instituție autonomă de stat
profesional organizare educaţională
Colegiul de Servicii și Turism
Curs de prelegeri cu exemple de sarcini practice
„Fundamentele mecanicii teoretice”
prin disciplinaMecanica tehnica
pentru studenti3 curs
specialități20.02.04 Securitate la incendiu
Kaliningrad
APROBA
Director adjunct SD GAU KO VEO KSTN.N. Miasnikov
APROBAT
Consiliul Metodologic al GAU KO VET KST
CONSIDERAT
La o ședință a PCC
Echipa editorială:
Kolganova A.A., metodolog
Falaleeva A.B., profesor de limba și literatura rusă
Tsvetaeva L.V., președintele PCCdiscipline generale de matematică și științe naturale
Compilat de:
Nezvanova I.V. Lector GAU KO VET KST
Conţinut
Informații teoretice
Informații teoretice
Exemple de rezolvare a problemelor practice
Dinamica: concepte de bază și axiome
Informații teoretice
Exemple de rezolvare a problemelor practice
Bibliografie
Informații teoretice
Statica: concepte de bază și axiome.
Statică - o secțiune de mecanică teoretică, care are în vedere proprietățile forțelor aplicate punctelor unui corp rigid și condițiile echilibrului acestora. Scopuri principale:
1. Transformarea sistemelor de forțe în sisteme echivalente de forțe.
2. Determinarea condiţiilor de echilibru pentru sistemele de forţe care acţionează asupra acestora solid.
punct material numit cel mai simplu model al unui corp material
orice formă, ale cărei dimensiuni sunt suficient de mici și care poate fi luată ca punct geometric având o anumită masă. Un sistem mecanic este orice set de puncte materiale. Un corp absolut rigid este un sistem mecanic, ale cărui distanțe între punctele nu se modifică sub nicio interacțiune.
Putere este o măsură a interacțiunii mecanice a corpurilor materiale între ele. Forța este o mărime vectorială, deoarece este determinată de trei elemente:
valoare numerică;
direcţie;
punctul de aplicare (A).
Unitatea de măsură a forței este Newton (N).

Figura 1.1
Un sistem de forțe este un set de forțe care acționează asupra unui corp.
Un sistem de forțe echilibrat (egal cu zero) este un sistem care, fiind aplicat unui corp, nu își schimbă starea.
Sistemul de forțe care acționează asupra corpului poate fi înlocuit cu o rezultantă care acționează ca un sistem de forțe.
Axiomele staticii.
Axioma 1: Dacă un sistem echilibrat de forțe este aplicat corpului, atunci acesta se mișcă uniform și rectiliniu sau este în repaus (legea inerției).
Axioma 2:
Un corp absolut rigid este în echilibru sub acțiunea a două forțe dacă și numai dacă aceste forțe sunt egale în valoare absolută, acționează într-o linie dreaptă și sunt direcționate în direcții opuse. Figura 1.2
Axioma 3:
Starea mecanică a corpului nu va fi perturbată dacă la sistemul de forțe care acționează asupra acestuia se adaugă sau se scade un sistem echilibrat de forțe.
Axioma 4: Rezultanta celor două forțe aplicate corpului este egală cu suma lor geometrică, adică este exprimată în valoare absolută și direcție prin diagonala paralelogramului construit pe aceste forțe ca pe laturi.
Figura 1.3.
Axioma 5:
Forțele cu care două corpuri acționează unul asupra celuilalt sunt întotdeauna egale în valoare absolută și direcționate de-a lungul unei linii drepte în direcții opuse.
Figura 1.4.
Tipuri de legături și reacțiile lor
conexiuni
se numesc orice restrictii care impiedica miscarea corpului in spatiu. Corpul, căutând sub acțiunea forțelor aplicate să se miște, care este împiedicat de legătură, va acționa asupra lui cu o anumită forță numită forța de presiune asupra conexiunii
. Conform legii egalității de acțiune și reacție, legătura va acționa asupra corpului cu același modul, dar forță direcționată opus.
Se numește forța cu care această legătură acționează asupra corpului, împiedicând una sau alta mișcare forța de reacție (reacția) legăturii
.
Unul dintre principiile fundamentale ale mecanicii este principiul eliberării
:
orice corp neliber poate fi considerat ca fiind liber, dacă aruncăm legăturile și înlocuim acțiunea lor cu reacțiile legăturilor.
Reacția de legătură este îndreptată în direcția opusă în cazul în care legătura nu permite corpului să se miște. Principalele tipuri de legături și reacțiile lor sunt prezentate în Tabelul 1.1.
Tabelul 1.1
Tipuri de legături și reacțiile lor
Nume comunicare
Simbol
1
Suprafață netedă (suport)
- suprafata (suportul), frecarea pe care corpul dat poate fi neglijat.
Cu sprijin gratuit, reacțiaeste îndreptată perpendicular pe tangenta prin punctDAR
contactul corpului1
cu suprafata de sprijin2
.

2
Fir (flexibil, inextensibil). Legătura, realizată sub formă de fir inextensibil, nu permite corpului să se îndepărteze de punctul de suspensie. Prin urmare, reacția firului este direcționată de-a lungul firului până la punctul de suspensie a acestuia.

3
lansetă fără greutate
– o tijă a cărei greutate poate fi neglijată în comparație cu sarcina percepută.
Reacția unei tije rectilinie cu balamale fără greutate este direcționată de-a lungul axei tijei.

4
Balamală mobilă, suport mobil articulat. Reacția este direcționată de-a lungul normalului la suprafața de susținere.

7
Închidere rigidă.
În planul înglobării rigide vor exista două componente ale reacției,
și momentul unei perechi de forțe, care împiedică rotirea fasciculului1
relativ la punctDAR
.
O atașare rigidă în spațiu ia toate cele șase grade de libertate de la corpul 1 - trei deplasări de-a lungul axelor de coordonate și trei rotații în jurul acestor axe.
Vor fi trei componente în înglobarea rigidă spațială,
,
și trei momente de perechi de forțe![]() .
.

Sistemul de forțe convergente
Un sistem de forțe convergente
numit sistem de forţe ale căror linii de acţiune se intersectează într-un punct. Două forțe care converg într-un punct, conform celei de-a treia axiome a staticii, pot fi înlocuite cu o singură forță -rezultanta
.
Vectorul principal al sistemului de forțe
- o valoare egală cu suma geometrică a forțelor sistemului.
Rezultanta unui sistem plan de forțe convergente poate fi definitgrafic și analitic.
Adăugarea unui sistem de forțe . Adunarea unui sistem plat de forțe convergente se realizează fie prin adăugarea succesivă de forțe cu construcția unei rezultante intermediare (Fig. 1.5), fie prin construirea unui poligon de forțe (Fig. 1.6).


Figura 1.5Figura 1.6
Proiecția forței pe axă
- o mărime algebrică egală cu produsul dintre modulul de forță și cosinusul unghiului dintre forță și direcția pozitivă a axei.
ProiecțieFX(fig.1.7) forţe pe osie Xpozitiv dacă α este acut, negativ dacă α este obtuz. Dacă putereaeste perpendiculară pe axă, atunci proiecția sa pe axă este zero.

Figura 1.7
Proiecția forței pe un plan Ohu– vector , încheiat între proiecțiile începutului și sfârșitului forțeila acest avion. Acestea. proiecția forței pe plan este o mărime vectorială, caracterizată nu numai printr-o valoare numerică, ci și prin direcția în planOhu (Fig. 1.8).

Figura 1.8
Apoi modulul de proiecție la avion Ohu va fi egal cu:
FX y = F cosα,
unde α este unghiul dintre direcția forțeiși proiecția acesteia.
Metoda analitica atribuiri de forță
.
Pentru metoda analitică de stabilire a forţeieste necesar să se aleagă un sistem de axe de coordonateOhz, în raport cu care se va determina direcția forței în spațiu.
Un vector care înfățișează puterea, se poate construi dacă se cunosc modulul acestei forțe și unghiurile α, β, γ pe care le formează forța cu axele de coordonate. PunctDAR aplicarea forței stabilite separat de coordonatele saleX,
la,
z. Puteți seta forța prin proiecțiile salefx,
fy,
fzpe axele de coordonate. Modulul de forță în acest caz este determinat de formula:
![]()
și cosinus de direcție:
,
.
Metoda analitică de adunare a forțelor : proiecția vectorului sumă pe o anumită axă este egală cu suma algebrică a proiecțiilor termenilor vectorilor pe aceeași axă, adică dacă:
apoi , , .
știind Rx, Ry, Rz, putem defini modulul
![]()
și cosinus de direcție:
, , .
Figura 1.9
Pentru echilibrul unui sistem de forțe convergente, este necesar și suficient ca rezultanta acestor forțe să fie egală cu zero.1) Condiție de echilibru geometric pentru un sistem de forțe convergent : pentru echilibrul unui sistem de forțe convergente, este necesar și suficient ca poligonul de forțe construit din aceste forțe
a fost închis (sfârșitul vectorului ultimului termen
forţa trebuie să coincidă cu începutul vectorului primului termen al forţei). Atunci vectorul principal al sistemului de forțe va fi zero ()
2)
Condiții analitice echilibru
.
Modulul vectorului principal al sistemului de forțe este determinat de formula.
![]() =0. Pentru că , atunci expresia rădăcină poate fi egală cu zero numai dacă fiecare termen dispare simultan, i.e.
=0. Pentru că , atunci expresia rădăcină poate fi egală cu zero numai dacă fiecare termen dispare simultan, i.e.
Rx= 0, Ry= 0, R z = 0.
Prin urmare, pentru echilibrul sistemului spațial al forțelor convergente, este necesar și suficient ca sumele proiecțiilor acestor forțe pe fiecare dintre cele trei coordonate ale axelor să fie egale cu zero:
Pentru echilibrul unui sistem plat de forțe convergente, este necesar și suficient ca suma proiecțiilor forțelor pe fiecare dintre cele două axe de coordonate să fie egală cu zero:
Adunarea a două forțe paralele în aceeași direcție.

Figura 1.9
Două forțe paralele în aceeași direcție sunt reduse la aceeași forța de acționare, paralele cu acestea și îndreptate în aceeași direcție. Mărimea rezultantei este egală cu suma mărimilor acestor forțe, iar punctul de aplicare a acesteia C împarte distanța dintre liniile de acțiune ale forțelor interne în părți invers proporționale cu mărimile acestor forțe, adicăB A C
R=F 1 +F 2
Adunarea a două forțe paralele inegale îndreptate în direcții opuse.
Două forțe antiparalele inegale sunt reduse la o forță rezultantă paralelă cu ele și îndreptate către forța mai mare. Mărimea rezultantei este egală cu diferența dintre mărimile acestor forțe, iar punctul de aplicare a acesteia, C, împarte distanța dintre liniile de acțiune ale forțelor din exterior în părți invers proporționale cu mărimile acestor forțe, că este
Pereche de forțe și moment de forță aproximativ un punct.
Moment de forță
relativ la punctul O se numește, luat cu semnul corespunzător, produsul mărimii forței cu distanța h de la punctul O la linia de acțiune a forței . Acest produs este luat cu un semn plus dacă forța tinde să rotească corpul în sens invers acelor de ceasornic, iar cu semnul -, dacă forța tinde să rotească corpul în sensul acelor de ceasornic, adică . Lungimea perpendicularei h se numeșteumărul puterii
punctul O. Efectul acțiunii forței i.e. accelerația unghiulară a corpului este mai mare, cu atât amploarea momentului de forță este mai mare.
Figura 1.11
Câteva forțe Un sistem se numește sistem format din două forțe paralele de mărime egală, direcționate în direcții opuse. Se numește distanța h dintre liniile de acțiune ale forțelorcupluri de umăr . Momentul unei perechi de forțe m(F,F") este produsul valorii uneia dintre forțele care alcătuiesc perechea și brațul perechii, luate cu semnul corespunzător.Se scrie astfel: m(F, F")= ± F × h, unde produsul se ia cu semnul plus dacă perechea de forțe tinde să rotească corpul în sens invers acelor de ceasornic și cu semnul minus dacă perechea de forțe tinde. pentru a roti corpul în sensul acelor de ceasornic.
Teorema privind suma momentelor de forță ale unei perechi.
Suma momentelor de forță ale perechii (F,F") față de orice punct 0 luat în planul de acțiune al perechii nu depinde de alegerea acestui punct și este egală cu momentul perechii.
Teorema perechilor echivalente. Consecințe.
Teorema. Două perechi ale căror momente sunt egale între ele sunt echivalente, adică. (F, F") ~ (P, P")
Corolarul 1 . O pereche de forțe poate fi transferată în orice loc din planul acțiunii sale, precum și rotită în orice unghi și poate schimba brațul și magnitudinea forțelor perechii, menținând în același timp momentul perechii.
Consecința 2. O pereche de forțe nu are o rezultantă și nu poate fi echilibrată de o forță situată în planul perechii.

Figura 1.12
Condiție de adunare și echilibru pentru un sistem de perechi pe un plan.
1. Teorema adunării perechilor aflate în același plan. Un sistem de perechi, situat arbitrar în același plan, poate fi înlocuit cu o pereche, al cărei moment este egală cu suma momentele acestor perechi.
2. Teorema asupra echilibrului unui sistem de perechi pe un plan.
Pentru ca un corp absolut rigid să fie în repaus sub acțiunea unui sistem de perechi, situat arbitrar în același plan, este necesar și suficient ca suma momentelor tuturor perechilor să fie egală cu zero, adică
Centrul de greutate
Gravitatie - rezultanta forţelor de atracţie către Pământ, distribuite pe întregul volum al corpului.
Centrul de greutate al corpului - acesta este un astfel de punct, asociat invariabil cu acest corp, prin care trece linia de acțiune a forței de gravitație a unui corp dat în orice poziție a corpului în spațiu.
Metode de găsire a centrului de greutate
1. Metoda simetriei:
1.1. Dacă un corp omogen are un plan de simetrie, atunci centrul de greutate se află în acest plan
1.2. Dacă un corp omogen are o axă de simetrie, atunci centrul de greutate se află pe această axă. Centrul de greutate al unui corp omogen de revoluție se află pe axa revoluției.
1.3 Dacă un corp omogen are două axe de simetrie, atunci centrul de greutate se află în punctul de intersecție a acestora.
2. Metoda împărțirii: Corpul este împărțit în cel mai mic număr piese a căror greutate şi poziţia centrelor de greutate sunt cunoscute.
3. Metoda maselor negative: La determinarea centrului de greutate al unui corp cu cavități libere, trebuie utilizată metoda de compartimentare, dar masa cavităților libere trebuie considerată negativă.
Coordonatele centrului de greutate figură plată:

Pozițiile centrelor de greutate ale simple forme geometrice poate fi calculată în funcţie de formule cunoscute. (Figura 1.13)

Notă: Centrul de greutate al simetriei figurii este pe axa de simetrie.
Centrul de greutate al tijei este la mijlocul înălțimii.
1.2. Exemple de rezolvare a problemelor practice
Exemplul 1:
O greutate este suspendată pe o tijă și este în echilibru. Determinați forțele din bară. (Figura 1.2.1)
Soluţie:
Forțele care apar în tijele de fixare sunt egale ca mărime cu forțele cu care tijele susțin sarcina. (a 5-a axiomă)
Determinăm direcțiile posibile ale reacțiilor legăturilor „tije rigide”.
Eforturile sunt direcționate de-a lungul tijelor.
Figura 1.2.1.
Să eliberăm punctul A de legături, înlocuind acțiunea legăturilor cu reacțiile lor. (Figura 1.2.2)
Să începem construcția cu o forță cunoscută desenând un vectorFla o oarecare scară.
De la sfârșitul vectoruluiFtrageți linii paralele cu reacțiileR 1 șiR 2 .
Figura 1.2.2
Intersectându-se, liniile creează un triunghi. (Figura 1.2.3.). Cunoscând scara construcțiilor și măsurând lungimea laturilor triunghiului, se poate determina magnitudinea reacțiilor din tije.
Pentru calcule mai precise, puteți utiliza relații geometrice, în special, teorema sinusului: raportul dintre latura triunghiului și sinusul unghiului opus este o valoare constantă
![]()
Pentru acest caz:
Figura 1.2.3
![]()
Cometariu: Dacă direcția vectorului (reacția de cuplare) pe o schemă dată și în triunghiul de forțe nu a coincis, atunci reacția pe schemă ar trebui direcționată în direcția opusă.
Exemplul 2:
Determinați mărimea și direcția sistemului plat rezultat de forțe convergente într-un mod analitic.
Soluţie:
Figura 1.2.4
1. Determinăm proiecțiile tuturor forțelor sistemului pe Ox (Figura 1.2.4)Adunând algebric proiecțiile, obținem proiecția rezultantei pe axa Ox.

Semnul indică faptul că rezultatul este îndreptat spre stânga.
2. Determinăm proiecțiile tuturor forțelor pe axa Oy:
Adunând algebric proiecțiile, obținem proiecția rezultantei pe axa Oy.
Semnul indică faptul că rezultanta este îndreptată în jos.
3. Determinați modulul rezultantei după mărimile proiecțiilor:
4. Determinați valoarea unghiului rezultantei cu axa Ox:

și valoarea unghiului cu axa y:
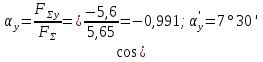
Exemplul 3:
Calculați suma momentelor forțelor raportate la punctul O (Figura 1.2.6).
OA= AB= LAD=DE=CB=2m
Figura 1.2.6
Soluţie:
1. Momentul forței relativ la un punct este numeric egal cu produsul modulului și brațul forței.
2. Momentul forței este egal cu zero dacă linia de acțiune a forței trece printr-un punct.
Exemplul 4:
Determinați poziția centrului de greutate al figurii prezentate în figura 1.2.7
Soluţie:
Împărțim cifra în trei:
1-dreptunghi
DAR 1 =10*20=200cm 2
2-triunghi
DAR 2 =1/2*10*15=75cm 2
3-tururi
DAR 3 =3,14*3 2 = 28,3 cm 2
Figura 1 CG: x 1 = 10 cm, y 1 = 5 cm
Figura 2 CG: x 2 =20+1/3*15=25cm, u 2 =1/3*10=3,3cm
Figura 3 CG: x 3 = 10 cm, y 3 = 5 cm
Este definit în mod similar pentru Cu = 4,5 cm
Cinematica: concepte de bază.
Parametri cinematici de bază
Traiectorie - linia pe care un punct material o conturează atunci când se deplasează în spațiu. Traiectoria poate fi o linie dreaptă și o curbă, o linie plată și o linie spațială.
Ecuația traiectoriei pentru mișcarea plană: y =f ( X)
Distanta parcursa. Calea este măsurată de-a lungul căii în direcția de mers. Denumire -S, unități de măsură - metri.
Ecuația mișcării punctuale este o ecuație care determină poziția unui punct în mișcare în funcție de timp.
Figura 2.1
Poziția unui punct în fiecare moment de timp poate fi determinată de distanța parcursă de-a lungul traiectoriei de la un punct fix, considerat ca origine (Figura 2.1). Acest tip de mișcare se numeștenatural . Astfel, ecuația mișcării poate fi reprezentată ca S = f (t).

Figura 2.2
Poziția unui punct poate fi determinată și dacă coordonatele sale sunt cunoscute ca o funcție a timpului (Figura 2.2). Apoi, în cazul mișcării pe un plan, trebuie date două ecuații:În cazul mișcării spațiale, se adaugă și o a treia coordonatăz= f 3 ( t)
Acest tip de mișcare se numeștecoordona .
Viteza de calatorie este o mărime vectorială care caracterizează în momentul de față viteza și direcția deplasării de-a lungul traiectoriei.
Viteza este un vector direcționat în orice moment tangențial la traiectoria către direcția de mișcare (Figura 2.3).
Figura 2.3
Dacă un punct acoperă distanțe egale în intervale egale de timp, atunci se numește mișcareauniformă .Viteza medie pe drum ΔSdefinit:
Unde∆S- distanta parcursa in timp Δt; Δ t- interval de timp.
Dacă un punct parcurge trasee inegale în intervale egale de timp, atunci se numește mișcareaneuniformă . În acest caz, viteza este variabilă și depinde de timpv= f( t)
Viteza curentă este definită ca
accelerație punctuală - o mărime vectorială care caracterizează rata de schimbare a vitezei în mărime și direcție.
Viteza unui punct atunci când se deplasează de la punctul M1 la punctul Mg se modifică în mărime și direcție. Valoarea medie a accelerației pentru această perioadă de timp
Accelerația curentă:
De obicei, pentru comoditate, sunt luate în considerare două componente de accelerație reciproc perpendiculare: normală și tangențială (Figura 2.4)
Accelerație normală a n , caracterizează schimbarea vitezei prin
direcție și este definită ca
Accelerația normală este întotdeauna direcționată perpendicular pe viteza spre centrul arcului.
Figura 2.4
Accelerația tangențială a t , caracterizează schimbarea vitezei în mărime și este întotdeauna direcționată tangențial la traiectorie; în timpul accelerației, direcția acesteia coincide cu direcția vitezei, iar în timpul decelerației, este îndreptată opus direcției vectorului viteză.![]()
Valoarea completă a accelerației este definită ca:
Analiza tipurilor și parametrilor cinematici ai mișcărilor
Mișcare uniformă - Aceasta este o mișcare cu o viteză constantă:
Pentru rectilinie mișcare uniformă:
Pentru mișcarea uniformă curbilinie:
![]()
Legea mișcării uniforme :
Mișcare egal-variabilă – este o mișcare cu o accelerație tangențială constantă:
Pentru mișcare uniformă rectilinie
Pentru mișcarea uniformă curbilinie:
![]()
Legea mișcării uniforme:
![]()
Grafice cinematice
Grafice cinematice - Acestea sunt grafice ale schimbărilor de cale, viteză și accelerație în funcție de timp.
Mișcare uniformă (Figura 2.5)

Figura 2.5
Mișcare egal-variabilă (figura 2.6)

Figura 2.6
Cele mai simple mișcări ale unui corp rigid
Mișcare înainte numită mișcarea unui corp rigid, în care orice linie dreaptă de pe corp în timpul mișcării rămâne paralelă cu poziția sa inițială (Figura 2.7)

Figura 2.7
În mișcarea de translație, toate punctele corpului se mișcă în același mod: vitezele și accelerațiile sunt aceleași în fiecare moment.
Lamișcare de rotație
toate punctele corpului descriu cercuri în jurul unei axe fixe comune.
Se numește axa fixă în jurul căreia se rotesc toate punctele corpuluiaxa de rotatie.
Pentru a descrie numai mișcarea de rotație a unui corp în jurul unei axe fixeopțiuni de colț. (Figura 2.8)
φ este unghiul de rotație al corpului;
ω – viteza unghiulară, determină modificarea unghiului de rotație pe unitatea de timp;
Modificarea vitezei unghiulare cu timpul este determinată de accelerația unghiulară:
2.2. Exemple de rezolvare a problemelor practice
Exemplul 1: Este dată ecuația de mișcare a unui punct. Determinați viteza punctului la sfârșitul celei de-a treia secunde de mișcare și viteza medie pentru primele trei secunde.
![]()
Soluţie:
1. Ecuația vitezei
2. Viteza la sfârșitul celei de-a treia secunde (t=3 c)
3. Viteza medie
Exemplul 2: Conform legii date a mișcării, determinați tipul de mișcare, viteza inițială și accelerația tangențială a punctului, timpul de oprire.
![]()
Soluţie:
1. Tipul de mișcare: la fel de variabil (![]() )
)
2. La compararea ecuaţiilor, este evident că
- traseul inițial parcurs înainte de începerea numărătorii inverse 10m;
- viteza initiala 20m/s
- accelerație tangențială constantă ![]()
- accelerația este negativă, prin urmare, mișcarea este lentă, accelerația este îndreptată în direcția opusă vitezei de mișcare.
3. Puteți determina momentul în care viteza punctului va fi egală cu zero.
3. Dinamica: concepte de bază și axiome
Dinamica - o sectiune de mecanica teoretica in care se stabileste o legatura intre miscarea corpurilor si fortele care actioneaza asupra lor.
În dinamică se rezolvă două tipuri de probleme:
determinați parametrii de mișcare în funcție de forțele date;
determinați forțele care acționează asupra corpului, în funcție de parametrii cinematici de mișcare dați.
Subpunct material
implică un anumit corp care are o anumită masă (adică conține o anumită cantitate de materie), dar nu are dimensiuni liniare (un volum infinitezimal de spațiu).
izolat
se ia în considerare un punct material, care nu este afectat de alte puncte materiale. În lumea reală, punctele materiale izolate, precum și corpurile izolate, nu există, acest concept este condiționat.
Cu mișcarea de translație, toate punctele corpului se mișcă în același mod, astfel încât corpul poate fi luat ca punct material.
Dacă dimensiunile corpului sunt mici în comparație cu traiectoria, acesta poate fi considerat și ca punct material, în timp ce punctul coincide cu centrul de greutate al corpului.
În timpul mișcării de rotație a corpului, punctele pot să nu se miște în același mod, în acest caz, unele prevederi ale dinamicii pot fi aplicate numai punctelor individuale, iar obiectul material poate fi considerat ca un set de puncte materiale.
Prin urmare, dinamica este împărțită în dinamica unui punct și dinamica unui sistem material.
Axiomele dinamicii
Prima axiomă ( principiul inerției): în fiecare punct material izolat este în repaus sau uniform şi mișcare rectilinie până când forţele aplicate îl scot din această stare.
Această stare se numește statinerţie. Îndepărtați punctul din această stare, adică. dă-i o accelerație, poate o forță externă.
Fiecare corp (punct) areinerţie. Măsura inerției este masa corpului.
Masa numitcantitatea de materie dintr-un corp în mecanica clasică, este considerată o valoare constantă. Unitatea de masă este kilogramul (kg).
A doua axiomă (A doua lege a lui Newton este legea de bază a dinamicii)
F=ma
Undet - masa punctuală, kg;A - accelerația punctuală, m/s 2 .
Accelerația dată unui punct material de o forță este proporțională cu mărimea forței și coincide cu direcția forței.
Gravitația acționează asupra tuturor corpurilor de pe Pământ, ea conferă corpului accelerația căderii libere, îndreptată spre centrul Pământului:
G=mg
Undeg- 9,81 m/s², accelerație în cădere liberă.
A treia axiomă (a treia lege a lui Newton): cuForțele de interacțiune a două corpuri sunt egale ca mărime și sunt direcționate de-a lungul aceleiași linii drepte în direcții diferite.
La interacțiune, accelerațiile sunt invers proporționale cu masele.
A patra axiomă (legea independenței acțiunii forțelor): toFiecare forță a sistemului de forțe acționează așa cum ar acționa singură.
Accelerația dată punctului de sistemul de forțe este egală cu suma geometrică a accelerațiilor transmise punctului de fiecare forță separat (Figura 3.1):

Figura 3.1
Conceptul de frecare. Tipuri de frecare.
Frecare-
rezistența care decurge din mișcarea unui corp aspru pe suprafața altuia. Frecarea de alunecare are ca rezultat frecare de alunecare, iar frecarea de rulare are ca rezultat frecare de balansare.
Frecare de alunecare
Figura 3.2.
Motivul este angajarea mecanică a proeminențelor. Forța de rezistență la mișcare în timpul alunecării se numește forța de frecare de alunecare (Figura 3.2)Legile frecării de alunecare:
1. Forța de frecare de alunecare este direct proporțională cu forța presiunii normale: 
UndeR- forta de presiune normala, indreptata perpendicular pe suprafata de sustinere;f- coeficient de frecare de alunecare.
Figura 3.3.
În cazul unui corp care se deplasează de-a lungul unui plan înclinat (Figura 3.3)frecare de rulare
Rezistența la rulare este legată de deformarea reciprocă a solului și a roții și este mult mai mică decât frecarea de alunecare.
Pentru rularea uniformă a roții, este necesar să aplicați forțăF dv (Figura 3.4)
Condiția de rulare a roții este ca momentul de mișcare să nu fie mai mic decât momentul de rezistență:
Figura 3.4.
Exemplul 1: Exemplul 2: La două puncte materiale de masăm 1 =2kg șim 2 = 5 kg se aplică forțe egale. Comparați mai repede valorile.Soluţie:
Conform celei de-a treia axiome, dinamica accelerației este invers proporțională cu masele: ![]()
Exemplul 3:
Determinați lucrul gravitației atunci când deplasați o sarcină din punctul A în punctul C de-a lungul unui plan înclinat (Figura 3. 7). Forța de gravitație a corpului este de 1500 N. AB=6m, BC=4m. Exemplul 3:
Determinați lucrul forței de tăiere în 3 minute. Viteza de rotație a piesei de prelucrat este de 120 rpm, diametrul piesei de prelucrat este de 40 mm, forța de tăiere este de 1 kN. (Figura 3.8)
Soluţie:
1. Lucrul cu mișcare rotativă:
2. Viteza unghiulara 120 rpm
Figura 3.8.
3. Numărul de rotații pentru un timp dat estez\u003d 120 * 3 \u003d 360 rev.Unghiul de rotație în acest timp φ=2πz\u003d 2 * 3,14 * 360 \u003d 2261 rad
4. Lucrați 3 ture:W\u003d 1 * 0,02 * 2261 \u003d 45,2 kJ
Bibliografie
Olofinskaya, V.P. „Mecanica tehnică”, „Forum” din Moscova 2011
Erdedi A.A. Erdedi N.A. Mecanica teoretică. Rezistența materialelor.- R-n-D; Phoenix, 2010
Mecanica teoretică este o ramură a mecanicii care stabilește legile de bază mișcare mecanicăși interacțiunea mecanică a corpurilor materiale.
Mecanica teoretică este o știință în care se studiază mișcările corpurilor în timp (mișcări mecanice). Acesta servește drept bază pentru alte secțiuni ale mecanicii (teoria elasticității, rezistența materialelor, teoria plasticității, teoria mecanismelor și mașinilor, hidroaerodinamică) și a multor discipline tehnice.
mișcare mecanică- aceasta este o schimbare în timp a poziţiei relative în spaţiu a corpurilor materiale.
Interacțiune mecanică- aceasta este o astfel de interacțiune, în urma căreia se schimbă mișcarea mecanică sau se schimbă poziția relativă a părților corpului.
Statica corpului rigid
Statică- Aceasta este o ramură a mecanicii teoretice, care se ocupă de problemele echilibrului corpurilor solide și de transformarea unui sistem de forțe în altul, echivalent cu acesta.
- Concepte de bază și legi ale staticii
- Corp absolut rigid(corp solid, corp) este corp material, distanța dintre orice puncte în care nu se modifică.
- Punct material este un corp ale cărui dimensiuni, în funcție de condițiile problemei, pot fi neglijate.
- corp liber este un corp, asupra căruia nu se impun restricții.
- Corp neliber (legat). este un corp a cărui mișcare este restricționată.
- Conexiuni- acestea sunt corpuri care impiedica miscarea obiectului luat in considerare (un corp sau un sistem de corpuri).
- Reacția de comunicare este o forță care caracterizează acțiunea unei legături asupra unui corp rigid. Dacă considerăm ca o acțiune forța cu care un corp rigid acționează asupra unei legături, atunci reacția legăturii este o contraacțiune. În acest caz, forța - acțiune se aplică conexiunii, iar reacția conexiunii este aplicată corpului solid.
- sistem mecanic este un set de corpuri sau puncte materiale interconectate.
- Solid poate fi considerat ca un sistem mecanic, ale cărui poziții și distanța dintre punctele nu se modifică.
- Putere este o mărime vectorială care caracterizează acțiunea mecanică a unui corp material asupra altuia.
Forța ca vector este caracterizată de punctul de aplicare, direcția de acțiune și valoarea absolută. Unitatea de măsură pentru modulul de forță este Newton. - linie de forţă este linia dreaptă de-a lungul căreia este îndreptat vectorul forță.
- Putere concentrată este forța aplicată într-un punct.
- Forțe distribuite (sarcină distribuită)- acestea sunt forte care actioneaza in toate punctele volumului, suprafetei sau lungimii corpului.
Sarcina distribuită este dată de forța care acționează pe unitatea de volum (suprafață, lungime).
Dimensiunea sarcinii distribuite este N / m 3 (N / m 2, N / m). - Forta externa este o forță care acționează dintr-un corp care nu aparține sistemului mecanic considerat.
- Forta interioara este forța care acționează asupra unui punct material al unui sistem mecanic din celălalt punct material aparţinând sistemului considerat.
- Sistemul de forță este totalitatea forțelor care acționează asupra unui sistem mecanic.
- Sistem plat de forțe este un sistem de forțe ale căror linii de acțiune se află în același plan.
- Sistemul spațial de forțe este un sistem de forțe ale căror linii de acțiune nu se află în același plan.
- Sistemul de forțe convergente este un sistem de forțe ale căror linii de acțiune se intersectează într-un punct.
- Sistem arbitrar de forțe este un sistem de forțe ale căror linii de acțiune nu se intersectează într-un punct.
- Sisteme de forțe echivalente- acestea sunt sisteme de forțe, a căror înlocuire una cu alta nu schimbă starea mecanică a corpului.
Denumirea acceptată: . - Echilibru O stare în care un corp rămâne staționar sau se mișcă uniform în linie dreaptă sub acțiunea forțelor.
- Sistem echilibrat de forțe- acesta este un sistem de forțe care, atunci când este aplicat unui corp solid liber, nu își schimbă starea mecanică (nu îl dezechilibrează).
 .
. - forță rezultantă este o forță a cărei acțiune asupra unui corp este echivalentă cu acțiunea unui sistem de forțe.
 .
. - Moment de putere este o valoare care caracterizează capacitatea de rotație a forței.
- Cuplu de putere este un sistem de două forțe paralele egale în valoare absolută direcționate opus.
Denumirea acceptată: .
Sub acțiunea câtorva forțe, corpul va efectua o mișcare de rotație. - Proiecția forței pe axă- acesta este un segment închis între perpendiculare desenate de la începutul și sfârșitul vectorului forță către această axă.
Proiecția este pozitivă dacă direcția segmentului coincide cu direcția pozitivă a axei. - Proiecția forței pe un plan este un vector pe un plan cuprins între perpendicularele trasate de la începutul și sfârșitul vectorului forță către acest plan.
- Legea 1 (legea inerției). Un punct material izolat este în repaus sau se mișcă uniform și rectiliniu.
Mișcarea uniformă și rectilinie a unui punct material este o mișcare prin inerție. Starea de echilibru a unui punct material și a unui corp rigid este înțeleasă nu numai ca stare de repaus, ci și ca o mișcare prin inerție. Pentru un corp rigid, există diferite tipuri de mișcare de inerție, de exemplu, rotația uniformă a unui corp rigid în jurul unei axe fixe. - Legea 2. Un corp rigid este în echilibru sub acțiunea a două forțe numai dacă aceste forțe sunt egale ca mărime și direcționate în direcții opuse de-a lungul linie comună actiuni.
Aceste două forțe se numesc echilibrate.
În general, se spune că forțele sunt echilibrate dacă corpul rigid căruia i se aplică aceste forțe este în repaus. - Legea 3. Fără a încălca starea (cuvântul „stare” aici înseamnă starea de mișcare sau de repaus) a unui corp rigid, se pot adăuga și elimina forțele de echilibrare.
Consecinţă. Fără a perturba starea unui corp rigid, forța poate fi transferată de-a lungul liniei sale de acțiune în orice punct al corpului.
Două sisteme de forțe sunt numite echivalente dacă unul dintre ele poate fi înlocuit cu altul fără a perturba starea corpului rigid. - Legea 4. Rezultanta a două forțe aplicate într-un punct este aplicată în același punct, este egală în valoare absolută cu diagonala paralelogramului construit pe aceste forțe și este îndreptată de-a lungul acestui
diagonalele.
Modulul rezultantei este: - Legea 5 (legea egalității de acțiune și reacție). Forțele cu care două corpuri acționează unul asupra celuilalt sunt egale ca mărime și sunt direcționate în direcții opuse de-a lungul unei linii drepte.
Trebuie avut în vedere faptul că acțiune- forta aplicata corpului B, și opoziţie- forta aplicata corpului DAR, nu sunt echilibrate, deoarece sunt atașate de corpuri diferite. - Legea 6 (legea întăririi). Echilibrul unui corp nesolid nu este perturbat atunci când acesta se solidifică.
Nu trebuie uitat că condițiile de echilibru, care sunt necesare și suficiente pentru un corp rigid, sunt necesare, dar insuficiente pentru corpul nerigid corespunzător. - Legea 7 (legea eliberării de obligațiuni). Un corp solid neliber poate fi considerat liber dacă este eliberat mental de legături, înlocuind acțiunea legăturilor cu reacțiile corespunzătoare ale legăturilor.
- Conexiunile și reacțiile lor
- Suprafață netedă restricționează mișcarea de-a lungul normalului la suprafața de sprijin. Reacția este direcționată perpendicular pe suprafață.
- Suport mobil articulat limitează mișcarea corpului de-a lungul normalului la planul de referință. Reacția este direcționată de-a lungul normalei la suprafața suport.
- Suport fix articulat contracarează orice mișcare într-un plan perpendicular pe axa de rotație.
- Lansetă articulată fără greutate contracarează mișcarea corpului de-a lungul liniei tijei. Reacția va fi direcționată de-a lungul liniei tijei.
- Terminare oarbă contracarează orice mișcare și rotație în plan. Actiunea sa poate fi inlocuita cu o forta prezentata sub forma a doua componente si o pereche de forte cu un moment.




Cinematică
Cinematică- o secțiune de mecanică teoretică, care are în vedere proprietățile geometrice generale ale mișcării mecanice, ca proces care se desfășoară în spațiu și timp. Obiectele în mișcare sunt considerate puncte geometrice sau corpuri geometrice.
- Concepte de bază ale cinematicii
- Legea mișcării unui punct (corp) este dependența de timp a poziției unui punct (corp) în spațiu.
- Traiectoria punctului este locul pozițiilor unui punct din spațiu în timpul mișcării sale.
- Viteza punctului (corpului).- aceasta este o caracteristică a schimbării în timp a poziției unui punct (corp) în spațiu.
- Accelerație punct (corp).- aceasta este o caracteristică a schimbării în timp a vitezei unui punct (corp).
- Determinarea caracteristicilor cinematice ale unui punct
- Traiectoria punctului
În sistemul de referință vectorială, traiectoria este descrisă prin expresia: .
În sistemul de referință de coordonate, traiectoria este determinată conform legii mișcării punctului și este descrisă de expresiile z = f(x,y)în spațiu, sau y = f(x)- in avion.
Într-un sistem de referință natural, traiectoria este predeterminată. - Determinarea vitezei unui punct dintr-un sistem de coordonate vectoriale
Când se specifică mișcarea unui punct într-un sistem de coordonate vectoriale, raportul dintre mișcare și intervalul de timp se numește valoarea medie a vitezei în acest interval de timp: .
Luând intervalul de timp ca valoare infinitezimală, se obține valoarea vitezei la un moment dat de timp ( valoare instantanee viteză): .
.
Vector viteza medie este îndreptat de-a lungul vectorului în direcția mișcării punctului, vectorul viteză instantanee este direcționat tangențial la traiectoria în direcția mișcării punctului.
Concluzie: viteza unui punct este o mărime vectorială egală cu derivata legii mișcării în raport cu timpul.
Proprietate derivată: derivata în timp a oricărei valori determină rata de modificare a acestei valori. - Determinarea vitezei unui punct într-un sistem de referință de coordonate
Rata de modificare a coordonatelor punctului: .
.
Modulul total al vitezei punctului la sistem dreptunghiular coordonatele vor fi: .
.
Direcția vectorului viteză este determinată de cosinusurile unghiurilor de virare: ,
,
unde sunt unghiurile dintre vectorul viteză și axele de coordonate. - Determinarea vitezei unui punct dintr-un sistem de referință natural
Viteza unui punct dintr-un sistem de referință natural este definită ca o derivată a legii de mișcare a unui punct: .
Conform concluziilor anterioare, vectorul viteză este direcționat tangențial la traiectorie în direcția mișcării punctului și în axe este determinat de o singură proiecție.
- Cinematica corpului rigid
- În cinematica corpurilor rigide se rezolvă două probleme principale:
1) sarcina de mișcare și determinarea caracteristicilor cinematice ale corpului în ansamblu;
2) determinarea caracteristicilor cinematice ale punctelor corpului. - Mișcarea de translație a unui corp rigid
Mișcarea de translație este o mișcare în care o linie dreaptă trasată prin două puncte ale corpului rămâne paralelă cu poziția inițială.
Teorema: în mișcare de translație, toate punctele corpului se mișcă pe aceleași traiectorii și în fiecare moment de timp au aceeași viteză și accelerație în valoare și direcție absolută.
Concluzie: mișcarea de translație a unui corp rigid este determinată de mișcarea oricăruia dintre punctele sale și, prin urmare, sarcina și studiul mișcării sale sunt reduse la cinematica unui punct. - Mișcarea de rotație a unui corp rigid în jurul unei axe fixe
Mișcarea de rotație a unui corp rigid în jurul unei axe fixe este mișcarea unui corp rigid în care două puncte aparținând corpului rămân nemișcate pe toată durata mișcării.
Poziția corpului este determinată de unghiul de rotație. Unitatea de măsură pentru un unghi este radianii. (Un radian este unghiul central al unui cerc a cărui lungime a arcului este egală cu raza, unghiul complet al cercului conține 2π radian.)
Legea mișcării de rotație a unui corp în jurul unei axe fixe.
Viteza unghiulară și accelerația unghiulară a corpului vor fi determinate prin metoda de diferențiere:
— viteza unghiulară, rad/s;
— accelerație unghiulară, rad/s².
Dacă tăiem corpul cu un plan perpendicular pe axă, alegeți un punct pe axa de rotație DINși un punct arbitrar M, apoi punctul M va descrie în jurul punctului DIN cerc cu raza R. Pe parcursul dt există o rotație elementară prin unghiul , în timp ce punctul M se va deplasa de-a lungul traiectoriei pe o distanţă .
.
Modul de viteză liniară: .
.
accelerație punctuală M cu o traiectorie cunoscută este determinată de componentele sale: ,
,
Unde .
.
Ca rezultat, obținem formule
accelerație tangențială: ;
;
acceleratie normala: .
.

Dinamica
Dinamica- Aceasta este o ramură a mecanicii teoretice, care studiază mișcările mecanice ale corpurilor materiale, în funcție de cauzele care le provoacă.
- Concepte de bază ale dinamicii
- inerţie- aceasta este proprietatea corpurilor materiale de a menține o stare de repaus sau o mișcare rectilinie uniformă până când forțele externe schimbă această stare.
- Greutate este o măsură cantitativă a inerției unui corp. Unitatea de masă este kilogramul (kg).
- Punct material este un corp cu o masă ale cărui dimensiuni sunt neglijate în rezolvarea acestei probleme.
- Centrul de masă al unui sistem mecanic este un punct geometric ale cărui coordonate sunt determinate de formulele:
Unde m k , x k , y k , z k- masa si coordonatele k- acel punct al sistemului mecanic, m este masa sistemului.
Într-un câmp uniform de greutate, poziția centrului de masă coincide cu poziția centrului de greutate. - Momentul de inerție al unui corp material în jurul axei este o măsură cantitativă a inerției în timpul mișcării de rotație.
Momentul de inerție al unui punct material în jurul axei este egal cu produsul dintre masa punctului și pătratul distanței punctului față de axă: .
.
Momentul de inerție al sistemului (corpului) în jurul axei este egal cu suma aritmetică momentele de inerție ale tuturor punctelor:
- Forța de inerție a unui punct material este o mărime vectorială egală în valoare absolută cu produsul dintre masa unui punct și modulul de accelerație și direcționată opus vectorului accelerație:
- Forța de inerție a unui corp material este o mărime vectorială egală în valoare absolută cu produsul dintre masa corporală și modulul de accelerație al centrului de masă al corpului și îndreptată opus vectorului de accelerație al centrului de masă: ,
unde este accelerația centrului de masă al corpului. - Impulsul de forță elementară este o mărime vectorială egală cu produsul vectorului forță cu un interval de timp infinitezimal dt:
.
Forța totală de impuls pe Δt este egală cu integrala din impulsuri elementare: .
. - Munca elementară de forță- aceasta este scalar dA, egal cu scalarul
Vedere: acest articol a fost citit de 32852 ori
Pdf Selectează limba... Rusă Ucraineană Engleză
Materialul complet este descărcat mai sus, după selectarea limbii
- Statică
- Concepte de bază de statică
- Tipuri de forță
- Axiomele staticii
- Conexiunile și reacțiile lor
- Sistemul de forțe convergente
- Metode de determinare a sistemului rezultant de forţe convergente
- Condiții de echilibru pentru un sistem de forțe convergente
- Momentul de forță în jurul centrului ca vector
- Valoarea algebrică a momentului de forță
- Proprietățile momentului de forță despre centru (punct)
- Teoria perechilor de forțe
- Adunarea a două forțe paralele în aceeași direcție
- Adunarea a două forțe paralele direcționate în direcții opuse
- Perechi de putere
- Teoremele cuplului de forțe
- Condiții pentru echilibrul unui sistem de perechi de forțe
- Maneta
- Sistemul de forțe plan arbitrar
- Cazuri de reducere a unui sistem plat de forțe la o formă mai simplă
- Condiții de echilibru analitic
- Centrul Forțelor Paralele. Centrul de greutate
- Centrul Forțelor Paralele
- Centrul de greutate al unui corp rigid și coordonatele acestuia
- Centrul de greutate al volumului, planurilor și liniilor
- Metode de determinare a poziției centrului de greutate
- Bazele jocurilor de forță
- Probleme și metode de rezistență a materialelor
- Clasificarea sarcinii
- Clasificarea elementelor structurale
- Deformari ale tijei
- Principalele ipoteze și principii
- Forțele interne. Metoda secțiunii
- Voltaj
- Tensiune și compresie
- Caracteristicile mecanice ale materialului
- Tensiuni admisibile
- Duritatea materialului
- Grafice ale forțelor și tensiunilor longitudinale
- Schimb
- Caracteristicile geometrice ale secțiunilor
- Torsiune
- îndoi
- Dependențe diferențiale în îndoire
- Rezistență la încovoiere
- tensiuni normale. Calculul puterii
- Tensiuni de forfecare la încovoiere
- Îndoire rigidă
- Elemente teorie generală stare de stres
- Teorii de forță
- Îndoirea cu răsucire
- Cinematică
- Cinematica punctuală
- Traiectoria punctului
- Metode de precizare a mișcării unui punct
- Viteza punctului
- accelerație punctuală
- Cinematica corpului rigid
- Mișcarea de translație a unui corp rigid
- Mișcarea de rotație a unui corp rigid
- Cinematica mecanismelor de viteză
- Mișcarea plan-paralelă a unui corp rigid
- Mișcare complexă a punctului
- Cinematica punctuală
- Dinamica
- Legile de bază ale dinamicii
- Dinamica punctului
- Ecuații diferențiale ale unui punct material liber
- Două probleme de dinamică a punctelor
- Dinamica corpului rigid
- Clasificarea forțelor care acționează asupra unui sistem mecanic
- Ecuații diferențiale ale mișcării unui sistem mecanic
- Teoreme generale de dinamică
- Teorema privind mișcarea centrului de masă al unui sistem mecanic
- Teorema privind modificarea impulsului
- Teorema privind modificarea momentului unghiular
- Teorema schimbării energiei cinetice
- Forțe care acționează în mașini
- Forțe în cuplarea unui angrenaj drept
- Frecare în mecanisme și mașini
- Frecare de alunecare
- frecare de rulare
- Eficienţă
- Piese de mașină
- Transmisii mecanice
- Tipuri de angrenaje mecanice
- Parametrii de bază și derivați ai angrenajelor mecanice
- angrenaje
- Angrenaje cu legături flexibile
- Arborii
- Scop și clasificare
- Calcul de proiectare
- Verificați calculul arborilor
- Rulmenți
- Lagăre simple
- Rulmenți de rulare
- Conectarea pieselor mașinii
- Tipuri de conexiuni detașabile și permanente
- Conexiuni cu cheie
- Transmisii mecanice
- Standardizarea normelor, interschimbabilitatea
- Toleranțe și aterizări
- Sistemul unificat de toleranțe și aterizări (ESDP)
- Deviația de formă și poziție
Format: pdf
Dimensiune: 4MB
Limba rusă
Un exemplu de calcul al unui angrenaj drept
Un exemplu de calcul al unui angrenaj drept. S-au efectuat alegerea materialului, calculul tensiunilor admisibile, calculul rezistenței la contact și la încovoiere.
Un exemplu de rezolvare a problemei de îndoire a fasciculului
În exemplu, sunt reprezentate diagrame ale forțelor transversale și ale momentelor încovoietoare, se găsește o secțiune periculoasă și este selectată o grindă I. În problemă, se analizează construcția diagramelor folosind dependențe diferențiale, se efectuează o analiză comparativă a diferitelor secțiuni transversale ale fasciculului.
Un exemplu de rezolvare a problemei torsiunii arborelui
Sarcina este de a testa rezistența unui arbore de oțel pentru un diametru dat, material și solicitări admisibile. În timpul soluției, se construiesc diagrame ale cuplurilor, tensiunilor tăietoare și unghiurilor de răsucire. Greutatea proprie a arborelui nu este luată în considerare
Un exemplu de rezolvare a problemei de tensiune-comprimare a unei tije
Sarcina este de a testa rezistența unei tije de oțel la solicitări admisibile date. În timpul soluției, se construiesc diagrame ale forțelor longitudinale, solicitărilor normale și deplasărilor. Greutatea proprie a barei nu este luată în considerare
Aplicarea teoremei de conservare a energiei cinetice
Un exemplu de rezolvare a problemei de aplicare a teoremei privind conservarea energiei cinetice a unui sistem mecanic
Determinarea vitezei și accelerației unui punct conform ecuațiilor de mișcare date
Un exemplu de rezolvare a problemei determinării vitezei și accelerației unui punct prin ecuații date miscarile
Determinarea vitezelor și accelerațiilor punctelor unui corp rigid în timpul mișcării plan-paralel
Un exemplu de rezolvare a problemei determinării vitezelor și accelerațiilor punctelor unui corp rigid în timpul mișcării plan-paralel
Determinarea forțelor în barele planare
Un exemplu de rezolvare a problemei determinării forțelor în barele unei ferme plane prin metoda Ritter și metoda tăierii nodului
1 tobogan
Curs de prelegeri de mecanică teoretică Dinamica (partea I) Bondarenko A.N. Moscova - 2007 Electronic curs de pregatire scrisă pe baza prelegerilor susținute de autor pentru studenții care studiază în specialitățile SZhD, PGS și SDM la NIIZhT și MIIT (1974-2006). Material educativ corespunde planuri calendaristice peste trei semestre. Pentru a implementa complet efectele de animație în timpul unei prezentări, trebuie să utilizați un vizualizator Power Point nu mai mic decât cel încorporat în Microsoft Office al sistemului de operare Windows-XP Professional. Comentariile și sugestiile pot fi trimise prin e-mail: [email protected]. Moscova Universitate de stat Căi Ferate (MIIT) Departamentul de Mecanică Teoretică Centrul Științific și Tehnic de Tehnologii de Transport

2 tobogan
Cuprins Cursul 1. Introducere în dinamică. Legile și axiomele dinamicii punctelor materiale. Ecuația de bază a dinamicii. Ecuații diferențiale și naturale ale mișcării. Două sarcini principale ale dinamicii. Exemple de rezolvare a problemei directe de dinamică Cursul 2. Rezolvarea problemei inverse de dinamică. Instrucțiuni generale pentru rezolvarea problemei inverse de dinamică. Exemple de rezolvare a problemei inverse a dinamicii. Mișcarea unui corp aruncat în unghi față de orizont, fără a ține cont de rezistența aerului. Curs 3. Oscilatii rectilinie ale unui punct material. Condiția pentru apariția oscilațiilor. Clasificarea vibrațiilor. Vibrații libere fără a ține cont de forțele de rezistență. vibrații amortizate. Scăderea oscilației. Curs 4. Oscilații forțate ale unui punct material. Rezonanţă. Influența rezistenței la mișcare în timpul vibrațiilor forțate. Cursul 5. Mișcarea relativă a unui punct material. Forțele de inerție. Cazuri speciale de mișcare pentru diferite tipuri de mișcare portabilă. Influența rotației Pământului asupra echilibrului și mișcării corpurilor. Curs 6. Dinamica unui sistem mecanic. sistem mecanic. Forțe externe și interne. Centrul de masă al sistemului. Teorema asupra mișcării centrului de masă. Legile de conservare. Un exemplu de rezolvare a problemei utilizării teoremei privind mișcarea centrului de masă. Curs 7. Impulsul de forta. Cantitatea de mișcare. Teorema privind modificarea impulsului. Legile de conservare. teorema lui Euler. Un exemplu de rezolvare a problemei privind utilizarea teoremei privind modificarea impulsului. moment de impuls. Teorema privind modificarea momentului unghiular Cursul 8. Legile de conservare. Elemente ale teoriei momentelor de inerție. Momentul cinetic al unui corp rigid. Ecuație diferențială rotirea unui corp rigid. Un exemplu de rezolvare a problemei utilizării teoremei privind modificarea momentului unghiular al sistemului. Teoria elementară a giroscopului. Literatură recomandată 1. Yablonsky A.A. Curs de mecanică teoretică. Partea 2. M.: facultate. 1977. 368 p. 2. Meshchersky I.V. Culegere de probleme de mecanică teoretică. M.: Știință. 1986 416 p. 3. Colectarea temelor pentru lucrările semestriale /Ed. A.A. Yablonsky. M.: Liceu. 1985. 366 p. 4. Bondarenko A.N. „Mecanica teoretică în exemple și sarcini. Dynamics” (manual electronic www.miit.ru/institut/ipss/faculties/trm/main.htm), 2004

3 slide
Cursul 1 Dinamica este o secțiune de mecanică teoretică care studiază mișcarea mecanică din cel mai general punct de vedere. Mișcarea este considerată în legătură cu forțele care acționează asupra obiectului. Secțiunea este formată din trei secțiuni: Dinamica unui punct material Dinamica Dinamica unui sistem mecanic Mecanica analitică ■ Dinamica unui punct - studiază mișcarea unui punct material, ținând cont de forțele care provoacă această mișcare. Obiectul principal este un punct material - un corp material cu o masă, ale cărei dimensiuni pot fi neglijate. Ipoteze de bază: - există un spațiu absolut (deține pur proprietăți geometrice independent de materie și de mișcarea ei. - există timp absolut (nu depinde de materie și de mișcarea ei). De aici rezultă: – există un cadru de referință absolut nemișcat. – timpul nu depinde de mișcarea cadrului de referință. – masele punctelor în mișcare nu depind de mișcarea cadrului de referință. Aceste ipoteze sunt folosite în mecanica clasică creată de Galileo și Newton. Are încă o gamă destul de largă de aplicații, întrucât sistemele mecanice considerate în științele aplicate nu au mase și viteze de mișcare atât de mari, pentru care este necesar să se țină cont de influența lor asupra geometriei spațiului, timpului, mișcării, asa cum se face in mecanică relativistă(teoria relativității). ■ Legile de bază ale dinamicii, descoperite mai întâi de Galileo și formulate de Newton, formează baza tuturor metodelor de descriere și analiză a mișcării sistemelor mecanice și a interacțiunii lor dinamice sub acțiunea diferitelor forțe. ■ Legea inerției (legea Galileo-Newton) - Un punct material izolat al unui corp își păstrează starea de repaus sau mișcarea rectilinie uniformă până când forțele aplicate îl forțează să schimbe această stare. Aceasta implică echivalența stării de repaus și a mișcării prin inerție (legea relativității a lui Galileo). Cadrul de referință, în raport cu care se îndeplinește legea inerției, se numește inerțial. Proprietatea unui punct material de a se strădui să mențină viteza de mișcare (starea sa cinematică) neschimbată se numește inerție. ■ Legea proporționalității forței și a accelerației (Ecuația de bază a dinamicii - legea lui Newton II) - Accelerația dată de forță unui punct material este direct proporțională cu forța și invers proporțională cu masa acestui punct: sau Aici m este masa punctului (o măsură a inerției), măsurată în kg, egală numeric cu greutatea împărțită la accelerația gravitației: F este forța care acționează, măsurată în N (1 N conferă o accelerație de 1 m/s2 unui punct de masa 1 kg, 1 N \u003d 1 / 9,81 kg-s). ■ Dinamica unui sistem mecanic - studiază mișcarea unui set de puncte materiale și corpuri rigide, combinate legi generale interacțiuni, ținând cont de forțele care provoacă această mișcare. ■ Mecanica analitica - studiaza miscarea sistemelor mecanice nelibere folosind metode analitice generale. unu

4 slide
Cursul 1 (continuare - 1.2) Ecuații diferențiale de mișcare a unui punct material: - ecuația diferențială de mișcare a unui punct în formă vectorială. - ecuaţii diferenţiale ale mişcării punctului sub formă de coordonate. Acest rezultat poate fi obținut prin proiecția formală a ecuației diferențiale vectoriale (1). După grupare, relația vectorială se descompune în trei ecuații scalare: În formă de coordonate: Folosim relația rază-vector cu coordonate și vectorul forță cu proiecții: ecuație diferențială a mișcării pe axe de coordonate naturale (în mișcare): sau: - ecuațiile naturale ale mișcării unui punct. ■ Ecuaţia de bază a dinamicii: - corespunde modului vectorial de precizare a mişcării unui punct. ■ Legea independenței acțiunii forțelor - Accelerația unui punct material sub acțiunea mai multor forțe este egală cu suma geometrică a accelerațiilor unui punct din acțiunea fiecăreia dintre forțe separat: sau Legea este valabilă. pentru orice stare cinematică a corpurilor. Forțele de interacțiune, fiind aplicate în diferite puncte (corpuri) nu sunt echilibrate. ■ Legea egalității acțiunii și reacției (legea a III-a a lui Newton) - Fiecărei acțiuni îi corespunde o reacție egală și direcționată opus: 2

5 slide
Două probleme principale de dinamică: 1. Problemă directă: Mișcarea este dată (ecuații de mișcare, traiectorie). Este necesar să se determine forțele sub acțiunea cărora are loc o anumită mișcare. 2. Problemă inversă: Sunt date forțele sub acțiunea cărora se produce mișcarea. Este necesar să se găsească parametrii de mișcare (ecuații de mișcare, traiectorie de mișcare). Ambele probleme sunt rezolvate folosind ecuația de bază a dinamicii și proiecția acesteia pe axele de coordonate. Dacă se ia în considerare mișcarea unui punct neliber, atunci, ca și în statică, se utilizează principiul eliberării din legături. Ca urmare a reacției, legăturile sunt incluse în compoziția forțelor care acționează asupra punctului material. Rezolvarea primei probleme este legată de operațiile de diferențiere. Rezolvarea problemei inverse necesită integrarea ecuațiilor diferențiale corespunzătoare, iar acest lucru este mult mai dificil decât diferențierea. Problema inversă este mai dificilă decât problema directă. Rezolvarea problemei directe a dinamicii - să ne uităm la exemple: Exemplul 1. O cabină cu greutatea G a unui lift este ridicată de un cablu cu o accelerație a . Determinați tensiunea cablului. 1. Selectați un obiect (cabina liftului se deplasează înainte și poate fi considerată ca punct material). 2. Aruncăm conexiunea (cablul) și o înlocuim cu reacția R. 3. Compunem ecuația de bază a dinamicii: Determinați reacția cablului: Determinați tensiunea cablului: Cu o mișcare uniformă a cabinei ay = 0 și tensiunea cablului este egală cu greutatea: T = G. Când cablul se rupe T = 0 şi acceleraţia cabinei este egală cu acceleraţia căderii libere: ay = -g. 3 4. Proiectăm ecuația de bază a dinamicii pe axa y: y Exemplul 2. Un punct de masă m se mișcă de-a lungul unei suprafețe orizontale (planul Oxy) conform ecuațiilor: x = a coskt, y = b coskt. Determinați forța care acționează asupra punctului. 1. Selectați un obiect (punct material). 2. Aruncăm legătura (planul) și o înlocuim cu reacția N. 3. Adăugăm la sistemul de forțe o forță necunoscută F. 4. Compuneți ecuația de bază a dinamicii: 5. Proiectați ecuația de bază a dinamicii pe axele x,y: Determinați proiecțiile forței: Modulul forței: Cosinusul direcției: Astfel, mărimea forței este proporțională cu distanța punctului la centrul de coordonate și este îndreptată spre centru de-a lungul liniei care leagă punctul de centru. Traiectoria mișcării punctului este o elipsă centrată la origine: O r Lecția 1 (continuare - 1.3)

6 diapozitiv
Cursul 1 (continuare 1.4) Exemplul 3: O sarcină cu greutatea G este suspendată pe un cablu de lungime l și se deplasează de-a lungul unui traseu circular într-un plan orizontal cu o anumită viteză. Unghiul de abatere al cablului de la verticală este egal cu. Determinați tensiunea cablului și viteza sarcinii. 1. Selectați un obiect (marfă). 2. Aruncați legătura (coarda) și înlocuiți-o cu reacția R. 3. Compuneți ecuația principală a dinamicii: Din a treia ecuație, determinați reacția cablului: Determinați tensiunea cablului: Înlocuiți valoarea reacției a cablului, accelerația normală în a doua ecuație și determinați viteza sarcinii: 4. Proiectați dinamica osiilor din ecuația principală,n,b: Exemplul 4: O mașină cu greutatea G se deplasează pe un pod convex (raza de curbură este R ) cu viteza V. Determinaţi presiunea maşinii pe pod. 1. Selectăm un obiect (o mașină, neglijăm dimensiunile și îl considerăm ca punct). 2. Aruncăm legătura (suprafață aspră) și o înlocuim cu reacțiile N și forța de frecare Ffr. 3. Compunem ecuația de bază a dinamicii: 4. Proiectăm ecuația de bază a dinamicii pe axa n: De aici determinăm reacția normală: Determinăm presiunea mașinii pe pod: De aici putem determina viteza corespunzătoare presiunii zero pe punte (Q = 0): 4

7 slide
Cursul 2 După înlocuirea valorilor găsite ale constantelor, obținem: Astfel, sub acțiunea aceluiași sistem de forțe, un punct material poate efectua toată clasa mişcări determinate de condiţiile iniţiale. Coordonatele inițiale țin cont de poziția inițială a punctului. Viteza inițială, dată de proiecții, ține cont de influența asupra mișcării acesteia de-a lungul secțiunii considerate a traiectoriei forțelor care au acționat asupra punctului înainte de a ajunge la această secțiune, i.e. starea cinematică inițială. Rezolvarea problemei inverse de dinamică - În cazul general al mișcării unui punct, forțele care acționează asupra punctului sunt variabile care depind de timp, coordonate și viteză. Mișcarea unui punct este descrisă de un sistem de trei ecuații diferențiale de ordinul doi: După integrarea fiecăreia dintre ele, vor exista șase constante C1, C2,..., C6: Valorile constantelor C1, C2,... ., C6 se găsesc din șase condiții inițiale la t = 0: Exemplul 1 al soluției problemei inverse: Un punct material liber de masă m se mișcă sub acțiunea unei forțe F, care este constantă ca mărime și mărime. . La momentul inițial, viteza punctului a fost v0 și a coincis în direcție cu forța. Determinați ecuația de mișcare a unui punct. 1. Compunem ecuația de bază a dinamicii: 3. Coborâm ordinea derivatei: 2. Alegem sistemul de referință cartezian, direcționând axa x de-a lungul direcției forței și proiectăm ecuația principală a dinamicii pe această axă: sau x y z 4. Separați variabilele: 5. Calculați integralele din ambele părți ale ecuației: 6. Să reprezentăm proiecția vitezei ca derivată în timp a coordonatei: 8. Calculați integralele ambelor părți ale ecuației: 7. Separați variabilele: 9. Pentru a determina valorile constantelor C1 și C2, folosim condițiile inițiale t = 0, vx = v0 , x = x0: Ca rezultat, obținem ecuația mișcării uniform variabile (de-a lungul axa x): 5

8 slide
Instructiuni generale pentru rezolvarea problemelor directe si inverse. Procedura de rezolvare: 1. Compilarea ecuației diferențiale a mișcării: 1.1. Alegeți un sistem de coordonate - dreptunghiular (fix) cu o traiectorie de mișcare necunoscută, natural (în mișcare) cu o traiectorie cunoscută, de exemplu, un cerc sau o linie dreaptă. În acest din urmă caz, poate fi utilizată o coordonată rectilinie. Punctul de referință trebuie combinat cu poziția inițială a punctului (la t = 0) sau cu poziția de echilibru a punctului, dacă există, de exemplu, atunci când punctul fluctuează. 6 1.2. Desenați un punct într-o poziție corespunzătoare unui moment de timp arbitrar (pentru t > 0), astfel încât coordonatele să fie pozitive (s > 0, x > 0). De asemenea, presupunem că proiecția vitezei în această poziție este de asemenea pozitivă. În cazul oscilațiilor, proiecția vitezei își schimbă semnul, de exemplu, la revenirea la poziția de echilibru. Aici ar trebui să presupunem că în momentul de timp considerat punctul se îndepărtează de poziția de echilibru. Implementarea acestei recomandări este importantă în viitor atunci când lucrați cu forțe de rezistență care depind de viteză. 1.3. Eliberați punctul material din legături, înlocuiți acțiunea lor cu reacții, adăugați forțe active. 1.4. Scrieți legea de bază a dinamicii în formă vectorială, proiectați pe axele selectate, exprimați forțele date sau reactive în termeni de timp, coordonate sau variabile de viteză, dacă acestea depind de acestea. 2. Rezolvarea ecuațiilor diferențiale: 2.1. Reduceți derivata dacă ecuația nu este redusă la forma canonică (standard). de exemplu: sau 2.2. Variabile separate, de exemplu: sau 2.4. Calculați Nu integrale definiteîn părțile din stânga și din dreapta ecuației, de exemplu: 2.3. Dacă există trei variabile în ecuație, atunci faceți o schimbare a variabilelor, de exemplu: și apoi separați variabilele. Cometariu. În loc să calculeze integrale nedefinite este posibil să se calculeze integrale definite cu o limită superioară variabilă. Limitele inferioare reprezintă valorile inițiale ale variabilelor (condițiile inițiale).Atunci nu este nevoie să găsiți separat constanta, care este inclusă automat în soluție, de exemplu: Folosind condițiile inițiale, de exemplu, t = 0 , vx = vx0, determinați constanta de integrare: 2.5. Exprimați viteza în termeni de derivată în timp a coordonatei, de exemplu, și repetați pașii 2.2 -2.4 Notă. Dacă ecuația este redusă la o formă canonică care are o soluție standard, atunci se folosește această soluție gata făcută. Constantele de integrare se regăsesc încă din condițiile inițiale. Vezi, de exemplu, oscilații (cursul 4, p. 8). Cursul 2 (continuare 2.2)

9 slide
Cursul 2 (continuare 2.3) Exemplul 2 de rezolvare a problemei inverse: Forța depinde de timp. O sarcină cu greutatea P începe să se deplaseze de-a lungul unei suprafețe orizontale netede sub acțiunea unei forțe F, a cărei mărime este proporțională cu timpul (F = kt). Determinați distanța parcursă de sarcină în timpul t. 3. Compuneți ecuația de bază a dinamicii: 5. Reduceți ordinea derivatei: 4. Proiectați ecuația de bază a dinamicii pe axa x: sau 7 6. Separați variabilele: 7. Calculați integralele ambelor părți ale ecuația: 9. Reprezentați proiecția vitezei ca derivată a coordonatei în raport cu timpul: 10. Calculați integralele ambelor părți ale ecuației: 9. Separați variabilele: 8. Determinați valoarea constantei C1 din condiția inițială t = 0, vx = v0=0: Ca rezultat, obținem ecuația mișcării (de-a lungul axei x), care dă valoarea distanței parcurse pentru timpul t: 1. Alegeți sistemul de referință ( coordonate carteziene) astfel încât corpul să aibă o coordonată pozitivă: 2. Luăm obiectul mișcării ca punct material (corpul se deplasează înainte), îl eliberăm de legătură (planul de referință) și îl înlocuim cu reacția (reacția normală a unui neted). suprafata): 11. Determinati valoarea constantei C2 din conditia initiala t = 0, x = x0=0: Problema inversa Exemplul 3: Forta depinde de coordonata. Un punct material de masă m este aruncat în sus de pe suprafața Pământului cu o viteză v0. Forța de gravitație a Pământului este invers proporțională cu pătratul distanței de la punct la centrul de greutate (centrul Pământului). Determinați dependența vitezei de distanța y până la centrul Pământului. 1. Alegem sistemul de referință (coordonate carteziane) astfel încât corpul să aibă o coordonată pozitivă: 2. Compunem ecuația de bază a dinamicii: 3. Proiectăm ecuația de bază a dinamicii pe axa y: sau Coeficientul de proporționalitate poate pot fi găsite folosind greutatea unui punct de pe suprafața Pământului: R Prin urmare diferența ecuației arată astfel: sau 4. Coborâți ordinul derivatei: 5. Schimbați variabila: 6. Separați variabilele: 7. Calculați integrale ale ambelor părți ale ecuației: 8. Înlocuiți limitele: Ca rezultat, obținem o expresie pentru viteza în funcție de coordonata y: Înălțimea maximă de zbor poate fi găsită prin echivalarea vitezei la zero: Altitudinea maximă de zbor când numitorul se întoarce la zero: De aici, la stabilirea razei Pământului și a accelerației căderii libere, se obține II viteza spatiala:

10 diapozitive
Cursul 2 (continuare 2.4) Exemplul 2 de rezolvare a problemei inverse: Forța depinde de viteză. O navă de masa m avea viteza v0. Rezistența apei la mișcarea navei este proporțională cu viteza. Determinați timpul necesar ca viteza navei să scadă la jumătate după oprirea motorului, precum și distanța parcursă de navă până la oprirea completă. 8 1. Alegem un sistem de referință (coordonate carteziane) astfel încât corpul să aibă o coordonată pozitivă: 2. Luăm obiectul mișcării ca punct material (nava se deplasează înainte), îl eliberăm de legături (apa) și îl înlocuim cu o reacție (forța de plutire - forța lui Arhimede), precum și forța de rezistență la mișcare. 3. Adăugați forța activă (gravitație). 4. Compunem ecuația principală a dinamicii: 5. Proiectăm ecuația principală a dinamicii pe axa x: sau 6. Coborâm ordinea derivatei: 7. Separăm variabilele: 8. Calculăm integralele din ambele părți ale ecuației: 9. Înlocuim limitele: Se obține o expresie care raportează viteza și timpul t, din care se poate determina timpul de mișcare: Timpul de mișcare, în timpul căruia viteza va scădea la jumătate: Este interesant de observat că atunci când viteza se apropie de zero, timpul de mișcare tinde spre infinit, adică. viteza finală nu poate fi zero. De ce nu „mișcare perpetuă”? Totuși, în acest caz, distanța parcursă până la oprire este o valoare finită. Pentru a determina distanța parcursă, apelăm la expresia obținută în urma scăderii ordinului derivatei și facem o schimbare de variabilă: După integrarea și înlocuirea limitelor, obținem: Distanța parcursă până la oprire: ■ Mișcarea unui punct aruncat într-un unghi față de orizont într-un câmp gravitațional uniform fără a ține cont de rezistența aerului Eliminând timpul din ecuațiile mișcării, obținem ecuația traiectoriei: Timpul de zbor se determină prin echivalarea coordonatei y la zero: Intervalul de zbor se determină înlocuind timp de zbor:

11 diapozitiv
Cursul 3 Oscilații rectilinii ale unui punct material - Mișcarea oscilatorie a unui punct material are loc cu condiția să existe o forță de restabilire care tinde să readucă punctul în poziția de echilibru pentru orice abatere de la această poziție. 9 Există o forță de restabilire, poziția de echilibru este stabilă Fără forță de restabilire, poziția de echilibru este instabilă Fără forță de restabilire, poziția de echilibru este indiferentă Este întotdeauna îndreptată spre poziția de echilibru, valoarea este direct proporțională cu alungirea (scurtarea) liniară a arcului, egală cu abaterea corpului de la poziția de echilibru: c este coeficientul de rigiditate a arcului, numeric egal cu forța sub căruia arcul își schimbă lungimea cu unu, măsurată în N/m în sistemul SI. x y O Tipuri de vibratii ale unui punct material: 1. Vibratii libere (fara a se tine cont de rezistenta mediului). 2. Oscilatii libere tinand cont de rezistenta mediului (oscilatii amortizate). 3. Vibrații forțate. 4. Oscilații forțate ținând cont de rezistența mediului. ■ Oscilaţii libere - apar doar sub acţiunea unei forţe de restabilire. Să notăm legea de bază a dinamicii: Să alegem un sistem de coordonate centrat pe poziția de echilibru (punctul O) și să proiectăm ecuația pe axa x: Să aducem ecuația rezultată la forma standard (canoică): Această ecuație este omogenă ecuație diferențială liniară de ordinul doi, a cărei formă a soluției este determinată de rădăcinile caracteristicii ecuației obținute cu ajutorul substituției universale: Rădăcinile ecuației caracteristice sunt imaginare și egale: Soluția generală a ecuației diferențiale are forma: Viteza punctului: Condiții inițiale: Definiți constantele: Deci, ecuația vibrațiilor libere are forma: Ecuația poate fi reprezentată printr-o expresie unică: unde a este amplitudinea, - faza inițială. Noile constante a și - sunt legate de constantele C1 și C2 prin relațiile: Să definim a și: Motivul apariției oscilațiilor libere este deplasarea inițială x0 și/sau viteza inițială v0.

12 slide
10 Cursul 3 (continuare 3.2) Oscilații amortizate ale unui punct material - Mișcarea oscilatorie a unui punct material are loc în prezența unei forțe de restabilire și a unei forțe de rezistență la mișcare. Se determină dependența forței de rezistență la mișcare de deplasare sau viteză natura fizica mediu sau comunicare care împiedică mișcarea. Cea mai simplă dependență este o dependență liniară de viteză (rezistența vâscoasă): - coeficientul de vâscozitate x y O din valorile rădăcinilor: 1. n< k – случай малого вязкого сопротивления: - корни комплексные, различные. или x = ae-nt x = -ae-nt Частота oscilații amortizate: Perioada: T* Scăderea oscilației: ai ai+1 Scăderea oscilației logaritmice: Oscilația scade foarte repede. Principala influență a forței de rezistență vâscoasă este o scădere a amplitudinii oscilației în timp. 2. n > k - cazul rezistenţei mari la vâscos: - rădăcinile sunt reale, diferite. sau - aceste funcții sunt aperiodice: 3. n = k: - rădăcinile sunt reale, multiple. aceste funcții sunt și aperiodice:

13 slide
Cursul 3 (continuare 3.3) Clasificarea soluţiilor de oscilaţii libere. Conexiuni cu arc. duritate echivalentă. y y 11 Dif. Caracterul ecuației. Ecuație Rădăcini char. ecuație Rezolvarea ecuației diferențiale Graficul nk n=k

14 slide
Cursul 4 Vibrații forțate ale unui punct material - Alături de forța de restabilire, acționează o forță în schimbare periodică, numită forță perturbatoare. Forța perturbatoare poate avea o natură diferită. De exemplu, într-un caz particular, efectul inerțial al unei mase dezechilibrate m1 a unui rotor în rotație determină proiecții de forță care se schimbă armonic: Ecuația principală a dinamicii: Proiecția ecuației dinamicii pe axă: Să aducem ecuația la standard forma: 12 Soluția acestei ecuații diferențiale neomogene constă din două părți x = x1 + x2: x1 este soluția generală a ecuației omogene corespunzătoare și x2 este o soluție particulară a ecuației neomogene: Selectăm soluția particulară sub formă de partea dreaptă: Egalitatea rezultată trebuie să fie satisfăcută pentru orice t . Atunci: sau Astfel, cu acțiunea simultană a forțelor restauratoare și perturbatoare, punctul material realizează un complex mișcare oscilantă, care este rezultatul adunării (suprapoziției) a oscilațiilor libere (x1) și forțate (x2). Dacă p< k (вынужденные колебания малой частоты), то фаза колебаний совпадает с фазой возмущающей силы: В итоге полное решение: или Общее решение: Постоянные С1 и С2, или a и определяются из начальных условий с использованием solutie completa(!): Astfel, o soluție particulară: Dacă p > k (oscilații forțate de înaltă frecvență), atunci faza oscilațiilor este opusă fazei forței perturbatoare:

15 slide
Cursul 4 (continuare 4.2) 13 Coeficient dinamic - raportul dintre amplitudinea oscilațiilor forțate și deviația statică a unui punct sub acțiunea unei forțe constante H = const: Amplitudinea oscilațiilor forțate: Abaterea statică poate fi găsită din ecuația de echilibru: Aici: Prin urmare: Astfel, la p< k (малая частота вынужденных колебаний) коэффициент динамичности: При p >k (frecvența înaltă a oscilațiilor forțate) coeficient dinamic: Rezonanța - apare atunci când frecvența oscilațiilor forțate coincide cu frecvența oscilațiilor naturale (p = k). Acest lucru se întâmplă cel mai adesea la pornirea și oprirea rotației rotoarelor prost echilibrate montate pe suspensii elastice. Ecuația diferențială a oscilațiilor cu frecvențe egale: O anumită soluție sub forma părții drepte nu poate fi luată, deoarece se va obţine o soluţie dependentă liniar (vezi soluţia generală). Soluție generală: Înlocuiți în ecuația diferențială: Să luăm o anumită soluție sub formă și să calculăm derivatele: Astfel, se obține soluția: sau Oscilațiile forțate la rezonanță au o amplitudine care crește nedefinit proporțional cu timpul. Influența rezistenței la mișcare în timpul vibrațiilor forțate. Ecuația diferențială în prezența rezistenței vâscoase are forma: Soluția generală este selectată din tabel (Lectura 3, p. 11) în funcție de raportul dintre n și k (vezi). Luăm o anumită soluție sub forma și calculăm derivatele: Înlocuire în ecuația diferențială: Echivalarea coeficienților la același funcții trigonometrice obținem un sistem de ecuații: Ridicând ambele ecuații la o putere și adunând lor, obținem amplitudinea oscilațiilor forțate: Împărțind a doua ecuație la prima, obținem defazatul oscilațiilor forțate: Astfel, ecuația de mișcare pentru oscilații forțate, ținând cont de rezistența la mișcare, de exemplu, la n< k (малое сопротивление): Вынужденные колебания при сопротивлении движению не затухают. Частота и период вынужденных колебаний равны частоте и периоду изменения возмущающей силы. Коэффициент динамичности при резонансе имеет конечную величину и зависит от соотношения n и к.

16 slide
Cursul 5 Mișcarea relativă a unui punct material - Să presupunem că sistemul de coordonate în mișcare (neinerțial) Oxyz se mișcă conform unei legi relativ la sistemul de coordonate fix (inerțial) O1x1y1z1. Mișcarea unui punct material M (x, y, z) față de sistemul mobil Oxyz este relativă, față de sistemul nemișcat O1x1y1z1 este absolută. Mișcarea sistemului mobil Oxyz în raport cu sistemul fix O1x1y1z1 este o mișcare portabilă. 14 z x1 y1 z1 O1 x y M x y z O partea dreapta: Termenii transferați au dimensiunea forțelor și sunt considerați ca forțe de inerție corespunzătoare egale cu: Atunci mișcarea relativă a unui punct poate fi considerată absolută, dacă la forțele care acționează se adaugă forțele de translație și Coriolis de inerție: În proiecții pe axele sistemului de coordonate în mișcare, avem: alt fel Mișcare de translație: 1. Rotație în jurul unei axe fixe: Dacă rotația este uniformă, atunci εe = 0: 2. Mișcare curbilinie de translație: Dacă mișcarea este rectilinie, atunci = : Dacă mișcarea este rectilinie și uniformă, atunci sistemul de mișcare este inerțiale și mișcarea relativă pot fi considerate absolute: Niciuna fenomene mecanice este imposibil să se detecteze mișcarea uniformă rectilinie (principiul relativității mecanica clasica). Influența rotației Pământului asupra echilibrului corpurilor - Să presupunem că corpul se află în echilibru pe suprafața Pământului la o latitudine arbitrară φ (paralele). Pământul se rotește în jurul axei sale de la vest la est cu o viteză unghiulară: raza Pământului este de aproximativ 6370 km. S R- reacție completă suprafață neuniformă. G - forța de atracție a Pământului către centru. Ф - forța centrifugă de inerție. Condiție de echilibru relativ: Rezultanța forțelor de atracție și inerție este forța gravitației (greutatea): Mărimea forței gravitaționale (greutatea) pe suprafața Pământului este P = mg. Forța centrifugă de inerție este o mică parte a forței gravitaționale: Deviația forței gravitaționale de la direcția forței de atracție este, de asemenea, mică: Astfel, influența rotației Pământului asupra echilibrului corpurilor este extrem de mică. și nu este luată în considerare în calculele practice. Valoarea maximă a forței de inerție (la φ = 0 - la ecuator) este doar 0,00343 din valoarea gravitației

17 slide
Cursul 5 (continuare 5.2) 15 Influența rotației Pământului asupra mișcării corpurilor în câmpul gravitațional al Pământului - Să presupunem că un corp cade pe Pământ de la o anumită înălțime H deasupra suprafeței Pământului la latitudinea φ . Să alegem un cadru de referință în mișcare, legat rigid de Pământ, care direcționează axele x, y tangențial la paralelă și la meridian: Ecuația mișcării relative: Aici, micșorarea forței centrifuge de inerție în comparație cu forța gravitației este luat in considerare. Astfel, forța gravitației este identificată cu forța gravitației. În plus, presupunem că gravitația este direcționată perpendicular pe suprafața Pământului datorită micșorării deviației sale, așa cum sa discutat mai sus. Accelerația Coriolis este egală și direcționată paralel cu axa y la vest. Forța de inerție Coriolis este direcționată în direcția opusă. Proiectăm ecuația mișcării relative pe axă: Soluția primei ecuații dă: Condiții inițiale: Soluția celei de-a treia ecuații oferă: Condiții inițiale: A treia ecuație ia forma: Condiții inițiale: Soluția ei dă: Soluția rezultată arată că corpul deviază spre est când cade. Să calculăm valoarea acestei abateri, de exemplu, la căderea de la o înălțime de 100 m. Găsim timpul de cădere din soluția celei de-a doua ecuații: Astfel, influența rotației Pământului asupra mișcării corpurilor este extrem de mică. pentru înălțimi și viteze practice și nu este luată în considerare în calculele tehnice. Rezolvarea celei de-a doua ecuații implică și existența unei viteze de-a lungul axei y, care ar trebui să provoace și să provoace accelerația corespunzătoare și forța de inerție Coriolis. Influența acestei viteze și a forței de inerție asociate acesteia asupra schimbării mișcării va fi chiar mai mică decât forța de inerție Coriolis considerată asociată cu viteza verticală.

18 slide
Cursul 6 Dinamica unui sistem mecanic. Un sistem de puncte materiale sau un sistem mecanic - Un set de puncte materiale sau acele puncte materiale unite prin legile generale ale interacțiunii (poziția sau mișcarea fiecăruia dintre punctele sau un corp depinde de poziția și mișcarea tuturor celorlalte). sistem de puncte libere - a cărui mișcare nu este limitată de nicio conexiune (de exemplu, un sistem planetar, în care planetele sunt considerate puncte materiale). Un sistem de puncte nelibere sau un sistem mecanic neliber - mișcarea punctelor materiale sau a corpurilor este limitată de constrângerile impuse sistemului (de exemplu, un mecanism, o mașină etc.). 16 Forțe care acționează asupra sistemului. Pe lângă clasificarea forțelor existentă anterior (forțe active și reactive), se introduce o nouă clasificare a forțelor: 1. Forțe externe (e) - care acționează asupra punctelor și corpurilor sistemului din puncte sau corpuri care nu fac parte din acesta. sistem. 2. Forțe interne (i) - forțe de interacțiune între punctele materiale sau corpurile incluse în sistemul dat. Aceeași forță poate fi atât forță externă, cât și forță internă. Totul depinde de ce sistem mecanic este luat în considerare. De exemplu: În sistemul Soarelui, Pământului și Lunii, toate forțele gravitaționale dintre ele sunt interne. Când luăm în considerare sistemul Pământului și Lunii, forțele gravitaționale aplicate din partea Soarelui sunt externe: C Z L Pe baza legii de acțiune și reacție, fiecărei forțe interne Fk îi corespunde o altă forță internă Fk', egală ca valoare absolută și opusă în direcţie. De aici rezultă două proprietăți remarcabile ale forțelor interne: Vectorul principal al tuturor forțelor interne ale sistemului este egal cu zero: Momentul principal al tuturor forțelor interne ale sistemului față de orice centru este egal cu zero: Sau în proiecții pe coordonate axe: Notă. Deși aceste ecuații sunt similare cu ecuațiile de echilibru, nu sunt, deoarece forțele interne sunt aplicate puncte diferite sau corpuri ale sistemului și pot provoca deplasarea acestor puncte (corpuri) unul față de celălalt. Din aceste ecuații rezultă că forțele interne nu afectează mișcarea unui sistem considerat ca un întreg. Centrul de masă al sistemului de puncte materiale. Pentru a descrie mișcarea sistemului în ansamblu, se introduce un punct geometric, numit centru de masă, al cărui vector rază este determinat de expresia, unde M este masa întregului sistem: Sau în proiecții pe coordonată axe: Formulele pentru centrul de masă sunt similare cu cele pentru centrul de greutate. Cu toate acestea, conceptul de centru de masă este mai general, deoarece nu este legat de forțele de greutate sau de forțele de greutate.

19 slide
Cursul 6 (continuare 6.2) 17 Teorema privind mișcarea centrului de masă al sistemului - Se consideră un sistem de n puncte materiale. Împărțim forțele aplicate fiecărui punct în cele externe și interne și le înlocuim cu rezultantele corespunzătoare Fke și Fki. Să notăm pentru fiecare punct ecuația de bază a dinamicii: sau Să însumăm aceste ecuații peste toate punctele: În partea stângă a ecuației, vom introduce masele sub semnul derivatei și vom înlocui suma derivatelor cu derivata a sumei: Din definiția centrului de masă: Înlocuiți în ecuația rezultată: obținem sau: Produsul dintre masa sistemului și accelerația masei sale centrale este egal cu vectorul principal al forțelor externe. În proiecțiile pe axele de coordonate: Centrul de masă al sistemului se mișcă ca punct material cu o masă egală cu masa întregului sistem, căruia i se aplică toate forțele externe care acționează asupra sistemului. Consecințe din teorema asupra mișcării centrului de masă al sistemului (legile conservării): 1. Dacă în intervalul de timp vectorul principal al forțelor externe ale sistemului este zero, Re = 0, atunci viteza centrului de masă este constantă, vC = const (centrul de masă se mișcă uniform rectiliniu - legea conservării centrului de masă al mișcării). 2. Dacă în intervalul de timp proiecția vectorului principal al forțelor externe ale sistemului pe axa x este egală cu zero, Rxe = 0, atunci viteza centrului de masă de-a lungul axei x este constantă, vCx = const (centrul de masă se mișcă uniform de-a lungul axei). Afirmații similare sunt adevărate pentru axele y și z. Exemplu: Două persoane de masele m1 și m2 se află într-o barcă de masa m3. La momentul inițial, barca cu oameni era în repaus. Determinați deplasarea bărcii dacă o persoană cu masa m2 s-a deplasat la prova bărcii la distanță a. 3. Dacă în intervalul de timp vectorul principal al forțelor externe ale sistemului este egal cu zero, Re = 0, iar în momentul inițial viteza centrului de masă este zero, vC = 0, atunci vectorul rază a centrul de masă rămâne constant, rC = const (centrul de masă este în repaus este legea conservării poziţiei centrului de masă). 4. Dacă în intervalul de timp proiecția vectorului principal al forțelor externe ale sistemului pe axa x este egală cu zero, Rxe = 0, iar în momentul inițial viteza centrului de masă de-a lungul acestei axe este zero. , vCx = 0, atunci coordonata centrului de masă de-a lungul axei x rămâne constantă, xC = const (centrul de masă nu se mișcă de-a lungul acestei axe). Afirmații similare sunt adevărate pentru axele y și z. 1. Obiectul de mișcare (o barcă cu oameni): 2. Aruncăm conexiunile (apa): 3. Înlocuim legătura cu o reacție: 4. Adăugăm forțe active: 5. Notează teorema despre centrul de masă: Proiectați pe axa x: O Stabiliți cât de departe trebuie să transferați la o persoană cu masa m1, astfel încât barca să rămână pe loc: Barca se va deplasa pe o distanță l în direcția opusă.

20 de diapozitive
Cursul 7 Impulsul forței este o măsură a interacțiunii mecanice care caracterizează transferul mișcării mecanice de la forțele care acționează asupra unui punct pentru o anumită perioadă de timp: 18 În proiecții pe axe de coordonate: În cazul unei forțe constante: În proiecții pe axe de coordonate: până la punctul de forțe în același interval de timp: Înmulțire cu dt: Integrare într-un interval de timp dat: Mărimea mișcării punctului este o măsură a mișcării mecanice, determinată de un vector egal cu produsul dintre masa punctului și vectorul său viteză: Teorema privind modificarea cantității de mișcare a sistemului – Se consideră sistemul n puncte materiale. Împărțim forțele aplicate fiecărui punct în cele externe și interne și le înlocuim cu rezultantele corespunzătoare Fke și Fki. Să scriem pentru fiecare punct ecuația de bază a dinamicii: sau Cantitatea de mișcare a unui sistem de puncte materiale - suma geometrică a cantităților de mișcare a punctelor materiale: Prin definiția centrului de masă: Vectorul impulsului sistemului este egal cu produsul dintre masa întregului sistem și vectorul viteză al centrului de masă al sistemului. Apoi: În proiecțiile pe axele de coordonate: Derivata în timp a vectorului impuls al sistemului este egală cu vectorul principal al forțelor externe ale sistemului. Să însumăm aceste ecuații peste toate punctele: În partea stângă a ecuației, introducem masele sub semnul derivatei și înlocuim suma derivatelor cu derivata sumei: Din definiția impulsului sistemului: În proiecțiile pe axele de coordonate:

21 slide
Teorema lui Euler - Aplicarea teoremei asupra modificării impulsului unui sistem la mișcarea unui mediu continuu (apa). 1. Selectăm ca obiect de mișcare volumul de apă situat în canalul curbiliniu al turbinei: 2. Aruncăm conexiunile și înlocuim acțiunea acestora cu reacții (Rpov - rezultanta forțelor de suprafață) 3. Adăugăm forțe active (Rb). - rezultanta forțelor corpului): 4. Scrieți teorema despre modificarea impulsului sistemului: Cantitatea de mișcare a apei la momentele t0 și t1 va fi reprezentată ca sume: Modificarea impulsului apei în intervalul de timp : Modificarea impulsului apei într-un interval de timp infinitezimal dt: , unde F1 F2 Luând produsul densității, aria secțiunii transversale și viteza pe secundă de masă, obținem: Înlocuind diferența de impuls a sistemului în teorema modificării , se obține: Consecințe din teoremă asupra modificării impulsului sistemului (legile conservării): 1. Dacă în intervalul de timp vectorul principal al forțelor externe ale sistemului este egal cu zero, Re = 0, atunci mișcarea vectorului mărime este constantă, Q = const este legea conservării impulsului sistemului). 2. Dacă în intervalul de timp proiecția vectorului principal al forțelor externe ale sistemului pe axa x este egală cu zero, Rxe = 0, atunci proiecția impulsului sistemului pe axa x este constantă, Qx = const. Afirmații similare sunt adevărate pentru axele y și z. Cursul 7 (continuare din 7.2) Exemplu: O grenadă de masă M, care zbura cu viteza v, a explodat în două părți. Viteza unuia dintre fragmentele de masă m1 a crescut în direcția de mișcare până la valoarea v1. Determinați viteza celui de-al doilea fragment. 1. Obiectul mișcării (grenada): 2. Obiectul este un sistem liber, nu există conexiuni și reacțiile lor. 3. Adăugați forțele active: 4. Scrieți teorema privind modificarea impulsului: Proiectați pe axă: β Împărțiți variabilele și integrați: Integrala dreaptă este aproape zero, deoarece timpul de explozie t

22 slide
Cursul 7 (continuare 7.3) 20 Momentul unghiular al unui punct sau momentul cinetic al mișcării în raport cu un anumit centru este o măsură a mișcării mecanice, determinată de un vector egal cu produsul vectorial dintre vectorul rază al unui punct material și vector al impulsului său: Momentul cinetic al unui sistem de puncte materiale relativ la un anumit centru este geometric suma momentelor numărului de mișcări ale tuturor punctelor materiale față de același centru: În proiecții pe axă: În proiecții pe axa: Teorema privind modificarea momentului impulsului sistemului - Se consideră un sistem de n puncte materiale. Împărțim forțele aplicate fiecărui punct în cele externe și interne și le înlocuim cu rezultantele corespunzătoare Fke și Fki. Să notăm pentru fiecare punct ecuația de bază a dinamicii: sau Să însumăm aceste ecuații pentru toate punctele: Să înlocuim suma derivatelor cu derivata sumei: Expresia dintre paranteze este momentul impulsului sistemului. De aici: Înmulțim vectorial fiecare dintre egalități cu raza-vector din stânga: Să vedem dacă este posibil să luăm semnul derivatei în afara produsului vectorial: Astfel, avem: centru. În proiecțiile pe axele de coordonate: Derivata momentului de impuls al sistemului față de o anumită axă în timp este egală cu momentul principal al forțelor externe ale sistemului față de aceeași axă.

23 slide
Cursul 8 21 ■ Consecințele teoremei asupra modificării momentului unghiular al sistemului (legile conservării): 1. Dacă în intervalul de timp vectorul momentului principal al forțelor externe ale sistemului relativ la un anumit centru este egal la zero, MOe = 0, atunci vectorul momentului unghiular al sistemului relativ la același centru este constant, KO = const este legea conservării impulsului a sistemului). 2. Dacă în intervalul de timp momentul principal al forțelor externe ale sistemului față de axa x este egal cu zero, Mxe = 0, atunci momentul unghiular al sistemului față de axa x este constant, Kx = const. Afirmații similare sunt adevărate pentru axele y și z. 2. Momentul de inerție al unui corp rigid în jurul unei axe: Momentul de inerție al unui punct material în jurul unei axe este egal cu produsul dintre masa punctului și pătratul distanței punctului față de axă. Momentul de inerție al unui corp rigid în jurul unei axe este egal cu suma produselor masei fiecărui punct și pătratul distanței acestui punct față de axă. ■ Elemente ale teoriei momentelor de inerție - Cu mișcarea de rotație a unui corp rigid, măsura inerției (rezistența la schimbarea în mișcare) este momentul de inerție în jurul axei de rotație. Luați în considerare conceptele de bază ale definiției și metodele de calcul a momentelor de inerție. 1. Momentul de inerție al unui punct material în jurul axei: La trecerea de la o masă discretă mică la o masă infinit mică a unui punct, limita unei astfel de sume este determinată de integrala: momentul axial de inerție al unui corp rigid . Pe lângă momentul de inerție axial al unui corp rigid, există și alte tipuri de momente de inerție: momentul de inerție centrifugal al unui corp rigid. momentul polar de inerție al unui corp rigid. 3. Teorema despre momentele de inerție ale unui corp rigid față de axele paralele - formula pentru trecerea la axele paralele: Moment de inerție față de axa de referință Momente statice de inerție față de axele de referință Masa corporală Distanța dintre axele z1 și z2 Astfel : momentele sunt zero:

24 slide
Cursul 8 (continuare 8.2) 22 Momentul de inerție al unei tije uniforme de secțiune constantă în jurul axei: x z L Selectați volumul elementar dV = Adx la distanță x: x dx Masa elementară: Pentru a calcula momentul de inerție cca. axa centrală(trecând prin centrul de greutate) este suficient să se schimbe locația axei și să se stabilească limitele de integrare (-L/2, L/2). Aici demonstrăm formula pentru trecerea la axe paralele: zС 5. Momentul de inerție al unui cilindru solid omogen în jurul axei de simetrie: H dr r Să evidențiem volumul elementar dV = 2πrdrH (cilindru subțire cu raza r) : Masa elementară: Aici folosim formula volumului cilindrului V=πR2H. Pentru a calcula momentul de inerție al unui cilindru tubular (gros), este suficient să stabilim limitele de integrare de la R1 la R2 (R2> R1): 6. Momentul de inerție al unui cilindru subțire în jurul axei de simetrie (t

25 diapozitiv
Cursul 8 (continuare 8.3) 23 ■ Ecuația diferențială de rotație a unui corp rigid în jurul unei axe: Să scriem o teoremă despre modificarea momentului unghiular al unui corp rigid care se rotește în jurul unei axe fixe: Momentul unui corp rigid în rotație este: Momentul a forțelor exterioare în jurul axei de rotație este egală cu cuplul (reacțiile și forța nu creează momente gravitaționale): înlocuim momentul cinetic și cuplul în teoremă Exemplu: Două persoane de aceeași greutate G1 = G2 atârnă de o frânghie aruncată. peste un bloc solid cu greutatea G3 = G1/4. La un moment dat, unul dintre ei a început să urce pe frânghie cu o viteză relativă u. Determinați viteza de ridicare a fiecărei persoane. 1. Selectați obiectul mișcării (bloc cu oameni): 2. Aruncați conexiunile (dispozitivul de susținere al blocului): 3. Înlocuiți legătura cu reacții (lagăr): 4. Adăugați forțe active (gravitație): 5. Notați teorema privind modificarea momentului cinetic al sistemului față de axa de rotație a blocului: R Deoarece momentul forțelor exterioare este egal cu zero, momentul cinetic trebuie să rămână constant: La momentul inițial de timp t = 0, există a fost echilibru și Kz0 = 0. După începutul mișcării unei persoane față de frânghie, întregul sistem a început să se miște, dar momentul cinetic al sistemului trebuie să rămână egal cu zero: Kz = 0. Momentul unghiular al sistem este suma momentelor unghiulare ale ambelor persoane și ale blocului: Aici v2 este viteza celei de-a doua persoane, egală cu viteza cablului, Exemplu: Determinați perioada de mici oscilații libere a unei tije omogene de masă M și lungime l, suspendat de un capăt pe o axă fixă de rotație. Sau: În cazul oscilațiilor mici sinφ φ: Perioada de oscilație: Momentul de inerție al tijei:

26 slide
Cursul 8 (continuare 8.4 - material suplimentar) 24 ■ Teoria elementară a giroscopului: Un giroscop este un corp rigid care se rotește în jurul axei de simetrie a materialului, unul dintre punctele căruia este fix. Un giroscop liber este fixat în așa fel încât centrul său de masă să rămână staționar, iar axa de rotație trece prin centrul de masă și poate lua orice poziție în spațiu, adică. axa de rotație își schimbă poziția ca și axa de rotație proprie a corpului în timpul mișcării sferice. Principala ipoteză a teoriei aproximative (elementare) a giroscopului este că vectorul de impuls (momentul cinetic) al rotorului este considerat a fi direcționat de-a lungul propriei axe de rotație. Astfel, în ciuda faptului că, în cazul general, rotorul participă la trei rotații, se ia în considerare doar viteza unghiulară a propriei rotații ω = dφ/dt. Baza pentru aceasta este că în tehnologie moderna rotorul giroscopului se rotește cu o viteză unghiulară de ordinul a 5000-8000 rad/s (aproximativ 50000-80000 rpm), în timp ce celelalte două viteze unghiulare asociate cu precesiunea și nutația propriei axe de rotație sunt de zeci de mii de ori mai mică decât această viteză. Proprietatea principală a unui giroscop liber este că axa rotorului păstrează aceeași direcție în spațiu față de sistemul de referință inerțial (stelar) (demonstrat de pendulul Foucault, care menține planul de balansare neschimbat față de stele, 1852). Aceasta rezultă din legea conservării momentului cinetic relativ la centrul de masă al rotorului, cu condiția să se neglijeze frecarea în lagărele axelor de suspensie a rotorului, cadrul exterior și interior: Acțiunea forței pe axa unei libere. giroscop. În cazul unei forțe aplicate axei rotorului, momentul forțelor exterioare față de centrul de masă nu este egal cu zero: ω ω С forță, iar spre vectorul momentului acestei forțe, adică. se va roti nu în jurul axei x (suspensia internă), ci în jurul axei y (suspensia externă). La terminarea forței, axa rotorului va rămâne în aceeași poziție, corespunzătoare ultimului timp al forței, deoarece din acest moment, momentul forțelor externe devine din nou egal cu zero. În cazul unei acțiuni de forță (impact) pe termen scurt, axa giroscopului practic nu își schimbă poziția. Astfel, rotirea rapidă a rotorului oferă giroscopului capacitatea de a contracara influențele aleatorii care urmăresc schimbarea poziția axei de rotație a rotorului, iar cu o acțiune constantă a forței, menține poziția planului perpendicular pe forța care acționează în care se află axa rotorului. Aceste proprietăți sunt utilizate în operarea sistemelor de navigație inerțiale.
Prelegeri de mecanică teoretică
Dinamica punctului
Cursul 1
Concepte de bază ale dinamicii
În capitolul Dinamica se studiază mişcarea corpurilor sub acţiunea forţelor aplicate acestora. Prin urmare, pe lângă acele concepte care au fost introduse în secțiune Cinematică, aici este necesar să se utilizeze concepte noi care reflectă specificul impactului forțelor asupra diferitelor corpuri și răspunsul corpurilor la aceste impacturi. Să luăm în considerare principalele concepte.
a) puterea
Forța este rezultatul cantitativ al impactului asupra unui anumit corp de către alte corpuri. Forța este o mărime vectorială (Fig. 1).
![]()
![]()
Punctul A de la începutul vectorului forță F numit punctul de aplicare a forței. Linia MN pe care se află vectorul forță se numește linie de forţă. Lungimea vectorului forță, măsurată la o anumită scară, se numește valoarea numerică sau modulul vectorului forță. Modulul de forță este notat cu sau . Acțiunea unei forțe asupra unui corp se manifestă fie prin deformarea acestuia, dacă corpul este staționar, fie prin conferirea lui de accelerație atunci când corpul se mișcă. Pe aceste manifestări de forță se bazează dispozitivul diverselor instrumente (contoare de forță sau dinamometre) pentru măsurarea forțelor.
b) sistemul de forţe
Se formează setul de forțe considerat sistem de forță. Orice sistem format din n forțe poate fi scris sub următoarea formă: ![]()
c) corp liber
Un corp care se poate mișca în spațiu în orice direcție fără a experimenta interacțiune directă (mecanică) cu alte corpuri se numește gratuit sau izolat. Influența unuia sau altui sistem de forțe asupra unui corp poate fi clarificată numai dacă acest corp este liber.
d) forța rezultantă
Dacă orice forță are asupra unui corp liber același efect ca un sistem de forțe, atunci această forță se numește rezultanta acestui sistem de forte. Aceasta este scrisă după cum urmează:
![]() ,
,
care înseamnă echivalenţă impactul asupra aceluiași corp liber al rezultantei și al unui sistem de n forțe.
Să trecem acum la considerarea unor concepte mai complexe legate de determinarea cantitativă a efectelor de rotație ale forțelor.
e) moment de forță relativ la un punct (centru)
Dacă corpul sub acțiunea unei forțe se poate roti în jurul unui punct fix O (Fig. 2), atunci pentru a cuantifica acest efect de rotație se introduce o mărime fizică, care se numește moment de forță în jurul unui punct (centru).

Se numește planul care trece printr-un punct fix dat și linia de acțiune a forței planul forței. În Fig. 2, acesta este planul ОАВ.
Momentul forței relativ la un punct (centru) este o mărime vectorială egală cu produsul vectorial al vectorului rază al punctului de aplicare a forței de către vectorul forță:
![]() ( 1)
( 1)
Conform regulii înmulțirii vectoriale a doi vectori, produsul lor vectorial este un vector perpendicular pe planul de localizare al vectorilor factor (în acest caz, planul triunghiului OAB), îndreptat în direcția din care tura cea mai scurtă a de la primul factor vector la al doilea factor de vector vizibil contra cronometru (Fig. 2). Cu această ordine a vectorilor factorilor produsului încrucișat (1), rotația corpului sub acțiunea forței va fi vizibilă împotriva cronometrului (Fig. 2) Deoarece vectorul este perpendicular pe planul forței , amplasarea sa in spatiu determina pozitia planului fortei.Valoarea numerica a vectorului momentului fortei fata de centru este egala cu dublul aria ОАВ si poate fi determinata prin formula:
![]() ,
(2)
,
(2)
Unde magnitudineah, egală cu cea mai scurtă distanță de la un punct dat O până la linia de acțiune a forței, se numește brațul forței.
Dacă poziția planului de acțiune al forței în spațiu nu este esențială pentru caracterizarea acțiunii de rotație a forței, atunci în acest caz, pentru a caracteriza acțiunea de rotație a forței, în locul vectorului momentului forței, moment algebric al forței:
![]() (3)
(3)
Momentul algebric al forței relativ la un centru dat este egal cu produsul dintre modulul de forță și umărul acestuia, luat cu semnul plus sau minus. În acest caz, un moment pozitiv corespunde rotației corpului sub acțiunea unei forțe date împotriva ceasului, iar un moment negativ corespunde rotației corpului în direcția ceasului. Din formulele (1), (2) și (3) rezultă că momentul fortei relativ la un punct este egal cu zero numai daca bratul acestei fortehzero. O astfel de forță nu poate roti corpul în jurul unui punct dat.
f) Momentul de forță în jurul axei
Dacă corpul sub acțiunea unei forțe se poate roti în jurul unei axe fixe (de exemplu, rotirea unui toc de ușă sau fereastră în balamale atunci când sunt deschise sau închise), atunci se introduce o mărime fizică pentru a cuantifica acest efect de rotație, care se numește moment de forță în jurul unei axe date.
 z
z
b Fxy
Figura 3 prezintă o diagramă în conformitate cu care se determină momentul forței în jurul axei z:
Unghiul este format din două direcții perpendiculare z și pe planurile triunghiurilor O abși, respectiv, OAV. Din moment ce O ab este proiecția lui ОАВ pe planul xy, apoi conform teoremei de stereometrie privind proiecția unei figuri plate pe un plan dat, avem:
unde semnul plus corespunde unei valori pozitive a cos, i.e. colțuri ascuțite, iar semnul minus corespunde valorii negative a cos, adică unghiurilor obtuze , datorită direcției vectorului . La rândul său, SO ab=1/2abh, Unde h ab . Valoarea segmentului ab este egală cu proiecția forței pe planul xy, adică . ab = F X y .
Pe baza celor de mai sus, precum și a egalităților (4) și (5), determinăm momentul forței în jurul axei z, după cum urmează:
Egalitatea (6) ne permite să formulăm următoarea definiție a momentului forței în jurul oricărei axe: Momentul forței în jurul unei axe date este egal cu proiecția pe această axă a vectorului momentului acestei forțe față de orice punct al forței. această axă și este definită ca produsul proiecției forței pe un plan perpendicular pe axa dată, luat cu un semn plus sau minus pe umărul acestei proiecții în raport cu punctul de intersecție al axei cu planul de proiecție. În acest caz, semnul momentului este considerat pozitiv dacă, privind din direcția pozitivă a axei, rotația corpului în jurul acestei axe este vizibilă contra cronometru. În caz contrar, momentul forței în jurul axei este considerat negativ. Deoarece această definiție a momentului de forță în raport cu axa este destul de greu de reținut, se recomandă să ne amintim formula (6) și Fig. 3, care explică această formulă.
Din formula (6) rezultă că momentul de forță în jurul axei este zero dacă este paralelă cu axa (în acest caz, proiecția sa pe un plan perpendicular pe axa este egală cu zero), sau linia de acțiune a forței intersectează axa (atunci brațul de proiecție h=0). Aceasta corespunde pe deplin sensului fizic al momentului de forță în jurul axei ca caracteristică cantitativă a acțiunii de rotație a forței asupra unui corp cu axă de rotație.
g) greutatea corporală
S-a remarcat de mult timp că sub influența unei forțe, corpul crește treptat viteză și continuă să se miște dacă forța este îndepărtată. Această proprietate a corpurilor de a rezista la schimbarea mișcării lor a fost numită inerţia sau inerţia corpurilor. Măsura cantitativă a inerției unui corp este masa acestuia. In afara de asta, masa corporală este o măsură cantitativă a efectului forțelor gravitaționale asupra unui corp dat cu cât masa corpului este mai mare, cu atât forța gravitațională acționează asupra corpului. După cum se va arăta mai jos, uh Aceste două definiții ale greutății corporale sunt legate.
Alte concepte și definiții ale dinamicii vor fi discutate mai târziu în secțiunile în care apar pentru prima dată.
2. Legături și reacții ale legăturilor
Mai devreme în secțiunea 1 punctul (c) a fost dat conceptul de corp liber, ca un corp care se poate mișca în spațiu în orice direcție fără a fi în contact direct cu alte corpuri. Majoritatea corpurilor reale care ne înconjoară sunt în contact direct cu alte corpuri și nu se pot mișca într-o direcție sau alta. Deci, de exemplu, corpurile situate pe suprafața mesei se pot deplasa în orice direcție, cu excepția direcției perpendiculare pe suprafața mesei în jos. Ușile cu balamale se pot roti, dar nu se pot deplasa înainte etc. Corpurile care nu se pot mișca în spațiu într-o direcție sau alta se numesc nu este gratis.
Tot ceea ce limitează mișcarea unui anumit corp în spațiu se numește legături. Acestea pot fi alte corpuri care împiedică mișcarea acestui corp în anumite direcții ( conexiuni fizice); mai larg, pot fi niste conditii impuse miscarii corpului, limitand aceasta miscare. Deci, puteți seta o condiție pentru ca mișcarea unui punct material să aibă loc de-a lungul unei curbe date. În acest caz, conexiunea este specificată matematic sub forma unei ecuații ( ecuația conexiunii). Problema tipurilor de link-uri va fi analizată mai detaliat mai jos.
Majoritatea legăturilor impuse corpurilor sunt practic legături fizice. Prin urmare, se pune întrebarea despre interacțiunea unui corp dat și legătura impusă acestui corp. La această întrebare se răspunde axioma despre interacțiunea corpurilor: Două corpuri acționează unul asupra celuilalt cu forțe egale ca mărime, opuse ca direcție și situate pe aceeași linie dreaptă. Aceste forțe se numesc forțe de interacțiune. Forțele de interacțiune sunt aplicate diferitelor corpuri care interacționează. Deci, de exemplu, în timpul interacțiunii dintre un corp dat și o conexiune, una dintre forțele de interacțiune este aplicată de pe partea laterală a corpului la conexiune, iar cealaltă forță de interacțiune este aplicată din partea conexiunii la corpul dat. . Această ultimă putere se numește forța de reacție a legăturii sau pur si simplu, reacția de conectare.
Când rezolvați probleme practice de dinamică, este necesar să puteți găsi direcția reacțiilor tipuri variate conexiuni. Regula generală pentru determinarea direcției unei reacții de legătură poate ajuta uneori în acest sens: reacția unei legături este întotdeauna îndreptată opus direcției în care această legătură împiedică mișcarea unui anumit corp. Dacă această direcție poate fi specificată cu siguranță, atunci reacția conexiunii va fi determinată de direcție. În caz contrar, direcția reacției de legătură este nedefinită și poate fi găsită numai din ecuațiile corespunzătoare de mișcare sau de echilibru ale corpului. Mai detaliat, problema tipurilor de legături și direcția reacțiilor acestora ar trebui studiată conform manualului: S.M. Targ Un scurt curs de mecanică teoretică „Școala superioară”, M., 1986. Cap.1, §3.
În secțiunea 1, litera (c), s-a spus că efectul oricărui sistem de forțe poate fi pe deplin determinat numai dacă acest sistem de forțe este aplicat unui corp liber. Deoarece majoritatea corpurilor nu sunt, de fapt, libere, atunci, pentru a studia mișcarea acestor corpuri, se pune întrebarea cum să facem aceste corpuri libere. Se răspunde la această întrebare axioma conexiunilor de prelegeri pe filozofie acasă. Prelegeri au fost... Psihologie socialași etnopsihologie. 3. Teoretic rezultatele în darwinismul social au fost...
teoretic Mecanica
Tutorial >> FizicaAbstract prelegeri pe subiect TEORETIC MECANICA Pentru studenții specialității: 260501,65 ... - full-time Rezumat prelegeriîntocmit pe baza: Butorin L.V., Busygina E.B. teoretic Mecanica. Ghid educațional și practic...




