Teraz sa pozrieme na transformáciu výrazov obsahujúcich logaritmy zo všeobecného hľadiska. Tu budeme analyzovať nielen transformáciu výrazov pomocou vlastností logaritmov, ale budeme uvažovať aj o transformácii výrazov pomocou logaritmov. všeobecný pohľad, ktoré obsahujú nielen logaritmy, ale aj mocniny, zlomky, odmocniny atď. Ako obvykle, všetok materiál dodáme s charakteristickými príkladmi podrobné popisy riešenia.

Navigácia na stránke.

Výrazy s logaritmami a logaritmické výrazy

Vykonávanie akcií so zlomkami

V predchádzajúcom odseku sme analyzovali hlavné transformácie, ktoré sa vykonávajú s jednotlivými zlomkami obsahujúcimi logaritmy. Tieto transformácie je samozrejme možné vykonať s každým jednotlivým zlomkom, ktorý je súčasťou zložitejšieho výrazu, napríklad predstavujúcom súčet, rozdiel, súčin a podiel podobných zlomkov. Ale okrem práce s jednotlivými zlomkami transformácia výrazov tohto druhu často zahŕňa vykonávanie vhodných akcií so zlomkami. Ďalej zvážime pravidlá, podľa ktorých sa tieto akcie vykonávajú.

Od ročníka 5-6 poznáme pravidlá, podľa ktorých . V článku všeobecný pohľad na operácie so zlomkami tieto pravidlá sme rozoslali s obyčajné zlomky na zlomky všeobecného tvaru A/B , kde A a B sú nejaké číselné, doslovné alebo variabilné výrazy a B je zhodne nenulové. Je jasné, že zlomky s logaritmami sú špeciálne prípady všeobecných zlomkov. A v tomto ohľade je zrejmé, že akcie so zlomkami, ktoré vo svojich záznamoch obsahujú logaritmy, sa vykonávajú podľa rovnakých pravidiel. menovite:

• Ak chcete sčítať alebo odčítať dva zlomky s rovnakými menovateľmi, podľa toho pridajte alebo odčítajte čitateľov a menovateľ ponechajte rovnaký.
• Na sčítanie alebo odčítanie dvoch zlomkov pomocou rôznych menovateľov, musíte ich priviesť k spoločnému menovateľovi a vykonať príslušné akcie podľa predchádzajúceho pravidla.
• Ak chcete vynásobiť dva zlomky, musíte napísať zlomok, ktorého čitateľ je súčinom čitateľov pôvodných zlomkov a menovateľ je súčinom menovateľov.
• Na delenie zlomku zlomkom je potrebné vynásobiť deliteľný zlomok prevrátenou hodnotou deliteľa, teda zlomkom s preskupeným čitateľom a menovateľom.

Tu je niekoľko príkladov vykonávania operácií so zlomkami obsahujúcimi logaritmy.

Príklad.

Vykonajte akcie so zlomkami obsahujúcimi logaritmy: a), b) , v) , G) .

Riešenie.

a) Menovatelia sčítaných zlomkov sú zjavne rovnaké. Preto podľa pravidla na sčítanie zlomkov s rovnakými menovateľmi sčítame čitateľov a menovateľa necháme rovnaký: .

b) Tu sú menovatelia rôzni. Preto najprv potrebujete priviesť zlomky k rovnakému menovateľovi. V našom prípade sú menovatele už prezentované ako súčin a zostáva nám vziať menovateľa prvého zlomku a doplniť k nemu chýbajúce faktory z menovateľa druhého zlomku. Dostaneme teda spoločného menovateľa formy . V tomto prípade sa odčítané zlomky redukujú na spoločného menovateľa pomocou ďalších faktorov vo forme logaritmu a výrazu x 2 · (x+1). Potom zostáva odčítať zlomky s rovnakými menovateľmi, čo nie je ťažké.

Takže riešenie je:

c) Je známe, že výsledkom násobenia zlomkov je zlomok, ktorého čitateľ je súčinom čitateľov a menovateľ je súčinom menovateľov, preto

Je ľahké vidieť, že je to možné redukcia frakcií o dva a o desiatkový logaritmus, ako výsledok máme .

d) Od delenia zlomkov prejdeme k násobeniu, pričom zlomok-deliteľa nahradíme jeho prevráteným. Takže

Čitateľ výsledného zlomku môže byť reprezentovaný ako , z ktorého je jasne viditeľný spoločný činiteľ čitateľa a menovateľa - súčiniteľ x, zlomok oň môžete zmenšiť:

odpoveď:

a), b) , v) , G) .

Malo by sa pamätať na to, že akcie so zlomkami sa vykonávajú s prihliadnutím na poradie, v ktorom sa akcie vykonávajú: najprv násobenie a delenie, potom sčítanie a odčítanie, a ak existujú zátvorky, najprv sa vykonajú akcie v zátvorkách.

Príklad.

Robte akcie so zlomkami .

Riešenie.

Najprv vykonáme sčítanie zlomkov v zátvorkách, po ktorých vykonáme násobenie:

odpoveď:

V tomto bode zostáva povedať nahlas tri pomerne zrejmé, ale zároveň dôležité body:

Konverzia výrazov pomocou vlastností logaritmov

Transformácia výrazov s logaritmami najčastejšie zahŕňa použitie identít vyjadrujúcich definíciu logaritmu a

Matematika. Tematické testy. Časť II. Príprava na jednotnú štátnu skúšku-2010. 10-11 ročníkov. Ed. Lysenko F.F. - Rostov n / D .: Legion, 2009. - 176s.

Matematika. POUŽITIE-2009. Tematické testy. Časť II (B4-B8, C1-C2) Ed. Lysenko F.F. - Rostov n/D: Legion, 2008 - 160 s.

Príručka pozostáva z testov z jednotlivých tém, ktoré sú v kurze matematiky tradičné, a preto sú spravidla súčasťou skúšky. Plne pokrývajú skupiny úloh so zvýšenou a vysokou úrovňou zložitosti POUŽITIA, okrem textových úloh a problémov v geometrii. Pre každú tému je ponúkaná jedna alebo viac testovacích sád. Každá sada obsahuje 10 testov, každý test obsahuje 8 úloh.

Účelom tejto knihy je vypracovať úlohy s krátkou a podrobnou odpoveďou na testy USE. Je to potrebné predovšetkým pre absolventov, ktorí očakávajú, že dostanú POUŽÍVAŤ dobré hodnotenie, ako aj pre žiakov 10. ročníka, ktorí si môžu upevniť preberané témy z pohľadu POUŽITIA. Navrhovaná príručka môže byť užitočná pre všetkých absolventov pripravujúcich sa na USE v matematike, ako aj pre učiteľov pripravujúcich študentov na USE.

Formát: djvu/zip (2009 , 176 s.)

Veľkosť: 2,5 MB

Stiahnuť / Stiahnuť súbor 14

Formát: pdf (2009 , 176 s.)

Veľkosť: 8,6 MB

Stiahnuť ▼: 14 .12.2018, odkazy odstránené na žiadosť vydavateľstva Legion (pozri pozn.)

Formát: djvu/zip (2008 , 160. roky.)

Veľkosť: 3 MB

Stiahnuť / Stiahnuť súbor 14 .12.2018, odkazy odstránené na žiadosť vydavateľstva Legion (pozri pozn.)

Formát: pdf (2008 , 160. roky.)

Veľkosť: 9,9 MB

Stiahnuť ▼: 14 .12.2018, odkazy odstránené na žiadosť vydavateľstva Legion (pozri pozn.)

Výchovno-metodický komplex "Matematika. Jednotná štátna skúška-2010" vyd. Lysenko F.F. a Kulabukhov S.Yu. obsahuje návody:
1. Matematika. Príprava na jednotnú štátnu skúšku-2010.
2. Reshebnik. Matematika. Príprava na jednotnú štátnu skúšku-2010.
3. Matematika. Tematické testy. Časť I (základná úroveň). Príprava na jednotnú štátnu skúšku-2010. 10-11 ročníkov.
4. Matematika. Tematické testy. Časť II. Príprava na jednotnú štátnu skúšku-2010. 10-11 ročníkov.
5. Matematika. Tematické testy: geometria, slovné úlohy. Príprava na jednotnú štátnu skúšku-2010. 10-11 ročníkov.
6. Matematika. Zbierka testov USE 2001 - 2010.
7. Matematika. Príprava na jednotnú štátnu skúšku-2010. Tréningové testy.
8. Vreckový sprievodca matematikou.

Obsah
Od autorov 11
§ 1. Identitné transformácie logaritmických výrazov 13
Možnosť číslo 113
Možnosť číslo 2 13
Možnosť číslo 3 14
Možnosť číslo 4 14
Možnosť číslo 5 15
Možnosť číslo 6 15
Možnosť číslo 7 16
Možnosť číslo 8 16
Možnosť číslo 9 17
Možnosť číslo 10 17
§ 2. Identitné premeny výrazov obsahujúcich 18. stupeň
Možnosť číslo 118
Možnosť číslo 2 19
Možnosť číslo 3 19
Možnosť číslo 4 20
Možnosť číslo 5 21
Možnosť číslo 6 21
Možnosť číslo 7 22
Možnosť číslo 8 23
Možnosť číslo 9 23
Možnosť číslo 10 24
§ 3. Identitné premeny iracionálnych výrazov 25
Možnosť číslo 1 25
Možnosť číslo 2 25
Možnosť číslo 3 26
Možnosť číslo 4 26
Možnosť číslo 5 27
Možnosť číslo 6 28
Možnosť číslo 7 28
Možnosť číslo 8 29
Možnosť číslo 9 30
Možnosť číslo 10 30
§ 4. Sústavy rovníc 31
Možnosť číslo 1 31
Možnosť číslo 2 32
Možnosť číslo 3 33
Možnosť číslo 4 33
Možnosť číslo 5 34
Možnosť číslo 6 35
Možnosť číslo 7 36
Možnosť číslo 8 37
Možnosť číslo 9 38
Možnosť číslo 10 39
§ 5. geometrický zmysel derivát 39
Možnosť číslo 1 39
Možnosť číslo 2 41
Možnosť číslo 3 43
Možnosť číslo 4 44
Možnosť číslo 5 46
Možnosť číslo 6 48
Možnosť číslo 7 50
Možnosť číslo 8 52
Možnosť číslo 9 54
Možnosť číslo 10 55
§ 6. Nerovnosti 56
Možnosť číslo 1 g 56
Možnosť číslo 2 57
Možnosť číslo 3 58
Možnosť číslo 4 58
Možnosť číslo 5 59
Možnosť číslo 6 60
Možnosť číslo 7 60
Možnosť číslo 8 61
Možnosť číslo 9 62
Možnosť číslo 10 63
§ 7. Iracionálne rovnice 63
Možnosť číslo 1 63
Možnosť číslo 2 64
Možnosť číslo 3 65
Možnosť číslo 4 65
Možnosť číslo 5 66
Možnosť číslo 6 66
Možnosť číslo 7 67
Možnosť číslo 8 67
Možnosť číslo 9 68
Možnosť č. Yu 68
§ 8. Goniometrické rovnice 69
Možnosť číslo 1 69
Možnosť číslo 2 69
Možnosť číslo 3 70
Možnosť číslo 4 70
Možnosť číslo 5 71
Možnosť číslo 6 72
Možnosť číslo 7 72
Možnosť číslo 8 73
Možnosť číslo 9 74
Možnosť číslo 10 74
§ 9. Logaritmické rovnice 75
Možnosť číslo 1 75
Možnosť číslo 2 75
Možnosť číslo 3 76
Možnosť číslo 4 76
Možnosť číslo 5 77
Možnosť číslo 6 77
Možnosť číslo 7 78
Možnosť č. 8 * 78
Možnosť číslo 9 79
Možnosť číslo 10 79
§ 10. Exponenciálne rovnice 80
Možnosť číslo 180
Možnosť číslo 2 80
Možnosť číslo 3 81
Možnosť číslo 4 81
Možnosť číslo 5 82
Možnosť číslo 6 82
Možnosť číslo 7 83
Možnosť číslo 8 83
Možnosť číslo 9 84
Možnosť číslo 10 84
§jedenásť. Periodicita, párne a nepárne funkcie 85
Možnosť číslo 1 85
Možnosť číslo 2 86
Možnosť číslo 3 87
Možnosť číslo 4 89
Možnosť číslo 5 90
Možnosť číslo 6 91
Možnosť číslo 7 92
Možnosť číslo 8 93
Možnosť číslo 9 94
Možnosť číslo 10 95
§ 12. Nuly komplexnej funkcie. Obmedzená funkcia 97
Možnosť číslo 1 97
Možnosť číslo 2 97
Možnosť číslo 3 98
Možnosť číslo 4 98
Možnosť číslo 5 99
Možnosť číslo 6 99
Možnosť číslo 7 100
Možnosť číslo 8 100
Možnosť číslo 9 101
Možnosť číslo 10 101
§ 13. Definičná oblasť, množina hodnôt, monotónnosť funkcií 102
Možnosť číslo 1 102
Možnosť číslo 2 102
Možnosť číslo 3 103
Možnosť číslo 4 103
Možnosť číslo 5 104
Možnosť číslo 6 104
Možnosť číslo 7 105
Možnosť číslo 8 105
Možnosť číslo 9 106
Možnosť číslo 10 107
§ 14. Extrémy funkcie. Najväčšie a najmenšie hodnoty funkcie 107
Možnosť číslo 1 107
Možnosť číslo 2 108
Možnosť číslo 3 108
Možnosť číslo 4 109
Možnosť číslo 5 109
Možnosť číslo 6 110
Možnosť číslo 7 110
Možnosť číslo 8 111
Možnosť číslo 9 111
Možnosť číslo 10 112
§ 15. Rôzne techniky riešenia logaritmických rovníc 113
Možnosť číslo 1 113
Možnosť číslo 2 113
Možnosť číslo 3 114
Možnosť číslo 4 114
Možnosť číslo 5 115
Možnosť číslo 6 115
Možnosť číslo 7 116
Možnosť číslo 8 116
Možnosť číslo 9 117
Možnosť číslo 10 117
§ 16. Rôzne techniky riešenia goniometrických rovníc 118
Možnosť číslo 1 118
Možnosť číslo 2 118
Možnosť číslo 3 118
Možnosť číslo 4 119
Možnosť číslo 5 119
Možnosť číslo 6 120
Možnosť číslo 7 120
Možnosť číslo 8 121
Možnosť číslo 9 121
Možnosť číslo 10 122
§ 17. Rôzne techniky riešenia iracionálnych rovníc 123
Možnosť číslo 1 123
Možnosť číslo 2 123
Možnosť číslo 3 124
Možnosť číslo 4 124
Možnosť číslo 5 125
Možnosť číslo 6 125
Možnosť číslo 7 125
Možnosť číslo 8 126
Možnosť číslo 9 126
Možnosť č. 10 127
§ 18. Rovnice obsahujúce premennú pod znamienkom modulo 127
Možnosť číslo 1 127
Možnosť číslo 2 128
Možnosť číslo 3 128
Možnosť číslo 4 129
Možnosť číslo 5 129
Možnosť číslo 6 130
Možnosť číslo 7 130
Možnosť číslo 8 131
Možnosť číslo 9 131
Možnosť číslo 10 131
§ 19. Rôzne spôsoby riešenia exponenciálne rovnice.132
Možnosť číslo 1 132
Možnosť číslo 2 133
Možnosť číslo 3 133
Možnosť číslo 4 134
Možnosť číslo 5 134
Možnosť číslo 6 135
Možnosť číslo 7 135
Možnosť číslo 8 135
Možnosť číslo 9 136
Možnosť číslo 10 136
§ 20. Rôzne techniky riešenia kombinovaných rovníc 137
Možnosť číslo 1 137
Možnosť číslo 2 137
Možnosť číslo 3 138
Možnosť číslo 4 138
Možnosť číslo 5 139
Možnosť číslo 6 139
Možnosť číslo 7 140
Možnosť číslo 8 140
Možnosť číslo 9 141
Možnosť číslo 10 141
§ 21. Rovnice s parametrom obsahujúcim modul 142
Možnosť číslo 1 142
Možnosť číslo 2 142
Možnosť číslo 3 143
Možnosť číslo 4 144
Možnosť číslo 5 144
Možnosť číslo 6 145
Možnosť číslo 7 146
Možnosť číslo 8 146
Možnosť číslo 9 147
Možnosť číslo 10 148
Odpovede 149
§ 1. Identitné transformácie logaritmických výrazov 149
§ 2. Identitné premeny výrazov obsahujúcich stupeň 150
§ 3. Identitné premeny iracionálnych výrazov 150
§ 4. Sústavy rovníc 151
§ 5. Geometrický význam derivátu 151
§ 6. Nerovnosti 152
§ 7. Iracionálne rovnice 152
§ 8. Goniometrické rovnice 153
§ 9. Logaritmické rovnice 153
§ 10. Exponenciálne rovnice 154
§jedenásť. Periodicita, párne a nepárne funkcie 154
§ 12. Nuly komplexnej funkcie. Obmedzená funkcia 155
§ 13. Definičná oblasť, množina hodnôt, monotónnosť funkcií 156
§ 14. Extrémy funkcie. Najväčšie a najmenšie hodnoty funkcie 158
§ pätnásť. Rôzne triky pri riešení logaritmických rovníc 159
§ 16. Rôzne techniky riešenia goniometrických rovníc 160
§ 17. Rôzne triky na riešenie iracionálnych rovníc 164
§ 18. Rovnice obsahujúce premennú pod znamienkom modulo 165
§ 19. Rôzne techniky riešenia exponenciálnych rovníc.166
§ 20. Rôzne techniky riešenia kombinovaných rovníc 167
§ 21. Rovnice s parametrom obsahujúcim modul 169
Literatúra 170

EGOROVÁ VICTORIA VALEREVNA

Učiteľ matematiky

najvyššej kvalifikačnej kategórii

TÉMA: „TRANSFORMÁCIA IDENTITY

LOGARITMICKÉ VÝRAZY"

Vedomosti a zručnosti, ktoré by si študenti mali osvojiť po preštudovaní tejto lekcie:

poznať definíciu logaritmu čísla, základnú logaritmickú identitu, vlastnosti logaritmov;

vedieť vykonávať transformácie výrazov obsahujúcich logaritmy, počítať logaritmy.

Literatúra:

1. Alimov Sh.A., Kolyagin Yu.M., Sidorov Yu.V. a iné Algebra a začiatok analýzy: učebnica pre ročníky 10-11 vzdelávacie inštitúcie. - M .: Vzdelávanie, 2001.

2. Kochagin V.V., Kochagina M.V., Intenzívny kurz prípravy na skúšku. – M.: Eksmo, 2009.

3. A. G. Merzlyak, V. B. Polonsky a M. S. Yakir, Algebraický simulátor: Sprievodca pre školákov a študentov vysokých škôl. – M.: Ileksa, 2005.

4. Gusev V.A., Mordkovich A.G. Matematika: Referenčné materiály: Kniha pre študentov. - M .: Vzdelávanie, 2001.

Plán lekcie:

Počas tried:

1) Logaritmus je Grécke slovo, ktorý pozostáva z 2 slov: „logos“ - vzťah, „aritmos“ - číslo. Takže logaritmus je číslo, ktoré meria pomer. V publikácii z roku 1614 sa uvádza, že Napier vynašiel logaritmy. Neskôr zostavil logaritmické tabuľky, ktoré sú nám dnes známe ako Bradysove tabuľky. Za menej ako storočie sa tabuľky rozšírili do celého sveta a stali sa nepostrádateľným výpočtovým nástrojom. V budúcnosti boli akoby zabudované do pohodlného zariadenia, ktoré mimoriadne urýchľuje proces výpočtu - logaritmického pravítka, ktoré sa používalo až do sedemdesiatych rokov dvadsiateho storočia.

Príloha 1.

2) logaritmus kladné číslob podľa rozumu a, navyše väčšie ako nula a nie rovné jednej,je exponent, na ktorý sa musí číslo zvýšiťa získať číslob.

Táto rovnosť vyjadrujúca definíciu logaritmu sa nazývazákladná logaritmická identita .

C

ALEBO 1

P

Základom stupňa a základom logaritmu je sedemnásť, čo znamená, že podľa základnej logaritmickej identity je hodnota výrazu tri.

Budeme pracovať verbálne:

SCH
ELCHOK

O dolná sekunda je nula päť desatín, takže výraz sa rovná aritmetickej druhej odmocnine z piatich.

P

dodatok 2.

Rovnosť znamená to

Z definície logaritmu sa získajú tieto dôležité rovnosti:

Napríklad:

P
dodatok 3.

Prejdime k USE priradenia:

Dodatok 4

3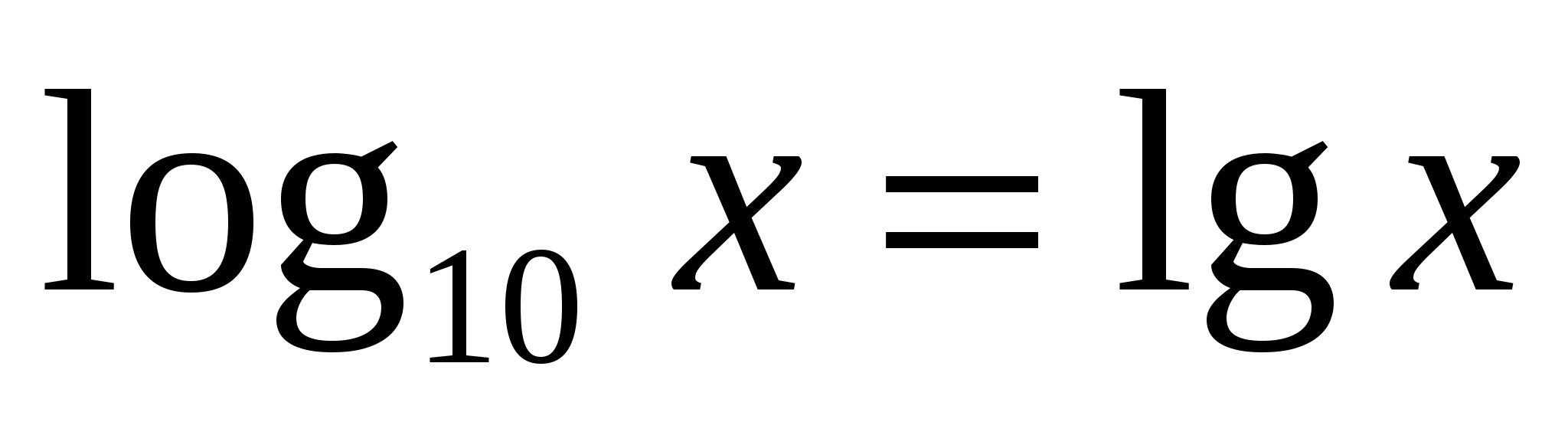
) Logaritmus základnej desiatky má špeciálny zápis a názov.desiatkový logaritmus .

L
aritme k základnie volalprirodzený logaritmus .

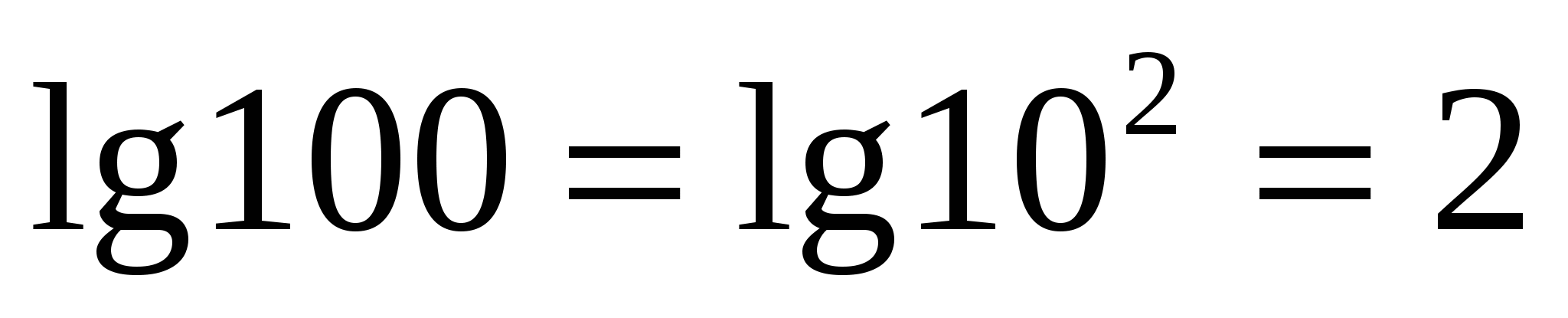
H
napríklad,

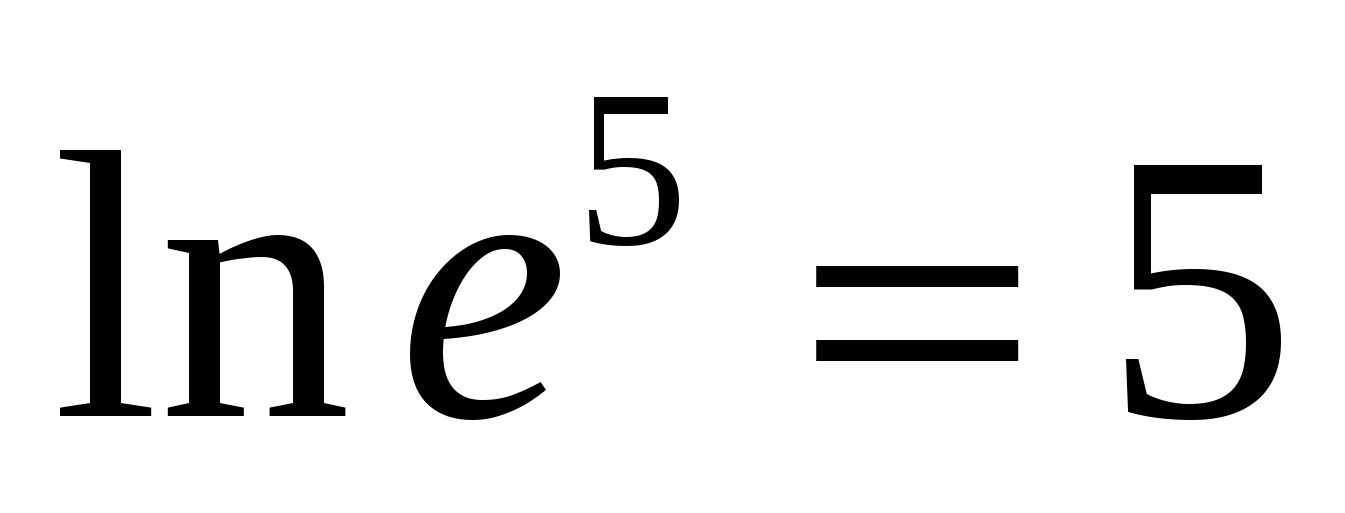
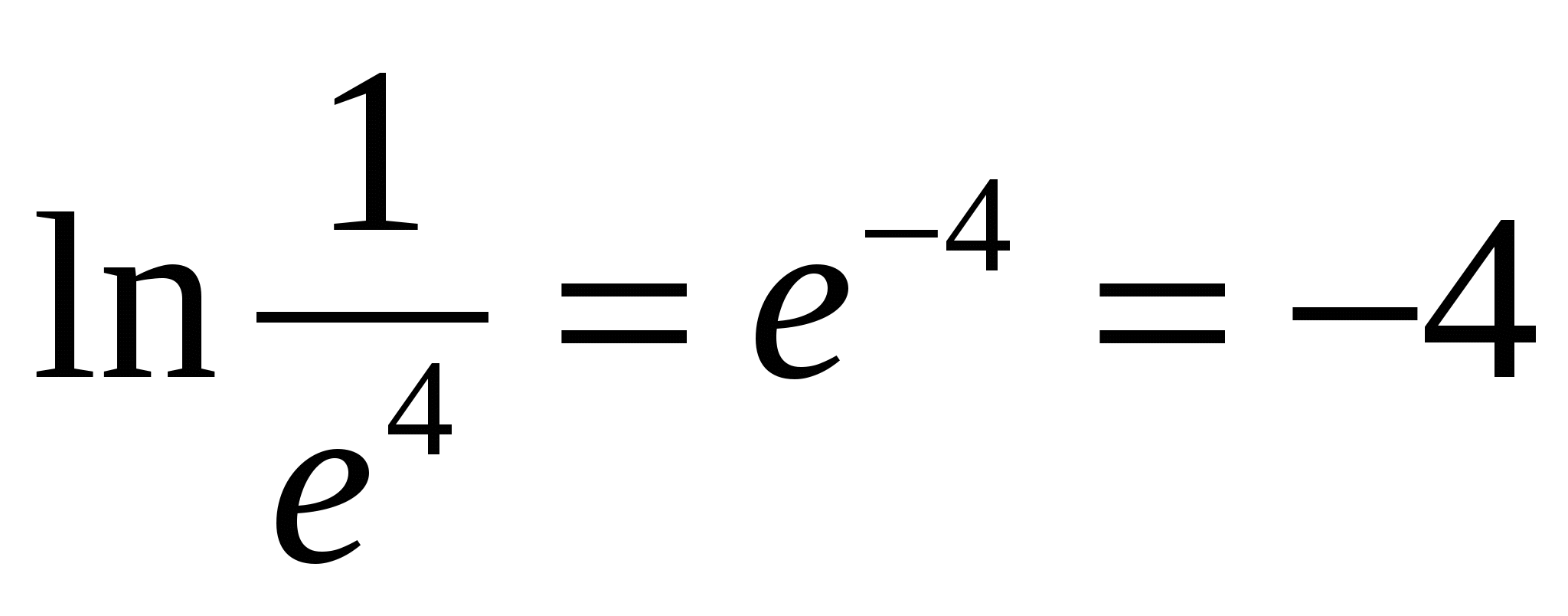
4) Z definície logaritmu vyplývajú nasledujúce vlastnosti. Všetky vlastnosti sú formulované a preukázané len pre kladné hodnoty premenných obsiahnutých pod logaritmickými znakmi.

Základný logaritmus súčinu dvoch kladných čísel a sa rovná súčtu logaritmy týchto čísel s rovnakým základom.

DER 2

Napríklad,

W
zadanie 1.

Úloha 2. Zjednodušte výraz

AT
Využime predchádzajúci príklad. Poďme vymeniť

Všimnite si, že logaritmus je na druhú, takže súčet musí byť tiež na druhú. Pomocou vzorca pre druhú mocninu súčtu otvorte zátvorky. Uvádzame podobné pojmy.

5) Logaritmus podielu sa rovná rozdielu medzi logaritmami dividendy a deliteľa.

C

Dávajte pozor na základňu stupňa a základňu logaritmu - sú rovnaké.

ALEBO 3

R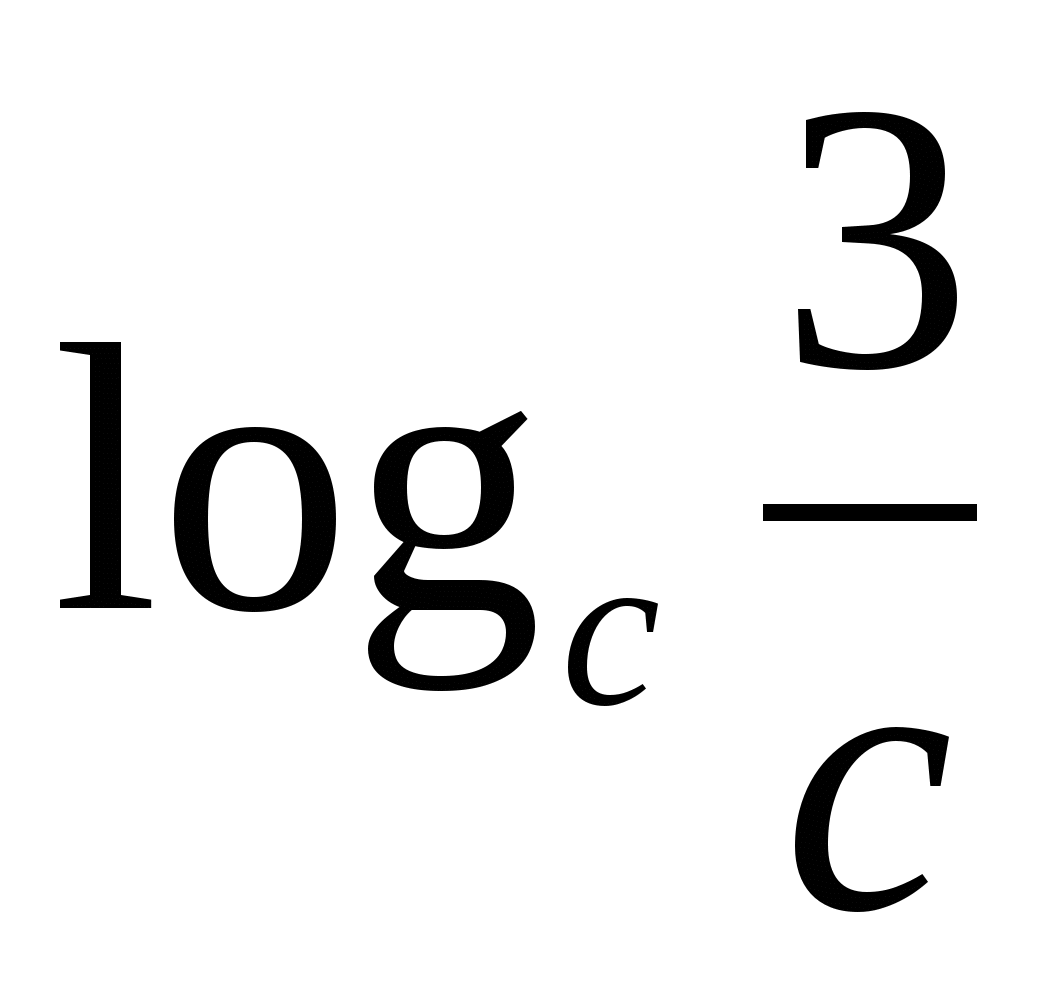

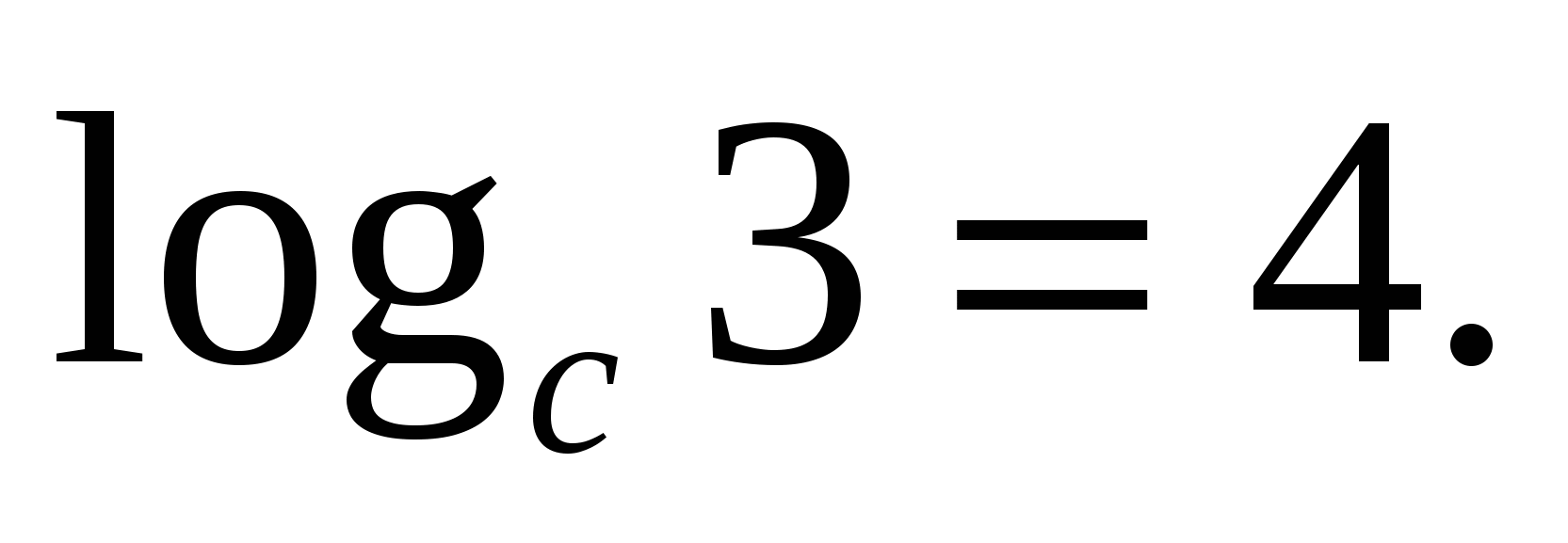Pozrime sa na použitie tohto vzorca s príkladom:

W
zadanie 1. Nájdite hodnotu výrazu if

Úloha 2. Nájdite hodnotu b podľa jeho logaritmu

6) Logaritmus stupňa k základnia , sa rovná produktu exponent na logaritmus v rovnakom základe.

DER 4

Napríklad,

W
zadanie 1. Vypočítajte, ak

Zjednodušme výraz

Vzorec

volal vzorec na prechod na nový základ.

W

zadanie 1. Vyjadrite pomocou logaritmu so základom 2.

Úloha 2. Vypočítajte

CER 5

CER 6

Napríklad,

W

zadanie 1. Vypočítajte

W
zadanie 2. Vypočítajte

9) Logaritmické transformácie môžete spustiť iba vtedy, ak ak si pamätáte všetky vlastnosti logaritmov. Po ich zopakovaní zvážime úlohy na transformáciu logaritmických výrazov z druhej strany.

Na prevod súčtu alebo rozdielu logaritmických výrazov niekedy stačí použiť definíciu logaritmu a najčastejšie vlastnosti logaritmu súčinu alebo kvocientu.

W
zadanie 1. Vypočítajte

Poďme to vyriešiť dvoma spôsobmi.

1 spôsobom pomocou definície logaritmu:

Metóda 2 založená na vlastnosť kvocientového logaritmu:

Úloha 2. Nájdite hodnotu výrazu

Najprv aplikujme vzorec logaritmus súčinu, potom definícia logaritmu.

Základná logaritmická identita sa používa pri konverzii výrazov obsahujúcich logaritmus v exponente. Myšlienkou takýchto operácií je dosiahnuť rovnakú základňu exponentu a základu logaritmu.

Niekedy je potrebné výraz transformovať podľa vlastností logaritmu a podľa vlastností stupňa pomocou prechodového vzorca možno ľahko prejsť z jednej základne na druhú. V ostatných prípadoch by sa mali použiť viaceré vlastnosti.

W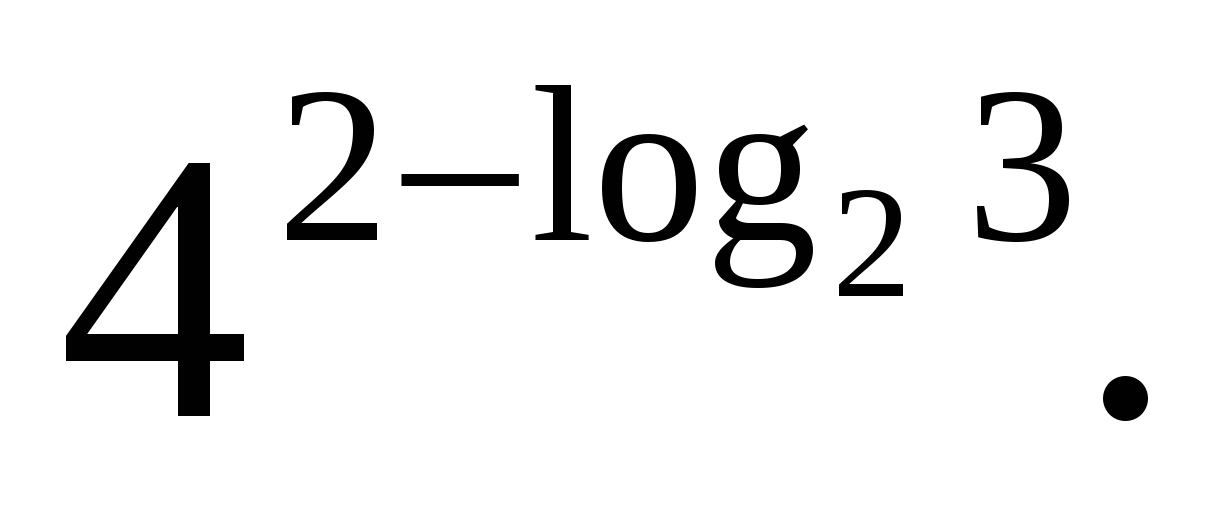
zadanie 3. Vypočítajte

W
zadanie 4. Nájdite hodnotu výrazu

Úloha 5. Nájdite hodnotu výrazu

W
zadanie 6. Vyjadrite ako rozdiel logaritmov

H
Najväčším problémom je transformácia logaritmických výrazov pod radikál. V procese transformácií je potrebné zvážiť moduly logaritmických výrazov, na odhalenie ktorých je potrebné porovnávať iracionálne čísla alebo racionálne a iracionálne čísla. Budeme konať dôsledne. Zvážte výraz pod vnútorným radikálom.

Nahradiť v pôvodnom výraze.

Treba poznamenať, že s transformáciou logaritmických výrazov sa môžeme stretnúť aj pri riešení rovníc a nerovníc alebo pri štúdiu funkcií, preto môžu byť v implicitnej forme prítomné aj v zadaniach skupín B a C.

10) Zhrnutie. Otázky:

Volá sa základný 10 logaritmus

základný logaritmus

hlavný logaritmus

prirodzený logaritmus

desiatkový logaritmus

2) Aké hodnoty môžuX vo výraze

Hodnota nie je definovaná

5) Uveďte pomer, ktorý platí pre všetkýchX ≠ 0 .

6) Zadajte správny pomer pre vzorec pre prechod na nový základ.

7) Označte správnu rovnosť pre

11) Kontrolné testovanie.

Podnesterská Štátna univerzita

ich. T.G. Ševčenko

Fakulta fyziky a matematiky

Katedra matematickej analýzy

a metódy vyučovania matematiky

KURZOVÁ PRÁCA

„Transformácie identity

exponenciálne a logaritmické

výrazy"

Práca dokončená:

študent skupiny ______

Fakulta fyziky a matematiky

_________________________

Skontrolovaná práca:

_________________________

Tiraspol, 2003

Úvod ……………………………………………………………………… 2

Kapitola 1

§jedna. Formovanie zručností pre aplikáciu špecifických typov transformácií………………………………………………………………………………………..4

§2. Vlastnosti organizácie znalostného systému pri štúdiu identických transformácií.…….………………………….………..………….5

§3. Matematický program ………………………………………….11

Kapitola 2

§jedna. Zovšeobecnenie pojmu titul………………………………………………..13

§2. Exponenciálna funkcia………………………………………………..15

§3. Logaritmická funkcia……………………………………………….16

Kapitola 3. Identické transformácie exponenciálnych a logaritmických výrazov v praxi ...................................... ...................................... 19

Záver………………………………………………………………………..24

Zoznam použitej literatúry……………………………………….25
Úvod

Táto práca sa bude zaoberať identickými transformáciami exponenciálnych a logaritmických funkcií, zváži metodológiu ich vyučovania v školskom kurze algebry a začiatok analýzy.

Prvá kapitola práce popisuje metodiku výučby identických transformácií v školskom kurze matematiky, obsahuje aj program z matematiky v kurze "Algebra a začiatky analýzy" so štúdiom exponenciálnych a logaritmických funkcií.

Druhá kapitola sa priamo zaoberá samotnými exponenciálnymi a logaritmickými funkciami, ich hlavnými vlastnosťami používanými pri identických transformáciách.

Treťou kapitolou je riešenie príkladov a úloh pomocou identických transformácií exponenciálnej a logaritmickej funkcie.

Štúdium rôznych premien výrazov a vzorcov zaberá značnú časť študijného času v rámci školskej matematiky. Najjednoduchšie transformácie založené na vlastnostiach aritmetických operácií sa už vykonávajú v Základná škola a v ročníkoch IV-V. Ale hlavnú záťaž na formovanie zručností a schopností vykonávať transformácie nesie kurz školskej algebry. Súvisí to jednak s prudkým nárastom počtu a rôznorodosti vykonaných transformácií, ako aj s komplikovaním činností na ich zdôvodnenie a objasnenie podmienok použiteľnosti, s identifikáciou a štúdiom zovšeobecnených pojmov identity, identickej transformácie, ekvivalentnej transformácie, stotožnenia sa s pojmami identity, identickej transformácie, ekvivalentnej transformácie. logický dôsledok.

Kultúra vykonávania identických transformácií sa vyvíja rovnakým spôsobom ako kultúra výpočtovej techniky, založená na solídnej znalosti vlastností operácií s objektmi (čísla, vektory, polynómy atď.) a algoritmov na ich implementáciu. Prejavuje sa nielen v schopnosti správne zdôvodniť transformácie, ale aj v schopnosti nájsť najkratšiu cestu k prechodu od pôvodného analytického výrazu k výrazu, ktorý najlepšie vyhovuje účelu transformácie, v schopnosti sledovať zmeny v oblasť definície analytických výrazov v reťazci identických transformácií, v rýchlosti a bezchybnom vykonávaní transformácií.

Dôležitým problémom pri vyučovaní matematiky je zabezpečenie vysokej kultúry výpočtov a identických transformácií. Tento problém však ešte zďaleka nie je vyriešený uspokojivo. Dôkazom toho sú štatistické údaje orgánov verejného školstva, v ktorých sa každoročne uvádzajú chyby a iracionálne spôsoby výpočtov a transformácií študentov. rôzne triedy pri robení kontrolné práce. Potvrdzujú to názory vyš vzdelávacie inštitúcie o kvalite matematických vedomostí a zručností uchádzačov. Nedá sa len súhlasiť so závermi orgánov verejného školstva a vysokých škôl, že to nestačí vysoký stupeň kultúra výpočtovej techniky a identické transformácie v stredná škola je dôsledkom formalizmu v poznaní žiakov, oddelenosti teórie od praxe.

Premeny identity a vyučovacie metódy

v školskom kurze algebry a začiatku analýzy.

§jedna. Formovanie aplikačných zručností

špecifické typy transformácií.

Systém metód a pravidiel na vykonávanie transformácií, ktorý sa používa vo fáze začiatkov algebry, má veľmi široký rozsah aplikácií: používa sa pri štúdiu celého kurzu matematiky. Tento systém však práve pre svoju nízku špecifickosť potrebuje dodatočné transformácie, ktoré zohľadňujú zvláštnosti štruktúry transformovaných výrazov a vlastnosti novozavedených operácií a funkcií. Vývoj zodpovedajúcich typov transformácií začína zavedením skrátených vzorcov násobenia. Potom uvažujeme o transformáciách spojených s operáciou umocňovania s rôznymi triedami elementárne funkcie- exponenciálny, mocninný, logaritmický, trigonometrický. Každý z týchto typov premien prechádza štádiom štúdia, v ktorom sa pozornosť sústreďuje na asimiláciu ich charakteristických čŕt.

S akumuláciou materiálu je možné vyčleniť spoločné črty všetkých uvažovaných transformácií a na tomto základe zaviesť koncepty identických a ekvivalentných transformácií.

Treba poznamenať, že pojem identickej transformácie sa v školskom kurze algebry podáva nie úplne všeobecne, ale iba v aplikácii na výrazy. Transformácie sú rozdelené do dvoch tried: identické transformácie sú transformácie výrazov a ekvivalentné transformácie sú transformácie vzorcov. V prípade, že je potrebné zjednodušiť jednu časť vzorca, je v tomto vzorci zvýraznený výraz, ktorý slúži ako argument pre použitú identickú transformáciu. Zodpovedajúci predikát sa považuje za nezmenený.

Pokiaľ ide o organizáciu integrálneho systému transformácií (syntézy), jeho hlavným cieľom je vytvoriť flexibilný a výkonný; prístroj vhodný na použitie pri riešení rôznych vzdelávacích úloh.

V priebehu algebry a na začiatku analýzy sa integrálny systém transformácií, už vytvorený vo svojich hlavných črtách, postupne zdokonaľuje. Pridávajú sa k nemu aj niektoré nové typy transformácií, ktoré ho však len obohacujú, rozširujú jeho možnosti, no nemenia jeho štruktúru. Metodológia štúdia týchto nových transformácií sa prakticky nelíši od tej, ktorá sa používa v kurze algebry.

§2. Vlastnosti organizácie systému úloh

pri štúdiu identických premien.

Základným princípom organizovania akéhokoľvek systému úloh je prezentovať ich od jednoduchých po zložité, berúc do úvahy potrebu študentov prekonať možné ťažkosti a vytvoriť problémové situácie. Uvedený základný princíp si vyžaduje konkretizáciu vo vzťahu k znakom tohto vzdelávacieho materiálu. Na popis rôznych systémov úloh v metodike matematiky sa používa koncept cyklu cvičení. Cyklus cvičení je charakterizovaný kombináciou v postupnosti cvičení niekoľkých aspektov štúdia a metód usporiadania materiálu. Vo vzťahu k identickým transformáciám môže byť myšlienka cyklu uvedená nasledovne.

Cyklus cvičení je spojený so štúdiom jednej identity, okolo ktorej sa zoskupujú ďalšie identity, ktoré sú s ňou v prirodzenom spojení. Zloženie cyklu spolu s výkonnými úlohami zahŕňa úlohy, ktoré si vyžadujú uznanie použiteľnosti uvažovanej identity. Študovaná identita sa používa na vykonávanie výpočtov v rôznych numerických doménach. Zohľadňuje sa špecifickosť identity; organizujú sa najmä obraty reči s tým spojené.

Úlohy v každom cykle sú rozdelené do dvoch skupín. Prvá zahŕňa úlohy vykonávané počas prvotného oboznámenia sa s identitou. Slúžia vzdelávací materiál na niekoľko po sebe nasledujúcich vyučovacích hodín, spojených jednou témou. Druhá skupina cvičení spája skúmanú identitu s rôznymi aplikáciami. Táto skupina netvorí kompozičnú jednotu – cvičenia sú tu roztrúsené na rôzne témy.

Opísaná štruktúra cyklu sa týka štádia formovania zručností pre aplikáciu konkrétnych typov transformácií. V konečnom štádiu – štádiu syntézy, sa cykly upravia. Najprv sa obe skupiny úloh spoja, čím sa vytvorí „rozložený“ cyklus a z prvej skupiny sa vylúčia tie najjednoduchšie, čo sa týka znenia či zložitosti úlohy. Zvyšné typy úloh sa stávajú zložitejšími. Po druhé, dochádza k zlučovaniu cyklov súvisiacich s rôznymi identitami, vďaka čomu sa zvyšuje úloha akcií na rozpoznanie použiteľnosti tej či onej identity.

Všímame si vlastnosti cyklov úloh súvisiacich s identitami pre elementárne funkcie. Tieto vlastnosti sú spôsobené skutočnosťou, že po prvé, zodpovedajúce identity sa skúmajú v súvislosti so štúdiom funkčného materiálu a po druhé, objavujú sa neskôr ako identity prvej skupiny a študujú sa pomocou už vytvorených zručností na vykonávanie identických transformácií. .

Každá novozavedená elementárna funkcia výrazne rozširuje rozsah čísel, ktoré je možné jednotlivo označiť a pomenovať. Preto by prvá skupina úloh cyklov mala obsahovať úlohy na vytvorenie spojenia medzi týmito novými číselnými oblasťami a pôvodnou oblasťou racionálnych čísel. Uvádzame príklady takýchto úloh.

Príklad 1 Vypočítajte:

Vedľa každého výrazu je identita v cykloch, pre ktoré môžu byť prítomné navrhované úlohy. Účelom takýchto úloh je osvojiť si vlastnosti záznamov vrátane symbolov nových operácií a funkcií a rozvíjať matematické rečové schopnosti.

Významná časť využitia transformácií identity spojených s elementárnymi funkciami pripadá na riešenie iracionálnych a transcendentálnych rovníc. Cykly súvisiace s asimiláciou identít zahŕňajú iba najjednoduchšie rovnice, ale už tu je vhodné vykonať prácu na zvládnutí metódy riešenia takýchto rovníc: jej redukciu nahradením neznámej rovnicou algebraickou.

Postupnosť krokov pre toto riešenie je nasledovná:

a) nájdite funkciu, pre ktorú môže byť táto rovnica reprezentovaná ako ;

b) urobte substitúciu a vyriešte rovnicu;

c) vyriešiť každú z rovníc , kde je množina koreňov rovnice .

Pri použití opísanej metódy sa krok b) často vykonáva implicitne bez zavedenia zápisu pre . Okrem toho si študenti často vyberajú z rôznych ciest vedúcich k nájdeniu odpovede, aby si vybrali tú, ktorá vedie k algebraickej rovnici rýchlejšie a jednoduchšie.

Príklad 2. Vyriešte rovnicu.

Prvý spôsob:

Druhý spôsob:

a)

b)

Tu je vidieť, že krok a) je pri prvom spôsobe náročnejší ako pri druhom. Prvý spôsob je „ťažší na začiatok“, aj keď ďalší priebeh riešenia je oveľa jednoduchší. Na druhej strane má druhý spôsob výhody, spočívajúce vo väčšej jednoduchosti, väčšej prepracovanosti pri výučbe redukcie na algebraickú rovnicu.

Pre školský kurz algebry sú typické úlohy, v ktorých je prechod na algebraickú rovnicu ešte jednoduchší ako v tomto príklade. Hlavná záťaž takýchto úloh súvisí s výberom kroku c) ako samostatnej súčasti procesu riešenia spojeného s využitím vlastností skúmanej elementárnej funkcie.

Príklad 3. Vyriešte rovnicu:

a) ; b) .

Tieto rovnice sú redukované na rovnice: a) alebo ; b) alebo. Na vyriešenie týchto rovníc je potrebná znalosť len tých najjednoduchších faktov o exponenciálnej funkcii: jej monotónnosti, rozsahu hodnôt. Rovnako ako predchádzajúci príklad, rovnice a) a b) možno priradiť k prvej skupine cyklu cvičení na riešenie kvadratických exponenciálnych rovníc.

Dostávame sa teda ku klasifikácii úloh v cykloch súvisiacich s riešením transcendentálnych rovníc vrátane exponenciálnej funkcie:

1) rovnice, ktoré sú redukované na rovnice tvaru a majú jednoduchú odpoveď, všeobecnú vo forme: ;

2) rovnice, ktoré sa redukujú na rovnice , kde je celé číslo alebo , kde ;

3) rovnice, ktoré sa redukujú na rovnice a vyžadujú explicitnú analýzu formy, v ktorej je číslo zapísané.

Podobné úlohy možno klasifikovať aj pre iné elementárne funkcie.

Značná časť identít naštudovaných v kurzoch algebry a algebry a začiatkov analýzy je v nich dokázaná alebo aspoň vysvetlená. Táto stránka štúdia identít má veľký význam pre oba kurzy, keďže demonštračné uvažovanie v nich prebieha s najväčšou jasnosťou a prísnosťou práve vo vzťahu k identitám. Okrem tohto materiálu sú dôkazy zvyčajne menej úplné, nie sú vždy odlíšené od zloženia použitých prostriedkov na odôvodnenie.

Vlastnosti aritmetických operácií sa používajú ako podpora, na ktorej sú postavené dôkazy totožnosti.

Vzdelávací vplyv výpočtov a identických transformácií možno smerovať do rozvoja logické myslenie, ak sa len od študentov systematicky vyžaduje zdôvodňovanie výpočtov a identických transformácií, rozvíjanie funkčného myslenia, čo sa dosahuje rôznymi spôsobmi. Dôležitosť výpočtov a rovnakých transformácií pri rozvoji vôle, pamäti, vynaliezavosti, sebaovládania a tvorivej iniciatívy je celkom zrejmá.

Požiadavky každodennej, priemyselnej výpočtovej praxe vyžadujú formovanie silných, automatizovaných zručností racionálnych výpočtov a rovnakých transformácií u študentov. Tieto zručnosti sa rozvíjajú v procese akejkoľvek výpočtovej práce, sú však potrebné špeciálne zručnosti. tréningové cvičenia v rýchlych výpočtoch a transformáciách.

Ak teda lekcia zahŕňa riešenie logaritmických rovníc pomocou základnej logaritmickej identity, potom je užitočné zahrnúť do plánu lekcie ústne cvičenia na zjednodušenie alebo výpočet hodnôt výrazov: , , . Účel cvičení je vždy študentom oznámený. Počas cvičenia môže byť potrebné vyžadovať od študentov, aby zdôvodnili jednotlivé transformácie, akcie alebo vyriešili celý problém, aj keď to nebolo plánované. Tam, kde sú možné rôzne spôsoby riešenia problému, je vždy žiaduce položiť si otázky: „Akým spôsobom bol problém vyriešený?“, „Kto vyriešil problém iným spôsobom?“

Pojmy identity a identickej transformácie sú explicitne zavedené v kurze algebry triedy VI. Samotnú definíciu identických výrazov nemožno prakticky použiť na preukázanie totožnosti dvoch výrazov a na pochopenie toho, že podstata identických transformácií spočíva v tom, že sa na výraz aplikujú definície a vlastnosti tých akcií, ktoré sú vo výraze naznačené, alebo sa pridajú k nemu výraz, ktorý sa zhodne rovná 0, alebo pri jeho vynásobení výrazom zhodne rovný jednej. Ale aj po zvládnutí týchto ustanovení študenti často nechápu, prečo nám tieto transformácie umožňujú tvrdiť, že pôvodné a výsledné výrazy sú totožné, t. mať rovnaké hodnoty pre všetky systémy (množiny) premenných hodnôt.

Je tiež dôležité zabezpečiť, aby študenti dobre pochopili, že takéto závery identických transformácií sú dôsledkom definícií a vlastností zodpovedajúcich akcií.

V 6. ročníku sa rozširuje aparát identických premien, nahromadený v minulých rokoch. Toto rozšírenie začína zavedením identity vyjadrujúcej vlastnosť súčinu mocnín s rovnakými základmi: , kde , sú celé čísla.

§3. Matematický program. V školskom kurze "Algebra a začiatky analýzy" študenti systematicky študujú exponenciálne a logaritmické funkcie a ich vlastnosti, identické transformácie logaritmických a exponenciálnych výrazov a ich aplikáciu na riešenie príslušných rovníc a nerovníc, oboznamujú sa so základnými pojmami, tvrdeniami. . V 11. ročníku hodiny algebry trvajú 3 hodiny týždenne, spolu 102 hodín ročne. Štúdium exponenciálnych, logaritmických a mocninových funkcií podľa programu trvá 36 hodín. Program zahŕňa úvahy a štúdium nasledujúcich problémov: Koncepcia titulu s racionálnym ukazovateľom. Riešenie iracionálnych rovníc. Exponenciálna funkcia, jej vlastnosti a graf. identické transformácie exponenciálnych výrazov. Riešenie exponenciálnych rovníc a nerovníc. Logaritmus čísla. Základné vlastnosti logaritmov. Logaritmická funkcia, jej vlastnosti a graf. Riešenie logaritmických rovníc a nerovníc. Derivácia exponenciálnej funkcie. Číslo a prirodzený logaritmus. Derivácia mocninovej funkcie. Hlavným cieľom časti o štúdiu exponenciálnych a logaritmických funkcií je oboznámiť študentov s exponenciálnymi, logaritmickými a mocninnými funkciami; naučiť žiakov riešiť exponenciálne a logaritmické rovnice a nerovnosti. Pojmy odmocniny tého stupňa a stupeň s racionálnym exponentom sú zovšeobecnením pojmov odmocniny a stupňa s celočíselným exponentom. Študenti by mali venovať pozornosť skutočnosti, že vlastnosti koreňov a stupňov s racionálnym exponentom, ktoré sa tu uvažujú, sú podobné tým vlastnostiam, ktoré boli študované skôr. odmocniny a stupne s celočíselnými exponentmi. Je potrebné venovať dostatok času vypracovaniu vlastností stupňov a formovaniu zručností pre identické transformácie. Pojem titul s iracionálny ukazovateľ zavedené na vizuálno-intuitívnom základe. Tento materiál hrá pomocnú úlohu a používa sa pri zavádzaní exponenciálnej funkcie. Štúdium vlastností exponenciálnych, logaritmických a mocninových funkcií je postavené v súlade s prijatými všeobecná schéma funkčný výskum. V tomto prípade je uvedený prehľad vlastností v závislosti od hodnôt parametrov. Exponenciálne a logaritmické nerovnice sú riešené na základe študovaných vlastností funkcií. Charakteristickou črtou predmetu je systematizácia a zovšeobecňovanie vedomostí študentov, upevňovanie a rozvoj zručností a schopností získaných v kurze algebry, ktorý sa uskutočňuje tak pri štúdiu nového materiálu, ako aj pri vykonávaní zovšeobecňujúceho opakovania.
Kapitola 2

§jedna. Zovšeobecnenie pojmu titul.

Definícia: Koreňom tého stupňa čistého je také číslo, ktorého tý stupeň sa rovná.

Podľa tejto definície je koreň tého stupňa čísla riešením rovnice. Počet koreňov tejto rovnice závisí od a . Uvažujme o funkcii. Ako je známe, v intervale sa táto funkcia zvyšuje pre ľubovoľnú a preberá všetky hodnoty z intervalu. Podľa koreňovej vety má rovnica pre ľubovoľný nezáporný koreň a navyše iba jeden. Nazýva sa aritmetický koreň tého stupňa čísla a označuje sa; číslo sa nazýva index koreňa a samotné číslo sa nazýva radikálny výraz. Znak sa nazýva aj radikál.

Definícia: Aritmetický koreň tého stupňa čísla je nezáporné číslo, ktorého tý stupeň je .

Pre párne, funkcia je párna. Z toho vyplýva, že ak, tak rovnica má okrem koreňa aj koreň. Ak , potom existuje iba jeden koreň: ; ak , potom táto rovnica nemá korene, pretože párna mocnina ľubovoľného čísla je nezáporná.

Pre nepárne hodnoty sa funkcia zvyšuje pozdĺž celej číselnej osi; jeho rozsah je množina všetkých reálnych čísel. Aplikovaním koreňovej vety zistíme, že rovnica má jeden koreň pre ľubovoľné a najmä pre . Tento koreň pre akúkoľvek hodnotu je označený .

Pre korene nepárneho stupňa platí rovnosť. Skutočne, t.j. číslo je tý koreň z . Ale taký koreň pre nepárne je jedinečný. V dôsledku toho, .

Poznámka 1: Pre akékoľvek skutočné

Pripomeňme si známe vlastnosti aritmetických koreňov t. stupňa.

Pre všetky prirodzené čísla platia celé číslo a všetky nezáporné celé čísla a rovnosti:

1.

2.

3.

4.

Stupeň s racionálnym exponentom.

Výraz je definovaný pre všetky a okrem prípadu, keď . Pripomeňte si vlastnosti takýchto právomocí.

Pre všetky čísla a všetky celé čísla a rovnosti platia:

Poznamenávame tiež, že ak , potom pre a pre .. a

Pre študentov študujúcich na jednotnú štátnu skúšku učitelia matematiky na strednej škole č. 26 v Jakutsku používajú zoznam obsahových otázok (kodifikátor) školského kurzu matematiky, ktorých asimilácia sa kontroluje pri zložení jednotnej štátnej skúšky v roku 2007 . voliteľný kurz v príprave na Zjednotené Štátna skúška je založená na opakovaní, systematizácii a prehlbovaní skôr získaných vedomostí. Kurzy prebiehajú formou bezplatnej...

Uvedené rovnosti pri prevode výrazov s logaritmami sa používajú sprava doľava aj zľava doprava.

Stojí za zmienku, že nie je potrebné zapamätať si dôsledky vlastností: pri vykonávaní transformácií si vystačíte so základnými vlastnosťami logaritmov a inými faktami (napríklad pre b≥0), z ktorých vyplývajú nasledujú následky. "Vedľajším efektom" tohto prístupu je len to, že riešenie bude trochu dlhšie. Napríklad, aby sme sa zaobišli bez následku, ktorý je vyjadrený vzorcom a počnúc iba základnými vlastnosťami logaritmov budete musieť vykonať reťaz transformácií nasledujúceho tvaru: .

To isté možno povedať o poslednej vlastnosti z vyššie uvedeného zoznamu, ktorá zodpovedá vzorcu , keďže to vyplýva aj zo základných vlastností logaritmov. Hlavná vec je pochopiť, že je vždy možné, aby stupeň kladného čísla s logaritmom v exponente zamenil základ stupňa a číslo pod znamienkom logaritmu. Pre spravodlivosť treba poznamenať, že príklady implementácie transformácií tohto druhu sú v praxi zriedkavé. Nižšie uvedieme niekoľko príkladov.

Prevod číselných výrazov pomocou logaritmov

Zapamätali sme si vlastnosti logaritmov, teraz je čas naučiť sa, ako ich uviesť do praxe pri transformácii výrazov. Je prirodzené začať s transformáciou číselných výrazov a nie výrazov s premennými, pretože je pohodlnejšie a jednoduchšie naučiť sa na nich základy. Tak to urobíme a začneme veľmi jednoduché príklady aby sme sa naučili, ako zvoliť požadovanú vlastnosť logaritmu, ale príklady budeme postupne komplikovať až do momentu, kedy bude potrebné použiť niekoľko vlastností za sebou, aby sme získali konečný výsledok.

Výber požadovanej vlastnosti logaritmov

Vlastností logaritmov nie je až tak málo a je jasné, že si z nich musíte vedieť vybrať tú vhodnú, ktorá v tomto konkrétnom prípade povedie k želanému výsledku. Zvyčajne to nie je ťažké urobiť porovnaním formy prevádzaného logaritmu alebo výrazu s typmi ľavej a pravej časti vzorcov vyjadrujúcich vlastnosti logaritmov. Ak zostane resp pravá časť jeden zo vzorcov sa zhoduje s daným logaritmom alebo výrazom, potom by sa s najväčšou pravdepodobnosťou mala pri transformácii použiť práve táto vlastnosť. Nasledujúce príklady to jasne dokazujú.

Začnime príkladmi transformácie výrazov pomocou definície logaritmu, ktorý zodpovedá vzorcu a log a b =b , a>0 , a≠1 , b>0 .

Príklad.

Vypočítajte, ak je to možné: a) 5 log 5 4 , b) 10 log(1+2 π) , c) , d) 2 log2 (-7) , e) .

Riešenie.

V príklade písmeno a) jasne ukazuje štruktúru a log a b , kde a=5 , b=4 . Tieto čísla spĺňajú podmienky a>0 , a≠1 , b>0 , takže môžete pokojne použiť rovnosť a log a b =b . Máme 5 log 5 4=4 .

b) Tu a=10, b=1+2 π, sú splnené podmienky a>0, a≠1, b>0. V tomto prípade platí rovnosť 10 lg(1+2 π) =1+2 π.

c) A v tomto príklade máme do činenia so stupňom tvaru a log a b , kde a b=ln15 . Takže .

Napriek tomu, že patrí do rovnakého tvaru a log a b (tu a=2 , b=−7 ), výraz pod písmenom d) nemožno previesť vzorcom a log a b =b . Dôvodom je, že to nedáva zmysel, pretože obsahuje záporné číslo pod znamienkom logaritmu. Navyše, číslo b=−7 nespĺňa podmienku b>0 , čo znemožňuje použiť vzorec a log a b =b , pretože vyžaduje podmienky a>0 , a≠1, b>0 . Nemôžeme teda hovoriť o výpočte hodnoty 2 log 2 (−7) . V tomto prípade by zápis 2 log 2 (−7) = −7 bol chybou.

Podobne v príklade pod písmenom e) nie je možné uviesť riešenie tvaru , keďže pôvodný výraz nedáva zmysel.

odpoveď:

a) 5 log 5 4 =4, b) 10 log(1+2 π) =1+2 π, c) , d), e) výrazy nedávajú zmysel.

Často je užitočné transformovať sa kladné číslo je reprezentovaná ako mocnina nejakého kladného a nejednotného čísla s logaritmom v exponente. Vychádza z rovnakej definície logaritmu a log a b =b , a>0 , a≠1 , b>0 , ale vzorec je aplikovaný sprava doľava, teda v tvare b=a log a b . Napríklad 3=e ln3 alebo 5=5 log 5 5 .

Prejdime k používaniu vlastností logaritmov na transformáciu výrazov.

Príklad.

Nájdite hodnotu výrazu: a) log −2 1, b) log 1 1, c) log 0 1, d) log 7 1, e) ln1, f) lg1, g) log 3,75 1, h) log 5 π 7 1 .

Riešenie.

V príkladoch pod písmenami a), b) a c) sú uvedené výrazy log −2 1 , log 1 1 , log 0 1 , ktoré nedávajú zmysel, pretože základ logaritmu by nemal obsahovať záporné číslo. , nula alebo jedna, pretože logaritmus sme definovali len pre kladný a nejednotkový základ. Preto v príkladoch a) - c) nemôže byť reč o hľadaní hodnoty výrazu.

Vo všetkých ostatných úlohách samozrejme základy logaritmov obsahujú kladné a nejednotkové čísla 7 , e , 10 , 3,75 a 5 π 7 a jednotky sú všade pod znamienkami logaritmov. A poznáme vlastnosť logaritmu jednoty: log a 1=0 pre ľubovoľné a>0 , a≠1 . Hodnoty výrazov b) - f) sa teda rovnajú nule.

odpoveď:

a), b), c) výrazy nedávajú zmysel, d) log 7 1=0, e) ln1=0, f) log1=0, g) log 3,75 1=0, h) log 5 e 7 1 =0.

Príklad.

Vypočítajte: a) , b) lne , c) lg10 , d) log 5 π 3 −2 (5 π 3 −2), e) log −3 (−3) , f) log 1 1 .

Riešenie.

Je jasné, že musíme použiť vlastnosť logaritmu základu, ktorá zodpovedá vzorcu log a a=1 pre a>0 , a≠1 . V úlohách pod všetkými písmenami sa číslo pod znakom logaritmu zhoduje s jeho základňou. Chcem teda hneď povedať, že hodnota každého z uvedených výrazov je 1 . Neunáhlite sa však k záverom: v úlohách pod písmenami a) - d) sa hodnoty výrazov skutočne rovnajú jednej a v úlohách e) a f) pôvodné výrazy nedávajú zmysel, takže nemôže treba povedať, že hodnoty týchto výrazov sa rovnajú 1.

odpoveď:

a) , b) lne=1, c) lg10=1, d) log 5 π 3 −2 (5 π 3 −2)=1, e), f) výrazy nedávajú zmysel.

Príklad.

Nájdite hodnotu: a) log 3 3 11 , b) , c) , d) log -10 (-10) 6 .

Riešenie.

Je zrejmé, že pod znakmi logaritmov sú niektoré stupne základne. Na základe toho chápeme, že tu je užitočná vlastnosť stupňa bázy: log a a p =p, kde a>0, a≠1 a p je ľubovoľné reálne číslo. Vzhľadom na to máme tieto výsledky: a) log 3 3 11 =11 , b) , v) . Je možné napísať podobnú rovnosť pre príklad pod písmenom d) tvaru log −10 (−10) 6 =6? Nie, nemôžete, pretože log −10 (−10) 6 nedáva zmysel.

odpoveď:

a) log 3 3 11 = 11, b) , v) d) výraz nedáva zmysel.

Príklad.

Vyjadrite výraz ako súčet alebo rozdiel logaritmov v rovnakom základe: a) , b) , c) log((-5) (-12)) .

Riešenie.

a) Súčin je pod znamienkom logaritmu a poznáme vlastnosť logaritmu súčinu log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y> 0 V našom prípade je číslo na báze logaritmu a čísla v súčine kladné, to znamená, že spĺňajú podmienky vybranej vlastnosti, preto ju môžeme bezpečne použiť: .

b) Tu použijeme vlastnosť logaritmu kvocientu , kde a>0 , a≠1 , x>0 , y>0 . V našom prípade je základom logaritmu kladné číslo e, čitateľ a menovateľ π sú kladné, čo znamená, že spĺňajú podmienky vlastnosti, takže máme právo použiť zvolený vzorec: .

c) Najprv si všimnite, že výraz lg((−5) (−12)) dáva zmysel. Zároveň však nemáme právo použiť vzorec pre logaritmus súčinu log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 , keďže čísla −5 a −12 sú záporné a nespĺňajú podmienky x>0 , y>0 . To znamená, že nie je možné vykonať takúto transformáciu: log((−5)(−12))=log(−5)+log(−12). Ale čo robiť? V takýchto prípadoch je potrebné pôvodný výraz vopred transformovať, aby sa predišlo záporným číslam. O podobných prípadoch premeny výrazov s záporné čísla pod znakom logaritmu budeme hovoriť podrobne v jednom z, ale zatiaľ uvedieme riešenie tohto príkladu, ktoré je vopred jasné a bez vysvetlenia: lg((−5)(−12))=lg(5 12)=lg5+lg12.

odpoveď:

a) , b) c) lg((-5) (-12))=lg5+lg12.

Príklad.

Zjednodušte výraz: a) log 3 0,25 + log 3 16 + log 3 0,5, b) .

Riešenie.

Tu nám pomôžu všetky rovnaké vlastnosti logaritmu súčinu a logaritmu kvocientu, ktoré sme použili v predchádzajúcich príkladoch, len teraz ich použijeme sprava doľava. To znamená, že prevedieme súčet logaritmov na logaritmus súčinu a rozdiel logaritmov na logaritmus kvocientu. Máme
a) log 3 0,25 + log 3 16 + log 3 0,5 = log 3 (0,25 16 0,5) = log 3 2.
b) .

odpoveď:

a) log 3 0,25+log 3 16+log 3 0,5=log 3 2, b) .

Príklad.

Zbavte sa stupňa pod znamienkom logaritmu: a) log 0,7 5 11, b) c) log3 (-5)6.

Riešenie.

Je ľahké vidieť, že máme do činenia s výrazmi ako log a b p . Zodpovedajúca vlastnosť logaritmu je log a b p = p log a b , kde a>0 , a≠1 , b>0 , p je ľubovoľné reálne číslo. To znamená, že za podmienok a>0 , a≠1 , b>0 z logaritmu stupňa log a b p môžeme prejsť k súčinu p·log a b . Vykonajte túto transformáciu s danými výrazmi.

a) V tomto prípade a = 0,7, b = 5 a p = 11. Takže log 0,7 5 11 = 11 log 0,7 5 .

b) Tu sú splnené podmienky a>0 , a≠1 , b>0. Preto

c) Výraz log 3 (−5) 6 má rovnakú štruktúru log a b p , a=3 , b=−5 , p=6 . Ale pre b nie je splnená podmienka b>0, čo znemožňuje použiť vzorec log a b p =p log a b . Tak prečo nemôžete dokončiť prácu? Je to možné, ale vyžaduje sa predbežná transformácia výrazu, ktorej sa budeme podrobne venovať nižšie v odseku pod nadpisom . Riešenie bude takéto: log 3 (−5) 6 = log 3 5 6 = 6 log 3 5.

odpoveď:

a) log 0,7 5 11 = 11 log 0,7 5 ,
b)
c) log3 (-5)6 = 6 log35.

Pomerne často sa musí vzorec pre logaritmus stupňa pri vykonávaní transformácií aplikovať sprava doľava vo forme p log a b \u003d log a b p (to si vyžaduje rovnaké podmienky pre a, b a p). Napríklad 3 ln5 = ln5 3 a lg2 log 2 3 = log 2 3 lg2.

Príklad.

a) Vypočítajte hodnotu log 2 5, ak je známe, že lg2≈0,3010 a lg5≈0,6990. b) Napíšte zlomok ako logaritmus so základom 3.

Riešenie.

a) Vzorec na prechod na nový základ logaritmu nám umožňuje tento logaritmus znázorniť ako pomer desiatkových logaritmov, ktorých hodnoty sú nám známe: . Zostáva len vykonať výpočty, máme .

b) Tu stačí použiť vzorec na prechod na nový základ a aplikovať ho sprava doľava, teda v tvare . Dostaneme .

odpoveď:

a) log 2 5≈2,3223, b) .

V tejto fáze sme dosť dôsledne uvažovali o transformácii najjednoduchších výrazov pomocou základných vlastností logaritmov a definície logaritmu. V týchto príkladoch sme museli použiť jednu vlastnosť a nič iné. Teraz môžete s čistým svedomím prejsť na príklady, ktorých transformácia si vyžaduje použitie niekoľkých vlastností logaritmov a iných dodatočných transformácií. Budeme sa im venovať v nasledujúcom odseku. Ešte predtým sa však krátko zastavme pri príkladoch aplikácie dôsledkov zo základných vlastností logaritmov.

Príklad.

a) Zbavte sa koreňa pod znakom logaritmu. b) Preveďte zlomok na logaritmus so základom 5. c) Zbavte sa mocností pod znakom logaritmu a na jeho základni. d) Vypočítajte hodnotu výrazu . e) Výraz nahraďte mocninou základom 3.

Riešenie.

a) Ak si pripomenieme dôsledok z vlastnosti logaritmu stupňa , potom môžete okamžite odpovedať: .

b) Tu použijeme vzorec sprava doľava, máme .

c) B tento prípad vzorec vedie k výsledku . Dostaneme .

d) A tu stačí použiť dôsledok, ktorému zodpovedá vzorec . Takže .

e) Vlastnosť logaritmu nám umožňuje dosiahnuť požadovaný výsledok: .

odpoveď:

a) . b) . v) . G) . e) .

Konzistentné používanie viacerých vlastností

Skutočné úlohy na transformáciu výrazov pomocou vlastností logaritmov sú zvyčajne zložitejšie ako tie, ktorým sme sa venovali v predchádzajúcom odseku. V nich sa výsledok spravidla nezíska v jednom kroku, ale riešenie už spočíva v postupnej aplikácii jednej vlastnosti za druhou spolu s ďalšími identickými transformáciami, ako sú otváranie zátvoriek, zmenšovanie podobných členov, zmenšovanie zlomkov atď. . Poďme si teda priblížiť takéto príklady. V tom nie je nič zložité, hlavnou vecou je konať opatrne a dôsledne a dodržiavať poradie, v ktorom sa akcie vykonávajú.

Príklad.

Vypočítajte hodnotu výrazu (log 3 15−log 3 5) 7 log 7 5.

Riešenie.

Rozdiel logaritmov v zátvorkách vlastnosťou logaritmu kvocientu možno nahradiť logaritmom log 3 (15:5) a potom vypočítať jeho hodnotu log 3 (15:5)=log 3 3=1 . A hodnota výrazu 7 log 7 5 podľa definície logaritmu je 5 . Nahradením týchto výsledkov do pôvodného výrazu dostaneme (log 3 15−log 3 5) 7 log 7 5 =1 5=5.

Tu je riešenie bez vysvetlenia:
(log 3 15−log 3 5) 7 log 7 5 = log 3 (15:5) 5=
= log 3 3 5 = 1 5 = 5.

odpoveď:

(log 3 15−log 3 5) 7 log 7 5 =5.

Príklad.

Akú hodnotu má číselný výraz log 3 log 2 2 3 −1 ?

Riešenie.

Najprv transformujme logaritmus, ktorý je pod znamienkom logaritmu, podľa vzorca pre logaritmus stupňa: log 2 2 3 =3. Takže log 3 log 2 2 3 = log 3 3 a potom log 3 3 = 1 . Takže log 3 log 2 2 3 −1=1−1=0 .

odpoveď:

log 3 log 2 2 3 −1=0 .

Príklad.

Zjednodušte výraz.

Riešenie.

Vzorec na prevod na nový základ logaritmu umožňuje, aby bol pomer logaritmov k jednej báze vyjadrený ako log 3 5 . V tomto prípade bude mať pôvodný výraz tvar . Podľa definície logaritmu 3 log 3 5 = 5 , tj a hodnota výsledného výrazu sa na základe rovnakej definície logaritmu rovná dvom.

Tu krátka verzia riešenie, ktoré sa zvyčajne uvádza: .

odpoveď:

.

Pre hladký prechod k informáciám z nasledujúceho odseku sa pozrime na výrazy 5 2+log 5 3 a lg0.01 . Ich štruktúra nezodpovedá žiadnej z vlastností logaritmov. Čo sa teda stane, ak ich nemožno previesť pomocou vlastností logaritmov? Je to možné, ak vykonáte predbežné transformácie, ktoré pripravia tieto výrazy na použitie vlastností logaritmov. Takže 5 2+log 5 3 =5 2 5 log 5 3 =25 3=75, a lg0,01=lg10-2 = -2. Ďalej podrobne pochopíme, ako sa takáto príprava výrazov vykonáva.

Príprava výrazov na použitie vlastností logaritmov

Logaritmy v konvertovanom výraze sa veľmi často líšia v štruktúre zápisu z ľavej a pravej časti vzorcov, ktoré zodpovedajú vlastnostiam logaritmov. Ale rovnako často transformácia týchto výrazov zahŕňa použitie vlastností logaritmov: ich použitie si vyžaduje iba predbežnú prípravu. A táto príprava spočíva vo vykonaní určitých identických transformácií, ktoré prinesú logaritmy do formy vhodnej na aplikáciu vlastností.

Aby sme boli spravodliví, poznamenávame, že takmer každá transformácia výrazov môže pôsobiť ako predbežná transformácia, od banálnej redukcie podobných výrazov až po aplikáciu. trigonometrické vzorce. Je to pochopiteľné, pretože konvertované výrazy môžu obsahovať akékoľvek matematické objekty: zátvorky, moduly, zlomky, odmocniny, stupne atď. Preto musíme byť pripravení vykonať akúkoľvek požadovanú transformáciu, aby sme mohli ďalej využívať vlastnosti logaritmov.

Hneď si povedzme, že v tejto časti si nekladieme za úlohu klasifikovať a analyzovať všetky mysliteľné predbežné transformácie, ktoré nám umožňujú v budúcnosti aplikovať vlastnosti logaritmu alebo definíciu logaritmu. Tu sa zameriame len na štyri z nich, ktoré sú najcharakteristickejšie a v praxi sa s nimi najčastejšie stretávame.

A teraz podrobne o každom z nich, po ktorom v rámci našej témy zostáva len zaoberať sa transformáciou výrazov s premennými pod znakmi logaritmov.

Výber mocnín pod znakom logaritmu a v jeho základe

Začnime hneď príkladom. Urobme logaritmus. Je zrejmé, že v tejto forme jej štruktúra neprispieva k použitiu vlastností logaritmov. Je možné tento výraz nejako transformovať, aby sme ho zjednodušili, alebo ešte lepšie vypočítať jeho hodnotu? Aby sme na túto otázku odpovedali, pozrime sa bližšie na čísla 81 a 1/9 v kontexte nášho príkladu. Tu je ľahké vidieť, že tieto čísla môžu byť vyjadrené ako mocnina 3 , skutočne 81=3 4 a 1/9=3 −2 . V tomto prípade je pôvodný logaritmus prezentovaný vo formulári a je možné použiť vzorec . takže, .

Analýza analyzovaného príkladu vedie k nasledujúcej myšlienke: ak je to možné, môžete sa pokúsiť zvýrazniť stupeň pod znamienkom logaritmu a na jeho základni, aby ste uplatnili vlastnosť logaritmu stupňa alebo jeho dôsledok. Zostáva len zistiť, ako tieto stupne vyčleniť. Dáme niekoľko odporúčaní k tejto otázke.

Niekedy je celkom zrejmé, že číslo pod znamienkom logaritmu a/alebo v jeho základni predstavuje nejakú celočíselnú mocninu, ako v príklade diskutovanom vyššie. Takmer neustále sa musíte zaoberať mocninami dvoch, ktoré sú dobre známe: 4=2 2 , 8=2 3 , 16=2 4 , 32=2 5 , 64=2 6 , 128=2 7 , 256=2 8 , 512 = 29, 1024 = 210. To isté možno povedať o stupňoch trojky: 9=3 2 , 27=3 3 , 81=3 4 , 243=3 5 , ... Vo všeobecnosti nezaškodí, ak existuje stupňová tabuľka prirodzené čísla do desiatich. Taktiež nie je ťažké pracovať s celočíselnými mocninami desať, sto, tisíc atď.

Príklad.

Vypočítajte hodnotu alebo zjednodušte výraz: a) log 6 216 , b) , c) log 0,000001 0,001 .

Riešenie.

a) Je zrejmé, že 216=63, takže log6216=log663=3.

b) Tabuľka mocnín prirodzených čísel nám umožňuje znázorniť čísla 343 a 1/243 ako mocniny 7 3 a 3 −4. Preto je to možné ďalšia transformácia daný logaritmus:

c) Keďže 0,000001 = 10 -6 a 0,001 = 10 -3, potom log 0,000001 0,001=log 10 −6 10 −3 =(−3)/(−6)=1/2.

odpoveď:

a) log 6 216=3, b) c) log 0,000001 0,001 = 1/2.

V zložitejších prípadoch sa musíte uchýliť k zvýrazneniu sily čísel.

Príklad.

Zmeňte výraz na jednoduchší tvar log 3 648 log 2 3 .

Riešenie.

Pozrime sa, v čom je rozšírenie čísla 648 hlavné faktory:

To znamená, 648=2 3 3 4 . Touto cestou, denník 3 648 denník 2 3= denník 3 (2 3 3 4) denník 2 3.

Teraz prevedieme logaritmus súčinu na súčet logaritmov, po ktorých použijeme vlastnosti logaritmu stupňa:
log 3 (2 3 3 4) log 2 3=(log 3 2 3 + log 3 3 4) log 2 3=
=(3 log 3 2+4) log 2 3 .

Na základe následku vlastnosti logaritmu stupňa, ktorý zodpovedá vzorcu , súčin log32 log23 je súčin a je známe, že sa rovná jednej. Vzhľadom na to dostaneme 3 denník 3 2 denník 2 3+4 denník 2 3=3 1+4 denník 2 3=3+4 denník 2 3.

odpoveď:

log 3 648 log 2 3=3+4 log 2 3.

Pomerne často sú výrazy pod znamienkom logaritmu a v jeho základe súčinom alebo pomerom koreňov a / alebo mocnín niektorých čísel, napríklad , . Podobné výrazy môžu byť vyjadrené ako stupeň. Na tento účel sa vykoná prechod z koreňov na stupne a aplikujú sa. Tieto transformácie vám umožňujú vybrať stupne pod znamienkom logaritmu a v jeho základni a potom použiť vlastnosti logaritmu.

Príklad.

Vypočítajte: a) , b).

Riešenie.

a) Výraz v základe logaritmu je súčinom mocnín s rovnakými základmi podľa zodpovedajúcej vlastnosti mocnín, ktoré máme 5 2 5 −0,5 5 −1 =5 2−0,5−1 =5 0,5.

Teraz preveďme zlomok pod znamienkom logaritmu: prejdime od koreňa k stupňu, po ktorom použijeme vlastnosť pomeru stupňov s rovnakými základmi: .

Zostáva nahradiť získané výsledky do pôvodného výrazu, použite vzorec a dokončite transformáciu:

b) Keďže 729=3 6 , a 1/9=3 −2 , pôvodný výraz možno prepísať ako .

Potom použite vlastnosť odmocniny exponentu, prejdite od odmocniny k exponentu a použite pomer mocnin na prevod základu logaritmu na mocninu: .

Ak vezmeme do úvahy posledný výsledok, máme .

odpoveď:

a) , b).

Je jasné, že vo všeobecnom prípade na získanie mocnín pod znamienkom logaritmu a v jeho základe môžu byť potrebné rôzne transformácie rôznych výrazov. Uveďme pár príkladov.

Príklad.

Akú hodnotu má výraz: a) , b) .

Riešenie.

Ďalej si všimneme, že daný výraz má tvar log A B p, kde A=2, B=x+1 a p=4. Číselné výrazy tohto druhu sme transformovali podľa vlastnosti logaritmu stupňa log a b p \u003d p log a b, preto s daným výrazom chcem urobiť to isté a ísť od log 2 (x + 1) 4 do 4 log 2 (x + 1) . A teraz vypočítame hodnotu pôvodného výrazu a výrazu získaného po transformácii, napríklad s x=−2 . Máme log 2 (−2+1) 4 = log 2 1 = 0 a 4 log 2 (−2+1)=4 log 2 (−1)- nezmyselný výraz. To vyvoláva legitímnu otázku: „Čo sme urobili zle“?

A dôvod je nasledovný: vykonali sme transformáciu log 2 (x+1) 4 =4 log 2 (x+1) , na základe vzorca log a b p =p log a b , ale máme právo použiť iba tento vzorec ak sú splnené podmienky a >0 , a≠1 , b>0 , p - ľubovoľné reálne číslo. To znamená, že transformácia, ktorú sme urobili, sa uskutoční, ak x+1>0 , čo je rovnaké x>−1 (pre A a p sú splnené podmienky). V našom prípade však ODZ premennej x pre pôvodný výraz pozostáva nielen z intervalu x> −1 , ale aj z intervalu x<−1 . Но для x<−1 мы не имели права осуществлять преобразование по выбранной формуле.

Potreba zohľadniť ODZ

Pokračujme v analýze transformácie nami zvoleného výrazu log 2 (x+1) 4 a teraz sa pozrime, čo sa stane s ODZ pri prechode na výraz 4 log 2 (x+1) . V predchádzajúcom odseku sme našli ODZ pôvodného výrazu - to je množina (−∞, −1)∪(−1, +∞) . Teraz nájdime oblasť prijateľných hodnôt premennej x pre výraz 4 log 2 (x+1) . Je určená podmienkou x+1>0 , ktorá zodpovedá množine (−1, +∞) . Je zrejmé, že pri prechode z log 2 (x+1) 4 na 4·log 2 (x+1) sa rozsah prípustných hodnôt zužuje. A dohodli sme sa, že sa vyhneme reformám, ktoré vedú k zúženiu ODZ, pretože to môže viesť k rôznym negatívnym dôsledkom.

Tu stojí za zmienku pre seba, že je užitočné kontrolovať ODZ v každom kroku transformácie a nedovoliť jej zúženie. A ak zrazu v niektorom štádiu transformácie došlo k zúženiu ODZ, potom sa oplatí veľmi pozorne pozrieť, či je táto transformácia prípustná a či sme mali právo ju vykonať.

Spravodlivo hovoríme, že v praxi musíme zvyčajne pracovať s výrazmi, v ktorých je ODZ premenných taká, že nám umožňuje používať vlastnosti logaritmov bez obmedzení v nám už známej forme, a to zľava doprava aj z sprava doľava pri vykonávaní transformácií. Rýchlo si na to zvyknete a transformácie začnete vykonávať mechanicky bez toho, aby ste premýšľali o tom, či je možné ich vykonať. A v takých chvíľach, ako by to chcelo šťastie, prekĺznu zložitejšie príklady, v ktorých nepresná aplikácia vlastností logaritmov vedie k chybám. Takže treba byť stále v strehu, a dbať na to, aby nedošlo k zúženiu ODZ.

Nezaškodí oddelene zdôrazniť hlavné transformácie založené na vlastnostiach logaritmov, ktoré sa musia vykonávať veľmi opatrne, čo môže viesť k zúženiu ODZ a v dôsledku toho k chybám:

Niektoré transformácie výrazov podľa vlastností logaritmov môžu viesť aj k opaku - rozšíreniu ODZ. Napríklad prechod zo 4 log 2 (x+1) na log 2 (x+1) 4 rozširuje ODZ z množiny (−1, +∞) na (−∞, −1)∪(−1, +∞ ). Takéto transformácie sa uskutočnia, ak zostanete v rámci ODZ pre pôvodný výraz. Takže práve spomínaná transformácia 4 log 2 (x+1)=log 2 (x+1) 4 prebieha na premennej ODZ x pre pôvodný výraz 4 log 2 (x+1) , teda keď x+1> 0 , čo je rovnaké ako (−1, +∞) .

Teraz, keď sme diskutovali o nuansách, ktorým musíte venovať pozornosť pri prevode výrazov s premennými pomocou vlastností logaritmov, zostáva zistiť, ako by sa tieto prevody mali vykonávať správne.

X+2>0. Funguje to v našom prípade? Aby sme odpovedali na túto otázku, pozrime sa na DPV premennej x. Je určená systémom nerovností , čo je ekvivalent podmienky x+2>0 (v prípade potreby pozri článok riešenie sústav nerovníc). Môžeme teda bezpečne aplikovať vlastnosť logaritmu stupňa.

Máme
3 log(x+2) 7 −log(x+2)−5 log(x+2) 4 =
=3 7 log(x+2)−log(x+2)−5 4 log(x+2)=
=21 log(x+2)-log(x+2)-20 log(x+2)=
=(21-1-20)lg(x+2)=0.

Môžete konať inak, pretože ODZ vám to umožňuje, napríklad takto:

odpoveď:

3 log(x+2) 7 −log(x+2)−5 log(x+2) 4 =0.

A čo robiť, keď na ODZ nie sú splnené podmienky spojené s vlastnosťami logaritmov? Budeme sa tomu venovať na príkladoch.

Žiadame, aby sme zjednodušili výraz lg(x+2) 4 −lg(x+2) 2 . Transformácia tohto výrazu na rozdiel od výrazu z predchádzajúceho príkladu neumožňuje voľné použitie vlastnosti logaritmu stupňa. prečo? ODV premennej x je v tomto prípade spojením dvoch intervalov x>−2 a x<−2 . При x>−2 môžeme bezpečne použiť vlastnosť logaritmu stupňa a postupovať ako v príklade vyššie: log(x+2) 4 −log(x+2) 2 = 4 log(x+2)−2 log(x+2)=2 log(x+2). Ale ODZ obsahuje ďalší interval x+2<0 , для которого последнее преобразование будет некорректно. Что же делать при x+2<0 ? В подобных случаях на помощь приходит . Определение модуля позволяет выражение x+2 при x+2<0 представить как −|x+2| . Тогда при x+2<0 от lg(x+2) 4 −lg(x+2) 2 переходим к log(−|x+2|) 4 −log(−|x+2|) 2 a ďalej v dôsledku energetických vlastností lg|x+2| 4−lg|x+2| 2. Výsledný výraz je možné transformovať pomocou vlastnosti logaritmu stupňa, pretože |x+2|>0 pre ľubovoľné hodnoty premennej. Máme log|x+2| 4−lg|x+2| 2 =4 log|x+2|−2 log|x+2|=2 log|x+2|. Teraz sa môžete zbaviť modulu, pretože splnil svoju úlohu. Keďže transformujeme na x+2<0 , то 2·lg|x+2|=2·lg(−(x+2)) . Итак, можно считать, что мы справились с поставленной задачей. Ответ: . Полученный результат можно записать компактно с использованием модуля как .

Uvažujme ešte jeden príklad, aby sme si prácu s modulmi objasnili. Uvažujme z výrazu prejsť na súčet a rozdiel logaritmov lineárnych binómov x−1 , x−2 a x−3 . Najprv nájdeme ODZ:

Na intervale (3, +∞) sú hodnoty výrazov x−1 , x−2 a x−3 kladné, takže môžeme bezpečne aplikovať vlastnosti logaritmu súčtu a rozdielu:

A na intervale (1, 2) sú hodnoty výrazu x−1 kladné a hodnoty výrazov x−2 a x−3 sú záporné. Preto na uvažovanom intervale reprezentujeme x−2 a x−3 pomocou modulo ako −|x−2| a −|x−3| resp. V čom

Teraz môžeme aplikovať vlastnosti logaritmu súčinu a kvocientu, keďže na uvažovanom intervale (1, 2) sú hodnoty výrazov x−1 , |x−2| a |x−3| - pozitívny.

Máme

Získané výsledky je možné kombinovať:

Vo všeobecnosti podobné uvažovanie umožňuje na základe vzorcov pre logaritmus súčinu, pomeru a stupňa získať tri prakticky užitočné výsledky, ktoré je celkom vhodné použiť:

• Logaritmus súčinu dvoch ľubovoľných výrazov X a Y tvaru log a (X·Y) možno nahradiť súčtom logaritmov log a |X|+log a |Y| , a>0, a≠1.
• Špeciálny logaritmus log a (X:Y) možno nahradiť rozdielom logaritmov log a |X|−log a |Y| , a>0 , a≠1, X a Y sú ľubovoľné výrazy.
• Od logaritmu nejakého výrazu B k párnej mocnine p tvaru log a B p možno prejsť k výrazu p log a |B| , kde a>0 , a≠1 , p je párne číslo a B je ľubovoľný výraz.

Podobné výsledky uvádza napríklad návod na riešenie exponenciálnych a logaritmických rovníc v zbierke úloh z matematiky pre uchádzačov o štúdium na vysokých školách, ktorú pripravil M. I. Skanavi.

Príklad.

Zjednodušte výraz .

Riešenie.

Bolo by dobré použiť vlastnosti logaritmu stupňa, súčtu a rozdielu. Ale môžeme to urobiť tu? Na zodpovedanie tejto otázky potrebujeme poznať ODZ.

Poďme si to definovať:

Je celkom zrejmé, že výrazy x+4 , x−2 a (x+4) 13 na rozsahu možných hodnôt premennej x môžu nadobúdať kladné aj záporné hodnoty. Preto sa budeme musieť prepracovať cez moduly.

Vlastnosti modulu vám umožňujú prepísať ako , tak

Nič vám tiež nebráni použiť vlastnosť logaritmu stupňa a potom priniesť podobné výrazy:

Ďalšia postupnosť transformácií vedie k rovnakému výsledku:

a keďže výraz x−2 môže nadobúdať kladné aj záporné hodnoty na ODZ, pri párnom exponente 14