Sada ćemo promatrati transformaciju izraza koji sadrže logaritme s općeg gledišta. Ovdje ćemo analizirati ne samo transformaciju izraza pomoću svojstava logaritama, već ćemo razmotriti i transformaciju izraza s logaritmima opći pogled, koji sadrže ne samo logaritme, već i potencije, razlomke, korijene itd. Kao i obično, sav materijal ćemo opskrbiti karakterističnim primjerima detaljni opisi rješenja.

Navigacija po stranici.

Izrazi s logaritmima i logaritamski izrazi

Izvođenje radnji s razlomcima

U prethodnom odlomku analizirali smo glavne transformacije koje se provode s pojedinim razlomcima koji sadrže logaritme. Ove se transformacije, naravno, mogu izvesti sa svakim pojedinačnim razlomkom koji je dio složenijeg izraza, na primjer, predstavljajući zbroj, razliku, umnožak i kvocijent sličnih razlomaka. Ali osim rada s pojedinačnim razlomcima, transformacija izraza ove vrste često uključuje izvođenje odgovarajućih radnji s razlomcima. Zatim ćemo razmotriti pravila po kojima se te radnje provode.

Od 5-6 razreda znamo pravila po kojima . U članku opći prikaz operacija s razlomcima podijelili smo ova pravila s obični razlomci u razlomke općeg oblika A/B, gdje su A i B neki numerički, doslovni ili varijabilni izrazi, a B je identički različit od nule. Jasno je da su razlomci s logaritmima posebni slučajevi općih razlomaka. I u tom smislu, jasno je da se radnje s razlomcima koji u svojim zapisima sadrže logaritme provode prema istim pravilima. Naime:

• Da biste dodali ili oduzeli dva razlomka s istim nazivnicima, dodajte ili oduzmite brojnike u skladu s tim, a nazivnik ostavite isti.
• Za zbrajanje ili oduzimanje dva razlomka s različite nazivnike, potrebno ih je dovesti pod zajednički nazivnik i izvršiti odgovarajuće radnje prema prethodnom pravilu.
• Da biste pomnožili dva razlomka, trebate napisati razlomak čiji je brojnik umnožak brojnika izvornih razlomaka, a nazivnik umnožak nazivnika.
• Da bismo razlomak podijelili s razlomkom, potrebno je djeljivi razlomak pomnožiti s recipročnom vrijednošću djelitelja, odnosno s razlomkom s premještenim brojnikom i nazivnikom.

Evo nekoliko primjera za izvođenje operacija s razlomcima koji sadrže logaritme.

Primjer.

Izvršite radnje s razlomcima koji sadrže logaritme: a), b) , u) , G) .

Riješenje.

a) Nazivnici zbrojenih razlomaka očito su isti. Dakle, prema pravilu zbrajanja razlomaka s istim nazivnicima, brojnike zbrajamo, a nazivnik ostavljamo isti: .

b) Ovdje su nazivnici različiti. Stoga, prvo trebate dovesti razlomke na isti nazivnik. U našem slučaju nazivnici su već prikazani kao umnošci, a nama preostaje uzeti nazivnik prvog razlomka i dodati mu faktore koji nedostaju iz nazivnika drugog razlomka. Tako dobivamo zajednički nazivnik oblika . U ovom slučaju, oduzeti razlomci se svode na zajednički nazivnik pomoću dodatnih faktora u obliku logaritma odnosno izraza x 2 ·(x+1). Nakon toga preostaje oduzeti razlomke s istim nazivnicima, što nije teško.

Dakle, rješenje je:

c) Poznato je da je rezultat množenja razlomaka razlomak čiji je brojnik umnožak brojnika, a nazivnik umnožak nazivnika, dakle

Lako je vidjeti da je moguće smanjenje frakcije s dva i decimalnim logaritmom, kao rezultat imamo .

d) Prelazimo s dijeljenja razlomaka na množenje, zamjenjujući razlomak-djelitelj njegovim recipročnim. Tako

Brojnik dobivenog razlomka može se prikazati kao , iz kojeg je jasno vidljiv zajednički faktor brojnika i nazivnika - faktor x, njime možete smanjiti razlomak:

Odgovor:

a), b) , u) , G) .

Treba imati na umu da se radnje s razlomcima provode uzimajući u obzir redoslijed izvođenja radnji: prvo množenje i dijeljenje, zatim zbrajanje i oduzimanje, a ako postoje zagrade, prvo se izvode radnje u zagradama.

Primjer.

Izvršite akcije s razlomcima .

Riješenje.

Prvo vršimo zbrajanje razlomaka u zagradama, nakon čega ćemo izvršiti množenje:

Odgovor:

U ovom trenutku preostaje naglas reći tri prilično očite, ali u isto vrijeme važne točke:

Pretvaranje izraza pomoću svojstava logaritama

Najčešće transformacija izraza s logaritmima uključuje korištenje identiteta koji izražavaju definiciju logaritma i

Matematika. Tematski testovi. Dio II. Priprema za Jedinstveni državni ispit-2010. 10-11 razreda. ur. Lysenko F.F. - Rostov n / D .: Legija, 2009. - 176s.

Matematika. UPOTREBA-2009. Tematski testovi. Dio II (B4-B8, C1-C2) Izd. Lysenko F.F. - Rostov n / D: Legija, 2008 - 160 str.

Priručnik se sastoji od testova po pojedinim temama, koje su tradicionalne u nastavi matematike i stoga su u pravilu uključene u ispit. U potpunosti pokrivaju skupine zadataka povećanog i visokog stupnja složenosti USE-a, osim tekstualnih zadataka i zadataka iz geometrije. Za svaku temu nudi se jedan ili više testova. Svaki set sadrži 10 testova, svaki test sadrži 8 zadataka.

Svrha ove knjige je razrada zadataka s kratkim i detaljnim odgovorom USE testova. Neophodan je prvenstveno za diplomante koji očekuju primanje KORISTI dobro ocjenjivanje, kao i za učenike 10. razreda, koji mogu objediniti obrađene teme sa stajališta USE-a. Predloženi priručnik može biti koristan svim maturantima koji se pripremaju za USE iz matematike, kao i nastavnicima koji pripremaju učenike za USE.

Format: djvu/zip (2009 , 176s.)

Veličina: 2,5 MB

Preuzimanje / Preuzimanje datoteke 14

Format: pdf (2009 , 176s.)

Veličina: 8,6 MB

Preuzimanje datoteka: 14 .12.2018, linkovi uklonjeni na zahtjev izdavačke kuće Legija (vidi napomenu)

Format: djvu/zip (2008 , 160s.)

Veličina: 3 MB

Preuzimanje / Preuzimanje datoteke 14 .12.2018, linkovi uklonjeni na zahtjev izdavačke kuće Legija (vidi napomenu)

Format: pdf (2008 , 160s.)

Veličina: 9,9 MB

Preuzimanje datoteka: 14 .12.2018, linkovi uklonjeni na zahtjev izdavačke kuće Legija (vidi napomenu)

Obrazovno-metodički kompleks "Matematika. Jedinstveni državni ispit-2010" ed. Lysenko F.F. i Kulabukhov S.Yu. uključuje upute:
1. Matematika. Priprema za Jedinstveni državni ispit-2010.
2. Reshebnik. Matematika. Priprema za Jedinstveni državni ispit-2010.
3. Matematika. Tematski testovi. I. dio (osnovna razina). Priprema za Jedinstveni državni ispit-2010. 10-11 razreda.
4. Matematika. Tematski testovi. Dio II. Priprema za Jedinstveni državni ispit-2010. 10-11 razreda.
5. Matematika. Tematski testovi: geometrija, tekstualni zadaci. Priprema za Jedinstveni državni ispit-2010. 10-11 razreda.
6. Matematika. Zbirka USE testova 2001. - 2010.
7. Matematika. Priprema za Jedinstveni državni ispit-2010. Testovi obuke.
8. Džepni vodič iz matematike.

Sadržaj
Od autora 11
§ 1. Transformacije identiteta logaritamskih izraza 13
Opcija broj 1 13
Opcija broj 2 13
Opcija broj 3 14
Opcija broj 4 14
Opcija broj 5 15
Opcija broj 6 15
Opcija broj 7 16
Opcija broj 8 16
Opcija broj 9 17
Opcija broj 10 17
§ 2. Transformacije identiteta izraza koji sadrže stupanj 18
Opcija broj 1 18
Opcija broj 2 19
Opcija broj 3 19
Opcija broj 4 20
Opcija broj 5 21
Opcija broj 6 21
Opcija broj 7 22
Opcija broj 8 23
Opcija broj 9 23
Opcija broj 10 24
§ 3. Transformacije identiteta iracionalnih izraza 25
Opcija broj 1 25
Opcija broj 2 25
Opcija broj 3 26
Opcija broj 4 26
Opcija broj 5 27
Opcija broj 6 28
Opcija broj 7 28
Opcija broj 8 29
Opcija broj 9 30
Opcija broj 10 30
§ 4. Sustavi jednadžbi 31
Opcija broj 1 31
Opcija broj 2 32
Opcija broj 3 33
Opcija broj 4 33
Opcija broj 5 34
Opcija broj 6 35
Opcija broj 7 36
Opcija broj 8 37
Opcija broj 9 38
Opcija broj 10 39
§ 5. geometrijski smisao izvedenica 39
Opcija broj 139
Opcija broj 2 41
Opcija broj 3 43
Opcija broj 4 44
Opcija broj 5 46
Opcija broj 6 48
Opcija broj 7 50
Opcija broj 8 52
Opcija broj 9 54
Opcija broj 10 55
§ 6. Nejednadžbe 56
Opcija broj 1 g 56
Opcija broj 2 57
Opcija broj 3 58
Opcija broj 4 58
Opcija broj 5 59
Opcija broj 6 60
Opcija broj 7 60
Opcija broj 8 61
Opcija broj 9 62
Opcija broj 10 63
§ 7. Iracionalne jednadžbe 63
Opcija broj 1 63
Opcija broj 2 64
Opcija broj 3 65
Opcija broj 4 65
Opcija broj 5 66
Opcija broj 6 66
Opcija broj 7 67
Opcija broj 8 67
Opcija broj 9 68
Opcija br. Yu 68
§ 8. Trigonometrijske jednadžbe 69
Opcija broj 1 69
Opcija broj 2 69
Opcija broj 3 70
Opcija broj 4 70
Opcija broj 5 71
Opcija broj 6 72
Opcija broj 7 72
Opcija broj 8 73
Opcija broj 9 74
Opcija broj 10 74
§ 9. Logaritamske jednadžbe 75
Opcija broj 1 75
Opcija broj 2 75
Opcija broj 3 76
Opcija broj 4 76
Opcija broj 5 77
Opcija broj 6 77
Opcija broj 7 78
Opcija br. 8 * 78
Opcija broj 9 79
Opcija broj 10 79
§ 10. Eksponencijalne jednadžbe 80
Opcija broj 1 80
Opcija broj 2 80
Opcija broj 3 81
Opcija broj 4 81
Opcija broj 5 82
Opcija broj 6 82
Opcija broj 7 83
Opcija broj 8 83
Opcija broj 9 84
Opcija broj 10 84
§jedanaest. Periodičnost, parne i neparne funkcije 85
Opcija broj 1 85
Opcija broj 2 86
Opcija broj 3 87
Opcija broj 4 89
Opcija broj 5 90
Opcija broj 6 91
Opcija broj 7 92
Opcija broj 8 93
Opcija broj 9 94
Opcija broj 10 95
§ 12. Nule složene funkcije. Ograničena funkcija 97
Opcija broj 197
Opcija broj 2 97
Opcija broj 3 98
Opcija broj 4 98
Opcija broj 5 99
Opcija broj 6 99
Opcija broj 7 100
Opcija broj 8 100
Opcija broj 9 101
Opcija broj 10 101
§ 13. Područje definiranja, skup vrijednosti, monotonost funkcija 102
Opcija broj 1 102
Opcija broj 2 102
Opcija broj 3 103
Opcija broj 4 103
Opcija broj 5 104
Opcija broj 6 104
Opcija broj 7 105
Opcija broj 8 105
Opcija broj 9 106
Opcija broj 10 107
§ 14. Ekstremumi funkcije. Najveća i najmanja vrijednost funkcije 107
Opcija broj 1 107
Opcija broj 2 108
Opcija broj 3 108
Opcija broj 4 109
Opcija broj 5 109
Opcija broj 6 110
Opcija broj 7 110
Opcija broj 8 111
Opcija broj 9 111
Opcija broj 10 112
§ 15. Razne tehnike rješavanja logaritamskih jednadžbi 113
Opcija broj 1 113
Opcija broj 2 113
Opcija broj 3 114
Opcija broj 4 114
Opcija broj 5 115
Opcija broj 6 115
Opcija broj 7 116
Opcija broj 8 116
Opcija broj 9 117
Opcija broj 10 117
§ 16. Razne tehnike rješavanja trigonometrijskih jednadžbi 118
Opcija broj 1 118
Opcija broj 2 118
Opcija broj 3 118
Opcija broj 4 119
Opcija broj 5 119
Opcija broj 6 120
Opcija broj 7 120
Opcija broj 8 121
Opcija broj 9 121
Opcija broj 10 122
§ 17. Razne tehnike rješavanja iracionalnih jednadžbi 123
Opcija broj 1 123
Opcija broj 2 123
Opcija broj 3 124
Opcija broj 4 124
Opcija broj 5 125
Opcija broj 6 125
Opcija broj 7 125
Opcija broj 8 126
Opcija broj 9 126
Opcija br. 10 127
§ 18. Jednadžbe koje sadrže varijablu pod znakom modula 127
Opcija broj 1 127
Opcija broj 2 128
Opcija broj 3 128
Opcija broj 4 129
Opcija broj 5 129
Opcija broj 6 130
Opcija broj 7 130
Opcija broj 8 131
Opcija broj 9 131
Opcija broj 10 131
§ 19. Različite metode rješavanja eksponencijalne jednadžbe.132
Opcija broj 1 132
Opcija broj 2 133
Opcija broj 3 133
Opcija broj 4 134
Opcija broj 5 134
Opcija broj 6 135
Opcija broj 7 135
Opcija broj 8 135
Opcija broj 9 136
Opcija broj 10 136
§ 20. Razne tehnike rješavanja kombiniranih jednadžbi 137
Opcija broj 1 137
Opcija broj 2 137
Opcija broj 3 138
Opcija broj 4 138
Opcija broj 5 139
Opcija broj 6 139
Opcija broj 7 140
Opcija broj 8 140
Opcija broj 9 141
Opcija broj 10 141
§ 21. Jednadžbe s parametrom koji sadrži modul 142
Opcija broj 1 142
Opcija broj 2 142
Opcija broj 3 143
Opcija broj 4 144
Opcija broj 5 144
Opcija broj 6 145
Opcija broj 7 146
Opcija broj 8 146
Opcija broj 9 147
Opcija broj 10 148
Odgovori 149
§ 1. Transformacije identiteta logaritamskih izraza 149
§ 2. Transformacije identiteta izraza koji sadrže stupanj 150
§ 3. Transformacije identiteta iracionalnih izraza 150
§ 4. Sustavi jednadžbi 151
§ 5. Geometrijsko značenje izvodnice 151
§ 6. Nejednadžbe 152
§ 7. Iracionalne jednadžbe 152
§ 8. Trigonometrijske jednadžbe 153
§ 9. Logaritamske jednadžbe 153
§ 10. Eksponencijalne jednadžbe 154
§jedanaest. Periodičnost, parne i neparne funkcije 154
§ 12. Nule složene funkcije. Ograničena funkcija 155
§ 13. Područje definiranja, skup vrijednosti, monotonost funkcija 156
§ 14. Ekstremumi funkcije. Najveća i najmanja vrijednost funkcije 158
§ petnaest. Razni trikovi pri rješavanju logaritamskih jednadžbi 159
§ 16. Razne tehnike rješavanja trigonometrijskih jednadžbi 160
§ 17. Razni trikovi za rješavanje iracionalnih jednadžbi 164
§ 18. Jednadžbe koje sadrže varijablu pod znakom modula 165
§ 19. Razne tehnike rješavanja eksponencijalnih jednadžbi.166
§ 20. Razne tehnike rješavanja kombiniranih jednadžbi 167
§ 21. Jednadžbe s parametrom koji sadrži modul 169
Književnost 170

EGOROVA VICTORIA VALEREVNA

Profesor matematike

najviša kvalifikacijska kategorija

TEMA: “TRANSFORMACIJA IDENTITETA

LOGARITAMSKI IZRAZI"

Znanja i vještine kojima bi učenici trebali ovladati nakon proučavanja ove lekcije:

poznavati definiciju logaritma broja, osnovni logaritamski identitet, svojstva logaritama;

znati izvoditi transformacije izraza koji sadrže logaritme, izračunavati logaritme.

Književnost:

1. Alimov Sh.A., Kolyagin Yu.M., Sidorov Yu.V. i dr. Algebra i početak analize: udžbenik za 10.-11 obrazovne ustanove. - M .: Obrazovanje, 2001.

2. Kochagin V.V., Kochagina M.V., Intenzivni tečaj pripreme za ispit. – M.: Eksmo, 2009.

3. A. G. Merzlyak, V. B. Polonsky i M. S. Yakir, Algebarski simulator: Vodič za školsku djecu i sveučilišne studente. – M.: Ileksa, 2005.

4. Gusev V.A., Mordkovich A.G. Matematika: Referentni materijali: Knjiga za studente. - M .: Obrazovanje, 2001.

Plan učenja:

Tijekom nastave:

1) Logaritam je grčka riječ, koji se sastoji od 2 riječi: “logos” - relacija, “arithmos” - broj. Dakle, logaritam je broj koji mjeri omjer. Publikacija iz 1614. izvijestila je da je Napier izumio logaritme. Kasnije je sastavio logaritamske tablice, koje su nam danas poznate kao Bradysove tablice. U manje od jednog stoljeća tablice su se proširile svijetom i postale neizostavan računalni alat. U budućnosti su, takoreći, ugrađeni u praktičan uređaj koji izuzetno ubrzava proces izračuna - klizač, koji se koristio do sedamdesetih godina dvadesetog stoljeća.

Prilog 1.

2) logaritam pozitivan brojb razumom a, štoviše veće od nule, a ne jednako jedan,je eksponent na koji se broj mora podićia da dobijem brojb.

Ova jednakost koja izražava definiciju logaritma naziva seosnovni logaritamski identitet .

C

ILI 1

P

Baza stupnja i baza logaritma su sedamnaest, što znači da je prema osnovnoj logaritamskoj identičnosti vrijednost izraza tri.

Radit ćemo usmeno:

SCH
ELCHOK

O donja sekunda je nula zarez pet desetinki, tako da je izraz jednak aritmetičkom kvadratnom korijenu od pet.

P

dodatak 2.

Jednakost znači da

Iz definicije logaritma dobivaju se sljedeće važne jednakosti:

Na primjer:

P
dodatak 3.

Prijeđimo na USE zadaci:

Dodatak 4

3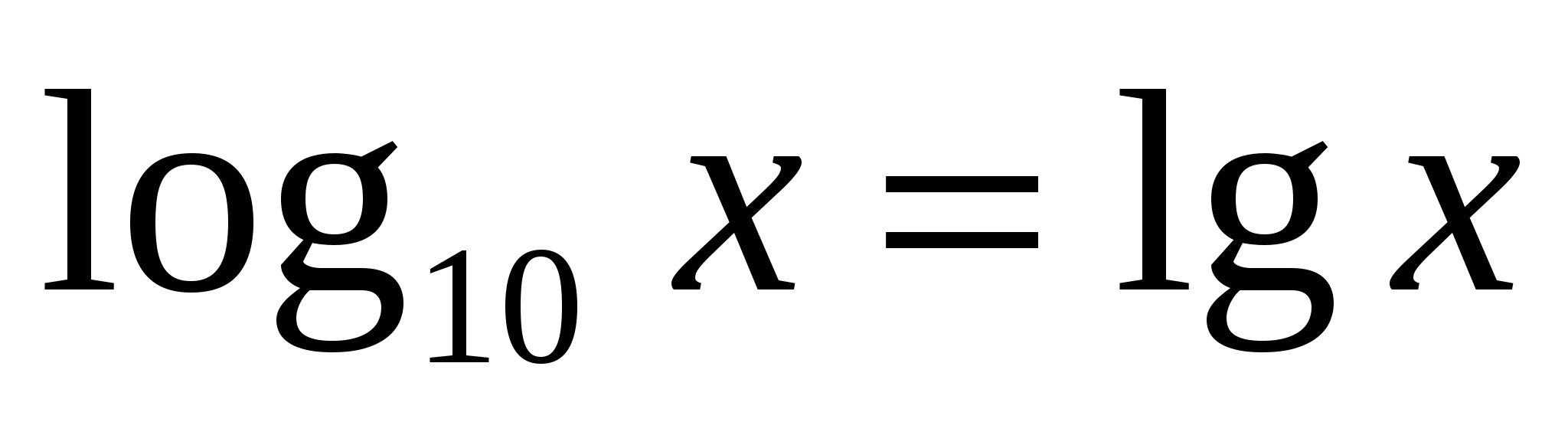
) Postoji posebna oznaka i naziv za logaritam s bazom deset.decimalni logaritam .

L
aritam prema bazie nazvaoprirodni logaritam .

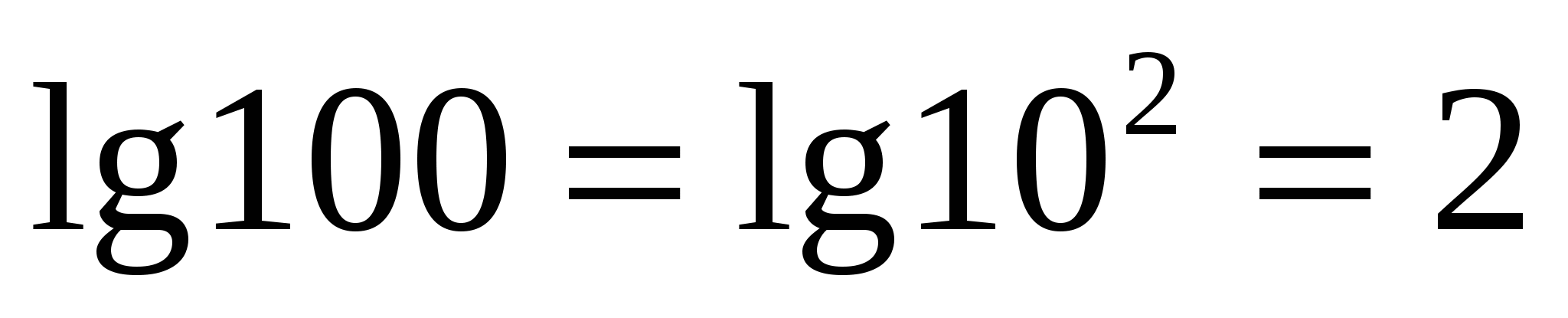
H
na primjer,

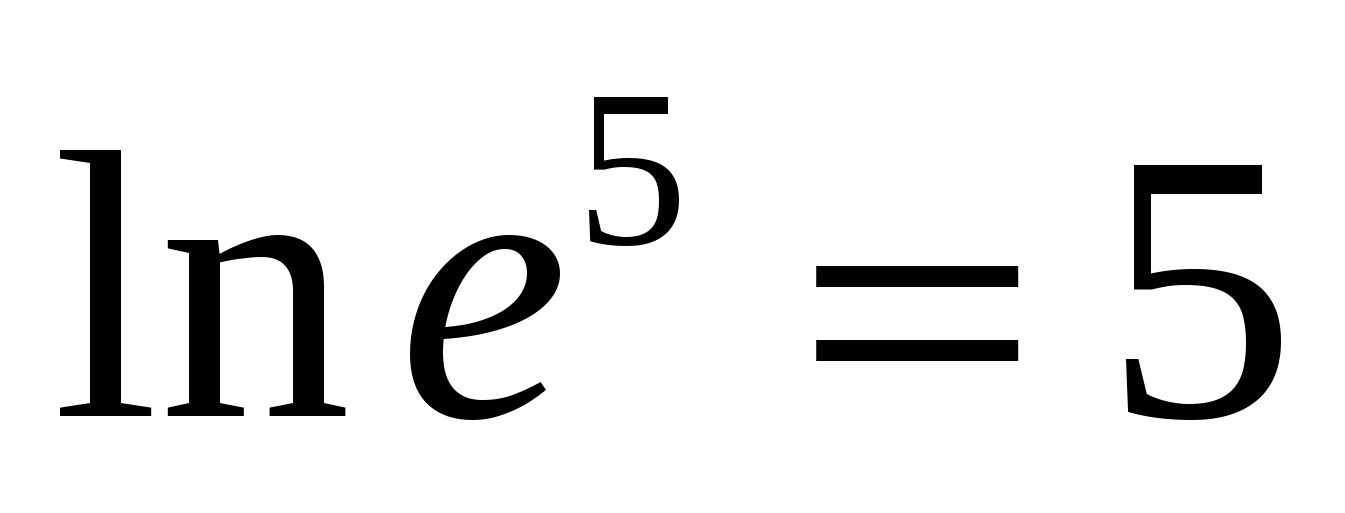
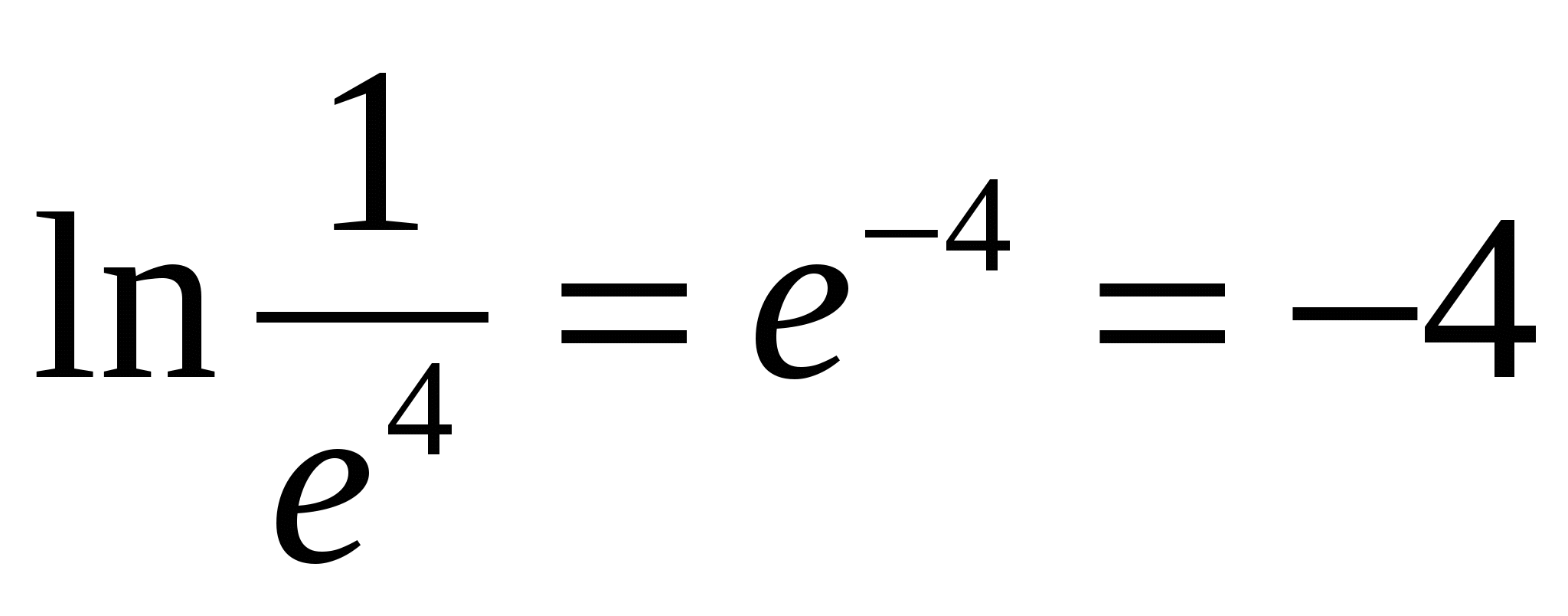
4) Sljedeća svojstva proizlaze iz definicije logaritma. Sva svojstva su formulirana i dokazana samo za pozitivne vrijednosti varijabli sadržanih pod predznacima logaritma.

Osnovni logaritam umnoška dvaju pozitivnih brojeva a jednak je zbroju logaritmi tih brojeva s istom bazom.

DER 2

Na primjer,

W
zadatak 1.

Zadatak 2. Pojednostavite izraz

NA
Poslužimo se prethodnim primjerom. Zamijenimo

Imajte na umu da je logaritam na kvadrat, pa zbroj također mora biti na kvadrat. Koristeći formulu za kvadrat zbroja, otvorite zagrade. Predstavljamo slične uvjete.

5) Logaritam količnika jednak je razlici logaritama djelitelja i djelitelja.

C

Obratite pozornost na bazu stupnja i bazu logaritma - one su iste.

ILI 3

R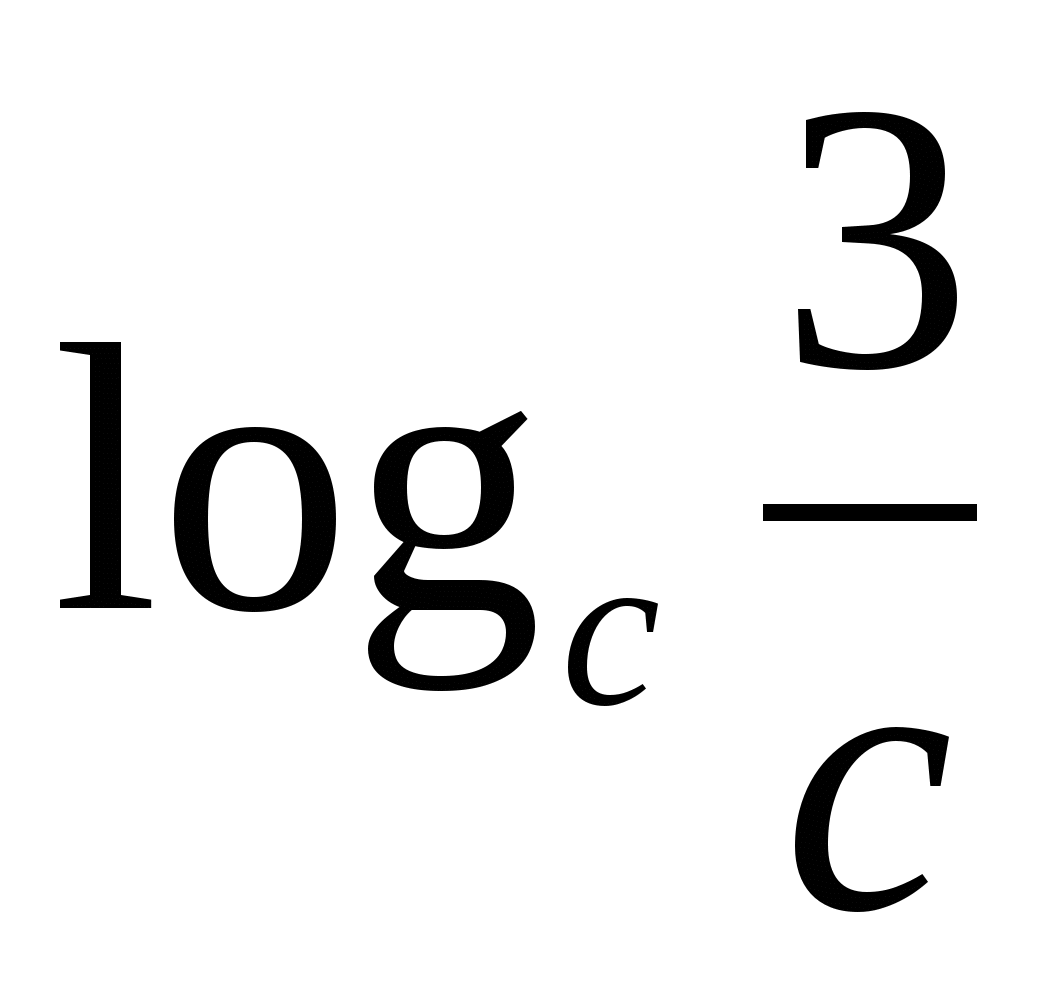

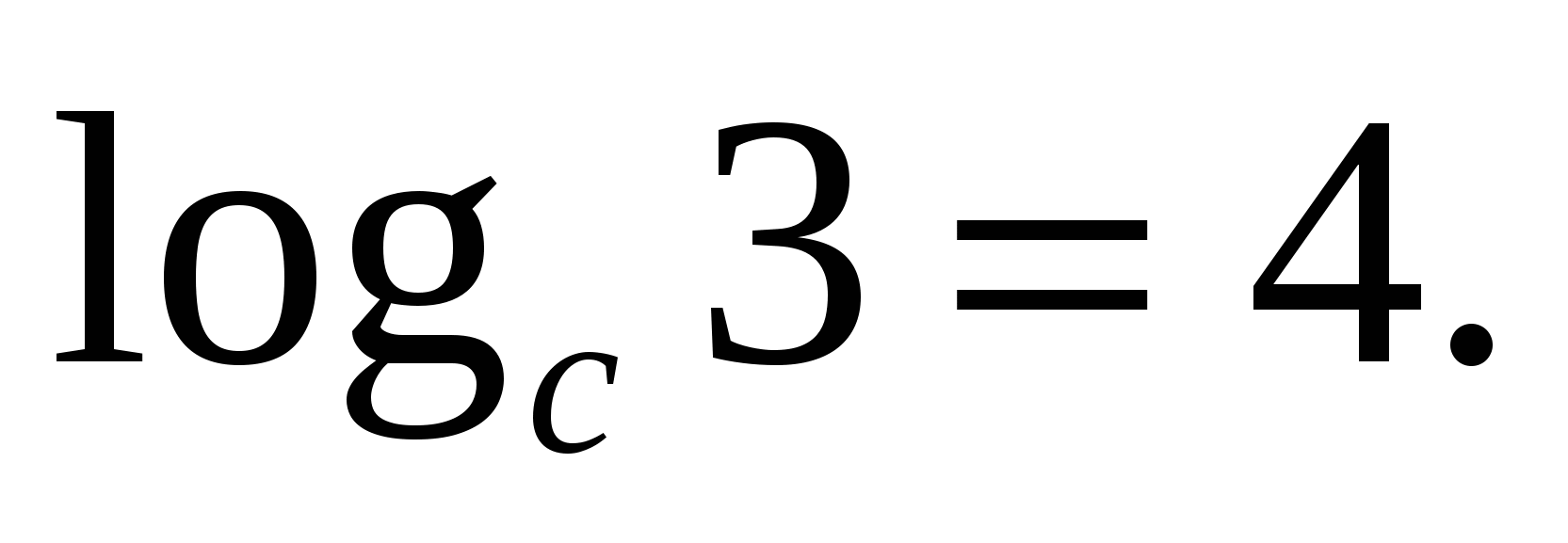Pogledajmo primjenu ove formule na primjeru:

W
zadatak 1. Odredi vrijednost izraza if

Zadatak 2. Pronađite vrijednost b svojim logaritmom

6) Logaritam stupnja prema bazia , jednak je proizvodu eksponent po logaritmu u istoj bazi.

DER 4

Na primjer,

W
zadatak 1. Izračunajte ako

Pojednostavimo izraz

Formula

nazvao formula za prijelaz na novu osnovu.

W

zadatak 1. Izrazite logaritmom s bazom 2.

Zadatak 2. Izračunati

CER 5

CER 6

Na primjer,

W

zadatak 1. Izračunati

W
zadatak 2. Izračunati

9) Logaritamske transformacije možete započeti samo ako ako zapamtite sva svojstva logaritama. Nakon što ih ponovimo, razmotrit ćemo zadatke za transformaciju logaritamskih izraza s druge strane.

Za pretvorbu zbroja ili razlike logaritamskih izraza ponekad je dovoljno koristiti se definicijom logaritma, a najčešće svojstvima logaritma umnoška ili kvocijenta.

W
zadatak 1. Izračunati

Riješimo to na dva načina.

1 način, koristeći definiciju logaritma:

Metoda 2 temelji se na svojstvo kvocijentnog logaritma:

Zadatak 2. Pronađite vrijednost izraza

Prvo primijenimo formulu logaritam umnoška, ​​zatim definicija logaritma.

Osnovni logaritamski identitet koristi se pri pretvorbi izraza koji sadrže logaritam u eksponentu. Ideja takvih operacija je da se baza eksponenta i baza logaritma izjednače.

Ponekad je potrebno transformirati izraz svojstvima logaritma i svojstvima stupnja, također može se lako prijeći s jedne baze na drugu pomoću formule prijelaza. U drugim slučajevima treba primijeniti više svojstava.

W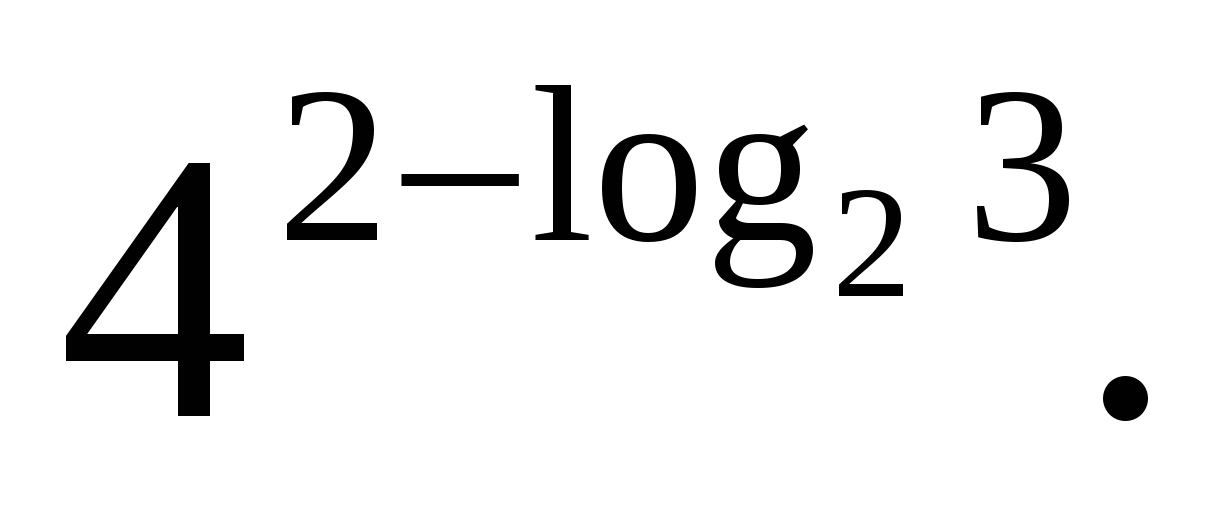
zadatak 3. Izračunati

W
zadatak 4. Pronađite vrijednost izraza

Zadatak 5. Pronađite vrijednost izraza

W
zadatak 6. Izrazite kao razliku logaritama

H
Najveća poteškoća je transformacija logaritamskih izraza pod radikalom. U procesu transformacija treba uzeti u obzir module logaritamskih izraza, za čije je otkrivanje potrebno usporediti iracionalne brojeve ili racionalne i iracionalne brojeve. Djelovat ćemo dosljedno. Razmotrimo izraz ispod unutarnjeg radikala.

Zamjena u izvornom izrazu.

Valja napomenuti da se transformacija logaritamskih izraza može susresti i pri rješavanju jednadžbi i nejednadžbi ili proučavanju funkcija, stoga u implicitnom obliku mogu biti prisutne i u zadacima skupine B i C.

10) Sažetak. Pitanja:

Logaritam s bazom 10 naziva se

osnovni logaritam

glavni logaritam

prirodni logaritam

decimalni logaritam

2) Koje vrijednosti mogux u izražavanju

Vrijednost nije definirana

5) Označite omjer koji vrijedi za svex ≠ 0 .

6) Navedite točan omjer za formulu za prijelaz na novu bazu.

7) Navedite točnu jednakost za

11) Kontrolno ispitivanje.

pridnjestrovskog Državno sveučilište

ih. T.G. Ševčenko

Fizičko-matematički fakultet

Zavod za matematičku analizu

i metodike nastave matematike

NASTAVNI RAD

„Transformacije identiteta

eksponencijalni i logaritamski

izrazi"

Radovi završeni:

student ______ grupe

Fizičko-matematički fakultet

_________________________

Provjereni rad:

_________________________

Tiraspol, 2003

Uvod…………………………………………………………………………2

Poglavlje 1

§jedan. Formiranje vještina za primjenu specifičnih vrsta transformacija…………………………………………………………………………………….4

§2. Značajke organizacije sustava znanja u proučavanju identičnih transformacija.…….………………………….………..………….5

§3. Program matematike ………………………………………….11

2. Poglavlje

§jedan. Generalizacija pojma stupnja……………………………………..13

§2. Eksponencijalna funkcija…………………………………………..15

§3. Logaritamska funkcija………………………………………….16

Poglavlje 3. Identične transformacije eksponencijalnih i logaritamskih izraza u praksi ...................................... ...... ...................................19

Zaključak…………………………………………………………………..24

Popis korištene literature…………………………………….25
Uvod

U ovom kolegiju će se razmotriti identične transformacije eksponencijalne i logaritamske funkcije, razmotriti metodologija njihovog poučavanja u školskom kolegiju algebre i početak analize.

Prvo poglavlje ovog rada opisuje metodologiju poučavanja identičnih transformacija u školskom kolegiju matematike, također uključuje program iz matematike u kolegiju "Algebra i početak analize" s proučavanjem eksponencijalnih i logaritamskih funkcija.

Drugo poglavlje bavi se izravno samim eksponencijalnim i logaritamskim funkcijama, njihovim glavnim svojstvima koja se koriste u identičnim transformacijama.

Treće poglavlje je rješavanje primjera i zadataka pomoću identične transformacije eksponencijalne i logaritamske funkcije.

Proučavanje različitih transformacija izraza i formula zauzima značajan dio vremena učenja u školskoj matematici. Najjednostavnije transformacije temeljene na svojstvima aritmetičkih operacija već se izvode u osnovna škola te u IV-V razredu. Ali glavni teret formiranja vještina i sposobnosti za izvođenje transformacija nosi tečaj školske algebre. To je povezano kako s naglim povećanjem broja i raznolikosti izvedenih transformacija, tako i s kompliciranjem aktivnosti za njihovo potkrijepljenje i razjašnjavanje uvjeta primjenjivosti, s identifikacijom i proučavanjem generaliziranih koncepata identiteta, identične transformacije, ekvivalentne transformacije, logična posljedica.

Kultura izvođenja identičnih transformacija razvija se na isti način kao i kultura računalstva, temeljena na dobrom poznavanju svojstava operacija nad objektima (brojevi, vektori, polinomi itd.) i algoritama za njihovu provedbu. Ono se ne očituje samo u sposobnosti ispravnog opravdavanja transformacija, već i u sposobnosti pronalaženja najkraćeg puta do prijelaza s izvornog analitičkog izraza na izraz koji najbolje odgovara svrsi transformacije, u sposobnosti praćenja promjena u domena definiranja analitičkih izraza u lancu identičnih transformacija, u brzini i bezgrešnom izvođenju transformacija.

Osiguravanje visoke kulture računanja i identičnih transformacija važan je problem u nastavi matematike. Međutim, ovaj problem još je daleko od zadovoljavajućeg rješenja. Dokaz za to su statistički podaci javnih prosvjetnih vlasti, u kojima se svake godine navode pogreške i neracionalne metode izračuna i transformacija koje su napravili učenici. razne klase dok radiš kontrolni radovi. To potvrđuju i mišljenja viših obrazovne ustanove o kvaliteti matematičkih znanja i vještina pristupnika. Ne može se ne složiti sa zaključcima javnih obrazovnih vlasti i sveučilišta da to nije dovoljno visoka razina kultura računalstva i identične transformacije u Srednja škola je posljedica formalizma u znanju učenika, odvajanja teorije od prakse.

Transformacije identiteta i metode poučavanja

u školskom tečaju algebre i početak analize.

§jedan. Formiranje vještina primjene

specifične vrste transformacija.

Sustav metoda i pravila za provođenje transformacija, korišten u fazi početaka algebre, ima vrlo širok raspon primjena: koristi se u proučavanju cijelog tečaja matematike. Međutim, upravo zbog svoje niske specifičnosti, ovaj sustav treba dodatne transformacije koje uzimaju u obzir osobitosti strukture transformiranih izraza i svojstva novouvedenih operacija i funkcija. Razvoj odgovarajućih vrsta transformacija počinje uvođenjem skraćenih formula množenja. Zatim razmatramo transformacije povezane s operacijom potenciranja, s različitim klasama elementarne funkcije- eksponencijalni, potencijski, logaritamski, trigonometrijski. Svaka od ovih vrsta transformacija prolazi kroz fazu proučavanja, u kojoj je pozornost usmjerena na asimilaciju njihovih karakterističnih značajki.

Nagomilavanjem materijala postaje moguće izdvojiti zajedničke značajke svih razmatranih transformacija i na temelju toga uvesti pojmove identične i ekvivalentne transformacije.

Treba napomenuti da je koncept identične transformacije dan u školskom tečaju algebre ne u punoj općenitosti, već samo u primjeni na izraze. Transformacije se dijele u dvije klase: identične transformacije su transformacije izraza, a ekvivalentne transformacije su transformacije formula. U slučaju kada postoji potreba za pojednostavljenjem jednog dijela formule, u ovoj formuli je istaknut izraz koji služi kao argument za primijenjenu identičnu transformaciju. Odgovarajući predikat smatra se nepromijenjenim.

Što se tiče organizacije cjelovitog sustava transformacija (sinteza), njegov glavni cilj je formiranje fleksibilnog i snažnog; uređaj pogodan za korištenje u rješavanju raznih obrazovnih zadataka.

Tijekom algebre i početaka analize nastavlja se postupno usavršavati integralni sustav transformacija, već formiran u svojim glavnim značajkama. Dodane su mu i neke nove vrste transformacija, ali one ga samo obogaćuju, proširuju njegove mogućnosti, ali ne mijenjaju njegovu strukturu. Metodologija proučavanja ovih novih transformacija praktički se ne razlikuje od one koja se koristi u tečaju algebre.

§2. Značajke organizacije sustava zadataka

u proučavanju identičnih transformacija.

Osnovno načelo organiziranja bilo kojeg sustava zadataka je prikazati ih od jednostavnih prema složenima, uzimajući u obzir potrebu učenika da prevladaju moguće poteškoće i stvore problemske situacije. Navedeno osnovno načelo zahtijeva konkretizaciju u odnosu na značajke ovog obrazovnog materijala. Za opis različitih sustava zadataka u metodici matematike koristi se koncept ciklusa vježbi. Ciklus vježbi karakterizira kombinacija u slijedu vježbi više aspekata učenja i načina sređivanja gradiva. U odnosu na identične transformacije, ideja ciklusa može se dati na sljedeći način.

Ciklus vježbi povezan je s proučavanjem jednog identiteta, oko kojeg se grupiraju drugi identiteti koji su s njim u prirodnoj vezi. Sastav ciklusa, uz izvedbene poslove, uključuje i poslove koji zahtijevaju prepoznavanje primjenjivosti razmatranog identiteta. Identitet koji se proučava koristi se za izvođenje izračuna na različitim numeričkim domenama. Uzima se u obzir specifičnost identiteta; posebno se organiziraju obrati govora povezani s njim.

Zadaci u svakom ciklusu podijeljeni su u dvije skupine. Prvi uključuje zadatke koji se obavljaju tijekom inicijalnog upoznavanja identiteta. Oni poslužuju obrazovni materijal za nekoliko uzastopnih lekcija, objedinjenih jednom temom. Druga skupina vježbi povezuje identitet koji se proučava s različitim primjenama. Ova grupa ne čini kompozicijsko jedinstvo - vježbe su ovdje razbacane po različitim temama.

Opisana struktura ciklusa odnosi se na stupanj formiranja vještina za primjenu pojedinih vrsta transformacija. U završnoj fazi - fazi sinteze, ciklusi se modificiraju. Prvo se kombiniraju obje skupine zadataka, tvoreći "razmotani" ciklus, a najjednostavniji u smislu riječi ili složenosti izvršenja zadataka isključeni su iz prve skupine. Preostale vrste zadataka postaju teže. Drugo, dolazi do stapanja ciklusa vezanih uz različite identitete, zbog čega se povećava uloga radnji za prepoznavanje primjenjivosti jednog ili drugog identiteta.

Uočavamo značajke ciklusa zadataka vezane uz identitete za elementarne funkcije. Ove značajke su posljedica činjenice da se, prvo, odgovarajući identiteti proučavaju u vezi s proučavanjem funkcionalnog materijala i, drugo, pojavljuju se kasnije od identiteta prve skupine i proučavaju se pomoću već formiranih vještina za provođenje identičnih transformacija. .

Svaka novouvedena elementarna funkcija oštro proširuje raspon brojeva koji se mogu pojedinačno označavati i imenovati. Stoga bi u prvoj skupini zadataka ciklusa trebali biti zadaci za uspostavljanje veze između ovih novih numeričkih područja i izvornog područja racionalnih brojeva. Dajemo primjere takvih zadataka.

Primjer 1 Izračunajte:

Uz svaki izraz nalazi se identitet, u ciklusima za koje mogu biti prisutni predloženi zadaci. Svrha takvih zadataka je ovladavanje značajkama zapisa, uključujući simbole novih operacija i funkcija, te razvijanje matematičkih govornih vještina.

Značajan dio korištenja transformacija identiteta povezanih s elementarnim funkcijama otpada na rješavanje iracionalnih i transcendentalnih jednadžbi. Ciklusi koji se odnose na asimilaciju identiteta uključuju samo najjednostavnije jednadžbe, ali već ovdje je preporučljivo raditi na ovladavanju metodom rješavanja takvih jednadžbi: smanjivanjem zamjenom nepoznate u algebarsku jednadžbu.

Redoslijed koraka za ovo rješenje je sljedeći:

a) pronaći funkciju za koju se ova jednadžba može prikazati kao ;

b) izvršiti zamjenu i riješiti jednadžbu;

c) riješiti svaku od jednadžbi , gdje je skup korijena jednadžbe .

Kada se koristi opisana metoda, korak b) se često izvodi implicitno, bez uvođenja notacije za . Osim toga, učenici često između različitih putova koji vode do odgovora biraju onaj koji brže i lakše vodi do algebarske jednadžbe.

Primjer 2. Riješite jednadžbu.

Prvi način:

Drugi način:

a)

b)

Ovdje se može vidjeti da je korak a) teži u prvoj metodi nego u drugoj. Prvi način je “teže započeti”, iako je daljnji tijek rješenja mnogo lakši. S druge strane, druga metoda ima prednosti koje se sastoje u većoj lakoći, većoj sofisticiranosti u podučavanju redukcije na algebarsku jednadžbu.

Za školski tečaj algebre tipični su zadaci u kojima je prijelaz na algebarsku jednadžbu još lakši nego u ovom primjeru. Glavni teret takvih zadataka odnosi se na odabir koraka c) kao neovisnog dijela procesa rješavanja povezanog s korištenjem svojstava elementarne funkcije koja se proučava.

Primjer 3. Riješite jednadžbu:

a) ; b) .

Te se jednadžbe svode na jednadžbe: a) ili ; b) ili. Za rješavanje ovih jednadžbi potrebno je poznavanje samo najjednostavnijih činjenica o eksponencijalnoj funkciji: njezina monotonost, raspon vrijednosti. Kao i prethodni primjer, jednadžbe a) i b) mogu se svrstati u prvu skupinu ciklusa vježbi za rješavanje kvadratnih eksponencijalnih jednadžbi.

Tako dolazimo do klasifikacije zadataka u ciklusima koji se odnose na rješavanje transcendentnih jednadžbi, uključujući eksponencijalnu funkciju:

1) jednadžbe koje se svode na jednadžbe oblika i imaju jednostavan odgovor, općeg oblika: ;

2) jednadžbe koje se svode na jednadžbe , gdje je cijeli broj, ili , gdje je ;

3) jednadžbe koje se svode na jednadžbe i zahtijevaju eksplicitnu analizu oblika u kojem je broj napisan.

Slični zadaci mogu se klasificirati za druge elementarne funkcije.

Značajan dio identiteta koji se proučavaju u kolegijima algebre i algebre i početaka analize u njima je dokazan ili barem objašnjen. Ova strana proučavanja identiteta ima veliki značaj za oba kolegija, budući da se u njima demonstrativno rasuđivanje provodi s najvećom jasnoćom i strogošću upravo u odnosu na identitete. Izvan ovog materijala, dokazi su obično manje potpuni, ne razlikuju se uvijek od sastava primijenjenih sredstava opravdanja.

Svojstva aritmetičkih operacija koriste se kao oslonac na kojem se grade dokazi identiteta.

Obrazovni učinak izračuna i identičnih transformacija može se usmjeriti na razvoj logično mišljenje, ako se samo od učenika sustavno zahtijeva opravdavanje izračuna i identičnih transformacija, razvijanje funkcionalnog mišljenja, što se postiže na razne načine. Vrlo je očita važnost kalkulacija i istovjetnih transformacija u razvoju volje, pamćenja, domišljatosti, samokontrole i kreativne inicijative.

Zahtjevi za svakodnevnom, industrijskom računalnom praksom zahtijevaju kod učenika formiranje jakih, automatiziranih vještina racionalnih proračuna i identičnih transformacija. Ove se vještine razvijaju u procesu bilo kojeg računalnog rada, međutim, potrebne su posebne vještine. vježbe treninga u brzim proračunima i transformacijama.

Dakle, ako lekcija uključuje rješavanje logaritamskih jednadžbi korištenjem osnovnog logaritamskog identiteta, tada je korisno u nastavni plan uključiti usmene vježbe za pojednostavljenje ili izračunavanje vrijednosti izraza: , , . Svrha vježbi uvijek se priopćava studentima. Tijekom vježbe može biti potrebno zahtijevati od učenika da obrazlože pojedine transformacije, radnje ili da riješe cijeli problem, čak i ako to nije planirano. Tamo gdje su mogući različiti načini rješavanja problema, uvijek je poželjno postaviti pitanja: “Na koji je način problem riješen?”, “Tko je problem riješio na drugačiji način?”

Koncepti identiteta i identične transformacije eksplicitno su predstavljeni u kolegiju algebre VI. razreda. Sama definicija identičnih izraza ne može se praktično koristiti za dokazivanje identičnosti dvaju izraza, te za razumijevanje da se bit identičnih transformacija sastoji u primjeni na izraz definicija i svojstava onih radnji koje su naznačene u izrazu, ili u zbrajanju njemu izraz koji je identički jednak 0, ili u množenju s izrazom identički jednak jedan. Ali, čak i nakon što su svladali ove odredbe, učenici često ne razumiju zašto nam te transformacije omogućuju da tvrdimo da su izvorni i rezultirajući izrazi identični, tj. uzeti iste vrijednosti za sve sustave (skupove) varijabilnih vrijednosti.

Također je važno osigurati da učenici dobro razumiju da su takvi zaključci identičnih transformacija posljedice definicija i svojstava odgovarajućih radnji.

U 6. razredu se proširuje aparat identičnih transformacija, akumuliran prethodnih godina. Ovo proširenje počinje uvođenjem identiteta koji izražava svojstvo umnoška potencija s istim bazama: , gdje su , cijeli brojevi.

§3. Program matematike. U školskom kolegiju „Algebra i počeci analize“ učenici sustavno proučavaju eksponencijalne i logaritamske funkcije i njihova svojstva, identične transformacije logaritamskih i eksponencijalnih izraza i njihovu primjenu na rješavanje odgovarajućih jednadžbi i nejednadžbi, upoznaju se s osnovnim pojmovima, tvrdnjama . U 11. razredu nastava algebre traje 3 sata tjedno, ukupno 102 sata godišnje. Za učenje eksponencijalne, logaritamske i potencije prema programu potrebno je 36 sati. Program uključuje razmatranje i proučavanje sljedećih pitanja: Pojam diplome s racionalnim pokazateljem. Rješenje iracionalnih jednadžbi. Eksponencijalna funkcija, njezina svojstva i graf. identične transformacije eksponencijalnih izraza. Rješavanje eksponencijalnih jednadžbi i nejednadžbi. Logaritam broja. Osnovna svojstva logaritama. Logaritamska funkcija, njezina svojstva i graf. Rješavanje logaritamskih jednadžbi i nejednadžbi. Derivacija eksponencijalne funkcije. Broj i prirodni logaritam. Derivacija funkcije potencije. Glavna svrha odjeljka o proučavanju eksponencijalnih i logaritamskih funkcija je upoznavanje učenika s eksponencijalnim, logaritamskim i potencijskim funkcijama; naučiti učenike rješavati eksponencijalne i logaritamske jednadžbe i nejednakosti. Koncepti korijena th stupnja i stupnja s racionalnim eksponentom su generalizacija pojmova kvadratnog korijena i stupnja s cjelobrojnim eksponentom. Učenici trebaju obratiti pozornost na činjenicu da su ovdje razmatrana svojstva korijena i stupnjeva s racionalnim eksponentom slična onim svojstvima koja su ranije proučavana. kvadratni korijeni a stupnjevi s cjelobrojnim eksponentima. Potrebno je posvetiti dovoljno vremena razradi svojstava stupnjeva i formiranju vještina za identične transformacije. Pojam diplome sa iracionalni pokazatelj uveden na vizualno-intuitivnoj osnovi. Ovaj materijal ima pomoćnu ulogu i koristi se pri uvođenju eksponencijalne funkcije. Proučavanje svojstava eksponencijalne, logaritamske i potencije izgrađeno je u skladu s prihvaćenim opća shema istraživanje funkcije. U ovom slučaju dan je pregled svojstava ovisno o vrijednostima parametara. Na temelju proučavanih svojstava funkcija rješavaju se eksponencijalne i logaritamske nejednadžbe. Karakteristična značajka kolegija je sistematizacija i generalizacija znanja učenika, konsolidacija i razvoj vještina i sposobnosti stečenih u kolegiju algebre, koji se provodi i pri proučavanju novog materijala i pri provođenju generalizirajućeg ponavljanja.
2. Poglavlje

§jedan. Generalizacija pojma stupnja.

Definicija: Korijen th stupnja čistoće je takav broj, čiji je th stupanj jednak.

Prema ovoj definiciji, korijen th stupnja broja je rješenje jednadžbe. Broj korijena ove jednadžbe ovisi o i . Razmotrimo funkciju. Kao što je poznato, na intervalu ova funkcija raste za bilo koji i uzima sve vrijednosti iz intervala. Prema teoremu o korijenu, jednadžba za bilo koji ima nenegativan korijen, štoviše, samo jedan. Naziva se aritmetičkim korijenom th stupnja broja i označava; broj se naziva indeks korijena, a sam broj naziva se radikalni izraz. Znak se također naziva radikal.

Definicija: Aritmetički korijen th stupnja broja je nenegativan broj čiji je th stupanj .

Za par, funkcija je parna. Slijedi da ako , onda jednadžba osim korijena ima i korijen . Ako je , tada postoji samo jedan korijen: ; ako je , tada ova jednadžba nema korijena, budući da je parna potencija bilo kojeg broja nenegativna.

Za neparne vrijednosti funkcija raste duž cijelog brojevnog pravca; njegov raspon je skup svih realnih brojeva. Primjenom teorema o korijenu nalazimo da jednadžba ima jedan korijen za bilo koji i, posebno, za . Ovaj korijen za bilo koju vrijednost je označen sa .

Za korijene neparnog stupnja jednakost vrijedi. Doista, tj. broj je th korijen od . Ali takav korijen za neparan je jedinstven. Posljedično,.

Primjedba 1: Za svaki pravi

Prisjetimo se dobro poznatih svojstava aritmetičkih korijena th stupnja.

Za svaki prirodni, cijeli broj i sve ne-negativne cijele brojeve i jednakosti su istinite:

1.

2.

3.

4.

Stupanj s racionalnim eksponentom.

Izraz je definiran za sve i , osim za slučaj kada je . Prisjetite se svojstava takvih ovlasti.

Za sve brojeve i sve cijele brojeve i jednakosti su istinite:

Također primjećujemo da ako , onda za i za .. i

Za učenike koji studiraju za jedinstveni državni ispit, nastavnici matematike u srednjoj školi br. 26 u Jakutsku koriste popis pitanja sadržaja (kodifikator) ​​školskog tečaja matematike, čija se asimilacija provjerava prilikom polaganja jedinstvenog državnog ispita 2007. . izborni predmet u pripremi za Unified Državni ispit temelji se na ponavljanju, usustavljivanju i produbljivanju ranije stečenih znanja. Nastava se održava u obliku besplatnih...

Navedene jednakosti pri pretvorbi izraza s logaritmima koriste se i s desna na lijevo i slijeva na desno.

Vrijedno je napomenuti da nije potrebno pamtiti posljedice svojstava: prilikom izvođenja transformacija možete se snaći s osnovnim svojstvima logaritama i drugim činjenicama (na primjer, onima za b≥0), iz kojih odgovarajuće slijede posljedice. “Nuspojava” ovakvog pristupa je samo to što će rješenje biti malo duže. Na primjer, kako bi se izbjegla posljedica, koja je izražena formulom , a polazeći samo od osnovnih svojstava logaritama, morat ćete provesti lanac transformacija sljedećeg oblika: .

Isto se može reći i za posljednje svojstvo s gornje liste, koje odgovara formuli , budući da to također proizlazi iz osnovnih svojstava logaritama. Najvažnije je razumjeti da je uvijek moguće da stupanj pozitivnog broja s logaritmom u eksponentu zamijeni bazu stupnja i broj pod znakom logaritma. Iskreno radi, napominjemo da su primjeri provedbe transformacija ove vrste rijetki u praksi. U nastavku ćemo dati nekoliko primjera.

Pretvaranje numeričkih izraza s logaritmima

Sjetili smo se svojstava logaritama, a sada je vrijeme da naučimo kako ih primijeniti u praksi za transformaciju izraza. Prirodno je započeti s transformacijom numeričkih izraza, a ne izraza s varijablama, jer je na njima praktičnije i lakše naučiti osnove. Tako ćemo i učiniti, a počet ćemo s vrlo jednostavni primjeri kako bismo naučili odabrati željeno svojstvo logaritma, no primjere ćemo postupno komplicirati, sve do trenutka kada će za konačni rezultat trebati primijeniti nekoliko svojstava zaredom.

Odabir željenog svojstva logaritama

Nema tako malo svojstava logaritama i jasno je da od njih treba znati odabrati ono odgovarajuće koje će u ovom konkretnom slučaju dovesti do željenog rezultata. Obično to nije teško učiniti usporedbom oblika logaritma ili izraza koji se pretvara s vrstama lijevog i desnog dijela formula koje izražavaju svojstva logaritama. Ako ostane ili desni dio jedna od formula podudara se s danim logaritmom ili izrazom, tada bi najvjerojatnije to svojstvo trebalo koristiti tijekom transformacije. Sljedeći primjeri to jasno pokazuju.

Počnimo s primjerima transformiranja izraza pomoću definicije logaritma, koji odgovara formuli a log a b =b , a>0 , a≠1 , b>0 .

Primjer.

Izračunajte, ako je moguće: a) 5 log 5 4 , b) 10 log(1+2 π) , c) , d) 2 log 2 (−7) , e) .

Riješenje.

U primjeru slovo a) jasno prikazuje strukturu a log a b , gdje je a=5 , b=4 . Ovi brojevi zadovoljavaju uvjete a>0 , a≠1 , b>0 , tako da možete slobodno koristiti jednakost a log a b =b . Imamo 5 log 5 4=4 .

b) Ovdje su a=10 , b=1+2 π , uvjeti a>0 , a≠1 , b>0 ispunjeni. U ovom slučaju vrijedi jednakost 10 lg(1+2 π) =1+2 π.

c) I u ovom primjeru imamo posla sa stupnjem oblika a log a b , gdje je i b=ln15 . Tako .

Unatoč tome što pripada istom obliku a log a b (ovdje a=2 , b=−7 ), izraz pod slovom d) ne može se pretvoriti formulom a log a b =b . Razlog je taj što nema smisla jer sadrži negativan broj ispod znaka logaritma. Štoviše, broj b=−7 ne zadovoljava uvjet b>0 , što onemogućuje pribjegavanje formuli a log a b =b , jer zahtijeva uvjete a>0 , a≠1 , b>0 . Dakle, ne možemo govoriti o izračunavanju vrijednosti 2 log 2 (−7) . U ovom slučaju pisanje 2 log 2 (−7) = −7 bila bi pogreška.

Isto tako, u primjeru pod slovom e) nemoguće je dati rješenje oblika , jer izvorni izraz nema smisla.

Odgovor:

a) 5 log 5 4 =4 , b) 10 log(1+2 π) =1+2 π , c) , d), e) izrazi nemaju smisla.

Često je korisno transformirati pozitivan broj predstavlja se kao potencija nekog pozitivnog i nejedan broja s logaritmom u eksponentu. Temelji se na istoj definiciji logaritma a log a b =b , a>0 , a≠1 , b>0 , ali se formula primjenjuje s desna na lijevo, odnosno u obliku b=a log a b . Na primjer, 3=e ln3 ili 5=5 log 5 5 .

Prijeđimo na korištenje svojstava logaritama za transformaciju izraza.

Primjer.

Odredite vrijednost izraza: a) log −2 1, b) log 1 1, c) log 0 1, d) log 7 1, e) ln1, f) lg1, g) log 3,75 1, h) log 5 π 7 1 .

Riješenje.

U primjerima pod slovima a), b) i c) navedeni su izrazi log −2 1 , log 1 1 , log 0 1 koji nemaju smisla jer baza logaritma ne smije sadržavati negativan broj , nula ili jedan, jer smo definirali logaritam samo za pozitivnu i nejediničnu bazu. Stoga u primjerima a) - c) ne može biti riječi o pronalaženju vrijednosti izraza.

U svim ostalim zadacima, očito, u bazama logaritama stoje pozitivni i nejedinički brojevi 7, e, 10, 3,75 odnosno 5 π 7, a jedinice su posvuda ispod predznaka logaritama. I znamo svojstvo logaritma jedinice: log a 1=0 za bilo koji a>0 , a≠1 . Dakle, vrijednosti izraza b) - f) jednake su nuli.

Odgovor:

a), b), c) izrazi nemaju smisla, d) log 7 1=0, e) ln1=0, f) log1=0, g) log 3,75 1=0, h) log 5 e 7 1 =0.

Primjer.

Izračunajte: a) , b) lne , c) lg10 , d) log 5 π 3 −2 (5 π 3 −2), e) log −3 (−3) , f) log 1 1 .

Riješenje.

Jasno je da moramo koristiti svojstvo logaritma baze, što odgovara formuli log a a=1 za a>0 , a≠1 . Doista, u zadacima pod svim slovima, broj pod znakom logaritma podudara se s njegovom bazom. Dakle, želim odmah reći da je vrijednost svakog od zadanih izraza 1 . Ipak, nemojte žuriti sa zaključcima: u zadacima pod slovima a) - d) vrijednosti izraza su stvarno jednake jedinici, a u zadacima e) i f) izvorni izrazi nemaju smisla, pa se ne može možemo reći da su vrijednosti ovih izraza jednake 1.

Odgovor:

a) , b) lne=1 , c) lg10=1 , d) log 5 π 3 −2 (5 π 3 −2)=1, e), f) izrazi nemaju smisla.

Primjer.

Odredite vrijednost: a) log 3 3 11 , b) , c) , d) log −10 (−10) 6 .

Riješenje.

Očito, pod predznacima logaritama su neki stupnjevi baze. Na temelju ovoga razumijemo da je svojstvo stupnja baze korisno ovdje: log a a p =p, gdje je a>0, a≠1 i p bilo koji realni broj. S obzirom na to, imamo sljedeće rezultate: a) log 3 3 11 =11 , b) , u) . Može li se slična jednakost napisati za primjer pod slovom d) oblika log −10 (−10) 6 =6? Ne, ne možete, jer log −10 (−10) 6 nema smisla.

Odgovor:

a) log 3 3 11 =11, b) , u) d) izraz nema smisla.

Primjer.

Izrazite izraz kao zbroj ili razliku logaritama u istoj bazi: a) , b) , c) log((−5) (−12)) .

Riješenje.

a) Umnožak je pod predznakom logaritma, a znamo svojstvo logaritma umnoška log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y> 0 . U našem slučaju, broj u bazi logaritma i brojevi u umnošku su pozitivni, odnosno zadovoljavaju uvjete odabranog svojstva, stoga ga možemo sigurno primijeniti: .

b) Ovdje koristimo svojstvo logaritma kvocijenta , gdje je a>0 , a≠1 , x>0 , y>0 . U našem slučaju baza logaritma je pozitivan broj e, brojnik i nazivnik π su pozitivni, što znači da zadovoljavaju uvjete svojstva, pa imamo pravo koristiti odabranu formulu: .

c) Prvo, primijetite da izraz lg((−5) (−12)) ima smisla. Ali u isto vrijeme, nemamo pravo primijeniti formulu za logaritam umnoška log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 , budući da su brojevi −5 i −12 negativni i ne zadovoljavaju uvjete x>0 , y>0 . Odnosno, nemoguće je izvršiti takvu transformaciju: log((−5)(−12))=log(−5)+log(−12). Ali što učiniti? U takvim slučajevima, izvorni izraz treba prethodno transformirati kako bi se izbjegli negativni brojevi. O sličnim slučajevima preoblikovanja izraza sa negativni brojevi pod znakom logaritma, govorit ćemo detaljno u jednom od, ali za sada ćemo dati rješenje ovog primjera, koji je unaprijed jasan i bez objašnjenja: lg((−5)(−12))=lg(5 12)=lg5+lg12.

Odgovor:

a) , b) , c) lg((−5) (−12))=lg5+lg12 .

Primjer.

Pojednostavite izraz: a) log 3 0,25 + log 3 16 + log 3 0,5, b) .

Riješenje.

Ovdje će nam pomoći sva ista svojstva logaritma umnoška i logaritma kvocijenta koja smo koristili u prethodnim primjerima, samo ćemo ih sada primijeniti s desna na lijevo. Odnosno, zbroj logaritama pretvaramo u logaritam umnoška, ​​a razliku logaritama u logaritam kvocijenta. Imamo
a) log 3 0,25+log 3 16+log 3 0,5=log 3 (0,25 16 0,5)=log 3 2.
b) .

Odgovor:

a) log 3 0,25+log 3 16+log 3 0,5=log 3 2, b) .

Primjer.

Riješite se stupnja ispod znaka logaritma: a) log 0,7 5 11, b) , c) log 3 (−5) 6 .

Riješenje.

Lako je vidjeti da imamo posla s izrazima poput log a b p . Odgovarajuće svojstvo logaritma je log a b p =p log a b , gdje je a>0 , a≠1 , b>0 , p bilo koji realan broj. To jest, pod uvjetima a>0 , a≠1 , b>0 od logaritma stupnja log a b p možemo ići do produkta p·log a b . Provedimo ovu transformaciju s danim izrazima.

a) U ovom slučaju a=0,7 , b=5 i p=11 . Dakle, log 0,7 5 11 =11 log 0,7 5 .

b) Ovdje su ispunjeni uvjeti a>0 , a≠1 , b>0. Zato

c) Izraz log 3 (−5) 6 ima istu strukturu log a b p , a=3 , b=−5 , p=6 . Ali za b, uvjet b>0 nije zadovoljen, što onemogućuje primjenu formule log a b p =p log a b . Pa zašto ne možete obaviti posao? Moguće je, ali potrebna je preliminarna transformacija izraza, o čemu ćemo detaljno raspravljati u nastavku u odlomku pod naslovom . Rješenje će biti ovako: log 3 (−5) 6 =log 3 5 6 =6 log 3 5.

Odgovor:

a) log 0,7 5 11 =11 log 0,7 5 ,
b)
c) log 3 (−5) 6 =6 log 3 5 .

Često se formula za logaritam stupnja pri izvođenju transformacija mora primijeniti s desna na lijevo u obliku p log a b \u003d log a b p (ovo zahtijeva iste uvjete za a, b i p). Na primjer, 3 ln5=ln5 3 i lg2 log 2 3=log 2 3 lg2 .

Primjer.

a) Izračunajte vrijednost log 2 5 ako je poznato da je lg2≈0,3010 i lg5≈0,6990. b) Zapišite razlomak kao logaritam bazi 3.

Riješenje.

a) Formula za prijelaz na novu bazu logaritma omogućuje nam da ovaj logaritam predstavimo kao omjer decimalnih logaritama, čije su nam vrijednosti poznate: . Ostaje samo izvršiti izračune, imamo .

b) Ovdje je dovoljno koristiti formulu za prijelaz na novu bazu i primijeniti je s desna na lijevo, odnosno u obliku . Dobivamo .

Odgovor:

a) log 2 5≈2,3223, b) .

U ovoj smo fazi prilično pažljivo razmotrili transformaciju najjednostavnijih izraza koristeći osnovna svojstva logaritama i definiciju logaritma. U ovim primjerima morali smo koristiti jedno svojstvo i ništa drugo. Sada, mirne savjesti, možete prijeći na primjere čija transformacija zahtijeva korištenje nekoliko svojstava logaritama i drugih dodatnih transformacija. Njima ćemo se pozabaviti u sljedećem paragrafu. Ali prije toga, zadržimo se kratko na primjerima primjene posljedica iz osnovnih svojstava logaritama.

Primjer.

a) Izbacite korijen pod predznakom logaritma. b) Pretvorite razlomak u logaritam s bazom 5. c) Oslobodite se potencija pod znakom logaritma i na njegovoj bazi. d) Izračunajte vrijednost izraza . e) Izraz zamijenite potencijom s bazom 3.

Riješenje.

a) Ako se prisjetimo korolarnog svojstva logaritma stupnja , tada možete odmah odgovoriti: .

b) Ovdje koristimo formulu s desna na lijevo, imamo .

c) B ovaj slučaj formula dovodi do rezultata . Dobivamo .

d) I ovdje je dovoljno primijeniti korolar kojem formula odgovara . Tako .

e) Svojstvo logaritma omogućuje postizanje željenog rezultata: .

Odgovor:

a) . b) . u) . G) . e) .

Dosljedna primjena višestrukih svojstava

Pravi zadaci transformacije izraza pomoću svojstava logaritama obično su kompliciraniji od onih kojima smo se bavili u prethodnom odlomku. U njima se u pravilu rezultat ne dobiva u jednom koraku, već se rješenje sastoji u sekvencijalnoj primjeni jednog svojstva za drugim, zajedno s dodatnim identičnim transformacijama, poput otvaranja zagrada, smanjivanja sličnih članova, smanjivanja razlomaka itd. . Priđimo dakle bliže takvim primjerima. U tome nema ništa komplicirano, glavna stvar je djelovati pažljivo i dosljedno, poštujući redoslijed izvođenja radnji.

Primjer.

Izračunajte vrijednost izraza (log 3 15−log 3 5) 7 log 7 5.

Riješenje.

Razliku logaritama u zagradama po svojstvu logaritma kvocijenta možemo zamijeniti logaritmom log 3 (15:5) , a zatim izračunati njegovu vrijednost log 3 (15:5)=log 3 3=1 . A vrijednost izraza 7 log 7 5 prema definiciji logaritma je 5 . Zamjenom ovih rezultata u izvorni izraz, dobivamo (log 3 15−log 3 5) 7 log 7 5 =1 5=5.

Evo rješenja bez objašnjenja:
(log 3 15−log 3 5) 7 log 7 5 =log 3 (15:5) 5=
= log 3 3 5=1 5=5 .

Odgovor:

(log 3 15−log 3 5) 7 log 7 5 =5.

Primjer.

Kolika je vrijednost brojčanog izraza log 3 log 2 2 3 −1 ?

Riješenje.

Prvo transformirajmo logaritam, koji je pod znakom logaritma, prema formuli logaritma stupnja: log 2 2 3 =3. Dakle, log 3 log 2 2 3 =log 3 3 i zatim log 3 3=1 . Dakle, log 3 log 2 2 3 −1=1−1=0 .

Odgovor:

log 3 log 2 2 3 −1=0 .

Primjer.

Pojednostavite izraz.

Riješenje.

Formula za pretvorbu u novu bazu logaritma omogućuje da se omjer logaritama prema jednoj bazi predstavi kao log 3 5 . U ovom slučaju, izvorni izraz će imati oblik . Po definiciji logaritma 3 log 3 5 =5 , tj , a vrijednost rezultirajućeg izraza, na temelju iste definicije logaritma, jednaka je dva.

Ovdje kratka verzija rješenje, koje se obično daje: .

Odgovor:

.

Za glatki prijelaz na informacije sljedećeg paragrafa, pogledajmo izraze 5 2+log 5 3 i lg0.01 . Njihova struktura ne odgovara niti jednom od svojstava logaritama. Dakle, što se događa ako se ne mogu pretvoriti korištenjem svojstava logaritama? To je moguće ako provedete preliminarne transformacije koje pripremaju ove izraze za primjenu svojstava logaritama. Tako 5 2+log 5 3 =5 2 5 log 5 3 =25 3=75, i lg0,01=lg10 −2 = −2 . Dalje ćemo detaljno razumjeti kako se takva priprema izraza provodi.

Priprema izraza za primjenu svojstava logaritama

Logaritmi u pretvorenom izrazu vrlo se često razlikuju po strukturi zapisa od lijevog i desnog dijela formula koje odgovaraju svojstvima logaritama. Ali isto tako često, transformacija ovih izraza uključuje korištenje svojstava logaritama: njihova upotreba zahtijeva samo prethodnu pripremu. A ta se priprema sastoji u provođenju određenih identičnih transformacija koje dovode logaritme u oblik pogodan za primjenu svojstava.

Iskreno radi, napominjemo da gotovo svaka transformacija izraza može djelovati kao preliminarna transformacija, od banalne redukcije sličnih izraza do primjene trigonometrijske formule. To je razumljivo jer pretvoreni izrazi mogu sadržavati bilo koje matematičke objekte: zagrade, module, razlomke, korijene, stupnjeve itd. Dakle, moramo biti spremni izvršiti bilo koju potrebnu transformaciju kako bismo dodatno iskoristili svojstva logaritama.

Recimo odmah da u ovom odjeljku ne postavljamo sebi zadatak klasificirati i analizirati sve zamislive preliminarne transformacije koje nam omogućuju da u budućnosti primijenimo svojstva logaritama ili definiciju logaritma. Ovdje ćemo se zadržati samo na četiri od njih, koji su najkarakterističniji i najčešće se susreću u praksi.

A sada detaljno o svakom od njih, nakon čega, u okviru naše teme, ostaje samo baviti se transformacijom izraza s varijablama pod znakovima logaritama.

Izbor potencija pod predznakom logaritma iu njegovoj bazi

Počnimo odmah s primjerom. Neka nam bude logaritam. Očito, u ovom obliku, njegova struktura nije pogodna za korištenje svojstava logaritama. Je li moguće nekako transformirati ovaj izraz kako bismo ga pojednostavili ili još bolje izračunali njegovu vrijednost? Da bismo odgovorili na ovo pitanje, pogledajmo pobliže brojeve 81 i 1/9 u kontekstu našeg primjera. Ovdje je lako vidjeti da se ti brojevi mogu predstaviti kao potencija broja 3, doista, 81=3 4 i 1/9=3 −2 . U ovom slučaju, izvorni logaritam je predstavljen u obliku i postaje moguće primijeniti formulu . Tako, .

Analiza analiziranog primjera dovodi do sljedeće ideje: ako je moguće, možete pokušati istaknuti stupanj ispod znaka logaritma i na njegovoj osnovi kako biste primijenili svojstvo logaritma stupnja ili njegove posljedice. Ostaje samo shvatiti kako izdvojiti ove stupnjeve. Dat ćemo neke preporuke o ovom pitanju.

Ponekad je posve očito da broj pod znakom logaritma i/ili u njegovoj bazi predstavlja neku cjelobrojnu potenciju, kao u primjeru koji je gore razmotren. Gotovo stalno morate imati posla s potencijama dvojke, koje su dobro poznate: 4=2 2 , 8=2 3 , 16=2 4 , 32=2 5 , 64=2 6 , 128=2 7 , 256=2 8 , 512= 2 9 , 1024=2 10 . Isto se može reći i za stupnjeve trojke: 9=3 2 , 27=3 3 , 81=3 4 , 243=3 5 , ... Općenito, ne šteti ako postoji tablica stupnjeva prirodni brojevi unutar deset. Također nije teško raditi s cjelobrojnim potencijama desetice, stotine, tisuće itd.

Primjer.

Izračunajte vrijednost ili pojednostavite izraz: a) log 6 216 , b) , c) log 0,000001 0,001 .

Riješenje.

a) Očito je 216=6 3 , pa je log 6 216=log 6 6 3 =3 .

b) Tablica potencija prirodnih brojeva omogućuje nam da brojeve 343 i 1/243 prikažemo kao potencije broja 7 3 odnosno 3 −4. Stoga je moguće sljedeća transformacija dati logaritam:

c) Kako je 0,000001=10 −6 i 0,001=10 −3, tada je log 0,000001 0,001=log 10 −6 10 −3 =(−3)/(−6)=1/2.

Odgovor:

a) log 6 216=3, b) , c) log 0,000001 0,001=1/2 .

U složenijim slučajevima, da biste istaknuli moć brojeva, morate pribjeći.

Primjer.

Promijenite izraz u jednostavniji oblik log 3 648 log 2 3 .

Riješenje.

Pogledajmo u što se sastoji proširenje broja 648 glavni faktori:

Odnosno, 648=2 3 3 4 . Na ovaj način, log 3 648 log 2 3=log 3 (2 3 3 4) log 2 3.

Sada pretvaramo logaritam umnoška u zbroj logaritama, nakon čega primjenjujemo svojstva logaritma stupnja:
log 3 (2 3 3 4) log 2 3=(log 3 2 3 + log 3 3 4) log 2 3=
=(3 log 3 2+4) log 2 3 .

Na temelju korolara svojstva logaritma stupnja, koji odgovara formuli , umnožak log32 log23 je umnožak , a poznato je da je jednak jedan. S obzirom na ovo, dobivamo 3 log 3 2 log 2 3+4 log 2 3=3 1+4 log 2 3=3+4 log 2 3.

Odgovor:

log 3 648 log 2 3=3+4 log 2 3.

Često su izrazi pod znakom logaritma iu njegovoj bazi umnošci ili omjeri korijena i/ili potencije nekih brojeva, na primjer, , . Slični izrazi mogu se prikazati kao stupanj. Da biste to učinili, provodi se prijelaz s korijena na stupnjeve i primjenjuju se i . Ove transformacije vam omogućuju da odaberete stupnjeve ispod znaka logaritma iu njegovoj bazi, a zatim primijenite svojstva logaritma.

Primjer.

Izračunaj: a) , b).

Riješenje.

a) Izraz u bazi logaritma je umnožak potencija s istim bazama, prema odgovarajućem svojstvu potencija imamo 5 2 5 −0,5 5 −1 =5 2−0,5−1 =5 0,5.

Sada pretvorimo razlomak pod znakom logaritma: pomaknimo se od korijena do stupnja, nakon čega ćemo koristiti svojstvo omjera stupnjeva s istim bazama: .

Ostaje zamijeniti dobivene rezultate u izvorni izraz, upotrijebiti formulu i dovršite transformaciju:

b) Budući da je 729=3 6 , a 1/9=3 −2 , izvorni izraz se može prepisati kao .

Zatim primijenite svojstvo korijena eksponenta, pomaknite se od korijena do eksponenta i upotrijebite svojstvo omjera potencija da pretvorite bazu logaritma u potenciju: .

Uzimajući u obzir posljednji rezultat, imamo .

Odgovor:

a) , b).

Jasno je da u općem slučaju, da bi se dobile potencije pod znakom logaritma iu njegovoj bazi, mogu biti potrebne različite transformacije različitih izraza. Navedimo par primjera.

Primjer.

Kolika je vrijednost izraza: a) , b) .

Riješenje.

Nadalje, napominjemo da navedeni izraz ima oblik log A B p , gdje je A=2 , B=x+1 i p=4 . Transformirali smo numeričke izraze ove vrste prema svojstvu logaritma stupnja log a b p \u003d p log a b, stoga, s danim izrazom, želim učiniti isto i ići od log 2 (x + 1) 4 na 4 log 2 (x + 1) . A sada izračunajmo vrijednost izvornog izraza i izraza dobivenog nakon transformacije, na primjer, s x=−2 . Imamo log 2 (−2+1) 4 =log 2 1=0 , i 4 log 2 (−2+1)=4 log 2 (−1)- besmislen izraz. To postavlja opravdano pitanje: “Što smo krivo učinili”?

A razlog je sljedeći: izvršili smo transformaciju log 2 (x+1) 4 =4 log 2 (x+1) , na temelju formule log a b p =p log a b , ali imamo pravo primijeniti samo ovu formulu ako su ispunjeni uvjeti a >0 , a≠1 , b>0 , p - bilo koji realni broj. Odnosno, transformacija koju smo napravili odvija se ako je x+1>0 , što je isto x>−1 (za A i p, uvjeti su ispunjeni). Međutim, u našem slučaju, ODZ varijable x za izvorni izraz sastoji se ne samo od intervala x> −1 , već i od intervala x<−1 . Но для x<−1 мы не имели права осуществлять преобразование по выбранной формуле.

Potreba uzimanja u obzir ODZ

Nastavimo analizirati transformaciju izraza log 2 (x+1) 4 koji smo odabrali, a sada da vidimo što se događa s ODZ-om kada prijeđemo na izraz 4 log 2 (x+1) . U prethodnom odlomku pronašli smo ODZ originalnog izraza - to je skup (−∞, −1)∪(−1, +∞) . Nađimo sada područje prihvatljivih vrijednosti varijable x za izraz 4 log 2 (x+1) . Određen je uvjetom x+1>0 , koji odgovara skupu (−1, +∞) . Očito je da se pri prelasku s log 2 (x+1) 4 na 4·log 2 (x+1) raspon dopuštenih vrijednosti sužava. I dogovorili smo se da ćemo izbjegavati reforme koje dovode do sužavanja ODZ-a jer to može dovesti do raznih negativnih posljedica.

Ovdje je vrijedno napomenuti da je korisno kontrolirati ODZ na svakom koraku transformacije i ne dopustiti da se suzi. A ako je odjednom u nekoj fazi transformacije došlo do sužavanja ODZ-a, onda je vrijedno pažljivo pogledati je li ta transformacija dopuštena i jesmo li je imali pravo provesti.

Poštenje radi, kažemo da u praksi obično moramo raditi s izrazima u kojima je ODZ varijabli takav da nam omogućuje korištenje svojstava logaritama bez ograničenja u obliku koji nam je već poznat, i slijeva na desno i s desna na lijevo, prilikom izvođenja transformacija. Brzo se naviknete na to i počnete mehanički provoditi transformacije, ne razmišljajući o tome je li ih bilo moguće izvesti. I u takvim trenucima, na sreću, provlače se složeniji primjeri u kojima netočna primjena svojstava logaritama dovodi do pogrešaka. Stoga morate uvijek biti na oprezu i paziti da ne dođe do suženja ODZ-a.

Ne boli posebno istaknuti glavne transformacije temeljene na svojstvima logaritama, koje se moraju provoditi vrlo pažljivo, što može dovesti do sužavanja DPV-a i kao rezultat toga do pogrešaka:

Neke transformacije izraza prema svojstvima logaritama mogu dovesti i do suprotnog - proširenja ODZ-a. Na primjer, prelazak s 4 log 2 (x+1) na log 2 (x+1) 4 proširuje ODZ sa skupa (−1, +∞) na (−∞, −1)∪(−1, +∞ ) . Takve se transformacije odvijaju ako ostanete unutar ODZ-a za izvorni izraz. Dakle, upravo spomenuta transformacija 4 log 2 (x+1)=log 2 (x+1) 4 odvija se na ODZ varijabli x za izvorni izraz 4 log 2 (x+1) , to jest, kada x+1> 0 , što je isto kao (−1, +∞) .

Sada kada smo razgovarali o nijansama na koje morate obratiti pozornost prilikom pretvaranja izraza s varijablama pomoću svojstava logaritama, ostaje nam otkriti kako se te pretvorbe trebaju ispravno izvršiti.

X+2>0. Radi li to u našem slučaju? Kako bismo odgovorili na ovo pitanje, pogledajmo DPV varijable x. Određuje se sustavom nejednakosti , što je ekvivalentno uvjetu x+2>0 (ako je potrebno, pogledajte članak rješavanje sustava nejednadžbi). Dakle, možemo sa sigurnošću primijeniti svojstvo logaritma stupnja.

Imamo
3 log(x+2) 7 −log(x+2)−5 log(x+2) 4 =
=3 7 log(x+2)−log(x+2)−5 4 log(x+2)=
=21 log(x+2)−log(x+2)−20 log(x+2)=
=(21−1−20)lg(x+2)=0 .

Možete postupiti drugačije, budući da vam ODZ to omogućuje, na primjer ovako:

Odgovor:

3 log(x+2) 7 −log(x+2)−5 log(x+2) 4 =0.

A što učiniti kada uvjeti povezani sa svojstvima logaritama nisu ispunjeni na ODZ-u? To ćemo riješiti na primjerima.

Neka se od nas traži da pojednostavimo izraz lg(x+2) 4 −lg(x+2) 2 . Transformacija ovog izraza, za razliku od izraza iz prethodnog primjera, ne dopušta slobodno korištenje svojstva logaritma stupnja. Zašto? ODZ varijable x u ovom slučaju je unija dvaju intervala x>−2 i x<−2 . При x>−2 možemo sigurno primijeniti svojstvo logaritma stupnja i nastaviti kao u gornjem primjeru: log(x+2) 4 −log(x+2) 2 =4 log(x+2)−2 log(x+2)=2 log(x+2). Ali ODZ sadrži još jedan interval x+2<0 , для которого последнее преобразование будет некорректно. Что же делать при x+2<0 ? В подобных случаях на помощь приходит . Определение модуля позволяет выражение x+2 при x+2<0 представить как −|x+2| . Тогда при x+2<0 от lg(x+2) 4 −lg(x+2) 2 переходим к log(−|x+2|) 4 −log(−|x+2|) 2 i dalje, zbog svojstava snage lg|x+2| 4−lg|x+2| 2. Rezultirajući izraz može se transformirati prema svojstvu logaritma stupnja, jer |x+2|>0 za bilo koju vrijednost varijable. Imamo log|x+2| 4−lg|x+2| 2 =4 log|x+2|−2 log|x+2|=2 log|x+2|. Sada se možete riješiti modula, jer je obavio svoj posao. Budući da se transformiramo na x+2<0 , то 2·lg|x+2|=2·lg(−(x+2)) . Итак, можно считать, что мы справились с поставленной задачей. Ответ: . Полученный результат можно записать компактно с использованием модуля как .

Razmotrimo još jedan primjer kako bismo rad s modulima učinili poznatijim. Shvatimo iz izraza prijeđite na zbroj i razliku logaritama linearnih binoma x−1 , x−2 i x−3 . Prvo nalazimo ODZ:

Na intervalu (3, +∞) vrijednosti izraza x−1 , x−2 i x−3 su pozitivne, pa možemo sa sigurnošću primijeniti svojstva logaritma zbroja i razlike:

I na intervalu (1, 2) vrijednosti izraza x−1 su pozitivne, a vrijednosti izraza x−2 i x−3 su negativne. Stoga, na intervalu koji razmatramo, predstavljamo x−2 i x−3 koristeći modul kao −|x−2| i −|x−3| odnosno. pri čemu

Sada možemo primijeniti svojstva logaritma umnoška i kvocijenta, jer na razmatranom intervalu (1, 2) vrijednosti izraza x−1 , |x−2| i |x−3| - pozitivno.

Imamo

Dobiveni rezultati mogu se kombinirati:

Općenito, slično razmišljanje omogućuje, na temelju formula za logaritam proizvoda, omjera i stupnja, da se dobiju tri praktično korisna rezultata koja su prilično prikladna za korištenje:

• Logaritam umnoška dva proizvoljna izraza X i Y oblika log a (X·Y) može se zamijeniti zbrojem logaritama log a |X|+log a |Y| , a>0 , a≠1 .
• Posebni logaritam log a (X:Y) može se zamijeniti razlikom logaritama log a |X|−log a |Y| , a>0 , a≠1 , X i Y su proizvoljni izrazi.
• Od logaritma nekog izraza B na parnu potenciju p oblika log a B p, može se prijeći na izraz p log a |B| , gdje je a>0 , a≠1 , p paran broj, a B proizvoljan izraz.

Slični rezultati dani su, primjerice, u uputama za rješavanje eksponencijalnih i logaritamskih jednadžbi u zbirci zadataka iz matematike za pristupnike sveučilištima, koju je uredio M. I. Skanavi.

Primjer.

Pojednostavite izraz .

Riješenje.

Bilo bi dobro primijeniti svojstva logaritma stupnja, zbroja i razlike. Ali možemo li to učiniti ovdje? Za odgovor na ovo pitanje moramo poznavati ODZ.

Definirajmo to:

Sasvim je očito da izrazi x+4 , x−2 i (x+4) 13 na rasponu mogućih vrijednosti varijable x mogu poprimiti i pozitivne i negativne vrijednosti. Stoga ćemo morati raditi kroz module.

Svojstva modula omogućuju vam prepisivanje kao , dakle

Također, ništa vas ne sprječava da upotrijebite svojstvo logaritma stupnja, a zatim donesete slične pojmove:

Drugi niz transformacija dovodi do istog rezultata:

a budući da izraz x−2 može poprimiti i pozitivne i negativne vrijednosti na ODZ, kada se uzima parni eksponent 14