Сега ще разгледаме преобразуването на изрази, съдържащи логаритми от обща гледна точка. Тук ще анализираме не само преобразуването на изрази, използващи свойствата на логаритмите, но ще разгледаме и преобразуването на изрази с логаритми общ изглед, които съдържат не само логаритми, но и степени, дроби, корени и др. Както обикновено, ще предоставим всички материали с характерни примери подробни описаниярешения.

Навигация в страницата.

Изрази с логаритми и логаритмични изрази

Извършване на действия с дроби

В предишния параграф разгледахме основните трансформации, които се извършват с отделни дроби, съдържащи логаритми. Тези трансформации, разбира се, могат да бъдат извършени с всяка отделна дроб, която е част от по-сложен израз, например представляващ сбора, разликата, произведението и частното на подобни дроби. Но в допълнение към работата с отделни дроби, преобразуването на изрази от този вид често включва извършване на подходящи действия с дроби. След това ще разгледаме правилата, по които се извършват тези действия.

От 5-6 клас знаем правилата, по които . В статията общ изглед на операциите с дробиразпространихме тези правила с обикновени дробив дроби от обща форма A/B, където A и B са някои числови, буквални или променливи изрази, а B е идентично различно от нула. Ясно е, че дроби с логаритми са частни случаи на общи дроби. И в тази връзка е ясно, че действията с дроби, които съдържат логаритми в своите записи, се извършват по същите правила. а именно:

• За да добавите или извадите две дроби с еднакви знаменатели, добавете или извадете съответно числителите и оставете знаменателя същия.
• За събиране или изваждане на две дроби с различни знаменатели, трябва да ги приведете към общ знаменател и да извършите съответните действия съгласно предходното правило.
• За да умножите две дроби, трябва да напишете дроб, чийто числител е произведението на числителите на първоначалните дроби, а знаменателят е произведението на знаменателите.
• За да разделите дроб на дроб, е необходимо да умножите делимата дроб по реципрочната стойност на делителя, т.е. по дробта с пренаредени числител и знаменател.

Ето няколко примера за извършване на операции с дроби, съдържащи логаритми.

Пример.

Извършете действия с дроби, съдържащи логаритми: а), б) , в) , G) .

Решение.

а) Знаменателите на добавените дроби очевидно са еднакви. Следователно, съгласно правилото за събиране на дроби с еднакви знаменатели, събираме числителите, а знаменателят оставяме същия: .

б) Тук знаменателите са различни. Следователно, първо трябва привеждане на дроби към един и същи знаменател. В нашия случай знаменателите вече са представени като произведения и ни остава да вземем знаменателя на първата дроб и да добавим към него липсващите множители от знаменателя на втората дроб. Така че получаваме общ знаменател на формата . В този случай извадените дроби се свеждат до общ знаменател, като се използват допълнителни множители под формата на логаритъм и съответно израза x 2 ·(x+1). След това остава да извадите дроби с еднакви знаменатели, което не е трудно.

Така че решението е:

в) Известно е, че резултатът от умножаването на дроби е дроб, чийто числител е произведение на числителите, а знаменателят е произведение на знаменателите, следователно

Лесно се вижда, че е възможно намаляване на фракциятас две и с десетичен логаритъм, като резултат имаме .

г) Преминаваме от деление на дроби към умножение, като заместваме делителя на дробта с реципрочната му стойност. Така

Числителят на получената дроб може да бъде представен като , от който ясно се вижда общият множител на числителя и знаменателя - множителят x, с който можете да намалите дробта:

Отговор:

а), б) , в) , G) .

Трябва да се помни, че действията с дроби се извършват, като се вземе предвид редът, в който се извършват действията: първо умножение и деление, след това събиране и изваждане, а ако има скоби, първо се извършват действия в скоби.

Пример.

Извършвайте действия с дроби .

Решение.

Първо, извършваме добавяне на дроби в скоби, след което ще извършим умножението:

Отговор:

В този момент остава да кажем на глас три доста очевидни, но в същото време важни точки:

Преобразуване на изрази с помощта на свойствата на логаритмите

Най-често преобразуването на изрази с логаритми включва използването на идентичности, изразяващи дефиницията на логаритъм и

Математика. Тематични тестове. Част II. Подготовка за Единния държавен изпит-2010. 10-11 клас. Изд. Лисенко F.F. - Ростов n / D .: Легион, 2009. - 176s.

Математика. УПОТРЕБА-2009. Тематични тестове. Част II (B4-B8, C1-C2) Изд. Лисенко F.F. - Ростов n / D: Легион, 2008 - 160 с.

Помагалото се състои от тестове по отделни теми, които са традиционни в курса по математика и затова по правило се включват в изпита. Те покриват изцяло групите задачи с повишено и високо ниво на сложност на USE, с изключение на текстови задачи и задачи по геометрия. За всяка тема се предлагат един или повече комплекта тестове. Всеки комплект съдържа 10 теста, всеки тест съдържа 8 задачи.

Целта на тази книга е да се разработят задачи с кратък и подробен отговор на USE тестовете. Необходимо е преди всичко за завършилите, които очакват да получат ИЗПОЛЗВАЙТЕ доброоценка, както и за ученици от 10 клас, които могат да затвърдят разгледаните теми от гледна точка на USE. Предложеното ръководство може да бъде полезно за всички завършили, подготвящи се за USE по математика, както и за учители, подготвящи ученици за USE.

формат: djvu/zip (2009 , 176s.)

Размерът: 2,5 MB

Изтегляне / Изтегляне на файл 14

формат: pdf (2009 , 176s.)

Размерът: 8,6 MB

Изтегли: 14 .12.2018 г., връзките премахнати по искане на издателство Легион (виж забележката)

формат: djvu/zip (2008 , 160-те.)

Размерът: 3 MB

Изтегляне / Изтегляне на файл 14 .12.2018 г., връзките премахнати по искане на издателство Легион (виж забележката)

формат: pdf (2008 , 160-те.)

Размерът: 9,9 MB

Изтегли: 14 .12.2018 г., връзките премахнати по искане на издателство Легион (виж забележката)

Учебно-методически комплекс "Математика. Единен държавен изпит-2010" изд. Лисенко F.F. и Кулабухов С.Ю. включва уроци:
1. Математика. Подготовка за Единния държавен изпит-2010.
2. Решебник. Математика. Подготовка за Единния държавен изпит-2010.
3. Математика. Тематични тестове. Част I (базово ниво). Подготовка за Единния държавен изпит-2010. 10-11 клас.
4. Математика. Тематични тестове. Част II. Подготовка за Единния държавен изпит-2010. 10-11 клас.
5. Математика. Тематични тестове: геометрия, текстови задачи. Подготовка за Единния държавен изпит-2010. 10-11 клас.
6. Математика. Колекция от USE тестове 2001 - 2010 г.
7. Математика. Подготовка за Единния държавен изпит-2010. Тренировъчни тестове.
8. Джобно помагало по математика.

Съдържание
От авторите 11
§ 1. Тъждествени трансформации на логаритмични изрази 13
Вариант номер 1 13
Вариант номер 2 13
Вариант номер 3 14
Вариант номер 4 14
Вариант номер 5 15
Вариант номер 6 15
Вариант номер 7 16
Вариант номер 8 16
Вариант номер 9 17
Вариант номер 10 17
§ 2. Тъждествени трансформации на изрази, съдържащи степен 18
Вариант номер 1 18
Вариант номер 2 19
Вариант номер 3 19
Вариант номер 4 20
Вариант номер 5 21
Вариант номер 6 21
Вариант номер 7 22
Вариант номер 8 23
Вариант номер 9 23
Вариант номер 10 24
§ 3. Тъждествени трансформации на ирационални изрази 25
Вариант номер 1 25
Вариант номер 2 25
Вариант номер 3 26
Вариант номер 4 26
Вариант номер 5 27
Вариант номер 6 28
Вариант номер 7 28
Вариант номер 8 29
Вариант номер 9 30
Вариант номер 10 30
§ 4. Системи уравнения 31
Вариант номер 1 31
Вариант номер 2 32
Вариант номер 3 33
Вариант номер 4 33
Вариант номер 5 34
Вариант номер 6 35
Вариант номер 7 36
Вариант номер 8 37
Вариант номер 9 38
Вариант номер 10 39
§ 5. геометричен смисълпроизводна 39
Вариант номер 1 39
Вариант номер 2 41
Вариант номер 3 43
Вариант номер 4 44
Вариант номер 5 46
Вариант номер 6 48
Вариант номер 7 50
Вариант номер 8 52
Вариант номер 9 54
Вариант номер 10 55
§ 6. Неравенства 56
Вариант номер 1 g 56
Вариант номер 2 57
Вариант номер 3 58
Вариант номер 4 58
Вариант номер 5 59
Вариант номер 6 60
Вариант номер 7 60
Вариант номер 8 61
Вариант номер 9 62
Вариант номер 10 63
§ 7. Ирационални уравнения 63
Вариант номер 1 63
Вариант номер 2 64
Вариант номер 3 65
Вариант номер 4 65
Вариант номер 5 66
Вариант номер 6 66
Вариант номер 7 67
Вариант номер 8 67
Вариант номер 9 68
Вариант № Ю 68
§ 8. Тригонометрични уравнения 69
Вариант номер 1 69
Вариант номер 2 69
Вариант номер 3 70
Вариант номер 4 70
Вариант номер 5 71
Вариант номер 6 72
Вариант номер 7 72
Вариант номер 8 73
Вариант номер 9 74
Вариант номер 10 74
§ 9. Логаритмични уравнения 75
Вариант номер 1 75
Вариант номер 2 75
Вариант номер 3 76
Вариант номер 4 76
Вариант номер 5 77
Вариант номер 6 77
Вариант номер 7 78
Вариант №8*78
Вариант номер 9 79
Вариант номер 10 79
§ 10. Показателни уравнения 80
Вариант номер 1 80
Вариант номер 2 80
Вариант номер 3 81
Вариант номер 4 81
Вариант номер 5 82
Вариант номер 6 82
Вариант номер 7 83
Вариант номер 8 83
Вариант номер 9 84
Вариант номер 10 84
§единадесет. Периодичност, четни и нечетни функции 85
Вариант номер 1 85
Вариант номер 2 86
Вариант номер 3 87
Вариант номер 4 89
Вариант номер 5 90
Вариант номер 6 91
Вариант номер 7 92
Вариант номер 8 93
Вариант номер 9 94
Вариант номер 10 95
§ 12. Нули на комплексна функция. Ограничена функция 97
Вариант номер 1 97
Вариант номер 2 97
Вариант номер 3 98
Вариант номер 4 98
Вариант номер 5 99
Вариант номер 6 99
Вариант номер 7 100
Вариант номер 8 100
Вариант номер 9 101
Вариант номер 10 101
§ 13. Област на дефиниране, множество от стойности, монотонност на функции 102
Вариант номер 1 102
Вариант номер 2 102
Вариант номер 3 103
Вариант номер 4 103
Вариант номер 5 104
Вариант номер 6 104
Вариант номер 7 105
Вариант номер 8 105
Вариант номер 9 106
Вариант номер 10 107
§ 14. Екстремуми на функция. Най-големите и най-малките стойности на функцията 107
Вариант номер 1 107
Вариант номер 2 108
Вариант номер 3 108
Вариант номер 4 109
Вариант номер 5 109
Вариант номер 6 110
Вариант номер 7 110
Вариант номер 8 111
Вариант номер 9 111
Вариант номер 10 112
§ 15. Различни техники за решаване на логаритмични уравнения 113
Вариант номер 1 113
Вариант номер 2 113
Вариант номер 3 114
Вариант номер 4 114
Вариант номер 5 115
Вариант номер 6 115
Вариант номер 7 116
Вариант номер 8 116
Вариант номер 9 117
Вариант номер 10 117
§ 16. Различни техники за решаване на тригонометрични уравнения 118
Вариант номер 1 118
Вариант номер 2 118
Вариант номер 3 118
Вариант номер 4 119
Вариант номер 5 119
Вариант номер 6 120
Вариант номер 7 120
Вариант номер 8 121
Вариант номер 9 121
Вариант номер 10 122
§ 17. Различни техники за решаване на ирационални уравнения 123
Вариант номер 1 123
Вариант номер 2 123
Вариант номер 3 124
Вариант номер 4 124
Вариант номер 5 125
Вариант номер 6 125
Вариант номер 7 125
Вариант номер 8 126
Вариант номер 9 126
Вариант № 10 127
§ 18. Уравнения, съдържащи променлива под знака на модул 127
Вариант номер 1 127
Вариант номер 2 128
Вариант номер 3 128
Вариант номер 4 129
Вариант номер 5 129
Вариант номер 6 130
Вариант номер 7 130
Вариант номер 8 131
Вариант номер 9 131
Вариант номер 10 131
§ 19. Различни методи за решаване експоненциални уравнения.132
Вариант номер 1 132
Вариант номер 2 133
Вариант номер 3 133
Вариант номер 4 134
Вариант номер 5 134
Вариант номер 6 135
Вариант номер 7 135
Вариант номер 8 135
Вариант номер 9 136
Вариант номер 10 136
§ 20. Различни техники за решаване на комбинирани уравнения 137
Вариант номер 1 137
Вариант номер 2 137
Вариант номер 3 138
Вариант номер 4 138
Вариант номер 5 139
Вариант номер 6 139
Вариант номер 7 140
Вариант номер 8 140
Вариант номер 9 141
Вариант номер 10 141
§ 21. Уравнения с параметър, съдържащ модул 142
Вариант номер 1 142
Вариант номер 2 142
Вариант номер 3 143
Вариант номер 4 144
Вариант номер 5 144
Вариант номер 6 145
Вариант номер 7 146
Вариант номер 8 146
Вариант номер 9 147
Вариант номер 10 148
Отговори 149
§ 1. Тъждествени трансформации на логаритмични изрази 149
§ 2. Тъждествени трансформации на изрази със степен 150
§ 3. Тъждествени трансформации на ирационални изрази 150
§ 4. Системи уравнения 151
§ 5. Геометричният смисъл на производната 151
§ 6. Неравенства 152
§ 7. Ирационални уравнения 152
§ 8. Тригонометрични уравнения 153
§ 9. Логаритмични уравнения 153
§ 10. Показателни уравнения 154
§единадесет. Периодичност, четни и нечетни функции 154
§ 12. Нули на комплексна функция. Ограничена функция 155
§ 13. Област на дефиниране, множество от стойности, монотонност на функции 156
§ 14. Екстремуми на функция. Най-големите и най-малките стойности на функцията 158
§ петнадесети. Разни триковепри решаване на логаритмични уравнения 159
§ 16. Различни техники за решаване на тригонометрични уравнения 160
§ 17. Различни трикове за решаване на ирационални уравнения 164
§ 18. Уравнения, съдържащи променлива под знака на модул 165
§ 19. Различни техники за решаване на експоненциални уравнения.166
§ 20. Различни техники за решаване на комбинирани уравнения 167
§ 21. Уравнения с параметър, съдържащ модул 169
Литература 170

ЕГОРОВА ВИКТОРИЯ ВАЛЕРЕВНА

Учител по математика

най-висока квалификационна категория

ТЕМА: „ТРАНСФОРМАЦИЯ НА ИДЕНТИЧНОСТТА

ЛОГАРИТМИЧНИ ИЗРАЖЕНИЯ"

Знания и умения, които учениците трябва да овладеят след изучаване на този урок:

познава дефиницията на логаритъм на число, основното логаритмично тъждество, свойствата на логаритмите;

да може да извършва трансформации на изрази, съдържащи логаритми, да пресмята логаритми.

Литература:

1. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. и др.. Алгебра и началото на анализа: учебник за 10-11 клас образователни институции. - М .: Образование, 2001.

2. Кочагин В.В., Кочагина М.В., Интензивен курс на подготовка за изпита. – М.: Ексмо, 2009.

3. А. Г. Мерзляк, В. Б. Полонски и М. С. Якир, Алгебричен симулатор: Ръководство за ученици и абитуриенти. – М.: Илекса, 2005.

4. Гусев В.А., Мордкович А.Г. Математика: Справочни материали: Книга за студенти. - М .: Образование, 2001.

План на урока:

По време на часовете:

1) Логаритъмът е гръцка дума, който се състои от 2 думи: “логос” - отношение, “аритмос” - число. Логаритъмът е числото, което измерва отношението. Публикация от 1614 г. съобщава, че Напиер е изобретил логаритмите. По-късно той съставя логаритмични таблици, които днес са ни известни като таблици на Брадис. За по-малко от век таблиците се разпространиха по целия свят и се превърнаха в незаменим компютърен инструмент. В бъдеще те бяха, така да се каже, вградени в удобно устройство, което изключително ускорява процеса на изчисление - слайд правило, което се използва до седемдесетте години на двадесети век.

Приложение 1.

2) логаритъм положително числоbпо разум а, освен това по-голямо от нула и не равно на единица,е степента, до която трябва да се повдигне дадено числоа за да получите номераb.

Това равенство, изразяващо определението на логаритъма, се наричаосновно логаритмично тъждество .

° С

ИЛИ 1

П

Основата на степента и основата на логаритъма са седемнадесет, което означава, че според основното логаритмично тъждество стойността на израза е три.

Ще работим устно:

SCH
ЕЛЧОК

О долната секунда е нула цяло пет десети, така че изразът е равен на аритметичния корен квадратен от пет.

П

приложение 2.

Равенство означава, че

От дефиницията на логаритъма се получават следните важни равенства:

Например:

П
приложение 3.

Да преминем към ИЗПОЛЗВАЙТЕ задания:

Приложение 4

3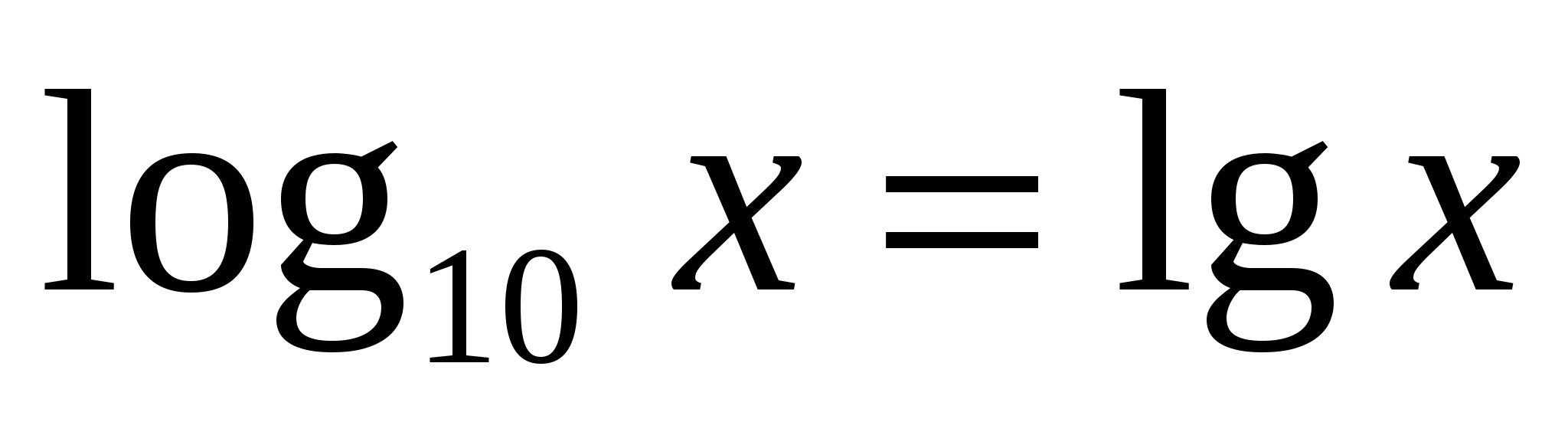
) Има специална нотация и име за логаритъм с основа десет.десетичен логаритъм .

Л
аритъм към основад Нареченнатурален логаритъм .

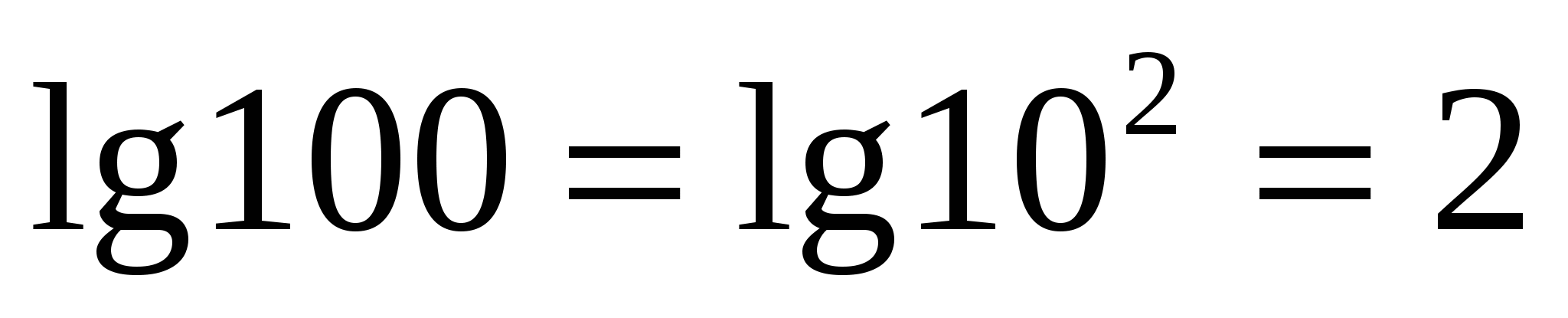
з
например,

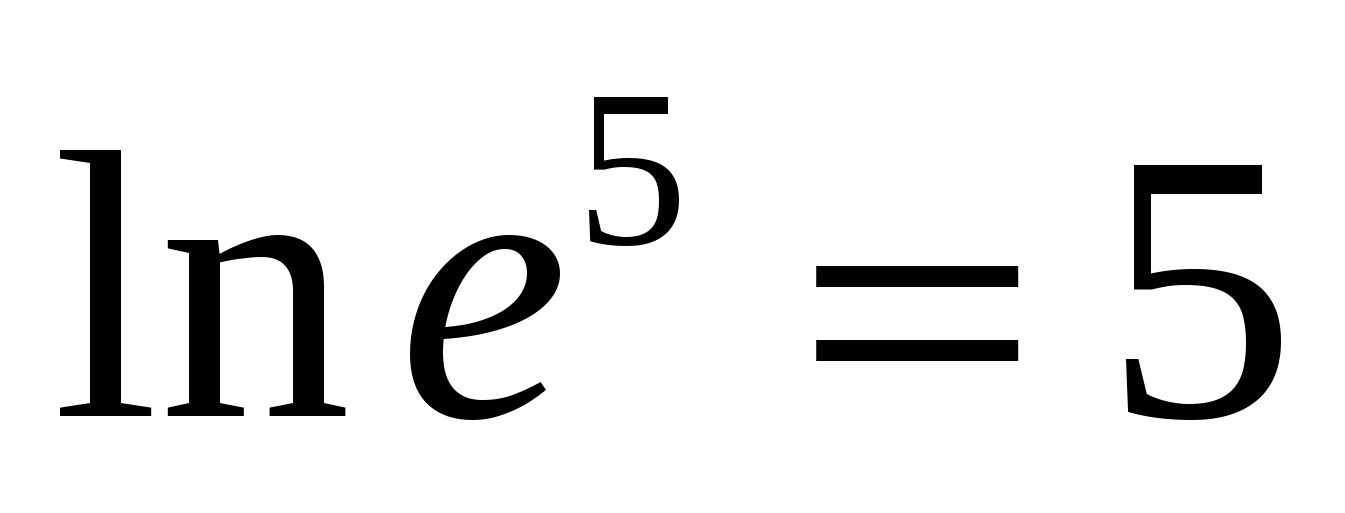
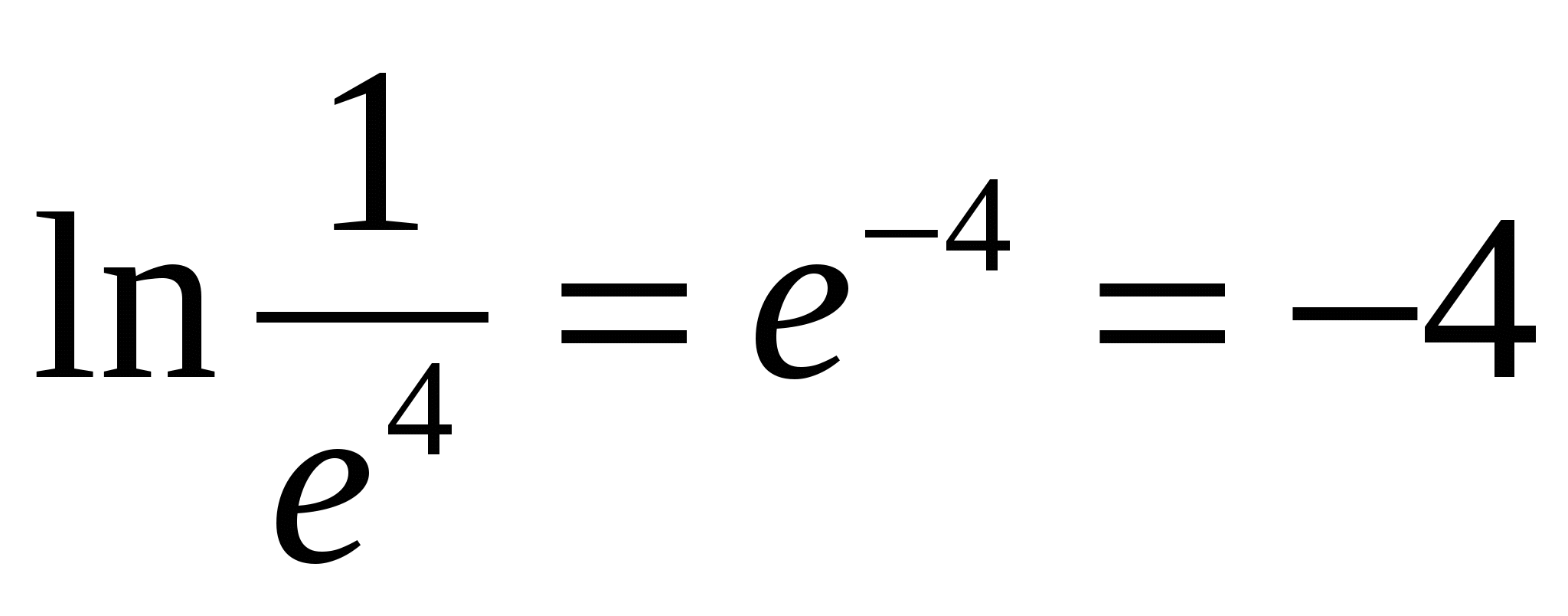
4) От дефиницията на логаритъма следват следните свойства. Всички свойства са формулирани и доказани само за положителни стойности на променливи, съдържащи се под логаритмични знаци.

Основен логаритъм от произведението на две положителни числа а е равно на суматалогаритми на тези числа с една и съща основа.

DER 2

Например,

У
задача 1.

Задача 2.Опростете израза

AT
Нека използваме предишния пример. Да заменим

Имайте предвид, че логаритъма е на квадрат, така че сумата също трябва да бъде на квадрат. Използвайки формулата за квадрат на сумата, отворете скобите. Представяме подобни условия.

5) Логаритъмът на частното е равен на разликата между логаритмите на делителя и делителя.

° С

Обърнете внимание на основата на степента и основата на логаритъма - те са еднакви.

ИЛИ 3

Р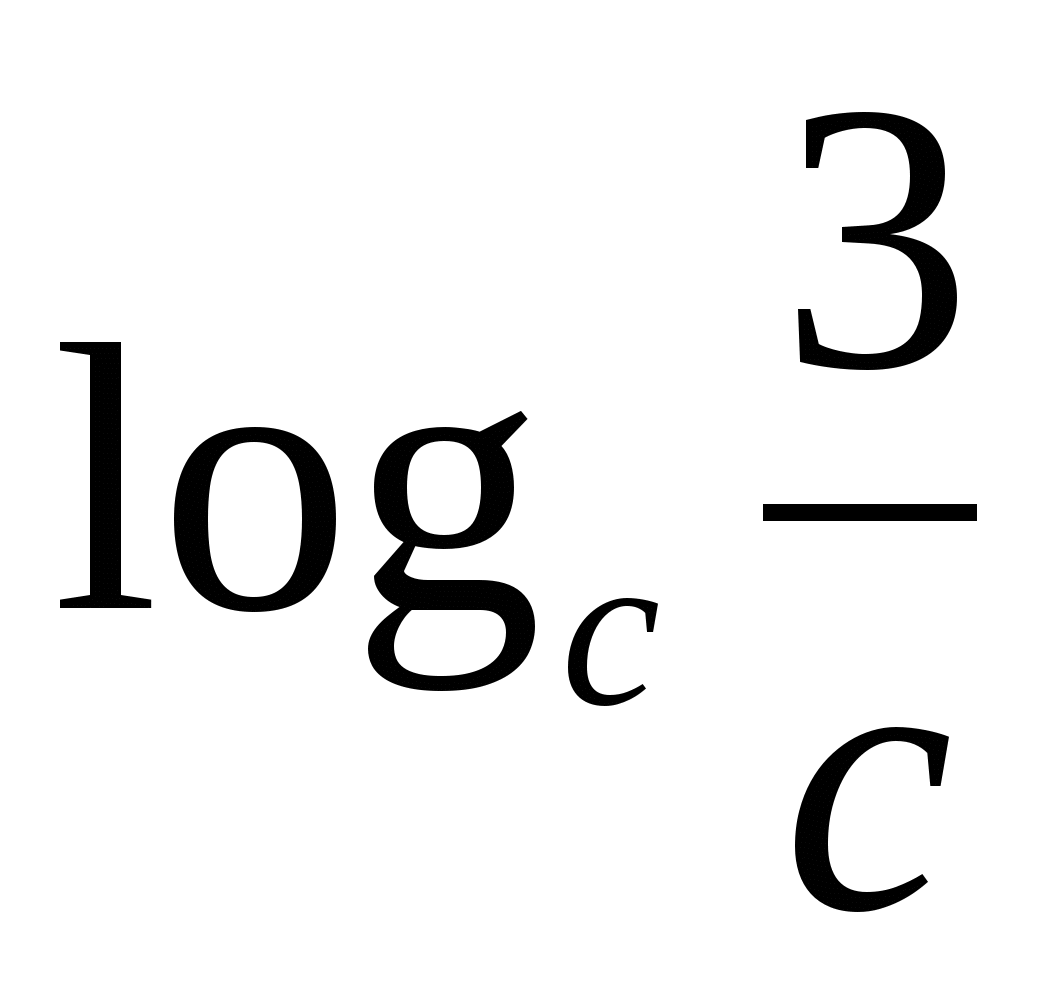

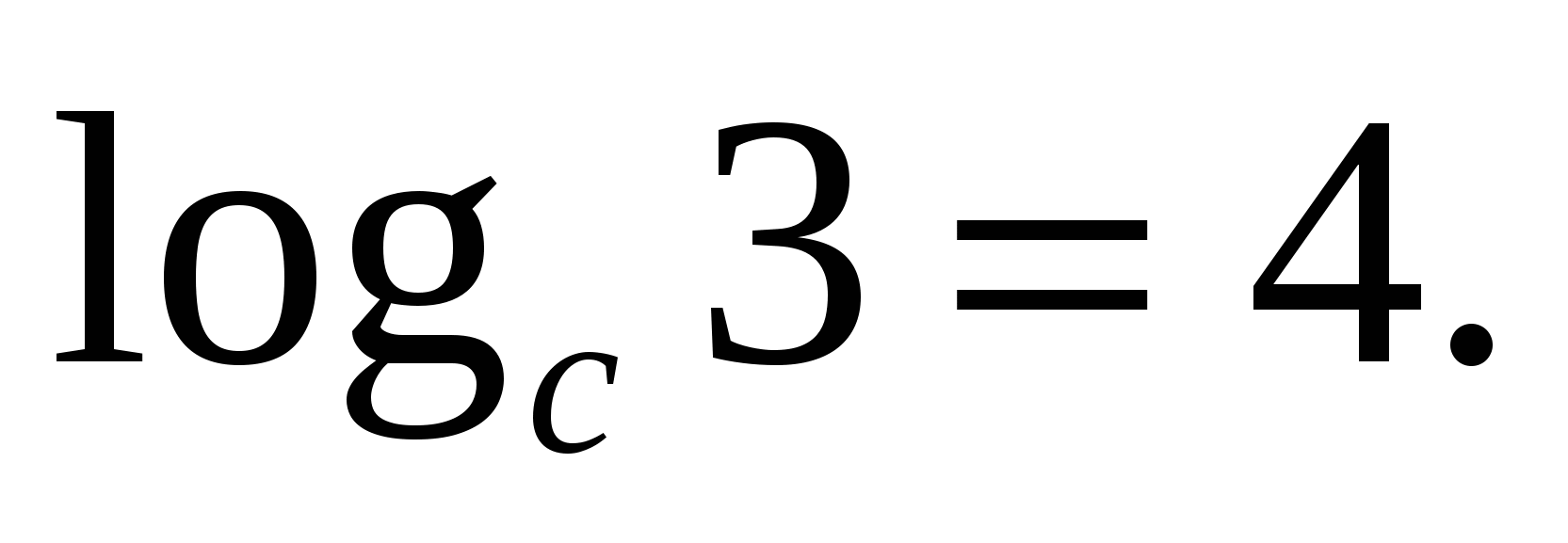Нека да разгледаме приложението на тази формула с пример:

У
задача 1.Намерете стойността на израза if

Задача 2.Намерете стойността bчрез своя логаритъм

6) Логаритъм на степента към основатаа , е равно на произведениетоекспонент за логаритъм в същата основа.

DER 4

Например,

У
задача 1.Изчислете дали

Нека опростим израза

Формула

Наречен формула за преминаване към нова основа.

У

задача 1.Изразете чрез логаритъм с основа 2.

Задача 2.Изчисли

CER 5

CER 6

Например,

У

задача 1.Изчисли

У
задача 2.Изчисли

9) Можете да започнете логаритмични трансформации само акоако помните всички свойства на логаритмите. След като ги повторим, ще разгледаме задачите за преобразуване на логаритмични изрази от другата страна.

За да преобразувате сумата или разликата на логаритмични изрази, понякога е достатъчно да използвате дефиницията на логаритъма и най-често свойствата на логаритъма на произведението или частното.

У
задача 1.Изчисли

Нека го решим по два начина.

1 начин, използвайки дефиницията на логаритъма:

Метод 2, базиран насвойство на частен логаритъм:

Задача 2.Намерете стойността на израз

Нека първо приложим формулаталогаритъма на произведението, след това дефиницията на логаритъма.

Основната логаритмична идентичност се използва при преобразуване на изрази, съдържащи логаритъм в степента. Идеята на такива операции е основата на експонентата и основата на логаритъма да бъдат равни.

Понякога е необходимо да се трансформира изражениетоот свойствата на логаритъма и от свойствата на степента, също човек може лесно да премине от една база към друга, използвайки формулата за преход. В други случаи трябва да се приложат множество свойства.

У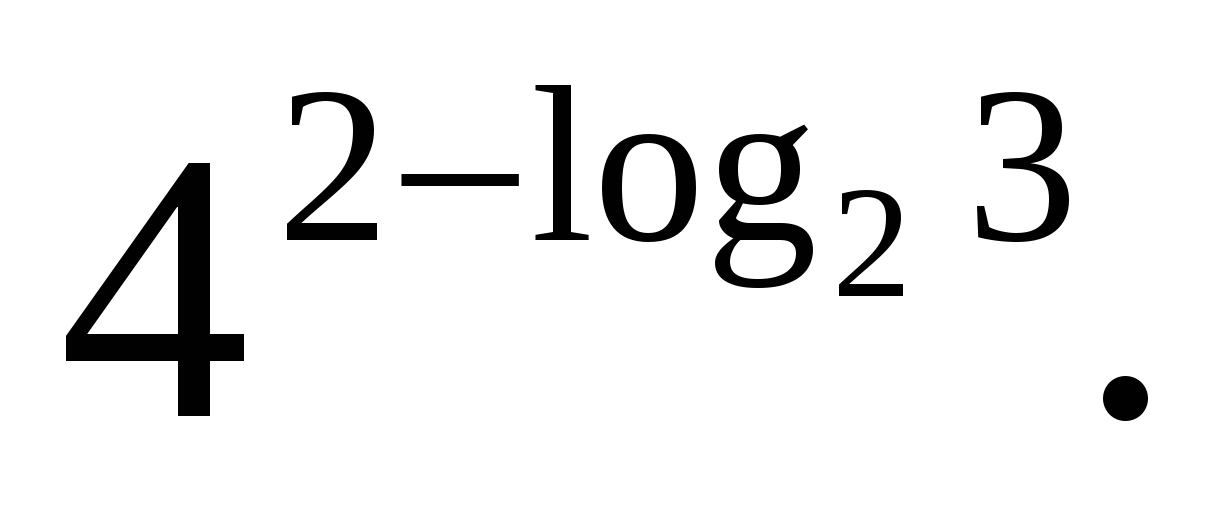
задача 3.Изчисли

У
задача 4.Намерете стойността на израз

Задача 5.Намерете стойността на израз

У
задача 6.Изразете като разлика на логаритми

з
Най-голямата трудност е преобразуването на логаритмични изрази под радикала. В процеса на трансформации трябва да се вземат предвид модулите на логаритмичните изрази, за разкриването на които е необходимо да се сравняват ирационални числа или рационални и ирационални числа. Ще действаме последователно. Разгледайте израза под вътрешния радикал.

Заместете в оригиналния израз.

Трябва да се отбележи, че преобразуването на логаритмични изрази може да се срещне и при решаване на уравнения и неравенства или изучаване на функции, следователно в неявна форма те могат да присъстват и в заданията на групи B и C.

10) Обобщаване. Въпроси:

Извиква се логаритъм с основа 10

основен логаритъм

главен логаритъм

натурален логаритъм

десетичен логаритъм

2) Какви ценности могатх в израза

Стойността не е дефинирана

5) Посочете съотношението, което е вярно за всичких ≠ 0 .

6) Посочете правилното съотношение за формулата за преход към нова база.

7) Посочете правилното равенство за

11) Контролно изпитване.

приднестровски Държавен университет

тях. Т.Г. Шевченко

Физико-математически факултет

Катедра по математически анализ

и методи на обучение по математика

КУРСОВА РАБОТА

„Трансформации на идентичността

експоненциална и логаритмична

изрази"

Завършена работа:

ученик от ______ група

Физико-математически факултет

_________________________

Проверена работа:

_________________________

Тираспол, 2003 г

Въведение…………………………………………………………………………2

Глава 1

§едно. Формиране на умения за прилагане на специфични видове трансформации………………………………………………………………………………….4

§2. Характеристики на организацията на система от знания при изучаването на идентични трансформации.…….……………………………………..………….5

§3. Програма по математика ……………………………………….11

Глава 2

§едно. Обобщение на понятието степен……………………………………..13

§2. Експоненциалната функция…………………………………………..15

§3. Логаритмична функция………………………………………….16

Глава 3. Тъждествени преобразувания на експоненциални и логаритмични изрази на практика ...................................... ...... ...................................19

Заключение…………………………………………………………………..24

Списък на използваната литература…………………………………….25
Въведение

Тази курсова работа ще разгледа идентични трансформации на експоненциалните и логаритмичните функции, ще разгледа методологията за преподаването им в училищния курс по алгебра и началото на анализа.

Първата глава на тази работа описва методологията за преподаване на идентични трансформации в училищния курс по математика, включва и програма по математика в курса "Алгебра и началото на анализа" с изучаване на експоненциални и логаритмични функции.

Втората глава се занимава директно със самите експоненциални и логаритмични функции, техните основни свойства, използвани при идентични трансформации.

Третата глава е решение на примери и задачи с помощта на идентични трансформации на експоненциалната и логаритмичната функция.

Изучаването на различни трансформации на изрази и формули заема значителна част от учебното време в курса на училищната математика. Най-простите трансформации, базирани на свойствата на аритметичните операции, вече се извършват в начално училищеи в IV-V клас. Но основната тежест върху формирането на умения и способности за извършване на трансформации се носи от курса на училищната алгебра. Това е свързано както с рязкото увеличаване на броя и разнообразието на извършваните трансформации, така и с усложняването на дейностите по тяхното обосноваване и изясняване на условията за приложимост, с идентифицирането и изучаването на обобщени понятия за идентичност, идентична трансформация, еквивалентна трансформация, логично следствие.

Културата на извършване на идентични трансформации се развива по същия начин като културата на изчисленията, основана на солидни познания за свойствата на операциите върху обекти (числа, вектори, полиноми и т.н.) и алгоритмите за тяхното изпълнение. Тя се проявява не само в способността за правилно обосноваване на трансформациите, но и в способността да се намери най-краткият път към прехода от оригиналния аналитичен израз към израза, който най-добре отговаря на целта на трансформацията, в способността да се проследяват промените в областта на дефиниране на аналитичните изрази във верига от идентични трансформации, в скоростта и безгрешното изпълнение на трансформациите.

Осигуряването на висока култура на изчисление и идентични трансформации е важен проблем в обучението по математика. Този проблем обаче все още е далеч от задоволителното си решение. Доказателство за това са статистическите данни на органите на общественото образование, в които ежегодно се посочват грешки и нерационални методи на изчисления и трансформации, извършвани от учениците. различни класоведокато правите контролни работи. Това се потвърждава от мненията на висш образователни институцииза качеството на математическите знания и умения на кандидатите. Не можем да не се съгласим с изводите на органите на народното образование и университетите, че не е достатъчно високо нивокултура на компютинг и идентични трансформации в гимназияе следствие от формализма в знанията на учениците, отделянето на теорията от практиката.

Трансформации на идентичността и методи на обучение

в училищния курс по алгебра и началото на анализа.

§едно. Формиране на умения за приложение

специфични видове трансформации.

Системата от методи и правила за извършване на трансформации, използвани на етапа на началото на алгебрата, има много широк спектър от приложения: използва се при изучаването на целия курс на математиката. Въпреки това, именно поради ниската си специфичност, тази система се нуждае от допълнителни трансформации, които да отчитат особеностите на структурата на трансформираните изрази и свойствата на нововъведените операции и функции. Разработването на съответните видове трансформации започва с въвеждането на съкратени формули за умножение. След това разглеждаме трансформациите, свързани с операцията за степенуване, с различни класове елементарни функции- експоненциална, степенна, логаритмична, тригонометрична. Всеки от тези видове трансформации преминава през етап на изследване, в който вниманието е насочено към усвояването на техните характерни черти.

С натрупването на материал става възможно да се отделят общите черти на всички разглеждани трансформации и на тази основа да се въведат понятията идентични и еквивалентни трансформации.

Трябва да се отбележи, че концепцията за идентична трансформация е дадена в училищния курс по алгебра не в пълна обобщеност, а само в приложение към изрази. Трансформациите са разделени на два класа: тъждествените трансформации са трансформации на изрази, а еквивалентните трансформации са трансформации на формули. В случай, че има нужда от опростяване на една част от формулата, в тази формула се маркира израз, който служи като аргумент за приложената идентична трансформация. Съответният предикат се счита за непроменен.

Що се отнася до организацията на интегрална система от трансформации (синтез), нейната основна цел е да формира гъвкава и мощна; уред, подходящ за използване при решаване на различни образователни задачи.

В хода на алгебрата и началото на анализа продължава постепенно да се усъвършенства цялостна система от трансформации, вече формирана в основните си характеристики. Към него се добавят и някои нови видове трансформации, но те само го обогатяват, разширяват възможностите му, но не променят структурата му. Методологията за изучаване на тези нови трансформации практически не се различава от тази, използвана в курса по алгебра.

§2. Характеристики на организацията на системата от задачи

при изследване на идентични трансформации.

Основният принцип за организиране на всяка система от задачи е да се представят от прости към сложни, като се вземе предвид необходимостта учениците да преодолеят възможни трудности и да създадат проблемни ситуации. Посоченият основен принцип изисква конкретизация по отношение на особеностите на този учебен материал. За описание на различни системи от задачи в методиката на математиката се използва понятието цикъл от упражнения. Цикълът от упражнения се характеризира с комбинирането в последователността на упражненията на няколко аспекта на изучаването и методите за подреждане на материала. Във връзка с идентични трансформации идеята за цикъл може да бъде дадена по следния начин.

Цикълът от упражнения е свързан с изучаването на една идентичност, около която се групират други идентичности, които са в естествена връзка с нея. Съставът на цикъла, наред с изпълнителните задачи, включва задачи, които изискват признаване на приложимостта на разглежданата идентичност. Изследваната идентичност се използва за извършване на изчисления в различни цифрови области. Отчита се спецификата на идентичността; по-специално се организират обрати на речта, свързани с него.

Задачите във всеки цикъл са разделени на две групи. Първият включва задачи, изпълнявани при първоначалното запознаване с идентичността. Те служат учебен материалза няколко последователни урока, обединени от една тема. Втората група упражнения свързва изследваната идентичност с различни приложения. Тази група не образува композиционно единство - упражненията тук са разпръснати по различни теми.

Описаната структура на цикъла се отнася до етапа на формиране на умения за прилагане на конкретни видове трансформации. На последния етап - етапът на синтеза, циклите се модифицират. Първо се обединяват двете групи задачи, образувайки "разгънат" цикъл, като от първата група се изключват най-простите по отношение на формулировката или сложността на задачата. Останалите видове задачи стават по-трудни. На второ място, има сливане на цикли, свързани с различни идентичности, поради което нараства ролята на действията за разпознаване на приложимостта на една или друга идентичност.

Отбелязваме характеристиките на циклите на задачите, свързани с идентичности за елементарни функции. Тези характеристики се дължат на факта, че, първо, съответните идентичности се изучават във връзка с изучаването на функционален материал и, второ, те се появяват по-късно от идентичностите от първата група и се изучават с помощта на вече формирани умения за извършване на идентични трансформации .

Всяка нововъведена елементарна функция рязко разширява областта на числата, които могат да бъдат обозначени и наименувани индивидуално. Следователно първата група задачи от циклите трябва да включва задачи за установяване на връзка между тези нови числови региони и оригиналния регион на рационални числа. Даваме примери за такива задачи.

Пример 1 Изчислете:

До всеки израз има идентичност, в циклите, за които могат да присъстват предложените задачи. Целта на такива задачи е да се овладеят характеристиките на записите, включително символи на нови операции и функции, и да се развият математически речеви умения.

Значителна част от използването на трансформации на идентичност, свързани с елементарни функции, се пада върху решаването на ирационални и трансцендентни уравнения. Циклите, свързани с асимилацията на идентичностите, включват само най-простите уравнения, но вече тук е препоръчително да се работи по овладяването на метода за решаване на такива уравнения: намаляването му чрез замяна на неизвестното с алгебрично уравнение.

Последователността от стъпки за това решение е следната:

а) намерете функция, за която това уравнение може да бъде представено като ;

б) направете заместване и решете уравнението;

в) решаване на всяко от уравненията , където е множеството от корените на уравнението .

Когато се използва описаният метод, стъпка b) често се изпълнява имплицитно, без да се въвежда нотация за . Освен това учениците често избират измежду различните пътища, водещи до намиране на отговор, за да изберат този, който води до алгебричното уравнение по-бързо и по-лесно.

Пример 2. Решете уравнението.

Първи начин:

Втори начин:

а)

б)

Тук може да се види, че стъпка а) е по-трудна при първия метод, отколкото при втория. Първият начин е „по-труден за стартиране“, въпреки че по-нататъшният ход на решението е много по-лесен. От друга страна, вторият метод има предимства, състоящи се в по-голяма лекота, по-голяма сложност при преподаване на редукция до алгебрично уравнение.

За училищен курс по алгебра са типични задачи, при които преходът към алгебрично уравнение е дори по-лесен, отколкото в този пример. Основното натоварване на такива задачи е свързано с избора на стъпка c) като независима част от процеса на решаване, свързана с използването на свойствата на елементарната функция, която се изследва.

Пример 3. Решете уравнението:

а) ; б) .

Тези уравнения се свеждат до уравненията: а) или ; б) или. За решаването на тези уравнения е необходимо познаване само на най-простите факти за експоненциалната функция: нейната монотонност, диапазон от стойности. Подобно на предишния пример, уравнения a) и b) могат да бъдат отнесени към първата група от цикъл от упражнения за решаване на квадратни експоненциални уравнения.

Така стигаме до класификацията на задачите в цикли, свързани с решаването на трансцендентни уравнения, включително експоненциална функция:

1) уравнения, които се свеждат до уравнения от формата и имат прост отговор, общ по форма: ;

2) уравнения, които се свеждат до уравнения , където е цяло число, или , където ;

3) уравнения, които се свеждат до уравнения и изискват ясен анализ на формата, в която е написано числото.

Подобни задачи могат да бъдат класифицирани за други елементарни функции.

В тях се доказват или поне обясняват значителна част от тъждествата, изучавани в курсовете по алгебра и алгебра и наченките на анализа. Тази страна на изследването на идентичностите има голямо значениеи за двата курса, тъй като демонстративното разсъждение в тях се извършва с най-голяма яснота и строгост именно по отношение на идентичностите. Извън този материал доказателствата обикновено са по-малко пълни, не винаги се разграничават от състава на приложените средства за обосновка.

Свойствата на аритметичните операции се използват като опора, върху която се изграждат доказателствата за идентичности.

Образователното въздействие на изчисленията и идентичните трансформации може да бъде насочено към развитието логично мислене, ако само от учениците се изисква систематично да обосновават изчисления и идентични трансформации, да развиват функционално мислене, което се постига по различни начини. Значението на изчисленията и идентичните трансформации в развитието на волята, паметта, изобретателността, самоконтрола и творческата инициатива е съвсем очевидно.

Изискванията на ежедневната индустриална компютърна практика изискват формирането на силни, автоматизирани умения за рационални изчисления и идентични трансформации у учениците. Тези умения се развиват в процеса на всяка изчислителна работа, но са необходими специални умения. тренировъчни упражненияв бързи изчисления и трансформации.

Така че, ако урокът включва решаване на логаритмични уравнения с помощта на основната логаритмична идентичност, тогава е полезно да включите устни упражнения в плана на урока, за да опростите или изчислите стойностите на изразите: , , . Целта на упражненията винаги се съобщава на учениците. По време на упражнението може да се наложи от учениците да обосноват отделни трансформации, действия или да решат целия проблем, дори ако това не е било планирано. Когато са възможни различни начини за решаване на даден проблем, винаги е желателно да се задават въпроси: „По какъв начин беше решен проблемът?“, „Кой реши проблема по различен начин?“

Понятията идентичност и идентично преобразуване, те са изрично въведени в курса по алгебра в VI клас. Самата дефиниция на идентични изрази не може да се използва практически, за да се докаже идентичността на два израза и да се разбере, че същността на идентичните трансформации се състои в прилагане към израза на определенията и свойствата на онези действия, които са посочени в израза, или в добавянето към него израз, който е идентично равен на 0, или при умножаването му по израз, идентично равен на единица. Но дори след като са усвоили тези разпоредби, учениците често не разбират защо тези трансформации ни позволяват да твърдим, че оригиналните и получените изрази са идентични, т.е. вземете едни и същи стойности за всякакви системи (набори) от променливи стойности.

Също така е важно да се гарантира, че учениците разбират добре, че такива заключения за идентични трансформации са следствия от дефинициите и свойствата на съответните действия.

В 6. клас се разширява натрупаният през предходните години апарат за тъждествени преобразувания. Това разширение започва с въвеждането на идентичност, изразяваща свойството на произведението на степени с еднакви бази: , където , са цели числа.

§3. Програма по математика. В училищния курс „Алгебра и началото на анализа“ учениците систематично изучават експоненциални и логаритмични функции и техните свойства, тъждествени преобразувания на логаритмични и експоненциални изрази и приложението им за решаване на съответните уравнения и неравенства, запознават се с основните понятия, твърдения . В 11 клас уроците по алгебра са 3 часа седмично, общо 102 часа годишно. За изучаване на експоненциалната, логаритмичната и степенната функции по програмата са необходими 36 часа. Програмата включва разглеждане и изучаване на следните въпроси: Концепцията за степен с рационален показател. Решение на ирационални уравнения. Експоненциална функция, нейните свойства и графика. идентични трансформации на експоненциални изрази. Решаване на показателни уравнения и неравенства. Логаритъм на число. Основни свойства на логаритмите. Логаритмична функция, нейните свойства и графика. Решаване на логаритмични уравнения и неравенства. Производна на експоненциална функция. Число и натурален логаритъм. Производна на степенна функция. Основната цел на раздела за изучаване на експоненциални и логаритмични функции е да запознае учениците с експоненциални, логаритмични и степенни функции; учат учениците да решават експоненциални и логаритмични уравненияи неравенства. Понятията корен от степен и степен с рационален показател са обобщение на понятията корен квадратен и степен с цяло число. Студентите трябва да обърнат внимание на факта, че свойствата на корени и степени с рационален показател, разглеждани тук, са подобни на онези свойства, които са били изучавани по-рано. квадратни корении степени с цели числа. Необходимо е да се отдели достатъчно време за разработване на свойствата на степени и формиране на умения за идентични трансформации. Понятието степен с ирационален показателвъведени на визуално-интуитивна основа. Този материал играе спомагателна роля и се използва при въвеждане на експоненциалната функция. Изследването на свойствата на експоненциалните, логаритмичните и степенните функции е изградено в съответствие с приетите обща схемафункционално изследване. В този случай е даден преглед на свойствата в зависимост от стойностите на параметрите. Въз основа на изучените свойства на функциите се решават показателните и логаритмичните неравенства. Характерна особеност на курса е систематизирането и обобщаването на знанията на учениците, консолидирането и развитието на уменията и способностите, придобити в курса по алгебра, което се извършва както при изучаване на нов материал, така и при провеждане на обобщаващо повторение.
Глава 2

§едно. Обобщение на понятието степен.

Определение: Коренът на степента на чистота е такова число, чиято степен е равна на.

Според тази дефиниция коренът на степен th на число е решение на уравнението. Броят на корените на това уравнение зависи от и . Нека разгледаме функция. Както е известно, на интервала тази функция нараства за всеки и приема всички стойности от интервала. Според теоремата за корена уравнението за всяко има неотрицателен корен и освен това само един. Нарича се аритметичен корен от степен th на число и се обозначава; числото се нарича индекс на корена, а самото число се нарича радикален израз. Знакът се нарича още радикал.

Определение: Аритметичният корен на степен th на число е неотрицателно число, чиято степен th е .

За четно, функцията е четно. От това следва, че ако , то уравнението освен корен има и корен . Ако , тогава има само един корен: ; ако , тогава това уравнение няма корени, тъй като четната степен на всяко число е неотрицателна.

За нечетни стойности функцията нараства по цялата числова линия; диапазонът му е множеството от всички реални числа. Прилагайки теоремата за корена, откриваме, че уравнението има един корен за всяко и по-специално за . Този корен за всяка стойност се означава с .

За корени с нечетна степен равенството е вярно. Наистина, , т.е. числото е корен th от . Но такъв корен за нечетно е уникален. Следователно,.

Забележка 1: За всяко реално

Припомнете си добре познатите свойства на аритметичните корени от степен th.

За всяко естествено, цяло число и всички неотрицателни цели числа и равенствата са верни:

1.

2.

3.

4.

Степен с рационален показател.

Изразът е дефиниран за всички и , с изключение на случая, когато . Припомнете си свойствата на такива мощности.

За всякакви числа и всички цели числа и равенства са верни:

Също така отбелязваме, че ако , тогава за и за .. и

За учениците, обучаващи се за Единния държавен изпит, учителите по математика в средно училище № 26 в Якутск използват списък с въпроси за съдържанието (кодификатор) на училищния курс по математика, чието усвояване се проверява при полагане на единния държавен изпит през 2007 г. . избираема дисциплинав подготовка за Обединеното Държавен изпитсе основава на повторение, систематизиране и задълбочаване на знания, придобити по-рано. Занятията се провеждат под формата на безплатни...

Изброените равенства при преобразуване на изрази с логаритми се използват както от дясно на ляво, така и от ляво на дясно.

Струва си да се отбележи, че не е необходимо да запомняте последствията от свойствата: когато извършвате трансформации, можете да се справите с основните свойства на логаритмите и други факти (например тези за b≥0), от които съответните следват последствията. „Страничният ефект“ на този подход е само, че решението ще бъде малко по-дълго. Например, за да се направи без последствието, което се изразява с формулата и започвайки само от основните свойства на логаритмите, ще трябва да извършите верига от трансформации от следния вид: .

Същото може да се каже и за последното свойство от горния списък, което отговаря на формулата , тъй като следва и от основните свойства на логаритмите. Основното нещо, което трябва да разберете, е, че винаги е възможно степента на положително число с логаритъм в степента да размени основата на степента и числото под знака на логаритъма. Честно казано, отбелязваме, че примерите за прилагане на трансформации от този вид са рядкост на практика. По-долу ще дадем няколко примера.

Преобразуване на числови изрази с логаритми

Спомнихме си свойствата на логаритмите, сега е време да научим как да ги прилагаме на практика, за да трансформираме изрази. Естествено е да започнете с трансформацията на числови изрази, а не на изрази с променливи, тъй като е по-удобно и по-лесно да научите основите върху тях. Така че ще направим и ще започнем с много прости примериза да научите как да изберете желаното свойство на логаритъма, но постепенно ще усложняваме примерите, до момента, в който ще трябва да се приложат няколко свойства подред, за да се получи крайният резултат.

Избор на желаното свойство на логаритмите

Не са толкова малко свойствата на логаритмите и е ясно, че трябва да можете да изберете подходящото от тях, което в конкретния случай ще доведе до желания резултат. Обикновено това не е трудно да се направи чрез сравняване на формата на логаритъма или израза, който се преобразува с типовете на лявата и дясната част на формулите, изразяващи свойствата на логаритмите. Ако остане или дясна частедна от формулите съвпада с дадения логаритъм или израз, тогава най-вероятно това свойство трябва да се използва по време на трансформацията. Следните примери ясно показват това.

Нека започнем с примери за преобразуване на изрази с помощта на дефиницията на логаритъм, който съответства на формулата a log a b =b , a>0 , a≠1 , b>0 .

Пример.

Изчислете, ако е възможно: a) 5 log 5 4 , b) 10 log(1+2 π) , c) , г) 2 log 2 (−7) , д) .

Решение.

В примера буква a) ясно показва структурата a log a b , където a=5 , b=4 . Тези числа отговарят на условията a>0 , a≠1 , b>0 , така че можете спокойно да използвате равенството a log a b =b . Имаме 5 log 5 4=4 .

б) Тук a=10 , b=1+2 π , условията a>0 , a≠1 , b>0 са изпълнени. В този случай се изпълнява равенството 10 lg(1+2 π) =1+2 π.

в) И в този пример имаме работа със степен от формата a log a b , където и b=ln15 . Така .

Въпреки че принадлежи към една и съща форма a log a b (тук a=2 , b=−7 ), изразът под буквата d) не може да бъде преобразуван по формулата a log a b =b . Причината е, че няма смисъл, защото съдържа отрицателно число под знака на логаритъма. Освен това числото b=−7 не отговаря на условието b>0 , което прави невъзможно прибягването до формулата a log a b =b , тъй като изисква условията a>0 , a≠1 , b>0 . Така че не можем да говорим за изчисляване на стойността 2 log 2 (−7) . В този случай писането на 2 log 2 (−7) = −7 би било грешка.

По същия начин в примера под буква д) е невъзможно да се даде решение на формата , тъй като оригиналният израз няма смисъл.

Отговор:

a) 5 log 5 4 =4 , b) 10 log(1+2 π) =1+2 π , c) , г), д) изразите нямат смисъл.

Често е полезно да се трансформирате положително числосе представя като степен на някакво положително и неединично число с логаритъм в степента. Тя се основава на същата дефиниция на логаритъма a log a b =b , a>0 , a≠1 , b>0 , но формулата се прилага отдясно наляво, тоест във формата b=a log a b . Например 3=e ln3 или 5=5 log 5 5 .

Нека да преминем към използването на свойствата на логаритмите за трансформиране на изрази.

Пример.

Намерете стойността на израза: a) log −2 1, b) log 1 1, c) log 0 1, d) log 7 1, e) ln1, f) lg1, g) log 3,75 1, h) log 5 π 7 1 .

Решение.

В примерите под букви а), б) и в) са дадени изразите log −2 1 , log 1 1 , log 0 1, които нямат смисъл, тъй като основата на логаритъма не трябва да съдържа отрицателно число , нула или единица, защото сме дефинирали логаритъм само за положителна и неединична основа. Следователно в примери а) - в) не може да става въпрос за намиране на стойността на израза.

Във всички останали задачи, очевидно, основите на логаритмите съдържат съответно положителни и неединични числа 7 , e , 10 , 3,75 и 5 π 7, а единиците са навсякъде под знаците на логаритмите. И знаем свойството на логаритъма от единица: log a 1=0 за всяко a>0, a≠1. По този начин стойностите на изразите b) - f) са равни на нула.

Отговор:

a), b), c) изразите нямат смисъл, d) log 7 1=0, e) ln1=0, f) log1=0, g) log 3,75 1=0, h) log 5 e 7 1 =0.

Пример.

Изчислете: а) , б) lne , в) lg10 , г) log 5 π 3 −2 (5 π 3 −2), д) log −3 (−3) , f) log 1 1 .

Решение.

Ясно е, че трябва да използваме свойството на логаритъма на основата, което съответства на формулата log a a=1 за a>0 , a≠1 . Действително в задачи под всички букви числото под знака на логаритъма съвпада с основата му. Затова искам веднага да кажа, че стойността на всеки от дадените изрази е 1. Все пак не бързайте със заключенията: в задачите под букви а) - г) стойностите на изразите наистина са равни на единица, а в задачите д) и е) оригиналните изрази нямат смисъл, така че не може да се каже, че стойностите на тези изрази са равни на 1.

Отговор:

а) , б) lne=1 , в) lg10=1 , г) log 5 π 3 −2 (5 π 3 −2)=1, д), е) изразите нямат смисъл.

Пример.

Намерете стойността: a) log 3 3 11 , b) , в), г) log −10 (−10) 6 .

Решение.

Очевидно под знаците на логаритмите са някои степени на основата. Въз основа на това разбираме, че свойството на степента на основата е полезно тук: log a a p =p, където a>0, a≠1 и p е всяко реално число. Имайки предвид това, имаме следните резултати: a) log 3 3 11 =11 , b) , в) . Може ли да се напише подобно равенство за примера под буква d) от вида log −10 (−10) 6 =6? Не, не можете, защото log −10 (−10) 6 няма смисъл.

Отговор:

а) log 3 3 11 =11, б) , в) г) изразът няма смисъл.

Пример.

Изразете израза като сбор или разлика от логаритми при една и съща основа: а) , b) , c) log((−5) (−12)) .

Решение.

а) Продуктът е под знака на логаритъма и знаем свойството на логаритъма на продукта log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y> 0 . В нашия случай числото в основата на логаритъма и числата в произведението са положителни, т.е. те отговарят на условията на избраното свойство, следователно можем безопасно да го приложим: .

б) Тук използваме свойството на логаритъма на частното, където a>0, a≠1, x>0, y>0. В нашия случай основата на логаритъма е положително число e, числителят и знаменателят π са положителни, което означава, че отговарят на условията на свойството, така че имаме право да използваме избраната формула: .

c) Първо, отбележете, че изразът lg((−5) (−12)) има смисъл. Но в същото време нямаме право да прилагаме формулата за логаритъм на произведението log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 , тъй като числата −5 и −12 са отрицателни и не отговарят на условията x>0 , y>0 . Тоест невъзможно е да се извърши такава трансформация: log((−5)(−12))=log(−5)+log(−12). Но какво да се прави? В такива случаи оригиналният израз трябва да бъде предварително трансформиран, за да се избегнат отрицателни числа. За подобни случаи на преобразуване на изрази с отрицателни числапод знака на логаритъма, ще говорим подробно в един от, но засега ще дадем решение на този пример, което е ясно предварително и без обяснение: lg((−5)(−12))=lg(5 12)=lg5+lg12.

Отговор:

а) , б) , в) lg((−5) (−12))=lg5+lg12 .

Пример.

Опростете израза: а) log 3 0,25 + log 3 16 + log 3 0,5, б) .

Решение.

Тук ще ни помогнат всички същите свойства на логаритъма на произведението и логаритъма на частното, които използвахме в предишните примери, само сега ще ги приложим отдясно наляво. Тоест, преобразуваме сумата от логаритми в логаритъм от произведението и разликата на логаритмите в логаритъм от частното. Ние имаме
а) log 3 0,25+log 3 16+log 3 0,5=log 3 (0,25 16 0,5)=log 3 2.
б) .

Отговор:

а) log 3 0,25+log 3 16+log 3 0,5=log 3 2, б) .

Пример.

Отървете се от степента под знака на логаритъма: а) log 0,7 5 11, б) , в) log 3 (−5) 6 .

Решение.

Лесно е да се види, че имаме работа с изрази като log a b p. Съответното свойство на логаритъма е log a b p =p log a b , където a>0 , a≠1 , b>0 , p е всяко реално число. Тоест, при условията a>0, a≠1, b>0 от логаритъма на степента log a b p можем да отидем до произведението p·log a b. Нека извършим тази трансформация с дадените изрази.

a) В този случай a=0,7 , b=5 и p=11 . Значи log 0,7 5 11 =11 log 0,7 5 .

б) Тук условията a>0 , a≠1 , b>0 са изпълнени. Ето защо

в) Изразът log 3 (−5) 6 има същата структура log a b p , a=3 , b=−5 , p=6 . Но за b условието b>0 не е изпълнено, което прави невъзможно прилагането на формулата log a b p =p log a b . Така че защо не можете да свършите работата? Възможно е, но е необходима предварителна трансформация на израза, която ще разгледаме подробно по-долу в параграфа под заглавието . Решението ще бъде така: log 3 (−5) 6 =log 3 5 6 =6 log 3 5.

Отговор:

а) log 0,7 5 11 =11 log 0,7 5 ,
б)
в) log 3 (−5) 6 =6 log 3 5 .

Доста често формулата за логаритъм на степента при извършване на трансформации трябва да се прилага отдясно наляво във формата p log a b \u003d log a b p (това изисква същите условия за a, b и p). Например, 3 ln5=ln5 3 и lg2 log 2 3=log 2 3 lg2 .

Пример.

а) Изчислете стойността на log 2 5, ако е известно, че lg2≈0,3010 и lg5≈0,6990. б) Запишете дробта като логаритъм при основа 3.

Решение.

а) Формулата за преход към нова основа на логаритъма ни позволява да представим този логаритъм като съотношение на десетични логаритми, стойностите на които са ни известни: . Остава само да извършим изчисленията, които имаме .

б) Тук е достатъчно да използвате формулата за прехода към нова база и да я приложите отдясно наляво, тоест във формата . Получаваме .

Отговор:

а) log 2 5≈2,3223, б) .

На този етап ние доста внимателно разгледахме трансформацията на най-простите изрази, използвайки основните свойства на логаритмите и дефиницията на логаритъм. В тези примери трябваше да използваме едно свойство и нищо друго. Сега с чиста съвест можете да преминете към примери, чиято трансформация изисква използването на няколко свойства на логаритми и други допълнителни трансформации. Ще се занимаем с тях в следващия параграф. Но преди това нека се спрем накратко на примери за прилагане на следствия от основните свойства на логаритмите.

Пример.

а) Отървете се от корена под знака на логаритъма. б) Преобразувайте дробта в логаритъм с основа 5. в) Отървете се от степените под знака на логаритъма и в основата му. г) Изчислете стойността на израза . д) Заменете израза със степен с основа 3.

Решение.

а) Ако си припомним следствието от свойството логаритъм на степента , тогава можете веднага да отговорите: .

б) Тук използваме формулата от дясно на ляво имаме .

в) Б този случайформула води до резултата . Получаваме .

г) И тук е достатъчно да приложим следствието, на което отговаря формулата . Така .

д) Свойството на логаритъма ни позволява да постигнем желания резултат: .

Отговор:

а) . б) . в) . G) . д) .

Последователно прилагане на множество свойства

Реалните задачи за преобразуване на изрази, използващи свойствата на логаритмите, обикновено са по-сложни от тези, които разгледахме в предишния параграф. При тях по правило резултатът не се получава на една стъпка, а решението вече се състои в последователно прилагане на едно свойство след друго, заедно с допълнителни идентични трансформации, като отваряне на скоби, редуциране на сходни членове, редуциране на дроби и т.н. . Така че нека се доближим до такива примери. В това няма нищо сложно, основното е да действате внимателно и последователно, като спазвате реда, в който се извършват действията.

Пример.

Изчислете стойността на израз (log 3 15−log 3 5) 7 log 7 5.

Решение.

Разликата на логаритмите в скоби със свойството на логаритъма на частното може да бъде заменена с логаритъм log 3 (15:5) и след това да се изчисли неговата стойност log 3 (15:5)=log 3 3=1 . И стойността на израза 7 log 7 5 по дефиницията на логаритъма е 5 . Замествайки тези резултати в оригиналния израз, получаваме (log 3 15−log 3 5) 7 log 7 5 =1 5=5.

Ето решение без обяснение:
(log 3 15−log 3 5) 7 log 7 5 =log 3 (15:5) 5=
= log 3 3 5=1 5=5 .

Отговор:

(log 3 15−log 3 5) 7 log 7 5 =5.

Пример.

Каква е стойността на числовия израз log 3 log 2 2 3 −1 ?

Решение.

Нека първо трансформираме логаритъма, който е под знака на логаритъма, според формулата на логаритъма на степента: log 2 2 3 =3. Така че log 3 log 2 2 3 =log 3 3 и след това log 3 3=1 . Така че log 3 log 2 2 3 −1=1−1=0 .

Отговор:

log 3 log 2 2 3 −1=0 .

Пример.

Опростете израза.

Решение.

Формулата за преобразуване в нова основа на логаритъма позволява съотношението на логаритмите към една основа да бъде представено като log 3 5 . В този случай оригиналният израз ще приеме формата . По дефиниция на логаритъма 3 log 3 5 =5 , т.е , а стойността на получения израз, по силата на същата дефиниция на логаритъма, е равна на две.

Тук кратка версиярешение, което обикновено се дава: .

Отговор:

.

За плавен преход към информацията от следващия параграф, нека да разгледаме изразите 5 2+log 5 3 и lg0.01. Тяхната структура не отговаря на нито едно от свойствата на логаритмите. И така, какво се случва, ако те не могат да бъдат преобразувани с помощта на свойствата на логаритмите? Възможно е, ако извършите предварителни трансформации, които подготвят тези изрази за прилагане на свойствата на логаритмите. Така 5 2+log 5 3 =5 2 5 log 5 3 =25 3=75, и lg0,01=lg10 −2 = −2 . По-нататък ще разберем подробно как се извършва такава подготовка на изрази.

Подготовка на изрази за прилагане на свойствата на логаритмите

Логаритмите в преобразувания израз много често се различават в структурата на нотацията от лявата и дясната част на формулите, които съответстват на свойствата на логаритмите. Но също толкова често преобразуването на тези изрази включва използването на свойствата на логаритмите: тяхното използване изисква само предварителна подготовка. И тази подготовка се състои в извършване на определени идентични трансформации, които привеждат логаритмите във форма, удобна за прилагане на свойства.

Честно казано, отбелязваме, че почти всяка трансформация на изрази може да действа като предварителни трансформации, от баналното редуциране на подобни термини до приложението тригонометрични формули. Това е разбираемо, тъй като преобразуваните изрази могат да съдържат всякакви математически обекти: скоби, модули, дроби, корени, степени и т.н. Следователно, човек трябва да е готов да извърши всяка необходима трансформация, за да се възползва допълнително от свойствата на логаритмите.

Нека кажем веднага, че в този раздел не си поставяме задачата да класифицираме и анализираме всички възможни предварителни трансформации, които ни позволяват да приложим свойствата на логаритмите или дефиницията на логаритъм в бъдеще. Тук ще се спрем само на четири от тях, които са най-характерните и най-често срещаните в практиката.

И сега подробно за всеки от тях, след което в рамките на нашата тема остава само да се занимаваме с трансформацията на изрази с променливи под знаците на логаритмите.

Подбор на степени под знака на логаритъма и в основата му

Нека започнем веднага с пример. Нека имаме логаритъм. Очевидно в тази форма неговата структура не е благоприятна за използването на свойствата на логаритмите. Възможно ли е по някакъв начин да се трансформира този израз, за ​​да се опрости или дори по-добре да се изчисли стойността му? За да отговорим на този въпрос, нека разгледаме по-подробно числата 81 и 1/9 в контекста на нашия пример. Тук е лесно да се види, че тези числа могат да бъдат представени като степен на 3, наистина, 81=3 4 и 1/9=3 −2. В този случай оригиналният логаритъм се представя във формуляра и става възможно прилагането на формулата . Така, .

Анализът на анализирания пример поражда следната идея: ако е възможно, можете да опитате да подчертаете степента под знака на логаритъма и в основата му, за да приложите свойството на логаритъма на степента или нейното следствие. Остава само да разберем как да разграничим тези степени. Ще дадем някои препоръки по този въпрос.

Понякога е съвсем очевидно, че числото под знака на логаритъма и/или в основата му представлява някаква цяла степен, както в примера, обсъден по-горе. Почти непрекъснато трябва да се справяте със степени на две, които са добре познати: 4=2 2 , 8=2 3 , 16=2 4 , 32=2 5 , 64=2 6 , 128=2 7 , 256=2 8 , 512= 2 9 , 1024=2 10 . Същото може да се каже и за степените на тройката: 9=3 2 , 27=3 3 , 81=3 4 , 243=3 5 , ... Като цяло не вреди, ако има степенна таблица естествени числа в рамките на десет. Също така не е трудно да се работи с цели степени на десет, сто, хиляда и т.н.

Пример.

Изчислете стойността или опростете израза: a) log 6 216 , b) , c) log 0,000001 0,001 .

Решение.

a) Очевидно е, че 216=6 3 , така че log 6 216=log 6 6 3 =3 .

б) Таблицата на степените на естествените числа ни позволява да представим числата 343 и 1/243 като степени съответно на 7 3 и 3 −4. Следователно е възможно следваща трансформациядаден логаритъм:

в) Тъй като 0,000001=10 −6 и 0,001=10 −3, тогава log 0,000001 0,001=log 10 −6 10 −3 =(−3)/(−6)=1/2.

Отговор:

а) log 6 216=3, б) , c) log 0,000001 0,001=1/2 .

В по-сложни случаи, за да подчертаете силата на числата, трябва да прибягвате до.

Пример.

Променете израза в по-простата форма log 3 648 log 2 3 .

Решение.

Нека да видим в какво се превръща числото 648 основни фактори:

Тоест 648=2 3 3 4 . По този начин, log 3 648 log 2 3=log 3 (2 3 3 4) log 2 3.

Сега преобразуваме логаритъма на продукта в сумата от логаритми, след което прилагаме свойствата на логаритъма на степента:
log 3 (2 3 3 4) log 2 3=(log 3 2 3 + log 3 3 4) log 2 3=
=(3 log 3 2+4) log 2 3 .

По силата на следствието от свойството на логаритъма на степента, което съответства на формулата , произведението log32 log23 е произведението и е известно, че е равно на едно. Имайки предвид това, получаваме 3 log 3 2 log 2 3+4 log 2 3=3 1+4 log 2 3=3+4 log 2 3.

Отговор:

log 3 648 log 2 3=3+4 log 2 3.

Доста често изрази под знака на логаритъма и в основата му са продукти или съотношения на корените и/или степените на някои числа, например, , . Подобни изрази могат да бъдат представени като степен. За да направите това, се извършва преходът от корени към степени и се прилагат и . Тези трансформации ви позволяват да изберете градусите под знака на логаритъма и в неговата основа и след това да приложите свойствата на логаритмите.

Пример.

Изчислете: а) , б).

Решение.

а) Изразът в основата на логаритъма е произведението на степени с еднакви основи, по съответното свойство на степени имаме 5 2 5 −0,5 5 −1 =5 2−0,5−1 =5 0,5.

Сега нека преобразуваме дроба под знака на логаритъма: нека преминем от корена към степента, след което ще използваме свойството на съотношението на градусите със същите основи: .

Остава да замените получените резултати в оригиналния израз, използвайте формулата и завършете трансформацията:

б) Тъй като 729=3 6 и 1/9=3 −2, оригиналният израз може да бъде пренаписан като .

След това приложете свойството корен на експонентата, преминете от корена към експонентата и използвайте свойството съотношение на степените, за да преобразувате основата на логаритъма в степен: .

Като вземем предвид последния резултат, имаме .

Отговор:

а) , б).

Ясно е, че в общия случай, за да се получат степени под знака на логаритъма и в неговата основа, може да са необходими различни трансформации на различни изрази. Нека дадем няколко примера.

Пример.

Каква е стойността на израза: а) , б) .

Решение.

Освен това отбелязваме, че даденият израз има формата log A B p , където A=2 , B=x+1 и p=4 . Преобразувахме числови изрази от този вид според свойството на логаритъма на степента log a b p \u003d p log a b, следователно с даден израз искам да направя същото и да премина от log 2 (x + 1) 4 до 4 log 2 (x + 1) . А сега нека изчислим стойността на оригиналния израз и израза, получен след трансформацията, например с x=−2 . Имаме log 2 (−2+1) 4 =log 2 1=0 и 4 log 2 (−2+1)=4 log 2 (−1)- безсмислен израз. Това повдига основателен въпрос: „Какво направихме погрешно“?

И причината е следната: извършихме трансформацията log 2 (x+1) 4 =4 log 2 (x+1) , въз основа на формулата log a b p =p log a b , но имаме право да приложим само тази формула ако са изпълнени условията a >0 , a≠1 , b>0 , p - всяко реално число. Тоест трансформацията, която направихме, се осъществява, ако x+1>0, което е същото x>−1 (за A и p условията са изпълнени). Въпреки това, в нашия случай, ODZ на променливата x за оригиналния израз се състои не само от интервала x> −1, но и от интервала x<−1 . Но для x<−1 мы не имели права осуществлять преобразование по выбранной формуле.

Необходимостта да се вземе предвид ODZ

Нека продължим да анализираме преобразуването на избрания от нас израз log 2 (x+1) 4 и сега нека видим какво се случва с ODZ при преминаване към израза 4 log 2 (x+1) . В предишния параграф открихме ODZ на оригиналния израз - това е множеството (−∞, −1)∪(−1, +∞) . Сега нека намерим областта на допустимите стойности на променливата x за израза 4 log 2 (x+1) . Определя се от условието x+1>0 , което съответства на множеството (−1, +∞) . Очевидно е, че при преминаване от log 2 (x+1) 4 към 4·log 2 (x+1), обхватът на допустимите стойности се стеснява. И се разбрахме да избягваме реформи, които водят до стесняване на ОДЗ, тъй като това може да доведе до различни негативни последици.

Тук си струва да отбележите за себе си, че е полезно да контролирате ODZ на всяка стъпка от трансформацията и да не позволявате тя да се стеснява. И ако изведнъж на някакъв етап от трансформацията е имало стесняване на ODZ, тогава си струва да разгледаме много внимателно дали тази трансформация е допустима и дали сме имали право да я извършим.

Честно казваме, че на практика обикновено трябва да работим с изрази, в които ODZ на променливите е такъв, че ни позволява да използваме свойствата на логаритмите без ограничения във формата, която вече ни е известна, както отляво надясно, така и от отдясно наляво, когато извършвате трансформации. Бързо свиквате с това и започвате да извършвате трансформациите механично, без да мислите дали е възможно да ги извършите. И в такива моменти, за късмет, се изплъзват по-сложни примери, в които неточното прилагане на свойствата на логаритмите води до грешки. Така че винаги трябва да сте нащрек и да се уверите, че няма стесняване на ODZ.

Не боли отделно да се подчертаят основните трансформации, базирани на свойствата на логаритмите, които трябва да се извършват много внимателно, което може да доведе до стесняване на ODZ и в резултат на това до грешки:

Някои трансформации на изрази според свойствата на логаритмите могат да доведат и до обратното - разширяване на ODZ. Например преминаването от 4 log 2 (x+1) към log 2 (x+1) 4 разширява ODZ от набора (−1, +∞) до (−∞, −1)∪(−1, +∞ ) . Такива трансформации се извършват, ако останете в рамките на ODZ за оригиналния израз. Така току-що споменатата трансформация 4 log 2 (x+1)=log 2 (x+1) 4 се извършва върху ODZ променливата x за оригиналния израз 4 log 2 (x+1) , тоест когато x+1> 0 , което е същото като (−1, +∞) .

Сега, след като обсъдихме нюансите, на които трябва да обърнете внимание, когато преобразувате изрази с променливи, използвайки свойствата на логаритмите, остава да разберем как тези преобразувания трябва да се извършват правилно.

X+2>0. Работи ли в нашия случай? За да отговорим на този въпрос, нека да разгледаме DPV на променливата x. Определя се от системата от неравенства , което е еквивалентно на условието x+2>0 (ако е необходимо, вижте статията решение на системи от неравенства). Така можем безопасно да приложим свойството на логаритъма на степента.

Ние имаме
3 log(x+2) 7 −log(x+2)−5 log(x+2) 4 =
=3 7 log(x+2)−log(x+2)−5 4 log(x+2)=
=21 log(x+2)−log(x+2)−20 log(x+2)=
=(21−1−20)lg(x+2)=0 .

Можете да действате по различен начин, тъй като ODZ ви позволява да направите това, например така:

Отговор:

3 log(x+2) 7 −log(x+2)−5 log(x+2) 4 =0.

И какво да направите, когато условията, свързани със свойствата на логаритмите, не са изпълнени на ODZ? Ще се справим с това с примери.

Нека трябва да опростим израза lg(x+2) 4 −lg(x+2) 2 . Преобразуването на този израз, за ​​разлика от израза от предишния пример, не позволява свободното използване на свойството логаритъм на степента. Защо? ODZ на променливата x в този случай е обединението на два интервала x>−2 и x<−2 . При x>−2 можем безопасно да приложим свойството на логаритъма на степента и да продължим както в примера по-горе: log(x+2) 4 −log(x+2) 2 =4 log(x+2)−2 log(x+2)=2 log(x+2). Но ODZ съдържа друг интервал x+2<0 , для которого последнее преобразование будет некорректно. Что же делать при x+2<0 ? В подобных случаях на помощь приходит . Определение модуля позволяет выражение x+2 при x+2<0 представить как −|x+2| . Тогда при x+2<0 от lg(x+2) 4 −lg(x+2) 2 переходим к log(−|x+2|) 4 −log(−|x+2|) 2и освен това, поради мощностните свойства на lg|x+2| 4−lg|x+2| 2. Полученият израз може да се трансформира според свойството на логаритъма на степента, тъй като |x+2|>0 за всякакви стойности на променливата. Ние имаме log|x+2| 4−lg|x+2| 2 =4 log|x+2|−2 log|x+2|=2 log|x+2|. Сега можете да се отървете от модула, тъй като той е свършил работата си. Тъй като трансформираме при x+2<0 , то 2·lg|x+2|=2·lg(−(x+2)) . Итак, можно считать, что мы справились с поставленной задачей. Ответ: . Полученный результат можно записать компактно с использованием модуля как .

Нека разгледаме още един пример, за да направим работата с модули позната. Нека разберем от израза преминете към сумата и разликата на логаритмите на линейните биноми x−1 , x−2 и x−3 . Първо намираме ODZ:

В интервала (3, +∞) стойностите на изразите x−1 , x−2 и x−3 са положителни, така че можем безопасно да приложим свойствата на логаритъма на сумата и разликата:

И на интервала (1, 2) стойностите на израза x−1 са положителни, а стойностите на изразите x−2 и x−3 са отрицателни. Следователно, в разглеждания интервал, представяме x−2 и x−3, използвайки модула като −|x−2| и −|x−3| съответно. При което

Сега можем да приложим свойствата на логаритъма на произведението и частното, тъй като върху разглеждания интервал (1, 2) стойностите на изразите x−1 , |x−2| и |x−3| - положителен.

Ние имаме

Получените резултати могат да се комбинират:

Като цяло подобно разсъждение позволява, въз основа на формулите за логаритъм на продукта, съотношението и степента, да се получат три практически полезни резултата, които са доста удобни за използване:

• Логаритъмът от произведението на два произволни израза X и Y от формата log a (X·Y) може да бъде заменен със сумата от логаритмите log a |X|+log a |Y| , a>0 , a≠1 .
• Специалният логаритъм log a (X:Y) може да бъде заменен с разликата на логаритмите log a |X|−log a |Y| , a>0 , a≠1 , X и Y са произволни изрази.
• От логаритъм на някакъв израз B към четна степен p във формата log a B p, може да се премине към израза p log a |B| , където a>0 , a≠1 , p е четно число и B е произволен израз.

Подобни резултати са дадени например в инструкциите за решаване на експоненциални и логаритмични уравнения в колекцията от задачи по математика за кандидати за университети, под редакцията на М. И. Сканави.

Пример.

Опростете израза .

Решение.

Би било добре да се прилагат свойствата на логаритъма на степента, сумата и разликата. Но можем ли да го направим тук? За да отговорим на този въпрос, трябва да знаем ОДЗ.

Нека го дефинираме:

Съвсем очевидно е, че изразите x+4 , x−2 и (x+4) 13 върху диапазона от възможни стойности на променливата x могат да приемат както положителни, така и отрицателни стойности. Следователно ще трябва да работим чрез модули.

Свойствата на модула ви позволяват да пренапишете като , така

Освен това нищо не ви пречи да използвате свойството на логаритъма на степента и след това да донесете подобни условия:

Друга последователност от трансформации води до същия резултат:

и тъй като изразът x−2 може да приема както положителни, така и отрицателни стойности на ODZ, когато се вземе четен показател 14