Použitie derivátu v rôznych oblastiach činnosti. Zaujímavá derivácia Ciele tejto práce: Zvážiť použitie derivácie v rôznych vedách Zoznámiť sa s vedcami, ktorí študovali deriváciu funkcie. Sila je odvodením práce vo vysídlení.

Ministerstvo školstva Saratovský región

Štátny autonómny profesionál vzdelávacia inštitúcia Saratovský región "Engels Polytechnic"

APLIKÁCIA DERIVÁTU V RÔZNYCH VEDECKÝCH OBLASTIACH

Vykonané: Sarkulova Nurgulya Sergejevna

študentka skupiny KShI-216/15

(dizajn, modelovanie a

technológia šitia)

vedecký poradca:

Verbitskaja Elena Vyacheslavovna

učiteľka matematiky GAPOU SO

"Engelsova polytechnika"

2016

Úvod

Úloha matematiky v rôznych oblastiach prírodných vied je veľmi veľká. Niet divu, že hovoria„Matematika je kráľovnou vied, jej fyzika pravá ruka, chémia zostala.

Predmetom skúmania je derivát.

Hlavným cieľom je ukázať význam derivácie nielen v matematike, ale aj v iných vedách, jej význam v modernom živote.

Diferenciálny počet je opis sveta okolo nás vytvorený matematickým jazykom. Derivát nám pomáha úspešne riešiť nielen matematické problémy, ale aj praktické úlohy v rôznych oblastiach vedy a techniky.

Derivácia funkcie sa používa všade tam, kde dochádza k nerovnomernému toku procesu: ide o nerovnomerný mechanický pohyb a striedavý prúd a chemické reakcie a rádioaktívny rozpad látky atď.

Kľúčové a tematické otázky tejto eseje:

1. História vzniku derivátu.

2. Prečo študovať derivácie funkcií?

3. Kde sa používajú deriváty?

4. Aplikácia derivátov vo fyzike, chémii, biológii a iných vedách.

5. Závery

Rozhodol som sa napísať prácu na tému „Aplikácia derivácie v rôznych oblastiach vedy“, pretože si myslím, že táto téma je veľmi zaujímavá, užitočná a relevantná.

Vo svojej práci budem hovoriť o aplikácii diferenciácie v rôznych oblastiach vedy, ako je chémia, fyzika, biológia, geografia atď. Všetky vedy sú predsa neoddeliteľne spojené, čo je veľmi dobre vidieť na príklade témy zvažujem.

Aplikácia derivátu v rôznych oblastiach vedy

Z kurzu algebry na strednej škole to už vieme derivát je hranica pomeru prírastku funkcie k prírastku jej argumentu, pretože prírastok argumentu má tendenciu k nule, ak takáto hranica existuje.

Akcia nájdenia derivácie sa nazýva jej diferenciácia a funkcia, ktorá má deriváciu v bode x, sa v tomto bode nazýva diferencovateľná. Funkcia, ktorá je diferencovateľná v každom bode intervalu, sa nazýva diferencovateľná na tomto intervale.

Pocta objaviť základné zákony matematickej analýzy patrí anglický fyzik a matematik Isaac Newton a nemecký matematik, fyzik, filozof Leibniz.

Newton predstavil pojem derivát, študoval zákony mechaniky, čím odhalil jeho mechanický význam.

Fyzikálny význam derivácie: derivácia funkcier= f(X) v bode X 0 je rýchlosť zmeny funkcief(X) v bode X 0 .

Leibniz prišiel ku konceptu derivácie vyriešením problému nakreslenia dotyčnice k derivačnej čiare, čím ju vysvetlil geometrický význam.

Geometrický význam derivácie je, že derivácia funguje v bodeX 0 rovná sklonu dotyčnice ku grafu funkcie nakreslenej v bode s osouX 0 .

Pojem derivácia a moderná notáciar" , f„Zaviedol ho J. Lagrange v roku 1797.

Ruský matematik V 19. storočí Panfuty Ľvovič Čebyšev povedal, že „mimoriadny význam majú tie vedecké metódy, ktoré nám umožňujú vyriešiť problém spoločný pre všetku praktickú ľudskú činnosť, napríklad ako naložiť s našimi prostriedkami, aby sme dosiahli čo najväčší úžitok“.

Zástupcovia rôznych špecialít sa v súčasnosti musia zaoberať takýmito úlohami:

Procesní inžinieri sa snažia organizovať výrobu tak, aby sa vyrobilo čo najviac produktov;

Dizajnéri sa snažia vyvinúť zariadenie pre vesmírna loď takže hmotnosť zariadenia je najmenšia;

Ekonómovia sa snažia plánovať prepojenia medzi závodom a zdrojmi surovín tak, aby náklady na dopravu boli minimálne.

Pri štúdiu akejkoľvek témy majú študenti otázku: „Prečo to potrebujeme? Ak odpoveď uspokojí zvedavosť, potom môžeme hovoriť o záujme študentov. Odpoveď na tému „Derivácia“ možno získať tak, že budeme vedieť, kde sa používajú derivácie funkcií.

Na zodpovedanie tejto otázky môžeme uviesť niektoré disciplíny a ich sekcie, v ktorých sa deriváty používajú.

Derivát v algebre:

1. Tangenta ku grafu funkcie

Graf dotyčnice k funkciif, diferencovateľné na x o , je priamka prechádzajúca bodom (x o ; f(x o )) a má sklonf“(x o).

y= f(x o) + f′(x o) (x - x o)

2. Vyhľadajte intervaly rastúcich a klesajúcich funkcií

Funkciay=f(x) sa počas intervalu zvyšujeX , ak k nejakému anerovnosť. Inými slovami, väčšia hodnota argumentu zodpovedá väčšej hodnote funkcie.

Funkciay=f(x) počas intervalu klesáX , ak k nejakému anerovnosť. Inými slovami, väčšia hodnota argumentu zodpovedá menšej hodnote funkcie.

3. Hľadanie extrémnych bodov funkcie

bod volalmaximálny bod funkciey=f(x) ak pre všetkýchX . Zavolá sa hodnota funkcie v maximálnom bodemaximálna funkcia a označujú.

bod volalminimálny bod funkciey=f(x) ak pre všetkýchX zo svojho okolia nerovnosť. Zavolá sa hodnota funkcie v minimálnom bodefunkčné minimum a označujú.

Pod susedstvom bodu pochopiť interval, kde je dostatočne malé kladné číslo.

Minimálne a maximálne body sa nazývajúextrémne body , a volajú sa funkčné hodnoty zodpovedajúce extrémnym bodomfunkčné extrémy .

4. Hľadajte intervaly konvexnosti a konkávnosti funkcie

Graf funkcií, je na tomto intervalekonvexné , neleží vyššie ako ktorákoľvek z jeho dotyčníc (obr. 1).

Graf funkcií, diferencovateľné na intervale, je na tomto intervalekonkávne , ak je graf tejto funkcie v intervale neleží nižšie ako ktorákoľvek z jeho dotyčníc (obr. 2).

Inflexný bod funkčného grafu sa nazýva bod oddeľujúci intervaly konvexnosti a konkávnosti.

5. Nájdenie inflexných bodov funkcie

Derivát vo fyzike:

1. Rýchlosť ako derivát cesty

2. Zrýchlenie ako derivácia rýchlostia =

3. Miera rozpadu rádioaktívne prvky 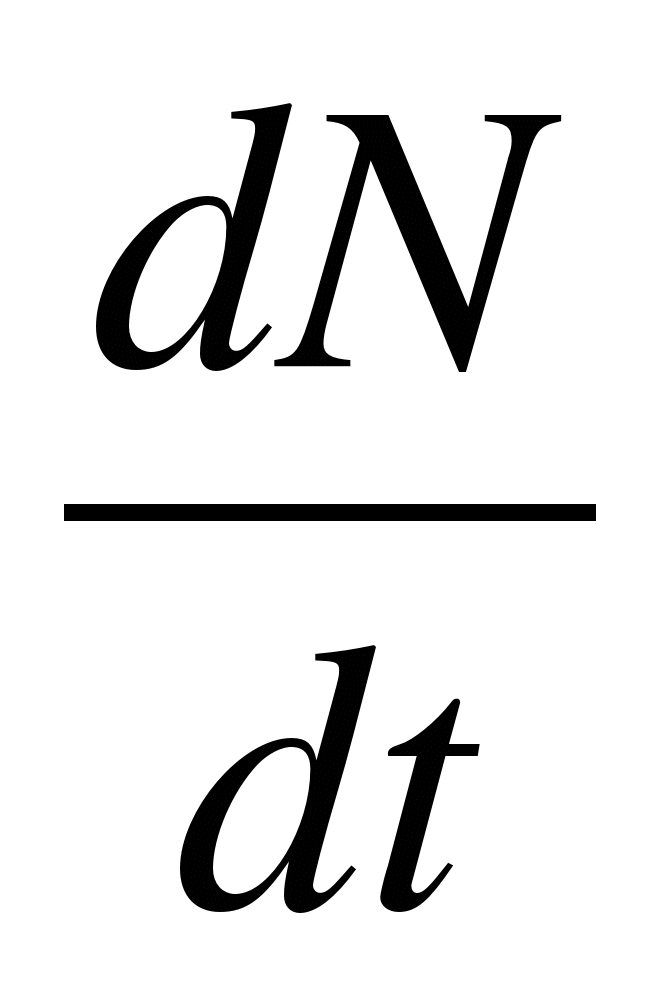= - λN

A tiež vo fyzike sa derivácia používa na výpočet:

Rýchlosti hmotný bod

Okamžitá rýchlosť ako fyzikálny význam derivátu

Okamžitá hodnota Napájanie striedavým prúdom

Okamžitá hodnota EMF elektromagnetickej indukcie

Maximálny výkon

Derivát v chémii:

A v chémii našiel diferenciálny počet široké uplatnenie pri konštrukcii matematických modelov chemické reakcie a následný popis ich vlastností.

Derivát v chémii sa používa na určenie veľmi dôležitej veci – rýchlosti chemická reakcia, jeden z rozhodujúcich faktorov, ktorý treba brať do úvahy v mnohých oblastiach vedeckej a priemyselnej činnosti. V(t) = p'(t)

Množstvo

in-va naraz t 0

p = p(t 0 )

Funkcia

Časový interval

∆t = t – t 0

Prírastok argumentu

Zmena množstva

∆p=p(t 0 + ∆t) – p(t 0 )

Prírastok funkcie

Priemerná rýchlosť chemickej reakcie

∆p/∆t

Pomer prírastku funkcie k prírastku argumentu

Deriváty v biológii:

Populácia je súbor jedincov daného druhu, ktorí zaberajú určitú oblasť územia v rámci druhu, voľne sa navzájom krížia a sú čiastočne alebo úplne izolovaní od iných populácií a je tiež základnou jednotkou evolúcie.

P \u003d x“ (t)

Derivát v geografii:

1. Niektoré významy v seizmografii

2. Vlastnosti elektromagnetického poľa pôda

3. Rádioaktivita jadrových geofyzikálnych parametrov

4. Mnoho významov v ekonomickej geografii

5. Odvoďte vzorec na výpočet počtu obyvateľov v území v čase t.

y'= do y

Myšlienka sociologického modelu Thomasa Malthusa je taká, že rast populácie je úmerný počtu obyvateľov v danom čase t až N(t). Malthusov model dobre fungoval na opis populácie USA v rokoch 1790 až 1860. Tento model už vo väčšine krajín neplatí.

Derivát v elektrotechnike:

V našich domovoch, v doprave, v továrňach: elektrický prúd funguje všade. Pod elektrickým prúdom rozumieme usmernený pohyb voľných elektricky nabitých častíc.

Kvantitatívna charakteristika elektrický prúd je súčasná sila.

V elektrickom obvode nabíjačka mení sa v čase podľa zákona q=q (t). Prúd I je deriváciou náboja q vzhľadom na čas.

V elektrotechnike sa využíva najmä striedavá prevádzka.

Elektrický prúd, ktorý sa mení s časom, sa nazýva striedavý prúd. Obvod striedavého prúdu môže obsahovať rôzne prvky: vykurovacie zariadenia, cievky, kondenzátory.

Generovanie striedavého elektrického prúdu je založené na zákone elektromagnetickej indukcie, ktorého formulácia obsahuje derivát magnetického toku.

Derivát v ekonómii:

Ekonomika je základom života a diferenciálny počet, prístroj na ekonomickú analýzu, v ňom zaujíma dôležité miesto. Základnou úlohou ekonomickej analýzy je študovať vzťahy ekonomických veličín vo forme funkcií.

Derivát v ekonómii rieši dôležité otázky:

1. Akým smerom sa zmenia príjmy štátu zvýšením daní alebo zavedením ciel?

2. Zvýšia sa alebo znížia sa príjmy spoločnosti s rastom ceny jej produktov?

Na vyriešenie týchto otázok je potrebné zostrojiť spojovacie funkcie vstupných premenných, ktoré sú následne študované metódami diferenciálneho počtu.

Taktiež pomocou extrému funkcie (derivátu) v ekonomike môžete nájsť najvyššiu produktivitu práce, maximálny zisk, maximálny výkon a minimálne náklady.

ZÁVER: derivát sa úspešne používa pri riešení rôznych aplikovaných problémov vo vede, technike a živote

Ako vidno z vyššie uvedeného, využitie derivačnej funkcie je veľmi rôznorodé, a to nielen pri štúdiu matematiky, ale aj v iných odboroch. Preto môžeme konštatovať, že štúdium témy: „Derivácia funkcie“ bude mať svoje uplatnenie aj v iných témach a predmetoch.

Presvedčili sme sa o dôležitosti naštudovania témy „Derivácia“, jej úlohe pri štúdiu procesov vedy a techniky, možnosti projektovania podľa skutočné udalosti matematické modely a riešiť dôležité problémy.

“Hudba môže povzniesť alebo upokojiť dušu,
Maľovanie lahodí oku,
Poézia - prebudiť pocity,
Filozofia - uspokojiť potreby mysle,
Inžinierstvo má zlepšiť materiálnu stránku života ľudí,
ALEmatematika môže dosiahnuť všetky tieto ciele.“

Tak povedal americký matematikMaurice Kline.

Bibliografia:

1. Bogomolov N.V., Samoylenko I.I. Matematika. - M.: Yurayt, 2015.

2. V. P. Grigoriev a Yu. A. Dubinsky, Základy vyššej matematiky. - M.: Akadémia, 2014.

3. Bavrin I.I. Základy vyššej matematiky. - M.: absolventská škola, 2013.

4. Bogomolov N.V. Praktické hodiny matematiky. - M.: Vysoká škola, 2013.

5. Bogomolov N.V. Zbierka úloh z matematiky. - M.: Drop, 2013.

6. Rybnikov K.A. Dejiny matematiky, Moskovská univerzita, M, 1960.

7. Vinogradov Yu.N., Gomola A.I., Potapov V.I., Sokolova E.V. – M.:Vydavateľské centrum "Akadémia", 2010

8 . Bašmakov M.I. Matematika: algebra a začiatky matematickej analýzy, geometria. - M.: Vydavateľské centrum "Akadémia", 2016

Pravidelné zdroje:

Noviny a časopisy: "Matematika", " Verejná lekcia»

Používanie internetových zdrojov, digitálnych knižníc:

www:egetutor.ru

matematika-na5.norod.ru

FGOU SPO

Novosibirsk poľnohospodárska vysoká škola

abstraktné

v odbore "matematika"

"Aplikácia derivátu vo vede a technike"

S. Razdolnoe 2008

Úvod

1. Teoretická časť

1.1 Problémy vedúce k pojmu derivát

1.2 Definícia derivátu

1.3 Všeobecné pravidlo pre nájdenie derivátu

1.4 Geometrický význam derivácie

1.5 Mechanický význam derivátu

1.6 Derivácia druhého rádu a jej mechanický význam

1.7 Definícia a geometrický význam diferenciálu

2. Skúmanie funkcií pomocou derivácie

Záver

Literatúra

Úvod

V prvej kapitole mojej eseje si povieme o koncepte derivácie, pravidlách jej aplikácie, o geometrickom a fyzický zmysel derivát. V druhej kapitole mojej eseje si povieme o využití derivátu vo vede a technike a o riešení problémov v tejto oblasti.

1. Teoretická časť

1.1 Problémy vedúce k pojmu derivát

Pri štúdiu určitých procesov a javov často vzniká problém určiť rýchlosť týchto procesov. Jeho riešenie vedie ku konceptu derivácie, čo je základný koncept diferenciálneho počtu.

Metóda diferenciálneho počtu vznikla v 17. a 18. storočí. Mená dvoch veľkých matematikov I. Newtona a G.V. Leibniz.

Newton prišiel k objavu diferenciálneho počtu pri riešení úloh o rýchlosti hmotného bodu v danom časovom okamihu (okamžitá rýchlosť).

Ako je známe, rovnomerný pohyb je pohyb, pri ktorom telo prejde rovnakú dĺžku dráhy v rovnakých časových intervaloch. Vzdialenosť, ktorú telo prejde za jednotku času, sa nazýva rýchlosť rovnomerný pohyb.

Najčastejšie sa však v praxi stretávame s nerovnomerným pohybom. Auto jazdiace po ceste spomaľuje na prechodoch a zrýchľuje ho v tých úsekoch, kde je cesta voľná; lietadlo pri pristávaní spomalí a pod. Preto sa najčastejšie musíme vysporiadať s tým, že v rovnakých časových intervaloch telo prechádza úsekmi dráhy rôznej dĺžky. Takýto pohyb sa nazýva nerovnomerné. Jeho rýchlosť sa nedá charakterizovať jedným číslom.

Na charakterizáciu nerovnomerného pohybu sa často používa koncept priemerná rýchlosť pohyb za čas ∆t٫, ktorý je určený vzťahom kde ∆s je dráha, ktorú teleso prejde za čas ∆t.

Takže s telom vo voľnom páde je priemerná rýchlosť jeho pohybu v prvých dvoch sekundách

V praxi taká charakteristika pohybu, ako je priemerná rýchlosť, hovorí o pohybe veľmi málo. V skutočnosti pri 4,9 m / s a pre 2. - 14,7 m / s, zatiaľ čo priemerná rýchlosť za prvé dve sekundy je 9,8 m / s. Priemerná rýchlosť počas prvých dvoch sekúnd nedáva žiadnu predstavu o tom, ako k pohybu došlo: keď sa telo pohybovalo rýchlejšie a keď pomalšie. Ak nastavíme priemerné rýchlosti pohybu pre každú sekundu zvlášť, tak napríklad budeme vedieť, že v 2. sekunde sa telo pohybovalo oveľa rýchlejšie ako v 1. Vo väčšine prípadov však oveľa rýchlejšie, než s čím nie sme spokojní. Koniec koncov, je ľahké pochopiť, že počas tejto 2. sekundy sa aj telo pohybuje rôznymi spôsobmi: na začiatku je to pomalšie, na konci rýchlejšie. A ako sa to posunie niekde uprostred tejto 2. sekundy? Inými slovami, ako určiť okamžitú rýchlosť?

Nech je pohyb telesa opísaný zákonom na čas rovný ∆t. V momente t0 telo prešlo cestou, momentálne - cestou. Preto za čas ∆t prešlo teleso určitú vzdialenosť a priemerná rýchlosť telesa za toto časové obdobie bude.

Čím kratší je časový interval ∆t, tým presnejšie je možné určiť, akou rýchlosťou sa teleso pohybuje v okamihu t0, keďže pohybujúce sa teleso nemôže v krátkom čase výrazne zmeniť svoju rýchlosť. Preto sa priemerná rýchlosť, keďže ∆t má tendenciu k nule, blíži k skutočnej rýchlosti pohybu a v limite udáva rýchlosť pohybu v danom čase t0 (okamžitá rýchlosť).

Touto cestou ,

Definícia 1. Okamžitá rýchlosť priamočiareho pohybu telesa v danom čase t0 je hranica priemernej rýchlosti za čas od t0 do t0+ ∆t, kedy sa časový interval ∆t blíži k nule.

Takže na nájdenie rýchlosti priamočiareho nerovnomerného pohybu v danom momente je potrebné nájsť hranicu pomeru prírastku dráhy ∆k prírastku času ∆t za podmienky t.j. Leibniz prišiel k objavu diferenciálneho počtu pri riešení problému konštrukcie dotyčnice ľubovoľnej krivky danej jeho rovnicou.

Riešenie tohto problému má veľký význam. Koniec koncov, rýchlosť pohybujúceho sa bodu smeruje pozdĺž dotyčnice k jeho trajektórii, preto sa pri určovaní rýchlosti projektilu na jeho trajektórii, rýchlosti akejkoľvek planéty na jej obežnej dráhe, obmedzuje na určenie smeru dotyčnice k krivka.

Definícia dotyčnice ako priamky, ktorá má len jeden spoločný bod s krivkou, ktorá platí pre kružnicu, je pre mnohé iné krivky nevhodná.

Nasledujúca definícia dotyčnice ku krivke nielen zodpovedá intuitívnej predstave o nej, ale umožňuje aj reálne nájsť jej smer, t.j. vypočítajte sklon dotyčnice.

Definícia 2. Tangenta ku krivke v bode M sa nazýva priamka MT, čo je hraničná poloha sečnice MM1, keď sa bod M1, pohybujúci sa po krivke, neobmedzene približuje k bodu M.

1.2 Definícia derivátu

Všimnite si, že pri určovaní dotyčnice ku krivke a okamžitej rýchlosti nerovnomerného pohybu sa vykonávajú v podstate rovnaké matematické operácie:

1. Daná hodnota argumentu sa inkrementuje a vypočíta sa nová hodnota funkcie zodpovedajúca novej hodnote argumentu.

2. Určite prírastok funkcie zodpovedajúci prírastku zvoleného argumentu.

3. Prírastok funkcie sa vydelí prírastkom argumentu.

4. Vypočítajte limit tohto pomeru za predpokladu, že prírastok argumentu má tendenciu k nule.

Riešenia mnohých problémov vedú k limitným prechodom tohto typu. Je potrebné zovšeobecniť a pomenovať túto pasáž až do krajnosti.

Rýchlosť zmeny funkcie v závislosti od zmeny argumentu možno samozrejme charakterizovať pomerom. Tento vzťah sa nazýva priemerná rýchlosť funkcia sa mení v intervale od do. Teraz musíme zvážiť limitu zlomku. Limit tohto pomeru, keďže prírastok argumentu má tendenciu k nule (ak táto limita existuje), je nejakou novou funkciou. Táto funkcia je označená symbolmi y', tzv derivát túto funkciu, keďže sa získava (vyrába) z funkcie Samotná funkcia sa volá primitívny funkcie vzhľadom na jej deriváciu

Definícia 3. derivát funkcie v danom bode pomenúvajú limitu pomeru prírastku funkcie ∆y k príslušnému prírastku argumentu ∆x za predpokladu, že ∆x→0, t.j.

1.3 Všeobecné pravidlo pre nájdenie derivátu

Operácia nájdenia derivácie nejakej funkcie sa nazýva diferenciácia funkcie a oblasť matematiky, ktorá študuje vlastnosti tejto operácie, je diferenciálny počet.

Ak má funkcia deriváciu v x=a, hovorí sa, že je diferencovateľné v tomto bode. Ak má funkcia deriváciu v každom bode v danom intervale, potom sa hovorí, že je diferencovateľné Na toto interval .

Definícia derivácie nielen plne charakterizuje koncept rýchlosti zmeny funkcie pri zmene argumentu, ale poskytuje aj spôsob, ako skutočne vypočítať deriváciu danej funkcie. Ak to chcete urobiť, musíte vykonať nasledujúce štyri akcie (štyri kroky) uvedené v definícii samotného derivátu:

1. Nájdite novú funkčnú hodnotu prezentáciou v túto funkciu namiesto x nová hodnota argumentu: .

2. Prírastok funkcie sa určí odčítaním danej hodnoty funkcie od jej novej hodnoty: .

3. Zostavte pomer prírastku funkcie k prírastku argumentu: .

4. Prejdite na limit a nájdite deriváciu: .

Všeobecne povedané, derivácia je „nová“ funkcia odvodená od danej funkcie podľa špecifikovaného pravidla.

1.4 Geometrický význam derivácie

Geometrická interpretácia derivátu, prvýkrát uvedená v koniec XVII v. Leibniz je nasledovný: hodnota derivácie funkcie v bode x sa rovná sklonu dotyčnice nakreslenej ku grafu funkcie v tom istom bode x, tie.

Rovnica dotyčnice, ako každá priamka prechádzajúca cez ňu daný bod v tomto smere má tvar – aktuálne súradnice. Ale rovnica dotyčnice bude tiež napísaná takto: . Normálna rovnica bude napísaná vo forme

1.5 Mechanický význam derivátu

Mechanickú interpretáciu derivátu ako prvý podal I. Newton. Spočíva v tomto: rýchlosť pohybu hmotného bodu v danom časovom okamihu sa rovná derivácii dráhy vzhľadom na čas, t.j. Ak je teda zákon pohybu hmotného bodu daný rovnicou, potom na nájdenie okamžitej rýchlosti bodu v určitom časovom okamihu musíte nájsť deriváciu a dosadiť do nej zodpovedajúcu hodnotu t.

1.6 Derivácia druhého rádu a jej mechanický význam

Dostávame (rovnicu z toho, čo bolo urobené v učebnici Lisichkin V.T. Soloveychik I.L. "Matematika" str. 240):

Touto cestou, zrýchlenie priamočiareho pohybu telesa v danom momente sa rovná druhej derivácii dráhy vzhľadom na čas, vypočítanej pre daný moment. Toto je mechanický význam druhej derivácie.

1.7 Definícia a geometrický význam diferenciálu

Definícia 4. Hlavná časť prírastku funkcie, lineárna vzhľadom na prírastok funkcie, lineárna vzhľadom na prírastok nezávislej premennej, sa nazýva diferenciál funkcií a označuje sa d, t.j. .

Funkčný diferenciál geometricky reprezentovaný prírastkom súradnice dotyčnice nakreslenej v bode M ( X ; r ) pre dané hodnoty x a ∆x.

kalkulácia diferenciál – .

Aplikácia diferenciálu v približných výpočtoch – , približná hodnota prírastku funkcie sa zhoduje s jej diferenciálom.

Veta 1. Ak je diferencovateľná funkcia rastie (klesá) v danom intervale, potom derivácia tejto funkcie nie je v tomto intervale záporná (nie kladná).

Veta 2. Ak je derivačná funkcia je v niektorom intervale kladná (záporná), potom funkcia v tomto intervale monotónne rastie (monotónne klesá).

Sformulujme teraz pravidlo na nájdenie intervalov monotónnosti funkcie

1. Vypočítajte deriváciu tejto funkcie.

2. Nájdite body, kde je nula alebo neexistujú. Tieto body sa nazývajú kritický pre funkciu

3. S nájdenými bodmi sa definičný obor funkcie rozdelí na intervaly, na ktorých si derivácia zachováva svoje znamienko. Tieto intervaly sú intervalmi monotónnosti.

4. Preskúmajte znamienko na každom z nájdených intervalov. Ak na uvažovanom intervale, potom sa na tomto intervale zvyšuje; ak, tak na takomto intervale klesá.

V závislosti od podmienok problému je možné zjednodušiť pravidlo na nájdenie intervalov monotónnosti.

Definícia 5. Bod sa nazýva maximálny (minimálny) bod funkcie, ak nerovnosť platí pre ľubovoľné x z nejakého okolia bodu.

Ak je maximálny (minimálny) bod funkcie, potom to hovoríme (minimálne) v bode. Maximálne a minimálne funkcie spájajú názov extrém funkcie a volajú sa maximálne a minimálne body extrémne body (extrémne body).

Veta 3.(nevyhnutný znak extrému). Ak a derivácia v tomto bode existuje, potom sa rovná nule: .

Veta 4.(dostatočný znak extrému). Ak derivát keď prechádza x a potom zmení znamenie a je extrémnym bodom funkcie .

Hlavné body štúdia derivátu:

1. Nájdite deriváciu.

2. Nájdite všetky kritické body z oblasti funkcie.

3. Nastavte znamienka derivácie funkcie pri prechode cez kritické body a vypíšte extrémne body.

4. Vypočítajte funkčné hodnoty v každom extrémnom bode.

2. Skúmanie funkcií s derivátom

Úloha č.1 . Zväzok denníka. Guľatina správnej formy bez chýb dreva s relatívne malým rozdielom v priemeroch hrubých a tenkých koncov sa nazýva priemyselná guľatina. Pri určovaní objemu priemyselnej guľatiny sa zvyčajne používa zjednodušený vzorec, kde dĺžka guľatiny je plocha jej priemerného prierezu. Zistite, či skutočný objem končí alebo podceňuje; odhadnúť relatívnu chybu.

Riešenie. Tvar okrúhleho obchodného dreva je blízky zrezanému kužeľu. Nech je polomer väčšieho, menšieho konca guľatiny. Potom jeho takmer presný objem (objem zrezaného kužeľa) možno, ako je známe, nájsť podľa vzorca. Nech je hodnota objemu vypočítaná podľa zjednodušeného vzorca. Potom;

Tie. . To znamená, že zjednodušený vzorec dáva podhodnotenie objemu. Povedzme si to teraz. Potom. To ukazuje, že relatívna chyba nezávisí od dĺžky guľatiny, ale je určená pomerom. Odkedy sa zvyšuje na intervale . To znamená, že relatívna chyba nepresahuje 3,7 %. V praxi lesníckej vedy sa takáto chyba považuje za celkom prijateľnú. S väčšou presnosťou je prakticky nemožné merať ani priemery koncov (pretože sú trochu odlišné od kruhov), ani dĺžku kmeňa, pretože nemerajú výšku, ale tvoriacu čiaru kužeľa (dĺžku poleno je desaťkrát väčšie ako priemer a to nevedie k veľkým chybám). Teda na prvý pohľad nesprávne, no o to viac jednoduchý vzorec lebo objem zrezaného kužeľa sa v reálnej situácii ukazuje ako celkom legitímny. Opakovane vykonané pomocou špeciálnych metód overovania ukázali, že pri hromadnom účtovaní priemyselného lesa relatívna chyba pri použití uvažovaného vzorca nepresahuje 4%.

Úloha č. 2 . Pri určovaní objemov jám, priekop vedier a iných nádob, ktoré majú tvar zrezaného kužeľa, sa niekedy v poľnohospodárskej praxi používa zjednodušený vzorec, kde je výška, sú plochy základov kužeľa. Zistite, či je skutočný objem nadhodnotený alebo podhodnotený, odhadnite relatívnu chybu za podmienok prirodzených pre prax: (- polomery základne, .

Riešenie. Označením cez skutočnú hodnotu objemu zrezaného kužeľa a cez hodnotu vypočítanú zjednodušeným vzorcom dostaneme: , t.j. . To znamená, že zjednodušený vzorec dáva nadhodnotenie objemu. Pri ďalšom opakovaní riešenia predchádzajúceho problému zistíme, že relatívna chyba nebude väčšia ako 6,7 %. Pravdepodobne je takáto presnosť prijateľná pri prideľovaní výkopových prác - napokon jamy nebudú ideálne kužele a zodpovedajúce parametre v reálnych podmienkach sa merajú veľmi zhruba.

Úloha č. 3 . V špeciálnej literatúre sa na určenie uhla β natočenia vretena frézky pri frézovaní spojok so zubami odvodzuje vzorec kde. Keďže tento vzorec je zložitý, odporúča sa vynechať jeho menovateľa a použiť zjednodušený vzorec. Pri akom (- celé číslo,) možno použiť tento vzorec, ak je pri určovaní uhla povolená chyba?

Riešenie. Presný vzorec po jednoduchom identické premeny možno spomenúť. Preto pri použití približného vzorca je povolená absolútna chyba, kde. Študujeme funkciu na intervale . V tomto prípade 0,06, t.j. roh patrí do prvej štvrtiny. Máme: . Všimnite si, že na uvažovanom intervale, a teda funkcia na tomto intervale klesá. Keďže ďalej, pre všetkých zvažovaných. Znamená, . Keďže je to radián, stačí vyriešiť nerovnosť. Vyriešením tejto nerovnosti výberom zistíme, že . Keďže funkcia klesá, z toho vyplýva

Záver

Použitie derivátu je pomerne široké a dá sa v tomto type práce úplne pokryť, ale pokúsil som sa pokryť hlavné body. V dnešnej dobe v súvislosti s vedecko-technický pokrok Najmä s rýchlym vývojom výpočtových systémov sa diferenciálny počet stáva čoraz dôležitejším pri riešení jednoduchých aj superzložitých problémov.

Literatúra

1. V.A. Petrov "Matematická analýza vo výrobných úlohách"

2. Soloveichik I.L., Lisichkin V.T. "Matematika"

Chaikin Semyon, Maysak Kirill, Zalogina Anastasia, Shakhzadova Anna

Tento vývoj obsahuje prezentáciu na tému "Aplikácia derivátu v chémii a biológii." Počas projektové aktivity bola vyslovená hypotéza, že derivát nachádza uplatnenie v týchto oblastiach vedy. Počas výskumná práca zistilo sa, aká je úloha derivátu v takých vedách ako chémia a biológia, kde a pri riešení akých problémov nachádza svoje uplatnenie. Na základe vykonanej práce sa dospelo k záveru, že hypotéza sa skutočne potvrdila.

Stiahnuť ▼:

Náhľad:

https://accounts.google.com

Popisy snímok:

hypotéza:

Náhľad:

Ak chcete použiť ukážku prezentácií, vytvorte si Google účet (účet) a prihláste sa: https://accounts.google.com

Popisy snímok:

Využitie derivátu v chémii a biológii Prácu realizovali študenti 11. ročníka MBOU strednej školy č. 6: Chaikin Semyon, Maisak Kirill, Zalogina Anastasia, Shakhzadova Anna Stavropol, 2014

hypotéza:

A v chémii našiel diferenciálny počet široké uplatnenie na zostavovanie matematických modelov chemických reakcií a následný popis ich vlastností. Chémia je veda o látkach, chemických premenách látok. Chémia študuje vzorce rôznych reakcií Rýchlosť chemickej reakcie je zmena koncentrácie reagujúcich látok za jednotku času. Aplikácia derivátu v chémii a biológii Stanovenie rýchlosti chemickej reakcie

Prečo potrebujeme deriváciu v reakciách? Pretože sa reakčná rýchlosť v počas procesu neustále mení, zvyčajne sa vyjadruje ako derivácia koncentrácie reaktantov v závislosti od času.

Vzorec derivátu v chémii Ak C (t) je zákon zmeny množstva látky, ktorá vstúpila do chemickej reakcie, potom sa rýchlosť v (t) chemickej reakcie v čase t rovná derivácii:

Určenie reakčnej rýchlosti Limit pomeru prírastkovej funkcie k prírastkovému argumentu, keďže Δt má tendenciu k nule, je rýchlosť chemickej reakcie v danom čase.

Chemická úloha: Nech je množstvo látky, ktorá vstúpila do chemickej reakcie, dané závislosťou: C (t) \u003d t 2 / 2 + 3 t -3 (mol) Nájdite rýchlosť chemickej reakcie po 3 sekundách. Riešenie: v (t) = C ‘(t) ; v(t) = t + 3; v (3) = 3+3 = 6. Odpoveď: 6 mol/s.

Biologický význam derivátu Vzťah medzi počtom jedincov populácie mikroorganizmov y a časom t jej rozmnožovania je daný rovnicou: y = x (t). Nech ∆ t je časový interval od nejakej počiatočnej hodnoty t po t + ∆ t . Potom y + ∆y = x (t + ∆ t) je nová hodnota veľkosti populácie zodpovedajúca momentu t + ∆ t a ∆ y + x (t + ∆ t) - x (t) je zmena v počet jedincov organizmov. Pomer je priemerná miera reprodukcie alebo, ako sa hovorí, priemerná produktivita obyvateľstva. Výpočtom dostaneme y ' = P (t) = x ' (t) , čiže produktivitu populácie v čase t .

Príklad Nech má bakteriálna populácia v čase t (c) x(t) jedincov. . Nájdite rýchlosť rastu populácie: a) v ľubovoľnom okamihu t , b) v okamihu t = 1 c . Riešenie: P = x'(t) = 200 t; P(l) = 200 (r/s). Odpoveď: 200 o/s.

Záver Pojem derivát je veľmi dôležitý v chémii a biológii, najmä pri určovaní rýchlosti reakcie.

Záver: Diferenciálny počet je opis sveta okolo nás, urobený v matematickom jazyku. Derivát je jedným z najdôležitejších pojmov v počte. Znalosť derivácie nám pomáha úspešne riešiť nielen matematické problémy, ale aj praktické problémy v rôznych oblastiach vedy, techniky a života.

Štátna univerzita v Južnom Sachaline

Katedra matematiky

Práca na kurze

Téma: Praktická aplikácia derivácie

Prednáša: Likhacheva O.N.

Južno-Sachalinsk

2002
Úvod

V tomto článku sa budem zaoberať aplikáciami derivátu v rôznych vedách a odvetviach. Práca je rozdelená do kapitol, z ktorých každá sa zaoberá jedným z aspektov diferenciálneho počtu (geometrický, fyzikálny význam atď.)

1. Pojem derivát

1-1. Historické informácie

Diferenciálny počet vytvorili Newton a Leibniz na konci 17. storočia na základe dvoch problémov:

1) o nájdení dotyčnice k ľubovoľnej priamke

2) o hľadaní rýchlosti s ľubovoľným zákonom pohybu

Ešte skôr sa s pojmom derivácie stretli v prácach talianskeho matematika Tartaglia (okolo 1500 - 1557) - tu sa v priebehu štúdia problematiky uhla sklonu pištole objavila tangenta, ktorá zaisťuje najväčší dosah. projektilu.

V 17. storočí sa na základe teórie pohybu G. Galilea aktívne rozvíjala kinematická koncepcia derivácie. Rôzne prezentácie sa začali objavovať v dielach Descarta, francúzskeho matematika Robervala a anglického vedca L. Gregoryho. Lopital, Bernoulli, Lagrange, Euler, Gauss výrazne prispeli k štúdiu diferenciálneho počtu.

1-2. Pojem derivát

Nech y \u003d f (x) je spojitá funkcia argumentu x, definovaného v intervale (a; b), a nech x 0 je ľubovoľný bod tohto intervalu

Argumentu x dáme prírastok ∆x, potom funkcia y = f(x) dostane prírastok ∆y = f(x + ∆x) - f(x). Limita, ku ktorej pomer ∆y / ∆x smeruje ako ∆x → 0, sa nazýva derivácia funkcie f(x).

1-3. Pravidlá diferenciácie a tabuľka derivácií

		(hriech x)" = cos x
	(1 / x)" = -1 / x2	(cos x)" = -sin x
	(√x)" = 1/2√x	(tg x)" = 1 / cos 2 x
(uv)" = u"v + uv"	(a x)" = a x log x	(ctg x)" = 1 / hriech 2 x
(u / v)"=(u"v - uv") / v 2		(arcsin x)" = 1 / √ (1- x 2)
	(log a x)" = (log a e) / x	(arccos x)" = -1 / √ (1- x 2)
	(ln x)" = 1 / x	(arctg x)" = 1 / √ (1+ x 2)
		(arcctg x)" = -1 / √ (1+ x 2)

2. Geometrický význam derivácie

2-1. Tangenta ku krivke

Nech máme krivku a na nej pevný bod M a bod N. Dotyčnicou k bodu M je priamka, ktorej polohu má tendenciu zaberať tetiva MN, ak sa k bodu N približujeme po nekonečne. krivka do M.

Uvažujme funkciu f(x) a krivku y = f(x) zodpovedajúcu tejto funkcii. Pre nejakú hodnotu x má funkcia hodnotu y = f(x). Tieto hodnoty na krivke zodpovedajú bodu M(x 0 , y 0). Zaveďme nový argument x 0 + ∆x, jeho hodnota zodpovedá hodnote funkcie y 0 + ∆y = f(x 0 + ∆x). Zodpovedajúci bod je N(x 0 + ∆x, y 0 + ∆y). Nakreslite sečnicu MN a označte φ uhol, ktorý zviera sečnica s kladným smerom osi Ox. Obrázok ukazuje, že ∆y / ∆x = tg φ. Ak sa teraz ∆x priblíži k 0, potom sa bod N bude pohybovať pozdĺž krivky, sečna MN sa bude otáčať okolo bodu M a uhol φ sa zmení. Ak, ako ∆x → 0, uhol φ smeruje k nejakému α, potom priamka prechádzajúca cez M a zvierajúca uhol α s kladným smerom osi x bude požadovanou dotyčnicou. Súčasne jeho koeficient sklonu:

To znamená, že hodnota derivácie f "(x) pre danú hodnotu argumentu x sa rovná dotyčnici uhla, ktorý zviera s kladným smerom osi Ox dotyčnica ku grafu funkcie f (x ) v bode M (x, f (x)).

Dotyčnica k priestorovej čiare má podobnú definíciu ako dotyčnica rovinnej krivky. V tomto prípade, ak je funkcia daná rovnicou z = f(x, y), sklony na osiach OX a OY sa budú rovnať parciálnym deriváciám f vzhľadom na x a y.

2-2. Dotyková rovina k povrchu

Dotyková rovina k povrchu v bode M je rovina obsahujúca dotyčnice ku všetkým priestorovým krivkám povrchu prechádzajúcich bodom M - bodom dotyku.

Zoberme plochu danú rovnicou F(x, y, z) = 0 a na nej nejaký obyčajný bod M(x 0 , y 0 , z 0). Uvažujme na ploche nejakú krivku L prechádzajúcu cez M. Nech je krivka daná rovnicami

x = φ(t); y = ψ(t); z = χ(t).

Dosadme tieto výrazy do rovnice povrchu. Rovnica sa zmení na identitu, pretože krivka leží celá na povrchu. Pomocou invariantnej vlastnosti tvaru diferenciálu diferencujeme výslednú rovnicu vzhľadom na t:

Rovnice dotyčnice ku krivke L v bode M majú tvar:

Pretože rozdiely x - x 0, y - y 0, z - z 0 sú úmerné zodpovedajúcim diferenciálom, výsledná rovnica roviny vyzerá takto:

F" x (x - x 0) + F" y (y - y 0) + F" z (z - z 0)=0

a pre konkrétny prípad z = f(x, y):

Z - z 0 \u003d F "x (x - x 0) + F" y (y - y 0)

Príklad: Nájdite rovnicu dotykovej roviny v bode (2a; a; 1,5a) hyperbolického paraboloidu

Riešenie:

Z" x \u003d x / a \u003d 2; Z" y \u003d -y / a \u003d -1

Rovnica požadovanej roviny:

Z - 1,5a = 2(x - 2a) - (Y - a) alebo Z = 2x - y - 1,5a

3-1. Bodová rýchlosť materiálu

Nech je závislosť dráhy s od času t v danom priamočiary pohyb hmotný bod je vyjadrený rovnicou s = f(t) a t 0 je určitý časový okamih. Zvážte iný čas t, označte ∆t = t - t 0 a vypočítajte prírastok dráhy: ∆s = f(t 0 + ∆t) - f(t 0). Pomer ∆s / ∆t sa nazýva priemerná rýchlosť pohybu za čas ∆t, ktorý uplynul od počiatočného momentu t 0 . Rýchlosť je limit tohto pomeru ako ∆t → 0.

Priemerné zrýchlenie nerovnomerného pohybu v intervale (t; t + ∆t) je hodnota =∆v / ∆t. Okamžité zrýchlenie hmotného bodu v čase t bude limitom priemerného zrýchlenia:

To znamená, že prvá časová derivácia (v "(t)).

Príklad: Závislosť dráhy prejdenej telom od času je daná rovnicou s \u003d A + Bt + Ct 2 + Dt 3 (C \u003d 0,1 m / s, D \u003d 0,03 m / s 2). Určite čas po začiatku pohybu, po ktorom sa zrýchlenie tela bude rovnať 2 m / s 2.

Riešenie:

v(t) = s"(t) = B + 2Ct + 3Dt2; a(t) = v"(t) = 2C + 6Dt = 0,2 + 0,18t = 2;

1,8 = 0,18 t; t = 10 s

3-2. Tepelná kapacita látky pri danej teplote

Na zvýšenie rôznych teplôt T o rovnakú hodnotu, ktorá sa rovná T 1 - T, na 1 kg. daná látka potrebuje iné množstvo tepla Q 1 - Q, a pomer

lebo táto látka nie je stála. Pre danú látku je teda množstvo tepla Q nelineárnou funkciou teploty T: Q = f(T). Potom ΔQ = f(t + ΔT) - f(T). Postoj

sa nazýva priemerná tepelná kapacita na intervale a hranica tohto výrazu pri ∆T → 0 sa nazýva tepelná kapacita danej látky pri teplote T.

3-3. Moc

Zmeniť mechanický pohyb teleso je spôsobené silami, ktoré naň pôsobia od iných telies. Aby bolo možné kvantitatívne charakterizovať proces výmeny energie medzi interagujúcimi telesami, v mechanike sa zavádza pojem práce sily. Aby sa charakterizovala rýchlosť vykonávania práce, zavádza sa pojem moci:

4. Diferenciálny počet v ekonómii

4-1. Funkčný výskum

Diferenciálny počet je matematický aparát široko používaný na ekonomickú analýzu. Základnou úlohou ekonomickej analýzy je študovať vzťahy ekonomických veličín zapísaných ako funkcie. Akým smerom sa zmenia vládne príjmy, ak sa zvýšia dane alebo sa zavedú dovozné clá? Zvýši sa alebo zníži príjem firmy, keď sa zvýši cena jej produktov? V akom pomere môže doplnkové vybavenie nahradiť dôchodcov? Na vyriešenie takýchto problémov je potrebné skonštruovať spojovacie funkcie premenných v nich zahrnutých, ktoré sa potom študujú pomocou metód diferenciálneho počtu. V ekonómii sa často vyžaduje nájsť najlepšiu alebo optimálnu hodnotu ukazovateľa: najvyššiu produktivitu práce, maximálny zisk, maximálny výkon, minimálne náklady atď. Každý ukazovateľ je funkciou jedného alebo viacerých argumentov. Nájdenie optimálnej hodnoty ukazovateľa sa teda redukuje na nájdenie extrému funkcie.

Podľa Fermatovej vety, ak je bod extrémom funkcie, potom v ňom derivácia buď neexistuje, alebo sa rovná 0. Typ extrému možno určiť jednou z postačujúcich podmienok pre extrém:

1) Nech je funkcia f(x) diferencovateľná v niektorom okolí bodu x 0 . Ak derivácia f "(x) pri prechode bodom x 0 zmení znamienko z + na -, potom x 0 je maximálny bod, ak z - do +, potom x 0 je minimálny bod, ak nemení znamienko , potom neexistuje žiadny extrém.

2) Nech je funkcia f (x) dvakrát diferencovateľná v niektorom okolí bodu x 0 a f "(x 0) \u003d 0, f "" (x 0) ≠ 0, potom v bode x 0 funkcia f (x 0) má maximum , ak f "" (x 0)< 0 и минимум, если f ""(x 0) > 0.

Okrem toho druhá derivácia charakterizuje konvexnosť funkcie (graf funkcie sa nazýva konvexný hore [dole] na intervale (a, b), ak sa nachádza na tomto intervale nie nad [nie pod] niektorou z jeho dotyčníc ).

Príklad: zvoliť optimálny objem produkcie firmy, ktorej ziskovú funkciu možno modelovať závislosťou:

π(q) = R(q) - C(q) = q2 - 8q + 10

Riešenie:

π"(q) = R"(q) - C"(q) = 2q - 8 = 0 → q extr = 4

Pre q< q extr = 4 → π"(q) < 0 и прибыль убывает

Pre q > q extr = 4 → π"(q) > 0 a zisk rastie

Keď q = 4, zisk nadobudne minimálnu hodnotu.

Aký je optimálny výstup pre firmu? Ak firma nemôže počas sledovaného obdobia vyprodukovať viac ako 8 jednotiek produkcie (p(q = 8) = p(q = 0) = 10), potom optimálnym riešením by bolo neprodukovať vôbec nič, ale získať príjem. z prenájmu priestorov a/alebo zariadení. Ak je firma schopná vyrobiť viac ako 8 jednotiek, tak optimálne pre firmu bude vyrábať na hranici svojej výrobnej kapacity.

4-2. Elasticita dopytu

Elasticita funkcie f (x) v bode x 0 sa nazýva limita

Dopyt je množstvo tovaru, ktoré kupujúci požaduje. Cenová elasticita dopytu E D je mierou toho, ako dopyt reaguje na zmeny cien. Ak │E D │>1, dopyt sa nazýva elastický, ak │E D │<1, то неэластичным. В случае E D =0 спрос называется совершенно неэластичным, т. е. изменение цены не приводит ни к какому изменению спроса. Напротив, если самое малое снижение цены побуждает покупателя увеличить покупки от 0 до предела своих возможностей, говорят, что спрос является совершенно эластичным. В зависимости от текущей эластичности спроса, предприниматель принимает решения о снижении или повышении цен на продукцию.

4-3. Limitná analýza

Dôležitou časťou metód diferenciálneho počtu používaných v ekonómii sú metódy limitnej analýzy, t. j. súbor metód na štúdium meniacich sa hodnôt nákladov alebo výsledkov so zmenami vo výrobe, spotrebe a pod. na základe analýzy ich hraničné hodnoty. Limitujúcim ukazovateľom (ukazovateľmi) funkcie je jej derivácia (v prípade funkcie jednej premennej) alebo parciálne derivácie (v prípade funkcie viacerých premenných)

V ekonomike sa často používajú priemery: priemerná produktivita práce, priemerné náklady, priemerný príjem, priemerný zisk a pod. zníži, ak sa znížia náklady. Na túto otázku nie je možné odpovedať pomocou priemerných hodnôt. Pri takýchto problémoch je potrebné určiť hranicu pomeru nárastu výsledku a nákladov, teda nájsť marginálny efekt. Preto je na ich riešenie potrebné použiť metódy diferenciálneho počtu.

5. Derivácia v približných výpočtoch

5-1. Interpolácia

Interpolácia je približný výpočet hodnôt funkcie z niekoľkých daných hodnôt. Interpolácia je široko používaná v kartografii, geológii, ekonómii a iných vedách. Najjednoduchšou možnosťou interpolácie je Lagrangeova forma, ale ak existuje veľa uzlových bodov a intervaly medzi nimi sú veľké, alebo ak chcete získať funkciu, ktorej zakrivenie je minimálne, potom sa uchýlite k interpolácii spline, ktorá poskytuje väčšiu presnosť.

Nech K n je sústava uzlových bodov a = x 0< x 1 <…< x n = b. Функция S k (x) называется сплайн-функцией S k (x) степени k≥0 на K n , если

a) S k (x) є C k -1 ()

b) S k (x) je polynóm stupňa najviac k

Spline funkcia Ŝ k (x) є S k (K n) sa nazýva interpolačná splajnová funkcia, ak Ŝ k (x j) = f(x j) pre j = 0,1,…,n

V aplikáciách často stačí zvoliť k=3 a aplikovať tzv kubická interpolácia.

Keďže s(x) je polynóm tretieho stupňa na každom parciálnom intervale, potom pre x є

Tu s 2 j , c j 1 , c j 0 sú neznáme pre j = 1, 2, …, n

Posledne menované sú vylúčené z dôvodu požiadavky s(x j) = y j:

Diferencovaním tejto funkcie a berúc do úvahy, že s "(x) musí byť spojité v celom intervale, a teda najmä v uzloch, nakoniec dostaneme sústavu rovníc:

vzhľadom na n+1 neznámych s 2 0 , s 2 1 ,…, s 2 n. Pre ich jednoznačné určenie sa v závislosti od úlohy pridávajú ďalšie dve rovnice:

normálny prípad (N):

Pravidelný prípad (P) (t.j.f(x+(x n -x 0))=f(X)):

Špecifikované vyhladenie na okrajoch:

Príklad: splajnová interpolácia funkcie f(x)=sin x, n=4.

Funkcia je periodická, preto používame prípad P.

Funkcia spline vyzerá takto:

5-2. Taylorov vzorec

Rozšírenie funkcií do nekonečných radov umožňuje získať hodnotu funkcie v danom bode s akoukoľvek presnosťou. Táto technika je široko používaná v programovaní a iných disciplínach.

Hovorí sa, že funkcia expanduje na danom intervale do mocninového radu, ak takýto mocninný rad existuje a 0 + a 1 (x - a) + a 2 (x - a) 2 + ... + a n (x - a ) n + ..., ktorá konverguje k tejto funkcii na tomto intervale. Dá sa dokázať, že tento rozklad je jedinečný:

Nech je funkcia f(x) v bode a nekonečne diferencovateľná. Mocninný rad formulára

sa nazýva Taylorov rad pre funkciu f(x), zapísaný v mocninách rozdielu (x - a). Vo všeobecnosti, aby Taylorov rad konvergoval k f(x), je potrebné a postačujúce, aby zvyšok radu smeroval k 0. Pre a = 0 sa Taylorov rad zvyčajne nazýva Maclaurinov rad.

I. M. Uvarenkov,

M. Z. Maller

Kurz matematickej analýzy, v.1

V. A. Dudarenko,

A.A. Dadayan

Matematická analýza

Diferenciálny a integrálny počet

T. I. Trofimová

Kurz fyziky

O. O. Zamkov

A. V. Tolstopjatenko

Yu. N. Cheremnykh

Matematické metódy v ekonómii

A. S. Solodovnikov

V. A. Babaitsev

A. V. Brailov

I.G. Shandra

Matematika v ekonómii

Úvod

1. Pojem derivát

1-1. Historické informácie

1-2. Pojem derivát

1-3. Pravidlá diferenciácie a tabuľka derivácií

2. Geometrický význam derivácie

2-1. Tangenta ku krivke

2-2. Dotyková rovina k povrchu

3. Použitie derivácie vo fyzike

3-1. Bodová rýchlosť materiálu

3-2. Tepelná kapacita pri danej teplote

3-3. Moc

4. Diferenciálny počet v ekonómii

4-1. Funkčný výskum

4-2. Elasticita dopytu

4-3. Limitná analýza

5. Derivácia v približných výpočtoch

5-1. Interpolácia

5-2. Taylorov vzorec

5-3. Približné výpočty

Záver

Zoznam použitej literatúry

Štátna univerzita v Južnom Sachaline

Katedra matematiky

Práca na kurze

Téma: Praktická aplikácia derivácie

Prednáša: Likhacheva O.N.

Južno-Sachalinsk

2002 Úvod

1. Pojem derivát

1-1. Historické informácie

Diferenciálny počet vytvorili Newton a Leibniz na konci 17. storočia na základe dvoch problémov:

1) o nájdení dotyčnice k ľubovoľnej priamke

2) o hľadaní rýchlosti s ľubovoľným zákonom pohybu

1-2. Pojem derivát

Nech y = f(x) je spojitá funkcia argumentu x, definovaného v intervale (a; b), a nech x0 je ľubovoľný bod tohto intervalu

Argumentu x dáme prírastok ∆x, potom funkcia y = f(x) dostane prírastok ∆y = f(x + ∆x) - f(x). Limita, ku ktorej pomer ∆y / ∆x smeruje ako ∆x → 0, sa nazýva derivácia funkcie f(x).

1-3. Pravidlá diferenciácie a tabuľka derivácií

C" = 0(xn) = nxn-1(sin x)" = cos xx" = 1(1 / x)" = -1 / x2(cos x)" = -sin x(Cu)"=Cu"( √x)" = 1 / 2√x(tg x)" = 1 / cos2 x(uv)" = u"v + uv"(ax)" = ax ln x(ctg x)" = 1 / sin2 x( u / v)"=(u"v - uv") / v2(ex)" = ex(arcsin x)" = 1 / √ (1- x2)(logax)" = (logae) / x(arccos x) " = -1 / √ (1- x2)(ln x)" = 1 / x(oblúk x)" = 1 / √ (1+ x2)(oblúk x)" = -1 / √ (1+ x2)

2. Geometrický význam derivácie

2-1. Tangenta ku krivke

Nech máme krivku a na nej pevný bod M a bod N. Dotyčnica k bodu M je priamka, ktorej polohu má tendenciu zaberať tetiva MN, ak sa k bodu N neobmedzene približujeme po krivka do M.

Uvažujme funkciu f(x) a krivku y = f(x) zodpovedajúcu tejto funkcii. Pre nejakú hodnotu x má funkcia hodnotu y = f(x). Tieto hodnoty na krivke zodpovedajú bodu M(x0, y0). Zavedieme nový argument x0 + ∆x, ktorého hodnota zodpovedá hodnote funkcie y0 + ∆y = f(x0 + ∆x). Zodpovedajúci bod je N(x0 + ∆x, y0 + ∆y). Nakreslite sečnicu MN a označte φ uhol, ktorý zviera sečnica s kladným smerom osi Ox. Obrázok ukazuje, že ∆y / ∆x = tg φ. Ak sa teraz ∆x priblíži k 0, potom sa bod N bude pohybovať pozdĺž krivky, sečna MN sa bude otáčať okolo bodu M a uhol φ sa zmení. Ak, ako ∆x → 0, uhol φ smeruje k nejakému α, potom priamka prechádzajúca cez M a zvierajúca uhol α s kladným smerom osi x bude požadovanou dotyčnicou. Súčasne jeho koeficient sklonu:

To znamená, že hodnota derivácie f "(x) pre danú hodnotu argumentu x sa rovná dotyčnici uhla, ktorý zviera s kladným smerom osi Ox dotyčnica ku grafu funkcie f (x ) v bode M (x, f (x)).

2-2. Dotyková rovina k povrchu

Dotyková rovina k povrchu v bode M je rovina obsahujúca dotyčnice ku všetkým priestorovým krivkám povrchu prechádzajúcich bodom M - bodom dotyku.

Vezmite plochu danú rovnicou F(x, y, z) = 0 a na nej nejaký obyčajný bod M(x0, y0, z0). Uvažujme na ploche nejakú krivku L prechádzajúcu cez M. Nech je krivka daná rovnicami

x = φ(t); y = ψ(t); z = χ(t).

Rovnice dotyčnice ku krivke L v bode M majú tvar:

Keďže rozdiely x - x0, y - y0, z - z0 sú úmerné zodpovedajúcim diferenciálom, výsledná rovnica roviny vyzerá takto:

F "x (x - x0) + F" y (y - y0) + F "z (z - z0) \u003d 0

a pre konkrétny prípad z = f(x, y):

Z - z0 \u003d F "x (x - x0) + F" y (y - y0)

Príklad: Nájdite rovnicu dotykovej roviny v bode (2a; a; 1,5a) hyperbolického paraboloidu

Riešenie:

Z"x \u003d x / a \u003d 2; Z"y \u003d -y / a \u003d -1

Rovnica požadovanej roviny:

Z - 1,5a = 2(x - 2a) - (Y - a) alebo Z = 2x - y - 1,5a

3. Použitie derivácie vo fyzike

3-1. Bodová rýchlosť materiálu

Nech je závislosť dráhy s od času t pri danom priamočiarom pohybe hmotného bodu vyjadrená rovnicou s = f(t) a t0 je nejaký časový okamih. Zvážte iný čas t, označte ∆t = t - t0 a vypočítajte prírastok dráhy: ∆s = f(t0 + ∆t) - f(t0). Pomer ∆s / ∆t sa nazýva priemerná rýchlosť pohybu za čas ∆t, ktorý uplynul od počiatočného momentu t0. Rýchlosť je limit tohto pomeru ako ∆t → 0.

Priemerné zrýchlenie nerovnomerného pohybu v intervale (t; t + ∆t) je hodnota =∆v / ∆t. Okamžité zrýchlenie hmotného bodu v čase t bude limitom priemerného zrýchlenia:

To znamená, že prvá časová derivácia (v "(t)).

Príklad:Časová závislosť dráhy prejdenej telesom je daná rovnicou s = A + Bt + Ct2 + Dt3 (C = 0,1 m/s, D = 0,03 m/s2). Určte čas po začatí pohybu, po ktorom bude zrýchlenie telesa rovné 2 m/s2.

Riešenie:

v(t) = s"(t) = B + 2Ct + 3Dt2; a(t) = v"(t) = 2C + 6Dt = 0,2 + 0,18 t = 2;

1,8 = 0,18 t; t = 10 s

3-2. Tepelná kapacita látky pri danej teplote

Na zvýšenie rôznych teplôt T o rovnakú hodnotu, ktorá sa rovná T1 - T, na 1 kg. daná látka potrebuje iné množstvo tepla Q1 - Q, a pomer

lebo táto látka nie je stála. Pre danú látku je teda množstvo tepla Q nelineárnou funkciou teploty T: Q = f(T). Potom ΔQ = f(t + ΔT) - f(T). Postoj

sa nazýva priemerná tepelná kapacita na intervale a hranica tohto výrazu pri ∆T → 0 sa nazýva tepelná kapacita danej látky pri teplote T.

3-3. Moc

Zmena mechanického pohybu telesa je spôsobená silami, ktoré naň pôsobia od iných telies. Aby bolo možné kvantitatívne charakterizovať proces výmeny energie medzi interagujúcimi telesami, v mechanike sa zavádza pojem práce sily. Aby sa charakterizovala rýchlosť vykonávania práce, zavádza sa pojem moci:

4. Diferenciálny počet v ekonómii

4-1. Funkčný výskum

Podľa Fermatovej vety, ak je bod extrémom funkcie, potom v ňom derivácia buď neexistuje, alebo sa rovná 0. Typ extrému možno určiť jednou z postačujúcich podmienok pre extrém:

1) Nech je funkcia f(x) diferencovateľná v niektorom okolí bodu x0. Ak derivácia f "(x) pri prechode bodom x0 zmení znamienko z + na -, potom x0 je maximálny bod, ak z - do +, potom x0 je minimálny bod, ak nezmení znamienko, potom tam nie je v tomto bode extrém.

2) Nech je funkcia f(x) dvakrát diferencovateľná v niektorom okolí bodu x0 a f "(x0) = 0, f ""(x0) ≠ 0, potom v bode x0 má funkcia f(x0) maximálne ak

Stiahnuť ▼:

Náhľad:

Popisy snímok:

Náhľad:

Popisy snímok:

Prečítajte si tiež