Korištenje derivata u različitim područjima djelatnosti. Zanimljiva derivacija Ciljevi ovog rada: Razmotriti upotrebu derivacije u raznim znanostima Upoznati se sa znanstvenicima koji su proučavali derivaciju funkcije. Sila je derivacija rada u pomaku.

Ministarstvo obrazovanja Saratovska regija

Državni autonomni stručni obrazovna ustanova Saratovska regija "Engels Polytechnic"

PRIMJENA DERIVATA U RAZLIČITIM PODRUČJIMA ZNANOSTI

Izvedena: Sarkulova Nurgulya Sergeevna

student grupe KShI-216/15

(Dizajn, modeliranje i

tehnologija šivanja)

znanstveni savjetnik:

Verbitskaya Elena Vyacheslavovna

nastavnik matematike GAPOU SO

"Veleučilište Engels"

2016

Uvod

Uloga matematike u raznim područjima prirodnih znanosti vrlo je velika. Nije ni čudo što kažu“Matematika je kraljica znanosti, njezina fizika desna ruka, kemija je ostala.

Predmet istraživanja je derivat.

Glavni cilj je ukazati na značaj derivacije ne samo u matematici, već iu drugim znanostima, njenu važnost u suvremenom životu.

Diferencijalni račun je opis svijeta oko nas, napravljen matematičkim jezikom. Izvedenica nam pomaže uspješno riješiti ne samo matematički problemi, ali i praktičnih zadataka iz različitih područja znanosti i tehnologije.

Derivacija funkcije koristi se gdje god postoji neravnomjeran tok procesa: to je neravnomjerno mehaničko kretanje, i izmjenična struja, i kemijske reakcije, i radioaktivni raspad tvari, itd.

Ključna i tematska pitanja ovog eseja:

1. Povijest nastanka izvedenice.

2. Zašto proučavati izvode funkcija?

3. Gdje se koriste izvedenice?

4. Primjena derivata u fizici, kemiji, biologiji i drugim znanostima.

5. Zaključci

Odlučio sam napisati rad na temu "Primjena derivata u raznim područjima znanosti", jer smatram da je ova tema vrlo zanimljiva, korisna i relevantna.

U svom radu govorit ću o primjeni diferencijacije u raznim područjima znanosti kao što su kemija, fizika, biologija, geografija itd. Uostalom, sve su znanosti neraskidivo povezane, što se vrlo jasno vidi na primjeru teme Razmišljam.

Primjena derivata u raznim područjima znanosti

To već znamo iz predmeta algebre u srednjoj školi izvedenica je granica omjera prirasta funkcije i prirasta njezinog argumenta jer priraštaj argumenta teži nuli, ako takva granica postoji.

Radnja pronalaženja derivacije naziva se njezino diferenciranje, a funkcija koja ima derivaciju u točki x diferencijabilna u toj točki. Funkcija koja je diferencijabilna u svakoj točki intervala naziva se diferencijabilna na tom intervalu.

Čast otkrivanja osnovnih zakona matematičke analize pripada engleski fizičar te matematičar Isaac Newton i njemački matematičar, fizičar, filozof Leibniz.

Newton je uveo pojam derivata, proučavajući zakone mehanike, otkrivajući time njegovo mehaničko značenje.

Fizičko značenje derivacije: derivacija funkcijeg= f(x) u točki x 0 je brzina promjene funkcijef(x) u točki x 0 .

Leibniz je došao do pojma izvodnice rješavajući problem povlačenja tangente na izvodnicu, čime je objasnio geometrijski smisao.

Geometrijsko značenje derivacije je da derivacija funkcionira u točkix 0 jednak nagibu tangente na graf funkcije nacrtan u točki s apscisomx 0 .

Pojam izvedenica i suvremeni zapisg" , f"Predstavio J. Lagrange 1797.

ruski matematičar U 19. stoljeću Panfuty Lvovich Chebyshev je rekao da su "od posebne važnosti one metode znanosti koje nam omogućuju da riješimo problem zajednički svim praktičnim ljudskim aktivnostima, na primjer, kako raspolagati našim sredstvima da postignemo najveću korist."

Predstavnici različitih specijalnosti moraju se nositi s takvim zadacima u naše vrijeme:

Procesni inženjeri nastoje organizirati proizvodnju na način da se proizvede što više proizvoda;

Dizajneri pokušavaju razviti uređaj za svemirski brod tako da je masa uređaja najmanja;

Ekonomisti pokušavaju isplanirati veze između postrojenja i izvora sirovina na način da troškovi transporta budu minimalni.

Prilikom proučavanja bilo koje teme, studenti imaju pitanje: "Zašto nam je ovo potrebno?" Ako odgovor zadovolji znatiželju, onda možemo govoriti o interesu učenika. Odgovor na temu "Derivacija" može se dobiti ako se zna gdje se koriste derivacije funkcija.

Da bismo odgovorili na ovo pitanje, možemo navesti neke discipline i njihove dijelove u kojima se koriste derivati.

Derivacija u algebri:

1. Tangenta na graf funkcije

Tangenta na graf funkcijef, diferencijabilan na x oko , je pravac koji prolazi točkom (x oko ; f(x o )) i imajući nagibf′(x o ).

y= f(x o ) + f′(x o ) (x - x o )

2. Traženje intervala rastućih i padajućih funkcija

Funkcijay=f(x) povećava se tijekom intervalax , ako postoji inejednakost. Drugim riječima, veća vrijednost argumenta odgovara većoj vrijednosti funkcije.

Funkcijay=f(x) smanjuje se tijekom intervalax , ako postoji inejednakost. Drugim riječima, manja vrijednost funkcije odgovara većoj vrijednosti argumenta.

3. Pronalaženje točaka ekstrema funkcije

Točka nazvaomaksimalna točka funkcijey=f(x) ako za svex . Vrijednost funkcije u točki maksimuma naziva semaksimalna funkcija i označavaju.

Točka nazvaominimalna točka funkcijey=f(x) ako za svex iz svog susjedstva nejednakost. Vrijednost funkcije u točki minimuma naziva seminimum funkcije i označavaju.

Ispod susjedstva točke razumjeti interval, gdje je dovoljno mali pozitivan broj.

Pozivaju se minimalne i maksimalne točkeekstremne točke , a nazivaju se vrijednosti funkcije koje odgovaraju točkama ekstremaekstremi funkcije .

4. Traženje intervala konveksnosti i konkavnosti funkcije

Grafikon funkcije, je na ovom intervalukonveksan , ne leži više od bilo koje njegove tangente (slika 1).

Grafikon funkcije, diferencijabilan na intervalu, je na ovom intervalukonkavan , ako je graf ove funkcije unutar intervala ne leži niže od bilo koje njegove tangente (slika 2).

Točkom infleksije grafa funkcije nazivamo točku koja razdvaja intervale konveksnosti i konkavnosti.

5. Određivanje točaka infleksije funkcije

Derivacija u fizici:

1. Brzina kao derivacija puta

2. Ubrzanje kao derivacija brzinea =

3. Stopa raspadanja radioaktivni elementi 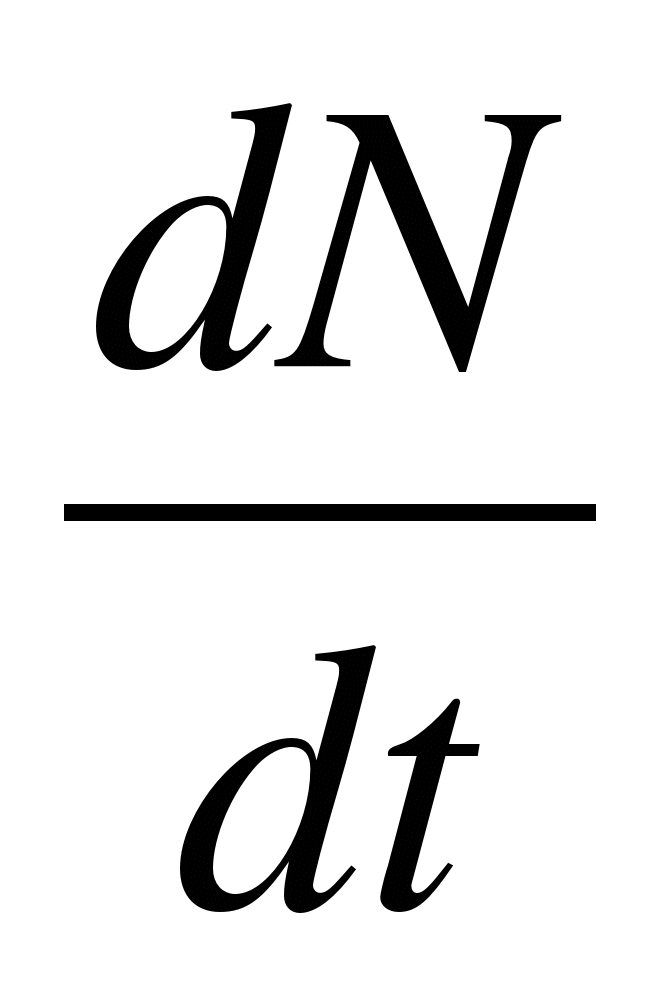= - λN

I također u fizici, derivat se koristi za izračunavanje:

Brzine materijalna točka

Trenutna brzina kao fizikalno značenje derivacije

Instant vrijednost AC napajanje

Trenutna vrijednost EMF elektromagnetske indukcije

Maksimalna snaga

Derivat u kemiji:

A u kemiji je diferencijalni račun našao široku primjenu za konstruiranje matematički modeli kemijske reakcije i naknadni opis njihovih svojstava.

Izvedenica u kemiji služi za određivanje vrlo bitne stvari – brzine kemijska reakcija, jedan od odlučujućih čimbenika koji se moraju uzeti u obzir u mnogim područjima znanstvene i industrijske djelatnosti. V(t) = p'(t)

Količina

in-va na vrijeme t 0

p = p(t 0 )

Funkcija

Vremenski interval

∆t = t– t 0

Povećanje argumenta

Promjena količine

∆p=p(t 0 + ∆t) – p(t 0 )

Povećanje funkcije

Prosječna brzina kemijske reakcije

∆p/∆t

Omjer prirasta funkcije i prirasta argumenta

Derivati u biologiji:

Populacija je skup jedinki određene vrste, koje zauzimaju određeno područje teritorija unutar raspona vrste, slobodno se međusobno križaju i djelomično ili potpuno izolirane od drugih populacija, a također je i elementarna jedinica evolucije .

P \u003d x‘ (t)

Derivacija u geografiji:

1. Neka značenja u seizmografiji

2. Značajke elektromagnetsko polje zemljište

3. Radioaktivnost nuklearnih geofizičkih indikatora

4. Mnoga značenja u ekonomskoj geografiji

5. Izvedite formulu za izračun broja stanovnika na teritoriju u trenutku t.

y'= do y

Ideja sociološkog modela Thomasa Malthusa je da je rast stanovništva proporcionalan broju stanovnika u određenom vremenu od t do N(t). Malthusov model dobro je funkcionirao za opisivanje stanovništva SAD-a od 1790. do 1860. Ovaj model više ne vrijedi u većini zemalja.

Izvod u elektrotehnici:

U našim domovima, u prijevozu, u tvornicama: električna struja radi posvuda. Pod električnom strujom podrazumijevamo usmjereno kretanje slobodnih električki nabijenih čestica.

Kvantitativna karakteristika električna struja je trenutna snaga.

U električnom krugu električno punjenje mijenja se tijekom vremena po zakonu q=q (t). Struja I je derivacija naboja q u odnosu na vrijeme.

U elektrotehnici se uglavnom koristi izmjenični rad.

Električna struja koja se mijenja s vremenom naziva se izmjenična struja. Krug izmjenične struje može sadržavati raznih elemenata: uređaji za grijanje, zavojnice, kondenzatori.

Proizvodnja izmjenične električne struje temelji se na zakonu elektromagnetske indukcije, čija formulacija sadrži derivaciju magnetskog toka.

Derivacija u ekonomiji:

Ekonomija je osnova života, a važno mjesto u njoj zauzima diferencijalni račun, aparat za ekonomsku analizu. Osnovna zadaća ekonomske analize je proučavanje odnosa ekonomskih veličina u obliku funkcija.

Derivat u ekonomiji rješava važna pitanja:

1. U kojem smjeru će se promijeniti dohodak države povećanjem poreza ili uvođenjem carina?

2. Hoće li se prihodi tvrtke povećati ili smanjiti s povećanjem cijene proizvoda?

Za rješavanje ovih pitanja potrebno je konstruirati funkcije povezivanja ulaznih varijabli koje se zatim proučavaju metodama diferencijalnog računa.

Također, korištenjem ekstrema funkcije (izvodnice) u gospodarstvu možete pronaći najveću produktivnost rada, maksimalnu dobit, maksimalnu proizvodnju i minimalne troškove.

ZAKLJUČAK: derivat se uspješno koristi u rješavanju različitih primijenjenih problema u znanosti, tehnologiji i životu

Kao što se može vidjeti iz navedenog, uporaba izvoda funkcije vrlo je raznolika, i to ne samo u proučavanju matematike, već iu drugim disciplinama. Stoga možemo zaključiti da će proučavanje teme: „Derivacija funkcije“ imati svoju primjenu iu drugim temama i predmetima.

Uvjerili smo se u važnost izučavanja teme „Derivativa“, njene uloge u proučavanju procesa znanosti i tehnologije, mogućnosti projektiranja prema stvarni događaji matematičke modele i rješavanje važnih problema.

“Glazba može podići ili umiriti dušu,
Slikanje je ugodno za oko,
Poezija - za buđenje osjećaja,
Filozofija - zadovoljiti potrebe uma,
Inženjering je poboljšati materijalnu stranu života ljudi,
ALImatematika može postići sve te ciljeve.”

Tako je rekao američki matematičarMaurice Kline.

Bibliografija:

1. Bogomolov N.V., Samoylenko I.I. Matematika. - M.: Yurayt, 2015.

2. V. P. Grigoriev i Yu. A. Dubinsky, Elementi više matematike. - M.: Akademija, 2014.

3. Bavrin I.I. Osnove više matematike. - M.: postdiplomske studije, 2013.

4. Bogomolov N.V. Praktična nastava iz matematike. - M.: Viša škola, 2013.

5. Bogomolov N.V. Zbirka zadataka iz matematike. - M.: Bustard, 2013.

6. Rybnikov K.A. Povijest matematike, Moscow University Press, M, 1960.

7. Vinogradov Yu.N., Gomola A.I., Potapov V.I., Sokolova E.V. – M.:Izdavački centar "Akademija", 2010

8 . Bashmakov M.I. Matematika: algebra i počeci matematičke analize, geometrija. - M.: Izdavački centar "Akademija", 2016

Periodični izvori:

Novine i časopisi: "Matematika", " Javni sat»

Korištenje internetskih resursa, digitalne knjižnice:

www:egetutor.ru

matematika-na5.norod.ru

FGOU SPO

Novosibirsk poljoprivredna škola

sažetak

u disciplini "matematika"

"Primjena derivata u znanosti i tehnologiji"

S. Razdolnoe 2008

Uvod

1. Teorijski dio

1.1 Problemi koji vode do koncepta derivata

1.2 Definicija izvedenice

1.3 Opće pravilo za pronalaženje derivacije

1.4 Geometrijsko značenje derivacije

1.5 Mehaničko značenje derivata

1.6 Derivat drugog reda i njegovo mehaničko značenje

1.7 Definicija i geometrijsko značenje diferencijala

2. Istraživanje funkcija uz pomoć derivacije

Zaključak

Književnost

Uvod

U prvom poglavlju mog eseja govorit ćemo o pojmu izvoda, pravilima za njegovu primjenu, o geometrijskim i fizički smisao izvedenica. U drugom poglavlju mog eseja govorit ćemo o upotrebi derivata u znanosti i tehnologiji te o rješavanju problema u tom području.

1. Teorijski dio

1.1 Problemi koji vode do koncepta derivata

Pri proučavanju pojedinih procesa i pojava često se javlja problem određivanja brzine tih procesa. Njegovo rješenje dovodi do koncepta derivacije, što je osnovni koncept diferencijalnog računa.

Metoda diferencijalnog računa nastala je u 17. i 18. stoljeću. Imena dvojice velikih matematičara, I. Newtona i G.V. Leibniz.

Newton je došao do otkrića diferencijalnog računa pri rješavanju problema o brzini materijalne točke u određenom trenutku vremena (trenutačna brzina).

Kao što je poznato, ravnomjerno kretanje je kretanje u kojem tijelo prijeđe jednaku duljinu puta u jednakim vremenskim intervalima. Put koji tijelo prijeđe u jedinici vremena naziva se ubrzati jednoliko kretanje.

Međutim, najčešće u praksi imamo posla s neravnomjernim kretanjem. Automobil koji vozi cestom usporava na prijelazima i ubrzava na onim dijelovima gdje je put slobodan; zrakoplov usporava pri slijetanju itd. Stoga se najčešće moramo suočiti s činjenicom da u jednakim vremenskim intervalima tijelo prolazi segmente puta različitih duljina. Takvo kretanje se zove neravnomjeran. Njegova brzina se ne može okarakterizirati jednim brojem.

Često se za karakterizaciju neravnomjernog gibanja koristi koncept Prosječna brzina kretanje tijekom vremena ∆t٫ koje je određeno relacijom gdje je ∆s put koji tijelo prijeđe za vrijeme ∆t.

Dakle, kod tijela u slobodnom padu prosječna brzina njegovog kretanja u prve dvije sekunde je

U praksi takva karakteristika kretanja kao što je prosječna brzina govori vrlo malo o kretanju. Doista, na 4,9 m / s, a za 2. - 14,7 m / s, dok je prosječna brzina za prve dvije sekunde 9,8 m / s. Prosječna brzina tijekom prve dvije sekunde ne daje nikakvu ideju o tome kako se kretanje dogodilo: kada se tijelo kretalo brže, a kada sporije. Zadamo li prosječne brzine gibanja za svaku sekundu posebno, tada ćemo znati npr. da se u 2. sekundi tijelo gibalo puno brže nego u 1. Međutim, u većini slučajeva puno brže nego što nismo zadovoljni. Uostalom, lako je razumjeti da se tijekom ove 2. sekunde i tijelo giba na različite načine: na početku je sporije, na kraju je brže. I kako se kreće negdje u sredini ove 2. sekunde? Drugim riječima, kako odrediti trenutnu brzinu?

Neka je gibanje tijela opisano zakonom za vrijeme jednako ∆t. U trenutku t0 tijelo je prošlo put, u trenutku - put. Dakle, tijekom vremena ∆t tijelo je prešlo put i prosječna brzina tijela u tom vremenskom razdoblju bit će.

Što je vremenski interval ∆t kraći, to se točnije može utvrditi kojom se brzinom tijelo giba u trenutku t0, jer tijelo koje se giba ne može bitno promijeniti svoju brzinu u kratkom vremenu. Prema tome, prosječna brzina dok ∆t teži nuli približava se stvarnoj brzini kretanja i u granici daje brzinu kretanja u danom trenutku t0 (trenutnu brzinu).

Na ovaj način ,

Definicija 1. Trenutačna brzina pravocrtnog gibanja tijela u određenom trenutku t0 naziva se granica prosječne brzine u vremenu od t0 do t0+ ∆t, kada vremenski interval ∆t teži nuli.

Dakle, da bi se našla brzina pravocrtnog nejednolikog gibanja u određenom trenutku, potrebno je pronaći granicu omjera prirasta puta ∆ prema vremenskom prirastu ∆t pod uvjetom tj. Leibniz je došao do otkrića diferencijalnog računa dok je rješavao problem konstruiranja tangente na bilo koju krivulju danu njegovom jednadžbom.

Rješenje za ovaj problem ima veliki značaj. Uostalom, brzina pokretne točke usmjerena je duž tangente na njezinu putanju, stoga se određivanje brzine projektila na njegovoj putanji, brzine bilo kojeg planeta u njegovoj orbiti, svodi na određivanje smjera tangente na putanju. zavoj.

Definicija tangente kao pravca koja ima samo jednu zajedničku točku s krivuljom, koja vrijedi za kružnicu, neprikladna je za mnoge druge krivulje.

Sljedeća definicija tangente na krivulju ne samo da odgovara intuitivnoj ideji o njoj, već vam također omogućuje da zapravo pronađete njen smjer, tj. izračunati nagib tangente.

Definicija 2. Tangens na krivulju u točki M naziva se pravac MT, koji je granični položaj sekante MM1, kada se točka M1, krećući se duž krivulje, neograničeno približava točki M.

1.2 Definicija izvedenice

Imajte na umu da se pri određivanju tangente na krivulju i trenutne brzine nejednolikog gibanja izvode uglavnom iste matematičke operacije:

1. Zadana vrijednost argumenta se povećava i nova vrijednost funkcije se izračunava koja odgovara novoj vrijednosti argumenta.

2. Odredite inkrement funkcije koji odgovara odabranom inkrementu argumenta.

3. Prirast funkcije dijeli se s prirastom argumenta.

4. Izračunajte granicu ovog omjera, pod uvjetom da prirast argumenta teži nuli.

Rješenja mnogih problema dovode do graničnih prijelaza ove vrste. Postaje neophodno generalizirati i dati ime ovom odlomku do granice.

Brzina promjene funkcije ovisno o promjeni argumenta može se očito karakterizirati omjerom. Ovaj odnos se zove Prosječna brzina funkcija se mijenja na intervalu od do. Sada trebamo razmotriti granicu razlomka. Granica ovog omjera dok prirast argumenta teži nuli (ako ta granica postoji) je neka nova funkcija. Ova funkcija je označena simbolima y', tzv izvedenica ovu funkciju, budući da je dobivena (proizvedena) iz funkcije Sama funkcija se zove primitivna funkcija u odnosu na svoju derivaciju

Definicija 3. izvedenica funkcije u danoj točki imenuju granicu omjera prirasta funkcije ∆y prema odgovarajućem prirastu argumenta ∆x, pod uvjetom da je ∆x→0, tj.

1.3 Opće pravilo za pronalaženje derivacije

Operacija nalaženja derivacije neke funkcije naziva se diferencijacija funkcije, a grana matematike koja proučava svojstva ove operacije je diferencijalni račun.

Ako funkcija ima izvod u x=a, onda se kaže da postoji diferencijabilan u ovom trenutku. Ako funkcija ima derivaciju u svakoj točki danog intervala, tada se kaže da postoji diferencijabilan Na ovo interval .

Definicija derivacije ne samo da u potpunosti karakterizira koncept stope promjene funkcije kada se argument promijeni, već također pruža način stvarnog izračuna derivacije dane funkcije. Da biste to učinili, morate izvršiti sljedeće četiri radnje (četiri koraka) navedene u definiciji same izvedenice:

1. Pronađite novu vrijednost funkcije predstavljanjem u ovu funkciju umjesto x, nova vrijednost argumenta: .

2. Prirast funkcije određuje se oduzimanjem zadane vrijednosti funkcije od njezine nove vrijednosti: .

3. Sastavite omjer prirasta funkcije i prirasta argumenta: .

4. Idite na limit na i pronađite izvod: .

Općenito govoreći, derivat je "nova" funkcija izvedena iz dane funkcije prema određenom pravilu.

1.4 Geometrijsko značenje derivacije

Geometrijska interpretacija derivacije, prvi put data u krajem XVII u. Leibniz je kako slijedi: vrijednost derivacije funkcije u točki x jednak je nagibu tangente povučene na graf funkcije u istoj točki x, oni.

Jednadžba tangente, kao i bilo koje ravne linije koja prolazi dana točka u ovom smjeru, ima oblik – trenutne koordinate. Ali jednadžba tangente također će biti zapisana na sljedeći način: . Normalna jednadžba bit će zapisana u obliku

1.5 Mehaničko značenje derivata

Mehaničko tumačenje izvedenice prvi je dao I. Newton. Sastoji se u sljedećem: brzina gibanja materijalne točke u određenom trenutku vremena jednaka je derivaciji putanje po vremenu, tj. Stoga, ako je zakon gibanja materijalne točke dan jednadžbom, tada da biste pronašli trenutnu brzinu točke u nekom određenom trenutku u vremenu, trebate pronaći derivaciju i zamijeniti odgovarajuću vrijednost t u nju.

1.6 Derivat drugog reda i njegovo mehaničko značenje

Dobivamo (jednadžbu iz onoga što je učinjeno u udžbeniku Lisichkin V.T. Soloveychik I.L. "Matematika" str. 240):

Na ovaj način, akceleracija pravocrtnog gibanja tijela u određenom trenutku jednaka je drugoj izvodnici puta po vremenu, izračunatoj za određeni trenutak. Ovo je mehaničko značenje druge izvedenice.

1.7 Definicija i geometrijsko značenje diferencijala

Definicija 4. Glavni dio prirasta funkcije, linearan u odnosu na priraštaj funkcije, linearan u odnosu na priraštaj nezavisne varijable, naziva se diferencijal funkcije i označava se s d, tj. .

Funkcijski diferencijal geometrijski predstavljen prirastom ordinate tangente povučene u točki M ( x ; g ) za zadane vrijednosti x i ∆x.

izračun diferencijal – .

Primjena diferencijala u aproksimativnim proračunima – , približna vrijednost prirasta funkcije podudara se s njezinim diferencijalom.

Teorem 1. Ako je diferencijabilna funkcija raste (opada) u zadanom intervalu, tada derivacija ove funkcije nije negativna (nije pozitivna) u tom intervalu.

Teorem 2. Ako je izvod funkcije pozitivna (negativna) u nekom intervalu, tada je funkcija u tom intervalu monotono rastuća (monotono padajuća).

Formulirajmo sada pravilo za pronalaženje intervala monotonosti funkcije

1. Izračunajte derivaciju ove funkcije.

2. Pronađite točke u kojima je nula ili ne postoji. Te se točke nazivaju kritično za funkciju

3. S pronađenim točkama domena funkcije se dijeli na intervale, na svakom od kojih izvod zadržava svoj predznak. Ovi intervali su intervali monotonosti.

4. Proučite znak na svakom od pronađenih intervala. Ako na razmatranom intervalu, onda na ovom intervalu raste; ako, onda se smanjuje na takvom intervalu.

Ovisno o uvjetima problema, pravilo za pronalaženje intervala monotonosti može se pojednostaviti.

Definicija 5. Točka se naziva maksimalna (minimalna) točka funkcije ako nejednakost vrijedi, odnosno, za bilo koji x iz neke okoline točke.

Ako je točka maksimuma (minimuma) funkcije, to kažemo (minimum) u točki. Maksimalne i minimalne funkcije objedinjuju naslov ekstremno funkcije, a zovu se točke maksimuma i minimuma ekstremne točke (ekstremne točke).

Teorem 3.(neophodan znak ekstrema). Ako a a derivacija postoji u ovoj točki, onda je jednaka nuli: .

Teorem 4.(dovoljan predznak ekstrema). Ako je izvedenica kada x prolazi a mijenja predznak, dakle a je ekstremna točka funkcije .

Glavne točke proučavanja derivata:

1. Nađi izvod.

2. Naći sve kritične točke iz domene funkcije.

3. Postavite predznake derivacije funkcije pri prolasku kroz kritične točke i ispišite točke ekstrema.

4. Izračunajte vrijednosti funkcije u svakoj ekstremnoj točki.

2. Istraživanje funkcija s derivacijom

Zadatak #1 . Volumen dnevnika. Trupci pravilnog oblika bez grešaka na drvu s relativno malom razlikom u promjeru debljeg i tankog kraja nazivaju se industrijska oblovina. Pri određivanju volumena industrijskog okruglog drveta obično se koristi pojednostavljena formula, gdje je duljina trupca, površina njegovog prosječnog presjeka. Saznajte da li stvarni volumen završava ili podcjenjuje; procijeniti relativnu pogrešku.

Riješenje. Oblik okruglog poslovnog drveta je blizak krnjem stošcu. Neka je radijus većeg, manjeg kraja trupca. Tada se njegov gotovo točan volumen (volumen krnjeg stošca) može, kao što je poznato, pronaći pomoću formule. Neka je vrijednost volumena izračunata pojednostavljenom formulom. Zatim;

Oni. . To znači da pojednostavljena formula daje podcijenjeni volumen. Stavimo to sada. Zatim. To pokazuje da relativna pogreška ne ovisi o duljini trupca, već je određena omjerom. Od kada raste na intervalu . Dakle, što znači da relativna pogreška ne prelazi 3,7%. U praksi šumarske znanosti takva se pogreška smatra sasvim prihvatljivom. S većom točnošću praktički je nemoguće izmjeriti ni promjere krajeva (jer se nešto razlikuju od krugova), ni duljinu trupca, jer ne mjere visinu, već generatrix stošca (duljina trupac je desetke puta veći od promjera, a to ne dovodi do velikih pogrešaka). Dakle, na prvi pogled netočno, ali više od toga jednostavna formula jer se volumen krnjeg stošca u stvarnoj situaciji pokazuje sasvim legitimnim. Opetovano provedeno uz pomoć posebnih metoda provjere pokazalo je da s masovnim obračunom industrijske šume relativna pogreška pri korištenju razmatrane formule ne prelazi 4%.

Zadatak #2 . Pri određivanju volumena jama, rovova kanti i drugih spremnika koji imaju oblik krnjeg stošca, u poljoprivrednoj praksi ponekad se koristi pojednostavljena formula, gdje je visina, područja baza stošca. Utvrdite je li stvarni volumen precijenjen ili podcijenjen, procijenite relativnu pogrešku pod uvjetom prirodnim za praksu: (- polumjeri baze, .

Riješenje. Označavajući kroz pravu vrijednost obujma krnjeg stošca, te kroz vrijednost izračunatu pojednostavljenom formulom, dobivamo: , tj. . To znači da pojednostavljena formula daje precijenjenu količinu. Ponavljajući dalje rješenje prethodnog problema, nalazimo da relativna pogreška neće biti veća od 6,7%. Vjerojatno je takva točnost prihvatljiva kada se racionira rad na iskopima - uostalom, jame neće biti idealni stožci, a odgovarajući parametri u stvarnim uvjetima mjere se vrlo grubo.

Zadatak #3 . U posebnoj literaturi, za određivanje kuta β rotacije vretena glodalice pri glodanju spojnica sa zubima, izvodi se formula gdje. Budući da je ova formula složena, preporuča se odbaciti njen nazivnik i koristiti pojednostavljenu formulu. Pri čemu (- cijeli broj,) se može koristiti ova formula ako je dopuštena pogreška pri određivanju kuta?

Riješenje. Točna formula nakon jednostavnog identične transformacije može se prisjetiti. Stoga je pri korištenju približne formule dopuštena apsolutna pogreška, gdje. Proučavamo funkciju na intervalu . U ovom slučaju 0,06, tj. kut pripada prvoj četvrtini. Imamo: . Primijetimo da je na intervalu koji razmatramo, a time i funkcija opadajuća na tom intervalu. Od dalje, za sve razmatrane. Sredstva, . Budući da se radi o radijanu, dovoljno je riješiti nejednadžbu. Rješavajući ovu nejednadžbu odabirom, nalazimo da je, . Kako je funkcija opadajuća, slijedi da

Zaključak

Upotreba izvedenice prilično je široka i može se u potpunosti pokriti ovom vrstom rada, ali pokušao sam pokriti glavne točke. Danas, u vezi s znanstveni i tehnološki napredak, posebno s brzom evolucijom računalnih sustava, diferencijalni račun postaje sve relevantniji u rješavanju jednostavnih i supersloženih problema.

Književnost

1. V.A. Petrov "Matematička analiza u proizvodnim zadacima"

2. Soloveichik I.L., Lisichkin V.T. "Matematika"

Chaikin Semyon, Maysak Kirill, Zalogina Anastasia, Shakhzadova Anna

Ovaj razvoj sadrži prezentaciju na temu "Primjena derivata u kemiji i biologiji." Tijekom projektne aktivnosti postavljena je hipoteza da derivat nalazi svoju primjenu u ovim područjima znanosti. Tijekom istraživački rad Saznalo se koja je uloga derivata u znanostima kao što su kemija i biologija, gdje i u rješavanju kojih problema nalazi svoju primjenu. Kao rezultat obavljenog rada zaključeno je da je hipoteza doista potvrđena.

Preuzimanje datoteka:

Pregled:

https://accounts.google.com

Naslovi slajdova:

Hipoteza:

Pregled:

Za korištenje pregleda prezentacija kreirajte Google račun (račun) i prijavite se: https://accounts.google.com

Naslovi slajdova:

Upotreba derivata u kemiji i biologiji. Rad su izveli učenici 11.B razreda MBOU srednje škole br. 6: Chaikin Semyon, Maysak Kirill, Zalogina Anastasia, Shakhzadova Anna Stavropol, 2014.

Hipoteza:

A u kemiji je diferencijalni račun pronašao široku primjenu za konstruiranje matematičkih modela kemijskih reakcija i naknadni opis njihovih svojstava. Kemija je znanost o tvarima, kemijskim pretvorbama tvari. Kemija proučava obrasce raznih reakcija.Brzina kemijske reakcije je promjena koncentracije reaktanata u jedinici vremena. Primjena derivata u kemiji i biologiji Određivanje brzine kemijske reakcije

Zašto nam treba derivat u reakcijama? Budući da se brzina reakcije v kontinuirano mijenja tijekom procesa, obično se izražava kao derivacija koncentracije reaktanata u odnosu na vrijeme.

Formula derivata u kemiji Ako je C (t) zakon promjene količine tvari koja je ušla u kemijsku reakciju, tada je brzina v (t) kemijske reakcije u trenutku t jednaka derivatu:

Određivanje brzine reakcije Granica omjera inkrementalne funkcije i inkrementalnog argumenta dok Δt teži nuli je brzina kemijske reakcije u danom trenutku

Zadatak iz kemije: Neka je količina tvari koja je ušla u kemijsku reakciju dana ovisnošću: C (t) \u003d t 2 / 2 + 3 t -3 (mol) Odredite brzinu kemijske reakcije nakon 3 sekunde. . Rješenje: v (t) = C ‘(t) ; v (t) = t + 3; v (3) = 3+3 = 6. Odgovor: 6 mol/s.

Biološko značenje izvedenice Neka je odnos između broja jedinki populacije mikroorganizama y i vremena t njezina razmnožavanja dan jednadžbom: y = x (t). Neka je ∆ t vremenski interval od neke početne vrijednosti t do t + ∆ t . Tada je y + ∆y = x (t + ∆ t) nova vrijednost veličine populacije koja odgovara trenutku t + ∆ t, a ∆ y + x (t + ∆ t) - x (t) je promjena u broj jedinki organizama. Omjer je prosječna stopa reprodukcije ili, kako se kaže, prosječna produktivnost stanovništva. Računanjem dobivamo y ' = P (t) = x ' (t) , odnosno produktivnost stanovništva u trenutku t .

Primjer Neka populacija bakterija u trenutku t (c) ima x(t) jedinki. . Odredite stopu rasta stanovništva: a) u proizvoljnom trenutku t , b) u trenutku t = 1 c . Rješenje: P = x'(t) = 200t; P(1) = 200 (r/s). Odgovor: 200 o/s.

Zaključak Pojam derivata vrlo je važan u kemiji i biologiji, posebice u određivanju brzine reakcije.

Zaključak: Diferencijalni račun je opis svijeta oko nas, napravljen matematičkim jezikom. Derivacija je jedan od najvažnijih pojmova u kalkulusu. Poznavanje derivacije pomaže nam da uspješno rješavamo ne samo matematičke probleme, već i praktične probleme iz raznih područja znanosti, tehnologije i života.

Državno sveučilište Južnog Sahalina

Odjel za matematiku

Tečajni rad

Tema: Praktična primjena derivata

Predavač: Likhacheva O.N.

Južno-Sahalinsk

2002. godine
Uvod

U ovom ću radu razmotriti primjene derivata u raznim znanostima i industrijama. Rad je podijeljen u poglavlja od kojih se svako bavi jednim od aspekata diferencijalnog računa (geometrijsko, fizičko značenje, itd.)

1. Pojam derivata

1-1. Povijesni podaci

Diferencijalni račun stvorili su Newton i Leibniz krajem 17. stoljeća na temelju dva problema:

1) o pronalaženju tangente na proizvoljnu liniju

2) o traženju brzine s proizvoljnim zakonom gibanja

Još ranije se koncept derivata susreo u djelima talijanskog matematičara Tartaglie (oko 1500. - 1557.) - ovdje se pojavila tangenta u tijeku proučavanja pitanja kuta nagiba pištolja, koji osigurava najveći domet projektila.

U 17. stoljeću, na temelju teorije gibanja G. Galilea, aktivno se razvijao kinematički koncept derivata. U djelima Descartesa, francuskog matematičara Robervala i engleskog znanstvenika L. Gregoryja počeli su se pojavljivati različiti prikazi. Lopital, Bernoulli, Lagrange, Euler, Gauss dali su veliki doprinos proučavanju diferencijalnog računa.

1-2. Pojam derivata

Neka je y \u003d f (x) kontinuirana funkcija argumenta x, definirana u intervalu (a; b), i neka je x 0 proizvoljna točka ovog intervala

Dajemo argumentu x prirast ∆x, tada će funkcija y = f(x) dobiti prirast ∆y = f(x + ∆x) - f(x). Granica kojoj teži omjer ∆y / ∆x pri ∆x → 0 zove se derivacija funkcije f(x).

1-3. Pravila diferenciranja i tablica derivacija

		(sin x)" = cos x
	(1 / x)" = -1 / x2	(cos x)" = -sin x
	(√x)" = 1 / 2√x	(tg x)" = 1 / cos 2 x
(uv)" = u"v + uv"	(a x)" = a x log x	(ctg x)" = 1 / sin 2 x
(u / v)"=(u"v - uv") / v 2		(arcsin x)" = 1 / √ (1- x 2)
	(log a x)" = (log a e) / x	(arccos x)" = -1 / √ (1- x 2)
	(ln x)" = 1 / x	(arctg x)" = 1 / √ (1+ x 2)
		(arcctg x)" = -1 / √ (1+ x 2)

2. Geometrijsko značenje derivacije

2-1. Tangenta na krivulju

Neka imamo krivulju i fiksnu točku M i na njoj točku N. Tangenta na točku M je pravac čiji položaj teži da zauzme tetiva MN, ako se točki N neograničeno približava duž krivulja do M.

Promotrimo funkciju f(x) i krivulju y = f(x) koja odgovara toj funkciji. Za neku vrijednost x funkcija ima vrijednost y = f(x). Ove vrijednosti na krivulji odgovaraju točki M(x 0 , y 0). Uvedimo novi argument x 0 + ∆x, čija vrijednost odgovara vrijednosti funkcije y 0 + ∆y = f(x 0 + ∆x). Odgovarajuća točka je N(x 0 + ∆x, y 0 + ∆y). Nacrtajte sekantu MN i sa φ označite kut koji sekanta tvori s pozitivnim smjerom osi Ox. Slika pokazuje da je ∆y / ∆x = tg φ. Ako se sada ∆x približi 0, tada će se točka N kretati duž krivulje, sekanta MN će se okretati oko točke M, a kut φ će se promijeniti. Ako pri ∆x → 0 kut φ teži nekom α, tada će pravac koji prolazi kroz M i zatvara kut α s pozitivnim smjerom osi apscisa biti tražena tangenta. U isto vrijeme, njegov koeficijent nagiba:

Odnosno, vrijednost derivacije f "(x) za danu vrijednost argumenta x jednaka je tangensu kuta koji s pozitivnim smjerom osi Ox tvori tangenta na graf funkcije f (x ) u točki M (x, f (x)).

Tangenta na prostornu liniju ima definiciju sličnu definiciji tangente na ravninsku krivulju. U ovom slučaju, ako je funkcija dana jednadžbom z = f(x, y), nagibi na osi OX i OY bit će jednaki parcijalnim derivatima f u odnosu na x i y.

2-2. Tangentna ravnina na površinu

Ravnina tangente na plohu u točki M je ravnina koja sadrži tangente na sve prostorne krivulje plohe koje prolaze kroz M - točku dodira.

Uzmimo površinu zadanu jednadžbom F(x, y, z) = 0 i neku običnu točku M(x 0 , y 0 , z 0) na njoj. Promotrimo na površini neku krivulju L koja prolazi kroz M. Neka je krivulja dana jednadžbama

x = φ(t); y = ψ(t); z = χ(t).

Zamijenimo ove izraze u jednadžbu površine. Jednadžba će se pretvoriti u identitet, budući da krivulja u potpunosti leži na površini. Koristeći svojstvo invarijantnosti oblika diferencijala, diferenciramo rezultirajuću jednadžbu s obzirom na t:

Jednadžbe tangente na krivulju L u točki M imaju oblik:

Budući da su razlike x - x 0, y - y 0, z - z 0 proporcionalne odgovarajućim diferencijalima, konačna jednadžba ravnine izgleda ovako:

F" x (x - x 0) + F" y (y - y 0) + F" z (z - z 0)=0

i za poseban slučaj z = f(x, y):

Z - z 0 \u003d F "x (x - x 0) + F" y (y - y 0)

Primjer: Nađite jednadžbu tangentne ravnine u točki (2a; a; 1,5a) hiperboličkog paraboloida.

Riješenje:

Z" x \u003d x / a \u003d 2; Z" y \u003d -y / a \u003d -1

Jednadžba željene ravnine:

Z - 1,5a = 2(x - 2a) - (Y - a) ili Z = 2x - y - 1,5a

3-1. Brzina materijalne točke

Neka je ovisnost puta s o vremenu t u zadanom pravocrtno gibanje materijalna točka izražava se jednadžbom s = f(t) i t 0 je određeni trenutak u vremenu. Razmotrimo drugo vrijeme t, označimo ∆t = t - t 0 i izračunajmo prirast puta: ∆s = f(t 0 + ∆t) - f(t 0). Omjer ∆s / ∆t naziva se prosječna brzina kretanja tijekom vremena ∆t proteklog od početnog trenutka t 0 . Brzina je granica ovog omjera kao ∆t → 0.

Prosječna akceleracija neravnomjernog gibanja u intervalu (t; t + ∆t) je vrijednost =∆v / ∆t. Trenutna akceleracija materijalne točke u trenutku t bit će granica prosječne akceleracije:

To jest, prvi vremenski izvod (v "(t)).

Primjer: Ovisnost puta koji je tijelo prešlo o vremenu dana je jednadžbom s \u003d A + Bt + Ct 2 + Dt 3 (C \u003d 0,1 m / s, D = 0,03 m / s 2). Odredite vrijeme nakon početka kretanja, nakon čega će ubrzanje tijela biti jednako 2 m / s 2.

Riješenje:

v(t) = s "(t) = B + 2Ct + 3Dt 2 ; a(t) = v"(t) = 2C + 6Dt = 0,2 + 0,18t = 2;

1,8 = 0,18 t; t = 10 s

3-2. Toplinski kapacitet tvari pri određenoj temperaturi

Za povećanje različitih temperatura T za istu vrijednost, jednaku T 1 - T, po 1 kg. određena tvar treba različitu količinu topline Q 1 - Q, i omjer

jer ova tvar nije konstantna. Dakle, za određenu tvar, količina topline Q je nelinearna funkcija temperature T: Q = f(T). Tada je ΔQ = f(t + ΔT) - f(T). Stav

naziva se prosječni toplinski kapacitet na intervalu , a granica ovog izraza pri ∆T → 0 naziva se toplinski kapacitet dane tvari pri temperaturi T.

3-3. Vlast

Promijeniti mehaničko kretanje Tijelo je uzrokovano silama koje na njega djeluju druga tijela. Da bi se kvantitativno okarakterizirao proces izmjene energije između tijela koja međusobno djeluju, u mehanici se uvodi pojam rada sile. Za karakterizaciju brzine obavljanja rada uvodi se koncept snage:

4. Diferencijalni račun u ekonomiji

4-1. Istraživanje funkcija

Diferencijalni račun je matematički aparat koji se široko koristi za ekonomsku analizu. Osnovni zadatak ekonomske analize je proučavanje odnosa ekonomskih veličina zapisanih kao funkcije. U kojem smjeru će se promijeniti državni prihod ako se povećaju porezi ili ako se uvedu uvozne carine? Hoće li se prihod poduzeća povećati ili smanjiti kada cijena njegovih proizvoda poraste? U kojem omjeru dodatna oprema može zamijeniti umirovljene radnike? Da bi se riješili takvi problemi, moraju se konstruirati funkcije povezivanja varijabli koje su u njih uključene, koje se zatim proučavaju pomoću metoda diferencijalnog računa. U ekonomiji se često traži pronaći najbolju ili optimalnu vrijednost pokazatelja: najveća produktivnost rada, maksimalni profit, maksimalni učinak, minimalni troškovi itd. Svaki pokazatelj je funkcija jednog ili više argumenata. Stoga se pronalaženje optimalne vrijednosti indikatora svodi na pronalaženje ekstremuma funkcije.

Prema Fermatovom teoremu, ako je točka ekstrem funkcije, tada derivacija u njoj ili ne postoji ili je jednaka 0. Vrsta ekstrema može se odrediti jednim od dovoljnih uvjeta za ekstrem:

1) Neka je funkcija f(x) diferencijabilna u nekoj okolini točke x 0 . Ako derivacija f "(x) pri prolasku kroz točku x 0 mijenja predznak od + do -, tada je x 0 maksimalna točka, ako od - do +, tada je x 0 minimalna točka, ako ne mijenja predznak , tada nema ekstrema.

2) Neka je funkcija f (x) dva puta diferencijabilna u nekoj okolini točke x 0, a f "(x 0) \u003d 0, f "" (x 0) ≠ 0, tada je u točki x 0 funkcija f (x 0) ima maksimum, ako je f ""(x 0)< 0 и минимум, если f ""(x 0) > 0.

Osim toga, druga derivacija karakterizira konveksnost funkcije (graf funkcije naziva se konveksnim gore [dolje] na intervalu (a, b) ako se nalazi na tom intervalu ne iznad [ne ispod] bilo koje svoje tangente ).

Primjer: odabrati optimalni obujam proizvodnje poduzeća, čija se funkcija dobiti može modelirati ovisnošću:

π(q) = R(q) - C(q) = q 2 - 8q + 10

Riješenje:

π"(q) = R"(q) - C"(q) = 2q - 8 = 0 → q extr = 4

Za q< q extr = 4 → π"(q) < 0 и прибыль убывает

Za q > q extr = 4 → π"(q) > 0 i dobit raste

Kada je q = 4, dobit ima minimalnu vrijednost.

Što je optimalni output za tvrtku? Ako tvrtka ne može proizvesti više od 8 jedinica outputa tijekom promatranog razdoblja (p(q = 8) = p(q = 0) = 10), tada bi optimalno rješenje bilo ne proizvoditi ništa, ali primati prihod od iznajmljivanja prostora i/ili opreme. Ako poduzeće može proizvesti više od 8 jedinica, tada će optimalni output za poduzeće biti na granici njegovog proizvodnog kapaciteta.

4-2. Elastičnost potražnje

Elastičnost funkcije f (x) u točki x 0 naziva se granica

Potražnja je količina dobra koju kupac traži. Cjenovna elastičnost potražnje E D je mjera kako potražnja reagira na promjene cijena. Ako je │E D │>1, tada se potražnja naziva elastičnom, ako je │E D │<1, то неэластичным. В случае E D =0 спрос называется совершенно неэластичным, т. е. изменение цены не приводит ни к какому изменению спроса. Напротив, если самое малое снижение цены побуждает покупателя увеличить покупки от 0 до предела своих возможностей, говорят, что спрос является совершенно эластичным. В зависимости от текущей эластичности спроса, предприниматель принимает решения о снижении или повышении цен на продукцию.

4-3. Analiza granica

Važan dio metoda diferencijalnog računa koji se koristi u ekonomiji su metode granične analize, tj. skup metoda za proučavanje promjena vrijednosti troškova ili rezultata s promjenama u proizvodnji, potrošnji itd. na temelju analize njihovih granične vrijednosti. Granični pokazatelj (indikatori) funkcije je njezina derivacija (u slučaju funkcije jedne varijable) ili parcijalne derivacije (u slučaju funkcije više varijabli)

U ekonomiji se često koriste prosjeci: prosječna produktivnost rada, prosječni troškovi, prosječni dohodak, prosječna dobit itd. Ali često se traži saznati za koliko će se rezultat povećati ako se troškovi povećaju ili obrnuto, koliko rezultat smanjit će se ako se smanje troškovi. Na ovo pitanje nemoguće je odgovoriti uz pomoć prosječnih vrijednosti. U takvim problemima potrebno je odrediti granicu omjera povećanja rezultata i troškova, odnosno pronaći granični učinak. Stoga je za njihovo rješavanje potrebno koristiti metode diferencijalnog računa.

5. Derivacija u približnim proračunima

5-1. Interpolacija

Interpolacija je približni izračun vrijednosti funkcije iz nekoliko zadanih vrijednosti. Interpolacija se široko koristi u kartografiji, geologiji, ekonomiji i drugim znanostima. Najjednostavnija opcija interpolacije je Lagrangeov oblik, ali kada postoji mnogo čvornih točaka i razmaci između njih su veliki, ili želite dobiti funkciju čija je zakrivljenost minimalna, tada se pribjegava interpolaciji spline, koja daje veću točnost.

Neka je K n sustav čvornih točaka a = x 0< x 1 <…< x n = b. Функция S k (x) называется сплайн-функцией S k (x) степени k≥0 на K n , если

a) S k (x) ê C k -1 ()

b) S k (x) je polinom stupnja najvišeg k

Spline funkcija Ŝ k (x) ê S k (K n) naziva se interpolirajuća spline funkcija ako je Ŝ k (x j) = f(x j) za j = 0,1,…,n

U primjenama je često dovoljno odabrati k=3 i primijeniti tzv kubična interpolacija.

Budući da je s(x) polinom trećeg stupnja na svakom parcijalnom intervalu, tada za x ê

Ovdje su s 2 j , c j 1 , c j 0 nepoznati za j = 1, 2, …, n

Potonji su isključeni zbog zahtjeva s(x j) = y j:

Diferencirajući ovu funkciju i uzimajući u obzir da s "(x) mora biti kontinuiran u cijelom intervalu i, prema tome, posebno u čvorovima, konačno dobivamo sustav jednadžbi:

s obzirom na n+1 nepoznanica s 2 0 , s 2 1 ,…, s 2 n. Za njihovo jednoznačno određivanje, ovisno o zadatku, dodaju se još dvije jednadžbe:

normalan slučaj (N):

Periodični slučaj (P) (tj.f(x+(x n -x 0))=f(x)):

Specificirano zaglađivanje na rubovima:

Primjer: spline interpolacija funkcije f(x)=sin x, n=4.

Funkcija je periodična, pa koristimo P slučaj.

Spline funkcija izgleda ovako:

5-2. Taylorova formula

Proširenje funkcija u beskonačne nizove omogućuje vam da dobijete vrijednost funkcije u danoj točki s bilo kojom točnošću. Ova tehnika se široko koristi u programiranju i drugim disciplinama.

Kaže se da se funkcija proširuje na danom intervalu u red potencija ako postoji takav red potencija a 0 + a 1 (x - a) + a 2 (x - a) 2 + ... + a n (x - a) ) n + ..., koja konvergira ovoj funkciji na ovom intervalu. Može se dokazati da je ova dekompozicija jedinstvena:

Neka je funkcija f(x) beskonačno diferencijabilna u točki a. Redovi potencija oblika

naziva se Taylorov red za funkciju f(x), zapisan u potencijama razlike (x - a). Općenito, da bi Taylorov red konvergirao k f(x), potrebno je i dovoljno da ostatak niza teži k 0. Za a = 0, Taylorov red se obično naziva Maclaurinov red.

I. M. Uvarenkov,

M. Z. Maller

Tečaj matematičke analize, v.1

V. A. Dudarenko,

A.A. Dadajan

Matematička analiza

Diferencijalni i integralni račun

T. I. Trofimova

Tečaj fizike

O. O. Zamkov

A. V. Tolstopjatenko

Yu N. Cheremnykh

Matematičke metode u ekonomiji

A. S. Solodovnikov

V. A. Babaitseva

A. V. Brailov

I.G. Shandra

Matematika u ekonomiji

Uvod

1. Pojam derivata

1-1. Povijesni podaci

1-2. Pojam derivata

1-3. Pravila diferenciranja i tablica derivacija

2. Geometrijsko značenje derivacije

2-1. Tangenta na krivulju

2-2. Tangentna ravnina na površinu

3. Korištenje izvoda u fizici

3-1. Brzina materijalne točke

3-2. Toplinski kapacitet pri određenoj temperaturi

3-3. Vlast

4. Diferencijalni račun u ekonomiji

4-1. Istraživanje funkcija

4-2. Elastičnost potražnje

4-3. Analiza granica

5. Derivacija u približnim proračunima

5-1. Interpolacija

5-2. Taylorova formula

5-3. Približni izračuni

Zaključak

Popis korištene literature

Državno sveučilište Južnog Sahalina

Odjel za matematiku

Tečajni rad

Tema: Praktična primjena derivata

Predavač: Likhacheva O.N.

Južno-Sahalinsk

2002. godine Uvod

1. Pojam derivata

1-1. Povijesni podaci

Diferencijalni račun stvorili su Newton i Leibniz krajem 17. stoljeća na temelju dva problema:

1) o pronalaženju tangente na proizvoljnu liniju

2) o traženju brzine s proizvoljnim zakonom gibanja

1-2. Pojam derivata

Neka je y = f(x) kontinuirana funkcija argumenta x definirana u intervalu (a; b) i neka je x0 proizvoljna točka tog intervala

Dajemo argumentu x prirast ∆x, tada će funkcija y = f(x) dobiti prirast ∆y = f(x + ∆x) - f(x). Granica kojoj teži omjer ∆y / ∆x pri ∆x → 0 zove se derivacija funkcije f(x).

1-3. Pravila diferenciranja i tablica derivacija

C" = 0(xn) = nxn-1(sin x)" = cos xx" = 1(1 / x)" = -1 / x2(cos x)" = -sin x(Cu)"=Cu"( √x)" = 1 / 2√x(tg x)" = 1 / cos2 x(uv)" = u"v + uv"(ax)" = ax ln x(ctg x)" = 1 / sin2 x( u / v)"=(u"v - uv") / v2(ex)" = ex(arcsin x)" = 1 / √ (1- x2)(logax)" = (logae) / x(arccos x) " = -1 / √ (1- x2)(ln x)" = 1 / x(arctg x)" = 1 / √ (1+ x2)(arctg x)" = -1 / √ (1+ x2)

2. Geometrijsko značenje derivacije

2-1. Tangenta na krivulju

Neka imamo krivulju i fiksnu točku M i na njoj točku N. Tangenta na točku M je pravac čiji položaj teži da zauzme tetiva MN, ako se točki N neograničeno približava duž krivulja do M.

Promotrimo funkciju f(x) i krivulju y = f(x) koja odgovara toj funkciji. Za neku vrijednost x funkcija ima vrijednost y = f(x). Ove vrijednosti na krivulji odgovaraju točki M(x0, y0). Uvodimo novi argument x0 + ∆x čija vrijednost odgovara vrijednosti funkcije y0 + ∆y = f(x0 + ∆x). Odgovarajuća točka je N(x0 + ∆x, y0 + ∆y). Nacrtajte sekantu MN i sa φ označite kut koji sekanta tvori s pozitivnim smjerom osi Ox. Slika pokazuje da je ∆y / ∆x = tg φ. Ako se sada ∆x približi 0, tada će se točka N kretati duž krivulje, sekanta MN će se okretati oko točke M, a kut φ će se promijeniti. Ako pri ∆x → 0 kut φ teži nekom α, tada će pravac koji prolazi kroz M i zatvara kut α s pozitivnim smjerom osi apscisa biti tražena tangenta. U isto vrijeme, njegov koeficijent nagiba:

Odnosno, vrijednost derivacije f "(x) za danu vrijednost argumenta x jednaka je tangensu kuta koji s pozitivnim smjerom osi Ox tvori tangenta na graf funkcije f (x ) u točki M (x, f (x)).

2-2. Tangentna ravnina na površinu

Ravnina tangente na plohu u točki M je ravnina koja sadrži tangente na sve prostorne krivulje plohe koje prolaze kroz M - točku dodira.

Uzmimo plohu zadanu jednadžbom F(x, y, z) = 0 i neku običnu točku M(x0, y0, z0) na njoj. Promotrimo na površini neku krivulju L koja prolazi kroz M. Neka je krivulja dana jednadžbama

x = φ(t); y = ψ(t); z = χ(t).

Jednadžbe tangente na krivulju L u točki M imaju oblik:

Budući da su razlike x - x0, y - y0, z - z0 proporcionalne odgovarajućim diferencijalima, konačna jednadžba ravnine izgleda ovako:

F "x (x - x0) + F" y (y - y0) + F "z (z - z0) \u003d 0

i za poseban slučaj z = f(x, y):

Z - z0 \u003d F "x (x - x0) + F" y (y - y0)

Primjer: Nađite jednadžbu tangentne ravnine u točki (2a; a; 1,5a) hiperboličkog paraboloida.

Riješenje:

Z"x \u003d x / a \u003d 2; Z"y \u003d -y / a = -1

Jednadžba željene ravnine:

Z - 1,5a = 2(x - 2a) - (Y - a) ili Z = 2x - y - 1,5a

3. Korištenje izvoda u fizici

3-1. Brzina materijalne točke

Neka je ovisnost puta s o vremenu t u zadanom pravocrtnom gibanju materijalne točke izražena jednadžbom s = f(t) i t0 je neki trenutak vremena. Razmotrimo drugo vrijeme t, označimo ∆t = t - t0 i izračunajmo prirast puta: ∆s = f(t0 + ∆t) - f(t0). Omjer ∆s / ∆t naziva se prosječna brzina kretanja tijekom vremena ∆t proteklog od početnog trenutka t0. Brzina je granica ovog omjera kao ∆t → 0.

Prosječna akceleracija neravnomjernog gibanja u intervalu (t; t + ∆t) je vrijednost =∆v / ∆t. Trenutna akceleracija materijalne točke u trenutku t bit će granica prosječne akceleracije:

To jest, prvi vremenski izvod (v "(t)).

Primjer: Vremenska ovisnost puta koji tijelo prijeđe dana je jednadžbom s = A + Bt + Ct2 + Dt3 (C = 0,1 m/s, D = 0,03 m/s2). Odredite vrijeme nakon početka gibanja nakon kojeg će akceleracija tijela biti jednaka 2 m/s2.

Riješenje:

v(t) = s"(t) = B + 2Ct + 3Dt2; a(t) = v"(t) = 2C + 6Dt = 0,2 + 0,18t = 2;

1,8 = 0,18 t; t = 10 s

3-2. Toplinski kapacitet tvari pri određenoj temperaturi

Za povećanje različitih temperatura T za istu vrijednost, jednaku T1 - T, po 1 kg. određena tvar treba različitu količinu topline Q1 - Q, i omjer

jer ova tvar nije konstantna. Dakle, za određenu tvar, količina topline Q je nelinearna funkcija temperature T: Q = f(T). Tada je ΔQ = f(t + ΔT) - f(T). Stav

naziva se prosječni toplinski kapacitet na intervalu , a granica ovog izraza pri ∆T → 0 naziva se toplinski kapacitet dane tvari pri temperaturi T.

3-3. Vlast

Promjena u mehaničkom gibanju tijela uzrokovana je silama koje na njega djeluju druga tijela. Da bi se kvantitativno okarakterizirao proces izmjene energije između tijela koja međusobno djeluju, u mehanici se uvodi pojam rada sile. Za karakterizaciju brzine obavljanja rada uvodi se koncept snage:

4. Diferencijalni račun u ekonomiji

4-1. Istraživanje funkcija

Prema Fermatovom teoremu, ako je točka ekstrem funkcije, tada derivacija u njoj ili ne postoji ili je jednaka 0. Vrsta ekstrema može se odrediti jednim od dovoljnih uvjeta za ekstrem:

1) Neka je funkcija f(x) diferencijabilna u nekoj okolini točke x0. Ako derivacija f "(x) pri prolasku kroz točku x0 promijeni predznak od + do -, tada je x0 maksimalna točka, ako od - do +, tada je x0 minimalna točka, ako ne promijeni predznak, tada postoji u ovom trenutku nije nikakav ekstrem.

2) Neka je funkcija f(x) dvostruko diferencijabilna u nekoj okolini točke x0 i f "(x0) = 0, f ""(x0) ≠ 0, tada u točki x0 funkcija f(x0) ima maksimalno ako

Preuzimanje datoteka:

Pregled:

Naslovi slajdova:

Pregled:

Naslovi slajdova:

Pročitajte također