Այժմ ընդհանուր տեսանկյունից կանդրադառնանք լոգարիթմներ պարունակող արտահայտությունների փոխակերպմանը։ Այստեղ մենք կվերլուծենք ոչ միայն արտահայտությունների փոխակերպումը, օգտագործելով լոգարիթմների հատկությունները, այլ կդիտարկենք արտահայտությունների փոխակերպումը լոգարիթմներով ընդհանուր տեսարան, որոնք պարունակում են ոչ միայն լոգարիթմներ, այլեւ հզորություններ, կոտորակներ, արմատներ եւ այլն։ Ինչպես միշտ, մենք բոլոր նյութերը կտրամադրենք բնորոշ օրինակներով մանրամասն նկարագրություններլուծումներ։
Էջի նավարկություն.
Արտահայտություններ լոգարիթմներով և լոգարիթմական արտահայտություններով
Կոտորակներով գործողություններ կատարելը
Նախորդ պարբերությունում մենք վերլուծեցինք հիմնական փոխակերպումները, որոնք կատարվում են լոգարիթմներ պարունակող առանձին կոտորակներով։ Այս փոխակերպումները, իհարկե, կարող են իրականացվել յուրաքանչյուր առանձին կոտորակի հետ, որն ավելի բարդ արտահայտության մաս է, օրինակ՝ ներկայացնելով համանման կոտորակների գումարը, տարբերությունը, արտադրյալը և գործակիցը։ Բայց բացի առանձին կոտորակների հետ աշխատելուց, այս տեսակի արտահայտությունների փոխակերպումը հաճախ ենթադրում է կոտորակների հետ համապատասխան գործողություններ կատարելը: Հաջորդիվ, մենք կքննարկենք այն կանոնները, որոնցով իրականացվում են այդ գործողությունները:
5-6-րդ դասարաններից մենք գիտենք այն կանոնները, որոնցով . Հոդվածում կոտորակների հետ գործողությունների ընդհանուր տեսքմենք տարածել ենք այս կանոնները սովորական կոտորակներ A/B ընդհանուր ձևի կոտորակների մեջ, որտեղ A-ն և B-ն թվային, բառացի կամ փոփոխականներով արտահայտություններ են, իսկ B-ն նույնականորեն հավասար չէ զրոյի: Հասկանալի է, որ լոգարիթմներով կոտորակները ընդհանուր կոտորակների հատուկ դեպքեր են։ Եվ այս առումով պարզ է, որ իրենց գրառումներում լոգարիթմներ պարունակող կոտորակների հետ գործողությունները կատարվում են նույն կանոններով։ Այսինքն:
- Նույն հայտարարներով երկու կոտորակներ գումարելու կամ հանելու համար համապատասխանաբար գումարեք կամ հանեք համարիչները, իսկ հայտարարը թողեք նույնը:
- հետ երկու կոտորակ գումարել կամ հանել տարբեր հայտարարներ, անհրաժեշտ է դրանք բերել ընդհանուր հայտարարի և կատարել համապատասխան գործողությունները՝ համաձայն նախորդ կանոնի։
- Երկու կոտորակ բազմապատկելու համար հարկավոր է գրել կոտորակ, որի համարիչը սկզբնական կոտորակների համարիչների արտադրյալն է, իսկ հայտարարը հայտարարների արտադրյալը։
- Կոտորակը կոտորակի վրա բաժանելու համար անհրաժեշտ է բաժանվող կոտորակը բազմապատկել բաժանարարի փոխադարձով, այսինքն՝ համարիչով և հայտարարով վերադասավորվող կոտորակով։
Ահա լոգարիթմներ պարունակող կոտորակների հետ գործողություններ կատարելու օրինակներ։
Օրինակ.
Կատարե՛ք գործողություններ լոգարիթմներ պարունակող կոտորակների հետ՝ ա), բ) 
, մեջ) 
, Գ) 
.
Լուծում.
ա) Ավելացված կոտորակների հայտարարներն ակնհայտորեն նույնն են. Հետևաբար, ըստ նույն հայտարարներով կոտորակների գումարման կանոնի, մենք գումարում ենք համարիչները, իսկ հայտարարը թողնում ենք նույնը. 
.
բ) Այստեղ հայտարարները տարբեր են. Հետեւաբար, նախ ձեզ հարկավոր է կոտորակները բերել նույն հայտարարի. Մեր դեպքում հայտարարներն արդեն ներկայացված են որպես արտադրյալներ, և մեզ մնում է վերցնել առաջին կոտորակի հայտարարը և դրան ավելացնել երկրորդ կոտորակի հայտարարից բացակայող գործոնները։ Այսպիսով, մենք ստանում ենք ձևի ընդհանուր հայտարար 
. Այս դեպքում հանված կոտորակները վերածվում են ընդհանուր հայտարարի՝ օգտագործելով լրացուցիչ գործոններ՝ համապատասխանաբար լոգարիթմի և x 2 ·(x+1) տեսքով: Դրանից հետո մնում է հանել նույն հայտարարներով կոտորակները, ինչը դժվար չէ։
Այսպիսով, լուծումը հետևյալն է. 
գ) Հայտնի է, որ կոտորակների բազմապատկման արդյունքը կոտորակն է, որի համարիչը համարիչների արտադրյալն է, իսկ հայտարարը հայտարարների արտադրյալն է, հետևաբար. 
Հեշտ է տեսնել, որ դա հնարավոր է ֆրակցիայի կրճատումերկուսով և տասնորդական լոգարիթմով, արդյունքում ունենք 
.
դ) Կոտորակների բաժանումից անցնում ենք բազմապատկման՝ կոտորակ-բաժանարարը փոխարինելով իր փոխադարձով։ Այսպիսով 
Ստացված կոտորակի համարիչը կարող է ներկայացվել որպես 
, որից հստակ երևում է համարիչի և հայտարարի ընդհանուր գործակիցը՝ x գործակիցը, դրանով կարող եք կրճատել կոտորակը. 
Պատասխան.
ա), բ) 
, մեջ) 
, Գ) 
.
Պետք է հիշել, որ կոտորակների հետ գործողություններն իրականացվում են՝ հաշվի առնելով գործողությունների կատարման հերթականությունը՝ սկզբում բազմապատկում և բաժանում, հետո գումարում և հանում, իսկ եթե կան փակագծեր, ապա նախ կատարվում են փակագծերի գործողություններ։
Օրինակ.
Կատարեք գործողություններ կոտորակներով 
.
Լուծում.
Նախ՝ փակագծերում կատարում ենք կոտորակների գումարում, որից հետո կիրականացնենք բազմապատկում. 
Պատասխան.
Այս պահին մնում է բարձրաձայն ասել երեք բավականին ակնհայտ, բայց միևնույն ժամանակ կարևոր կետեր.
Արտահայտությունների փոխակերպում՝ օգտագործելով լոգարիթմների հատկությունները
Ամենից հաճախ լոգարիթմներով արտահայտությունների փոխակերպումը ներառում է նույնականությունների օգտագործում, որոնք արտահայտում են լոգարիթմի սահմանումը և
Մաթեմատիկա. Թեմատիկ թեստեր. Մաս II. Պետական միասնական քննության նախապատրաստում-2010թ. 10-11 դասարաններ. Էդ. Լիսենկո Ֆ.Ֆ. - Ռոստով n / D .: Լեգեոն, 2009. - 176s.
Մաթեմատիկա. ՕԳՏԱԳՈՐԾՈՒՄ-2009. Թեմատիկ թեստեր. Մաս II (B4-B8, C1-C2) Ed. Լիսենկո Ֆ.Ֆ. - Ռոստով n / D: Legion, 2008 - 160 p.
Ձեռնարկը բաղկացած է առանձին թեմաներով թեստերից, որոնք ավանդական են մաթեմատիկայի դասընթացում և հետևաբար, որպես կանոն, ներառված են քննության մեջ։ Դրանք ամբողջությամբ ընդգրկում են USE-ի բարձրացված և բարդության բարձր մակարդակի առաջադրանքների խմբերը, բացառությամբ տեքստային առաջադրանքների և երկրաչափության խնդիրների: Յուրաքանչյուր թեմայի համար առաջարկվում է մեկ կամ մի քանի թեստային փաթեթ: Յուրաքանչյուր հավաքածու պարունակում է 10 թեստ, յուրաքանչյուր թեստը պարունակում է 8 առաջադրանք:
Այս գրքի նպատակն է մշակել առաջադրանքներ USE թեստերի կարճ և մանրամասն պատասխաններով: Դա անհրաժեշտ է առաջին հերթին այն շրջանավարտների համար, ովքեր ակնկալում են ստանալ ՕԳՏԱԳՈՐԾԵԼ լավգնահատումը, ինչպես նաև 10-րդ դասարանի սովորողների համար, ովքեր կարող են համախմբել ընդգրկված թեմաները USE-ի տեսանկյունից: Առաջարկվող ձեռնարկը կարող է օգտակար լինել բոլոր շրջանավարտներին, ովքեր պատրաստվում են մաթեմատիկայի USE-ին, ինչպես նաև ուսուցիչներին, ովքեր պատրաստում են ուսանողներին USE-ին:
Ձևաչափ: djvu/zip (2009 , 176 թ.)
Չափը: 2,5 ՄԲ
Ներբեռնեք / Ներբեռնեք ֆայլը 14
Ձևաչափ: pdf (2009 , 176 թ.)
Չափը: 8,6 ՄԲ
Ներբեռնել: 14 .12.2018, հղումները հեռացվել են Legion հրատարակչության խնդրանքով (տես ծանոթագրությունը)
Ձևաչափ: djvu/zip (2008 , 160-ական թթ.)
Չափը: 3 ՄԲ
Ներբեռնեք / Ներբեռնեք ֆայլը 14 .12.2018, հղումները հեռացվել են Legion հրատարակչության խնդրանքով (տես ծանոթագրությունը)
Ձևաչափ: pdf (2008 , 160-ական թթ.)
Չափը: 9,9 ՄԲ
Ներբեռնել: 14 .12.2018, հղումները հեռացվել են Legion հրատարակչության խնդրանքով (տես ծանոթագրությունը)
Ուսումնամեթոդական համալիր «Մաթեմատիկա. միասնական պետական քննություն-2010» հրատ. Լիսենկո Ֆ.Ֆ. and Kulabukhov S.Yu. ներառում է ձեռնարկներ.
1.
Մաթեմատիկա. Պետական միասնական քննության նախապատրաստում-2010թ.
2. Ռեշեբնիկ. Մաթեմատիկա. Պետական միասնական քննության նախապատրաստում-2010թ.
3. Մաթեմատիկա. Թեմատիկ թեստեր. Մաս I (հիմնական մակարդակ): Պետական միասնական քննության նախապատրաստում-2010թ. 10-11 դասարաններ.
4. Մաթեմատիկա. Թեմատիկ թեստեր. Մաս II. Պետական միասնական քննության նախապատրաստում-2010թ. 10-11 դասարաններ.
5.
Մաթեմատիկա. Թեմատիկ թեստեր՝ երկրաչափություն, բառային խնդիրներ: Պետական միասնական քննության նախապատրաստում-2010թ. 10-11 դասարաններ.
6.
Մաթեմատիկա. USE թեստերի հավաքածու 2001 - 2010 թթ.
7. Մաթեմատիկա. Պետական միասնական քննության նախապատրաստում-2010թ. Վերապատրաստման թեստեր.
8. Մաթեմատիկայի գրպանային ուղեցույց:
Բովանդակություն
Հեղինակներից 11
§ 1. Լոգարիթմական արտահայտությունների ինքնության փոխակերպումներ 13
Տարբերակ թիվ 1 13
Տարբերակ թիվ 2 13
Տարբերակ թիվ 3 14
Տարբերակ թիվ 4 14
Տարբերակ թիվ 5 15
Տարբերակ թիվ 6 15
Տարբերակ թիվ 7 16
Տարբերակ թիվ 8 16
Տարբերակ թիվ 9 17
Տարբերակ թիվ 10 17
§ 2. 18 աստիճան պարունակող արտահայտությունների ինքնության փոխակերպումներ
Տարբերակ թիվ 1 18
Տարբերակ թիվ 2 19
Տարբերակ թիվ 3 19
Տարբերակ թիվ 4 20
Տարբերակ թիվ 5 21
Տարբերակ թիվ 6 21
Տարբերակ թիվ 7 22
Տարբերակ թիվ 8 23
Տարբերակ թիվ 9 23
Տարբերակ թիվ 10 24
§ 3. Իռացիոնալ արտահայտությունների ինքնության փոխակերպումներ 25
Տարբերակ թիվ 1 25
Տարբերակ թիվ 2 25
Տարբերակ թիվ 3 26
Տարբերակ թիվ 4 26
Տարբերակ թիվ 5 27
Տարբերակ թիվ 6 28
Տարբերակ թիվ 7 28
Տարբերակ թիվ 8 29
Տարբերակ թիվ 9 30
Տարբերակ թիվ 10 30
§ 4. Հավասարումների համակարգեր 31
Տարբերակ թիվ 1 31
Տարբերակ թիվ 2 32
Տարբերակ թիվ 3 33
Տարբերակ թիվ 4 33
Տարբերակ թիվ 5 34
Տարբերակ թիվ 6 35
Տարբերակ թիվ 7 36
Տարբերակ թիվ 8 37
Տարբերակ թիվ 9 38
Տարբերակ թիվ 10 39
§ 5. երկրաչափական իմաստածանցյալ 39
Տարբերակ թիվ 1 39
Տարբերակ թիվ 2 41
Տարբերակ թիվ 3 43
Տարբերակ թիվ 4 44
Տարբերակ թիվ 5 46
Տարբերակ թիվ 6 48
Տարբերակ թիվ 7 50
Տարբերակ թիվ 8 52
Տարբերակ թիվ 9 54
Տարբերակ թիվ 10 55
§ 6. Անհավասարություններ 56
Տարբերակ թիվ 1 գ 56
Տարբերակ թիվ 2 57
Տարբերակ թիվ 3 58
Տարբերակ թիվ 4 58
Տարբերակ թիվ 5 59
Տարբերակ թիվ 6 60
Տարբերակ թիվ 7 60
Տարբերակ թիվ 8 61
Տարբերակ թիվ 9 62
Տարբերակ թիվ 10 63
§ 7. Իռացիոնալ հավասարումներ 63
Տարբերակ թիվ 1 63
Տարբերակ թիվ 2 64
Տարբերակ թիվ 3 65
Տարբերակ թիվ 4 65
Տարբերակ թիվ 5 66
Տարբերակ թիվ 6 66
Տարբերակ թիվ 7 67
Տարբերակ թիվ 8 67
Տարբերակ թիվ 9 68
Տարբերակ թիվ Յու 68
§ 8. Եռանկյունաչափական հավասարումներ 69
Տարբերակ թիվ 1 69
Տարբերակ թիվ 2 69
Տարբերակ թիվ 3 70
Տարբերակ թիվ 4 70
Տարբերակ թիվ 5 71
Տարբերակ թիվ 6 72
Տարբերակ թիվ 7 72
Տարբերակ թիվ 8 73
Տարբերակ թիվ 9 74
Տարբերակ թիվ 10 74
§ 9. Լոգարիթմական հավասարումներ 75
Տարբերակ թիվ 1 75
Տարբերակ թիվ 2 75
Տարբերակ թիվ 3 76
Տարբերակ թիվ 4 76
Տարբերակ թիվ 5 77
Տարբերակ թիվ 6 77
Տարբերակ թիվ 7 78
Տարբերակ թիվ 8 * 78
Տարբերակ թիվ 9 79
Տարբերակ թիվ 10 79
§ 10. Էքսպոնենցիալ հավասարումներ 80
Տարբերակ թիվ 1 80
Տարբերակ թիվ 2 80
Տարբերակ թիվ 3 81
Տարբերակ թիվ 4 81
Տարբերակ թիվ 5 82
Տարբերակ թիվ 6 82
Տարբերակ թիվ 7 83
Տարբերակ թիվ 8 83
Տարբերակ թիվ 9 84
Տարբերակ թիվ 10 84
§ տասնմեկ. Պարբերականություն, զույգ և կենտ ֆունկցիաներ 85
Տարբերակ թիվ 1 85
Տարբերակ թիվ 2 86
Տարբերակ թիվ 3 87
Տարբերակ թիվ 4 89
Տարբերակ թիվ 5 90
Տարբերակ թիվ 6 91
Տարբերակ թիվ 7 92
Տարբերակ թիվ 8 93
Տարբերակ թիվ 9 94
Տարբերակ թիվ 10 95
§ 12. Բարդ ֆունկցիայի զրոներ. Սահմանափակ գործառույթ 97
Տարբերակ թիվ 1 97
Տարբերակ թիվ 2 97
Տարբերակ թիվ 3 98
Տարբերակ թիվ 4 98
Տարբերակ թիվ 5 99
Տարբերակ թիվ 6 99
Տարբերակ թիվ 7 100
Տարբերակ թիվ 8 100
Տարբերակ թիվ 9 101
Տարբերակ թիվ 10 101
§ 13. Սահմանման տիրույթ, արժեքների բազմություն, ֆունկցիաների միապաղաղություն 102.
Տարբերակ թիվ 1 102
Տարբերակ թիվ 2 102
Տարբերակ թիվ 3 103
Տարբերակ թիվ 4 103
Տարբերակ թիվ 5 104
Տարբերակ թիվ 6 104
Տարբերակ թիվ 7 105
Տարբերակ թիվ 8 105
Տարբերակ թիվ 9 106
Տարբերակ թիվ 10 107
§ 14. Ֆունկցիայի ծայրահեղություն. 107 ֆունկցիայի ամենամեծ և ամենափոքր արժեքները
Տարբերակ թիվ 1 107
Տարբերակ թիվ 2 108
Տարբերակ թիվ 3 108
Տարբերակ թիվ 4 109
Տարբերակ թիվ 5 109
Տարբերակ թիվ 6 110
Տարբերակ թիվ 7 110
Տարբերակ թիվ 8 111
Տարբերակ թիվ 9 111
Տարբերակ թիվ 10 112
§ 15. Լոգարիթմական հավասարումների լուծման տարբեր տեխնիկա 113
Տարբերակ թիվ 1 113
Տարբերակ թիվ 2 113
Տարբերակ թիվ 3 114
Տարբերակ թիվ 4 114
Տարբերակ թիվ 5 115
Տարբերակ թիվ 6 115
Տարբերակ թիվ 7 116
Տարբերակ թիվ 8 116
Տարբերակ թիվ 9 117
Տարբերակ թիվ 10 117
§ 16. Եռանկյունաչափական հավասարումների լուծման տարբեր տեխնիկա 118
Տարբերակ թիվ 1 118
Տարբերակ թիվ 2 118
Տարբերակ թիվ 3 118
Տարբերակ թիվ 4 119
Տարբերակ թիվ 5 119
Տարբերակ թիվ 6 120
Տարբերակ թիվ 7 120
Տարբերակ թիվ 8 121
Տարբերակ թիվ 9 121
Տարբերակ թիվ 10 122
§ 17. Իռացիոնալ հավասարումների լուծման տարբեր տեխնիկա 123
Տարբերակ թիվ 1 123
Տարբերակ թիվ 2 123
Տարբերակ թիվ 3 124
Տարբերակ թիվ 4 124
Տարբերակ թիվ 5 125
Տարբերակ թիվ 6 125
Տարբերակ թիվ 7 125
Տարբերակ թիվ 8 126
Տարբերակ թիվ 9 126
Տարբերակ թիվ 10 127
§ 18. 127 մոդուլային նշանի տակ փոփոխական պարունակող հավասարումներ
Տարբերակ թիվ 1 127
Տարբերակ թիվ 2 128
Տարբերակ թիվ 3 128
Տարբերակ թիվ 4 129
Տարբերակ թիվ 5 129
Տարբերակ թիվ 6 130
Տարբերակ թիվ 7 130
Տարբերակ թիվ 8 131
Տարբերակ թիվ 9 131
Տարբերակ թիվ 10 131
§ 19. Լուծման տարբեր մեթոդներ էքսպոնենցիալ հավասարումներ.132
Տարբերակ թիվ 1 132
Տարբերակ թիվ 2 133
Տարբերակ թիվ 3 133
Տարբերակ թիվ 4 134
Տարբերակ թիվ 5 134
Տարբերակ թիվ 6 135
Տարբերակ թիվ 7 135
Տարբերակ թիվ 8 135
Տարբերակ թիվ 9 136
Տարբերակ թիվ 10 136
§ 20. Համակցված հավասարումների լուծման տարբեր տեխնիկա 137
Տարբերակ թիվ 1 137
Տարբերակ թիվ 2 137
Տարբերակ թիվ 3 138
Տարբերակ թիվ 4 138
Տարբերակ թիվ 5 139
Տարբերակ թիվ 6 139
Տարբերակ թիվ 7 140
Տարբերակ թիվ 8 140
Տարբերակ թիվ 9 141
Տարբերակ թիվ 10 141
§ 21. 142 մոդուլ պարունակող պարամետրով հավասարումներ
Տարբերակ թիվ 1 142
Տարբերակ թիվ 2 142
Տարբերակ թիվ 3 143
Տարբերակ թիվ 4 144
Տարբերակ թիվ 5 144
Տարբերակ թիվ 6 145
Տարբերակ թիվ 7 146
Տարբերակ թիվ 8 146
Տարբերակ թիվ 9 147
Տարբերակ թիվ 10 148
Պատասխաններ 149
§ 1. Լոգարիթմական արտահայտությունների ինքնության փոխակերպումներ 149
§ 2. 150 աստիճան պարունակող արտահայտությունների ինքնության փոխակերպումներ
§ 3. Իռացիոնալ արտահայտությունների ինքնության փոխակերպումներ 150
§ 4. Հավասարումների համակարգեր 151
§ 5. Ածանցյալի երկրաչափական իմաստը 151
§ 6. Անհավասարություններ 152
§ 7. Իռացիոնալ հավասարումներ 152
§ 8. Եռանկյունաչափական հավասարումներ 153
§ 9. Լոգարիթմական հավասարումներ 153
§ 10. Էքսպոնենցիալ հավասարումներ 154
§ տասնմեկ. Պարբերականություն, զույգ և կենտ ֆունկցիաներ 154
§ 12. Բարդ ֆունկցիայի զրոներ. Սահմանափակ գործառույթ 155
§ 13. Սահմանման տիրույթ, արժեքների բազմություն, ֆունկցիաների միապաղաղություն 156.
§ 14. Ֆունկցիայի ծայրահեղություն. 158 ֆունկցիայի ամենամեծ և ամենափոքր արժեքները
§ տասնհինգ. Տարբեր հնարքներ 159 լոգարիթմական հավասարումներ լուծելիս
§ 16. Եռանկյունաչափական հավասարումների լուծման տարբեր տեխնիկա 160
§ 17. Իռացիոնալ հավասարումների լուծման տարբեր հնարքներ 164
§ 18. 165 մոդուլային նշանի տակ փոփոխական պարունակող հավասարումներ
§ 19. Էքսպոնենցիալ հավասարումների լուծման տարբեր տեխնիկա.166
§ 20. Համակցված հավասարումների լուծման տարբեր տեխնիկա 167
§ 21. 169 մոդուլ պարունակող պարամետրով հավասարումներ
Գրականություն 170
ԷԳՈՐՈՎԱ ՎԻԿՏՈՐԻԱ ՎԱԼԵՐԵՎՆԱ
Մաթեմատիկայի ուսուցիչ
բարձրագույն որակավորման կատեգորիա
ԹԵՄԱ՝ «ԻՆՔՈՒԹՅԱՆ ՓՈՓՈԽԱՆՈՒՄ
լոգարիթմական արտահայտություններ»
Գիտելիքներ և հմտություններ, որոնք ուսանողները պետք է տիրապետեն այս դասն ուսումնասիրելուց հետո.
իմանալ թվի լոգարիթմի սահմանումը, հիմնական լոգարիթմական ինքնությունը, լոգարիթմների հատկությունները.
կարողանալ կատարել լոգարիթմներ պարունակող արտահայտությունների փոխակերպումներ, հաշվարկել լոգարիթմներ.
Գրականություն:
1. Ալիմով Շ.Ա., Կոլյագին Յու.Մ., Սիդորով Յու.Վ. և այլք Հանրահաշիվ և վերլուծության սկիզբ՝ դասագիրք 10-11-րդ դասարանների համար ուսումնական հաստատություններ. - Մ.: Կրթություն, 2001:
2. Kochagin V.V., Kochagina M.V., Քննությանը նախապատրաստվելու ինտենսիվ կուրս. - Մ.: Էքսմո, 2009:
3. A. G. Merzlyak, V. B. Polonsky և M. S. Yakir, Հանրահաշվական սիմուլյատոր. ուղեցույց դպրոցականների և բուհ ընդունվողների համար: - Մ.: Իլեքսա, 2005:
4. Գուսև Վ.Ա., Մորդկովիչ Ա.Գ. Մաթեմատիկա. Տեղեկատվական նյութեր. Գիրք ուսանողների համար. - Մ.: Կրթություն, 2001:
Դասի պլան:
Դասերի ընթացքում.
1) Լոգարիթմն է Հունարեն բառ, որը բաղկացած է 2 բառից՝ «լոգոներ»՝ հարաբերություն, «արիթմոս»՝ թիվ։ Այսպիսով, լոգարիթմը այն թիվն է, որը չափում է հարաբերակցությունը: 1614 թվականին հրապարակված մի հրապարակում նշվում էր, որ Նապիերը հորինել է լոգարիթմներ։ Հետագայում նա կազմել է լոգարիթմական աղյուսակներ, որոնք այժմ մեզ հայտնի են որպես Բրադիսի աղյուսակներ։ Մեկ դարից էլ քիչ ժամանակում աղյուսակները տարածվել են ամբողջ աշխարհում և դարձել հաշվողական անփոխարինելի գործիք: Ապագայում դրանք, կարծես, կառուցվել են հարմար սարքի մեջ, որը չափազանց արագացնում է հաշվարկի գործընթացը՝ սլայդի կանոն, որն օգտագործվում էր մինչև քսաներորդ դարի յոթանասունական թվականները:
Հավելված 1.
2) լոգարիթմ դրական թիվբպատճառաբանությամբ ա, ընդ որում զրոյից մեծ և ոչ հավասար մեկի,այն ցուցանիշն է, որին պետք է բարձրացվի թիվըա համարը ստանալու համարբ.
Լոգարիթմի սահմանումն արտահայտող այս հավասարությունը կոչվում էհիմնական լոգարիթմական ինքնությունը .
Գ 
ԿԱՄ 1
Պ 
Աստիճանի հիմքը և լոգարիթմի հիմքը տասնյոթն են, ինչը նշանակում է, որ ըստ հիմնական լոգարիթմական նույնության արտահայտության արժեքը երեքն է։
Մենք բանավոր կաշխատենք.
SCH 
ԷԼՉՈԿ
Օ ներքևի վայրկյանը զրոյական կետն է հինգ տասներորդական, ուստի արտահայտությունը հավասար է հինգի թվաբանական քառակուսի արմատին:
Պ 
հավելված 2.
Հավասարություն նշանակում է, որ
Լոգարիթմի սահմանումից ստացվում են հետևյալ կարևոր հավասարությունները.
Օրինակ:
Պ 
հավելված 3.
Անցնենք ՕԳՏԱԳՈՐԾԵԼ առաջադրանքներ:
Հավելված 4
3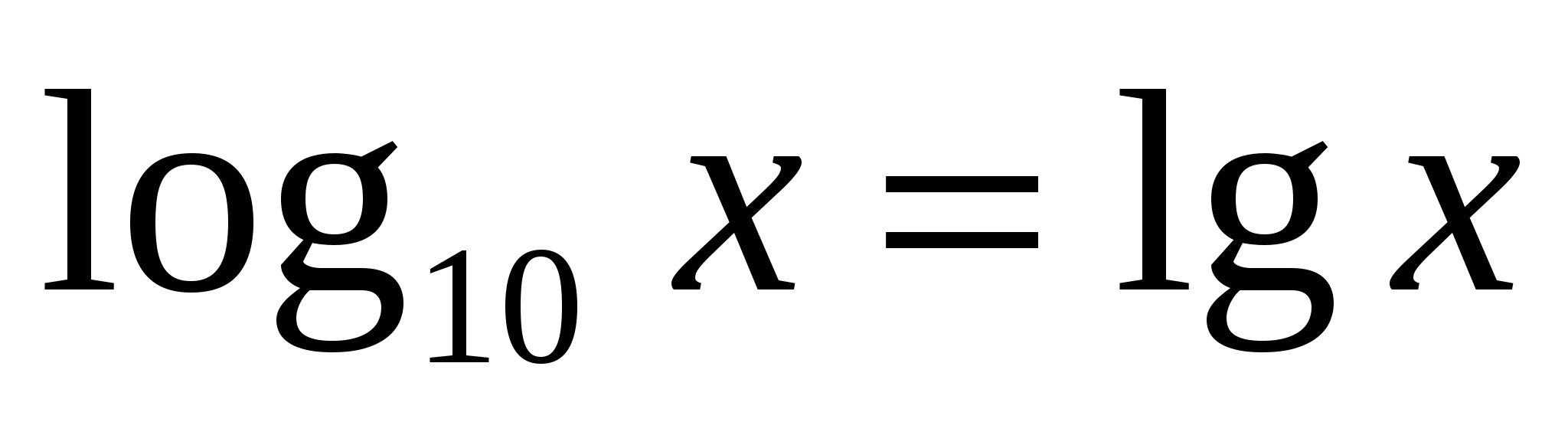
)
Տասը հիմքի լոգարիթմի համար կա հատուկ նշում և անվանում։տասնորդական լոգարիթմ
.
Լ 
թվաբանություն՝ հիմքե
կանչեցբնական լոգարիթմ
.
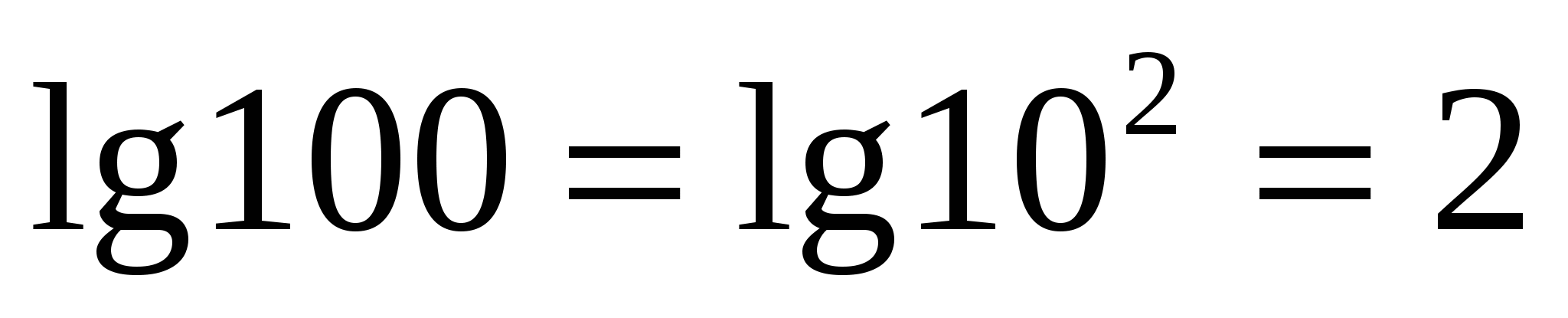
Հ 
օրինակ,
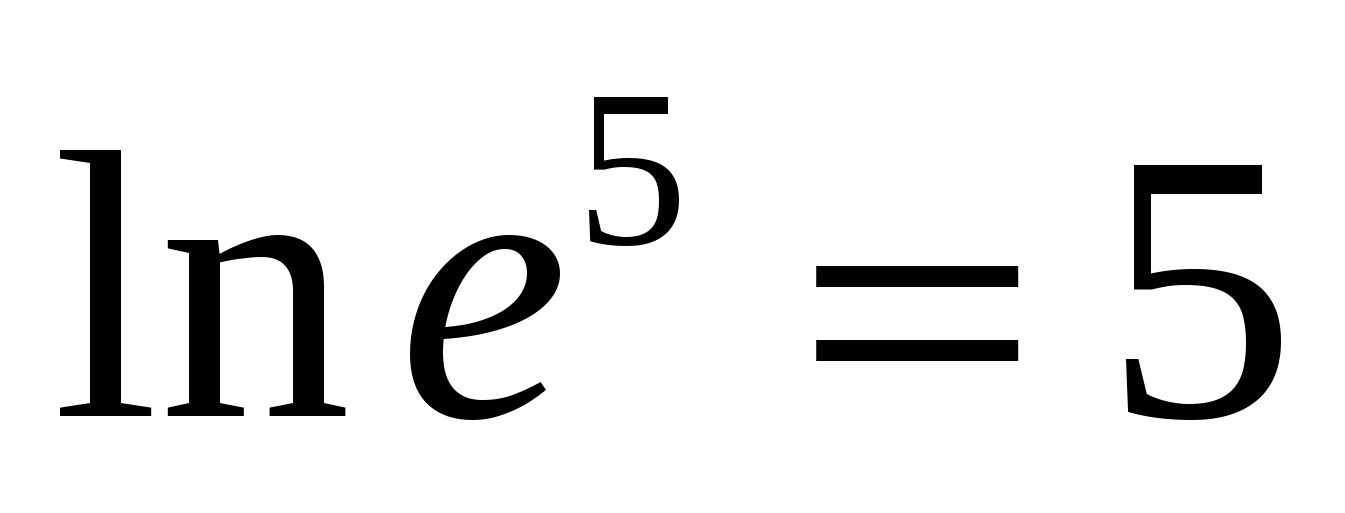
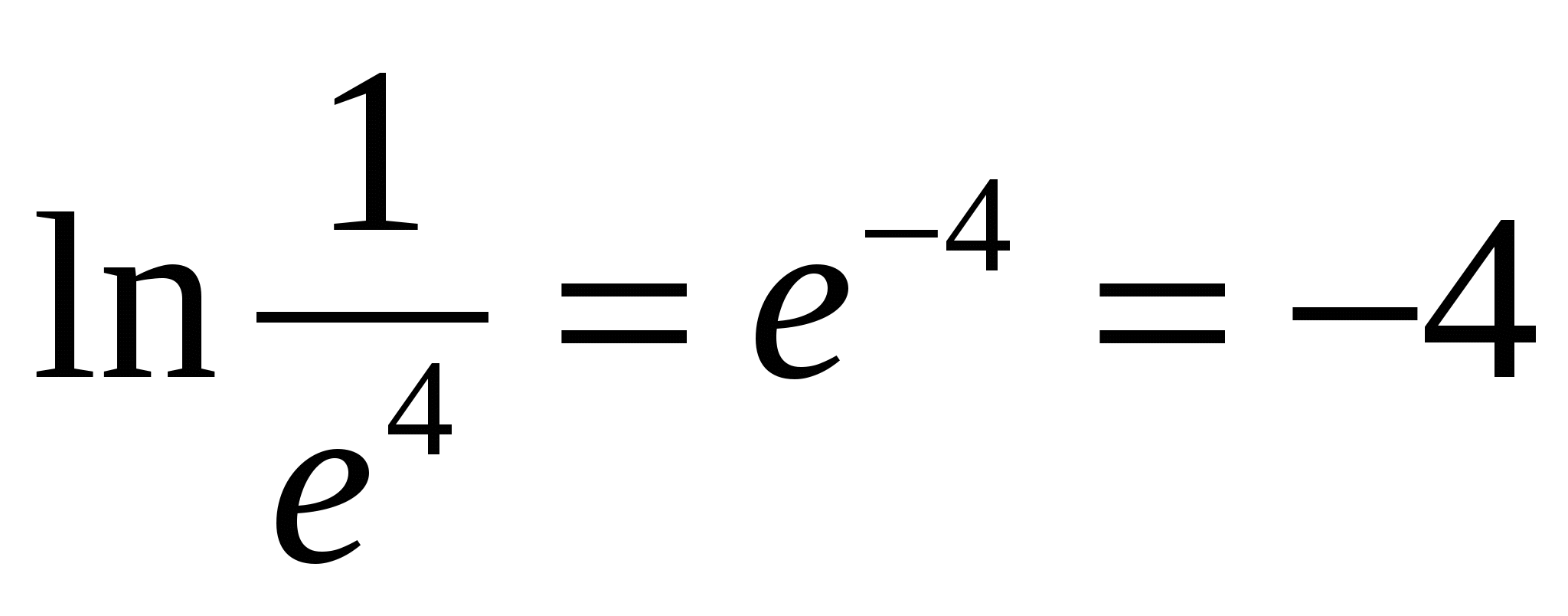
4) Լոգարիթմի սահմանումից բխում են հետևյալ հատկությունները. Բոլոր հատկությունները ձևակերպված և ապացուցված են միայն լոգարիթմական նշանների տակ պարունակվող փոփոխականների դրական արժեքների համար:
Երկու դրական թվերի արտադրյալի բազային լոգարիթմ ա հավասար է գումարիննույն հիմքով այս թվերի լոգարիթմները:
DER 2
Օրինակ,
Վ 
հանձնարարություն 1.
Առաջադրանք 2.Պարզեցրեք արտահայտությունը
AT 
Եկեք օգտագործենք նախորդ օրինակը: Եկեք փոխարինենք
Նշենք, որ լոգարիթմը քառակուսի է, ուստի գումարը նույնպես պետք է քառակուսի լինի: Օգտագործելով գումարի քառակուսու բանաձևը՝ բացեք փակագծերը։ Ներկայացնում ենք նմանատիպ տերմիններ.
5) քանորդի լոգարիթմը հավասար է դիվիդենտի և բաժանարարի լոգարիթմների տարբերությանը:
Գ
Ուշադրություն դարձրեք աստիճանի հիմքին և լոգարիթմի հիմքին. դրանք նույնն են:
ԿԱՄ 3Ռ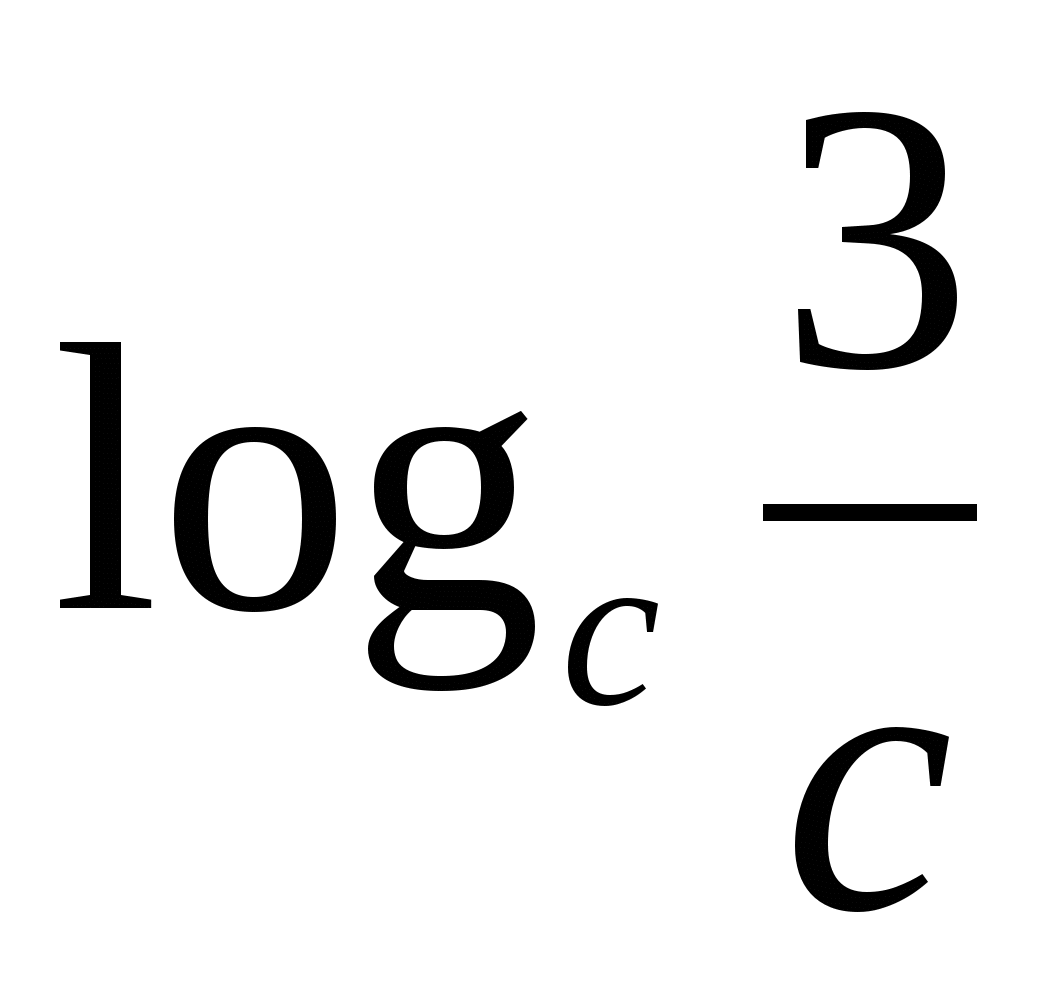 
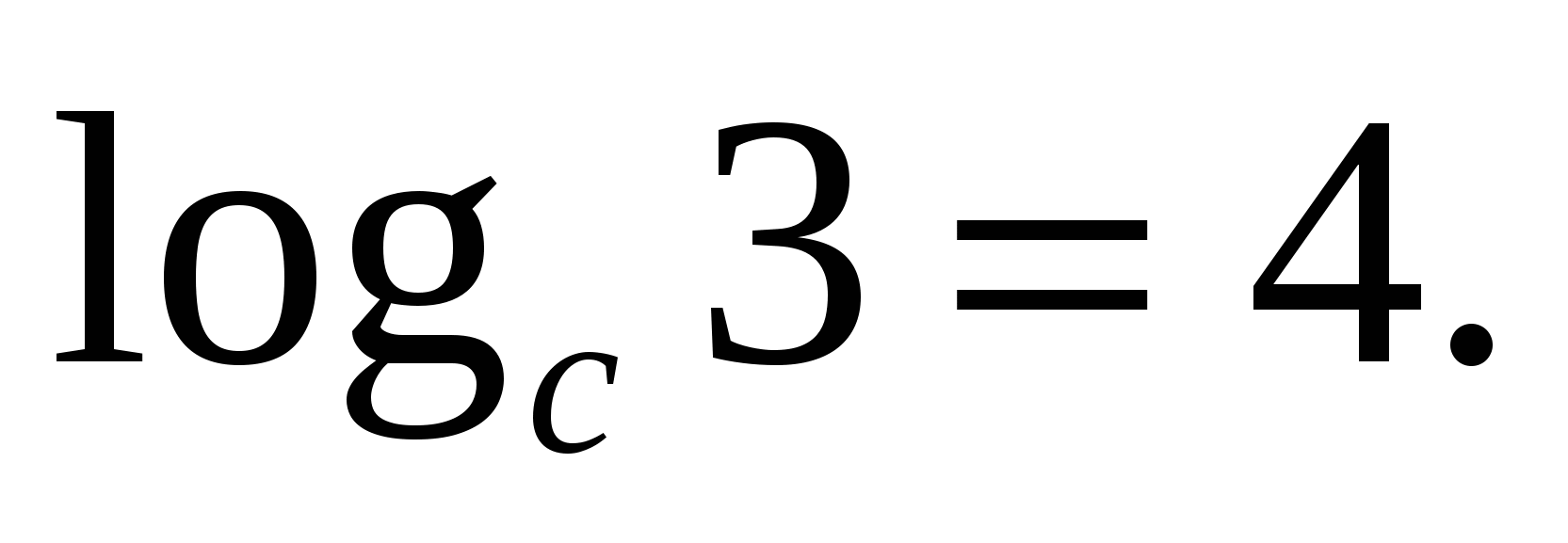Դիտարկենք այս բանաձևի կիրառումը օրինակով.
Վ 
հանձնարարություն 1.Գտե՛ք արտահայտության արժեքը, եթե
Առաջադրանք 2.Գտեք արժեքը բիր լոգարիթմով
6) Հիմքի աստիճանի լոգարիթմըա , հավասար է արտադրանքինցուցիչ մեկ լոգարիթմի վրա նույն հիմքում:
DER 4
Օրինակ,
Վ 
հանձնարարություն 1.Հաշվեք, եթե
Պարզեցնենք արտահայտությունը
Բանաձև
կանչեց նոր հիմքի անցնելու բանաձևը.
Վ 
հանձնարարություն 1.Արտահայտի՛ր 2 հիմքով լոգարիթմի տեսքով:
Առաջադրանք 2.Հաշվիր
CER 5
CER 6
Օրինակ,
Վ 
հանձնարարություն 1.Հաշվիր
Վ 
հանձնարարություն 2.Հաշվիր
9) Դուք կարող եք սկսել լոգարիթմական փոխակերպումներ միայն այն դեպքում, եթեեթե հիշում եք լոգարիթմների բոլոր հատկությունները. Դրանք կրկնելուց հետո մենք կդիտարկենք լոգարիթմական արտահայտությունները մյուս կողմից փոխակերպելու առաջադրանքներ:
Լոգարիթմական արտահայտությունների գումարը կամ տարբերությունը փոխակերպելու համար երբեմն բավական է օգտագործել լոգարիթմի սահմանումը, իսկ ամենից հաճախ՝ արտադրյալի կամ գործակիցի լոգարիթմի հատկությունները։
Վ 
հանձնարարություն 1.Հաշվիր
Եկեք լուծենք այն երկու ճանապարհով.
1 ճանապարհ, օգտագործելով լոգարիթմի սահմանումը.
Մեթոդ 2-ի վրա հիմնվածքանորդ լոգարիթմի հատկություն.
Առաջադրանք 2.Գտեք արտահայտության արժեքը
Եկեք նախ կիրառենք բանաձևըարտադրանքի լոգարիթմը, ապա լոգարիթմի սահմանումը։
Հիմնական լոգարիթմական ինքնությունը օգտագործվում է ցուցիչում լոգարիթմ պարունակող արտահայտությունները փոխակերպելիս: Նման գործողությունների գաղափարն այն է, որ ցուցիչի հիմքը և լոգարիթմի հիմքը հավասար լինեն:
Երբեմն անհրաժեշտ է փոխակերպել արտահայտությունըլոգարիթմի հատկություններով և աստիճանի հատկություններով նույնպես կարելի է հեշտությամբ տեղափոխել մի բազայից մյուսը՝ օգտագործելով անցումային բանաձևը: Այլ դեպքերում, պետք է կիրառվեն մի քանի հատկություններ:
Վ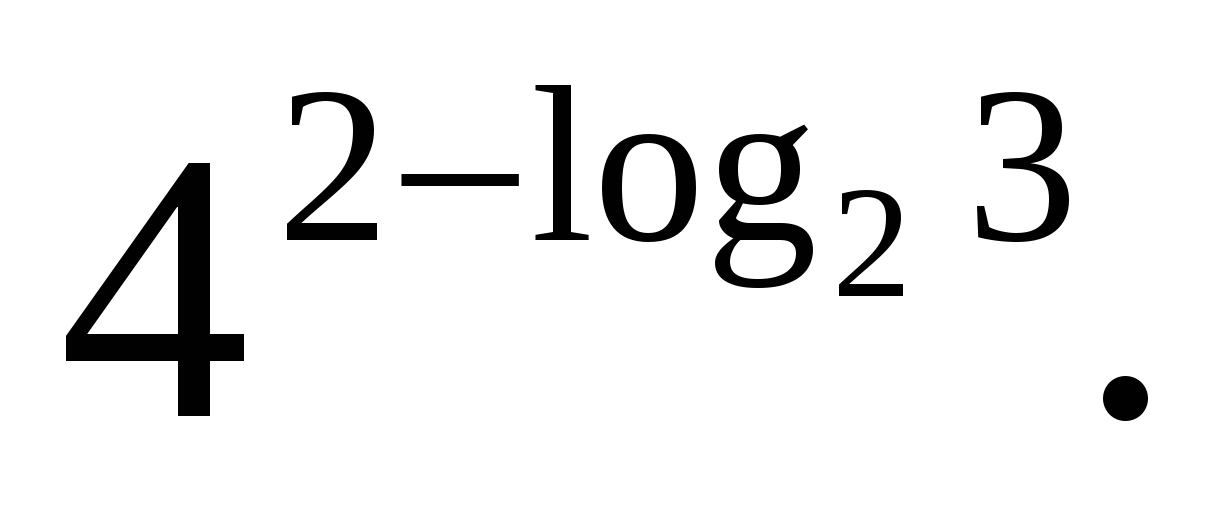 
հանձնարարություն 3.Հաշվիր
Վ 
հանձնարարություն 4.Գտեք արտահայտության արժեքը
Առաջադրանք 5.Գտեք արտահայտության արժեքը
Վ 
հանձնարարություն 6.Արտահայտեք որպես լոգարիթմների տարբերություն
Հ 
Ամենամեծ դժվարությունը լոգարիթմական արտահայտությունների փոխակերպումն է արմատականի տակ։ Փոխակերպումների գործընթացում պետք է դիտարկել լոգարիթմական արտահայտությունների մոդուլները, որոնց բացահայտման համար անհրաժեշտ է համեմատել իռացիոնալ թվերը կամ ռացիոնալ և իռացիոնալ թվերը։ Մենք գործելու ենք հետևողական. Դիտարկենք արտահայտությունը ներքին ռադիկալի տակ:
Փոխարինել սկզբնական արտահայտության մեջ:
Հարկ է նշել, որ լոգարիթմական արտահայտությունների փոխակերպմանը կարելի է հանդիպել նաև հավասարումներ և անհավասարություններ լուծելիս կամ ֆունկցիաները ուսումնասիրելիս, հետևաբար, անուղղակի ձևով դրանք կարող են լինել նաև B և C խմբերի հանձնարարություններում։
10) Ամփոփում Հարցեր.
Բազային 10 լոգարիթմը կոչվում է
հիմնական լոգարիթմ
հիմնական լոգարիթմ
բնական լոգարիթմ
տասնորդական լոգարիթմ
2) Ինչ արժեքներ կարող ենx
արտահայտության մեջ 
Արժեքը սահմանված չէ
5) Նշեք այն հարաբերակցությունը, որը ճիշտ է բոլորի համարx ≠ 0 .
6) Նշեք նոր բազայի անցնելու բանաձևի ճիշտ հարաբերակցությունը:
7) Նշեք ճիշտ հավասարությունը
11)
Վերահսկիչ փորձարկում.
Մերձդնեստրյան Պետական համալսարան
նրանց. Տ.Գ. Շևչենկո
ֆիզիկամաթեմատիկական ֆակուլտետ
Մաթեմատիկական անալիզի բաժին
և մաթեմատիկայի դասավանդման մեթոդները
ԴԱՍԸՆԹԱՑ ԱՇԽԱՏԱՆՔ
«Ինքնության փոխակերպումներ
էքսպոնենցիալ և լոգարիթմական
արտահայտությունները"
Ավարտված աշխատանք.
______ խմբի աշակերտ
ֆիզիկամաթեմատիկական ֆակուլտետ
_________________________
Ստուգված աշխատանք.
_________________________
Տիրասպոլ, 2003 թ
Ներածություն …………………………………………………………………………………… 2
Գլուխ 1
§մեկ. Փոխակերպումների հատուկ տեսակների կիրառման հմտությունների ձևավորում………………………………………………………………………………………………………………………………………………………………………………………….
§2. Գիտելիքների համակարգի կազմակերպման առանձնահատկությունները նույնական փոխակերպումների ուսումնասիրության մեջ…………………………………………..…………….
§3. Մաթեմատիկա ծրագիր …………………………………………….11
Գլուխ 2
§մեկ. Աստիճանի հասկացության ընդհանրացում…………………………………………..13
§2. Էքսպոնենցիալ ֆունկցիան…………………………………………………..15
§3. Լոգարիթմական ֆունկցիա………………………………………….16
Գլուխ 3. Էքսպոնենցիալ և լոգարիթմական արտահայտությունների նույնական փոխակերպումները պրակտիկայում ...................................... ...................................19
Եզրակացություն……………………………………………………………………………………………..
Օգտագործված գրականության ցանկ………………………………………….25
Ներածություն
Այս կուրսային աշխատանքում դիտարկվելու են էքսպոնենցիալ և լոգարիթմական ֆունկցիաների նույնական փոխակերպումները, դիտարկվելու են հանրահաշվի դպրոցական դասընթացում դրանք դասավանդելու մեթոդաբանությունը և վերլուծության սկիզբը:
Այս աշխատանքի առաջին գլուխը նկարագրում է մաթեմատիկայի դպրոցական դասընթացում նույնական փոխակերպումների ուսուցման մեթոդաբանությունը, այն նաև ներառում է մաթեմատիկայի ծրագիր «Հանրահաշիվ և վերլուծության սկիզբ» դասընթացում էքսպոնենցիալ և լոգարիթմական ֆունկցիաների ուսումնասիրությամբ:
Երկրորդ գլուխն ուղղակիորեն վերաբերում է էքսպոնենցիալ և լոգարիթմական ֆունկցիաներին, դրանց հիմնական հատկություններին, որոնք օգտագործվում են նույնական փոխակերպումների ժամանակ:
Երրորդ գլուխը օրինակների և խնդիրների լուծումն է՝ օգտագործելով էքսպոնենցիալ և լոգարիթմական ֆունկցիաների նույնական փոխակերպումները։
Դպրոցական մաթեմատիկայի դասընթացում ուսումնառության ժամանակի զգալի մասը զբաղեցնում է արտահայտությունների և բանաձևերի տարբեր փոխակերպումների ուսումնասիրությունը։ Թվաբանական գործողությունների հատկությունների վրա հիմնված ամենապարզ փոխակերպումները արդեն կատարվում են տարրական դպրոցիսկ IV-V դասարաններում. Բայց փոխակերպումներ կատարելու հմտությունների և կարողությունների ձևավորման հիմնական բեռը կրում է դպրոցական հանրահաշվի ընթացքը։ Սա կապված է ինչպես կատարված փոխակերպումների քանակի և բազմազանության կտրուկ աճի, այնպես էլ դրանց հիմնավորման և կիրառելիության պայմանների հստակեցման գործողությունների բարդության, ինքնության, նույնական փոխակերպման, համարժեք փոխակերպման ընդհանրացված հասկացությունների նույնականացման և ուսումնասիրության հետ, տրամաբանական հետևանք.
Նույնական փոխակերպումների կատարման մշակույթը զարգանում է այնպես, ինչպես հաշվողական մշակույթը՝ հիմնված օբյեկտների (թվեր, վեկտորներ, բազմանդամներ և այլն) գործողությունների հատկությունների և դրանց իրականացման ալգորիթմների ամուր իմացության վրա: Այն դրսևորվում է ոչ միայն փոխակերպումները ճիշտ հիմնավորելու ունակությամբ, այլև սկզբնական վերլուծական արտահայտությունից դեպի այն արտահայտությունը, որը լավագույնս համապատասխանում է վերափոխման նպատակին անցում կատարելու ամենակարճ ճանապարհը գտնելու ունակությամբ, փոփոխությունները հետևելու ունակությամբ: վերլուծական արտահայտությունների սահմանման տիրույթը նույնական փոխակերպումների շղթայում, փոխակերպումների արագության և սխալ կատարման մեջ:
Հաշվարկների բարձր մշակույթի և նույնական փոխակերպումների ապահովումը մաթեմատիկայի դասավանդման կարևոր խնդիր է: Սակայն այս խնդիրը դեռ հեռու է բավարար լուծում ստանալուց։ Դրա վառ ապացույցն են հանրակրթական մարմինների վիճակագրական տվյալները, որոնցում ամեն տարի նշվում են ուսանողների կողմից կատարված հաշվարկների ու փոխակերպումների սխալներն ու իռացիոնալ մեթոդները։ տարբեր դասերկատարելիս հսկիչ աշխատանքներ. Դա հաստատում են բարձրագույնների կարծիքները ուսումնական հաստատություններդիմորդների մաթեմատիկական գիտելիքների և հմտությունների որակի մասին։ Չի կարելի չհամաձայնել հանրակրթական մարմինների և բուհերի եզրակացությունների հետ, որ դա բավարար չէ բարձր մակարդակհաշվողական մշակույթ և նույնական փոխակերպումներ ավագ դպրոցուսանողների գիտելիքների ֆորմալիզմի, տեսության պրակտիկայի տարանջատման հետևանք է։
Ինքնության փոխակերպումներ և ուսուցման մեթոդներ
հանրահաշվի դպրոցական դասընթացում և վերլուծության սկզբում։
§մեկ. Կիրառական հմտությունների ձևավորում
փոխակերպումների հատուկ տեսակներ.
Փոխակերպումների իրականացման մեթոդների և կանոնների համակարգը, որն օգտագործվում է հանրահաշվի սկզբի փուլում, ունի կիրառությունների շատ լայն շրջանակ. այն օգտագործվում է մաթեմատիկայի ողջ դասընթացի ուսումնասիրության մեջ։ Այնուամենայնիվ, հենց իր ցածր յուրահատկության պատճառով այս համակարգը կարիք ունի լրացուցիչ փոխակերպումների, որոնք հաշվի են առնում վերափոխված արտահայտությունների կառուցվածքի առանձնահատկությունները և նոր ներդրված գործողությունների և գործառույթների հատկությունները: Փոխակերպումների համապատասխան տեսակների մշակումը սկսվում է կրճատված բազմապատկման բանաձևերի ներդրմամբ։ Այնուհետև մենք դիտարկում ենք փոխակերպումները, որոնք կապված են հզորության գործողության հետ, տարբեր դասերի հետ տարրական գործառույթներ- էքսպոնենցիալ, հզորություն, լոգարիթմական, եռանկյունաչափական: Այս տեսակի փոխակերպումներից յուրաքանչյուրն անցնում է ուսումնասիրության մի փուլ, որտեղ ուշադրությունը կենտրոնացված է նրանց բնորոշ հատկանիշների յուրացման վրա։
Նյութի կուտակմամբ հնարավոր է դառնում առանձնացնել դիտարկվող բոլոր փոխակերպումների ընդհանուր հատկանիշները և դրա հիման վրա ներմուծել նույնական և համարժեք փոխակերպումների հասկացությունները։
Հարկ է նշել, որ նույնական փոխակերպման հասկացությունը հանրահաշվի դպրոցական դասընթացում տրված է ոչ թե լրիվ ընդհանրությամբ, այլ միայն արտահայտությունների կիրառման մեջ։ Փոխակերպումները բաժանվում են երկու դասի՝ նույնական փոխակերպումները արտահայտությունների փոխակերպումներ են, իսկ համարժեք փոխակերպումները՝ բանաձևերի փոխակերպումներ։ Այն դեպքում, երբ բանաձևի մի մասը պարզեցնելու անհրաժեշտություն կա, այս բանաձևում ընդգծվում է արտահայտություն, որը ծառայում է որպես կիրառական նույնական փոխակերպման փաստարկ։ Համապատասխան պրեդիկատը համարվում է անփոփոխ։
Ինչ վերաբերում է փոխակերպումների (սինթեզի) ինտեգրալ համակարգի կազմակերպմանը, ապա դրա հիմնական նպատակն է ձևավորել ճկուն և հզոր; ապարատ, որը հարմար է տարբեր կրթական խնդիրներ լուծելու համար:
Հանրահաշվի ընթացքում և վերլուծության սկզբում աստիճանաբար շարունակում է կատարելագործվել իր հիմնական հատկանիշներով արդեն ձևավորված փոխակերպումների ինտեգրալ համակարգը։ Դրան ավելանում են նաև փոխակերպումների որոշ նոր տեսակներ, որոնք միայն հարստացնում են, ընդլայնում են նրա հնարավորությունները, բայց չեն փոխում կառուցվածքը։ Այս նոր փոխակերպումների ուսումնասիրման մեթոդաբանությունը գործնականում չի տարբերվում հանրահաշվի ընթացքում կիրառվող մեթոդաբանությունից։
§2. Առաջադրանքի համակարգի կազմակերպման առանձնահատկությունները
նույնական փոխակերպումների ուսումնասիրության մեջ։
Առաջադրանքների ցանկացած համակարգի կազմակերպման հիմնական սկզբունքը դրանք պարզից բարդ ներկայացնելն է՝ հաշվի առնելով ուսանողների համար հնարավոր դժվարությունները հաղթահարելու և ստեղծելու անհրաժեշտությունը. խնդրահարույց իրավիճակներ. Նշված հիմնական սկզբունքը պահանջում է կոնկրետացում այս ուսումնական նյութի առանձնահատկությունների հետ կապված: Մաթեմատիկայի մեթոդաբանության մեջ առաջադրանքների տարբեր համակարգեր նկարագրելու համար օգտագործվում է վարժությունների ցիկլի հայեցակարգը: Զորավարժությունների ցիկլը բնութագրվում է ուսումնասիրության մի քանի ասպեկտների և նյութի դասավորության մեթոդների վարժությունների հաջորդականության մեջ: Նույնական փոխակերպումների առնչությամբ ցիկլի գաղափարը կարող է տրվել հետևյալ կերպ.
Վարժությունների ցիկլը կապված է մեկ ինքնության ուսումնասիրության հետ, որի շուրջ խմբավորվում են այլ ինքնություններ, որոնք բնական կապի մեջ են դրա հետ։ Ցիկլի կազմը, կատարողական առաջադրանքների հետ մեկտեղ, ներառում է առաջադրանքներ, որոնք պահանջում են դիտարկվող ինքնության կիրառելիության ճանաչում: Ուսումնասիրվող ինքնությունը օգտագործվում է տարբեր թվային տիրույթների վրա հաշվարկներ կատարելու համար: Ինքնության առանձնահատկությունը հաշվի է առնվում. մասնավորապես կազմակերպվում են դրա հետ կապված խոսքի շրջադարձեր։
Յուրաքանչյուր ցիկլի առաջադրանքները բաժանված են երկու խմբի. Առաջինը ներառում է ինքնության հետ նախնական ծանոթության ընթացքում կատարվող առաջադրանքներ։ Ծառայում են ուսումնական նյութմի քանի անընդմեջ դասերի համար՝ միավորված մեկ թեմայով. Վարժությունների երկրորդ խումբը կապում է ուսումնասիրվող ինքնությունը տարբեր կիրառությունների հետ: Այս խումբը կոմպոզիցիոն միասնություն չի կազմում. այստեղ վարժությունները ցրված են տարբեր թեմաներով։
Ցիկլի նկարագրված կառուցվածքը վերաբերում է փոխակերպումների կոնկրետ տեսակների կիրառման հմտությունների ձևավորման փուլին։ Վերջնական փուլում՝ սինթեզի փուլում, ցիկլերը փոփոխվում են։ Նախ՝ առաջադրանքների երկու խմբերն էլ համակցվում են՝ ձևավորելով «բացված» ցիկլ, իսկ ամենապարզները՝ ձևակերպման կամ առաջադրանքի բարդության առումով, դուրս են մնում առաջին խմբից։ Մնացած առաջադրանքների տեսակները դառնում են ավելի բարդ: Երկրորդ, տեղի է ունենում տարբեր ինքնությունների հետ կապված ցիկլերի միաձուլում, որի պատճառով մեծանում է այս կամ այն ինքնության կիրառելիությունը ճանաչելու գործողությունների դերը:
Մենք նշում ենք տարրական գործառույթների նույնականացման հետ կապված առաջադրանքների ցիկլերի առանձնահատկությունները: Այս հատկանիշները պայմանավորված են նրանով, որ նախ՝ համապատասխան նույնականությունները ուսումնասիրվում են ֆունկցիոնալ նյութի ուսումնասիրության հետ կապված, և երկրորդ՝ դրանք ի հայտ են գալիս ավելի ուշ, քան առաջին խմբի ինքնությունները և ուսումնասիրվում են՝ օգտագործելով արդեն իսկ ձևավորված հմտությունները՝ նույնական փոխակերպումներ իրականացնելու համար։ .
Յուրաքանչյուր նոր ներդրված տարրական ֆունկցիա կտրուկ ընդլայնում է թվերի շրջանակը, որոնք կարող են նշանակվել և անվանվել առանձին: Հետևաբար, ցիկլերի առաջադրանքների առաջին խումբը պետք է ներառի առաջադրանքներ՝ կապ հաստատելու այս նոր թվային շրջանների և ռացիոնալ թվերի սկզբնական շրջանի միջև: Մենք տալիս ենք նման առաջադրանքների օրինակներ:
Օրինակ 1 Հաշվարկել.
Յուրաքանչյուր արտահայտության կողքին կա ինքնություն, այն ցիկլերում, որոնց համար առաջարկվող առաջադրանքները կարող են ներկա լինել: Նման առաջադրանքների նպատակն է տիրապետել գրառումների առանձնահատկություններին, ներառյալ նոր գործողությունների և գործառույթների խորհրդանիշները և զարգացնել մաթեմատիկական խոսքի հմտությունները:
Տարրական ֆունկցիաների հետ կապված ինքնության փոխակերպումների օգտագործման զգալի մասը բաժին է ընկնում իռացիոնալ և տրանսցենդենտալ հավասարումների լուծմանը։ Ինքնությունների յուրացման հետ կապված ցիկլերը ներառում են միայն ամենապարզ հավասարումները, բայց արդեն այստեղ նպատակահարմար է աշխատանքներ տանել նման հավասարումների լուծման մեթոդի յուրացման ուղղությամբ՝ նվազեցնելով այն՝ անհայտը հանրահաշվական հավասարման փոխարինելով:
Այս լուծման համար քայլերի հաջորդականությունը հետևյալն է.
ա) գտնել մի ֆունկցիա, որի համար այս հավասարումը կարող է ներկայացվել որպես.
բ) կատարել փոխարինում և լուծել հավասարումը.
գ) լուծել յուրաքանչյուր հավասարում, որտեղ է հավասարման արմատների բազմությունը:
Նկարագրված մեթոդի կիրառման ժամանակ քայլ բ) հաճախ կատարվում է անուղղակիորեն՝ առանց նոտագրման: Բացի այդ, ուսանողները հաճախ ընտրում են պատասխան գտնելու տանող տարբեր ուղիներից ընտրել այն, որն ավելի արագ և հեշտ է տանում դեպի հանրահաշվական հավասարումը:
Օրինակ 2. Լուծե՛ք հավասարումը.
Առաջին ճանապարհը.
Երկրորդ ճանապարհը.
ա) 
բ) 
Այստեղ երևում է, որ ա) քայլն ավելի դժվար է առաջին մեթոդով, քան երկրորդում։ Առաջին ճանապարհը «ավելի դժվար է սկսել», թեև լուծման հետագա ընթացքը շատ ավելի հեշտ է։ Մյուս կողմից, երկրորդ մեթոդն ունի առավելություններ, որոնք բաղկացած են հանրահաշվական հավասարման ուսուցման ավելի մեծ հեշտությունից, ավելի բարդությունից:
Հանրահաշվի դպրոցական դասընթացի համար բնորոշ են առաջադրանքները, որոնցում հանրահաշվական հավասարման անցումը նույնիսկ ավելի հեշտ է, քան այս օրինակում: Նման առաջադրանքների հիմնական բեռը վերաբերում է գ) քայլի ընտրությանը որպես լուծման գործընթացի անկախ մաս, որը կապված է ուսումնասիրվող տարրական ֆունկցիայի հատկությունների օգտագործման հետ:
Օրինակ 3. Լուծե՛ք հավասարումը.
ա) 
; բ) 
.
Այս հավասարումները կրճատվում են հավասարումների՝ ա) կամ ; բ) կամ. Այս հավասարումները լուծելու համար պահանջվում է էքսպոնենցիալ ֆունկցիայի մասին միայն պարզագույն փաստերի իմացություն՝ միապաղաղություն, արժեքների տիրույթ։ Ինչպես նախորդ օրինակը, ա) և բ) հավասարումները կարող են վերագրվել քառակուսի էքսպոնենցիալ հավասարումների լուծման վարժությունների ցիկլի առաջին խմբին։
Այսպիսով, մենք գալիս ենք առաջադրանքների դասակարգմանը ցիկլերում, որոնք կապված են տրանսցենդենտալ հավասարումների լուծման հետ, ներառյալ էքսպոնենցիալ ֆունկցիան.
1) հավասարումներ, որոնք վերածվում են ձևի հավասարումների և ունեն պարզ պատասխան, ձևով ընդհանուր.
2) հավասարումներ, որոնք վերածվում են հավասարումների, որտեղ ամբողջ թիվ է, կամ որտեղ;
3) հավասարումներ, որոնք վերածվում են հավասարումների և պահանջում են թվի գրված ձևի հստակ վերլուծություն:
Նմանատիպ առաջադրանքները կարող են դասակարգվել այլ տարրական գործառույթների համար:
Հանրահաշվի և հանրահաշվի դասընթացներում ուսումնասիրված ինքնությունների զգալի մասը և վերլուծության սկիզբը դրանցում ապացուցված կամ գոնե բացատրված է։ Ինքնությունների ուսումնասիրության այս կողմն ունի մեծ նշանակություներկու դասընթացի համար էլ, քանի որ դրանցում ցուցադրական հիմնավորումն իրականացվում է առավելագույն հստակությամբ և խստությամբ հենց ինքնությունների հետ կապված: Այս նյութից դուրս ապացույցները սովորաբար պակաս ամբողջական են, միշտ չէ, որ տարբերվում են կիրառվող հիմնավորման միջոցների կազմից։
Թվաբանական գործողությունների հատկությունները օգտագործվում են որպես հենարան, որի վրա կառուցվում են ինքնության ապացույցները։
Հաշվարկների և նույնական վերափոխումների կրթական ազդեցությունը կարող է ուղղվել զարգացմանը տրամաբանական մտածողություն, եթե միայն ուսանողներից համակարգված պահանջվի հիմնավորել հաշվարկները և նույնական փոխակերպումները, զարգացնել ֆունկցիոնալ մտածողությունը, որը ձեռք է բերվում տարբեր ձևերով։ Հաշվարկների և նույնական փոխակերպումների կարևորությունը կամքի, հիշողության, հնարամտության, ինքնատիրապետման, ստեղծագործական նախաձեռնության զարգացման գործում միանգամայն ակնհայտ է։
Առօրյա, արդյունաբերական հաշվողական պրակտիկայի պահանջները պահանջում են ուսանողների մոտ ռացիոնալ հաշվարկների և նույնական փոխակերպումների ուժեղ, ավտոմատացված հմտությունների ձևավորում: Այս հմտությունները զարգանում են ցանկացած հաշվողական աշխատանքի ընթացքում, սակայն անհրաժեշտ են հատուկ հմտություններ: վերապատրաստման վարժություններարագ հաշվարկների և փոխակերպումների մեջ։
Այսպիսով, եթե դասը ներառում է լոգարիթմական հավասարումների լուծում՝ օգտագործելով հիմնական լոգարիթմական ինքնությունը, ապա օգտակար է դասի պլանում ներառել բանավոր վարժություններ՝ արտահայտությունների արժեքները պարզեցնելու կամ հաշվարկելու համար. 
. Զորավարժությունների նպատակը միշտ հաղորդվում է ուսանողներին: Վարժության ընթացքում կարող է անհրաժեշտ լինել ուսանողներից պահանջել հիմնավորել անհատական վերափոխումները, գործողությունները կամ լուծել ամբողջ խնդիրը, նույնիսկ եթե դա նախատեսված չէր: Այնտեղ, որտեղ հնարավոր են խնդրի լուծման տարբեր ուղիներ, միշտ ցանկալի է հարցեր տալ՝ «Ի՞նչ ճանապարհով է լուծվել խնդիրը», «Ո՞վ է այլ կերպ լուծել խնդիրը»:
Ինքնության և նույնական փոխակերպման հասկացությունները, դրանք հստակորեն ներդրված են հանրահաշվի VI դասի դասընթացում: Նույնական արտահայտությունների սահմանումը գործնականում չի կարող օգտագործվել երկու արտահայտությունների նույնությունն ապացուցելու և հասկանալու համար, որ նույնական փոխակերպումների էությունը կայանում է նրանում, որ արտահայտությունը կիրառելու է այն գործողությունների սահմանումները և հատկությունները, որոնք նշված են արտահայտության մեջ, կամ ավելացնելով. նրան մի արտահայտություն, որը նույնականորեն հավասար է 0-ի, կամ այն բազմապատկելիս նույնականորեն հավասար արտահայտությամբ մեկին: Բայց, նույնիսկ յուրացնելով այս դրույթները, ուսանողները հաճախ չեն հասկանում, թե ինչու են այս փոխակերպումները թույլ տալիս մեզ պնդել, որ սկզբնական և ստացված արտահայտությունները նույնական են, այսինքն. Վերցրեք նույն արժեքները փոփոխական արժեքների ցանկացած համակարգի (կոմպլեկտների) համար:
Կարևոր է նաև ապահովել, որ ուսանողները լավ հասկանան, որ նույնական փոխակերպումների նման եզրակացությունները համապատասխան գործողությունների սահմանումների և հատկությունների հետևանք են:
Նախորդ տարիներին կուտակված նույնական կերպարանափոխությունների ապարատը ընդլայնվում է 6-րդ դասարանում։ Այս ընդլայնումը սկսվում է նույնականության ներմուծմամբ, որն արտահայտում է նույն հիմքերով հզորությունների արտադրյալի հատկությունը. , որտեղ , ամբողջ թվեր են։
§3. Մաթեմատիկայի ծրագիր. «Հանրահաշիվը և վերլուծության սկիզբը» դպրոցական դասընթացում ուսանողները համակարգված ուսումնասիրում են էքսպոնենցիալ և լոգարիթմական ֆունկցիաները և դրանց հատկությունները, լոգարիթմական և էքսպոնենցիալ արտահայտությունների նույնական փոխակերպումները և դրանց կիրառումը համապատասխան հավասարումների և անհավասարությունների լուծման համար, ծանոթանում են հիմնական հասկացություններին, պնդումներին: . 11-րդ դասարանում հանրահաշվի դասաժամերը շաբաթական 3 ժամ են՝ ընդհանուր տարեկան 102 ժամ: Ըստ ծրագրի էքսպոնենցիալ, լոգարիթմական և ուժային ֆունկցիաները ուսումնասիրելու համար պահանջվում է 36 ժամ։ Ծրագիրը ներառում է հետևյալ հարցերի քննարկում և ուսումնասիրություն. Իռացիոնալ հավասարումների լուծում. Էքսպոնենցիալ ֆունկցիա, նրա հատկությունները և գրաֆիկը: էքսպոնենցիալ արտահայտությունների նույնական փոխակերպումներ։ Էքսպոնենցիալ հավասարումների և անհավասարությունների լուծում. Թվի լոգարիթմ. Լոգարիթմների հիմնական հատկությունները. Լոգարիթմական ֆունկցիան, դրա հատկությունները և գրաֆիկը: Լոգարիթմական հավասարումների և անհավասարությունների լուծում. Էքսպոնենցիալ ֆունկցիայի ածանցյալ։ Թիվ և բնական լոգարիթմ. Հզորության ֆունկցիայի ածանցյալ: Էքսպոնենցիալ և լոգարիթմական ֆունկցիաների ուսումնասիրության բաժնի հիմնական նպատակն է ուսանողներին ծանոթացնել էքսպոնենցիալ, լոգարիթմական և ուժային ֆունկցիաներին. սովորեցնել ուսանողներին լուծել էքսպոնենցիալ և լոգարիթմական հավասարումներև անհավասարություններ։ Երրորդ աստիճանի արմատ և ռացիոնալ ցուցիչով աստիճան հասկացությունները քառակուսի արմատ և աստիճան ամբողջ թվով ցուցիչով հասկացությունների ընդհանրացումն են։ Ուսանողները պետք է ուշադրություն դարձնեն այն փաստին, որ այստեղ դիտարկված ռացիոնալ ցուցիչով արմատների և աստիճանների հատկությունները նման են այն հատկություններին, որոնք ուսումնասիրվել են ավելի վաղ: քառակուսի արմատներև աստիճաններ՝ ամբողջ թվերի ցուցիչներով: Անհրաժեշտ է բավարար ժամանակ հատկացնել աստիճանների հատկությունների մշակմանը և նույնական փոխակերպումների հմտությունների ձևավորմանը: Գիտական աստիճանի հասկացությունը հետ իռացիոնալ ցուցանիշներկայացվել է տեսողական-ինտուիտիվ հիմունքներով: Այս նյութը կատարում է օժանդակ դեր և օգտագործվում է էքսպոնենցիալ ֆունկցիան ներմուծելիս։ Էքսպոնենցիալ, լոգարիթմական և ուժային ֆունկցիաների հատկությունների ուսումնասիրությունը կառուցված է ընդունված համաձայն. ընդհանուր սխեմանֆունկցիայի հետազոտություն։ Այս դեպքում, կախված պարամետրերի արժեքներից, տրվում է հատկությունների ակնարկ: Էքսպոնենցիալ և լոգարիթմական անհավասարությունները լուծվում են ֆունկցիաների ուսումնասիրված հատկությունների հիման վրա։ Դասընթացի բնորոշ առանձնահատկությունն ուսանողների գիտելիքների համակարգումն ու ընդհանրացումն է, հանրահաշվի ընթացքում ձեռք բերված հմտությունների և կարողությունների համախմբումն ու զարգացումը, որն իրականացվում է ինչպես նոր նյութ ուսումնասիրելիս, այնպես էլ ընդհանրացնող կրկնություն կատարելիս:
Գլուխ 2
§մեկ. աստիճան հասկացության ընդհանրացում.
Սահմանում. Մաքուրի րդ աստիճանի արմատը այնպիսի թիվ է, որի 3-րդ աստիճանը հավասար է։
Համաձայն այս սահմանման՝ թվի րդ աստիճանի արմատը հավասարման լուծում է։ Այս հավասարման արմատների թիվը կախված է և. Դիտարկենք մի ֆունկցիա. Ինչպես հայտնի է, միջակայքում այս ֆունկցիան մեծանում է ցանկացածի համար և վերցնում է բոլոր արժեքները միջակայքից: Արմատային թեորեմով ցանկացածի համար հավասարումը ունի ոչ բացասական արմատ, ընդ որում՝ միայն մեկը։ Այն կոչվում է թվի րդ աստիճանի թվաբանական արմատ և նշանակում. թիվը կոչվում է արմատի ինդեքս, իսկ ինքնին թիվը՝ արմատական արտահայտություն։ Նշանը կոչվում է նաև ռադիկալ:
Սահմանում. Թվի րդ աստիճանի թվաբանական արմատը ոչ բացասական թիվ է, որի րդ աստիճանը .
Նույնիսկ համար ֆունկցիան հավասար է: Հետևում է , որ եթե , ապա հավասարումը , բացի արմատից , ունի նաև արմատ : Եթե , ապա կա միայն մեկ արմատ. եթե , ապա այս հավասարումն արմատներ չունի, քանի որ ցանկացած թվի զույգ ուժը ոչ բացասական է:
Կենտ արժեքների դեպքում ֆունկցիան մեծանում է ամբողջ թվային գծի երկայնքով. նրա միջակայքը բոլոր իրական թվերի բազմությունն է: Կիրառելով արմատի թեորեմը, մենք գտնում ենք, որ հավասարումը ունի մեկ արմատ ցանկացած և, մասնավորապես, համար . Ցանկացած արժեքի այս արմատը նշվում է .
Կենտ աստիճանի արմատների համար հավասարությունը ճշմարիտ է: Իրոք, , այսինքն. թիվը -ի րդ արմատն է։ Բայց տարօրինակի նման արմատը եզակի է: Հետևաբար, .
Դիտողություն 1. Ցանկացած իրականի համար
Հիշեք րդ աստիճանի թվաբանական արմատների հայտնի հատկությունները:
Ցանկացած բնական, ամբողջ և ցանկացած ոչ բացասական ամբողջ թվերի և հավասարումների համար ճշմարիտ են.
1. 
2. 
3. 
4. 
Աստիճան ռացիոնալ ցուցիչով:
Արտահայտությունը սահմանվում է բոլորի և , բացառությամբ այն դեպքի, երբ . Հիշեք նման ուժերի հատկությունները:
Ցանկացած թվերի և ցանկացած ամբողջ թվերի և հավասարումների համար ճշմարիտ են.
Մենք նաև նշում ենք, որ եթե, ապա հանուն և .. և
Պետական միասնական քննության համար սովորող ուսանողների համար Յակուտսկի թիվ 26 միջնակարգ դպրոցի մաթեմատիկայի ուսուցիչներն օգտագործում են դպրոցական մաթեմատիկայի դասընթացի բովանդակային հարցերի ցանկը (կոդավորիչ), որոնց յուրացումը ստուգվում է 2007 թվականին միասնական պետական քննություն հանձնելիս։ . ընտրովի դասընթացՄիասնությանը նախապատրաստվելիս Պետական քննությունհիմնված է ավելի վաղ ձեռք բերված գիտելիքների կրկնության, համակարգման և խորացման վրա: Դասընթացներն անցկացվում են անվճար...
Թվարկված հավասարությունները լոգարիթմներով արտահայտությունները փոխակերպելիս օգտագործվում են ինչպես աջից ձախ, այնպես էլ ձախից աջ։
Հարկ է նշել, որ անհրաժեշտ չէ անգիր անել հատկությունների հետևանքները. փոխակերպումներ կատարելիս կարող եք յոլա գնալ լոգարիթմների հիմնական հատկություններից և այլ փաստերից (օրինակ՝ b≥0-ի համար), որոնցից համապատասխան. հետևանքները. Այս մոտեցման «կողմնակի ազդեցությունը» միայն այն է, որ լուծումը մի փոքր ավելի երկար կլինի։ Օրինակ՝ առանց հետևանքի անելու համար, որն արտահայտվում է բանաձևով 
և ելնելով միայն լոգարիթմների հիմնական հատկություններից, դուք պետք է կատարեք հետևյալ ձևի փոխակերպումների շղթա. 
.
Նույնը կարելի է ասել վերը նշված ցանկից վերջին հատկության մասին, որը համապատասխանում է բանաձևին 
, քանի որ դա բխում է նաև լոգարիթմների հիմնական հատկություններից։ Հիմնական բանը հասկանալն այն է, որ ցուցիչում լոգարիթմ ունեցող դրական թվի աստիճանը միշտ էլ հնարավոր է փոխել աստիճանի հիմքը և թիվը լոգարիթմի նշանի տակ: Արդարության համար մենք նշում ենք, որ նման փոխակերպումների իրականացման օրինակները գործնականում հազվադեպ են: Ստորև մենք կտանք մի քանի օրինակ:
Թվային արտահայտությունների փոխակերպում լոգարիթմներով
Մենք հիշեցինք լոգարիթմների հատկությունները, այժմ ժամանակն է սովորել, թե ինչպես դրանք կիրառել գործնականում արտահայտությունները փոխակերպելու համար: Բնական է սկսել թվային արտահայտությունների, այլ ոչ թե փոփոխականներով արտահայտությունների փոխակերպումից, քանի որ դրանց վրա հիմունքները սովորելը ավելի հարմար և հեշտ է: Այսպիսով, մենք կանենք, և մենք կսկսենք շատից պարզ օրինակներսովորել, թե ինչպես ընտրել լոգարիթմի ցանկալի հատկությունը, բայց մենք աստիճանաբար կբարդացնենք օրինակները, մինչև այն պահը, երբ վերջնական արդյունք ստանալու համար անհրաժեշտ կլինի անընդմեջ կիրառել մի քանի հատկություններ:
Ընտրելով լոգարիթմների ցանկալի հատկությունը
Լոգարիթմների հատկությունները այնքան էլ քիչ չեն, և պարզ է, որ պետք է կարողանալ դրանցից ընտրել համապատասխանը, ինչը կոնկրետ դեպքում կբերի ցանկալի արդյունքի։ Սովորաբար դա դժվար չէ անել՝ համեմատելով փոխարկվող լոգարիթմի կամ արտահայտության ձևը լոգարիթմների հատկություններն արտահայտող բանաձևերի ձախ և աջ մասերի տեսակների հետ։ Եթե մնացել է կամ աջ մասԲանաձևերից մեկը համընկնում է տվյալ լոգարիթմի կամ արտահայտության հետ, ապա, ամենայն հավանականությամբ, հենց այս հատկությունն է, որ պետք է օգտագործվի փոխակերպման ժամանակ։ Հետևյալ օրինակները հստակորեն ցույց են տալիս դա։
Սկսենք արտահայտությունների փոխակերպման օրինակներից՝ օգտագործելով լոգարիթմի սահմանումը, որը համապատասխանում է a log a b =b , a>0, a≠1, b>0 բանաձևին:
Օրինակ.
Հաշվեք, եթե հնարավոր է. ա) 5 լոգ 5 4 , բ) 10 լոգ (1+2 π) , գ) 
, դ) 2 log 2 (−7) , e) .
Լուծում.
Օրինակում a) տառը հստակ ցույց է տալիս a log a b կառուցվածքը, որտեղ a=5, b=4: Այս թվերը բավարարում են a>0, a≠1, b>0 պայմանները, այնպես որ կարող եք ապահով կերպով օգտագործել a log a b =b հավասարությունը: Մենք ունենք 5 լոգ 5 4=4:
բ) Այստեղ a=10 , b=1+2 π , a>0 , a≠1 , b>0 պայմանները կատարվում են: Այս դեպքում տեղի է ունենում 10 lg(1+2 π) =1+2 π հավասարությունը։
գ) Եվ այս օրինակում մենք գործ ունենք a log a b ձևի աստիճանի հետ, որտեղ և b=ln15: Այսպիսով 
.
Չնայած a log a b ձևին պատկանելուն (այստեղ a=2, b=−7), d տառի տակ արտահայտությունը չի կարող փոխարկվել a log a b =b բանաձևով։ Պատճառն այն է, որ դա իմաստ չունի, քանի որ այն պարունակում է բացասական թիվ լոգարիթմի նշանի տակ։ Ավելին, b=−7 թիվը չի բավարարում b>0 պայմանին, ինչը անհնարին է դարձնում a log a b =b բանաձևին դիմելը, քանի որ այն պահանջում է a>0, a≠1, b>0 պայմանները։ Այսպիսով, մենք չենք կարող խոսել 2 log 2 (−7) արժեքի հաշվարկման մասին: Այս դեպքում 2 log 2 (−7) = −7 գրելը սխալ կլինի։
Նմանապես, ե) տառի տակ գտնվող օրինակում հնարավոր չէ ձևի լուծում տալ 
, քանի որ բնօրինակ արտահայտությունը իմաստ չունի։
Պատասխան.
ա) 5 լոգ 5 4 =4 , բ) 10 լոգ (1+2 π) =1+2 π , գ) , դ), ե) արտահայտությունները իմաստ չունեն։
Հաճախ օգտակար է փոխակերպվել դրական թիվներկայացվում է որպես որոշ դրական և ոչ մեկ թվի ուժ՝ ցուցիչում լոգարիթմով: Այն հիմնված է a log a b =b, a>0, a≠1, b>0 լոգարիթմի նույն սահմանման վրա, սակայն բանաձևը կիրառվում է աջից ձախ, այսինքն՝ b=a log a b ձևով: Օրինակ՝ 3=e ln3 կամ 5=5 log 5 5:
Եկեք անցնենք արտահայտությունների փոխակերպման համար լոգարիթմների հատկությունների օգտագործմանը:
Օրինակ.
Գտե՛ք արտահայտության արժեքը՝ ա) log −2 1, բ) log 1 1, գ) log 0 1, դ) log 7 1, ե) ln1, զ) lg1, է) log 3,75 1, ը) log 5։ π 7 1 .
Լուծում.
ա), բ) և գ տառերի տակ գտնվող օրինակներում բերված են log −2 1, log 1 1, log 0 1 արտահայտությունները, որոնք իմաստ չունեն, քանի որ լոգարիթմի հիմքը չպետք է բացասական թիվ պարունակի։ , զրո կամ մեկ, քանի որ մենք լոգարիթմ ենք սահմանել միայն դրական և ոչ միավոր հիմքի համար։ Ուստի ա) - գ) օրինակներում խոսք չի կարող լինել արտահայտության արժեքը գտնելու մասին։
Բոլոր մյուս առաջադրանքներում, ակնհայտ է, որ լոգարիթմների հիմքերը պարունակում են համապատասխանաբար դրական և ոչ միավոր թվեր, համապատասխանաբար, 7, e, 10, 3.75 և 5 π 7, և միավորներն ամենուր գտնվում են լոգարիթմների նշանների ներքո: Եվ մենք գիտենք միասնության լոգարիթմի հատկությունը՝ log a 1=0 ցանկացած a>0 , a≠1 : Այսպիսով, b) - f) արտահայտությունների արժեքները հավասար են զրոյի:
Պատասխան.
ա), բ), գ) արտահայտությունները իմաստ չունեն, դ) log 7 1=0, ե) ln1=0, զ) log1=0, է) log 3.75 1=0, ը) log 5 e 7 1 =0.
Օրինակ.
Հաշվեք՝ ա) , բ) lne , գ) lg10 , դ) log 5 π 3 −2 (5 π 3 −2), ե) log −3 (−3) , f) log 1 1 .
Լուծում.
Հասկանալի է, որ մենք պետք է օգտագործենք հիմքի լոգարիթմի հատկությունը, որը համապատասխանում է log a a=1 բանաձևին a>0, a≠1-ի համար: Իրոք, բոլոր տառերի տակ առաջադրանքներում լոգարիթմի նշանի տակ թիվը համընկնում է դրա հիմքի հետ: Այսպիսով, ուզում եմ անմիջապես ասել, որ տրված արտահայտություններից յուրաքանչյուրի արժեքը 1 է։ Այնուամենայնիվ, մի շտապեք եզրակացություններ անել. ա) - դ) տառերի տակ առաջադրանքներում արտահայտությունների արժեքները իսկապես հավասար են մեկին, իսկ առաջադրանքներում e) և զ) բնօրինակ արտահայտությունները իմաստ չունեն, ուստի դա չի կարող. ասենք, որ այս արտահայտությունների արժեքները հավասար են 1-ի:
Պատասխան.
ա) , բ) lne=1, գ) lg10=1, դ) log 5 π 3 −2 (5 π 3 −2)=1, ե), զ) արտահայտությունները իմաստ չունեն։
Օրինակ.
Գտե՛ք արժեքը՝ ա) log 3 3 11 , բ) 
, գ) , դ) լոգ −10 (−10) 6.
Լուծում.
Ակնհայտ է, որ լոգարիթմների նշանների տակ գտնվում են հիմքի որոշ աստիճաններ: Ելնելով դրանից՝ մենք հասկանում ենք, որ հիմքի աստիճանի հատկությունն այստեղ օգտակար է. log a a p =p, որտեղ a>0, a≠1 և p ցանկացած իրական թիվ է: Հաշվի առնելով դա՝ մենք ունենք հետևյալ արդյունքները՝ ա) log 3 3 11 =11 , բ) 
, մեջ) 
. Հնարավո՞ր է օրինակի համար նմանատիպ հավասարություն գրել log −10 (−10) 6 =6 ձևի դ) տառի տակ։ Ոչ, դուք չեք կարող, քանի որ log −10 (−10) 6-ն իմաստ չունի:
Պատասխան.
ա) մատյան 3 3 11 = 11, բ) , մեջ) դ) արտահայտությունը իմաստ չունի.
Օրինակ.
Արտահայտությունն արտահայտեք նույն հիմքում լոգարիթմների գումարի կամ տարբերության տեսքով. ա) 
, բ) , գ) լոգ((−5) (−12)) .
Լուծում.
ա) Արտադրյալը գտնվում է լոգարիթմի նշանի տակ, և մենք գիտենք արտադրյալի լոգարիթմի հատկությունը log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y> 0 . Մեր դեպքում լոգարիթմի հիմքում թվերը և արտադրյալի թվերը դրական են, այսինքն՝ բավարարում են ընտրված հատկության պայմանները, հետևաբար, մենք կարող ենք ապահով կիրառել այն. 
.
բ) Այստեղ մենք օգտագործում ենք քանորդի լոգարիթմի հատկությունը, որտեղ a>0, a≠1, x>0, y>0: Մեր դեպքում լոգարիթմի հիմքը դրական e թիվ է, π համարիչը և հայտարարը դրական են, ինչը նշանակում է, որ դրանք բավարարում են հատկության պայմաններին, ուստի մենք իրավունք ունենք օգտագործել ընտրված բանաձևը. 
.
գ) Նախ նշենք, որ lg((−5) (−12)) արտահայտությունը իմաստ ունի։ Բայց միևնույն ժամանակ մենք իրավունք չունենք լոգարիթմի լոգարիթմի բանաձևը կիրառելու a (x y)=log a x+log a y, a>0, a≠1, x>0, y>0. , քանի որ −5 և −12 թվերը բացասական են և չեն բավարարում x>0 , y>0 պայմանները։ Այսինքն, անհնար է իրականացնել նման վերափոխում. log((−5)(−12))=log(−5)+log(−12). Բայց ի՞նչ անել։ Նման դեպքերում բնօրինակ արտահայտությունը պետք է նախապես փոխակերպվի բացասական թվերից խուսափելու համար: հետ արտահայտությունների փոխակերպման նմանատիպ դեպքերի մասին բացասական թվերլոգարիթմի նշանի տակ մենք մանրամասն կխոսենք մեկում, բայց առայժմ լուծում կտանք այս օրինակին, որը նախապես պարզ է և առանց բացատրության. lg((-5)(-12))=lg(5 12)=lg5+lg12.
Պատասխան.
ա) , բ) , գ) lg((−5) (−12))=lg5+lg12.
Օրինակ.
Պարզեցրե՛ք արտահայտությունը՝ ա) log 3 0,25 + log 3 16 + log 3 0,5, բ) .
Լուծում.
Այստեղ մեզ կօգնեն արտադրանքի լոգարիթմի բոլոր նույն հատկությունները և գործակիցի լոգարիթմը, որոնք մենք օգտագործել ենք նախորդ օրինակներում, միայն հիմա մենք դրանք կկիրառենք աջից ձախ: Այսինքն՝ մենք լոգարիթմների գումարը վերածում ենք արտադրյալի լոգարիթմի, իսկ լոգարիթմների տարբերությունը՝ քանորդի լոգարիթմին։ Մենք ունենք
ա) log 3 0.25+log 3 16+log 3 0.5=log 3 (0.25 16 0.5)=log 3 2.
բ) 
.
Պատասխան.
ա) log 3 0.25+log 3 16+log 3 0.5=log 3 2, բ) 
.
Օրինակ.
Ազատվեք աստիճանից լոգարիթմի նշանի տակ՝ ա) լոգ 0,7 5 11, բ) 
, գ) լոգ 3 (−5) 6.
Լուծում.
Հեշտ է հասկանալ, որ մենք գործ ունենք այնպիսի արտահայտությունների հետ, ինչպիսին log a b p. Լոգարիթմի համապատասխան հատկությունն է log a b p =p log a b , որտեղ a>0 , a≠1 , b>0 , p ցանկացած իրական թիվ է։ Այսինքն՝ a>0, a≠1, b>0 log a b p աստիճանի լոգարիթմից կարող ենք գնալ p·log a b արտադրյալին: Այս փոխակերպումն իրականացնենք տրված արտահայտություններով.
ա) Այս դեպքում a=0.7, b=5 և p=11: Այսպիսով, log 0.7 5 11 =11 log 0.7 5:
բ) Այստեղ կատարվում են a>0, a≠1, b>0 պայմանները: Ահա թե ինչու 
գ) log 3 (−5) 6 արտահայտությունն ունի նույն կառուցվածքը log a b p , a=3 , b=−5 , p=6 : Բայց b-ի համար b>0 պայմանը չի բավարարվում, ինչը անհնարին է դարձնում log a b p =p log a b բանաձևի կիրառումը: Ուրեմն ինչո՞ւ չեք կարողանում գործն ավարտել: Հնարավոր է, բայց պահանջվում է արտահայտության նախնական վերափոխում, որը մենք մանրամասն կքննարկենք ստորև՝ վերնագրի տակ գտնվող պարբերությունում: Լուծումը կլինի այսպիսին. log 3 (−5) 6 =log 3 5 6 =6 log 3 5.
Պատասխան.
ա) լոգ 0,7 5 11 = 11 լոգ 0,7 5,
բ)
գ) լոգ 3 (−5) 6 =6 լոգ 3 5:
Հաճախ փոխակերպումներ իրականացնելիս աստիճանի լոգարիթմի բանաձևը պետք է կիրառվի աջից ձախ p log a b \u003d log a b p ձևով (սա պահանջում է նույն պայմանները a, b և p): Օրինակ՝ 3 ln5=ln5 3 և lg2 log 2 3=log 2 3 lg2:
Օրինակ.
ա) Հաշվե՛ք log 2 5-ի արժեքը, եթե հայտնի է, որ lg2≈0.3010 և lg5≈0.6990. բ) Կոտորակը որպես լոգարիթմ գրի՛ր 3-ի հիմքում:
Լուծում.
ա) Լոգարիթմի նոր հիմքի անցնելու բանաձևը թույլ է տալիս մեզ ներկայացնել այս լոգարիթմը որպես տասնորդական լոգարիթմների հարաբերակցություն, որոնց արժեքները մեզ հայտնի են. Մնում է միայն հաշվարկներն իրականացնել, ունենք 
.
բ) Այստեղ բավական է օգտագործել նոր բազայի անցնելու բանաձևը և կիրառել այն աջից ձախ, այսինքն՝ ձևով. 
. Մենք ստանում ենք 
.
Պատասխան.
ա) log 2 5≈2.3223, բ) .
Այս փուլում մենք բավականին մանրակրկիտ դիտարկել ենք ամենապարզ արտահայտությունների փոխակերպումը` օգտագործելով լոգարիթմների հիմնական հատկությունները և լոգարիթմի սահմանումը: Այս օրինակներում մենք պետք է օգտագործեինք մեկ գույք և ուրիշ ոչինչ: Այժմ, մաքուր խղճով, կարող եք անցնել օրինակներին, որոնց փոխակերպումը պահանջում է լոգարիթմների մի քանի հատկությունների և այլ լրացուցիչ փոխակերպումների օգտագործում: Դրանցով կզբաղվենք հաջորդ պարբերությունում։ Բայց մինչ այդ հակիրճ անդրադառնանք լոգարիթմների հիմնական հատկություններից հետևանքների կիրառման օրինակներին։
Օրինակ.
ա) Ազատվել արմատից լոգարիթմի նշանի տակ. բ) Կոտորակը դարձրեք 5 հիմքի լոգարիթմի: գ) Ազատվեք լոգարիթմի նշանի տակ և դրա հիմքում գտնվող հզորություններից: դ) Հաշվիր արտահայտության արժեքը 
. ե) արտահայտությունը փոխարինի՛ր 3 հիմքով հզորությամբ։
Լուծում.
ա) Եթե հետևանքը հիշենք աստիճանի լոգարիթմի հատկությունից 
, ապա անմիջապես կարող եք պատասխանել. 
.
բ) Այստեղ մենք օգտագործում ենք բանաձևը 
աջից ձախ ունենք 
.
գ) Բ այս դեպքըբանաձևը հանգեցնում է արդյունքի . Մենք ստանում ենք 
.
դ) Եվ այստեղ բավական է կիրառել այն եզրակացությունը, որին համապատասխանում է բանաձեւը 
. Այսպիսով 
.
ե) Լոգարիթմի հատկությունը թույլ է տալիս մեզ հասնել ցանկալի արդյունքի. 
.
Պատասխան.
ա) . բ) . մեջ) 
. է) 
. ե) .
Հետևողականորեն կիրառելով բազմաթիվ հատկություններ
Լոգարիթմների հատկությունների օգտագործմամբ արտահայտությունների փոխակերպման իրական առաջադրանքները սովորաբար ավելի բարդ են, քան նախորդ պարբերությունում քննարկվածները: Դրանցում, որպես կանոն, արդյունքը չի ստացվում մեկ քայլով, այլ լուծումն արդեն իսկ բաղկացած է գույքի հաջորդական կիրառումից մյուսի հետևից՝ լրացուցիչ նույնական փոխակերպումների հետ միասին, ինչպիսիք են փակագծերը բացելը, նման տերմինների կրճատումը, կոտորակների կրճատումը և այլն։ . Այսպիսով, եկեք ավելի մոտենանք նման օրինակներին: Սրանում ոչ մի բարդ բան չկա, գլխավորը զգույշ և հետևողական գործելն է՝ պահպանելով գործողությունների կատարման հերթականությունը։
Օրինակ.
Հաշվիր արտահայտության արժեքը (log 3 15−log 3 5) 7 log 7 5.
Լուծում.
Փակագծերում գտնվող լոգարիթմների տարբերությունը քանորդի լոգարիթմի հատկությամբ կարելի է փոխարինել լոգարիթմի log 3-ով (15:5), այնուհետև հաշվարկել դրա արժեքը log 3 (15:5)=log 3 3=1: Իսկ 7 log 7 5 արտահայտության արժեքը լոգարիթմի սահմանմամբ 5 է։ Այս արդյունքները փոխարինելով սկզբնական արտահայտությամբ՝ ստանում ենք (log 3 15−log 3 5) 7 log 7 5 =1 5=5.
Ահա մի լուծում առանց բացատրության.
(log 3 15−log 3 5) 7 log 7 5 =log 3 (15:5) 5=
= log 3 3 5=1 5=5 .
Պատասխան.
(log 3 15−log 3 5) 7 log 7 5 =5.
Օրինակ.
Որքա՞ն է log 3 log 2 2 3 −1 թվային արտահայտության արժեքը:
Լուծում.
Նախ փոխակերպենք լոգարիթմը, որը գտնվում է լոգարիթմի նշանի տակ, ըստ աստիճանի լոգարիթմի բանաձևի՝ log 2 2 3 =3։ Այսպիսով, log 3 log 2 2 3 =log 3 3 և ապա log 3 3=1: Այսպիսով, log 3 log 2 2 3 −1=1−1=0:
Պատասխան.
log 3 log 2 2 3 −1=0 .
Օրինակ.
Պարզեցրեք արտահայտությունը.
Լուծում.
Լոգարիթմի նոր հիմքի վերածելու բանաձևը թույլ է տալիս լոգարիթմների և մեկ հիմքի հարաբերակցությունը ներկայացնել որպես log 3 5: Այս դեպքում բնօրինակ արտահայտությունը կունենա . Լոգարիթմի սահմանմամբ 3 log 3 5 =5 , այսինքն 
, և ստացված արտահայտության արժեքը, լոգարիթմի նույն սահմանման ուժով, հավասար է երկուսի։
Այստեղ կարճ տարբերակլուծում, որը սովորաբար տրվում է. 
.
Պատասխան.
.
Հաջորդ պարբերության տեղեկատվությանը սահուն անցնելու համար եկեք նայենք 5 2+log 5 3 և lg0.01 արտահայտություններին: Նրանց կառուցվածքը չի համապատասխանում լոգարիթմների ոչ մի հատկության։ Այսպիսով, ի՞նչ է տեղի ունենում, եթե դրանք չեն կարող փոխակերպվել՝ օգտագործելով լոգարիթմների հատկությունները: Դա հնարավոր է, եթե իրականացնեք նախնական փոխակերպումներ, որոնք պատրաստում են այս արտահայտությունները լոգարիթմների հատկությունները կիրառելու համար: Այսպիսով 5 2+log 5 3 =5 2 5 log 5 3 =25 3=75, 
և lg0,01=lg10 −2 = −2: Այնուհետև մենք մանրամասն կհասկանանք, թե ինչպես է իրականացվում արտահայտությունների նման պատրաստումը։
Արտահայտությունների պատրաստում լոգարիթմների հատկությունները կիրառելու համար
Փոխակերպված արտահայտության մեջ լոգարիթմները շատ հաճախ նշումների կառուցվածքով տարբերվում են բանաձևերի ձախ և աջ մասերից, որոնք համապատասխանում են լոգարիթմների հատկություններին: Բայց նույնքան հաճախ, այս արտահայտությունների փոխակերպումը ներառում է լոգարիթմների հատկությունների օգտագործումը. դրանց օգտագործումը միայն նախնական նախապատրաստություն է պահանջում: Եվ այս պատրաստումը բաղկացած է որոշակի նույնական փոխակերպումներ իրականացնելուց, որոնք լոգարիթմները բերում են հատկությունների կիրառման համար հարմար ձևի:
Արդարության համար մենք նշում ենք, որ արտահայտությունների գրեթե ցանկացած փոխակերպում կարող է հանդես գալ որպես նախնական փոխակերպումներ՝ սկսած նմանատիպ տերմինների սովորական կրճատումից մինչև կիրառում։ եռանկյունաչափական բանաձևեր. Սա հասկանալի է, քանի որ փոխարկված արտահայտությունները կարող են պարունակել ցանկացած մաթեմատիկական օբյեկտ՝ փակագծեր, մոդուլներ, կոտորակներ, արմատներ, աստիճաններ և այլն։ Այսպիսով, պետք է պատրաստ լինել կատարել ցանկացած անհրաժեշտ փոխակերպում, որպեսզի հետագայում օգտվենք լոգարիթմների հատկություններից:
Անմիջապես ասենք, որ այս բաժնում մենք մեզ խնդիր չենք դնում դասակարգել և վերլուծել բոլոր հնարավոր նախնական փոխակերպումները, որոնք թույլ են տալիս մեզ ապագայում կիրառել լոգարիթմների հատկությունները կամ լոգարիթմի սահմանումը: Այստեղ մենք կկենտրոնանանք դրանցից միայն չորսի վրա, որոնք ամենաբնորոշն են և առավել հաճախ հանդիպող գործնականում:
Իսկ հիմա դրանցից յուրաքանչյուրի մասին մանրամասն, որից հետո մեր թեմայի շրջանակներում մնում է միայն զբաղվել լոգարիթմների նշանների տակ փոփոխականներով արտահայտությունների փոխակերպմամբ։
Հզորությունների ընտրություն լոգարիթմի նշանի տակ և դրա հիմքում
Անմիջապես սկսենք օրինակով. Եկեք ունենանք լոգարիթմ. Ակնհայտ է, որ այս ձևով նրա կառուցվածքը չի նպաստում լոգարիթմների հատկությունների օգտագործմանը: Հնարավո՞ր է ինչ-որ կերպ փոխակերպել այս արտահայտությունը՝ այն պարզեցնելու կամ նույնիսկ ավելի լավ հաշվարկելու համար դրա արժեքը: Այս հարցին պատասխանելու համար եկեք ավելի մոտիկից նայենք 81 և 1/9 թվերին մեր օրինակի համատեքստում: Այստեղ հեշտ է տեսնել, որ այս թվերը կարող են ներկայացվել որպես 3-ի, իսկապես, 81=3 4 և 1/9=3 −2 աստիճանի: Այս դեպքում սկզբնական լոգարիթմը ներկայացվում է ձևով և հնարավոր է դառնում կիրառել բանաձևը . Այսպիսով, 
.
Վերլուծված օրինակի վերլուծությունից առաջանում է հետևյալ միտքը՝ հնարավորության դեպքում կարող եք փորձել ընդգծել աստիճանը լոգարիթմի նշանի տակ և դրա հիմքում՝ աստիճանի լոգարիթմի հատկությունը կամ դրա հետևանքը կիրառելու համար։ Մնում է միայն պարզել, թե ինչպես կարելի է առանձնացնել այս աստիճանները։ Այս հարցում մենք մի քանի առաջարկություններ կտանք։
Երբեմն միանգամայն ակնհայտ է, որ լոգարիթմի նշանի տակ և/կամ դրա հիմքում գտնվող թիվը ներկայացնում է որոշակի ամբողջ հզորություն, ինչպես վերը քննարկված օրինակում: Գրեթե անընդհատ դուք պետք է գործ ունենաք երկու ուժերի հետ, որոնք լավ ծանոթ են՝ 4=2 2, 8=2 3, 16=2 4, 32=2 5, 64=2 6, 128=2 7, 256=2 8. , 512= 2 9 , 1024=2 10 ։ Նույնը կարելի է ասել եռյակի աստիճանների մասին՝ 9=3 2 , 27=3 3 , 81=3 4 , 243=3 5 , ... Ընդհանրապես չի վնասում, եթե կա. աստիճանի աղյուսակ բնական թվեր տասի ընթացքում։ Դժվար չէ նաև աշխատել տասը, հարյուր, հազար և այլն ամբողջ հզորություններով։
Օրինակ.
Հաշվիր արժեքը կամ պարզեցրու արտահայտությունը՝ ա) log 6 216 , բ) , գ) log 0,000001 0,001 .
Լուծում.
ա) Ակնհայտորեն, 216=6 3, ուրեմն log 6 216=log 6 6 3 =3:
բ) Բնական թվերի հզորությունների աղյուսակը թույլ է տալիս 343 և 1/243 թվերը ներկայացնել որպես համապատասխանաբար 7 3 և 3 −4 թվերի ուժեր։ Ուստի հնարավոր է հաջորդ վերափոխումըտրված լոգարիթմ. 
գ) Քանի որ 0,000001=10 −6 և 0,001=10 −3, ապա log 0,000001 0,001=log 10 −6 10 −3 =(−3)/(−6)=1/2.
Պատասխան.
ա) լոգ 6 216=3, բ) 
, գ) լոգ 0.000001 0.001=1/2.
Ավելի բարդ դեպքերում թվերի ուժերն ընդգծելու համար պետք է դիմել.
Օրինակ.
Արտահայտությունը փոխեք ավելի պարզ ձևի log 3 648 log 2 3:
Լուծում.
Տեսնենք, թե ինչի մեջ է 648 թվի ընդլայնումը հիմնական գործոնները:
Այսինքն՝ 648=2 3 3 4: Այս կերպ, log 3 648 log 2 3=log 3 (2 3 3 4) log 2 3.
Այժմ արտադրյալի լոգարիթմը վերածում ենք լոգարիթմների գումարի, որից հետո կիրառում ենք աստիճանի լոգարիթմի հատկությունները.
log 3 (2 3 3 4) log 2 3=(log 3 2 3 + log 3 3 4) log 2 3=
=(3 log 3 2+4) log 2 3 .
Աստիճանի լոգարիթմի հատկության հետևանքի ուժով, որը համապատասխանում է բանաձևին. , log32 log23 արտադրյալը արտադրյալն է, և հայտնի է, որ այն հավասար է մեկի։ Սա հաշվի առնելով՝ մենք ստանում ենք 3 log 3 2 log 2 3+4 log 2 3=3 1+4 log 2 3=3+4 log 2 3.
Պատասխան.
log 3 648 log 2 3=3+4 log 2 3.
Շատ հաճախ լոգարիթմի նշանի տակ և դրա հիմքում արտահայտությունները որոշ թվերի արմատների և/կամ հզորությունների արտադրյալներ կամ հարաբերակցություններ են, օրինակ՝ , . Նմանատիպ արտահայտությունները կարող են ներկայացվել որպես աստիճան: Դրա համար իրականացվում է արմատներից աստիճանների անցում, և կիրառվում են: Այս փոխակերպումները թույլ են տալիս ընտրել աստիճանները լոգարիթմի նշանի տակ և դրա հիմքում, այնուհետև կիրառել լոգարիթմի հատկությունները։
Օրինակ.
Հաշվիր՝ ա) 
, բ).
Լուծում.
ա) Լոգարիթմի հիմքում արտահայտված արտահայտությունը նույն հիմքերով հզորությունների արտադրյալն է՝ մեր ունեցած հզորությունների համապատասխան հատկությամբ. 5 2 5 −0,5 5 −1 =5 2−0,5−1 =5 0,5.
Այժմ փոխարկենք կոտորակը լոգարիթմի նշանի տակ՝ արմատից անցնենք աստիճանի, որից հետո կօգտագործենք աստիճանների հարաբերակցության հատկությունը նույն հիմքերով. 
.
Մնում է ստացված արդյունքները փոխարինել սկզբնական արտահայտությամբ, օգտագործել բանաձևը և ավարտիր վերափոխումը. 
բ) Քանի որ 729=3 6, և 1/9=3 −2, սկզբնական արտահայտությունը կարող է վերագրվել որպես .
Այնուհետև կիրառեք ցուցիչի արմատի հատկությունը, արմատից շարժվեք դեպի աստիճան և օգտագործեք հզորությունների հարաբերակցության հատկությունը՝ լոգարիթմի հիմքը հզորության փոխարկելու համար. 
.
Հաշվի առնելով վերջին արդյունքը՝ ունենք 
.
Պատասխան.
ա) 
, բ).
Հասկանալի է, որ ընդհանուր դեպքում լոգարիթմի նշանի տակ և դրա հիմքում հզորություններ ստանալու համար կարող են պահանջվել տարբեր արտահայտությունների տարբեր փոխակերպումներ։ Բերենք մի երկու օրինակ։
Օրինակ.
Ո՞րն է արտահայտության արժեքը. ա) 
, բ) 
.
Լուծում.
Այնուհետև նշում ենք, որ տրված արտահայտությունն ունի log A B p ձևը, որտեղ A=2, B=x+1 և p=4: Մենք վերափոխեցինք այս տեսակի թվային արտահայտությունները ըստ աստիճանի log a b p \u003d p log a b աստիճանի լոգարիթմի հատկության, հետևաբար, տրված արտահայտությամբ ես ուզում եմ անել նույնը և գնալ log 2-ից (x + 1) 4: դեպի 4 log 2 (x + 1) . Իսկ հիմա հաշվարկենք սկզբնական արտահայտության արժեքը և փոխակերպումից հետո ստացված արտահայտությունը, օրինակ, x=−2-ով։ Մենք ունենք log 2 (−2+1) 4 =log 2 1=0 , և 4 log 2 (−2+1)=4 log 2 (−1)- անիմաստ արտահայտություն. Սա օրինաչափ հարց է առաջացնում. «Ի՞նչ ենք մենք սխալ արել»:
Իսկ պատճառը հետևյալն է՝ մենք կատարել ենք փոխակերպման log 2 (x+1) 4 =4 log 2 (x+1) log a b p =p log a b բանաձևը, բայց մենք իրավունք ունենք կիրառել միայն այս բանաձևը։ եթե a >0, a≠1, b>0, p - ցանկացած իրական թիվ: Այսինքն՝ մեր կատարած փոխակերպումը տեղի է ունենում, եթե x+1>0 , որը նույնն է x>−1 (A-ի և p-ի համար պայմանները բավարարված են): Այնուամենայնիվ, մեր դեպքում, սկզբնական արտահայտության համար x փոփոխականի ODZ-ը բաղկացած է ոչ միայն x> −1 միջակայքից, այլ նաև x միջակայքից։<−1 . Но для x<−1 мы не имели права осуществлять преобразование по выбранной формуле.
ՕՁՀ-ն հաշվի առնելու անհրաժեշտությունը
Շարունակենք վերլուծել մեր ընտրած log 2 (x+1) 4 արտահայտության փոխակերպումը, իսկ հիմա տեսնենք, թե ինչ է տեղի ունենում ODZ-ի հետ 4 log 2 (x+1) արտահայտությանն անցնելիս: Նախորդ պարբերությունում մենք գտանք սկզբնական արտահայտության ODZ - սա բազմությունն է (−∞, −1)∪(−1, +∞) ։ Այժմ եկեք գտնենք x փոփոխականի ընդունելի արժեքների տարածքը 4 log 2 (x+1) արտահայտության համար: Այն որոշվում է x+1>0 պայմանով, որը համապատասխանում է (−1, +∞) բազմությանը։ Ակնհայտ է, որ log 2 (x+1) 4-ից 4·log 2 (x+1) անցնելիս թույլատրելի արժեքների շրջանակը նեղանում է։ Եվ մենք պայմանավորվեցինք խուսափել բարեփոխումներից, որոնք հանգեցնում են ՕԶՀ-ի նեղացմանը, քանի որ դա կարող է հանգեցնել տարբեր բացասական հետեւանքների:
Այստեղ արժե ինքներդ նշել, որ օգտակար է վերահսկել ODZ-ը փոխակերպման յուրաքանչյուր քայլում և թույլ չտալ, որ այն նեղանա: Եվ եթե հանկարծ փոխակերպման ինչ-որ փուլում տեղի ունեցավ ՕՁ-ի նեղացում, ապա արժե շատ ուշադիր նայել, թե արդյոք այդ փոխակերպումը թույլատրելի է, և արդյոք մենք իրավունք ունեինք այն իրականացնելու։
Արդարության համար մենք ասում ենք, որ գործնականում մենք սովորաբար պետք է աշխատենք արտահայտությունների հետ, որոնցում փոփոխականների ODZ-ն այնպիսին է, որ թույլ է տալիս մեզ օգտագործել լոգարիթմների հատկությունները առանց սահմանափակումների, ինչպես արդեն գիտենք, այնպես էլ ձախից աջ: իսկ աջից ձախ՝ փոխակերպումներ կատարելիս։ Դուք արագ ընտելանում եք դրան, և սկսում եք մեխանիկորեն իրականացնել փոխակերպումները՝ չմտածելով, թե արդյոք հնարավոր էր դրանք իրականացնել։ Եվ նման պահերին, ինչպես բախտը բերեց, սայթաքում են ավելի բարդ օրինակներ, որոնցում լոգարիթմների հատկությունների ոչ ճշգրիտ կիրառումը հանգեցնում է սխալների։ Այսպիսով, դուք պետք է միշտ զգոն լինեք և համոզվեք, որ ODZ-ի նեղացում չկա:
Չի խանգարում առանձին ընդգծել հիմնական փոխակերպումները, որոնք հիմնված են լոգարիթմների հատկությունների վրա, որոնք պետք է իրականացվեն շատ ուշադիր, ինչը կարող է հանգեցնել ODZ-ի նեղացման, և արդյունքում՝ սխալների.
Արտահայտությունների որոշ փոխակերպումներ՝ ըստ լոգարիթմների հատկությունների, կարող են հանգեցնել նաև հակառակի՝ ODZ-ի ընդլայնմանը։ Օրինակ, 4 log 2-ից (x+1) անցնելով log 2 (x+1) 4, ODZ-ը (−1, +∞) բազմությունից երկարացնում է մինչև (−∞, −1)∪(−1, +∞): ) . Նման փոխակերպումները տեղի են ունենում, եթե դուք մնում եք ODZ-ի սահմաններում սկզբնական արտահայտության համար: Այսպիսով, վերափոխումը հենց նոր նշված 4 log 2 (x+1)=log 2 (x+1) 4 տեղի է ունենում ODZ փոփոխականի վրա՝ 4 log 2 (x+1) սկզբնական արտահայտության համար, այսինքն, երբ x+1> 0, որը նույնն է, ինչ (−1, +∞) .
Այժմ, երբ մենք քննարկեցինք այն նրբությունները, որոնց վրա պետք է ուշադրություն դարձնեք լոգարիթմների հատկությունների օգտագործմամբ արտահայտությունները փոփոխականներով փոխակերպելիս, մնում է պարզել, թե ինչպես պետք է այդ փոխարկումները ճիշտ իրականացվեն:
X+2>0. Արդյո՞ք դա աշխատում է մեր դեպքում: Այս հարցին պատասխանելու համար եկեք նայենք x փոփոխականի DPV-ին: Այն որոշվում է անհավասարությունների համակարգով 
, որը համարժեք է x+2>0 պայմանին (անհրաժեշտության դեպքում տե՛ս հոդվածը անհավասարությունների համակարգերի լուծում) Այսպիսով, մենք կարող ենք ապահով կերպով կիրառել աստիճանի լոգարիթմի հատկությունը։
Մենք ունենք
3 log(x+2) 7 −log(x+2)−5 log(x+2) 4 =
=3 7 log(x+2)−log(x+2)−5 4 log(x+2)=
=21 log(x+2)−log(x+2)−20 log(x+2)=
=(21−1−20)lg(x+2)=0 .
Դուք կարող եք այլ կերպ վարվել, քանի որ ODZ-ն թույլ է տալիս դա անել, օրինակ այսպես. 
Պատասխան.
3 log(x+2) 7 −log(x+2)−5 log(x+2) 4 =0.
Իսկ ի՞նչ անել, երբ ODZ-ում լոգարիթմների հատկությունների հետ կապված պայմանները չեն պահպանվում: Սրա հետ կզբաղվենք օրինակներով։
Եկեք մեզանից պահանջենք պարզեցնել lg(x+2) 4 −lg(x+2) 2 արտահայտությունը: Այս արտահայտության փոխակերպումը, ի տարբերություն նախորդ օրինակի արտահայտության, թույլ չի տալիս ազատորեն օգտագործել աստիճանի լոգարիթմի հատկությունը։ Ինչո՞ւ։ x փոփոխականի ODZ-ն այս դեպքում x>−2 և x երկու ինտերվալների միավորումն է<−2 . При x>−2 մենք կարող ենք ապահով կերպով կիրառել աստիճանի լոգարիթմի հատկությունը և շարունակել այնպես, ինչպես վերը նշված օրինակում. log(x+2) 4 −log(x+2) 2 =4 log(x+2)−2 log(x+2)=2 log(x+2). Բայց ODZ-ը պարունակում է մեկ այլ միջակայք x+2<0 , для которого последнее преобразование будет некорректно. Что же делать при x+2<0 ? В подобных случаях на помощь приходит . Определение модуля позволяет выражение x+2 при x+2<0 представить как −|x+2| . Тогда при x+2<0 от lg(x+2) 4 −lg(x+2) 2 переходим к log(−|x+2|) 4 −log(−|x+2|) 2և հետագայում, lg|x+2|-ի հզորության հատկությունների շնորհիվ 4−lg|x+2| 2 . Ստացված արտահայտությունը կարող է փոխակերպվել ըստ աստիճանի լոգարիթմի հատկության, քանի որ փոփոխականի ցանկացած արժեքի համար |x+2|>0: Մենք ունենք տեղեկամատյան|x+2| 4−lg|x+2| 2 =4 լոգ|x+2|−2 լոգ|x+2|=2 լոգ|x+2|. Այժմ դուք կարող եք ազատվել մոդուլից, քանի որ այն կատարել է իր գործը: Քանի որ մենք փոխակերպվում ենք x+2-ով<0 , то 2·lg|x+2|=2·lg(−(x+2)) . Итак, можно считать, что мы справились с поставленной задачей. Ответ: . Полученный результат можно записать компактно с использованием модуля как .
Դիտարկենք ևս մեկ օրինակ՝ մոդուլների հետ աշխատանքը ծանոթ դարձնելու համար: Եկեք պատկերացնենք արտահայտությունից 
անցնել x−1 , x−2 և x−3 գծային երկանդամների լոգարիթմների գումարին և տարբերությանը։ Նախ մենք գտնում ենք ODZ-ը. 
(3, +∞) ինտերվալի վրա x−1, x−2 և x−3 արտահայտությունների արժեքները դրական են, ուստի մենք կարող ենք ապահով կերպով կիրառել գումարի և տարբերության լոգարիթմի հատկությունները. 
Իսկ (1, 2) միջակայքում x−1 արտահայտության արժեքները դրական են, իսկ x−2 և x−3 արտահայտությունների արժեքները՝ բացասական։ Հետևաբար, դիտարկվող միջակայքում մենք ներկայացնում ենք x−2 և x−3 մոդուլը՝ օգտագործելով −|x−2| եւ −|x−3| համապատասխանաբար. Որտեղ 
Այժմ մենք կարող ենք կիրառել արտադրյալի լոգարիթմի և գործակիցի հատկությունները, քանի որ դիտարկված միջակայքում (1, 2) նշվում են x−1 , |x−2| արտահայտությունների արժեքները։ եւ |x−3| - դրական.
Մենք ունենք 
Ստացված արդյունքները կարելի է համատեղել.
Ընդհանուր առմամբ, նմանատիպ հիմնավորումը թույլ է տալիս, հիմնվելով արտադրանքի լոգարիթմի, հարաբերակցության և աստիճանի բանաձևերի վրա, ստանալ երեք գործնականորեն օգտակար արդյունք, որոնք բավականին հարմար են օգտագործման համար.
- Logar a (X·Y) ձևի X և Y երկու կամայական արտահայտությունների արտադրյալի լոգարիթմը կարելի է փոխարինել log a |X|+log a |Y| , a>0, a≠1.
- Հատուկ լոգարիթմի log a (X:Y) կարելի է փոխարինել լոգարիթմների տարբերությամբ log a |X|−log a |Y| , a>0, a≠1, X և Y կամայական արտահայտություններ են:
- Որոշ B արտահայտության լոգարիթմից log a B p ձևի զույգ հզորության p-ին կարելի է անցնել p log a |B| , որտեղ a>0, a≠1, p զույգ թիվ է, իսկ B-ն կամայական արտահայտություն է:
Նմանատիպ արդյունքներ են տրված, օրինակ, բուհերի դիմորդների համար մաթեմատիկայի խնդիրների հավաքածուում էքսպոնենցիալ և լոգարիթմական հավասարումների լուծման հրահանգներում, որը խմբագրվել է M. I. Skanavi-ի կողմից:
Օրինակ.
Պարզեցրեք արտահայտությունը 
.
Լուծում.
Լավ կլինի կիրառել աստիճանի, գումարի և տարբերության լոգարիթմի հատկությունները։ Բայց կարո՞ղ ենք դա անել այստեղ: Այս հարցին պատասխանելու համար մենք պետք է իմանանք ODZ-ին:
Եկեք սահմանենք այն. 
Ակնհայտ է, որ x+4, x−2 և (x+4) 13 արտահայտությունները x փոփոխականի հնարավոր արժեքների տիրույթում կարող են ընդունել և՛ դրական, և՛ բացասական արժեքներ: Հետեւաբար, մենք ստիպված կլինենք աշխատել մոդուլների միջոցով: 
Մոդուլի հատկությունները թույլ են տալիս վերաշարադրել ինչպես, այնպես 
Բացի այդ, ոչինչ չի խանգարում ձեզ օգտագործել աստիճանի լոգարիթմի հատկությունը, այնուհետև բերել նման տերմիններ. 
Փոխակերպումների մեկ այլ հաջորդականություն հանգեցնում է նույն արդյունքին. 
և քանի որ x−2 արտահայտությունը կարող է ընդունել և՛ դրական, և՛ բացասական արժեքներ ODZ-ի վրա, երբ վերցնում ենք զույգ ցուցիչ 14:
