Acum ne vom uita la transformarea expresiilor care conțin logaritmi din punct de vedere general. Aici vom analiza nu numai transformarea expresiilor folosind proprietățile logaritmilor, dar vom lua în considerare transformarea expresiilor cu logaritmi vedere generala, care conțin nu numai logaritmi, ci și puteri, fracții, rădăcini etc. Ca de obicei, vom furniza toate materialele cu exemple caracteristice descrieri detaliate solutii.

Navigare în pagină.

Expresii cu logaritmi și expresii logaritmice

Efectuarea de acțiuni cu fracții

În paragraful anterior, am examinat principalele transformări care sunt efectuate cu fracții individuale care conțin logaritmi. Aceste transformări, desigur, pot fi efectuate cu fiecare fracție individuală care face parte dintr-o expresie mai complexă, de exemplu, reprezentând suma, diferența, produsul și câtul fracțiilor similare. Dar, pe lângă lucrul cu fracții individuale, transformarea expresiilor de acest fel implică adesea efectuarea de acțiuni adecvate cu fracții. În continuare, vom lua în considerare regulile după care se realizează aceste acțiuni.

Din clasele 5-6, cunoaștem regulile după care . In articol vedere generală a operaţiilor cu fracţii am vehiculat aceste reguli cu fracții obișnuiteîn fracții de formă generală A/B , unde A și B sunt niște expresii numerice, literale sau cu variabile, iar B nu este identic egal cu zero. Este clar că fracțiile cu logaritmi sunt cazuri speciale de fracții generale. Și în acest sens, este clar că acțiunile cu fracții care conțin logaritmi în înregistrările lor se desfășoară după aceleași reguli. Și anume:

• Pentru a adăuga sau scădea două fracții cu aceiași numitori, adunați sau scădeți numărătorii în consecință și lăsați numitorul același.
• Pentru a adăuga sau scădea două fracții cu numitori diferiti, trebuie să le aduceți la un numitor comun și să efectuați acțiunile corespunzătoare conform regulii anterioare.
• Pentru a înmulți două fracții, trebuie să scrieți o fracție al cărei numărător este produsul numărătorilor fracțiilor originale, iar numitorul este produsul numitorilor.
• Pentru a împărți o fracție la o fracție, este necesar să înmulțiți fracția divizibilă cu reciproca divizorului, adică cu fracția cu numărătorul și numitorul rearanjate.

Iată câteva exemple pentru efectuarea de operații cu fracții care conțin logaritmi.

Exemplu.

Efectuați acțiuni cu fracții care conțin logaritmi: a), b) , în) , G) .

Soluţie.

a) Numitorii fracțiilor adăugate sunt în mod evident aceiași. Prin urmare, conform regulii de adunare a fracțiilor cu aceiași numitori, adunăm numărătorii și lăsăm numitorul același: .

b) Aici numitorii sunt diferiți. Prin urmare, mai întâi aveți nevoie aduce fracțiile la același numitor. În cazul nostru, numitorii sunt deja prezentați ca produse și rămâne să luăm numitorul primei fracții și să adăugăm la acesta factorii lipsă de la numitorul celei de-a doua fracții. Deci obținem un numitor comun al formei . În acest caz, fracțiile scăzute sunt reduse la un numitor comun folosind factori suplimentari sub forma unui logaritm și, respectiv, expresia x 2 ·(x+1). După aceea, rămâne să scădem fracții cu aceiași numitori, ceea ce nu este dificil.

Deci solutia este:

c) Se știe că rezultatul înmulțirii fracțiilor este o fracție, al cărei numărător este produsul numărătorilor, iar numitorul este produsul numitorilor, prin urmare

Este ușor de văzut că este posibil reducerea fracției cu doi și după logaritmul zecimal, ca rezultat avem .

d) Trecem de la împărțirea fracțiilor la înmulțire, înlocuind divizorul de fracții cu reciproca acestuia. Asa de

Numătorul fracției rezultate poate fi reprezentat ca , din care factorul comun al numărătorului și numitorului este clar vizibil - factorul x, puteți reduce fracția cu acesta:

Răspuns:

a), b) , în) , G) .

Trebuie amintit că acțiunile cu fracții sunt efectuate ținând cont de ordinea în care sunt efectuate acțiunile: mai întâi înmulțirea și împărțirea, apoi adunarea și scăderea, iar dacă există paranteze, atunci se efectuează mai întâi acțiunile dintre paranteze.

Exemplu.

Faceți acțiuni cu fracții .

Soluţie.

Mai întâi, efectuăm adunarea fracțiilor dintre paranteze, după care vom efectua înmulțirea:

Răspuns:

În acest moment, rămâne să spunem cu voce tare trei puncte destul de evidente, dar în același timp importante:

Conversia expresiilor folosind proprietățile logaritmilor

Cel mai adesea, transformarea expresiilor cu logaritmi implică utilizarea identităților care exprimă definiția logaritmului și

Matematica. Teste tematice. Partea a II-a. Pregătirea pentru Examenul Unificat de Stat-2010. 10-11 clase. Ed. Lysenko F.F. - Rostov n/D .: Legion, 2009. - 176s.

Matematica. USE-2009. Teste tematice. Partea a II-a (B4-B8, C1-C2) Ed. Lysenko F.F. - Rostov n/D: Legiunea, 2008 - 160 p.

Manualul constă în teste pe subiecte individuale, care sunt tradiționale în cursul de matematică și, prin urmare, de regulă, sunt incluse în examen. Acestea acoperă pe deplin grupurile de sarcini de un nivel crescut și ridicat de complexitate al USE, cu excepția sarcinilor text și a problemelor de geometrie. Pentru fiecare subiect sunt oferite una sau mai multe suite de testare. Fiecare set conține 10 teste, fiecare test conține 8 sarcini.

Scopul acestei cărți este de a elabora sarcini cu un răspuns scurt și detaliat al testelor USE. Este necesar în primul rând pentru absolvenții care se așteaptă să primească UTILIZAȚI bine evaluare, precum și pentru elevii clasei a X-a, care pot consolida temele abordate din punctul de vedere al USE. Manualul propus poate fi util tuturor absolvenților care se pregătesc pentru USE la matematică, precum și profesorilor care pregătesc elevii pentru USE.

Format: djvu/zip (2009 , 176s.)

Marimea: 2,5 MB

Descărcați / descărcați fișierul 14

Format: pdf (2009 , 176s.)

Marimea: 8,6 MB

Descarca: 14 .12.2018, link-uri eliminate la cererea editurii Legiunea (vezi nota)

Format: djvu/zip (2008 , 160 de ani.)

Marimea: 3 MB

Descărcați / descărcați fișierul 14 .12.2018, link-uri eliminate la cererea editurii Legiunea (vezi nota)

Format: pdf (2008 , 160 de ani.)

Marimea: 9,9 MB

Descarca: 14 .12.2018, link-uri eliminate la cererea editurii Legiunea (vezi nota)

Complex educativ-metodic "Matematică. Examenul de stat unificat-2010" ed. Lysenko F.F. și Kulabukhov S.Yu. include tutoriale:
1. Matematica. Pregătirea pentru Examenul Unificat de Stat-2010.
2. Reşebnik. Matematica. Pregătirea pentru Examenul Unificat de Stat-2010.
3. Matematica. Teste tematice. Partea I (nivel de bază). Pregătirea pentru Examenul Unificat de Stat-2010. 10-11 clase.
4. Matematica. Teste tematice. Partea a II-a. Pregătirea pentru Examenul Unificat de Stat-2010. 10-11 clase.
5. Matematica. Teste tematice: geometrie, probleme de cuvinte. Pregătirea pentru Examenul Unificat de Stat-2010. 10-11 clase.
6. Matematica. Culegere de teste USE 2001 - 2010.
7. Matematica. Pregătirea pentru Examenul Unificat de Stat-2010. Teste de antrenament.
8. Ghid de buzunar la matematică.

Cuprins
De la autori 11
§ 1. Transformări identitare ale expresiilor logaritmice 13
Opțiunea numărul 1 13
Opțiunea numărul 2 13
Opțiunea numărul 3 14
Opțiunea numărul 4 14
Opțiunea numărul 5 15
Opțiunea numărul 6 15
Opțiunea numărul 7 16
Opțiunea numărul 8 16
Opțiunea numărul 9 17
Opțiunea numărul 10 17
§ 2. Transformări identitare ale expresiilor care conţin gradul 18
Opțiunea numărul 1 18
Opțiunea numărul 2 19
Opțiunea numărul 3 19
Opțiunea numărul 4 20
Opțiunea numărul 5 21
Opțiunea numărul 6 21
Opțiunea numărul 7 22
Opțiunea numărul 8 23
Opțiunea numărul 9 23
Opțiunea numărul 10 24
§ 3. Transformări identitare ale expresiilor iraționale 25
Opțiunea numărul 1 25
Opțiunea numărul 2 25
Opțiunea numărul 3 26
Opțiunea numărul 4 26
Opțiunea numărul 5 27
Opțiunea numărul 6 28
Opțiunea numărul 7 28
Opțiunea numărul 8 29
Opțiunea numărul 9 30
Opțiunea numărul 10 30
§ 4. Sisteme de ecuații 31
Opțiunea numărul 1 31
Opțiunea numărul 2 32
Opțiunea numărul 3 33
Opțiunea numărul 4 33
Opțiunea numărul 5 34
Opțiunea numărul 6 35
Opțiunea numărul 7 36
Opțiunea numărul 8 37
Opțiunea numărul 9 38
Opțiunea numărul 10 39
§ 5. sens geometric derivat 39
Opțiunea numărul 1 39
Opțiunea numărul 2 41
Opțiunea numărul 3 43
Opțiunea numărul 4 44
Opțiunea numărul 5 46
Opțiunea numărul 6 48
Opțiunea numărul 7 50
Opțiunea numărul 8 52
Opțiunea numărul 9 54
Opțiunea numărul 10 55
§ 6. Inegalități 56
Opțiunea numărul 1 g 56
Opțiunea numărul 2 57
Opțiunea numărul 3 58
Opțiunea numărul 4 58
Opțiunea numărul 5 59
Opțiunea numărul 6 60
Opțiunea numărul 7 60
Opțiunea numărul 8 61
Opțiunea numărul 9 62
Opțiunea numărul 10 63
§ 7. Ecuații iraționale 63
Opțiunea numărul 1 63
Opțiunea numărul 2 64
Opțiunea numărul 3 65
Opțiunea numărul 4 65
Opțiunea numărul 5 66
Opțiunea numărul 6 66
Opțiunea numărul 7 67
Opțiunea numărul 8 67
Opțiunea numărul 9 68
Opțiunea nr. Yu 68
§ 8. Ecuații trigonometrice 69
Opțiunea numărul 1 69
Opțiunea numărul 2 69
Opțiunea numărul 3 70
Opțiunea numărul 4 70
Opțiunea numărul 5 71
Opțiunea numărul 6 72
Opțiunea numărul 7 72
Opțiunea numărul 8 73
Opțiunea numărul 9 74
Opțiunea numărul 10 74
§ 9. Ecuații logaritmice 75
Opțiunea numărul 1 75
Opțiunea numărul 2 75
Opțiunea numărul 3 76
Opțiunea numărul 4 76
Opțiunea numărul 5 77
Opțiunea numărul 6 77
Opțiunea numărul 7 78
Opțiunea nr. 8 * 78
Opțiunea numărul 9 79
Opțiunea numărul 10 79
§ 10. Ecuații exponențiale 80
Opțiunea numărul 1 80
Opțiunea numărul 2 80
Opțiunea numărul 3 81
Opțiunea numărul 4 81
Opțiunea numărul 5 82
Opțiunea numărul 6 82
Opțiunea numărul 7 83
Opțiunea numărul 8 83
Opțiunea numărul 9 84
Opțiunea numărul 10 84
§unsprezece. Periodicitate, funcții pare și impare 85
Opțiunea numărul 1 85
Opțiunea numărul 2 86
Opțiunea numărul 3 87
Opțiunea numărul 4 89
Opțiunea numărul 5 90
Opțiunea numărul 6 91
Opțiunea numărul 7 92
Opțiunea numărul 8 93
Opțiunea numărul 9 94
Opțiunea numărul 10 95
§ 12. Zerurile unei funcţii complexe. Funcție limitată 97
Opțiunea numărul 1 97
Opțiunea numărul 2 97
Opțiunea numărul 3 98
Opțiunea numărul 4 98
Opțiunea numărul 5 99
Opțiunea numărul 6 99
Opțiunea numărul 7 100
Opțiunea numărul 8 100
Opțiunea numărul 9 101
Opțiunea numărul 10 101
§ 13. Domeniul definiției, set de valori, monotonitatea funcțiilor 102
Opțiunea numărul 1 102
Opțiunea numărul 2 102
Opțiunea numărul 3 103
Opțiunea numărul 4 103
Opțiunea numărul 5 104
Opțiunea numărul 6 104
Opțiunea numărul 7 105
Opțiunea numărul 8 105
Opțiunea numărul 9 106
Opțiunea numărul 10 107
§ 14. Extreme ale unei funcţii. Cele mai mari și cele mai mici valori ale funcției 107
Opțiunea numărul 1 107
Opțiunea numărul 2 108
Opțiunea numărul 3 108
Opțiunea numărul 4 109
Opțiunea numărul 5 109
Opțiunea numărul 6 110
Opțiunea numărul 7 110
Opțiunea numărul 8 111
Opțiunea numărul 9 111
Opțiunea numărul 10 112
§ 15. Diverse tehnici de rezolvare a ecuaţiilor logaritmice 113
Opțiunea numărul 1 113
Opțiunea numărul 2 113
Opțiunea numărul 3 114
Opțiunea numărul 4 114
Opțiunea numărul 5 115
Opțiunea numărul 6 115
Opțiunea numărul 7 116
Opțiunea numărul 8 116
Opțiunea numărul 9 117
Opțiunea numărul 10 117
§ 16. Diverse tehnici de rezolvare a ecuaţiilor trigonometrice 118
Opțiunea numărul 1 118
Opțiunea numărul 2 118
Opțiunea numărul 3 118
Opțiunea numărul 4 119
Opțiunea numărul 5 119
Opțiunea numărul 6 120
Opțiunea numărul 7 120
Opțiunea numărul 8 121
Opțiunea numărul 9 121
Opțiunea numărul 10 122
§ 17. Diverse tehnici de rezolvare a ecuaţiilor iraţionale 123
Opțiunea numărul 1 123
Opțiunea numărul 2 123
Opțiunea numărul 3 124
Opțiunea numărul 4 124
Opțiunea numărul 5 125
Opțiunea numărul 6 125
Opțiunea numărul 7 125
Opțiunea numărul 8 126
Opțiunea numărul 9 126
Opțiunea nr. 10 127
§ 18. Ecuații care conțin o variabilă sub semnul modulo 127
Opțiunea numărul 1 127
Opțiunea numărul 2 128
Opțiunea numărul 3 128
Opțiunea numărul 4 129
Opțiunea numărul 5 129
Opțiunea numărul 6 130
Opțiunea numărul 7 130
Opțiunea numărul 8 131
Opțiunea numărul 9 131
Opțiunea numărul 10 131
§ 19. Diverse metode de rezolvare ecuații exponențiale.132
Opțiunea numărul 1 132
Opțiunea numărul 2 133
Opțiunea numărul 3 133
Opțiunea numărul 4 134
Opțiunea numărul 5 134
Opțiunea numărul 6 135
Opțiunea numărul 7 135
Opțiunea numărul 8 135
Opțiunea numărul 9 136
Opțiunea numărul 10 136
§ 20. Diverse tehnici de rezolvare a ecuaţiilor combinate 137
Opțiunea numărul 1 137
Opțiunea numărul 2 137
Opțiunea numărul 3 138
Opțiunea numărul 4 138
Opțiunea numărul 5 139
Opțiunea numărul 6 139
Opțiunea numărul 7 140
Opțiunea numărul 8 140
Opțiunea numărul 9 141
Opțiunea numărul 10 141
§ 21. Ecuații cu un parametru care conține modulul 142
Opțiunea numărul 1 142
Opțiunea numărul 2 142
Opțiunea numărul 3 143
Opțiunea numărul 4 144
Opțiunea numărul 5 144
Opțiunea numărul 6 145
Opțiunea numărul 7 146
Opțiunea numărul 8 146
Opțiunea numărul 9 147
Opțiunea numărul 10 148
Răspunsurile 149
§ 1. Transformările identitare ale expresiilor logaritmice 149
§ 2. Transformări identitare ale expresiilor care conţin gradul 150
§ 3. Transformări identitare ale expresiilor iraționale 150
§ 4. Sisteme de ecuații 151
§ 5. Sensul geometric al derivatului 151
§ 6. Inegalităţi 152
§ 7. Ecuații iraționale 152
§ 8. Ecuații trigonometrice 153
§ 9. Ecuații logaritmice 153
§ 10. Ecuații exponențiale 154
§unsprezece. Periodicitate, funcții pare și impare 154
§ 12. Zerurile unei funcţii complexe. Funcție limitată 155
§ 13. Domeniul definirii, setul de valori, monotonitatea functiilor 156
§ 14. Extreme ale unei funcţii. Cele mai mari și cele mai mici valori ale funcției 158
§ cincisprezece. Diverse trucuri la rezolvarea ecuațiilor logaritmice 159
§ 16. Diverse tehnici de rezolvare a ecuaţiilor trigonometrice 160
§ 17. Diverse trucuri pentru rezolvarea ecuaţiilor iraţionale 164
§ 18. Ecuații care conțin o variabilă sub semnul modulo 165
§ 19. Diverse tehnici de rezolvare a ecuaţiilor exponenţiale.166
§ 20. Diverse tehnici de rezolvare a ecuaţiilor combinate 167
§ 21. Ecuații cu un parametru care conține modulul 169
Literatura 170

EGOROVA VICTORIA VALEREVNA

Profesor de matematică

cea mai înaltă categorie de calificare

TEMA: „TRANSFORMAREA IDENTITATII

EXPRESII LOGARITMICE"

Cunoștințe și abilități pe care elevii ar trebui să le stăpânească după ce au studiat această lecție:

cunoașteți definiția logaritmului unui număr, identitatea logaritmică de bază, proprietățile logaritmilor;

să poată efectua transformări ale expresiilor care conțin logaritmi, să calculeze logaritmi.

Literatură:

1. Alimov Sh.A., Kolyagin Yu.M., Sidorov Yu.V. şi altele.Algebra şi începutul analizei: un manual pentru clasele 10-11 institutii de invatamant. - M .: Educație, 2001.

2. Kochagin V.V., Kochagina M.V., Curs intensiv de pregătire pentru examen. – M.: Eksmo, 2009.

3. A. G. Merzlyak, V. B. Polonsky și M. S. Yakir, Simulator algebric: un ghid pentru școlari și solicitanți. – M.: Ileksa, 2005.

4. Gusev V.A., Mordkovich A.G. Matematică: Materiale de referință: O carte pentru elevi. - M .: Educație, 2001.

Planul lecției:

În timpul orelor:

1) Logaritmul este cuvânt grecesc, care constă din 2 cuvinte: „logos” - relație, „arithmos” - număr. Deci logaritmul este numărul care măsoară raportul. O publicație din 1614 a raportat că Napier a inventat logaritmi. Mai târziu, el a compilat tabele logaritmice, care acum ne sunt cunoscute ca tabelele lui Bradys. În mai puțin de un secol, tabelele s-au răspândit în întreaga lume și au devenit un instrument de calcul indispensabil. În viitor, acestea au fost, parcă, încorporate într-un dispozitiv convenabil care accelerează extrem de mult procesul de calcul - o regulă de calcul, care a fost folosită până în anii șaptezeci ai secolului XX.

Atasamentul 1.

2) logaritm număr pozitivb prin rațiune A, în plus mai mare decât zero și nu egal cu unu,este exponentul la care trebuie ridicat un numărA pentru a obține numărulb.

Această egalitate care exprimă definiția logaritmului se numeșteidentitate logaritmică de bază .

C

SAU 1

P

Baza gradului și baza logaritmului sunt șaptesprezece, ceea ce înseamnă că, conform identității logaritmice de bază, valoarea expresiei este de trei.

Vom lucra verbal:

SCH
ELCHOK

O secunda de jos este zero virgulă cinci zecimi, deci expresia este egală cu rădăcina pătrată aritmetică a lui cinci.

P

anexa 2.

Egalitatea înseamnă că

Din definiția logaritmului se obțin următoarele egalități importante:

De exemplu:

P
anexa 3.

Să trecem la USE sarcini:

Anexa 4

3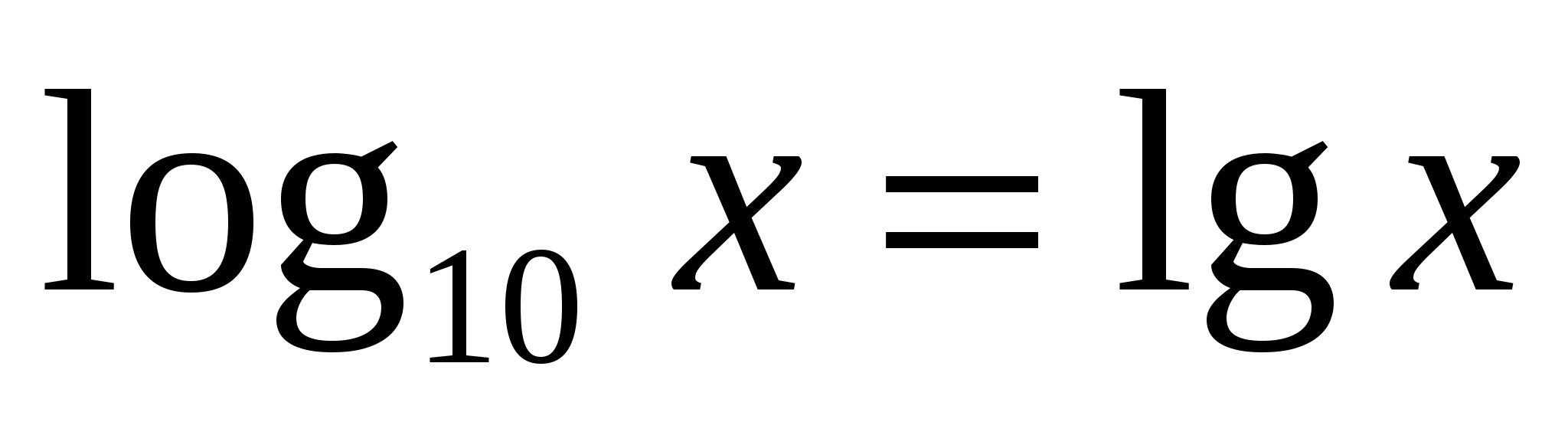
) Există o notație și un nume special pentru logaritmul de bază zece.logaritm zecimal .

L
aritmul la bazăe numitlogaritmul natural .

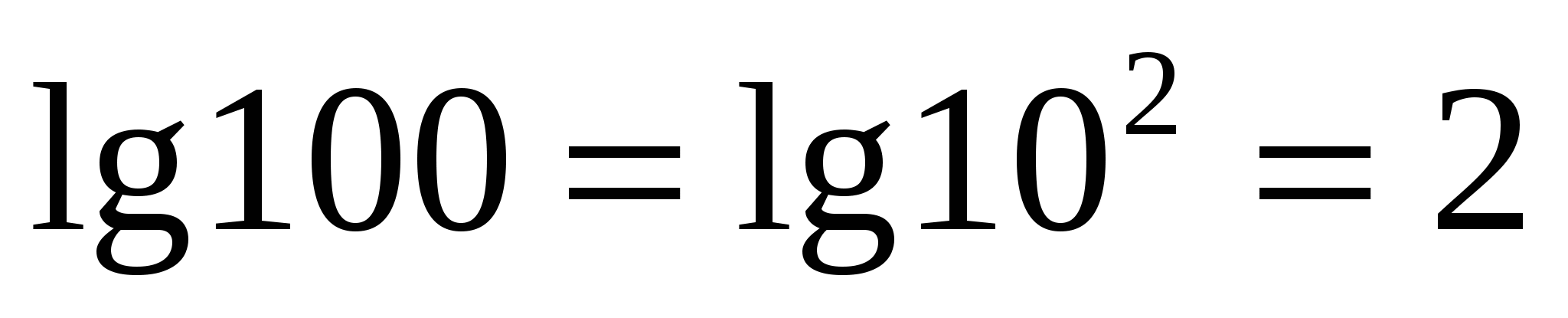
H
de exemplu,

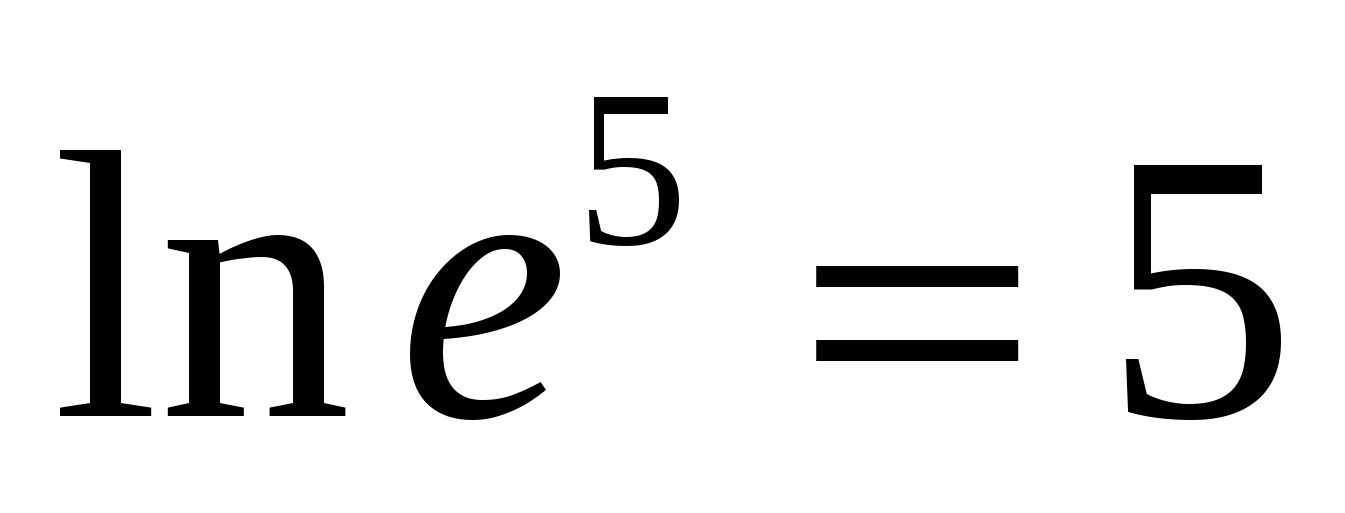
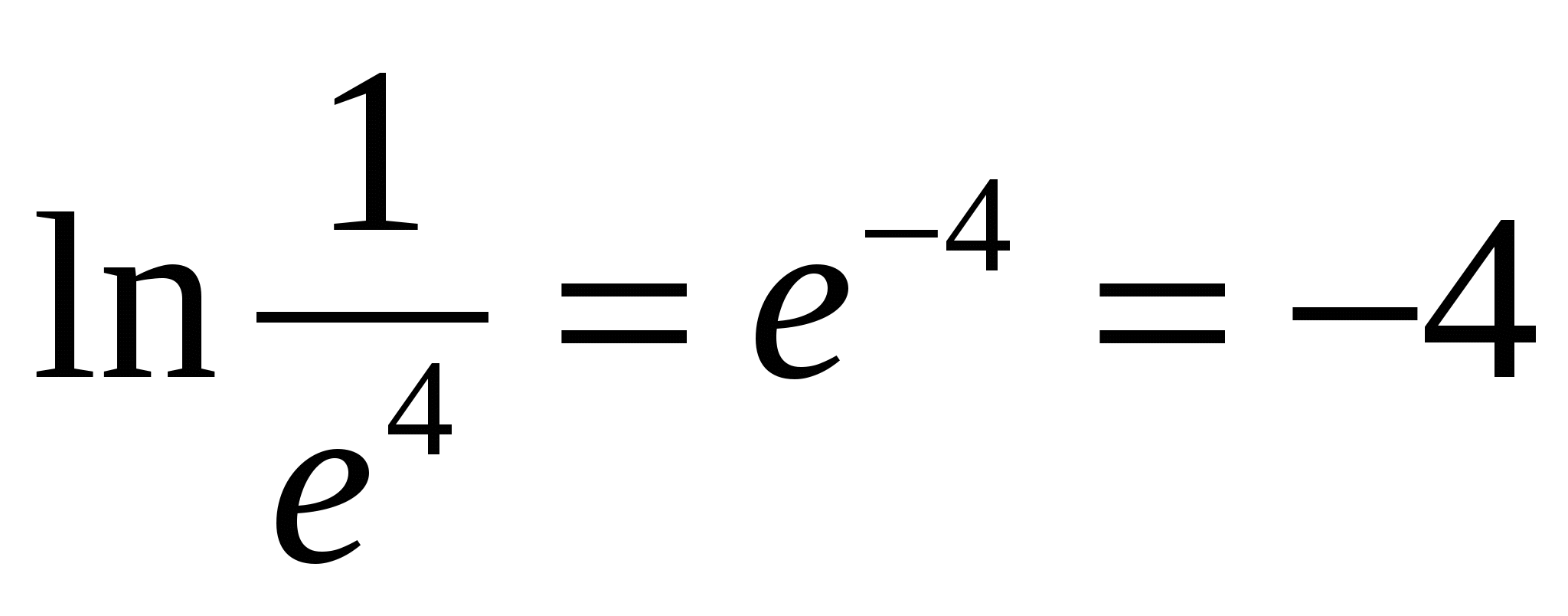
4) Următoarele proprietăți rezultă din definiția logaritmului. Toate proprietățile sunt formulate și dovedite numai pentru valorile pozitive ale variabilelor conținute sub semne logaritmice.

Logaritmul de bază al produsului a două numere pozitive A este egală cu suma logaritmi ale acestor numere cu aceeași bază.

DER 2

De exemplu,

W
Alocarea 1.

Sarcina 2. Simplificați expresia

LA
Să folosim exemplul anterior. Să înlocuim

Rețineți că logaritmul este pătrat, deci și suma trebuie să fie pătrat. Folosind formula pentru pătratul sumei, deschideți parantezele. Prezentăm termeni similari.

5) Logaritmul coeficientului este egal cu diferența dintre logaritmii dividendului și divizorului.

C

Atenție la baza gradului și la baza logaritmului - sunt aceleași.

SAU 3

R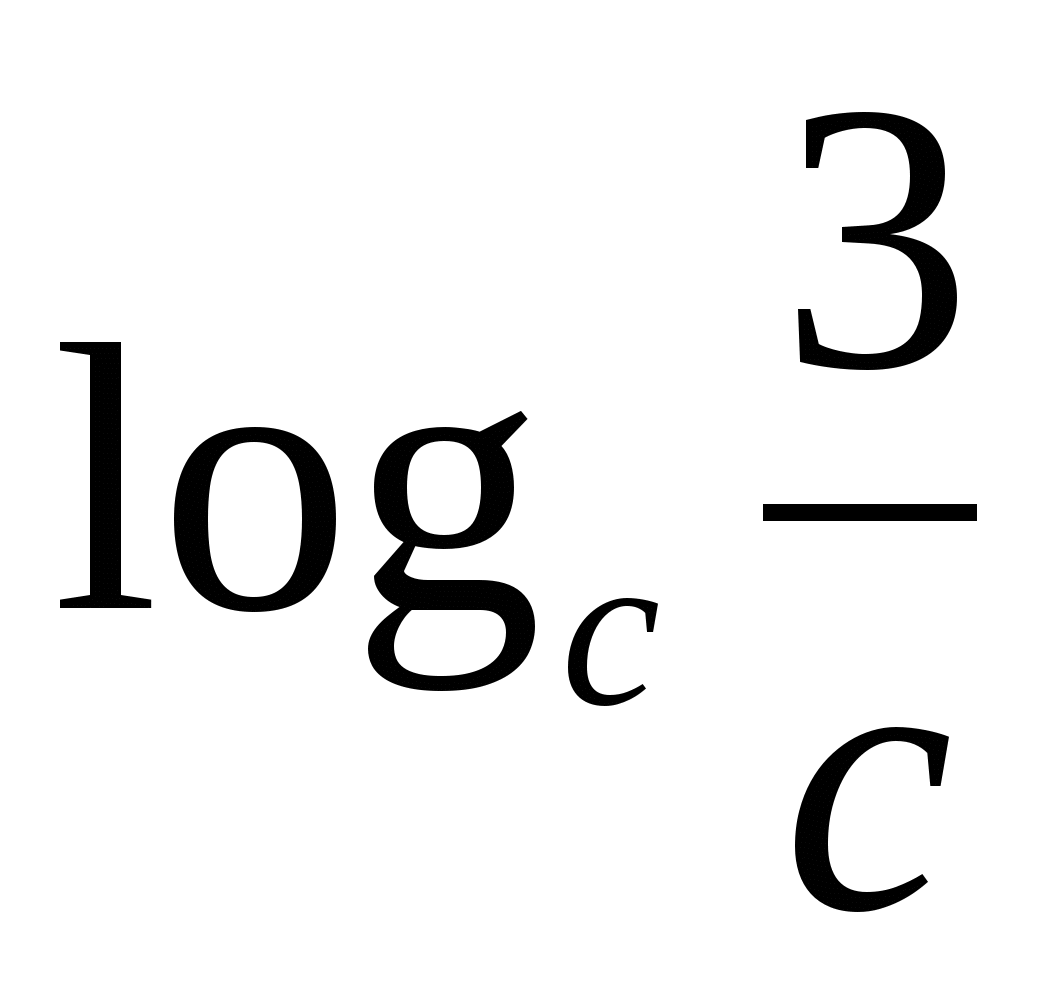

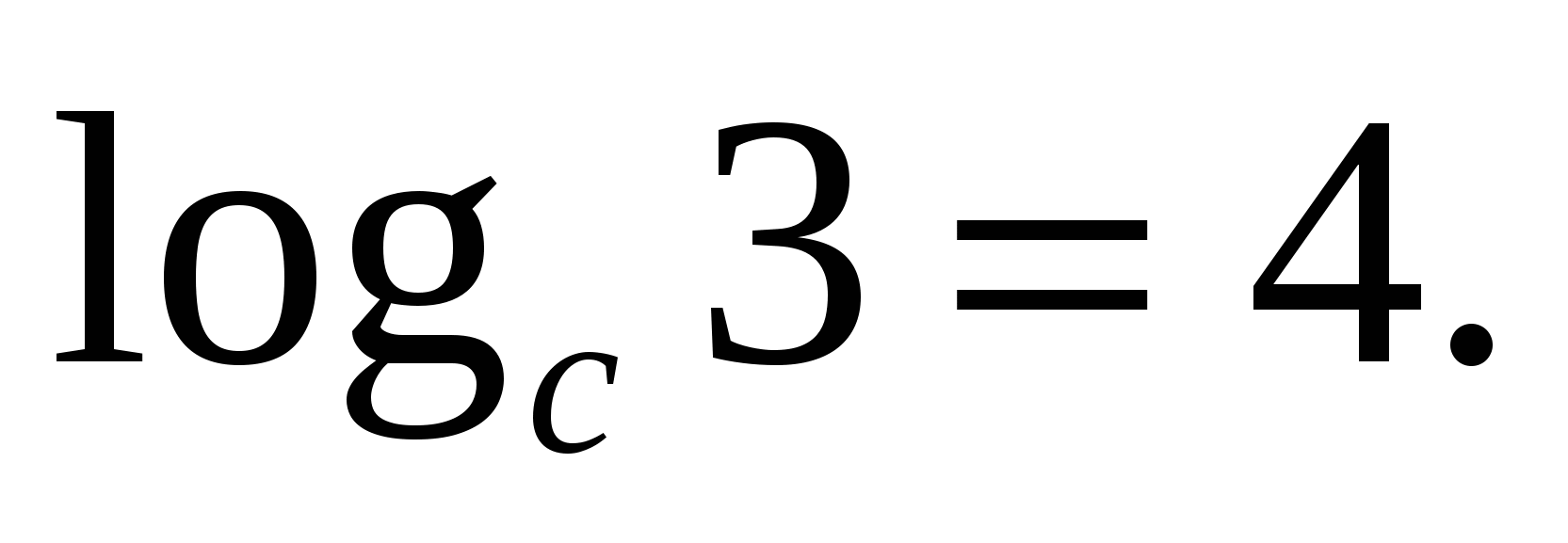Să ne uităm la aplicarea acestei formule cu un exemplu:

W
Alocarea 1. Găsiți valoarea expresiei dacă

Sarcina 2. Găsiți valoarea b prin logaritmul său

6) Logaritmul gradului la bazăA , este egal cu produsul exponent pe logaritm în aceeași bază.

DER 4

De exemplu,

W
Alocarea 1. Calculați dacă

Să simplificăm expresia

Formulă

numit formula de tranziție la o nouă bază.

W

Alocarea 1. Exprimați în termeni de logaritm cu baza 2.

Sarcina 2. calculati

CER 5

CER 6

De exemplu,

W

Alocarea 1. calculati

W
sarcina 2. calculati

9) Puteți începe transformări logaritmice numai dacă dacă vă amintiți toate proprietățile logaritmilor. După ce le-am repetat, vom lua în considerare sarcini pentru transformarea expresiilor logaritmice din cealaltă parte.

Pentru a converti suma sau diferența expresiilor logaritmice, uneori este suficient să folosiți definiția logaritmului și cel mai adesea proprietățile logaritmului produsului sau al coeficientului.

W
Alocarea 1. calculati

Să o rezolvăm în două moduri.

1 mod, folosind definiția logaritmului:

Metoda 2 bazată pe Proprietatea logaritmului coeficientului:

Sarcina 2. Găsiți valoarea unei expresii

Mai întâi să aplicăm formula logaritmul produsului, apoi definiția logaritmului.

Identitatea logaritmică de bază este utilizată la conversia expresiilor care conțin un logaritm în exponent. Ideea unor astfel de operații este de a obține baza exponentului și baza logaritmului egale.

Uneori este necesar să se transforme expresia de proprietățile logaritmului și de proprietățile gradului, de asemenea se poate trece cu ușurință de la o bază la alta folosind formula de tranziție. În alte cazuri, ar trebui aplicate mai multe proprietăți.

W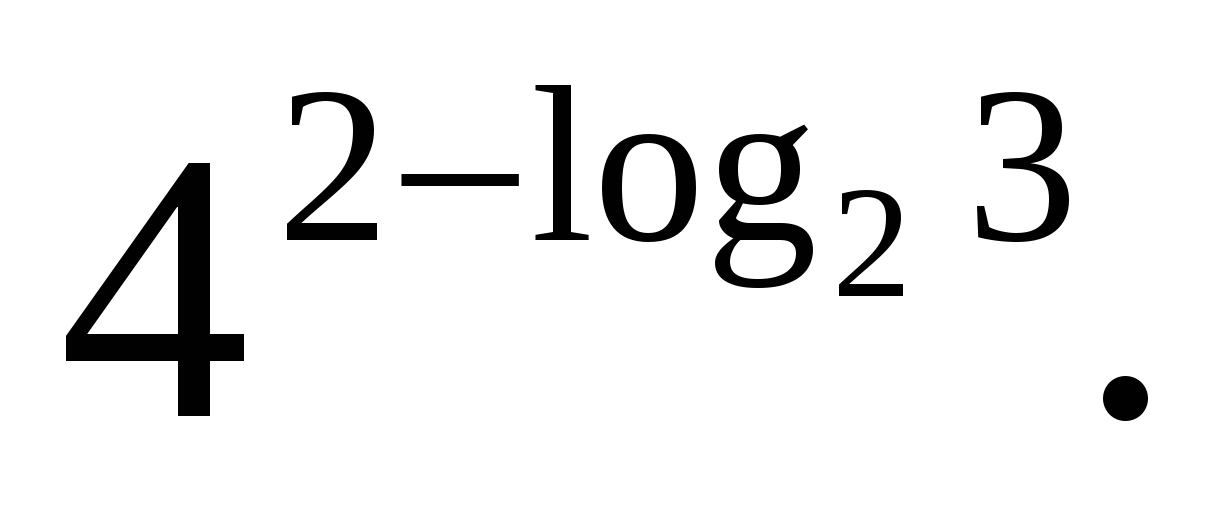
sarcina 3. calculati

W
sarcina 4. Găsiți valoarea unei expresii

Sarcina 5. Găsiți valoarea unei expresii

W
sarcina 6. Exprimați ca diferență de logaritmi

H
Cea mai mare dificultate este transformarea expresiilor logaritmice sub radical. În procesul transformărilor, trebuie luate în considerare modulele expresiilor logaritmice, pentru a căror dezvăluire este necesară compararea numerelor iraționale sau a numerelor raționale și iraționale. Vom acționa consecvent. Luați în considerare expresia sub radicalul interior.

Înlocuiți în expresia originală.

De remarcat că transformarea expresiilor logaritmice poate fi întâlnită și la rezolvarea ecuațiilor și inegalităților sau studierea funcțiilor, prin urmare, sub formă implicită, acestea pot fi prezente și în atribuțiile grupelor B și C.

10) Rezumat Întrebări:

Se numește logaritmul de bază 10

logaritm de bază

logaritmul principal

logaritmul natural

logaritm zecimal

2) Ce valori potX în exprimare

Valoarea nu este definită

5) Indicați raportul care este adevărat pentru toțiX ≠ 0 .

6) Specificați raportul corect pentru formula de tranziție la o nouă bază.

7) Indicați egalitatea corectă pentru

11) Testarea de control.

transnistreană Universitate de stat

lor. T.G. Şevcenko

Facultatea de Fizică și Matematică

Departamentul de Analiză Matematică

și metode de predare a matematicii

LUCRARE DE CURS

„Transformări de identitate

exponențial și logaritmic

expresii"

Lucrare finalizata:

elev din grupa ______

Facultatea de Fizică și Matematică

_________________________

Lucrare verificata:

_________________________

Tiraspol, 2003

Introducere……………………………………………………………………………… 2

Capitolul 1

§unu. Formarea deprinderilor de aplicare a unor tipuri specifice de transformări…………………………………………………………………………………………….4

§2. Trăsături ale organizării unui sistem de cunoștințe în studiul transformărilor identice……….………………………….………..…………..5

§3. Programul de matematică ……………………………………….11

capitolul 2

§unu. Generalizarea conceptului de grad………………………………………………..13

§2. Funcția exponențială……………………………………………………..15

§3. Funcția logaritmică………………………………………….16

Capitolul 3. Transformări identice ale expresiilor exponențiale și logaritmice în practică ...................................... ......................................................19

Concluzie………………………………………………………………………..24

Lista literaturii utilizate…………………………………………….25
Introducere

Acest lucru de curs va lua în considerare transformările identice ale funcțiilor exponențiale și logaritmice, va lua în considerare metodologia de predare a acestora în cursul școlar de algebră și începutul analizei.

Primul capitol al acestei lucrări descrie metodologia de predare a transformărilor identice în cursul școlar de matematică, include și un program de matematică la cursul „Algebra și începutul analizei” cu studiul funcțiilor exponențiale și logaritmice.

Al doilea capitol tratează direct funcțiile exponențiale și logaritmice în sine, principalele lor proprietăți utilizate în transformări identice.

Al treilea capitol este rezolvarea de exemple și probleme folosind transformările identice ale funcțiilor exponențiale și logaritmice.

Studiul diferitelor transformări ale expresiilor și formulelor ocupă o parte semnificativă a timpului de studiu în cursul matematicii școlare. Cele mai simple transformări bazate pe proprietățile operațiilor aritmetice sunt deja efectuate în scoala primara iar în clasele IV-V. Dar sarcina principală a formării deprinderilor și abilităților de a efectua transformări este suportată de cursul algebrei școlare. Aceasta este legată atât de creșterea bruscă a numărului și varietatea transformărilor efectuate, cât și de complicarea activităților de fundamentare a acestora și de clarificare a condițiilor de aplicabilitate, cu identificarea și studiul conceptelor generalizate de identitate, transformare identică, transformare echivalentă, consecință logică.

Cultura efectuării transformărilor identice se dezvoltă în același mod ca și cultura calculului, bazată pe o cunoaștere solidă a proprietăților operațiilor asupra obiectelor (numere, vectori, polinoame etc.) și a algoritmilor de implementare a acestora. Se manifestă nu numai prin capacitatea de a justifica corect transformările, ci și prin capacitatea de a găsi calea cea mai scurtă către trecerea de la expresia analitică originală la expresia care se potrivește cel mai bine scopului transformării, în capacitatea de a urmări schimbările în domeniul definirii expresiilor analitice într-un lanț de transformări identice, în execuția rapidă și fără erori a transformărilor.

Asigurarea unei culturi înalte a calculului și a transformărilor identice este o problemă importantă în predarea matematicii. Cu toate acestea, această problemă este încă departe de a fi rezolvată satisfăcător. Dovadă în acest sens sunt datele statistice ale autorităților din învățământul public, în care anual se constată erori și metode iraționale de calcule și transformări efectuate de elevi. diverse claseîn timp ce face lucrări de control. Acest lucru este confirmat de opiniile superioarelor institutii de invatamant despre calitatea cunoștințelor și aptitudinilor matematice ale solicitanților. Nu se poate decât să fie de acord cu concluziile autorităților din învățământul public și ale universităților că nu este suficient nivel inalt cultura de calcul și transformări identice în liceu este o consecință a formalismului în cunoașterea studenților, separarea teoriei de practică.

Transformări identitare și metode de predare

în cursul şcolar de algebră şi începutul analizei.

§unu. Formarea abilităților de aplicare

tipuri specifice de transformări.

Sistemul de metode și reguli de efectuare a transformărilor, utilizat în stadiul începuturilor algebrei, are o gamă foarte largă de aplicații: este utilizat în studiul întregului curs de matematică. Cu toate acestea, tocmai din cauza specificității sale scăzute, acest sistem are nevoie de transformări suplimentare care să țină cont de particularitățile structurii expresiilor transformate și de proprietățile operațiilor și funcțiilor nou introduse. Dezvoltarea tipurilor corespunzătoare de transformări începe cu introducerea formulelor de înmulțire abreviate. Apoi luăm în considerare transformările asociate cu operația de exponențiere, cu diferite clase functii elementare- exponenţial, putere, logaritmic, trigonometric. Fiecare dintre aceste tipuri de transformări trece printr-o etapă de studiu, în care atenția este concentrată pe asimilarea trăsăturilor lor caracteristice.

Odată cu acumularea de material, devine posibilă evidențierea trăsăturilor comune tuturor transformărilor luate în considerare și, pe această bază, introducerea conceptelor de transformări identice și echivalente.

Trebuie remarcat faptul că conceptul unei transformări identice este dat în cursul școlar de algebră nu în generalitate deplină, ci doar în aplicare la expresii. Transformările sunt împărțite în două clase: transformările identice sunt transformări ale expresiilor, iar transformările echivalente sunt transformări ale formulelor. În cazul în care este necesară simplificarea unei părți a formulei, în această formulă este evidențiată o expresie, care servește drept argument pentru transformarea identică aplicată. Predicatul corespunzător este considerat neschimbat.

În ceea ce privește organizarea unui sistem integral de transformări (sinteză), scopul său principal este formarea unui sistem flexibil și puternic; aparat adecvat pentru a fi utilizat în rezolvarea unei varietăți de sarcini educaționale.

În cursul algebrei și începutul analizei, un sistem integral de transformări, deja format în principalele sale caracteristici, continuă să fie îmbunătățit treptat. I se adaugă și unele noi tipuri de transformări, dar nu fac decât să-l îmbogățească, să-i extindă capacitățile, dar nu îi schimbă structura. Metodologia de studiu a acestor noi transformări practic nu diferă de cea folosită în cursul algebrei.

§2. Caracteristici ale organizării sistemului de sarcini

în studiul transformărilor identice.

Principiul de bază al organizării oricărui sistem de sarcini este de a le prezenta de la simplu la complex, ținând cont de necesitatea elevilor de a depăși dificultățile fezabile și de a crea situații problematice. Principiul de bază precizat necesită concretizare în raport cu trăsăturile acestui material educațional. Pentru a descrie diverse sisteme de sarcini din metodologia matematicii, se folosește conceptul de ciclu de exerciții. Ciclul de exerciții se caracterizează prin combinarea în succesiunea de exerciții a mai multor aspecte ale studiului și metode de aranjare a materialului. În legătură cu transformările identice, ideea unui ciclu poate fi dată după cum urmează.

Ciclul de exerciții este legat de studiul unei identități, în jurul căreia se grupează alte identități, care se află într-o legătură firească cu aceasta. Alcătuirea ciclului, împreună cu sarcinile executive, include sarcini care necesită recunoașterea aplicabilității identității luate în considerare. Identitatea studiată este utilizată pentru a efectua calcule pe diverse domenii numerice. Se ține cont de specificul identității; în special, sunt organizate rânduri de vorbire asociate acestuia.

Sarcinile din fiecare ciclu sunt împărțite în două grupe. Prima include sarcini efectuate în timpul cunoașterii inițiale cu identitatea. Ei servesc material educațional pentru mai multe lecții consecutive, unite printr-o singură temă. Al doilea grup de exerciții leagă identitatea studiată cu diverse aplicații. Acest grup nu formează o unitate compozițională - exercițiile de aici sunt împrăștiate pe diverse subiecte.

Structura descrisă a ciclului se referă la etapa de formare a deprinderilor de aplicare a unor tipuri specifice de transformări. În etapa finală - etapa de sinteză, ciclurile sunt modificate. În primul rând, ambele grupuri de sarcini sunt combinate, formând un ciclu „desfășurat”, iar cele mai simple în ceea ce privește formularea sau complexitatea executării sarcinilor sunt excluse din primul grup. Tipurile rămase de sarcini devin mai dificile. În al doilea rând, există o contopire a ciclurilor legate de diferite identități, datorită căreia rolul acțiunilor de recunoaștere a aplicabilității uneia sau alteia identități crește.

Remarcăm caracteristicile ciclurilor de sarcini legate de identități pentru funcții elementare. Aceste caracteristici se datorează faptului că, în primul rând, identitățile corespunzătoare sunt studiate în legătură cu studiul materialului funcțional și, în al doilea rând, apar mai târziu decât identitățile primului grup și sunt studiate folosind abilități deja formate pentru a efectua transformări identice. .

Fiecare funcție elementară nou introdusă extinde drastic gama de numere care pot fi desemnate și denumite individual. Prin urmare, primul grup de sarcini ale ciclurilor ar trebui să includă sarcini pentru a stabili o conexiune între aceste noi regiuni numerice și regiunea inițială a numerelor raționale. Dăm exemple de astfel de sarcini.

Exemplul 1 Calculați:

Lângă fiecare expresie, există o identitate, în ciclurile pentru care sarcinile propuse pot fi prezente. Scopul unor astfel de sarcini este de a stăpâni caracteristicile înregistrărilor, inclusiv simbolurile de noi operațiuni și funcții, și de a dezvolta abilități de vorbire matematică.

O parte semnificativă a utilizării transformărilor identitare asociate cu funcțiile elementare revine soluției ecuațiilor iraționale și transcendentale. Ciclurile legate de asimilarea identităților cuprind doar cele mai simple ecuații, dar deja aici este recomandabil să se lucreze la stăpânirea metodei de rezolvare a unor astfel de ecuații: reducerea acesteia prin înlocuirea necunoscutului cu o ecuație algebrică.

Secvența de pași pentru această soluție este următoarea:

a) găsiți o funcție pentru care această ecuație poate fi reprezentată ca ;

b) faceți o înlocuire și rezolvați ecuația;

c) rezolvați fiecare dintre ecuațiile , unde este mulțimea rădăcinilor ecuației .

Atunci când se folosește metoda descrisă, pasul b) este adesea efectuat implicit, fără a introduce o notație pentru . În plus, elevii aleg adesea dintre diferitele căi care duc la găsirea unui răspuns, să o aleagă pe cea care duce la ecuația algebrică mai rapid și mai ușor.

Exemplul 2. Rezolvați ecuația.

Prima cale:

A doua cale:

A)

b)

Se poate observa aici că pasul a) este mai dificil în prima metodă decât în ​​a doua. Prima modalitate este „mai greu de început”, deși următorul curs al soluției este mult mai ușor. Pe de altă parte, a doua metodă are avantaje, constând într-o ușurință mai mare, o mai mare sofisticare în predarea reducerii la o ecuație algebrică.

Pentru un curs școlar de algebră, sarcinile sunt tipice în care trecerea la o ecuație algebrică este chiar mai ușoară decât în ​​acest exemplu. Sarcina principală a unor astfel de sarcini se referă la selectarea etapei c) ca parte independentă a procesului de soluție asociată cu utilizarea proprietăților funcției elementare studiate.

Exemplul 3. Rezolvați ecuația:

A) ; b) .

Aceste ecuații se reduc la ecuațiile: a) sau ; b) sau. Pentru a rezolva aceste ecuații, este necesară cunoașterea doar a celor mai simple fapte despre funcția exponențială: monotonitatea acesteia, intervalul de valori. La fel ca exemplul anterior, ecuațiile a) și b) pot fi atribuite primei grupe a unui ciclu de exerciții pentru rezolvarea ecuațiilor exponențiale pătratice.

Astfel, ajungem la clasificarea sarcinilor în cicluri legate de rezolvarea ecuațiilor transcendentale, incluzând o funcție exponențială:

1) ecuatii care se reduc la ecuatii de forma si au un raspuns simplu, general ca forma: ;

2) ecuații care se reduc la ecuații , unde este un număr întreg, sau , unde ;

3) ecuații care se reduc la ecuații și necesită o analiză explicită a formei în care este scris numărul.

Sarcini similare pot fi clasificate pentru alte funcții elementare.

O parte semnificativă a identităților studiate la cursurile de algebră și algebră și începuturile analizei sunt dovedite în acestea sau cel puțin explicate. Această latură a studiului identităţilor are mare importanță pentru ambele cursuri, întrucât raționamentul demonstrativ în ele se realizează cu cea mai mare claritate și rigoare tocmai în raport cu identitățile. În afara acestui material, dovezile sunt de obicei mai puțin complete, nu se disting întotdeauna de componența mijloacelor de justificare aplicate.

Proprietățile operațiilor aritmetice sunt folosite ca suport pe care se construiesc dovezile identităților.

Impactul educațional al calculelor și transformărilor identice poate fi direcționat spre dezvoltare gandire logica, dacă numai elevilor li se cere sistematic să justifice calcule și transformări identice, să dezvolte gândirea funcțională, care se realizează în diverse moduri. Importanța calculelor și a transformărilor identice în dezvoltarea voinței, memoriei, ingeniozității, autocontrolului și inițiativei creatoare este destul de evidentă.

Solicitările pentru practica de calcul industrială de zi cu zi necesită formarea unor abilități puternice, automate de calcule raționale și transformări identice la studenți. Aceste abilități sunt dezvoltate în procesul oricărei lucrări de calcul, cu toate acestea, sunt necesare abilități speciale. exerciții de antrenamentîn calcule și transformări rapide.

Deci, dacă lecția implică rezolvarea ecuațiilor logaritmice folosind identitatea logaritmică de bază, atunci este util să includeți exerciții orale în planul lecției pentru a simplifica sau calcula valorile expresiilor: , , . Scopul exercițiilor este întotdeauna comunicat elevilor. În timpul exercițiului, poate fi necesar să se solicite elevilor să justifice transformări, acțiuni individuale sau să rezolve întreaga problemă, chiar dacă acest lucru nu a fost planificat. Acolo unde sunt posibile moduri diferite de rezolvare a unei probleme, este întotdeauna de dorit să se pună întrebări: „În ce mod a fost rezolvată problema?”, „Cine a rezolvat problema într-un mod diferit?”

Conceptele de identitate și transformare identică, sunt introduse explicit în cursul de algebră clasa a VI-a. Însăși definiția expresiilor identice nu poate fi folosită practic pentru a dovedi identitatea a două expresii și pentru a înțelege că esența transformărilor identice constă în aplicarea expresiei a definițiilor și proprietăților acelor acțiuni care sunt indicate în expresie, sau în adăugarea acestora. lui o expresie care este identic egală cu 0, sau înmulțind-o cu o expresie identic egală cu unu. Dar, chiar dacă stăpânesc aceste prevederi, elevii de multe ori nu înțeleg de ce aceste transformări ne permit să afirmăm că expresiile originale și cele rezultate sunt identice, adică. luați aceleași valori pentru orice sisteme (seturi) de valori variabile.

De asemenea, este important să ne asigurăm că elevii înțeleg bine că astfel de concluzii ale transformărilor identice sunt consecințe ale definițiilor și proprietăților acțiunilor corespunzătoare.

Aparatul transformărilor identice, acumulat în anii anteriori, se extinde în clasa a VI-a. Această extensie începe cu introducerea unei identități care exprimă proprietatea produsului de puteri cu aceleași baze: , unde , sunt numere întregi.

§3. Programul de matematică. La cursul școlar „Algebra și începuturile analizei”, elevii studiază sistematic funcțiile exponențiale și logaritmice și proprietățile lor, transformările identice ale expresiilor logaritmice și exponențiale și aplicarea acestora la rezolvarea ecuațiilor și inegalităților corespunzătoare, se familiarizează cu conceptele de bază, enunțurile. . În clasa a XI-a, lecțiile de algebră durează 3 ore pe săptămână, pentru un total de 102 ore pe an. Este nevoie de 36 de ore pentru a studia funcțiile exponențiale, logaritmice și de putere conform programului. Programul include luarea în considerare și studiul următoarelor aspecte: Conceptul de diplomă cu un indicator rațional. Rezolvarea ecuațiilor iraționale. O funcție exponențială, proprietățile și graficul acesteia. transformări identice ale expresiilor exponenţiale. Rezolvarea ecuațiilor exponențiale și a inegalităților. Logaritmul unui număr. Proprietățile de bază ale logaritmilor. Funcția logaritmică, proprietățile și graficul acesteia. Rezolvarea ecuațiilor și inegalităților logaritmice. Derivată a funcției exponențiale. Numărul și logaritmul natural. Derivată a unei funcții de putere. Scopul principal al secțiunii despre studiul funcțiilor exponențiale și logaritmice este de a familiariza elevii cu funcțiile exponențiale, logaritmice și de putere; invata elevii sa rezolve exponential si ecuații logaritmiceși inegalități. Conceptele de rădăcină de gradul al-lea și de gradul cu exponent rațional sunt o generalizare a conceptelor de rădăcină pătrată și gradul cu exponent întreg. Elevii ar trebui să acorde atenție faptului că proprietățile rădăcinilor și gradelor cu un exponent rațional luate în considerare aici sunt similare cu acele proprietăți care au fost studiate mai devreme. rădăcini pătrateși grade cu exponenți întregi. Este necesar să se dedice suficient timp elaborării proprietăților gradelor și formării abilităților pentru transformări identice. Conceptul de grad cu indicator irațional introdus pe o bază vizual-intuitivă. Acest material joacă un rol auxiliar și este utilizat la introducerea funcției exponențiale. Studiul proprietăților funcțiilor exponențiale, logaritmice și de putere este construit în conformitate cu normele acceptate. schema generala cercetarea funcţiei. În acest caz, se oferă o prezentare generală a proprietăților în funcție de valorile parametrilor. Inegalitățile exponențiale și logaritmice sunt rezolvate pe baza proprietăților studiate ale funcțiilor. O trăsătură caracteristică a cursului este sistematizarea și generalizarea cunoștințelor studenților, consolidarea și dezvoltarea abilităților și abilităților dobândite în cursul de algebră, care se realizează atât la studierea materialelor noi, cât și la efectuarea unei repetiții generalizatoare.
capitolul 2

§unu. Generalizarea conceptului de grad.

Definiție: Rădăcina gradului de puritate este un astfel de număr, al cărui grad este egal cu.

Conform acestei definiții, rădăcina gradului al treilea al unui număr este o soluție a ecuației. Numărul de rădăcini ale acestei ecuații depinde de și . Să luăm în considerare o funcție. După cum se știe, pe interval această funcție crește pentru oricare și ia toate valorile din intervalul . După teorema rădăcinii, ecuația pentru oricare are o rădăcină nenegativă și, în plus, doar una. Se numește rădăcina aritmetică a gradului al-lea al unui număr și se notează; numărul se numește indicele rădăcinii, iar numărul însuși se numește expresie radicală. Semnul este numit și radical.

Definiție: Rădăcina aritmetică a gradului al treilea al unui număr este un număr nenegativ al cărui grad este .

Pentru chiar, funcția este pare. Rezultă că dacă , atunci ecuația , pe lângă rădăcină , are și rădăcină . Dacă , atunci există o singură rădăcină: ; dacă , atunci această ecuație nu are rădăcini, deoarece puterea pară a oricărui număr este nenegativă.

Pentru valorile impare, funcția crește de-a lungul întregii linii numerice; intervalul său este mulțimea tuturor numerelor reale. Aplicând teorema rădăcinii, constatăm că ecuația are o rădăcină pentru oricare și, în special, pentru . Această rădăcină pentru orice valoare este notă cu .

Pentru rădăcinile de grad impar, egalitatea este adevărată. Într-adevăr, , i.e. numărul este rădăcina-a a lui . Dar o astfel de rădăcină pentru ciudat este unică. Prin urmare, .

Observație 1: Pentru orice real

Amintiți-vă proprietățile binecunoscute ale rădăcinilor aritmetice de gradul al treilea.

Pentru orice natural, întreg și orice numere întregi și egalități nenegative sunt adevărate:

1.

2.

3.

4.

Grad cu un exponent rațional.

Expresia este definită pentru toate și , cu excepția cazului în care . Amintiți-vă proprietățile unor astfel de puteri.

Pentru orice numere și orice numere întregi și egalități sunt adevărate:

De asemenea, menționăm că dacă , atunci pentru și pentru .. și

Pentru studenții care studiază pentru examenul de stat unificat, profesorii de matematică de la școala secundară nr. 26 din Yakutsk folosesc o listă de întrebări de conținut (codificator) ale cursului de matematică școlară, a căror asimilare este verificată la promovarea examenului de stat unificat în 2007. . curs opționalîn pregătirea pentru Unificare Examen de stat se bazează pe repetarea, sistematizarea și aprofundarea cunoștințelor dobândite anterior. Cursurile se desfășoară sub formă de...

Egalitățile enumerate la conversia expresiilor cu logaritmi sunt utilizate atât de la dreapta la stânga, cât și de la stânga la dreapta.

Este de remarcat faptul că nu este necesar să memorați consecințele proprietăților: atunci când efectuați transformări, vă puteți descurca cu proprietățile de bază ale logaritmilor și ale altor fapte (de exemplu, cele pentru b≥0), din care corespunzătoare urmează consecințele. „Efectul secundar” al acestei abordări este doar că soluția va fi puțin mai lungă. De exemplu, pentru a face fără consecință, care este exprimată prin formula , și pornind doar de la proprietățile de bază ale logaritmilor, va trebui să efectuați un lanț de transformări de următoarea formă: .

Același lucru se poate spune despre ultima proprietate din lista de mai sus, care corespunde formulei , deoarece rezultă și din proprietățile de bază ale logaritmilor. Principalul lucru de înțeles este că este întotdeauna posibil ca gradul unui număr pozitiv cu un logaritm în exponent să schimbe baza gradului și numărul de sub semnul logaritmului. Pentru dreptate, observăm că exemplele care implică implementarea unor transformări de acest fel sunt rare în practică. Vom da mai jos câteva exemple.

Conversia expresiilor numerice cu logaritmi

Ne-am amintit de proprietățile logaritmilor, acum este timpul să învățăm cum să le punem în practică pentru a transforma expresiile. Este firesc să începeți cu transformarea expresiilor numerice și nu a expresiilor cu variabile, deoarece este mai convenabil și mai ușor să învățați elementele de bază despre ele. Așa că vom face, și vom începe cu o foarte exemple simple pentru a învăța cum să alegem proprietatea dorită a logaritmului, dar vom complica treptat exemplele, până în momentul în care vor trebui aplicate mai multe proprietăți la rând pentru a obține rezultatul final.

Selectarea proprietății dorite a logaritmilor

Nu există atât de puține proprietăți ale logaritmilor și este clar că trebuie să puteți alege cea potrivită dintre ele, ceea ce în acest caz particular va duce la rezultatul dorit. De obicei, acest lucru nu este dificil de realizat comparând forma logaritmului sau expresiei convertite cu tipurile părților din stânga și din dreapta ale formulelor care exprimă proprietățile logaritmilor. Dacă este lăsat sau partea dreaptă una dintre formule coincide cu logaritmul sau expresia dată, atunci, cel mai probabil, această proprietate ar trebui utilizată în timpul transformării. Următoarele exemple demonstrează clar acest lucru.

Să începem cu exemple de transformare a expresiilor folosind definiția logaritmului, care corespunde formulei a log a b =b , a>0 , a≠1 , b>0 .

Exemplu.

Calculați, dacă este posibil: a) 5 log 5 4 , b) 10 log(1+2 π) , c) , d) 2 log 2 (−7) , e) .

Soluţie.

În exemplu, litera a) arată clar structura a log a b , unde a=5 , b=4 . Aceste numere îndeplinesc condițiile a>0 , a≠1 , b>0 , astfel încât puteți utiliza în siguranță egalitatea a log a b =b . Avem 5 log 5 4=4 .

b) Aici a=10 , b=1+2 π , sunt îndeplinite condițiile a>0 , a≠1 , b>0. În acest caz are loc egalitatea 10 lg(1+2 π) =1+2 π.

c) Și în acest exemplu avem de-a face cu un grad de forma a log a b , unde și b=ln15 . Asa de .

În ciuda faptului că aparține aceleiași forme a log a b (aici a=2 , b=−7 ), expresia de sub litera d) nu poate fi convertită prin formula a log a b =b . Motivul este că nu are sens deoarece conține un număr negativ sub semnul logaritmului. Mai mult, numărul b=−7 nu satisface condiția b>0 , ceea ce face imposibilă recurgerea la formula a log a b =b , întrucât necesită condițiile a>0 , a≠1 , b>0 . Deci, nu putem vorbi despre calcularea valorii 2 log 2 (−7) . În acest caz, scrierea 2 log 2 (−7) = −7 ar fi o eroare.

În mod similar, în exemplul de sub litera e) este imposibil să se ofere o soluție a formei , deoarece expresia originală nu are sens.

Răspuns:

a) 5 log 5 4 =4 , b) 10 log(1+2 π) =1+2 π , c) , d), e) expresiile nu au sens.

Este adesea util să se transforme număr pozitiv este reprezentat ca o putere a unui număr pozitiv și non-unu cu un logaritm în exponent. Se bazează pe aceeași definiție a logaritmului a log a b =b , a>0 , a≠1 , b>0 , dar formula se aplică de la dreapta la stânga, adică sub forma b=a log a b . De exemplu, 3=e ln3 sau 5=5 log 5 5 .

Să trecem la utilizarea proprietăților logaritmilor pentru a transforma expresii.

Exemplu.

Aflați valoarea expresiei: a) log −2 1, b) log 1 1, c) log 0 1, d) log 7 1, e) ln1, f) lg1, g) log 3,75 1, h) log 5 π 7 1 .

Soluţie.

În exemplele de sub literele a), b) și c), sunt date expresiile log −2 1 , log 1 1 , log 0 1, care nu au sens, deoarece baza logaritmului nu trebuie să conțină un număr negativ. , zero sau unu, deoarece am definit logaritmul numai pentru o bază pozitivă și non-unită. Prin urmare, în exemplele a) - c) nu se poate pune problema găsirii valorii expresiei.

În toate celelalte sarcini, în mod evident, bazele logaritmilor conțin numere pozitive și non-unități 7 , e , 10 , 3.75 și respectiv 5 π 7, iar unitățile sunt peste tot sub semnele logaritmilor. Și cunoaștem proprietatea logaritmului unității: log a 1=0 pentru orice a>0 , a≠1 . Astfel, valorile expresiilor b) - f) sunt egale cu zero.

Răspuns:

a), b), c) expresiile nu au sens, d) log 7 1=0, e) ln1=0, f) log1=0, g) log 3,75 1=0, h) log 5 e 7 1 =0 .

Exemplu.

Calculați: a) , b) lne , c) lg10 , d) log 5 π 3 −2 (5 π 3 −2), e) log −3 (−3) , f) log 1 1 .

Soluţie.

Este clar că trebuie să folosim proprietatea logaritmului bazei, care corespunde formulei log a a=1 pentru a>0 , a≠1 . Într-adevăr, în sarcinile sub toate literele, numărul de sub semnul logaritmului coincide cu baza acestuia. Astfel, vreau să spun imediat că valoarea fiecăreia dintre expresiile date este 1 . Cu toate acestea, nu vă grăbiți să trageți concluzii: în sarcinile de la literele a) - d) valorile expresiilor sunt într-adevăr egale cu unu, iar în sarcinile e) și f) expresiile originale nu au sens, deci nu se poate. se spune că valorile acestor expresii sunt egale cu 1.

Răspuns:

a) , b) lne=1 , c) lg10=1 , d) log 5 π 3 −2 (5 π 3 −2)=1, e), f) expresiile nu au sens.

Exemplu.

Aflați valoarea: a) log 3 3 11 , b) , c) , d) log −10 (−10) 6 .

Soluţie.

Evident, sub semnele logaritmilor sunt niște grade de bază. Pe baza acestui fapt, înțelegem că proprietatea gradului bazei este utilă aici: log a a p =p, unde a>0, a≠1 și p este orice număr real. Având în vedere acest lucru, avem următoarele rezultate: a) log 3 3 11 =11 , b) , în) . Este posibil să scrieți o egalitate similară pentru exemplul sub litera d) de forma log −10 (−10) 6 =6? Nu, nu poți, pentru că log −10 (−10) 6 nu are sens.

Răspuns:

a) log 3 3 11 =11, b) , în) d) expresia nu are sens.

Exemplu.

Exprimați expresia ca sumă sau diferență de logaritmi din aceeași bază: a) , b) , c) log((−5) (−12)) .

Soluţie.

a) Produsul este sub semnul logaritmului și cunoaștem proprietatea logaritmului produsului log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y> 0 . În cazul nostru, numărul din baza logaritmului și numerele din produs sunt pozitive, adică îndeplinesc condițiile proprietății selectate, prin urmare, o putem aplica în siguranță: .

b) Aici folosim proprietatea logaritmului coeficientului , unde a>0 , a≠1 , x>0 , y>0 . În cazul nostru, baza logaritmului este un număr pozitiv e, numărătorul și numitorul π sunt pozitive, ceea ce înseamnă că îndeplinesc condițiile proprietății, deci avem dreptul să folosim formula aleasă: .

c) În primul rând, rețineți că expresia lg((−5) (−12)) are sens. Dar, în același timp, nu avem dreptul să aplicăm formula pentru logaritmul produsului log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 , întrucât numerele −5 și −12 sunt negative și nu îndeplinesc condițiile x>0 , y>0 . Adică, este imposibil să efectuați o astfel de transformare: log((−5)(−12))=log(−5)+log(−12). Dar ce să faci? În astfel de cazuri, expresia originală trebuie să fie pre-transformată pentru a evita numerele negative. Despre cazuri similare de transformare a expresiilor cu numere negative sub semnul logaritmului, vom vorbi în detaliu într-unul dintre, dar deocamdată vom oferi o soluție acestui exemplu, care este clară în prealabil și fără explicații: lg((−5)(−12))=lg(5 12)=lg5+lg12.

Răspuns:

A) , b) , c) lg((−5) (−12))=lg5+lg12 .

Exemplu.

Simplificați expresia: a) log 3 0,25 + log 3 16 + log 3 0,5, b) .

Soluţie.

Aici ne vor ajuta toate aceleași proprietăți ale logaritmului produsului și ale logaritmului coeficientului pe care le-am folosit în exemplele anterioare, abia acum le vom aplica de la dreapta la stânga. Adică convertim suma logaritmilor în logaritmul produsului, iar diferența logaritmilor în logaritmul coeficientului. Avem
A) log 3 0,25+log 3 16+log 3 0,5=log 3 (0,25 16 0,5)=log 3 2.
b) .

Răspuns:

A) log 3 0,25+log 3 16+log 3 0,5=log 3 2, b) .

Exemplu.

Scăpați de gradul sub semnul logaritmului: a) log 0,7 5 11, b) , c) log 3 (−5) 6 .

Soluţie.

Este ușor de observat că avem de-a face cu expresii precum log a b p . Proprietatea corespunzătoare a logaritmului este log a b p =p log a b , unde a>0 , a≠1 , b>0 , p este orice număr real. Adică în condițiile a>0 , a≠1 , b>0 din logaritmul gradului log a b p putem merge la produsul p·log a b . Să realizăm această transformare cu expresiile date.

a) În acest caz a=0,7 , b=5 și p=11 . Deci log 0,7 5 11 =11 log 0,7 5 .

b) Aici , sunt îndeplinite condițiile a>0 , a≠1 , b>0. De aceea

c) Expresia log 3 (−5) 6 are aceeași structură log a b p , a=3 , b=−5 , p=6 . Dar pentru b, condiția b>0 nu este îndeplinită, ceea ce face imposibilă aplicarea formulei log a b p =p log a b . Deci, de ce nu poți termina treaba? Este posibil, dar este necesară o transformare prealabilă a expresiei, pe care o vom discuta în detaliu mai jos în paragraful de la rubrica . Soluția va fi așa: log 3 (−5) 6 =log 3 5 6 =6 log 3 5.

Răspuns:

a) log 0,7 5 11 =11 log 0,7 5 ,
b)
c) log 3 (−5) 6 =6 log 3 5 .

Destul de des, formula pentru logaritmul gradului atunci când se efectuează transformări trebuie aplicată de la dreapta la stânga sub forma p log a b \u003d log a b p (acest lucru necesită aceleași condiții pentru a, b și p). De exemplu, 3 ln5=ln5 3 și lg2 log 2 3=log 2 3 lg2 .

Exemplu.

a) Calculați valoarea log 2 5 dacă se știe că lg2≈0,3010 și lg5≈0,6990. b) Scrieți fracția ca logaritm în baza 3.

Soluţie.

a) Formula pentru trecerea la o nouă bază a logaritmului ne permite să reprezentăm acest logaritm ca raport al logaritmilor zecimal, ale căror valori ne sunt cunoscute: . Rămâne doar să facem calculele, avem .

b) Aici este suficient să folosiți formula pentru trecerea la o nouă bază și să o aplicați de la dreapta la stânga, adică sub forma . Primim .

Răspuns:

a) log 2 5≈2,3223, b) .

În această etapă, am analizat destul de atent transformarea celor mai simple expresii folosind proprietățile de bază ale logaritmilor și definiția unui logaritm. În aceste exemple, a trebuit să folosim o proprietate și nimic altceva. Acum, cu conștiința curată, puteți trece la exemple a căror transformare necesită utilizarea mai multor proprietăți ale logaritmilor și alte transformări suplimentare. Ne vom ocupa de ele în paragraful următor. Dar înainte de asta, să ne oprim pe scurt asupra exemplelor de aplicare a consecințelor din proprietățile de bază ale logaritmilor.

Exemplu.

a) Scăpați de rădăcina sub semnul logaritmului. b) Convertiți fracția într-un logaritm de bază 5. c) Scapa de puterile de sub semnul logaritmului si de la baza lui. d) Calculați valoarea expresiei . e) Înlocuiți expresia cu o putere cu baza 3.

Soluţie.

a) Dacă amintim corolarul din proprietatea logaritmului gradului , atunci poți răspunde imediat: .

b) Aici folosim formula de la dreapta la stânga, avem .

c) B acest caz formula conduce la rezultat . Primim .

d) Și aici este suficient să aplicăm corolarul căruia îi corespunde formula . Asa de .

e) Proprietatea logaritmului ne permite să obținem rezultatul dorit: .

Răspuns:

A) . b) . în) . G) . e) .

Aplicarea constantă a mai multor proprietăți

Sarcinile reale pentru transformarea expresiilor folosind proprietățile logaritmilor sunt de obicei mai complicate decât cele de care ne-am ocupat în paragraful anterior. În ele, de regulă, rezultatul nu se obține într-o singură etapă, dar soluția constă deja în aplicarea secvențială a unei proprietăți după alta, împreună cu transformări identice suplimentare, precum deschiderea parantezelor, reducerea termenilor similari, reducerea fracțiilor etc. . Deci haideți să ne apropiem de astfel de exemple. Nu este nimic complicat în acest sens, principalul lucru este să acționați cu atenție și consecvență, respectând ordinea în care sunt efectuate acțiunile.

Exemplu.

Calculați valoarea unei expresii (log 3 15−log 3 5) 7 log 7 5.

Soluţie.

Diferența de logaritmi între paranteze prin proprietatea logaritmului coeficientului poate fi înlocuită cu logaritmul log 3 (15:5) și apoi se calculează valoarea sa log 3 (15:5)=log 3 3=1 . Iar valoarea expresiei 7 log 7 5 după definiția logaritmului este 5 . Înlocuind aceste rezultate în expresia originală, obținem (log 3 15−log 3 5) 7 log 7 5 =1 5=5.

Iată o soluție fără explicații:
(log 3 15−log 3 5) 7 log 7 5 =log 3 (15:5) 5=
= log 3 3 5=1 5=5 .

Răspuns:

(log 3 15−log 3 5) 7 log 7 5 =5.

Exemplu.

Care este valoarea expresiei numerice log 3 log 2 2 3 −1 ?

Soluţie.

Să transformăm mai întâi logaritmul, care se află sub semnul logaritmului, după formula logaritmului gradului: log 2 2 3 =3. Deci log 3 log 2 2 3 =log 3 3 și apoi log 3 3=1 . Deci log 3 log 2 2 3 −1=1−1=0 .

Răspuns:

log 3 log 2 2 3 −1=0 .

Exemplu.

Simplificați expresia.

Soluţie.

Formula de conversie la o nouă bază a logaritmului permite ca raportul dintre logaritmi și o bază să fie reprezentat ca log 3 5 . În acest caz, expresia originală va lua forma . Prin definiția logaritmului 3 log 3 5 =5 , adică , iar valoarea expresiei rezultate, în virtutea aceleiași definiții a logaritmului, este egală cu doi.

Aici versiune scurta soluție, care este de obicei dată: .

Răspuns:

.

Pentru o tranziție lină la informațiile din următorul paragraf, să aruncăm o privire la expresiile 5 2+log 5 3 și lg0.01 . Structura lor nu se potrivește cu niciuna dintre proprietățile logaritmilor. Deci, ce se întâmplă dacă nu pot fi convertite folosind proprietățile logaritmilor? Este posibil dacă efectuați transformări preliminare care pregătesc aceste expresii pentru aplicarea proprietăților logaritmilor. Asa de 5 2+log 5 3 =5 2 5 log 5 3 =25 3=75, și lg0,01=lg10 −2 = −2 . Mai departe vom înțelege în detaliu cum se realizează o astfel de pregătire a expresiilor.

Pregătirea expresiilor pentru aplicarea proprietăților logaritmilor

Logaritmii din expresia convertită diferă foarte des în structura notației din părțile din stânga și din dreapta ale formulelor care corespund proprietăților logaritmilor. Dar la fel de des, transformarea acestor expresii implică utilizarea proprietăților logaritmilor: utilizarea lor necesită doar o pregătire preliminară. Și această pregătire constă în efectuarea anumitor transformări identice care aduc logaritmii într-o formă convenabilă pentru aplicarea proprietăților.

Pentru dreptate, observăm că aproape orice transformare a expresiilor poate acționa ca transformări preliminare, de la reducerea banală a termenilor similari la aplicare. formule trigonometrice. Acest lucru este de înțeles, deoarece expresiile convertite pot conține orice obiecte matematice: paranteze, module, fracții, rădăcini, grade etc. Astfel, trebuie să fii pregătit să efectueze orice transformare necesară pentru a beneficia în continuare de proprietățile logaritmilor.

Să spunem imediat că în această secțiune nu ne propunem sarcina de a clasifica și analiza toate transformările preliminare imaginabile care ne permit să aplicăm proprietățile logaritmilor sau definiția unui logaritm în viitor. Aici ne vom concentra doar pe patru dintre ele, care sunt cele mai caracteristice și cel mai des întâlnite în practică.

Și acum în detaliu despre fiecare dintre ele, după care, în cadrul subiectului nostru, rămâne doar să ne ocupăm de transformarea expresiilor cu variabile sub semnele logaritmilor.

Selectarea puterilor sub semnul logaritmului și în baza acestuia

Să începem imediat cu un exemplu. Să avem un logaritm. Evident, în această formă, structura sa nu este propice utilizării proprietăților logaritmilor. Este posibil să transformăm cumva această expresie pentru a o simplifica, sau chiar mai bine să-i calculăm valoarea? Pentru a răspunde la această întrebare, să aruncăm o privire mai atentă la numerele 81 și 1/9 în contextul exemplului nostru. Este ușor de observat aici că aceste numere pot fi reprezentate ca o putere a lui 3 , într-adevăr, 81=3 4 și 1/9=3 −2 . În acest caz, logaritmul original este prezentat sub formă și devine posibilă aplicarea formulei . Asa de, .

Analiza exemplului analizat dă naștere următoarei idei: dacă este posibil, puteți încerca să evidențiați gradul sub semnul logaritmului și la baza acestuia pentru a aplica proprietatea logaritmului gradului sau consecința acestuia. Rămâne doar să ne dăm seama cum să evidențiem aceste grade. Vom oferi câteva recomandări cu privire la această problemă.

Uneori este destul de evident că numărul de sub semnul logaritmului și/sau din baza lui reprezintă o putere întreagă, ca în exemplul discutat mai sus. Aproape constant ai de-a face cu puteri a lui doi, care sunt bine familiare: 4=2 2 , 8=2 3 , 16=2 4 , 32=2 5 , 64=2 6 , 128=2 7 , 256=2 8 , 512= 2 9 , 1024=2 10 . Același lucru se poate spune despre gradele triplei: 9=3 2 , 27=3 3 , 81=3 4 , 243=3 5 , ... În general, nu strica dacă există tabelul de grade numere naturale în termen de zece. De asemenea, nu este dificil să lucrezi cu puteri întregi de zece, sută, mii etc.

Exemplu.

Calculați valoarea sau simplificați expresia: a) log 6 216 , b) , c) log 0,000001 0,001 .

Soluţie.

a) Evident, 216=6 3 , deci log 6 216=log 6 6 3 =3 .

b) Tabelul puterilor numerelor naturale ne permite să reprezentăm numerele 343 și 1/243 ca puteri ale 7 3 și, respectiv, 3 −4. Prin urmare, este posibil următoarea transformare logaritm dat:

c) Deoarece 0,000001=10 −6 și 0,001=10 −3, atunci log 0,000001 0,001=log 10 −6 10 −3 =(−3)/(−6)=1/2.

Răspuns:

a) log 6 216=3, b) , c) log 0,000001 0,001=1/2 .

În cazuri mai complexe, pentru a evidenția puterile numerelor, trebuie să apelezi.

Exemplu.

Schimbați expresia la forma mai simplă log 3 648 log 2 3 .

Soluţie.

Să vedem în ce extinde numărul 648 factori primi:

Adică 648=2 3 3 4 . În acest fel, log 3 648 log 2 3=log 3 (2 3 3 4) log 2 3.

Acum convertim logaritmul produsului în suma logaritmilor, după care aplicăm proprietățile logaritmului gradului:
log 3 (2 3 3 4) log 2 3=(log 3 2 3 + log 3 3 4) log 2 3=
=(3 log 3 2+4) log 2 3 .

În virtutea corolarului proprietății logaritmului gradului, care corespunde formulei , produsul log32 log23 este produsul și se știe că este egal cu unu. Având în vedere acest lucru, obținem 3 log 3 2 log 2 3+4 log 2 3=3 1+4 log 2 3=3+4 log 2 3.

Răspuns:

log 3 648 log 2 3=3+4 log 2 3.

Destul de des, expresiile sub semnul logaritmului și în baza acestuia sunt produse sau rapoarte ale rădăcinilor și/sau puterilor unor numere, de exemplu, , . Expresii similare pot fi reprezentate ca grad. Pentru a face acest lucru, se realizează tranziția de la rădăcini la grade și se aplică. Aceste transformări vă permit să selectați gradele sub semnul logaritmului și în baza acestuia și apoi să aplicați proprietățile logaritmilor.

Exemplu.

Calculați: a) , b).

Soluţie.

a) Expresia din baza logaritmului este produsul puterilor cu aceleași baze, prin proprietatea corespunzătoare a puterilor pe care o avem 5 2 5 −0,5 5 −1 =5 2−0,5−1 =5 0,5.

Acum să transformăm fracția sub semnul logaritmului: să trecem de la rădăcină la grad, după care vom folosi proprietatea raportului de grade cu aceleași baze: .

Rămâne să înlocuiți rezultatele obținute în expresia originală, folosiți formula și terminați transformarea:

b) Deoarece 729=3 6 , și 1/9=3 −2 , expresia originală poate fi rescrisă ca .

Apoi, aplicați proprietatea rădăcinii exponentului, treceți de la rădăcină la exponent și utilizați proprietatea raportului puterilor pentru a converti baza logaritmului într-o putere: .

Ținând cont de ultimul rezultat, avem .

Răspuns:

A) , b).

Este clar că în cazul general, pentru a obține puteri sub semnul logaritmului și în baza acestuia, pot fi necesare diverse transformări ale diferitelor expresii. Să dăm câteva exemple.

Exemplu.

Care este valoarea expresiei: a) , b) .

Soluţie.

Mai mult, observăm că expresia dată are forma log A B p , unde A=2 , B=x+1 și p=4 . Am transformat expresii numerice de acest fel în funcție de proprietatea logaritmului gradului log a b p \u003d p log a b, prin urmare, cu o expresie dată, vreau să fac același lucru și să merg de la log 2 (x + 1) 4 la 4 log 2 (x + 1) . Și acum să calculăm valoarea expresiei inițiale și a expresiei obținute după transformare, de exemplu, cu x=−2 . Avem log 2 (−2+1) 4 =log 2 1=0 , și 4 log 2 (−2+1)=4 log 2 (−1)- expresie lipsită de sens. Acest lucru ridică o întrebare legitimă: „Cu ce ​​am greșit”?

Și motivul este următorul: am efectuat transformarea log 2 (x+1) 4 =4 log 2 (x+1) , pe baza formulei log a b p =p log a b , dar avem dreptul să aplicăm doar această formulă dacă condițiile a >0 , a≠1 , b>0 , p - orice număr real. Adică, transformarea pe care am făcut-o are loc dacă x+1>0 , care este același x>−1 (pentru A și p sunt îndeplinite condițiile). Totuși, în cazul nostru, ODV-ul variabilei x pentru expresia originală constă nu numai din intervalul x> −1 , ci și din intervalul x<−1 . Но для x<−1 мы не имели права осуществлять преобразование по выбранной формуле.

Necesitatea de a lua în considerare ODZ

Să continuăm să analizăm transformarea expresiei log 2 (x+1) 4 pe care am ales-o, iar acum să vedem ce se întâmplă cu ODZ la trecerea la expresia 4·log 2 (x+1) . În paragraful anterior, am găsit ODZ a expresiei originale - aceasta este mulțimea (−∞, −1)∪(−1, +∞) . Acum să găsim aria valorilor acceptabile ale variabilei x pentru expresia 4 log 2 (x+1) . Este determinată de condiția x+1>0 , care corespunde mulțimii (−1, +∞) . Este evident că atunci când treceți de la log 2 (x+1) 4 la 4·log 2 (x+1), intervalul de valori admisibile se îngustează. Și am convenit să evităm reformele care duc la o îngustare a ODZ, deoarece aceasta poate duce la diverse consecințe negative.

Aici merită să rețineți că este util să controlați ODZ la fiecare pas al transformării și să nu îi permiteți să se îngusteze. Și dacă dintr-o dată, într-un anumit stadiu al transformării, a existat o îngustare a ODZ, atunci merită să ne uităm foarte atent dacă această transformare este permisă și dacă am avut dreptul să o realizăm.

Sincer, spunem că în practică trebuie să lucrăm de obicei cu expresii în care ODZ a variabilelor este de așa natură încât ne permite să folosim proprietățile logaritmilor fără restricții în forma deja cunoscută nouă, atât de la stânga la dreapta, cât și de la de la dreapta la stânga, la efectuarea transformărilor. Te obișnuiești repede cu asta și începi să faci transformările mecanic, fără să te gândești dacă a fost posibil să le realizezi. Și în astfel de momente, după noroc, se strecoară exemple mai complexe, în care aplicarea inexactă a proprietăților logaritmilor duce la erori. Deci, trebuie să fiți mereu în alertă și să vă asigurați că nu există nicio îngustare a ODZ.

Nu strică să evidențiezi separat principalele transformări bazate pe proprietățile logaritmilor, care trebuie efectuate cu mare atenție, ceea ce poate duce la o îngustare a ODZ și, ca urmare, la erori:

Unele transformări ale expresiilor în funcție de proprietățile logaritmilor pot duce și la opus - extinderea ODZ. De exemplu, trecerea de la 4 log 2 (x+1) la log 2 (x+1) 4 extinde ODZ de la mulțimea (−1, +∞) la (−∞, −1)∪(−1, +∞ ). Astfel de transformări au loc dacă rămâneți în ODZ pentru expresia originală. Deci transformarea tocmai menționată 4 log 2 (x+1)=log 2 (x+1) 4 are loc pe variabila ODZ x pentru expresia originală 4 log 2 (x+1) , adică atunci când x+1> 0 , care este același cu (−1, +∞) .

Acum că am discutat nuanțele cărora trebuie să le acordați atenție atunci când convertiți expresii cu variabile folosind proprietățile logaritmilor, rămâne să ne dăm seama cum trebuie efectuate corect aceste conversii.

X+2>0. Functioneaza in cazul nostru? Pentru a răspunde la această întrebare, să aruncăm o privire la DPV a variabilei x. Este determinată de sistemul de inegalități , care este echivalentă cu condiția x+2>0 (dacă este necesar, vezi articolul rezolvarea sistemelor de inegalități). Astfel, putem aplica în siguranță proprietatea logaritmului gradului.

Avem
3 log(x+2) 7 −log(x+2)−5 log(x+2) 4 =
=3 7 log(x+2)−log(x+2)−5 4 log(x+2)=
=21 log(x+2)−log(x+2)−20 log(x+2)=
=(21−1−20)lg(x+2)=0 .

Puteți acționa diferit, deoarece ODZ vă permite să faceți acest lucru, de exemplu astfel:

Răspuns:

3 log(x+2) 7 −log(x+2)−5 log(x+2) 4 =0.

Și ce să faci atunci când condițiile asociate cu proprietățile logaritmilor nu sunt îndeplinite pe ODZ? Ne vom ocupa de asta cu exemple.

Să ni se ceară să simplificăm expresia lg(x+2) 4 −lg(x+2) 2 . Transformarea acestei expresii, spre deosebire de expresia din exemplul precedent, nu permite folosirea liberă a proprietății logaritmului gradului. De ce? ODZ a variabilei x în acest caz este unirea a două intervale x>−2 și x<−2 . При x>−2 putem aplica în siguranță proprietatea logaritmului gradului și procedăm ca în exemplul de mai sus: log(x+2) 4 −log(x+2) 2 =4 log(x+2)−2 log(x+2)=2 log(x+2). Dar ODZ conține un alt interval x+2<0 , для которого последнее преобразование будет некорректно. Что же делать при x+2<0 ? В подобных случаях на помощь приходит . Определение модуля позволяет выражение x+2 при x+2<0 представить как −|x+2| . Тогда при x+2<0 от lg(x+2) 4 −lg(x+2) 2 переходим к log(−|x+2|) 4 −log(−|x+2|) 2și mai departe, datorită proprietăților de putere ale lui lg|x+2| 4−lg|x+2| 2. Expresia rezultată poate fi transformată în funcție de proprietatea logaritmului gradului, deoarece |x+2|>0 pentru orice valoare a variabilei. Avem log|x+2| 4−lg|x+2| 2 =4 log|x+2|−2 log|x+2|=2 log|x+2|. Acum puteți scăpa de modul, deoarece și-a făcut treaba. Deoarece transformăm la x+2<0 , то 2·lg|x+2|=2·lg(−(x+2)) . Итак, можно считать, что мы справились с поставленной задачей. Ответ: . Полученный результат можно записать компактно с использованием модуля как .

Să luăm în considerare încă un exemplu pentru a face lucrul cu modulele familiar. Să concepem din expresie treceți la suma și diferența logaritmilor binoamelor liniare x−1 , x−2 și x−3 . Mai întâi găsim ODZ:

Pe intervalul (3, +∞), valorile expresiilor x−1 , x−2 și x−3 sunt pozitive, deci putem aplica în siguranță proprietățile logaritmului sumei și diferenței:

Și pe intervalul (1, 2), valorile expresiei x−1 sunt pozitive, iar valorile expresiilor x−2 și x−3 sunt negative. Prin urmare, pe intervalul luat în considerare, reprezentăm x−2 și x−3 folosind modulo ca −|x−2| și −|x−3| respectiv. în care

Acum putem aplica proprietățile logaritmului produsului și al coeficientului, deoarece pe intervalul considerat (1, 2) valorile expresiilor x−1 , |x−2| și |x−3| - pozitiv.

Avem

Rezultatele obținute pot fi combinate:

În general, un raționament similar permite, pe baza formulelor pentru logaritmul produsului, raportului și gradului, să se obțină trei rezultate practic utile care sunt destul de convenabile de utilizat:

• Logaritmul produsului a două expresii arbitrare X și Y de forma log a (X·Y) poate fi înlocuit cu suma logaritmilor log a |X|+log a |Y| , a>0, a≠1.
• Logaritmul special log a (X:Y) poate fi înlocuit cu diferența logaritmilor log a |X|−log a |Y| , a>0 , a≠1 , X și Y sunt expresii arbitrare.
• De la logaritmul unei expresii B la o putere pare p de forma log a B p, se poate trece la expresia p log a |B| , unde a>0 , a≠1 , p este un număr par și B este o expresie arbitrară.

Rezultate similare sunt date, de exemplu, în instrucțiunile de rezolvare a ecuațiilor exponențiale și logaritmice din colecția de probleme de matematică pentru solicitanții la universități, editată de M. I. Skanavi.

Exemplu.

Simplificați expresia .

Soluţie.

Ar fi bine să aplici proprietățile logaritmului gradului, sumei și diferenței. Dar o putem face aici? Pentru a răspunde la această întrebare, trebuie să cunoaștem ODZ.

Să o definim:

Este destul de evident că expresiile x+4 , x−2 și (x+4) 13 pe intervalul de valori posibile ale variabilei x pot lua atât valori pozitive, cât și negative. Prin urmare, va trebui să lucrăm prin module.

Proprietățile modulului vă permit să rescrieți ca , deci

De asemenea, nimic nu vă împiedică să utilizați proprietatea logaritmului gradului și apoi să aduceți termeni similari:

O altă secvență de transformări duce la același rezultat:

și deoarece expresia x−2 poate lua atât valori pozitive, cât și negative pe ODZ, atunci când se ia un exponent par 14