Dabar pažvelgsime į reiškinių, turinčių logaritmus, transformaciją bendruoju požiūriu. Čia analizuosime ne tik išraiškų transformaciją naudojant logaritmų savybes, bet nagrinėsime išraiškų transformaciją logaritmais bendras vaizdas, kuriuose yra ne tik logaritmai, bet ir laipsniai, trupmenos, šaknys ir kt. Kaip įprasta, mes pateiksime visą medžiagą su būdingais pavyzdžiais detalius aprašymus sprendimus.
Puslapio naršymas.
Išraiškos su logaritmais ir logaritminės išraiškos
Veiksmų su trupmenomis atlikimas
Ankstesnėje pastraipoje išanalizavome pagrindines transformacijas, kurios atliekamos su atskiromis trupmenomis, turinčiomis logaritmus. Žinoma, šias transformacijas galima atlikti su kiekviena atskira trupmena, kuri yra sudėtingesnės išraiškos dalis, pavyzdžiui, vaizduojanti panašių trupmenų sumą, skirtumą, sandaugą ir koeficientą. Tačiau be darbo su atskiromis trupmenomis, tokio pobūdžio išraiškų transformavimas dažnai apima atitinkamų veiksmų su trupmenomis atlikimą. Toliau apsvarstysime taisykles, pagal kurias šie veiksmai atliekami.
Nuo 5-6 klasių žinome taisykles, pagal kurias . Straipsnyje bendras operacijų su trupmenomis vaizdas mes išplatinome šias taisykles paprastosios trupmenosį bendrosios formos A/B trupmenas, kur A ir B yra kai kurie skaitiniai, pažodiniai arba išraiškos su kintamaisiais, o B identiškai nėra lygus nuliui. Aišku, kad trupmenos su logaritmais yra ypatingi bendrųjų trupmenų atvejai. Ir šiuo atžvilgiu aišku, kad veiksmai su trupmenomis, kurių įrašuose yra logaritmų, atliekami pagal tas pačias taisykles. Būtent:
- Norėdami pridėti arba atimti dvi trupmenas su tais pačiais vardikliais, atitinkamai pridėkite arba atimkite skaitiklius, o vardiklį palikite tą patį.
- Norėdami pridėti arba atimti dvi trupmenas su skirtingus vardiklius, reikia juos suvesti į bendrą vardiklį ir atlikti atitinkamus veiksmus pagal ankstesnę taisyklę.
- Norint padauginti dvi trupmenas, reikia parašyti trupmeną, kurios skaitiklis yra pradinių trupmenų skaitiklių sandauga, o vardiklis – vardklių sandauga.
- Norint padalyti trupmeną iš trupmenos, dalijamąją trupmeną reikia padauginti iš daliklio atvirkštinės vertės, tai yra, iš trupmenos, kurios skaitiklis ir vardiklis yra pertvarkyti.
Štai keli pavyzdžiai, kaip atlikti operacijas su trupmenomis, kuriose yra logaritmų.
Pavyzdys.
Atlikite veiksmus su trupmenomis, kuriose yra logaritmų: a), b) 
, in) 
, G) 
.
Sprendimas.
a) Sudėtinių trupmenų vardikliai akivaizdžiai yra vienodi. Todėl pagal trupmenų su tais pačiais vardikliais pridėjimo taisyklę pridedame skaitiklius, o vardiklį paliekame tą patį: 
.
b) Čia vardikliai yra skirtingi. Todėl pirmiausia reikia suvesti trupmenas į tą patį vardiklį. Mūsų atveju vardikliai jau pateikiami kaip sandaugai, o mums belieka paimti pirmosios trupmenos vardiklį ir prie jo pridėti trūkstamus veiksnius iš antrosios trupmenos vardiklio. Taigi gauname bendrą formos vardiklį 
. Šiuo atveju atimtos trupmenos sumažinamos iki bendro vardiklio, naudojant papildomus veiksnius atitinkamai logaritmo forma ir išraiška x 2 ·(x+1). Po to belieka atimti trupmenas su tais pačiais vardikliais, o tai nėra sunku.
Taigi sprendimas yra: 
c) Žinoma, kad trupmenų dauginimo rezultatas yra trupmena, kurios skaitiklis yra skaitiklių sandauga, o vardiklis yra vardklių sandauga, todėl 
Nesunku pastebėti, kad tai įmanoma frakcijos sumažinimas dviem ir dešimtainiu logaritmu, todėl turime 
.
d) Nuo trupmenų dalybos pereiname prie daugybos, trupmeną-daliklį pakeisdami jo abipuse. Taigi 
Gautos trupmenos skaitiklis gali būti pavaizduotas kaip 
, iš kurio aiškiai matomas bendras skaitiklio ir vardiklio koeficientas - koeficientas x, juo galite sumažinti trupmeną: 
Atsakymas:
a), b) 
, in) 
, G) 
.
Reikėtų atsiminti, kad veiksmai su trupmenomis atliekami atsižvelgiant į veiksmų atlikimo tvarką: pirmiausia daugyba ir padalijimas, tada sudėjimas ir atėmimas, o jei yra skliaustų, tada pirmiausia atliekami veiksmai skliausteliuose.
Pavyzdys.
Atlikite veiksmus su trupmenomis 
.
Sprendimas.
Pirma, sudedame trupmenas skliausteliuose, po to atliksime dauginimą: 
Atsakymas:
Šiuo metu belieka garsiai pasakyti tris gana akivaizdžius, bet kartu svarbius dalykus:
Reiškių konvertavimas naudojant logaritmų savybes
Dažniausiai išraiškų transformavimas logaritmais apima tapatybių, išreiškiančių logaritmo apibrėžimą ir naudojimą.
Matematika. Teminiai testai. II dalis. Pasirengimas vieningam valstybiniam egzaminui-2010. 10-11 klasių. Red. Lysenko F.F. - Rostovas n / D .: Legionas, 2009. - 176s.
Matematika. NAUDOJIMAS-2009. Teminiai testai. II dalis (B4-B8, C1-C2) Red. Lysenko F.F. - Rostovas n / D: Legionas, 2008 - 160 p.
Vadovas susideda iš testų atskiromis temomis, kurios yra tradicinės matematikos kursuose ir todėl paprastai įtraukiamos į egzaminą. Jie visiškai apima padidinto ir didelio USE sudėtingumo užduočių grupes, išskyrus tekstines užduotis ir geometrijos problemas. Kiekvienai temai siūlomas vienas ar daugiau testų rinkinių. Kiekviename rinkinyje yra 10 testų, kiekviename teste yra 8 užduotys.
Šios knygos tikslas – parengti užduotis su trumpais ir išsamiais USE testų atsakymais. Ji pirmiausia reikalinga absolventams, kurie tikisi gauti NAUDOTI gerai vertinimas, taip pat 10 klasės mokiniams, kurie gali įtvirtinti nagrinėjamas temas VARTOJIMO požiūriu. Siūlomas vadovas gali būti naudingas visiems absolventams, besiruošiantiems matematikos USE, taip pat mokytojams, ruošiantiems studentus USE.
Formatas: djvu/zip (2009 , 176s.)
Dydis: 2,5 MB
Atsisiųsti / atsisiųsti failą 14
Formatas: pdf (2009 , 176s.)
Dydis: 8,6 MB
Parsisiųsti: 14 .12.2018, nuorodos pašalintos Legion leidyklos prašymu (žr. pastabą)
Formatas: djvu/zip (2008 , 160 m.)
Dydis: 3 MB
Atsisiųsti / atsisiųsti failą 14 .12.2018, nuorodos pašalintos Legion leidyklos prašymu (žr. pastabą)
Formatas: pdf (2008 , 160 m.)
Dydis: 9,9 MB
Parsisiųsti: 14 .12.2018, nuorodos pašalintos Legion leidyklos prašymu (žr. pastabą)
Edukacinis-metodinis kompleksas "Matematika. Vieningas valstybinis egzaminas-2010" red. Lysenko F.F. ir Kulabukhovas S.Yu. apima pamokas:
1.
Matematika. Pasirengimas vieningam valstybiniam egzaminui-2010.
2. Rešebnikas. Matematika. Pasirengimas vieningam valstybiniam egzaminui-2010.
3. Matematika. Teminiai testai. I dalis (pagrindinis lygis). Pasirengimas vieningam valstybiniam egzaminui-2010. 10-11 klasių.
4. Matematika. Teminiai testai. II dalis. Pasirengimas vieningam valstybiniam egzaminui-2010. 10-11 klasių.
5.
Matematika. Teminiai testai: geometrija, tekstiniai uždaviniai. Pasirengimas vieningam valstybiniam egzaminui-2010. 10-11 klasių.
6.
Matematika. 2001–2010 m. NAUDOJIMO testų rinkinys.
7. Matematika. Pasirengimas vieningam valstybiniam egzaminui-2010. Treniruočių testai.
8. Kišeninis matematikos vadovas.
Turinys
Iš autorių 11
§ 1. Logaritminių išraiškų tapatybės transformacijos 13
Pasirinkimo numeris 113
Pasirinkimo numeris 2 13
Pasirinkimo numeris 3 14
Pasirinkimo numeris 4 14
Pasirinkimo numeris 5 15
Pasirinkimo numeris 6 15
Pasirinkimo numeris 7 16
Pasirinkimo numeris 8 16
Pasirinkimo numeris 9 17
Pasirinkimo numeris 10 17
§ 2. Posakių, turinčių 18 laipsnį, tapatybės transformacijos
Pasirinkimo numeris 118
Pasirinkimo numeris 2 19
Pasirinkimo numeris 3 19
Pasirinkimo numeris 4 20
Pasirinkimo numeris 5 21
Pasirinkimo numeris 6 21
Pasirinkimo numeris 7 22
Pasirinkimo numeris 8 23
Pasirinkimo numeris 9 23
Pasirinkimo numeris 10 24
§ 3. Iracionalių posakių tapatybės transformacijos 25
Pasirinkimo numeris 1 25
Pasirinkimo numeris 2 25
Pasirinkimo numeris 3 26
Pasirinkimo numeris 4 26
Pasirinkimo numeris 5 27
Pasirinkimo numeris 6 28
Pasirinkimo numeris 7 28
Pasirinkimo numeris 8 29
Pasirinkimo numeris 9 30
Pasirinkimo numeris 10 30
§ 4. Lygčių sistemos 31
Pasirinkimo numeris 1 31
Pasirinkimo numeris 2 32
Pasirinkimo numeris 3 33
Pasirinkimo numeris 4 33
Pasirinkimo numeris 5 34
Pasirinkimo numeris 6 35
Pasirinkimo numeris 7 36
Pasirinkimo numeris 8 37
Pasirinkimo numeris 9 38
Pasirinkimo numeris 10 39
§ 5. geometrine prasme išvestinė 39
Pasirinkimo numeris 1 39
Pasirinkimo numeris 2 41
Pasirinkimo numeris 3 43
Pasirinkimo numeris 4 44
Pasirinkimo numeris 5 46
Pasirinkimo numeris 6 48
Pasirinkimo numeris 750
Pasirinkimo numeris 8 52
Pasirinkimo numeris 9 54
Pasirinkimo numeris 10 55
§ 6. Nelygybės 56
Pasirinkimo numeris 1 g 56
Pasirinkimo numeris 2 57
Pasirinkimo numeris 3 58
Pasirinkimo numeris 4 58
Pasirinkimo numeris 5 59
Pasirinkimo numeris 6 60
Pasirinkimo numeris 7 60
Pasirinkimo numeris 8 61
Pasirinkimo numeris 9 62
Pasirinkimo numeris 10 63
§ 7. Iracionalios lygtys 63
Pasirinkimo numeris 1 63
Pasirinkimo numeris 2 64
Pasirinkimo numeris 3 65
Pasirinkimo numeris 4 65
Pasirinkimo numeris 5 66
Pasirinkimo numeris 6 66
Pasirinkimo numeris 7 67
Pasirinkimo numeris 8 67
Pasirinkimo numeris 9 68
Galimybė Nr. Yu 68
§ 8. Trigonometrinės lygtys 69
Pasirinkimo numeris 1 69
Pasirinkimo numeris 2 69
Pasirinkimo numeris 3 70
Pasirinkimo numeris 4 70
Pasirinkimo numeris 5 71
Pasirinkimo numeris 6 72
Pasirinkimo numeris 7 72
Pasirinkimo numeris 8 73
Pasirinkimo numeris 9 74
Pasirinkimo numeris 10 74
§ 9. Logaritminės lygtys 75
Pasirinkimo numeris 1 75
Pasirinkimo numeris 2 75
Pasirinkimo numeris 3 76
Pasirinkimo numeris 4 76
Pasirinkimo numeris 5 77
Pasirinkimo numeris 6 77
Pasirinkimo numeris 7 78
Variantas Nr.8 * 78
Pasirinkimo numeris 9 79
Pasirinkimo numeris 10 79
§ 10. Eksponentinės lygtys 80
Pasirinkimo numeris 1 80
Pasirinkimo numeris 2 80
Pasirinkimo numeris 3 81
Pasirinkimo numeris 4 81
Pasirinkimo numeris 5 82
Pasirinkimo numeris 6 82
Pasirinkimo numeris 7 83
Pasirinkimo numeris 8 83
Pasirinkimo numeris 9 84
Pasirinkimo numeris 10 84
§vienuolika. Periodiškumas, lyginės ir nelyginės funkcijos 85
Pasirinkimo numeris 1 85
Pasirinkimo numeris 2 86
Pasirinkimo numeris 3 87
Pasirinkimo numeris 4 89
Pasirinkimo numeris 5 90
Pasirinkimo numeris 6 91
Pasirinkimo numeris 7 92
Pasirinkimo numeris 8 93
Pasirinkimo numeris 9 94
Pasirinkimo numeris 10 95
§ 12. Sudėtinės funkcijos nuliai. Ribota funkcija 97
Pasirinkimo numeris 1 97
Pasirinkimo numeris 2 97
Pasirinkimo numeris 3 98
Pasirinkimo numeris 4 98
Pasirinkimo numeris 5 99
Pasirinkimo numeris 6 99
Pasirinkimo numeris 7 100
Pasirinkimo numeris 8 100
Pasirinkimo numeris 9 101
Pasirinkimo numeris 10 101
§ 13. Apibrėžimo sritis, reikšmių rinkinys, funkcijų monotoniškumas 102
Pasirinkimo numeris 1 102
Pasirinkimo numeris 2 102
Pasirinkimo numeris 3 103
Pasirinkimo numeris 4 103
Pasirinkimo numeris 5 104
Pasirinkimo numeris 6 104
Pasirinkimo numeris 7 105
Pasirinkimo numeris 8 105
Pasirinkimo numeris 9 106
Pasirinkimo numeris 10 107
§ 14. Funkcijos ekstremumai. Didžiausia ir mažiausia funkcijos 107 reikšmės
Pasirinkimo numeris 1 107
Pasirinkimo numeris 2 108
Pasirinkimo numeris 3 108
Pasirinkimo numeris 4 109
Pasirinkimo numeris 5 109
Pasirinkimo numeris 6 110
Pasirinkimo numeris 7 110
Pasirinkimo numeris 8 111
Pasirinkimo numeris 9 111
Pasirinkimo numeris 10 112
§ 15. Įvairūs logaritminių lygčių sprendimo būdai 113
Pasirinkimo numeris 1 113
Pasirinkimo numeris 2 113
Pasirinkimo numeris 3 114
Pasirinkimo numeris 4 114
Pasirinkimo numeris 5 115
Pasirinkimo numeris 6 115
Pasirinkimo numeris 7 116
Pasirinkimo numeris 8 116
Pasirinkimo numeris 9 117
Pasirinkimo numeris 10 117
§ 16. Įvairūs trigonometrinių lygčių sprendimo būdai 118
Pasirinkimo numeris 1 118
Pasirinkimo numeris 2 118
Pasirinkimo numeris 3 118
Pasirinkimo numeris 4 119
Pasirinkimo numeris 5 119
Pasirinkimo numeris 6 120
Pasirinkimo numeris 7 120
Pasirinkimo numeris 8 121
Pasirinkimo numeris 9 121
Pasirinkimo numeris 10 122
§ 17. Įvairūs iracionaliųjų lygčių sprendimo būdai 123
Pasirinkimo numeris 1 123
Pasirinkimo numeris 2 123
Pasirinkimo numeris 3 124
Pasirinkimo numeris 4 124
Pasirinkimo numeris 5 125
Pasirinkimo numeris 6 125
Pasirinkimo numeris 7 125
Pasirinkimo numeris 8 126
Pasirinkimo numeris 9 126
Variantas Nr.10 127
§ 18. Lygtys, kuriose yra kintamasis po modulio ženklu 127
Pasirinkimo numeris 1 127
Pasirinkimo numeris 2 128
Pasirinkimo numeris 3 128
Pasirinkimo numeris 4 129
Pasirinkimo numeris 5 129
Pasirinkimo numeris 6 130
Pasirinkimo numeris 7 130
Pasirinkimo numeris 8 131
Pasirinkimo numeris 9 131
Pasirinkimo numeris 10 131
§ 19. Įvairūs sprendimo būdai eksponentinės lygtys.132
Pasirinkimo numeris 1 132
Pasirinkimo numeris 2 133
Pasirinkimo numeris 3 133
Pasirinkimo numeris 4 134
Pasirinkimo numeris 5 134
Pasirinkimo numeris 6 135
Pasirinkimo numeris 7 135
Pasirinkimo numeris 8 135
Pasirinkimo numeris 9 136
Pasirinkimo numeris 10 136
§ 20. Įvairūs kombinuotųjų lygčių sprendimo būdai 137
Pasirinkimo numeris 1 137
Pasirinkimo numeris 2 137
Pasirinkimo numeris 3 138
Pasirinkimo numeris 4 138
Pasirinkimo numeris 5 139
Pasirinkimo numeris 6 139
Pasirinkimo numeris 7 140
Pasirinkimo numeris 8 140
Pasirinkimo numeris 9 141
Pasirinkimo numeris 10 141
§ 21. Lygtys su parametru, kuriame yra 142 modulis
Pasirinkimo numeris 1 142
Pasirinkimo numeris 2 142
Pasirinkimo numeris 3 143
Pasirinkimo numeris 4 144
Pasirinkimo numeris 5 144
Pasirinkimo numeris 6 145
Pasirinkimo numeris 7 146
Pasirinkimo numeris 8 146
Pasirinkimo numeris 9 147
Pasirinkimo numeris 10 148
Atsakymai 149
§ 1. Logaritminių reiškinių tapatumo transformacijos 149
§ 2. Posakių, turinčių 150 laipsnį, tapatybės transformacijos
§ 3. Iracionaliųjų posakių tapatumo transformacijos 150
§ 4. Lygčių sistemos 151
§ 5. Geometrinė vedinio reikšmė 151
§ 6. Nelygybės 152
§ 7. Iracionaliosios lygtys 152
§ 8. Trigonometrinės lygtys 153
§ 9. Logaritminės lygtys 153
§ 10. Eksponentinės lygtys 154
§vienuolika. Periodiškumas, lyginės ir nelyginės funkcijos 154
§ 12. Sudėtinės funkcijos nuliai. Ribota funkcija 155
§ 13. Apibrėžimo sritis, reikšmių rinkinys, funkcijų monotoniškumas 156
§ 14. Funkcijos ekstremumai. Didžiausia ir mažiausia funkcijos 158 reikšmės
§ penkiolika. Įvairūs triukai sprendžiant logaritmines lygtis 159
§ 16. Įvairūs trigonometrinių lygčių sprendimo būdai 160
§ 17. Įvairios gudrybės sprendžiant iracionaliąsias lygtis 164
§ 18. Lygtys, kuriose yra kintamasis po modulio ženklu 165
§ 19. Įvairūs eksponentinių lygčių sprendimo būdai.166
§ 20. Įvairūs kombinuotųjų lygčių sprendimo būdai 167
§ 21. Lygtys su parametru, kuriame yra 169 modulis
Literatūra 170
EGOROVA VIKTORIJA VALEREVNA
Matematikos mokytojas
aukščiausia kvalifikacinė kategorija
TEMA: „TAPATYBĖS TRANSFORMACIJA
LOGARITMINĖS IŠRAIKOS"
Žinios ir įgūdžiai, kuriuos mokiniai turėtų įgyti baigę šią pamoką:
žinoti skaičiaus logaritmo apibrėžimą, pagrindinį logaritminį tapatumą, logaritmų savybes;
mokėti atlikti logaritmus turinčių reiškinių transformacijas, skaičiuoti logaritmus.
Literatūra:
1. Alimov Sh.A., Kolyagin Yu.M., Sidorov Yu.V. ir kt.. Algebra ir analizės pradžia: vadovėlis 10-11 klasei švietimo įstaigų. - M .: Švietimas, 2001 m.
2. Kochagin V.V., Kochagina M.V., Intensyvus pasirengimo egzaminui kursas. – M.: Eksmo, 2009.
3. A. G. Merzlyak, V. B. Polonsky ir M. S. Yakir, Algebrinis simuliatorius: vadovas moksleiviams ir stojantiesiems į universitetus. – M.: Ileksa, 2005.
4. Gusevas V.A., Mordkovičius A.G. Matematika: informacinė medžiaga: Knyga studentams. - M .: Švietimas, 2001 m.
Pamokos planas:
Užsiėmimų metu:
1) Logaritmas yra Graikiškas žodis, kurį sudaro 2 žodžiai: „logos“ – santykis, „aritmos“ – skaičius. Taigi logaritmas yra skaičius, kuris matuoja santykį. 1614 m. leidinys pranešė, kad Napier išrado logaritmus. Vėliau jis sudarė logaritmines lenteles, kurios dabar mums žinomos kaip Bradiso lentelės. Mažiau nei per šimtmetį lentelės išplito visame pasaulyje ir tapo nepakeičiamu skaičiavimo įrankiu. Ateityje jie buvo tarsi įmontuoti į patogų įrenginį, itin pagreitinantį skaičiavimo procesą – skaidrių taisyklę, kuri buvo naudojama iki XX amžiaus aštuntojo dešimtmečio.
1 priedas.
2) logaritmas teigiamas skaičiusb dėl priežasties a, be to didesnis už nulį ir nelygus vienetui,yra rodiklis, iki kurio turi būti padidintas skaičiusa norėdami gauti numerįb.
Ši lygybė, išreiškianti logaritmo apibrėžimą, vadinamapagrindinė logaritminė tapatybė .
C 
ARBA 1
P 
Laipsnio bazė ir logaritmo bazė yra septyniolika, tai reiškia, kad pagal pagrindinį logaritminį tapatumą išraiškos reikšmė yra trys.
Dirbsime žodžiu:
SCH 
ELCHOK
O apatinė sekundė yra nulis taško penkios dešimtosios, taigi išraiška yra lygi aritmetinei kvadratinei šakniai iš penkių.
P 
2 priedas.
Lygybė reiškia kad
Iš logaritmo apibrėžimo gaunamos šios svarbios lygybės:
Pavyzdžiui:
P 
3 priedas.
Pereikime prie NAUDOTI užduotis:
4 priedas
3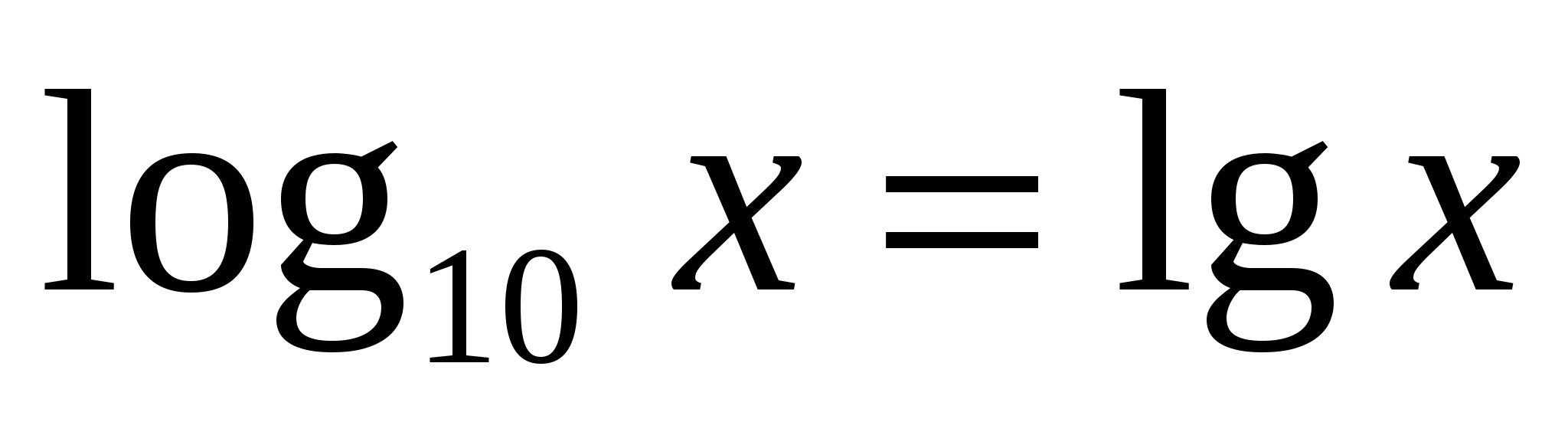
)
Yra specialus dešimties bazinio logaritmo žymėjimas ir pavadinimas.dešimtainis logaritmas
.
L 
aritmas į bazęe
paskambinonatūralusis logaritmas
.
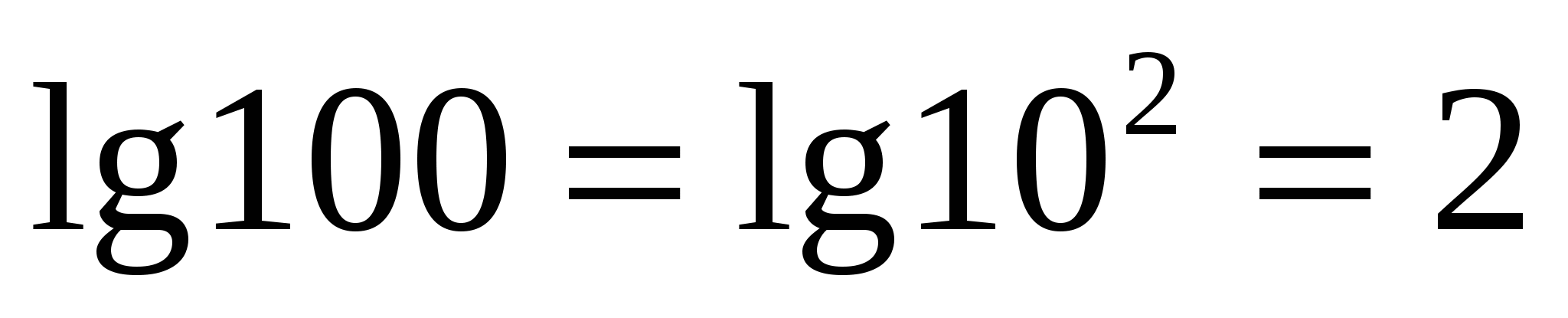
H 
pavyzdžiui,
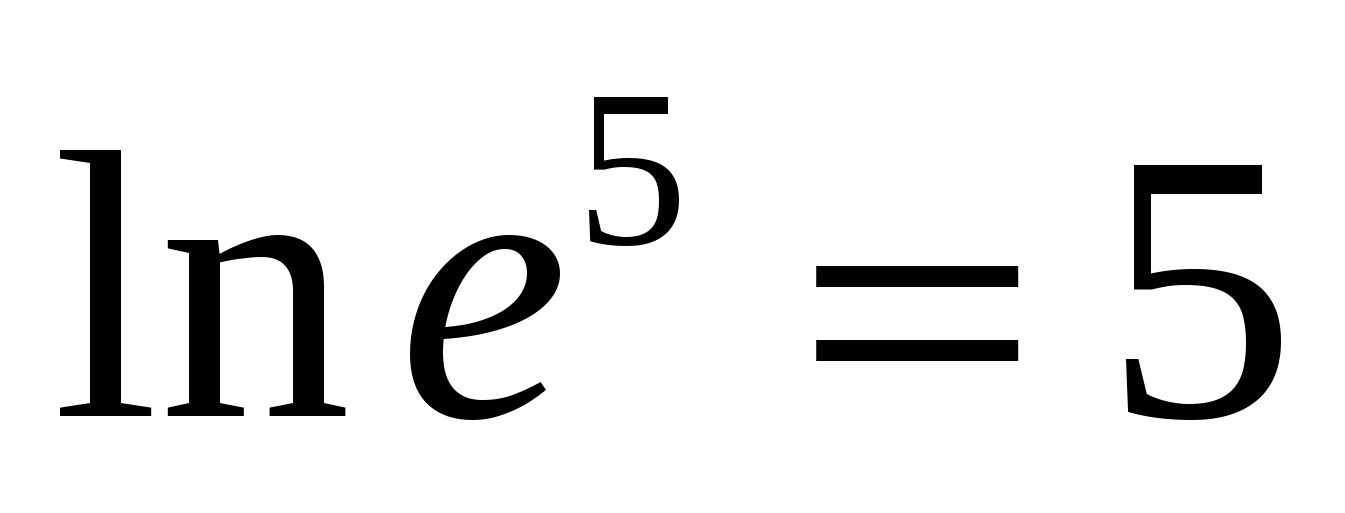
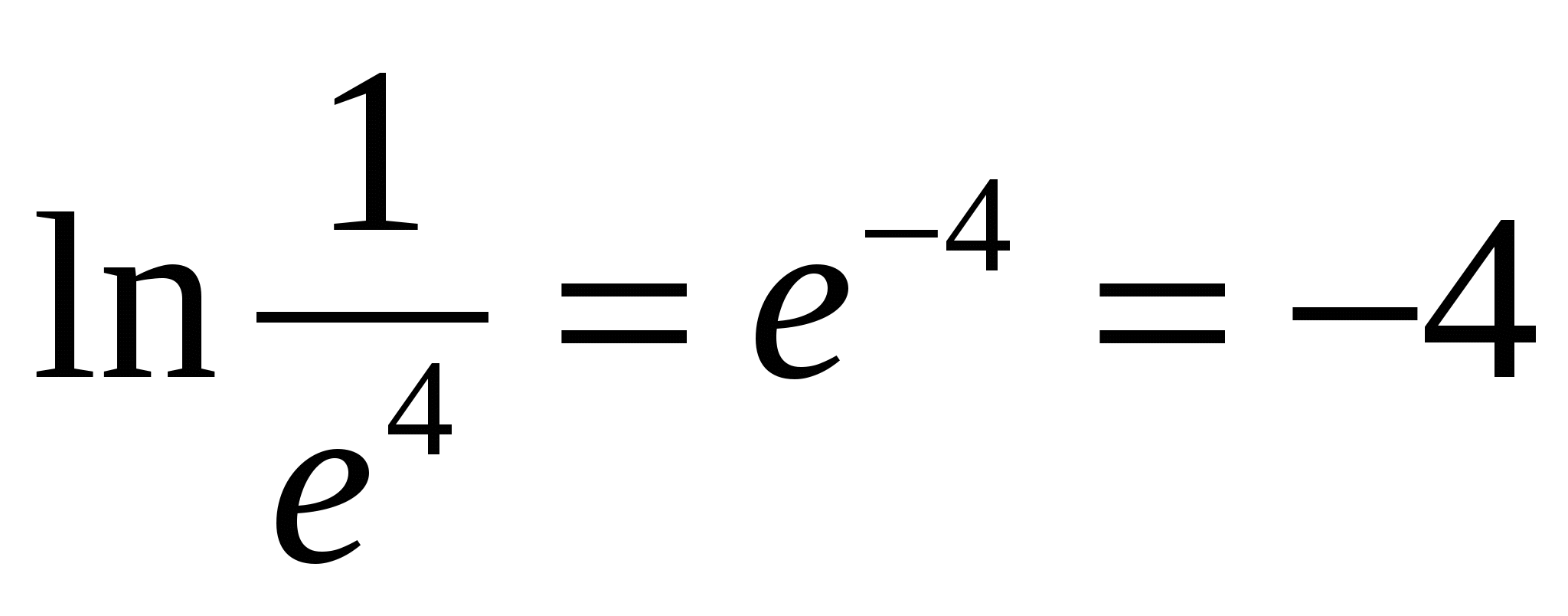
4) Šios savybės išplaukia iš logaritmo apibrėžimo. Visos savybės yra suformuluotos ir įrodytos tik teigiamoms kintamųjų, esančių po logaritmo ženklais, reikšmėmis.
Dviejų teigiamų skaičių sandaugos bazinis logaritmas a yra lygi sumaišių skaičių logaritmai su ta pačia baze.
DER 2
Pavyzdžiui,
Z 
1 užduotis.
2 užduotis. Supaprastinkite išraišką
AT 
Naudokime ankstesnį pavyzdį. Pakeiskime
Atkreipkite dėmesį, kad logaritmas yra kvadratas, todėl suma taip pat turi būti pakelta kvadratu. Naudodami sumos kvadrato formulę, atidarykite skliaustus. Pateikiame panašias sąlygas.
5) Dalinio logaritmas lygus dividendo ir daliklio logaritmų skirtumui.
C
Atkreipkite dėmesį į laipsnio pagrindą ir logaritmo pagrindą - jie yra vienodi.
ARBA 3R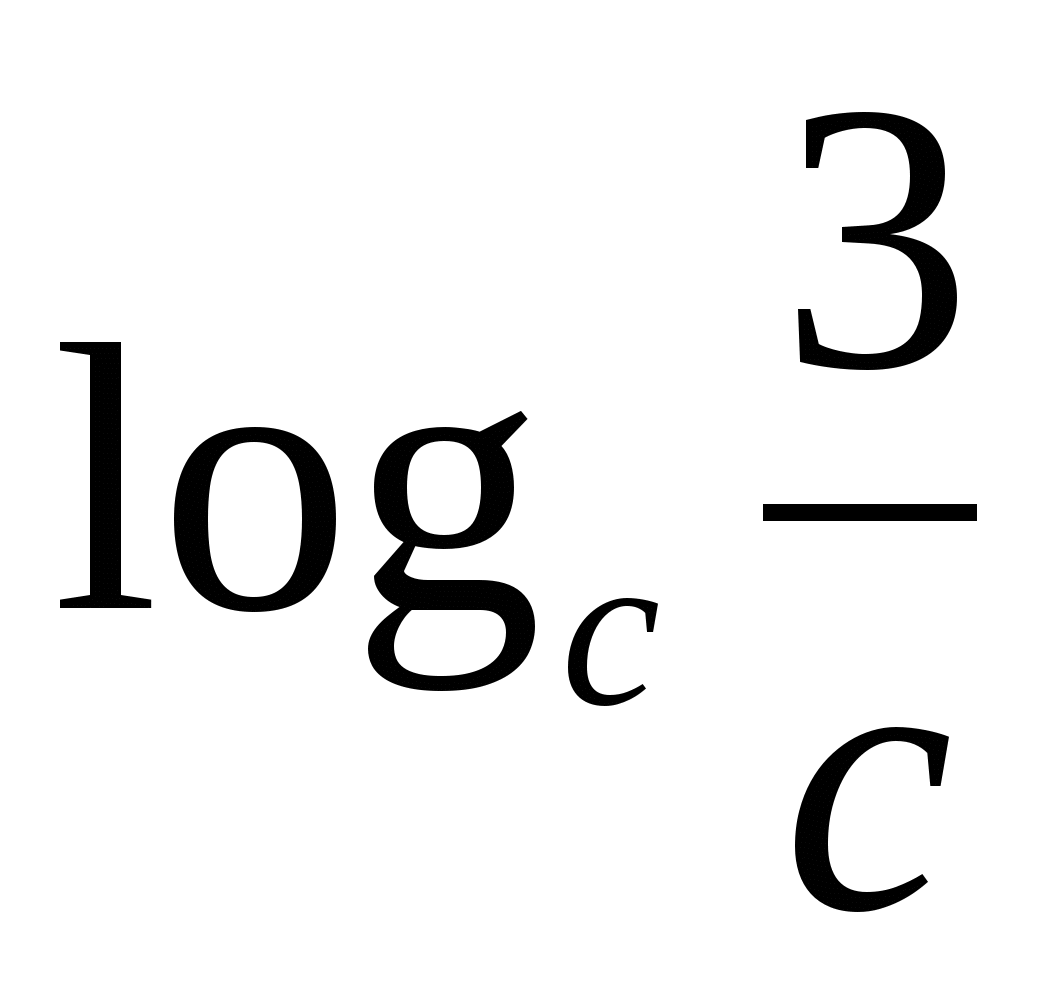 
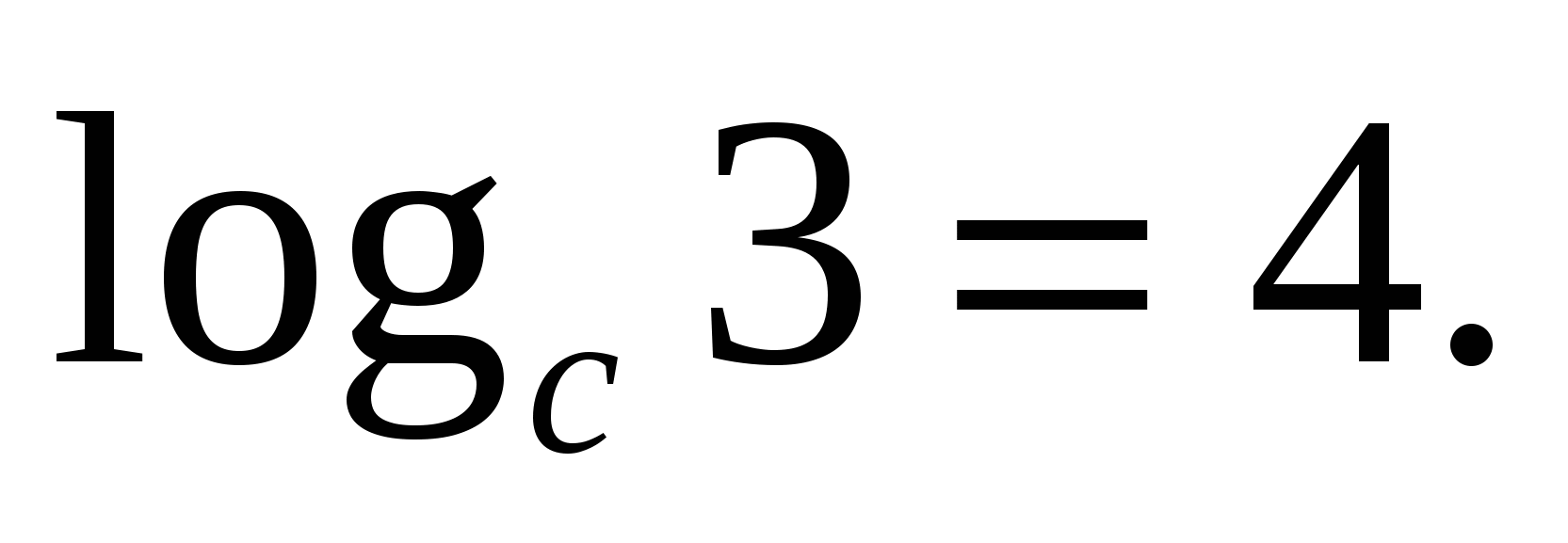Pažvelkime į šios formulės taikymą su pavyzdžiu:
Z 
1 užduotis. Raskite išraiškos reikšmę if
2 užduotis. Raskite vertę b pagal jo logaritmą
6) Laipsnio logaritmas iki pagrindoa , yra lygus produktui eksponentas logaritmui toje pačioje bazėje.
DER 4
Pavyzdžiui,
Z 
1 užduotis. Apskaičiuokite, jei
Supaprastinkime išraišką
Formulė
paskambino perėjimo prie naujo pagrindo formulė.
Z 
1 užduotis. Išreikškite logaritmu su 2 baze.
2 užduotis. Apskaičiuoti
CER 5
CER 6
Pavyzdžiui,
Z 
1 užduotis. Apskaičiuoti
Z 
2 užduotis. Apskaičiuoti
9) Galite pradėti logaritmines transformacijas tik tada, jei jei prisiminsite visas logaritmų savybes. Jas pakartoję, apsvarstysime logaritminių išraiškų transformavimo užduotis iš kitos pusės.
Norint konvertuoti logaritminių išraiškų sumą arba skirtumą, kartais pakanka naudoti logaritmo apibrėžimą, o dažniausiai sandaugos ar koeficiento logaritmo savybes.
Z 
1 užduotis. Apskaičiuoti
Išspręskime tai dviem būdais.
1 būdas, naudojant logaritmo apibrėžimą:
2 metodas pagrįstas koeficiento logaritmo savybė:
2 užduotis. Raskite išraiškos reikšmę
Pirmiausia pritaikykime formulę sandaugos logaritmas, tada logaritmo apibrėžimas.
Pagrindinė logaritminė tapatybė naudojama konvertuojant išraiškas, kurių eksponente yra logaritmas. Tokių operacijų idėja yra lygiuoti eksponento bazę ir logaritmo bazę.
Kartais reikia transformuoti išraišką pagal logaritmo savybes ir laipsnio savybes naudojant perėjimo formulę galima lengvai pereiti iš vienos bazės į kitą. Kitais atvejais turėtų būti taikomos kelios savybės.
Z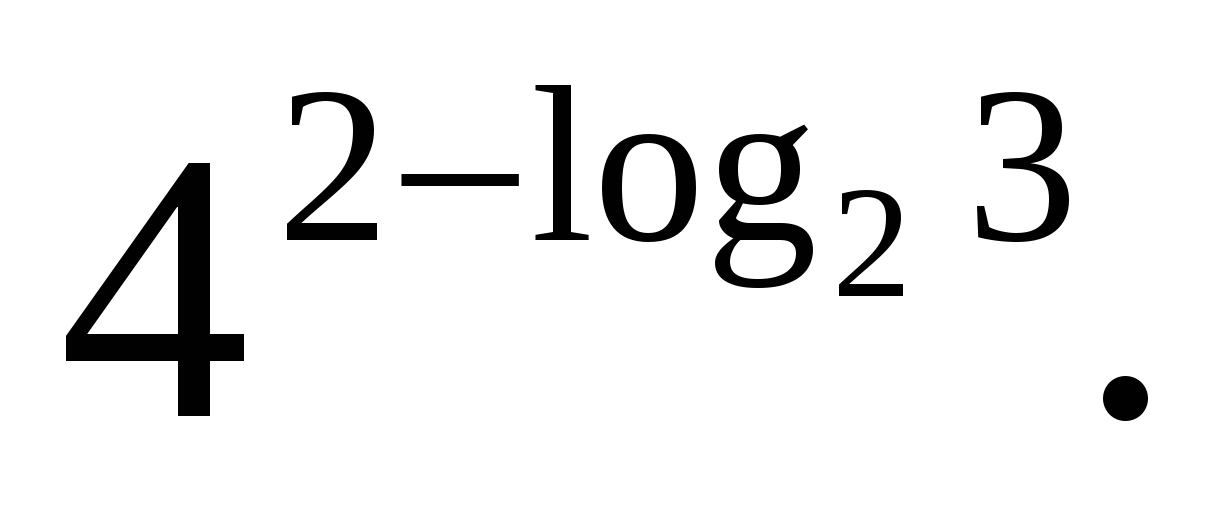 
3 užduotis. Apskaičiuoti
Z 
4 užduotis. Raskite išraiškos reikšmę
5 užduotis. Raskite išraiškos reikšmę
Z 
6 užduotis. Išreikškite kaip logaritmų skirtumą
H 
Didžiausias sunkumas yra logaritminių išraiškų transformavimas į radikalą. Transformacijų procese reikia atsižvelgti į logaritminių reiškinių modulius, kurių atskleidimui reikia palyginti iracionaliuosius skaičius arba racionaliuosius ir iracionaliuosius skaičius. Veiksime nuosekliai. Apsvarstykite išraišką po vidiniu radikalu.
Pakeisti pradinėje išraiškoje.
Pažymėtina, kad su logaritminių išraiškų transformacija galima susidurti ir sprendžiant lygtis bei nelygybes ar tiriant funkcijas, todėl numanoma forma jos gali būti ir B bei C grupių priskyrime.
10) Apibendrinimas. Klausimai:
Vadinamas 10 bazinis logaritmas
pagrindinis logaritmas
pagrindinis logaritmas
natūralusis logaritmas
dešimtainis logaritmas
2) Kokios vertybės galix
išraiškoje 
Vertė neapibrėžta
5) Nurodykite santykį, kuris tinka visiemsx ≠ 0 .
6) Nurodykite teisingą perėjimo prie naujos bazės formulės santykį.
7) Nurodykite teisingą lygybę
11)
Kontrolinis bandymas.
Padniestrės Valstijos universitetas
juos. T.G. Ševčenka
Fizikos ir matematikos fakultetas
Matematinės analizės katedra
ir matematikos mokymo metodus
KURSINIS DARBAS
„Tapatybės transformacijos
eksponentinis ir logaritminis
išraiškos"
Darbai baigti:
______ grupės mokinys
Fizikos ir matematikos fakultetas
_________________________
Patikrintas darbas:
_________________________
Tiraspolis, 2003 m
Įvadas…………………………………………………………………………2
1 skyrius
§ vienas. Konkrečių tipų transformacijų taikymo įgūdžių formavimas……………………………………………………………………………………….4
§2. Žinių sistemos organizavimo ypatumai tiriant identiškas transformacijas.…….………………………….………..…………….5
§3. Matematikos programa ………………………………………….11
2 skyrius
§ vienas. Laipsnio sampratos apibendrinimas………………………………………..13
§2. Eksponentinė funkcija……………………………………………..15
§3. Logaritminė funkcija…………………………………………….16
3 skyrius. Identiškos eksponentinių ir logaritminių išraiškų transformacijos praktikoje ................................................ ......................................19
Išvada…………………………………………………………………..24
Naudotos literatūros sąrašas……………………………………….25
Įvadas
Šiame kursiniame darbe bus nagrinėjamos identiškos eksponentinės ir logaritminės funkcijų transformacijos, nagrinėjama jų mokymo mokykliniame algebros kurse metodika ir analizės pradžia.
Pirmajame šio darbo skyriuje aprašoma identiškų transformacijų mokymo mokykliniame matematikos kurse metodika, taip pat įtraukta matematikos programa kurse „Algebra ir analizės pradžia“ su eksponentinių ir logaritminių funkcijų tyrimu.
Antrame skyriuje tiesiogiai aptariamos pačios eksponentinės ir logaritminės funkcijos, pagrindinės jų savybės, naudojamos identiškose transformacijose.
Trečias skyrius – pavyzdžių ir uždavinių sprendimas, naudojant identiškas eksponentinių ir logaritminių funkcijų transformacijas.
Įvairių posakių ir formulių transformacijų studijos užima nemažą mokyklinės matematikos kurso studijų laiko dalį. Paprasčiausios transformacijos, pagrįstos aritmetinių operacijų savybėmis, jau atliekamos pradinė mokykla ir IV-V klasėse. Tačiau pagrindinė našta formuojant įgūdžius ir gebėjimus atlikti transformacijas tenka mokyklinės algebros eigai. Tai lemia tiek staigus atliekamų transformacijų skaičiaus ir įvairovės padidėjimas, tiek joms pagrįsti ir pritaikymo sąlygų patikslinimas, identifikuojant ir tiriant apibendrintas tapatumo, identiškos transformacijos, lygiavertės transformacijos sąvokas. logiška pasekmė.
Identiškų transformacijų atlikimo kultūra vystosi taip pat, kaip ir skaičiavimo kultūra, pagrįsta tvirtomis žiniomis apie operacijų su objektais savybes (skaičius, vektorius, polinomus ir kt.) ir jų įgyvendinimo algoritmus. Ji pasireiškia ne tik gebėjimu teisingai pagrįsti transformacijas, bet ir gebėjimu rasti trumpiausią kelią į perėjimą nuo pirminės analitinės išraiškos prie labiausiai transformacijos tikslą atitinkančios išraiškos, gebėjimu sekti pokyčius Analitinių išraiškų apibrėžimo sritis identiškų transformacijų grandinėje, transformacijų vykdymo greičiu ir be klaidų.
Aukštos skaičiavimo kultūros ir identiškų transformacijų užtikrinimas yra svarbi matematikos mokymo problema. Tačiau ši problema dar toli gražu nėra išspręsta patenkinamai. To įrodymas – valstybinių švietimo institucijų statistiniai duomenys, kuriuose kasmet konstatuojamos klaidos ir neracionalūs mokinių atliktų skaičiavimų ir perskaičiavimų metodai. įvairios klasės darant valdymo darbai. Tai patvirtina aukštesniųjų nuomonės švietimo įstaigų apie pretendentų matematinių žinių ir įgūdžių kokybę. Galima nesutikti su valstybinių švietimo institucijų ir universitetų išvadomis, kad to nepakanka aukštas lygis skaičiavimo kultūra ir identiškos transformacijos vidurinė mokykla yra formalizmo studentų žiniose pasekmė, teorijos atskyrimas nuo praktikos.
Tapatybės transformacijos ir mokymo metodai
mokykliniame algebros kurse ir analizės pradžioje.
§ vienas. Taikymo įgūdžių formavimas
specifinių tipų transformacijos.
Transformacijų atlikimo technikų ir taisyklių sistema, naudojama algebros pradžios stadijoje, turi labai platų pritaikymo spektrą: ji naudojama studijuojant visą matematikos kursą. Tačiau būtent dėl mažo specifiškumo šiai sistemai reikia papildomų transformacijų, kurios atsižvelgtų į transformuojamų išraiškų struktūros ypatumus bei naujai įvestų operacijų ir funkcijų savybes. Atitinkamų transformacijų tipų kūrimas prasideda sutrumpintų daugybos formulių įvedimu. Tada apsvarstysime transformacijas, susijusias su eksponencijos operacija, su skirtingomis klasėmis elementarios funkcijos- eksponentinis, galios, logaritminis, trigonometrinis. Kiekvienas iš šių transformacijų tipų pereina tyrimo etapą, kurio metu dėmesys sutelkiamas į jiems būdingų bruožų įsisavinimą.
Sukaupus medžiagą, atsiranda galimybė išskirti bendrus visų nagrinėjamų transformacijų bruožus ir tuo remiantis įvesti identiškų ir lygiaverčių transformacijų sąvokas.
Pažymėtina, kad identiškos transformacijos sąvoka mokykliniame algebros kurse pateikiama ne visapusiškai, o tik taikant išraiškas. Transformacijos skirstomos į dvi klases: identiškos transformacijos yra reiškinių transformacijos, o ekvivalentinės – formulių transformacijos. Tuo atveju, kai reikia supaprastinti vieną formulės dalį, šioje formulėje paryškinama išraiška, kuri yra pritaikytos identiškos transformacijos argumentas. Atitinkamas predikatas laikomas nepakitusiu.
Kalbant apie vientisos transformacijų sistemos (sintezės) organizavimą, pagrindinis jos tikslas yra suformuoti lanksčią ir galingą; aparatai, tinkami naudoti sprendžiant įvairias edukacines užduotis.
Algebros eigoje ir analizės pradžioje toliau palaipsniui tobulinama integrali transformacijų sistema, jau susiformavusi pagrindiniais bruožais. Prie jo pridedami ir kai kurie nauji transformacijų tipai, tačiau jie jį tik praturtina, išplečia galimybes, bet nekeičia struktūros. Šių naujų transformacijų tyrimo metodika praktiškai nesiskiria nuo naudojamos algebroje.
§2. Užduočių sistemos organizavimo ypatumai
tiriant identiškas transformacijas.
Pagrindinis bet kokios užduočių sistemos organizavimo principas yra pateikti jas nuo paprastų iki sudėtingų, atsižvelgiant į mokinių poreikį įveikti įmanomus sunkumus ir sukurti problemines situacijas. Nurodytas pagrindinis principas reikalauja sukonkretinti šios mokomosios medžiagos ypatybes. Matematikos metodikoje įvairioms užduočių sistemoms apibūdinti vartojama pratimų ciklo sąvoka. Pratimų ciklas pasižymi kelių studijų aspektų ir medžiagos išdėstymo metodų deriniu pratimų sekoje. Kalbant apie identiškas transformacijas, ciklo idėja gali būti pateikta taip.
Pratimų ciklas susietas su vienos tapatybės tyrinėjimu, aplink kurią grupuojamos kitos tapatybės, kurios yra natūraliai su ja susijusios. Ciklo sudėtis kartu su vykdomosiomis užduotimis apima užduotis, kurioms reikia pripažinti nagrinėjamos tapatybės pritaikomumą. Tiriama tapatybė naudojama įvairių skaitmeninių sričių skaičiavimams atlikti. Atsižvelgiama į tapatybės specifiką; ypač organizuojami su juo susiję kalbos posūkiai.
Kiekvieno ciklo užduotys suskirstytos į dvi grupes. Pirmoji apima užduotis, atliekamas pirminės pažinties su tapatybe metu. Jie tarnauja mokomoji medžiaga kelioms pamokoms iš eilės, kurias vienija viena tema. Antroji pratimų grupė sieja tiriamą tapatybę su įvairiomis programomis. Ši grupė nesudaro kompozicinės vienybės – čia atliekami pratimai išsibarstę po įvairias temas.
Apibūdinta ciklo struktūra nurodo įgūdžių formavimosi etapą taikyti specifinius transformacijų tipus. Paskutiniame etape - sintezės etape, ciklai modifikuojami. Pirmiausia sujungiamos abi užduočių grupės, suformuojant „išskleistą“ ciklą, o iš pirmosios grupės išskiriamos pačios paprasčiausios pagal formuluotę ar užduoties sudėtingumą. Likusios užduočių rūšys tampa sunkesnės. Antra, vyksta su skirtingomis tapatybėmis susijusių ciklų susiliejimas, dėl kurio didėja veiksmų vaidmuo atpažinti vienos ar kitos tapatybės pritaikomumą.
Atkreipiame dėmesį į užduočių ciklų ypatybes, susijusias su elementarių funkcijų tapatybėmis. Šios ypatybės atsiranda dėl to, kad, pirma, atitinkamos tapatybės tiriamos atliekant funkcinės medžiagos tyrimą ir, antra, jos atsiranda vėliau nei pirmosios grupės tapatybės ir tiriamos naudojant jau suformuotus įgūdžius identiškoms transformacijoms atlikti. .
Kiekviena naujai įdiegta elementari funkcija smarkiai išplečia skaičių, kuriuos galima priskirti ir pavadinti atskirai, diapazoną. Todėl į pirmąją ciklų užduočių grupę turėtų būti įtrauktos užduotys, skirtos nustatyti ryšį tarp šių naujų skaitinių sričių ir pradinės racionaliųjų skaičių srities. Pateikiame tokių užduočių pavyzdžių.
1 pavyzdys Apskaičiuokite:
Šalia kiekvienos išraiškos yra tapatybė, cikluose, kuriems gali būti siūlomos užduotys. Tokių užduočių tikslas – įsisavinti įrašų ypatybes, įskaitant naujų operacijų ir funkcijų simbolius, lavinti matematinius kalbos įgūdžius.
Nemaža dalis tapatybės transformacijų, susijusių su elementariomis funkcijomis, panaudojimo tenka iracionaliųjų ir transcendentinių lygčių sprendimui. Su tapatybių įsisavinimu susiję ciklai apima tik paprasčiausias lygtis, tačiau jau čia patartina įsisavinti tokių lygčių sprendimo metodą: jį redukuoti, pakeičiant nežinomą algebrine lygtimi.
Šio sprendimo veiksmų seka yra tokia:
a) rasti funkciją, kuriai ši lygtis gali būti pavaizduota kaip ;
b) atlikti keitimą ir išspręsti lygtį;
c) išspręskite kiekvieną lygtį , kur yra lygties šaknų aibė.
Naudojant aprašytą metodą, b) veiksmas dažnai atliekamas netiesiogiai, neįvedant žymėjimo . Be to, studentai dažnai renkasi iš įvairių kelių, leidžiančių rasti atsakymą, kad galėtų greičiau ir lengviau pasirinkti tą, kuris veda į algebrinę lygtį.
2 pavyzdys. Išspręskite lygtį.
Pirmas būdas:
Antras būdas:
a) 
b) 
Čia matyti, kad a) žingsnis yra sunkesnis pirmuoju metodu nei antrasis. Pirmasis būdas yra „sunkesnis pradžia“, nors tolimesnė sprendimo eiga yra daug lengvesnė. Kita vertus, antrasis metodas turi pranašumų, nes yra lengvesnis ir sudėtingesnis mokant redukuoti į algebrinę lygtį.
Mokykliniam algebros kursui būdingos užduotys, kuriose perėjimas prie algebrinės lygties yra dar lengvesnis nei šiame pavyzdyje. Pagrindinė tokių užduočių apkrova yra susijusi su c) žingsnio, kaip savarankiškos sprendimo proceso dalies, susijusios su tiriamos elementarios funkcijos savybių naudojimu, pasirinkimu.
3 pavyzdys. Išspręskite lygtį:
a) 
; b) 
.
Šios lygtys redukuojamos į lygtis: a) arba ; b) arba. Norint išspręsti šias lygtis, reikia žinoti tik pačius paprasčiausius faktus apie eksponentinę funkciją: jos monotoniškumą, reikšmių diapazoną. Kaip ir ankstesniame pavyzdyje, lygtys a) ir b) gali būti priskirtos pirmajai kvadratinių eksponentinių lygčių sprendimo pratimų ciklo grupei.
Taigi, mes priėjome prie užduočių klasifikavimo ciklais, susijusiais su transcendentinių lygčių sprendimu, įskaitant eksponentinę funkciją:
1) lygtys, redukuotos į formos lygtis ir turinčios paprastą atsakymą, bendros formos: ;
2) lygtys, kurios redukuoja į lygtis , kur yra sveikasis skaičius arba , kur ;
3) lygtys, kurios redukuojasi į lygtis ir reikalauja aiškios skaičiaus užrašymo formos analizės.
Panašios užduotys gali būti priskirtos ir kitoms elementarioms funkcijoms.
Juose įrodoma ar bent paaiškinama nemaža dalis algebros ir algebros kursuose tirtų tapatybių bei analizės užuomazgų. Ši tapatybių tyrimo pusė turi didelę reikšmę abiem kursams, nes demonstratyvūs samprotavimai juose atliekami su didžiausiu aiškumu ir griežtumu būtent tapatybių atžvilgiu. Išskyrus šią medžiagą, įrodymai paprastai yra mažiau išsamūs, jie ne visada skiriasi nuo taikomų pateisinimo priemonių sudėties.
Aritmetinių operacijų savybės naudojamos kaip atrama, ant kurios statomi tapatybių įrodymai.
Skaičiavimų ir identiškų transformacijų edukacinis poveikis gali būti nukreiptas į plėtrą loginis mąstymas, jei tik iš studentų sistemingai reikalaujama pagrįsti skaičiavimus ir identiškas transformacijas, ugdyti funkcinį mąstymą, kuris pasiekiamas įvairiais būdais. Skaičiavimų ir identiškų transformacijų svarba ugdant valią, atmintį, išradingumą, susivaldymą, kūrybinę iniciatyvą yra gana akivaizdi.
Kasdienio, pramoninio skaičiavimo praktikos poreikiai reikalauja, kad studentai suformuotų stiprius, automatizuotus racionalių skaičiavimų ir identiškų transformacijų įgūdžius. Šie įgūdžiai ugdomi atliekant bet kokį skaičiavimo darbą, tačiau reikia specialių įgūdžių. treniruočių pratimai greituose skaičiavimuose ir transformacijose.
Taigi, jei pamokoje sprendžiamos logaritminės lygtys naudojant pagrindinę logaritminę tapatybę, į pamokos planą naudinga įtraukti žodinius pratimus, kad būtų supaprastintos arba apskaičiuotos posakių reikšmės: , , 
. Mokiniams visada pranešama apie pratybų tikslą. Pratimo metu gali tekti reikalauti, kad mokiniai pagrįstų atskirus pokyčius, veiksmus ar išspręstų visą problemą, net jei tai nebuvo planuota. Kai galimi skirtingi problemos sprendimo būdai, visada pageidautina užduoti klausimus: „Kaip problema buvo išspręsta?“, „Kas išsprendė problemą kitaip?
Tapatumo ir identiškos transformacijos sąvokos yra aiškiai supažindintos su VI klasės algebros kursu. Pats identiškų posakių apibrėžimas negali būti praktiškai naudojamas dviejų posakių tapatumui įrodyti ir suprasti, kad identiškų transformacijų esmė yra pritaikyti išraiškai tų veiksmų, kurie nurodyti reiškinyje, apibrėžimus ir savybes arba pridėti į jį išraišką, kuri identiškai lygi 0, arba padauginus ją iš išraiškos, identiškai lygi vienetui. Tačiau net ir įsisavinę šias nuostatas, studentai dažnai nesupranta, kodėl šios transformacijos leidžia teigti, kad pradinė ir gauta išraiška yra tapačios, t.y. paimkite tas pačias reikšmes bet kurioms kintamųjų verčių sistemoms (rinkiniams).
Taip pat svarbu užtikrinti, kad studentai gerai suprastų, jog tokios identiškų transformacijų išvados yra atitinkamų veiksmų apibrėžimų ir savybių pasekmės.
6 klasėje plečiamas identiškų virsmų aparatas, sukauptas ankstesniais metais. Šis plėtinys pradedamas įvedus tapatybę, išreiškiančią galių sandaugą su tomis pačiomis bazėmis: , kur , yra sveikieji skaičiai.
§3. Matematikos programa. Mokykliniame kurse „Algebra ir analizės užuomazgos“ mokiniai sistemingai mokosi eksponentinių ir logaritminių funkcijų bei jų savybių, logaritminių ir eksponentinių reiškinių identiškų transformacijų bei jų pritaikymo sprendžiant atitinkamas lygtis ir nelygybes, susipažįsta su pagrindinėmis sąvokomis, teiginiais. . 11 klasėje algebros pamokos trunka 3 valandas per savaitę, iš viso 102 valandas per metus. Eksponentinės, logaritminės ir galios funkcijų studijavimas pagal programą trunka 36 valandas. Programa apima šių klausimų svarstymą ir studijas: Laipsnio samprata su racionaliu rodikliu. Iracionaliųjų lygčių sprendimas. Eksponentinė funkcija, jos savybės ir grafikas. identiškos eksponentinių išraiškų transformacijos. Eksponentinių lygčių ir nelygybių sprendimas. Skaičiaus logaritmas. Pagrindinės logaritmų savybės. Logaritminė funkcija, jos savybės ir grafikas. Logaritminių lygčių ir nelygybių sprendimas. Eksponentinės funkcijos išvestinė. Skaičius ir natūralusis logaritmas. Galios funkcijos išvestinė. Pagrindinis eksponentinių ir logaritminių funkcijų tyrimo skyriaus tikslas – supažindinti studentus su eksponentinės, logaritminės ir laipsnio funkcijomis; mokyti mokinius spręsti eksponentinį ir logaritmines lygtis ir nelygybės. Laipsnio šaknies ir laipsnio su racionaliuoju rodikliu sąvokos yra kvadratinės šaknies ir laipsnio su sveikuoju skaičiumi sąvokų apibendrinimas. Studentai turėtų atkreipti dėmesį į tai, kad čia nagrinėjamų šaknų ir laipsnių savybės su racionaliuoju rodikliu yra panašios į tas savybes, kurios buvo ištirtos anksčiau. kvadratinės šaknys ir laipsniai su sveikaisiais rodikliais. Būtina skirti pakankamai laiko laipsnių savybėms išsiaiškinti ir identiškų transformacijų įgūdžių formavimui. Laipsnio samprata su neracionalus rodiklisįvesta vizualiai-intuityviu pagrindu. Ši medžiaga atlieka pagalbinį vaidmenį ir naudojama įvedant eksponentinę funkciją. Eksponentinių, logaritminių ir laipsnių funkcijų savybių tyrimas atliekamas pagal priimtą bendra schema funkcijų tyrimas. Šiuo atveju, atsižvelgiant į parametrų reikšmes, pateikiama savybių apžvalga. Remiantis ištirtomis funkcijų savybėmis, sprendžiamos eksponentinės ir logaritminės nelygybės. Būdingas kurso bruožas – studentų žinių sisteminimas ir apibendrinimas, algebros kurse įgytų įgūdžių ir gebėjimų įtvirtinimas ir ugdymas, kuris atliekamas tiek studijuojant naują medžiagą, tiek atliekant apibendrinantį kartojimą.
2 skyrius
§ vienas. Laipsnio sampratos apibendrinimas.
Apibrėžimas: th grynumo laipsnio šaknis yra toks skaičius, kurio th laipsnis yra lygus.
Pagal šį apibrėžimą skaičiaus th laipsnio šaknis yra lygties sprendimas. Šios lygties šaknų skaičius priklauso nuo ir . Panagrinėkime funkciją. Kaip žinoma, intervale ši funkcija padidėja bet kuriam ir paima visas reikšmes iš intervalo . Pagal šaknies teoremą bet kurios lygtis turi neneigiamą šaknį, be to, tik vieną. Jis vadinamas skaičiaus th laipsnio aritmetine šaknimi ir žymimas; skaičius vadinamas šaknies indeksu, o pats skaičius – radikaliąja išraiška. Ženklas taip pat vadinamas radikalu.
Apibrėžimas: skaičiaus th laipsnio aritmetinė šaknis yra neneigiamas skaičius, kurio laipsnis yra .
Netgi funkcija yra lygi. Iš to išplaukia, kad jei , tai lygtis, be šaknies, taip pat turi šaknį. Jei , tada yra tik viena šaknis: ; jei , tai ši lygtis neturi šaknų, nes bet kurio skaičiaus net galia yra neneigiama.
Nelyginėms reikšmėms funkcija didėja visoje skaičių eilutėje; jo diapazonas yra visų realiųjų skaičių aibė. Taikydami šaknies teoremą, mes nustatome, kad lygtis turi vieną šaknį bet kuriai ir ypač . Ši bet kurios reikšmės šaknis žymima .
Nelyginio laipsnio šaknims lygybė yra tiesa. Išties, , t.y. skaičius yra šaknis iš . Tačiau tokia nelyginio šaknis yra unikali. Vadinasi,.
1 pastaba: bet kokiam tikram
Prisiminkite gerai žinomas laipsnio aritmetinių šaknų savybes.
Bet kokiems natūraliems , sveikieji ir bet kokie neneigiami sveikieji skaičiai ir lygybės yra teisingi:
1. 
2. 
3. 
4. 
Laipsnis su racionaliuoju rodikliu.
Išraiška apibrėžiama visiems ir , išskyrus atvejį, kai . Prisiminkite tokių galių savybes.
Bet kokiems skaičiams ir bet kokiems sveikiesiems skaičiams bei lygybėms yra teisingi:
Taip pat pažymime, kad jei , tada už ir už .. ir
Mokiniams, besimokantiems laikyti vieningą valstybinį egzaminą, Jakutsko 26-osios vidurinės mokyklos matematikos mokytojai naudoja mokyklinio matematikos kurso turinio klausimų sąrašą (kodifikatorių), kurio įsisavinimas tikrinamas laikant vieningą valstybinį egzaminą 2007 m. . pasirenkamasis kursas ruošiantis Unifikacijai Valstybinis egzaminas remiasi anksčiau įgytų žinių kartojimu, sisteminimu ir gilinimu. Užsiėmimai vyksta nemokamai...
Išvardytos lygybės konvertuojant išraiškas logaritmais naudojamos tiek iš dešinės į kairę, tiek iš kairės į dešinę.
Verta paminėti, kad nebūtina įsiminti savybių pasekmių: atlikdami transformacijas galite apsieiti su pagrindinėmis logaritmų savybėmis ir kitais faktais (pavyzdžiui, kai b≥0), iš kurių atitinkamos seka pasekmės. Šio metodo „šalutinis poveikis“ yra tik tai, kad sprendimas bus šiek tiek ilgesnis. Pavyzdžiui, norint apsieiti be pasekmės, kuri išreiškiama formule 
, ir pradedant tik nuo pagrindinių logaritmų savybių, turėsite atlikti tokios formos transformacijų grandinę: 
.
Tą patį galima pasakyti apie paskutinę savybę iš aukščiau pateikto sąrašo, kuri atitinka formulę 
, nes tai išplaukia ir iš pagrindinių logaritmų savybių. Svarbiausia suprasti, kad teigiamo skaičiaus laipsnis su logaritmu eksponente visada gali pakeisti laipsnio bazę ir skaičių po logaritmo ženklu. Sąžiningai pažymime, kad praktikoje retai pasitaiko pavyzdžių, susijusių su tokio pobūdžio transformacijų įgyvendinimu. Toliau pateiksime keletą pavyzdžių.
Skaitinių išraiškų konvertavimas logaritmais
Prisiminėme logaritmų ypatybes, dabar laikas išmokti juos pritaikyti praktiškai transformuojant išraiškas. Natūralu pradėti nuo skaitinių išraiškų, o ne reiškinių su kintamaisiais transformavimo, nes jais patogiau ir lengviau išmokti pagrindus. Taigi mes padarysime ir pradėsime nuo labai paprasti pavyzdžiai išmokti pasirinkti norimą logaritmo savybę, tačiau pavyzdžius palaipsniui komplikuosime iki to momento, kai norint gauti galutinį rezultatą reikės taikyti kelias savybes iš eilės.
Norimos logaritmų savybės pasirinkimas
Logaritmų savybių yra ne tiek ir mažai, ir aišku, kad iš jų reikia mokėti pasirinkti tinkamą, kuri šiuo konkrečiu atveju lems norimą rezultatą. Paprastai tai padaryti nesunku lyginant konvertuojamo logaritmo ar išraiškos formą su logaritmų savybes išreiškiančių formulių kairiosios ir dešiniosios dalių tipais. Jei paliktas arba dešinioji dalis viena iš formulių sutampa su pateiktu logaritmu ar išraiška, tada greičiausiai būtent šią savybę reikia naudoti transformuojant. Toliau pateikti pavyzdžiai tai aiškiai parodo.
Pradėkime nuo reiškinių transformavimo pavyzdžių, naudojant logaritmo apibrėžimą, kuris atitinka formulę a log a b =b , a>0 , a≠1 , b>0 .
Pavyzdys.
Jei įmanoma, apskaičiuokite: a) 5 log 5 4 , b) 10 log(1+2 π) , c) 
, d) 2 log 2 (−7) , e) .
Sprendimas.
Pavyzdyje raidė a) aiškiai parodo struktūrą a log a b , kur a=5 , b=4 . Šie skaičiai atitinka sąlygas a>0 , a≠1 , b>0 , todėl galite saugiai naudoti lygybę a log a b =b . Turime 5 log 5 4=4 .
b) Čia a=10 , b=1+2 π , sąlygos a>0 , a≠1 , b>0 tenkinamos. Šiuo atveju įvyksta lygybė 10 lg(1+2 π) =1+2 π.
c) Šiame pavyzdyje kalbame apie a log a b formos laipsnį, kur ir b=ln15 . Taigi 
.
Nepaisant to, kad ji priklauso tai pačiai formai a log a b (čia a=2 , b=−7 ), išraiška po raide d) negali būti konvertuojama pagal formulę a log a b =b . Priežastis ta, kad tai nėra prasminga, nes jame yra neigiamas skaičius po logaritmo ženklu. Be to, skaičius b=−7 netenkina sąlygos b>0 , todėl neįmanoma pasinaudoti formule a log a b =b , nes tam reikalingos sąlygos a>0 , a≠1 , b>0 . Taigi, mes negalime kalbėti apie reikšmės 2 log 2 (−7) skaičiavimą. Šiuo atveju parašyti 2 log 2 (−7) = −7 būtų klaida.
Panašiai ir pavyzdyje po raide e) neįmanoma pateikti formos sprendimo 
, nes pradinė išraiška neturi prasmės.
Atsakymas:
a) 5 log 5 4 =4, b) 10 log(1+2 π) =1+2 π , c) , d), e) posakiai neturi prasmės.
Dažnai naudinga transformuotis teigiamas skaičius vaizduojamas kaip tam tikro teigiamo ir nevieno skaičiaus laipsnis su logaritmu eksponente. Jis pagrįstas tuo pačiu logaritmo apibrėžimu a log a b =b , a>0 , a≠1 , b>0 , tačiau formulė taikoma iš dešinės į kairę, tai yra b=a log a b forma. Pavyzdžiui, 3=e ln3 arba 5=5 log 5 5 .
Pereikime prie logaritmų savybių panaudojimo išraiškoms transformuoti.
Pavyzdys.
Raskite išraiškos reikšmę: a) log −2 1, b) log 1 1, c) log 0 1, d) log 7 1, e) ln1, f) lg1, g) log 3,75 1, h) log 5 π 7 1 .
Sprendimas.
Pavyzdžiuose po raidėmis a), b) ir c) pateiktos išraiškos log −2 1, log 1 1, log 0 1, kurios nėra prasmės, nes logaritmo bazėje neturi būti neigiamo skaičiaus. , nulis arba vienas, nes apibrėžėme logaritmą tik teigiamai ir ne vienetinei bazei. Todėl a) - c) pavyzdžiuose negali būti nė kalbos apie išraiškos reikšmės radimą.
Akivaizdu, kad visose kitose užduotyse logaritmų bazėse yra atitinkamai teigiami ir nevienetiniai skaičiai 7 , e , 10 , 3,75 ir 5 π 7, o vienetai visur yra po logaritmų ženklais. Ir žinome vienybės logaritmo savybę: log a 1=0 bet kuriam a>0 , a≠1 . Taigi b) - f) išraiškų reikšmės yra lygios nuliui.
Atsakymas:
a), b), c) posakiai neturi prasmės, d) log 7 1=0, e) ln1=0, f) log1=0, g) log 3,75 1=0, h) log 5 e 7 1 =0.
Pavyzdys.
Apskaičiuokite: a) , b) lne , c) lg10 , d) log 5 π 3 -2 (5 π 3 -2), e) log −3 (−3) , f) log 1 1 .
Sprendimas.
Aišku, kad turime naudoti pagrindo logaritmo savybę, kuri atitinka formulę log a a=1, kai a>0 , a≠1 . Iš tiesų, užduotyse po visomis raidėmis skaičius po logaritmo ženklu sutampa su jo pagrindu. Taigi iš karto noriu pasakyti, kad kiekvienos pateiktos išraiškos reikšmė yra 1 . Tačiau neskubėkite daryti išvadų: užduotyse po raidėmis a) - d) posakių reikšmės tikrai lygios vienetui, o e) ir f) užduotyse originalūs posakiai neturi prasmės, todėl negali Sakoma, kad šių išraiškų reikšmės yra lygios 1.
Atsakymas:
a) , b) lne=1 , c) lg10=1 , d) log 5 π 3 −2 (5 π 3 −2)=1, e), f) posakiai neturi prasmės.
Pavyzdys.
Raskite reikšmę: a) log 3 3 11 , b) 
, c) , d) log −10 (−10) 6 .
Sprendimas.
Akivaizdu, kad po logaritmų ženklais yra tam tikri bazės laipsniai. Remdamiesi tuo suprantame, kad čia naudinga pagrindo laipsnio savybė: log a a p =p, kur a>0, a≠1 ir p yra bet koks realusis skaičius. Atsižvelgdami į tai, gauname tokius rezultatus: a) log 3 3 11 =11 , b) 
, in) 
. Ar galima panašią lygybę pavyzdžiui užrašyti po formos log −10 (−10) 6 =6 raide d)? Ne, negalite, nes log −10 (−10) 6 neturi prasmės.
Atsakymas:
a) log 3 3 11 = 11, b) , in) d) posakis neturi prasmės.
Pavyzdys.
Išreikškite išraišką kaip logaritmų sumą arba skirtumą toje pačioje bazėje: a) 
, b) , c) log((−5) (−12)) .
Sprendimas.
a) sandauga yra po logaritmo ženklu ir žinome sandaugos logaritmo savybę log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y> 0 . Mūsų atveju skaičius logaritmo bazėje ir skaičiai sandaugoje yra teigiami, tai yra, atitinka pasirinktos savybės sąlygas, todėl galime drąsiai ją taikyti: 
.
b) Čia naudojame koeficiento logaritmo savybę, kur a>0 , a≠1 , x>0 , y>0 . Mūsų atveju logaritmo pagrindas yra teigiamas skaičius e, skaitiklis ir vardiklis π yra teigiami, vadinasi, atitinka savybės sąlygas, todėl turime teisę naudoti pasirinktą formulę: 
.
c) Pirma, atkreipkite dėmesį, kad išraiška lg((-5) (-12)) yra prasminga. Bet tuo pačiu neturime teisės taikyti sandaugos logaritmo formulės log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 , kadangi skaičiai −5 ir −12 yra neigiami ir neatitinka sąlygų x>0 , y>0 . Tai yra, tokios transformacijos atlikti neįmanoma: log((-5)(-12))=log(-5)+log(-12). Bet ką daryti? Tokiais atvejais pirminę išraišką reikia iš anksto paversti, kad būtų išvengta neigiamų skaičių. Apie panašius posakių transformavimo atvejus su neigiami skaičiai po logaritmo ženklu mes išsamiai kalbėsime viename iš, bet kol kas pateiksime šio pavyzdžio sprendimą, kuris yra aiškus iš anksto ir be paaiškinimo: lg((-5)(-12))=lg(5 12)=lg5+lg12.
Atsakymas:
a) , b) , c) lg((−5) (−12))=lg5+lg12 .
Pavyzdys.
Supaprastinkite išraišką: a) log 3 0,25 + log 3 16 + log 3 0,5, b) .
Sprendimas.
Čia mums padės visos tos pačios sandaugos logaritmo ir koeficiento logaritmo savybės, kurias naudojome ankstesniuose pavyzdžiuose, tik dabar jas pritaikysime iš dešinės į kairę. Tai yra, logaritmų sumą paverčiame sandaugos logaritmu, o logaritmų skirtumą – koeficiento logaritmu. Mes turime
a) log 3 0,25 + log 3 16 + log 3 0,5 = log 3 (0,25 16 0,5) = log 3 2.
b) 
.
Atsakymas:
a) log 3 0,25+log 3 16+log 3 0,5=log 3 2, b) 
.
Pavyzdys.
Atsikratykite laipsnio po logaritmo ženklu: a) log 0,7 5 11, b) 
, c) log 3 (−5) 6 .
Sprendimas.
Nesunku suprasti, kad turime reikalą su tokiais posakiais kaip log a b p . Atitinkama logaritmo savybė yra log a b p =p log a b , kur a>0 , a≠1 , b>0 , p yra bet koks realusis skaičius. Tai yra, esant sąlygoms a>0 , a≠1 , b>0 iš laipsnio log a b p logaritmo galime pereiti prie sandaugos p·log a b . Atlikime šią transformaciją pateiktomis išraiškomis.
a) Šiuo atveju a=0,7 , b=5 ir p=11 . Taigi log 0,7 5 11 =11 log 0,7 5 .
b) Čia įvykdomos sąlygos a>0 , a≠1 , b>0. Štai kodėl 
c) Išraiška log 3 (−5) 6 turi tokią pačią struktūrą log a b p , a=3 , b=−5 , p=6 . Tačiau b sąlyga b>0 netenkinama, todėl neįmanoma taikyti formulės log a b p =p log a b . Tai kodėl negalite atlikti darbo? Tai įmanoma, tačiau reikalinga išankstinė išraiškos transformacija, kurią išsamiai aptarsime toliau esančioje pastraipoje antraštėje . Sprendimas bus toks: log 3 (−5) 6 =log 3 5 6 =6 log 3 5.
Atsakymas:
a) log 0,7 5 11 = 11 log 0,7 5,
b)
c) log 3 (−5) 6 =6 log 3 5 .
Gana dažnai laipsnio logaritmo formulė, atliekant transformacijas, turi būti taikoma iš dešinės į kairę forma p log a b \u003d log a b p (tam reikalingos tos pačios sąlygos a, b ir p). Pavyzdžiui, 3 ln5=ln5 3 ir lg2 log 2 3=log 2 3 lg2 .
Pavyzdys.
a) Apskaičiuokite log 2 5 reikšmę, jei žinoma, kad lg2≈0,3010 ir lg5≈0,6990. b) Parašykite trupmeną logaritmu į 3 pagrindą.
Sprendimas.
a) Perėjimo prie naujos logaritmo bazės formulė leidžia mums pavaizduoti šį logaritmą kaip dešimtainių logaritmų santykį, kurių reikšmės mums žinomos: . Belieka tik atlikti skaičiavimus, mes turime 
.
b) Čia pakanka naudoti perėjimo prie naujos bazės formulę ir taikyti ją iš dešinės į kairę, tai yra formoje 
. Mes gauname 
.
Atsakymas:
a) log 2 5≈2,3223, b) .
Šiame etape mes gana kruopščiai apsvarstėme paprasčiausių išraiškų transformaciją, naudodami pagrindines logaritmų savybes ir logaritmo apibrėžimą. Šiuose pavyzdžiuose turėjome naudoti vieną nuosavybę ir nieko kito. Dabar ramia sąžine galite pereiti prie pavyzdžių, kurių transformacijai reikia panaudoti keletą logaritmų savybių ir kitų papildomų transformacijų. Su jais kalbėsime kitoje pastraipoje. Tačiau prieš tai trumpai apsistokime prie pagrindinių logaritmų savybių pasekmių taikymo pavyzdžių.
Pavyzdys.
a) Atsikratykite šaknies po logaritmo ženklu. b) Paverskite trupmeną į 5 bazinį logaritmą. c) Atsikratykite galių po logaritmo ženklu ir jo pagrindu. d) Apskaičiuokite išraiškos reikšmę 
. e) Pakeiskite išraišką laipsniu su 3 baze.
Sprendimas.
a) Jei priminsime išvadą iš laipsnio logaritmo savybės 
, tuomet galite iš karto atsakyti: 
.
b) Čia naudojame formulę 
iš dešinės į kairę, turime 
.
c) B Ši byla formulė veda prie rezultato . Mes gauname 
.
d) Ir čia pakanka pritaikyti išvadą, kurią atitinka formulė 
. Taigi 
.
e) Logaritmo savybė leidžia pasiekti norimą rezultatą: 
.
Atsakymas:
a) . b) . in) 
. G) 
. e) .
Nuoseklus kelių savybių taikymas
Realios užduotys, skirtos išraiškoms transformuoti naudojant logaritmų savybes, paprastai yra sudėtingesnės nei tos, kurias nagrinėjome ankstesnėje pastraipoje. Juose, kaip taisyklė, rezultatas gaunamas ne vienu žingsniu, o sprendimas jau susideda iš nuoseklaus vienos savybės pritaikymo po kitos kartu su papildomomis identiškomis transformacijomis, tokiomis kaip skliaustų atidarymas, panašių terminų redukavimas, trupmenų mažinimas ir kt. . Taigi, eikime arčiau tokių pavyzdžių. Čia nėra nieko sudėtingo, svarbiausia elgtis atsargiai ir nuosekliai, laikantis veiksmų atlikimo tvarkos.
Pavyzdys.
Apskaičiuokite išraiškos reikšmę (log 3 15–log 3 5) 7 log 7 5.
Sprendimas.
Logaritmų skirtumą skliausteliuose pagal koeficiento logaritmo savybę galima pakeisti logaritmu log 3 (15:5) , o tada apskaičiuoti jo reikšmę log 3 (15:5)=log 3 3=1 . O išraiškos 7 log 7 5 reikšmė pagal logaritmo apibrėžimą yra 5 . Pakeitę šiuos rezultatus į pradinę išraišką, gauname (log 3 15−log 3 5) 7 log 7 5 =1 5=5.
Čia yra sprendimas be paaiškinimo:
(log 3 15–log 3 5) 7 log 7 5 =log 3 (15:5) 5=
= log 3 3 5=1 5=5 .
Atsakymas:
(log 3 15−log 3 5) 7 log 7 5 =5.
Pavyzdys.
Kokia yra skaitinės išraiškos log 3 log 2 2 3 −1 reikšmė?
Sprendimas.
Pirmiausia transformuokime logaritmą, esantį po logaritmo ženklu, pagal laipsnio logaritmo formulę: log 2 2 3 =3. Taigi log 3 log 2 2 3 =log 3 3 ir tada log 3 3 = 1 . Taigi log 3 log 2 2 3 −1=1−1=0 .
Atsakymas:
log 3 log 2 2 3 −1=0 .
Pavyzdys.
Supaprastinkite išraišką.
Sprendimas.
Konvertavimo į naują logaritmo bazę formulė leidžia logaritmų ir vienos bazės santykį pavaizduoti kaip log 3 5 . Tokiu atveju pradinė išraiška bus formos . Pagal logaritmo apibrėžimą 3 log 3 5 =5 , tai yra 
, o gautos išraiškos reikšmė pagal tą patį logaritmo apibrėžimą yra lygi dviem.
Čia trumpa versija sprendimas, kuris paprastai pateikiamas: 
.
Atsakymas:
.
Kad perėjimas prie kitos pastraipos informacijos būtų sklandus, pažvelkime į išraiškas 5 2+log 5 3 ir lg0.01 . Jų struktūra neatitinka jokių logaritmų savybių. Taigi, kas atsitiks, jei jų negalima konvertuoti naudojant logaritmų savybes? Tai įmanoma, jei atliksite išankstines transformacijas, kurios paruošia šias išraiškas logaritmų savybėms taikyti. Taigi 5 2+log 5 3 =5 2 5 log 5 3 =25 3=75, 
ir lg0,01=lg10 −2 = −2 . Toliau mes išsamiai suprasime, kaip atliekamas toks posakių rengimas.
Reiškių ruošimas logaritmų savybėms taikyti
Logaritmai konvertuotoje išraiškoje labai dažnai skiriasi žymėjimo struktūra nuo kairėje ir dešinėje formulių dalių, atitinkančių logaritmų savybes. Tačiau taip pat dažnai šių posakių transformacija apima logaritmų savybių naudojimą: jų naudojimui reikia tik išankstinio pasiruošimo. Ir šis paruošimas susideda iš tam tikrų identiškų transformacijų, kurios logaritmams suteikia formą, patogią savybėms taikyti.
Sąžiningai pažymime, kad beveik bet kokia išraiškų transformacija gali veikti kaip preliminari transformacija, nuo banalaus panašių terminų sumažinimo iki taikymo trigonometrines formules. Tai suprantama, nes konvertuotose išraiškose gali būti bet kokių matematinių objektų: skliaustų, modulių, trupmenų, šaknų, laipsnių ir kt. Taigi, norint dar labiau pasinaudoti logaritmų savybėmis, reikia būti pasiruošus atlikti bet kokią reikiamą transformaciją.
Iš karto pasakykime, kad šiame skyriuje mes nekeliame sau užduoties klasifikuoti ir analizuoti visas įsivaizduojamas išankstines transformacijas, leidžiančias ateityje pritaikyti logaritmų savybes ar logaritmo apibrėžimą. Čia sutelksime dėmesį tik į keturis iš jų, kurie yra būdingiausi ir dažniausiai sutinkami praktikoje.
Ir dabar išsamiai apie kiekvieną iš jų, po kurio mūsų temos rėmuose belieka tik nagrinėti išraiškų su kintamaisiais transformaciją logaritmų ženklais.
Galių pasirinkimas po logaritmo ženklu ir jo bazėje
Iš karto pradėkime nuo pavyzdžio. Paimkime logaritmą. Akivaizdu, kad tokia forma jo struktūra nėra palanki logaritmų savybių naudojimui. Ar galima kaip nors transformuoti šią išraišką, kad ją supaprastintume, ar dar geriau apskaičiuoti jos vertę? Norėdami atsakyti į šį klausimą, atidžiau pažvelkime į skaičius 81 ir 1/9 mūsų pavyzdžio kontekste. Čia nesunku pastebėti, kad šie skaičiai gali būti pavaizduoti kaip 3 laipsniai, iš tikrųjų 81 = 3 4 ir 1/9 = 3 −2 . Tokiu atveju formoje pateikiamas pradinis logaritmas ir atsiranda galimybė pritaikyti formulę . Taigi, 
.
Analizuojant analizuojamą pavyzdį kyla tokia mintis: jei įmanoma, galite pabandyti paryškinti laipsnį po logaritmo ženklu ir jo pagrindu, kad būtų pritaikyta laipsnio logaritmo savybė arba jo pasekmė. Belieka tik išsiaiškinti, kaip išskirti šiuos laipsnius. Pateiksime keletą rekomendacijų šiuo klausimu.
Kartais visiškai akivaizdu, kad skaičius po logaritmo ženklu ir (arba) jo bazėje reiškia tam tikrą sveikojo skaičiaus galią, kaip ir aukščiau aptartame pavyzdyje. Beveik nuolat tenka susidurti su gerai žinomomis dviejų galiomis: 4=2 2 , 8=2 3 , 16=2 4 , 32=2 5 , 64=2 6 , 128=2 7 , 256=2 8 , 512 = 2 9 , 1024 = 2 10 . Tą patį galima pasakyti ir apie trigubo laipsnius: 9=3 2 , 27=3 3 , 81=3 4 , 243=3 5 , ... Apskritai, neskauda, jei yra laipsnių lentelė natūraliuosius skaičius per dešimt. Taip pat nesunku dirbti su dešimties, šimto, tūkstančio ir pan.
Pavyzdys.
Apskaičiuokite reikšmę arba supaprastinkite išraišką: a) log 6 216 , b) , c) log 0,000001 0,001 .
Sprendimas.
a) Akivaizdu, kad 216=6 3, taigi log 6 216=log 6 6 3 =3.
b) Natūraliųjų skaičių laipsnių lentelė leidžia pavaizduoti skaičius 343 ir 1/243 atitinkamai kaip 7 3 ir 3 −4 laipsnius. Todėl galima kita transformacija duotas logaritmas: 
c) Kadangi 0,000001 = 10 -6 ir 0,001 = 10 -3, tada log 0,000001 0,001 = log 10 −6 10 −3 = (−3)/(−6) = 1/2.
Atsakymas:
a) log 6 216 = 3, b) 
, c) log 0,000001 0,001=1/2 .
Sudėtingesniais atvejais, norėdami pabrėžti skaičių galias, turite pasinaudoti.
Pavyzdys.
Pakeiskite išraišką į paprastesnę formą log 3 648 log 2 3 .
Sprendimas.
Pažiūrėkime, į ką išplečiamas skaičius 648 pagrindiniai veiksniai:
Tai yra, 648=2 3 3 4 . Šiuo būdu, log 3 648 log 2 3=log 3 (2 3 3 4) log 2 3.
Dabar paverčiame sandaugos logaritmą į logaritmų sumą, po to taikome laipsnio logaritmo savybes:
log 3 (2 3 3 4) log 2 3=(log 3 2 3 + log 3 3 4) log 2 3=
=(3 log 3 2+4) log 2 3 .
Dėl laipsnio logaritmo savybės, atitinkančios formulę, pasekmė , sandauga log32 log23 yra sandauga , ir žinoma, kad jis lygus vienetui. Atsižvelgdami į tai, gauname 3 log 3 2 log 2 3+4 log 2 3=3 1+4 log 2 3=3+4 log 2 3.
Atsakymas:
log 3 648 log 2 3=3+4 log 2 3.
Gana dažnai posakiai po logaritmo ženklu ir jo bazėje yra kai kurių skaičių šaknų ir (arba) laipsnių sandaugai arba santykiai, pavyzdžiui, , . Panašios išraiškos gali būti pavaizduotos kaip laipsnis. Norėdami tai padaryti, atliekamas perėjimas nuo šaknų iki laipsnių ir yra taikomas. Šios transformacijos leidžia pasirinkti laipsnius po logaritmo ženklu ir jo bazėje, o tada taikyti logaritmų savybes.
Pavyzdys.
Apskaičiuokite: a) 
, b).
Sprendimas.
a) Logaritmo pagrindo išraiška yra tų pačių bazių laipsnių sandauga pagal atitinkamą mūsų turimų galių savybę 5 2 5 −0,5 5 −1 =5 2−0,5−1 =5 0,5.
Dabar paverskime trupmeną po logaritmo ženklu: pereikime nuo šaknies į laipsnį, po kurio naudosime laipsnių santykio savybę su tomis pačiomis bazėmis: 
.
Belieka gautus rezultatus pakeisti pradine išraiška, naudoti formulę ir užbaigti transformaciją: 
b) Kadangi 729=3 6 ir 1/9=3 −2 , pradinė išraiška gali būti perrašyta kaip .
Tada pritaikykite laipsnio šaknies savybę, pereikite nuo šaknies prie laipsnio ir naudokite laipsnių santykio savybę logaritmo bazei konvertuoti į laipsnį: 
.
Atsižvelgdami į paskutinį rezultatą, turime 
.
Atsakymas:
a) 
, b).
Aišku, kad bendru atveju, norint gauti galias po logaritmo ženklu ir jo bazėje, gali prireikti įvairių įvairių posakių transformacijų. Pateikime porą pavyzdžių.
Pavyzdys.
Kokia yra išraiškos reikšmė: a) 
, b) 
.
Sprendimas.
Be to, pastebime, kad pateikta išraiška turi formą log A B p , kur A=2 , B=x+1 ir p=4 . Tokio pobūdžio skaitines išraiškas transformavome pagal laipsnio log a b p \u003d p log a b logaritmo savybę, todėl su nurodyta išraiška noriu padaryti tą patį ir pereiti nuo log 2 (x + 1) 4 iki 4 log 2 (x + 1) . O dabar apskaičiuokime pradinės išraiškos reikšmę ir po transformacijos gautą išraišką, pavyzdžiui, su x=−2 . Turime log 2 (−2+1) 4 =log 2 1=0 , ir 4 log 2 (−2+1) = 4 log 2 (−1)- beprasmiška išraiška. Tai kelia teisėtą klausimą: „Ką mes padarėme ne taip“?
O priežastis tokia: atlikome transformaciją log 2 (x+1) 4 =4 log 2 (x+1) , remiantis formule log a b p =p log a b , bet turime teisę taikyti tik šią formulę jei sąlygos a >0 , a≠1 , b>0 , p - bet koks realusis skaičius. Tai yra, mūsų atlikta transformacija įvyksta, jei x+1>0 , tai yra tas pats x>−1 (A ir p sąlygos yra įvykdytos). Tačiau mūsų atveju pradinės išraiškos kintamojo x ODZ susideda ne tik iš intervalo x> −1 , bet ir iš intervalo x<−1 . Но для x<−1 мы не имели права осуществлять преобразование по выбранной формуле.
Reikia atsižvelgti į ODZ
Toliau analizuosime pasirinktos išraiškos log 2 (x+1) 4 transformaciją, o dabar pažiūrėkime, kas atsitiks su ODZ pereinant prie reiškinio 4·log 2 (x+1) . Ankstesnėje pastraipoje radome pradinės išraiškos ODZ – tai rinkinys (−∞, −1)∪(−1, +∞) . Dabar suraskime kintamojo x priimtinų reikšmių plotą 4 log 2 (x+1) . Jis nustatomas pagal sąlygą x+1>0 , kuri atitinka aibę (−1, +∞) . Akivaizdu, kad pereinant nuo log 2 (x+1) 4 iki 4·log 2 (x+1), leistinų reikšmių diapazonas susiaurėja. Ir sutarėme vengti reformų, kurios veda į ODZ susiaurėjimą, nes tai gali sukelti įvairių neigiamų pasekmių.
Čia verta atkreipti dėmesį į tai, kad kiekviename transformacijos etape naudinga valdyti ODZ ir neleisti jam susiaurėti. Ir jei staiga kažkuriame pertvarkos etape ODZ susiaurėjo, tuomet verta labai atidžiai pasidomėti, ar ši pertvarka yra leistina ir ar turėjome teisę ją vykdyti.
Teisybės dėlei sakome, kad praktikoje dažniausiai tenka dirbti su išraiškomis, kuriose kintamųjų ODZ yra toks, kad leistų be apribojimų naudoti logaritmų savybes mums jau žinoma forma tiek iš kairės į dešinę, tiek iš iš dešinės į kairę, atliekant transformacijas. Greitai prie to pripranti ir transformacijas pradedi vykdyti mechaniškai, negalvodamas, ar buvo įmanoma jas atlikti. Ir tokiais momentais, kaip pasisektų, praslysta sudėtingesni pavyzdžiai, kuriuose netikslus logaritmų savybių pritaikymas sukelia klaidų. Taigi jūs turite visada būti budrūs ir įsitikinti, kad ODZ nesusiaurėja.
Nepakenks atskirai pabrėžti pagrindines transformacijas, pagrįstas logaritmų savybėmis, kurios turi būti atliekamos labai atsargiai, o tai gali lemti ODZ susiaurėjimą ir dėl to klaidų:
Kai kurios išraiškų transformacijos pagal logaritmų savybes gali sukelti ir priešingą – ODZ išplėtimą. Pavyzdžiui, pereinant nuo 4 log 2 (x+1) į log 2 (x+1) 4, ODZ išplečiamas nuo aibės (−1, +∞) iki (−∞, −1)∪(−1, +∞ ). Tokios transformacijos įvyksta, jei liekate pirminės išraiškos ODZ ribose. Taigi ką tik minėta transformacija 4 log 2 (x+1)=log 2 (x+1) 4 vyksta ODZ kintamajame x pradinei išraiškai 4 log 2 (x+1), tai yra, kai x+1> 0 , kuris yra toks pat kaip (−1, +∞) .
Dabar, kai aptarėme niuansus, į kuriuos reikia atkreipti dėmesį konvertuojant išraiškas su kintamaisiais naudojant logaritmų savybes, belieka išsiaiškinti, kaip teisingai atlikti šias konversijas.
X+2>0 . Ar tai veikia mūsų atveju? Norėdami atsakyti į šį klausimą, pažvelkime į x kintamojo DPV. Jį lemia nelygybių sistema 
, kuri atitinka sąlygą x+2>0 (jei reikia, žr. straipsnį nelygybių sistemų sprendimas). Taigi galime saugiai taikyti laipsnio logaritmo savybę.
Mes turime
3 log(x+2) 7 −log(x+2)−5 log(x+2) 4 =
=3 7 log(x+2)–log(x+2)–5 4 log(x+2)=
=21 log(x+2)−log(x+2)−20 log(x+2)=
=(21−1−20)lg(x+2)=0 .
Galite elgtis kitaip, nes ODZ leidžia tai padaryti, pavyzdžiui, taip: 
Atsakymas:
3 log(x+2) 7 −log(x+2)−5 log(x+2) 4 =0.
O ką daryti, kai ODZ nesilaikoma su logaritmų savybėmis susijusių sąlygų? Mes tai spręsime pavyzdžiais.
Reikės supaprastinti išraišką lg(x+2) 4 −lg(x+2) 2 . Šios išraiškos transformacija, skirtingai nei išraiška iš ankstesnio pavyzdžio, neleidžia laisvai naudotis laipsnio logaritmo savybe. Kodėl? Kintamojo x ODZ šiuo atveju yra dviejų intervalų x>−2 ir x sąjunga<−2 . При x>−2 galime saugiai pritaikyti laipsnio logaritmo savybę ir elgtis taip, kaip nurodyta aukščiau pateiktame pavyzdyje: log(x+2) 4 −log(x+2) 2 =4 log(x+2)−2 log(x+2)=2 log(x+2). Tačiau ODZ yra kitas intervalas x+2<0 , для которого последнее преобразование будет некорректно. Что же делать при x+2<0 ? В подобных случаях на помощь приходит . Определение модуля позволяет выражение x+2 при x+2<0 представить как −|x+2| . Тогда при x+2<0 от lg(x+2) 4 −lg(x+2) 2 переходим к log(−|x+2|) 4 −log(−|x+2|) 2 ir toliau dėl lg|x+2| galios savybių 4−lg|x+2| 2. Gautą išraišką galima transformuoti pagal laipsnio logaritmo savybę, nes |x+2|>0 bet kurioms kintamojo reikšmėms. Mes turime log|x+2| 4−lg|x+2| 2 =4 log|x+2|−2 log|x+2|=2 log|x+2|. Dabar galite atsikratyti modulio, nes jis atliko savo darbą. Kadangi transformuojame ties x+2<0 , то 2·lg|x+2|=2·lg(−(x+2)) . Итак, можно считать, что мы справились с поставленной задачей. Ответ: . Полученный результат можно записать компактно с использованием модуля как .
Panagrinėkime dar vieną pavyzdį, kad būtų lengviau dirbti su moduliais. Supraskime iš posakio 
pereiti prie tiesinių dvinarių x−1 , x−2 ir x−3 logaritmų sumos ir skirtumo. Pirmiausia randame ODZ: 
Intervale (3, +∞) reiškinių x−1, x−2 ir x−3 reikšmės yra teigiamos, todėl galime saugiai taikyti sumos ir skirtumo logaritmo savybes: 
O intervale (1, 2) išraiškos x−1 reikšmės yra teigiamos, o išraiškų x−2 ir x−3 reikšmės yra neigiamos. Todėl nagrinėjamame intervale x−2 ir x−3 pavaizduojame modulį kaip −|x−2| ir −|x−3| atitinkamai. Kuriame 
Dabar galime pritaikyti sandaugos logaritmo ir koeficiento savybes, nes nagrinėjamame intervale (1, 2) reikšmių x−1 , |x−2| ir |x−3| - teigiamas.
Mes turime 
Gauti rezultatai gali būti derinami:
Apskritai, panašus samprotavimas leidžia, remiantis sandaugos, santykio ir laipsnio logaritmo formulėmis, gauti tris praktiškai naudingus rezultatus, kuriuos gana patogu naudoti:
- Dviejų savavališkų log a (X·Y) reiškinių X ir Y sandaugos logaritmą galima pakeisti logaritmų suma log a |X|+log a |Y| , a>0 , a≠1 .
- Specialusis logaritmas log a (X:Y) gali būti pakeistas logaritmų log a skirtumu |X|−log a |Y| , a>0 , a≠1 , X ir Y yra savavališkos išraiškos.
- Iš kokios nors išraiškos B logaritmo iki lyginės laipsnio p formos log a B p, galima pereiti prie išraiškos p log a |B| , kur a>0, a≠1, p yra lyginis skaičius, o B yra savavališka išraiška.
Panašūs rezultatai pateikiami, pavyzdžiui, M. I. Skanavi redaguotose eksponentinių ir logaritminių lygčių sprendimo instrukcijose matematikos uždavinių rinkinyje stojantiesiems į universitetus.
Pavyzdys.
Supaprastinkite išraišką 
.
Sprendimas.
Būtų gerai pritaikyti laipsnio, sumos ir skirtumo logaritmo savybes. Bet ar galime tai padaryti čia? Norėdami atsakyti į šį klausimą, turime žinoti ODZ.
Apibrėžkime tai: 
Visiškai akivaizdu, kad kintamojo x galimų reikšmių diapazono išraiškos x+4 , x−2 ir (x+4) 13 gali turėti ir teigiamas, ir neigiamas reikšmes. Todėl turėsime dirbti per modulius. 
Modulio ypatybės leidžia perrašyti kaip , so 
Be to, niekas netrukdo naudoti laipsnio logaritmo savybę ir tada pateikti tokius terminus: 
Kita transformacijų seka lemia tą patį rezultatą: 
ir kadangi išraiška x−2 gali turėti ir teigiamas, ir neigiamas ODZ reikšmes, imant lyginį eksponentą 14
