Utilizarea derivatului în diverse domenii de activitate. O derivată interesantă Obiectivele acestei lucrări: Să ia în considerare utilizarea derivatei în diverse științe Să se familiarizeze cu oamenii de știință care au studiat derivata unei funcții. Forța este derivata muncii în deplasare.

Ministerul Educației Regiunea Saratov

Profesionist autonom de stat instituție educațională Regiunea Saratov „Politehnica Engels”

APLICAREA DERIVATULUI ÎN DIFERITE DOMENIILE ȘTIINȚEI

Efectuat: Sarkulova Nurgulya Sergheevna

elev al grupei KShI-216/15

(Design, modelare și

tehnologie de cusut)

consilier științific:

Verbitskaya Elena Vyacheslavovna

profesor de matematică GAPOU SO

„Politehnica engleză”

2016

Introducere

Rolul matematicii în diverse domenii ale științelor naturii este foarte mare. Nu e de mirare că spun ei„Matematica este regina științelor, fizica ei mana dreapta, a rămas chimia.

Subiectul cercetării este derivatul.

Scopul principal este de a arăta semnificația derivatului nu numai în matematică, ci și în alte științe, importanța sa în viața modernă.

Calculul diferențial este o descriere a lumii din jurul nostru, realizată în limbaj matematic. Derivatul ne ajută să rezolvăm cu succes nu numai probleme de matematică, dar și sarcini practice în diverse domenii ale științei și tehnologiei.

Derivata unei funcții este utilizată oriunde există un flux de proces neuniform: aceasta este o mișcare mecanică neuniformă și curent alternativ și reacții chimice și dezintegrare radioactivă substanțe etc.

Întrebări cheie și tematice ale acestui eseu:

1. Istoria originii derivatului.

2. De ce să studiem derivatele funcțiilor?

3. Unde se folosesc derivatele?

4. Aplicarea derivaților în fizică, chimie, biologie și alte științe.

5. Concluzii

Am decis să scriu o lucrare pe tema „Aplicarea derivatului în diverse domenii ale științei”, pentru că acest subiect mi se pare foarte interesant, util și relevant.

În lucrarea mea, voi vorbi despre aplicarea diferențierii în diverse domenii ale științei, cum ar fi chimia, fizica, biologia, geografia etc. La urma urmei, toate științele sunt indisolubil legate, ceea ce se vede foarte clar în exemplul subiectului. Iau în considerare.

Aplicarea derivatului în diverse domenii ale științei

De la cursul de algebră din liceu, știm deja asta derivat este limita raportului dintre incrementul funcției și incrementul argumentului său, deoarece incrementul argumentului tinde spre zero, dacă există o astfel de limită.

Acțiunea de a găsi o derivată se numește diferențiere, iar o funcție care are o derivată într-un punct x se numește diferențiabilă în acel punct. O funcție care este diferențiabilă în fiecare punct al unui interval se numește diferențiabilă în acel interval.

Onoarea de a descoperi legile de bază ale analizei matematice îi aparține fizician englezși matematicianul Isaac Newton și matematicianul, fizicianul, filozoful german Leibniz.

Newton a introdus conceptul de derivat, studiind legile mecanicii, dezvăluind astfel sensul său mecanic.

Semnificația fizică a derivatei: derivata unei funcțiiy= f(X) la punct X 0 este rata de schimbare a funcțieif(X) la punct X 0 .

Leibniz a ajuns la conceptul de derivată rezolvând problema trasării unei tangente la o dreaptă derivată, explicând-o astfel sens geometric.

Sensul geometric al derivatei este că derivata funcționează într-un punctX 0 egală cu panta tangentei la graficul funcției trasate în punctul cu abscisaX 0 .

Termenul derivat și notația modernăy" , f„Introdus de J. Lagrange în 1797.

matematician rusÎn secolul al XIX-lea, Panfuty Lvovich Chebyshev spunea că „de o importanță deosebită sunt acele metode ale științei care ne permit să rezolvăm o problemă comună tuturor activităților umane practice, de exemplu, cum să dispunem de mijloacele noastre pentru a obține cel mai mare beneficiu”.

Reprezentanții diferitelor specialități trebuie să se ocupe de astfel de sarcini în timpul nostru:

Inginerii de proces încearcă să organizeze producția în așa fel încât să fie produse cât mai multe produse;

Designerii încearcă să dezvolte un dispozitiv pentru nava spatiala astfel încât masa dispozitivului să fie cea mai mică;

Economiștii încearcă să planifice legăturile dintre fabrică și sursele de materii prime în așa fel încât costurile de transport să fie minime.

Când studiază orice subiect, elevii au o întrebare: „De ce avem nevoie de asta?” Dacă răspunsul satisface curiozitatea, atunci putem vorbi despre interesul elevilor. Răspunsul la subiectul „Derivată” poate fi obținut știind unde sunt folosite derivatele funcțiilor.

Pentru a răspunde la această întrebare, putem enumera câteva discipline și secțiunile lor în care sunt utilizate derivate.

Derivată în algebră:

1. Tangenta la graficul functiei

Graficul tangent la funcțief, diferentiabil la x despre , este o dreaptă care trece prin punctul (x despre ; f(x o )) și având o pantăf′(x o ).

y= f(x o ) + f′(x o ) (x - x o )

2. Căutați intervale de funcții crescătoare și descrescătoare

Funcţiey=f(x) crește pe intervalX , dacă pentru vreunul șiinegalitatea. Cu alte cuvinte, o valoare mai mare a argumentului corespunde unei valori mai mari a funcției.

Funcţiey=f(x) scade pe intervalX , dacă pentru vreunul șiinegalitatea. Cu alte cuvinte, o valoare mai mare a argumentului corespunde unei valori mai mici a funcției.

3. Găsirea punctelor extreme ale unei funcții

Punct numitpunct maxim funcțiiy=f(x) dacă pentru toţiX . Se numește valoarea funcției în punctul maximfunctia maxima si denota.

Punct numitpunct minim funcțiiy=f(x) dacă pentru toţiX din vecinătatea ei inegalitatea. Se numește valoarea funcției în punctul minimfuncția minimă si denota.

Sub vecinătatea unui punct înțelege intervalul, Unde este un număr pozitiv suficient de mic.

Se numesc punctele minime și maximepuncte extremum , iar valorile funcției corespunzătoare punctelor extreme sunt numitefuncția extremă .

4. Căutați intervale de convexitate și concavitate ale unei funcții

Graficul funcției, este în acest intervalconvex , nu se află mai sus decât oricare dintre tangentele sale (Fig. 1).

Graficul funcției, diferentiabil pe interval, este în acest intervalconcav , dacă graficul acestei funcţii se află în interval nu se află mai jos decât oricare dintre tangentele sale (Fig. 2).

Punctul de inflexiune al graficului funcției se numește punctul care separă intervalele de convexitate și concavitate.

5. Aflarea punctelor de inflexiune ale unei functii

Derivată în fizică:

1. Viteza ca derivat al traseului

2. Accelerația ca derivată a vitezeiA =

3. Rata de dezintegrare elemente radioactive 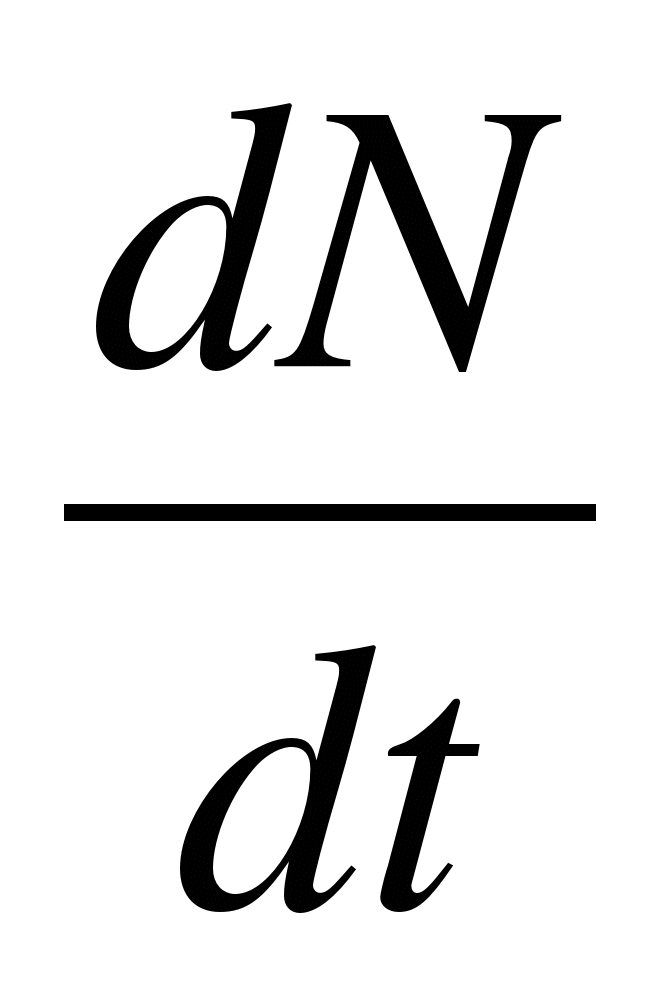= - λN

Și, de asemenea, în fizică, derivata este folosită pentru a calcula:

Viteze punct material

Viteza instantanee ca sens fizic al derivatului

Valoare instantanee alimentare de curent alternativ

Valoarea instantanee a EMF de inducție electromagnetică

Putere maxima

Derivat în chimie:

Și în chimie, calculul diferențial a găsit o largă aplicație pentru construcție modele matematice reacții chimice și descrierea ulterioară a proprietăților acestora.

Derivatul în chimie este folosit pentru a determina un lucru foarte important - viteza reactie chimica, unul dintre factorii determinanți care trebuie luați în considerare în multe domenii ale activității științifice și industriale. V(t) = p'(t)

Cantitate

in-va la un moment dat t 0

p = p(t 0 )

Funcţie

Interval de timp

∆t = t– t 0

Argument Increment

Modificarea cantității

∆p=p(t 0 + ∆t) – p(t 0 )

Creșterea funcției

Viteza medie a unei reacții chimice

∆p/∆t

Raportul dintre creșterea funcției și creșterea argumentului

Derivat în biologie:

O populație este un ansamblu de indivizi ai unei anumite specii care ocupă o anumită zonă a teritoriului din raza de acțiune a speciei, încrucișându-se liber între ei și izolați parțial sau complet de alte populații și este, de asemenea, o unitate elementară de evoluție.

P \u003d x‘ (t)

Derivată în geografie:

1. Câteva sensuri în seismografie

2. Caracteristici câmp electromagnetic teren

3. Radioactivitatea indicatorilor geofizici nucleari

4. Multe sensuri în geografia economică

5. Deduceți o formulă de calcul a populației din teritoriu la momentul t.

y'= la y

Ideea modelului sociologic al lui Thomas Malthus este că creșterea populației este proporțională cu populația la un moment dat t prin N(t). Modelul Malthus a funcționat bine pentru a descrie populația SUA din 1790 până în 1860. Acest model nu mai este valabil în majoritatea țărilor.

Derivat în inginerie electrică:

În casele noastre, în transport, în fabrici: curentul electric funcționează peste tot. Sub curent electric, înțelegeți mișcarea direcționată a particulelor libere încărcate electric.

Caracteristica cantitativă curent electric este puterea curentă.

Într-un circuit electric incarcare electrica se modifică în timp conform legii q=q (t). Curentul I este derivata sarcinii q în raport cu timpul.

În inginerie electrică, funcționarea AC este utilizată în principal.

Curentul electric care se modifică în timp se numește curent alternativ. Circuitul AC poate conține diverse elemente: dispozitive de încălzire, bobine, condensatoare.

Producerea curentului electric alternativ se bazează pe legea inducției electromagnetice, a cărei formulare conține derivata fluxului magnetic.

Derivat în economie:

Economia este baza vieții, iar calculul diferențial, un aparat de analiză economică, ocupă un loc important în ea. Sarcina de bază a analizei economice este de a studia relațiile cantităților economice sub formă de funcții.

Derivatul în economie rezolvă întrebări importante:

1. În ce direcție se vor schimba veniturile statului odată cu creșterea impozitelor sau odată cu introducerea taxelor vamale?

2. Veniturile companiei vor crește sau vor scădea odată cu creșterea prețului produselor sale?

Pentru a rezolva aceste întrebări, este necesar să se construiască funcțiile de conexiune ale variabilelor de intrare, care sunt apoi studiate prin metodele de calcul diferențial.

De asemenea, folosind extremul funcției (derivate) din economie, puteți găsi cea mai mare productivitate a muncii, profit maxim, producție maximă și costuri minime.

CONCLUZIE: derivatul este folosit cu succes în rezolvarea diverselor probleme aplicate în știință, tehnologie și viață

După cum se poate observa din cele de mai sus, utilizarea derivatei unei funcții este foarte diversă și nu numai în studiul matematicii, ci și în alte discipline. Prin urmare, putem concluziona că studiul temei: „Derivata unei funcții” își va avea aplicarea și în alte subiecte și materii.

Am fost convinși de importanța studierii temei „Derivată”, rolul acesteia în studiul proceselor științei și tehnologiei, posibilitatea de a proiecta în funcție de evenimente reale modele matematice și rezolva probleme importante.

“Muzica poate ridica sau calma sufletul,
Pictura este plăcută ochiului,
Poezie - pentru a trezi sentimente,
Filosofie - pentru a satisface nevoile minții,
Ingineria este de a îmbunătăți partea materială a vieții oamenilor,
DARmatematica poate atinge toate aceste obiective.”

Așa a spus matematicianul americanMaurice Kline.

Bibliografie:

1. Bogomolov N.V., Samoylenko I.I. Matematica. - M.: Yurayt, 2015.

2. V. P. Grigoriev și Yu. A. Dubinsky, Elemente de matematică superioară. - M.: Academia, 2014.

3. Bavrin I.I. Fundamentele matematicii superioare. - M.: facultate, 2013.

4. Bogomolov N.V. Lecții practice de matematică. - M.: Liceu, 2013.

5. Bogomolov N.V. Culegere de probleme de matematică. - M.: Dropia, 2013.

6. Rybnikov K.A. Istoria matematicii, Moscow University Press, M, 1960.

7. Vinogradov Yu.N., Gomola A.I., Potapov V.I., Sokolova E.V. – M.:Centrul editorial „Academia”, 2010

8 . Bashmakov M.I. Matematică: algebră și începuturile analizei matematice, geometrie. - M.: Centrul editorial „Academia”, 2016

Surse periodice:

Ziare și reviste: „Matematică”, „ Lecție publică»

Utilizarea resurselor de internet, biblioteci digitale:

www:egetutor.ru

matematica-na5.norod.ru

FGOU SPO

Novosibirsk facultate de agricultură

abstract

la disciplina „matematică”

„Aplicarea derivatului în știință și tehnologie”

S. Razdolnoe 2008

Introducere

1. Partea teoretică

1.1 Probleme care duc la conceptul de derivată

1.2 Definiție derivată

1.3 Regula generală pentru găsirea derivatei

1.4 Sensul geometric al derivatei

1.5 Sensul mecanic al derivatului

1.6 Derivată de ordinul doi și semnificația sa mecanică

1.7 Definiția și semnificația geometrică a diferenţialului

2. Investigarea funcţiilor cu ajutorul derivatei

Concluzie

Literatură

Introducere

În primul capitol al eseului meu, vom vorbi despre conceptul de derivată, regulile de aplicare a acestuia, despre geometric și simțul fizic derivat. În al doilea capitol al eseului meu, vom vorbi despre utilizarea derivatului în știință și tehnologie și despre rezolvarea problemelor din acest domeniu.

1. Partea teoretică

1.1 Probleme care duc la conceptul de derivată

La studierea anumitor procese și fenomene, apare adesea problema determinării vitezei acestor procese. Soluția sa conduce la conceptul de derivată, care este conceptul de bază al calculului diferențial.

Metoda calculului diferențial a fost creată în secolele al XVII-lea și al XVIII-lea. Numele a doi mari matematicieni, I. Newton și G.V. Leibniz.

Newton a ajuns la descoperirea calculului diferențial atunci când rezolva probleme despre viteza unui punct material la un moment dat de timp (viteza instantanee).

După cum se știe, mișcare uniformă este o mișcare în care un corp parcurge lungimi egale ale traseului în intervale egale de timp. Se numește distanța parcursă de un corp într-o unitate de timp viteză mișcare uniformă.

Cu toate acestea, cel mai adesea în practică avem de-a face cu mișcări inegale. O mașină care circulă pe șosea încetinește la treceri și o accelerează în acele tronsoane în care poteca este liberă; aeronava încetinește la aterizare etc. Prin urmare, cel mai adesea trebuie să ne confruntăm cu faptul că în intervale de timp egale corpul trece pe segmente de cale de lungimi diferite. O astfel de mișcare se numește neuniformă. Viteza sa nu poate fi caracterizată de un singur număr.

Adesea, pentru a caracteriza mișcarea neuniformă, se folosește conceptul viteza medie mișcarea în timpul ∆t٫ care este determinată de relația în care ∆s este calea parcursă de corp în timpul ∆t.

Deci, cu un corp în cădere liberă, viteza medie a mișcării sale în primele două secunde este

În practică, o astfel de caracteristică a mișcării precum viteza medie spune foarte puțin despre mișcare. Într-adevăr, la 4,9 m/s, iar pentru al doilea - 14,7 m/s, în timp ce viteza medie pentru primele două secunde este de 9,8 m/s. Viteza medie în primele două secunde nu oferă nicio idee despre cum a avut loc mișcarea: când corpul s-a mișcat mai repede și când mai lent. Dacă setăm separat vitezele medii de mișcare pentru fiecare secundă, atunci vom ști, de exemplu, că în a 2-a secundă corpul s-a mișcat mult mai repede decât în a 1-a. Cu toate acestea, în majoritatea cazurilor, mult mai rapid decât nu suntem mulțumiți. La urma urmei, este ușor de înțeles că în această a 2-a secundă și corpul se mișcă în moduri diferite: la început este mai lent, la sfârșit este mai rapid. Și cum se mișcă undeva la mijlocul acestei a doua secunde? Cu alte cuvinte, cum se determină viteza instantanee?

Fie ca mișcarea corpului să fie descrisă de lege pentru un timp egal cu ∆t. În momentul t0 corpul a trecut de cale, în momentul de față - calea. Prin urmare, în timpul ∆t, corpul a parcurs o distanță și viteza medie a corpului în această perioadă de timp va fi.

Cu cât intervalul de timp ∆t este mai scurt, cu atât mai precis se poate stabili cu ce viteză se mișcă corpul în momentul t0, deoarece un corp în mișcare nu își poate schimba semnificativ viteza într-o perioadă scurtă de timp. Prin urmare, viteza medie pe măsură ce ∆t tinde spre zero se apropie de viteza reală de mișcare și, în limită, dă viteza de deplasare la un moment dat t0 (viteza instantanee).

În acest fel ,

Definiția 1. Viteza instantanee a mișcării rectilinie a corpului la un moment dat t0 se numește limita vitezei medii în timpul de la t0 la t0+ ∆t, când intervalul de timp ∆t tinde spre zero.

Deci, pentru a găsi viteza mișcării rectilinie neuniforme la un moment dat, este necesar să se găsească limita raportului dintre incrementul de cale ∆ și incrementul de timp ∆t în condiția i.e. Leibniz a ajuns la descoperirea calculului diferențial în timp ce rezolva problema construirii unei tangente la orice curbă dată de ecuația sa.

Soluția la această problemă are mare importanță. La urma urmei, viteza unui punct în mișcare este direcționată de-a lungul unei tangente la traiectoria sa, prin urmare, determinarea vitezei unui proiectil pe traiectoria sa, viteza oricărei planete pe orbita sa, se reduce la determinarea direcției tangentei la curba.

Definiția unei tangente ca drepte care are un singur punct comun cu o curbă, care este valabilă pentru un cerc, este nepotrivită pentru multe alte curbe.

Următoarea definiție a unei tangente la o curbă nu corespunde numai ideii intuitive despre ea, dar vă permite și să găsiți direcția acesteia, de exemplu. calculați panta tangentei.

Definiția 2. Tangentă la curba în punctul M se numește linie dreaptă MT, care este poziția limită a secantei MM1, când punctul M1, deplasându-se de-a lungul curbei, se apropie de punctul M la nesfârșit.

1.2 Definiție derivată

Rețineți că la determinarea tangentei la curbă și a vitezei instantanee a mișcării neuniforme, în esență se efectuează aceleași operații matematice:

1. Valoarea dată a argumentului este incrementată și se calculează o nouă valoare a funcției corespunzătoare noii valori a argumentului.

2. Determinați incrementul funcției corespunzător incrementului argumentului selectat.

3. Incrementul funcției este împărțit la incrementul argumentului.

4. Calculați limita acestui raport, cu condiția ca incrementul argumentului să tinde spre zero.

Rezolvarea multor probleme duc la limitarea tranzițiilor de acest tip. Devine necesar să facem o generalizare și să dăm un nume acestui pasaj până la limită.

Rata de modificare a funcției în funcție de schimbarea argumentului poate fi, evident, caracterizată printr-un raport. Această relație se numește viteza medie funcția se modifică pe intervalul de la până la. Acum trebuie să luăm în considerare limita unei fracții.Limita acestui raport, deoarece incrementul argumentului tinde spre zero (dacă această limită există) este o nouă funcție a. Această funcție este notă prin simbolurile y', numite derivat această funcție, deoarece se obține (produce) din funcție Funcția însăși este numită primitiv funcţie în raport cu derivata sa

Definiția 3. derivat funcțiile la un punct dat numesc limita raportului dintre incrementul funcției ∆y și incrementul corespunzător al argumentului ∆x, cu condiția ca ∆x→0, i.e.

1.3 Regula generală pentru găsirea derivatei

Operația de găsire a derivatei unei funcții se numește diferenţiere funcţii, iar ramura matematicii care studiază proprietăţile acestei operaţii este calcul diferenţial.

Dacă o funcție are o derivată la x=a, atunci se spune că este diferentiabilîn acest moment. Dacă o funcție are o derivată în fiecare punct dintr-un interval dat, atunci se spune că este diferentiabil Pe aceasta interval .

Definiția derivatei nu numai că caracterizează pe deplin conceptul de rata de modificare a unei funcții atunci când argumentul se schimbă, dar oferă și o modalitate de a calcula efectiv derivata unei anumite funcții. Pentru a face acest lucru, trebuie să efectuați următoarele patru acțiuni (patru pași) indicate în definiția derivatului în sine:

1. Găsiți o nouă valoare a funcției prezentând în această funcțieîn loc de x, noua valoare a argumentului: .

2. Creșterea funcției se determină scăzând valoarea dată a funcției din noua ei valoare: .

3. Compuneți raportul dintre incrementul funcției și incrementul argumentului: .

4. Mergeți la limita la și găsiți derivata: .

În general, o derivată este o funcție „nouă” derivată dintr-o funcție dată conform unei reguli specificate.

1.4 Sensul geometric al derivatei

Interpretarea geometrică a derivatei, dată mai întâi în sfârşitul XVII-leaîn. Leibniz este după cum urmează: valoarea derivatei functiei în punctul x este egal cu panta tangentei trasate la graficul funcției în același punct x, acestea.

Ecuația unei tangente, ca orice dreaptă care trece prin punct datîn această direcție, are forma – coordonatele curente. Dar ecuația tangentei se va scrie și astfel: . Ecuația normală va fi scrisă sub formă

1.5 Sensul mecanic al derivatului

Interpretarea mecanică a derivatei a fost dată mai întâi de I. Newton. Constă în următoarele: viteza de deplasare a unui punct material la un moment dat de timp este egală cu derivata traseului în raport cu timpul, adică. Astfel, dacă legea mișcării unui punct material este dată de o ecuație, atunci pentru a găsi viteza instantanee a unui punct la un anumit moment de timp, trebuie să găsiți derivata și să înlocuiți valoarea corespunzătoare a lui t în ea.

1.6 Derivată de ordinul doi și semnificația sa mecanică

Obținem (o ecuație din ceea ce s-a făcut în manualul Lisichkin V.T. Soloveychik I.L. „Matematică” p. 240):

În acest fel, accelerația mișcării rectilinie a corpului la un moment dat este egală cu derivata a doua a drumului în raport cu timpul, calculată pentru un moment dat. Acesta este sensul mecanic al derivatei a doua.

1.7 Definiția și semnificația geometrică a diferenţialului

Definiția 4. Partea principală a incrementului unei funcții, liniară în raport cu incrementul funcției, liniară în raport cu incrementul variabilei independente, se numește diferenţial funcții și se notează cu d, adică. .

Diferenţial de funcţie reprezentat geometric prin incrementul ordonatei tangentei trasate în punct M ( X ; y ) pentru valorile date ale lui x și ∆x.

calcul diferenţial – .

Aplicarea diferenţialului în calcule aproximative – , valoarea aproximativă a incrementului funcției coincide cu diferența acesteia.

Teorema 1. Dacă funcţia diferenţiabilă crește (descrește) într-un interval dat, atunci derivata acestei funcții nu este negativă (nu pozitivă) în acest interval.

Teorema 2. Dacă funcţia derivată este pozitiv (negativ) într-un anumit interval, atunci funcția din acest interval este monoton crescător (monoton descrescător).

Să formulăm acum regula pentru găsirea intervalelor de monotonitate ale funcției

1. Calculați derivata acestei funcții.

2. Găsiți punctele în care este zero sau nu există. Aceste puncte sunt numite critic pentru functie

3. Cu punctele găsite, domeniul funcției este împărțit în intervale, pe fiecare dintre care derivata își păstrează semnul. Aceste intervale sunt intervale de monotonitate.

4. Examinați semnul de pe fiecare dintre intervalele găsite. Dacă pe intervalul considerat, atunci pe acest interval crește; daca, atunci scade pe un astfel de interval.

În funcție de condițiile problemei, regula de găsire a intervalelor de monotonitate poate fi simplificată.

Definiția 5. Un punct se numește punct maxim (minim) al unei funcții dacă inegalitatea este valabilă, respectiv, pentru orice x dintr-o vecinătate a punctului.

Dacă este punctul maxim (minim) al funcției, atunci spunem că (minim) la punct. Funcțiile maxime și minime unesc numele extremum funcții și sunt numite punctele maxime și minime puncte extreme (puncte extreme).

Teorema 3.(semnul necesar al unui extremum). În cazul în care un și derivata există în acest punct, atunci este egală cu zero: .

Teorema 4.(semn suficient de extremum). Dacă derivatul când trece x A schimba semnul, atunci A este punctul extremum al funcției .

Principalele puncte ale studiului derivatului:

1. Găsiți derivata.

2. Găsiți toate punctele critice din domeniul funcției.

3. Stabiliți semnele derivatei funcției la trecerea prin punctele critice și scrieți punctele extreme.

4. Calculați valorile funcției la fiecare punct extrem.

2. Investigarea funcțiilor cu derivata

Sarcina 1 . Volumul jurnalului. Buștenii de formă corectă fără defecte ale lemnului cu o diferență relativ mică în diametrele capetelor groase și subțiri se numesc lemn rotund industrial. La determinarea volumului de lemn industrial rotund, se utilizează de obicei o formulă simplificată, unde este lungimea buștenului, este aria secțiunii sale medii. Aflați dacă volumul real se termină sau subestimează; estimați eroarea relativă.

Soluţie. Forma unei cherestea rotundă de afaceri este aproape de un trunchi de con. Fie raza capătului mai mare și mai mic al bușteanului. Apoi, volumul său aproape exact (volumul unui trunchi de con) poate fi găsit, după cum se știe, prin formula. Fie valoarea volumului calculată prin formula simplificată. Apoi;

Acestea. . Aceasta înseamnă că formula simplificată oferă o subestimare a volumului. Să o punem acum. Apoi. Aceasta arată că eroarea relativă nu depinde de lungimea jurnalului, ci este determinată de raport. De când crește pe interval . Prin urmare, ceea ce înseamnă că eroarea relativă nu depășește 3,7%. În practica științei forestiere, o astfel de eroare este considerată destul de acceptabilă. Cu o precizie mai mare, este practic imposibil să se măsoare fie diametrele capetelor (pentru că sunt oarecum diferite de cercurile), fie lungimea buștenului, deoarece măsoară nu înălțimea, ci generatria conului (lungimea de bușteanul este de zeci de ori mai mare decât diametrul, iar acest lucru nu duce la erori mari). Astfel, la prima vedere incorect, dar mai mult formulă simplă pentru că volumul unui trunchi de con într-o situație reală se dovedește a fi destul de legitim. Efectuate în mod repetat cu ajutorul unor metode speciale de verificare a arătat că, la contabilizarea în masă a pădurii industriale, eroarea relativă la utilizarea formulei luate în considerare nu depășește 4%.

Sarcina #2 . La determinarea volumelor de gropi, șanțuri de găleți și alte containere care au forma unui trunchi de con, uneori se folosește o formulă simplificată în practica agricolă, unde este înălțimea, sunt zonele bazelor conului. Aflați dacă volumul real este supraestimat sau subestimat, evaluați eroarea relativă în condițiile naturale pentru practică: (- razele de bază, .

Soluţie. Notând prin valoarea adevărată a volumului trunchiului de con, și prin valoarea calculată prin formula simplificată, obținem: , i.e. . Aceasta înseamnă că formula simplificată oferă o supraestimare a volumului. Repetând în continuare soluția problemei precedente, constatăm că eroarea relativă nu va fi mai mare de 6,7%. Probabil, o astfel de precizie este acceptabilă atunci când raționalizarea lucrărilor de excavare - la urma urmei, gropile nu vor fi conuri ideale, iar parametrii corespunzători în condiții reale sunt măsurați foarte aproximativ.

Sarcina #3 . În literatura specială, pentru a determina unghiul β de rotație al axului unei mașini de frezat la frezarea cuplajelor cu dinți, se derivă o formulă unde. Deoarece această formulă este complexă, se recomandă să renunți la numitorul și să folosești o formulă simplificată. La ce (- un număr întreg) poate fi utilizată această formulă dacă este permisă o eroare la determinarea unghiului?

Soluţie. Formula exactă după simplă transformări identice poate fi adus în minte. Prin urmare, atunci când se utilizează o formulă aproximativă, este permisă o eroare absolută, unde. Studiem funcția pe intervalul . În acest caz, 0,06, adică colțul aparține primului sfert. Avem: . Rețineți că pe intervalul luat în considerare și, prin urmare, funcția este în scădere pe acest interval. De mai departe, pentru toți considerați. Mijloace, . Deoarece este un radian, este suficient să rezolvi inegalitatea. Rezolvând această inegalitate prin selecție, constatăm că, . Deoarece funcția este în scădere, rezultă că

Concluzie

Utilizarea derivatului este destul de largă și poate fi acoperită pe deplin în acest tip de lucrări, dar am încercat să acoper principalele puncte. În zilele noastre, în legătură cu progresul științific și tehnologic, în special odată cu evoluția rapidă a sistemelor de calcul, calculul diferențial devine din ce în ce mai relevant în rezolvarea problemelor atât simple, cât și supercomplexe.

Literatură

1. V.A. Petrov „Analiza matematică în sarcinile de producție”

2. Soloveichik I.L., Lisichkin V.T. "Matematica"

Chaikin Semyon, Maysak Kirill, Zalogina Anastasia, Shakhzadova Anna

Această dezvoltare conține o prezentare pe tema „Aplicarea derivatului în chimie și biologie”. Pe parcursul activitati ale proiectului a fost înaintată o ipoteză că derivatul își găsește aplicarea în aceste domenii ale științei. Pe parcursul muncă de cercetare s-a aflat care este rolul derivatului în științe precum chimia și biologia, unde și în rezolvarea problemelor își găsește aplicarea. În urma muncii depuse, s-a ajuns la concluzia că ipoteza a fost într-adevăr confirmată.

Descarca:

Previzualizare:

https://accounts.google.com

Subtitrările slide-urilor:

Ipoteză:

Previzualizare:

Pentru a utiliza previzualizarea prezentărilor, creați un cont Google (cont) și conectați-vă: https://accounts.google.com

Subtitrările slide-urilor:

Utilizarea derivatului în chimie și biologie Lucrarea a fost efectuată de elevii clasei 11B ai școlii secundare MBOU Nr. 6: Chaikin Semyon, Maysak Kirill, Zalogina Anastasia, Shakhzadova Anna Stavropol, 2014

Ipoteză:

Și în chimie, calculul diferențial a găsit o largă aplicație pentru construirea de modele matematice ale reacțiilor chimice și descrierea ulterioară a proprietăților acestora. Chimia este știința substanțelor, a transformărilor chimice ale substanțelor. Chimia studiază modelele diferitelor reacții.Viteza unei reacții chimice este modificarea concentrației de reactanți pe unitatea de timp. Aplicarea derivatului în chimie și biologie Determinarea vitezei unei reacții chimice

De ce avem nevoie de un derivat în reacții? Deoarece viteza de reacție v se modifică continuu în timpul procesului, este de obicei exprimată ca derivată a concentrației reactanților în funcție de timp.

Formula derivată în chimie Dacă C (t) este legea modificării cantității de substanță care a intrat într-o reacție chimică, atunci viteza v (t) a reacției chimice la momentul t este egală cu derivata:

Determinarea vitezei de reacție Limita raportului dintre funcția incrementală și argumentul incremental deoarece Δt tinde spre zero este viteza unei reacții chimice la un moment dat

Sarcină de chimie: Fie cantitatea de substanță care a intrat într-o reacție chimică să fie dată de dependența: C (t) \u003d t 2 / 2 + 3 t -3 (mol) Aflați viteza reacției chimice după 3 secunde . Rezolvare: v (t) = C ‘(t) ; v (t) = t + 3; v (3) = 3+3 = 6. Răspuns: 6 mol/s.

Semnificaţia biologică a derivatei Fie relaţia dintre numărul de indivizi ai unei populaţii de microorganisme y şi timpul t de reproducere a acesteia să fie dată de ecuaţia: y = x (t). Fie ∆ t intervalul de timp de la o valoare inițială t la t + ∆ t . Atunci y + ∆y \u003d x (t + ∆ t) este noua valoare a mărimii populației corespunzătoare momentului t + ∆ t, iar ∆ y + x (t + ∆ t) - x (t) este modificarea în numărul de indivizi ai organismelor. Raportul este rata medie de reproducere sau, după cum se spune, productivitatea medie a populației. Calculând, obținem y ' = P (t) = x ' (t) , sau productivitatea populației la momentul t .

Exemplu Fie populația bacteriană la momentul t (c) să aibă x(t) indivizi. . Aflați rata de creștere a populației: a) la un moment arbitrar t , b) la momentul t = 1 c . Rezolvare: P = x'(t) = 200t; P(1) = 200 (r/s). Răspuns: 200 o/s.

Concluzie Conceptul de derivat este foarte important în chimie și biologie, în special în determinarea vitezei unei reacții.

Concluzie: Calculul diferențial este o descriere a lumii din jurul nostru, realizată în limbaj matematic. Derivata este unul dintre cele mai importante concepte în calcul. Cunoașterea derivatei ne ajută să rezolvăm cu succes nu numai probleme matematice, ci și probleme practice din diverse domenii ale științei, tehnologiei și vieții.

Universitatea de Stat din Sakhalin de Sud

Departamentul de Matematică

Lucrări de curs

Tema: Aplicarea practică a derivatului

Lector: Lihacheva O.N.

Iuzhno-Sahalinsk

2002
Introducere

În această lucrare, voi lua în considerare aplicațiile derivatului în diverse științe și industrii. Lucrarea este împărțită în capitole, fiecare dintre ele tratând unul dintre aspectele calculului diferențial (geometrie, semnificație fizică etc.)

1. Conceptul de derivat

1-1. Informații istorice

Calculul diferențial a fost creat de Newton și Leibniz la sfârșitul secolului al XVII-lea pe baza a două probleme:

1) despre găsirea unei tangente la o dreaptă arbitrară

2) pe căutarea vitezei cu o lege arbitrară a mișcării

Chiar și mai devreme, conceptul de derivat a fost întâlnit în lucrările matematicianului italian Tartaglia (circa 1500 - 1557) - aici a apărut o tangentă în cursul studierii problemei unghiului de înclinare al pistolului, care asigură cea mai mare rază de acțiune. a proiectilului.

În secolul al XVII-lea, pe baza teoriei mișcării lui G. Galileo, a fost dezvoltat activ conceptul cinematic al derivatului. În lucrările lui Descartes, matematicianul francez Roberval și savantul englez L. Gregory au început să apară diverse prezentări. Lopital, Bernoulli, Lagrange, Euler, Gauss au adus o mare contribuție la studiul calculului diferențial.

1-2. Conceptul de derivat

Fie y \u003d f (x) o funcție continuă a argumentului x, definită în intervalul (a; b), și fie x 0 un punct arbitrar al acestui interval

Dăm argumentului x un increment ∆x, apoi funcția y = f(x) va primi un increment ∆y = f(x + ∆x) - f(x). Limita către care tinde raportul ∆y / ∆x ca ∆x → 0 se numește derivată a funcției f(x).

1-3. Reguli de diferențiere și tabelul derivatelor

		(sin x)" = cos x
	(1 / x)" = -1 / x2	(cos x)" = -sin x
	(√x)" = 1 / 2√x	(tg x)" = 1 / cos 2 x
(uv)" = u"v + uv"	(a x)" = a x log x	(ctg x)" = 1 / sin 2 x
(u / v)"=(u"v - uv") / v 2		(arcsin x)" = 1 / √ (1- x 2)
	(log a x)" = (log a e) / x	(arccos x)" = -1 / √ (1- x 2)
	(ln x)" = 1 / x	(arctg x)" = 1 / √ (1+ x 2)
		(arcctg x)" = -1 / √ (1+ x 2)

2. Sensul geometric al derivatului

2-1. Tangenta la curba

Să avem pe ea o curbă și un punct fix M și un punct N. O tangentă la punctul M este o dreaptă, a cărei poziție tinde să fie ocupată de coarda MN, dacă punctul N este abordat nelimitat de-a lungul curba spre M.

Se consideră funcția f(x) și curba y = f(x) corespunzătoare acestei funcții. Pentru o anumită valoare x, funcția are valoarea y = f(x). Aceste valori de pe curbă corespund punctului M(x 0 , y 0). Să introducem un nou argument x 0 + ∆x, valoarea acestuia corespunde valorii funcției y 0 + ∆y = f(x 0 + ∆x). Punctul corespunzător este N(x 0 + ∆x, y 0 + ∆y). Se trasează secanta MN și se notează cu φ unghiul format de secanta cu direcția pozitivă a axei Ox. Figura arată că ∆y / ∆x = tg φ. Dacă acum ∆x se apropie de 0, atunci punctul N se va deplasa de-a lungul curbei, secanta MN se va roti în jurul punctului M, iar unghiul φ se va schimba. Dacă, ca ∆x → 0, unghiul φ tinde spre ceva α, atunci linia dreaptă care trece prin M și care face unghiul α cu direcția pozitivă a axei absciselor va fi tangenta necesară. În același timp, coeficientul său de pantă:

Adică, valoarea derivatei f "(x) pentru o valoare dată a argumentului x este egală cu tangentei unghiului format cu direcția pozitivă a axei Ox de tangenta la graficul funcției f (x). ) în punctul M (x, f (x)).

O tangentă la o linie spațială are o definiție similară cu cea a unei tangente la o curbă plană. În acest caz, dacă funcția este dată de ecuația z = f(x, y), pantele la axele OX și OY vor fi egale cu derivatele parțiale ale lui f față de x și y.

2-2. Plan tangent la suprafață

Planul tangent la suprafața în punctul M este planul care conține tangentele la toate curbele spațiale ale suprafeței care trec prin M - punctul de contact.

Luați suprafața dată de ecuația F(x, y, z) = 0 și un punct obișnuit M(x 0 , y 0 , z 0) pe ea. Se consideră la suprafață o curbă L care trece prin M. Fie curba dată de ecuații

x = φ(t); y = ψ(t); z = χ(t).

Să substituim aceste expresii în ecuația suprafeței. Ecuația se va transforma într-o identitate, deoarece curba se află în întregime pe suprafață. Folosind proprietatea de invarianță a formei diferențialei, diferențiem ecuația rezultată în raport cu t:

Ecuațiile tangentei la curba L în punctul M au forma:

Deoarece diferențele x - x 0, y - y 0, z - z 0 sunt proporționale cu diferențele corespunzătoare, ecuația finală a planului arată astfel:

F" x (x - x 0) + F" y (y - y 0) + F" z (z - z 0)=0

iar pentru cazul particular z = f(x, y):

Z - z 0 \u003d F "x (x - x 0) + F" y (y - y 0)

Exemplu: Aflați ecuația planului tangent în punctul (2a; a; 1,5a) al paraboloidului hiperbolic

Soluţie:

Z" x \u003d x / a \u003d 2; Z" y \u003d -y / a \u003d -1

Ecuația planului dorit:

Z - 1,5a = 2(x - 2a) - (Y - a) sau Z = 2x - y - 1,5a

3-1. Viteza punctului material

Fie dependența căii s de timpul t într-un dat mișcare rectilinie punctul material este exprimat prin ecuația s = f(t) și t 0 este un anumit moment în timp. Luați în considerare un alt timp t, notați ∆t = t - t 0 și calculați incrementul de cale: ∆s = f(t 0 + ∆t) - f(t 0). Raportul ∆s / ∆t se numește viteza medie de mișcare în timpul ∆t scurs din momentul inițial t 0 . Viteza este limita acestui raport ca ∆t → 0.

Accelerația medie a mișcării neuniforme în intervalul (t; t + ∆t) este valoarea =∆v / ∆t. Accelerația instantanee a unui punct material la momentul t va fi limita accelerației medii:

Adică prima derivată de timp (v "(t)).

Exemplu: Dependența traseului parcurs de corp în timp este dată de ecuația s \u003d A + Bt + Ct 2 + Dt 3 (C \u003d 0,1 m / s, D \u003d 0,03 m / s 2). Determinați timpul după începerea mișcării, după care accelerația corpului va fi egală cu 2 m / s 2.

Soluţie:

v(t) = s "(t) = B + 2Ct + 3Dt 2 ; a(t) = v"(t) = 2C + 6Dt = 0,2 + 0,18t = 2;

1,8 = 0,18t; t = 10 s

3-2. Capacitatea termică a unei substanțe la o anumită temperatură

Pentru a crește diferite temperaturi T cu aceeași valoare, egală cu T 1 - T, la 1 kg. o anumită substanță are nevoie de o cantitate diferită de căldură Q 1 - Q și raportul

căci această substanţă nu este constantă. Astfel, pentru o substanță dată, cantitatea de căldură Q este o funcție neliniară a temperaturii T: Q = f(T). Atunci ΔQ = f(t + ΔT) - f(T). Atitudine

se numește capacitatea termică medie pe intervalul , iar limita acestei expresii la ∆T → 0 se numește capacitatea termică a substanței date la temperatura T.

3-3. Putere

Schimbare mișcare mecanică corpul este cauzat de forțele care acționează asupra lui de la alte corpuri. Pentru a caracteriza cantitativ procesul de schimb de energie între corpurile care interacționează, în mecanică este introdus conceptul de lucru al unei forțe. Pentru a caracteriza rata de lucru, se introduce conceptul de putere:

4. Calcul diferențial în economie

4-1. Cercetarea funcției

Calculul diferențial este un aparat matematic utilizat pe scară largă pentru analiza economică. Sarcina de bază a analizei economice este de a studia relațiile cantităților economice scrise ca funcții. În ce direcție se vor schimba veniturile guvernamentale dacă vor crește taxele sau dacă sunt introduse taxe de import? Venitul firmei va crește sau va scădea atunci când prețul produselor sale crește? În ce proporție echipamentele suplimentare pot înlocui lucrătorii pensionari? Pentru rezolvarea unor astfel de probleme trebuie construite funcțiile de conexiune ale variabilelor incluse în ele, care apoi sunt studiate folosind metodele calculului diferențial. În economie, este adesea necesar să se găsească cea mai bună sau optimă valoare a unui indicator: cea mai mare productivitate a muncii, profit maxim, producție maximă, costuri minime etc. Fiecare indicator este o funcție a unuia sau mai multor argumente. Astfel, găsirea valorii optime a indicatorului se reduce la găsirea extremului funcției.

Conform teoremei lui Fermat, dacă un punct este un extremum al unei funcții, atunci derivata fie nu există în el, fie este egală cu 0. Tipul unui extremum poate fi determinat de una dintre condițiile suficiente pentru un extremum:

1) Fie funcția f(x) diferențiabilă într-o vecinătate a punctului x 0 . Dacă derivata f "(x) la trecerea prin punctul x 0 își schimbă semnul de la + la -, atunci x 0 este punctul maxim, dacă de la - la +, atunci x 0 este punctul minim, dacă nu își schimbă semnul , atunci nu există extremum.

2) Fie funcția f (x) să fie de două ori diferențiabilă într-o vecinătate a punctului x 0 și f "(x 0) \u003d 0, f "" (x 0) ≠ 0, apoi în punctul x 0 funcția f (x 0) are un maxim, dacă f ""(x 0)< 0 и минимум, если f ""(x 0) > 0.

În plus, derivata a doua caracterizează convexitatea funcției (graficul funcției se numește convex în sus [în jos] pe intervalul (a, b) dacă este situat pe acest interval nu deasupra [nu sub] oricare dintre tangentele sale ).

Exemplu: alegeți volumul optim de producție de către firmă, a cărui funcție de profit poate fi modelată prin dependență:

π(q) = R(q) - C(q) = q 2 - 8q + 10

Soluţie:

π"(q) = R"(q) - C"(q) = 2q - 8 = 0 → q extr = 4

Pentru q< q extr = 4 → π"(q) < 0 и прибыль убывает

Pentru q > q extr = 4 → π"(q) > 0 și profitul crește

Când q = 4, profitul ia valoarea minimă.

Care este rezultatul optim pentru firmă? Dacă firma nu poate produce mai mult de 8 unități de producție în perioada analizată (p(q = 8) = p(q = 0) = 10), atunci soluția optimă ar fi să nu producă nimic, decât să primești venit din inchiriere spatii si/sau echipamente. Dacă firma este capabilă să producă mai mult de 8 unități, atunci optimul pentru firmă va fi să producă la limita capacității sale de producție.

4-2. Elasticitatea cererii

Elasticitatea funcției f (x) în punctul x 0 se numește limită

Cererea este cantitatea de bun cerută de cumpărător. Elasticitatea prețului a cererii E D este o măsură a modului în care cererea răspunde la schimbările de preț. Dacă │E D │>1, atunci cererea se numește elastică, dacă │E D │<1, то неэластичным. В случае E D =0 спрос называется совершенно неэластичным, т. е. изменение цены не приводит ни к какому изменению спроса. Напротив, если самое малое снижение цены побуждает покупателя увеличить покупки от 0 до предела своих возможностей, говорят, что спрос является совершенно эластичным. В зависимости от текущей эластичности спроса, предприниматель принимает решения о снижении или повышении цен на продукцию.

4-3. Analiza limitelor

O secțiune importantă a metodelor de calcul diferențial utilizate în economie o reprezintă metodele de analiză limitativă, adică un set de metode pentru studierea valorilor variabile ale costurilor sau rezultatelor cu modificări ale producției, consumului etc., pe baza unei analize a acestora. valori limitative. Indicatorul limitator (indicatorii) unei funcții este derivata acesteia (în cazul unei funcții a unei variabile) sau derivatele parțiale (în cazul unei funcții a mai multor variabile)

În economie, se folosesc adesea medii: productivitatea medie a muncii, costurile medii, venitul mediu, profitul mediu etc. Dar adesea se cere să se afle cu ce sumă va crește rezultatul dacă costurile sunt crescute sau invers, cât de mult va fi rezultatul. va scădea dacă costurile sunt reduse. Este imposibil să răspunzi la această întrebare cu ajutorul valorilor medii. În astfel de probleme, este necesar să se determine limita raportului dintre creșterea rezultatului și costurilor, adică să se găsească efectul marginal. Prin urmare, pentru a le rezolva, este necesar să folosiți metodele de calcul diferențial.

5. Derivată în calcule aproximative

5-1. Interpolare

Interpolarea este calculul aproximativ al valorilor unei funcții din mai multe valori date. Interpolarea este utilizată pe scară largă în cartografie, geologie, economie și alte științe. Cea mai simplă opțiune de interpolare este forma Lagrange, dar când există multe puncte nodale și intervalele dintre ele sunt mari, sau doriți să obțineți o funcție a cărei curbură este minimă, atunci recurgeți la interpolarea spline, care oferă o precizie mai mare.

Fie K n un sistem de puncte nodale a = x 0< x 1 <…< x n = b. Функция S k (x) называется сплайн-функцией S k (x) степени k≥0 на K n , если

a) S k (x) є C k -1 ()

b) S k (x) este un polinom de grad cel mult k

O funcție spline Ŝ k (x) є S k (K n) se numește funcție spline de interpolare dacă Ŝ k (x j) = f(x j) pentru j = 0,1,…,n

În aplicații, este adesea suficient să alegeți k=3 și să aplicați așa-numitul interpolare cubică.

Deoarece s(x) este un polinom de gradul trei pe fiecare interval parțial, atunci pentru x є

Aici s 2 j , c j 1 , c j 0 sunt necunoscute pentru j = 1, 2, …, n

Acestea din urmă sunt excluse din cauza cerinței s(x j) = y j:

Diferențiând această funcție și ținând cont de faptul că s "(x) trebuie să fie continuu pe tot intervalul și, prin urmare, în special, la noduri, obținem în final sistemul de ecuații:

în raport cu n+1 necunoscute s 2 0 , s 2 1 ,…, s 2 n. Pentru determinarea lor fără ambiguitate, în funcție de sarcină, se mai adaugă două ecuații:

caz normal(N):

Caz periodic (P) (adicăf(x+(x n -x 0))=f(X)):

Netezire specificată pe margini:

Exemplu: interpolarea spline a funcției f(x)=sin x, n=4.

Funcția este periodică, deci folosim cazul P.

Funcția spline arată astfel:

5-2. formula Taylor

Extinderea funcțiilor în serii infinite vă permite să obțineți valoarea funcției la un punct dat cu orice precizie. Această tehnică este utilizată pe scară largă în programare și alte discipline.

Se spune că o funcție se extinde pe un interval dat într-o serie de puteri dacă există o astfel de serie de puteri a 0 + a 1 (x - a) + a 2 (x - a) 2 + ... + a n (x - a) ) n + ..., care converge către această funcție pe acest interval. Se poate dovedi că această descompunere este unică:

Fie funcția f(x) diferențiabilă la infinit în punctul a. Seria de putere a formei

se numește seria Taylor pentru funcția f(x), scrisă în puteri ale diferenței (x - a). În general, pentru ca seria Taylor să convergă către f(x), este necesar și suficient ca restul seriei să tinde spre 0. Pentru a = 0, seria Taylor este de obicei numită seria Maclaurin.

I. M. Uvarenkov,

M. Z. Maller

Curs de analiză matematică, v.1

V. A. Dudarenko,

A.A. Dadayan

Analiza matematică

Calcul diferențial și integral

T. I. Trofimova

curs de fizica

O. O. Zamkov

A. V. Tolstopiatenko

Yu. N. Cheremnykh

Metode matematice în economie

A. S. Solodovnikov

V. A. Babaitsev

A. V. Brailov

IG. Shandra

Matematică în economie

Introducere

1. Conceptul de derivat

1-1. Informații istorice

1-2. Conceptul de derivat

1-3. Reguli de diferențiere și tabelul derivatelor

2. Sensul geometric al derivatului

2-1. Tangenta la curba

2-2. Plan tangent la suprafață

3. Utilizarea derivatei în fizică

3-1. Viteza punctului material

3-2. Capacitatea termică la o temperatură dată

3-3. Putere

4. Calcul diferenţial în economie

4-1. Cercetarea funcției

4-2. Elasticitatea cererii

4-3. Analiza limitelor

5. Derivată în calcule aproximative

5-1. Interpolare

5-2. formula Taylor

5-3. Calcule aproximative

Concluzie

Lista literaturii folosite

Universitatea de Stat din Sakhalin de Sud

Departamentul de Matematică

Lucrări de curs

Tema: Aplicarea practică a derivatului

Lector: Lihacheva O.N.

Iuzhno-Sahalinsk

2002 Introducere

1. Conceptul de derivat

1-1. Informații istorice

Calculul diferențial a fost creat de Newton și Leibniz la sfârșitul secolului al XVII-lea pe baza a două probleme:

1) despre găsirea unei tangente la o dreaptă arbitrară

2) pe căutarea vitezei cu o lege arbitrară a mișcării

1-2. Conceptul de derivat

Fie y = f(x) o funcție continuă a argumentului x, definită în intervalul (a; b), și fie x0 un punct arbitrar al acestui interval

1-3. Reguli de diferențiere și tabelul derivatelor

C" = 0(xn) = nxn-1(sin x)" = cos xx" = 1(1 / x)" = -1 / x2(cos x)" = -sin x(Cu)"=Cu"( √x)" = 1 / 2√x(tg x)" = 1 / cos2 x(uv)" = u"v + uv"(ax)" = ax ln x(ctg x)" = 1 / sin2 x( u / v)"=(u"v - uv") / v2(ex)" = ex(arcsin x)" = 1 / √ (1- x2)(logax)" = (logae) / x(arccos x) " = -1 / √ (1- x2)(ln x)" = 1 / x(arctg x)" = 1 / √ (1+ x2)(arctg x)" = -1 / √ (1+ x2)

2. Sensul geometric al derivatului

2-1. Tangenta la curba

Se consideră funcția f(x) și curba y = f(x) corespunzătoare acestei funcții. Pentru o anumită valoare x, funcția are valoarea y = f(x). Aceste valori de pe curbă corespund punctului M(x0, y0). Introducem un nou argument x0 + ∆x, valoarea lui corespunde valorii funcției y0 + ∆y = f(x0 + ∆x). Punctul corespunzător este N(x0 + ∆x, y0 + ∆y). Se trasează secanta MN și se notează cu φ unghiul format de secanta cu direcția pozitivă a axei Ox. Figura arată că ∆y / ∆x = tg φ. Dacă acum ∆x se apropie de 0, atunci punctul N se va deplasa de-a lungul curbei, secanta MN se va roti în jurul punctului M, iar unghiul φ se va schimba. Dacă, ca ∆x → 0, unghiul φ tinde spre ceva α, atunci linia dreaptă care trece prin M și care face unghiul α cu direcția pozitivă a axei absciselor va fi tangenta necesară. În același timp, coeficientul său de pantă:

2-2. Plan tangent la suprafață

Planul tangent la suprafața în punctul M este planul care conține tangentele la toate curbele spațiale ale suprafeței care trec prin M - punctul de contact.

Luați o suprafață dată de ecuația F(x, y, z) = 0 și un punct obișnuit M(x0, y0, z0) pe ea. Se consideră la suprafață o curbă L care trece prin M. Fie curba dată de ecuații

x = φ(t); y = ψ(t); z = χ(t).

Ecuațiile tangentei la curba L în punctul M au forma:

Deoarece diferențele x - x0, y - y0, z - z0 sunt proporționale cu diferențele corespunzătoare, ecuația finală a planului arată astfel:

F "x (x - x0) + F" y (y - y0) + F "z (z - z0) \u003d 0

iar pentru cazul particular z = f(x, y):

Z - z0 \u003d F "x (x - x0) + F" y (y - y0)

Exemplu: Aflați ecuația planului tangent în punctul (2a; a; 1,5a) al paraboloidului hiperbolic

Soluţie:

Z"x \u003d x / a \u003d 2; Z"y \u003d -y / a \u003d -1

Ecuația planului dorit:

Z - 1,5a = 2(x - 2a) - (Y - a) sau Z = 2x - y - 1,5a

3. Utilizarea derivatei în fizică

3-1. Viteza punctului material

Fie ca dependența traseului s de timpul t într-o mișcare rectilinie dată a unui punct material să fie exprimată prin ecuația s = f(t) și t0 este un anumit moment de timp. Luați în considerare un alt timp t, notați ∆t = t - t0 și calculați incrementul de cale: ∆s = f(t0 + ∆t) - f(t0). Raportul ∆s / ∆t se numește viteza medie de mișcare în timpul ∆t scurs din momentul inițial t0. Viteza este limita acestui raport ca ∆t → 0.

Accelerația medie a mișcării neuniforme în intervalul (t; t + ∆t) este valoarea =∆v / ∆t. Accelerația instantanee a unui punct material la momentul t va fi limita accelerației medii:

Adică prima derivată de timp (v "(t)).

Exemplu: Dependența de timp a traseului parcurs de corp este dată de ecuația s = A + Bt + Ct2 + Dt3 (C = 0,1 m/s, D = 0,03 m/s2). Determinați timpul după începerea mișcării, după care accelerația corpului va fi egală cu 2 m/s2.

Soluţie:

v(t) = s"(t) = B + 2Ct + 3Dt2; a(t) = v"(t) = 2C + 6Dt = 0,2 + 0,18t = 2;

1,8 = 0,18t; t = 10 s

3-2. Capacitatea termică a unei substanțe la o anumită temperatură

Pentru a crește diferite temperaturi T cu aceeași valoare, egală cu T1 - T, la 1 kg. o anumită substanță are nevoie de o cantitate diferită de căldură Q1 - Q și raportul

se numește capacitatea termică medie pe intervalul , iar limita acestei expresii la ∆T → 0 se numește capacitatea termică a substanței date la temperatura T.

3-3. Putere

O modificare a mișcării mecanice a unui corp este cauzată de forțele care acționează asupra lui de la alte corpuri. Pentru a caracteriza cantitativ procesul de schimb de energie între corpurile care interacționează, în mecanică este introdus conceptul de lucru al unei forțe. Pentru a caracteriza rata de lucru, se introduce conceptul de putere:

4. Calcul diferenţial în economie

4-1. Cercetarea funcției

1) Fie funcția f(x) diferențiabilă într-o vecinătate a punctului x0. Dacă derivata f "(x) la trecerea prin punctul x0 își schimbă semnul de la + la -, atunci x0 este punctul maxim, dacă de la - la +, atunci x0 este punctul minim, dacă nu își schimbă semnul, atunci există nu este un extremum în acest moment.

2) Fie funcția f(x) diferențiabilă de două ori într-o vecinătate a punctului x0 și f „(x0) = 0, f „”(x0) ≠ 0, atunci în punctul x0 funcția f(x0) are un maxim dacă

Descarca:

Previzualizare:

Subtitrările slide-urilor:

Previzualizare:

Subtitrările slide-urilor:

Citeste si