लॉगरिदमिक अभिव्यक्तियों की पहचान परिवर्तन। घातीय और लघुगणकीय अभिव्यक्तियों के समान परिवर्तन। चर के साथ एक लघुगणकीय व्यंजक को कैसे परिवर्तित करें

अब हम एक सामान्य दृष्टिकोण से लघुगणक वाले व्यंजकों के रूपांतरण को देखेंगे। यहां हम लॉगरिदम के गुणों का उपयोग करके न केवल अभिव्यक्तियों के परिवर्तन का विश्लेषण करेंगे, बल्कि हम लॉगरिदम के साथ अभिव्यक्तियों के परिवर्तन पर भी विचार करेंगे। सामान्य दृष्टि से, जिसमें न केवल लघुगणक होते हैं, बल्कि शक्तियाँ, अंश, मूल आदि भी होते हैं। हमेशा की तरह, हम सभी सामग्री को विशिष्ट उदाहरणों के साथ आपूर्ति करेंगे विस्तृत विवरणसमाधान।

पृष्ठ नेविगेशन।

लघुगणक और लघुगणक व्यंजकों के साथ व्यंजक

भिन्नों के साथ क्रिया करना

पिछले पैराग्राफ में, हमने मुख्य परिवर्तनों का विश्लेषण किया था जो लॉगरिदम वाले अलग-अलग अंशों के साथ किए जाते हैं। इन परिवर्तनों को, निश्चित रूप से, प्रत्येक व्यक्तिगत अंश के साथ किया जा सकता है जो कि अधिक जटिल अभिव्यक्ति का हिस्सा है, उदाहरण के लिए, समान अंशों के योग, अंतर, उत्पाद और भागफल का प्रतिनिधित्व करना। लेकिन अलग-अलग भिन्नों के साथ काम करने के अलावा, इस प्रकार के व्यंजकों के रूपांतरण में अक्सर भिन्नों के साथ उपयुक्त क्रियाएं करना शामिल होता है। अगला, हम उन नियमों पर विचार करेंगे जिनके द्वारा ये क्रियाएं की जाती हैं।

ग्रेड 5-6 से हम उन नियमों को जानते हैं जिनके द्वारा . लेख में भिन्नों के साथ संचालन का सामान्य दृश्यहमने इन नियमों को परिचालित किया है साधारण अंशसामान्य रूप ए/बी के अंशों में, जहां ए और बी कुछ संख्यात्मक, शाब्दिक या चर के साथ अभिव्यक्ति हैं, और बी समान रूप से शून्य के बराबर नहीं है। यह स्पष्ट है कि लघुगणक वाले भिन्न सामान्य भिन्नों के विशेष मामले हैं। और इस संबंध में, यह स्पष्ट है कि उनके रिकॉर्ड में लॉगरिदम वाले अंशों के साथ क्रियाएं समान नियमों के अनुसार की जाती हैं। अर्थात्:

एक ही हर के साथ दो भिन्नों को जोड़ने या घटाने के लिए, अंशों को तदनुसार जोड़ें या घटाएं, और हर को वही छोड़ दें।
के साथ दो भिन्नों को जोड़ने या घटाने के लिए विभिन्न भाजक, आपको उन्हें एक सामान्य भाजक के पास लाना होगा और पिछले नियम के अनुसार उचित कार्य करना होगा।
दो भिन्नों को गुणा करने के लिए, आपको एक ऐसी भिन्न लिखनी होगी जिसका अंश मूल भिन्नों के अंशों का गुणनफल हो और हर हर का गुणनफल हो।
किसी भिन्न को भिन्न से विभाजित करने के लिए, विभाज्य भिन्न को भाजक के व्युत्क्रम से गुणा करना आवश्यक है, अर्थात अंश और हर को पुनर्व्यवस्थित करके अंश से गुणा करना आवश्यक है।

लॉगरिदम वाले भिन्नों के साथ संचालन करने के लिए यहां कुछ उदाहरण दिए गए हैं।

उदाहरण।

लघुगणक वाले भिन्नों के साथ क्रिया करें: a), b) , में) , जी) .

समाधान।

a) जोड़े गए भिन्नों के हर स्पष्ट रूप से समान हैं। इसलिए, समान हर के साथ भिन्न जोड़ने के नियम के अनुसार, हम अंश जोड़ते हैं, और हर को वही छोड़ देते हैं: .

b) यहाँ हर अलग हैं। इसलिए, पहले आपको चाहिए भिन्नों को एक ही हर में लाएँ. हमारे मामले में, हर को पहले से ही उत्पादों के रूप में प्रस्तुत किया जाता है, और यह हमारे लिए रहता है कि हम पहले अंश के हर को लें और दूसरे अंश के हर से लापता कारकों को जोड़ें। तो हमें फॉर्म का एक आम भाजक मिलता है . इस मामले में, घटाए गए अंशों को क्रमशः लघुगणक और व्यंजक x 2 ·(x+1) के रूप में अतिरिक्त कारकों का उपयोग करके एक सामान्य हर में घटाया जाता है। उसके बाद, एक ही हर के साथ अंशों को घटाना रहता है, जो मुश्किल नहीं है।

तो समाधान है:

ग) यह ज्ञात है कि भिन्नों को गुणा करने का परिणाम एक भिन्न होता है, जिसका अंश अंशों का गुणनफल होता है, और हर हर का गुणनफल होता है, इसलिए

यह देखना आसान है कि यह संभव है अंश में कमीदो से और दशमलव लघुगणक द्वारा, परिणामस्वरूप हमारे पास है .

d) हम भिन्नों के विभाजन से गुणा की ओर जाते हैं, भिन्न-भाजक को उसके व्युत्क्रम से बदल देते हैं। इसलिए

परिणामी भिन्न के अंश को इस प्रकार दर्शाया जा सकता है , जिसमें से अंश और हर का उभयनिष्ठ गुणनखंड स्पष्ट रूप से दिखाई देता है - गुणन x, आप इसके द्वारा भिन्न को कम कर सकते हैं:

उत्तर:

ए), बी) , में) , जी) .

यह याद रखना चाहिए कि अंशों के साथ क्रियाओं को उस क्रम को ध्यान में रखते हुए किया जाता है जिसमें क्रियाएं की जाती हैं: पहले गुणा और भाग, फिर जोड़ और घटाव, और यदि कोष्ठक हैं, तो कोष्ठक में क्रियाएं पहले की जाती हैं।

उदाहरण।

भिन्नों के साथ क्रिया करें .

समाधान।

सबसे पहले, हम कोष्ठक में भिन्नों का योग करते हैं, जिसके बाद हम गुणा करेंगे:

उत्तर:

इस बिंदु पर, यह जोर से तीन स्पष्ट रूप से कहना बाकी है, लेकिन एक ही समय में महत्वपूर्ण बिंदु:

लघुगणक के गुणों का उपयोग करके व्यंजकों को परिवर्तित करना

अक्सर, लघुगणक के साथ अभिव्यक्तियों के परिवर्तन में लघुगणक की परिभाषा को व्यक्त करने वाली पहचान का उपयोग शामिल होता है और

गणित। विषयगत परीक्षण। भाग द्वितीय। एकीकृत राज्य परीक्षा-2010 की तैयारी। 10-11 ग्रेड। ईडी। लिसेंको एफ.एफ. - रोस्तोव एन / डी।: लीजन, 2009. - 176 एस।

गणित। यूएसई-2009। विषयगत परीक्षण। भाग II (B4-B8, C1-C2) एड। लिसेंको एफ.एफ. - रोस्तोव एन / डी: लीजन, 2008 - 160 पी।

मैनुअल में व्यक्तिगत विषयों पर परीक्षण होते हैं, जो गणित के पाठ्यक्रम में पारंपरिक होते हैं और इसलिए, एक नियम के रूप में, परीक्षा में शामिल होते हैं। वे पाठ कार्यों और ज्यामिति में समस्याओं को छोड़कर, USE की बढ़ी हुई और उच्च स्तर की जटिलता के कार्यों के समूहों को पूरी तरह से कवर करते हैं। प्रत्येक विषय के लिए एक या अधिक परीक्षण सूट पेश किए जाते हैं। प्रत्येक सेट में 10 परीक्षण होते हैं, प्रत्येक परीक्षण में 8 कार्य होते हैं।

इस पुस्तक का उद्देश्य यूएसई परीक्षणों के संक्षिप्त और विस्तृत उत्तर के साथ कार्यों को हल करना है। यह मुख्य रूप से उन स्नातकों के लिए आवश्यक है जो प्राप्त करने की उम्मीद करते हैं अच्छा उपयोग करेंमूल्यांकन, साथ ही 10 वीं कक्षा के छात्रों के लिए, जो यूएसई के दृष्टिकोण से कवर किए गए विषयों को समेकित कर सकते हैं। प्रस्तावित मैनुअल गणित में यूएसई की तैयारी करने वाले सभी स्नातकों के साथ-साथ यूएसई के लिए छात्रों को तैयार करने वाले शिक्षकों के लिए उपयोगी हो सकता है।

प्रारूप:डीजेवीयू/ज़िप (2009 , 176 एस।)

आकार: 2.5 एमबी

फ़ाइल डाउनलोड / डाउनलोड करें 14

प्रारूप:पीडीएफ (2009 , 176 एस।)

आकार: 8.6 एमबी

डाउनलोड: 14 .12.2018, लीजन पब्लिशिंग हाउस के अनुरोध पर हटाए गए लिंक (नोट देखें)

प्रारूप:डीजेवीयू/ज़िप (2008 , 160 एस।)

आकार: 3 एमबी

फ़ाइल डाउनलोड / डाउनलोड करें 14 .12.2018, लीजन पब्लिशिंग हाउस के अनुरोध पर हटाए गए लिंक (नोट देखें)

प्रारूप:पीडीएफ (2008 , 160 एस।)

आकार: 9.9 एमबी

डाउनलोड: 14 .12.2018, लीजन पब्लिशिंग हाउस के अनुरोध पर हटाए गए लिंक (नोट देखें)

शैक्षिक-विधि जटिल "गणित। एकीकृत राज्य परीक्षा -2010" एड। लिसेंको एफ.एफ. और कुलबुखोव एस.यू. ट्यूटोरियल शामिल हैं:
1. गणित। एकीकृत राज्य परीक्षा-2010 की तैयारी।
2. रेशेबनिक। गणित। एकीकृत राज्य परीक्षा-2010 की तैयारी।
3. गणित। विषयगत परीक्षण। भाग I (मूल स्तर)। एकीकृत राज्य परीक्षा-2010 की तैयारी। 10-11 ग्रेड।
4. गणित। विषयगत परीक्षण। भाग द्वितीय। एकीकृत राज्य परीक्षा-2010 की तैयारी। 10-11 ग्रेड।
5. गणित। विषयगत परीक्षण: ज्यामिति, शब्द समस्याएं। एकीकृत राज्य परीक्षा-2010 की तैयारी। 10-11 ग्रेड।
6. गणित। USE परीक्षणों का संग्रह 2001 - 2010।
7. गणित। एकीकृत राज्य परीक्षा-2010 की तैयारी। प्रशिक्षण परीक्षण।
8. गणित के लिए पॉकेट गाइड।

विषयसूची
लेखकों से 11
§ 1. लघुगणकीय व्यंजकों के पहचान परिवर्तन 13
विकल्प संख्या 1 13
विकल्प संख्या 2 13
विकल्प संख्या 3 14
विकल्प संख्या 4 14
विकल्प संख्या 5 15
विकल्प संख्या 6 15
विकल्प संख्या 7 16
विकल्प संख्या 8 16
विकल्प संख्या 9 17
विकल्प संख्या 10 17
§ 2. डिग्री 18 . वाले व्यंजकों के पहचान परिवर्तन
विकल्प संख्या 1 18
विकल्प संख्या 2 19
विकल्प संख्या 3 19
विकल्प संख्या 4 20
विकल्प संख्या 5 21
विकल्प संख्या 6 21
विकल्प संख्या 7 22
विकल्प संख्या 8 23
विकल्प संख्या 9 23
विकल्प संख्या 10 24
§ 3. अपरिमेय व्यंजकों के पहचान परिवर्तन 25
विकल्प संख्या 1 25
विकल्प संख्या 2 25
विकल्प संख्या 3 26
विकल्प संख्या 4 26
विकल्प संख्या 5 27
विकल्प संख्या 6 28
विकल्प संख्या 7 28
विकल्प संख्या 8 29
विकल्प संख्या 9 30
विकल्प संख्या 10 30
4. समीकरणों की प्रणाली 31
विकल्प संख्या 1 31
विकल्प संख्या 2 32
विकल्प संख्या 3 33
विकल्प संख्या 4 33
विकल्प संख्या 5 34
विकल्प संख्या 6 35
विकल्प संख्या 7 36
विकल्प संख्या 8 37
विकल्प संख्या 9 38
विकल्प संख्या 10 39
5. ज्यामितीय अर्थव्युत्पन्न 39
विकल्प संख्या 1 39
विकल्प संख्या 2 41
विकल्प संख्या 3 43
विकल्प संख्या 4 44
विकल्प संख्या 5 46
विकल्प संख्या 6 48
विकल्प संख्या 7 50
विकल्प संख्या 8 52
विकल्प संख्या 9 54
विकल्प संख्या 10 55
6. असमानताएं 56
विकल्प संख्या 1 जी 56
विकल्प संख्या 2 57
विकल्प संख्या 3 58
विकल्प संख्या 4 58
विकल्प संख्या 5 59
विकल्प संख्या 6 60
विकल्प संख्या 7 60
विकल्प संख्या 8 61
विकल्प संख्या 9 62
विकल्प संख्या 10 63
7. अपरिमेय समीकरण 63
विकल्प संख्या 1 63
विकल्प संख्या 2 64
विकल्प संख्या 3 65
विकल्प संख्या 4 65
विकल्प संख्या 5 66
विकल्प संख्या 6 66
विकल्प संख्या 7 67
विकल्प संख्या 8 67
विकल्प संख्या 9 68
विकल्प संख्या यू 68
8. त्रिकोणमितीय समीकरण 69
विकल्प संख्या 1 69
विकल्प संख्या 2 69
विकल्प संख्या 3 70
विकल्प संख्या 4 70
विकल्प संख्या 5 71
विकल्प संख्या 6 72
विकल्प संख्या 7 72
विकल्प संख्या 8 73
विकल्प संख्या 9 74
विकल्प संख्या 10 74
9. लघुगणक समीकरण 75
विकल्प संख्या 1 75
विकल्प संख्या 2 75
विकल्प संख्या 3 76
विकल्प संख्या 4 76
विकल्प संख्या 5 77
विकल्प संख्या 6 77
विकल्प संख्या 7 78
विकल्प संख्या 8 * 78
विकल्प संख्या 9 79
विकल्प संख्या 10 79
10. घातीय समीकरण 80
विकल्प संख्या 1 80
विकल्प संख्या 2 80
विकल्प संख्या 3 81
विकल्प संख्या 4 81
विकल्प संख्या 5 82
विकल्प संख्या 6 82
विकल्प संख्या 7 83
विकल्प संख्या 8 83
विकल्प संख्या 9 84
विकल्प संख्या 10 84
§ग्यारह। आवर्त, सम और विषम फलन 85
विकल्प संख्या 1 85
विकल्प संख्या 2 86
विकल्प संख्या 3 87
विकल्प संख्या 4 89
विकल्प संख्या 5 90
विकल्प संख्या 6 91
विकल्प संख्या 7 92
विकल्प संख्या 8 93
विकल्प संख्या 9 94
विकल्प संख्या 10 95
§ 12. एक जटिल फलन के शून्य। सीमित समारोह 97
विकल्प संख्या 1 97
विकल्प संख्या 2 97
विकल्प संख्या 3 98
विकल्प संख्या 4 98
विकल्प संख्या 5 99
विकल्प संख्या 6 99
विकल्प संख्या 7 100
विकल्प संख्या 8 100
विकल्प संख्या 9 101
विकल्प संख्या 10 101
13. परिभाषा का क्षेत्र, मूल्यों का समूह, कार्यों की एकरसता 102
विकल्प संख्या 1 102
विकल्प संख्या 2 102
विकल्प संख्या 3 103
विकल्प संख्या 4 103
विकल्प संख्या 5 104
विकल्प संख्या 6 104
विकल्प संख्या 7 105
विकल्प संख्या 8 105
विकल्प संख्या 9 106
विकल्प संख्या 10 107
§ 14. एक समारोह की चरम सीमा। फ़ंक्शन का सबसे बड़ा और सबसे छोटा मान 107
विकल्प संख्या 1 107
विकल्प संख्या 2 108
विकल्प संख्या 3 108
विकल्प संख्या 4 109
विकल्प संख्या 5 109
विकल्प संख्या 6 110
विकल्प संख्या 7 110
विकल्प संख्या 8 111
विकल्प संख्या 9 111
विकल्प संख्या 10 112
15. लघुगणकीय समीकरणों को हल करने की विभिन्न तकनीकें 113
विकल्प संख्या 1 113
विकल्प संख्या 2 113
विकल्प संख्या 3 114
विकल्प संख्या 4 114
विकल्प संख्या 5 115
विकल्प संख्या 6 115
विकल्प संख्या 7 116
विकल्प संख्या 8 116
विकल्प संख्या 9 117
विकल्प संख्या 10 117
16. त्रिकोणमितीय समीकरणों को हल करने की विभिन्न तकनीकें 118
विकल्प संख्या 1 118
विकल्प संख्या 2 118
विकल्प संख्या 3 118
विकल्प संख्या 4 119
विकल्प संख्या 5 119
विकल्प संख्या 6 120
विकल्प संख्या 7 120
विकल्प संख्या 8 121
विकल्प संख्या 9 121
विकल्प संख्या 10 122
17. अपरिमेय समीकरणों को हल करने की विभिन्न तकनीकें 123
विकल्प संख्या 1 123
विकल्प संख्या 2 123
विकल्प संख्या 3 124
विकल्प संख्या 4 124
विकल्प संख्या 5 125
विकल्प संख्या 6 125
विकल्प संख्या 7 125
विकल्प संख्या 8 126
विकल्प संख्या 9 126
विकल्प संख्या 10 127
18. मॉडुलो साइन 127 . के तहत एक चर वाले समीकरण
विकल्प संख्या 1 127
विकल्प संख्या 2 128
विकल्प संख्या 3 128
विकल्प संख्या 4 129
विकल्प संख्या 5 129
विकल्प संख्या 6 130
विकल्प संख्या 7 130
विकल्प संख्या 8 131
विकल्प संख्या 9 131
विकल्प संख्या 10 131
§ 19. हल करने के लिए विभिन्न तरीके घातीय समीकरण.132
विकल्प संख्या 1 132
विकल्प संख्या 2 133
विकल्प संख्या 3 133
विकल्प संख्या 4 134
विकल्प संख्या 5 134
विकल्प संख्या 6 135
विकल्प संख्या 7 135
विकल्प संख्या 8 135
विकल्प संख्या 9 136
विकल्प संख्या 10 136
20. संयुक्त समीकरणों को हल करने की विभिन्न तकनीकें 137
विकल्प संख्या 1 137
विकल्प संख्या 2 137
विकल्प संख्या 3 138
विकल्प संख्या 4 138
विकल्प संख्या 5 139
विकल्प संख्या 6 139
विकल्प संख्या 7 140
विकल्प संख्या 8 140
विकल्प संख्या 9 141
विकल्प संख्या 10 141
21. मॉड्यूल 142 युक्त पैरामीटर वाले समीकरण
विकल्प संख्या 1 142
विकल्प संख्या 2 142
विकल्प संख्या 3 143
विकल्प संख्या 4 144
विकल्प संख्या 5 144
विकल्प संख्या 6 145
विकल्प संख्या 7 146
विकल्प संख्या 8 146
विकल्प संख्या 9 147
विकल्प संख्या 10 148
उत्तर 149
1. लघुगणकीय अभिव्यक्तियों के पहचान परिवर्तन 149
§ 2. 150 . की डिग्री वाले भावों की पहचान परिवर्तन
§ 3. अपरिमेय व्यंजकों के पहचान परिवर्तन 150
§ 4. समीकरणों की प्रणाली 151
5. व्युत्पन्न 151 . का ज्यामितीय अर्थ
6. असमानताएं 152
7. अपरिमेय समीकरण 152
8. त्रिकोणमितीय समीकरण 153
9. लघुगणक समीकरण 153
10. घातीय समीकरण 154
§ग्यारह। आवर्त, सम और विषम फलन 154
§ 12. एक जटिल फलन के शून्य। सीमित कार्य 155
§ 13. परिभाषा का क्षेत्र, मूल्यों का समूह, कार्यों की एकरसता 156
§ 14. एक समारोह की चरम सीमा। फ़ंक्शन का सबसे बड़ा और सबसे छोटा मान 158
§ पंद्रह। विभिन्न तरकीबेंलघुगणक समीकरणों को हल करते समय 159
§ 16. त्रिकोणमितीय समीकरणों को हल करने की विभिन्न तकनीकें 160
17. अपरिमेय समीकरणों को हल करने की विभिन्न तरकीबें 164
18. मॉडुलो साइन 165 . के तहत एक चर वाले समीकरण
§ 19. घातांकीय समीकरणों को हल करने के लिए विभिन्न तकनीकें।166
20. संयुक्त समीकरणों को हल करने की विभिन्न तकनीकें 167
21. मॉड्यूल 169 . वाले पैरामीटर वाले समीकरण
साहित्य 170

ईगोरोवा विक्टोरिया वलेरेवना

गणित के शिक्षक

उच्चतम योग्यता श्रेणी

विषय: "पहचान परिवर्तन"

लघुगणक व्यंजक"

इस पाठ का अध्ययन करने के बाद छात्रों को जिन ज्ञान और कौशलों में महारत हासिल करनी चाहिए:

किसी संख्या के लघुगणक की परिभाषा, मूल लघुगणकीय पहचान, लघुगणक के गुण जान सकेंगे;

लघुगणक वाले व्यंजकों का रूपांतरण करने में सक्षम हों, लघुगणक की गणना करें।

साहित्य:

1. अलीमोव श.ए., कोल्यागिन यू.एम., सिदोरोव यू.वी. और अन्य। बीजगणित और विश्लेषण की शुरुआत: ग्रेड 10-11 . के लिए एक पाठ्यपुस्तक शिक्षण संस्थानों. - एम।: शिक्षा, 2001।

2. कोचागिन वी.वी., कोचागिना एम.वी., परीक्षा की तैयारी का गहन पाठ्यक्रम। - एम .: एक्समो, 2009।

3. A. G. Merzlyak, V. B. Polonsky, और M. S. Yakir, बीजगणितीय सिम्युलेटर: स्कूली बच्चों और विश्वविद्यालय के प्रवेशकों के लिए एक गाइड। - एम .: इलेक्सा, 2005।

4. गुसेव वी.ए., मोर्दकोविच ए.जी. गणित: संदर्भ सामग्री: छात्रों के लिए एक किताब। - एम।: शिक्षा, 2001।

शिक्षण योजना:

कक्षाओं के दौरान:

1) लघुगणक है ग्रीक शब्द, जिसमें 2 शब्द हैं: "लोगो" - संबंध, "अरिथमोस" - संख्या। तो लघुगणक वह संख्या है जो अनुपात को मापती है। 1614 में एक प्रकाशन ने बताया कि नेपियर ने लघुगणक का आविष्कार किया था। बाद में, उन्होंने लघुगणकीय तालिकाओं का संकलन किया, जिन्हें अब हम ब्रैडी की सारणी के रूप में जानते हैं। एक सदी से भी कम समय में, टेबल दुनिया भर में फैल गए हैं और एक अनिवार्य कंप्यूटिंग टूल बन गए हैं। भविष्य में, वे, जैसा कि थे, एक सुविधाजनक उपकरण में बनाया गया था जो गणना प्रक्रिया को बहुत तेज करता है - एक स्लाइड नियम, जिसका उपयोग बीसवीं शताब्दी के सत्तर के दशक तक किया जाता था।

अनुलग्नक 1।

2) लोगारित्म सकारात्मक संख्याबीवजह से एक, इसके अतिरिक्त शून्य से बड़ा और एक के बराबर नहीं,वह घातांक है जिस पर एक संख्या बढ़ाई जानी चाहिएएक नंबर पाने के लिएबी।

लघुगणक की परिभाषा को व्यक्त करने वाली यह समानता कहलाती हैबुनियादी लघुगणकीय पहचान .

सी

या 1

पी

डिग्री का आधार और लघुगणक का आधार सत्रह है, जिसका अर्थ है कि मूल लघुगणकीय पहचान के अनुसार व्यंजक का मान तीन है।

हम मौखिक रूप से काम करेंगे:

SCH
एल्चोक

हे निचला दूसरा शून्य दशमलव पाँच दसवां है, इसलिए व्यंजक पाँच के अंकगणितीय वर्गमूल के बराबर है।

पी

परिशिष्ट 2।

समानता मतलब कि

लघुगणक की परिभाषा से, निम्नलिखित महत्वपूर्ण समानताएँ प्राप्त होती हैं:

उदाहरण के लिए:

पी
परिशिष्ट 3.

चलिए आगे बढ़ते हैं कार्य का उपयोग करें:

परिशिष्ट 4

3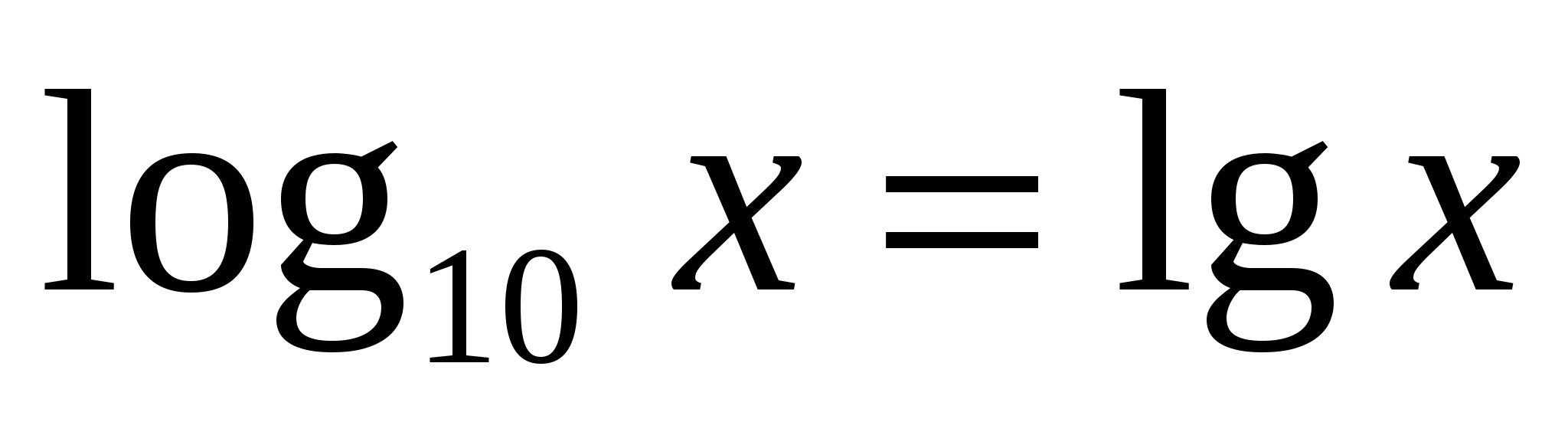
) आधार दस लघुगणक के लिए एक विशेष अंकन और नाम है।दशमलव लघुगणक .

ली
आधार के लिए अंकगणितइ बुलायाप्राकृतिक .

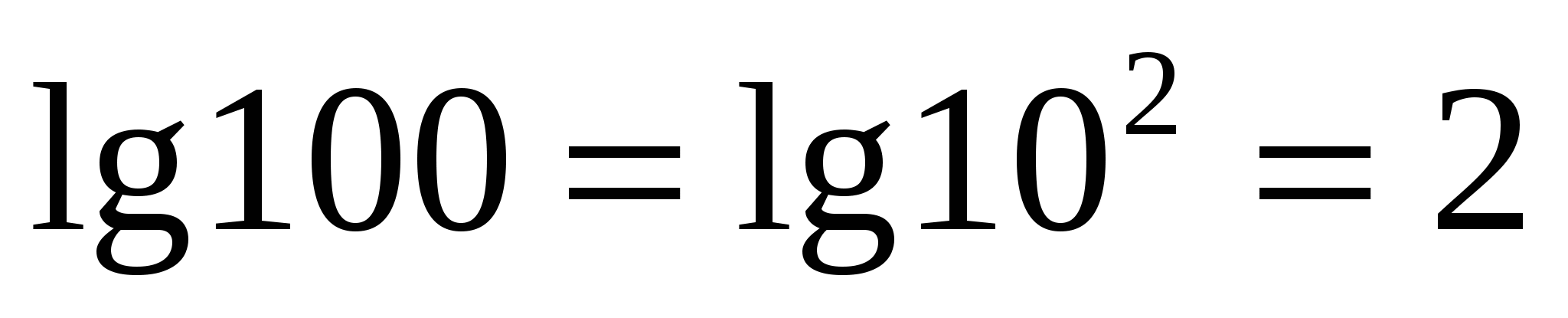
एच
उदाहरण के लिए,

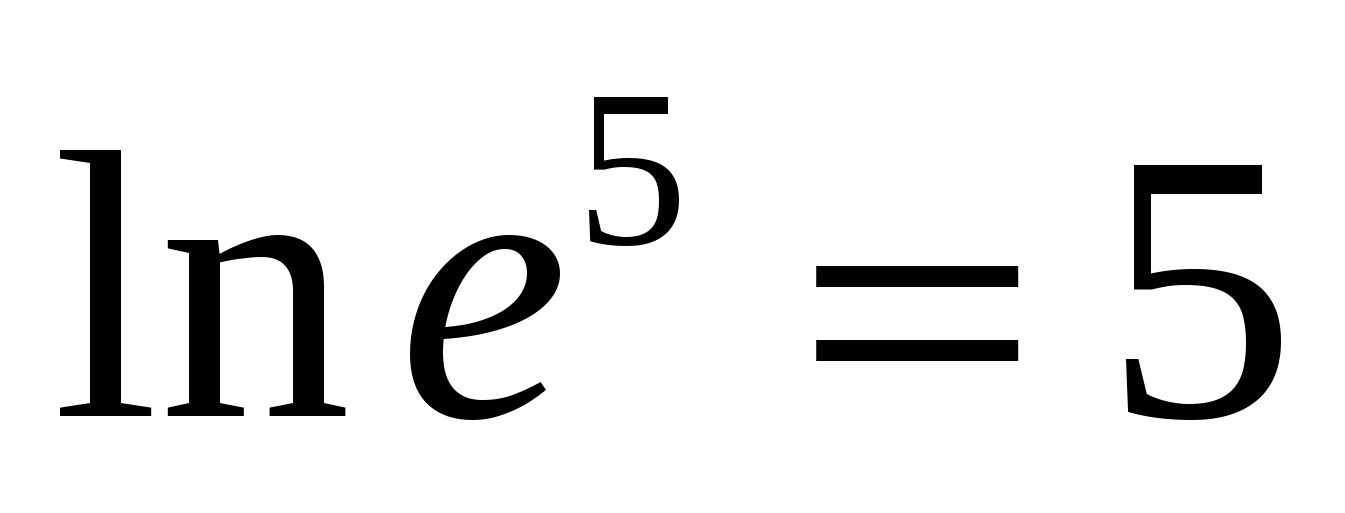
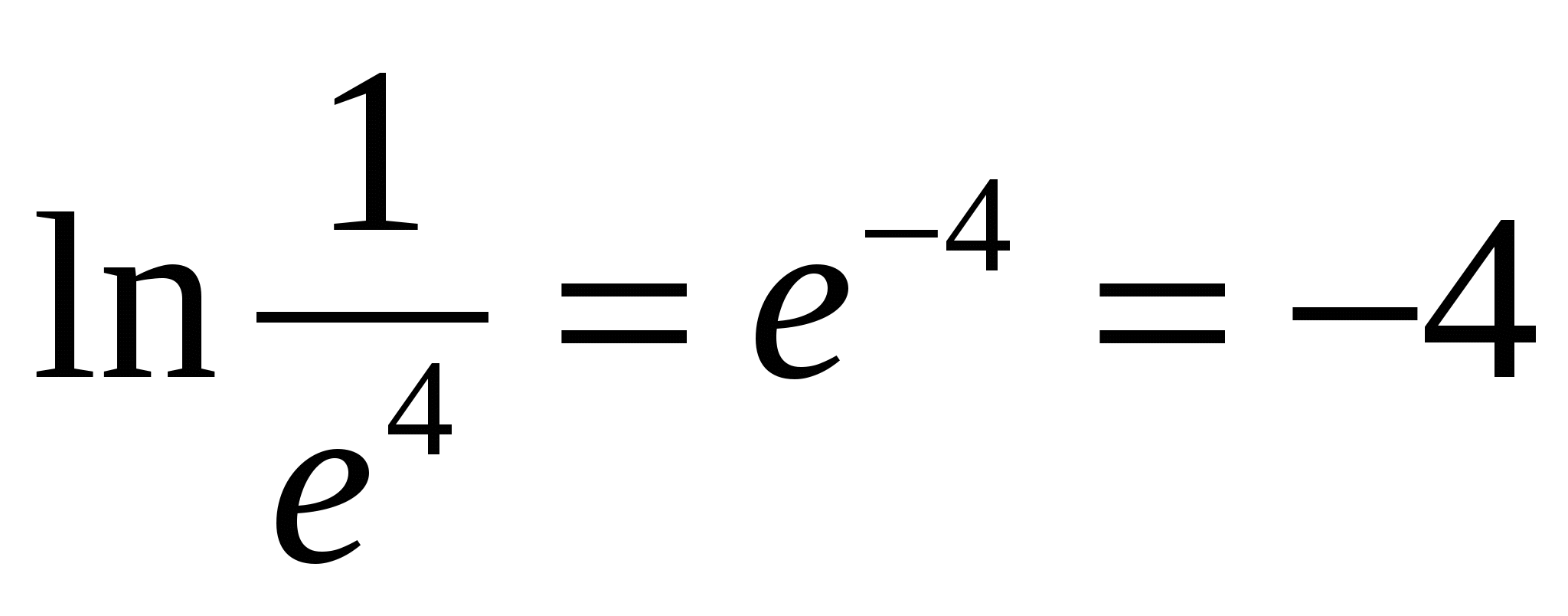
4) निम्नलिखित गुण लघुगणक की परिभाषा से अनुसरण करते हैं। सभी गुण केवल लघुगणक संकेतों के तहत निहित चर के सकारात्मक मूल्यों के लिए तैयार और सिद्ध होते हैं।

दो धनात्मक संख्याओं के गुणनफल का आधार लघुगणक एक योग के बराबर हैएक ही आधार के साथ इन संख्याओं के लघुगणक।

डीईआर 2

उदाहरण के लिए,

जेड
असाइनमेंट 1।

कार्य 2.व्यंजक को सरल कीजिए

पर
आइए पिछले उदाहरण का उपयोग करें। आइए बदलें

ध्यान दें कि लघुगणक चुकता है, इसलिए योग भी चुकता होना चाहिए। योग के वर्ग के सूत्र का प्रयोग करते हुए कोष्ठकों को खोलिए। हम समान शब्द प्रस्तुत करते हैं।

5) भागफल का लघुगणक भाज्य और भाजक के लघुगणक के बीच के अंतर के बराबर होता है।

सी

डिग्री के आधार और लघुगणक के आधार पर ध्यान दें - वे समान हैं।

या 3

आर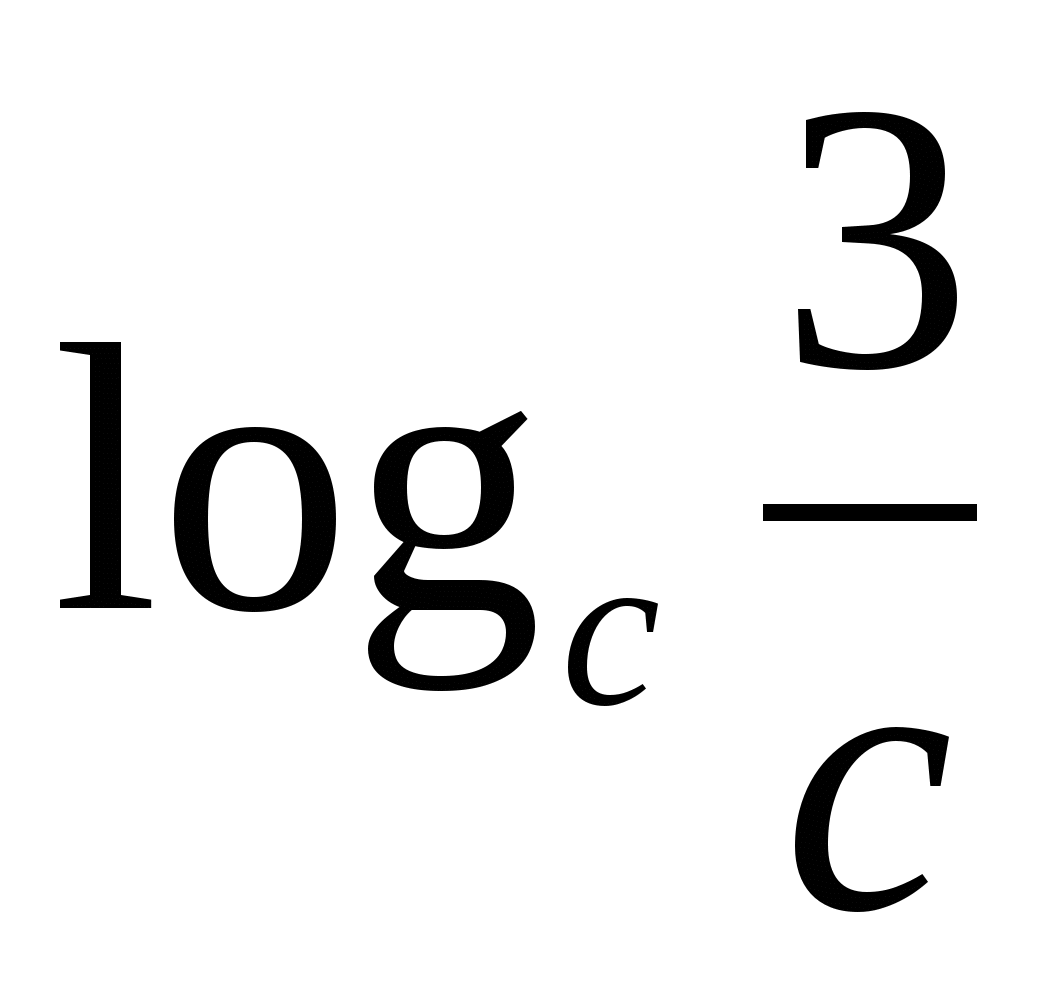

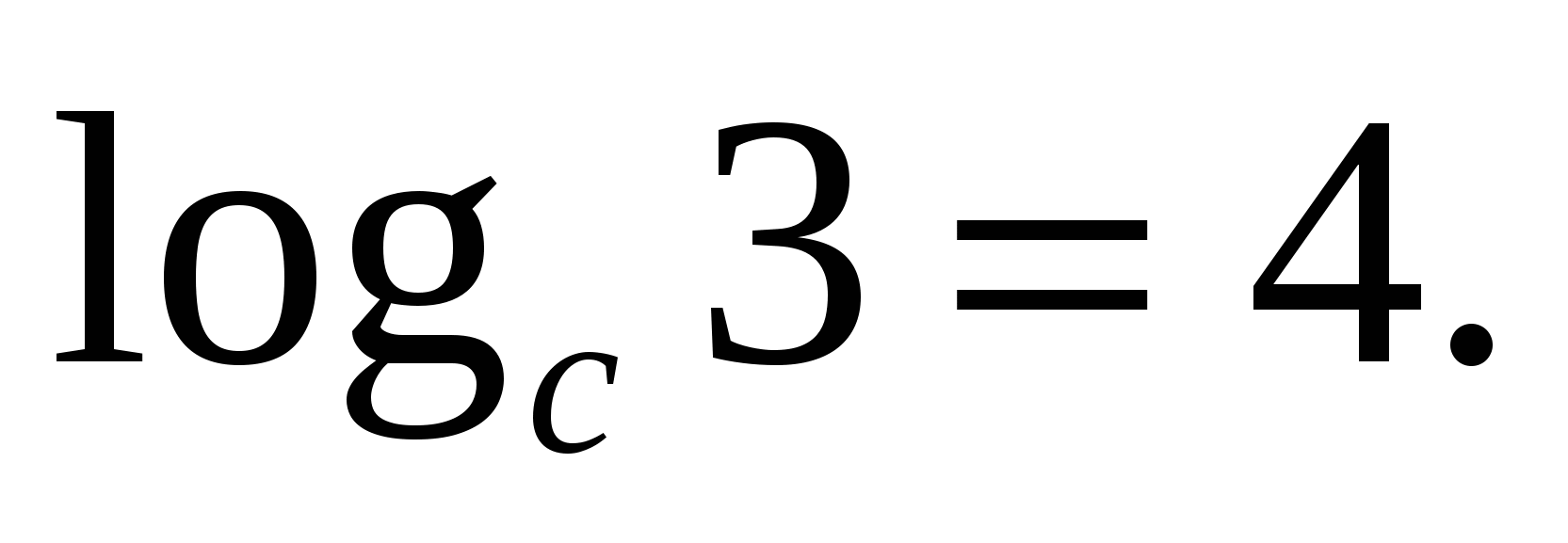आइए एक उदाहरण के साथ इस सूत्र के अनुप्रयोग को देखें:

जेड
असाइनमेंट 1।व्यंजक का मान ज्ञात कीजिए यदि

कार्य 2.मान ज्ञात कीजिए बीइसके लघुगणक द्वारा

6) आधार से डिग्री का लघुगणकएक , उत्पाद के बराबर हैएक ही आधार में प्रति लघुगणक घातांक।

डीईआर 4

उदाहरण के लिए,

जेड
असाइनमेंट 1।गणना करें यदि

आइए अभिव्यक्ति को सरल बनाएं

सूत्र

बुलाया एक नए आधार पर संक्रमण के लिए सूत्र।

जेड

असाइनमेंट 1।आधार 2 वाले लघुगणक के रूप में व्यक्त करें।

कार्य 2.गणना

सीईआर 5

सीईआर 6

उदाहरण के लिए,

जेड

असाइनमेंट 1।गणना

जेड
असाइनमेंट 2.गणना

9) आप लघुगणक परिवर्तन तभी प्रारंभ कर सकते हैं जबयदि आपको लघुगणक के सभी गुण याद हैं। उन्हें दोहराने के बाद, हम दूसरी तरफ से लघुगणकीय अभिव्यक्तियों को बदलने के कार्यों पर विचार करेंगे।

लॉगरिदमिक अभिव्यक्तियों के योग या अंतर को परिवर्तित करने के लिए, कभी-कभी लॉगरिदम की परिभाषा का उपयोग करना पर्याप्त होता है, और अक्सर उत्पाद या भागफल के लॉगरिदम के गुण।

जेड
असाइनमेंट 1।गणना

आइए इसे दो तरह से हल करें।

1 तरीका, लघुगणक की परिभाषा का उपयोग करते हुए:

विधि 2 पर आधारितभागफल लघुगणक गुण:

कार्य 2.व्यंजक का मान ज्ञात कीजिए

आइए पहले सूत्र लागू करेंउत्पाद का लघुगणक, फिर लघुगणक की परिभाषा।

घातांक में लघुगणक वाले व्यंजकों को परिवर्तित करते समय मूल लघुगणकीय पहचान का उपयोग किया जाता है। इस तरह के संचालन का विचार घातांक के आधार और लघुगणक के आधार को बराबर करना है।

कभी-कभी अभिव्यक्ति को बदलना आवश्यक होता हैलघुगणक के गुणों से और डिग्री के गुणों से भी कोई व्यक्ति संक्रमण सूत्र का उपयोग करके आसानी से एक आधार से दूसरे आधार पर जा सकता है। अन्य मामलों में, एकाधिक गुणों को लागू किया जाना चाहिए।

जेड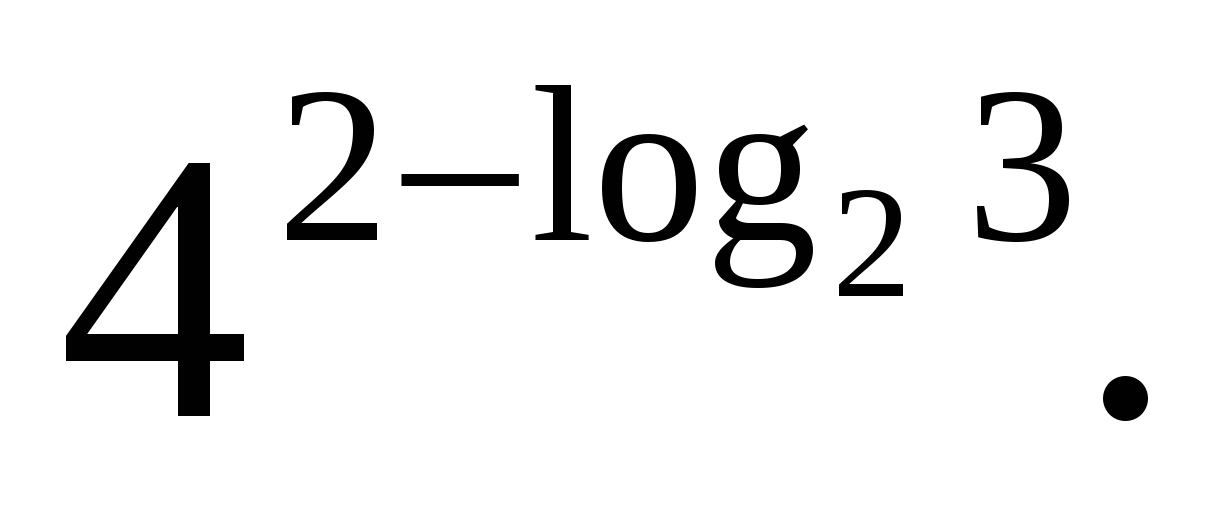
असाइनमेंट 3.गणना

जेड
असाइनमेंट 4.व्यंजक का मान ज्ञात कीजिए

कार्य 5.व्यंजक का मान ज्ञात कीजिए

जेड
कार्य 6.लघुगणक के अंतर के रूप में व्यक्त करें

एच
रेडिकल के तहत लॉगरिदमिक अभिव्यक्तियों का परिवर्तन सबसे बड़ी कठिनाई है। रूपांतरण की प्रक्रिया में, किसी को लघुगणकीय व्यंजकों के मॉड्यूल पर विचार करना होता है, जिसके प्रकटीकरण के लिए अपरिमेय संख्याओं या परिमेय और अपरिमेय संख्याओं की तुलना करने की आवश्यकता होती है। हम लगातार कार्रवाई करेंगे। आंतरिक मूलक के तहत अभिव्यक्ति पर विचार करें।

मूल अभिव्यक्ति में स्थानापन्न करें।

यह ध्यान दिया जाना चाहिए कि समीकरणों और असमानताओं को हल करते समय या कार्यों का अध्ययन करते समय लॉगरिदमिक अभिव्यक्तियों के परिवर्तन का भी सामना किया जा सकता है, इसलिए, एक निहित रूप में, वे समूह बी और सी के असाइनमेंट में भी उपस्थित हो सकते हैं।

10) संक्षेप में।

आधार 10 लघुगणक कहलाता है

मूल लघुगणक

मुख्य लघुगणक

प्राकृतिक

दशमलव लघुगणक

2) क्या मूल्य कर सकते हैंएक्स अभिव्यक्ति में

मान परिभाषित नहीं है

5) उस अनुपात को इंगित करें जो सभी के लिए सत्य हैएक्स ≠ 0 .

6) नए आधार पर संक्रमण के लिए सूत्र के लिए सही अनुपात निर्दिष्ट करें।

7) के लिए सही समानता का संकेत दें

11) नियंत्रण परीक्षण।

ट्रांसनिस्ट्रियन स्टेट यूनिवर्सिटी

उन्हें। टी.जी. शेवचेंको

भौतिकी और गणित के संकाय

गणितीय विश्लेषण विभाग

और गणित पढ़ाने के तरीके

पाठ्यक्रम कार्य

"पहचान परिवर्तन

घातीय और लघुगणक

भाव"

काम पूरा हो गया है:

______ समूह का छात्र

भौतिकी और गणित के संकाय

_________________________

जांचा गया काम:

_________________________

तिरस्पोल, 2003

परिचय ……………………………………………………………………… 2

अध्याय 1

§एक। विशिष्ट प्रकार के परिवर्तनों को लागू करने के लिए कौशल का निर्माण……………………………………………………………………………….4

2. समान परिवर्तनों के अध्ययन में एक ज्ञान प्रणाली के संगठन की विशेषताएं।

3. गणित कार्यक्रम ……………………………………….11

अध्याय 2

§एक। डिग्री की अवधारणा का सामान्यीकरण…………………………………..13

2. घातांकीय फलन………………………………..15

3. लॉगरिदमिक फ़ंक्शन ………………………………….16

अध्याय 3. व्यवहार में घातीय और लघुगणकीय अभिव्यक्तियों के समान परिवर्तन ...................................................19

निष्कर्ष……………………………………………………..24

प्रयुक्त साहित्य की सूची………………………………….25
परिचय

यह पाठ्यक्रम कार्य घातीय और लघुगणकीय कार्यों के समान परिवर्तनों पर विचार करेगा, बीजगणित के स्कूल पाठ्यक्रम और विश्लेषण की शुरुआत में उन्हें पढ़ाने की पद्धति पर विचार करेगा।

इस काम का पहला अध्याय गणित के स्कूल पाठ्यक्रम में समान परिवर्तनों को पढ़ाने की पद्धति का वर्णन करता है, इसमें घातीय और लघुगणक कार्यों के अध्ययन के साथ "बीजगणित और विश्लेषण की शुरुआत" पाठ्यक्रम में गणित में एक कार्यक्रम भी शामिल है।

दूसरा अध्याय सीधे घातीय और लॉगरिदमिक कार्यों से संबंधित है, उनके मुख्य गुण समान परिवर्तनों में उपयोग किए जाते हैं।

तीसरा अध्याय घातीय और लघुगणकीय कार्यों के समान परिवर्तनों का उपयोग करके उदाहरणों और समस्याओं का समाधान है।

अभिव्यक्ति और सूत्रों के विभिन्न परिवर्तनों का अध्ययन स्कूली गणित के पाठ्यक्रम में अध्ययन के समय का एक महत्वपूर्ण हिस्सा लेता है। अंकगणितीय संक्रियाओं के गुणों के आधार पर सरलतम परिवर्तन पहले से ही किए जा चुके हैं प्राथमिक स्कूलऔर ग्रेड IV-V में। लेकिन परिवर्तन करने के लिए कौशल और क्षमताओं के निर्माण पर मुख्य बोझ स्कूल बीजगणित के पाठ्यक्रम द्वारा वहन किया जाता है। यह प्रदर्शन किए गए परिवर्तनों की संख्या और विविधता में तेज वृद्धि के साथ जुड़ा हुआ है, और गतिविधियों की जटिलता के साथ उन्हें प्रमाणित करने और प्रयोज्यता की शर्तों को स्पष्ट करने के साथ, पहचान की सामान्यीकृत अवधारणाओं की पहचान और अध्ययन के साथ, समान परिवर्तन, समकक्ष परिवर्तन, तार्किक परिणाम।

समान परिवर्तन करने की संस्कृति उसी तरह विकसित होती है जैसे कंप्यूटिंग की संस्कृति, वस्तुओं (संख्याओं, वैक्टर, बहुपद, आदि) और उनके कार्यान्वयन के लिए एल्गोरिदम पर संचालन के गुणों के ठोस ज्ञान के आधार पर। यह न केवल परिवर्तनों को सही ढंग से सही ठहराने की क्षमता में प्रकट होता है, बल्कि मूल विश्लेषणात्मक अभिव्यक्ति से उस अभिव्यक्ति तक संक्रमण के लिए सबसे छोटा रास्ता खोजने की क्षमता में भी प्रकट होता है जो परिवर्तन के उद्देश्य के लिए सबसे उपयुक्त है, परिवर्तनों को ट्रैक करने की क्षमता में परिवर्तनों की गति और त्रुटि-मुक्त निष्पादन में, समान परिवर्तनों की श्रृंखला में विश्लेषणात्मक अभिव्यक्तियों की परिभाषा का क्षेत्र। ।

गणना और समान परिवर्तनों की उच्च संस्कृति सुनिश्चित करना गणित पढ़ाने में एक महत्वपूर्ण समस्या है। हालाँकि, यह समस्या अभी भी संतोषजनक ढंग से हल होने से बहुत दूर है। इसका प्रमाण सार्वजनिक शिक्षा अधिकारियों का सांख्यिकीय डेटा है, जिसमें छात्रों द्वारा की गई गणना और परिवर्तन की त्रुटियों और तर्कहीन तरीकों को सालाना कहा जाता है। विभिन्न वर्गकरते हुए नियंत्रण कार्य. इसकी पुष्टि उच्चतर के मतों से होती है शिक्षण संस्थानोंआवेदकों के गणितीय ज्ञान और कौशल की गुणवत्ता के बारे में। कोई भी सार्वजनिक शिक्षा अधिकारियों और विश्वविद्यालयों के इस निष्कर्ष से सहमत नहीं हो सकता है कि यह पर्याप्त नहीं है उच्च स्तरकंप्यूटिंग और समान परिवर्तनों की संस्कृति उच्च विद्यालयछात्रों के ज्ञान में औपचारिकता का परिणाम है, सिद्धांत को व्यवहार से अलग करना।

पहचान परिवर्तन और शिक्षण विधियों

बीजगणित के स्कूल पाठ्यक्रम और विश्लेषण की शुरुआत में।

§एक। आवेदन कौशल का गठन

विशिष्ट प्रकार के परिवर्तन।

बीजगणित की शुरुआत के चरण में उपयोग किए जाने वाले परिवर्तनों को करने के लिए तकनीकों और नियमों की प्रणाली में अनुप्रयोगों की एक विस्तृत श्रृंखला है: इसका उपयोग गणित के पूरे पाठ्यक्रम के अध्ययन में किया जाता है। हालांकि, इसकी कम विशिष्टता के कारण, इस प्रणाली को अतिरिक्त परिवर्तनों की आवश्यकता है जो रूपांतरित अभिव्यक्तियों की संरचना की ख़ासियत और नए शुरू किए गए कार्यों और कार्यों के गुणों को ध्यान में रखते हैं। संबंधित प्रकार के परिवर्तनों का विकास संक्षिप्त गुणन फ़ार्मुलों की शुरूआत के साथ शुरू होता है। फिर हम विभिन्न वर्गों के साथ घातांक संचालन से जुड़े परिवर्तनों पर विचार करते हैं प्राथमिक कार्य- घातीय, शक्ति, लघुगणक, त्रिकोणमितीय। इस प्रकार के प्रत्येक परिवर्तन अध्ययन के एक चरण से गुजरते हैं, जिसमें उनकी विशिष्ट विशेषताओं को आत्मसात करने पर ध्यान केंद्रित किया जाता है।

सामग्री के संचय के साथ, विचाराधीन सभी परिवर्तनों की सामान्य विशेषताओं को अलग करना संभव हो जाता है और इस आधार पर, समान और समकक्ष परिवर्तनों की अवधारणाओं को पेश करना संभव हो जाता है।

यह ध्यान दिया जाना चाहिए कि एक समान परिवर्तन की अवधारणा बीजगणित के स्कूल पाठ्यक्रम में पूर्ण व्यापकता में नहीं, बल्कि केवल अभिव्यक्तियों के आवेदन में दी गई है। रूपांतरणों को दो वर्गों में विभाजित किया गया है: समान परिवर्तन अभिव्यक्ति के परिवर्तन हैं, और समकक्ष परिवर्तन सूत्रों के परिवर्तन हैं। मामले में जब सूत्र के एक भाग को सरल बनाने की आवश्यकता होती है, तो इस सूत्र में एक अभिव्यक्ति को हाइलाइट किया जाता है, जो लागू समान परिवर्तन के लिए एक तर्क के रूप में कार्य करता है। संबंधित विधेय को अपरिवर्तित माना जाता है।

परिवर्तनों (संश्लेषण) की एक अभिन्न प्रणाली के संगठन के लिए, इसका मुख्य लक्ष्य एक लचीला और शक्तिशाली बनाना है; विभिन्न प्रकार के शैक्षिक कार्यों को हल करने में उपयोग के लिए उपयुक्त उपकरण।

बीजगणित और विश्लेषण की शुरुआत के दौरान, इसकी मुख्य विशेषताओं में पहले से ही गठित परिवर्तनों की एक अभिन्न प्रणाली में धीरे-धीरे सुधार जारी है। इसमें कुछ नए प्रकार के परिवर्तन भी जोड़े जाते हैं, लेकिन वे केवल इसे समृद्ध करते हैं, इसकी क्षमताओं का विस्तार करते हैं, लेकिन इसकी संरचना को नहीं बदलते हैं। इन नए परिवर्तनों का अध्ययन करने की पद्धति व्यावहारिक रूप से बीजगणित के पाठ्यक्रम में उपयोग की जाने वाली पद्धति से भिन्न नहीं है।

2. कार्य प्रणाली के संगठन की विशेषताएं

समान परिवर्तनों के अध्ययन में।

कार्यों की किसी भी प्रणाली को व्यवस्थित करने का मूल सिद्धांत छात्रों को व्यवहार्य कठिनाइयों को दूर करने और बनाने की आवश्यकता को ध्यान में रखते हुए उन्हें सरल से जटिल तक प्रस्तुत करना है। समस्या की स्थिति. निर्दिष्ट बुनियादी सिद्धांत को इस शैक्षिक सामग्री की विशेषताओं के संबंध में ठोसकरण की आवश्यकता है। गणित की पद्धति में कार्यों की विभिन्न प्रणालियों का वर्णन करने के लिए, अभ्यासों के चक्र की अवधारणा का उपयोग किया जाता है। अभ्यास के चक्र को अध्ययन के कई पहलुओं के अभ्यास के क्रम में संयोजन और सामग्री की व्यवस्था के तरीकों की विशेषता है। समान परिवर्तनों के संबंध में, एक चक्र का विचार इस प्रकार दिया जा सकता है।

अभ्यास का चक्र एक पहचान के अध्ययन से जुड़ा है, जिसके चारों ओर अन्य पहचान समूहीकृत हैं, जो इसके साथ एक प्राकृतिक संबंध में हैं। कार्यकारी कार्यों के साथ-साथ चक्र की संरचना में ऐसे कार्य शामिल हैं जिन्हें माना पहचान की प्रयोज्यता की मान्यता की आवश्यकता होती है। अध्ययन के तहत पहचान का उपयोग विभिन्न संख्यात्मक डोमेन पर गणना करने के लिए किया जाता है। पहचान की विशिष्टता को ध्यान में रखा जाता है; खासतौर पर इससे जुड़े टर्न ऑफ स्पीच का आयोजन किया जाता है।

प्रत्येक चक्र में कार्यों को दो समूहों में बांटा गया है। पहले में पहचान के साथ प्रारंभिक परिचय के दौरान किए गए कार्य शामिल हैं। वे सेवा करते हैं शैक्षिक सामग्रीलगातार कई पाठों के लिए, एक विषय से एकजुट। अभ्यास का दूसरा समूह अध्ययन के तहत पहचान को विभिन्न अनुप्रयोगों से जोड़ता है। यह समूह एक रचनात्मक एकता नहीं बनाता है - यहां अभ्यास विभिन्न विषयों पर बिखरे हुए हैं।

चक्र की वर्णित संरचना विशिष्ट प्रकार के परिवर्तनों को लागू करने के लिए कौशल के गठन के चरण को संदर्भित करती है। अंतिम चरण में - संश्लेषण का चरण, चक्रों को संशोधित किया जाता है। सबसे पहले, कार्यों के दोनों समूहों को संयुक्त किया जाता है, जिससे एक "खुला" चक्र बनता है, और शब्दों या कार्य की जटिलता के मामले में सबसे सरल लोगों को पहले समूह से बाहर रखा जाता है। शेष प्रकार के कार्य अधिक कठिन हो जाते हैं। दूसरे, विभिन्न पहचानों से संबंधित चक्रों का विलय होता है, जिससे एक या दूसरी पहचान की प्रयोज्यता को पहचानने के लिए क्रियाओं की भूमिका बढ़ जाती है।

हम प्राथमिक कार्यों के लिए सर्वसमिकाओं से संबंधित कार्य चक्रों की विशेषताओं पर ध्यान देते हैं। ये विशेषताएं इस तथ्य के कारण हैं कि, सबसे पहले, कार्यात्मक सामग्री के अध्ययन के संबंध में संबंधित पहचान का अध्ययन किया जाता है और दूसरा, वे पहले समूह की पहचान की तुलना में बाद में प्रकट होते हैं और समान परिवर्तनों को करने के लिए पहले से ही गठित कौशल का उपयोग करके अध्ययन किया जाता है। .

प्रत्येक नया शुरू किया गया प्राथमिक कार्य तेजी से संख्याओं की सीमा का विस्तार करता है जिसे व्यक्तिगत रूप से नामित और नामित किया जा सकता है। इसलिए, चक्रों के कार्यों के पहले समूह में इन नए संख्यात्मक क्षेत्रों और परिमेय संख्याओं के मूल क्षेत्र के बीच संबंध स्थापित करने के लिए कार्य शामिल होने चाहिए। हम ऐसे कार्यों का उदाहरण देते हैं।

उदाहरण 1 गणना करें:

प्रत्येक अभिव्यक्ति के आगे, चक्रों में एक पहचान होती है जिसके लिए प्रस्तावित कार्य मौजूद हो सकते हैं। इस तरह के कार्यों का उद्देश्य रिकॉर्ड की विशेषताओं में महारत हासिल करना है, जिसमें नए संचालन और कार्यों के प्रतीक शामिल हैं, और गणितीय भाषण कौशल विकसित करना है।

प्राथमिक कार्यों से जुड़े पहचान परिवर्तनों के उपयोग का एक महत्वपूर्ण हिस्सा तर्कहीन और पारलौकिक समीकरणों के समाधान पर पड़ता है। पहचान के आत्मसात से संबंधित चक्रों में केवल सबसे सरल समीकरण शामिल हैं, लेकिन पहले से ही ऐसे समीकरणों को हल करने की विधि में महारत हासिल करने के लिए काम करना उचित है: अज्ञात को बीजीय समीकरण में बदलकर इसे कम करना।

इस समाधान के लिए चरणों का क्रम इस प्रकार है:

ए) एक फ़ंक्शन ढूंढें जिसके लिए इस समीकरण को इस प्रकार दर्शाया जा सकता है;

बी) एक प्रतिस्थापन करें और समीकरण को हल करें;

सी) प्रत्येक समीकरण को हल करें, जहां समीकरण की जड़ों का सेट है।

वर्णित विधि का उपयोग करते समय, चरण बी) अक्सर के लिए एक संकेतन शुरू किए बिना, परोक्ष रूप से किया जाता है। इसके अलावा, छात्र अक्सर उत्तर खोजने के लिए विभिन्न पथों में से एक को चुनते हैं, जो कि बीजीय समीकरण को तेज और आसान बनाता है।

उदाहरण 2. समीकरण को हल करें।

पहला तरीका:

दूसरा तरीका:

एक)

बी)

यह यहाँ देखा जा सकता है कि चरण a) पहली विधि में दूसरे की तुलना में अधिक कठिन है। पहला तरीका "शुरू करने में कठिन" है, हालांकि समाधान का आगे का तरीका बहुत आसान है। दूसरी ओर, दूसरी विधि के फायदे हैं, जिसमें अधिक आसानी से, एक बीजीय समीकरण को कम करने के लिए शिक्षण में अधिक परिष्कार शामिल है।

बीजगणित में एक स्कूल पाठ्यक्रम के लिए, ऐसे कार्य विशिष्ट होते हैं जिनमें बीजीय समीकरण में संक्रमण इस उदाहरण की तुलना में और भी आसान होता है। ऐसे कार्यों का मुख्य भार चरण सी के चयन से संबंधित है) अध्ययन के तहत प्राथमिक कार्य के गुणों के उपयोग से जुड़े समाधान प्रक्रिया के एक स्वतंत्र भाग के रूप में।

उदाहरण 3. समीकरण को हल करें:

एक) ; बी) .

इन समीकरणों को समीकरणों में घटाया जाता है: a) या ; बी) या। इन समीकरणों को हल करने के लिए, घातीय फ़ंक्शन के बारे में केवल सबसे सरल तथ्यों का ज्ञान आवश्यक है: इसकी एकरसता, मूल्यों की सीमा। पिछले उदाहरण की तरह, समीकरण ए) और बी) द्विघात घातीय समीकरणों को हल करने के लिए अभ्यास के चक्र के पहले समूह के लिए जिम्मेदार ठहराया जा सकता है।

इस प्रकार, हम एक घातीय कार्य सहित, पारलौकिक समीकरणों के समाधान से संबंधित चक्रों में कार्यों के वर्गीकरण पर आते हैं:

1) समीकरण जो फॉर्म के समीकरणों में कम हो जाते हैं और जिनका एक सरल उत्तर होता है, सामान्य रूप में: ;

2) समीकरण जो समीकरणों को कम करते हैं, जहां एक पूर्णांक है, या जहां;

3) समीकरण जो समीकरणों को कम करते हैं और जिस रूप में संख्या लिखी जाती है, उसके स्पष्ट विश्लेषण की आवश्यकता होती है।

इसी तरह के कार्यों को अन्य प्राथमिक कार्यों के लिए वर्गीकृत किया जा सकता है।

बीजगणित और बीजगणित के पाठ्यक्रमों में अध्ययन की गई पहचानों का एक महत्वपूर्ण हिस्सा और विश्लेषण की शुरुआत उनमें सिद्ध होती है या कम से कम व्याख्या की जाती है। सर्वसमिकाओं के अध्ययन के इस पक्ष में है बहुत महत्वदोनों पाठ्यक्रमों के लिए, क्योंकि उनमें प्रदर्शनकारी तर्क सबसे बड़ी स्पष्टता और पहचान के संबंध में कठोरता के साथ किया जाता है। इस सामग्री के बाहर, सबूत आमतौर पर कम पूर्ण होते हैं, यह हमेशा औचित्य के लागू साधनों की संरचना से अलग नहीं होता है।

अंकगणितीय संक्रियाओं के गुणों का उपयोग एक समर्थन के रूप में किया जाता है जिस पर पहचान के प्रमाण बनाए जाते हैं।

गणना और समान परिवर्तनों के शैक्षिक प्रभाव को विकास के लिए निर्देशित किया जा सकता है तार्किक सोच, यदि केवल छात्रों को कार्यात्मक सोच विकसित करने के लिए गणना और समान परिवर्तनों को सही ठहराने के लिए व्यवस्थित रूप से आवश्यक है, जो विभिन्न तरीकों से प्राप्त किया जाता है। इच्छा, स्मृति, सरलता, आत्म-नियंत्रण और रचनात्मक पहल के विकास में गणना और समान परिवर्तनों का महत्व काफी स्पष्ट है।

दैनिक, औद्योगिक कंप्यूटिंग अभ्यास की मांगों के लिए छात्रों में तर्कसंगत गणना और समान परिवर्तनों के मजबूत, स्वचालित कौशल के गठन की आवश्यकता होती है। ये कौशल किसी भी कम्प्यूटेशनल कार्य की प्रक्रिया में विकसित होते हैं, हालांकि, विशेष कौशल की आवश्यकता होती है। प्रशिक्षण अभ्यासतेजी से गणना और परिवर्तनों में।

इसलिए, यदि पाठ में मूल लघुगणकीय पहचान का उपयोग करके लघुगणकीय समीकरणों को हल करना शामिल है, तो अभिव्यक्ति के मूल्यों को सरल या गणना करने के लिए पाठ योजना में मौखिक अभ्यास शामिल करना उपयोगी है: . अभ्यास का उद्देश्य हमेशा छात्रों को बताया जाता है। अभ्यास के दौरान, छात्रों को व्यक्तिगत परिवर्तनों, कार्यों को सही ठहराने या पूरी समस्या को हल करने की आवश्यकता हो सकती है, भले ही यह योजनाबद्ध न हो। जहां किसी समस्या को हल करने के विभिन्न तरीके संभव हैं, वहां हमेशा प्रश्न पूछना वांछनीय है: "समस्या को किस तरह हल किया गया?", "समस्या को अलग तरीके से किसने हल किया?"

पहचान और समान परिवर्तन की अवधारणाएं, उन्हें स्पष्ट रूप से कक्षा VI बीजगणित पाठ्यक्रम में पेश किया गया है। समान अभिव्यक्तियों की परिभाषा का व्यावहारिक रूप से दो अभिव्यक्तियों की पहचान को साबित करने के लिए उपयोग नहीं किया जा सकता है, और यह समझने के लिए कि समान परिवर्तनों का सार अभिव्यक्ति में उन क्रियाओं की परिभाषाओं और गुणों को लागू करना है जो अभिव्यक्ति में इंगित किए गए हैं, या जोड़ने में इसके लिए एक व्यंजक जो समान रूप से 0 के बराबर है, या इसे समान रूप से एक के बराबर व्यंजक से गुणा करने पर। लेकिन, इन प्रावधानों में महारत हासिल करने के बाद भी, छात्र अक्सर यह नहीं समझते हैं कि ये परिवर्तन हमें यह कहने की अनुमति क्यों देते हैं कि मूल और परिणामी अभिव्यक्ति समान हैं, अर्थात। चर मानों के किसी भी सिस्टम (सेट) के लिए समान मान लें।

यह सुनिश्चित करना भी महत्वपूर्ण है कि छात्र अच्छी तरह से समझें कि समान परिवर्तनों के ऐसे निष्कर्ष संबंधित क्रियाओं की परिभाषाओं और गुणों के परिणाम हैं।

पिछले वर्षों में संचित समान परिवर्तनों के तंत्र का विस्तार छठी कक्षा में किया जा रहा है। यह विस्तार एक पहचान की शुरूआत के साथ शुरू होता है जो समान आधारों के साथ शक्तियों के उत्पाद की संपत्ति को व्यक्त करता है: जहां, पूर्णांक हैं।

3. गणित कार्यक्रम। स्कूल पाठ्यक्रम "बीजगणित और विश्लेषण की शुरुआत" में, छात्र व्यवस्थित रूप से घातीय और लॉगरिदमिक कार्यों और उनके गुणों का अध्ययन करते हैं, लॉगरिदमिक और घातीय अभिव्यक्तियों के समान परिवर्तन और संबंधित समीकरणों और असमानताओं को हल करने के लिए उनके आवेदन, बुनियादी अवधारणाओं, बयानों से परिचित होते हैं . 11वीं कक्षा में, बीजगणित के पाठ में सप्ताह में 3 घंटे, साल में कुल 102 घंटे लगते हैं। कार्यक्रम के अनुसार घातांक, लघुगणक और शक्ति कार्यों का अध्ययन करने में 36 घंटे लगते हैं। कार्यक्रम में निम्नलिखित मुद्दों पर विचार और अध्ययन शामिल है: एक तर्कसंगत संकेतक के साथ एक डिग्री की अवधारणा। अपरिमेय समीकरणों का हल। एक घातीय कार्य, इसके गुण और ग्राफ। घातीय अभिव्यक्तियों के समान परिवर्तन। घातीय समीकरणों और असमानताओं का समाधान। किसी संख्या का लघुगणक। लघुगणक के मूल गुण। लॉगरिदमिक फ़ंक्शन, इसके गुण और ग्राफ। लघुगणकीय समीकरणों और असमानताओं का समाधान। घातीय फ़ंक्शन का व्युत्पन्न। संख्या और प्राकृतिक लघुगणक। एक शक्ति समारोह का व्युत्पन्न। घातीय और लघुगणक कार्यों के अध्ययन पर अनुभाग का मुख्य उद्देश्य छात्रों को घातीय, लघुगणक और शक्ति कार्यों से परिचित कराना है; छात्रों को घातीय हल करना सिखाएं और लघुगणक समीकरणऔर असमानताएं। वें डिग्री की जड़ की अवधारणा और एक तर्कसंगत घातांक के साथ डिग्री वर्गमूल की अवधारणाओं का एक सामान्यीकरण और एक पूर्णांक घातांक के साथ डिग्री है। छात्रों को इस तथ्य पर ध्यान देना चाहिए कि यहां पर विचार किए गए तर्कसंगत घातांक वाले मूल और डिग्री के गुण उन गुणों के समान हैं जिनका अध्ययन पहले किया जा चुका है। वर्गमूलऔर पूर्णांक घातांक के साथ डिग्री। डिग्री के गुणों और समान परिवर्तनों के लिए कौशल के निर्माण के लिए पर्याप्त समय देना आवश्यक है। डिग्री की अवधारणा के साथ तर्कहीन संकेतकएक दृश्य-सहज आधार पर पेश किया गया। यह सामग्री एक सहायक भूमिका निभाती है और इसका उपयोग घातीय फ़ंक्शन को पेश करते समय किया जाता है। घातीय, लघुगणक और शक्ति कार्यों के गुणों का अध्ययन स्वीकृत के अनुसार बनाया गया है सामान्य योजनासमारोह अनुसंधान। इस मामले में, पैरामीटर मानों के आधार पर गुणों का अवलोकन दिया जाता है। कार्यों के अध्ययन किए गए गुणों के आधार पर घातीय और लघुगणकीय असमानताओं को हल किया जाता है। पाठ्यक्रम की एक विशिष्ट विशेषता छात्रों के ज्ञान का व्यवस्थितकरण और सामान्यीकरण है, बीजगणित के दौरान हासिल किए गए कौशल और क्षमताओं का समेकन और विकास, जो नई सामग्री का अध्ययन करते समय और एक सामान्य दोहराव का संचालन करते समय किया जाता है।
अध्याय 2

§एक। डिग्री की अवधारणा का सामान्यीकरण।

परिभाषा: शुद्ध की th डिग्री की जड़ एक ऐसी संख्या है, जिसका th अंश बराबर होता है।

इस परिभाषा के अनुसार, किसी संख्या की th डिग्री का मूल समीकरण का हल होता है। इस समीकरण के मूलों की संख्या और पर निर्भर करती है। आइए एक समारोह पर विचार करें। जैसा कि ज्ञात है, अंतराल पर यह फ़ंक्शन किसी के लिए बढ़ता है और अंतराल से सभी मान लेता है। मूल प्रमेय के अनुसार, किसी के लिए समीकरण का एक गैर-ऋणात्मक मूल होता है, और इसके अलावा, केवल एक। इसे किसी संख्या की th डिग्री का अंकगणितीय मूल कहा जाता है और इसे निरूपित किया जाता है; संख्या को मूल का सूचकांक कहा जाता है, और संख्या को ही मूलक व्यंजक कहा जाता है। संकेत को एक कट्टरपंथी भी कहा जाता है।

परिभाषा: किसी संख्या की th डिग्री का अंकगणितीय मूल एक गैर-ऋणात्मक संख्या होती है जिसकी th डिग्री होती है।

सम के लिए, फलन सम है। यह इस प्रकार है कि यदि, तो समीकरण, जड़ के अतिरिक्त, भी एक जड़ है। यदि , तो केवल एक ही जड़ है: ; यदि , तो इस समीकरण का कोई मूल नहीं है, क्योंकि किसी भी संख्या की सम घात ऋणात्मक नहीं होती है।

विषम मानों के लिए, फलन पूर्ण संख्या रेखा के अनुदिश बढ़ता है; इसका परिसर सभी वास्तविक संख्याओं का समुच्चय है। मूल प्रमेय को लागू करने पर, हम पाते हैं कि समीकरण में किसी के लिए एक मूल है और, विशेष रूप से, के लिए। किसी भी मान के लिए इस रूट को द्वारा दर्शाया जाता है।

विषम कोटि के मूलों के लिए समानता सत्य है। दरअसल, यानी। संख्या का वां मूल है। लेकिन विषम के लिए ऐसी जड़ अद्वितीय है। फलस्वरूप, ।

टिप्पणी 1: किसी भी वास्तविक के लिए

वें डिग्री के अंकगणितीय जड़ों के प्रसिद्ध गुणों को याद करें।

किसी भी प्राकृतिक, पूर्णांक और किसी भी गैर-ऋणात्मक पूर्णांक और समानता के लिए सत्य हैं:

एक तर्कसंगत घातांक के साथ डिग्री।

व्यंजक को सभी के लिए परिभाषित किया गया है और , उस स्थिति को छोड़कर जब . ऐसी शक्तियों के गुणों को याद करें।

किसी भी संख्या के लिए, और कोई भी पूर्णांक और समानताएं मान्य हैं:

हम यह भी नोट करते हैं कि यदि , तो के लिए और के लिए .. और

यूनिफाइड स्टेट परीक्षा के लिए अध्ययन करने वाले छात्रों के लिए, याकुतस्क में माध्यमिक विद्यालय नंबर 26 में गणित के शिक्षक स्कूल गणित पाठ्यक्रम के सामग्री प्रश्नों (कोडिफायर) की एक सूची का उपयोग करते हैं, जिसके आत्मसात की जाँच 2007 में एकीकृत राज्य परीक्षा उत्तीर्ण करते समय की जाती है। . वैकल्पिक पाठ्यक्रमयूनिफाइड की तैयारी में राज्य परीक्षापूर्व में अर्जित ज्ञान की पुनरावृत्ति, व्यवस्थितकरण और गहनता पर आधारित है। कक्षाएं मुफ्त के रूप में आयोजित की जाती हैं ...

लघुगणक के साथ व्यंजकों को परिवर्तित करते समय सूचीबद्ध समानताएं दाएं से बाएं और बाएं से दाएं दोनों का उपयोग करती हैं।

यह ध्यान देने योग्य है कि गुणों के परिणामों को याद रखना आवश्यक नहीं है: परिवर्तन करते समय, आप लघुगणक और अन्य तथ्यों (उदाहरण के लिए, b≥0 के लिए) के मूल गुणों के साथ प्राप्त कर सकते हैं, जिससे संबंधित परिणाम अनुसरण करते हैं। इस दृष्टिकोण का "दुष्प्रभाव" केवल इतना है कि समाधान थोड़ा लंबा होगा। उदाहरण के लिए, परिणाम के बिना करने के लिए, जो सूत्र द्वारा व्यक्त किया गया है , और केवल लघुगणक के मूल गुणों से शुरू करते हुए, आपको निम्नलिखित रूप के परिवर्तनों की एक श्रृंखला को पूरा करना होगा: .

उपरोक्त सूची से अंतिम संपत्ति के बारे में भी यही कहा जा सकता है, जो सूत्र से मेल खाती है , क्योंकि यह लघुगणक के मूल गुणों से भी अनुसरण करता है। समझने वाली मुख्य बात यह है कि घातांक में एक लघुगणक के साथ एक सकारात्मक संख्या की डिग्री के लिए डिग्री के आधार और लघुगणक के संकेत के तहत संख्या को स्वैप करना हमेशा संभव होता है। निष्पक्षता में, हम ध्यान दें कि इस तरह के परिवर्तनों के कार्यान्वयन से जुड़े उदाहरण व्यवहार में दुर्लभ हैं। हम नीचे कुछ उदाहरण देंगे।

लघुगणक के साथ संख्यात्मक अभिव्यक्तियों को परिवर्तित करना

हमें लघुगणक के गुण याद आ गए, अब यह सीखने का समय है कि व्यंजकों को बदलने के लिए उन्हें कैसे व्यवहार में लाया जाए। संख्यात्मक अभिव्यक्तियों के परिवर्तन के साथ शुरू करना स्वाभाविक है, न कि चर के साथ अभिव्यक्ति, क्योंकि उन पर मूल बातें सीखना अधिक सुविधाजनक और आसान है। तो हम करेंगे, और हम बहुत से शुरू करेंगे सरल उदाहरणलॉगरिदम की वांछित संपत्ति का चयन कैसे करें, यह जानने के लिए, लेकिन हम धीरे-धीरे उदाहरणों को जटिल बना देंगे, उस समय तक जब अंतिम परिणाम प्राप्त करने के लिए कई गुणों को एक पंक्ति में लागू करने की आवश्यकता होगी।

लघुगणक के वांछित गुण का चयन

लॉगरिदम के इतने कम गुण नहीं हैं, और यह स्पष्ट है कि आपको उनमें से उपयुक्त एक को चुनने में सक्षम होने की आवश्यकता है, जो इस विशेष मामले में वांछित परिणाम की ओर ले जाएगा। आमतौर पर लघुगणक के गुणों को व्यक्त करने वाले सूत्रों के बाएँ और दाएँ भागों के प्रकारों के साथ परिवर्तित किए जा रहे लघुगणक या व्यंजक के रूप की तुलना करके ऐसा करना कठिन नहीं है। अगर छोड़ दिया या दाहिना भागसूत्रों में से एक दिए गए लघुगणक या अभिव्यक्ति के साथ मेल खाता है, तो, सबसे अधिक संभावना है, यह वह संपत्ति है जिसका उपयोग परिवर्तन के दौरान किया जाना चाहिए। निम्नलिखित उदाहरण स्पष्ट रूप से इसे प्रदर्शित करते हैं।

आइए लघुगणक की परिभाषा का उपयोग करते हुए व्यंजकों को रूपांतरित करने के उदाहरणों के साथ प्रारंभ करें, जो सूत्र a log a b =b , a>0 , a≠1 , b>0 के संगत है।

उदाहरण।

गणना करें, यदि संभव हो तो: ए) 5 लॉग 5 4, बी) 10 लॉग(1+2 π), सी) , डी) 2 लॉग 2 (−7) , ई) ।

समाधान।

उदाहरण में, अक्षर a) स्पष्ट रूप से संरचना a log a b दिखाता है, जहां a=5 , b=4 । ये संख्याएँ a>0 , a≠1 , b>0 शर्तों को पूरा करती हैं, ताकि आप समानता a log a b =b का सुरक्षित रूप से उपयोग कर सकें। हमारे पास 5 लघुगणक 5 4=4 है।

बी) यहां a=10 , b=1+2 π , शर्तें a>0 , a≠1 , b>0 पूरी होती हैं। इस मामले में, समानता 10 एलजी(1+2 π) = 1+2 होती है।

ग) और इस उदाहरण में हम a log a b , जहां और b=ln15 रूप की एक डिग्री के साथ काम कर रहे हैं। इसलिए .

एक ही रूप a log a b (यहां a=2 , b=−7 ) से संबंधित होने के बावजूद, अक्षर d के अंतर्गत व्यंजक को a log a b =b सूत्र द्वारा परिवर्तित नहीं किया जा सकता है। इसका कारण यह है कि इसका कोई मतलब नहीं है क्योंकि इसमें लघुगणक चिह्न के तहत एक ऋणात्मक संख्या होती है। इसके अलावा, संख्या b=−7 b>0 शर्त को पूरा नहीं करती है, जिससे a log a b =b सूत्र का सहारा लेना असंभव हो जाता है, क्योंकि इसके लिए a>0 , a≠1 , b>0 शर्तों की आवश्यकता होती है। इसलिए, हम मान 2 log 2 (−7) की गणना के बारे में बात नहीं कर सकते। इस मामले में, 2 लॉग 2 (−7) = −7 लिखना एक त्रुटि होगी।

इसी तरह, पत्र ई के तहत उदाहरण में) फॉर्म का समाधान देना असंभव है , चूंकि मूल अभिव्यक्ति का कोई मतलब नहीं है।

उत्तर:

ए) 5 लॉग 5 4 =4, बी) 10 लॉग(1+2 ) = 1+2 π, सी) , d), e) भावों का कोई मतलब नहीं है।

यह अक्सर बदलने के लिए उपयोगी होता है सकारात्मक संख्याघातांक में एक लघुगणक के साथ कुछ सकारात्मक और गैर-एक संख्या की शक्ति के रूप में दर्शाया गया है। यह लघुगणक a log a b =b , a>0 , a≠1 , b>0 की समान परिभाषा पर आधारित है, लेकिन सूत्र को दाएं से बाएं, यानी b=a log a b के रूप में लागू किया जाता है। उदाहरण के लिए, 3=e ln3 या 5=5 log 5 5 ।

आइए व्यंजकों को रूपांतरित करने के लिए लघुगणक के गुणों का उपयोग करने के लिए आगे बढ़ते हैं।

उदाहरण।

व्यंजक का मान ज्ञात कीजिए: a) log −2 1, b) log 1 1, c) log 0 1, d) log 7 1, e) ln1, f) lg1, g) log 3.75 1, h) log 5 7 1.

समाधान।

अक्षरों a), b) और c) के उदाहरणों में, व्यंजक log −2 1 , log 1 1 , log 0 1 दिए गए हैं, जिनका कोई अर्थ नहीं है, क्योंकि लघुगणक के आधार में ऋणात्मक संख्या नहीं होनी चाहिए। , शून्य या एक, क्योंकि हमने केवल धनात्मक और गैर-इकाई आधार के लिए लघुगणक को परिभाषित किया है। इसलिए, उदाहरणों में a) - c) व्यंजक का मान ज्ञात करने का प्रश्न ही नहीं उठता।

अन्य सभी कार्यों में, जाहिर है, लॉगरिदम के आधार में सकारात्मक और गैर-इकाई संख्याएं होती हैं 7, ई, 10, 3.75 और 5 7 क्रमशः, और इकाइयां लॉगरिदम के संकेतों के तहत हर जगह हैं। और हम एकता के लघुगणक के गुण को जानते हैं: किसी भी a>0 , a≠1 के लिए a 1=0 लॉग करें। इस प्रकार, भावों के मान b) - f) शून्य के बराबर हैं।

उत्तर:

ए), बी), सी) अभिव्यक्तियों का कोई मतलब नहीं है, डी) लॉग 7 1 = 0, ई) एलएन 1 = 0, एफ) लॉग 1 = 0, जी) लॉग 3.75 1 = 0, एच) लॉग 5 ई 7 1 = 0।

उदाहरण।

गणना करें: a) , b) lne , c) lg10 , d) लॉग 5 3 −2 (5 π 3 −2), ई) लॉग −3 (−3) , f) लॉग 1 1 ।

समाधान।

यह स्पष्ट है कि हमें आधार के लघुगणक के गुण का उपयोग करना होगा, जो कि a>0 , a≠1 के लिए सूत्र लॉग a = 1 के संगत है। दरअसल, सभी अक्षरों के तहत कार्यों में, लघुगणक के चिह्न के नीचे की संख्या इसके आधार के साथ मेल खाती है। इस प्रकार, मैं तुरंत कहना चाहता हूं कि दिए गए व्यंजकों में से प्रत्येक का मान 1 है। हालांकि, निष्कर्ष पर जल्दी मत करो: अक्षरों के तहत कार्यों में ए) - डी) भावों के मूल्य वास्तव में एक के बराबर हैं, और कार्यों में ई) और एफ) मूल भावों का कोई मतलब नहीं है, इसलिए यह नहीं हो सकता कहा जा सकता है कि इन भावों के मान 1 के बराबर हैं।

उत्तर:

a) , b) lne=1 , c) lg10=1 , d) लॉग 5 π 3 −2 (5 π 3 −2)=1, ई), एफ) भाव समझ में नहीं आता।

उदाहरण।

मान ज्ञात कीजिए: a) log 3 3 11 , b) , c) , d) लॉग −10 (−10) 6 ।

समाधान।

जाहिर है, लॉगरिदम के संकेतों के तहत आधार की कुछ डिग्री होती है। इसके आधार पर, हम समझते हैं कि आधार की घात का गुण यहाँ उपयोगी है: log a p =p, जहाँ a>0, a≠1 और p कोई वास्तविक संख्या है। इसे ध्यान में रखते हुए, हमारे पास निम्नलिखित परिणाम हैं: ए) लॉग 3 3 11 =11, बी) , में) . क्या फॉर्म लॉग -10 (−10) 6 =6 के अक्षर d के तहत उदाहरण के लिए समान समानता लिखना संभव है? नहीं, आप नहीं कर सकते, क्योंकि लॉग −10 (−10) 6 का कोई मतलब नहीं है।

उत्तर:

क) लघुगणक 3 3 11 =11, ख) , में) d) अभिव्यक्ति का कोई मतलब नहीं है।

उदाहरण।

व्यंजक को एक ही आधार में लघुगणक के योग या अंतर के रूप में व्यक्त करें: a) , बी) , सी) लॉग ((−5) (−12)) ।

समाधान।

ए) उत्पाद लॉगरिदम के संकेत के तहत है, और हम उत्पाद लॉग के लॉगरिदम की संपत्ति जानते हैं a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y> 0. हमारे मामले में, लघुगणक के आधार में संख्या और उत्पाद में संख्या सकारात्मक हैं, अर्थात, वे चयनित संपत्ति की शर्तों को पूरा करते हैं, इसलिए, हम इसे सुरक्षित रूप से लागू कर सकते हैं: .

बी) यहां हम भागफल के लघुगणक के गुण का उपयोग करते हैं, जहां a>0 , a≠1 , x>0 , y>0 । हमारे मामले में, लघुगणक का आधार एक सकारात्मक संख्या ई है, अंश और हर π सकारात्मक हैं, जिसका अर्थ है कि वे संपत्ति की शर्तों को पूरा करते हैं, इसलिए हमें चुने हुए सूत्र का उपयोग करने का अधिकार है: .

सी) सबसे पहले, ध्यान दें कि अभिव्यक्ति lg((−5) (−12)) समझ में आता है। लेकिन साथ ही, हमें उत्पाद के लघुगणक के लिए सूत्र लागू करने का अधिकार नहीं है लॉग a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 , क्योंकि संख्याएँ −5 और -12 ऋणात्मक हैं और x>0 , y>0 शर्तों को पूरा नहीं करती हैं। यही है, इस तरह के परिवर्तन को अंजाम देना असंभव है: लॉग((−5)(−12))=लॉग(−5)+लॉग(−12). पर क्या करूँ! ऐसे मामलों में, ऋणात्मक संख्याओं से बचने के लिए मूल व्यंजक को पूर्व-रूपांतरित करने की आवश्यकता होती है। अभिव्यक्तियों के परिवर्तन के समान मामलों के बारे में ऋणात्मक संख्यालघुगणक के संकेत के तहत, हम में से एक में विस्तार से बात करेंगे, लेकिन अभी के लिए हम इस उदाहरण का समाधान देंगे, जो पहले से स्पष्ट है और बिना स्पष्टीकरण के: एलजी((−5)(−12))=lg(5 12)=lg5+lg12.

उत्तर:

एक) , बी) , सी) lg((−5) (−12))=lg5+lg12 ।

उदाहरण।

व्यंजक को सरल कीजिए: क) लघुगणक 3 0.25 + लघुगणक 3 16 + लघुगणक 3 0.5, ख) ।

समाधान।

यहां हमें उत्पाद के लघुगणक के सभी समान गुणों और भागफल के लघुगणक से मदद मिलेगी जो हमने पिछले उदाहरणों में उपयोग किया था, केवल अब हम उन्हें दाएं से बाएं लागू करेंगे। अर्थात्, हम लघुगणक के योग को उत्पाद के लघुगणक में और लघुगणक के अंतर को भागफल के लघुगणक में परिवर्तित करते हैं। हमारे पास है
एक) लॉग 3 0.25+लॉग 3 16+लॉग 3 0.5=लॉग 3 (0.25 16 0.5)=लॉग 3 2.
बी) .

उत्तर:

एक) लॉग 3 0.25+लॉग 3 16+लॉग 3 0.5=लॉग 3 2, बी) .

उदाहरण।

लघुगणक के संकेत के तहत डिग्री से छुटकारा पाएं: ए) लॉग 0.7 5 11, बी) , सी) लॉग 3 (−5) 6।

समाधान।

यह देखना आसान है कि हम log a b p जैसे व्यंजकों के साथ काम कर रहे हैं। लघुगणक का संगत गुण है log a b p =p log a b , जहां a>0 , a≠1 , b>0 , p कोई वास्तविक संख्या है। अर्थात्, शर्तों के तहत a>0 , a≠1 , b>0 डिग्री लॉग a b p के लॉगरिदम से हम उत्पाद p·log a b पर जा सकते हैं। आइए इस परिवर्तन को दिए गए भावों के साथ करें।

ए) इस मामले में a=0.7 , b=5 और p=11 । अतः लघुगणक 0.7 5 11 =11 लघुगणक 0.7 5।

बी) यहां, शर्तें a>0 , a≠1 , b>0 पूरी होती हैं। इसीलिए

c) व्यंजक log 3 (−5) 6 की संरचना समान है log a b p , a=3 , b=−5 , p=6 । लेकिन b के लिए, शर्त b>0 संतुष्ट नहीं है, जिससे सूत्र log a b p =p log a b को लागू करना असंभव हो जाता है। तो आप काम क्यों नहीं करवा सकते? यह संभव है, लेकिन अभिव्यक्ति के प्रारंभिक परिवर्तन की आवश्यकता है, जिसके बारे में हम नीचे शीर्षक के तहत पैराग्राफ में विस्तार से चर्चा करेंगे। समाधान इस प्रकार होगा: लॉग 3 (−5) 6 =लॉग 3 5 6 =6 लॉग 3 5.

उत्तर:

क) लघुगणक 0.7 5 11 =11 लघुगणक 0.7 5 ,
बी)
ग) लघुगणक 3 (−5) 6 =6 लघुगणक 3 5 ।

अक्सर, परिवर्तन करते समय डिग्री के लघुगणक के लिए सूत्र को पी लॉग ए बी \u003d लॉग ए बी पी के रूप में दाएं से बाएं से लागू करना पड़ता है (इसके लिए ए, बी और पी के लिए समान शर्तों की आवश्यकता होती है)। उदाहरण के लिए, 3 ln5=ln5 3 और lg2 log 2 3=log 2 3 lg2 ।

उदाहरण।

ए) लॉग 2 5 के मान की गणना करें यदि यह ज्ञात है कि lg2≈0.3010 और lg5≈0.6990। b) भिन्न को आधार 3 के लघुगणक के रूप में लिखिए।

समाधान।

a) लघुगणक के एक नए आधार में संक्रमण का सूत्र हमें इस लघुगणक को दशमलव लघुगणक के अनुपात के रूप में प्रस्तुत करने की अनुमति देता है, जिसके मान हमें ज्ञात हैं: . यह केवल गणना करने के लिए बनी हुई है, हमारे पास है .

बी) यहां एक नए आधार पर संक्रमण के लिए सूत्र का उपयोग करना और इसे दाएं से बाएं, यानी फॉर्म में लागू करना पर्याप्त है . हम पाते हैं .

उत्तर:

ए) लॉग 2 5≈2.3223, बी) .

इस स्तर पर, हमने लॉगरिदम के मूल गुणों और लघुगणक की परिभाषा का उपयोग करते हुए सरलतम अभिव्यक्तियों के परिवर्तन पर गंभीरता से विचार किया है। इन उदाहरणों में, हमें एक संपत्ति का उपयोग करना था और कुछ नहीं। अब, एक स्पष्ट विवेक के साथ, आप उन उदाहरणों पर आगे बढ़ सकते हैं जिनके परिवर्तन के लिए लघुगणक के कई गुणों और अन्य अतिरिक्त परिवर्तनों के उपयोग की आवश्यकता होती है। हम उनके साथ अगले पैराग्राफ में निपटेंगे। लेकिन इससे पहले, आइए हम संक्षेप में लघुगणक के मूल गुणों से परिणामों के अनुप्रयोग के उदाहरणों पर ध्यान दें।

उदाहरण।

a) लॉगरिदम के चिन्ह के तहत जड़ से छुटकारा पाएं। b) भिन्न को आधार 5 लघुगणक में बदलें। ग) लघुगणक के चिह्न और उसके आधार पर शक्तियों से छुटकारा पाएं। डी) अभिव्यक्ति के मूल्य की गणना करें . e) व्यंजक को आधार 3 से घात से बदलें।

समाधान।

ए) यदि हम डिग्री के लघुगणक के गुण से उपफल को याद करते हैं , तो आप तुरंत उत्तर दे सकते हैं: .

बी) यहां हम सूत्र का उपयोग करते हैं दाएं से बाएं, हमारे पास है .

ग) बी ये मामलासूत्र परिणाम की ओर ले जाता है . हम पाते हैं .

d) और यहाँ यह उस परिणाम को लागू करने के लिए पर्याप्त है जिससे सूत्र मेल खाता है . इसलिए .

ई) लघुगणक की संपत्ति हमें वांछित परिणाम प्राप्त करने की अनुमति देता है: .

उत्तर:

एक) . बी) . में) . जी) . इ) .

लगातार कई गुण लागू करना

लॉगरिदम के गुणों का उपयोग करके अभिव्यक्तियों को बदलने के लिए वास्तविक कार्य आमतौर पर उन कार्यों की तुलना में अधिक जटिल होते हैं जिन्हें हमने पिछले पैराग्राफ में निपटाया था। उनमें, एक नियम के रूप में, परिणाम एक चरण में प्राप्त नहीं होता है, लेकिन समाधान पहले से ही एक के बाद एक संपत्ति के अनुक्रमिक अनुप्रयोग में होता है, साथ में अतिरिक्त समान परिवर्तन, जैसे कि कोष्ठक खोलना, समान शब्दों को कम करना, अंशों को कम करना, आदि। . तो आइए ऐसे उदाहरणों के करीब आते हैं। इसमें कुछ भी जटिल नहीं है, मुख्य बात यह है कि क्रियाओं को करने के क्रम को देखते हुए सावधानीपूर्वक और लगातार कार्य करना है।

उदाहरण।

एक व्यंजक के मान की गणना करें (लॉग 3 15−लॉग 3 5) 7 लॉग 7 5.

समाधान।

भागफल के लघुगणक के गुण द्वारा कोष्ठकों में लघुगणक के अंतर को लघुगणक लॉग 3 (15:5) द्वारा प्रतिस्थापित किया जा सकता है, और फिर इसके मान की गणना करें लॉग 3 (15:5)=log 3 3=1 । और लघुगणक की परिभाषा के अनुसार व्यंजक 7 log 7 5 का मान 5 है। इन परिणामों को मूल व्यंजक में प्रतिस्थापित करने पर, हम प्राप्त करते हैं (लॉग 3 15−लॉग 3 5) 7 लॉग 7 5 =1 5=5.

यहाँ स्पष्टीकरण के बिना एक समाधान है:
(लॉग 3 15−लॉग 3 5) 7 लॉग 7 5 =लॉग 3 (15:5) 5=
= लघुगणक 3 3 5=1 5=5 ।

उत्तर:

(लॉग 3 15−लॉग 3 5) 7 लॉग 7 5 =5.

उदाहरण।

संख्यात्मक व्यंजक log 3 log 2 2 3 −1 का मान क्या है?

समाधान।

आइए पहले लघुगणक को रूपांतरित करें, जो लघुगणक के चिह्न के नीचे है, डिग्री के लघुगणक के सूत्र के अनुसार: लॉग 2 2 3 =3। अतः 3 log 2 2 3 =log 3 3 और फिर 3 3=1 log कीजिये। अतः 3 लघुगणक 2 2 3 −1=1−1=0 लघुगणक करें।

उत्तर:

लघुगणक 3 लघुगणक 2 2 3 −1=0 .

उदाहरण।

अभिव्यक्ति को सरल बनाएं।

समाधान।

लघुगणक के एक नए आधार में बदलने का सूत्र लघुगणक के एक आधार के अनुपात को लघुगणक 3 5 के रूप में प्रदर्शित करने की अनुमति देता है। इस मामले में, मूल अभिव्यक्ति रूप ले लेगी। लघुगणक की परिभाषा के अनुसार 3 लघुगणक 3 5 =5 , अर्थात् , और परिणामी व्यंजक का मान, लघुगणक की समान परिभाषा के आधार पर, दो के बराबर है।

यहां लघु संस्करणसमाधान, जो आमतौर पर दिया जाता है: .

उत्तर:

अगले पैराग्राफ की जानकारी के लिए एक सहज संक्रमण के लिए, आइए भावों पर एक नज़र डालें 5 2+log 5 3 , तथा lg0.01 । उनकी संरचना लघुगणक के किसी भी गुण में फिट नहीं होती है। तो क्या होगा यदि उन्हें लघुगणक के गुणों का उपयोग करके परिवर्तित नहीं किया जा सकता है? यह संभव है यदि आप प्रारंभिक परिवर्तन करते हैं जो लघुगणक के गुणों को लागू करने के लिए इन अभिव्यक्तियों को तैयार करते हैं। इसलिए 5 2+लॉग 5 3 =5 2 5 लॉग 5 3 =25 3=75, और lg0,01=lg10 −2 = −2 । आगे हम विस्तार से समझेंगे कि अभिव्यक्ति की ऐसी तैयारी कैसे की जाती है।

लघुगणक के गुणों को लागू करने के लिए व्यंजक तैयार करना

रूपांतरित व्यंजक में लघुगणक अक्सर सूत्र के बाएँ और दाएँ भागों से संकेतन की संरचना में भिन्न होते हैं जो लघुगणक के गुणों के अनुरूप होते हैं। लेकिन जैसा कि अक्सर होता है, इन अभिव्यक्तियों के परिवर्तन में लघुगणक के गुणों का उपयोग शामिल होता है: उनके उपयोग के लिए केवल प्रारंभिक तैयारी की आवश्यकता होती है। और इस तैयारी में कुछ समान परिवर्तनों को अंजाम देना शामिल है जो लॉगरिदम को गुणों को लागू करने के लिए सुविधाजनक रूप में लाते हैं।

निष्पक्षता में, हम ध्यान दें कि अभिव्यक्तियों का लगभग कोई भी परिवर्तन प्रारंभिक परिवर्तनों के रूप में कार्य कर सकता है, समान शर्तों की सामान्य कमी से लेकर आवेदन तक त्रिकोणमितीय सूत्र. यह समझ में आता है, क्योंकि परिवर्तित अभिव्यक्तियों में कोई भी गणितीय वस्तु हो सकती है: कोष्ठक, मॉड्यूल, अंश, मूल, डिग्री, आदि। इस प्रकार, लघुगणक के गुणों से अधिक लाभ के लिए किसी भी आवश्यक परिवर्तन को करने के लिए तैयार रहना चाहिए।

आइए तुरंत कहें कि इस खंड में हम उन सभी कल्पनीय प्रारंभिक परिवर्तनों को वर्गीकृत और विश्लेषण करने का कार्य निर्धारित नहीं करते हैं जो हमें भविष्य में लॉगरिदम के गुणों या लॉगरिदम की परिभाषा को लागू करने की अनुमति देते हैं। यहां हम उनमें से केवल चार पर ध्यान केंद्रित करेंगे, जो सबसे अधिक विशिष्ट हैं और व्यवहार में सबसे अधिक बार सामने आते हैं।

और अब उनमें से प्रत्येक के बारे में विस्तार से, जिसके बाद, हमारे विषय के ढांचे के भीतर, यह केवल लघुगणक के संकेतों के तहत चर के साथ अभिव्यक्तियों के परिवर्तन से निपटने के लिए बनी हुई है।

लघुगणक के संकेत के तहत और उसके आधार में शक्तियों का चयन

आइए एक उदाहरण के साथ तुरंत शुरू करें। आइए एक लघुगणक प्राप्त करें। जाहिर है, इस रूप में, इसकी संरचना लघुगणक के गुणों के उपयोग के अनुकूल नहीं है। क्या इसे सरल बनाने के लिए किसी तरह इस अभिव्यक्ति को बदलना संभव है, या इसके मूल्य की बेहतर गणना करना भी संभव है? इस प्रश्न का उत्तर देने के लिए, आइए हमारे उदाहरण के संदर्भ में संख्या 81 और 1/9 पर करीब से नज़र डालें। यहां यह देखना आसान है कि इन संख्याओं को 3 की घात के रूप में दर्शाया जा सकता है, वास्तव में, 81=3 4 और 1/9=3 −2। इस मामले में, मूल लघुगणक को रूप में प्रस्तुत किया जाता है और सूत्र को लागू करना संभव हो जाता है . इसलिए, .

विश्लेषण किए गए उदाहरण का विश्लेषण निम्नलिखित विचार को जन्म देता है: यदि संभव हो, तो आप डिग्री या उसके परिणाम के लॉगरिदम की संपत्ति को लागू करने के लिए लॉगरिदम के संकेत के तहत और उसके आधार पर डिग्री को हाइलाइट करने का प्रयास कर सकते हैं। यह केवल यह पता लगाना बाकी है कि इन डिग्रियों को कैसे अलग किया जाए। हम इस मुद्दे पर कुछ सिफारिशें देंगे।

कभी-कभी यह बिल्कुल स्पष्ट होता है कि लघुगणक के चिह्न के नीचे की संख्या और / या इसके आधार में कुछ पूर्णांक शक्ति का प्रतिनिधित्व करता है, जैसा कि ऊपर चर्चा किए गए उदाहरण में है। लगभग लगातार आपको दो की शक्तियों से निपटना पड़ता है, जो अच्छी तरह से परिचित हैं: 4=2 2 , 8=2 3 , 16=2 4 , 32=2 5 , 64=2 6 , 128=2 7, 256=2 8 , 512= 2 9 , 1024=2 10। ट्रिपल की डिग्री के बारे में भी यही कहा जा सकता है: 9=3 2 , 27=3 3 , 81=3 4 , 243=3 5 , ... सामान्य तौर पर, यह चोट नहीं करता है अगर वहाँ है डिग्री तालिका प्राकृतिक संख्या दस के भीतर। दस, सौ, हजार आदि की पूर्णांक घातों के साथ कार्य करना भी कठिन नहीं है।

उदाहरण।

मान परिकलित करें या व्यंजक को सरल करें: a) log 6 216 , b) , c) log 0.000001 0.001 ।

समाधान।

a) स्पष्ट रूप से, 216=6 3 , इसलिए log 6 216=log 6 6 3 =3 ।

b) प्राकृत संख्याओं की घातों की तालिका हमें संख्या 343 और 1/243 को क्रमशः 7 3 और 3 −4 की घातों के रूप में निरूपित करने की अनुमति देती है। इसलिए संभव है अगला परिवर्तनदिया गया लघुगणक:

ग) चूंकि 0.000001=10 −6 और 0.001=10 −3, तो लॉग 0.000001 0.001=लॉग 10 −6 10 −3 =(−3)/(−6)=1/2.

उत्तर:

क) लघुगणक 6 216=3, ख) , सी) लॉग 0.000001 0.001=1/2।

अधिक जटिल मामलों में, संख्याओं की शक्तियों को उजागर करने के लिए, आपको इसका सहारा लेना होगा।

उदाहरण।

व्यंजक को सरल रूप में बदलें log 3 648 log 2 3 .

समाधान।

आइए देखें कि संख्या 648 का विस्तार क्या है प्रधान कारण:

अर्थात्, 648=2 3 3 4 । इस तरह, लॉग 3 648 लॉग 2 3=लॉग 3 (2 3 3 4) लॉग 2 3.

अब हम उत्पाद के लघुगणक को लघुगणक के योग में परिवर्तित करते हैं, जिसके बाद हम डिग्री के लघुगणक के गुण लागू करते हैं:
लॉग 3 (2 3 3 4) लॉग 2 3=(लॉग 3 2 3 + लॉग 3 3 4) लॉग 2 3=
=(3 लघुगणक 3 2+4) लघुगणक 2 3 .

डिग्री के लघुगणक के गुण के परिणाम के आधार पर, जो सूत्र से मेल खाती है , उत्पाद log32 log23 उत्पाद है, और इसे एक के बराबर माना जाता है। इसे ध्यान में रखते हुए, हम प्राप्त करते हैं 3 लघुगणक 3 2 लघुगणक 2 3+4 लघुगणक 2 3=3 1+4 लघुगणक 2 3=3+4 लघुगणक 2 3.

उत्तर:

लघुगणक 3 648 लघुगणक 2 3=3+4 लघुगणक 2 3.

अक्सर, लघुगणक के चिह्न के तहत और उसके आधार में अभिव्यक्ति कुछ संख्याओं की जड़ों और / या शक्तियों के उत्पाद या अनुपात होते हैं, उदाहरण के लिए, . इसी तरह के भावों को एक डिग्री के रूप में दर्शाया जा सकता है। ऐसा करने के लिए, जड़ों से डिग्री तक संक्रमण किया जाता है, और लागू किया जाता है। ये परिवर्तन आपको लघुगणक के चिह्न के तहत और उसके आधार में डिग्री का चयन करने की अनुमति देते हैं, और फिर लघुगणक के गुणों को लागू करते हैं।

उदाहरण।

गणना करें: ए) , बी)।

समाधान।

ए) लॉगरिदम के आधार में अभिव्यक्ति समान आधार वाली शक्तियों का उत्पाद है, हमारे पास शक्तियों की संबंधित संपत्ति द्वारा 5 2 5 −0.5 5 −1 =5 2−0.5−1 =5 0.5.

अब हम अंश को लघुगणक के चिह्न के तहत परिवर्तित करते हैं: आइए मूल से डिग्री तक चलते हैं, जिसके बाद हम समान आधारों के साथ डिग्री के अनुपात की संपत्ति का उपयोग करेंगे: .

यह मूल अभिव्यक्ति में प्राप्त परिणामों को प्रतिस्थापित करने के लिए बनी हुई है, सूत्र का उपयोग करें और परिवर्तन समाप्त करें:

ख) चूंकि 729=3 6 , और 1/9=3 −2 , मूल व्यंजक को इस रूप में फिर से लिखा जा सकता है।

इसके बाद, घातांक के मूल के गुण को लागू करें, मूल से घातांक तक जाएँ, और लघुगणक के आधार को घात में बदलने के लिए घातों के अनुपात गुण का उपयोग करें: .

अंतिम परिणाम को ध्यान में रखते हुए, हमारे पास है .

उत्तर:

एक) , बी)।

यह स्पष्ट है कि सामान्य स्थिति में, लघुगणक के संकेत के तहत और उसके आधार में शक्ति प्राप्त करने के लिए, विभिन्न अभिव्यक्तियों के विभिन्न परिवर्तनों की आवश्यकता हो सकती है। आइए एक दो उदाहरण दें।

उदाहरण।

अभिव्यक्ति का मूल्य क्या है: ए) , बी) .

समाधान।

इसके अलावा, हम देखते हैं कि दिए गए व्यंजक का रूप log A B p है, जहाँ A=2 , B=x+1 और p=4 । हमने डिग्री लॉग ए बी पी \u003d पी लॉग ए बी के लॉगरिदम की संपत्ति के अनुसार इस तरह के संख्यात्मक अभिव्यक्तियों को बदल दिया है, इसलिए, किसी दिए गए अभिव्यक्ति के साथ, मैं वही करना चाहता हूं, और लॉग 2 (x + 1) 4 से जाना चाहता हूं 4 लॉग 2 (x + 1) तक। और अब हम मूल व्यंजक के मान और रूपांतरण के बाद प्राप्त व्यंजक की गणना करते हैं, उदाहरण के लिए, x=−2 के साथ। हमारे पास लघुगणक 2 (−2+1) 4 =log 2 1=0 , और . है 4 लघुगणक 2 (−2+1)=4 लघुगणक 2 (−1)- अर्थहीन अभिव्यक्ति। यह एक वैध सवाल उठाता है: "हमने क्या गलत किया"?

और इसका कारण इस प्रकार है: हमने रूपांतरण लॉग 2 (x+1) 4 =4 लॉग 2 (x+1) किया, सूत्र के आधार पर लॉग a b p =p log a b , लेकिन हमें केवल इस सूत्र को लागू करने का अधिकार है अगर शर्तें a >0 , a≠1 , b>0 , p - कोई वास्तविक संख्या। अर्थात्, हमने जो परिवर्तन किया है वह तब होता है जब x+1>0 , जो समान x>−1 है (A और p के लिए, शर्तें पूरी होती हैं)। हालांकि, हमारे मामले में, मूल व्यंजक के लिए चर x के ODZ में न केवल अंतराल x> −1 होता है, बल्कि अंतराल x का भी होता है।<−1 . Но для x<−1 мы не имели права осуществлять преобразование по выбранной формуле.

ओडीजेड को ध्यान में रखने की जरूरत

आइए हम अभिव्यक्ति लॉग 2 (x+1) 4 के परिवर्तन का विश्लेषण करना जारी रखें, और अब देखते हैं कि अभिव्यक्ति 4 लॉग 2 (x+1) को पास करते समय ओडीजेड का क्या होता है। पिछले पैराग्राफ में, हमें मूल व्यंजक का ODZ मिला - यह समुच्चय (−∞, −1)∪(−1, +∞) है। अब आइए व्यंजक 4 log 2 (x+1) के लिए चर x के स्वीकार्य मानों का क्षेत्रफल ज्ञात करें। यह शर्त x+1>0 द्वारा निर्धारित किया जाता है, जो समुच्चय (−1, +∞) से मेल खाती है। यह स्पष्ट है कि लॉग 2 (x+1) 4 से 4·लॉग 2 (x+1) पर जाने पर, स्वीकार्य मानों की सीमा कम हो जाती है। और हम उन सुधारों से बचने के लिए सहमत हुए जो ओडीजेड को संकुचित करते हैं, क्योंकि इससे विभिन्न नकारात्मक परिणाम हो सकते हैं।

यहां यह अपने लिए ध्यान देने योग्य है कि परिवर्तन के प्रत्येक चरण में ODZ को नियंत्रित करना उपयोगी है और इसे संकीर्ण नहीं होने देना है। और अगर अचानक परिवर्तन के किसी चरण में ODZ का संकुचन हुआ, तो यह बहुत ध्यान से देखने योग्य है कि क्या यह परिवर्तन अनुमेय है और क्या हमें इसे करने का अधिकार है।

निष्पक्षता में, हम कहते हैं कि व्यवहार में हमें आमतौर पर उन अभिव्यक्तियों के साथ काम करना पड़ता है जिनमें चर का ODZ ऐसा होता है कि यह हमें पहले से ही ज्ञात रूप में, बाएं से दाएं और दोनों से, प्रतिबंधों के बिना लघुगणक के गुणों का उपयोग करने की अनुमति देता है। परिवर्तन करते समय दाएं से बाएं। आप जल्दी से इसके अभ्यस्त हो जाते हैं, और आप परिवर्तनों को यांत्रिक रूप से करना शुरू कर देते हैं, बिना यह सोचे कि क्या उन्हें पूरा करना संभव है। और ऐसे क्षणों में, जैसा कि भाग्य के पास होता है, अधिक जटिल उदाहरण सामने आते हैं, जिसमें लघुगणक के गुणों का गलत अनुप्रयोग त्रुटियों की ओर जाता है। इसलिए आपको हमेशा सतर्क रहने की जरूरत है, और सुनिश्चित करें कि ODZ की कोई संकीर्णता नहीं है।

लॉगरिदम के गुणों के आधार पर मुख्य परिवर्तनों को अलग से उजागर करने में कोई दिक्कत नहीं होती है, जिसे बहुत सावधानी से किया जाना चाहिए, जिससे ओडीजेड का संकुचन हो सकता है, और परिणामस्वरूप, त्रुटियां हो सकती हैं:

लघुगणक के गुणों के अनुसार अभिव्यक्तियों के कुछ परिवर्तन भी विपरीत हो सकते हैं - ODZ का विस्तार। उदाहरण के लिए, 4 लॉग 2 (x+1) से लॉग 2 (x+1) 4 पर जाने से ODZ सेट (−1, +∞) से (−∞, −1)∪(−1, +∞) तक बढ़ जाता है ) . यदि आप मूल अभिव्यक्ति के लिए ODZ के भीतर रहते हैं तो ऐसे परिवर्तन होते हैं। तो परिवर्तन ने अभी उल्लेख किया है 4 लॉग 2 (x+1)=log 2 (x+1) 4 ओडीजेड चर x पर मूल अभिव्यक्ति 4 लॉग 2 (x+1) के लिए होता है, अर्थात, जब x+1> 0 , जो (−1, +∞) के समान है।

अब जब हमने उन बारीकियों पर चर्चा कर ली है, जिन पर आपको ध्यान देने की आवश्यकता है, जब लॉगरिदम के गुणों का उपयोग करके चर के साथ अभिव्यक्तियों को परिवर्तित किया जाता है, तो यह पता लगाना बाकी है कि इन रूपांतरणों को सही तरीके से कैसे किया जाना चाहिए।

एक्स+2>0। क्या यह हमारे मामले में काम करता है? इस प्रश्न का उत्तर देने के लिए, आइए x चर के DPV पर एक नज़र डालते हैं। यह असमानताओं की प्रणाली द्वारा निर्धारित किया जाता है , जो शर्त के बराबर है x+2>0 (यदि आवश्यक हो, तो लेख देखें असमानताओं की प्रणालियों का समाधान) इस प्रकार, हम डिग्री के लघुगणक की संपत्ति को सुरक्षित रूप से लागू कर सकते हैं।

हमारे पास है
3 लॉग(x+2) 7 −log(x+2)−5 लॉग(x+2) 4 =
=3 7 लॉग(x+2)−log(x+2)−5 4 लॉग(x+2)=
=21 लॉग(x+2)−लॉग(x+2)−20 लॉग(x+2)=
=(21−1−20)lg(x+2)=0 ।

आप अलग तरह से कार्य कर सकते हैं, क्योंकि ODZ आपको ऐसा करने की अनुमति देता है, उदाहरण के लिए इस तरह:

उत्तर:

3 लॉग(x+2) 7 −log(x+2)−5 लॉग(x+2) 4 =0.

और जब ODZ पर लॉगरिदम के गुणों से जुड़ी शर्तें पूरी नहीं होती हैं तो क्या करें? हम इससे उदाहरणों के साथ निपटेंगे।

आइए हम व्यंजक lg(x+2) 4 −lg(x+2) 2 को सरल बनाएं। इस अभिव्यक्ति का परिवर्तन, पिछले उदाहरण से अभिव्यक्ति के विपरीत, डिग्री के लघुगणक की संपत्ति के मुक्त उपयोग की अनुमति नहीं देता है। क्यों? इस मामले में चर x का ODZ दो अंतरालों x>−2 और x . का मिलन है<−2 . При x>-2 हम डिग्री के लघुगणक की संपत्ति को सुरक्षित रूप से लागू कर सकते हैं और ऊपर दिए गए उदाहरण के अनुसार आगे बढ़ सकते हैं: log(x+2) 4 −log(x+2) 2 =4 log(x+2)−2 log(x+2)=2 log(x+2). लेकिन ODZ में एक और अंतराल x+2 . है<0 , для которого последнее преобразование будет некорректно. Что же делать при x+2<0 ? В подобных случаях на помощь приходит . Определение модуля позволяет выражение x+2 при x+2<0 представить как −|x+2| . Тогда при x+2<0 от lg(x+2) 4 −lg(x+2) 2 переходим к लॉग(−|x+2|) 4 −log(−|x+2|) 2और आगे, lg|x+2| . के शक्ति गुणों के कारण 4−एलजी|x+2| 2. परिणामी अभिव्यक्ति को डिग्री के लघुगणक की संपत्ति के अनुसार रूपांतरित किया जा सकता है, क्योंकि |x+2|>0 चर के किसी भी मान के लिए। हमारे पास है लॉग|एक्स+2| 4−एलजी|x+2| 2 =4 लॉग|x+2|−2 लॉग|x+2|=2 लॉग|x+2|. अब आप मॉड्यूल से छुटकारा पा सकते हैं, क्योंकि इसने अपना काम कर दिया है। चूँकि हम x+2 . पर रूपांतरित हो रहे हैं<0 , то 2·lg|x+2|=2·lg(−(x+2)) . Итак, можно считать, что мы справились с поставленной задачей. Ответ: . Полученный результат можно записать компактно с использованием модуля как .

आइए मॉड्यूल के साथ काम करने को परिचित बनाने के लिए एक और उदाहरण पर विचार करें। आइए हम अभिव्यक्ति से कल्पना करें रैखिक द्विपद x−1 , x−2 और x−3 के लघुगणक के योग और अंतर को पास करें। सबसे पहले हम ODZ पाते हैं:

अंतराल (3, +∞) पर, x−1, x−2 और x−3 व्यंजकों के मान सकारात्मक हैं, इसलिए हम योग और अंतर के लघुगणक के गुणों को सुरक्षित रूप से लागू कर सकते हैं:

और अंतराल (1, 2) पर, व्यंजक x−1 के मान धनात्मक हैं, और व्यंजकों x−2 और x−3 के मान ऋणात्मक हैं। इसलिए, विचाराधीन अंतराल पर, हम मॉड्यूलो का उपयोग करके −|x−2| के रूप में x−2 और x−3 का प्रतिनिधित्व करते हैं। और −|x−3| क्रमश। जिसमें

अब हम गुणनफल और भागफल के लघुगणक के गुणों को लागू कर सकते हैं, क्योंकि माना अंतराल (1, 2) पर x−1 , |x−2| और |x−3| - सकारात्मक।

हमारे पास है

प्राप्त परिणामों को जोड़ा जा सकता है:

सामान्य तौर पर, समान तर्क उत्पाद, अनुपात और डिग्री के लघुगणक के सूत्रों के आधार पर, तीन व्यावहारिक रूप से उपयोगी परिणाम प्राप्त करने की अनुमति देता है जो उपयोग करने के लिए काफी सुविधाजनक हैं:

लॉग a (X·Y) के रूप के दो स्वेच्छिक व्यंजकों X और Y के गुणनफल का लघुगणक लघुगणक के योग द्वारा प्रतिस्थापित किया जा सकता है log a |X|+log a |Y| , a>0 , a≠1 ।
विशेष लघुगणक लॉग a (X:Y) को लघुगणक लॉग a |X|−log a |Y| के अंतर से बदला जा सकता है। , a>0 , a≠1 , X और Y मनमाना व्यंजक हैं।
कुछ व्यंजक B के लघुगणक से लॉग a B p के सम घात p तक, व्यंजक p log a |B| , जहां a>0 , a≠1 , p एक सम संख्या है और B एक मनमाना व्यंजक है।

इसी तरह के परिणाम दिए गए हैं, उदाहरण के लिए, एम। आई। स्कैनवी द्वारा संपादित विश्वविद्यालयों के आवेदकों के लिए गणित में समस्याओं के संग्रह में घातीय और लॉगरिदमिक समीकरणों को हल करने के निर्देश में।

उदाहरण।

व्यंजक को सरल कीजिए .

समाधान।

डिग्री, योग और अंतर के लघुगणक के गुणों को लागू करना अच्छा होगा। लेकिन क्या हम इसे यहाँ कर सकते हैं? इस प्रश्न का उत्तर देने के लिए, हमें ODZ को जानना होगा।

आइए इसे परिभाषित करें:

यह बिल्कुल स्पष्ट है कि चर x के संभावित मानों की सीमा पर x+4 , x−2 और (x+4) 13 व्यंजक सकारात्मक और नकारात्मक दोनों मान ले सकते हैं। इसलिए हमें मॉड्यूल के जरिए काम करना होगा।