Използването на производното в различни сфери на дейност. Интересна производна Целите на тази работа: Да се разгледа използването на производната в различни науки Да се запознаят с учени, които са изучавали производната на функция. Силата е производната на работата при изместване.

Министерство на образованието Саратовска област

Държавен автономен професионалист образователна институцияСаратовска област "Енгелс Политехника"

ПРИЛОЖЕНИЕ НА ПРОИЗВОДНАТА В РАЗЛИЧНИ ОБЛАСТИ НА НАУКАТА

Изпълнено: Саркулова Нургуля Сергеевна

студент от група КШИ-216/15

(Дизайн, моделиране и

технология на шиене)

научен съветник:

Вербицкая Елена Вячеславовна

учител по математика GAPOU SO

"Енгелс политехника"

2016

Въведение

Ролята на математиката в различни области на естествените науки е много голяма. Нищо чудно, че казват„Математиката е кралицата на науките, нейната физика дясна ръка, химията остана.

Предмет на изследване е производното.

Водеща цел е да се покаже значението на производната не само в математиката, но и в други науки, нейното значение в съвременния живот.

Диференциалното смятане е описание на света около нас, направено на математически език. Производната ни помага успешно да решаваме не само задачи по математика, но и практически задачи в различни области на науката и техниката.

Производната на функция се използва навсякъде, където има неравномерно протичане на процеса: това е неравномерно механично движение, променлив ток, химични реакции и радиоактивно разпаданевещества и др.

Ключови и тематични въпроси на това есе:

1. Историята на произхода на производното.

2. Защо да изучаваме производни на функции?

3. Къде се използват деривати?

4. Приложение на производните във физиката, химията, биологията и други науки.

5. Изводи

Реших да напиша статия на тема "Приложение на производната в различни области на науката", защото смятам, че тази тема е много интересна, полезна и актуална.

В работата си ще говоря за приложението на диференциацията в различни области на науката, като химия, физика, биология, география и др. В крайна сметка всички науки са неразривно свързани, което се вижда много ясно в примера на темата обмислям.

Приложение на производната в различни области на науката

От курса по алгебра в гимназията вече знаем товапроизводна е границата на отношението на нарастването на функцията към нарастването на нейния аргумент, тъй като нарастването на аргумента клони към нула, ако такова ограничение съществува.

Действието за намиране на производна се нарича нейно диференциране, а функция, която има производна в точка x, се нарича диференцируема в тази точка. Функция, която е диференцируема във всяка точка на интервал, се нарича диференцируема на този интервал.

Честта да открие основните закони на математическия анализ принадлежи на английски физики математикът Исак Нютон и немският математик, физик, философ Лайбниц.

Нютон въвежда понятието производна, изучавайки законите на механиката, като по този начин разкрива нейното механично значение.

Физическото значение на производната: производната на функцияг= f(х) в точката х 0 е скоростта на промяна на функциятаf(х) в точката х 0 .

Лайбниц стига до концепцията за производна чрез решаване на проблема за начертаване на допирателна към производна линия, като по този начин я обяснява геометричен смисъл.

Геометричният смисъл на производната е, че производната функционира в точках 0 равен на наклона на допирателната към графиката на функцията, начертана в точката с абсцисатах 0 .

Терминът производна и съвременна нотацияг" , f„Въведено от J. Lagrange през 1797г.

Руски математикПрез 19 век Панфути Львович Чебишев казва, че „от особено значение са онези методи на науката, които ни позволяват да разрешим проблем, общ за цялата практическа човешка дейност, например как да се разпореждаме със средствата си, за да постигнем най-голяма полза“.

Представители на различни специалности трябва да се справят с такива задачи в наше време:

Инженерите по процеси се опитват да организират производството по такъв начин, че да се произвеждат възможно най-много продукти;

Дизайнерите се опитват да разработят устройство за космически корабтака че масата на устройството да е най-малка;

Икономистите се опитват да планират връзките между завода и източниците на суровини по такъв начин, че транспортните разходи да бъдат минимални.

Когато изучават всяка тема, учениците имат въпрос: „Защо имаме нужда от това?“ Ако отговорът задоволи любопитството, тогава можем да говорим за интерес на учениците. Отговорът на темата "Производна" може да бъде получен, като се знае къде се използват производни на функции.

За да отговорим на този въпрос, можем да изброим някои дисциплини и техните раздели, в които се използват производни.

Производна в алгебрата:

1. Допирателна към графиката на функцията

Графика на допирателна към функцияе, диференцируеми при xотносно , е права, минаваща през точката (xотносно ; f(х о )) и с наклонf′(x o ).

y= f(x o ) + f′(x o ) (x - x o )

2. Търсене на интервали на нарастващи и намаляващи функции

функцияy=f(x) нараства през интервалах , ако има такива инеравенството. С други думи, по-голяма стойност на аргумента съответства на по-голяма стойност на функцията.

функцияy=f(x) намалява през интервалах , ако има такива инеравенството. С други думи, по-голяма стойност на аргумента съответства на по-малка стойност на функцията.

3. Намиране на точки на екстремум на функция

точка Нареченмаксимална точка функцииy=f(x) ако за всичких . Извиква се стойността на функцията в максималната точкамаксимална функция и обозначават.

точка Нареченминимална точка функцииy=f(x) ако за всичких от съседството си неравенството. Извиква се стойността на функцията в минималната точкафункционален минимум и обозначават.

Под съседство на точка разберете интервала, където е достатъчно малко положително число.

Извикват се минималните и максималните точкиекстремни точки , и се извикват стойностите на функцията, съответстващи на екстремалните точкиекстремуми на функцията .

4. Търсене на интервали на изпъкналост и вдлъбнатост на функция

Функционална графика, е на този интервализпъкнал , лежи не по-високо от която и да е от неговите допирателни (фиг. 1).

Функционална графика, диференцируеми на интервала, е на този интервалвдлъбнат , ако графиката на тази функция е в интервала лежи не по-ниско от която и да е от неговите допирателни (фиг. 2).

Инфлексната точка на графиката на функцията се нарича точката, разделяща интервалите на изпъкналост и вдлъбнатост.

5. Намиране на инфлексните точки на функция

Производна във физиката:

1. Скоростта като производна на пътя

2. Ускорението като производна на скоросттаа =

3. Скорост на разпад радиоактивни елементи 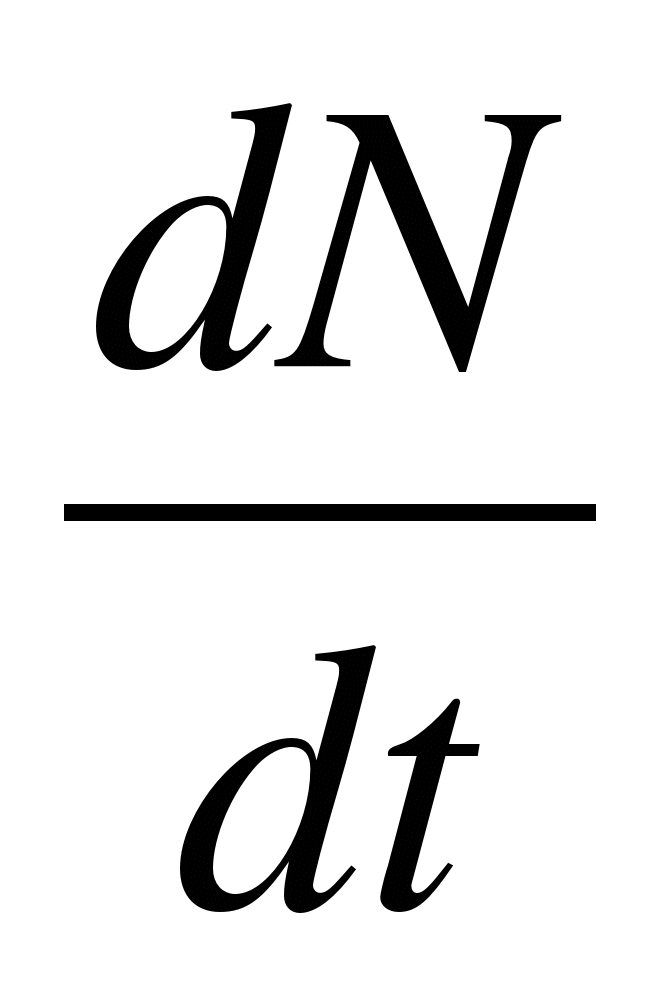= - λN

А също и във физиката, производната се използва за изчисляване:

Скорости материална точка

Моментната скорост като физически смисъл на производната

Незабавна стойност AC захранване

Моментна стойност на ЕМП на електромагнитната индукция

Максимална сила

Производно в химията:

А в химията диференциалното смятане намери широко приложение за конструиране математически моделихимични реакции и последващо описание на техните свойства.

Производната в химията се използва за определяне на много важно нещо - скоростта химическа реакция, един от решаващите фактори, които трябва да се вземат предвид в много области на научната и промишлена дейност. V(t) = p'(t)

Количество

в-ва наведнъж T 0

p = p(t 0 )

функция

Времеви интервал

∆t = t– t 0

Увеличаване на аргумента

Промяна в количеството

∆p=p(t 0 + ∆t) – p(t 0 )

Увеличаване на функцията

Средна скорост на химична реакция

∆p/∆t

Съотношение на увеличението на функцията към увеличението на аргумента

Производно в биологията:

Популацията е съвкупност от индивиди от даден вид, заемащи определена част от територията в рамките на ареала на вида, свободно кръстосващи се помежду си и частично или напълно изолирани от други популации, а също така е елементарна единица на еволюцията .

P \u003d x‘ (t)

Производна в географията:

1. Някои значения в сеизмографията

2. Характеристики електромагнитно полеземя

3. Радиоактивност на ядрени геофизични параметри

4. Много значения в икономическата география

5. Изведете формула за изчисляване на населението на територията в момент t.

y'= към y

Идеята на социологическия модел на Томас Малтус е, че нарастването на населението е пропорционално на населението в даден момент от t до N(t).Моделът на Малтус работи добре за описание на населението на САЩ от 1790 до 1860 г. Този модел вече не е валиден в повечето държави.

Производна в електротехниката:

В домовете ни, в транспорта, във фабриките: електрическият ток работи навсякъде. Под електрически ток се разбира насоченото движение на свободни електрически заредени частици.

Количествена характеристика електрически токе силата на тока.

В електрическа верига електрически зарядсе променя във времето по закона q=q (t). Токът I е производната на заряда q спрямо времето.

В електротехниката се използва главно AC работа.

Електрическият ток, който се променя с времето, се нарича променлив ток. AC веригата може да съдържа различни елементи: нагреватели, намотки, кондензатори.

Производството на променлив електрически ток се основава на закона за електромагнитната индукция, формулировката на който съдържа производната на магнитния поток.

Производна в икономиката:

Икономиката е основата на живота, а диференциалното смятане, апарат за икономически анализ, заема важно място в нея. Основната задача на икономическия анализ е да изследва връзките на икономическите величини под формата на функции.

Производната в икономиката решава важни въпроси:

1. В каква посока ще се променят доходите на държавата с увеличаване на данъците или с въвеждането на мита?

2. Приходите на компанията ще се увеличат или намалят с увеличаване на цената на нейните продукти?

За да се решат тези въпроси, е необходимо да се конструират функциите на свързване на входните променливи, които след това се изучават с методите на диференциалното смятане.

Също така, използвайки екстремума на функцията (производна) в икономиката, можете да намерите най-високата производителност на труда, максималната печалба, максималната продукция и минималните разходи.

ЗАКЛЮЧЕНИЕ: производната се използва успешно при решаването на различни приложни проблеми в науката, технологиите и живота

Както може да се види от горното, използването на производната на функция е много разнообразно и не само в изучаването на математика, но и в други дисциплини. Следователно можем да заключим, че изучаването на темата: „Производна на функция“ ще има своето приложение и в други теми и предмети.

Бяхме убедени в важността на изучаването на темата „Производна“, нейната роля в изучаването на процесите на науката и технологиите, възможността за проектиране съгл. реални събитияматематически модели и решаване на важни проблеми.

“Музиката може да повдигне или успокои душата,
Рисуването е приятно за окото,
Поезия - за събуждане на чувства,
Философия - да задоволи нуждите на ума,
Инженерството е да подобри материалната страна на живота на хората,
НОматематиката може да постигне всички тези цели.

Така каза американският математикМорис Клайн.

Библиография:

1. Богомолов Н.В., Самойленко И.И. Математика. - М.: Юрайт, 2015.

2. В. П. Григориев и Ю. А. Дубински, Елементи на висшата математика. - М.: Академия, 2014.

3. Баврин И.И. Основи на висшата математика. - М.: висше училище, 2013.

4. Богомолов Н.В. Практически уроци по математика. - М.: Висше училище, 2013.

5. Богомолов Н.В. Сборник задачи по математика. - М.: Дропла, 2013.

6. Рибников К.А. История на математиката, Издателство на Московския университет, М, 1960 г.

7. Виноградов Ю.Н., Гомола А.И., Потапов В.И., Соколова Е.В. – М.:Издателски център "Академия", 2010г

8 . Башмаков M.I. Математика: алгебра и началото на математическия анализ, геометрия. - М.: Издателски център "Академия", 2016 г

Периодични източници:

Вестници и списания: "Математика", " Публичен урок»

Използване на интернет ресурси, цифрови библиотеки:

www:egetutor.ru

matematika-na5.norod.ru

FGOU SPO

Новосибирск земеделски техникум

абстрактно

по дисциплина "математика"

"Приложение на производната в науката и технологиите"

С. Раздолное 2008г

Въведение

1. Теоретична част

1.1 Проблеми, водещи до концепцията за производна

1.2 Производна дефиниция

1.3 Общо правило за намиране на производната

1.4 Геометричен смисъл на производната

1.5 Механично значение на производната

1.6 Производна от втори ред и нейното механично значение

1.7 Определение и геометричен смисъл на диференциала

2. Изследване на функции с помощта на производната

Заключение

Литература

Въведение

В първата глава на моето есе ще говорим за концепцията за производна, правилата за нейното приложение, за геометричните и физически смисълпроизводна. Във втората глава на моето есе ще говорим за използването на производната в науката и технологиите и за решаването на проблеми в тази област.

1. Теоретична част

1.1 Проблеми, водещи до концепцията за производна

При изучаването на определени процеси и явления често възниква проблемът с определянето на скоростта на тези процеси. Неговото решение води до концепцията за производна, която е основната концепция на диференциалното смятане.

Методът на диференциалното смятане е създаден през 17-ти и 18-ти век. Имената на двама велики математици И. Нютон и Г.В. Лайбниц.

Нютон стига до откритието на диференциалното смятане при решаване на задачи за скоростта на материална точка в даден момент от време (моментна скорост).

Както е известно, равномерно движениее движение, при което тялото изминава равни дължини на пътя за равни интервали от време. Нарича се разстоянието, изминато от тялото за единица време скорост равномерно движение.

Най-често обаче на практика имаме работа с неравномерно движение. Автомобил, който се движи по пътя, забавя на прелезите и ускорява в участъците, където пътят е свободен; самолетът забавя при кацане и т.н. Следователно най-често трябва да се справяме с факта, че през равни интервали от време тялото преминава отрязъци с различна дължина. Такова движение се нарича неравен.Скоростта му не може да се характеризира с едно число.

Често, за да се характеризира неравномерното движение, се използва понятието Средната скоростдвижение за времето ∆t٫, което се определя от връзката където ∆s е пътят, изминат от тялото за времето ∆t.

И така, при свободно падане на тяло средната скорост на движението му през първите две секунди е

На практика такава характеристика на движението като средна скорост говори много малко за движението. Наистина, при 4,9 m / s, а за 2-ри - 14,7 m / s, докато средната скорост за първите две секунди е 9,8 m / s. Средната скорост през първите две секунди не дава представа как е станало движението: кога тялото се е движило по-бързо и кога по-бавно. Ако зададем средните скорости на движение за всяка секунда поотделно, тогава ще знаем например, че през 2-рата секунда тялото се е движило много по-бързо, отколкото през 1-вата. Въпреки това, в повечето случаи много по-бързо, отколкото не сме доволни. В крайна сметка е лесно да се разбере, че през тази 2-ра секунда тялото също се движи по различни начини: в началото е по-бавно, в края е по-бързо. И как се движи някъде по средата на тази 2-ра секунда? С други думи, как да определим моментната скорост?

Нека движението на тялото се описва от закона за време равно на ∆t. В момента t0 тялото е изминало пътя, в момента - пътя. Следователно за времето ∆t тялото е изминало разстояние и средната скорост на тялото за този период от време ще бъде.

Колкото по-кратък е интервалът от време ∆t, толкова по-точно е възможно да се установи с каква скорост се движи тялото в момента t0, тъй като движещо се тяло не може значително да промени скоростта си за кратък период от време. Следователно средната скорост, когато ∆t клони към нула, се доближава до действителната скорост на движение и в границите дава скоростта на движение в даден момент t0 (моментна скорост).

По този начин ,

Определение 1. Незабавна скоростна праволинейно движение на тялото в даден момент t0 се нарича границата на средната скорост за времето от t0 до t0+ ∆t, когато интервалът от време ∆t клони към нула.

Така че, за да се намери скоростта на праволинейно неравномерно движение в даден момент, е необходимо да се намери границата на отношението на нарастването на пътя ∆ към увеличението на времето ∆t при условие, т.е. Лайбниц стига до откритието на диференциалното смятане, докато решава проблема с конструирането на допирателна към всяка крива, дадена от неговото уравнение.

Решението на този проблем има голямо значение. В крайна сметка скоростта на движеща се точка е насочена по допирателната към нейната траектория, така че определянето на скоростта на снаряд по нейната траектория, скоростта на всяка планета в нейната орбита, се свежда до определяне на посоката на допирателната към кривата .

Определението за допирателна като права линия, която има само една обща точка с крива, което е валидно за окръжност, е неподходящо за много други криви.

Следната дефиниция на допирателна към крива не само отговаря на интуитивната представа за нея, но също така ви позволява действително да намерите нейната посока, т.е. изчислете наклона на тангентата.

Определение 2. Допирателнакъм кривата в точката M се нарича правата линия MT, която е граничното положение на секущата MM1, когато точката M1, движеща се по кривата, се приближава неограничено до точката M.

1.2 Производна дефиниция

Обърнете внимание, че при определяне на допирателната към кривата и моментната скорост на неравномерно движение се извършват по същество същите математически операции:

1. Дадената стойност на аргумента се увеличава и се изчислява нова стойност на функцията, съответстваща на новата стойност на аргумента.

2. Определете нарастването на функцията, съответстващо на избраното увеличение на аргумента.

3. Приращението на функцията се дели на приращението на аргумента.

4. Изчислете границата на това съотношение, при условие че нарастването на аргумента клони към нула.

Решенията на много проблеми водят до гранични преходи от този тип. Става необходимо да се направи обобщение и да се даде име на този пасаж до краен предел.

Скоростта на промяна на функцията в зависимост от промяната на аргумента очевидно може да се характеризира с отношение. Тази връзка се нарича Средната скорост функцията се променя в интервала от до. Сега трябва да разгледаме границата на дроб. Границата на това съотношение, когато нарастването на аргумента клони към нула (ако тази граница съществува) е някаква нова функция на. Тази функция се означава със символите у', т.нар производнатази функция, тъй като се получава (произведе) от функцията Самата функция се извиква примитивенфункция по отношение на нейната производна

Определение 3. производнафункции в дадена точка назовават границата на отношението на нарастването на функцията ∆y към съответното нарастване на аргумента ∆x, при условие че ∆x→0, т.е.

1.3 Общо правило за намиране на производната

Операцията за намиране на производната на някаква функция се нарича диференциацияфункции, а клонът на математиката, който изучава свойствата на тази операция, е диференциално смятане.

Ако една функция има производна при x=a, тогава се казва, че е такава диференцируемив този момент. Ако една функция има производна във всяка точка от даден интервал, тогава се казва, че е такава диференцируемиПо този интервал .

Дефиницията на производната не само напълно характеризира концепцията за скоростта на промяна на функция, когато аргументът се промени, но също така предоставя начин за действително изчисляване на производната на дадена функция. За да направите това, трябва да извършите следните четири действия (четири стъпки), посочени в дефиницията на самата производна:

1. Намерете нова функционална стойност чрез представяне в тази функциявместо x, новата стойност на аргумента: .

2. Приращението на функцията се определя, като дадената стойност на функцията се извади от новата й стойност: .

3. Съставете отношението на нарастването на функцията към нарастването на аргумента: .

4. Отидете до границата при и намерете производната: .

Най-общо казано, производната е „нова“ функция, получена от дадена функция съгласно определено правило.

1.4 Геометричен смисъл на производната

Геометричната интерпретация на производната, дадена за първи път в края на XVIIв. Лайбниц е както следва: стойността на производната на функцията в точката x е равен на наклона на допирателната, начертана към графиката на функцията в същата точка x,тези.

Уравнението на допирателната, като всяка права линия, минаваща през нея дадена точкав тази посока, има формата – текущи координати. Но уравнението на допирателната също ще бъде написано както следва: . Нормалното уравнение ще бъде записано във формата

1.5 Механично значение на производната

Механичното тълкуване на производната е дадено за първи път от И. Нютон. Състои се в следното: скоростта на движение на материална точка в даден момент от време е равна на производната на пътя по време, т.е. По този начин, ако законът за движение на материална точка е даден от уравнение, тогава, за да намерите моментната скорост на точка в определен момент от времето, трябва да намерите производната и да замените съответната стойност на t в нея .

1.6 Производна от втори ред и нейното механично значение

Получаваме (уравнение от направеното в учебника Lisichkin V.T. Soloveychik I.L. "Математика" стр. 240):

По този начин, ускорението на праволинейното движение на тялото в даден момент е равно на втората производна на пътя по време, изчислена за даден момент.Това е механичният смисъл на втората производна.

1.7 Определение и геометричен смисъл на диференциала

Определение 4.Главната част от нарастването на функция, линейна спрямо нарастването на функцията, линейна спрямо нарастването на независимата променлива, се нарича диференциалфункции и се означава с d, т.е. .

Функционален диференциал геометрично представена чрез нарастване на ординатата на допирателната, начертана в точката М ( х ; г ) за дадени стойности на x и ∆x.

изчисление диференциал – .

Приложение на диференциала при приближени изчисления – , приблизителната стойност на нарастването на функцията съвпада с нейния диференциал.

Теорема 1. Ако диференцируемата функция нараства (намалява) в даден интервал, тогава производната на тази функция не е отрицателна (не е положителна) в този интервал.

Теорема 2. Ако производната функция е положителна (отрицателна) в някакъв интервал, то функцията в този интервал е монотонно нарастваща (монотонно намаляваща).

Нека сега формулираме правилото за намиране на интервали на монотонност на функцията

1. Изчислете производната на тази функция.

2. Намерете точки, където е нула или не съществува. Тези точки се наричат критиченза функция

3. С намерените точки областта на функцията се разделя на интервали, на всеки от които производната запазва своя знак. Тези интервали са интервали на монотонност.

4. Разгледайте знака на всеки от намерените интервали. Ако на разглеждания интервал, тогава на този интервал се увеличава; ако, тогава намалява на такъв интервал.

В зависимост от условията на задачата, правилото за намиране на интервали на монотонност може да бъде опростено.

Определение 5.Точка се нарича точка на максимум (минимум) на функция, ако неравенството е в сила, съответно за всяко x от някаква околност на точката.

Ако е максималната (минималната) точка на функцията, тогава казваме това (минимум)в точката. Максималните и минималните функции обединяват името екстремумфункции, като точките максимум и минимум се извикват екстремни точки (крайни точки).

Теорема 3.(необходим знак за екстремум). Ако и производната съществува в тази точка, тогава тя е равна на нула: .

Теорема 4.(достатъчен знак за екстремум). Ако производната когато x преминава през а променя знака, тогава а е екстремната точка на функцията .

Основните точки на изследването на производната:

1. Намерете производната.

2. Намерете всички критични точки от домейна на функцията.

3. Задайте знаците на производната на функцията при преминаване през критичните точки и изпишете точките на екстремума.

4. Изчислете стойностите на функцията във всяка крайна точка.

2. Изследване на функции с производна

Задача №1 . Дневник обем.Дървени трупи с правилна форма без дървесни дефекти със сравнително малка разлика в диаметрите на дебелите и тънките краища се наричат промишлена кръгла дървесина. При определяне на обема на индустриалния кръгъл дървен материал обикновено се използва опростена формула, където е дължината на трупа, е площта на средното му сечение. Разберете дали реалният обем свършва или подценява; оценка на относителната грешка.

Решение. Формата на кръглия бизнес дървен материал е близка до пресечен конус. Нека е радиусът на по-големия, по-малкия край на дънера. Тогава неговият почти точен обем (обемът на пресечен конус) може, както е известно, да се намери по формулата. Нека е стойността на обема, изчислена по опростената формула. Тогава;

Тези. . Това означава, че опростената формула дава подценяване на обема. Нека го поставим сега. Тогава. Това показва, че относителната грешка не зависи от дължината на трупа, а се определя от съотношението. От кога се увеличава на интервала. Следователно, което означава, че относителната грешка не надвишава 3,7%. В практиката на горската наука такава грешка се счита за напълно приемлива. С по-голяма точност е практически невъзможно да се измерят нито диаметрите на краищата (тъй като те са малко по-различни от кръговете), нито дължината на трупа, тъй като те измерват не височината, а генератора на конуса (дължината на трупът е десетки пъти по-голям от диаметъра и това не води до големи грешки). Така на пръв поглед неправилно, но повече проста формулатъй като обемът на пресечен конус в реална ситуация се оказва съвсем легитимен. Многократно проведено с помощта на специални методи за проверка показа, че при масовото отчитане на промишлената гора относителната грешка при използване на разглежданата формула не надвишава 4%.

Задача №2 . При определяне на обемите на ями, траншеи на кофи и други контейнери, които имат формата на пресечен конус, понякога в селскостопанската практика се използва опростена формула, където е височината, са площите на основите на конуса. Разберете дали реалният обем е надценен или подценен, оценете относителната грешка при естествените условия за практика: (- основни радиуси, .

Решение. Означавайки чрез истинската стойност на обема на пресечения конус и чрез стойността, изчислена по опростената формула, получаваме: , т.е. . Това означава, че опростената формула дава надценка на обема. Повтаряйки по-нататък решението на предишната задача, откриваме, че относителната грешка ще бъде не повече от 6,7%. Вероятно такава точност е приемлива при разпределяне на изкопните работи - в края на краищата ямите няма да бъдат идеални конуси и съответните параметри в реални условия се измерват много грубо.

Задача №3 . В специална литература, за да се определи ъгълът β на въртене на шпиндела на фреза при фрезоване на съединители със зъби, се извежда формула, където. Тъй като тази формула е сложна, се препоръчва да се отхвърли нейният знаменател и да се използва опростена формула. При какво (- цяло число) може да се използва тази формула, ако е допусната грешка при определяне на ъгъла?

Решение.Точната формула след проста идентични трансформацииможе да се доведе до ума. Следователно, когато се използва приблизителна формула, се допуска абсолютна грешка, където. Изучаваме функцията на интервала . В случая 0,06, т.е. ъгълът принадлежи към първата четвърт. Ние имаме: . Забележете, че на разглеждания интервал и следователно функцията е намаляваща на този интервал. Тъй като по-нататък, за всички разгледани. Означава,. Тъй като е радиан, това е достатъчно за решаване на неравенството. Решавайки това неравенство чрез селекция, намираме, че . Тъй като функцията е намаляваща, следва, че

Заключение

Използването на производното е доста широко и може да бъде напълно обхванато в този тип работа, но аз се опитах да покрия основните точки. В наши дни във връзка с научно-техническия прогрес, особено с бързото развитие на изчислителните системи, диференциалното смятане става все по-уместно при решаването както на прости, така и на свръхсложни проблеми.

Литература

1. В.А. Петров "Математически анализ в производствени задачи"

2. Соловейчик И.Л., Лисичкин В.Т. "математика"

Чайкин Семьон, Майсак Кирил, Залогина Анастасия, Шахзадова Анна

Тази разработка съдържа презентация на тема „Приложение на производното в химията и биологията“. По време на дейности по проектабеше изложена хипотеза, че производната намира своето приложение в тези области на науката. По време на изследователска работабеше установено каква е ролята на производната в такива науки като химия и биология, къде и при решаването на какви проблеми намира своето приложение. В резултат на извършената работа се стигна до заключението, че хипотезата наистина се потвърждава.

Изтегли:

Преглед:

https://accounts.google.com

Надписи на слайдове:

Хипотеза:

Преглед:

За да използвате визуализацията на презентации, създайте акаунт в Google (акаунт) и влезте: https://accounts.google.com

Надписи на слайдове:

Използването на производната в химията и биологията. Работата е извършена от ученици от 11 Б клас на средно училище № 6 на MBOU: Чайкин Семьон, Майсак Кирил, Залогина Анастасия, Шахзадова Анна Ставропол, 2014 г.

Хипотеза:

А в химията диференциалното смятане намери широко приложение за конструиране на математически модели на химични реакции и последващо описание на техните свойства. Химията е наука за веществата, химичните превръщания на веществата. Химията изучава моделите на различни реакции.Скоростта на химичната реакция е промяната в концентрацията на реагентите за единица време. Приложение на производното в химията и биологията. Определяне на скоростта на химична реакция

Защо се нуждаем от производни в реакциите? Тъй като скоростта на реакцията v се променя непрекъснато по време на процеса, тя обикновено се изразява като производна на концентрацията на реагентите по отношение на времето.

Производната формула в химията Ако C (t) е законът за промяна на количеството вещество, което е влязло в химическа реакция, тогава скоростта v (t) на химическата реакция в момент t е равна на производната:

Определяне на скоростта на реакцията Границата на съотношението на инкременталната функция към инкременталния аргумент, когато Δt клони към нула, е скоростта на химическа реакция в даден момент

Задача по химия: Нека количеството вещество, което е влязло в химична реакция, се дава от зависимостта: C (t) \u003d t 2 / 2 + 3 t -3 (mol) Намерете скоростта на химичната реакция след 3 секунди . Решение: v (t) = C ‘(t) ; v (t) = t + 3; v (3) = 3+3 = 6. Отговор: 6 mol/s.

Биологично значение на производната Нека връзката между броя на индивидите в популация от микроорганизми y и времето t на нейното размножаване се дава от уравнението: y = x (t). Нека ∆ t е интервалът от време от някаква начална стойност t до t + ∆ t . Тогава y + ∆y \u003d x (t + ∆ t) е новата стойност на размера на популацията, съответстваща на момента t + ∆ t, а ∆ y + x (t + ∆ t) - x (t) е промяната в броя на индивидите на организмите. Коефициентът е средната скорост на възпроизводство или, както се казва, средната производителност на населението. Изчислявайки, получаваме y ' = P (t) = x ' (t) , или производителността на населението в момент t .

Пример Нека бактериалната популация в момент t (c) има x(t) индивида. . Намерете скоростта на нарастване на населението: а) в произволен момент t , б) в момент t = 1 c . Решение: P = x'(t) = 200t; P(1) = 200 (r/s). Отговор: 200 o/s.

Заключение Концепцията за производно е много важна в химията и биологията, особено при определяне на скоростта на реакцията.

Заключение: Диференциалното смятане е описание на света около нас, направено на математически език. Производната е едно от най-важните понятия в смятането. Познаването на производната ни помага успешно да решаваме не само математически задачи, но и практически задачи в различни области на науката, технологиите и живота.

Южносахалински държавен университет

Катедра по математика

Курсова работа

Тема: Практическо приложение на производната

Лектор: Лихачева О.Н.

Южно-Сахалинск

2002 г
Въведение

В тази статия ще разгледам приложенията на производната в различни науки и индустрии. Работата е разделена на глави, всяка от които се занимава с един от аспектите на диференциалното смятане (геометричен, физически смисъл и т.н.)

1. Понятието производна

1-1. Историческа информация

Диференциалното смятане е създадено от Нютон и Лайбниц в края на 17 век въз основа на два проблема:

1) за намиране на допирателна към произволна права

2) за търсене на скорост с произволен закон на движение

Още по-рано концепцията за производна се среща в произведенията на италианския математик Тарталия (около 1500 - 1557 г.) - тук се появява допирателна в хода на изучаването на въпроса за ъгъла на наклона на пистолета, който осигурява най-голям обхват на снаряда.

През 17 век, въз основа на теорията за движението на Г. Галилей, активно се развива кинематичната концепция за производната. Различни презентации започват да се появяват в трудовете на Декарт, френския математик Робервал и английския учен Л. Грегъри. Лопитал, Бернули, Лагранж, Ойлер, Гаус имат голям принос в изучаването на диференциалното смятане.

1-2. Понятието производно

Нека y \u003d f (x) е непрекъсната функция на аргумента x, определен в интервала (a; b), и нека x 0 е произволна точка от този интервал

Даваме на аргумента x увеличение ∆x, тогава функцията y = f(x) ще получи увеличение ∆y = f(x + ∆x) - f(x). Границата, към която отношението ∆y / ∆x клони при ∆x → 0, се нарича производна на функцията f(x).

1-3. Правила за диференциране и таблица на производните

		(sin x)" = cos x
	(1 / x)" = -1 / x2	(cos x)" = -sin x
	(√x)" = 1 / 2√x	(tg x)" = 1 / cos 2 x
(uv)" = u"v + uv"	(a x)" = a x log x	(ctg x)" = 1 / sin 2 x
(u / v)"=(u"v - uv") / v 2		(arcsin x)" = 1 / √ (1- x 2)
	(log a x)" = (log a e) / x	(arccos x)" = -1 / √ (1- x 2)
	(ln x)" = 1 / x	(arctg x)" = 1 / √ (1+ x 2)
		(arcctg x)" = -1 / √ (1+ x 2)

2. Геометричният смисъл на производната

2-1. Допирателна към крива

Нека имаме крива и фиксирана точка M и точка N върху нея.Допирателната към точката M е права линия, чиято позиция се стреми да бъде заета от хордата MN, ако точката N се приближава неограничено по протежение на крива към М.

Разгледайте функцията f(x) и кривата y = f(x), съответстваща на тази функция. За някаква стойност x функцията има стойност y = f(x). Тези стойности на кривата съответстват на точката M(x 0 , y 0). Нека въведем нов аргумент x 0 + ∆x, чиято стойност съответства на стойността на функцията y 0 + ∆y = f(x 0 + ∆x). Съответстващата точка е N(x 0 + ∆x, y 0 + ∆y). Начертайте секанса MN и означете с φ ъгъла, образуван от секанса с положителната посока на оста Ox. Фигурата показва, че ∆y / ∆x = tg φ. Ако сега ∆x се доближи до 0, тогава точката N ще се движи по кривата, секущата MN ще се върти около точката M и ъгълът φ ще се промени. Ако при ∆x → 0 ъгълът φ клони към някакво α, тогава правата, минаваща през M и сключваща ъгъл α с положителната посока на абсцисната ос, ще бъде търсената допирателна. В същото време неговият коефициент на наклон:

Тоест стойността на производната f "(x) за дадена стойност на аргумента x е равна на тангенса на ъгъла, образуван с положителната посока на оста Ox от допирателната към графиката на функцията f (x ) в точката M (x, f (x)).

Допирателната към пространствена линия има определение, подобно на това на допирателната към равнинна крива. В този случай, ако функцията е дадена от уравнението z = f(x, y), наклоните по осите OX и OY ще бъдат равни на частните производни на f по отношение на x и y.

2-2. Допирателна равнина към повърхност

Допирателната равнина към повърхнината в точка М е равнината, съдържаща допирателните към всички пространствени криви на повърхнината, минаващи през М - точката на контакт.

Вземете повърхността, дадена от уравнението F(x, y, z) = 0 и някаква обикновена точка M(x 0 , y 0 , z 0) върху нея. Да разгледаме на повърхността някаква крива L, минаваща през M. Нека кривата е дадена от уравненията

x = φ(t); y = ψ(t); z = χ(t).

Нека заместим тези изрази в уравнението на повърхността. Уравнението ще се превърне в идентичност, тъй като кривата лежи изцяло на повърхността. Използвайки свойството за инвариантност на формата на диференциала, диференцираме полученото уравнение по отношение на t:

Уравненията на допирателната към кривата L в точка M имат формата:

Тъй като разликите x - x 0, y - y 0, z - z 0 са пропорционални на съответните диференциали, крайното уравнение на равнината изглежда така:

F" x (x - x 0) + F" y (y - y 0) + F" z (z - z 0)=0

и за частния случай z = f(x, y):

Z - z 0 \u003d F "x (x - x 0) + F" y (y - y 0)

Пример:Намерете уравнението на допирателната равнина в точката (2a; a; 1,5a) на хиперболичния параболоид

Решение:

Z" x \u003d x / a \u003d 2; Z" y \u003d -y / a = -1

Уравнението на желаната равнина:

Z - 1,5a = 2(x - 2a) - (Y - a) или Z = 2x - y - 1,5a

3-1. Скорост на материалната точка

Нека зависимостта на пътя s от времето t в дадено праволинейно движениематериална точка се изразява чрез уравнението s = f(t) и t 0 е определен момент от времето. Помислете за друго време t, означете ∆t = t - t 0 и изчислете увеличението на пътя: ∆s = f(t 0 + ∆t) - f(t 0). Отношението ∆s / ∆t се нарича средната скорост на движение за времето ∆t, изтекло от началния момент t 0 . Скоростта е границата на това съотношение като ∆t → 0.

Стойността е средното ускорение на неравномерното движение в интервала (t; t + ∆t). =∆v / ∆t. Моментното ускорение на материална точка в момент t ще бъде границата на средното ускорение:

Това е първата производна по време (v "(t)).

Пример:Зависимостта на пътя, изминат от тялото от времето, се дава от уравнението s \u003d A + Bt + Ct 2 + Dt 3 (C = 0,1 m / s, D = 0,03 m / s 2). Определете времето след началото на движението, след което ускорението на тялото ще бъде равно на 2 m / s 2.

Решение:

v(t) = s "(t) = B + 2Ct + 3Dt 2; a(t) = v"(t) = 2C + 6Dt = 0,2 + 0,18t = 2;

1,8 = 0,18t; t = 10 s

3-2. Топлинният капацитет на дадено вещество при дадена температура

За увеличаване на различните температури T със същата стойност, равна на T 1 - T, на 1 kg. дадено вещество се нуждае от различно количество топлина Q 1 - Q, и отношението

за това вещество не е константа. По този начин за дадено вещество количеството топлина Q е нелинейна функция на температурата T: Q = f(T). Тогава ΔQ = f(t + ΔT) - f(T). Поведение

се нарича среден топлинен капацитет на интервала , а границата на този израз при ∆T → 0 се нарича топлинен капацитет на даденото вещество при температура T.

3-3. Мощност

промяна механично движениетялото се причинява от сили, действащи върху него от други тела. За да се характеризира количествено процеса на обмен на енергия между взаимодействащи тела, в механиката се въвежда понятието работа на сила. За да се характеризира скоростта на извършване на работа, се въвежда понятието мощност:

4. Диференциално смятане в икономиката

4-1. Функционално изследване

Диференциалното смятане е математически апарат, широко използван за икономически анализ. Основната задача на икономическия анализ е да изследва връзките на икономическите величини, записани като функции. В каква посока ще се променят държавните приходи, ако се увеличат данъците или ако се въведат вносни мита? Ще се увеличат или ще намалят приходите на фирмата, когато цената на нейните продукти се увеличи? В какво съотношение допълнителното оборудване може да замести пенсионираните работници? За решаването на такива проблеми трябва да се конструират функциите на свързване на включените в тях променливи, които след това се изучават с помощта на методите на диференциалното смятане. В икономиката често се изисква да се намери най-добрата или оптимална стойност на даден показател: най-висока производителност на труда, максимална печалба, максимална продукция, минимални разходи и т.н. Всеки показател е функция на един или повече аргументи. По този начин намирането на оптималната стойност на индикатора се свежда до намиране на екстремума на функцията.

Според теоремата на Ферма, ако една точка е екстремум на функция, тогава производната или не съществува в нея, или е равна на 0. Видът на екстремума може да се определи от едно от достатъчните условия за екстремум:

1) Нека функцията f(x) е диференцируема в някаква околност на точката x 0 . Ако производната f "(x) при преминаване през точката x 0 променя знака от + на -, тогава x 0 е максималната точка, ако от - към +, тогава x 0 е минималната точка, ако не променя знака , тогава няма екстремум.

2) Нека функцията f (x) е два пъти диференцируема в някаква околност на точката x 0 и f "(x 0) \u003d 0, f "" (x 0) ≠ 0, тогава в точката x 0 функцията f (x 0) има максимум, ако f ""(x 0)< 0 и минимум, если f ""(x 0) > 0.

В допълнение, втората производна характеризира изпъкналостта на функцията (графиката на функцията се нарича изпъкнала нагоре [надолу] на интервала (a, b), ако се намира на този интервал не над [не под] нито една от нейните допирателни ).

Пример:изберете оптималния обем на производство на фирмата, чиято функция на печалбата може да се моделира чрез зависимостта:

π(q) = R(q) - C(q) = q 2 - 8q + 10

Решение:

π"(q) = R"(q) - C"(q) = 2q - 8 = 0 → q extr = 4

За q< q extr = 4 → π"(q) < 0 и прибыль убывает

За q > q extr = 4 → π"(q) > 0 и печалбата се увеличава

Когато q = 4, печалбата приема минималната стойност.

Каква е оптималната продукция за фирмата? Ако фирмата не може да произведе повече от 8 единици продукция през разглеждания период (p(q = 8) = p(q = 0) = 10), тогава оптималното решение би било да не произвежда нищо, но да получава доход от отдаване под наем на помещения и/или оборудване. Ако фирмата е в състояние да произведе повече от 8 единици, тогава оптималното за фирмата ще бъде да произвежда на границата на производствения си капацитет.

4-2. Еластичност на търсенето

Еластичността на функцията f (x) в точката x 0 се нарича граница

Търсенето е количеството стока, търсено от купувача. Ценовата еластичност на търсенето E D е мярка за това как търсенето реагира на промените в цените. Ако │E D │>1, тогава търсенето се нарича еластично, ако │E D │<1, то неэластичным. В случае E D =0 спрос называется совершенно неэластичным, т. е. изменение цены не приводит ни к какому изменению спроса. Напротив, если самое малое снижение цены побуждает покупателя увеличить покупки от 0 до предела своих возможностей, говорят, что спрос является совершенно эластичным. В зависимости от текущей эластичности спроса, предприниматель принимает решения о снижении или повышении цен на продукцию.

4-3. Анализ на границите

Важен раздел от методите на диференциалното смятане, използвани в икономиката, са методите за ограничаващ анализ, т.е. набор от методи за изучаване на променящите се стойности на разходите или резултатите с промени в производството, потреблението и т.н. въз основа на анализ на техните гранични стойности. Ограничаващият индикатор (индикатори) на функция е нейната производна (в случай на функция на една променлива) или частични производни (в случай на функция на няколко променливи)

В икономиката често се използват средни стойности: средна производителност на труда, средни разходи, среден доход, средна печалба и т.н. Но често се изисква да се разбере с каква сума ще се увеличи резултатът, ако разходите се увеличат или обратно, колко резултатът ще намалее, ако се намалят разходите. Невъзможно е да се отговори на този въпрос с помощта на средни стойности. При такива задачи е необходимо да се определи границата на съотношението на увеличението на резултата и разходите, т.е. да се намери пределният ефект. Следователно, за решаването им е необходимо да се използват методите на диференциалното смятане.

5. Производна при приближени изчисления

5-1. Интерполация

Интерполацията е приблизителното изчисляване на стойностите на функция от няколко дадени стойности. Интерполацията се използва широко в картографията, геологията, икономиката и други науки. Най-простата опция за интерполация е формата на Лагранж, но когато има много възлови точки и интервалите между тях са големи или искате да получите функция, чиято кривина е минимална, тогава прибягвайте до сплайн интерполация, която дава по-голяма точност.

Нека K n е система от възлови точки a = x 0< x 1 <…< x n = b. Функция S k (x) называется сплайн-функцией S k (x) степени k≥0 на K n , если

а) S k (x) є C k -1 ()

b) S k (x) е полином със степен най-висока k

Сплайн функция Ŝ k (x) є S k (K n) се нарича интерполираща сплайн функция, ако Ŝ k (x j) = f(x j) за j = 0,1,…,n

В приложенията често е достатъчно да изберете k=3 и да приложите т.нар кубична интерполация.

Тъй като s(x) е полином от трета степен на всеки частичен интервал, тогава за x є

Тук s 2 j , c j 1 , c j 0 са неизвестни за j = 1, 2, …, n

Последните са изключени поради изискването s(x j) = y j:

Диференцирайки тази функция и като вземем предвид, че s "(x) трябва да бъде непрекъснат през целия интервал и, следователно, по-специално във възлите, най-накрая получаваме системата от уравнения:

по отношение на n+1 неизвестни s 2 0 , s 2 1 ,…, s 2 n. За еднозначното им определяне в зависимост от задачата се добавят още две уравнения:

нормален случай(Н):

Периодичен случай (P) (т.е.е(x+(x n -x 0))=е(х)):

Определено изглаждане на границите:

Пример:сплайн интерполация на функцията f(x)=sin x, n=4.

Функцията е периодична, така че използваме случая P.

Сплайн функцията изглежда така:

5-2. Формула на Тейлър

Разширяването на функциите в безкрайни серии ви позволява да получите стойността на функцията в дадена точка с всякаква точност. Тази техника се използва широко в програмирането и други дисциплини.

За дадена функция се казва, че се разширява в даден интервал в степенна редица, ако съществува такава степенна редица a 0 + a 1 (x - a) + a 2 (x - a) 2 + ... + a n (x - a ) n + ..., която сходна към тази функция на този интервал. Може да се докаже, че това разлагане е уникално:

Нека функцията f(x) е безкрайно диференцируема в точка a. Степенен ред на формата

се нарича ред на Тейлър за функцията f(x), записана в степени на разликата (x - a). Като цяло, за да се сближи редът на Тейлър към f(x), е необходимо и достатъчно остатъкът от реда да клони към 0. За a = 0, редът на Тейлър обикновено се нарича ред на Маклорен.

И. М. Уваренков,

М. З. Малер

Курс по математически анализ, т.1

В. А. Дударенко,

А.А. Дадаян

Математически анализ

Диференциално и интегрално смятане

Т. И. Трофимова

Курс по физика

О. О. Замков

А. В. Толстопятенко

Ю. Н. Черемних

Математически методи в икономиката

А. С. Солодовников

В. А. Бабайцев

А. В. Браилов

И.Г. Шандра

Математика в икономиката

Въведение

1. Понятието производна

1-1. Историческа информация

1-2. Понятието производно

1-3. Правила за диференциране и таблица на производните

2. Геометричният смисъл на производната

2-1. Допирателна към крива

2-2. Допирателна равнина към повърхност

3. Използване на производната във физиката

3-1. Скорост на материалната точка

3-2. Топлинна мощност при дадена температура

3-3. Мощност

4. Диференциално смятане в икономиката

4-1. Функционално изследване

4-2. Еластичност на търсенето

4-3. Анализ на границите

5. Производна при приближени изчисления

5-1. Интерполация

5-2. Формула на Тейлър

5-3. Приблизителни изчисления

Заключение

Списък на използваната литература

Южносахалински държавен университет

Катедра по математика

Курсова работа

Тема: Практическо приложение на производната

Лектор: Лихачева О.Н.

Южно-Сахалинск

2002 г Въведение

1. Понятието производна

1-1. Историческа информация

Диференциалното смятане е създадено от Нютон и Лайбниц в края на 17 век въз основа на два проблема:

1) за намиране на допирателна към произволна права

2) за търсене на скорост с произволен закон на движение

1-2. Понятието производно

Нека y = f(x) е непрекъсната функция на аргумента x, дефиниран в интервала (a; b), и нека x0 е произволна точка от този интервал

1-3. Правила за диференциране и таблица на производните

C" = 0(xn) = nxn-1(sin x)" = cos xx" = 1(1 / x)" = -1 / x2(cos x)" = -sin x(Cu)"=Cu"( √x)" = 1 / 2√x(tg x)" = 1 / cos2 x(uv)" = u"v + uv"(ax)" = ax ln x(ctg x)" = 1 / sin2 x( u / v)"=(u"v - uv") / v2(ex)" = ex(arcsin x)" = 1 / √ (1- x2)(logax)" = (logae) / x(arccos x) " = -1 / √ (1- x2)(ln x)" = 1 / x(arctg x)" = 1 / √ (1+ x2)(arctg x)" = -1 / √ (1+ x2)

2. Геометричният смисъл на производната

2-1. Допирателна към крива

Разгледайте функцията f(x) и кривата y = f(x), съответстваща на тази функция. За някаква стойност x функцията има стойност y = f(x). Тези стойности на кривата съответстват на точката M(x0, y0). Въвеждаме нов аргумент x0 + ∆x, чиято стойност съответства на стойността на функцията y0 + ∆y = f(x0 + ∆x). Съответстващата точка е N(x0 + ∆x, y0 + ∆y). Начертайте секанса MN и означете с φ ъгъла, образуван от секанса с положителната посока на оста Ox. Фигурата показва, че ∆y / ∆x = tg φ. Ако сега ∆x се доближи до 0, тогава точката N ще се движи по кривата, секущата MN ще се върти около точката M и ъгълът φ ще се промени. Ако при ∆x → 0 ъгълът φ клони към някакво α, тогава правата, минаваща през M и сключваща ъгъл α с положителната посока на абсцисната ос, ще бъде търсената допирателна. В същото време неговият коефициент на наклон:

2-2. Допирателна равнина към повърхност

Вземете повърхност, дадена от уравнението F(x, y, z) = 0 и някаква обикновена точка M(x0, y0, z0) върху нея. Да разгледаме на повърхността някаква крива L, минаваща през M. Нека кривата е дадена от уравненията

x = φ(t); y = ψ(t); z = χ(t).

Уравненията на допирателната към кривата L в точка M имат формата:

Тъй като разликите x - x0, y - y0, z - z0 са пропорционални на съответните диференциали, крайното уравнение на равнината изглежда така:

F "x (x - x0) + F" y (y - y0) + F "z (z - z0) \u003d 0

и за частния случай z = f(x, y):

Z - z0 \u003d F "x (x - x0) + F" y (y - y0)

Пример:Намерете уравнението на допирателната равнина в точката (2a; a; 1,5a) на хиперболичния параболоид

Решение:

Z"x \u003d x / a \u003d 2; Z"y \u003d -y / a = -1

Уравнението на желаната равнина:

Z - 1,5a = 2(x - 2a) - (Y - a) или Z = 2x - y - 1,5a

3. Използване на производната във физиката

3-1. Скорост на материалната точка

Нека зависимостта на пътя s от времето t при дадено праволинейно движение на материална точка се изрази чрез уравнението s = f(t) и t0 е някакъв момент от време. Помислете за друго време t, означете ∆t = t - t0 и изчислете увеличението на пътя: ∆s = f(t0 + ∆t) - f(t0). Съотношението ∆s / ∆t се нарича средната скорост на движение за времето ∆t, изминало от началния момент t0. Скоростта е границата на това съотношение като ∆t → 0.

Това е първата производна по време (v "(t)).

Пример:Времевата зависимост на пътя, изминат от тялото, се дава от уравнението s = A + Bt + Ct2 + Dt3 (C = 0,1 m/s, D = 0,03 m/s2). Определете времето след началото на движението, след което ускорението на тялото ще бъде равно на 2 m/s2.

Решение:

v(t) = s"(t) = B + 2Ct + 3Dt2; a(t) = v"(t) = 2C + 6Dt = 0,2 + 0,18t = 2;

1,8 = 0,18t; t = 10 s

3-2. Топлинният капацитет на дадено вещество при дадена температура

За увеличаване на различните температури T със същата стойност, равна на T1 - T, за 1 kg. дадено вещество се нуждае от различно количество топлина Q1 - Q, и отношението

3-3. Мощност

Промяната в механичното движение на тялото се причинява от сили, действащи върху него от други тела. За да се характеризира количествено процеса на обмен на енергия между взаимодействащи тела, в механиката се въвежда понятието работа на сила. За да се характеризира скоростта на извършване на работа, се въвежда понятието мощност:

4. Диференциално смятане в икономиката

4-1. Функционално изследване

1) Нека функцията f(x) е диференцируема в някаква околност на точката x0. Ако производната f "(x) при преминаване през точката x0 променя знака от + на -, тогава x0 е максималната точка, ако от - към +, тогава x0 е минималната точка, ако не променя знака, тогава там не е крайност в този момент.

2) Нека функцията f(x) е два пъти диференцируема в някаква околност на точката x0 и f "(x0) = 0, f ""(x0) ≠ 0, тогава в точката x0 функцията f(x0) има максимум ако

Изтегли:

Преглед:

Надписи на слайдове:

Преглед:

Надписи на слайдове:

Прочетете също