Застосування похідної у різних сферах діяльності. Цікава похідна Цілі даної роботи: Розглянути застосування похідної в різних науках Познайомитися з вченими, що вивчали похідну функції. Сила є похідною роботи з переміщення

Міністерство освіти Саратівської області

Державне автономне професійне освітня установаСаратовській області «Енгельський політехнікум»

ВИКОРИСТАННЯ ВИРОБНИЧОЇ У РОЗДРІБНИХ ОБЛАСТЯХ НАУКИ

Виконала: Саркулова Нургуля Сергіївна

студентка групи КШІ-216/15

(Конструювання, моделювання та

технологія швейних виробів)

Науковий керівник:

Вербицька Олена В'ячеславівна

викладач математики ГАПОУ СО

«Енгельський політехнікум»

2016

Вступ

Роль математики у різних галузях природознавства дуже велика. Недарма кажуть«Математика – цариця наук, фізика її права рука, хімія - ліва».

Предмет дослідження – похідна.

Провідна мета - показати значимість похідної у математиці, а й у інших науках, її важливість у житті.

Диференціальне обчислення – це опис навколишнього світу, виконане математичною мовою. Похідна допомагає нам успішно вирішувати не лише математичні задачі, а й завдання практичного характеру у різних галузях науки і техніки.

Похідна функції використовується усюди, де є нерівномірне перебіг процесу: це і нерівномірний механічний рух, і змінний струм, і хімічні реакції та радіоактивний розпадречовини тощо.

Ключовий та тематичний питання даного реферату:

1. Історія виникнення похідної.

2. Навіщо вивчати похідні функції?

3. Де використовуються похідні?

4. Застосування похідних у фізиці, хімії, біології та інших науках.

5. Висновки

Я вирішила написати роботу на тему «Застосування похідної у різних галузях науки», бо вважаю цю тему дуже цікавою, корисною та актуальною.

У своїй роботі я розповім про застосування диференціювання в різних галузях науки, таких як хімія, фізика, біологія, географія і т. д. Адже всі науки нерозривно пов'язані між собою, що дуже добре видно на прикладі теми, що розглядається мною.

Застосування похідної у різних галузях науки

З курсу алгебри старших класів ми знаємо, щопохідна - це межа відношення збільшення функції до збільшення її аргументу при прагненні збільшення аргументу до нуля, якщо така межа існує.

Дія знаходження похідної називається її диференціюванням, а функцію, що має похідну в точці х, називають диференційованою в цій точці. Функція, що диференціюється в кожній точці проміжку, називається диференційованою в цьому проміжку.

Честь відкриття основних законів математичного аналізу належить англійського фізиката математику Ісааку Ньютону та німецькому математику, фізику, філософу Лейбніцу.

Ньютон ввів поняття похідної, вивчаючи закони механіки, цим розкрив її механічний сенс.

Фізичний зміст похідної: похідна функціїy= f(x) у точці x 0 – це швидкість зміни функціїf(x) у точці x 0 .

Лейбніц дійшов поняття похідної, вирішуючи завдання проведення дотичної до похідної лінії, пояснивши цим її геометричний зміст.

Геометричний зміст похідної полягає в тому, що похідна функція в точціx 0 дорівнює кутовому коефіцієнту дотичної до графіка функції, проведеної в точці з абсцисоюx 0 .

Термін похідна та сучасні позначенняy" , fВвів Ж. Лагранж в 1797р.

Російський математик 19 століття Панфутій Львович Чебишев говорив, що «особливу важливість мають ті методи науки, які дозволяють вирішувати завдання, загальне для всієї практичної діяльності людини, наприклад, як мати свої засоби для досягнення найбільшої вигоди».

З такими завданнями в наш час доводиться мати справу представникам різних спеціальностей:

Інженери технологи намагаються так організувати виробництво, щоб випускалося якнайбільше продукції;

Конструктори намагаються розробити прилад для космічного кораблятак, щоб маса приладу була найменшою;

Економісти намагаються спланувати зв'язки заводу із джерелами сировини так, щоб транспортні витрати виявилися мінімальними.

Під час вивчення будь-якої теми в учнів виникає запитання: «Навіщо це треба?». Якщо відповідь задовольнить цікавість, можна говорити про зацікавленість учнів. Відповідь на тему «Похідна» можна отримати, знаючи, де використовуються похідні функції.

Щоб відповісти на це питання, можна перерахувати деякі дисципліни та їх розділи, у яких використовуються похідні.

Похідна в алгебрі:

1. Дотична до графіка функції

Стосовна графіку функціїf, що диференціюється в точці xпро , - Це пряма, що проходить через точку (xпро; f(x про )) і має кутовий коефіцієнтf'(x про).

y = f(x про) + f′(x про ) (x – x про )

2. Пошук проміжків зростання та зменшення функції

Функціяy=f(x) зростає на інтерваліX , якщо для будь-яких івиконується нерівність. Інакше кажучи – більшого значення аргументу відповідає більше значення функції.

Функціяy=f(x) зменшується на інтерваліX , якщо для будь-яких івиконується нерівність. Інакше кажучи – більшого значення аргументу відповідає менше значення функції.

3. Пошук точок екстремуму функції

Крапку називаютьточкою максимуму функціїy=f(x) якщо для всіхx . Значення функції у точці максимуму називаютьмаксимумом функції і позначають.

Крапку називаютьточкою мінімуму функціїy=f(x) якщо для всіхx з її околиці справедлива нерівність. Значення функції у точці мінімуму називаютьмінімумом функції і позначають.

Під околицею точки розуміють інтервал, де - Досить мале позитивне число.

Точки мінімуму та максимуму називаютьточками екстремуму , а значення функції, що відповідають точкам екстремуму, називаютьекстремумами функції .

4. Пошук проміжків опуклості та увігнутості функції

Графік функції, є на цьому інтерваліопуклим , лежить не вище за будь-яку свою дотичну (рис. 1).

Графік функції, що диференціюється на інтервалі, є на цьому інтерваліувігнутим , якщо графік цієї функції в межах інтервалу лежить не нижче за будь-яку свою дотичну (рис. 2).

Точкою перегину графіка функції називається точка, що розділяє проміжки опуклості та увігнутості.

5. Пошук точок вигину функції

Похідна у фізиці:

1. Швидкість як похідна дорога

2. Прискорення як похідна швидкостіa =

3. Швидкість розпаду радіоактивних елементів 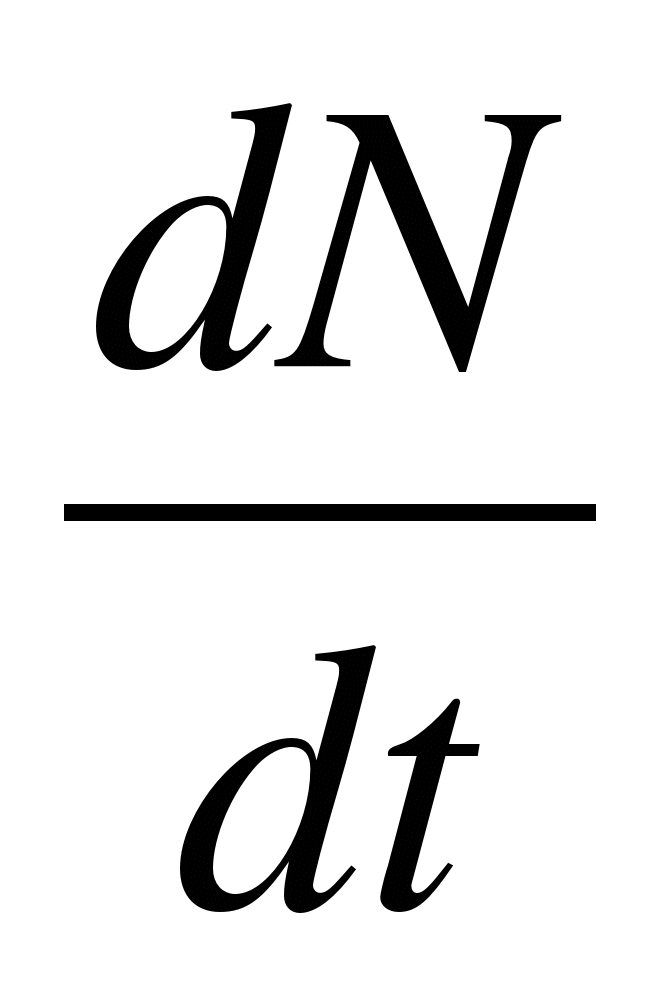= - λN

А також у фізиці похідну застосовують для обчислення:

Швидкості матеріальної точки

Миттєва швидкість як фізичний сенс похідної

Миттєве значеннясили змінного струму

Миттєве значення ЕРС електромагнітної індукції

Максимальну потужність

Похідна в хімії:

І в хімії знайшло широке застосування диференціальне літочислення для побудови математичних моделейхімічних реакцій та подальшого опису їх властивостей.

Похідну в хімії використовують для визначення дуже важливої речі – швидкості хімічної реакції, одного з вирішальних факторів, який потрібно враховувати у багатьох галузях науково-виробничої діяльності. V(t) = p '(t)

Кількість

в-ва на момент часу t 0

p = p(t 0 )

Функція

Інтервал часу

∆t = t-t 0

Приріст аргументу

Зміна кількості в-ва

∆p = p (t 0 + ∆ t) – p(t 0 )

Збільшення функції

Середня швидкість хімічної реакції

∆p/∆t

Відношення прирощення функції до прирощення аргументу

Похідна у біології:

Популяція – це сукупність особин даного виду, які займають певну ділянку території всередині ареалу виду, що вільно схрещуються між собою і частково або повністю ізольованих з інших популяцій, а також є елементарною одиницею еволюції.

Р = х (t)

Похідна у географії:

1. Деякі значення у сейсмографії

2. Особливості електромагнітного поляземлі

3. Радіоактивність ядерно-геоіфзичексих показників

4. Багато значення в економічній географії

5. Вивести формулу для обчислення чисельності населення на території у момент часу t.

у’= до у

Ідея соціологічної моделі Томаса Мальтуса полягає в тому, що приріст населення пропорційно числу населення в даний момент часу t через N(t). Модель Мальтуса непогано діяла для опису чисельності населення США з 1790 по 1860 роки. Нині ця модель у більшості країн не діє

Похідна в електротехніці:

У наших будинках, на транспорті, на заводах: усюди працює електричний струм. Під електричним струмом розуміють спрямований рух вільних електрично заряджених частинок.

Кількісною характеристикою електричного струмує сила струму.

У ланцюзі електричного струму електричний зарядзмінюється з часом за законом q=q(t). Сила струму I є похідною заряду q за часом.

У електротехніці переважно використовується робота змінного струму.

Електричний струм, що змінюється з часом, називають змінним. Ланцюг змінного струму може містити різні елементиКабіна: нагрівальні прилади, котушки, конденсатори.

Отримання змінного електричного струму ґрунтується на законі електромагнітної індукції, формулювання якого містить похідну магнітного потоку.

Похідна в економіці:

Економіка - основа життя, а в ній важливе місце займає диференціальне числення - апарат для економічного аналізу. Базове завдання економічного аналізу – вивчення зв'язків економічних величин як функцій.

Похідна в економіці вирішує важливі питання:

1. У якому напрямку зміниться дохід держави при збільшенні податків або запровадженні мит?

2. Збільшиться чи зменшиться виручка фірми зі збільшенням ціни її продукцию?

Для вирішення цих питань необхідно побудувати функції зв'язку вхідних змінних, які потім вивчаються способами диференціального обчислення.

Також за допомогою екстремуму функції (похідної) в економіці можна знайти найвищу продуктивність праці, максимальний прибуток, максимальний випуск та мінімальні витрати.

ВИСНОВОК: похідна успішно застосовується при вирішенні різних прикладних завдань у науці, техніці та житті

Як очевидно з вищепереліченого застосування похідної функції дуже різноманітне і як щодо математики, а й інших дисциплін. Тому можна дійти невтішного висновку, що вивчення теми: «Похідна функції» матиме своє застосування інших темах і предметах.

Ми переконалися у важливості вивчення теми "Похідна", її ролі у дослідженні процесів науки і техніки, у можливості конструювання по реальним подіямматематичні моделі і вирішувати важливі завдання.

“Музика може піднімати або утихомирювати душу,
Живопис – радувати око,
Поезія – пробуджувати почуття,
Філософія – задовольняти потреби розуму,
Інженерна справа – удосконалювати матеріальний бік життя людей,
Аматематика здатна досягти всіх цих цілей”.

Так сказав американський математикМоріс Клайн.

Список використаної літератури:

1. Богомолов Н.В., Самойленко І.І. Математика. – К.: Юрайт, 2015.

2. Григор'єв В.П., Дубінський Ю.А, Елементи вищої математики. – К.: Академія, 2014.

3. Баврін І.І. Основи вищої математики. - М: вища школа, 2013.

4. Богомолов Н.В. Практичні заняття з математики. – К.: Вища школа, 2013.

5. Богомолов Н.В. Збірник задач з математики. - М: Дрофа, 2013.

6. Рибніков К.А. Історія математики, "Видавництво Московського університету", М, 1960.

7. Виноградов Ю.М., Гомола А.І., Потапов В.І., Соколова О.В. - М.:Видавничий центр "Академія", 2010

8 . Башмаков М.І. Математика: алгебра та початку математичного аналізу, геометрія. - М.: Видавничий центр «Академія», 2016

Періодичні джерела:

Газети та журнали: «Математика», « Відкритий урок»

Використання ресурсів мережі Інтернет, електронних бібліотек:

www:egetutor.ru

matematika-na5.norod.ru

ФГОУ СПО

Новосибірський аграрний коледж

Реферат

з дисципліни «математика»

«Застосування похідної в науці та техніці»

С. Роздольне 2008 р.

Вступ

1. Теоретична частина

1.1 Завдання, що призводять до поняття похідної

1.2 Визначення похідної

1.3 Загальне правило знаходження похідної

1.4 Геометричний зміст похідної

1.5 Механічний зміст похідної

1.6 Похідна другого порядку та її механічний зміст

1.7 Визначення та геометричний зміст диференціала

2. Дослідження функцій за допомогою похідної

Висновок

Література

Вступ

У першому розділі мого реферату йтиметься про поняття похідної, правила її застосування, про геометричне і фізичному сенсіпохідною. У другому розділі мого реферату йтиметься про застосування похідної в науці і техніці і вирішенні завдань у цій галузі.

1. Теоретична частина

1.1 Завдання, що призводять до поняття похідної

При вивченні тих чи інших процесів та явищ часто виникає завдання визначення швидкості цих процесів. Її рішення призводить до поняття похідної, що є основним поняттям диференціального обчислення.

Метод диференціального обчислення було створено XVII і XVIII ст. З виникненням цього пов'язані імена двох великих математиків – І. Ньютона і Г.В. Лейбниця.

Ньютон дійшов відкриття диференціального обчислення під час вирішення завдань про швидкість руху матеріальної точки на даний час (миттєвої швидкості).

Як відомо, рівномірним рухомназивають такий рух, у якому тіло у рівні проміжки часу проходить рівні за довжиною відрізки шляху. Шлях, пройдений тілом за одиницю часу, називають швидкістю рівномірного руху.

Проте найчастіше практично маємо справу з нерівномірним рухом. Автомобіль, що їде дорогою, уповільнює рух у переходів і прискорює його на тих ділянках, де шлях вільний; літак знижує швидкість при приземленні тощо. Тому найчастіше нам доводиться мати справу з тим, що за рівні відрізки часу тіло проходить різні за довжиною відрізки колії. Такий рух називають нерівномірним.Його швидкість не можна охарактеризувати одним числом.

Часто для характеристики нерівномірного руху користуються поняттям середньої швидкостіруху за час ∆t, яке визначається співвідношенням де ∆s – шлях, пройдений тілом за час ∆t.

Так, при вільному падінні тіла середня швидкість його руху за перші дві секунди є

Майже така характеристика руху, як середня швидкість, говорить про рух дуже мало. Дійсно, при 4,9 м/с, а за 2-у – 14,7 м/с, тоді як середня швидкість за перші дві секунди становить 9,8 м/с. Середня швидкість протягом перших двох секунд не дає уявлення про те, як відбувався рух: коли тіло рухалося швидше, а коли повільніше. Якщо ж задати середні швидкості руху кожної секунди окремо, ми знатимемо, наприклад, що у 2-ю секунду тіло рухалося значно швидше, ніж у 1-ю. Однак у більшості випадків значно швидше, ніж нас мало влаштовує. Адже неважко зрозуміти, що протягом цієї другої секунди тіло також рухається по-різному: на початку повільніше, наприкінці швидше. А як воно рухається десь у середині цієї 2 секунди? Інакше кажучи, як визначити миттєву швидкість?

Нехай рух тіла описується законом Розглянемо шлях, пройдений тілом протягом часу від t0до t0 + ∆t, тобто. за час, що дорівнює ∆t. У момент t0тілом пройдено шлях, у момент – шлях. Тому за час ∆t тіло пройшло шлях і середня швидкість руху тіла за цей проміжок часу становитиме.

Чим менший проміжок часу ∆t, тим точніше можна встановити, з якою швидкістю рухається тіло в момент t0, оскільки тіло, що рухається, не може значно змінити швидкість за малий проміжок часу. Тому середня швидкість при прагненні ∆t до нуля наближається до дійсної швидкості руху і межі дає швидкість руху в даний момент часу t0 (миттєву швидкість).

Таким чином ,

Визначення 1. Миттєва швидкістьпрямолінійного руху тіла в даний момент часу t0називається межа середньої швидкості за час від t0 до t0+ ∆t, коли проміжок часу ∆t прагне нуля.

Отже, щоб знайти швидкість прямолінійного нерівномірного руху на даний момент, потрібно знайти межу відношення збільшення шляху ∆до збільшення часу ∆t за умови тобто. Лейбніц прийшов до відкриття диференціального обчислення при вирішенні задачі про побудову дотичної до будь-якої кривої, заданої своїм рівнянням.

Вирішення цього завдання має велике значення. Адже швидкість точки, що рухається, спрямована по дотичній до її траєкторії, тому визначення швидкості снаряда на його траєкторії, швидкості будь-якої планети на її орбіті зводиться, до визначення напрямку дотичної до кривої.

Визначення дотичної як прямої, що має з кривою лише одну загальну точку, справедливе для кола, непридатне для багатьох інших кривих.

Нижче представлене визначення дотичної до кривої, як відповідає інтуїтивному уявленню неї, а й дозволяє фактично шукати її напрям, тобто. обчислювати кутовий коефіцієнт дотичної.

Визначення 2. Стосуєтьсядо кривої в точці М називається пряма МТ, яка є граничним положенням січної ММ1, коли точка М1, переміщаючись кривою, необмежено наближається до точки М.

1.2 Визначення похідної

Зауважимо, що при визначенні дотичної до кривої та миттєвої швидкості нерівномірного руху, по суті, виконуються ті самі математичні операції:

1. Заданого значення аргументу дають приріст і обчислюють нове значення функції, що відповідає новому значенню аргументу.

2. Визначають збільшення функції, що відповідає обраному збільшенню аргументу.

3. Збільшення функції поділяють на збільшення аргументу.

4. Обчислюють межу цього відношення за умови, що збільшення аргументу прагне нуля.

До граничних переходів такого типу призводять розв'язання багатьох завдань. Виникає необхідність зробити узагальнення і дати назву цьому граничному переходу.

Швидкість зміни функції залежно від зміни аргументу, очевидно, можна охарактеризувати ставленням. Це ставлення називається середньою швидкістю зміни функції на відрізку від до. Зараз потрібно розглянути межу дробу Межа цього відношення при прагненні збільшення аргументу до нуля (якщо ця межа існує) є деякою новою функцією від. Цю функцію позначають символами y', називають похіднийданої функції оскільки вона отримана (вироблена) з функції Сама ж функція називається первісноїфункцією по відношенню до своєї похідної

Визначення 3. Похіднийфункції у цій точці називають межу відношення збільшення функції ∆y до відповідного прирощення аргументу ∆x за умови, що ∆x→0, тобто.

1.3 Загальне правило знаходження похідної

Операцію відшукання похідної деякої функції називають диференціюваннямфункції, а розділ математики, що вивчає властивості цієї операції, - диференціальним обчисленням.

Якщо функція має похідну у точці x=a, то кажуть, що вона диференційованау цій точці. Якщо функція має похідну в кожній точці цього проміжку, то кажуть, що вона диференційованана цьому проміжку .

Визначення похідної як з вичерпною повнотою характеризує поняття швидкості зміни функції за зміни аргументу, а й дає спосіб фактичного обчислення похідної цієї функції. Для цього необхідно виконати наступні чотири дії (чотири кроки), зазначені у самому визначенні похідної:

1. Знаходять нове значення функції, представивши в цю функціюзамість x нове значення аргумента: .

2. Визначають збільшення функції, вираховуючи це значення функції з її нового значення: .

3. Складають відношення збільшення функції до збільшення аргументу: .

4. Переходять до межі і знаходять похідну: .

Взагалі, похідна – це «нова» функція, вироблена від цієї функції за вказаним правилом.

1.4 Геометричний зміст похідної

Геометрична інтерпретація похідної, вперше дана в наприкінці XVIIв. Лейбніца, полягає в наступному: значення похідної функції у точці x дорівнює кутовому коефіцієнту дотичної, проведеної до графіка функції у тій точці x,тобто.

Рівняння дотичної, як і будь-якої прямої, що проходить через дану точкуу цьому напрямі, має вигляд – поточні координати. Але й рівняння дотичної запишеться так: . Рівняння нормалі запишеться як.

1.5 Механічний зміст похідної

Механічне тлумачення похідної було вперше дано І. Ньютон. Воно полягає в наступному: швидкість руху матеріальної точки в даний час дорівнює похідної шляху за часом, тобто. Отже, якщо закон руху матеріальної точки заданий рівнянням, то знаходження миттєвої швидкості точки у якийсь певний час потрібно знайти похідну і підставити у ній відповідне значення t.

1.6 Похідна другого порядку та її механічний зміст

Отримаємо (рівняння з зробленого у підручнику Лисичкін В.Т. Соловейчик І.Л. «математика» с. 240):

Таким чином, прискорення прямолінійного руху тіла в даний момент дорівнює другий похідний шлях за часом, обчисленої для даного моменту.У цьому полягає механічний зміст другий похідної.

1.7 Визначення та геометричний зміст диференціала

Визначення 4.Головна частина прирощення функції, лінійна щодо прирощення функції, лінійна щодо прирощення незалежною зміною, називається диференціаломфункції та позначається знаком d, тобто. .

Диференціал функції геометрично зображується збільшенням ординати дотичної, проведеної в точці M ( x ; y ) при даних значеннях x та ∆x.

Обчислення диференціала – .

Застосування диференціала у наближених обчисленнях – , наближене значення збільшення функції збігається з її диференціалом.

Теорема 1. Якщо функція, що диференціюється зростає (зменшується) у цьому інтервалі, то похідна цієї функції не негативна (не позитивна) у цьому інтервалі.

Теорема 2. Якщо похідна функція позитивна (негативна) в якому інтервалі, то функція в цьому інтервалі монотонно зростає (монотонно убуває).

Сформулюємо тепер правило знаходження інтервалів монотонності функції

1. Обчислюють похідну цієї функції.

2. Знаходять точки, у яких дорівнює нулю чи немає. Ці точки називаються критичнимидля функції

3. Знайденими точками область визначення функції розбивається на інтервали, кожному з яких похідна зберігає свій знак. Ці інтервали є інтервалами монотонності.

4. Досліджують знак на кожному із знайдених інтервалів. Якщо на аналізованому інтервалі, то цьому інтервалі зростає; якщо ж, то на такому інтервалі зменшується.

Залежно та умовами завдання правило знаходження інтервалів монотонності може спрощуватися.

Визначення 5.Точка називається точкою максимуму (мінімуму) функції, якщо має місце нерівність відповідно для будь-якого x з якої околиці точки.

Якщо - точка максимуму (мінімуму) функції, то кажуть, що (мінімум)у точці. Максимум та мінімум функції об'єднують назву екстремумфункції, а точки максимуму та мінімуму називають точками екстремуму (екстремальними точками).

Теорема 3.(Необхідна ознака екстремуму). Якщо і похідна в цій точці існує, вона дорівнює нулю: .

Теорема 4.(Достатня ознака екстремуму). Якщо похідна при переході x через a змінює знак, то a є точкою екстремуму функції .

Основні моменти дослідження похідної:

1. Знаходять похідну.

2. Знаходять всі критичні точки з області визначення функції.

3. Встановлюють знаки похідної функції під час переходу через критичні точки і виписують точки екстремуму.

4. Обчислюють значення функції у кожній екстремальній точці.

2. Дослідження функцій за допомогою похідної

Завдання №1 . Об'єм колоди.Круглим діловим лісом називають колоди правильної форми без дефектів деревини з відносно невеликою різницею діаметрів товстого та тонкого кінців. При визначенні обсягів круглого ділового лісу зазвичай застосовують спрощену формулу, де – довжина колоди – площа його середнього перерізу. З'ясуйте, завершується чи занижується реальний обсяг; оцініть відносну похибку.

Рішення. Форма круглого ділового лісу близька до усіченого конуса. Нехай – радіус більшого, меншого кінця колоди. Тоді його майже точний обсяг (обсяг усіченого конуса) можна, як відомо, знайти за такою формулою. Нехай значення об'єму, обчислене за спрощеною формулою. Тоді;

Тобто. . Значить спрощена формула дає заниження величини обсягу. Покладемо тепер. Тоді. Звідси видно, що відносна похибка залежить від довжини колоди, а визначається ставленням. Оскільки при зростає на проміжку. Тому, отже, відносна похибка вбирається у 3,7%. У практиці лісознавства така похибка вважається цілком допустимою. З більшою точністю практично неможливо виміряти ні діаметри торців (адже вони дещо відрізняються від кіл), ні довжину колоди, оскільки вимірюють не висоту, а утворює конуса (довжина колоди в десятки разів більша за діаметр, і це не призводить до великих похибок). Таким чином, на перший погляд неправильна, але більше проста формуладля обсягу усіченого конуса у реальній ситуації виявляється цілком правомірною. Багаторазово проведені з допомогою спеціальних методів перевірки показали, що з масовому обліку ділового лісу відносна похибка під час використання аналізованої формули вбирається у 4%.

Завдання №2 . При визначенні обсягів ям, траншей відер та інших ємностей, що мають форму усіченого конуса, у с/г практиці іноді користуються спрощеною формулою, де – висота – площі основ конуса. З'ясуйте, завищується чи занижується при цьому реальний обсяг, оцініть відносну похибку за умови природної для практики умови: (– радіуси підстав, .

Рішення. Позначивши через справжнє значення обсягу зрізаного конуса, а через значення, обчислене за спрощеною формулою, отримаємо: , тобто. . Значить спрощена формула дає завищення величини обсягу. Повторивши подальше вирішення попереднього завдання, знайдемо, що відносна похибка буде не більше 6,7%. Ймовірно, така точність допустима при нормуванні землерийних робіт - адже ями не будуть ідеальними конусами, та й відповідні параметри в реальних умовах вимірюють дуже грубо.

Завдання №3 . У спеціальній літературі для визначення кута повороту шпинделя фрезерного верстата при фрезеруванні муфт з зубами виводиться формула, де. Так як ця формула складна, рекомендується відкинути її знаменник і користуватися спрощеною формулою. При яких (– ціле число) можна користуватися цією формулою, якщо при визначенні кута допускається похибка?

Рішення.Точну формулу після нескладних тотожних перетвореньможна привести до вигляду. Тому за використання наближеної формули допускається абсолютна похибка, де. Досліджуємо функцію на відрізку. У цьому 0,06, тобто. кут належить першій чверті. Маємо: . Зауважимо, що на проміжку, що розглядається, а значить, функція на цьому проміжку зменшується. Оскільки далі, то за всіх розглянутих. Отже, . Оскільки радіан, досить вирішити нерівність. Вирішуючи це нерівність підбором, знаходимо, що, . Через те, що функція зменшується, слідує, що.

Висновок

Застосування похідної досить широко, і його можна повністю охопити у роботі такого типу, проте спробував розкрити основні базові моменти. У наш час, у зв'язку з науково-технічним прогресом, зокрема з швидкої еволюцією обчислювальних систем, диференціальне обчислення стає дедалі актуальними у вирішенні як простих, і надскладних завдань.

Література

1. В.А. Петров «Математичний аналіз у виробничих завданнях»

2. Соловійчик І.Л., Лисичкін В.Т. «Математика»

Чайкін Семен, Майсак Кирило, Залогіна Анастасія, Шахзадова Анна

Дана розробка містить презентацію на тему "Застосування похідної в хімії та біології". В ході проектної діяльностібула висунута гіпотеза про те, що похідна знаходить своє застосування у цих галузях науки. В ході дослідницької роботибуло з'ясовано, яка роль похідної таких науках як хімія і біологія, де й під час вирішення яких завдань вона знаходить своє застосування. В результаті виконаної роботи дійшли висновку, що гіпотеза справді підтвердилася.

Завантажити:

Попередній перегляд:

https://accounts.google.com

Підписи до слайдів:

Гіпотеза:

Попередній перегляд:

Щоб скористатися попереднім переглядом презентацій, створіть собі обліковий запис Google і увійдіть до нього: https://accounts.google.com

Підписи до слайдів:

Застосування похідної в хімії та біології Роботу виконали учні 11В класу МБОУ ЗОШ №6: Чайкін Семен, Майсак Кирило, Залогіна Анастасія, Шахзадова Анна м. Ставрополь, 2014 рік

Гіпотеза:

І в хімії знайшло широке застосування диференціальне літочислення для побудови математичних моделей хімічних реакцій та подальшого опису їх властивостей. Хімія - це наука про речовини, про хімічні перетворення речовин. Хімія вивчає закономірності перебігу різних реакцій Швидкістю хімічної реакції називається зміна концентрації речовин, що реагують, в одиницю часу. Використання похідної в хімії та біології Визначення швидкості хімічної реакції

Навіщо потрібна похідна у реакціях? Так як швидкість реакції v безперервно змінюється в ході процесу, її зазвичай виражають похідної концентрації речовин, що реагують за часом.

Формула похідної в хімії Якщо C (t) – закон зміни кількості речовини, що вступила в хімічну реакцію, швидкість v (t) хімічної реакції в момент часу t дорівнює похідній:

Визначення швидкості реакції Межа відношення прирощеної функції до прирощеного аргументу при прагненні Δt до нуля - є швидкість хімічної реакції в даний момент часу

Завдання з хімії: Нехай кількість речовини, що вступила в хімічну реакцію, задається залежністю: С (t) = t 2 /2 + 3 t –3 (моль) Знайти швидкість хімічної реакції через 3 секунди. Рішення: v (t) = З '(t); v(t) = t + 3; v (3) = 3+3 = 6. Відповідь: 6 моль\с.

Біологічний сенс похідної Нехай залежність між числом особин популяції мікроорганізмів у та часом t її розмноження задана рівнянням: у = x(t). Нехай t - проміжок часу від деякого початкового значення t до t + t . Тоді у + ∆у = x (t + ∆ t) - нове значення чисельності популяції, що відповідає моменту t + ∆ t, а ∆ y + x (t + ∆ t) - x (t) - зміна числа особин організмів. Ставлення є середньою швидкістю розмноження чи середньої продуктивністю життєдіяльності популяції. Обчислюючи, отримуємо y = P (t) = x (t), або продуктивність життєдіяльності популяції в момент часу t.

Приклад Популяція бактерій в момент t (с) налічує x (t) особин. . Знайти швидкість зростання популяції: а) у довільний момент t б) у момент t = 1 c . Рішення: P = x'(t) = 200t; P(1) = 200 (про/с). Відповідь: 200 про/с.

Поняття похідної дуже важливе в хімії та в біології, особливо при визначенні швидкості перебігу реакції.

Висновок: Диференціальне обчислення- це опис навколишнього світу, виконане математичною мовою. Похідна - одне з найважливіших понять математичного аналізу. Знання похідної допомагає нам успішно вирішувати як математичні завдання, а й завдання практичного характеру у різних галузях науки, техніки і життя.

Південно-Сахалінський Державний Університет

Кафедра математики

Курсова робота

Тема: Практичне застосування похідної

Викладач: Лихачова О. Н.

Південно-Сахалінськ

2002р
Вступ

У цій роботі я розгляну застосування похідної у різних науках та галузях. Робота розбита на глави, у кожній з яких розглядається одна із сторін диференціального обчислення (геометричний, фізичний зміст тощо).

1. Поняття похідної

1-1. Історичні відомості

Диференціальне числення було створено Ньютоном і Лейбніцем наприкінці 17 століття на основі двох завдань:

1) про розшук дотичної до довільної лінії

2) про розшук швидкості при довільному законі руху

Ще раніше поняття похідної зустрічалося на роботах італійського математика Тартальи (близько 1500 - 1557 рр.) - тут виникла дотична під час вивчення питання куті нахилу зброї, у якому забезпечується максимальна дальність польоту снаряда.

У 17 столітті на основі вчення Г.Галілея про рух активно розвивалася кінематична концепція похідної. Різні виклади стали зустрічатися у роботах у Декарта, французького математика Роберваля, англійського вченого Л. Грегорі. Великий внесок у вивчення диференціального обчислення зробили Лопіталь, Бернуллі, Лагранж, Ейлер, Гаус.

1-2. Поняття похідної

Нехай y = f(x) є безперервна функція аргументу x, визначена в проміжку (a; b), і нехай х 0 - довільна точка цього проміжку

Дамо аргументу x збільшення ∆x, тоді функція y = f(x) отримає збільшення ∆y = f(x + ∆x) - f(x). Межа, якої прагне відношення ∆y / ∆x при ∆x → 0, називається похідною від функції f(x).

1-3. Правила диференціювання та таблиця похідних

		(sin x)" = cos x
	(1 / x)" = -1 / x 2	(cos x)" = -sin x
	(√x)" = 1 / 2√x	(tg x)" = 1 / cos 2 x
(uv)" = u"v + uv"	(a x)" = a x ln x	(ctg x)" = 1 / sin 2 x
(u / v) "= (u "v - uv") / v 2		(arcsin x)" = 1 / √ (1- x 2)
	(log a x)" = (log a e) / x	(arccos x)" = -1 / √ (1- x 2)
	(ln x)" = 1 / x	(arctg x)" = 1 / √ (1+ x 2)
		(arcctg x)" = -1 / √ (1+ x 2)

2. Геометричний зміст похідної

2-1. Стосовна до кривої

Нехай маємо криву і на ній фіксовану точку M і точку N. Стосовною точкою M називається пряма, положення якої прагне зайняти хорда MN, якщо точку N необмежено наближати по кривій до M.

Розглянемо функцію f(x) та відповідну цій функції криву y = f(x). За деякого значення x функція має значення y = f(x). Цим значенням кривою відповідає точка M(x 0 , y 0). Введемо новий аргумент x 0 + ∆x, його значення відповідає значення функції y 0 + ∆y = f(x 0 + ∆x). Відповідна точка - N(x 0 + ∆x, y 0 + ∆y). Проведемо сікучу MN і позначимо φ кут, утворений січною з позитивним напрямом осі Ox. З малюнка видно, що ∆y / ∆x = tg? Якщо тепер ∆x буде наближатися до 0, точка N переміщатиметься вздовж кривої, що січе MN - повертатиметься навколо точки M, а кут φ - змінюватись. Якщо при ∆x → 0 кут φ прагне деякого α, то пряма, яка проходить через M і складова з позитивним напрямом осі абсцис кут α, буде шуканою дотичною. При цьому, її кутовий коефіцієнт:

Тобто значення похідної f "(x) при даному значенні аргументу x дорівнює тангенсу кута, утвореного з позитивним напрямом осі Ox, що стосується графіку функції f(x) у точці M(x, f(x)).

Стосовна до просторової лінії має визначення, аналогічне визначенню дотичної до плоскої кривої. У цьому випадку, якщо функція задана рівнянням z = f(x, y), кутові коефіцієнти при осях OX і OY дорівнюють приватним похідним f по x і y.

2-2. Дотична площина до поверхні

Стосовною площиною до поверхні в точці M називається площина, що містить дотичні до всіх просторових кривих поверхні, що проходять через M - точку торкання.

Візьмемо поверхню, задану рівнянням F(x, y, z) = 0 і якусь звичайну точку M(x 0 , y 0 , z 0) на ній. Розглянемо на поверхні деяку криву L, що проходить через M. Нехай крива задана рівняннями

x =? (t); y = ψ(t); z = χ(t).

Підставимо в рівняння поверхні ці вирази. Рівняння перетвориться на тотожність, тому що крива цілком лежить на поверхні. Використовуючи властивість інваріантності форми диференціала, продиференціюємо отримане рівняння t:

Рівняння дотичної до кривої L у точці M мають вигляд:

Оскільки різниці x - x 0 , y - y 0 , z - z 0 пропорційні відповідним диференціалам, то остаточне рівняння площини виглядає так:

F" x (x - x 0) + F" y (y - y 0) + F" z (z - z 0) = 0

і для окремого випадку z = f(x, y):

Z - z 0 = F "x (x - x 0) + F" y (y - y 0)

Приклад:Знайти рівняння дотичної площини в точці (2a; a; 1,5a) гіперболічного параболоїда

Рішення:

Z" x = x / a = 2; Z" y = -y / a = -1

Рівняння площини:

Z - 1.5a = 2(x - 2a) - (Y - a) або Z = 2x - y - 1.5a

3-1. Швидкість матеріальної точки

Нехай залежність шляху s від часу t у даному прямолінійному русіматеріальної точки виражається рівнянням s = f(t) і t 0 деякий момент часу. Розглянемо інший момент часу t, позначимо ∆t = t - t 0 і обчислимо збільшення шляху: ∆s = f(t 0 + ∆t) - f(t 0). Відношення ∆s / ∆t називають середньою швидкістю руху за час ∆t, що протік від вихідного моменту t 0 . Швидкістю називають межу цього відношення при ∆t → 0.

Середнє прискорення нерівномірного руху в інтервалі (t; t + ∆t) – це величина = ∆v / ∆t. Миттєвим прискоренням матеріальної точки в момент часу t буде межа середнього прискорення:

Тобто перша похідна за часом (v"(t)).

Приклад:Залежність пройденого тілом шляху іноді задається рівнянням s = A + Bt + Ct 2 +Dt 3 (C = 0,1 м/с, D = 0,03 м/с 2). Визначити час після початку руху, через яке прискорення тіла дорівнюватиме 2 м/с 2 .

Рішення:

v(t) = s"(t) = B + 2Ct + 3Dt 2; a(t) = v"(t) = 2C + 6Dt = 0,2 + 0,18t = 2;

1,8 = 0,18t; t = 10 c

3-2. Теплоємність речовини за даної температури

Для підвищення різних температур T на те саме значення, що дорівнює T 1 - T, на 1 кг. даної речовини необхідна різна кількість теплоти Q 1 - Q, причому відношення

для цієї речовини не є постійним. Таким чином, для даної речовини кількість теплоти Q є нелінійною функцією температури T: Q = f(T). Тоді Q = f(t + T) - f(T). Ставлення

називається середньою теплоємністю на відрізку, а межа цього виразу при ∆T → 0 називається теплоємністю даної речовини при температурі T.

3-3. Потужність

Зміна механічного рухутіла викликається силами, які діють нього із боку інших тіл. Щоб кількісно характеризувати процес обміну енергією між тілами, що взаємодіють, в механіці вводиться поняття роботи сили. Щоб охарактеризувати швидкість роботи, вводять поняття потужності:.

4. Диференціальне обчислення економіки

4-1. Дослідження функцій

Диференціальне обчислення - широко застосовуваний економічного аналізу математичний апарат. Базовим завданням економічного аналізу вивчення зв'язків економічних величин, записаних як функцій. У якому напрямі зміниться дохід держави зі збільшенням податків чи запровадження імпортних мит? Чи збільшиться чи зменшиться виручка фірми при підвищенні ціни на її продукцію? У якій пропорції додаткове обладнання може замінити працівників, що вибувають? Для вирішення подібних завдань повинні бути побудовані функції зв'язку змінних, що входять до них, які потім вивчаються за допомогою методів диференціального обчислення. В економіці дуже часто потрібно знайти найкраще чи оптимальне значення показника: найвищу продуктивність праці, максимальний прибуток, максимальний випуск, мінімальні витрати тощо. буд. Кожен показник є функцією від однієї чи кількох аргументів. Таким чином, знаходження оптимального значення показника зводиться до знаходження екстремуму функції.

По теоремі Ферма, якщо точка є екстремумом функції, то похідна у ній або немає, або дорівнює 0. Тип екстремуму можна визначити за однією з достатніх умов екстремуму:

1) Нехай функція f(x) диференційована в околиці точки x 0 . Якщо похідна f "(x) при переході через точку x 0 змінює знак з + на -, то x 0 - точка максимуму, якщо з - на +, то x 0 - точка мінімуму, якщо не змінює знак, то в цій точці немає екстремуму.

2) Нехай функція f(x) двічі диференційована в околиці точки x 0 , причому f "(x 0) = 0, f ""(x 0) ≠ 0, то в точці x 0 функція f(x 0) має максимум якщо f ""(x 0)< 0 и минимум, если f ""(x 0) > 0.

Крім того, друга похідна характеризує опуклість функції (графік функції називається опуклим вгору [вниз] на інтервалі (a, b), якщо він на цьому інтервалі розташований не вище [не нижче] будь-якої своєї дотичної).

Приклад:вибрати оптимальний обсяг виробництва фірмою, функція прибутку якої може бути змодельована залежністю:

π(q) = R(q) - C(q) = q 2 - 8q + 10

Рішення:

π"(q) = R"(q) - C"(q) = 2q - 8 = 0 → q extr = 4

При q< q extr = 4 → π"(q) < 0 и прибыль убывает

За q > q extr = 4 → π"(q) > 0 і прибуток зростає

При q = 4 прибуток набуває мінімального значення.

Яким буде оптимальний обсяг випуску для фірми? Якщо фірма не може виробляти за аналізований період більше 8 одиниць продукції (p(q = 8) = p(q = 0) = 10), то оптимальним рішенням взагалі нічого не вироблятиме, а отримувати дохід від здачі в оренду приміщень та/або обладнання. Якщо фірма здатна виробляти більше 8 одиниць, то оптимальним для фірми буде випуск межі своїх виробничих потужностей.

4-2. Еластичність попиту

Еластичність функції f(x) у точці x 0 називають межу

Попит - це кількість товару, яку покупець потребує. Цінова еластичність попиту E D - це величина, що характеризує те, як попит реагує зміну ціни. Якщо │E D │>1, то попит називається еластичним, якщо │E D │<1, то неэластичным. В случае E D =0 спрос называется совершенно неэластичным, т. е. изменение цены не приводит ни к какому изменению спроса. Напротив, если самое малое снижение цены побуждает покупателя увеличить покупки от 0 до предела своих возможностей, говорят, что спрос является совершенно эластичным. В зависимости от текущей эластичности спроса, предприниматель принимает решения о снижении или повышении цен на продукцию.

4-3. Граничний аналіз

p align="justify"> Важливий розділ методів диференціального обчислення, що використовуються в економіці - методи граничного аналізу, тобто сукупність прийомів дослідження змінних величин витрат або результатів при змінах обсягів виробництва, споживання і т. п. на основі аналізу їх граничних значень. Граничний показник (показники) функції – це її похідна (у разі функції однієї змінної) або приватні похідні (у разі функції кількох змінних)

В економіці часто використовуються середні величини: середня продуктивність праці, середні витрати, середній дохід, середній прибуток і т. д. Але часто потрібно дізнатися, яку величину зросте результат, якщо будуть збільшені витрати або навпаки, наскільки зменшиться результат, якщо витрати скоротяться. За допомогою середніх величин відповідь це питання отримати неможливо. У подібних завданнях потрібно визначити межу відношення приростів результату та витрат, тобто знайти граничний ефект. Отже, для їх вирішення необхідне застосування методів диференціального обчислення.

5. Похідна у наближених обчисленнях

5-1. Інтерполяція

Інтерполяцією називається наближене обчислення значень функції за декількома даними її значень. Інтерполяція широко використовується у картографії, геології, економіці та інших науках. Найпростішим варіантом інтерполяції є форма Лагранжа, але коли вузлових точок багато і інтервали між ними великі, або потрібно отримати функцію, кривизна якої мінімальна вдаються до сплайн-інтерполяції, що дає більшу точність.

Нехай K n – система вузлових точок a = x 0< x 1 <…< x n = b. Функция S k (x) называется сплайн-функцией S k (x) степени k≥0 на K n , если

а) S k (x) є C k -1 ()

б) S k (x) - багаточлен ступеня не більшого k

Сплайн-функція Ŝk(x) є Sk(Kn) називається інтерполюючою сплайн-функцією, якщо Ŝk(xj) = f(xj) для j = 0,1,…,n

У додатках часто досить вибрати k=3 і застосувати т. зв. кубічну інтерполяцію.

Т. до. s(x) на кожному частковому інтервалі є багаточлен третього ступеня, то для x є

Тут s 2 j , c j 1 , c j 0 невідомі для j = 1, 2, …, n

Останні виключаються з вимоги s(x j) = y j:

Диференціюючи цю функцію і враховуючи, що s"(x) по всьому інтервалі і, отже, зокрема, у вузлах має бути безперервна, остаточно отримуємо систему рівнянь:

щодо n+1 невідомих s 2 0 s 2 1 ... s 2 n. Для однозначного їх визначення залежно від завдання додаються ще два рівняння:

Нормальний випадок(N):

Періодичний випадок (P) (тобто.f(x+(x n -x 0)) =f(x)):

Задане згладжування на кордонах:

Приклад:сплайн-інтерполяція функції f(x)=sin x, n=4.

Функція періодична, тому використовуємо випадок P.

Сплайн-функція виходить така:

5-2. Формула Тейлора

Розкладання функцій у нескінченні ряди дозволяє отримати значення функції у цій точці з точністю. Цей прийом широко використовується у програмуванні та інших дисциплінах.

Кажуть, що функція розкладається на даному проміжку в статечний ряд, якщо існує такий статечний ряд a 0 + a 1 (x - a) + a 2 (x - a) 2 + … + a n (x - a) n + …, який у цьому проміжку сходить до цієї функції. Можна довести, що це розкладання єдине:

Нехай функція f(x) нескінченно диференційована у точці a. Ступеневий ряд виду

називається рядом Тейлора для функції f(x), записаним за ступенями різниці (x - a). Взагалі, щоб ряд Тейлора сходився до f(x) необхідно і достатньо, щоб залишковий член ряду прагнув 0. При a = 0 ряд Тейлора зазвичай називають рядом Маклорена.

І. М. Уваренков,

М. З. Маллер

Курс математичного аналізу, т.1

В. А. Дударенко,

А.А. Дадаян

Математичний аналіз

Диференціальне та інтегральне обчислення

Т. І. Трофімова

Курс фізики

О. О. Замков

О. В. Толстоп'ятенко

Ю. Н. Черемних

Математичні методи економіки

А. С. Солодовников

В. А. Бабайцев

А. В. Браїлов

І.Г. Шандра

Математика економіки

Вступ

1. Поняття похідної

1-1. Історичні відомості

1-2. Поняття похідної

1-3. Правила диференціювання та таблиця похідних

2. Геометричний зміст похідної

2-1. Стосовна до кривої

2-2. Дотична площина до поверхні

3. Використання похідної у фізиці

3-1. Швидкість матеріальної точки

3-2. Теплоємність за даної температури

3-3. Потужність

4. Диференціальне обчислення економіки

4-1. Дослідження функцій

4-2. Еластичність попиту

4-3. Граничний аналіз

5. Похідна у наближених обчисленнях

5-1. Інтерполяція

5-2. Формула Тейлора

5-3. Наближені обчислення

Висновок

Список використаної літератури

Південно-Сахалінський Державний Університет

Кафедра математики

Курсова робота

Тема: Практичне застосування похідної

Викладач: Лихачова О. Н.

Південно-Сахалінськ

2002р Вступ

1. Поняття похідної

1-1. Історичні відомості

Диференціальне числення було створено Ньютоном і Лейбніцем наприкінці 17 століття на основі двох завдань:

1) про розшук дотичної до довільної лінії

2) про розшук швидкості при довільному законі руху

Ще раніше поняття похідної зустрічалося на роботах італійського математика Тартальї (близько 1500 - 1557 рр.) - тут виникла дотична під час вивчення питання куті нахилу зброї, у якому забезпечується максимальна дальність польоту снаряда.

1-2. Поняття похідної

Нехай y = f(x) є безперервна функція аргументу x, визначена в проміжку (a; b), і нехай х0 – довільна точка цього проміжку

1-3. Правила диференціювання та таблиця похідних

C" = 0(xn) = nxn-1(sin x)" = cos xx" = 1(1/x)" = -1 / x2(cos x)" = -sin x(Cu)"=Cu"( √x)" = 1 / 2√x(tg x)" = 1 / cos2 x(uv)" = u"v + uv"(ax)" = ax ln x(ctg x)" = 1 / sin2 x( u / v) "= (u "v - uv") / v2 (ex) "= ex (arcsin x)" = 1 / √ (1-x2) (logax)" = (logae) / x (arccos x) " = -1 / √ (1- x2) (ln x)" = 1 / x (arctg x)" = 1 / √ (1+ x2) (arcctg x)" = -1 / √ (1+ x2)

2. Геометричний зміст похідної

2-1. Стосовна до кривої

Розглянемо функцію f(x) та відповідну цій функції криву y = f(x). За деякого значення x функція має значення y = f(x). Цим значенням на кривій відповідає точка M(x0, y0). Введемо новий аргумент x0 + ∆x, його значення відповідає значення функції y0 + ∆y = f(x0 + ∆x). Відповідна точка - N(x0 + ∆x, y0 + ∆y). Проведемо сікучу MN і позначимо φ кут, утворений січною з позитивним напрямом осі Ox. З малюнка видно, що ∆y / ∆x = tg? Якщо тепер ∆x буде наближатися до 0, точка N переміщатиметься вздовж кривої, що січе MN - повертатиметься навколо точки M, а кут φ - змінюватись. Якщо при ∆x → 0 кут φ прагне деякого α, то пряма, яка проходить через M і складова з позитивним напрямом осі абсцис кут α, буде шуканою дотичною. При цьому, її кутовий коефіцієнт:

2-2. Дотична площина до поверхні

Візьмемо поверхню, задану рівнянням F(x, y, z) = 0 і якусь звичайну точку M(x0, y0, z0) у ній. Розглянемо на поверхні деяку криву L, що проходить через M. Нехай крива задана рівняннями

x =? (t); y = ψ(t); z = χ(t).

Рівняння дотичної до кривої L у точці M мають вигляд:

Т. до. різниці x - x0, y - y0, z - z0 пропорційні відповідним диференціалам, то остаточне рівняння площини виглядає так:

F"x(x - x0) + F"y(y - y0) + F"z(z - z0) = 0

і для окремого випадку z = f(x, y):

Z - z0 = F"x(x - x0) + F"y(y - y0)

Приклад:Знайти рівняння дотичної площини в точці (2a; a; 1,5a) гіперболічного параболоїда

Рішення:

Z"x=x/a=2; Z"y=-y/a=-1

Рівняння площини:

Z - 1.5a = 2(x - 2a) - (Y - a) або Z = 2x - y - 1.5a

3. Використання похідної у фізиці

3-1. Швидкість матеріальної точки

Нехай залежність шляху s від часу t в даному прямолінійному русі матеріальної точки виражається рівнянням s = f (t) і t0 деякий момент часу. Розглянемо інший момент часу t, позначимо ∆t = t - t0 і обчислимо збільшення шляху: ∆s = f(t0 + ∆t) - f(t0). Відношення ∆s / ∆t називають середньою швидкістю руху за час ∆t, що протік від вихідного моменту t0. Швидкістю називають межу цього відношення при ∆t → 0.

Тобто перша похідна за часом (v"(t)).

Приклад:Залежність пройденого тілом шляху іноді задається рівнянням s = A + Bt + Ct2 + Dt3 (C = 0,1 м/с, D = 0,03 м/с2). Визначити час після початку руху, через яке прискорення тіла дорівнюватиме 2 м/с2.

Рішення:

v(t) = s"(t) = B + 2Ct + 3Dt2; a(t) = v"(t) = 2C + 6Dt = 0,2 + 0,18t = 2;

1,8 = 0,18t; t = 10 c

3-2. Теплоємність речовини за даної температури

Для підвищення різних температур T на те саме значення, рівне T1 - T, на 1 кг. даної речовини необхідна різна кількість теплоти Q1 - Q, причому відношення

3-3. Потужність

Зміна механічного руху тіла викликається силами, які діють нього із боку інших тіл. Щоб кількісно характеризувати процес обміну енергією між тілами, що взаємодіють, в механіці вводиться поняття роботи сили. Щоб охарактеризувати швидкість роботи, вводять поняття потужності:.

4. Диференціальне обчислення економіки

4-1. Дослідження функцій

1) Нехай функція f(x) диференційована в околиці точки x0. Якщо похідна f "(x) при переході через точку x0 змінює знак з + на - то x0 - точка максимуму, якщо з - на +, то x0 - точка мінімуму, якщо не змінює знак, то в цій точці немає екстремуму.

2) Нехай функція f(x) двічі диференційована в околиці точки x0, причому f "(x0) = 0, f ""(x0) ≠ 0, то в точці x0 функція f(x0) має максимум, якщо

Завантажити:

Попередній перегляд:

Підписи до слайдів:

Попередній перегляд:

Підписи до слайдів:

Читайте також