Ածանցյալի օգտագործումը գործունեության տարբեր ոլորտներում: Հետաքրքիր ածանցյալ Այս աշխատանքի նպատակները. Դիտարկել ածանցյալի օգտագործումը տարբեր գիտություններում Ծանոթանալ այն գիտնականների հետ, ովքեր ուսումնասիրել են ֆունկցիայի ածանցյալը: Ուժը աշխատանքի ածանցյալն է տեղաշարժում:

Կրթության նախարարություն Սարատովի մարզ

Պետական ինքնավար պրոֆեսիոնալ ուսումնական հաստատությունՍարատովի շրջան «Էնգելսի պոլիտեխնիկ»

Ածանցյալի ԿԻՐԱՌՈՒՄԸ ԳԻՏՈՒԹՅԱՆ ՏԱՐԲԵՐ ՈԼՈՐՏՆԵՐՈՒՄ

Կատարվել է՝ Սարկուլովա Նուրգուլյա Սերգեևնա

ԿՇԻ-216/15 խմբի աշակերտ

(Դիզայն, մոդելավորում և

կարի տեխնոլոգիա)

գիտական խորհրդատու:

Վերբիցկայա Ելենա Վյաչեսլավովնա

մաթեմատիկայի ուսուցիչ ԳԱՊՈՒ ՍՈ

«Էնգելսի պոլիտեխնիկ»

2016

Ներածություն

Շատ մեծ է մաթեմատիկայի դերը բնագիտության տարբեր բնագավառներում։ Զարմանալի չէ, որ ասում են«Մաթեմատիկան գիտությունների թագուհին է, նրա ֆիզիկան աջ ձեռք, քիմիա է մնացել։

Հետազոտության առարկան ածանցյալն է։

Առաջատար նպատակն է ցույց տալ ածանցյալի նշանակությունը ոչ միայն մաթեմատիկայի, այլ նաև այլ գիտությունների մեջ, դրա կարևորությունը ժամանակակից կյանքում։

Դիֆերենցիալ հաշվարկը մեզ շրջապատող աշխարհի նկարագրությունն է՝ արված մաթեմատիկական լեզվով։ Ածանցյալն օգնում է մեզ հաջողությամբ լուծել ոչ միայն մաթեմատիկական խնդիրներ, այլ նաև գործնական առաջադրանքներ գիտության և տեխնիկայի տարբեր ոլորտներում։

Ֆունկցիայի ածանցյալն օգտագործվում է ամենուր, որտեղ առկա է գործընթացի անհավասար հոսք. սա անհավասար մեխանիկական շարժում է, և փոփոխական հոսանք, և քիմիական ռեակցիաներ և ռադիոակտիվ քայքայումընյութեր և այլն:

Այս շարադրության հիմնական և թեմատիկ հարցերը.

1. Ածանցյալի ծագման պատմությունը.

2. Ինչու՞ ուսումնասիրել ֆունկցիաների ածանցյալները:

3. Որտե՞ղ են օգտագործվում ածանցյալները:

4. Ածանցյալների կիրառումը ֆիզիկայում, քիմիայում, կենսաբանության մեջ և այլ գիտություններում:

5. Եզրակացություններ

Որոշեցի հոդված գրել «Ածանցյալի կիրառումը գիտության տարբեր բնագավառներում» թեմայով, քանի որ կարծում եմ այս թեման շատ հետաքրքիր է, օգտակար և տեղին։

Իմ աշխատանքում ես կխոսեմ գիտության տարբեր ոլորտներում տարբերակման կիրառման մասին՝ քիմիա, ֆիզիկա, կենսաբանություն, աշխարհագրություն և այլն։ Ի վերջո, բոլոր գիտությունները անքակտելիորեն կապված են, ինչը շատ պարզ երևում է թեմայի օրինակում։ Ես դիտարկում եմ.

Ածանցյալի կիրառումը գիտության տարբեր բնագավառներում

Ավագ դպրոցի հանրահաշվի դասընթացից մենք դա արդեն գիտենքածանցյալ ֆունկցիայի աճի հարաբերակցության սահմանն է իր արգումենտի աճին, քանի որ արգումենտի աճը ձգտում է զրոյի, եթե այդպիսի սահման գոյություն ունի:

Ածանցյալ գտնելու գործողությունը կոչվում է դրա տարբերակում, իսկ այն ֆունկցիան, որը x կետում ունի ածանցյալ՝ այդ կետում դիֆերենցիալ։ Այն ֆունկցիան, որը տարբերվում է ինտերվալի յուրաքանչյուր կետում, կոչվում է տարբերվող այդ միջակայքում:

Մաթեմատիկական վերլուծության հիմնական օրենքները բացահայտելու պատիվը պատկանում է անգլիացի ֆիզիկոսև մաթեմատիկոս Իսահակ Նյուտոնը և գերմանացի մաթեմատիկոս, ֆիզիկոս, փիլիսոփա Լայբնիցը։

Նյուտոնը ներմուծեց ածանցյալ հասկացությունը՝ ուսումնասիրելով մեխանիկայի օրենքները՝ դրանով իսկ բացահայտելով դրա մեխանիկական նշանակությունը։

Ածանցյալի ֆիզիկական իմաստը՝ ֆունկցիայի ածանցյալy= զ(x) կետում x 0 ֆունկցիայի փոփոխության արագությունն էզ(x) կետում x 0 .

Լայբնիցը եկել է ածանցյալ հասկացությանը՝ լուծելով ածանցյալ գծին շոշափող գծելու խնդիրը՝ դրանով բացատրելով այն. երկրաչափական իմաստ.

Ածանցյալի երկրաչափական իմաստն այն է, որ ածանցյալը գործում է մի կետումx 0 հավասար է աբսցիսով կետում գծված ֆունկցիայի գրաֆիկին շոշափողի թեքությանըx 0 .

Ածանցյալ և ժամանակակից նշում տերմինըy" , զ«Ներկայացրել է Ջ.Լագրանժը 1797 թ.

Ռուս մաթեմատիկոս 19-րդ դարում Պանֆուտի Լվովիչ Չեբիշևն ասաց, որ «առանձնահատուկ նշանակություն ունեն գիտության այն մեթոդները, որոնք թույլ են տալիս մեզ լուծել մի խնդիր, որը ընդհանուր է մարդկային բոլոր գործնական գործունեության համար, օրինակ՝ ինչպես տնօրինել մեր միջոցները առավելագույն օգուտ ստանալու համար»:

Մեր ժամանակներում տարբեր մասնագիտությունների ներկայացուցիչներ պետք է զբաղվեն այսպիսի խնդիրներով.

Գործընթացի ինժեներները փորձում են արտադրությունը կազմակերպել այնպես, որ հնարավորինս շատ ապրանքներ արտադրվեն.

Դիզայներները փորձում են սարք մշակել տիեզերանավայնպես, որ սարքի զանգվածը ամենափոքրն է.

Տնտեսագետները փորձում են գործարանի և հումքի աղբյուրների միջև կապը պլանավորել այնպես, որ տրանսպորտային ծախսերը նվազագույն լինեն։

Ցանկացած թեմա ուսումնասիրելիս ուսանողներին հարց է առաջանում. «Ինչու՞ մեզ դա պետք է»: Եթե պատասխանը բավարարում է հետաքրքրությունը, ապա կարելի է խոսել ուսանողների հետաքրքրության մասին։ «Ածանցյալ» թեմայի պատասխանը կարելի է ստանալ՝ իմանալով, թե որտեղ են օգտագործվում ֆունկցիաների ածանցյալները։

Այս հարցին պատասխանելու համար մենք կարող ենք թվարկել որոշ առարկաներ և դրանց բաժինները, որոնցում օգտագործվում են ածանցյալներ:

Ածանցյալ հանրահաշիվում.

1. Ֆունկցիայի գրաֆիկին շոշափող

Շոշափում է ֆունկցիայի գրաֆիկըզ, տարբերվող x-ովմասին , կետով անցնող ուղիղ է (xմասին ; զ(x o )) ու թեքություն ունենալըզ«(x o):

y= զ(x o ) + զ′(x o ) (x - x o )

2. Փնտրել մեծացող և նվազող ֆունկցիաների միջակայքերը

Գործառույթy=f(x) ավելանում է ընդմիջման ընթացքումX , եթե որևէ մեկի համար ևանհավասարությունը. Այլ կերպ ասած, արգումենտի ավելի մեծ արժեքը համապատասխանում է ֆունկցիայի ավելի մեծ արժեքին:

Գործառույթy=f(x) նվազում է ընդմիջման ընթացքումX , եթե որևէ մեկի համար ևանհավասարությունը. Այլ կերպ ասած, արգումենտի ավելի մեծ արժեքը համապատասխանում է ֆունկցիայի ավելի փոքր արժեքին:

3. Ֆունկցիայի ծայրահեղ կետերի հայտնաբերում

կետ կանչեցառավելագույն միավոր գործառույթներըy=f(x) եթե բոլորի համարx . Ֆունկցիայի արժեքը առավելագույն կետում կոչվում էառավելագույն գործառույթ և նշել.

կետ կանչեցնվազագույն միավոր գործառույթներըy=f(x) եթե բոլորի համարx իր հարեւանությամբ անհավասարությունը. Ֆունկցիայի արժեքը նվազագույն կետում կոչվում էգործառույթի նվազագույնը և նշել.

Մի կետի հարևանությամբ հասկանալ միջակայքը, որտեղ բավական փոքր դրական թիվ է:

Նվազագույն և առավելագույն միավորները կոչվում ենծայրահեղ կետեր , և կոչվում են ծայրահեղ կետերին համապատասխանող ֆունկցիաների արժեքներըֆունկցիա ծայրահեղ .

4. Որոնել ֆունկցիայի ուռուցիկության և գոգավորության միջակայքերը

Ֆունկցիայի գրաֆիկ, այս միջակայքում էուռուցիկ , գտնվում է ոչ ավելի բարձր, քան նրա շոշափողներից որևէ մեկը (նկ. 1):

Ֆունկցիայի գրաֆիկ, տարբերվող միջակայքում, այս միջակայքում էգոգավոր , եթե այս ֆունկցիայի գրաֆիկը գտնվում է միջակայքում գտնվում է ոչ ավելի ցածր, քան նրա շոշափողներից որևէ մեկը (նկ. 2):

Ֆունկցիայի գրաֆիկի թեքության կետը կոչվում է ուռուցիկության և գոգավորության միջակայքերը բաժանող կետ:

5. Գտնել ֆունկցիայի թեքման կետերը

Ածանցյալը ֆիզիկայում.

1. Արագությունը՝ որպես ճանապարհի ածանցյալ

2. Արագացումը որպես արագության ածանցյալա =

3. Քայքայման արագություն ռադիոակտիվ տարրեր 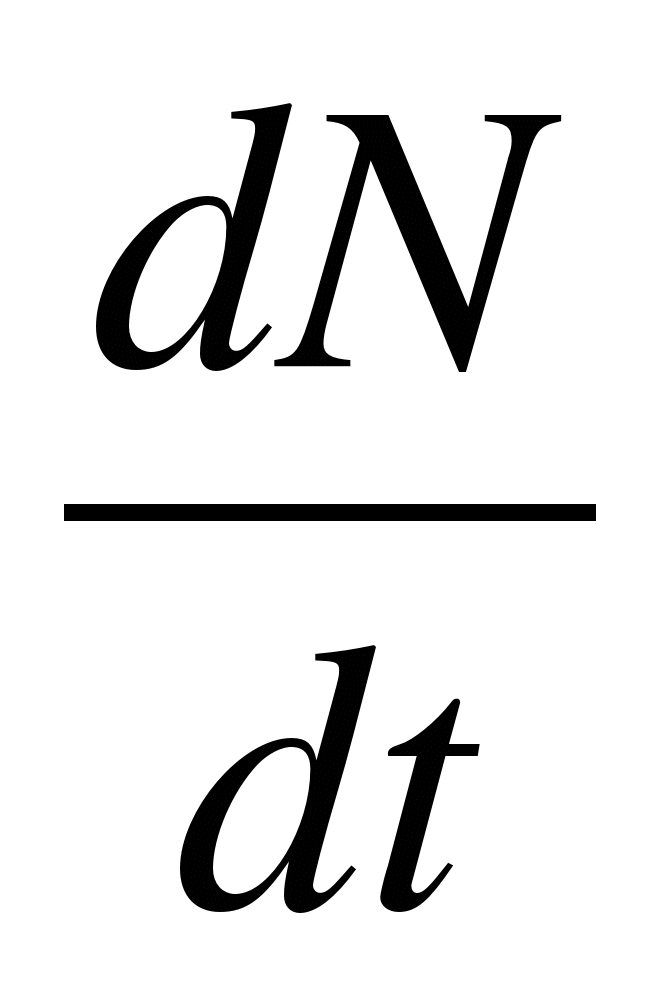= - λN

Եվ նաև ֆիզիկայում ածանցյալն օգտագործվում է հաշվարկելու համար.

Արագություններ նյութական կետ

Ակնթարթային արագությունը որպես ածանցյալի ֆիզիկական նշանակություն

Ակնթարթային արժեք AC հոսանք

Էլեկտրամագնիսական ինդուկցիայի EMF-ի ակնթարթային արժեքը

Max Power

Ածանցյալը քիմիայում.

Իսկ քիմիայում դիֆերենցիալ հաշվարկը լայն կիրառություն է գտել կառուցման համար մաթեմատիկական մոդելներքիմիական ռեակցիաները և դրանց հատկությունների հետագա նկարագրությունը:

Քիմիայի մեջ ածանցյալը օգտագործվում է որոշելու համար շատ կարևոր բան՝ արագությունը քիմիական ռեակցիա, որոշիչ գործոններից մեկը, որը պետք է հաշվի առնել գիտական և արդյունաբերական գործունեության բազմաթիվ ոլորտներում. V(t) = p'(t)

Քանակ

in-va միաժամանակ տ 0

p = p (t 0 )

Գործառույթ

Ժամանակի ընդմիջում

∆t = t– t 0

Փաստարկի ավելացում

Քանակի փոփոխություն

∆p=p(t 0 + ∆t) – p(t 0 )

Ֆունկցիայի ավելացում

Քիմիական ռեակցիայի միջին արագությունը

∆p/∆t

Գործառույթի ավելացման հարաբերակցությունը արգումենտի աճին

Ածանցյալ կենսաբանության մեջ.

Պոպուլյացիան տվյալ տեսակի անհատների ամբողջությունն է, որը զբաղեցնում է տարածքի որոշակի տարածք տեսակների միջակայքում, ազատորեն խառնվում են միմյանց և մասամբ կամ ամբողջությամբ մեկուսացված այլ պոպուլյացիաներից, ինչպես նաև էվոլյուցիայի տարրական միավոր է:

P \u003d x‘ (t)

Ածանցյալ աշխարհագրության մեջ.

1. Որոշ իմաստներ սեյսմոգրաֆիայում

2. Առանձնահատկություններ էլեկտրամագնիսական դաշտհողատարածք

3. Միջուկային երկրաֆիզիկական պարամետրերի ռադիոակտիվություն

4. Բազմաթիվ իմաստներ տնտեսական աշխարհագրության մեջ

5. Տարածքի բնակչության թվաքանակի հաշվարկման բանաձև բերեք t ժամանակում.

y'= դեպի y

Թոմաս Մալթուսի սոցիոլոգիական մոդելի գաղափարը կայանում է նրանում, որ բնակչության աճը համաչափ է բնակչության թվին տվյալ պահին t-ից մինչև N(t): Մալթուսի մոդելը լավ աշխատեց 1790-ից 1860 թվականներին ԱՄՆ բնակչությունը նկարագրելու համար: Այս մոդելն այլևս չի գործում շատ երկրներում:

Ածանցյալը էլեկտրատեխնիկայում.

Մեր տներում, տրանսպորտում, գործարաններում. էլեկտրական հոսանքն աշխատում է ամենուր։ Էլեկտրական հոսանքի տակ հասկանալ ազատ էլեկտրական լիցքավորված մասնիկների ուղղորդված շարժումը:

Քանակական բնութագիր էլեկտրական հոսանքներկայիս ուժն է:

Էլեկտրական շղթայում էլեկտրական լիցքավորումժամանակի ընթացքում փոփոխվում է ըստ օրենքի q=q (t). I հոսանքը ժամանակի նկատմամբ q լիցքի ածանցյալն է։

Էլեկտրատեխնիկայում հիմնականում օգտագործվում է AC շահագործումը:

Ժամանակի ընթացքում փոփոխվող էլեկտրական հոսանքը կոչվում է փոփոխական հոսանք։ AC շղթան կարող է պարունակել տարբեր տարրերՋեռուցման սարքեր, կծիկներ, կոնդենսատորներ:

Փոփոխական էլեկտրական հոսանքի արտադրությունը հիմնված է էլեկտրամագնիսական ինդուկցիայի օրենքի վրա, որի ձևակերպումը պարունակում է մագնիսական հոսքի ածանցյալ։

Ածանցյալը տնտեսագիտության մեջ.

Տնտեսագիտությունը կյանքի հիմքն է, և դրանում կարևոր տեղ է գրավում դիֆերենցիալ հաշվարկը՝ տնտեսական վերլուծության ապարատը։ Տնտեսական վերլուծության հիմնական խնդիրն է ուսումնասիրել տնտեսական մեծությունների փոխհարաբերությունները ֆունկցիաների տեսքով։

Տնտեսագիտության մեջ ածանցյալը լուծում է կարևոր հարցեր.

1. Ի՞նչ ուղղությամբ կփոխվեն պետության եկամուտները հարկերի ավելացմամբ, թե մաքսատուրքերի ներդրմամբ։

2. Արդյո՞ք ընկերության եկամուտը կավելանա, թե՞ կնվազի իր արտադրանքի գնի բարձրացմամբ:

Այս հարցերը լուծելու համար անհրաժեշտ է կառուցել մուտքային փոփոխականների միացման ֆունկցիաները, որոնք այնուհետեւ ուսումնասիրվում են դիֆերենցիալ հաշվարկի մեթոդներով։

Նաև, օգտագործելով տնտեսության մեջ ֆունկցիայի (ածանցյալի) ծայրահեղությունը, կարող եք գտնել աշխատանքի ամենաբարձր արտադրողականությունը, առավելագույն շահույթը, առավելագույն արտադրանքը և նվազագույն ծախսերը:

ԵԶՐԱԿԱՑՈՒԹՅՈՒՆ. ածանցյալը հաջողությամբ օգտագործվում է գիտության, տեխնիկայի և կյանքի տարբեր կիրառական խնդիրների լուծման համար

Ինչպես երևում է վերը նշվածից, ֆունկցիայի ածանցյալի օգտագործումը շատ բազմազան է և ոչ միայն մաթեմատիկայի, այլ նաև այլ առարկաների ուսումնասիրության մեջ։ Ուստի կարող ենք եզրակացնել, որ թեմայի ուսումնասիրությունը՝ «Ֆունկցիայի ածանցյալը» իր կիրառությունը կունենա այլ թեմաներում և առարկաներում։

Համոզվեցինք «Ածանցյալ» թեմայի ուսումնասիրության կարևորության, գիտության և տեխնիկայի գործընթացների ուսումնասիրության մեջ դրա դերի, ըստ նախագծման հնարավորության. իրական իրադարձություններմաթեմատիկական մոդելներ և լուծել կարևոր խնդիրներ:

“Երաժշտությունը կարող է բարձրացնել կամ հանգստացնել հոգին,
Նկարչությունը հաճելի է աչքին,
Պոեզիա - զգացմունքներ արթնացնել,
Փիլիսոփայություն - բավարարել մտքի կարիքները,
Ինժեներությունը մարդկանց կյանքի նյութական կողմի բարելավումն է,
ԲԱՅՑմաթեմատիկան կարող է հասնել այս բոլոր նպատակներին»։

Այսպես է ասել ամերիկացի մաթեմատիկոսըՄորիս Քլայն.

Մատենագիտություն:

1. Բոգոմոլով Ն.Վ., Սամոյլենկո Ի.Ի. Մաթեմատիկա. - Մ.՝ Յուրայթ, 2015թ.

2. Վ.Պ.Գրիգորիև և Յու.Ա.Դուբինսկի, Բարձրագույն մաթեմատիկայի տարրեր: - Մ.: Ակադեմիա, 2014:

3. Բավրին Ի.Ի. Բարձրագույն մաթեմատիկայի հիմունքներ. - Մ.: ավարտական դպրոց, 2013.

4. Բոգոմոլով Ն.Վ. Գործնական դասեր մաթեմատիկայից. - Մ.: Բարձրագույն դպրոց, 2013 թ.

5. Բոգոմոլով Ն.Վ. Մաթեմատիկայի խնդիրների ժողովածու. - Մ.: Բուստարդ, 2013:

6. Ռիբնիկով Կ.Ա. Մաթեմատիկայի պատմություն, Մոսկվայի համալսարանի հրատ., Մ, 1960։

7. Վինոգրադով Յու.Ն., Գոմոլա Ա.Ի., Պոտապով Վ.Ի., Սոկոլովա Է.Վ. - Մ.:«Ակադեմիա» հրատարակչական կենտրոն, 2010 թ

8 . Բաշմակով Մ.Ի. Մաթեմատիկա՝ հանրահաշիվ և մաթեմատիկական վերլուծության սկիզբ, երկրաչափություն։ - Մ.: «Ակադեմիա» հրատարակչական կենտրոն, 2016 թ

Պարբերական աղբյուրներ.

Թերթեր և ամսագրեր՝ «Մաթեմատիկա», « Հանրային դաս»

Ինտերնետային ռեսուրսների օգտագործում, էլեկտրոնային գրադարաններ:

www:egetutor.ru

matematika-na5.norod.ru

FGOU SPO

Նովոսիբիրսկ գյուղատնտեսական քոլեջ

վերացական

«մաթեմատիկա» առարկայից

«Ածանցյալի կիրառումը գիտության և տեխնիկայի մեջ»

S. Razdolnoe 2008 թ

Ներածություն

1. Տեսական մաս

1.1 Ածանցյալ հասկացությանը տանող խնդիրներ

1.2 Ածանցյալ սահմանում

1.3 Ածանցյալը գտնելու ընդհանուր կանոն

1.4 Ածանցյալի երկրաչափական նշանակությունը

1.5 Ածանցյալի մեխանիկական նշանակությունը

1.6 Երկրորդ կարգի ածանցյալը և դրա մեխանիկական նշանակությունը

1.7 Դիֆերենցիալի սահմանումը և երկրաչափական նշանակությունը

2. Գործառույթների ուսումնասիրություն ածանցյալի օգնությամբ

Եզրակացություն

գրականություն

Ներածություն

Էսսեիս առաջին գլխում կխոսենք ածանցյալ հասկացության, դրա կիրառման կանոնների, երկրաչափական և. ֆիզիկական զգացողությունածանցյալ. Իմ շարադրության երկրորդ գլխում մենք կխոսենք գիտության և տեխնիկայի մեջ ածանցյալի օգտագործման և այս ոլորտում խնդիրների լուծման մասին:

1. Տեսական մաս

1.1 Ածանցյալ հասկացությանը տանող խնդիրներ

Որոշ գործընթացներ և երևույթներ ուսումնասիրելիս հաճախ խնդիր է առաջանում այդ գործընթացների արագությունը որոշելու համար։ Դրա լուծումը հանգեցնում է ածանցյալ հասկացության, որը դիֆերենցիալ հաշվարկի հիմնական հասկացությունն է:

Դիֆերենցիալ հաշվարկի մեթոդը ստեղծվել է 17-18-րդ դարերում։ Երկու մեծ մաթեմատիկոսների՝ Ի.Նյուտոնի և Գ.Վ. Լայբնիցը։

Նյուտոնը հայտնաբերեց դիֆերենցիալ հաշվարկը ժամանակի տվյալ պահին (ակնթարթային արագություն) նյութական կետի արագության վերաբերյալ խնդիրներ լուծելիս:

Ինչպես հայտնի է, միասնական շարժումշարժում է, որի ժամանակ մարմինը անցնում է ճանապարհի հավասար երկարություններ ժամանակի հավասար ընդմիջումներով: Մարմնի անցած տարածությունը ժամանակի միավորում կոչվում է արագություն միատեսակ շարժում.

Այնուամենայնիվ, ամենից հաճախ գործնականում գործ ունենք անհավասար շարժման հետ։ Ճանապարհով ընթացող մեքենան անցումներում դանդաղեցնում է արագությունը և արագացնում այն այն հատվածներում, որտեղ ճանապարհը պարզ է. ինքնաթիռը դանդաղում է վայրէջքի ժամանակ և այլն: Հետևաբար, ամենից հաճախ մենք պետք է գործ ունենանք այն փաստի հետ, որ մարմինը հավասար ժամանակային ընդմիջումներով անցնում է տարբեր երկարությունների ճանապարհի հատվածներ: Նման շարժումը կոչվում է անհավասար.Նրա արագությունը չի կարող բնութագրվել մեկ թվով:

Հաճախ անհավասար շարժումը բնութագրելու համար օգտագործվում է հայեցակարգը Միջին արագությունըշարժում ∆t ժամանակի ընթացքում, որը որոշվում է այն հարաբերությամբ, որտեղ ∆s-ն մարմնի անցած ճանապարհն է ∆t ժամանակի ընթացքում:

Այսպիսով, ազատ անկման մեջ գտնվող մարմնի դեպքում առաջին երկու վայրկյանում նրա շարժման միջին արագությունը կազմում է

Գործնականում շարժման այնպիսի հատկանիշը, ինչպիսին է միջին արագությունը, շատ քիչ բան է ասում շարժման մասին: Իրոք, 4,9 մ/վ-ում, իսկ 2-րդի համար՝ 14,7 մ/վրկ, մինչդեռ առաջին երկու վայրկյանի միջին արագությունը 9,8 մ/վ է: Առաջին երկու վայրկյանների ընթացքում միջին արագությունը որևէ պատկերացում չի տալիս այն մասին, թե ինչպես է տեղի ունեցել շարժումը. երբ մարմինը շարժվեց ավելի արագ, և երբ ավելի դանդաղ: Եթե յուրաքանչյուր վայրկյանի համար շարժման միջին արագությունները սահմանենք առանձին, ապա կիմանանք, օրինակ, որ 2-րդ վայրկյանում մարմինը շատ ավելի արագ է շարժվել, քան 1-ին։ Այնուամենայնիվ, շատ դեպքերում շատ ավելի արագ, քան մենք չենք բավարարվում: Ի վերջո, հեշտ է հասկանալ, որ այս 2-րդ վայրկյանում մարմինը նույնպես տարբեր կերպ է շարժվում՝ սկզբում ավելի դանդաղ է, վերջում՝ ավելի արագ։ Իսկ ինչպե՞ս է այն շարժվում ինչ-որ տեղ այս 2-րդ վայրկյանի մեջտեղում։ Այսինքն՝ ինչպե՞ս որոշել ակնթարթային արագությունը։

Օրենքով թող նկարագրվի մարմնի շարժումը ∆t-ին հավասար ժամանակի համար։ t0 պահին մարմինն անցել է ճանապարհը, տվյալ պահին՝ ճանապարհը։ Հետևաբար, ∆t ժամանակի ընթացքում մարմինը անցել է մի տարածություն, և մարմնի միջին արագությունը այս ժամանակահատվածում կլինի:

Որքան կարճ է ժամանակի Δt միջակայքը, այնքան ավելի ճշգրիտ է հնարավոր պարզել, թե ինչ արագությամբ է շարժվում մարմինը t0 պահին, քանի որ շարժվող մարմինը չի կարող էապես փոխել արագությունը կարճ ժամանակահատվածում: Հետևաբար, միջին արագությունը, քանի որ ∆t-ը հակված է զրոյի, մոտենում է շարժման իրական արագությանը և սահմանի մեջ տալիս է շարժման արագությունը տվյալ պահին t0 (ակնթարթային արագություն):

Այս կերպ ,

Սահմանում 1. Ակնթարթային արագությունմարմնի ուղղագիծ շարժման տրված t0 ժամանակում կոչվում է միջին արագության սահման t0-ից t0+ ∆t ժամանակի ընթացքում, երբ ∆t ժամանակային միջակայքը ձգտում է զրոյի:

Այսպիսով, ուղղագիծ անհավասարաչափ շարժման արագությունը տվյալ պահին գտնելու համար անհրաժեշտ է գտնել ուղու աճի Δ-ի ժամանակի աճի հարաբերակցության սահմանը` պայմանով, այսինքն. Լայբնիցը հայտնաբերեց դիֆերենցիալ հաշվարկը՝ լուծելով իր հավասարմամբ տրված ցանկացած կորի շոշափող շոշափող խնդիրը։

Այս խնդրի լուծումն ունի մեծ նշանակություն. Ի վերջո, շարժվող կետի արագությունն ուղղված է իր հետագծին շոշափող երկայնքով, հետևաբար, իր հետագծի վրա արկի արագությունը որոշելը, իր ուղեծրի վրա գտնվող ցանկացած մոլորակի արագությունը, կրճատվում է մինչև շոշափողի ուղղությունը որոշելու համար: կոր.

Շոշափողի սահմանումը որպես ուղիղ գիծ, որն ունի կորի հետ միայն մեկ ընդհանուր կետ, որը վավեր է շրջանագծի համար, պիտանի չէ շատ այլ կորերի համար:

Կորին շոշափողի հետևյալ սահմանումը ոչ միայն համապատասխանում է դրա մասին ինտուիտիվ գաղափարին, այլև թույլ է տալիս իրականում գտնել դրա ուղղությունը, այսինքն. հաշվարկել շոշափողի թեքությունը.

Սահմանում 2. Շոշափողդեպի M կետի կորը կոչվում է MT ուղիղ գիծ, որը MM1 հատվածի սահմանային դիրքն է, երբ M1 կետը, շարժվելով կորի երկայնքով, անորոշ ժամանակով մոտենում է M կետին:

1.2 Ածանցյալ սահմանում

Նկատի ունեցեք, որ կորի շոշափումը և անհավասար շարժման ակնթարթային արագությունը որոշելիս, ըստ էության, կատարվում են նույն մաթեմատիկական գործողությունները.

1. Փաստարկի տրված արժեքը ավելացվում է և արգումենտի նոր արժեքին համապատասխան ֆունկցիայի նոր արժեք է հաշվարկվում։

2. Որոշեք ընտրված արգումենտի ավելացմանը համապատասխանող ֆունկցիայի աճը:

3. Ֆունկցիայի աճը բաժանվում է փաստարկի աճի վրա։

4. Հաշվի՛ր այս հարաբերակցության սահմանը՝ պայմանով, որ փաստարկի աճը հակված է զրոյի:

Բազմաթիվ խնդիրների լուծումները հանգեցնում են այս տեսակի սահմանափակ անցումների: Անհրաժեշտ է դառնում ընդհանրացում կատարել և այս հատվածին մինչև վերջ անուն տալ։

Գործառույթի փոփոխության արագությունը՝ կախված փաստարկի փոփոխությունից, ակնհայտորեն կարելի է բնութագրել հարաբերակցությամբ։ Այս հարաբերությունը կոչվում է Միջին արագությունը ֆունկցիան փոխվում է մինչև ինտերվալով: Այժմ մենք պետք է դիտարկենք կոտորակի սահմանը:Այս հարաբերակցության սահմանը, քանի որ արգումենտի աճը հակված է զրոյի (եթե այս սահմանը գոյություն ունի) որոշ նոր ֆունկցիա է: Այս ֆունկցիան նշվում է y' խորհրդանիշներով, որոնք կոչվում են ածանցյալայս ֆունկցիան, քանի որ այն ստացվում է (արտադրվում է) ֆունկցիայից պարզունակֆունկցիան իր ածանցյալի նկատմամբ

Սահմանում 3. ածանցյալֆունկցիաները տվյալ կետում անվանում են ∆y ֆունկցիայի աճի հարաբերակցության սահմանը ∆x արգումենտի համապատասխան աճին, պայմանով, որ ∆x→0, այսինքն.

1.3 Ածանցյալը գտնելու ընդհանուր կանոն

Որոշ ֆունկցիայի ածանցյալը գտնելու գործողությունը կոչվում է տարբերակումֆունկցիաները, իսկ մաթեմատիկայի այն ճյուղը, որն ուսումնասիրում է այս գործողության հատկությունները դիֆերենցիալ հաշվարկ.

Եթե ֆունկցիան ունի x=a ածանցյալ, ապա այն կոչվում է տարբերակելիայս պահին: Եթե ֆունկցիան ունի ածանցյալ տվյալ միջակայքի յուրաքանչյուր կետում, ապա այն կոչվում է տարբերակելիԱյս մասին ընդմիջում .

Ածանցյալի սահմանումը ոչ միայն ամբողջությամբ բնութագրում է արգումենտի փոփոխման ժամանակ ֆունկցիայի փոփոխության արագության հայեցակարգը, այլ նաև հնարավորություն է տալիս իրականում հաշվարկել տվյալ ֆունկցիայի ածանցյալը։ Դա անելու համար դուք պետք է կատարեք հետևյալ չորս գործողությունները (չորս քայլ), որոնք նշված են հենց ածանցյալի սահմանման մեջ.

1. Գտեք նոր ֆունկցիայի արժեքը՝ ներկայացնելով in այս գործառույթը x-ի փոխարեն փաստարկի նոր արժեքը՝ .

2. Ֆունկցիայի աճը որոշվում է ֆունկցիայի տրված արժեքը նրա նոր արժեքից հանելով՝ .

3. Կազմե՛ք ֆունկցիայի աճի հարաբերակցությունը արգումենտի ավելացմանը՝ .

4. Գնացեք մինչև սահմանաչափը և գտեք ածանցյալը.

Ընդհանուր առմամբ, ածանցյալը «նոր» ֆունկցիա է, որը ստացվում է տվյալ ֆունկցիայից՝ ըստ սահմանված կանոնի:

1.4 Ածանցյալի երկրաչափական նշանակությունը

Ածանցյալի երկրաչափական մեկնաբանությունը, առաջինը տրված է վերջ XVIIմեջ Լայբնիցը հետևյալն է. ֆունկցիայի ածանցյալի արժեքը x կետում հավասար է նույն x կետի ֆունկցիայի գրաֆիկին գծված շոշափողի թեքությանը,դրանք.

Շոշափողի հավասարումը, ինչպես միջով անցնող ցանկացած ուղիղ գիծ տրված կետայս ուղղությամբ ունի ձև՝ ընթացիկ կոորդինատներ: Բայց շոշափող հավասարումը նույնպես կգրվի հետևյալ կերպ. Նորմալ հավասարումը կգրվի ձևով

1.5 Ածանցյալի մեխանիկական նշանակությունը

Ածանցյալի մեխանիկական մեկնաբանությունն առաջին անգամ տվել է Ի.Նյուտոնը։ Այն բաղկացած է հետևյալից. նյութական կետի շարժման արագությունը ժամանակի տվյալ պահին հավասար է ուղու ածանցյալին ժամանակի նկատմամբ, այսինքն. Այսպիսով, եթե նյութական կետի շարժման օրենքը տրված է հավասարմամբ, ապա ժամանակի որոշակի պահի կետի ակնթարթային արագությունը գտնելու համար անհրաժեշտ է գտնել ածանցյալը և դրանում փոխարինել t-ի համապատասխան արժեքը:

1.6 Երկրորդ կարգի ածանցյալը և դրա մեխանիկական նշանակությունը

Մենք ստանում ենք (հավասարում այն ամենից, ինչ արվել է Lisichkin V.T. Soloveychik I.L. «Մաթեմատիկա» էջ 240 դասագրքում).

Այս կերպ, մարմնի ուղղագիծ շարժման արագացումը տվյալ պահին հավասար է ուղու երկրորդ ածանցյալին ժամանակի նկատմամբ՝ հաշվարկված տվյալ պահի համար։Սա երկրորդ ածանցյալի մեխանիկական նշանակությունն է։

1.7 Դիֆերենցիալի սահմանումը և երկրաչափական նշանակությունը

Սահմանում 4.Ֆունկցիայի աճի հիմնական մասը՝ գծային՝ ֆունկցիայի աճի նկատմամբ, գծային՝ անկախ փոփոխականի աճի նկատմամբ, կոչվում է. դիֆերենցիալգործառույթներ և նշանակվում է d-ով, այսինքն. .

Ֆունկցիայի դիֆերենցիալ երկրաչափորեն ներկայացված է կետում գծված շոշափողի օրդինատի աճով Մ ( x ; y ) x-ի և ∆x-ի տրված արժեքների համար:

հաշվարկ դիֆերենցիալ – .

Դիֆերենցիալի կիրառումը մոտավոր հաշվարկներում – , ֆունկցիայի աճի մոտավոր արժեքը համընկնում է նրա դիֆերենցիալի հետ։

Թեորեմ 1. Եթե դիֆերենցիալ ֆունկցիան մեծանում (նվազում է) տվյալ ինտերվալում, ապա այս ֆունկցիայի ածանցյալը բացասական չէ (ոչ դրական) այս միջակայքում։

Թեորեմ 2. Եթե ածանցյալ ֆունկցիան ինչ-որ միջակայքում դրական է (բացասական), ապա այս ինտերվալում ֆունկցիան միապաղաղ աճում է (միապաղաղ նվազում):

Այժմ ձևակերպենք ֆունկցիայի միապաղաղության միջակայքերը գտնելու կանոնը

1. Հաշվիր այս ֆունկցիայի ածանցյալը:

2. Գտեք այն կետերը, որտեղ զրո է կամ գոյություն չունի: Այս կետերը կոչվում են քննադատականֆունկցիայի համար

3. Գտնված կետերով ֆունկցիայի տիրույթը բաժանվում է ընդմիջումների, որոնցից յուրաքանչյուրի վրա ածանցյալը պահպանում է իր նշանը։ Այս ինտերվալները միապաղաղության միջակայքեր են։

4. Քննեք հայտնաբերված միջակայքներից յուրաքանչյուրի նշանը: Եթե դիտարկված միջակայքում, ապա այս միջակայքում ավելանում է. եթե, ապա այն նվազում է նման ընդմիջումով:

Կախված խնդրի պայմաններից՝ միապաղաղության միջակայքերը գտնելու կանոնը կարող է պարզեցվել։

Սահմանում 5.Կետը կոչվում է ֆունկցիայի առավելագույն (նվազագույն) կետ, եթե անհավասարությունը համապատասխանաբար պահպանվում է կետի ինչ-որ հարևանությամբ գտնվող ցանկացած x-ի համար:

Եթե ֆունկցիայի առավելագույն (նվազագույն) կետն է, ապա ասում ենք (նվազագույն)կետում։ Առավելագույն և նվազագույն գործառույթները միավորում են վերնագիրը ծայրահեղությունֆունկցիաները, և կոչվում են առավելագույն և նվազագույն միավորներ ծայրահեղ կետեր (ծայրահեղ կետեր):

Թեորեմ 3.(էքստրեմումի անհրաժեշտ նշան): Եթե և ածանցյալը գոյություն ունի այս կետում, ապա այն հավասար է զրոյի. .

Թեորեմ 4.(ծայրահեղության բավարար նշան): Եթե ածանցյալը երբ x անցնում է միջով ա փոխում է նշանը, ապա ա ֆունկցիայի ծայրահեղ կետն է .

Ածանցյալի ուսումնասիրության հիմնական կետերը.

1. Գտի՛ր ածանցյալը:

2. Գտեք բոլոր կրիտիկական կետերը ֆունկցիայի տիրույթից:

3. Սահմանե՛ք ֆունկցիայի ածանցյալի նշանները կրիտիկական կետերով անցնելիս և դուրս գրե՛ք ծայրահեղ կետերը։

4. Հաշվեք ֆունկցիայի արժեքները յուրաքանչյուր ծայրահեղ կետում:

2. Գործառույթների ուսումնասիրություն ածանցյալի հետ

Առաջադրանք թիվ 1 . Մատյանների ծավալը:Ճիշտ ձևի գերանները, առանց փայտի թերությունների, հաստ և բարակ ծայրերի տրամագծերի համեմատաբար փոքր տարբերությամբ կոչվում են արդյունաբերական կլոր փայտ: Արդյունաբերական կլոր փայտանյութի ծավալը որոշելիս սովորաբար օգտագործվում է պարզեցված բանաձև, որտեղ գտնվում է գերանի երկարությունը, նրա միջին հատվածի տարածքն է: Պարզեք, թե իրական ծավալը ավարտվում է, թե թերագնահատում; գնահատել հարաբերական սխալը.

Լուծում. Կլոր բիզնես փայտանյութի ձևը մոտ է կտրված կոնին: Թող լինի գերանի ավելի մեծ, փոքր ծայրի շառավիղը: Այնուհետեւ նրա գրեթե ճշգրիտ ծավալը (կտրված կոնի ծավալը), ինչպես հայտնի է, կարելի է գտնել բանաձեւով. Թող լինի պարզեցված բանաձևով հաշվարկված ծավալի արժեքը: Հետո;

Նրանք. . Սա նշանակում է, որ պարզեցված բանաձեւը տալիս է ծավալի թերագնահատում։ Եկեք հիմա դնենք: Հետո. Սա ցույց է տալիս, որ հարաբերական սխալը կախված չէ գրանցամատյանի երկարությունից, այլ որոշվում է հարաբերակցությամբ: Երբվանից ինտերվալով ավելանում է: Հետեւաբար, ինչը նշանակում է, որ հարաբերական սխալը չի գերազանցում 3,7%-ը։ Անտառագիտության պրակտիկայում նման սխալը համարվում է միանգամայն ընդունելի։ Ավելի մեծ ճշգրտությամբ գործնականում անհնար է չափել կամ ծայրերի տրամագծերը (քանի որ դրանք որոշակիորեն տարբերվում են շրջանակներից), կամ գերանի երկարությունը, քանի որ չափում են ոչ թե բարձրությունը, այլ կոնի գեներատորը (երկարությունը գերանը տասնյակ անգամ ավելի մեծ է, քան տրամագիծը, և դա մեծ սխալների չի հանգեցնում): Այսպիսով, առաջին հայացքից սխալ, բայց ավելին պարզ բանաձեւքանի որ իրական իրավիճակում կտրված կոնի ծավալը միանգամայն օրինական է ստացվում: Ստուգման հատուկ մեթոդների օգնությամբ բազմիցս իրականացվածը ցույց է տվել, որ արդյունաբերական անտառի զանգվածային հաշվառման դեպքում դիտարկվող բանաձևի օգտագործման հարաբերական սխալը չի գերազանցում 4%-ը։

Առաջադրանք թիվ 2 . Կտրված կոնի ձև ունեցող փոսերի, դույլերի խրամուղիների և այլ տարաների ծավալները որոշելիս գյուղատնտեսական պրակտիկայում երբեմն օգտագործվում է պարզեցված բանաձև, որտեղ բարձրությունն է, կոնի հիմքերի տարածքներն են: Պարզեք՝ իրական ծավալը գերագնահատված է, թե թերագնահատված, գնահատեք հարաբերական սխալը գործնականում բնական պայմանով. (- բազային շառավիղներ, .

Լուծում. Նշելով կտրված կոնի ծավալի իրական արժեքով և պարզեցված բանաձևով հաշվարկված արժեքով, մենք ստանում ենք. . Սա նշանակում է, որ պարզեցված բանաձեւը տալիս է ծավալի գերագնահատում։ Հետագա կրկնելով նախորդ խնդրի լուծումը, մենք գտնում ենք, որ հարաբերական սխալը կլինի ոչ ավելի, քան 6,7%: Հավանաբար, նման ճշգրտությունը ընդունելի է պեղումների աշխատանքի ռացիոնալացման ժամանակ. ի վերջո, փոսերը իդեալական կոններ չեն լինի, իսկ իրական պայմաններում համապատասխան պարամետրերը չափվում են շատ կոպիտ:

Առաջադրանք թիվ 3 . Հատուկ գրականության մեջ ֆրեզերային մեքենայի ողնաշարի պտտման β անկյունը որոշելու համար կցորդիչները ատամներով ֆրեզերելիս, ստացվում է բանաձև, որտեղ. Քանի որ այս բանաձևը բարդ է, խորհուրդ է տրվում հրաժարվել դրա հայտարարից և օգտագործել պարզեցված բանաձև: Ո՞ր դեպքում (- ամբողջ թվով) կարող է օգտագործվել այս բանաձևը, եթե անկյունը որոշելիս սխալ է թույլատրվում:

Լուծում.Ճշգրիտ բանաձեւը պարզից հետո նույնական փոխակերպումներկարելի է հիշել. Ուստի մոտավոր բանաձեւ օգտագործելիս բացարձակ սխալ է թույլատրվում, որտեղ. Մենք ուսումնասիրում ենք ֆունկցիան ինտերվալի վրա: Այս դեպքում 0.06, այսինքն. անկյունը պատկանում է առաջին քառորդին։ Մենք ունենք: . Նկատի ունեցեք, որ դիտարկվող միջակայքում, հետևաբար, ֆունկցիան նվազում է այս միջակայքում: Հետագայում, բոլորի համար: Նշանակում է, . Քանի որ դա ռադիան է, բավական է լուծել անհավասարությունը։ Այս անհավասարությունը լուծելով ընտրությամբ՝ մենք գտնում ենք, որ, . Քանի որ ֆունկցիան նվազում է, հետևում է

Եզրակացություն

Ածանցյալի օգտագործումը բավականին լայն է և կարող է ամբողջությամբ լուսաբանվել այս տեսակի աշխատանքում, բայց ես փորձել եմ լուսաբանել հիմնական կետերը: Մեր օրերում, կապված գիտական և տեխնոլոգիական առաջընթաց, մասնավորապես հաշվողական համակարգերի արագ էվոլյուցիայի հետ մեկտեղ, դիֆերենցիալ հաշվարկը դառնում է ավելի ու ավելի արդիական ինչպես պարզ, այնպես էլ գերբարդ խնդիրների լուծման համար:

գրականություն

1. Վ.Ա. Պետրով «Մաթեմատիկական վերլուծություն արտադրական առաջադրանքներում»

2. Սոլովեյչիկ Ի.Լ., Լիսիչկին Վ.Տ. "Մաթեմատիկա"

Չայկին Սեմյոն, Մայսակ Կիրիլ, Զալոգինա Անաստասիա, Շախզադովա Աննա

Այս մշակումը պարունակում է շնորհանդես «Ածանցյալի կիրառումը քիմիայի և կենսաբանության մեջ» թեմայով: ընթացքում ծրագրի գործողություններըառաջ քաշվեց վարկած, որ ածանցյալն իր կիրառությունն է գտնում գիտության այս ոլորտներում։ ընթացքում հետազոտական աշխատանքպարզվեց, թե ինչ դեր ունի ածանցյալը այնպիսի գիտություններում, ինչպիսիք են քիմիան և կենսաբանությունը, որտեղ և ինչ խնդիրների լուծման մեջ է այն գտնում իր կիրառությունը։ Կատարված աշխատանքի արդյունքում եզրակացություն է արվել, որ վարկածն իսկապես հաստատվել է։

Ներբեռնել:

Նախադիտում:

https://accounts.google.com

Սլայդների ենթագրեր.

Վարկած.

Նախադիտում:

Ներկայացումների նախադիտումն օգտագործելու համար ստեղծեք Google հաշիվ (հաշիվ) և մուտք գործեք՝ https://accounts.google.com

Սլայդների ենթագրեր.

Ածանցյալի օգտագործումը քիմիայի և կենսաբանության մեջ Աշխատանքն իրականացվել է MBOU թիվ 6 միջնակարգ դպրոցի 11B դասարանի աշակերտների կողմից՝ Չայկին Սեմյոն, Մաիսակ Կիրիլ, Զալոգինա Անաստասիա, Շախզադովա Աննա Ստավրոպոլ, 2014թ.

Վարկած.

Իսկ քիմիայում դիֆերենցիալ հաշվարկը լայն կիրառություն է գտել քիմիական ռեակցիաների մաթեմատիկական մոդելների կառուցման և դրանց հատկությունների հետագա նկարագրության համար։ Քիմիան նյութերի գիտություն է, նյութերի քիմիական փոխակերպումները։ Քիմիան ուսումնասիրում է տարբեր ռեակցիաների օրինաչափությունները Քիմիական ռեակցիայի արագությունը միավոր ժամանակում արձագանքող նյութերի կոնցենտրացիայի փոփոխությունն է։ Ածանցյալի կիրառումը քիմիայում և կենսաբանության մեջ Քիմիական ռեակցիայի արագության որոշում

Ինչու՞ մեզ պետք է ածանցյալ ռեակցիաներում: Քանի որ ռեակցիայի արագությունը v անընդհատ փոխվում է գործընթացի ընթացքում, այն սովորաբար արտահայտվում է որպես ռեակտիվների կոնցենտրացիայի ածանցյալ՝ կապված ժամանակի հետ։

Ածանցյալ բանաձևը քիմիայում Եթե C (t) քիմիական ռեակցիայի մեջ մտած նյութի քանակի փոփոխության օրենքն է, ապա t ժամանակում քիմիական ռեակցիայի v (t) արագությունը հավասար է ածանցյալին.

Ռեակցիայի արագության որոշումը Աճող ֆունկցիայի հարաբերակցության սահմանը աճող փաստարկին, քանի որ Δt-ը հակված է զրոյի, դա տվյալ պահին քիմիական ռեակցիայի արագությունն է։

Քիմիայի առաջադրանք. Քիմիական ռեակցիայի մեջ մտած նյութի քանակությունը տրվի կախվածությամբ՝ C (t) \u003d t 2 / 2 + 3 t -3 (մոլ) Գտեք քիմիական ռեակցիայի արագությունը 3 վայրկյանից հետո: Լուծում` v (t) = C ‘(t) ; v (t) = t + 3; v (3) = 3+3 = 6. Պատասխան՝ 6 մոլ/վրկ.

Ածանցյալի կենսաբանական նշանակությունը Թող y միկրոօրգանիզմների պոպուլյացիայի անհատների թվի և նրա վերարտադրության t ժամանակի հարաբերությունը տրվի y = x (t) հավասարմամբ: Թող ∆ t լինի ժամանակային միջակայքը t որոշ սկզբնական արժեքից մինչև t + ∆ t: Այնուհետև y + ∆y = x (t + ∆ t) պոպուլյացիայի չափի նոր արժեքն է, որը համապատասխանում է t + ∆ t պահին, իսկ ∆ y + x (t + ∆ t) - x (t) փոփոխությունն է. օրգանիզմների անհատների թիվը. Հարաբերակցությունը վերարտադրության միջին տեմպն է կամ, ինչպես ասում են, բնակչության միջին արտադրողականությունը։ Հաշվարկելով՝ մենք ստանում ենք y ' = P (t) = x ' (t) , կամ բնակչության արտադրողականությունը t պահին:

Օրինակ Թող բակտերիաների պոպուլյացիան t (c) ժամանակ ունենա x(t) անհատներ: . Գտե՛ք բնակչության աճի տեմպը՝ ա) t կամայական պահին, բ) t = 1 c պահին: Լուծում` P = x'(t) = 200t; P (1) = 200 (r / s): Պատասխան՝ 200 օ/վ:

Եզրակացություն Ածանցյալ հասկացությունը շատ կարևոր է քիմիայի և կենսաբանության մեջ, հատկապես ռեակցիայի արագությունը որոշելիս:

Եզրակացություն. Դիֆերենցիալ հաշվարկը մեզ շրջապատող աշխարհի նկարագրությունն է՝ արված մաթեմատիկական լեզվով: Ածանցյալը հաշվարկի ամենակարևոր հասկացություններից մեկն է։ Ածանցյալի իմացությունն օգնում է մեզ հաջողությամբ լուծել ոչ միայն մաթեմատիկական, այլ նաև գիտության, տեխնիկայի և կյանքի տարբեր ոլորտների գործնական խնդիրները:

Հարավային Սախալինի պետական համալսարան

մաթ

Դասընթացի աշխատանք

Թեմա՝ Ածանցյալի գործնական կիրառում

Դասախոս՝ Լիխաչևա Օ.Ն.

Յուժնո-Սախալինսկ

2002 թ
Ներածություն

Այս հոդվածում ես կքննարկեմ ածանցյալի կիրառությունները տարբեր գիտությունների և արդյունաբերության մեջ: Աշխատանքը բաժանված է գլուխների, որոնցից յուրաքանչյուրը վերաբերում է դիֆերենցիալ հաշվարկի ասպեկտներից մեկին (երկրաչափական, ֆիզիկական իմաստ և այլն):

1. Ածանցյալ հասկացությունը

1-1. Պատմական տեղեկություններ

Դիֆերենցիալ հաշվարկը ստեղծվել է Նյուտոնի և Լայբնիցի կողմից 17-րդ դարի վերջին երկու խնդիրների հիման վրա.

1) կամայական գծին շոշափող գտնելու մասին

2) շարժման կամայական օրենքով արագության որոնման մասին

Նույնիսկ ավելի վաղ, ածանցյալ հասկացությունը հանդիպում էր իտալացի մաթեմատիկոս Տարտալյայի աշխատություններում (մոտ 1500 - 1557 թթ.) - այստեղ հրացանի թեքության անկյան հարցի ուսումնասիրության ընթացքում հայտնվեց շոշափողություն, որն ապահովում է ամենամեծ հեռահարությունը: արկի։

17-րդ դարում Գ.Գալիլեոյի շարժման տեսության հիման վրա ակտիվորեն զարգացել է ածանցյալի կինեմատիկական հայեցակարգը։ Տարբեր ներկայացումներ սկսեցին հայտնվել Դեկարտի, ֆրանսիացի մաթեմատիկոս Ռոբերվալի և անգլիացի գիտնական Լ.Գրիգորիի աշխատություններում։ Լոպիտալը, Բեռնուլին, Լագրանժը, Էյլերը, Գաուսը մեծ ներդրում են ունեցել դիֆերենցիալ հաշվարկի ուսումնասիրության մեջ։

1-2. Ածանցյալ հասկացությունը

Թող y \u003d f (x) լինի x արգումենտի շարունակական ֆունկցիան, որը սահմանված է (a; b) միջակայքում, իսկ x 0-ն այս միջակայքի կամայական կետն է:

x արգումենտին տալիս ենք ∆x աճ, ապա y = f(x) ֆունկցիան կստանա աճ ∆y = f(x + ∆x) - f(x): Այն սահմանը, որին ∆y / ∆x հարաբերակցությունը ձգտում է որպես ∆x → 0, կոչվում է f(x) ֆունկցիայի ածանցյալ։

1-3. Ածանցյալների տարբերակման կանոններ և աղյուսակ

		(մեղք x)» = cos x
	(1 / x)" = -1 / x2	(cos x)» = -sin x
	(√x)" = 1 / 2√x	(tg x)" = 1 / cos 2 x
(UV)" = u"v + uv"	(a x)" = a x log x	(ctg x)» = 1 / մեղք 2 x
(u / v)"=(u"v - uv") / v 2		(arcsin x)" = 1 / √ (1- x 2)
	(log a x)" = (log a e) / x	(arccos x)" = -1 / √ (1- x 2)
	(ln x)» = 1 / x	(arctg x)" = 1 / √ (1+ x 2)
		(arcctg x)" = -1 / √ (1+ x 2)

2. Ածանցյալի երկրաչափական նշանակությունը

2-1. Շոշափող կորին

Եկեք ունենանք կոր և հաստատուն M կետ և դրա վրա N կետ: M կետին շոշափողն ուղիղ գիծ է, որի դիրքը հակված է զբաղեցնելու MN ակորդը, եթե N կետին անորոշ կերպով մոտենա երկայնքով: կորը դեպի Մ.

Դիտարկենք այս ֆունկցիային համապատասխան f(x) ֆունկցիան և y = f(x) կորը։ Որոշ x արժեքի համար ֆունկցիան ունի y = f(x) արժեքը: Այս արժեքները կորի վրա համապատասխանում են M կետին (x 0, y 0): Ներկայացնենք նոր արգումենտ x 0 + ∆x, որի արժեքը համապատասխանում է y ֆունկցիայի արժեքին 0 + ∆y = f(x 0 + ∆x): Համապատասխան կետն է N(x 0 + ∆x, y 0 + ∆y): Գծե՛ք MN հատվածը և φ-ով նշանակե՛ք կտրվածքով գոյացած անկյունը Ox առանցքի դրական ուղղությամբ։ Նկարը ցույց է տալիս, որ ∆y / ∆x = tg φ: Եթե այժմ ∆x-ը մոտենա 0-ին, ապա N կետը կշարժվի կորի երկայնքով, MN հատվածը կպտտվի M կետի շուրջ, և φ անկյունը կփոխվի։ Եթե, ինչպես ∆x → 0, φ անկյունը հակված է որոշ α-ի, ապա M-ով անցնող և աբսցիսային առանցքի դրական ուղղությամբ α անկյունը կազմող ուղիղ գիծը կլինի ցանկալի շոշափողը։ Միևնույն ժամանակ, դրա թեքության գործակիցը.

Այսինքն, f «(x) ածանցյալի արժեքը x փաստարկի տրված արժեքի համար հավասար է այն անկյան շոշափմանը, որը ձևավորվում է Ox առանցքի դրական ուղղությամբ f (x) ֆունկցիայի գրաֆիկի շոշափմամբ։ ) M կետում (x, f (x)):

Տիեզերական գծի շոշափողն ունի հարթ կորի շոշափողի սահմանում: Այս դեպքում, եթե ֆունկցիան տրված է z = f(x, y) հավասարմամբ, ապա OX և OY առանցքների թեքությունները հավասար կլինեն f-ի մասնակի ածանցյալներին x-ի և y-ի նկատմամբ:

2-2. Մակերեւույթին շոշափող հարթություն

M կետում մակերևույթին շոշափող հարթությունն այն հարթությունն է, որը պարունակում է շոշափողներ M-ով անցնող մակերեսի բոլոր տարածական կորերին՝ շփման կետ:

Վերցրեք F(x, y, z) = 0 հավասարման տրված մակերեսը և դրա վրա գտնվող մի սովորական կետ M(x 0, y 0, z 0): Մակերեւույթի վրա դիտարկենք M-ի միջով անցնող L կորը: Թող կորը տրվի հավասարումներով

x = φ (t); y = ψ(t); z = χ(t).

Եկեք այս արտահայտությունները փոխարինենք մակերեսի հավասարման մեջ: Հավասարումը կվերածվի նույնականության, քանի որ կորը ամբողջությամբ գտնվում է մակերեսի վրա: Օգտագործելով դիֆերենցիալի ձևի ինվարիանտության հատկությունը՝ մենք տարբերում ենք ստացված հավասարումը t-ի նկատմամբ.

M կետում L կորի շոշափողի հավասարումները ունեն ձև.

Քանի որ x - x 0, y - y 0, z - z 0 տարբերությունները համաչափ են համապատասխան դիֆերենցիալներին, ինքնաթիռի վերջնական հավասարումն ունի հետևյալ տեսքը.

F" x (x - x 0) + F" y (y - y 0) + F" z (z - z 0)=0

իսկ կոնկրետ դեպքի համար z = f(x, y):

Z - z 0 \u003d F "x (x - x 0) + F" y (y - y 0)

Օրինակ:Գտե՛ք շոշափող հարթության հավասարումը հիպերբոլիկ պարաբոլոիդի (2a; a; 1,5a) կետում.

Լուծում:

Z" x \u003d x / a \u003d 2; Z" y \u003d -y / a \u003d -1

Ցանկալի հարթության հավասարումը.

Z - 1.5a = 2 (x - 2a) - (Y - a) կամ Z = 2x - y - 1.5a

3-1. Նյութական կետի արագություն

Թող s-ի ուղու կախվածությունը տրվածում t ժամանակից ուղղագիծ շարժումնյութական կետը արտահայտվում է s = f(t) հավասարմամբ, իսկ t 0-ը ժամանակի որոշակի պահ է: Դիտարկենք մեկ այլ ժամանակ t, նշանակենք ∆t = t - t 0 և հաշվարկենք ճանապարհի աճը՝ ∆s = f(t 0 + ∆t) - f(t 0): ∆s / ∆t հարաբերակցությունը կոչվում է շարժման միջին արագություն t 0 սկզբնական պահից անցած ∆t ժամանակի ընթացքում: Արագությունը այս հարաբերակցության սահմանն է՝ Δt → 0:

Անհավասար շարժման միջին արագացումը միջակայքում (t; t + ∆t) արժեքն է =∆v / ∆t. Նյութական կետի ակնթարթային արագացումը t ժամանակում կլինի միջին արագացման սահմանը.

Այսինքն՝ առաջին անգամ ածանցյալը (v «(t)):

Օրինակ:Մարմնի անցած ճանապարհի կախվածությունը ժամանակից տրված է s \u003d A + Bt + Ct 2 + Dt 3 հավասարմամբ (C \u003d 0,1 մ / վ, D \u003d 0,03 մ / վ 2): Որոշեք շարժումը սկսելուց հետո ժամանակը, որից հետո մարմնի արագացումը հավասար կլինի 2 մ/վրկ 2-ի:

Լուծում:

v(t) = s "(t) = B + 2Ct + 3Dt 2; a(t) = v"(t) = 2C + 6Dt = 0.2 + 0.18t = 2;

1,8 = 0,18 տ; t = 10 վ

3-2. Նյութի ջերմունակությունը տվյալ ջերմաստիճանում

T տարբեր ջերմաստիճանները նույն արժեքով բարձրացնելու համար, որը հավասար է T 1 - T, 1 կգ-ի դիմաց: տվյալ նյութին անհրաժեշտ է տարբեր քանակությամբ ջերմություն Q 1 - Q, և հարաբերակցությունը

քանի որ այս նյութը հաստատուն չէ: Այսպիսով, տվյալ նյութի համար Q ջերմության քանակը T ջերմաստիճանի ոչ գծային ֆունկցիան է՝ Q = f(T): Այնուհետեւ ΔQ = f(t + ΔT) - f(T): Վերաբերմունք

կոչվում է միջին ջերմունակություն միջակայքում, իսկ այս արտահայտության սահմանը ∆T → 0-ում կոչվում է տվյալ նյութի ջերմունակություն T ջերմաստիճանում։

3-3. Ուժ

Փոփոխություն մեխանիկական շարժումմարմինը առաջանում է նրա վրա այլ մարմինների ուժերով: Փոխազդող մարմինների միջև էներգիայի փոխանակման գործընթացը քանակականորեն բնութագրելու համար մեխանիկայում ներդրվում է ուժի աշխատանքի հասկացությունը։ Աշխատանքի կատարման արագությունը բնութագրելու համար ներկայացվում է ուժ հասկացությունը.

4. Դիֆերենցիալ հաշվարկը տնտեսագիտության մեջ

4-1. Ֆունկցիոնալ հետազոտություն

Դիֆերենցիալ հաշվարկը մաթեմատիկական ապարատ է, որը լայնորեն օգտագործվում է տնտեսական վերլուծության համար: Տնտեսական վերլուծության հիմնական խնդիրն է ուսումնասիրել տնտեսական մեծությունների հարաբերությունները, որոնք գրված են որպես գործառույթ: Ի՞նչ ուղղությամբ կփոխվեն կառավարության եկամուտները, եթե հարկերը բարձրացվեն կամ ներմուծվեն մաքսատուրքեր։ Արդյո՞ք ընկերության եկամուտը կավելանա կամ կնվազի, երբ իր արտադրանքի գինը բարձրանա: Ի՞նչ համամասնությամբ լրացուցիչ սարքավորումները կարող են փոխարինել թոշակառու աշխատողներին: Նման խնդիրներ լուծելու համար պետք է կառուցվեն դրանցում ներառված փոփոխականների միացման ֆունկցիաները, որոնք այնուհետեւ ուսումնասիրվում են դիֆերենցիալ հաշվարկի մեթոդներով։ Տնտեսագիտության մեջ հաճախ պահանջվում է գտնել ցուցիչի լավագույն կամ օպտիմալ արժեքը՝ աշխատանքի ամենաբարձր արտադրողականությունը, առավելագույն շահույթը, առավելագույն արդյունքը, նվազագույն ծախսերը և այլն։ Յուրաքանչյուր ցուցանիշ մեկ կամ մի քանի փաստարկների ֆունկցիա է։ Այսպիսով, ցուցիչի օպտիմալ արժեքը գտնելը կրճատվում է ֆունկցիայի ծայրահեղության հայտնաբերման վրա:

Ֆերմայի թեորեմի համաձայն, եթե կետը ֆունկցիայի ծայրահեղություն է, ապա ածանցյալը կամ գոյություն չունի դրանում կամ հավասար է 0-ի: Ծայրահեղության տեսակը կարող է որոշվել ծայրահեղության համար բավարար պայմաններից մեկով.

1) Եկեք f(x) ֆունկցիան տարբերվող լինի x 0 կետի ինչ-որ հարևանությամբ: Եթե f "(x) ածանցյալը x 0 կետով անցնելիս փոխում է նշանը +-ից -, ապա x 0-ը առավելագույն կետն է, եթե --ից +, ապա x 0-ը նվազագույն կետն է, եթե այն չի փոխում նշանը: , ուրեմն ծայրահեղություն չկա։

2) Թող f (x) ֆունկցիան երկու անգամ տարբերելի լինի x 0 կետի ինչ-որ հարևանությամբ, իսկ f "(x 0) \u003d 0, f "" (x 0) ≠ 0, ապա x 0 կետում ֆունկցիան. f (x 0) ունի առավելագույնը, եթե f ""(x 0)< 0 и минимум, если f ""(x 0) > 0.

Բացի այդ, երկրորդ ածանցյալը բնութագրում է ֆունկցիայի ուռուցիկությունը (ֆունկցիայի գծապատկերը կոչվում է ուռուցիկ վերև [ներքև] (a, b) միջակայքում, եթե այն գտնվում է այս ինտերվալի վրա ոչ ավելի բարձր [ոչ ներքև] նրա շոշափողներից որևէ մեկից։ )

Օրինակ:ընտրել ընկերության կողմից արտադրության օպտիմալ ծավալը, որի շահույթի ֆունկցիան կարելի է մոդելավորել կախվածությամբ.

π(q) = R(q) - C(q) = q 2 - 8q + 10

Լուծում:

π"(q) = R"(q) - C"(q) = 2q - 8 = 0 → q extr = 4

Ք–ի համար< q extr = 4 → π"(q) < 0 и прибыль убывает

q > q extr = 4 → π"(q) > 0-ի համար և շահույթը մեծանում է

Երբ q = 4, շահույթը վերցնում է նվազագույն արժեքը:

Ո՞րն է ընկերության համար օպտիմալ արդյունքը: Եթե ընկերությունը չի կարող արտադրել ավելի քան 8 միավոր արդյունք դիտարկվող ժամանակահատվածում (p(q = 8) = p(q = 0) = 10), ապա օպտիմալ լուծումը կլինի ընդհանրապես ոչինչ չարտադրելը, այլ եկամուտ ստանալը: տարածքներ և/կամ սարքավորումներ վարձակալելուց: Եթե ֆիրման ի վիճակի է արտադրել ավելի քան 8 միավոր, ապա ֆիրմայի համար օպտիմալը կլինի իր արտադրական հզորությունների սահմաններում արտադրել:

4-2. Պահանջարկի առաձգականություն

f (x) ֆունկցիայի առաձգականությունը x 0 կետում կոչվում է սահման

Պահանջարկը գնորդի կողմից պահանջվող ապրանքի քանակությունն է: Պահանջարկի գնային առաձգականությունը E D-ն չափում է, թե ինչպես է պահանջարկը արձագանքում գների փոփոխություններին: Եթե │E D │>1, ապա պահանջարկը կոչվում է առաձգական, եթե │E D │<1, то неэластичным. В случае E D =0 спрос называется совершенно неэластичным, т. е. изменение цены не приводит ни к какому изменению спроса. Напротив, если самое малое снижение цены побуждает покупателя увеличить покупки от 0 до предела своих возможностей, говорят, что спрос является совершенно эластичным. В зависимости от текущей эластичности спроса, предприниматель принимает решения о снижении или повышении цен на продукцию.

4-3. Սահմանային վերլուծություն

Տնտեսագիտության մեջ օգտագործվող դիֆերենցիալ հաշվարկի մեթոդների կարևոր բաժինը սահմանափակման վերլուծության մեթոդներն են, այսինքն՝ ծախսերի կամ արդյունքների փոփոխվող արժեքների ուսումնասիրման մեթոդների մի շարք՝ արտադրության, սպառման և այլնի փոփոխություններով՝ հիմնված դրանց վերլուծության վրա։ սահմանափակող արժեքներ. Ֆունկցիայի սահմանափակող ցուցիչը (ներ)ն է նրա ածանցյալը (մեկ փոփոխականի ֆունկցիայի դեպքում) կամ մասնակի ածանցյալները (մի քանի փոփոխականների ֆունկցիայի դեպքում)

Տնտեսագիտության մեջ հաճախ օգտագործվում են միջիններ՝ աշխատանքի միջին արտադրողականություն, միջին ծախսեր, միջին եկամուտ, միջին շահույթ և այլն: Բայց հաճախ պահանջվում է պարզել, թե ինչ չափով կավելանա արդյունքը, եթե ծախսերը մեծանան, կամ հակառակը, որքան արդյունքը: կնվազի, եթե ծախսերը կրճատվեն: Այս հարցին հնարավոր չէ պատասխանել միջին արժեքների օգնությամբ։ Նման խնդիրների դեպքում պահանջվում է որոշել արդյունքի և ծախսերի աճի հարաբերակցության սահմանը, այսինքն՝ գտնել սահմանային էֆեկտը։ Ուստի դրանք լուծելու համար անհրաժեշտ է օգտագործել դիֆերենցիալ հաշվարկի մեթոդները։

5. Ածանցյալը մոտավոր հաշվարկներում

5-1. Ինտերպոլացիա

Ինտերպոլացիան մի քանի տրված արժեքներից ֆունկցիայի արժեքների մոտավոր հաշվարկն է: Ինտերպոլյացիան լայնորեն կիրառվում է քարտեզագրության, երկրաբանության, տնտեսագիտության և այլ գիտությունների մեջ։ Ամենապարզ ինտերպոլացիայի տարբերակը Լագրանժի ձևն է, բայց երբ կան բազմաթիվ հանգուցային կետեր, և դրանց միջև ընդմիջումները մեծ են, կամ ցանկանում եք ստանալ մի ֆունկցիա, որի կորությունը նվազագույն է, ապա դիմեք spline interpolation-ին, որն ավելի մեծ ճշգրտություն է տալիս:

Թող K n-ը լինի a = x 0 հանգուցային կետերի համակարգ< x 1 <…< x n = b. Функция S k (x) называется сплайн-функцией S k (x) степени k≥0 на K n , если

ա) S k (x) є C k -1 ()

բ) S k (x)-ը առավելագույնը k աստիճանի բազմանդամ է

Skline ֆունկցիան Ŝ k (x) є S k (K n) կոչվում է ինտերբոլացնող սպլայն ֆունկցիա, եթե Ŝ k (x j) = f(x j) j = 0,1,…,n համար:

Հավելվածներում հաճախ բավական է ընտրել k=3 և կիրառել այսպես կոչված խորանարդ ինտերպոլացիա.

Քանի որ s(x)-ը երրորդ աստիճանի բազմանդամ է յուրաքանչյուր մասնակի միջակայքում, ապա x є-ի համար

Այստեղ s 2 j , c j 1 , c j 0 անհայտ են j = 1, 2, …, n համար

Վերջիններս բացառվում են s(x j) = y j պահանջի պատճառով:

Տարբերակելով այս ֆունկցիան և հաշվի առնելով, որ s "(x)-ը պետք է շարունակական լինի ամբողջ միջակայքում և, հետևաբար, մասնավորապես, հանգույցներում, վերջապես ստանում ենք հավասարումների համակարգը.

n+1 անհայտների նկատմամբ s 2 0 , s 2 1 ,…, s 2 n. Նրանց միանշանակ որոշման համար, կախված առաջադրանքից, ավելացվում են ևս երկու հավասարումներ.

նորմալ դեպք (N):

Պարբերական դեպք (P) (այսինքն.զ(x+(x n -x 0))=զ(x)):

Սահմանների վրա նշված հարթեցում.

Օրինակ: f(x)=sin x, n=4 ֆունկցիայի spline ինտերպոլացիա:

Ֆունկցիան պարբերական է, ուստի մենք օգտագործում ենք P դեպքը։

Spline ֆունկցիան ունի հետևյալ տեսքը.

5-2. Թեյլորի բանաձեւը

Գործառույթների անվերջ շարքերի ընդլայնումը թույլ է տալիս ցանկացած ճշգրտությամբ ստանալ ֆունկցիայի արժեքը տվյալ կետում։ Այս տեխնիկան լայնորեն կիրառվում է ծրագրավորման և այլ բնագավառներում։

Ֆունկցիան կոչվում է, որ ընդլայնվում է տրված միջակայքում և վերածվում է հզորության շարքի, եթե գոյություն ունի այդպիսի հզորության շարք a 0 + a 1 (x - a) + a 2 (x - a) 2 + ... + a n (x - a. ) n + ..., որը համընկնում է այս ֆունկցիային այս միջակայքում: Կարելի է ապացուցել, որ այս տարրալուծումը եզակի է.

Թող f(x) ֆունկցիան անվերջ տարբերակելի լինի a կետում: Ձևի ուժային շարք

կոչվում է Թեյլորի շարք f(x) ֆունկցիայի համար, որը գրված է տարբերության հզորություններով (x - a): Ընդհանուր առմամբ, որպեսզի Թեյլորի շարքը համընկնի f(x-ին), անհրաժեշտ և բավարար է, որ շարքի մնացորդը ձգվի դեպի 0: a = 0-ի համար Թեյլորի շարքը սովորաբար կոչվում է Մակլաուրինի շարք:

Ի.Մ.Ուվարենկով,

M. Z. Maller

Մաթեմատիկական վերլուծության դասընթաց, հ.1

Վ.Ա.Դուդարենկո,

Ա.Ա. Դադայանը

Մաթեմատիկական վերլուծություն

Դիֆերենցիալ և ինտեգրալ հաշվարկ

T. I. Տրոֆիմովա

Ֆիզիկայի դասընթաց

O. O. Zamkov

Ա.Վ.Տոլստոպյատենկո

Յու.Ն.Չերեմնիխ

Մաթեմատիկական մեթոդները տնտեսագիտության մեջ

Ա.Ս. Սոլոդովնիկով

Վ.Ա.Բաբաիցև

A. V. Brailov

Ի.Գ. Շանդրա

Մաթեմատիկա տնտեսագիտության մեջ

Ներածություն

1. Ածանցյալ հասկացությունը

1-1. Պատմական տեղեկություններ

1-2. Ածանցյալ հասկացությունը

1-3. Ածանցյալների տարբերակման կանոններ և աղյուսակ

2. Ածանցյալի երկրաչափական նշանակությունը

2-1. Շոշափող կորին

2-2. Մակերեւույթին շոշափող հարթություն

3. Ածանցյալի օգտագործումը ֆիզիկայում

3-1. Նյութական կետի արագություն

3-2. Ջերմային հզորությունը տվյալ ջերմաստիճանում

3-3. Ուժ

4. Դիֆերենցիալ հաշվարկը տնտեսագիտության մեջ

4-1. Ֆունկցիոնալ հետազոտություն

4-2. Պահանջարկի առաձգականություն

4-3. Սահմանային վերլուծություն

5. Ածանցյալը մոտավոր հաշվարկներում

5-1. Ինտերպոլացիա

5-2. Թեյլորի բանաձեւը

5-3. Մոտավոր հաշվարկներ

Եզրակացություն

Օգտագործված գրականության ցանկ

Հարավային Սախալինի պետական համալսարան

մաթ

Դասընթացի աշխատանք

Թեմա՝ Ածանցյալի գործնական կիրառում

Դասախոս՝ Լիխաչևա Օ.Ն.

Յուժնո-Սախալինսկ

2002 թ Ներածություն

1. Ածանցյալ հասկացությունը

1-1. Պատմական տեղեկություններ

Դիֆերենցիալ հաշվարկը ստեղծվել է Նյուտոնի և Լայբնիցի կողմից 17-րդ դարի վերջին երկու խնդիրների հիման վրա.

1) կամայական գծին շոշափող գտնելու մասին

2) շարժման կամայական օրենքով արագության որոնման մասին

Նույնիսկ ավելի վաղ ածանցյալ հասկացությունը հանդիպում էր իտալացի մաթեմատիկոս Տարտալյայի աշխատություններում (մոտ 1500 - 1557 թթ.) - այստեղ հրացանի թեքության անկյան հարցի ուսումնասիրության ընթացքում հայտնվեց շոշափողություն, որն ապահովում է ամենամեծ հեռահարությունը: արկի։

1-2. Ածանցյալ հասկացությունը

Թող y = f(x) լինի x արգումենտի շարունակական ֆունկցիան, որը սահմանված է (a; b) միջակայքում, իսկ x0-ն այս ինտերվալի կամայական կետն է:

1-3. Ածանցյալների տարբերակման կանոններ և աղյուսակ

C" = 0(xn) = nxn-1(sin x)" = cos xx" = 1(1 / x)" = -1 / x2(cos x)" = -sin x(Cu)"=Cu"( √x)" = 1 / 2 u / v)"=(u"v - uv") / v2(ex)" = ex(arcsin x)" = 1 / √ (1- x2) (logax)" = (logae) / x(arccos x) " = -1 / √ (1- x2) (ln x)" = 1 / x (arctg x)" = 1 / √ (1+ x2) (arctg x)" = -1 / √ (1+ x2)

2. Ածանցյալի երկրաչափական նշանակությունը

2-1. Շոշափող կորին

Դիտարկենք այս ֆունկցիային համապատասխան f(x) ֆունկցիան և y = f(x) կորը։ Որոշ x արժեքի համար ֆունկցիան ունի y = f(x) արժեքը: Այս արժեքները կորի վրա համապատասխանում են M (x0, y0) կետին: Մենք ներկայացնում ենք նոր արգումենտ x0 + ∆x, որի արժեքը համապատասխանում է y0 + ∆y = f(x0 + ∆x) ֆունկցիայի արժեքին: Համապատասխան կետն է՝ N(x0 + ∆x, y0 + ∆y): Գծե՛ք MN հատվածը և φ-ով նշանակե՛ք կտրվածքով գոյացած անկյունը Ox առանցքի դրական ուղղությամբ։ Նկարը ցույց է տալիս, որ ∆y / ∆x = tg φ: Եթե այժմ ∆x-ը մոտենա 0-ին, ապա N կետը կշարժվի կորի երկայնքով, MN հատվածը կպտտվի M կետի շուրջ, և φ անկյունը կփոխվի։ Եթե, ինչպես ∆x → 0, φ անկյունը հակված է որոշ α-ի, ապա M-ով անցնող և աբսցիսային առանցքի դրական ուղղությամբ α անկյունը կազմող ուղիղ գիծը կլինի ցանկալի շոշափողը։ Միևնույն ժամանակ, դրա թեքության գործակիցը.

2-2. Մակերեւույթին շոշափող հարթություն

Վերցրեք մի մակերես, որը տրված է F(x, y, z) = 0 հավասարմամբ և դրա վրա գտնվող մի սովորական կետ M(x0, y0, z0): Մակերեւույթի վրա դիտարկենք M-ի միջով անցնող L կորը: Թող կորը տրվի հավասարումներով

x = φ (t); y = ψ(t); z = χ(t).

M կետում L կորի շոշափողի հավասարումները ունեն ձև.

Քանի որ x - x0, y - y0, z - z0 տարբերությունները համաչափ են համապատասխան դիֆերենցիալներին, ինքնաթիռի վերջնական հավասարումն ունի հետևյալ տեսքը.

F "x (x - x0) + F" y (y - y0) + F "z (z - z0) \u003d 0

իսկ կոնկրետ դեպքի համար z = f(x, y):

Z - z0 \u003d F "x (x - x0) + F" y (y - y0)

Օրինակ:Գտե՛ք շոշափող հարթության հավասարումը հիպերբոլիկ պարաբոլոիդի (2a; a; 1,5a) կետում.

Լուծում:

Z"x \u003d x / a \u003d 2; Z"y \u003d -y / a \u003d -1

Ցանկալի հարթության հավասարումը.

Z - 1.5a = 2 (x - 2a) - (Y - a) կամ Z = 2x - y - 1.5a

3. Ածանցյալի օգտագործումը ֆիզիկայում

3-1. Նյութական կետի արագություն

Թող s ուղու կախվածությունը t ժամանակից նյութական կետի տրված ուղղագիծ շարժումով արտահայտվի s = f(t) հավասարումով, իսկ t0-ը ժամանակի ինչ-որ պահ է: Դիտարկենք մեկ այլ ժամանակ t, նշանակենք ∆t = t - t0 և հաշվարկենք ճանապարհի աճը՝ ∆s = f(t0 + ∆t) - f(t0): ∆s / ∆t հարաբերակցությունը կոչվում է շարժման միջին արագություն t0 սկզբնական պահից անցած ∆t ժամանակի ընթացքում: Արագությունը այս հարաբերակցության սահմանն է՝ Δt → 0:

Այսինքն՝ առաջին անգամ ածանցյալը (v «(t)):

Օրինակ:Մարմնի անցած ուղու ժամանակային կախվածությունը տրվում է s = A + Bt + Ct2 + Dt3 (C = 0,1 մ/վ, D = 0,03 մ/վ2) հավասարումով։ Որոշեք շարժումը սկսելուց հետո այն ժամանակը, որից հետո մարմնի արագացումը հավասար կլինի 2 մ/վ2:

Լուծում:

v(t) = s"(t) = B + 2Ct + 3Dt2; a(t) = v"(t) = 2C + 6Dt = 0.2 + 0.18t = 2;

1,8 = 0,18 տ; t = 10 վ

3-2. Նյութի ջերմունակությունը տվյալ ջերմաստիճանում

T-ի տարբեր ջերմաստիճանները նույն արժեքով բարձրացնելու համար, որը հավասար է T1 - T-ի, 1 կգ-ի դիմաց: տվյալ նյութին անհրաժեշտ է տարբեր քանակությամբ ջերմություն Q1 - Q, և հարաբերակցությունը

3-3. Ուժ

Մարմնի մեխանիկական շարժման փոփոխությունը պայմանավորված է այլ մարմիններից նրա վրա ազդող ուժերի պատճառով: Փոխազդող մարմինների միջև էներգիայի փոխանակման գործընթացը քանակականորեն բնութագրելու համար մեխանիկայում ներդրվում է ուժի աշխատանքի հասկացությունը։ Աշխատանքի կատարման արագությունը բնութագրելու համար ներկայացվում է ուժ հասկացությունը.

4. Դիֆերենցիալ հաշվարկը տնտեսագիտության մեջ

4-1. Ֆունկցիոնալ հետազոտություն

1) Եկեք f(x) ֆունկցիան տարբերակելի լինի x0 կետի ինչ-որ հարևանությամբ: Եթե f "(x) ածանցյալը x0 կետով անցնելիս փոխում է նշանը +-ից -, ապա x0-ը առավելագույն կետն է, եթե --ից +, ապա x0-ը նվազագույն կետն է, եթե այն չի փոխում նշանը, ապա այս պահին ծայրահեղություն չէ:

2) Թող f(x) ֆունկցիան երկու անգամ տարբերվող լինի x0 կետի ինչ-որ հարևանությամբ, և f "(x0) = 0, f ""(x0) ≠ 0, ապա x0 կետում f(x0) ֆունկցիան ունի. առավելագույնը, եթե

Ներբեռնել:

Նախադիտում:

Սլայդների ենթագրեր.

Նախադիտում:

Սլայդների ենթագրեր.

Կարդացեք նաև