állami autonóm intézmény
szakmai oktatási szervezet
Szolgáltatási és Idegenforgalmi Főiskola
Előadások menete gyakorlati feladatok példáival
"Az elméleti mechanika alapjai"
fegyelem szerintMűszaki mechanika
diákoknak3 tanfolyam
szakterületek20.02.04 Tűzbiztonság
Kalinyingrád
JÓVÁHAGY
Az SD GAU KO VEO KSTN.N. igazgatóhelyettese. Myasnikova
JÓVÁHAGYOTT
GAU KO VET KST Módszertani Tanácsa
FIGYELEMBE VETT
A PCC ülésén
Szerkesztői csapat:
Kolganova A.A., módszertanos
Falaleeva A.B., orosz nyelv és irodalom tanár
Tsvetaeva L.V., a PCC elnökeáltalános matematikai és természettudományi diszciplínák
Összeállította:
Nezvanova I.V. Előadó GAU KO VET KST
Tartalom
Elméleti információk
Elméleti információk
Példák gyakorlati problémák megoldására
Dinamika: alapfogalmak és axiómák
Elméleti információk
Példák gyakorlati problémák megoldására
Bibliográfia
Elméleti információk
Statika: alapfogalmak és axiómák.
Statika - az elméleti mechanika egy része, amely a merev test pontjaira ható erők tulajdonságait, egyensúlyi feltételeit veszi figyelembe. Főbb célok:
1. Erőrendszerek átalakítása egyenértékű erőrendszerekké.
2. A rá ható erőrendszerek egyensúlyi feltételeinek meghatározása szilárd.
anyagi pont az anyagi test legegyszerűbb modelljének nevezik
bármilyen alakzat, amelynek méretei elég kicsik, és amely meghatározott tömegű geometriai pontnak tekinthető. A mechanikai rendszer anyagi pontok tetszőleges halmaza. Az abszolút merev test olyan mechanikai rendszer, amelynek pontjai közötti távolságok semmilyen kölcsönhatás során nem változnak.
Erő az anyagi testek egymással való mechanikai kölcsönhatásának mértéke. Az erő egy vektormennyiség, mivel három elem határozza meg:
numerikus érték;
irány;
alkalmazási pont (A).
Az erő mértékegysége Newton (N).

1.1. ábra
Az erőrendszer egy testre ható erők összessége.
A kiegyensúlyozott (nullával egyenlő) erőrendszer olyan rendszer, amely egy testre alkalmazva nem változtatja meg annak állapotát.
A testre ható erőrendszer helyettesíthető egy eredővel, amely erőrendszerként működik.
A statika axiómái.
1. axióma: Ha kiegyensúlyozott erőrendszer hat a testre, akkor egyenletesen és egyenesen mozog, vagy nyugalomban van (a tehetetlenség törvénye).
2. axióma:
Egy abszolút merev test akkor és csak akkor van egyensúlyban két erő hatására, ha ezek az erők abszolút értékűek, egy egyenesben hatnak és ellentétes irányúak. 1.2. ábra
3. axióma:
A test mechanikai állapotát nem zavarja meg, ha a rá ható erőrendszerhez hozzáadunk vagy kivonunk egy kiegyensúlyozott erőrendszert.
4. axióma: A testre ható két erő eredője egyenlő a geometriai összegükkel, azaz abszolút értékben és irányban az ezekre az erőkre, mint az oldalakra épített paralelogramma átlója fejezi ki.
1.3. ábra.
5. axióma:
Azok az erők, amelyekkel két test hat egymásra, abszolút értékűek, és egy egyenes mentén ellentétes irányban irányulnak.
1.4. ábra.
A kötések típusai és reakcióik
kapcsolatokat
Minden olyan korlátozást nevezünk, amely megakadályozza a test mozgását a térben. A fellépő erők hatására elmozdulni igyekvő test, amelyet a kapcsolat megakadályoz, egy bizonyos erővel, ún. a csatlakozásra ható nyomáserő
. A cselekvés és a reakció egyenlőségének törvénye szerint a kapcsolat azonos modulussal, de ellentétes irányú erővel hat a testre.
Azt az erőt, amellyel ez a kapcsolat a testre hat, megakadályozva egyik vagy másik mozgást, ún a kötés reakcióereje (reakciója).
.
A mechanika egyik alapelve az felszabadulás elve
:
bármely nem szabad test szabadnak tekinthető, ha a kötéseket elvetjük és hatásukat a kötések reakcióival helyettesítjük.
A kötésreakció az ellenkező irányba irányul, mint ahol a kötés nem engedi a testet elmozdulni. A kötések főbb típusait és reakcióit az 1.1. táblázat mutatja be.
1.1. táblázat
A kötések típusai és reakcióik
Kommunikációs név
Szimbólum
1
Sima felület (támaszték)
- felület (támaszték), súrlódás, amelyen az adott test elhanyagolható.
Ingyenes támogatással a reakcióa ponton átmenő érintőre merőlegesen irányulDE
testkontaktus1
tartófelülettel2
.

2
Menet (rugalmas, nyújthatatlan). A nyújthatatlan menet formájában kialakított csatlakozás nem teszi lehetővé a test elmozdulását a felfüggesztés helyétől. Ezért a menet reakciója a menet mentén a felfüggesztés pontjáig irányul.

3
súlytalan rúd
– olyan rúd, amelynek súlya az észlelt terheléshez képest elhanyagolható.
A súlytalan csuklós egyenes vonalú rúd reakciója a rúd tengelye mentén irányul.

4
Mozgatható zsanér, csuklós mozgatható támaszték. A reakció a normál mentén a támasztófelületre irányul.

7
Merev zárás.
A merev beágyazás síkjában a reakció két komponense lesz,
és egy erőpár pillanata, amely megakadályozza a gerenda elfordulását1
ponthoz képestDE
.
Egy merev rögzítés a térben elveszi mind a hat szabadsági fokot az 1. testtől – három elmozdulás a koordinátatengelyek mentén és három elfordulás e tengelyek körül.
A térbeli merev beágyazásban három összetevő lesz,
,
és három pillanatnyi erőpár![]() .
.

Összetartó erőrendszer
Összetartó erők rendszere
olyan erőrendszernek nevezzük, amelynek hatásvonalai egy pontban metszik egymást. Két, egy pontban konvergáló erő a statika harmadik axiómája szerint egy erővel helyettesíthető -eredő
.
Az erőrendszer fővektora
- a rendszer erőinek geometriai összegével egyenlő érték.
Konvergáló erők síkrendszerének eredője meg lehet határoznigrafikusan és elemzőleg.
Erőrendszer összeadása . A konvergáló erők lapos rendszerének összeadása vagy az erők egymás utáni összeadásával, közbenső eredő felépítésével (1.5. ábra), vagy egy erőpoligon felépítésével (1.6. ábra).


1.5. ábra 1.6. ábra
Erő vetülete a tengelyre
- algebrai mennyiség, amely egyenlő az erőmodulus és az erő és a tengely pozitív iránya közötti szög koszinuszának szorzatával.
KivetítésFx(1.7. ábra) tengelyenkénti erők xpozitív, ha α akut, negatív, ha α tompa. Ha erőtmerőleges a tengelyre, akkor a vetülete a tengelyre nulla.

1.7. ábra
Erő vetítése egy síkon Ohu– vektor , amely az erő kezdetének és végének vetületei között következett beerre a síkra. Azok. az erő síkra vetítése egy vektormennyiség, amelyet nemcsak számérték, hanem a síkban lévő irány is jellemez.Ohu (1.8. ábra).

1.8. ábra
Aztán a vetítési modul a repülőhöz Ohu egyenlő lesz:
Fxy = F cosα,
ahol α az erő iránya közötti szögés annak vetülete.
Analitikai módszer erőkiosztások
.
Az erő beállításának analitikai módszeréhezkoordinátatengely-rendszert kell választaniOhz, amelyhez képest az erő iránya a térben meghatározásra kerül.
Az erőt ábrázoló vektor, akkor állítható elő, ha ismerjük ennek az erőnek a modulusát és azokat az α, β, γ szögeket, amelyeket az erő a koordinátatengelyekkel alkot. PontDE erő alkalmazása koordinátáival külön beállítvax,
nál nél,
z. Az erőt a vetületei alapján állíthatja befx,
fy,
F za koordináta tengelyeken. Az erő modulusát ebben az esetben a következő képlet határozza meg:
![]()
és irány koszinusz:
,
.
Erők összeadásának analitikai módszere : az összegvektor valamely tengelyre vetítése megegyezik a vektorok tagjainak ugyanarra a tengelyre vetített vetületeinek algebrai összegével, azaz ha:
akkor , , .
Tudva Rx, Ry, Rz, definiálhatjuk a modult
![]()
és irány koszinusz:
, , .
1.9. ábra
Egy konvergáló erőrendszer egyensúlyához szükséges és elegendő, hogy ezen erők eredője nullával egyenlő.1) Geometriai egyensúlyi feltétel konvergáló erőrendszerhez : egy konvergáló erőrendszer egyensúlyához szükséges és elegendő, hogy az erőpoligon ezekből az erőkből épüljön fel.
zárva volt (az utolsó tag vektorának vége
az erőnek egybe kell esnie az erő első tagjának vektorának kezdetével). Ekkor az erőrendszer fővektora az lesz nulla ()
2)
Analitikai feltételek egyensúlyi
.
Az erőrendszer fővektorának modulját a képlet határozza meg.
![]() =0. Mert a , akkor a gyökkifejezés csak akkor lehet nulla, ha minden tag egyidejűleg eltűnik, pl.
=0. Mert a , akkor a gyökkifejezés csak akkor lehet nulla, ha minden tag egyidejűleg eltűnik, pl.
Rx= 0, Ry= 0, R z = 0.
Ezért a konvergáló erők térbeli rendszerének egyensúlyához szükséges és elegendő, hogy ezeknek az erőknek a vetületeinek összege a tengely mindhárom koordinátájára nulla legyen:
A konvergáló erők lapos rendszerének egyensúlyához szükséges és elegendő, hogy a két koordinátatengelyre eső erővetületek összege nulla legyen:
Két párhuzamos, azonos irányú erő összeadása.

1.9. ábra
Két, azonos irányú párhuzamos erő azonosra redukálódik működő erő, velük párhuzamosan és ugyanabba az irányba irányítva. Az eredő nagysága megegyezik ezen erők nagyságának összegével, és alkalmazásának pontja C osztja az erők hatásvonalai közötti távolságot belsőleg ezeknek az erőknek a nagyságával fordítottan arányos részekre, azazB A C
R=F 1 +F 2
Két, egymással ellentétes irányú, egyenlőtlen párhuzamos erő összeadása.
Két egyenlőtlen antipárhuzamos erő egy velük párhuzamos eredő erőre redukálódik, és a nagyobb erő felé irányul. Az eredő nagysága egyenlő ezen erők nagysága közötti különbséggel, és alkalmazásának pontja, C, a külső erők hatásvonalai közötti távolságot ezen erők nagyságával fordítottan arányos részekre osztja, van
Erőpár és erőnyomaték egy pont körül.
Az erő pillanata
az O ponthoz viszonyítva a megfelelő előjellel felvetve az erő nagyságának az O pont és az erő hatásvonala közötti h távolság szorzatát nevezzük. . Ezt a terméket pluszjellel kell venni, ha az erő hajlamos a testet az óramutató járásával ellentétes irányba forgatni, és a - jellel, ha az erő hajlamos a testet az óramutató járásával megegyező irányba forgatni, azaz . A h merőleges hosszát únaz erő vállát
pont O. Az erőhatás hatása i.e. a test szöggyorsulása annál nagyobb, minél nagyobb az erőnyomaték nagysága.
1.11. ábra
Pár erő Rendszernek nevezzük azt a rendszert, amely két párhuzamos, azonos nagyságú, ellentétes irányú erőből áll. Az erők hatásvonalai közötti h távolságot únvállpárok . Egy erőpár pillanata m(F,F") a párt alkotó egyik erő értékének és a pár karjának szorzata a megfelelő előjellel.Ez a következőképpen írható: m(F, F")= ± F × h, ahol a szorzatot plusz előjellel vesszük, ha az erőpár hajlamos a testet az óramutató járásával ellentétes irányba forgatni, és mínusz előjellel, ha az erőpár hajlamos. hogy a testet az óramutató járásával megegyező irányba forgatjuk.
A tétel egy pár erőnyomatékainak összegéről.
Az (F,F") pár erőnyomatékainak összege a pár hatássíkjában felvett bármely 0 ponthoz képest nem függ ennek a pontnak a megválasztásától, és egyenlő a pár nyomatékával.
Tétel ekvivalens párokról. Következmények.
Tétel. Két olyan pár, amelyek pillanatai egyenlőek egymással, ekvivalens, azaz. (F, F") ~ (P, P")
Következmény 1 . Egy erőpár a cselekvés síkjában tetszőleges helyre átvihető, valamint tetszőleges szögben elforgatható, és megváltoztathatja a pár erőinek karját és nagyságát, miközben megtartja a pár pillanatát.
2. következmény. Egy erőpárnak nincs eredője, és nem lehet kiegyensúlyozni a pár síkjában fekvő egyetlen erővel.

1.12. ábra
Összeadás és egyensúlyi feltétel egy síkon lévő párrendszerhez.
1. Tétel az azonos síkban fekvő párok összeadásáról. Egy síkban tetszőlegesen elhelyezkedő párok rendszere helyettesíthető egy párral, amelynek pillanata egyenlő az összeggel e párok pillanatai.
2. Tétel egy párrendszer síkbeli egyensúlyáról.
Ahhoz, hogy egy abszolút merev test nyugalomban legyen egy párrendszer hatására, tetszőlegesen ugyanabban a síkban, szükséges és elegendő, hogy az összes pár nyomatékainak összege nulla legyen, azaz
Gravitáció középpontja
Gravitáció - a Föld vonzási erőinek eredője, a test teljes térfogatán elosztva.
A test súlypontja - ez egy olyan pont, amely változatlanul ehhez a testhez kapcsolódik, és amelyen egy adott test gravitációs erejének hatásvonala áthalad a test bármely helyén a térben.
A súlypont megtalálásának módszerei
1. Szimmetriás módszer:
1.1. Ha egy homogén testnek van szimmetriasíkja, akkor a súlypont ebben a síkban van
1.2. Ha egy homogén testnek van szimmetriatengelye, akkor a súlypont ezen a tengelyen található. Egy homogén forradalomtest súlypontja a forradalom tengelyén fekszik.
1.3 Ha egy homogén testnek két szimmetriatengelye van, akkor a tömegközéppont ezek metszéspontjában van.
2. Split módszer: A testet felosztják legkisebb szám olyan részek, amelyek gravitációja és a súlypontok helyzete ismert.
3. Negatív tömegek módszere: Szabad üregekkel rendelkező test tömegközéppontjának meghatározásakor a felosztási módszert kell alkalmazni, de a szabad üregek tömegét negatívnak kell tekinteni.
A súlypont koordinátái lapos alak:

Az egyszerű súlypontok helyzete geometriai formák szerint lehet számolni ismert képletek. (1.13. ábra)

Jegyzet: Az ábra szimmetriájának súlypontja a szimmetriatengelyen van.
A rúd súlypontja a magasság közepén van.
1.2. Példák gyakorlati problémák megoldására
1. példa:
Egy súly egy rúdon van felfüggesztve, és egyensúlyban van. Határozza meg a rúdban lévő erőket. (1.2.1. ábra)
Megoldás:
A rögzítőrudakban fellépő erők egyenlőek azokkal az erőkkel, amelyekkel a rudak a terhelést támogatják. (5. axióma)
Meghatározzuk a kötések „merev rudak” reakcióinak lehetséges irányait.
Az erőfeszítések a rudak mentén irányulnak.
1.2.1. ábra.
Szabadítsuk meg az A pontot a kötésektől, helyettesítve a kötések hatását azok reakcióival. (1.2.2. ábra)
Kezdjük a konstrukciót ismert erővel vektor rajzolásávalFvalamilyen léptékben.
A vektor végétőlFhúzz párhuzamos vonalakat a reakciókkalR 1 ésR 2 .
1.2.2. ábra
Az egymást metsző vonalak háromszöget hoznak létre. (1.2.3. ábra). A konstrukciók léptékének ismeretében és a háromszög oldalainak hosszának mérésével meg lehet határozni a pálcákban fellépő reakciók nagyságát.
A pontosabb számításokhoz használhat geometriai összefüggéseket, különösen a szinusztételt: a háromszög oldalának és az ellenkező szög szinuszának aránya állandó érték
![]()
Erre az esetre:
1.2.3. ábra
![]()
Megjegyzés: Ha a vektor (csatolási reakció) iránya egy adott sémán és az erőháromszögben nem egyezik, akkor a reakciót a sémán az ellenkező irányba kell irányítani.
2. példa:
Határozza meg analitikus módon a konvergáló erők eredő lapos rendszerének nagyságát és irányát!
Megoldás:
1.2.4. ábra
1. Határozzuk meg a rendszer összes erőjének vetületét az oxra (1.2.4. ábra)A vetületeket algebrailag összeadva megkapjuk az eredő vetületét az Ox tengelyre.

A jel azt jelzi, hogy az eredő balra irányul.
2. Meghatározzuk az összes erő vetületét az Oy tengelyre:
A vetületeket algebrailag összeadva megkapjuk az eredő vetületét az Oy tengelyre.
A jel azt jelzi, hogy az eredő lefelé irányul.
3. Határozza meg az eredő modulusát a vetületek nagyságával:
4. Határozza meg az eredő Ox tengellyel bezárt szögének értékét!

és az y tengellyel bezárt szög értéke:
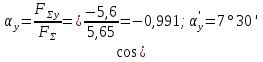
3. példa:
Számítsa ki az O ponthoz viszonyított erőnyomatékok összegét (1.2.6. ábra).
OA= AB= NÁL NÉLD=DE=CB=2m
1.2.6. ábra
Megoldás:
1. A ponthoz viszonyított erőnyomaték számszerűen egyenlő a modul és az erő karjának szorzatával.
2. Az erőnyomaték egyenlő nullával, ha az erő hatásvonala egy ponton halad át.
4. példa:
Határozza meg az 1.2.7. ábrán látható ábra súlypontjának helyzetét!
Megoldás:
Három részre osztjuk az ábrát:
1-téglalap
DE 1 =10*20=200cm 2
2-háromszög
DE 2 =1/2*10*15=75cm 2
3 körös
DE 3 =3,14*3 2 = 28,3 cm 2
1. ábra CG: x 1 =10 cm, y 1 = 5 cm
2. ábra CG: x 2 =20+1/3*15=25cm, u 2 =1/3*10=3,3cm
3. ábra CG: x 3 =10 cm, y 3 = 5 cm
Hasonlóképpen van meghatározva a Val vel = 4,5 cm
Kinematika: alapfogalmak.
Alapvető kinematikai paraméterek
Röppálya - az a vonal, amelyet egy anyag pont körvonalaz, amikor a térben mozog. A pálya lehet egyenes és görbe, sík és térbeli vonal.
A sík mozgásának pályaegyenlete: y =f ( x)
Megtett távolság. Az utat a menetirány mentén mérjük. Megnevezés -S, mértékegységek - méter.
Pontmozgási egyenlet egy egyenlet, amely egy mozgó pont helyzetét az idő függvényében határozza meg.
2.1. ábra
Egy pont helyzete az egyes időpillanatokban a pálya mentén megtett távolság alapján határozható meg valamely fix ponttól, amelyet origónak tekintünk (2.1. ábra). Ezt a fajta mozgást úntermészetes . Így a mozgásegyenlet a következőképpen ábrázolható: S = f (t).

2.2. ábra
Egy pont helyzete akkor is meghatározható, ha a koordinátáit az idő függvényében ismerjük (2.2. ábra). Ekkor síkban történő mozgás esetén két egyenletet kell megadni:Térbeli mozgás esetén egy harmadik koordináta is hozzáadásra kerülz= f 3 ( t)
Ezt a fajta mozgást únkoordináta .
Utazási sebesség egy vektormennyiség, amely az adott pillanatban a pálya mentén történő mozgás sebességét és irányát jellemzi.
A sebesség egy vektor, amely bármely pillanatban érintőlegesen irányul a pályára a mozgás iránya felé (2.3. ábra).
2.3. ábra
Ha egy pont egyenlő időközönként egyenlő távolságokat tesz meg, akkor a mozgást hívjákegyenruha .Átlagsebesség az úton ΔSmeghatározott:
ahol∆S- időben megtett távolság Δt; Δ t- időintervallum.
Ha egy pont egyenlőtlen időközönként egyenlőtlen utakat tesz meg, akkor a mozgást únegyenetlen . Ebben az esetben a sebesség változó és időfüggőv= f( t)
Az aktuális sebességet a következőképpen határozzuk meg
pont gyorsulás - a sebesség nagyságrendi és irányú változásának mértékét jellemző vektormennyiség.
Egy pont sebessége az M1 pontból az Mg pontba való mozgáskor nagyságrendben és irányban változik. A gyorsulás átlagos értéke erre az időszakra
Jelenlegi gyorsulás:
Általában a kényelem kedvéért két egymásra merőleges gyorsulási összetevőt veszünk figyelembe: a normált és az érintőlegest (2.4. ábra).
Normál gyorsulás a n , a sebesség változását azzal jellemzi
irányát és úgy határozzuk meg
A normál gyorsulás mindig a sebességre merőlegesen irányul az ív középpontja felé.
2.4. ábra
Tangenciális gyorsulás a t , a sebesség nagyságrendi változását jellemzi, és mindig érintőlegesen irányul a pályára; gyorsításkor iránya egybeesik a sebesség irányával, lassításkor pedig a sebességvektor irányával ellentétes.![]()
A teljes gyorsulás értékét a következőképpen határozzuk meg:
A mozgások típusainak és kinematikai paramétereinek elemzése
Egységes mozgás - Ez egy állandó sebességű mozgás:
Egyenes vonalúhoz egyenletes mozgás:
A görbe vonalú egyenletes mozgáshoz:
![]()
Az egyenletes mozgás törvénye :
Egyenlő változó mozgás – állandó tangenciális gyorsulású mozgás:
Egyenes vonalú egyenletes mozgáshoz
A görbe vonalú egyenletes mozgáshoz:
![]()
Az egyenletes mozgás törvénye:
![]()
Kinematikai grafikonok
Kinematikai grafikonok - ezek az út, a sebesség és a gyorsulás időtől függő változásainak grafikonjai.
Egyenletes mozgás (2.5. ábra)

2.5. ábra
Egyenlő változó mozgás (2.6. ábra)

2.6. ábra
A merev test legegyszerűbb mozdulatai
Előre mozgás merev test mozgásának nevezzük, amelyben a test bármely egyenes vonala mozgás közben párhuzamos marad a kezdeti helyzetével (2.7. ábra).

2.7. ábra
A transzlációs mozgásban a test minden pontja ugyanúgy mozog: a sebességek és a gyorsulások minden pillanatban azonosak.
Nál nélforgó mozgás
a test minden pontja egy közös rögzített tengely körüli köröket ír le.
A rögzített tengelyt, amely körül a test minden pontja forog, nevezzükforgástengely.
Csak egy test fix tengely körüli forgó mozgásának leírásárasarok opciók. (2.8. ábra)
φ a test elfordulási szöge;
ω – szögsebesség, meghatározza a forgásszög változását egységnyi idő alatt;
A szögsebesség időbeli változását a szöggyorsulás határozza meg:
2.2. Példák gyakorlati problémák megoldására
1. példa: Adott egy pont mozgásegyenlete. Határozza meg a pont sebességét a mozgás harmadik másodpercének végén és az átlagos sebességet az első három másodpercben.
![]()
Megoldás:
1. A sebesség egyenlete
2. Sebesség a harmadik másodperc végén (t=3 c)
3. Átlagsebesség
2. példa: Az adott mozgástörvény szerint határozza meg a mozgás típusát, a pont kezdősebességét és érintőleges gyorsulását, a megállás idejét!
![]()
Megoldás:
1. Mozgás típusa: egyformán változó (![]() )
)
2. Az egyenletek összehasonlításakor nyilvánvaló, hogy
- a visszaszámlálás kezdete előtt megtett kezdeti út 10 méterrel;
- kezdeti sebesség 20m/s
- állandó tangenciális gyorsulás ![]()
- a gyorsulás negatív, ezért a mozgás lassú, a gyorsulás a mozgási sebességgel ellentétes irányba irányul.
3. Meghatározhatja azt az időt, amikor a pont sebessége egyenlő lesz nullával.
3. Dinamika: alapfogalmak és axiómák
Dinamika - az elméleti mechanika azon része, amelyben a testek mozgása és a rájuk ható erők között kapcsolat jön létre.
A dinamikában kétféle probléma oldható meg:
határozza meg a mozgási paramétereket az adott erők szerint;
határozza meg a testre ható erőket, a mozgás adott kinematikai paraméterei szerint.
Alattanyagi pont
egy bizonyos testet jelent, amelynek bizonyos tömege van (azaz bizonyos mennyiségű anyagot tartalmaz), de nincs lineáris mérete (végtelenül kicsi tértérfogat).
izolált
olyan tárgyi pontot vesznek figyelembe, amelyet más anyagi pontok nem érintenek. A való világban izolált anyagi pontok, mint az elszigetelt testek, nem léteznek, ez a fogalom feltételes.
Transzlációs mozgásnál a test minden pontja egyformán mozog, így a test anyagi pontnak vehető fel.
Ha a test méretei a pályához képest kicsik, akkor anyagi pontnak is tekinthető, miközben a pont egybeesik a test súlypontjával.
A test forgó mozgása során előfordulhat, hogy a pontok nem egyformán mozognak, ebben az esetben a dinamika egyes rendelkezései csak egyes pontokra vonatkoztathatók, az anyagi tárgy pedig anyagi pontok halmazának tekinthető.
Ezért a dinamika fel van osztva egy pont dinamikájára és egy anyagrendszer dinamikájára.
A dinamika axiómái
Első axióma ( tehetetlenségi elv): in bármely izolált anyagpont nyugalomban van vagy egyenletes és egyenes vonalú mozgás amíg az alkalmazott erők ki nem hozzák ebből az állapotból.
Ezt az állapotot államnak neveziktehetetlenség. Távolítsa el a pontot ebből az állapotból, azaz. adj neki némi gyorsulást, esetleg külső erőt.
Minden testnek (pontnak) vantehetetlenség. A tehetetlenség mértéke a test tömege.
Tömeg hívottaz anyag mennyisége egy testben a klasszikus mechanikában állandó értéknek számít. A tömeg mértékegysége a kilogramm (kg).
Második axióma (Newton második törvénye a dinamika alaptörvénye)
F=ma
aholt - ponttömeg, kg;a - pontgyorsulás, m/s 2 .
Egy anyagi pontra erő által adott gyorsulás arányos az erő nagyságával, és egybeesik az erő irányával.
A gravitáció a Föld minden testére hat, a testnek a szabadesés gyorsulását adja, a Föld közepe felé irányítva:
G=mg
aholg- 9,81 m/s², szabadesési gyorsulás.
Harmadik axióma (Newton harmadik törvénye): -valKét test kölcsönhatási ereje egyenlő nagyságú, és ugyanazon egyenes mentén különböző irányokba irányul.
Ha kölcsönhatásba lépnek, a gyorsulások fordítottan arányosak a tömegekkel.
Negyedik axióma (az erők működésének függetlenségének törvénye): ahhozAz erőrendszerben minden erő úgy működik, mintha egyedül cselekedne.
Az erőrendszer által a pontra adott gyorsulás egyenlő az egyes erők által a pontra adott gyorsulások geometriai összegével (3.1. ábra):

3.1. ábra
A súrlódás fogalma. A súrlódás típusai.
Súrlódás-
az egyik durva testnek a másik felületén való mozgásából eredő ellenállás. A csúszósúrlódás csúszósúrlódást, a gördülési súrlódás pedig lengősúrlódást eredményez.
Csúszó súrlódás
3.2. ábra.
Ennek oka a nyúlványok mechanikus összekapcsolódása. A csúszás során a mozgással szembeni ellenállás erejét csúszási súrlódási erőnek nevezzük (3.2. ábra).A csúszósúrlódás törvényei:
1. A csúszósúrlódási erő egyenesen arányos a normál nyomás erejével: 
aholR- normál nyomású erő, amely a támasztófelületre merőlegesen irányul;f- csúszósúrlódási együttható.
3.3. ábra.
Ferde sík mentén mozgó test esetén (3.3. ábra)gördülési súrlódás
A gördülési ellenállás a talaj és a kerék kölcsönös deformációjához kapcsolódik, és sokkal kisebb, mint a csúszósúrlódás.
A kerék egyenletes gördüléséhez erőt kell alkalmazniF dv (3.4. ábra)
A kerék gördülési feltétele, hogy a mozgási nyomaték nem lehet kisebb, mint az ellenállási nyomaték:
3.4. ábra.
1. példa: 2. példa: Két anyagi tömegponthozm 1 =2kg ésm 2 = 5 kg egyenlő erőket alkalmazunk. Hasonlítsa össze az értékeket gyorsabban.Megoldás:
A harmadik axióma szerint a gyorsulási dinamika fordítottan arányos a tömegekkel: ![]()
3. példa:
Határozza meg a gravitáció munkáját, amikor egy terhet ferde sík mentén mozgatunk A pontból C pontba (3. 7. ábra). A test gravitációs ereje 1500 N. AB=6m, BC=4m. 3. példa:
Határozza meg a vágóerő munkáját 3 perc alatt. A munkadarab forgási sebessége 120 ford./perc, a munkadarab átmérője 40mm, a forgácsolóerő 1kN. (3.8. ábra)
Megoldás:
1. Munkavégzés forgó mozgással:
2. Szögfordulatszám 120 ford./perc
3.8. ábra.
3. A fordulatok száma adott időre azz\u003d 120 * 3 \u003d 360 rev.Forgatási szög ez idő alatt φ=2πz\u003d 2 * 3,14 * 360 \u003d 2261 rad
4. Dolgozzon 3 fordulatig:W\u003d 1 * 0,02 * 2261 \u003d 45,2 kJ
Bibliográfia
Olofinszkaja, V.P. "Műszaki mechanika", Moszkva "Fórum" 2011
Erdedi A.A. Erdedi N.A. Elméleti mechanika. Az anyagok szilárdsága.- R-n-D; Főnix, 2010
Elméleti mechanika a mechanikának az alaptörvényeket leíró ága mechanikus mozgásés az anyagi testek mechanikai kölcsönhatása.
Az elméleti mechanika olyan tudomány, amelyben a testek időbeli mozgását (mechanikai mozgását) tanulmányozzák. Alapjául szolgál a mechanika más szekcióinak (rugalmasság elmélete, anyagok ellenállása, plaszticitás elmélete, mechanizmusok és gépek elmélete, hidroaerodinamika) és számos műszaki tudományág számára.
mechanikus mozgás- ez az anyagi testek térbeli relatív helyzetének időbeli változása.
Mechanikai kölcsönhatás- ez egy olyan kölcsönhatás, amelynek következtében megváltozik a mechanikai mozgás, vagy megváltozik a testrészek egymáshoz viszonyított helyzete.
Merev test statika
Statika- Ez az elméleti mechanika egyik ága, amely a szilárd testek egyensúlyának és az egyik erőrendszernek egy másik, azzal egyenértékű erőrendszerré való átalakulásának problémájával foglalkozik.
- A statika alapfogalmai és törvényei
- Abszolút merev test(szilárd test, test) van anyagi test, azon pontok közötti távolság, amelyekben nem változik.
- Anyagi pont olyan test, amelynek méretei a probléma feltételeinek megfelelően elhanyagolhatók.
- laza test egy test, amelynek mozgására nincs korlátozás.
- Nem szabad (kötött) test olyan test, amelynek mozgása korlátozott.
- Kapcsolatok- ezek olyan testek, amelyek megakadályozzák a vizsgált tárgy (test vagy testrendszer) mozgását.
- Kommunikációs reakció egy olyan erő, amely egy kötés merev testre gyakorolt hatását jellemzi. Ha azt az erőt tekintjük, amellyel egy merev test egy kötésre hat, akkor a kötés reakciója ellenhatás. Ebben az esetben az erő - hatás a kapcsolatra, a kapcsolat reakciója pedig a szilárd testre érvényesül.
- mechanikus rendszer egymással összefüggő testek vagy anyagi pontok összessége.
- Szilárd mechanikai rendszernek tekinthető, amelynek helyzete és pontjai közötti távolság nem változik.
- Erő Az egyik anyagtestnek a másikra gyakorolt mechanikai hatását jellemző vektormennyiség.
Az erőt mint vektort az alkalmazási pont, a hatás iránya és az abszolút érték jellemzi. Az erőmodulus mértékegysége Newton. - Az erő hatásvonala az az egyenes, amely mentén az erővektor irányul.
- Koncentrált erő az egy pontban kifejtett erő.
- Megosztott erők (elosztott terhelés)- ezek a test térfogatának, felületének vagy hosszának minden pontjára ható erők.
Az elosztott terhelést az egységnyi térfogatra (felületre, hosszra) ható erő adja meg.
Az elosztott terhelés mérete N / m 3 (N / m 2, N / m). - Külső erő a vizsgált mechanikai rendszerhez nem tartozó testből ható erő.
- belső erő egy mechanikai rendszer anyagi pontjára a másikból ható erő anyagi pont a figyelembe vett rendszerhez tartozó.
- Erőrendszer a mechanikai rendszerre ható erők összessége.
- Lapos erőrendszer olyan erőrendszer, amelynek hatásvonalai ugyanabban a síkban fekszenek.
- Az erők térbeli rendszere olyan erőrendszer, amelynek hatásvonalai nem egy síkban fekszenek.
- Összetartó erőrendszer olyan erőrendszer, amelynek hatásvonalai egy pontban metszik egymást.
- Önkényes erőrendszer olyan erőrendszer, amelynek hatásvonalai nem egy pontban metszik egymást.
- Egyenértékű erőrendszerek- ezek olyan erőrendszerek, amelyek egymásra cseréje nem változtatja meg a test mechanikai állapotát.
Elfogadott megnevezés: . - Egyensúlyi Olyan állapot, amelyben egy test álló helyzetben marad, vagy egyenletesen, egyenes vonalban mozog erők hatására.
- Kiegyensúlyozott erőrendszer- ez egy olyan erőrendszer, amely egy szabad szilárd testre hatva nem változtatja meg annak mechanikai állapotát (nem teszi kiegyensúlyozatlanná).
 .
. - eredő erő olyan erő, amelynek a testre gyakorolt hatása egyenértékű egy erőrendszer hatásával.
 .
. - A hatalom pillanata az erő forgási képességét jellemző érték.
- Hatalom pár két párhuzamos, abszolút értékű, egymással ellentétes irányú erőből álló rendszer.
Elfogadott megnevezés: .
Néhány erő hatására a test forgó mozgást végez. - Erő vetülete a tengelyre- ez egy szakasz, amely az erővektor elejétől és végétől erre a tengelyre húzott merőlegesek közé van zárva.
A vetítés akkor pozitív, ha a szakasz iránya egybeesik a tengely pozitív irányával. - Erő vetítése egy síkon egy vektor egy síkon, amely az erővektor elejétől és végétől erre a síkra húzott merőlegesek közé van zárva.
- 1. törvény (tehetetlenségi törvény). Egy elszigetelt anyagpont nyugalomban van, vagy egyenletesen és egyenesen mozog.
Egy anyagi pont egyenletes és egyenes vonalú mozgása tehetetlenségi mozgás. Egy anyagi pont és egy merev test egyensúlyi állapotán nemcsak nyugalmi állapotot értünk, hanem tehetetlenségi mozgásként is. Merev test esetén többféle tehetetlenségi mozgás létezik, például egy merev test egyenletes forgása egy rögzített tengely körül. - 2. törvény. Egy merev test csak akkor van egyensúlyban két erő hatására, ha ezek az erők egyenlő nagyságúak és ellentétes irányba irányulnak. közös vonal akciókat.
Ezt a két erőt kiegyensúlyozottnak nevezzük.
Általánosságban elmondható, hogy az erők kiegyensúlyozottak, ha a merev test, amelyre ezeket az erőket kifejtik, nyugalomban van. - 3. törvény. A merev test állapotának megsértése nélkül (az "állapot" szó itt mozgási vagy nyugalmi állapotot jelent) hozzáadhat és elvethet egyensúlyozó erőket.
Következmény. A merev test állapotának megzavarása nélkül az erő hatásvonala mentén átvihető a test bármely pontjára.
Két erőrendszert ekvivalensnek nevezünk, ha az egyik a merev test állapotának megzavarása nélkül helyettesíthető egy másikkal. - 4. törvény. Az egy pontban kifejtett két erő eredője ugyanabban a pontban érvényesül, abszolút értékében egyenlő az ezekre az erőkre épített paralelogramma átlójával, és ennek mentén irányul.
Diagonal vonalok.
Az eredő modulusa: - 5. törvény (a cselekvés és a reakció egyenlőségének törvénye). Azok az erők, amelyekkel két test hat egymásra, egyenlő nagyságúak, és egy egyenes mentén ellentétes irányba irányulnak.
Ezt szem előtt kell tartani akció- a testre ható erő B, és ellenzék- a testre ható erő DE, nincsenek kiegyensúlyozottak, mivel különböző testekhez kapcsolódnak. - 6. törvény (a keményedés törvénye). A nem szilárd test egyensúlya nem bomlik meg, amikor megszilárdul.
Nem szabad elfelejteni, hogy az egyensúlyi feltételek, amelyek egy merev testhez szükségesek és elegendőek, szükségesek, de nem elegendőek a megfelelő nem merev testhez. - 7. törvény (a kötvények alóli felmentés törvénye). Egy nem szabad szilárd test akkor tekinthető szabadnak, ha mentálisan felszabadul a kötésektől, és a kötések hatását a kötések megfelelő reakcióival helyettesíti.
- Kapcsolatok és reakcióik
- Sima felület korlátozza a mozgást a támasztófelület normál irányában. A reakció a felületre merőlegesen irányul.
- Csuklós mozgatható támaszték korlátozza a test mozgását a normál mentén a referenciasíkra. A reakció a normál mentén a támasztófelület felé irányul.
- Csuklós fix támaszték ellensúlyoz minden mozgást a forgástengelyre merőleges síkban.
- Csuklós súlytalan rúd ellensúlyozza a test mozgását a rúd vonala mentén. A reakciót a rúd vonala mentén irányítjuk.
- Vak befejezés ellensúlyoz minden mozgást és forgást a síkban. Hatása helyettesíthető két komponens formájában megjelenő erővel és egy nyomatékos erőpárral.




Kinematika
Kinematika- az elméleti mechanika olyan része, amely a mechanikai mozgás általános geometriai tulajdonságait térben és időben lezajló folyamatnak tekinti. A mozgó tárgyakat geometriai pontoknak vagy geometriai testeknek tekintjük.
- Kinematikai alapfogalmak
- Egy pont (test) mozgásának törvénye egy pont (test) térbeli helyzetének időfüggősége.
- Pont pályája a térbeli pont pozícióinak helye a mozgása során.
- Pont (test) sebesség- ez egy pont (test) térbeli helyzetének időbeli változásának jellemzője.
- Pont (test) gyorsulás- ez egy pont (test) sebességének időbeli változásának jellemzője.
- Egy pont kinematikai jellemzőinek meghatározása
- Pont pályája
A vektor vonatkoztatási rendszerben a pályát a következő kifejezés írja le: .
A koordináta-referenciarendszerben a pályát a pontmozgás törvénye szerint határozzák meg, és a kifejezésekkel írják le z = f(x,y) térben, ill y = f(x)- a repülőben.
A természetes vonatkoztatási rendszerben a pálya előre meghatározott. - Egy pont sebességének meghatározása vektorkoordináta-rendszerben
Egy pont mozgásának megadásakor vektorkoordináta-rendszerben a mozgás és az időintervallum arányát a sebesség átlagértékének nevezzük ebben az időintervallumban: .
Ha az időintervallumot végtelenül kicsi értéknek vesszük, akkor megkapjuk a sebesség értékét egy adott időpillanatban ( pillanatnyi érték sebesség): .
.
Vektor átlagsebesség a vektor mentén a pont mozgásának irányába irányul, a pillanatnyi sebességvektor a pont mozgásának irányába mutató pályára érintőlegesen irányul.
Következtetés: egy pont sebessége a mozgástörvény időbeli deriváltjával egyenlő vektormennyiség.
Származékos tulajdonság: bármely érték időbeli deriváltja határozza meg ennek az értéknek a változási sebességét. - Egy pont sebességének meghatározása koordináta-referenciarendszerben
Pontkoordináták változásának sebessége: .
.
Teljes pontsebesség modulus at téglalap alakú rendszer koordináták lesznek: .
.
A sebességvektor irányát a kormányszögek koszinuszai határozzák meg: ,
,
hol vannak a sebességvektor és a koordinátatengelyek közötti szögek. - Egy pont sebességének meghatározása természetes vonatkoztatási rendszerben
A természetes vonatkoztatási rendszerben egy pont sebességét a pont mozgástörvényének deriváltjaként határozzuk meg: .
A korábbi következtetések szerint a sebességvektor a pont mozgásának irányában érintőlegesen irányul a pályára, és a tengelyekben csak egy vetület határozza meg.
- Merev test kinematikája
- A merev testek kinematikájában két fő probléma oldódik meg:
1) a mozgás feladata és a test egészének kinematikai jellemzőinek meghatározása;
2) a test pontjainak kinematikai jellemzőinek meghatározása. - Merev test transzlációs mozgása
A transzlációs mozgás olyan mozgás, amelyben a test két pontján keresztül húzott egyenes párhuzamos marad az eredeti helyzetével.
Tétel: transzlációs mozgásban a test minden pontja ugyanazon a pályán mozog, és minden időpillanatban azonos sebességgel és gyorsulással rendelkezik a nagyságban és irányban.
Következtetés: egy merev test transzlációs mozgását bármely pontjának mozgása határozza meg, ezért a mozgásának feladata és tanulmányozása egy pont kinematikájára redukálódik. - Merev test forgó mozgása rögzített tengely körül
A merev test fix tengely körüli forgó mozgása egy merev test olyan mozgása, amelyben a testhez tartozó két pont a mozgás teljes ideje alatt mozdulatlan marad.
A test helyzetét a forgásszög határozza meg. A szög mértékegysége a radián. (A radián annak a körnek a középponti szöge, amelynek ívhossza megegyezik a sugárral, a kör teljes szöge tartalmazza 2π radián.)
A test fix tengely körüli forgási törvénye.
A test szögsebességét és szöggyorsulását a differenciálási módszerrel határozzuk meg:
— szögsebesség, rad/s;
— szöggyorsulás, rad/s².
Ha a testet a tengelyre merőleges síkkal vágjuk, válasszunk egy pontot a forgástengelyen TÓL TŐLés egy tetszőleges pont M, akkor a lényeg M leírja a lényeget TÓL TŐL sugarú kör R. Alatt dt van egy elemi elforgatás a szögön keresztül, míg a pont M a pálya mentén halad egy távolságig .
.
Lineáris sebesség modul: .
.
pont gyorsulás M ismert pályával az összetevői határozzák meg: ,
,
ahol .
.
Ennek eredményeként képleteket kapunk
érintőleges gyorsulás: ;
;
normál gyorsulás: .
.

Dinamika
Dinamika- Ez az elméleti mechanika egyik ága, amely az anyagi testek mechanikai mozgásait vizsgálja, az azokat kiváltó okoktól függően.
- A dinamika alapfogalmai
- tehetetlenség- ez az anyagi testek azon tulajdonsága, hogy nyugalmi állapotot vagy egyenletes egyenes vonalú mozgást tartsanak fenn, amíg a külső erők ezt az állapotot meg nem változtatják.
- Súly egy test tehetetlenségének mennyiségi mértéke. A tömeg mértékegysége kilogramm (kg).
- Anyagi pont olyan tömegű test, amelynek méreteit ennek a feladatnak a megoldása során figyelmen kívül hagyjuk.
- Mechanikai rendszer tömegközéppontja egy geometriai pont, amelynek koordinátáit a következő képletek határozzák meg:
ahol m k , x k , y k , z k- tömeg és koordináták k- a mechanikai rendszer azon pontja, m a rendszer tömege.
Egyenletes gravitációs térben a tömegközéppont helyzete egybeesik a tömegközéppont helyzetével. - Anyagi test tehetetlenségi nyomatéka a tengely körül a forgó mozgás során fellépő tehetetlenség mennyiségi mértéke.
Egy anyagi pont tehetetlenségi nyomatéka a tengely körül egyenlő a pont tömegének és a pont tengelytől való távolságának négyzetével: .
.
A rendszer (test) tehetetlenségi nyomatéka a tengely körül egyenlő számtani összeg minden pont tehetetlenségi nyomatéka:
- Anyagi pont tehetetlenségi ereje egy olyan vektormennyiség, amely abszolút értékben egyenlő egy pont tömegének és a gyorsulási modul szorzatával, és a gyorsulási vektorral ellentétes irányban irányul:
- Anyagi test tehetetlenségi ereje a test tömegének és a test tömegközéppontja gyorsulási moduljának szorzatával abszolút értékben egyenlő vektormennyiség, amely a tömegközéppont gyorsulási vektorával ellentétes irányban irányul:
ahol a test tömegközéppontjának gyorsulása. - Elemi Erő Impulzus egy vektormennyiség, amely egyenlő az erővektor végtelen kis időintervallum szorzatával dt:
.
Teljes impulzuserő per Δt egyenlő az integrállal elemi impulzusokból: .
. - Elemi erőmunka- ez skalár dA, egyenlő a skalárral
Kilátás: Ezt a cikket eddig 32852 alkalommal olvasták
Pdf Nyelv kiválasztása... Orosz Ukrán Angol
A teljes anyag fentebb, a nyelv kiválasztása után letölthető
- Statika
- A statika alapfogalmai
- Erőfajták
- A statika axiómái
- Kapcsolatok és reakcióik
- Összetartó erőrendszer
- A konvergáló erők eredő rendszerének meghatározására szolgáló módszerek
- Egyensúlyi feltételek egy konvergáló erőrendszerhez
- A középpontra, mint vektorra vonatkozó erőnyomaték
- Az erőnyomaték algebrai értéke
- A középpontra (pontra) vonatkozó erőnyomaték tulajdonságai
- Az erőpárok elmélete
- Két párhuzamos, azonos irányú erő összeadása
- Két párhuzamos, ellentétes irányú erő összeadása
- Erőpárok
- Erőpár tétel
- Egy erőpárok rendszerének egyensúlyi feltételei
- Emelőkar
- Önkényes sík erőrendszer
- Egy lapos erőrendszer egyszerűbb formára való redukálásának esetei
- Analitikai egyensúlyi feltételek
- Párhuzamos erők középpontja. Gravitáció középpontja
- Párhuzamos Erők Központja
- A merev test súlypontja és koordinátái
- Térfogat súlypontja, síkok és vonalak
- A súlypont helyzetének meghatározására szolgáló módszerek
- Az Erő Racsetek alapjai
- Az anyagok ellenállásának problémái és módszerei
- Terhelés besorolása
- A szerkezeti elemek osztályozása
- Rúd deformációk
- Főbb hipotézisek és alapelvek
- Belső erők. Szakasz módszer
- Feszültség
- Feszülés és tömörítés
- Az anyag mechanikai jellemzői
- Megengedett feszültségek
- Anyagkeménység
- A hosszanti erők és feszültségek diagramjai
- Váltás
- Metszetek geometriai jellemzői
- Csavarás
- hajlít
- Differenciális függőségek a hajlításban
- Hajlító szilárdság
- normál stresszek. Szilárdsági számítás
- Nyírófeszültségek hajlításkor
- Hajlítási merevség
- Elemek általános elmélet stressz állapot
- Erőelméletek
- Hajlítás csavarással
- Kinematika
- Pontkinematika
- Pont pályája
- Egy pont mozgásának meghatározására szolgáló módszerek
- Pont sebessége
- pont gyorsulás
- Merev test kinematikája
- Merev test transzlációs mozgása
- Merev test forgó mozgása
- A fogaskerekes mechanizmusok kinematikája
- Merev test síkpárhuzamos mozgása
- Komplex pontmozgás
- Pontkinematika
- Dinamika
- A dinamika alaptörvényei
- Pontdinamika
- Egy szabad anyagi pont differenciálegyenletei
- A pontdinamika két problémája
- Merev test dinamika
- A mechanikai rendszerre ható erők osztályozása
- Mechanikai rendszer mozgásdifferenciálegyenletei
- Általános dinamikai tételek
- Tétel egy mechanikai rendszer tömegközéppontjának mozgásáról
- Tétel az impulzus változásáról
- Tétel a szögimpulzus változásáról
- Kinetikus energia változási tétel
- A gépekben ható erők
- Erők a homlokkerekes fogaskerék bekapcsolásakor
- Súrlódás a mechanizmusokban és gépekben
- Csúszó súrlódás
- gördülési súrlódás
- Hatékonyság
- Gép alkatrészek
- Mechanikus sebességváltók
- A mechanikus fogaskerekek típusai
- A mechanikus hajtóművek alapvető és származtatott paraméterei
- fogaskerekek
- Sebességváltók rugalmas linkekkel
- Tengelyek
- Cél és osztályozás
- Tervezési számítás
- Ellenőrizze a tengelyek számítását
- Csapágyak
- Siklócsapágyak
- Gördülőcsapágyak
- Gépalkatrészek csatlakoztatása
- A levehető és állandó csatlakozások típusai
- Kulcsos csatlakozások
- Mechanikus sebességváltók
- Normák szabványosítása, felcserélhetőség
- Tűrések és leszállások
- A tűrések és leszállások egységes rendszere (ESDP)
- Az alak és a hely eltérése
Formátum: pdf
Méret: 4MB
orosz nyelv
Példa a homlokkerekes fogaskerék számítására
Példa a homlokkerekes fogaskerék számítására. Megtörtént az anyagválasztás, a megengedett feszültségek számítása, az érintkezési és hajlítószilárdság számítása.
Példa a sugárhajlítási probléma megoldására
A példában a keresztirányú erők és a hajlítónyomatékok diagramjait készítjük, veszélyes szakaszt találunk, és egy I-gerenda kerül kiválasztásra. A feladatban differenciális függőségek felhasználásával diagramok felépítését elemeztem, különböző gerenda keresztmetszetek összehasonlító elemzését végeztem el.
Példa a tengelycsavarodás problémájának megoldására
A feladat egy acéltengely szilárdságának vizsgálata adott átmérőhöz, anyaghoz és megengedett feszültségekhez. A megoldás során a nyomatékok, nyírófeszültségek és csavarási szögek diagramjai készülnek. A tengely önsúlyát nem veszik figyelembe
Példa a rúd feszítésének-tömörítésének problémájának megoldására
A feladat egy acélrúd szilárdságának vizsgálata adott megengedett feszültségeknél. A megoldás során a hosszirányú erők, normál feszültségek és elmozdulások diagramjai készülnek. A rúd önsúlyát nem vesszük figyelembe
A kinetikus energia megmaradás tételének alkalmazása
Példa a mechanikai rendszer kinetikus energiájának megmaradásáról szóló tétel alkalmazásának problémájának megoldására
Egy pont sebességének és gyorsulásának meghatározása a megadott mozgásegyenletek szerint
Példa egy pont sebességének és gyorsulásának meghatározására adott egyenletek mozgások
Merev test pontjai sebességének és gyorsulásának meghatározása síkpárhuzamos mozgás közben
Példa a merev test pontjai sebességének és gyorsulásainak meghatározására síkpárhuzamos mozgás közben
Erők meghatározása lapos rácsos rudaknál
Példa a lapos rácsozat rudaiban lévő erők Ritter módszerrel és csomóvágási módszerrel történő meghatározására
1 csúszda
Előadások az elméleti mechanikáról Dinamika (I rész) Bondarenko A.N. Moszkva - 2007 Elektronikus képzés a szerző előadásai alapján íródott a NIIZhT és a MIIT SZhD, PGS és SDM szakán tanuló hallgatók számára (1974-2006). Oktatási anyag megfelel naptári tervek több mint három félév. Az animációs effektusok teljes körű megvalósításához a prezentáció során legalább a Windows XP Professional operációs rendszer Microsoft Office-jába beépített Power Point megjelenítőt kell használnia. Észrevételeiket, javaslataikat e-mailben küldhetik el: [e-mail védett]. Moszkva Állami Egyetem Vasút (MIIT) Elméleti Mechanikai Tanszék Közlekedéstechnológiai Tudományos és Műszaki Központ

2 csúszda
Tartalom 1. előadás. Bevezetés a dinamikába. Az anyagi pontdinamika törvényei és axiómái. A dinamika alapegyenlete. Differenciál- és természetes mozgásegyenletek. A dinamika két fő feladata. Példák a dinamika közvetlen problémájának megoldására 2. előadás A dinamika inverz problémájának megoldása. Általános utasítások a dinamika inverz problémájának megoldásához. Példák a dinamika inverz problémájának megoldására. A horizonthoz képest szögben eldobott test mozgása a légellenállás figyelembevétele nélkül. 3. előadás Anyagi pont egyenes irányú rezgései. Az oszcillációk előfordulásának feltétele. A rezgések osztályozása. Szabad rezgések az ellenállási erők figyelembevétele nélkül. csillapított rezgések. Az oszcilláció csökkenése. 4. előadás Anyagi pont kényszerrezgései. Rezonancia. A mozgással szembeni ellenállás befolyása kényszerrezgések során. 5. előadás Anyagi pont relatív mozgása. Tehetetlenségi erők. Különleges mozgási esetek különféle hordozható mozgásokhoz. A Föld forgásának hatása a testek egyensúlyára és mozgására. 6. előadás Mechanikai rendszer dinamikája. mechanikus rendszer. Külső és belső erők. A rendszer tömegközéppontja. Tétel a tömegközéppont mozgásáról. Természetvédelmi törvények. Példa a tömegközéppont mozgására vonatkozó tétel alkalmazásának problémájának megoldására. 7. előadás. Erőimpulzus. A mozgás mennyisége. Tétel az impulzus változásáról. Természetvédelmi törvények. Euler-tétel. Példa a feladat megoldására az impulzusváltozásra vonatkozó tétel felhasználásáról. lendület pillanata. A szögimpulzus megváltoztatásának tétele 8. előadás Megmaradási törvények. A tehetetlenségi nyomatékok elméletének elemei. Merev test kinetikus momentuma. Differenciálegyenlet merev test forgása. Példa a rendszer impulzusimpulzusának változására vonatkozó tétel alkalmazásának problémájának megoldására. A giroszkóp elemi elmélete. Ajánlott irodalom 1. Yablonsky A.A. Elméleti mechanika tanfolyam. 2. rész. M.: elvégezni az iskolát. 1977. 368 p. 2. Mescserszkij I.V. Feladatgyűjtemény az elméleti mechanikában. M.: Tudomány. 1986 416 p. 3. Feladatgyűjtés a kurzusokhoz /Szerk. A.A. Yablonsky. M.: Felsőiskola. 1985. 366 p. 4. Bondarenko A.N. „Elméleti mechanika példákban és feladatokban. Dynamics” (elektronikus kézikönyv www.miit.ru/institut/ipss/faculties/trm/main.htm), 2004

3 csúszda
Az 1. előadás Dinamika az elméleti mechanika egy része, amely a mechanikai mozgást a legáltalánosabb szemszögből vizsgálja. A mozgást a tárgyra ható erőkkel összefüggésben tekintjük. A rész három részből áll: Anyagi pont dinamikája Mechanikai rendszer dinamikája Analitikai mechanika ■ Pont dinamikája - egy anyagi pont mozgását vizsgálja, figyelembe véve az ezt a mozgást okozó erőket. A fő tárgy egy anyagi pont - egy tömegű anyagi test, amelynek méretei elhanyagolhatók. Alapfeltevés: - abszolút tér van (tisztán rendelkezik geometriai tulajdonságok független az anyagtól és annak mozgásától. - abszolút idő van (nem függ az anyagtól és annak mozgásától). Innen következik: – abszolút mozdulatlan vonatkoztatási rendszer van. – az idő nem függ a vonatkoztatási rendszer mozgásától. – a mozgó pontok tömege nem függ a vonatkoztatási rendszer mozgásától. Ezeket a feltételezéseket a Galileo és Newton által létrehozott klasszikus mechanika használja. Alkalmazási köre továbbra is meglehetősen széles, mivel az alkalmazott tudományokban figyelembe vett mechanikai rendszerek nem rendelkeznek olyan nagy tömeggel és mozgási sebességgel, amelyhez figyelembe kell venni a tér, az idő, a mozgás geometriájára gyakorolt hatásukat, ahogy az ben történik relativisztikus mechanika(relativitáselmélet). ■ A dinamika alaptörvényei, amelyeket először Galilei fedezett fel és Newton fogalmazott meg, minden módszer alapját képezik a mechanikai rendszerek mozgásának és dinamikus kölcsönhatásának leírására és elemzésére különböző erők hatására. ■ Tehetetlenségi törvény (Galileo-Newton törvény) – Egy test izolált anyagi pontja mindaddig megtartja nyugalmi állapotát vagy egyenletes egyenes vonalú mozgását, amíg az alkalmazott erők ezt az állapot megváltoztatására nem kényszerítik. Ez magában foglalja a nyugalmi állapot és a mozgás tehetetlenségi ekvivalenciáját (Galilei relativitás törvénye). Azt a vonatkoztatási rendszert, amelyhez képest a tehetetlenségi törvény teljesül, tehetetlenséginek nevezzük. Az anyagi pontnak azt a tulajdonságát, hogy törekedjen mozgásának sebességének (kinematikai állapotának) változatlanságára, tehetetlenségnek nevezzük. ■ Az erő és a gyorsulás arányosságának törvénye (Dinamika alapegyenlete - Newton II. törvénye) - Egy anyagi pontra erővel adott gyorsulás egyenesen arányos ennek a pontnak az erővel és fordítottan arányos ennek a pontnak a tömegével: vagy Itt m a a pont tömege (a tehetetlenség mértéke), kg-ban mérve, számszerűen egyenlő a tömeggel osztva a gravitációs gyorsulással: F a ható erő, N-ben mérve (1 N 1 m/s2 gyorsulást ad egy pontra tömeg 1 kg, 1 N \u003d 1 / 9,81 kg-s). ■ Mechanikai rendszer dinamikája – anyagi pontok és merev testek halmazának mozgását vizsgálja, kombinálva általános törvények kölcsönhatásokat, figyelembe véve azokat az erőket, amelyek ezt a mozgást okozzák. ■ Analitikai mechanika – nem szabad mechanikai rendszerek mozgását tanulmányozza általános analitikai módszerekkel. egy

4 csúszda
1. előadás (folytatás - 1.2) Anyagi pont mozgási differenciálegyenletei: - pont mozgásának differenciálegyenlete vektor alakban. - pontmozgás differenciálegyenletei koordináta alakban. Ezt az eredményt az (1) vektor-differenciálegyenlet formális vetületével kaphatjuk meg. Csoportosítás után a vektorrelációt három skaláris egyenletre bontjuk: Koordináta formában: A sugár-vektor koordinátákkal és az erővektor kapcsolatát vetületekkel használjuk: mozgás differenciálegyenlete természetes (mozgó) koordináta tengelyeken: vagy: - pont természetes mozgásegyenletei. ■ A dinamika alapegyenlete: - egy pont mozgásának vektoros módjának felel meg. ■ Az erők hatásának függetlenségének törvénye - Egy anyagi pont gyorsulása több erő hatására megegyezik egy pont gyorsulásának geometriai összegével, amely az egyes erők hatásából származik külön-külön: vagy A törvény érvényes testek bármely kinematikai állapotára. A különböző pontokra (testekre) ható kölcsönhatási erők nincsenek kiegyensúlyozva. ■ A cselekvés és a reakció egyenlőségének törvénye (Newton III. törvénye) – Minden cselekvés egyenlő és ellentétes irányú reakciónak felel meg: 2

5 csúszda
A dinamika két fő problémája: 1. Közvetlen probléma: A mozgás adott (mozgásegyenletek, pálya). Meg kell határozni azokat az erőket, amelyek hatására egy adott mozgás bekövetkezik. 2. Inverz probléma: Adottak azok az erők, amelyek hatására a mozgás létrejön. Meg kell találni a mozgási paramétereket (mozgásegyenletek, mozgási pálya). Mindkét feladat megoldása a dinamika alapegyenletével és annak a koordinátatengelyekre való vetítésével történik. Ha egy nem szabad pont mozgását vesszük figyelembe, akkor a statikához hasonlóan a kötésektől való felszabadulás elvét alkalmazzuk. A reakció eredményeként a kötések bekerülnek az anyagi pontra ható erők összetételébe. Az első probléma megoldása a differenciálási műveletekhez kapcsolódik. Az inverz probléma megoldásához a megfelelő differenciálegyenletek integrálása szükséges, és ez sokkal nehezebb, mint a differenciálás. Az inverz probléma nehezebb, mint a közvetlen probléma. A dinamika közvetlen problémájának megoldása - nézzünk példákat: Példa 1. Egy felvonó G súlyú kabinját a gyorsulású kábel emeli meg. Határozza meg a kábel feszességét. 1. Válasszon ki egy tárgyat (a liftfülke előrehalad, és anyagi pontnak tekinthető). 2. Eldobjuk a csatlakozást (kábelt) és helyettesítjük az R reakcióval. 3. Állítsa össze a dinamika alapegyenletét: Határozza meg a kábel reakcióját: Határozza meg a kábelfeszességet: A fülke egyenletes mozgásával ay = 0 és a a kábel feszessége egyenlő a súllyal: T = G. Amikor a kábel elszakad, T = 0 és a kabin gyorsulása megegyezik a szabadesés gyorsulásával: ay = -g. 3 4. Az y tengelyre vetítjük a dinamika alapegyenletét: y 2. példa Egy m tömegű pont egy vízszintes felületen (az Oxy-síkon) mozog a következő egyenletek szerint: x = a coskt, y = b coskt. Határozza meg a pontra ható erőt! 1. Válasszon ki egy objektumot (anyagpont). 2. Eldobjuk az összefüggést (síkot) és helyettesítjük az N reakcióval. 3. Adjunk hozzá egy ismeretlen F erőt az erőrendszerhez 4. Állítsuk össze a dinamika alapegyenletét: 5. Vetítsük rá a dinamika alapegyenletét tengelyek x,y: Határozza meg az erővetületeket: Erőmodulus: Iránykoszinusz: Így az erő nagysága arányos a pontnak a koordináták középpontjától való távolságával, és a pontot a középponttal összekötő egyenes mentén a középpont felé irányul. A pont mozgásának pályája egy ellipszis, amelynek középpontja az origóban van: O r 1. előadás (folytatás - 1.3)

6 csúszda
1. előadás (1.4 folytatás) 3. példa: Egy l hosszúságú kábelre egy G súlyú terhet függesztünk fel, és egy vízszintes síkban, bizonyos sebességgel körpályán mozog. A kábel függőlegestől való eltérési szöge egyenlő. Határozza meg a kábel feszességét és a terhelés sebességét. 1. Válasszon ki egy tárgyat (rakományt). 2. Dobja el a csatlakozást (kötelet) és cserélje ki az R reakcióval. 3. Állítsa össze a dinamikai főegyenletet: A harmadik egyenletből határozza meg a kábel reakcióját: Határozza meg a kábel feszültségét: Helyettesítse be a reakció értékét a kábel normál gyorsulása a második egyenletbe, és meghatározza a terhelés sebességét: 4. Vetítse ki a főegyenletet tengelydinamika,n,b: 4. példa: G súlyú autó egy konvex hídon mozog (görbületi sugár R) V sebességgel. Határozza meg az autó nyomását a hídon! 1. Kijelölünk egy tárgyat (autó, a méreteket elhanyagoljuk és pontnak tekintjük). 2. Eldobjuk a csatlakozást (durva felület), és helyettesítjük az N reakciókkal és az Ffr súrlódási erővel. 3. Összeállítjuk a dinamika alapegyenletét: 4. Az n tengelyre vetítjük a dinamika alapegyenletét: Innen határozzuk meg a normál reakciót: Meghatározzuk az autó nyomását a hídon: Innen tudjuk meghatározni a sebességet a hídon lévő nulla nyomásnak megfelelő (Q = 0): 4

7 csúszda
2. előadás Az állandók talált értékeinek behelyettesítése után a következőket kapjuk: Így ugyanazon erőrendszer hatására egy anyagi pont teljesíthet egész osztály a kezdeti feltételek által meghatározott mozgások. A kezdeti koordináták figyelembe veszik a pont kezdeti helyzetét. A vetületek által adott kezdősebesség figyelembe veszi a pálya figyelembe vett szakaszán való mozgására gyakorolt hatását azoknak az erőknek, amelyek a pontra hatnak, mielőtt erre a szakaszra érkeztek volna, pl. kezdeti kinematikai állapot. A dinamika inverz problémájának megoldása - Egy pont mozgásának általános esetben a pontra ható erők időtől, koordinátáktól és sebességtől függő változók. Egy pont mozgását három másodrendű differenciálegyenletből álló rendszer írja le: Mindegyik integrálása után hat konstans lesz C1, C2,…., C6: A C1, C2,… állandók értékei. ., C6 található hat kezdeti feltételből t = 0-nál: A megoldási inverz probléma 1. példája: Egy m tömegű szabad anyagpont elmozdul egy F erő hatására, amelynek nagysága és nagysága állandó. . A kezdeti pillanatban a pont sebessége v0 volt, és iránya egybeesett az erővel. Határozzuk meg egy pont mozgásegyenletét! 1. Összeállítjuk a dinamika alapegyenletét: 3. Csökkentjük a derivált sorrendjét: 2. A derékszögű vonatkoztatási rendszert választjuk, az x tengelyt az erő iránya mentén irányítva, és erre a tengelyre vetítjük a dinamika főegyenletét: vagy x y z 4. Válasszuk szét a változókat: 5. Számítsuk ki az integrálokat az egyenlet mindkét részéből: 6. A sebességvetítést ábrázoljuk a koordináta időbeli deriváltjaként: 8. Számítsuk ki az egyenlet mindkét részének integrálját! 7. A változók szétválasztása: 9. A C1 és C2 állandók értékének meghatározásához a kezdeti feltételeket használjuk: t = 0, vx = v0 , x = x0: Ennek eredményeként megkapjuk az egyenletesen változó mozgás egyenletét. (az x tengely mentén): 5

8 csúszda
Általános utasítások direkt és inverz problémák megoldásához. Megoldási eljárás: 1. A mozgási differenciálegyenlet összeállítása: 1.1. Válasszon egy koordinátarendszert - téglalap alakú (rögzített) ismeretlen mozgási pályával, természetes (mozgó) ismert pályával, például kör vagy egyenes. Ez utóbbi esetben egy egyenes koordináta használható. A referenciapontot kombinálni kell a pont kezdeti helyzetével (t = 0-nál) vagy a pont egyensúlyi helyzetével, ha létezik, például amikor a pont ingadozik. 6 1.2. Rajzoljunk egy pontot egy tetszőleges időpillanatnak megfelelő pozícióba (t > 0 esetén), hogy a koordináták pozitívak legyenek (s > 0, x > 0). Azt is feltételezzük, hogy ebben a helyzetben a sebesség vetülete is pozitív. Lengések esetén a sebességvetítés előjelet vált, például az egyensúlyi helyzetbe való visszatéréskor. Itt azt kell feltételezni, hogy a vizsgált időpillanatban a pont eltávolodik az egyensúlyi helyzettől. Ennek az ajánlásnak a végrehajtása fontos a jövőben, amikor a sebességtől függő ellenállási erőkkel dolgozunk. 1.3. Oldja fel az anyagi pontot a kötésekből, cserélje ki hatásukat reakciókra, adjon hozzá aktív erőket. 1.4. Írja le a dinamika alaptörvényét vektoros formában, vetítse ki a kiválasztott tengelyekre, fejezze ki adott vagy reaktív erőket időben, koordinátákkal vagy sebességváltozókkal, ha ezektől függ. 2. Differenciálegyenletek megoldása: 2.1. Csökkentse a derivált, ha az egyenlet nem redukálódik kanonikus (standard) alakra. például: vagy 2.2. Külön változók, például: vagy 2.4. Számolj nem határozott integrálok az egyenlet bal és jobb részében például: 2.3. Ha három változó van az egyenletben, akkor módosítsa a változókat, például: majd válassza szét a változókat. Megjegyzés. Számítás helyett határozatlan integrálok változó felső határú határozott integrálokat lehet számítani. Az alsó határértékek a változók kezdeti értékeit jelentik (kezdeti feltételek), ekkor nincs szükség az állandó külön meghatározására, ami automatikusan bekerül a megoldásba, pl.: A kezdeti feltételekkel pl. t = 0 , vx = vx0, határozza meg az integráció állandóját: 2.5. Adja meg a sebességet például a koordináta időbeli deriváltjával, és ismételje meg a 2.2 -2.4 lépéseket Megjegyzés. Ha az egyenletet olyan kanonikus formára redukáljuk, amely standard megoldással rendelkezik, akkor ezt a kész megoldást használjuk. Az integráció állandói továbbra is a kezdeti feltételekből származnak. Lásd például az oszcillációkat (4. előadás, 8. o.). 2. előadás (2.2 folytatás)

9 csúszda
2. előadás (2.3 folytatás) 2. példa az inverz probléma megoldására: Az erő időtől függ. Egy P súlyú teher egy sima vízszintes felület mentén mozogni kezd F erő hatására, amelynek nagysága arányos az idővel (F = kt). Határozza meg a rakomány által megtett távolságot t időben! 3. Összeállítjuk a dinamika főegyenletét: 5. Csökkentjük a derivált sorrendjét: 4. A dinamika főegyenletét az x tengelyre vetítjük: vagy 7 6. Elválasztjuk a változókat: 7. Kiszámoljuk az integrálokat az egyenlet mindkét részéből: 9. A sebesség vetületét a koordináta időbeli deriváltjaként ábrázoljuk: 10. Számítsuk ki mindkét egyenletrész integrálját: 9. Válasszuk szét a változókat: 8. Határozzuk meg az értéket a C1 konstans t = 0 kezdeti feltételből, vx = v0=0: Ennek eredményeként megkapjuk a mozgásegyenletet (x tengely mentén), amely megadja a megtett út értékét t időre: 1. Válasszon a referenciarendszer ( Derékszögű koordináták) úgy, hogy a testnek pozitív koordinátája legyen: 2. A mozgás tárgyát anyagi pontnak vesszük (a test előrehalad), kiszabadítjuk a kapcsolatból (referenciasík) és helyettesítjük a reakcióval (egy sima normál reakciója). felület): 11. Határozza meg a C2 konstans értékét a kezdeti feltételből t = 0, x = x0=0: Inverz probléma 3. példa: Az erő a koordinátától függ. Egy m tömegű anyagpont v0 sebességgel felfelé dobódik a Föld felszínéről. A Föld gravitációs ereje fordítottan arányos a pont és a gravitációs középpont (a Föld középpontja) közötti távolság négyzetével. Határozza meg a sebesség függését a Föld középpontjától mért y távolságtól! 1. A vonatkoztatási rendszert (derékszögű koordináták) úgy választjuk meg, hogy a test pozitív koordinátájú legyen: 2. Összeállítjuk a dinamika főegyenletét: 3. A dinamika főegyenletét az y tengelyre vetítjük: vagy Az arányossági együttható Megtalálható a Föld felszínén lévő pont súlyával: R Ebből az egyenlet differenciálműve így néz ki: vagy 4. Csökkentse a derivált sorrendjét: 5. Változtassa meg a változót: 6. válassza szét a változókat: 7. Számítsa ki a az egyenlet mindkét oldalának integráljai: 8. Helyettesítsük be a határértékeket: Ennek eredményeként az y koordináta függvényében kapunk egy kifejezést a sebességre: A maximális magasságú repülést a sebesség nullával való egyenlővé tételével kaphatjuk meg: A maximális repülési magasság amikor a nevező nullára fordul: Innen a Föld sugarának és a szabadesés gyorsulásának beállításakor II. térsebesség:

10 csúszda
2. előadás (2.4 folytatás) 2. példa az inverz probléma megoldására: Az erő sebességtől függ. Egy m tömegű hajó sebessége v0 volt. A víz ellenállása a hajó mozgásával arányos a sebességgel. Határozza meg azt az időt, amely alatt a hajó sebessége felére csökken a motor leállítása után, valamint azt a távolságot, amelyet a hajó megtett a teljes megállásig. 8 1. Válasszunk egy vonatkoztatási rendszert (derékszögű koordináták), hogy a test pozitív koordinátájú legyen: 2. A mozgás tárgyát anyagi pontnak vesszük (a hajó előrehalad), megszabadítjuk a kötésektől (víz) és kicseréljük. reakcióval (felhajtóerő - Archimedes erő), valamint a mozgással szembeni ellenállás erejével. 3. Adjunk hozzá aktív erőt (gravitáció). 4. Állítsa össze a dinamika alapegyenletét: 5. Vetítse ki a dinamika alapegyenletét az x tengelyre: vagy 6. Csökkentse a derivált sorrendjét: 7. Válassza szét a változókat: 8. Számítsa ki az egyenlet mindkét oldalának integrálját : 9. Helyettesítsd be a határértékeket: Kapunk egy kifejezést, amely a sebességet és a t időt kapcsolja össze, amelyből meghatározható a mozgás ideje: A mozgás ideje, amely alatt a sebesség a felére csökken: Érdekes megjegyezni, hogy amikor a sebesség a nullához közelít, a mozgás ideje a végtelenbe hajlik, i.e. a végsebesség nem lehet nulla. Miért nem "örökmozgó"? Ebben az esetben azonban a megállóig megtett távolság véges érték. A megtett távolság meghatározásához a derivált sorrendjének csökkentése után kapott kifejezésre térünk át, és változtatjuk a változót: Integrálás és határértékek behelyettesítése után a következőt kapjuk: Megállóig megtett távolság: ■ Egy pontra dobott pont mozgása. a horizonttal bezárt szög egyenletes gravitációs térben a légellenállás figyelembe vétele nélkül A mozgásegyenletekből az időt kiszűrve a pályaegyenletet kapjuk: A repülési időt úgy határozzuk meg, hogy az y koordinátát nullával egyenlővé tesszük: A repülési tartományt úgy határozzuk meg, hogy helyettesítjük repülési idő:

11 csúszda
3. előadás Anyagi pont egyenes irányú oszcillációi - Egy anyagi pont oszcilláló mozgása a következő feltételek mellett történik: van egy helyreállító erő, amely a pontot az egyensúlyi helyzetbe igyekszik visszahelyezni az ettől a pozíciótól való bármilyen eltérés esetén. 9 Helyreállító erő van, az egyensúlyi helyzet stabil Nincs helyreállító erő, az egyensúlyi helyzet instabil Nincs helyreállító erő, az egyensúlyi helyzet közömbös Mindig az egyensúlyi helyzet felé irányul, az érték egyenesen arányos a rugó lineáris nyúlásával (rövidülésével), egyenlő a test egyensúlyi helyzettől való eltérésével: c a rugó merevségi együtthatója, számszerűen egyenlő a rugó alatti erővel. amelynek hosszát a rugó eggyel megváltoztatja, N/m-ben mérve az SI rendszerben. x y O Anyagi pont rezgésének fajtái: 1. Szabad rezgések (a közeg ellenállásának figyelembevétele nélkül). 2. Szabad rezgések a közeg ellenállását figyelembe véve (csillapított rezgések). 3. Kényszerrezgések. 4. Kényszer rezgések a közeg ellenállásának figyelembevételével. ■ Szabad oszcillációk – csak egy helyreállító erő hatására lépnek fel. Írjuk fel a dinamika alaptörvényét: Válasszunk egy koordinátarendszert, amelynek középpontja az egyensúlyi helyzetben (O pont) van, és vetítsük az egyenletet az x tengelyre: A kapott egyenletet hozzuk a standard (kanonikus) alakba: a felhasználásával kapott egyenletből. az univerzális behelyettesítés: A karakterisztikus egyenlet gyökei képzeletbeliek és egyenlőek: A differenciálegyenlet általános megoldásának formája: Pontsebesség: Kiindulási feltételek: Határozza meg az állandókat: Tehát a szabad rezgések egyenlete a következő formában van: Az egyenlet egytagú kifejezéssel ábrázolható: ahol a az amplitúdó, - kezdeti fázis. Az új a és - állandók a C1 és C2 állandókhoz kapcsolódnak a következő összefüggésekkel: Határozzuk meg a és: A szabad rezgések előfordulásának oka az x0 kezdeti elmozdulás és/vagy a v0 kezdősebesség.

12 csúszda
10 3. előadás (3.2 folytatás) Anyagi pont csillapított oszcillációi - Egy anyagi pont lengőmozgása helyreállító erő és mozgással szembeni ellenállási erő jelenlétében történik. Meghatározzuk a mozgással szembeni ellenállás erejének az elmozdulástól vagy sebességtől való függését fizikai természet mozgást akadályozó környezet vagy kommunikáció. A legegyszerűbb függés a sebességtől való lineáris függés (viszkózus ellenállás): - x y O viszkozitási együttható a gyökerek értékéből: 1. n< k – случай малого вязкого сопротивления: - корни комплексные, различные. или x = ae-nt x = -ae-nt Частота csillapított oszcillációk: Periódus: T* Oszcilláció csökkenés: ai ai+1 Logaritmikus rezgés csökkenés: Az oszcilláció nagyon gyorsan lecseng. A viszkózus ellenállási erő fő hatása az oszcillációs amplitúdó időbeli csökkenése. 2. n > k - nagy viszkózus ellenállás esete: - a gyökerek valódiak, különbözőek. vagy - ezek a függvények periodikusak: 3. n = k: - a gyökök valósak, többszörösek. ezek a funkciók is periodikusak:

13 csúszda
3. előadás (3.3. folytatás) A szabad rezgések megoldásainak osztályozása. Rugós csatlakozások. egyenértékű keménység. y y 11 Diff. Egyenlet karakter. Egyenlet gyökér karakter. egyenletek Differenciálegyenlet megoldása Grafikon nk n=k

14 csúszda
4. előadás Anyagi pont kényszerrezgései - A helyreállító erővel együtt egy periodikusan változó erő hat, ezt perturbáló erőnek nevezzük. A zavaró erőnek más természete lehet. Például egy adott esetben egy forgó rotor m1 kiegyensúlyozatlan tömegének tehetetlenségi hatása harmonikusan változó erővetületeket okoz: A dinamika főegyenlete: A dinamika egyenletének vetülete a tengelyre: Hozzuk az egyenletet a szabványba. forma: 12 Ennek az inhomogén differenciálegyenletnek a megoldása két részből áll: x = x1 + x2: x1 a megfelelő homogén egyenlet általános megoldása, x2 pedig az inhomogén egyenlet konkrét megoldása: Kiválasztjuk az adott megoldást a következő formában: a jobb oldal: A kapott egyenlőségnek minden t-re teljesülnie kell. Ekkor: vagy Így a helyreállító és a zavaró erők egyidejű hatására az anyagi pont komplexet hajt végre oszcilláló mozgás, ami a szabad (x1) és a kényszerített (x2) rezgések összeadásának (szuperpozíciójának) eredménye. Ha p< k (вынужденные колебания малой частоты), то фаза колебаний совпадает с фазой возмущающей силы: В итоге полное решение: или Общее решение: Постоянные С1 и С2, или a и определяются из начальных условий с использованием komplett megoldás(!): Így egy sajátos megoldás: Ha p > k (nagy frekvenciájú kényszerrezgés), akkor a rezgések fázisa ellentétes a zavaró erő fázisával:

15 csúszda
4. előadás (4.2. folytatás) 13 Dinamikus együttható - a kényszerrezgések amplitúdójának és egy pont statikus eltérésének aránya állandó erő hatására H = const: A kényszerrezgések amplitúdója: A statikus eltérés a egyensúlyi egyenlet: Itt: Innen: Így a p< k (малая частота вынужденных колебаний) коэффициент динамичности: При p >k (kényszerrezgések magas frekvenciája) dinamikus együttható: Rezonancia - akkor jön létre, ha a kényszerrezgések frekvenciája egybeesik a természetes rezgések frekvenciájával (p = k). Ez leggyakrabban a rugalmas felfüggesztésekre szerelt, rosszul kiegyensúlyozott rotorok forgásának elindításakor és leállításakor fordul elő. Az egyenlő frekvenciájú rezgések differenciálegyenlete: Egy adott megoldás a jobb oldal formájában nem vehető fel, mert lineárisan függő megoldást kapunk (lásd az általános megoldást). Általános megoldás: Helyettesítsük be a differenciálegyenletben: Vegyünk egy adott megoldást a formába, és számoljuk ki a deriváltokat: Így a megoldást kapjuk: vagy A rezonanciabeli kényszerrezgések amplitúdója korlátlanul növekszik az idővel arányosan. A mozgással szembeni ellenállás befolyása kényszerrezgések során. A viszkózus ellenállás jelenlétében a differenciálegyenlet a következőképpen alakul: Az általános megoldást a táblázatból választjuk ki (3. előadás, 11. o.) n és k arányától függően (lásd). Vegyünk egy adott megoldást a formában, és kiszámítjuk a deriváltokat: Helyettesítsük a differenciálegyenletben: Az együtthatók egyenlítésével trigonometrikus függvények egyenletrendszert kapunk: Ha mindkét egyenletet hatványra emeljük és összeadjuk, megkapjuk a kényszerrezgések amplitúdóját: A második egyenletet elosztva az elsővel, megkapjuk a kényszerrezgések fáziseltolódását: Így az egyenlet a mozgás kényszerített rezgések esetén, figyelembe véve a mozgással szembeni ellenállást, például n-nél< k (малое сопротивление): Вынужденные колебания при сопротивлении движению не затухают. Частота и период вынужденных колебаний равны частоте и периоду изменения возмущающей силы. Коэффициент динамичности при резонансе имеет конечную величину и зависит от соотношения n и к.

16 csúszda
5. előadás Anyagi pont relatív mozgása - Tegyük fel, hogy az Oxyz mozgó (nem inerciális) koordinátarendszer valamilyen törvény szerint mozog az O1x1y1z1 rögzített (inerciális) koordinátarendszerhez képest. Egy anyagi M (x, y, z) pont mozgása az Oxyz mobilrendszerhez képest relatív, az O1x1y1z1 mozdulatlan rendszerhez képest abszolút. Az Oxyz mobil rendszer mozgása az O1x1y1z1 fix rendszerhez képest hordozható mozgás. 14 z x1 y1 z1 O1 x y M x y z O jobb oldal: Az átvitt tagok erődimenzióval rendelkeznek, és a megfelelő tehetetlenségi erőknek tekintendők, amelyek egyenlőek: Ekkor egy pont relatív mozgása abszolútnak tekinthető, ha a ható erőkhöz hozzáadjuk a transzlációs és Coriolis tehetetlenségi erőket: Vetítésekben a mozgó koordináta-rendszer tengelyeire a következőket kapjuk: másfajta transzlációs mozgás: 1. Rögzített tengely körüli forgás: Ha a forgás egyenletes, akkor εe = 0: 2. Transzlációs görbe vonalú mozgás: Ha a mozgás egyenes vonalú, akkor = : Ha a mozgás egyenes és egyenletes, akkor a mozgó rendszer az inerciális és a relatív mozgás abszolútnak tekinthető: Nincs mechanikai jelenségek Az egyenes vonalú egyenletes mozgást lehetetlen észlelni (relativitáselmélet klasszikus mechanika). A Föld forgásának hatása a testek egyensúlyára - Tegyük fel, hogy a test egyensúlyban van a Föld felszínén egy tetszőleges φ szélességen (párhuzamos). A Föld tengelye körül nyugatról keletre szögsebességgel forog: A Föld sugara körülbelül 6370 km. S R - teljes reakció egyenetlen felület. G - a Föld vonzási ereje a középponthoz. Ф - centrifugális tehetetlenségi erő. Relatív egyensúlyi feltétel: A vonzás és a tehetetlenségi erők eredője a gravitációs erő (súly): A Föld felszínére ható gravitációs erő (súly) nagysága P = mg. A centrifugális tehetetlenségi erő a gravitációs erő kis töredéke: A gravitációs erőnek a vonzási erő irányától való eltérése is kicsi: Így a Föld forgásának hatása a testek egyensúlyára rendkívül kicsi és a gyakorlati számítások során nem veszik figyelembe. A tehetetlenségi erő maximális értéke (φ = 0-nál - az egyenlítőn) csak 0,00343 a gravitáció értékének

17 csúszda
5. előadás (5.2 folytatás) 15 A Föld forgásának hatása a testek mozgására a Föld gravitációs mezőjében - Tegyük fel, hogy egy test a φ szélességi fokon a Föld felszíne felett bizonyos H magasságból zuhan a Földre. Válasszunk a Földhöz mereven kapcsolódó mozgó vonatkoztatási rendszert, amely az x, y tengelyeket érintőlegesen irányítja a párhuzamosra és a meridiánra: Relatív mozgás egyenlete: Itt a centrifugális tehetetlenségi erő kicsinysége a gravitációs erőhöz képest. figyelembe veszik. Így a gravitációs erőt a gravitációs erővel azonosítjuk. Ezen túlmenően feltételezzük, hogy a gravitáció a Föld felszínére merőlegesen irányul az elhajlásának kicsinysége miatt, amint azt fentebb tárgyaltuk. A Coriolis-gyorsulás megegyezik az y tengellyel párhuzamosan nyugatra. A Coriolis tehetetlenségi erő az ellenkező irányba irányul. A relatív mozgás egyenletét a tengelyre vetítjük: Az első egyenlet megoldása adja: Kiindulási feltételek: A harmadik egyenlet megoldása adja: Kiindulási feltételek: A harmadik egyenlet a következő alakot ölti: Kiindulási feltételek: Megoldása adja: A kapott megoldást azt mutatja, hogy a test leesésekor keletre tér el. Számítsuk ki ennek az eltérésnek az értékét például 100 m magasságból zuhanáskor Az esési időt a második egyenlet megoldásából találjuk meg: Így a Föld forgásának befolyása a testek mozgására rendkívül kicsi gyakorlati magasságokhoz és sebességekhez, és nem veszik figyelembe a műszaki számítások során. A második egyenlet megoldása magában foglalja az y tengely menti sebesség létezését is, aminek a megfelelő gyorsulást és a Coriolis tehetetlenségi erőt is elő kell idéznie és előidéznie. Ennek a sebességnek és a vele járó tehetetlenségi erőnek a mozgásváltozásra gyakorolt hatása még kisebb lesz, mint a függőleges sebességhez kapcsolódó figyelembe vett Coriolis tehetetlenségi erő.

18 csúszda
6. előadás Mechanikai rendszer dinamikája. Anyagi pontok rendszere vagy mechanikai rendszer - Anyagi pontok halmaza, vagy azok az anyagi pontok, amelyeket a kölcsönhatás általános törvényei egyesítenek (az egyes pontok vagy testek helyzete vagy mozgása az összes többi helyétől és mozgásától függ) szabad pontok rendszere - amelynek mozgását semmilyen kapcsolat nem korlátozza (például bolygórendszer, amelyben a bolygókat anyagi pontoknak tekintjük). Nem szabad pontok rendszere vagy nem szabad mechanikai rendszer - az anyagi pontok vagy testek mozgását korlátozzák a rendszerre támasztott korlátok (például egy mechanizmus, egy gép stb.). 16 A rendszerre ható erők. Az erők korábban létező osztályozása (aktív és reaktív erők) mellett új erőosztályozást vezetnek be: 1. Külső erők (e) - a rendszer pontjaira és testeire ható pontokból vagy testekből, amelyek nem részei ennek. rendszer. 2. Belső erők (i) - az adott rendszerben szereplő anyagi pontok vagy testek közötti kölcsönhatás erői. Ugyanaz az erő lehet külső és belső erő is. Minden attól függ, hogy melyik mechanikai rendszerről van szó. Például: A Nap, a Föld és a Hold rendszerében a köztük lévő összes gravitációs erő belső. A Föld és a Hold rendszerét tekintve a Nap oldaláról fellépő gravitációs erők külsőek: C Z L A hatás és a reakció törvénye alapján minden Fk belső erő egy másik belső erőnek Fk' felel meg, amely abszolút értékű és ellentétes irány. A belső erők két figyelemreméltó tulajdonsága következik ebből: A rendszer összes belső erőjének fővektora nulla: A rendszer összes belső erőjének főmomentuma bármely középponthoz viszonyítva nullával egyenlő: Vagy a koordinátára vetítésekben tengelyek: Megjegyzés. Bár ezek az egyenletek hasonlóak az egyensúlyi egyenletekhez, nem azok, mivel a belső erők különböző pontokat vagy a rendszer testei és ezeknek a pontoknak (testeknek) egymáshoz viszonyított elmozdulását idézhetik elő. Ezekből az egyenletekből következik, hogy a belső erők nem befolyásolják a rendszer egészének mozgását. Az anyagi pontrendszer tömegközéppontja. A rendszer egészének mozgásának leírására bevezetünk egy geometriai pontot, az úgynevezett tömegközéppontot, amelynek sugárvektorát a kifejezés határozza meg, ahol M a teljes rendszer tömege: Vagy a koordinátára vetítésekben tengelyek: A tömegközéppont képletei hasonlóak a tömegközéppont képleteihez. A tömegközéppont fogalma azonban általánosabb, mivel nem kapcsolódik sem a gravitációs, sem a gravitációs erőkhöz.

19 csúszda
6. előadás (6.2 folytatás) 17 Tétel a rendszer tömegközéppontjának mozgásáról - Tekintsünk egy n anyagi pontból álló rendszert. Az egyes pontokra kifejtett erőket felosztjuk külső és belső erőkre, és helyettesítjük a megfelelő Fke és Fki eredővel. Írjuk fel minden pontra a dinamika alapegyenletét: vagy Adjuk össze ezeket az egyenleteket az összes ponton: Az egyenlet bal oldalán bevezetjük a tömegeket a derivált jele alá, és a derivált összegét helyettesítjük a deriválttal. összegének: A tömegközéppont definíciójából: Helyettesítsük be a kapott egyenletbe: kapjuk vagy: A rendszer tömegének és középponti tömegének gyorsulásának szorzata egyenlő a külső erők fővektorával. A koordinátatengelyekre vetítéseknél: A rendszer tömegközéppontja az egész rendszer tömegével megegyező tömegű anyagi pontként mozog, amelyre a rendszerre ható összes külső erő hat. Következmények a rendszer tömegközéppontjának mozgására vonatkozó tételből (megmaradási törvények): 1. Ha az időintervallumban a rendszer külső erőinek fővektora nulla, Re = 0, akkor a középpont sebessége a tömeg állandó, vC = const (a tömegközéppont egyenletesen egyenesen mozog - a mozgás tömegközéppont megmaradásának törvénye). 2. Ha az időintervallumban a rendszer külső erőinek fővektorának x tengelyre vetülete nulla, Rxe = 0, akkor a tömegközéppont sebessége az x tengely mentén állandó, vCx = const (a tömegközéppont egyenletesen mozog a tengely mentén). Hasonló állítások igazak az y és z tengelyekre. Példa: Két m1 és m2 tömegű ember van egy m3 tömegű csónakban. A kezdeti pillanatban a hajó az emberekkel nyugalomban volt. Határozza meg a csónak elmozdulását, ha egy m2 tömegű személy a csónak orrába mozdult a távolságra. 3. Ha az időintervallumban a rendszer külső erőinek fővektora nulla, Re = 0, és a kezdeti pillanatban a tömegközéppont sebessége nulla, vC = 0, akkor a rendszer sugárvektora tömegközéppont állandó marad, rC = const (a tömegközéppont nyugalomban van, a tömegközéppont helyzetének megmaradásának törvénye). 4. Ha az időintervallumban a rendszer külső erőinek fővektorának x tengelyre vetülete nulla, Rxe = 0, és a kezdeti pillanatban a tömegközéppont sebessége e tengely mentén nulla. , vCx = 0, akkor a tömegközéppont x tengely menti koordinátája állandó marad, xC = const (a tömegközéppont ezen tengely mentén nem mozog). Hasonló állítások igazak az y és z tengelyekre. 1. A mozgás tárgya (csónak emberekkel): 2. Eldobjuk a kapcsolatokat (víz): 3. A kapcsolatot egy reakcióval helyettesítjük: 4. Összeadjuk az aktív erőket: 5. Írjuk fel a tömegközéppontra vonatkozó tételt: Vetítés az x tengelyre: O Határozza meg, milyen messzire kell átszállnia egy m1 tömegű személyre, hogy a csónak a helyén maradjon: A hajó l távolságot fog elmozdulni az ellenkező irányba.

20 csúszda
7. előadás Az erőimpulzus a mechanikai kölcsönhatás mértéke, amely egy adott idő alatt egy pontra ható erők mechanikai mozgásának átadását jellemzi: 18 Koordinátatengelyekre vetítésekben: Állandó erő esetén: Vetítésekben koordinátatengelyekre: ugyanabban az időintervallumban az erők pontjára: Szorozzuk meg dt-vel: Integráljuk egy adott időintervallumban: A pont mozgásának mértéke a mechanikai mozgás mértéke, amelyet egy vektor határozza meg, amely egyenlő a pont tömege és sebességének vektora: Tétel a rendszer mozgási mennyiségének változásáról – Tekintsük a rendszer n anyagi pontját. Az egyes pontokra kifejtett erőket felosztjuk külső és belső erőkre, és helyettesítjük a megfelelő Fke és Fki eredővel. Írjuk fel minden pontra a dinamika alapegyenletét: vagy Anyagi pontrendszer mozgási mennyisége - anyagi pontok mozgásmennyiségeinek geometriai összege: A tömegközéppont definíciója szerint: A tömegközéppont lendületének vektora rendszer egyenlő a teljes rendszer tömegének és a rendszer tömegközéppontjának sebességvektorának szorzatával. Ekkor: A koordinátatengelyekre vetítéseknél: A rendszer impulzusvektorának időbeli deriváltja megegyezik a rendszer külső erőinek fővektorával. Összegezzük ezeket az egyenleteket az összes ponton: Az egyenlet bal oldalán a tömegeket a derivált jele alá vezetjük, és a deriváltak összegét az összeg deriváltjával helyettesítjük: A rendszer impulzusának definíciójából: A koordinátatengelyekre vetítéseknél:

21 csúszda
Euler-tétel - A rendszer lendületének változásáról szóló tétel alkalmazása folytonos közeg (víz) mozgására. 1. A mozgás tárgyául a turbina görbe csatornájában elhelyezkedő víz térfogatát választjuk ki: 2. Eldobjuk a kötéseket, és hatásukat reakciókkal helyettesítjük (Rpov - a felületi erők eredője) 3. Adjunk hozzá aktív erőket (Rb). - testerők eredője): 4. Írja fel a rendszer impulzusának változásáról szóló tételt: A víz mozgásának mennyiségét t0 és t1 időpontokban összegként ábrázoljuk: A víz impulzusának változása az időben intervallum : A víz impulzusának változása végtelenül kicsi dt időintervallumban: , ahol F1 F2 A sűrűség, a keresztmetszeti terület és a másodpercenkénti tömegsebesség szorzatát véve a következőt kapjuk: A rendszer impulzusának különbségét behelyettesítve a változásba tétel, a következőt kapjuk: Következmények a rendszer impulzusának változására vonatkozó tételből (megmaradási törvények): 1. Ha az időintervallumban a rendszer külső erőinek fővektora nulla, Re = 0, akkor a mennyiségvektor mozgása állandó, Q = const a rendszer impulzusmegmaradásának törvénye). 2. Ha az időintervallumban a rendszer külső erőinek fővektorának x tengelyre vetülete nulla, Rxe = 0, akkor a rendszer impulzusának x tengelyre vetítése állandó, Qx = konst. Hasonló állítások igazak az y és z tengelyekre. 7. előadás (a 7.2 folytatása) Példa: Egy M tömegű gránát, amely v sebességgel repült, két részre robbant. Az egyik m1 tömegű töredék sebessége a mozgás irányában v1 értékre nőtt. Határozza meg a második töredék sebességét! 1. A mozgás tárgya (gránát): 2. A tárgy szabad rendszer, nincsenek összefüggések és reakcióik. 3. Aktív erők összeadása: 4. Írja fel az impulzus változására vonatkozó tételt: Vetítsen a tengelyre: β Ossza el a változókat és integrálja: A jobboldali integrál majdnem nulla, mert robbanási idő t

22 csúszda
7. előadás (7.3. folytatás) 20 Egy pont szögimpulzusa vagy egy bizonyos középponthoz viszonyított kinetikus mozgásnyomatéka a mechanikai mozgás mértéke, amelyet egy olyan vektor határoz meg, amely egyenlő egy anyagi pont sugárvektorának és a impulzusvektora: Anyagi pontrendszer egy bizonyos középponthoz viszonyított kinetikus nyomatéka geometriai az összes anyagi pont azonos középponthoz viszonyított impulzusnyomatékának összege: Tengely vetületekben: Tengely vetületeiben : Tétel a rendszer impulzusnyomatékának változásáról - Tekintsünk egy n anyagi pontból álló rendszert. Az egyes pontokra kifejtett erőket felosztjuk külső és belső erőkre, és helyettesítjük a megfelelő Fke és Fki eredővel. Írjuk fel minden pontra a dinamika alapegyenletét: vagy Adjuk össze ezeket az egyenleteket minden pontra: Cseréljük le a deriváltak összegét az összeg deriváltjával: A zárójelben lévő kifejezés a rendszer lendületi nyomatéka. Innen: Az egyenlőségeket vektorosan megszorozzuk a bal oldali sugárvektorral: Nézzük meg, hogy lehetséges-e a derivált előjelét a vektorszorzaton kívülre vinni: Így kaptuk: középpont. A koordinátatengelyekre történő vetítéseknél: A rendszer impulzusnyomatékának valamely időtengelyhez viszonyított deriváltja megegyezik a rendszer külső erőinek ugyanarra a tengelyre vonatkoztatott főnyomatékával.

23 csúszda
8. előadás 21 ■ Következmények a rendszer impulzusimpulzusának változására vonatkozó tételből (megmaradási törvények): 1. Ha az időintervallumban a rendszer külső erőinek főmomentumának vektora egy bizonyos középponthoz képest egyenlő nullához, MOe = 0, akkor a rendszer azonos középponthoz viszonyított impulzusimpulzusának vektora állandó, KO = const a rendszer impulzusmegmaradásának törvénye). 2. Ha az időintervallumban a rendszer külső erőinek főmomentuma az x tengelyhez képest nulla, Mxe = 0, akkor a rendszer x tengelyhez viszonyított szögnyomatéka állandó, Kx = const. Hasonló állítások igazak az y és z tengelyekre. 2. Merev test tehetetlenségi nyomatéka egy tengely körül: Egy anyagi pont tengely körüli tehetetlenségi nyomatéka egyenlő a pont tömegének és a pont tengely távolságának négyzetével. A merev test tehetetlenségi nyomatéka egy tengely körül egyenlő az egyes pontok tömegének és a pont tengelytől való távolságának négyzetének szorzatának összegével. ■ A tehetetlenségi nyomaték elméletének elemei - Merev test forgómozgásakor a tehetetlenségi nyomaték (a mozgásváltozással szembeni ellenállás) a forgástengely körüli tehetetlenségi nyomaték. Tekintsük a definíció alapfogalmait és a tehetetlenségi nyomatékok számítási módszereit. 1. Anyagi pont tehetetlenségi nyomatéka a tengely körül: Egy pont diszkrét kis tömegéről végtelenül kis tömegre való átmenetben az ilyen összeg határát a merev test integrál: axiális tehetetlenségi nyomatéka határozza meg. . A merev test tengelyirányú tehetetlenségi nyomatékán kívül más típusú tehetetlenségi nyomatékok is léteznek: a merev test centrifugális tehetetlenségi nyomatéka. merev test poláris tehetetlenségi nyomatéka. 3. A merev test tehetetlenségi nyomatékairól szóló tétel párhuzamos tengelyekre - a párhuzamos tengelyekre való átmenet képlete: Tehetetlenségi nyomaték a vonatkoztatási tengely körül Statikus tehetetlenségi nyomatékok a vonatkoztatási tengelyekre A testtömegnyomatékok nullák:

24 csúszda
8. előadás (folytatás 8.2) 22 Állandó keresztmetszetű egyenletes rúd tehetetlenségi nyomatéka a tengely körül: x z L Válassza ki az elemi térfogatot dV = Adx távolságban x: x dx Elemi tömeg: A tehetetlenségi nyomaték kiszámításához kb. központi tengely(a súlyponton áthaladva) elegendő a tengely helyét megváltoztatni és beállítani az integrációs határokat (-L/2, L/2). Itt bemutatjuk a párhuzamos tengelyekre való átmenet képletét: zС 5. Homogén tömör henger tehetetlenségi nyomatéka a szimmetriatengelyhez viszonyítva: H dr r Különítsük el a dV = 2πrdrH elemi térfogatot (r sugarú vékony henger) ): Elemi tömeg: Itt a V=πR2H hengertérfogat képletet használjuk. Egy üreges (vastag) henger tehetetlenségi nyomatékának kiszámításához elegendő beállítani az integrálási határokat R1-ről R2-re (R2> R1): 6. Vékony henger tehetetlenségi nyomatéka a szimmetriatengely körül (t)

25 csúszda
8. előadás (folytatás 8.3) 23 ■ Merev test tengely körüli forgásának differenciálegyenlete: Írjunk egy tételt egy rögzített tengely körül forgó merev test impulzusimpulzusának megváltoztatásáról: A forgó merev test impulzusa: A nyomaték A forgástengely körüli külső erők egyenlő a nyomatékkal (a reakciók és az erő nem hoz létre gravitációs nyomatékot): A tételbe behelyettesítjük a mozgási nyomatékot és a forgatónyomatékot Példa: Két azonos súlyú, G1 = G2 ember lóg egy kötélen G3 = G1/4 súllyal egy tömör tömb fölé dobva. Valamikor egyikük relatív u sebességgel mászni kezdett a kötélen. Határozza meg az egyes személyek emelési sebességét. 1. Válassza ki a mozgás tárgyát (blokk emberekkel): 2. Dobja el a kapcsolatokat (a blokk tartószerkezete): 3. Cserélje ki a kapcsolatot reakciókkal (csapágy): 4. Adjon hozzá aktív erőket (gravitáció): 5. Írja le tétel a rendszer mozgási nyomatékának a blokk forgástengelyéhez viszonyított megváltoztatásáról: R Mivel a külső erők nyomatéka egyenlő nullával, a kinetikus nyomatéknak állandónak kell maradnia: A kezdeti t = 0 időpillanatban ott egyensúly volt, és Kz0 = 0. Egy ember kötélhez viszonyított mozgásának kezdete után az egész rendszer mozogni kezdett, de a rendszer kinetikai nyomatékának nullával egyenlőnek kell maradnia: Kz = 0. A szögimpulzus rendszer mind az emberek, mind a blokk kinetikai momentumainak összege: Itt v2 a második személy sebessége, megegyezik a kábel sebességével.vége egy rögzített forgástengelyhez. Vagy: Kis oszcillációk esetén sinφ φ: Lengés periódusa: A rúd tehetetlenségi nyomatéka:

26 csúszda
8. előadás (folytatás 8.4 - kiegészítő anyag) 24 ■ A giroszkóp elemi elmélete: A giroszkóp az anyagszimmetria tengelye körül forgó merev test, melynek egyik pontja rögzített. A szabad giroszkóp úgy van rögzítve, hogy a tömegközéppontja mozdulatlan marad, a forgástengely pedig átmegy a tömegközépponton, és bármilyen pozíciót felvehet a térben, pl. a forgástengely úgy változtatja helyzetét, mint a test saját forgástengelye gömbmozgás közben. A giroszkóp közelítő (elemi) elméletének fő feltételezése, hogy a forgórész impulzusvektorát (kinetikus nyomatékát) a saját forgástengelye mentén irányítottnak tekintjük. Így annak ellenére, hogy általános esetben a forgórész három forgásban vesz részt, csak a saját forgásának ω = dφ/dt szögsebességét vesszük figyelembe. Ennek az az alapja, hogy in modern technológia a giroszkóp forgórésze körülbelül 5000-8000 rad/s (körülbelül 50000-80000 ford/perc) szögsebességgel forog, míg a másik két szögsebesség, amely a saját forgástengelyének precessziójához és nutációjához kapcsolódik, több tízezerszer kisebb, mint ezt a sebességet. A szabad giroszkóp fő tulajdonsága, hogy a forgórész tengelye ugyanazt az irányt tartja a térben a tehetetlenségi (csillag) vonatkoztatási rendszerhez képest (ezt a Foucault-inga mutatja, amely a lengéssíkot változatlanul tartja a csillagokhoz képest, 1852). Ez a forgórész tömegközéppontjához viszonyított kinetikus nyomaték megmaradásának törvényéből következik, feltéve, hogy a súrlódást a forgórész felfüggesztési tengelyeinek csapágyaiban, a külső és a belső keretben figyelmen kívül hagyjuk: Erőhatás egy szabad tengelyre giroszkóp. A forgórész tengelyére ható erő esetén a külső erők tömegközépponthoz viszonyított nyomatéka nem egyenlő nullával: ω ω С erő, és ezen erő nyomatékának vektora felé, azaz. nem az x tengely körül fog forogni (belső felfüggesztés), hanem az y tengely körül (külső felfüggesztés). Az erő megszűnésekor a forgórész tengelye ugyanabban a helyzetben marad, ami megfelel az erő utolsó idejének, mert ettől az időponttól kezdve a külső erők pillanata ismét nullával egyenlő. Rövid távú erőhatás (ütés) esetén a giroszkóp tengelye gyakorlatilag nem változtatja meg a helyzetét. Így a forgórész gyors forgása lehetővé teszi a giroszkóp számára, hogy ellensúlyozza azokat a véletlenszerű behatásokat, amelyek a forgórész forgástengelyének helyzetét kívánják megváltoztatni, és állandó erőhatás mellett megtartja a sík helyzetét merőlegesen a ható erő, amelyben a forgórész tengelye fekszik. Ezeket a tulajdonságokat az inerciális navigációs rendszerek működésében használják.
Előadások az elméleti mechanikáról
Pontdinamika
1. előadás
A dinamika alapfogalmai
fejezetben Dinamika a testek mozgását vizsgálják a rájuk ható erők hatására. Ezért a szakaszban bevezetett fogalmakon kívül kinematika, itt olyan új fogalmakat kell alkalmazni, amelyek tükrözik az erők különböző testekre gyakorolt hatásának sajátosságait és a testek reakcióit ezekre a hatásokra. Tekintsük e fogalmak főbb elemeit.
a) erő
Az erő egy adott testre más testek által gyakorolt hatás mennyiségi eredménye. Az erő egy vektormennyiség (1. ábra).
![]()
![]()
Az erővektor kezdetének A pontja F hívott az erő alkalmazási pontja. Az MN egyenest, amelyen az erővektor található, hívjuk erővonal. Az erővektor egy bizonyos skálán mért hosszát ún az erővektor számértéke vagy modulusa. Az erőmodul jelölése vagy . A testre ható erőhatás vagy annak alakváltozásában nyilvánul meg, ha a test álló helyzetben van, vagy abban, hogy a test mozgása során gyorsulást kölcsönöz neki. Az erő ezen megnyilvánulásaira épül a különféle erőmérők (erőmérők vagy dinamométerek) eszközei az erők mérésére.
b) erőrendszer
Az erők figyelembe vett halmaza kialakul erőrendszer. Bármely n erőből álló rendszer felírható a következő formában: ![]()
c) szabad test
Olyan testet nevezünk, amely a térben bármilyen irányban mozoghat anélkül, hogy közvetlen (mechanikai) kölcsönhatást tapasztalna más testekkel ingyenes vagy izolált. Egyik vagy másik erőrendszer befolyása egy testre csak akkor tisztázható, ha ez a test szabad.
d) eredő erő
Ha bármely erő olyan hatással van egy szabad testre, mint valamilyen erőrendszer, akkor ezt az erőt nevezzük ennek az erőrendszernek az eredménye. Ez így van leírva:
![]() ,
,
ami azt jelenti egyenértékűség az eredő és valamilyen n erőrendszer becsapódása ugyanarra a szabad testre.
Térjünk most át az erők forgási hatásainak mennyiségi meghatározásához kapcsolódó összetettebb fogalmak mérlegelésére.
e) egy ponthoz (középponthoz) viszonyított erőnyomaték
Ha a test egy erő hatására el tud forogni valamilyen fix O pont körül (2. ábra), akkor ennek a forgási hatásnak a számszerűsítésére bevezetünk egy fizikai mennyiséget, amelyet ún. pontra (középre) vonatkozó erőnyomaték.

Az adott fix ponton és az erő hatásvonalán áthaladó síkot ún erő síkja. A 2. ábrán ez a ОАВ sík.
A ponthoz (középponthoz) viszonyított erőnyomaték egy olyan vektormennyiség, amely egyenlő az erőnek az erővektor általi alkalmazási pontjának sugárvektorának vektorszorzatával:
![]() ( 1)
( 1)
A két vektor vektorszorzásának szabálya szerint vektorszorzatuk a faktorok vektorainak elhelyezkedési síkjára (jelen esetben az OAB háromszög síkjára) merőleges vektor, amely abba az irányba irányul, ahonnan a legrövidebb. a faktor első vektorának elforgatása a faktor második vektorához látható az órával szemben (2. ábra). Az (1) keresztszorzat tényezőinek ilyen sorrendjével a test forgása az erő hatására látható lesz az órával szemben (2. ábra). Mivel a vektor merőleges a keresztszorzat síkjára erő, térbeli elhelyezkedése meghatározza az erő síkjának helyzetét Az erőnyomaték vektorának a középponthoz viszonyított számértéke egyenlő a ОАВ terület kétszeresével, és a következő képlettel határozható meg:
![]() ,
(2)
,
(2)
ahol nagyságrendűh, amely egyenlő egy adott O pont és az erő hatásvonala közötti legrövidebb távolsággal, az erő karjának nevezzük.
Ha az erő hatássíkjának térbeli helyzete nem lényeges az erő forgási hatásának jellemzéséhez, akkor ebben az esetben az erő forgási hatásának jellemzéséhez az erőnyomaték vektora helyett algebrai erőnyomaték:
![]() (3)
(3)
Az egy adott középponthoz viszonyított algebrai erőnyomaték egyenlő az erőmodulus és a váll szorzatával, plusz vagy mínusz előjellel. Ebben az esetben a pozitív momentum a test forgásának felel meg adott erő hatására az órával szemben, a negatív nyomaték pedig a test forgásának az óra irányában. Az (1), (2) és (3) képletekből az következik, hogy ponthoz viszonyított erőnyomaték csak akkor egyenlő nullával, ha ennek az erőnek a karjahnulla. Ilyen erő nem tudja elforgatni a testet egy adott pont körül.
f) A tengely körüli erőnyomaték
Ha egy test erő hatására el tud forogni valamilyen rögzített tengely körül (például ajtó- vagy ablakkeret forgása a zsanérokban, amikor kinyitják vagy zárják), akkor ennek a forgási hatásnak a számszerűsítésére bevezetünk egy fizikai mennyiséget, amely nak, nek hívják adott tengely körüli erőnyomaték.
 z
z
b Fxy
A 3. ábra egy diagramot mutat, amely alapján meghatározzuk a z tengely körüli erőnyomatékot:
A szöget két merőleges z irány és az O háromszögek síkjai alkotják abés OAV, ill. O óta ab a ОАВ xy síkra vetítése, akkor a sík alak adott síkra vetítésére vonatkozó sztereometriai tétel szerint van:
ahol a plusz előjel a cos pozitív értékének felel meg, azaz. éles sarkok, a mínusz előjel pedig a cos, azaz a tompaszögek negatív értékének felel meg, ami a vektor irányából adódik. Viszont az SO ab=1/2abh, ahol h ab . A szegmens értéke ab egyenlő az xy síkra vetített erővel, azaz. . ab = F xy .
A fentiek, valamint a (4) és (5) egyenlőségek alapján a következőképpen határozzuk meg a z tengely körüli erőnyomatékot:
A (6) egyenlőség lehetővé teszi, hogy a következő definíciót fogalmazzuk meg az erőnyomaték bármely tengely körüli meghatározására: Egy adott tengely körüli erőnyomaték egyenlő az erő nyomatékának vektorának erre a tengelyre való vetületével bármely tengelyre vonatkoztatva. ezt a tengelyt, és az adott tengelyre merőleges síkra való erővetítés szorzataként határozzuk meg, plusz vagy mínusz előjellel a vetület vállán a tengely és a vetítési sík metszéspontjához képest. Ebben az esetben a pillanat előjele akkor tekinthető pozitívnak, ha a tengely pozitív irányából nézve a test e tengely körüli forgása látható az órával szemben. Ellenkező esetben a tengely körüli erőnyomaték negatívnak tekinthető. Mivel a tengelyhez viszonyított erőnyomatéknak ezt a definícióját meglehetősen nehéz megjegyezni, ezért ajánlott megjegyezni a (6) képletet és a 3. ábrát, amely ezt a képletet magyarázza.
A (6) képletből az következik a tengely körüli erőnyomaték nulla, ha párhuzamos a tengellyel (ebben az esetben a tengelyre merőleges síkra vetülete nulla), vagy az erő hatásvonala metszi a tengelyt (akkor a vetítőkar h=0). Ez teljes mértékben megfelel a tengely körüli erőnyomaték fizikai jelentésének, mint a forgástengelyű testre gyakorolt forgó erőhatás mennyiségi jellemzőjének.
g) testtömeg
Régóta megfigyelték, hogy egy erő hatására a test fokozatosan felveszi a sebességet, és tovább mozog, ha az erőt megszüntetik. A testeknek ezt a tulajdonságát, hogy ellenállnak a mozgásuk változásának, nevezték a testek tehetetlensége vagy tehetetlensége. Egy test tehetetlenségének mennyiségi mértéke a tömege. Kívül, A testtömeg a gravitációs erők adott testre gyakorolt hatásának mennyiségi mértéke minél nagyobb a test tömege, annál nagyobb gravitációs erő hat a testre. Amint az alább látható lesz, uh A testsúly két definíciója összefügg.
A dinamika egyéb fogalmairól és definícióiról később, azokban a részekben lesz szó, ahol először előfordulnak.
2. Kötések és kötések reakciói
Korábban az 1. szakasz c) pontjában megadták a szabad test fogalmát, mint olyan testet, amely a térben bármilyen irányba mozoghat anélkül, hogy más testekkel közvetlenül érintkezne. A minket körülvevő valódi testek többsége közvetlen kapcsolatban áll más testekkel, és nem tud egyik vagy másik irányba mozogni. Így például az asztal felületén elhelyezkedő testek bármilyen irányba mozoghatnak, kivéve az asztal felületére merőleges irányt lefelé. A csuklós ajtók foroghatnak, de nem mozoghatnak előre, stb. Azokat a testeket, amelyek a térben egyik vagy másik irányba nem tudnak elmozdulni, ún. nem ingyenes.
Mindent, ami egy adott test mozgását a térben korlátozza, kötésnek nevezzük. Ezek lehetnek más testek, amelyek megakadályozzák ennek a testnek a mozgását bizonyos irányban ( fizikai kapcsolatok); tágabb értelemben lehet, hogy a test mozgását bizonyos feltételek szabják, amelyek korlátozzák ezt a mozgást. Tehát beállíthat egy feltételt, hogy egy anyagi pont egy adott görbe mentén elmozduljon. Ebben az esetben a kapcsolat matematikailag egyenlet formájában van megadva ( kapcsolódási egyenlet). A linkek típusának kérdésével az alábbiakban részletesebben foglalkozunk.
A testekre fektetett kötések többsége gyakorlatilag fizikai kötés. Felmerül tehát a kérdés egy adott test interakciójáról és az erre a testre háruló kapcsolatról. Erre a kérdésre ad választ a testek kölcsönhatására vonatkozó axióma: Két test egyenlő nagyságú, ellentétes irányú és ugyanazon az egyenesen elhelyezkedő erőkkel hat egymásra. Ezeket az erőket interakciós erőknek nevezzük. A kölcsönhatási erők különböző kölcsönható testekre vonatkoznak. Tehát például egy adott test és egy kapcsolat kölcsönhatása során az egyik kölcsönhatási erő a test oldaláról a kapcsolatra, a másik kölcsönhatási erő pedig a kapcsolat oldaláról hat az adott testre. . Ezt az utolsó hatalmat nevezzük kötés reakcióereje vagy egyszerűen kapcsolódási reakció.
A dinamika gyakorlati problémáinak megoldása során meg kell tudni találni a reakciók irányát különféle típusok kapcsolatokat. Ebben néha segíthet a kötésreakció irányának meghatározására vonatkozó általános szabály: A kötés reakciója mindig azzal az iránnyal ellentétes irányban irányul, amelyben ez a kötés megakadályozza az adott test mozgását. Ha ez az irány határozottan megadható, akkor a kapcsolat reakcióját az irány határozza meg. Ellenkező esetben a kötésreakció iránya határozatlan, és csak a test megfelelő mozgási vagy egyensúlyi egyenleteiből állapítható meg. Részletesebben a kötéstípusok és reakcióik irányának kérdését érdemes tanulmányozni a tankönyv szerint: S.M. Targ Elméleti mechanika rövid kurzusa "Felsőiskola", M., 1986. 1. fejezet, 3. §.
Az 1. szakasz c) pontjában elhangzott, hogy bármely erőrendszer hatása csak akkor határozható meg teljes mértékben, ha ezt az erőrendszert egy szabad testre alkalmazzuk. Mivel a legtöbb test valójában nem szabad, ezért e testek mozgásának tanulmányozásához felvetődik a kérdés, hogyan lehet ezeket a testeket szabaddá tenni. Erre a kérdésre megvan a válasz előadások összefüggéseinek axiómája tovább filozófia otthon. Előadások voltak... szociálpszichológiaés etnopszichológia. 3. Elméleti A szociáldarwinizmus eredményei...
elméleti Mechanika
Oktatóanyag >> FizikaAbsztrakt előadások tovább tantárgy ELMÉLETI MECHANIKA A szakos hallgatóknak: 260501,65 ... - nappali tagozatos Absztrakt előadások alapján összeállított: Butorin L.V., Busygina E.B. elméleti Mechanika. Oktatási és gyakorlati útmutató...




