Darinio naudojimas įvairiose veiklos srityse. Įdomi išvestinė Šio darbo tikslai: Apsvarstyti išvestinės panaudojimą įvairiuose moksluose Susipažinti su mokslininkais, tyrusiais funkcijos išvestinę. Jėga yra darbo poslinkyje išvestinė.

Mokslo Ministerija Saratovo sritis

Valstybinis autonominis profesionalas švietimo įstaiga Saratovo sritis „Engelso politechnika“

IŠVEDINĖS TAIKYMAS ĮVAIRINGOSE MOKSLO SRITYSE

Atlikta: Sarkulova Nurgulya Sergeevna

KShI-216/15 grupės mokinys

(Dizainas, modeliavimas ir

siuvimo technologija)

mokslinis patarėjas:

Verbitskaja Elena Viačeslavovna

matematikos mokytojas GAPOU SO

„Engelso politechnika“

2016

Įvadas

Matematikos vaidmuo įvairiose gamtos mokslų srityse yra labai didelis. Nenuostabu, kad jie sako„Matematika yra mokslų, jos fizikos karalienė dešinė ranka, chemija liko.

Tyrimo objektas – išvestinė.

Pagrindinis tikslas – parodyti išvestinės reikšmę ne tik matematikoje, bet ir kituose moksluose, jos svarbą šiuolaikiniame gyvenime.

Diferencialinis skaičiavimas – tai mus supančio pasaulio aprašymas, atliktas matematine kalba. Išvestinė padeda mums sėkmingai išspręsti ne tik matematikos uždaviniai, bet ir praktines užduotis įvairiose mokslo ir technologijų srityse.

Funkcijos išvestinė naudojama visur, kur vyksta netolygus proceso srautas: tai netolygus mechaninis judėjimas, kintamoji srovė, cheminės reakcijos ir radioaktyvusis skilimas medžiagos ir kt.

Pagrindiniai ir teminiai šio rašinio klausimai:

1. Darinio atsiradimo istorija.

2. Kodėl verta tirti funkcijų išvestinius?

3. Kur naudojamos išvestinės priemonės?

4. Darinių taikymas fizikoje, chemijoje, biologijoje ir kituose moksluose.

5. Išvados

Nusprendžiau parašyti pranešimą tema „Išvestinės taikymas įvairiose mokslo srityse“, nes manau, kad ši tema yra labai įdomi, naudinga ir aktuali.

Savo darbe kalbėsiu apie diferenciacijos taikymą įvairiose mokslo srityse, tokiose kaip chemija, fizika, biologija, geografija ir kt.. Juk visi mokslai yra neatsiejamai susiję, kas labai aiškiai matyti temos pavyzdyje as svarstau.

Išvestinės taikymas įvairiose mokslo srityse

Iš vidurinės mokyklos algebros kurso mes tai jau žinome išvestinė yra funkcijos padidėjimo santykio su jos argumento prieaugio riba, nes argumento padidėjimas linkęs į nulį, jei tokia riba yra.

Išvestinės radimo veiksmas vadinamas jos diferenciacija, o funkcija, kuri taške x turi išvestinę, tame taške vadinama diferencijuojama. Funkcija, kuri yra diferencijuojama kiekviename intervalo taške, vadinama diferencijuojama tame intervale.

Garbė atrasti pagrindinius matematinės analizės dėsnius priklauso anglų fizikas ir matematikas Isaacas Newtonas bei vokiečių matematikas, fizikas, filosofas Leibnicas.

Niutonas pristatė darinio sąvoką, tyrinėdamas mechanikos dėsnius, taip atskleisdamas jo mechaninę prasmę.

Fizinė išvestinės reikšmė: funkcijos išvestinėy= f(x) taške x 0 yra funkcijos kitimo greitisf(x) taške x 0 .

Leibnicas prie išvestinės sąvokos atėjo išspręsdamas išvestinės linijos liestinės nubrėžimo problemą, taip ją paaiškindamas. geometrine prasme.

Išvestinės geometrinė reikšmė yra ta, kad išvestinė funkcija taškex 0 lygus funkcijos grafiko liestinės nuolydžiui, nubrėžtam taške su abscisėmisx 0 .

Terminas vedinys ir šiuolaikinis žymėjimasy" , f„J.Lagrange’o pristatytas 1797 m.

rusų matematikas XIX amžiuje Panfuty Lvovich Chebyshev sakė, kad „ypač svarbūs yra tie mokslo metodai, kurie leidžia išspręsti visai praktinei žmogaus veiklai būdingą problemą, pavyzdžiui, kaip disponuoti savo priemonėmis, kad būtų pasiekta didžiausia nauda“.

Įvairių specialybių atstovai mūsų laikais turi susidoroti su tokiomis užduotimis:

Procesų inžinieriai stengiasi organizuoti gamybą taip, kad būtų pagaminama kuo daugiau produktų;

Dizaineriai bando sukurti įrenginį erdvėlaivis kad prietaiso masė būtų mažiausia;

Ekonomistai gamyklos ir žaliavų šaltinių sąsajas stengiasi suplanuoti taip, kad transportavimo išlaidos būtų minimalios.

Studijuodami bet kurią temą, studentams kyla klausimas: „Kam mums to reikia? Jei atsakymas tenkina smalsumą, galime kalbėti apie mokinių susidomėjimą. Atsakymą į temą „Išvestinė“ galima gauti žinant, kur naudojami funkcijų išvestiniai.

Norėdami atsakyti į šį klausimą, galime išvardyti kai kurias disciplinas ir jų skyrius, kuriuose vartojami dariniai.

Išvestinė algebroje:

1. Funkcijos grafiko liestinė

Funkcijos grafiko liestinėf, skiriasi ties x apie , yra tiesė, einanti per tašką (x apie ; f(x o )) ir turintis nuolydįf“(x o ).

y= f(x o ) + f'(x o ) (x - x o )

2. Didėjančių ir mažėjančių funkcijų intervalų paieška

Funkcijay=f(x) didėja per intervaląX , jei kam irnelygybę. Kitaip tariant, didesnė argumento reikšmė atitinka didesnę funkcijos reikšmę.

Funkcijay=f(x) per intervalą mažėjaX , jei kam irnelygybę. Kitaip tariant, didesnė argumento reikšmė atitinka mažesnę funkcijos reikšmę.

3. Funkcijos ekstremalių taškų radimas

tašką paskambinomaksimalus taškas funkcijasy=f(x) jei už visusx . Iškviečiama funkcijos reikšmė didžiausiame taškemaksimali funkcija ir žymėti.

tašką paskambinominimalus taškas funkcijasy=f(x) jei už visusx iš savo kaimynystės nelygybę. Iškviečiama funkcijos reikšmė minimaliame taškefunkcijos minimumas ir žymėti.

Pagal taško kaimynystę suprasti intervalą, kur yra pakankamai mažas teigiamas skaičius.

Vadinami minimalūs ir didžiausi taškaiekstremalūs taškai , ir iškviečiamos funkcijos reikšmės, atitinkančios ekstremumo taškusfunkcijos ekstremumai .

4. Funkcijos išgaubimo ir įgaubimo intervalų paieška

Funkcijų grafikas, yra šiame intervaleišgaubtas , yra ne aukščiau už bet kurią jo liestinę (1 pav.).

Funkcijų grafikas, skiriasi intervalu, yra šiame intervaleįgaubtas , jei šios funkcijos grafikas yra intervale yra ne žemesnė už bet kurią jo liestinę (2 pav.).

Funkcijos grafiko vingio tašku vadinamas taškas, skiriantis išgaubto ir įgaubto intervalus.

5. Funkcijos vingio taškų radimas

Išvestinė fizikoje:

1. Greitis kaip kelio išvestinė

2. Pagreitis kaip greičio išvestinėa =

3. Skilimo greitis radioaktyvieji elementai 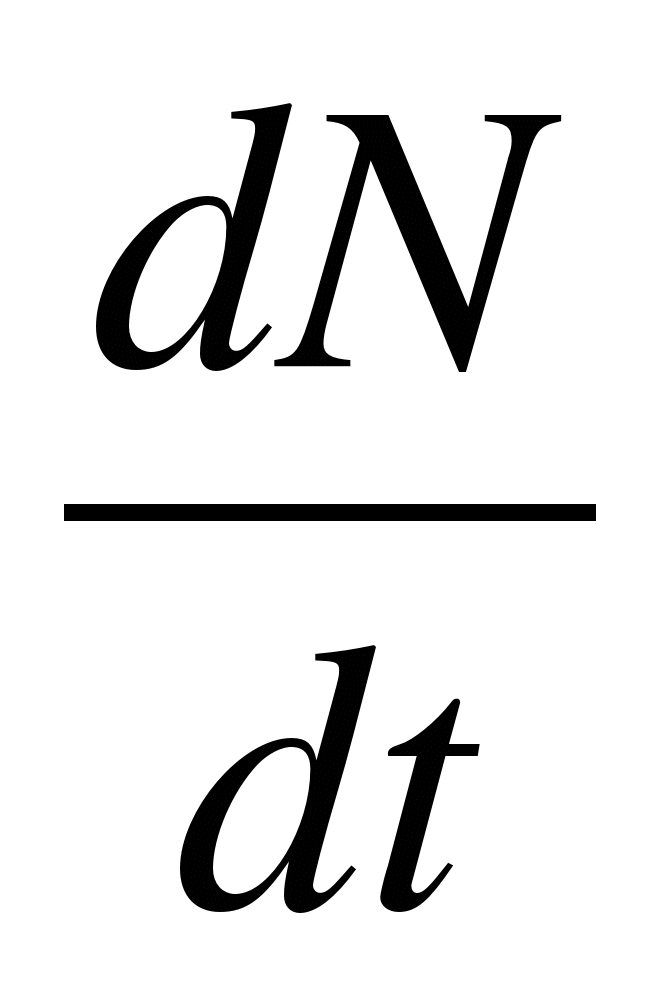= - λN

Taip pat fizikoje išvestinė naudojama apskaičiuojant:

Greičiai materialus taškas

Momentinis greitis kaip fizinė išvestinės reikšmė

Momentinė vertė kintamoji srovė

Momentinė elektromagnetinės indukcijos EML vertė

Maksimali galia

Darinys chemijoje:

O chemijoje diferencialinis skaičiavimas buvo plačiai pritaikytas konstruojant matematiniai modeliai cheminės reakcijos ir tolesnis jų savybių aprašymas.

Išvestinė chemijoje naudojama norint nustatyti labai svarbų dalyką – greitį cheminė reakcija, vienas iš lemiamų veiksnių, į kurį būtina atsižvelgti daugelyje mokslo ir pramonės veiklos sričių. V(t) = p'(t)

Kiekis

in-va vienu metu t 0

p = p(t 0 )

Funkcija

Laiko intervalas

∆t = t–t 0

Argumento padidėjimas

Kiekio pasikeitimas

∆p=p(t 0 + ∆t) – p(t 0 )

Funkcijų padidėjimas

Vidutinis cheminės reakcijos greitis

∆p/∆t

Funkcijos prieaugio ir argumento prieaugio santykis

Darinys biologijoje:

Populiacija yra tam tikros rūšies individų rinkinys, užimantis tam tikrą teritorijos plotą rūšies diapazone, laisvai kryžminantis vienas su kitu ir iš dalies arba visiškai izoliuotas nuo kitų populiacijų, taip pat elementarus evoliucijos vienetas. .

P \u003d x‘ (t)

Išvestinė geografijoje:

1. Kai kurios reikšmės seismografijoje

2. Savybės elektromagnetinis laukasžemė

3. Branduolinių geofizinių parametrų radioaktyvumas

4. Daug reikšmių ekonominėje geografijoje

5. Išveskite formulę, kaip apskaičiuoti gyventojų skaičių teritorijoje laiko momentu t.

y'= į y

Thomaso Malthuso sociologinio modelio idėja yra ta, kad gyventojų skaičiaus augimas yra proporcingas gyventojų skaičiui tam tikru laiku nuo t iki N(t). Malthuso modelis puikiai pasiteisino apibūdinant JAV gyventojus nuo 1790 iki 1860 m. Daugumoje šalių šis modelis nebegalioja.

Elektrotechnikos vedinys:

Mūsų namuose, transporte, gamyklose: elektros srovė veikia visur. Pagal elektros srovę supraskite kryptingą laisvų elektriškai įkrautų dalelių judėjimą.

Kiekybinė charakteristika elektros srovė yra srovės stiprumas.

Elektros grandinėje elektros krūvis kinta laikui bėgant pagal dėsnį q=q (t). Srovė I yra krūvio q išvestinė laiko atžvilgiu.

Elektros inžinerijoje daugiausia naudojamas kintamosios srovės veikimas.

Laikui bėgant besikeičianti elektros srovė vadinama kintamąja srove. Kintamosios srovės grandinėje gali būti įvairių elementų: šildymo prietaisai, gyvatukai, kondensatoriai.

Kintamosios elektros srovės gamyba grindžiama elektromagnetinės indukcijos dėsniu, kurio formulėje yra magnetinio srauto darinys.

Ekonomikos darinys:

Ekonomika yra gyvybės pagrindas, o joje svarbią vietą užima diferencialinis skaičiavimas – ekonominės analizės aparatas. Pagrindinis ekonominės analizės uždavinys – ištirti ekonominių dydžių ryšius funkcijų pavidalu.

Ekonomikos išvestinė priemonė išsprendžia svarbius klausimus:

1. Kokia kryptimi keisis valstybės pajamos, padidėjus mokesčiams ar įvedus muitus?

2. Ar įmonės pajamos padidės ar mažės brangstant jos produkcijai?

Norint išspręsti šiuos klausimus, reikia sukonstruoti įvesties kintamųjų ryšio funkcijas, kurios vėliau tiriamos diferencialinio skaičiavimo metodais.

Taip pat ekonomikoje naudojant funkcijos ekstremumą (išvestinę išvestinę) galima rasti didžiausią darbo našumą, maksimalų pelną, maksimalią produkciją ir minimalias išlaidas.

IŠVADA: išvestinė sėkmingai naudojama sprendžiant įvairias taikomąsias mokslo, technikos ir gyvenimo problemas

Kaip matyti iš aukščiau pateikto, funkcijos išvestinės panaudojimas yra labai įvairus ir ne tik matematikos, bet ir kitų disciplinų studijose. Todėl galime daryti išvadą, kad temos: „Funkcijos išvestinė“ tyrimas turės savo pritaikymą kitose temose ir dalykuose.

Įsitikinome temos „Išvestinė“ studijavimo svarba, jos vaidmeniu mokslo ir technikos procesų tyrime, galimybe projektuoti pagal tikrų įvykių matematinius modelius ir išspręsti svarbias problemas.

“Muzika gali pakylėti ar nuraminti sielą,
Tapyba džiugina akį,
Poezija - pažadinti jausmus,
Filosofija – patenkinti proto poreikius,
Inžinerija turi pagerinti materialinę žmonių gyvenimo pusę,
BETmatematika gali pasiekti visus šiuos tikslus“.

Taip sakė amerikiečių matematikasMaurice'as Kline'as.

Bibliografija:

1. Bogomolovas N.V., Samoylenko I.I. Matematika. - M.: Yurayt, 2015 m.

2. V. P. Grigorjevas ir Yu. A. Dubinskis, Aukštosios matematikos elementai. - M.: Akademija, 2014 m.

3. Bavrinas I.I. Aukštosios matematikos pagrindai. - M.: baigti mokyklą, 2013.

4. Bogomolovas N.V. Praktinės matematikos pamokos. - M.: Aukštoji mokykla, 2013 m.

5. Bogomolovas N.V. Matematikos uždavinių rinkinys. - M.: Bustard, 2013 m.

6. Rybnikovas K.A. Matematikos istorija, Maskvos universiteto leidykla, M, 1960 m.

7. Vinogradovas Yu.N., Gomola A.I., Potapovas V.I., Sokolova E.V. – M.:Leidybos centras „Akademija“, 2010 m

8 . Bašmakovas M.I. Matematika: algebra ir matematinės analizės pradžia, geometrija. - M.: Leidybos centras „Akademija“, 2016 m

Periodiniai šaltiniai:

Laikraščiai ir žurnalai: „Matematika“, „ Vieša pamoka»

Interneto išteklių naudojimas, skaitmenines bibliotekas:

www:egetutor.ru

matematika-na5.norod.ru

FGOU SPO

Novosibirskas žemės ūkio kolegija

abstrakčiai

disciplinoje "matematika"

„Išvestinės priemonės taikymas moksle ir technikoje“

S. Razdolnoe 2008 m

Įvadas

1. Teorinė dalis

1.1 Problemos, lemiančios išvestinės priemonės sampratą

1.2 Išvestinis apibrėžimas

1.3 Bendroji išvestinės priemonės radimo taisyklė

1.4 Geometrinė išvestinės reikšmė

1.5 Mechaninė išvestinės reikšmė

1.6 Antrosios eilės vedinys ir jo mechaninė reikšmė

1.7 Diferencialo apibrėžimas ir geometrinė reikšmė

2. Funkcijų tyrimas išvestinės pagalba

Išvada

Literatūra

Įvadas

Pirmajame mano rašinio skyriuje kalbėsime apie išvestinės sąvoką, jos taikymo taisykles, apie geometrines ir fizinis pojūtis išvestinė. Antrame mano rašinio skyriuje kalbėsime apie darinio panaudojimą moksle ir technikoje bei apie šios srities problemų sprendimą.

1. Teorinė dalis

1.1 Problemos, lemiančios išvestinės priemonės sampratą

Tiriant tam tikrus procesus ir reiškinius, dažnai iškyla šių procesų greičio nustatymo problema. Jo sprendimas veda prie išvestinės sąvokos, kuri yra pagrindinė diferencialinio skaičiavimo sąvoka.

Diferencialinio skaičiavimo metodas buvo sukurtas XVII–XVIII a. Dviejų puikių matematikų – I. Niutono ir G. V. – vardai. Leibnicas.

Niutonas atėjo prie diferencialinio skaičiavimo atradimo spręsdamas uždavinius apie materialaus taško greitį tam tikru laiko momentu (momentinis greitis).

Kaip žinoma, vienodas judėjimas yra judėjimas, kai kūnas vienodais laiko intervalais nukeliauja vienodo ilgio kelią. Atstumas, kurį kūnas nukeliauja per laiko vienetą, vadinamas greitis vienodas judesys.

Tačiau dažniausiai praktikoje susiduriame su netolygiu judėjimu. Keliu važiuojantis automobilis sankryžose sulėtina greitį ir padidina jį tose atkarpose, kur kelias laisvas; orlaivis lėtėja leidžiantis ir pan. Todėl dažniausiai tenka susidurti su tuo, kad vienodais laiko intervalais kūnas praeina skirtingo ilgio kelio atkarpas. Toks judėjimas vadinamas netolygus. Jo greičio negalima apibūdinti vienu skaičiumi.

Dažnai ši sąvoka naudojama netolygiam judėjimui apibūdinti Vidutinis greitis judėjimas per laiką ∆t٫, kuris nustatomas pagal ryšį, kur ∆s yra kūno nueitas kelias per laiką ∆t.

Taigi, kai kūnas krinta laisvai, jo vidutinis judėjimo greitis per pirmąsias dvi sekundes yra

Praktikoje tokia judėjimo charakteristika kaip vidutinis greitis labai mažai ką pasako apie judėjimą. Iš tiesų, 4,9 m / s, o 2 - 14,7 m / s, o vidutinis greitis per pirmąsias dvi sekundes yra 9,8 m / s. Vidutinis greitis per pirmąsias dvi sekundes nesuteikia jokio supratimo, kaip įvyko judėjimas: kada kūnas judėjo greičiau, o kada lėčiau. Jei kiekvienai sekundei atskirai nustatysime vidutinius judėjimo greičius, tai žinosime, pavyzdžiui, kad 2 sekundę kūnas judėjo daug greičiau nei 1-ąją. Tačiau daugeliu atvejų daug greičiau, nei nesame patenkinti. Juk nesunku suprasti, kad per šią 2 sekundę kūnas taip pat juda įvairiai: pradžioje lėčiau, pabaigoje greičiau. Ir kaip jis juda kažkur šios 2 sekundės viduryje? Kitaip tariant, kaip nustatyti momentinį greitį?

Tegul kūno judėjimą apibūdina įstatymas laikui, lygiam ∆t. Šiuo metu t0 kūnas praėjo kelią, šiuo metu - kelią. Todėl per laiką ∆t kūnas nukeliavo atstumą ir vidutinis kūno greitis per šį laikotarpį bus toks.

Kuo trumpesnis laiko intervalas ∆t, tuo tiksliau galima nustatyti, kokiu greičiu juda kūnas momentu t0, nes judantis kūnas negali reikšmingai pakeisti savo greičio per trumpą laiką. Todėl vidutinis greitis, kai ∆t linkęs į nulį, artėja prie faktinio judėjimo greičio ir, esant ribinei, suteikia judėjimo greitį tam tikru laiku t0 (momentinis greitis).

Šiuo būdu ,

1 apibrėžimas. Momentinis greitis Tiesinio kūno judėjimo tam tikru laiku t0 vadinama vidutinio greičio riba per laiką nuo t0 iki t0+ ∆t, kai laiko intervalas ∆t linkęs į nulį.

Taigi, norint rasti tiesiojo netolygaus judėjimo greitį tam tikru momentu, reikia rasti kelio ∆ prieaugio ir laiko prieaugio ∆t santykio ribą, esant sąlygai t.y. Leibnicas atrado diferencialinį skaičiavimą spręsdamas bet kurios kreivės, pateiktos pagal jo lygtį, liestinės sudarymo problemą.

Šios problemos sprendimas turi didelę reikšmę. Juk judančio taško greitis nukreiptas išilgai jo trajektorijos liestinės, todėl nustatant sviedinio greitį jo trajektorijoje, bet kurios jo orbitoje skriejančios planetos greitis sumažinamas iki kreivės liestinės krypties nustatymo. .

Liestinės, kaip tiesės, turinčios tik vieną bendrą tašką su kreive, apibrėžimas, kuris galioja apskritimui, netinka daugeliui kitų kreivių.

Toliau pateiktas kreivės liestinės apibrėžimas ne tik atitinka intuityvią mintį apie ją, bet ir leidžia realiai rasti jos kryptį, t.y. apskaičiuokite liestinės nuolydį.

2 apibrėžimas. Tangentasį kreivę taške M vadinama tiese MT, kuri yra ribinė sekanto MM1 padėtis, kai taškas M1, judantis išilgai kreivės, neribotai artėja prie taško M.

1.2 Išvestinis apibrėžimas

Atkreipkite dėmesį, kad nustatant kreivės liestinę ir momentinį netolygaus judėjimo greitį, iš esmės atliekamos tos pačios matematinės operacijos:

1. Nurodyta argumento reikšmė padidinama ir apskaičiuojama nauja funkcijos reikšmė, atitinkanti naują argumento reikšmę.

2. Nustatykite funkcijos prieaugį, atitinkantį pasirinktą argumento prieaugį.

3. Funkcijos prieaugis dalijamas iš argumento prieaugio.

4. Apskaičiuokite šio santykio ribą, jei argumento prieaugis yra lygus nuliui.

Daugelio problemų sprendimai apriboja tokio tipo perėjimus. Tampa būtina padaryti apibendrinimą ir suteikti šiai ištraukai pavadinimą iki ribos.

Funkcijos kitimo greitis, priklausantis nuo argumento pasikeitimo, akivaizdžiai gali būti apibūdinamas santykiu. Šis ryšys vadinamas Vidutinis greitis funkcija keičiasi intervalu nuo iki. Dabar turime atsižvelgti į trupmenos ribą. Šio santykio riba, nes argumento prieaugis linkęs į nulį (jei tokia riba egzistuoja), yra kažkokia nauja funkcija. Ši funkcija žymima simboliais y', vadinamais išvestinėši funkcija, nes ji gaunama (pagaminama) iš funkcijos Pati funkcija vadinama primityvus funkcija jos išvestinės atžvilgiu

3 apibrėžimas. išvestinė funkcijos duotame taške įvardija funkcijos ∆y prieaugio santykio su atitinkamu argumento ∆x prieaugiu ribą, su sąlyga, kad ∆x→0, t.y.

1.3 Bendroji išvestinės priemonės radimo taisyklė

Kai kurios funkcijos išvestinės radimo operacija vadinama diferenciacija funkcijos, o šios operacijos savybes tirianti matematikos šaka yra diferencialinis skaičiavimas.

Jei funkcija turi išvestinę ties x=a, tada sakoma, kad ji yra skiriasiŠiuo atveju. Jei funkcija turi išvestinę kiekviename tam tikro intervalo taške, tada sakoma, kad ji yra skiriasi Ant šito intervalas .

Išvestinės apibrėžimas ne tik visiškai charakterizuoja funkcijos kitimo greičio pasikeitus argumentui sampratą, bet ir suteikia galimybę realiai apskaičiuoti tam tikros funkcijos išvestinę. Norėdami tai padaryti, turite atlikti šiuos keturis veiksmus (keturis veiksmus), nurodytus pačios išvestinės priemonės apibrėžime:

1. Raskite naują funkcijos reikšmę pateikdami in šią funkciją vietoj x nauja argumento reikšmė: .

2. Funkcijos prieaugis nustatomas iš naujos jos reikšmės atėmus pateiktą funkcijos reikšmę: .

3. Sudarykite funkcijos prieaugio ir argumento prieaugio santykį: .

4. Eikite į ribą ties ir suraskite išvestinę: .

Paprastai tariant, išvestinė yra „nauja“ funkcija, gauta iš tam tikros funkcijos pagal nurodytą taisyklę.

1.4 Geometrinė išvestinės reikšmė

Pirmą kartą pateikta išvestinės geometrinė interpretacija pabaigos XVII in. Leibnicas yra toks: funkcijos išvestinės reikšmė taške x yra lygus funkcijos grafiko liestinės nuolydžiui tame pačiame taške x, tie.

Liestinės lygtis, kaip ir bet kuri einanti tiesė duotas taškasšia kryptimi, turi formą – dabartinės koordinatės. Tačiau liestinės lygtis taip pat bus parašyta taip: . Normalioji lygtis bus parašyta forma

1.5 Mechaninė išvestinės reikšmė

Mechaninę vedinio interpretaciją pirmasis pateikė I. Niutonas. Jis susideda iš to: materialaus taško judėjimo greitis tam tikru laiko momentu yra lygus kelio išvestinei laiko atžvilgiu, t.y. Taigi, jei materialaus taško judėjimo dėsnis pateikiamas lygtimi, tai norint rasti momentinį taško greitį tam tikru laiko momentu, reikia rasti išvestinę ir į ją pakeisti atitinkamą t reikšmę. .

1.6 Antrosios eilės vedinys ir jo mechaninė reikšmė

Gauname (lygtis iš to, kas buvo padaryta vadovėlyje Lisichkin V.T. Soloveychik I.L. „Matematika“ p. 240):

Šiuo būdu, kūno tiesinio judėjimo pagreitis tam tikru momentu yra lygus antrajai kelio išvestinei laiko atžvilgiu, skaičiuojamai tam tikram momentui. Tai mechaninė antrojo darinio reikšmė.

1.7 Diferencialo apibrėžimas ir geometrinė reikšmė

4 apibrėžimas. Pagrindinė funkcijos prieaugio dalis, tiesinė funkcijos prieaugio atžvilgiu, tiesinė nepriklausomo kintamojo prieaugio atžvilgiu, vadinama diferencialas funkcijas ir žymimas d, t.y. .

Funkcinis diferencialas geometriškai pavaizduotas taške nubrėžtos liestinės ordinatės prieaugiu M ( x ; y ) nurodytoms x ir ∆x reikšmėms.

skaičiavimas diferencialas – .

Diferencialo taikymas apytiksliuose skaičiavimuose – , apytikslė funkcijos prieaugio reikšmė sutampa su jos diferencialu.

1 teorema. Jei diferencijuojamoji funkcija didėja (mažėja) duotame intervale, tai šios funkcijos išvestinė šiame intervale nėra neigiama (ne teigiama).

2 teorema. Jei išvestinė funkcija yra teigiamas (neigiamas) kokiame nors intervale, tai funkcija šiame intervale monotoniškai didėja (monotoniškai mažėja).

Dabar suformuluokime taisyklę, kaip rasti funkcijos monotoniškumo intervalus

1. Apskaičiuokite šios funkcijos išvestinę.

2. Raskite taškus, kuriuose yra nulis arba jų nėra. Šie taškai vadinami kritiškas už funkciją

3. Su rastais taškais funkcijos sritis padalinama į intervalus, kurių kiekviename išvestinė išlaiko savo ženklą. Šie intervalai yra monotoniškumo intervalai.

4. Išnagrinėkite kiekvieno rasto intervalo ženklą. Jei nagrinėjamame intervale, tai šiuo intervalu didėja; jei, tai tokiu intervalu jis mažėja.

Atsižvelgiant į problemos sąlygas, monotoniškumo intervalų nustatymo taisyklė gali būti supaprastinta.

5 apibrėžimas. Taškas vadinamas maksimaliu (minimaliu) funkcijos tašku, jei nelygybė galioja atitinkamai bet kuriam x iš tam tikros taško kaimynystės.

Jei yra maksimalus (minimalus) funkcijos taškas, tai sakome (minimumas) taške. Maksimalios ir minimalios funkcijos vienija pavadinimą ekstremumas funkcijos, o iškviečiami didžiausi ir mažiausi taškai ekstremalūs taškai (kraštutiniai taškai).

3 teorema.(būtinas ekstremumo požymis). Jeigu ir išvestinė egzistuoja šiame taške, tada ji yra lygi nuliui: .

4 teorema.(pakankamas ekstremumo požymis). Jei išvestinė kai x praeina a tada pakeičia ženklą a yra funkcijos kraštutinis taškas .

Pagrindiniai darinio tyrimo dalykai:

1. Raskite išvestinę.

2. Raskite visus svarbiausius funkcijos srities taškus.

3. Per kritinius taškus nustatykite funkcijos išvestinės ženklus ir išrašykite ekstremumo taškus.

4. Apskaičiuokite funkcijų reikšmes kiekviename kraštutiniame taške.

2. Funkcijų tyrimas naudojant išvestinę

1 užduotis . Žurnalo tūris. Taisyklingos formos rąstai be medienos defektų, kurių storų ir plonų galų skersmenų skirtumas santykinai nedidelis, vadinami pramonine apvalia mediena. Nustatant pramoninės apvalios medienos tūrį, dažniausiai naudojama supaprastinta formulė, kur rąsto ilgis yra jo vidutinio pjūvio plotas. Sužinokite, ar tikrasis tūris baigiasi, ar neįvertinamas; įvertinti santykinę paklaidą.

Sprendimas. Apvalios verslo medienos forma artima nupjautam kūgiui. Leisti būti didesnio, mažesnio rąsto galo spindulys. Tada beveik tikslų jo tūrį (nupjauto kūgio tūrį), kaip žinoma, galima rasti pagal formulę. Tegul yra tūrio vertė, apskaičiuota pagal supaprastintą formulę. Tada;

Tie. . Tai reiškia, kad supaprastinta formulė nepakankamai įvertina tūrį. Padėkime dabar. Tada. Tai rodo, kad santykinė paklaida nepriklauso nuo rąsto ilgio, o nustatoma pagal santykį. Nuo kada didėja intervalas. Todėl, o tai reiškia, kad santykinė paklaida neviršija 3,7%. Miškų mokslo praktikoje tokia klaida laikoma gana priimtina. Didesniu tikslumu praktiškai neįmanoma išmatuoti nei galų skersmenų (nes jie šiek tiek skiriasi nuo apskritimų), nei rąsto ilgio, nes matuojamas ne aukštis, o kūgio generatorius (ilgis). rąstas yra dešimtis kartų didesnis už skersmenį, ir tai nesukelia didelių klaidų). Taigi, iš pirmo žvilgsnio neteisinga, bet daugiau paprasta formule nes nupjauto kūgio tūris realioje situacijoje pasirodo visai teisėtas. Pakartotinai, naudojant specialius patikrinimo metodus, nustatyta, kad masiškai apskaitant pramoninį mišką santykinė paklaida naudojant nagrinėjamą formulę neviršija 4%.

2 užduotis . Nustatant duobių, kaušų tranšėjų ir kitų nupjauto kūgio formos konteinerių tūrius, žemės ūkio praktikoje kartais naudojama supaprastinta formulė, kur yra aukštis, yra kūgio pagrindų plotai. Išsiaiškinkite, ar tikrasis tūris pervertintas, ar neįvertintas, įvertinkite santykinę paklaidą pagal natūralią praktikos sąlygą: (- baziniai spinduliai, .

Sprendimas. Žymėdami per tikrąją nupjauto kūgio tūrio reikšmę, o per supaprastinta formule apskaičiuotą reikšmę gauname: , t.y. . Tai reiškia, kad supaprastinta formulė pervertina tūrį. Toliau kartodami ankstesnės problemos sprendimą, matome, kad santykinė paklaida bus ne didesnė kaip 6,7%. Ko gero, normuojant kasimo darbus toks tikslumas priimtinas – juk duobės nebus idealūs kūgiai, o atitinkami parametrai realiomis sąlygomis matuojami labai grubiai.

3 užduotis . Specialiojoje literatūroje, norint nustatyti frezavimo staklių suklio sukimosi kampą β frezuojant movas su dantimis, išvesta formulė kur. Kadangi ši formulė yra sudėtinga, rekomenduojama atsisakyti jos vardiklio ir naudoti supaprastintą formulę. Kokiu atveju (- sveikasis skaičius) galima naudoti šią formulę, jei nustatant kampą leidžiama klaida?

Sprendimas. Tiksli formulė po paprastos identiškos transformacijos galima atvesti į galvą. Todėl, naudojant apytikslę formulę, leidžiama absoliuti paklaida, kur. Mes tiriame intervalo funkciją. Šiuo atveju 0,06, t.y. kampinis priklauso pirmajam ketvirčiui. Mes turime: . Atkreipkite dėmesį, kad nagrinėjamame intervale, taigi, funkcija mažėja šiame intervale. Kadangi toliau, visiems atsižvelgiant į. Reiškia,. Kadangi tai yra radianas, to pakanka išspręsti nelygybę. Išspręsdami šią nelygybę atrankos būdu, mes nustatome, kad . Kadangi funkcija mažėja, iš to išplaukia

Išvada

Išvestinės naudojimas yra gana platus ir gali būti visiškai aprėptas tokio pobūdžio darbuose, tačiau aš pabandžiau aprėpti pagrindinius dalykus. Šiais laikais, ryšium su mokslo ir technologijų pažanga, ypač sparčiai tobulėjant kompiuterinėms sistemoms, diferencialinis skaičiavimas tampa vis aktualesnis sprendžiant tiek paprastas, tiek itin sudėtingas problemas.

Literatūra

1. V.A. Petrovas „Matematinė analizė atliekant gamybos užduotis“

2. Soloveicchik I.L., Lisichkin V.T. "Matematika"

Chaikinas Semjonas, Maysakas Kirilas, Zalogina Anastasija, Shakhzadova Anna

Šioje plėtroje pateikiamas pristatymas tema „Išvestinės taikymas chemijoje ir biologijoje“. Per projekto veikla buvo iškelta hipotezė, kad išvestinė randa savo pritaikymą šiose mokslo srityse. Per tiriamasis darbas išsiaiškinta, koks yra darinio vaidmuo tokiuose moksluose kaip chemija ir biologija, kur ir kokias problemas sprendžiant jis pritaikomas. Atlikus darbus buvo padaryta išvada, kad hipotezė tikrai pasitvirtino.

Parsisiųsti:

Peržiūra:

https://accounts.google.com

Skaidrių antraštės:

Hipotezė:

Peržiūra:

Norėdami naudoti pristatymų peržiūrą, susikurkite „Google“ paskyrą (paskyrą) ir prisijunkite: https://accounts.google.com

Skaidrių antraštės:

Darinio panaudojimas chemijoje ir biologijoje Darbą atliko MBOU 6 vidurinės mokyklos 11B klasės mokiniai: Chaikin Semyon, Maysak Kirill, Zalogina Anastasia, Shakhzadova Anna Stavropol, 2014 m.

Hipotezė:

O chemijoje diferencialinis skaičiavimas buvo plačiai pritaikytas kuriant matematinius cheminių reakcijų modelius ir vėliau aprašant jų savybes. Chemija yra mokslas apie medžiagas, cheminius medžiagų virsmus. Chemija tiria įvairių reakcijų dėsningumus.Cheminės reakcijos greitis – tai reaguojančių medžiagų koncentracijos pokytis per laiko vienetą. Darinio taikymas chemijoje ir biologijoje Cheminės reakcijos greičio nustatymas

Kodėl reakcijose mums reikia išvestinės? Kadangi reakcijos greitis v nuolat kinta proceso metu, jis dažniausiai išreiškiamas kaip reagentų koncentracijos išvestinė laiko atžvilgiu.

Išvestinė formulė chemijoje Jei C (t) yra į cheminę reakciją patekusios medžiagos kiekio kitimo dėsnis, tai cheminės reakcijos greitis v (t) momentu t yra lygus išvestinei:

Reakcijos greičio nustatymas Prieauginės funkcijos ir prieauginio argumento santykio riba, nes Δt linksta į nulį, yra cheminės reakcijos greitis tam tikru metu

Chemijos užduotis: Į cheminę reakciją patekusios medžiagos kiekį pateiksime pagal priklausomybę: C (t) \u003d t 2 / 2 + 3 t -3 (mol) Raskite cheminės reakcijos greitį po 3 sekundžių . Sprendimas: v (t) = C ‘(t) ; v (t) = t + 3; v (3) = 3+3 = 6. Atsakymas: 6 mol/s.

Biologinė išvestinės reikšmė Tegul ryšys tarp mikroorganizmų populiacijos y individų skaičiaus ir jos dauginimosi laiko t pateikiamas lygtimi: y = x (t). Tegu ∆ t yra laiko intervalas nuo kokios nors pradinės reikšmės t iki t + ∆ t . Tada y + ∆y \u003d x (t + ∆ t) yra nauja populiacijos dydžio reikšmė, atitinkanti momentą t + ∆ t, o ∆ y + x (t + ∆ t) - x (t) yra pokytis organizmų individų skaičiumi. Santykis yra vidutinis reprodukcijos greitis arba, kaip sakoma, vidutinis gyventojų produktyvumas. Skaičiuodami gauname y ' = P (t) = x ' (t) , arba populiacijos produktyvumą momentu t .

Pavyzdys Tegul bakterijų populiacija laiko momentu t (c) turi x(t) individų. . Raskite populiacijos augimo tempą: a) savavališku momentu t , b) momentu t = 1 c . Sprendimas: P = x'(t) = 200t; P(1) = 200 (r/s). Atsakymas: 200 o/s.

Išvada Darinio sąvoka labai svarbi chemijoje ir biologijoje, ypač nustatant reakcijos greitį.

Išvada: Diferencialinis skaičiavimas yra mus supančio pasaulio aprašymas, atliktas matematine kalba. Išvestinė yra viena iš svarbiausių skaičiavimo sąvokų. Išvestinės žinios mums padeda sėkmingai spręsti ne tik matematines, bet ir praktines įvairių mokslo, technikos ir gyvenimo sričių problemas.

Pietų Sachalino valstybinis universitetas

Matematikos katedra

Kursinis darbas

Tema: Praktinis išvestinės taikymas

Lektorius: Likhacheva O.N.

Južno-Sachalinskas

2002 m
Įvadas

Šiame darbe apžvelgsiu darinio pritaikymą įvairiuose moksluose ir pramonės šakose. Darbas suskirstytas į skyrius, kurių kiekviename nagrinėjamas vienas iš diferencialinio skaičiavimo aspektų (geometrinė, fizinė reikšmė ir kt.)

1. Išvestinės sąvoka

1-1. Istorinė informacija

Diferencialinį skaičiavimą sukūrė Niutonas ir Leibnicas XVII amžiaus pabaigoje, remdamiesi dviem problemomis:

1) apie savavališkos tiesės liestinės radimą

2) dėl greičio paieškos pagal savavališką judėjimo dėsnį

Dar anksčiau su darinio sąvoka buvo susidurta italų matematiko Tartaglia (apie 1500 - 1557 m.) darbuose - čia, tiriant ginklo pasvirimo kampo klausimą, atsirado liestinė, kuri užtikrina didžiausią diapazoną. sviedinio.

XVII amžiuje G. Galilėjaus judėjimo teorijos pagrindu buvo aktyviai plėtojama darinio kinematinė samprata. Įvairių pristatymų pradėjo atsirasti Dekarto, prancūzų matematiko Robervalio, anglų mokslininko L. Gregory darbuose. Lopital, Bernoulli, Lagrange, Euler, Gauss labai prisidėjo prie diferencialinio skaičiavimo tyrimo.

1-2. Darinio samprata

Tegul y \u003d f (x) yra nuolatinė argumento x funkcija, apibrėžta intervale (a; b), ir tegul x 0 yra savavališkas šio intervalo taškas

Argumentui x suteikiame prieaugį ∆x, tada funkcija y = f(x) gaus prieaugį ∆y = f(x + ∆x) - f(x). Riba, iki kurios santykis ∆y / ∆x yra ∆x → 0, vadinama funkcijos f(x) išvestine.

1-3. Diferencijavimo taisyklės ir išvestinių lentelė

		(sin x)" = cos x
	(1 / x)" = -1 / x2	(cos x)" = -sin x
	(√x)" = 1 / 2√x	(tg x)" = 1 / cos 2 x
(uv)" = u"v + uv"	(a x)" = a x log x	(ctg x)" = 1 / sin 2 x
(u / v)"=(u"v - uv") / v 2		(arcsin x)" = 1 / √ (1- x 2)
	(log a x)" = (log a e) / x	(arccos x)" = -1 / √ (1 - x 2)
	(ln x)" = 1 / x	(arctg x)" = 1 / √ (1+ x 2)
		(arcctg x)" = -1 / √ (1+ x 2)

2. Išvestinės geometrinė reikšmė

2-1. Kreivės liestinė

Turėkime kreivę ir fiksuotą tašką M bei tašką N. Taško M liestinė yra tiesi linija, kurios vietą linkusi užimti styga MN, jei taškas N neribotai artėja išilgai taško N. kreivė į M.

Apsvarstykite funkciją f(x) ir šią funkciją atitinkančią kreivę y = f(x). Kai kurios reikšmės x funkcija turi reikšmę y = f(x). Šios kreivės reikšmės atitinka tašką M(x 0 , y 0). Įveskime naują argumentą x 0 + ∆x, jo reikšmė atitinka funkcijos y 0 + ∆y = f(x 0 + ∆x) reikšmę. Atitinkamas taškas yra N(x 0 + ∆x, y 0 + ∆y). Nubraižykite sekantą MN ir φ pažymėkite sekanto suformuotą kampą su teigiama Ox ašies kryptimi. Paveikslėlyje parodyta, kad ∆y / ∆x = tg φ. Jei dabar ∆x artėja prie 0, tai taškas N judės išilgai kreivės, sekantas MN pasisuks aplink tašką M ir kampas φ pasikeis. Jei, kaip ∆x → 0, kampas φ yra linkęs į α, tai tiesė, einanti per M ir sudaranti kampą α su teigiama abscisių ašies kryptimi, bus reikalinga liestinė. Tuo pačiu metu jo nuolydžio koeficientas:

Tai reiškia, kad išvestinės f "(x) reikšmė tam tikrai argumento x reikšmei yra lygi kampo, kurį su Ox ašies teigiama kryptimi sudaro funkcijos f (x) grafiko liestinė, liestine. ) taške M (x, f (x)).

Erdvės linijos liestinės apibrėžimas panašus į plokštumos kreivės liestinės apibrėžimą. Šiuo atveju, jei funkcija pateikta lygtimi z = f(x, y), nuolydžiai ties OX ir OY ašimis bus lygūs dalinėms f išvestinėms x ir y atžvilgiu.

2-2. Paviršiaus liestinės plokštuma

Paviršiaus liestinė taške M yra plokštuma, kurioje yra visų paviršiaus erdvinių kreivių, einančių per M – sąlyčio tašką, liestinės.

Paimkite paviršių, pateiktą lygtimi F(x, y, z) = 0, ir kokį nors paprastą tašką M(x 0 , y 0 , z 0) ant jo. Paviršiuje apsvarstykite kokią nors kreivę L, einančią per M. Kreivę pateiksime lygtimis

x = φ(t); y = ψ(t); z = χ(t).

Pakeiskime šias išraiškas į paviršiaus lygtį. Lygtis pavirs tapatybe, nes kreivė yra tik paviršiuje. Naudodami diferencialo formos nekintamumo savybę, gautą lygtį diferencijuojame t atžvilgiu:

Kreivės L liestinės taške M lygtys yra tokios formos:

Kadangi skirtumai x - x 0, y - y 0, z - z 0 yra proporcingi atitinkamiems diferencialams, galutinė plokštumos lygtis atrodo taip:

F" x (x - x 0) + F" y (y - y 0) + F" z (z - z 0) = 0

ir konkrečiu atveju z = f(x, y):

Z - z 0 \u003d F "x (x - x 0) + F" y (y - y 0)

Pavyzdys: Raskite liestinės plokštumos hiperbolinio paraboloido taške (2a; a; 1,5a) lygtį

Sprendimas:

Z" x \u003d x / a \u003d 2; Z" y \u003d -y / a \u003d -1

Norimos plokštumos lygtis:

Z - 1,5a = 2 (x - 2a) - (Y - a) arba Z = 2x - y - 1,5a

3-1. Medžiagos taško greitis

Tegu kelio s priklausomybė nuo laiko t duotoje tiesinis judėjimas materialusis taškas išreiškiamas lygtimi s = f(t), o t 0 yra tam tikras laiko momentas. Apsvarstykite kitą laiką t, pažymėkite ∆t = t - t 0 ir apskaičiuokite kelio prieaugį: ∆s = f(t 0 + ∆t) - f(t 0). Santykis ∆s / ∆t vadinamas vidutiniu judėjimo greičiu per laiką ∆t, praėjusį nuo pradinio momento t 0 . Greitis yra šio santykio riba kaip ∆t → 0.

Vidutinis netolygaus judėjimo pagreitis intervale (t; t + ∆t) yra reikšmė =∆v / ∆t. Momentinis materialaus taško pagreitis momentu t bus vidutinio pagreičio riba:

Tai yra, pirmą kartą išvestinė (v "(t)).

Pavyzdys: Kūno nuvažiuoto kelio priklausomybė nuo laiko apskaičiuojama pagal lygtį s \u003d A + Bt + Ct 2 + Dt 3 (C \u003d 0,1 m / s, D \u003d 0,03 m / s 2). Nustatykite laiką po judėjimo pradžios, po kurio kūno pagreitis bus lygus 2 m / s 2.

Sprendimas:

v(t) = s "(t) = B + 2Ct + 3Dt 2; a(t) = v"(t) = 2C + 6Dt = 0,2 + 0,18t = 2;

1,8 = 0,18 t; t = 10 s

3-2. Medžiagos šiluminė talpa tam tikroje temperatūroje

Norėdami padidinti skirtingas temperatūras T ta pačia verte, lygia T 1 - T, 1 kg. tam tikrai medžiagai reikia kitokio šilumos kiekio Q 1 - Q ir santykio

nes ši medžiaga nėra pastovi. Taigi tam tikros medžiagos šilumos kiekis Q yra netiesinė temperatūros T funkcija: Q = f(T). Tada ΔQ = f(t + ΔT) - f(T). Požiūris

vadinama vidutine šilumine talpa intervale , o šios išraiškos riba esant ∆T → 0 vadinama duotosios medžiagos šilumine talpa esant T temperatūrai.

3-3. Galia

Keisti mechaninis judėjimas kūną sukelia jėgos, veikiančios jį iš kitų kūnų. Siekiant kiekybiškai apibūdinti energijos mainų tarp sąveikaujančių kūnų procesą, mechanikoje įvedama jėgos darbo samprata. Norint apibūdinti darbo tempą, įvedama galios sąvoka:

4. Diferencialinis skaičiavimas ekonomikoje

4-1. Funkcijų tyrimas

Diferencialinis skaičiavimas yra matematinis aparatas, plačiai naudojamas ekonominei analizei. Pagrindinis ekonominės analizės uždavinys – ištirti ekonominių dydžių, užrašytų kaip funkcijos, ryšius. Kokia kryptimi keisis vyriausybės pajamos, jei bus padidinti mokesčiai arba įvesti importo muitai? Ar įmonės pajamos padidės ar sumažės, kai pabrangs jos produktai? Kokia dalimi papildoma įranga gali pakeisti į pensiją išėjusius darbuotojus? Norint išspręsti tokias problemas, turi būti sukonstruotos į juos įtrauktų kintamųjų ryšio funkcijos, kurios vėliau tiriamos diferencialinio skaičiavimo metodais. Ekonomikoje dažnai reikalaujama rasti geriausią arba optimalią rodiklio reikšmę: didžiausias darbo našumas, maksimalus pelnas, maksimali produkcija, minimalios išlaidos ir kt. Kiekvienas rodiklis yra vieno ar kelių argumentų funkcija. Taigi optimalios rodiklio reikšmės radimas sumažinamas iki funkcijos ekstremumo radimo.

Pagal Ferma teoremą, jei taškas yra funkcijos ekstremumas, tai išvestinė jame arba neegzistuoja, arba lygi 0. Ekstremo tipą galima nustatyti pagal vieną iš pakankamų ekstremumo sąlygų:

1) Tegul funkcija f(x) yra diferencijuojama kurioje nors taško x 0 kaimynystėje. Jei išvestinė f "(x) eidama per tašką x 0 pakeičia ženklą iš + į -, tai x 0 yra maksimalus taškas, jei nuo - iki +, tai x 0 yra mažiausias taškas, jei jis nekeičia ženklo , tada nėra ekstremumo.

2) Tegul funkcija f (x) yra du kartus diferencijuojama kurioje nors taško x 0 kaimynystėje, o f "(x 0) \u003d 0, f "" (x 0) ≠ 0, tada taške x 0 funkcija f (x 0) turi maksimumą , jei f ""(x 0)< 0 и минимум, если f ""(x 0) > 0.

Be to, antroji išvestinė apibūdina funkcijos išgaubimą (funkcijos grafikas vadinamas išgaubtu aukštyn [žemyn] intervale (a, b), jei jis yra šiame intervale ne aukščiau [ne žemiau] bet kurios jo liestinės ).

Pavyzdys: pasirinkti optimalią įmonės gamybos apimtį, kurios pelno funkcija gali būti modeliuojama pagal priklausomybę:

π(q) = R(q) - C(q) = q 2 - 8q + 10

Sprendimas:

π"(q) = R"(q) - C"(q) = 2q - 8 = 0 → q extr = 4

Dėl q< q extr = 4 → π"(q) < 0 и прибыль убывает

Jei q > q extr = 4 → π"(q) > 0 ir pelnas didėja

Kai q = 4, pelnas įgyja mažiausią reikšmę.

Kokia yra optimali įmonės produkcija? Jei įmonė per nagrinėjamą laikotarpį negali pagaminti daugiau nei 8 vienetų produkcijos (p(q = 8) = p(q = 0) = 10), tai optimalus sprendimas būtų visiškai nieko negaminti, o gauti pajamų. iš patalpų ir/ar įrangos nuomos. Jeigu firma sugeba pagaminti daugiau nei 8 vienetus, tai firmai optimaliausia bus gaminti ties savo gamybos pajėgumų riba.

4-2. Paklausos elastingumas

Funkcijos f (x) tamprumas taške x 0 vadinamas riba

Paklausa – tai prekės kiekis, kurio reikalauja pirkėjas. Paklausos elastingumas kainai E D yra matas, kaip paklausa reaguoja į kainų pokyčius. Jei │E D │>1, tada paklausa vadinama elastinga, jei │E D │<1, то неэластичным. В случае E D =0 спрос называется совершенно неэластичным, т. е. изменение цены не приводит ни к какому изменению спроса. Напротив, если самое малое снижение цены побуждает покупателя увеличить покупки от 0 до предела своих возможностей, говорят, что спрос является совершенно эластичным. В зависимости от текущей эластичности спроса, предприниматель принимает решения о снижении или повышении цен на продукцию.

4-3. Ribų analizė

Svarbi ekonomikoje naudojamų diferencialinio skaičiavimo metodų dalis yra ribojimo analizės metodai, t. y. metodų rinkinys, skirtas kintančių sąnaudų ar rezultatų vertei tirti keičiantis gamybai, vartojimui ir pan., remiantis jų analize. ribines vertes. Funkcijos ribojantis rodiklis (rodikliai) yra jos išvestinė (vieno kintamojo funkcijos atveju) arba dalinės išvestinės (jeigu funkcija iš kelių kintamųjų)

Ekonomikoje dažnai naudojami vidurkiai: vidutinis darbo našumas, vidutinės išlaidos, vidutinės pajamos, vidutinis pelnas ir kt. Tačiau dažnai reikia išsiaiškinti, kokia suma padidės rezultatas, jei padidės sąnaudos, ar atvirkščiai, kiek bus rezultatas. sumažės, jei bus sumažintos išlaidos. Neįmanoma atsakyti į šį klausimą naudojant vidutines vertes. Tokiose problemose reikia nustatyti rezultato ir sąnaudų padidėjimo santykio ribą, t.y. rasti ribinį efektą. Todėl joms išspręsti būtina naudoti diferencialinio skaičiavimo metodus.

5. Išvestinė apytiksliais skaičiavimais

5-1. Interpoliacija

Interpoliacija yra apytikslis funkcijos reikšmių apskaičiavimas iš kelių nurodytų verčių. Interpoliacija plačiai naudojama kartografijoje, geologijoje, ekonomikoje ir kituose moksluose. Paprasčiausias interpoliacijos variantas yra Lagranžo forma, tačiau kai mazginių taškų yra daug ir intervalai tarp jų dideli arba norite gauti funkciją, kurios kreivumas būtų minimalus, tuomet naudokite splaino interpoliaciją, kuri suteikia didesnį tikslumą.

Tegu K n mazginių taškų sistema a = x 0< x 1 <…< x n = b. Функция S k (x) называется сплайн-функцией S k (x) степени k≥0 на K n , если

a) S k (x) є C k -1 ()

b) S k (x) yra daugiausiai k laipsnio daugianario

Splaino funkcija Ŝ k (x) є S k (K n) vadinama interpoliuojančia splaino funkcija, jei Ŝ k (x j) = f(x j), kai j = 0,1,…,n

Aplikacijose dažnai užtenka pasirinkti k=3 ir taikyti vadinamąjį kubinė interpoliacija.

Kadangi s(x) yra trečiojo laipsnio daugianomas kiekviename daliniame intervale, tada x є

Čia s 2 j , c j 1 , c j 0 yra nežinomi, kai j = 1, 2, …, n

Pastarieji neįtraukiami dėl reikalavimo s(x j) = y j:

Diferencijuodami šią funkciją ir atsižvelgdami į tai, kad s "(x) turi būti nenutrūkstamas per visą intervalą, taigi, ypač mazguose, galiausiai gauname lygčių sistemą:

n+1 nežinomųjų atžvilgiu s 2 0 , s 2 1 ,…, s 2 n. Kad jie būtų vienareikšmiškai nustatyti, priklausomai nuo užduoties, pridedamos dar dvi lygtys:

normalus atvejis (N):

Periodinis atvejis (P) (t.y.f(x+(x n -x 0))=f(x)):

Nurodytas sienų išlyginimas:

Pavyzdys: funkcijos f(x)=sin x, n=4 spline interpoliacija.

Funkcija yra periodinė, todėl naudojame P atvejį.

Spline funkcija atrodo taip:

5-2. Taylor formulė

Funkcijų išplėtimas į begalines eilutes leidžia bet kokiu tikslumu gauti funkcijos reikšmę tam tikrame taške. Ši technika plačiai naudojama programavimo ir kitose disciplinose.

Sakoma, kad funkcija tam tikru intervalu išsiplečia į laipsnių eilutę, jei egzistuoja tokia laipsnių eilutė a 0 + a 1 (x - a) + a 2 (x - a) 2 + ... + a n (x - a) ) n + ..., kuris konverguoja į šią funkciją šiame intervale. Galima įrodyti, kad šis skilimas yra unikalus:

Tegul funkcija f(x) taške a yra be galo diferencijuota. Formos galių serija

vadinama Taylor eilute funkcijai f(x), parašyta skirtumo (x - a) laipsniais. Apskritai, kad Teiloro eilutė suartėtų su f(x), būtina ir pakanka, kad likusi eilutės dalis būtų lygi 0. Jei a = 0, Teiloro eilutė paprastai vadinama Maclaurino eilute.

I. M. Uvarenkovas,

M. Z. Malleris

Matematinės analizės kursas, v.1

V. A. Dudarenko,

A.A. Dadayanas

Matematinė analizė

Diferencialinis ir integralinis skaičiavimas

T. I. Trofimova

Fizikos kursas

O. O. Zamkovas

A. V. Tolstopyatenko

Yu. N. Čeremnychas

Matematiniai metodai ekonomikoje

A. S. Solodovnikovas

V. A. Babicevas

A. V. Brailovas

I.G. Šandra

Matematika ekonomikoje

Įvadas

1. Išvestinės sąvoka

1-1. Istorinė informacija

1-2. Darinio samprata

1-3. Diferencijavimo taisyklės ir išvestinių lentelė

2. Išvestinės geometrinė reikšmė

2-1. Kreivės liestinė

2-2. Paviršiaus liestinės plokštuma

3. Išvestinės naudojimas fizikoje

3-1. Medžiagos taško greitis

3-2. Šilumos talpa tam tikroje temperatūroje

3-3. Galia

4. Diferencialinis skaičiavimas ekonomikoje

4-1. Funkcijų tyrimas

4-2. Paklausos elastingumas

4-3. Ribų analizė

5. Išvestinė apytiksliais skaičiavimais

5-1. Interpoliacija

5-2. Taylor formulė

5-3. Apytiksliai skaičiavimai

Išvada

Naudotos literatūros sąrašas

Pietų Sachalino valstybinis universitetas

Matematikos katedra

Kursinis darbas

Tema: Praktinis išvestinės taikymas

Lektorius: Likhacheva O.N.

Južno-Sachalinskas

2002 m Įvadas

1. Išvestinės sąvoka

1-1. Istorinė informacija

Diferencialinį skaičiavimą sukūrė Niutonas ir Leibnicas XVII amžiaus pabaigoje, remdamiesi dviem problemomis:

1) apie savavališkos tiesės liestinės radimą

2) dėl greičio paieškos pagal savavališką judėjimo dėsnį

1-2. Darinio samprata

Tegul y = f(x) yra nuolatinė argumento x funkcija, apibrėžta intervale (a; b), o x0 yra savavališkas šio intervalo taškas

Argumentui x suteikiame prieaugį ∆x, tada funkcija y = f(x) gaus prieaugį ∆y = f(x + ∆x) - f(x). Riba, iki kurios santykis ∆y / ∆x yra ∆x → 0, vadinama funkcijos f(x) išvestine.

1-3. Diferencijavimo taisyklės ir išvestinių lentelė

C" = 0(xn) = nxn-1(sin x)" = cos xx" = 1(1 / x)" = -1 / x2(cos x)" = -sin x(Cu)"=Cu"( √x)" = 1 / 2√x(tg x)" = 1 / cos2 x(uv)" = u"v + uv"(ax)" = ax ln x(ctg x)" = 1 / sin2 x( u / v)"=(u"v - uv") / v2(ex)" = ex(arcsin x)" = 1 / √ (1-x2)(logax)" = (logae) / x(arccos x) " = -1 / √ (1- x2) (ln x)" = 1 / x (arctg x)" = 1 / √ (1 + x2) (arctg x)" = -1 / √ (1 + x2)

2. Išvestinės geometrinė reikšmė

2-1. Kreivės liestinė

Turėkime kreivę ir fiksuotą tašką M bei tašką N. Taško M liestinė yra tiesi linija, kurios vietą linkusi užimti styga MN, jei taškas N neribotai artėja išilgai taško N. kreivė į M.

Apsvarstykite funkciją f(x) ir šią funkciją atitinkančią kreivę y = f(x). Kai kurios reikšmės x funkcija turi reikšmę y = f(x). Šios kreivės reikšmės atitinka tašką M(x0, y0). Pateikiame naują argumentą x0 + ∆x, jo reikšmė atitinka funkcijos y0 + ∆y = f(x0 + ∆x) reikšmę. Atitinkamas taškas yra N(x0 + ∆x, y0 + ∆y). Nubraižykite sekantą MN ir φ pažymėkite sekanto suformuotą kampą su teigiama Ox ašies kryptimi. Paveikslėlyje parodyta, kad ∆y / ∆x = tg φ. Jei dabar ∆x artėja prie 0, tai taškas N judės išilgai kreivės, sekantas MN pasisuks aplink tašką M ir kampas φ pasikeis. Jei, kaip ∆x → 0, kampas φ yra linkęs į α, tai tiesė, einanti per M ir sudaranti kampą α su teigiama abscisių ašies kryptimi, bus reikalinga liestinė. Tuo pačiu metu jo nuolydžio koeficientas:

2-2. Paviršiaus liestinės plokštuma

Paviršiaus liestinė taške M yra plokštuma, kurioje yra visų paviršiaus erdvinių kreivių, einančių per M – sąlyčio tašką, liestinės.

Paimkite paviršių, pateiktą lygtimi F(x, y, z) = 0, ir kokį nors paprastą tašką M(x0, y0, z0). Paviršiuje apsvarstykite kokią nors kreivę L, einančią per M. Kreivę pateiksime lygtimis

x = φ(t); y = ψ(t); z = χ(t).

Kreivės L liestinės taške M lygtys yra tokios formos:

Kadangi skirtumai x - x0, y - y0, z - z0 yra proporcingi atitinkamiems diferencialams, galutinė plokštumos lygtis atrodo taip:

F "x (x - x0) + F" y (y - y0) + F "z (z - z0) \u003d 0

ir konkrečiu atveju z = f(x, y):

Z - z0 \u003d F "x (x - x0) + F" y (y - y0)

Pavyzdys: Raskite liestinės plokštumos hiperbolinio paraboloido taške (2a; a; 1,5a) lygtį

Sprendimas:

Z"x \u003d x / a \u003d 2; Z"y \u003d -y / a \u003d -1

Norimos plokštumos lygtis:

Z - 1,5a = 2 (x - 2a) - (Y - a) arba Z = 2x - y - 1,5a

3. Išvestinės naudojimas fizikoje

3-1. Medžiagos taško greitis

Tegul kelio s priklausomybė nuo laiko t tam tikrame materialaus taško tiesiame judėjime išreiškiama lygtimi s = f(t), o t0 yra tam tikras laiko momentas. Apsvarstykite kitą laiką t, pažymėkite ∆t = t - t0 ir apskaičiuokite kelio prieaugį: ∆s = f(t0 + ∆t) - f(t0). Santykis ∆s / ∆t vadinamas vidutiniu judėjimo greičiu per laiką ∆t, praėjusį nuo pradinio momento t0. Greitis yra šio santykio riba kaip ∆t → 0.

Vidutinis netolygaus judėjimo pagreitis intervale (t; t + ∆t) yra reikšmė =∆v / ∆t. Momentinis materialaus taško pagreitis momentu t bus vidutinio pagreičio riba:

Tai yra, pirmą kartą išvestinė (v "(t)).

Pavyzdys: Kūno nueito kelio priklausomybė nuo laiko pateikiama lygtimi s = A + Bt + Ct2 + Dt3 (C = 0,1 m/s, D = 0,03 m/s2). Nustatykite laiką po judėjimo pradžios, po kurio kūno pagreitis bus lygus 2 m/s2.

Sprendimas:

v(t) = s"(t) = B + 2Ct + 3Dt2; a(t) = v"(t) = 2C + 6Dt = 0,2 + 0,18t = 2;

1,8 = 0,18 t; t = 10 s

3-2. Medžiagos šiluminė talpa tam tikroje temperatūroje

Norėdami padidinti skirtingas temperatūras T ta pačia verte, lygia T1 - T, 1 kg. tam tikrai medžiagai reikia kitokio šilumos kiekio Q1 - Q ir santykio

nes ši medžiaga nėra pastovi. Taigi tam tikros medžiagos šilumos kiekis Q yra netiesinė temperatūros T funkcija: Q = f(T). Tada ΔQ = f(t + ΔT) - f(T). Požiūris

vadinama vidutine šilumine talpa intervale , o šios išraiškos riba esant ∆T → 0 vadinama duotosios medžiagos šilumine talpa esant T temperatūrai.

3-3. Galia

Kūno mechaninio judėjimo pasikeitimą sukelia jėgos, veikiančios jį iš kitų kūnų. Siekiant kiekybiškai apibūdinti energijos mainų tarp sąveikaujančių kūnų procesą, mechanikoje įvedama jėgos darbo samprata. Norint apibūdinti darbo tempą, įvedama galios sąvoka:

4. Diferencialinis skaičiavimas ekonomikoje

4-1. Funkcijų tyrimas

Pagal Ferma teoremą, jei taškas yra funkcijos ekstremumas, tai išvestinė jame arba neegzistuoja, arba lygi 0. Ekstremo tipą galima nustatyti pagal vieną iš pakankamų ekstremumo sąlygų:

1) Tegul funkcija f(x) yra diferencijuojama kurioje nors taško x0 kaimynystėje. Jei išvestinė f "(x) eidama per tašką x0 pakeičia ženklą iš + į -, tai x0 yra maksimalus taškas, jei nuo - iki +, tai x0 yra mažiausias taškas, jei jis nekeičia ženklo, tada ten šiuo metu nėra ekstremumas.

2) Tegul funkcija f(x) yra du kartus diferencijuojama kurioje nors taško x0 kaimynystėje, o f "(x0) = 0, f ""(x0) ≠ 0, tada taške x0 funkcija f(x0) turi maksimaliai jei

Parsisiųsti:

Peržiūra:

Skaidrių antraštės:

Peržiūra:

Skaidrių antraštės:

Taip pat skaitykite