Math-Calculator-Online v.1.0
Kalkulačka vykonáva tieto operácie: sčítanie, odčítanie, násobenie, delenie, práca s desatinnými miestami, extrahovanie odmocniny, umocnenie, výpočet percent a ďalšie operácie.
Riešenie:
Ako používať matematickú kalkulačku
| kľúč | Označenie | Vysvetlenie |
|---|---|---|
| 5 | čísla 0-9 | arabské číslice. Zadajte prirodzené celé čísla, nulu. Ak chcete získať záporné celé číslo, stlačte kláves +/- |
| . | bodkočiarka) | Oddeľovač desatinných miest. Ak pred bodkou (čiarkou) nie je žiadna číslica, kalkulačka automaticky nahradí bodku nulou. Napríklad: napíše sa 0,5 - 0,5 |
| + | znamienko plus | Sčítanie čísel (celé, desatinné zlomky) |
| - | znamienko mínus | Odčítanie čísel (celé, desatinné zlomky) |
| ÷ | deliaci znak | Delenie čísel (celé, desatinné zlomky) |
| X | znak násobenia | Násobenie čísel (celé čísla, desatinné miesta) |
| √ | koreň | Extrahovanie koreňa z čísla. Po opätovnom stlačení tlačidla "root" sa z výsledku vypočíta koreň. Napríklad: druhá odmocnina z 16 = 4; druhá odmocnina zo 4 = 2 |
| x2 | kvadratúra | Umocnenie čísla. Keď znova stlačíte tlačidlo "štvorce", výsledok sa odmocní. Napríklad: štvorec 2 = 4; štvorec 4 = 16 |
| 1/x | zlomok | Výstup na desatinné miesta. V čitateli 1 v menovateli vstupné číslo |
| % | percent | Získajte percento z čísla. Ak chcete pracovať, musíte zadať: číslo, z ktorého sa vypočíta percento, znamienko (plus, mínus, delenie, násobenie), koľko percent v číselnej forme, tlačidlo "%" |
| ( | otvorená konzola | Otvorená zátvorka na nastavenie priority hodnotenia. Vyžaduje sa uzavretá zátvorka. Príklad: (2+3)*2=10 |
| ) | uzavretá konzola | Uzavretá zátvorka na nastavenie priority hodnotenia. Povinná otvorená zátvorka |
| ± | plus mínus | Zmení znamienko na opačné |
| = | rovná sa | Zobrazí výsledok riešenia. Medzivýpočty a výsledok sa tiež zobrazujú nad kalkulačkou v poli "Riešenie". |
| ← | vymazanie postavy | Vymaže posledný znak |
| OD | resetovať | Tlačidlo reštart. Úplne resetuje kalkulačku na "0" |
Algoritmus online kalkulačky s príkladmi
Doplnenie.
Sčítanie celého čísla prirodzené čísla { 5 + 7 = 12 }
Pridanie celých prírodných a záporné čísla { 5 + (-2) = 3 }
Desatinné sčítanie zlomkové čísla { 0,3 + 5,2 = 5,5 }
Odčítanie.
Odčítanie celých prirodzených čísel ( 7 - 5 = 2 )
Odčítanie celých prirodzených a záporných čísel ( 5 - (-2) = 7 )
Odčítanie desatinných zlomkových čísel ( 6,5 - 1,2 = 4,3 )
Násobenie.
Súčin celých prirodzených čísel ( 3 * 7 = 21 )
Súčin celých prirodzených a záporných čísel ( 5 * (-3) = -15 )
Súčin desatinných zlomkových čísel ( 0,5 * 0,6 = 0,3 )
divízie.
Delenie celých prirodzených čísel ( 27 / 3 = 9 )
Delenie celých prirodzených a záporných čísel ( 15 / (-3) = -5 )
Delenie desatinných zlomkových čísel ( 6,2 / 2 = 3,1 )
Extrahovanie koreňa z čísla.
Extrahovanie koreňa celého čísla ( root(9) = 3 )
Extrahovanie odmocniny desatinných miest ( odmocnina (2.5) = 1.58 )
Extrahovanie koreňa zo súčtu čísel ( root(56 + 25) = 9)
Extrahovanie odmocniny z rozdielu čísel ( odmocnina (32 - 7) = 5)
Umocnenie čísla.
Umocnenie celého čísla ( (3) 2 = 9 )
Umocnenie desatinných miest ( (2,2) 2 = 4,84 )
Previesť na desatinné zlomky.
Výpočet percent čísla
Zvýšiť 230 o 15 % ( 230 + 230 * 0,15 = 264,5 )
Znížiť číslo 510 o 35 % ( 510 - 510 * 0,35 = 331,5 )
18 % z čísla 140 je ( 140 * 0,18 = 25,2 )
Farafonová Natália Igorevna
Po absolvovaní témy „Akcie s desatinnými zlomkami“ na precvičenie zručností počítania a kontrolu asimilácie materiálu môžete individuálna práca so študentmi na kartičkách. Každý žiak musí splniť všetky úlohy bez chýb. Pre každú akciu je prezentovaných veľa možností, čo umožňuje každému študentovi vyriešiť úlohu pre každú akciu s desatinnými zlomkami niekoľkokrát a dosiahnuť bezchybný výsledok alebo dokončiť úlohu s minimálnym počtom chýb. Keďže každý žiak plní individuálnu úlohu, učiteľ má možnosť tak, ako sú mu predložené splnené úlohy, s každým žiakom o nich osobne diskutovať. Ak žiak urobil chyby, učiteľ ich opraví a ponúkne vykonanie úlohy z inej možnosti. Teda, kým študent nesplní celú úlohu alebo jej väčšinu bez chýb. Karty sa najlepšie robia na farebnom papieri.
V poslednej fáze práce môžeme ponúknuť riešenie príkladu obsahujúceho niekoľko akcií.
Za každú správne dokončenú možnosť, bez ohľadu na pokus, pri ktorom bola úloha dokončená správne, môžu študenti dostať známku výborná, po dokončení celej práce môžete podľa uváženia učiteľa nastaviť priemernú známku.
Pridávanie desatinných miest.
1 možnosť
7,468 + 2,85
9,6 + 0,837
38,64 + 8,4
3,9 + 26,117
Možnosť 2
19,45 + 34,8
4,9 + 0,716
75,86 + 4,2
5,6 + 44,408
3 možnosť
24,38 + 7,9
6,5 + 0,952
48,59 + 1,8
35,906 + 2,8
4 možnosť
7,6 + 319,75
888,99 + 4,5
64,15 + 18,9
4,5 + 0,738
5 možnosť
7,62 + 8,9
25,38 + 0,09
12,842 + 8,6
412 + 78,83
6 možnosť
70,7 + 3,8645
3,65 + 0,89
61,22 + 31.719
12,842 + 8,6
Odpovede: 1. možnosť: 10,318; 10,437; 47,04; 30,017;
Možnosť 2: 54,25; 5,616; 80,06; 50,008;
3. možnosť: 32,28; 7,452; 50,19; 38,706;
4. možnosť: 327,35; 893,49; 83,05; 5,238;
5. možnosť: 16,52; 25,47; 21,442; 490,83;
6 možnosť: 74,5645; 4,54; 92,939; 21,442;
Odčítanie desatinných miest.
1 možnosť
26,38 - 9,69
41,12 - 8,6
5,2 - 3,445
7 - 0,346
Možnosť 2
47,62 - 8,78
54,06 - 9,1
7,1 - 6,346
3 - 1,551
3 možnosť
50,41 - 9,62
72,03 - 6,3
9,2 - 5,453
4 - 2,662
4 možnosť
60,01 - 8,364
123,61 - 69,8
8,7 - 4,915
10 - 3,817
5 možnosť
6,52 - 3,8
7,41 - 0,758
67,351 - 9,7
22 - 0,618
6 možnosť
4,5 - 0,496
61,3 - 20,3268
24,7 - 15,276
50 - 2,38
Odpovede: 1 možnosť: 16,69; 32,52; 1,755; 6,654;
Možnosť 2: 38,84; 44,96; 0,754; 1,449;
3. možnosť: 40,79; 65,73; 3,747; 1,338;
4. možnosť: 51,646; 53,81; 3,785; 6,183;
5. možnosť: 2,72; 6,652; 57,651; 21,382;
6 možnosť: 4,004; 40,9732; 9,424; 47,62;
Násobenie desatinných miest.
1 možnosť
7,4 3,5
20.2 3.04
0,68 0,65
2,5 840
Možnosť 2
2,8 9,7
6.05 7.08
0,024 0,35
560 3.4
3 možnosť
6,8 5,9
6.06 8.05
0,65 0,014
720 4.6
4 možnosť
34,7 8,4
9.06 7.08
0,038 0,29
3,6 540
5 možnosť
62,4 2,5
0,038 9
1,8 0,009
4,125 0,16
6 možnosť
0,28 45
20.6 30.5
2,3 0,0024
0,0012 0,73
7 možnosť
68 0,15
0,08 0,012
1,4 1,04
0,32 2,125
8 možnosť
4,125 0,16
0,0012 0,73
1,4 1,04
720 4.6
Odpovede: 1. možnosť: 25,9; 61,408; 0,442; 2100;
Možnosť 2: 27,16; 42,834; 0,0084; 1904;
3. možnosť: 40,12; 48,783; 0,0091; 3312;
4. možnosť: 291,48; 64,1448; 0,01102; 1944;
5. možnosť: 156; 0,342; 0,0162; 0,66;
6 možnosť: 12,6; 628,3; 0,00552; 0,000876;
7 možnosť: 10,2; 0,00096; 1,456; 0,68;
8 možnosť: 0,66; 0,000876; 1,456; 3312;
Delenie desatinného čísla prirodzeným číslom.
1 možnosť
62,5: 25
0,5: 25
9,6: 12
1,08: 8
Možnosť 2
0,28: 7
0,2: 4
16,9: 13
22,5: 15
3 možnosť
0,75: 15
0,7: 35
1,6: 8
0,72: 6
4 možnosť
2,4: 6
1,5: 75
0,12: 4
1,69: 13
5 možnosť
3,5: 175
1,8: 24
10,125: 9
0,48: 16
6 možnosť
0,35: 7
1,2: 3
0,2: 5
7,2: 144
7 možnosť
151,2: 63
4,8: 32
0,7: 25
2,3: 40
8 možnosť
397,8: 78
5,2: 65
0,9: 750
3,4: 80
9 možnosť
478,8: 84
7,3: 4
0,6: 750
5,7: 80
10 možnosť
699,2: 92
1,8: 144
0,7: 875
6,3: 24
Odpovede: 1 možnosť: 2,5; 0,02; 0,8; 0,135;
Možnosť 2: 0,04; 0,05; 1,3; 1,5;
3. možnosť: 0,05; 0,02; 0,2; 0,12;
4. možnosť: 0,4; 0,02; 0,03; 0,13;
5. možnosť: 0,02; 0,075; 1,125; 0,03;
6 možnosť: 0,05; 0,4; 0,04; 0,05;
7 možnosť: 2,4; 0,15; 0,28; 0,0575;
8 možnosť: 5.1; 0,08; 0,0012; 0,0425;
9 možnosť: 5,7; 1,825; 0,0008; 0,07125;
10 možnosť: 7,6; 0,0125; 0,0008; 0,2625;
Rozdelenie podľa desiatkový.
1 možnosť
32: 1,25
54: 12,5
6: 125
Možnosť 2
50,02: 6,1
34,2: 9,5
67,6: 6,5
3 možnosť
2,8036: 0,4
3,1: 0,025
0,0008: 0,16
4 možnosť
4: 32
303: 75
687,4: 10
1,59: 100
5 možnosť
5: 16
336: 35
412,5: 10
24,3: 100
6 možnosť
41,82: 6,8
73,44: 3,6
7,2: 0,045
32,89: 4,6
Odpovede: 1. možnosť: 25,6; 4,32; 0,048;
Možnosť 2: 8,2; 3,6; 10,4;
3. možnosť: 7,009; 124; 0,005;
4. možnosť: 0,125; 4,04; 68,74; 0,0159;
5. možnosť: 0,3125; 9,6; 41,25; 0,243;
6 možnosť: 6,15; 20,4; 160; 7,15;
Spoločné akcie s desatinnými zlomkami.
824,72 - 475: (0,071 + 0,929) + 13,8
(7 351 + 12 649) 105 – 95,48 – 4,52
(3,82 – 1,084 + 12,264) (4,27 + 1,083 – 3,353) + 83
278 - 16,7 - (15,75 + 24,328 + 39,2)
57,18 42 – 74,1: 13 + 21,35: 7
(18,8: 16 + 9,86 3) 40 - 12,73
(2 – 0,25 0,8) : (0,16: 0,5 – 0,02)
(3,625 + 0,25 + 2,75) : (28,75 + 92,25 - 15) : 0,0625
Odpovede: 1) 363,52; 2) 2000; 3) 113; 4) 182,022; 5) 2398,91; 6) 1217,47; 7) 6; 8) 1.
Z mnohých zlomkov nájdených v aritmetike si zvláštnu pozornosť zaslúžia tie, ktoré majú v menovateli 10, 100, 1000 – vo všeobecnosti akákoľvek mocnina desiatky. Tieto zlomky majú špeciálny názov a zápis.
Desatinné číslo je akékoľvek číslo, ktorého menovateľom je mocnina desať.
Desatinné príklady:
Prečo bolo vôbec potrebné izolovať takéto frakcie? Prečo potrebujú vlastný vstupný formulár? Sú na to minimálne tri dôvody:
- Desatinné čísla sa porovnávajú oveľa jednoduchšie. Pamätajte: na porovnanie bežných zlomkov je potrebné ich od seba odčítať a najmä priviesť zlomky k spoločnému menovateľovi. V desatinných zlomkoch sa nič z toho nevyžaduje;
- Zníženie výpočtov. Desatinné miesta sčítavajú a násobia podľa vlastných pravidiel a po troche cviku s nimi budete pracovať oveľa rýchlejšie ako s obyčajnými;
- Jednoduchosť nahrávania. Na rozdiel od bežných zlomkov sa desatinné miesta píšu na jeden riadok bez straty prehľadnosti.
Väčšina kalkulačiek dáva odpovede aj v desatinných číslach. V niektorých prípadoch môže iný formát záznamu spôsobiť problémy. Napríklad, čo ak požadujete zmenu vo výške 2/3 rubľov v obchode :)
Pravidlá zápisu desatinných zlomkov
Hlavnou výhodou desatinných zlomkov je pohodlný a vizuálny zápis. menovite:
Desatinný zápis je forma desatinného zápisu kde celú časť sa oddeľuje od zlomku pravidelnou bodkou alebo čiarkou. V tomto prípade sa samotný oddeľovač (bodka alebo čiarka) nazýva desatinná čiarka.
Napríklad 0,3 (čítaj: „nulové celé číslo, 3 desatiny“); 7,25 (7 celých čísel, 25 stotín); 3,049 (3 celé čísla, 49 tisícin). Všetky príklady sú prevzaté z predchádzajúcej definície.
Pri písaní sa ako desatinná čiarka zvyčajne používa čiarka. Tu a nižšie sa čiarka použije aj na celom webe.
Ak chcete zapísať ľubovoľný desatinný zlomok v určenom tvare, musíte vykonať tri jednoduché kroky:
- Vypíšte samostatne čitateľa;
- Posuňte desatinnú čiarku doľava o toľko miest, koľko je núl v menovateli. Predpokladajme, že na začiatku je desatinná čiarka napravo od všetkých číslic;
- Ak sa desatinná čiarka posunula a za ňou sú na konci záznamu nuly, treba ich prečiarknuť.
Stáva sa, že v druhom kroku čitateľ nemá dostatok číslic na dokončenie posunu. V tomto prípade sú chýbajúce pozície vyplnené nulami. A vo všeobecnosti je možné priradiť ľubovoľný počet núl naľavo od akéhokoľvek čísla bez poškodenia zdravia. Je to škaredé, ale niekedy užitočné.
Na prvý pohľad sa tento algoritmus môže zdať dosť komplikovaný. V skutočnosti je všetko veľmi, veľmi jednoduché - stačí trochu cvičiť. Pozrite si príklady:
Úloha. Pre každý zlomok uveďte jeho desatinný zápis:
Čitateľ prvého zlomku: 73. Desatinnú čiarku posunieme o jedno znamienko (pretože menovateľ je 10) - dostaneme 7,3.
Čitateľ druhého zlomku: 9. Desatinnú čiarku posunieme o dve číslice (pretože menovateľ je 100) - dostaneme 0,09. Musel som pridať jednu nulu za desatinnú čiarku a ešte jednu pred ňu, aby som nezanechal zvláštny zápis ako „.09“.
Čitateľ tretieho zlomku: 10029. Desatinnú čiarku posunieme o tri číslice (pretože menovateľ je 1000) - dostaneme 10,029.
Čitateľ posledného zlomku: 10500. Bod opäť posunieme o tri číslice - dostaneme 10,500. Na konci čísla sú nuly navyše. Prečiarkneme ich – dostaneme 10,5.
Venujte pozornosť posledným dvom príkladom: číslam 10,029 a 10,5. Podľa pravidiel musia byť nuly vpravo prečiarknuté, ako sa to robí v poslednom príklade. V žiadnom prípade to však nerobte s nulami, ktoré sú vo vnútri čísla (ktoré sú obklopené inými číslicami). Preto sme dostali 10,029 a 10,5, a nie 1,29 a 1,5.
Takže sme prišli na definíciu a formu zaznamenávania desatinných zlomkov. Teraz poďme zistiť, ako previesť bežné zlomky na desatinné miesta - a naopak.
Zmena zo zlomkov na desatinné miesta
Uvažujme jednoduchý číselný zlomok tvaru a/b. Môžete použiť základnú vlastnosť zlomku a vynásobiť čitateľa a menovateľa takým číslom, aby ste dostali mocninu desať nižšie. Predtým si však prečítajte nasledujúce informácie:
Existujú menovatele, ktoré sa neredukujú na mocninu desiatich. Naučte sa rozpoznávať takéto zlomky, pretože s nimi nie je možné pracovať podľa nižšie opísaného algoritmu.
To je všetko. Ako pochopiť, či je menovateľ znížený na desať alebo nie?
Odpoveď je jednoduchá: zohľadnite menovateľa hlavné faktory. Ak sú v expanzii prítomné iba faktory 2 a 5, toto číslo možno znížiť na mocninu desať. Ak existujú iné čísla (3, 7, 11 - čokoľvek), na stupeň desať môžete zabudnúť.
Úloha. Skontrolujte, či je možné špecifikované zlomky reprezentovať ako desatinné miesta:
Vypíšeme a rozkladáme menovateľov týchto zlomkov:
20 \u003d 4 5 \u003d 2 2 5 - prítomné sú iba čísla 2 a 5. Preto môže byť zlomok znázornený ako desatinné číslo.
12 \u003d 4 3 \u003d 2 2 3 - existuje „zakázaný“ faktor 3. Zlomok nemožno reprezentovať ako desatinné číslo.
640 \u003d 8 8 10 \u003d 2 3 2 3 2 5 \u003d 2 7 5. Všetko je v poriadku: okrem čísel 2 a 5 nie je nič. Zlomok je znázornený ako desatinné číslo.
48 \u003d 6 8 \u003d 2 3 2 3 \u003d 2 4 3. Znova sa „vynoril“ faktor 3. Nemožno ho reprezentovať ako desatinný zlomok.
Takže sme prišli na menovateľa - teraz zvážime celý algoritmus na prepnutie na desatinné zlomky:
- Faktorizujte menovateľ pôvodného zlomku a uistite sa, že je vo všeobecnosti reprezentovateľný ako desatinné číslo. Tie. skontrolujte, či sú v expanzii prítomné iba faktory 2 a 5. V opačnom prípade algoritmus nefunguje;
- Spočítajte, koľko dvojiek a pätiek je prítomných v rozklade (nebudú tam žiadne iné čísla, pamätáte?). Vyberte si takú dodatočnú násobilku, aby sa počet dvojiek a pätiek rovnal.
- Vlastne vynásobte čitateľa a menovateľa pôvodného zlomku týmto faktorom – dostaneme požadované zobrazenie, t.j. menovateľom bude mocnina desať.
Samozrejme aj doplnkový faktor sa rozloží len na dvojky a päťky. Zároveň, aby ste si nekomplikovali život, mali by ste si zo všetkých možných vybrať ten najmenší takýto faktor.
A ešte jedna vec: ak je v pôvodnom zlomku celočíselná časť, nezabudnite tento zlomok previesť na nesprávny - a až potom použiť opísaný algoritmus.
Úloha. Preveďte tieto čísla na desatinné miesta:
Rozložme menovateľa prvého zlomku na faktor: 4 = 2 · 2 = 2 2 . Preto môže byť zlomok reprezentovaný ako desatinné číslo. V expanzii sú dve dvojky a žiadne päťky, takže dodatočný faktor je 5 2 = 25. Počet dvojok a pätiek sa mu bude rovnať. Máme:
Teraz sa poďme zaoberať druhým zlomkom. Za týmto účelom si všimnite, že 24 \u003d 3 8 \u003d 3 2 3 - v expanzii je trojica, takže zlomok nemôže byť reprezentovaný ako desatinné číslo.
Posledné dva zlomky majú menovateľov 5 (prvočíslo) a 20 = 4 5 = 2 2 5 – všade sú len dvojky a päťky. Zároveň v prvom prípade „pre úplné šťastie“ nie je dostatok multiplikátora 2 a v druhom - 5. Dostávame:
Prechod z desatinných miest na bežné
Spätný prevod - z desiatkového zápisu na normálny - je oveľa jednoduchší. Neexistujú žiadne obmedzenia a špeciálne kontroly, takže desatinný zlomok môžete vždy previesť na klasický „dvojposchodový“.
Algoritmus prekladu je nasledujúci:
- Prečiarknite všetky nuly na ľavej strane desatinnej čiarky, ako aj desatinnú čiarku. Toto bude čitateľ požadovaného zlomku. Hlavná vec - nepreháňajte to a neprečiarknite vnútorné nuly obklopené inými číslami;
- Vypočítajte, koľko číslic je v pôvodnom desatinnom zlomku za desatinnou čiarkou. Vezmite číslo 1 a pridajte toľko núl doprava, koľko ste spočítali znakov. Toto bude menovateľ;
- Vlastne zapíšte zlomok, ktorého čitateľa a menovateľa sme práve našli. Ak je to možné, znížte. Ak v pôvodnom zlomku bola celočíselná časť, teraz dostaneme nesprávny zlomok, ktorý je veľmi vhodný pre ďalšie výpočty.
Úloha. Previesť desatinné miesta na obyčajné: 0,008; 3,107; 2,25; 7,2008.
Naľavo prečiarkneme nuly a čiarky - dostaneme nasledujúce čísla (budú to čitatelia): 8; 3107; 225; 72008.
V prvom a druhom zlomku za desatinnou čiarkou sú 3 desatinné miesta, v druhom - 2 a v treťom - až 4 desatinné miesta. Dostaneme menovateľov: 1000; 1000; 100; 10 000.
Nakoniec spojme čitateľov a menovateľov do obyčajných zlomkov:

Ako je zrejmé z príkladov, výsledný podiel sa môže veľmi často znížiť. Ešte raz poznamenávam, že každý desatinný zlomok môže byť reprezentovaný ako obyčajný. Opačná transformácia nie je vždy možná.
V tomto návode sa pozrieme na každú z týchto operácií jednu po druhej.
Obsah lekciePridávanie desatinných miest
Ako vieme, desatinný zlomok pozostáva z celočíselnej časti a zlomkovej časti. Pri pridávaní desatinných miest sa celé číslo a zlomkové časti pridávajú oddelene.
Pridajme napríklad desatinné miesta 3,2 a 5,3. Je vhodnejšie pridať desatinné zlomky do stĺpca.
Najprv si tieto dva zlomky zapíšeme do stĺpca, pričom celé časti musia byť pod celými časťami a zlomkové pod zlomkové. V škole je táto požiadavka tzv "čiarka pod čiarkou" .
Zlomky napíšeme do stĺpca tak, aby bola čiarka pod čiarkou:
Sčítame zlomkové časti: 2 + 3 = 5. Päť zapíšeme do zlomkovej časti našej odpovede:
Teraz spočítame celé časti: 3 + 5 = 8. Osem zapíšeme do celočíselnej časti našej odpovede:
Teraz oddelíme celočíselnú časť od zlomkovej časti čiarkou. Aby sme to dosiahli, opäť sa riadime pravidlom "čiarka pod čiarkou" :
Odpoveď som dostal 8.5. Takže výraz 3,2 + 5,3 sa rovná 8,5
3,2 + 5,3 = 8,5
V skutočnosti nie je všetko také jednoduché, ako sa na prvý pohľad zdá. Aj tu sú úskalia, o ktorých si teraz povieme.
Miesta v desatinných číslach
Desatinné čísla, rovnako ako bežné čísla, majú svoje vlastné číslice. Toto sú desiate miesta, sté miesta, tisíciny. V tomto prípade číslice začínajú za desatinnou čiarkou.
Prvá číslica za desatinnou čiarkou zodpovedá za desatinné miesto, druhá číslica za desatinnou čiarkou za desatinné miesto, tretia číslica za desatinnou čiarkou za tisícinu.
Číslice v desatinných zlomkoch ukladajú niektoré užitočná informácia. Predovšetkým uvádzajú, koľko desatín, stotín a tisícin je v desatinnej čiarke.
Uvažujme napríklad desatinné číslo 0,345
Pozícia, kde sa nachádza trojka, je tzv desiate miesto
Pozícia, kde sa štvorka nachádza, sa nazýva stotinové miesto
Pozícia, kde sa nachádza päťka, sa nazýva tisíciny

Pozrime sa na tento údaj. Vidíme, že v kategórii desatiniek je trojka. To naznačuje, že v desatinnom zlomku 0,345 sú tri desatiny.
Ak sčítame zlomky, dostaneme pôvodný desatinný zlomok 0,345

Najprv sme dostali odpoveď, ale previedli sme ju na desatinné číslo a dostali sme 0,345.
Pri pridávaní desatinných miest platia rovnaké pravidlá ako pri pridávaní obyčajných čísel. Sčítanie desatinných zlomkov prebieha po čísliciach: desatiny sa pripočítavajú k desatinám, stotiny k stotinám, tisíciny k tisícinám.
Preto pri pridávaní desatinných zlomkov je potrebné dodržiavať pravidlo "čiarka pod čiarkou". Čiarka pod čiarkou poskytuje rovnaké poradie, v ktorom sa pridávajú desatiny k desatinám, stotiny až stotiny, tisíciny až tisíciny.
Príklad 1 Nájdite hodnotu výrazu 1,5 + 3,4
Najprv sčítame zlomkové časti 5 + 4 = 9. Deväť zapíšeme do zlomkovej časti našej odpovede:
Teraz spočítame celé časti 1 + 3 = 4. Zapíšeme štyri v celočíselnej časti našej odpovede:
Teraz oddelíme celočíselnú časť od zlomkovej časti čiarkou. Aby sme to dosiahli, opäť dodržiavame pravidlo „čiarka pod čiarkou“:
Odpoveď som dostal 4.9. Takže hodnota výrazu 1,5 + 3,4 je 4,9
Príklad 2 Nájdite hodnotu výrazu: 3,51 + 1,22
Tento výraz zapíšeme do stĺpca, pričom dodržíme pravidlo „čiarka pod čiarkou“
Najprv pridajte zlomkovú časť, konkrétne stotiny 1+2=3. Trojku píšeme v stotej časti našej odpovede:
Teraz pridajte desatiny 5+2=7. Sedem si zapíšeme do desiatej časti našej odpovede:
Teraz pridajte celé časti 3+1=4. Zapíšeme štyri v celej časti našej odpovede:
Celú časť oddeľujeme od zlomkovej časti čiarkou, pričom dodržiavame pravidlo „čiarka pod čiarkou“:
Dostal som odpoveď 4,73. Takže hodnota výrazu 3,51 + 1,22 je 4,73
3,51 + 1,22 = 4,73
Rovnako ako pri obyčajných číslach, pri sčítaní desatinných zlomkov platí . V tomto prípade sa do odpovede zapíše jedna číslica a zvyšok sa prenesie na ďalšiu číslicu.
Príklad 3 Nájdite hodnotu výrazu 2,65 + 3,27
Tento výraz zapíšeme do stĺpca:
Pridajte stotiny 5+7=12. Číslo 12 sa nezmestí do stotiny našej odpovede. Preto v stotej časti napíšeme číslo 2 a prenesieme jednotku na ďalší bit:
Teraz sčítame desatiny 6+2=8 plus jednotku, ktorú sme dostali z predchádzajúcej operácie, dostaneme 9. Do desatiny našej odpovede napíšeme číslo 9:
Teraz pridajte celé časti 2+3=5. Do celočíselnej časti našej odpovede napíšeme číslo 5:
Dostali sme odpoveď 5,92. Takže hodnota výrazu 2,65 + 3,27 je 5,92
2,65 + 3,27 = 5,92
Príklad 4 Nájdite hodnotu výrazu 9,5 + 2,8
Napíšte tento výraz do stĺpca
Sčítame zlomkové časti 5 + 8 = 13. Číslo 13 sa nezmestí do zlomkovej časti našej odpovede, preto si najskôr zapíšeme číslo 3, a jednotku prenesieme na ďalšiu číslicu, alebo radšej prenesieme na celé číslo. časť:
Teraz sčítame celé časti 9+2=11 plus jednotku, ktorú sme dostali z predchádzajúcej operácie, dostaneme 12. Do celočíselnej časti našej odpovede napíšeme číslo 12:
Celú časť oddeľte od zlomkovej časti čiarkou:
Odpoveď som dostal 12.3. Takže hodnota výrazu 9,5 + 2,8 je 12,3
9,5 + 2,8 = 12,3
Pri sčítavaní desatinných zlomkov musí byť počet číslic za desatinnou čiarkou v oboch zlomkoch rovnaký. Ak nie je dostatok číslic, potom sú tieto miesta v zlomkovej časti vyplnené nulami.
Príklad 5. Nájdite hodnotu výrazu: 12,725 + 1,7
Pred napísaním tohto výrazu do stĺpca urobme rovnaký počet číslic za desatinnou čiarkou v oboch zlomkoch. Desatinný zlomok 12,725 má za desatinnou čiarkou tri číslice, zatiaľ čo zlomok 1,7 iba jednu. Takže v zlomku 1,7 na konci musíte pridať dve nuly. Potom dostaneme zlomok 1 700. Teraz môžete tento výraz zapísať do stĺpca a začať počítať:

Pridajte tisíciny 5+0=5. Číslo 5 napíšeme do tisíciny našej odpovede:

Pridajte stotiny 2+0=2. Číslo 2 napíšeme do stej časti našej odpovede:

Pridajte desatiny 7+7=14. Číslo 14 sa nezmestí do desatiny našej odpovede. Preto si najprv zapíšeme číslo 4 a prenesieme jednotku na ďalší bit:

Teraz sčítame celé časti 12+1=13 plus jednotku, ktorú sme dostali z predchádzajúcej operácie, dostaneme 14. Do celočíselnej časti našej odpovede napíšeme číslo 14:

Celú časť oddeľte od zlomkovej časti čiarkou:

Dostal som odpoveď 14 425. Takže hodnota výrazu 12,725+1,700 je 14,425
12,725+ 1,700 = 14,425
Odčítanie desatinných miest
Pri odčítaní desatinných zlomkov musíte dodržiavať rovnaké pravidlá ako pri pridávaní: „čiarka pod čiarkou“ a „rovnaký počet číslic za desatinnou čiarkou“.
Príklad 1 Nájdite hodnotu výrazu 2,5 − 2,2
Tento výraz zapíšeme do stĺpca, pričom dodržíme pravidlo „čiarka pod čiarkou“:
Vypočítame zlomkovú časť 5−2=3. V desiatej časti našej odpovede píšeme číslo 3:
Vypočítajte časť celého čísla 2−2=0. Do celočíselnej časti našej odpovede napíšeme nulu:
Celú časť oddeľte od zlomkovej časti čiarkou:
Dostali sme odpoveď 0,3. Takže hodnota výrazu 2,5 − 2,2 sa rovná 0,3
2,5 − 2,2 = 0,3
Príklad 2 Nájdite hodnotu výrazu 7,353 - 3,1
V tomto výraze iná sumačíslice za desatinnou čiarkou. V zlomku 7,353 sú za desatinnou čiarkou tri číslice a v zlomku 3,1 len jedna. To znamená, že v zlomku 3.1 treba na koniec pridať dve nuly, aby bol počet číslic v oboch zlomkoch rovnaký. Potom dostaneme 3100.
Teraz môžete tento výraz napísať do stĺpca a vypočítať ho:

Dostal som odpoveď 4,253. Takže hodnota výrazu 7,353 − 3,1 je 4,253
7,353 — 3,1 = 4,253
Rovnako ako pri bežných číslach, niekedy si budete musieť požičať jedno zo susedného bitu, ak odčítanie nebude možné.
Príklad 3 Nájdite hodnotu výrazu 3,46 − 2,39
Odčítajte stotiny 6-9. Od čísla 6 neodčítajte číslo 9. Preto musíte zobrať jednotku zo susednej číslice. Po požičaní jedničky zo susednej číslice sa číslo 6 zmení na číslo 16. Teraz môžeme vypočítať stotiny z 16−9=7. Sedem zapíšeme do stej časti našej odpovede:
Teraz odpočítajte desatiny. Keďže sme brali jednu jednotku v kategórii desatiny, číslo, ktoré sa tam nachádzalo, sa znížilo o jednotku. Inými slovami, desiate miesto teraz nie je číslo 4, ale číslo 3. Vypočítajme desatiny z 3−3=0. V desiatej časti našej odpovede píšeme nulu:
Teraz odčítajte časti celého čísla 3−2=1. Jednotku zapíšeme do celočíselnej časti našej odpovede:
Celú časť oddeľte od zlomkovej časti čiarkou:
Dostal som odpoveď 1.07. Takže hodnota výrazu 3,46−2,39 sa rovná 1,07
3,46−2,39=1,07
Príklad 4. Nájdite hodnotu výrazu 3−1.2
Tento príklad odpočítava desatinné číslo od celého čísla. Napíšme tento výraz do stĺpca tak, aby celá časť desatinného zlomku 1,23 bola pod číslom 3
Teraz urobme rovnaký počet číslic za desatinnou čiarkou. Ak to chcete urobiť, za číslom 3 vložte čiarku a pridajte jednu nulu:
Teraz odčítajte desatiny: 0-2. Od nuly neodčítajte číslo 2. Preto je potrebné vziať jednotku zo susednej číslice. Požičaním jedničky zo susednej číslice sa 0 zmení na číslo 10. Teraz môžete vypočítať desatiny z 10−2=8. Osem si zapíšeme do desiatej časti našej odpovede:
Teraz odčítajte celé časti. Predtým sa číslo 3 nachádzalo v celom čísle, ale jednu jednotku sme si z neho požičali. V dôsledku toho sa zmenil na číslo 2. Preto odpočítame 1 od 2. 2−1=1. Jednotku zapíšeme do celočíselnej časti našej odpovede:
Celú časť oddeľte od zlomkovej časti čiarkou:
Odpoveď som dostal 1.8. Takže hodnota výrazu 3−1,2 je 1,8
Desatinné násobenie
Násobenie desatinných miest je jednoduché a dokonca zábavné. Ak chcete násobiť desatinné miesta, musíte ich vynásobiť ako bežné čísla, pričom čiarky ignorujte.
Po prijatí odpovede je potrebné oddeliť celú časť od zlomkovej časti čiarkou. Ak to chcete urobiť, musíte spočítať počet číslic za desatinnou čiarkou v oboch zlomkoch, potom spočítať rovnaký počet číslic vpravo v odpovedi a dať čiarku.
Príklad 1 Nájdite hodnotu výrazu 2,5 × 1,5
Tieto desatinné zlomky vynásobíme ako obyčajné čísla, čiarky ignorujeme. Ak chcete čiarky ignorovať, môžete si dočasne predstaviť, že úplne chýbajú:

Dostali sme 375. V tomto čísle je potrebné oddeliť celú časť od zlomkovej časti čiarkou. Aby ste to dosiahli, musíte spočítať počet číslic za desatinnou čiarkou v zlomkoch 2,5 a 1,5. V prvom zlomku je za desatinnou čiarkou jedna číslica, v druhom zlomku je tiež jedna. Celkovo dve čísla.
Vraciame sa k číslu 375 a začíname sa pohybovať sprava doľava. Musíme spočítať dve číslice sprava a dať čiarku:

Dostal som odpoveď 3,75. Takže hodnota výrazu 2,5 × 1,5 je 3,75
2,5 x 1,5 = 3,75
Príklad 2 Nájdite hodnotu výrazu 12,85 × 2,7
Vynásobme tieto desatinné miesta, pričom čiarky ignorujeme:

Dostali sme 34695. V tomto čísle musíte oddeliť celú časť od zlomkovej časti čiarkou. Aby ste to dosiahli, musíte vypočítať počet číslic za desatinnou čiarkou v zlomkoch 12,85 a 2,7. V zlomku 12,85 sú za desatinnou čiarkou dve číslice, v zlomku 2,7 jedna číslica - spolu tri číslice.
Vraciame sa k číslu 34695 a začíname sa pohybovať sprava doľava. Musíme spočítať tri číslice sprava a dať čiarku:

Dostal som odpoveď 34 695. Takže hodnota výrazu 12,85 × 2,7 je 34,695
12,85 x 2,7 = 34,695
Násobenie desatinného čísla obyčajným číslom
Niekedy nastanú situácie, keď potrebujete vynásobiť desatinný zlomok bežným číslom.
Ak chcete vynásobiť desatinné a obyčajné číslo, musíte ich vynásobiť bez ohľadu na čiarku v desatinnej čiarke. Po prijatí odpovede je potrebné oddeliť celú časť od zlomkovej časti čiarkou. Ak to chcete urobiť, musíte spočítať počet číslic za desatinnou čiarkou v desatinnom zlomku, potom v odpovedi spočítať rovnaký počet číslic vpravo a dať čiarku.
Napríklad vynásobte 2,54 číslom 2
Desatinný zlomok 2,54 vynásobíme obvyklým číslom 2, pričom čiarku ignorujeme:

Dostali sme číslo 508. V tomto čísle je potrebné oddeliť časť celého čísla od zlomkovej časti čiarkou. Aby ste to dosiahli, musíte spočítať počet číslic za desatinnou čiarkou v zlomku 2,54. Zlomok 2,54 má za desatinnou čiarkou dve číslice.
Vraciame sa k číslu 508 a začíname sa pohybovať sprava doľava. Musíme spočítať dve číslice sprava a dať čiarku:

Odpoveď som dostal 5.8. Takže hodnota výrazu 2,54 × 2 je 5,08
2,54 x 2 = 5,08
Násobenie desatinných miest 10, 100, 1000
Násobenie desatinných miest 10, 100 alebo 1000 sa vykonáva rovnakým spôsobom ako násobenie desatinných miest bežnými číslami. Je potrebné vykonať násobenie, ignorovať čiarku v desatinnom zlomku, potom v odpovedi oddeliť časť celého čísla od zlomkovej časti a počítať rovnaký počet číslic napravo, ako bolo číslic za desatinnou čiarkou v desatinnej čiarke zlomok.
Napríklad vynásobte 2,88 číslom 10
Vynásobme desatinný zlomok 2,88 10, pričom čiarku v desatinnom zlomku ignorujeme:

Dostali sme 2880. V tomto čísle je potrebné oddeliť celú časť od zlomkovej časti čiarkou. Ak to chcete urobiť, musíte spočítať počet číslic za desatinnou čiarkou v zlomku 2,88. Vidíme, že v zlomku 2,88 sú za desatinnou čiarkou dve číslice.
Vraciame sa k číslu 2880 a začíname sa pohybovať sprava doľava. Musíme spočítať dve číslice sprava a dať čiarku:

Dostal som odpoveď 28.80. Poslednú nulu vyhodíme - dostaneme 28.8. Takže hodnota výrazu 2,88 × 10 je 28,8
2,88 x 10 = 28,8
Existuje druhý spôsob, ako vynásobiť desatinné zlomky 10, 100, 1000. Táto metóda je oveľa jednoduchšia a pohodlnejšia. Spočíva v tom, že čiarka v desatinnom zlomku sa posunie doprava o toľko číslic, koľko núl je v násobidle.
Napríklad predchádzajúci príklad 2,88×10 vyriešime týmto spôsobom. Bez uvedenia akýchkoľvek výpočtov sa okamžite pozrieme na faktor 10. Zaujíma nás, koľko núl je v ňom. Vidíme, že má jednu nulu. Teraz v zlomku 2,88 posunieme desatinnú čiarku doprava o jednu číslicu, dostaneme 28,8.
2,88 x 10 = 28,8
Skúsme vynásobiť 2,88 číslom 100. Hneď sa pozrieme na faktor 100. Zaujíma nás, koľko núl je v ňom. Vidíme, že má dve nuly. Teraz v zlomku 2,88 posunieme desatinnú čiarku doprava o dve číslice, dostaneme 288
2,88 x 100 = 288
Skúsme vynásobiť 2,88 číslom 1000. Hneď sa pozrieme na faktor 1000. Zaujíma nás, koľko núl je v ňom. Vidíme, že má tri nuly. Teraz v zlomku 2,88 posunieme desatinnú čiarku doprava o tri číslice. Tretia číslica tam nie je, preto pridáme ďalšiu nulu. Výsledkom je 2880.
2,88 x 1 000 = 2 880
Násobenie desatinných miest 0,1 0,01 a 0,001
Násobenie desatinných miest 0,1, 0,01 a 0,001 funguje rovnakým spôsobom ako násobenie desatinného miesta desatinným číslom. Je potrebné násobiť zlomky ako obyčajné čísla a do odpovede dať čiarku, pričom treba počítať toľko číslic vpravo, koľko je číslic za desatinnou čiarkou v oboch zlomkoch.
Napríklad vynásobte 3,25 číslom 0,1
Tieto zlomky násobíme ako obyčajné čísla, čiarky ignorujeme:

Dostali sme 325. V tomto čísle je potrebné oddeliť celú časť od zlomkovej časti čiarkou. Aby ste to dosiahli, musíte vypočítať počet číslic za desatinnou čiarkou v zlomkoch 3,25 a 0,1. V zlomku 3,25 sú za desatinnou čiarkou dve číslice, v zlomku 0,1 jedna číslica. Spolu tri čísla.
Vraciame sa k číslu 325 a začíname sa pohybovať sprava doľava. Musíme spočítať tri číslice vpravo a dať čiarku. Po spočítaní troch číslic zistíme, že číslam je koniec. V tomto prípade musíte pridať jednu nulu a dať čiarku:

Dostali sme odpoveď 0,325. Takže hodnota výrazu 3,25 × 0,1 je 0,325
3,25 x 0,1 = 0,325
Existuje druhý spôsob, ako násobiť desatinné miesta 0,1, 0,01 a 0,001. Táto metóda je oveľa jednoduchšia a pohodlnejšia. Spočíva v tom, že čiarka v desatinnom zlomku sa posunie doľava o toľko číslic, koľko núl je v násobidle.
Napríklad predchádzajúci príklad 3,25 × 0,1 vyriešime týmto spôsobom. Bez akýchkoľvek výpočtov sa okamžite pozrieme na faktor 0,1. Zaujíma nás, koľko núl je v ňom. Vidíme, že má jednu nulu. Teraz v zlomku 3,25 posunieme desatinnú čiarku doľava o jednu číslicu. Posunutím čiarky o jednu číslicu doľava vidíme, že pred tromi už nie sú žiadne číslice. V tomto prípade pridajte jednu nulu a vložte čiarku. V dôsledku toho dostaneme 0,325
3,25 x 0,1 = 0,325
Skúsme vynásobiť 3,25 číslom 0,01. Okamžite sa pozrite na multiplikátor 0,01. Zaujíma nás, koľko núl je v ňom. Vidíme, že má dve nuly. Teraz v zlomku 3,25 posunieme čiarku doľava o dve číslice, dostaneme 0,0325
3,25 x 0,01 = 0,0325
Skúsme vynásobiť 3,25 číslom 0,001. Okamžite sa pozrite na multiplikátor 0,001. Zaujíma nás, koľko núl je v ňom. Vidíme, že má tri nuly. Teraz v zlomku 3,25 posunieme desatinnú čiarku doľava o tri číslice, dostaneme 0,00325
3,25 × 0,001 = 0,00325
Nezamieňajte násobenie desatinných miest 0,1, 0,001 a 0,001 s násobením 10, 100, 1000. Bežná chyba väčšina ľudí.
Pri násobení 10, 100, 1000 sa čiarka posunie doprava o toľko číslic, koľko núl je v násobidle.
A pri násobení 0,1, 0,01 a 0,001 sa čiarka posunie doľava o toľko číslic, koľko je núl v násobidle.
Ak je to spočiatku ťažké zapamätať, môžete použiť prvú metódu, v ktorej sa násobenie vykonáva ako pri bežných číslach. V odpovedi budete musieť oddeliť časť celého čísla od zlomkovej časti tak, že spočítate toľko číslic napravo, koľko je číslic za desatinnou čiarkou v oboch zlomkoch.
Delenie menšieho čísla väčším. Pokročilá úroveň.
V jednej z predchádzajúcich lekcií sme si povedali, že pri delení menšieho čísla väčším dostaneme zlomok, v čitateli ktorého je delenec a v menovateli deliteľ.
Ak chcete napríklad rozdeliť jedno jablko na dve, musíte do čitateľa napísať 1 (jedno jablko) a do menovateľa napísať 2 (dvaja priatelia). Výsledkom je zlomok. Takže každý priateľ dostane jablko. Inými slovami, polovica jablka. Zlomok je odpoveďou na problém ako rozdeliť jedno jablko medzi dve

Ukázalo sa, že tento problém môžete ďalej vyriešiť, ak vydelíte 1 číslom 2. Koniec koncov, zlomková čiara v ľubovoľnom zlomku znamená delenie, čo znamená, že toto delenie je povolené aj v zlomku. Ale ako? Sme zvyknutí, že dividenda je vždy väčšia ako deliteľ. A tu je naopak dividenda menšia ako deliteľ.
Všetko sa vyjasní, ak si zapamätáme, že zlomok znamená drvenie, delenie, delenie. To znamená, že jednotku možno rozdeliť na toľko častí, koľko chcete, a nie iba na dve časti.
Pri delení menšieho čísla väčším sa získa desatinný zlomok, v ktorom bude celá časť 0 (nula). Zlomková časť môže byť čokoľvek.
Vydeľme teda 1 2. Vyriešme tento príklad s rohom:
Človek sa nedá len tak rozdeliť na dve časti. Ak položíte otázku "koľko dvoch je v jednom" , potom bude odpoveď 0. Preto v súkromí napíšeme 0 a dáme čiarku:
Teraz, ako obvykle, vynásobíme podiel deliteľom, aby sme vytiahli zvyšok:
Nastal moment, kedy je možné jednotku rozdeliť na dve časti. Ak to chcete urobiť, pridajte ďalšiu nulu napravo od prijatej:
Dostali sme 10. 10 vydelíme 2, dostaneme 5. Päť zapíšeme do zlomkovej časti našej odpovede:
Teraz vyberieme posledný zvyšok na dokončenie výpočtu. Vynásobte 5 x 2, dostaneme 10
Dostali sme odpoveď 0,5. Takže zlomok je 0,5
Polovicu jablka je možné zapísať aj pomocou desatinného zlomku 0,5. Ak spočítame tieto dve polovice (0,5 a 0,5), dostaneme opäť pôvodné jedno celé jablko: 

Tento bod možno pochopiť aj vtedy, ak si predstavíme, ako sa 1 cm delí na dve časti. Ak rozdelíte 1 centimeter na 2 časti, dostanete 0,5 cm

Príklad 2 Nájdite hodnotu výrazu 4:5
Koľko pätiek je v štyroch? Vôbec nie. Píšeme súkromne 0 a dáme čiarku:
Vynásobíme 0 5, dostaneme 0. Pod štvorku napíšeme nulu. Okamžite odpočítajte túto nulu od dividendy:
Teraz začneme štvoricu deliť (rozdeľovať) na 5 častí. Aby sme to urobili, napravo od 4 pripočítame nulu a vydelíme 40 5, dostaneme 8. Osmičku píšeme súkromne.

Príklad dokončíme vynásobením 8 x 5 a dostaneme 40:

Dostali sme odpoveď 0,8. Takže hodnota výrazu 4: 5 je 0,8
Príklad 3 Nájdite hodnotu výrazu 5: 125
Koľko čísel 125 je v piatich? Vôbec nie. Súkromne napíšeme 0 a dáme čiarku:

Vynásobíme 0 5, dostaneme 0. Pod päťku napíšeme 0. Okamžite odpočítajte od piatich 0
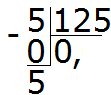
Teraz začneme deliť (rozdeľovať) päťku na 125 častí. Aby sme to dosiahli, napravo od tejto päťky napíšeme nulu:

Vydeľte 50 číslom 125. Koľko čísel 125 je v 50? Vôbec nie. Takže v kvociente opäť napíšeme 0

Vynásobíme 0 125, dostaneme 0. Túto nulu napíšeme pod 50. Hneď od 50 odčítame 0
Teraz rozdelíme číslo 50 na 125 častí. Aby sme to urobili, napravo od 50 napíšeme ďalšiu nulu:
Vydeľte 500 číslom 125. Koľko čísel je 125 v čísle 500. V čísle 500 sú štyri čísla 125. Štyri píšeme súkromne:

Príklad dokončíme vynásobením 4 číslom 125 a dostaneme 500

Dostali sme odpoveď 0,04. Takže hodnota výrazu 5:125 je 0,04
Delenie čísel bez zvyšku
Dajme teda do podielu za jednotkou čiarku, čím označíme, že delenie celých častí je ukončené a prejdeme k zlomkovej časti:
Pridajte nulu k zvyšku 4
Teraz vydelíme 40 5, dostaneme 8. Osem píšeme súkromne:
40-40=0. Prijaté 0 vo zvyšku. Rozdelenie je teda úplne dokončené. Delením 9 5 získame desatinné číslo 1,8:
9: 5 = 1,8
Príklad 2. Vydeľte 84 číslom 5 bezo zvyšku
Najprv vydelíme 84 5 ako zvyčajne so zvyškom:

Prijaté v súkromí 16 a 4 ďalšie v zostatku. Teraz tento zvyšok vydelíme 5. Do súkromného čísla vložíme čiarku a k zvyšku 4 pridáme 0

Teraz vydelíme 40 5, dostaneme 8. Osem zapíšeme do podielu za desatinnou čiarkou:

a dokončite príklad kontrolou, či je tam ešte zvyšok:

Delenie desatinnej čiarky bežným číslom
Desatinný zlomok, ako vieme, pozostáva z celého čísla a zlomkovej časti. Pri delení desatinného zlomku bežným číslom v prvom rade potrebujete:
- vydeľte celú časť desatinného zlomku týmto číslom;
- po rozdelení celočíselnej časti musíte do súkromnej časti okamžite vložiť čiarku a pokračovať vo výpočte ako pri bežnom delení.
Napríklad vydeľme 4,8 2
Napíšme tento príklad ako roh:

Teraz vydelme celú časť 2. Štyri delené dvoma sú dve. Dvojku napíšeme súkromne a okamžite dáme čiarku:

Teraz vynásobíme podiel deliteľom a uvidíme, či existuje zvyšok z delenia:

4-4 = 0. Zvyšok nula. Zatiaľ nepíšeme nulu, keďže riešenie nie je dokončené. Potom pokračujeme vo výpočte, ako pri bežnom delení. Zoberte 8 a vydeľte ho 2

8: 2 = 4. Štyri zapíšeme do podielu a hneď ho vynásobíme deliteľom:

Odpoveď som dostal 2.4. Hodnota výrazu 4,8: 2 sa rovná 2,4
Príklad 2 Nájdite hodnotu výrazu 8,43:3

Vydelíme 8 číslom 3, dostaneme 2. Hneď za dvojku dajte čiarku:

Teraz vynásobíme podiel deliteľom 2 × 3 = 6. Šestku napíšeme pod osmičku a zvyšok nájdeme:
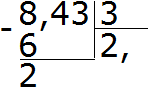

Vydelíme 24 3, dostaneme 8. Osmičku píšeme súkromne. Okamžite to vynásobíme deliteľom, aby sme našli zvyšok delenia:

24-24 = 0. Zvyšok je nula. Nula ešte nie je zaznamenaná. Vezmite posledné tri z dividend a vydeľte ich 3, dostaneme 1. Okamžite vynásobte 1 x 3, aby ste dokončili tento príklad:

Dostal som odpoveď 2,81. Takže hodnota výrazu 8,43: 3 sa rovná 2,81
Delenie desatinnej čiarky desatinnou čiarkou
Ak chcete rozdeliť desatinný zlomok na desatinný zlomok v deleni a v deliteľovi, posuňte čiarku doprava o rovnaký počet číslic, aký je za desatinnou čiarkou v deliteľovi, a potom vydeľte bežným číslom.
Napríklad vydeľte 5,95 číslom 1,7
Napíšme tento výraz ako roh

Teraz v deleni a v deliteľovi posunieme čiarku doprava o rovnaký počet číslic, koľko je za desatinnou čiarkou v deliteľovi. Deliteľ má jednu číslicu za desatinnou čiarkou. Čiarku teda musíme posunúť v dividende a v deliteľovi o jednu číslicu doprava. Prenáša sa:

Po posunutí desatinnej čiarky doprava o jednu číslicu sa desatinný zlomok 5,95 zmenil na zlomok 59,5. A desatinný zlomok 1,7 sa po posunutí desatinnej čiarky doprava o jednu číslicu zmenil na obvyklé číslo 17. A už vieme, ako sa desatinný zlomok delí obvyklým číslom. Ďalší výpočet nie je ťažký:

Čiarka je presunutá doprava, aby sa uľahčilo delenie. To je povolené vzhľadom na skutočnosť, že pri vynásobení alebo delení dividendy a deliteľa rovnakým číslom sa podiel nemení. Čo to znamená?
Toto je jeden z zaujímavé funkcie divízie. Nazýva sa to súkromný majetok. Uvažujme výraz 9: 3 = 3. Ak sa v tomto výraze delenec a deliteľ vynásobia alebo vydelia rovnakým číslom, potom sa podiel 3 nezmení.
Vynásobme dividendu a deliteľa 2 a uvidíme, čo sa stane:
(9 × 2): (3 × 2) = 18: 6 = 3
Ako vidno z príkladu, kvocient sa nezmenil.
To isté sa stane, keď nesieme čiarku v dividende a v deliteľovi. V predchádzajúcom príklade, kde sme vydelili 5,91 číslom 1,7, sme v dividende a deliteľovi posunuli čiarku o jedno číslo doprava. Po posunutí čiarky sa zlomok 5,91 previedol na zlomok 59,1 a zlomok 1,7 sa previedol na obvyklé číslo 17.
V skutočnosti sa v tomto procese uskutočnilo násobenie číslom 10. Takto to vyzeralo:
5,91 × 10 = 59,1
Preto počet číslic za desatinnou čiarkou v deliteľovi závisí od toho, čím sa bude delenec a deliteľ násobiť. Inými slovami, počet číslic za desatinnou čiarkou v deliteľovi určí, o koľko číslic v deliteľovi a v deliteľovi sa čiarka posunie doprava.
Desatinné delenie 10, 100, 1000
Delenie desatinného čísla 10, 100 alebo 1000 sa vykonáva rovnakým spôsobom ako . Napríklad vydeľme 2,1 10. Vyriešme tento príklad s rohom:

Existuje však aj druhý spôsob. Je ľahší. Podstatou tejto metódy je, že čiarka v delenci sa posunie doľava o toľko číslic, koľko núl je v deliteľovi.
Vyriešme predchádzajúci príklad týmto spôsobom. 2,1: 10. Pozeráme sa na rozdeľovač. Zaujíma nás, koľko núl je v ňom. Vidíme, že je tam jedna nula. Takže v deliteľnom 2.1 musíte posunúť čiarku doľava o jednu číslicu. Čiarku posunieme o jednu číslicu doľava a vidíme, že už nezostali žiadne číslice. V tomto prípade pred číslo pridáme ešte jednu nulu. V dôsledku toho dostaneme 0,21
Skúsme vydeliť 2,1 číslom 100. V čísle 100 sú dve nuly. Takže v deliteľnom 2.1 musíte posunúť čiarku doľava o dve číslice:
2,1: 100 = 0,021
Skúsme vydeliť 2,1 číslom 1000. V čísle 1000 sú tri nuly. Takže v deliteľnom 2.1 musíte posunúť čiarku doľava o tri číslice:
2,1: 1000 = 0,0021
Desatinné delenie 0,1, 0,01 a 0,001
Delenie desatinného čísla 0,1, 0,01 a 0,001 sa vykonáva rovnakým spôsobom ako . V dividende a v deliteľovi musíte posunúť čiarku doprava o toľko číslic, koľko je za desatinnou čiarkou v deliteľovi.
Napríklad vydeľme 6,3 číslom 0,1. V prvom rade posunieme čiarky v delenci a v deliteľovi doprava o rovnaký počet číslic, koľko je za desatinnou čiarkou v deliteľovi. Deliteľ má jednu číslicu za desatinnou čiarkou. Čiarky v dividende a v deliteľovi teda posunieme o jednu číslicu doprava.
Po posunutí desatinnej čiarky doprava o jednu číslicu sa desatinný zlomok 6,3 zmení na obvyklé číslo 63 a desatinný zlomok 0,1 po posunutí desatinnej čiarky doprava o jednu číslicu na jednotku. A delenie 63 číslom 1 je veľmi jednoduché:
Takže hodnota výrazu 6,3: 0,1 sa rovná 63
Existuje však aj druhý spôsob. Je ľahšia. Podstatou tejto metódy je, že čiarka v dividende sa prenesie doprava o toľko číslic, koľko núl je v deliteľovi.
Vyriešme predchádzajúci príklad týmto spôsobom. 6,3:0,1. Pozrime sa na rozdeľovač. Zaujíma nás, koľko núl je v ňom. Vidíme, že je tam jedna nula. Takže v deliteľnom 6.3 musíte posunúť čiarku doprava o jednu číslicu. Čiarku posunieme doprava o jednu číslicu a dostaneme 63
Skúsme vydeliť 6,3 číslom 0,01. Deliteľ 0,01 má dve nuly. Takže v deliteľnom 6.3 musíte posunúť čiarku doprava o dve číslice. Ale v dividende je len jedna číslica za desatinnou čiarkou. V tomto prípade treba na koniec pridať ešte jednu nulu. Výsledkom je 630
Skúsme vydeliť 6,3 číslom 0,001. Deliteľ 0,001 má tri nuly. Takže v deliteľnom 6.3 musíte posunúť čiarku doprava o tri číslice:
6,3: 0,001 = 6300
Úlohy na samostatné riešenie
Páčila sa vám lekcia?
Pridajte sa k nám nová skupina Vkontakte a začnite dostávať upozornenia o nových lekciách
Stĺpcová kalkulačka pre Android zariadenia bude skvelým pomocníkom pre moderných školákov. Program nielenže dáva správnu odpoveď na matematickú akciu, ale tiež jasne ukazuje jej postupné riešenie. Ak potrebujete zložitejšie kalkulačky, môžete sa pozrieť na alebo pokročilé inžinierska kalkulačka.
Zvláštnosti
Hlavnou črtou programu je jedinečnosť výpočtu matematických operácií. Zobrazenie procesu výpočtu v stĺpci umožňuje študentom sa s ním podrobnejšie zoznámiť, pochopiť algoritmus riešenia a nielen získať hotový výsledok a prepísať ho do poznámkového bloku. Táto funkcia má oproti iným kalkulačkám obrovskú výhodu. V škole učitelia často vyžadujú, aby sa priebežné výpočty zapisovali, aby sa ubezpečili, že ich študent robí vo svojej mysli a skutočne rozumie algoritmu riešenia problémov. Mimochodom, máme ďalší program podobného druhu - .
Ak chcete začať používať program, musíte si stiahnuť kalkulačku v stĺpci v systéme Android. Môžete to urobiť na našej webovej stránke úplne zadarmo bez dodatočných registrácií a SMS. Po inštalácii sa otvorí hlavná stránka vo forme listu notebooku v klietke, na ktorom sú v skutočnosti výsledky výpočtov a ich podrobné riešenie. V spodnej časti je panel s tlačidlami:
- čísla.
- Znaky aritmetických operácií.
- Vymažte predtým zadané znaky.
Zadávanie sa vykonáva podľa rovnakého princípu ako na. Všetok rozdiel je len v rozhraní aplikácie – všetky matematické výpočty a ich výsledky sa zobrazujú vo virtuálnom žiackom notebooku.

Aplikácia vám umožňuje rýchlo a správne vykonávať štandardné matematické výpočty pre študenta v stĺpci:
- násobenie;
- rozdelenie;
- prídavok;
- odčítanie.
Príjemným doplnkom aplikácie je funkcia denného pripomenutia. domáca úloha matematiky. Ak chcete, urobte si domácu úlohu. Ak ju chcete povoliť, prejdite do nastavení (stlačte tlačidlo vo forme ozubeného kolieska) a začiarknite políčko pripomenutia.
Výhody a nevýhody
- Pomáha študentovi nielen rýchlo získať správny výsledok matematických výpočtov, ale aj pochopiť samotný princíp výpočtu.
- Veľmi jednoduché, intuitívne rozhranie pre každého užívateľa.
- Aplikáciu môžete nainštalovať aj na najlacnejšie zariadenie Android s operačným systémom 2.2 a novším.
- Kalkulačka ukladá históriu matematických výpočtov, ktorú možno kedykoľvek vymazať.
Kalkulačka je obmedzená v matematických operáciách, takže nebude fungovať pri zložitých výpočtoch, ktoré by mohla zvládnuť inžinierska kalkulačka. Avšak vzhľadom na účel samotnej aplikácie - jasne demonštrovať študentom Základná škola princíp výpočtu v stĺpci, to by sa nemalo považovať za nevýhodu.
Aplikácia bude zároveň výborným pomocníkom nielen pre školákov, ale aj rodičov, ktorí chcú svoje dieťa zaujať matematikou a naučiť ho správne a dôsledne počítať. Ak ste už aplikáciu Stacked Calculator použili, zanechajte svoje dojmy nižšie v komentároch.




