A származék felhasználása különböző tevékenységi területeken. Egy érdekes derivált A munka céljai: A derivált különféle tudományokban való használatának átgondolása Megismerkedni olyan tudósokkal, akik egy függvény deriváltját tanulmányozták. Az erő az elmozdulásban végzett munka származéka.

Oktatási Minisztérium Szaratov régió

Állami Autonóm Szakember oktatási intézmény Szaratov régió "Engels Polytechnic"

A DERIVATÍV ALKALMAZÁSA KÜLÖNBÖZŐ TUDOMÁNYTERÜLETEKEN

Teljesített: Sarkulova Nurgulya Sergeevna

a KShI-216/15 csoport tanulója

(Tervezés, modellezés és

varrás technológia)

tudományos tanácsadója:

Verbitskaya Elena Vyacheslavovna

matematika tanár GAPOU SO

"Engels Polytechnic"

2016

Bevezetés

A matematika szerepe a természettudomány különböző területein igen nagy. Nem csoda, hogy azt mondják„A matematika a tudományok királynője, fizikája jobb kéz, a kémia maradt.

A kutatás tárgya a származék.

Vezető cél, hogy ne csak a matematikában, hanem más tudományokban is megmutassa a derivált jelentőségét, jelentőségét a modern életben.

A differenciálszámítás a minket körülvevő világ leírása, matematikai nyelven. A derivált nem csak a sikeres megoldásban segít matematikai feladatok, hanem gyakorlati feladatok is a tudomány és a technika különböző területein.

Egy függvény deriváltját mindenhol használjuk, ahol egyenetlen folyamat áramlás van: ez egyenetlen mechanikai mozgás, váltakozó áram és kémiai reakciók, ill. radioaktív bomlás anyagok stb.

Az esszé legfontosabb és tematikus kérdései:

1. A származék keletkezésének története.

2. Miért érdemes a függvények deriváltjait tanulmányozni?

3. Hol használják a származékokat?

4. Származékok alkalmazása a fizikában, kémiában, biológiában és más tudományokban.

5. Következtetések

Úgy döntöttem, hogy írok egy tanulmányt "A származék alkalmazása a tudomány különböző területein" témában, mert úgy gondolom, hogy ez a téma nagyon érdekes, hasznos és releváns.

Munkámban a differenciálás alkalmazásáról fogok beszélni a tudomány különböző területein, például kémiában, fizikában, biológiában, földrajzban stb. Hiszen minden tudomány elválaszthatatlanul összefügg, ami a téma példáján nagyon jól látható. fontolgatom.

A származék alkalmazása a tudomány különböző területein

A középiskolai algebratanfolyamból ezt már tudjuk derivált a függvény növekménye és argumentuma növekménye arányának határa, mivel az argumentum növekménye nullára hajlik, ha létezik ilyen korlát.

A derivált megtalálásának műveletét differenciálásnak nevezzük, és azt a függvényt, amelynek egy x pontban deriváltja van, abban a pontban differenciálhatónak nevezzük. Az intervallum minden pontján differenciálható függvényt az adott intervallumon differenciálhatónak nevezzük.

A matematikai elemzés alaptörvényeinek felfedezésének megtiszteltetése angol fizikus valamint Isaac Newton matematikus és Leibniz német matematikus, fizikus, filozófus.

Newton bevezette a derivált fogalmát, tanulmányozva a mechanika törvényeit, feltárva ezzel annak mechanikai jelentését.

A derivált fizikai jelentése: egy függvény deriváltjay= f(x) azon a ponton x 0 a függvény változási sebességef(x) azon a ponton x 0 .

Leibniz úgy jutott el a derivált fogalmához, hogy megoldotta azt a problémát, hogy egy derivált egyeneshez érintőt vonjunk, így magyarázza meg azt geometriai érzék.

A derivált geometriai jelentése az, hogy a derivált függvény egy pontbanx 0 egyenlő az abszcissza pontban megrajzolt függvény grafikonjának érintőjének meredekségévelx 0 .

A származékos kifejezés és a modern jelölésy" , f"J. Lagrange vezette be 1797-ben.

orosz matematikus A 19. században Panfuty Lvovics Csebisev azt mondta, hogy "különös jelentőséggel bírnak azok a tudomány módszerei, amelyek lehetővé teszik számunkra, hogy megoldjunk egy olyan problémát, amely minden gyakorlati emberi tevékenységre jellemző, például, hogyan rendelkezzünk eszközeinkkel a legnagyobb haszon elérése érdekében".

A különböző szakterületek képviselőinek korunkban ilyen feladatokkal kell megküzdeniük:

A folyamatmérnökök igyekeznek a termelést úgy megszervezni, hogy minél több termék készüljön el;

A tervezők egy olyan eszközt próbálnak kifejleszteni űrhajó hogy a készülék tömege a legkisebb legyen;

A közgazdászok igyekeznek úgy megtervezni az üzem és a nyersanyagforrások közötti kapcsolatokat, hogy a szállítási költségek minimálisak legyenek.

Bármilyen téma tanulmányozásakor a hallgatóknak kérdésük van: „Miért van szükségünk erre?” Ha a válasz kielégíti a kíváncsiságot, akkor beszélhetünk a hallgatók érdeklődéséről. A "Származék" témára a választ úgy kaphatja meg, ha tudja, hol használják a függvények deriváltjait.

A kérdés megválaszolásához felsorolhatunk néhány tudományágat és azok szakaszait, amelyekben származékokat használnak.

Származék az algebrában:

1. A függvénygráf érintője

Függvénygráf érintőjef, x-ben differenciálható ról ről , az (x) ponton áthaladó egyenes ról ről ; f(x o )) és lejtősf′(x o ).

y= f(x o ) + f′(x o ) (x - x o )

2. Növekvő és csökkenő függvények intervallumainak keresése

Funkcióy=f(x) növekszik az intervallum soránx , ha van ilyen ésaz egyenlőtlenséget. Más szavakkal, az argumentum nagyobb értéke a függvény nagyobb értékének felel meg.

Funkcióy=f(x) az intervallum alatt csökkenx , ha van ilyen ésaz egyenlőtlenséget. Más szóval, az argumentum nagyobb értéke a függvény kisebb értékének felel meg.

3. Függvény szélsőpontjainak keresése

Pont hívottmaximális pont funkciókaty=f(x) ha mindenértx . A függvény értékét a maximum pontban hívjukfunkció maximum és jelöljük.

Pont hívottminimum pont funkciókaty=f(x) ha mindenértx szomszédságából az egyenlőtlenséget. A függvény értékét a minimumpontban hívjukfunkció minimum és jelöljük.

Egy pont szomszédságában intervallum megértése, ahol elég kicsi pozitív szám.

A minimum és maximum pontokat hívjukszélsőséges pontok , és a szélsőpontoknak megfelelő függvényértékeket hívjuk megfunkció szélsőségei .

4. Egy függvény konvexitási és konkávsági intervallumainak keresése

Függvénygrafikon, ezen az intervallumon vankonvex , nem fekszik magasabban egyik érintőjénél sem (1. ábra).

Függvénygrafikon, az intervallumon differenciálható, ezen az intervallumon vanhomorú , ha ennek a függvénynek a grafikonja az intervallumon belül van nem fekszik alacsonyabban egyik érintőjénél sem (2. ábra).

A függvénygráf inflexiós pontját a konvexitás és a konkávság intervallumait elválasztó pontnak nevezzük.

5. Egy függvény inflexiós pontjainak megtalálása

Származék a fizikában:

1. A sebesség, mint az útvonal származéka

2. A gyorsulás mint a sebesség deriváltjaa =

3. Bomlási sebesség radioaktív elemek 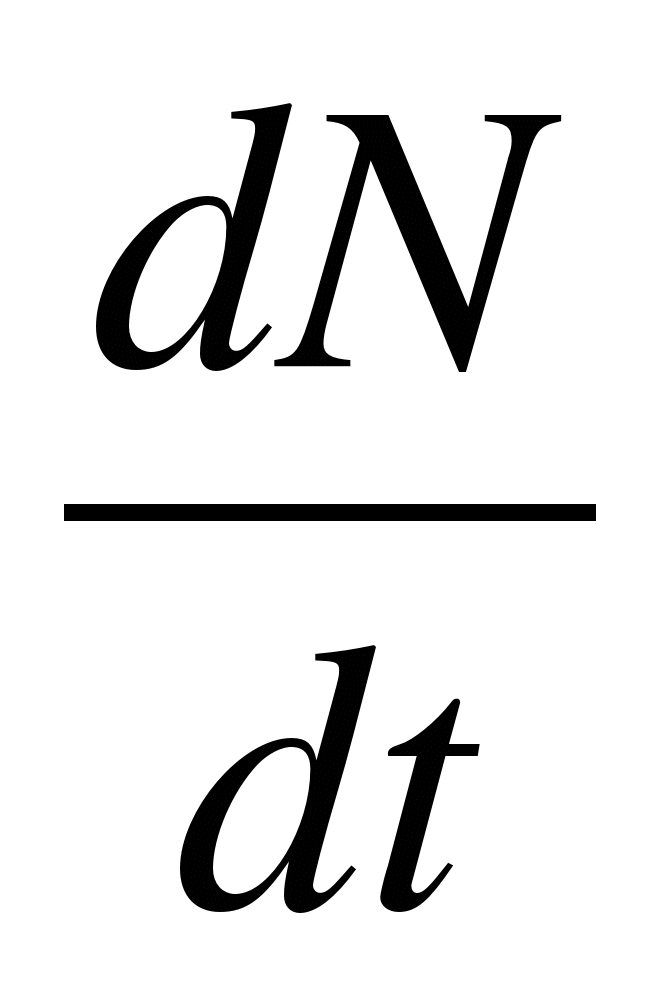= - λN

És a fizikában is a derivált számítja ki:

Sebesség anyagi pont

A pillanatnyi sebesség mint a származék fizikai jelentése

Azonnali érték AC táp

Az elektromágneses indukció EMF pillanatnyi értéke

Max erő

Származék a kémiában:

A kémiában pedig a differenciálszámítást széles körben alkalmazzák a konstrukciókban matematikai modellek kémiai reakciók és tulajdonságaik későbbi leírása.

A kémiában a származékot egy nagyon fontos dolog – a sebesség – meghatározására használják kémiai reakció, az egyik döntő tényező, amelyet a tudományos és ipari tevékenység számos területén figyelembe kell venni. V(t) = p'(t)

Mennyiség

in-va egy adott időpontban t 0

p = p(t 0 )

Funkció

Időintervallum

∆t = t–t 0

Érv növekménye

Mennyiségi változás

∆p=p(t 0 + ∆t) – p(t 0 )

Funkciónövekedés

A kémiai reakció átlagos sebessége

∆p/∆t

A függvénynövekmény és az argumentumnövekmény aránya

Származék a biológiában:

A populáció egy adott faj egyedeinek gyűjteménye, amelyek a faj elterjedési területén belül a terület egy bizonyos részét foglalják el, egymással szabadon kereszteződve, részben vagy teljesen elszigetelve más populációktól, és egyben az evolúció elemi egysége is.

P \u003d x’ (t)

Származék a földrajzból:

1. Néhány jelentés a szeizmográfiában

2. Jellemzők elektromágneses mező föld

3. Maggeofizikai paraméterek radioaktivitása

4. Sok jelentés a gazdaságföldrajzban

5. Készítsen képletet a területen t időpontban lévő népesség kiszámításához.

y'= y-re

Thomas Malthus szociológiai modelljének gondolata az, hogy a népességnövekedés arányos a népesség számával egy adott időpontban t-től N(t-ig). A Malthus-modell jól bevált az Egyesült Államok népességének leírására 1790 és 1860 között. Ez a modell a legtöbb országban már nem érvényes.

Villamosmérnöki származéka:

Otthonunkban, közlekedésben, gyárakban: mindenhol működik az elektromos áram. Az elektromos áram alatt értse a szabad elektromosan töltött részecskék irányított mozgását.

Mennyiségi jellemző elektromos áram az aktuális erősség.

Egy elektromos áramkörben elektromos töltés q=q (t) törvény szerint idővel változik. Az I áram a q töltés deriváltja az idő függvényében.

Az elektrotechnikában főként váltakozó áramú üzemet alkalmaznak.

Az időben változó elektromos áramot váltakozó áramnak nevezzük. Az AC áramkör tartalmazhat különféle elemek: fűtőberendezések, tekercsek, kondenzátorok.

A váltakozó elektromos áram előállítása az elektromágneses indukció törvényén alapul, melynek összetétele tartalmazza a mágneses fluxus deriváltját.

Származék a közgazdaságtanban:

A közgazdaságtan az élet alapja, és fontos helyet foglal el benne a differenciálszámítás, a közgazdasági elemzés apparátusa. A közgazdasági elemzés alapvető feladata a közgazdasági mennyiségek összefüggéseinek vizsgálata függvény formájában.

A származék a közgazdaságtanban fontos kérdéseket old meg:

1. Milyen irányba változik az állam bevétele az adóemeléssel vagy a vámok bevezetésével?

2. Növekszik-e vagy csökken-e a cég bevétele termékei árának emelkedésével?

E kérdések megoldásához szükséges a bemeneti változók kapcsolódási függvényeinek megalkotása, amelyeket ezután differenciálszámítás módszerével vizsgálunk.

Ezenkívül a függvény (derivált) extrémumát használva a gazdaságban megtalálhatja a legmagasabb munkatermelékenységet, maximális profitot, maximális kibocsátást és minimális költségeket.

KÖVETKEZTETÉS: a származékot sikeresen használják a tudomány, a technológia és az élet különböző alkalmazott problémáinak megoldására

Mint a fentiekből is látszik, egy függvény deriváltjának használata igen sokrétű, és nemcsak a matematika, hanem más tudományágak tanulmányozásában is. Ebből arra következtethetünk, hogy a „Függvény deriváltja” témakör tanulmányozása más témákban és tárgyakban is alkalmazható lesz.

Meggyőződésünk volt a „Származék” témakör tanulmányozásának fontosságáról, a tudomány és a technológia folyamatainak vizsgálatában betöltött szerepéről, a szerinti tervezés lehetőségéről. valós események matematikai modelleket, és fontos problémákat megoldani.

“A zene felemelheti vagy megnyugtathatja a lelket,
A festészet kellemes a szemnek,
Költészet - érzések felébresztése,
Filozófia – az elme szükségleteinek kielégítése,
A mérnöki tevékenység célja az emberek életének anyagi oldalának javítása,
DEa matematika mindezeket a célokat elérheti.”

Így mondta az amerikai matematikusMaurice Kline.

Bibliográfia:

1. Bogomolov N.V., Samoylenko I.I. Matematika. - M.: Yurayt, 2015.

2. V. P. Grigorjev és Yu. A. Dubinsky, A felsőbb matematika elemei. - M.: Akadémia, 2014.

3. Bavrin I.I. A felsőbb matematika alapjai. -M.: elvégezni az iskolát, 2013.

4. Bogomolov N.V. Gyakorlati órák matematikából. - M.: Felsőiskola, 2013.

5. Bogomolov N.V. Matematikai feladatgyűjtemény. - M.: Túzok, 2013.

6. Rybnikov K.A. Matematikatörténet, Moszkvai Egyetemi Kiadó, M, 1960.

7. Vinogradov Yu.N., Gomola A.I., Potapov V.I., Sokolova E.V. – M.:"Akadémia" Kiadói Központ, 2010

8 . Bashmakov M.I. Matematika: algebra és a matematikai elemzés kezdetei, geometria. - M.: "Akadémia" Kiadói Központ, 2016

Időszakos források:

Újságok és folyóiratok: "Matematika", " Nyilvános óra»

Internetes források használata, digitális könyvtárak:

www:egetutor.ru

matematika-na5.norod.ru

FGO SPO

Novoszibirszk mezőgazdasági főiskola

absztrakt

a "matematika" tudományágban

"A származék alkalmazása a tudományban és a technológiában"

S. Razdolnoe 2008

Bevezetés

1. Elméleti rész

1.1 A derivált fogalmához vezető problémák

1.2 Származékos definíció

1.3 A származék megtalálásának általános szabálya

1.4 A derivált geometriai jelentése

1.5 A származék mechanikai jelentése

1.6 Másodrendű származék és mechanikai jelentése

1.7 A differenciál definíciója és geometriai jelentése

2. Függvények vizsgálata a derivált segítségével

Következtetés

Irodalom

Bevezetés

Esszém első fejezetében szó lesz a derivált fogalmáról, alkalmazásának szabályairól, a geometriai ill. fizikai érzék derivált. Esszém második fejezetében a származék tudományban és technológiában való használatáról, valamint az e területen felmerülő problémák megoldásáról lesz szó.

1. Elméleti rész

1.1 A derivált fogalmához vezető problémák

Egyes folyamatok, jelenségek tanulmányozása során gyakran felmerül e folyamatok sebességének meghatározása. Megoldása elvezet a derivált fogalmához, amely a differenciálszámítás alapfogalma.

A differenciálszámítás módszerét a 17. és 18. században alkották meg. Két nagy matematikus, I. Newton és G.V. Leibniz.

Newton a differenciálszámítás felfedezéséhez egy anyagi pont adott időpillanatbeli sebességével (pillanatnyi sebességgel) kapcsolatos problémák megoldása során jutott el.

Mint ismeretes, egységes mozgás olyan mozgás, amelyben egy test egyenlő időközönként egyenlő hosszúságú utat tesz meg. A test által időegység alatt megtett távolságot ún sebesség egyenletes mozgás.

A gyakorlatban azonban leggyakrabban egyenetlen mozgással van dolgunk. Az úton haladó autó az átkelőhelyeken lassít, és azokon a szakaszokon gyorsít, ahol szabad az út; leszálláskor lelassul a gép stb. Ezért leggyakrabban azzal kell számolnunk, hogy a test egyenlő időintervallumokban halad át különböző hosszúságú útszakaszokon. Az ilyen mozgást ún egyenetlen. Sebessége nem jellemezhető egyetlen számmal.

Gyakran az egyenetlen mozgás jellemzésére használják ezt a fogalmat átlagsebesség mozgás a ∆t٫ idő alatt, amelyet a reláció határoz meg, ahol ∆s a test által ∆t idő alatt megtett út.

Tehát szabadesésben lévő test esetén a mozgásának átlagos sebessége az első két másodpercben

A gyakorlatban a mozgás olyan jellemzője, mint az átlagos sebesség, nagyon keveset mond a mozgásról. Valójában 4,9 m / s és a 2. - 14,7 m / s, míg az átlagos sebesség az első két másodpercben 9,8 m / s. Az első két másodperc átlagos sebessége nem ad fogalmat arról, hogyan történt a mozgás: mikor mozgott gyorsabban a test, és mikor lassabban. Ha minden másodpercre külön beállítjuk az átlagos mozgási sebességeket, akkor tudni fogjuk például, hogy a 2. másodpercben a test sokkal gyorsabban mozgott, mint az 1. másodpercben. Azonban a legtöbb esetben sokkal gyorsabban, mint amivel nem vagyunk elégedettek. Hiszen könnyen érthető, hogy ebben a 2. másodpercben a test is különbözőképpen mozog: az elején lassabban, a végén gyorsabban. És hogyan mozog valahol ennek a 2. másodpercnek a közepén? Más szóval, hogyan határozható meg a pillanatnyi sebesség?

A test mozgását írja le a törvény ∆t-vel egyenlő ideig. Abban a pillanatban, hogy t0 a test áthaladt az ösvényen, jelenleg - az ösvényen. Ezért a ∆t idő alatt a test megtett egy távolságot, és a test átlagos sebessége ezen időtartam alatt ez lesz.

Minél rövidebb a ∆t időintervallum, annál pontosabban meg lehet állapítani, hogy a test mekkora sebességgel mozog t0 pillanatban, mivel egy mozgó test nem tudja rövid időn belül jelentősen megváltoztatni a sebességét. Ezért az átlagos sebesség, mivel ∆t nullára hajlik, megközelíti a tényleges mozgási sebességet, és határértékben megadja a mozgás sebességét egy adott t0 időpontban (pillanatnyi sebesség).

Ily módon ,

1. definíció. Azonnali sebesség A test egyenes vonalú mozgásának egy adott t0 időpontban az átlagsebesség határát t0-tól t0+ ∆t-ig tartjuk, amikor a ∆t időintervallum nullára tart.

Tehát ahhoz, hogy egy adott pillanatban meg lehessen találni az egyenes vonalú nem egyenletes mozgás sebességét, meg kell találni a ∆ út növekményének a ∆t időnövekedéshez viszonyított arányának határát az ún. Leibniz a differenciálszámítás felfedezéséhez érkezett, miközben megoldotta azt a problémát, hogy az egyenlete által adott bármely görbe érintőjét megszerkesztse.

A probléma megoldása megvan nagyon fontos. Végül is egy mozgó pont sebessége a pályájának érintője mentén irányul, ezért a pályáján lévő lövedék sebességének meghatározásakor a pályáján lévő bármely bolygó sebességét a pályán lévő érintő irányának meghatározására redukáljuk. ív.

Az érintő definíciója olyan egyenesként, amelynek csak egy közös pontja van a görbével, amely körre érvényes, sok más görbére alkalmatlan.

A görbe érintőjének alábbi definíciója nem csak a vele kapcsolatos intuitív elképzelésnek felel meg, hanem lehetővé teszi az irányának tényleges megtalálását is, pl. számítsa ki az érintő meredekségét.

2. definíció. Tangens Az M pontban lévő görbét MT egyenesnek nevezzük, amely az MM1 szekáns határhelyzete, amikor az M1 pont a görbe mentén haladva korlátlanul megközelíti az M pontot.

1.2 Származékos definíció

Vegye figyelembe, hogy a görbe érintőjének és az egyenetlen mozgás pillanatnyi sebességének meghatározásakor lényegében ugyanazokat a matematikai műveleteket hajtják végre:

1. Az argumentum adott értéke növekszik, és a függvény új értékét számítja ki az argumentum új értékének megfelelően.

2. Határozza meg a kiválasztott argumentumnövekménynek megfelelő függvénynövekményt.

3. A függvény növekményét elosztjuk az argumentum növekményével.

4. Számítsa ki ennek az aránynak a határát, feltéve, hogy az argumentum növekménye nullára hajlik!

Számos probléma megoldása korlátozza az ilyen típusú átmeneteket. Szükség van egy általánosításra, és a végletekig el kell nevezni ezt a részt.

A függvény változási sebessége az argumentum változásától függően nyilvánvalóan egy aránnyal jellemezhető. Ezt a kapcsolatot úgy hívják átlagsebesség a funkció a tól ig intervallumban változik. Most figyelembe kell vennünk a tört határát, ennek az aránynak a határa, mivel az argumentum növekménye nullára hajlik (ha ez a határ létezik), ennek valami új függvénye. Ezt a függvényt az y' szimbólumok jelölik, amelyeket hívnak derivált ezt a függvényt, hiszen a függvényből kapjuk (előállítjuk) Magát a függvényt nevezzük primitív függvény a származékához képest

3. definíció. derivált függvények egy adott pontban megnevezik a ∆y függvény növekményének és az ∆x argumentum megfelelő növekményének arányának határát, feltéve, hogy ∆x→0, azaz.

1.3 A származék megtalálásának általános szabálya

Valamely függvény deriváltjának megtalálásának műveletét ún különbségtétel függvények, és a matematikának az e művelet tulajdonságait vizsgáló ága az differenciálszámítás.

Ha egy függvénynek van deriváltja az x=a helyen, akkor azt mondjuk, hogy az megkülönböztethető ezen a ponton. Ha egy függvénynek egy adott intervallum minden pontjában van deriváltja, akkor azt mondjuk, hogy az megkülönböztethető Ezen intervallum .

A derivált definíciója nemcsak teljes mértékben jellemzi a függvény változási sebességének fogalmát az argumentum megváltozásakor, hanem lehetőséget ad egy adott függvény deriváltjának tényleges kiszámítására is. Ehhez a következő négy műveletet (négy lépést) kell végrehajtania, amelyek a származék definíciójában szerepelnek:

1. Keressen egy új függvényértéket az in bemutatásával ezt a funkciót x helyett az argumentum új értéke: .

2. A függvény növekményét úgy határozzuk meg, hogy a függvény adott értékét kivonjuk az új értékéből: .

3. Állítsa össze a függvény növekményének és az argumentum növekményének arányát: .

4. Menjen a határértékre, és keresse meg a deriváltot: .

Általánosságban elmondható, hogy a derivált egy „új” függvény, amely egy adott függvényből egy meghatározott szabály szerint származtatott.

1.4 A derivált geometriai jelentése

A derivált geometriai értelmezése, először a késő XVII ban ben. Leibniz a következő: a függvény deriváltjának értéke az x pontban egyenlő a függvény grafikonjára ugyanabban az x pontban húzott érintő meredekségével, azok.

Az érintő egyenlete, mint bármely áthaladó egyenes adott pont ebben az irányban a formája – aktuális koordináták. De az érintőegyenletet a következőképpen is felírjuk: . A normál egyenlet az alakban lesz felírva

1.5 A származék mechanikai jelentése

A derivált mechanikus értelmezését először I. Newton adta meg. Ez a következőkből áll: egy anyagi pont mozgási sebessége egy adott időpillanatban megegyezik az út időbeli deriváltjával, azaz. Tehát, ha egy anyagi pont mozgástörvényét egy egyenlet adja meg, akkor egy pont pillanatnyi sebességének meghatározásához egy adott időpillanatban meg kell találni a derivált, és be kell cserélni a megfelelő t értékét. .

1.6 Másodrendű származék és mechanikai jelentése

Azt kapjuk (egyenlet abból, amit Lisichkin V.T. Soloveychik I.L. "Matematika" 240. o. című tankönyvében tettek):

Ily módon a test egyenes vonalú mozgásának gyorsulása egy adott pillanatban megegyezik az út adott pillanatra számított időbeli második deriváltjával. Ez a második származék mechanikus jelentése.

1.7 A differenciál definíciója és geometriai jelentése

4. definíció. A függvény növekményének fő részét, a függvény növekedéséhez képest lineáris, a független változó növekedéséhez képest lineárisan ún. differenciális függvények, és d-vel jelöljük, azaz. .

Funkció differenciál geometriailag a pontba húzott érintő ordinátájának növekedésével ábrázolva M ( x ; y ) adott x és ∆x értékekre.

számítás differenciális – .

A differenciál alkalmazása közelítő számításokban – , a függvény növekményének közelítő értéke egybeesik a differenciáljával.

1. tétel. Ha a differenciálható függvény növekszik (csökken) egy adott intervallumban, akkor ennek a függvénynek a deriváltja nem negatív (nem pozitív) ebben az intervallumban.

2. tétel. Ha a derivált függvény pozitív (negatív) valamilyen intervallumban, akkor a függvény ebben az intervallumban monoton növekvő (monoton csökkenő).

Fogalmazzuk meg most a függvény monotonitási intervallumainak megtalálásának szabályát

1. Számítsa ki ennek a függvénynek a deriváltját!

2. Keressen pontokat, ahol nulla vagy nem létezik. Ezeket a pontokat ún kritikai funkcióhoz

3. A talált pontokkal a függvény tartománya intervallumokra van felosztva, amelyek mindegyikén a derivált megtartja előjelét. Ezek az intervallumok a monotonitás intervallumai.

4. Vizsgálja meg a jelet az egyes talált intervallumokon. Ha a figyelembe vett intervallumon, akkor ezen az intervallumon növekszik; ha, akkor ilyen intervallumon csökken.

A probléma körülményeitől függően a monotonitási intervallumok megtalálásának szabálya egyszerűsíthető.

5. definíció. Egy pontot egy függvény maximális (minimális) pontjának nevezünk, ha az egyenlőtlenség a pont valamely környezetéből származó bármely x-re érvényes.

Ha a függvény maximális (minimális) pontja, akkor ezt mondjuk (minimális) azon a ponton. Maximum és minimum függvények egyesítik a nevet extrémum függvényeket, és a maximum és minimum pontokat hívjuk meg szélsőpontok (extrém pontok).

3. tétel.(az extrémum szükséges jele). Ha egy és a derivált ezen a ponton létezik, akkor egyenlő nullával: .

4. tétel.(elegendő extrémum jele). Ha a származék amikor x áthalad a akkor előjelet vált a a függvény szélsőpontja .

A derivált vizsgálatának főbb pontjai:

1. Keresse meg a származékot.

2. Keresse meg az összes kritikus pontot a függvény tartományából.

3. Állítsa be a függvény deriváltjának előjeleit a kritikus pontokon való áthaladáskor, és írja ki a szélsőpontokat!

4. Számítsa ki a függvényértékeket minden szélső pontban.

2. Függvények vizsgálata a származékkal

1. feladat . Napló hangereje. A megfelelő formájú, fahibák nélküli rönköket, amelyek vastag és vékony végeinek átmérője viszonylag kis különbséggel rendelkezik, ipari kerekfának nevezzük. Az ipari körfa térfogatának meghatározásakor általában egyszerűsített képletet használnak, ahol a rönk hossza az átlagos metszet területe. Tudja meg, hogy a valódi mennyiség véget ér-e vagy alábecsüli-e; becsülje meg a relatív hibát.

Megoldás. A kerek üzleti fa alakja közel áll a csonka kúphoz. Legyen a rönk nagyobb, kisebb végének sugara. Ekkor a majdnem pontos térfogata (a csonka kúp térfogata) – mint ismeretes – a képlettel meghatározható. Legyen az egyszerűsített képlettel számított térfogatérték. Akkor;

Azok. . Ez azt jelenti, hogy az egyszerűsített képlet alábecsüli a térfogatot. Tegyük fel most. Akkor. Ez azt mutatja, hogy a relatív hiba nem a rönk hosszától függ, hanem az arány határozza meg. Mióta nő az intervallumon. Ezért, ami azt jelenti, hogy a relatív hiba nem haladja meg a 3,7%-ot. Az erdőtudomány gyakorlatában egy ilyen hiba meglehetősen elfogadhatónak tekinthető. Nagyobb pontossággal gyakorlatilag lehetetlen megmérni sem a végek átmérőjét (mert ezek némileg eltérnek a köröktől), sem a rönk hosszát, mivel nem a magasságot, hanem a kúp generatrixát (a kúp hosszát) mérik. a rönk több tízszer nagyobb, mint az átmérő, és ez nem vezet nagy hibákhoz). Így első látásra helytelen, de több egyszerű képlet mert egy csonkakúp térfogata valós helyzetben egészen jogosnak bizonyul. Speciális igazolási módszerekkel ismételten elvégzett vizsgálat azt mutatta, hogy az ipari erdő tömeges elszámolásával a relatív hiba a figyelembe vett képlet használatakor nem haladja meg a 4%-ot.

2. feladat . A gödrök, vödrök és egyéb csonka kúp alakú tartályok térfogatának meghatározásakor a mezőgazdasági gyakorlatban néha egyszerűsített képletet használnak, ahol a magasság a kúp alapjainak területe. Állapítsa meg, hogy a valós térfogat túl- vagy alulbecsült-e, becsülje meg a relatív hibát a gyakorlatra természetes feltétel mellett: (- alapsugár, .

Megoldás. A csonkakúp térfogatának valós értékén keresztül jelölve, és az egyszerűsített képlettel számított értéken keresztül kapjuk: , azaz. . Ez azt jelenti, hogy az egyszerűsített képlet túlbecsüli a térfogatot. Az előző feladat megoldását tovább ismételve azt találjuk, hogy a relatív hiba nem haladja meg a 6,7%-ot. Valószínűleg ez a pontosság elfogadható az ásatási munkák arányosítása során - elvégre a gödrök nem lesznek ideális kúpok, és a megfelelő paramétereket valós körülmények között nagyon durván mérik.

3. feladat . A szakirodalomban a marógép orsójának β elfordulási szögének meghatározására fogazott tengelykapcsolók marásakor egy képletet vezetnek le, ahol. Mivel ez a képlet összetett, ajánlatos elvetni a nevezőt, és egyszerűsített képletet használni. Milyen (- egész szám,) esetén használható ez a képlet, ha a szög meghatározásakor hiba megengedett?

Megoldás. A pontos képlet egyszerű után azonos átalakulások eszünkbe lehet juttatni. Ezért közelítő képlet használatakor abszolút hiba megengedett, ahol. Tanulmányozzuk a függvényt az intervallumon. Ebben az esetben 0,06, azaz. a szöglet az első negyedhez tartozik. Nekünk van: . Vegye figyelembe, hogy a vizsgált intervallumon, és így a függvény ezen az intervallumon csökken. Mivel tovább, minden tekintetben. Azt jelenti,. Mivel ez egy radián, elegendő az egyenlőtlenség feloldásához. Ezt az egyenlőtlenséget kiválasztással megoldva azt találjuk, hogy, . Mivel a függvény csökken, ebből az következik

Következtetés

A származék használata meglehetősen tág, és az ilyen típusú munkákban teljes mértékben lefedhető, de megpróbáltam kitérni a főbb pontokra. Napjainkban azzal kapcsolatban tudományos és technológiai haladás, különösen a számítástechnikai rendszerek gyors fejlődésével a differenciálszámítás egyre relevánsabb mind az egyszerű, mind a szuperbonyolult problémák megoldásában.

Irodalom

1. V.A. Petrov "Matematikai elemzés a termelési feladatokban"

2. Soloveicchik I.L., Lisichkin V.T. "Matematika"

Chaikin Semyon, Maysak Kirill, Zalogina Anastasia, Shakhzadova Anna

Ez a fejlesztés egy előadást tartalmaz "A származék alkalmazása a kémiában és a biológiában" témában. Alatt projekt tevékenységek felterjesztették azt a hipotézist, hogy a származékot ezeken a tudományterületeken alkalmazzák. Alatt kutatómunka kiderült, hogy mi a szerepe a származéknak olyan tudományokban, mint a kémia és a biológia, hol és milyen problémák megoldásában találja alkalmazását. Az elvégzett munka eredményeként arra a következtetésre jutottak, hogy a hipotézis valóban beigazolódott.

Letöltés:

Előnézet:

https://accounts.google.com

Diák feliratai:

Hipotézis:

Előnézet:

A prezentációk előnézetének használatához hozzon létre egy Google-fiókot (fiókot), és jelentkezzen be: https://accounts.google.com

Diák feliratai:

A származék használata a kémiában és a biológiában A munkát az MBOU 6. számú középiskola 11B osztályos diákjai végezték: Chaikin Semyon, Maisak Kirill, Zalogina Anastasia, Shakhzadova Anna Stavropol, 2014

Hipotézis:

A kémiában pedig a differenciálszámítást széles körben alkalmazzák a kémiai reakciók matematikai modelljeinek megalkotására és tulajdonságaik későbbi leírására. A kémia az anyagok tudománya, az anyagok kémiai átalakulása. A kémia a különféle reakciók mintázatait vizsgálja A kémiai reakció sebessége a reagáló anyagok koncentrációjának egységnyi idő alatti változása. A származék alkalmazása a kémiában és a biológiában Kémiai reakció sebességének meghatározása

Miért van szükségünk deriváltra a reakciókban? Mivel a v reakciósebesség a folyamat során folyamatosan változik, általában a reaktánsok koncentrációjának időbeli származékaként fejezik ki.

A derivált képlet a kémiában Ha C (t) a kémiai reakcióba lépett anyag mennyiségének változásának törvénye, akkor a kémiai reakció sebessége v (t) a t időpontban egyenlő a származékkal:

A reakciósebesség meghatározása A növekményes függvény és a növekményes argumentum arányának határa, mivel Δt nullára hajlik, a kémiai reakció sebessége egy adott időpontban

Kémiai feladat: Adja meg a kémiai reakcióba lépett anyag mennyiségét a függőség: C (t) \u003d t 2 / 2 + 3 t -3 (mol) Határozza meg a kémiai reakció sebességét 3 másodperc után! Megoldás: v (t) = C ‘(t) ; v (t) = t + 3; v (3) = 3+3 = 6. Válasz: 6 mol/s.

A származék biológiai jelentése Adjuk meg az y mikroorganizmusok populációjának egyedszáma és szaporodási t ideje közötti összefüggést a következő egyenlettel: y = x (t). Legyen ∆ t valamely t kezdeti érték és t + ∆ t közötti időintervallum. Ekkor y + ∆y = x (t + ∆ t) a populáció méretének új értéke, amely megfelel a t + ∆ t pillanatnak, és ∆ y + x (t + ∆ t) - x (t) a változás az élőlények egyedeinek száma. Az arány az átlagos szaporodási ráta, vagy ahogy mondani szokás, a népesség átlagos termelékenysége. Kiszámítva azt kapjuk, hogy y ' = P (t) = x ' (t) , vagyis a sokaság termelékenysége t időpontban.

Példa Legyen a t (c) időpontban a baktériumpopulációnak x(t) egyede. . Határozzuk meg a népességnövekedés ütemét: a) tetszőleges t pillanatban, b) t = 1 c pillanatban. Megoldás: P = x'(t) = 200t; P(1) = 200 (r/s). Válasz: 200 o/s.

Következtetés A származék fogalma nagyon fontos a kémiában és a biológiában, különösen a reakció sebességének meghatározásában.

Következtetés: A differenciálszámítás a minket körülvevő világ leírása, matematikai nyelven. A derivált a számítás egyik legfontosabb fogalma. A derivált ismerete nemcsak matematikai, hanem gyakorlati problémákat is segít sikeresen megoldani a tudomány, a technika és az élet különböző területein.

Dél-Szahalin Állami Egyetem

Matematika Tanszék

Tanfolyami munka

Téma: A derivált gyakorlati alkalmazása

Előadó: Likhacheva O.N.

Juzsno-Szahalinszk

2002
Bevezetés

Ebben a cikkben a származékok különböző tudományokban és iparágakban való alkalmazásait vizsgálom meg. A munka fejezetekre tagolódik, amelyek mindegyike a differenciálszámítás egy-egy aspektusával foglalkozik (geometriai, fizikai jelentés stb.)

1. A származék fogalma

1-1. Történelmi információk

A differenciálszámítást Newton és Leibniz alkotta meg a 17. század végén két probléma alapján:

1) egy tetszőleges egyenes érintőjének megtalálásáról

2) a sebesség önkényes mozgástörvénnyel való kereséséről

Már korábban is találkoztak a derivált fogalmával Tartaglia olasz matematikus (körülbelül 1500 - 1557) munkáiban - itt egy érintő jelent meg a pisztoly dőlésszögének kérdéskörének tanulmányozása során, amely biztosítja a legnagyobb hatótávolságot. a lövedéké.

A 17. században G. Galileo mozgáselmélete alapján a derivált kinematikai koncepciója aktívan fejlődött. Különféle előadások kezdtek megjelenni Descartes, a francia matematikus, Roberval és az angol tudós, L. Gregory munkáiban. Lopital, Bernoulli, Lagrange, Euler, Gauss nagyban hozzájárult a differenciálszámítás tanulmányozásához.

1-2. A származék fogalma

Legyen y \u003d f (x) az (a; b) intervallumban definiált x argumentum folytonos függvénye, és legyen x 0 ennek az intervallumnak tetszőleges pontja

Az x argumentumnak ∆x növekményt adunk, ekkor az y = f(x) függvény ∆y = f(x + ∆x) - f(x) növekményt kap. Azt a határt, amelyre a ∆y / ∆x arány ∆x → 0-ra hajlik, az f(x) függvény deriváltjának nevezzük.

1-3. A differenciálás szabályai és a származékok táblázata

		(sin x)" = cos x
	(1/x)" = -1/x2	(cos x)" = -sin x
	(√x)" = 1 / 2√x	(tg x)" = 1 / cos 2 x
(uv)" = u"v + uv"	(a x)" = a x log x	(ctg x)" = 1 / sin 2 x
(u / v)"=(u"v - uv") / v 2		(arcsin x)" = 1 / √ (1- x 2)
	(log a x)" = (log a e) / x	(arccos x)" = -1 / √ (1- x 2)
	(ln x)" = 1 / x	(arctg x)" = 1 / √ (1+ x 2)
		(arcctg x)" = -1 / √ (1+ x 2)

2. A származék geometriai jelentése

2-1. Görbe érintő

Legyen egy görbénk és rajta egy fix M pont és egy N. Az M pont érintője egy egyenes, amelynek pozícióját hajlamos az MN húr elfoglalni, ha az N pontot korlátlanul közelítjük meg a vonal mentén. görbe M-re.

Tekintsük az f(x) függvényt és a függvénynek megfelelő y = f(x) görbét. Valamely x érték esetén a függvény értéke y = f(x). A görbén ezek az értékek az M(x 0 , y 0) pontnak felelnek meg. Vezessünk be egy új x 0 + ∆x argumentumot, melynek értéke megfelel az y 0 + ∆y = f(x 0 + ∆x) függvény értékének. A megfelelő pont N(x 0 + ∆x, y 0 + ∆y). Rajzolja meg az MN szekánst, és jelölje φ-vel a szekáns által az Ox tengely pozitív irányával bezárt szöget. Az ábrán látható, hogy ∆y / ∆x = tg φ. Ha most ∆x megközelíti a 0-t, akkor az N pont elmozdul a görbén, a szekáns MN elfordul az M pont körül, és a φ szög megváltozik. Ha ∆x → 0-ként a φ szög valamilyen α-ra hajlik, akkor az M-en átmenő és az abszcissza tengelyének pozitív irányával α szöget bezáró egyenes lesz a szükséges érintő. Ugyanakkor a lejtési együtthatója:

Azaz az f "(x) derivált értéke az x argumentum adott értékéhez egyenlő annak a szögnek az érintőjével, amelyet az f (x) függvény grafikonjának érintője az Ox tengely pozitív irányával alkot. ) az M (x, f (x) pontban).

A térvonal érintőjének definíciója hasonló a síkgörbe érintőjéhez. Ebben az esetben, ha a függvényt a z = f(x, y) egyenlet adja meg, az OX és OY tengelyeken lévő meredekségek egyenlőek lesznek f parciális deriváltjaival x és y vonatkozásában.

2-2. A felület érintő síkja

A felület érintősíkja az M pontban az a sík, amely tartalmazza a felület minden térbeli görbéjének érintőit, amelyek M-en - az érintkezési ponton - haladnak át.

Vegyük az F(x, y, z) = 0 egyenlet által adott felületet és rajta valamilyen közönséges M(x 0, y 0, z 0) pontot. Tekintsünk a felületen valamilyen M-en átmenő L görbét. Adják meg a görbét az egyenletek

x = φ(t); y = ψ(t); z = χ(t).

Helyettesítsük be ezeket a kifejezéseket a felület egyenletébe. Az egyenlet azonossággá válik, mivel a görbe teljes egészében a felszínen fekszik. A differenciál alakjának invariancia tulajdonságát felhasználva megkülönböztetjük a kapott egyenletet t vonatkozásában:

Az L görbe érintőjének egyenlete az M pontban a következő:

Mivel az x - x 0, y - y 0, z - z 0 különbségek arányosak a megfelelő differenciálokkal, a sík végső egyenlete így néz ki:

F" x (x - x 0) + F" y (y - y 0) + F" z (z - z 0)=0

és az adott esetben z = f(x, y):

Z - z 0 \u003d F "x (x - x 0) + F" y (y - y 0)

Példa: Határozzuk meg az érintősík egyenletét a hiperbolikus paraboloid (2a; a; 1,5a) pontjában

Megoldás:

Z" x \u003d x / a \u003d 2; Z" y \u003d -y / a \u003d -1

A kívánt sík egyenlete:

Z - 1,5a = 2 (x - 2a) - (Y - a) vagy Z = 2x - y - 1,5a

3-1. Anyagpont sebesség

Legyen az s út függése az adott t időtől egyenes vonalú mozgás az anyagi pontot az s = f(t) egyenlet fejezi ki, és t 0 egy bizonyos időpillanat. Tekintsünk egy másik t időpontot, jelöljük ∆t = t - t 0-t, és számítsuk ki az útnövekményt: ∆s = f(t 0 + ∆t) - f(t 0). A ∆s / ∆t arányt a t 0 kezdeti pillanattól eltelt ∆t idő alatti átlagos mozgási sebességnek nevezzük. A sebesség ennek az aránynak a határa: ∆t → 0.

Az egyenetlen mozgás átlagos gyorsulása az intervallumban (t; t + ∆t) az érték =∆v / ∆t. Egy anyagi pont pillanatnyi gyorsulása t időpontban lesz az átlagos gyorsulás határa:

Vagyis az első derivált (v "(t)).

Példa: A test által megtett út időtől való függését az s \u003d A + Bt + Ct 2 + Dt 3 egyenlet adja meg (C \u003d 0,1 m / s, D \u003d 0,03 m / s 2). Határozza meg a mozgás megkezdése utáni időt, amely után a test gyorsulása 2 m / s 2 lesz.

Megoldás:

v(t) = s "(t) = B + 2Ct + 3Dt 2; a(t) = v"(t) = 2C + 6Dt = 0,2 + 0,18t = 2;

1,8 = 0,18 t; t = 10 s

3-2. Egy anyag hőkapacitása adott hőmérsékleten

Különböző T hőmérsékletek növelése ugyanazzal az értékkel, amely egyenlő T 1 - T értékkel, 1 kg-onként. adott anyagnak más hőmennyiségre van szüksége Q 1 - Q, és az arány

mert ez az anyag nem állandó. Így egy adott anyagra a Q hőmennyiség a T hőmérséklet nemlineáris függvénye: Q = f(T). Ekkor ΔQ = f(t + ΔT) - f(T). Hozzáállás

intervallumon az átlagos hőkapacitásnak nevezzük, és ennek a kifejezésnek a határát ∆T → 0 esetén az adott anyag hőkapacitásának nevezzük T hőmérsékleten.

3-3. Erő

változás mechanikus mozgás testet más testekből rá ható erők okozzák. A kölcsönható testek közötti energiacsere folyamatának kvantitatív jellemzése érdekében a mechanikában bevezetik az erő munkájának fogalmát. A munkavégzés ütemének jellemzésére bevezetjük a hatalom fogalmát:

4. Differenciálszámítás a közgazdaságtanban

4-1. Funkciókutatás

A differenciálszámítás egy matematikai eszköz, amelyet széles körben használnak gazdasági elemzésre. A közgazdasági elemzés alapvető feladata a függvényként felírt közgazdasági mennyiségek összefüggéseinek vizsgálata. Milyen irányba változik az állam bevétele, ha emelik az adókat vagy ha bevezetik az importvámokat? Növekszik vagy csökken-e a cég bevétele, ha termékeinek ára nő? Milyen arányban pótolhatják a nyugdíjas munkavállalókat a kiegészítő felszerelések? Az ilyen problémák megoldásához meg kell alkotni a bennük szereplő változók kapcsolódási függvényeit, amelyeket azután a differenciálszámítás módszereivel tanulmányozunk. A közgazdaságtanban gyakran meg kell találni egy mutató legjobb vagy optimális értékét: a legmagasabb munkatermelékenységet, maximális profitot, maximális kibocsátást, minimális költségeket stb. Minden mutató egy vagy több érv függvénye. Így a mutató optimális értékének megtalálása a függvény szélsőértékének megtalálására redukálódik.

Fermat tétele szerint, ha egy pont egy függvény szélsőpontja, akkor a derivált vagy nem létezik benne, vagy egyenlő 0-val. A szélsőség típusát a szélsőértékre vonatkozó elegendő feltétel valamelyikével határozhatjuk meg:

1) Legyen az f(x) függvény az x 0 pont valamely környezetében differenciálható. Ha az f "(x) derivált az x 0 ponton áthaladva előjelet vált +-ról -ra, akkor x 0 a maximális pont, ha -ból +-ra, akkor x 0 a minimumpont, ha nem változtat előjelet , akkor nincs extrémum.

2) Legyen az f (x) függvény kétszer differenciálható az x 0 pont valamelyik környezetében, és f "(x 0) \u003d 0, f "" (x 0) ≠ 0, akkor az x 0 pontban a függvény f (x 0) maximummal rendelkezik, ha f ""(x 0)< 0 и минимум, если f ""(x 0) > 0.

Ezenkívül a második derivált a függvény konvexitását jellemzi (a függvény grafikonját konvexnek nevezzük fel [le] az (a, b) intervallumon, ha ezen az intervallumon nem magasabb [nem alacsonyabb], mint bármelyik érintők).

Példa: válassza ki a vállalat optimális termelési volumenét, amelynek profitfüggvénye a függéssel modellezhető:

π(q) = R(q) - C(q) = q 2 - 8q + 10

Megoldás:

π"(q) = R"(q) - C"(q) = 2q - 8 = 0 → q extr = 4

A q< q extr = 4 → π"(q) < 0 и прибыль убывает

q > q esetén extr = 4 → π"(q) > 0 és a profit nő

Ha q = 4, akkor a nyereség a minimális értéket veszi fel.

Mi az optimális teljesítmény a cég számára? Ha a vállalat nem tud 8 egységnél többet termelni a vizsgált időszakban (p(q = 8) = p(q = 0) = 10), akkor az optimális megoldás az lenne, ha semmit sem termelne, hanem bevételhez jutna. helyiségek és/vagy berendezések bérbeadásából. Ha a cég 8 egységnél többet tud előállítani, akkor a cég számára az lesz az optimális, ha a termelési kapacitása határán termel.

4-2. A kereslet rugalmassága

Az f (x) függvény rugalmasságát az x 0 pontban határértéknek nevezzük

A kereslet a vevő által keresett áru mennyisége. A kereslet árrugalmassága E D annak mértéke, hogy a kereslet hogyan reagál az árváltozásokra. Ha │E D │>1, akkor a keresletet rugalmasnak nevezzük, ha │E D │<1, то неэластичным. В случае E D =0 спрос называется совершенно неэластичным, т. е. изменение цены не приводит ни к какому изменению спроса. Напротив, если самое малое снижение цены побуждает покупателя увеличить покупки от 0 до предела своих возможностей, говорят, что спрос является совершенно эластичным. В зависимости от текущей эластичности спроса, предприниматель принимает решения о снижении или повышении цен на продукцию.

4-3. Limit elemzés

A közgazdaságtanban alkalmazott differenciálszámítás módszereinek fontos részét képezik a limitáló elemzés módszerei, azaz a költségek vagy eredmények változó értékeinek tanulmányozására szolgáló módszerek a termelési, fogyasztási stb. mennyiségek változásai alapján. határértékeik elemzéséről. Egy függvény korlátozó mutatója(i) a deriváltja (egy változó függvénye esetén) vagy parciális deriváltjai (több változó függvénye esetén)

A közgazdaságtanban gyakran használnak átlagokat: átlagos munkatermelékenység, átlagos költségek, átlagjövedelem, átlagos nyereség stb. De gyakran meg kell találni, hogy mennyivel nő az eredmény, ha a költségeket növelik, vagy fordítva, mennyivel. csökkenni fog, ha csökkennek a költségek. Átlagértékek segítségével erre a kérdésre nem lehet válaszolni. Ilyen problémáknál meg kell határozni az eredmény és a költségek növekedésének arányának határát, vagyis a határhatást. Ezért ezek megoldásához a differenciálszámítás módszereit kell alkalmazni.

5. Derivált közelítő számításokban

5-1. Interpoláció

Az interpoláció egy függvény értékeinek hozzávetőleges kiszámítása több megadott értékből. Az interpolációt széles körben használják a térképészetben, a geológiában, a közgazdaságtanban és más tudományokban. A legegyszerűbb interpolációs lehetőség a Lagrange-forma, de ha sok csomópont van, és a közöttük lévő intervallumok nagyok, vagy olyan függvényt szeretnénk kapni, amelynek görbülete minimális, akkor folyamodjunk spline interpolációhoz, amely nagyobb pontosságot ad.

Legyen K n a = x 0 csomópontok rendszere< x 1 <…< x n = b. Функция S k (x) называется сплайн-функцией S k (x) степени k≥0 на K n , если

a) S k (x) є C k -1 ()

b) S k (x) legfeljebb k fokú polinom

A Ŝ k (x) є S k (K n) spline függvényt interpoláló spline függvénynek nevezzük, ha Ŝ k (x j) = f(x j) j = 0,1,…,n esetén

Az alkalmazásokban gyakran elég a k=3-at választani és alkalmazni az ún köbös interpoláció.

Mivel s(x) harmadfokú polinom minden parciális intervallumon, akkor x esetén є

Itt s 2 j , c j 1 , c j 0 ismeretlenek j = 1, 2, …, n esetén

Ez utóbbiak az s(x j) = y j követelmény miatt ki vannak zárva:

Megkülönböztetve ezt a függvényt, és figyelembe véve, hogy s "(x)-nek folytonosnak kell lennie a teljes intervallumon, és ezért különösen a csomópontoknál, végül megkapjuk az egyenletrendszert:

n+1 ismeretlenhez képest s 2 0, s 2 1,…, s 2 n. Az egyértelmű meghatározás érdekében a feladattól függően további két egyenletet adunk hozzá:

normál eset (N):

Időszakos eset(P) (azazf(x+(x n -x 0))=f(x)):

Meghatározott simítás a szegélyeken:

Példa: az f(x)=sin x, n=4 függvény spline interpolációja.

A függvény periodikus, ezért a P esetet használjuk.

A spline függvény így néz ki:

5-2. Taylor képlet

A függvények végtelen sorozatokba való kiterjesztése lehetővé teszi, hogy egy adott pontban tetszőleges pontossággal megkapjuk a függvény értékét. Ezt a technikát széles körben használják a programozásban és más tudományágakban.

Egy függvényről azt mondjuk, hogy adott intervallumon hatványsorrá bővül, ha létezik ilyen hatványsor a 0 + a 1 (x - a) + a 2 (x - a) 2 + ... + a n (x - a) ) n + ..., amely ezen az intervallumon konvergál ehhez a függvényhez. Bizonyítható, hogy ez a dekompozíció egyedi:

Legyen az f(x) függvény végtelenül differenciálható az a pontban. Az űrlap hatványsorai

az f(x) függvény Taylor-sorozatának nevezzük, a különbség hatványaiban (x - a) írva. Általánosságban elmondható, hogy ahhoz, hogy a Taylor-sor f(x)-hez konvergáljon, szükséges és elégséges, hogy a sorozat többi része 0-ra hajlik. A = 0 esetén a Taylor-sort általában Maclaurin-sornak nevezik.

I. M. Uvarenkov,

M. Z. Maller

Matematikai elemzés tanfolyam, v.1

V. A. Dudarenko,

A.A. Dadayan

Matematikai elemzés

Differenciál- és integrálszámítás

T. I. Trofimova

Fizika tanfolyam

O. O. Zamkov

A. V. Tolsztopjatenko

Yu. N. Cheremnykh

Matematikai módszerek a közgazdaságtanban

A. S. Solodovnikov

V. A. Babacev

A. V. Brailov

I.G. Shandra

Matematika a közgazdaságtanban

Bevezetés

1. A származék fogalma

1-1. Történelmi információk

1-2. A származék fogalma

1-3. A differenciálás szabályai és a származékok táblázata

2. A származék geometriai jelentése

2-1. Görbe érintő

2-2. A felület érintő síkja

3. A derivált használata a fizikában

3-1. Anyagpont sebesség

3-2. Hőteljesítmény adott hőmérsékleten

3-3. Erő

4. Differenciálszámítás a közgazdaságtanban

4-1. Funkciókutatás

4-2. A kereslet rugalmassága

4-3. Limit elemzés

5. Derivált közelítő számításokban

5-1. Interpoláció

5-2. Taylor képlet

5-3. Hozzávetőleges számítások

Következtetés

Felhasznált irodalom jegyzéke

Dél-Szahalin Állami Egyetem

Matematika Tanszék

Tanfolyami munka

Téma: A derivált gyakorlati alkalmazása

Előadó: Likhacheva O.N.

Juzsno-Szahalinszk

2002 Bevezetés

1. A származék fogalma

1-1. Történelmi információk

A differenciálszámítást Newton és Leibniz alkotta meg a 17. század végén két probléma alapján:

1) egy tetszőleges egyenes érintőjének megtalálásáról

2) a sebesség önkényes mozgástörvénnyel való kereséséről

Már korábban is találkoztak a derivált fogalmával Tartaglia olasz matematikus (körülbelül 1500 - 1557) munkáiban - itt egy érintő jelent meg a fegyver dőlésszögének kérdéskörének tanulmányozása során, amely biztosítja a legnagyobb hatótávolságot. a lövedéké.

1-2. A származék fogalma

Legyen y = f(x) az (a; b) intervallumban definiált x argumentum folytonos függvénye, és legyen x0 ennek az intervallumnak tetszőleges pontja

1-3. A differenciálás szabályai és a származékok táblázata

C" = 0(xn) = nxn-1(sin x)" = cos xx" = 1(1 / x)" = -1 / x2(cos x)" = -sin x(Cu)"=Cu"( √x)" = 1 / 2√x(tg x)" = 1 / cos2 x(uv)" = u"v + uv"(ax)" = ax ln x(ctg x)" = 1 / sin2 x( u / v)"=(u"v - uv") / v2(ex)" = ex(arcsin x)" = 1 / √ (1-x2)(logax)" = (logae) / x(arccos x) " = -1 / √ (1- x2) (ln x)" = 1 / x (arctg x)" = 1 / √ (1+ x2) (arctg x)" = -1 / √ (1+ x2)

2. A származék geometriai jelentése

2-1. Görbe érintő

Tekintsük az f(x) függvényt és a függvénynek megfelelő y = f(x) görbét. Valamely x érték esetén a függvény értéke y = f(x). A görbén ezek az értékek az M(x0, y0) pontnak felelnek meg. Bevezetünk egy új x0 + ∆x argumentumot, melynek értéke megfelel az y0 + ∆y = f(x0 + ∆x) függvény értékének. A megfelelő pont N(x0 + ∆x, y0 + ∆y). Rajzolja meg az MN szekánst, és jelölje φ-vel a szekáns által az Ox tengely pozitív irányával bezárt szöget. Az ábrán látható, hogy ∆y / ∆x = tg φ. Ha most ∆x megközelíti a 0-t, akkor az N pont elmozdul a görbén, a szekáns MN elfordul az M pont körül, és a φ szög megváltozik. Ha ∆x → 0-ként a φ szög valamilyen α-ra hajlik, akkor az M-en átmenő és az abszcissza tengelyének pozitív irányával α szöget bezáró egyenes lesz a szükséges érintő. Ugyanakkor a lejtési együtthatója:

2-2. A felület érintő síkja

A felület érintősíkja az M pontban az a sík, amely tartalmazza a felület minden térbeli görbéjének érintőit, amelyek M-en - az érintkezési ponton - haladnak át.

Vegyünk egy F(x, y, z) = 0 egyenlet által adott felületet és egy M(x0, y0, z0) közönséges pontot. Tekintsünk a felületen valamilyen M-en átmenő L görbét. Adják meg a görbét az egyenletek

x = φ(t); y = ψ(t); z = χ(t).

Az L görbe érintőjének egyenlete az M pontban a következő:

Mivel az x - x0, y - y0, z - z0 különbségek arányosak a megfelelő differenciálokkal, a sík végső egyenlete így néz ki:

F "x (x - x0) + F" y (y - y0) + F "z (z - z0) \u003d 0

és az adott esetben z = f(x, y):

Z - z0 \u003d F "x (x - x0) + F" y (y - y0)

Példa: Határozzuk meg az érintősík egyenletét a hiperbolikus paraboloid (2a; a; 1,5a) pontjában

Megoldás:

Z"x \u003d x / a \u003d 2; Z"y \u003d -y / a \u003d -1

A kívánt sík egyenlete:

Z - 1,5a = 2 (x - 2a) - (Y - a) vagy Z = 2x - y - 1,5a

3. A derivált használata a fizikában

3-1. Anyagpont sebesség

Legyen az s út t időtől való függése egy anyagi pont adott egyenes vonalú mozgásában az s = f(t) egyenlettel, és t0 valamilyen időpillanat. Tekintsünk egy másik t időpontot, jelöljük ∆t = t - t0, és számítsuk ki az útnövekményt: ∆s = f(t0 + ∆t) - f(t0). A ∆s / ∆t arányt a t0 kezdeti pillanattól eltelt ∆t idő alatti átlagos mozgási sebességnek nevezzük. A sebesség ennek az aránynak a határa: ∆t → 0.

Az egyenetlen mozgás átlagos gyorsulása az intervallumban (t; t + ∆t) az érték =∆v / ∆t. Egy anyagi pont pillanatnyi gyorsulása t időpontban lesz az átlagos gyorsulás határa:

Vagyis az első derivált (v "(t)).

Példa: A test által megtett út időfüggését az s = A + Bt + Ct2 + Dt3 egyenlet adja meg (C = 0,1 m/s, D = 0,03 m/s2). Határozza meg azt az időt a mozgás megkezdése után, amely után a test gyorsulása 2 m/s2 lesz.

Megoldás:

v(t) = s"(t) = B + 2Ct + 3Dt2; a(t) = v"(t) = 2C + 6Dt = 0,2 + 0,18t = 2;

1,8 = 0,18 t; t = 10 s

3-2. Egy anyag hőkapacitása adott hőmérsékleten

Különböző T hőmérsékletek növelése ugyanazzal az értékkel, amely egyenlő T1 - T értékkel, 1 kg-onként. adott anyagnak más hőmennyiségre van szüksége Q1 - Q, és az arány

mert ez az anyag nem állandó. Így egy adott anyagra a Q hőmennyiség a T hőmérséklet nemlineáris függvénye: Q = f(T). Ekkor ΔQ = f(t + ΔT) - f(T). Hozzáállás

intervallumon az átlagos hőkapacitásnak nevezzük, és ennek a kifejezésnek a határát ∆T → 0 esetén az adott anyag hőkapacitásának nevezzük T hőmérsékleten.

3-3. Erő

Egy test mechanikai mozgásában bekövetkező változást más testekből rá ható erők okozzák. A kölcsönható testek közötti energiacsere folyamatának kvantitatív jellemzése érdekében a mechanikában bevezetik az erő munkájának fogalmát. A munkavégzés ütemének jellemzésére bevezetjük a hatalom fogalmát:

4. Differenciálszámítás a közgazdaságtanban

4-1. Funkciókutatás

1) Legyen az f(x) függvény az x0 pont valamely környezetében differenciálható. Ha az f "(x) derivált az x0 ponton áthaladva előjelet változtat +-ról -ra, akkor x0 a maximális pont, ha -ból +-ra, akkor x0 a minimumpont, ha nem változtat előjelet, akkor ott ezen a ponton nem extrémum.

2) Legyen az f(x) függvény kétszer differenciálható az x0 pont valamelyik környezetében, és f "(x0) = 0, f ""(x0) ≠ 0, akkor az x0 pontban az f(x0) függvény maximum ha

Letöltés:

Előnézet:

Diák feliratai:

Előnézet:

Diák feliratai:

Olvassa el is