Sinuso (), kosinuso (), liestinės (), kotangento () sąvokos yra neatsiejamai susijusios su kampo sąvoka. Norėdami gerai suprasti šias, iš pirmo žvilgsnio, sudėtingas sąvokas (kurios daugeliui moksleivių kelia siaubą) ir įsitikinti, kad „velnias nėra toks baisus, kaip jis nupieštas“, pradėkime nuo pradžių. ir suprasti kampo sąvoką.
Kampo sąvoka: radianas, laipsnis
Pažiūrėkime į paveikslėlį. Vektorius „pasuko“ taško atžvilgiu tam tikru dydžiu. Taigi šio sukimosi matas pradinės padėties atžvilgiu bus kampas.
Ką dar reikia žinoti apie kampo sąvoką? Na, žinoma, kampo vienetai!
Kampas, tiek geometrijoje, tiek trigonometrijoje, gali būti matuojamas laipsniais ir radianais.
Kampas ties (vienu laipsniu) yra centrinis apskritimo kampas, pagrįstas apskritimo lanku, lygiu apskritimo daliai. Taigi visas apskritimas susideda iš apskritimo lankų „gabalų“ arba apskritimo aprašytas kampas yra lygus.
Tai yra, aukščiau pateiktame paveikslėlyje parodytas kampas, kuris yra lygus, tai yra, šis kampas pagrįstas apskritimo lanku, kurio dydis yra apskritimas.
Kampu radianais vadinamas centrinis apskritimo kampas, pagrįstas apskritimo lanku, kurio ilgis lygus apskritimo spinduliui. Na, ar supratai? Jei ne, pažiūrėkime į paveikslėlį.
Taigi paveiksle parodytas kampas, lygus radianui, tai yra, šis kampas pagrįstas apskritimo lanku, kurio ilgis lygus apskritimo spinduliui (ilgis lygus ilgiui arba spindulys lygus lanko ilgis). Taigi, lanko ilgis apskaičiuojamas pagal formulę:
Kur yra centrinis kampas radianais.
Na, žinodami tai, ar galite atsakyti, kiek radianų yra apskritimu apibūdinamas kampas? Taip, tam reikia atsiminti apskritimo perimetro formulę. Štai ir ji:
Na, dabar susiekime šias dvi formules ir gaukime, kad apskritimu aprašytas kampas yra lygus. Tai yra, koreliuodami vertę laipsniais ir radianais, tai gauname. Atitinkamai,. Kaip matote, skirtingai nei "laipsniai", žodis "radianas" yra praleistas, nes matavimo vienetas paprastai yra aiškus iš konteksto.
Kiek yra radianų? Teisingai!
Supratau? Tada pritvirtinkite priekyje:
Bet kokių sunkumų? Tada žiūrėk atsakymai:
Statusis trikampis: sinusas, kosinusas, liestinė, kampo kotangentas
Taigi, išsiaiškinus kampo sąvoką. Bet kas yra kampo sinusas, kosinusas, liestinė, kotangentas? Išsiaiškinkime. Tam mums padės stačiakampis trikampis.
Kaip vadinamos stačiojo trikampio kraštinės? Teisingai, hipotenuzė ir kojos: hipotenuzė yra pusė, esanti priešais stačią kampą (mūsų pavyzdyje tai yra pusė); kojos yra dvi likusios pusės ir (gretimos stačiu kampu), be to, jei svarstysime kojas kampo atžvilgiu, tada koja yra gretima, o koja yra priešinga. Taigi, dabar atsakykime į klausimą: kas yra kampo sinusas, kosinusas, tangentas ir kotangentas?
Kampo sinusas yra priešingos (tolimosios) kojos ir hipotenuzės santykis.
mūsų trikampyje.
Kampo kosinusas- tai yra gretimos (artimos) kojos ir hipotenuzės santykis.
mūsų trikampyje.
Kampo liestinė- tai priešingos (tolimosios) kojos ir gretimos (artimos) santykis.
mūsų trikampyje.
Kampo kotangentas- tai gretimos (artimos) kojos ir priešingos (toli) santykis.
mūsų trikampyje.
Šie apibrėžimai yra būtini Prisiminti! Kad būtų lengviau atsiminti, kurią koją iš ko padalinti, turite tai aiškiai suprasti liestinė ir kotangentas sėdi tik kojos, o hipotenuzė atsiranda tik viduje sinusas ir kosinusas. Ir tada jūs galite sugalvoti asociacijų grandinę. Pavyzdžiui, šis:
kosinusas→lietimas→lietimas→gretima;
Kotangentas→lietimas→lietimas→gretima.
Visų pirma, reikia atsiminti, kad sinusas, kosinusas, liestinė ir kotangentas kaip trikampio kraštinių santykiai nepriklauso nuo šių kraštinių ilgių (vienu kampu). Nepasitikėk? Tada įsitikinkite, žiūrėdami į paveikslėlį:
Apsvarstykite, pavyzdžiui, kampo kosinusą. Pagal apibrėžimą iš trikampio: , bet kampo kosinusą galime apskaičiuoti iš trikampio: . Matote, kraštinių ilgiai skirtingi, bet vieno kampo kosinuso reikšmė vienoda. Taigi sinuso, kosinuso, liestinės ir kotangento reikšmės priklauso tik nuo kampo dydžio.
Jei suprantate apibrėžimus, eikite į priekį ir pataisykite juos!
Žemiau esančiame paveikslėlyje parodytam trikampiui randame.
Na, ar gavai? Tada pabandykite patys: apskaičiuokite tą patį kampui.
Vienetinis (trigonometrinis) apskritimas
Suprasdami laipsnių ir radianų sąvokas, laikėme apskritimą, kurio spindulys lygus. Toks ratas vadinamas vienišas. Tai labai naudinga tiriant trigonometriją. Todėl mes apie tai pasikalbėsime šiek tiek išsamiau.
Kaip matote, šis ratas yra įmontuotas Dekarto sistema koordinates. Apskritimo spindulys lygus vienetui, o apskritimo centras yra pradžioje, spindulio vektoriaus pradinė padėtis fiksuojama išilgai teigiamos ašies krypties (mūsų pavyzdyje tai yra spindulys).
Kiekvienas apskritimo taškas atitinka du skaičius: koordinatę išilgai ašies ir koordinatę išilgai ašies. Kas yra šie koordinačių skaičiai? Ir apskritai, ką jie turi bendro su nagrinėjama tema? Norėdami tai padaryti, prisiminkite apie svarstomą stačiakampį trikampį. Viršuje esančiame paveikslėlyje galite pamatyti du ištisus stačiuosius trikampius. Apsvarstykite trikampį. Jis yra stačiakampis, nes yra statmenas ašiai.
Kas lygu iš trikampio? Teisingai. Be to, mes žinome, kad yra vieneto apskritimo spindulys, todėl . Pakeiskite šią reikšmę mūsų kosinuso formule. Štai kas nutinka:
O kas lygu iš trikampio? Na žinoma, ! Pakeiskite spindulio reikšmę į šią formulę ir gaukite:
Taigi, ar galite man pasakyti, kokios yra apskritimui priklausančio taško koordinatės? Na, niekaip? O jei tai supranti ir tėra skaičiai? Kokią koordinatę ji atitinka? Na, žinoma, koordinatė! Kokią koordinatę ji atitinka? Teisingai, derinkite! Taigi, esmė.
O kas tada yra lygūs ir? Teisingai, naudokime atitinkamus liestinės ir kotangento apibrėžimus ir gaukime, kad a.
O jei kampas didesnis? Štai, pavyzdžiui, kaip šiame paveikslėlyje:
Kas pasikeitė šiame pavyzdyje? Išsiaiškinkime. Dėl to vėl kreipiamės į taisyklingas trikampis. Apsvarstykite statųjį trikampį: kampą (kaip greta kampo). Kokia kampo sinuso, kosinuso, tangento ir kotangento reikšmė? Taip, mes laikomės atitinkamų apibrėžimų trigonometrinės funkcijos:
Na, kaip matote, kampo sinuso reikšmė vis tiek atitinka koordinatę; kampo kosinuso reikšmė – koordinatė; ir atitinkamų santykių liestinės ir kotangento reikšmės. Taigi šie santykiai taikomi bet kokiems spindulio vektoriaus sukimams.
Jau buvo minėta, kad pradinė spindulio vektoriaus padėtis yra išilgai teigiamos ašies krypties. Iki šiol mes sukome šį vektorių prieš laikrodžio rodyklę, bet kas atsitiks, jei pasuksime jį pagal laikrodžio rodyklę? Nieko nepaprasto, gausite ir tam tikro dydžio kampą, bet tik jis bus neigiamas. Taigi, sukdami spindulio vektorių prieš laikrodžio rodyklę, gauname teigiami kampai, o sukant pagal laikrodžio rodyklę - neigiamas.
Taigi, mes žinome, kad visas spindulio vektoriaus apsisukimas aplink apskritimą yra arba. Ar galima pasukti spindulio vektorių ar per? Na, žinoma, galite! Todėl pirmuoju atveju spindulio vektorius padarys vieną pilną apsisukimą ir sustos padėtyje arba.
Antruoju atveju, tai yra, spindulio vektorius padarys tris pilnus apsisukimus ir sustos padėtyje arba.
Taigi iš aukščiau pateiktų pavyzdžių galime daryti išvadą, kad kampai, kurie skiriasi arba (kur yra bet koks sveikas skaičius), atitinka tą pačią spindulio vektoriaus padėtį.
Žemiau esančiame paveikslėlyje parodytas kampas. Tas pats vaizdas atitinka kampą ir pan. Šį sąrašą galima tęsti neribotą laiką. Visi šie kampai gali būti parašyti naudojant bendrą formulę arba (kur yra bet koks sveikasis skaičius)
Dabar, žinodami pagrindinių trigonometrinių funkcijų apibrėžimus ir naudodami vieneto apskritimą, pabandykite atsakyti, kam lygios reikšmės:
Štai vieneto ratas, kuris jums padės:
Bet kokių sunkumų? Tada išsiaiškinkime. Taigi mes žinome, kad:
Iš čia nustatome taškų koordinates, atitinkančias tam tikrus kampo matmenis. Na, pradėkime iš eilės: kampas ties atitinka tašką su koordinatėmis, todėl:
Neegzistuoja;
Be to, laikydamiesi tos pačios logikos, sužinome, kad kampai atitinka atitinkamai taškus su koordinatėmis. Tai žinant, nesunku nustatyti trigonometrinių funkcijų reikšmes atitinkamuose taškuose. Pirmiausia išbandykite patys, tada patikrinkite atsakymus.
Atsakymai:
Neegzistuoja
Neegzistuoja
Neegzistuoja
Neegzistuoja
Taigi galime sudaryti tokią lentelę:
Nereikia atsiminti visų šių vertybių. Pakanka prisiminti vienetinio apskritimo taškų koordinačių ir trigonometrinių funkcijų verčių atitikimą:
Bet kampų trigonometrinių funkcijų reikšmės ir, pateiktos toliau esančioje lentelėje, reikia atsiminti:
Nebijokite, dabar parodysime vieną iš pavyzdžių gana paprastas atitinkamų reikšmių įsiminimas:
Norint naudoti šį metodą, labai svarbu atsiminti visų trijų kampo matmenų sinuso reikšmes (), taip pat kampo liestinės reikšmę. Žinant šias reikšmes, gana paprasta atkurti visą lentelę – kosinuso reikšmės perkeliamos pagal rodykles, tai yra:
Žinodami tai, galite atkurti reikšmes. Skaitiklis „ “ atitiks, o vardiklis „ “. Kotangentinės reikšmės perkeliamos pagal paveikslėlyje parodytas rodykles. Jei tai suprasite ir atsimenate diagramą su rodyklėmis, pakaks prisiminti visą lentelės vertę.
Apskritimo taško koordinatės
Ar įmanoma apskritime rasti tašką (jo koordinates), žinant apskritimo centro koordinates, jo spindulį ir sukimosi kampą?
Na, žinoma, galite! Iškelkime bendroji formulė rasti taško koordinates.
Pavyzdžiui, turime tokį ratą:
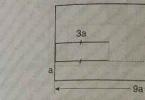
Mums duota, kad taškas yra apskritimo centras. Apskritimo spindulys lygus. Reikia rasti taško koordinates, gautas sukant tašką laipsniais.
Kaip matyti iš paveikslo, taško koordinatė atitinka atkarpos ilgį. Atkarpos ilgis atitinka apskritimo centro koordinatę, tai yra lygus. Atkarpos ilgį galima išreikšti naudojant kosinuso apibrėžimą:
Tada turime taško koordinatę.
Pagal tą pačią logiką randame taško y koordinatės reikšmę. Šiuo būdu,
Taigi į bendras vaizdas taško koordinatės nustatomos pagal formules:
Apskritimo centro koordinatės,
apskritimo spindulys,
Spindulio vektoriaus sukimosi kampas.
Kaip matote, mūsų svarstomo vieneto apskritimo formulės yra žymiai sumažintos, nes centro koordinatės yra lygios nuliui, o spindulys yra lygus vienetui:
Na, pabandykime paragauti šias formules, praktikuodami rasti taškus ant apskritimo?
1. Raskite vienetinio apskritimo taško koordinates, gautas įjungus tašką.
2. Raskite vienetinio apskritimo taško koordinates, gautas sukant tašką.
3. Raskite vienetinio apskritimo taško koordinates, gautas įjungus tašką.
4. Taškas – apskritimo centras. Apskritimo spindulys lygus. Reikia rasti taško, gauto pasukus pradinį spindulio vektorių, koordinates.
5. Taškas – apskritimo centras. Apskritimo spindulys lygus. Reikia rasti taško, gauto pasukus pradinį spindulio vektorių, koordinates.
Sunku rasti apskritimo taško koordinates?
Išspręskite šiuos penkis pavyzdžius (arba gerai supraskite sprendimą) ir sužinosite, kaip juos rasti!
1.
Galima matyti, kad. Ir mes žinome, kas atitinka visą pradinio taško posūkį. Taigi norimas taškas bus toje pačioje padėtyje kaip ir sukant. Tai žinodami randame norimas taško koordinates:
2. Apskritimas yra vienetas su centru taške, o tai reiškia, kad galime naudoti supaprastintas formules:
Galima matyti, kad. Žinome, kas atitinka du pilnus pradinio taško apsisukimus. Taigi norimas taškas bus toje pačioje padėtyje kaip ir sukant. Tai žinodami randame norimas taško koordinates:
Sinusas ir kosinusas yra lentelės reikšmės. Prisimename jų vertybes ir gauname:
Taigi norimas taškas turi koordinates.
3. Apskritimas yra vienetas su centru taške, o tai reiškia, kad galime naudoti supaprastintas formules:
Galima matyti, kad. Pavaizduokime nagrinėjamą pavyzdį paveikslėlyje:
Spindulys sudaro kampus, kurių ašis lygi ir. Žinodami, kad kosinuso ir sinuso lentelės reikšmės yra lygios, ir nustačius, kad kosinusas čia turi neigiamą reikšmę, o sinusas yra teigiamas, turime:
Panašūs pavyzdžiai išsamiau analizuojami tiriant trigonometrinių funkcijų mažinimo formules temoje.
Taigi norimas taškas turi koordinates.
4.
Spindulio vektoriaus sukimosi kampas (pagal sąlygą)
Norėdami nustatyti atitinkamus sinuso ir kosinuso ženklus, sudarome vienetinį apskritimą ir kampą:
Kaip matote, vertė, tai yra, yra teigiama, o vertė, tai yra, yra neigiama. Žinodami atitinkamų trigonometrinių funkcijų lentelių reikšmes, gauname, kad:
Pakeiskime gautas reikšmes į savo formulę ir suraskime koordinates:
Taigi norimas taškas turi koordinates.
5. Norėdami išspręsti šią problemą, naudojame formules bendra forma, kur
Apskritimo centro koordinatės (mūsų pavyzdyje
Apskritimo spindulys (pagal sąlygą)
Spindulio vektoriaus sukimosi kampas (pagal sąlygą).
Pakeiskite visas reikšmes į formulę ir gaukite:
ir - lentelės reikšmės. Prisimename ir pakeičiame juos į formulę:
Taigi norimas taškas turi koordinates.
SANTRAUKA IR PAGRINDINĖ FORMULĖ
Kampo sinusas yra priešingos (tolimosios) kojos ir hipotenuzės santykis.
Kampo kosinusas yra gretimos (artimos) kojos ir hipotenuzės santykis.
Kampo liestinė yra priešingos (tolimosios) kojos ir gretimos (artimos) santykis.
Kampo kotangentas yra gretimos (artimos) kojos santykis su priešinga (toli).
Šiame straipsnyje mes išsamiai apžvelgsime . Pagrindinis trigonometrinės tapatybės yra lygybės, nustatančios ryšį tarp vieno kampo sinuso, kosinuso, liestinės ir kotangento ir leidžiančios rasti bet kurią iš šių trigonometrinių funkcijų per žinomą kitą.
Iš karto išvardijame pagrindines trigonometrines tapatybes, kurias analizuosime šiame straipsnyje. Jas užrašome į lentelę, o žemiau pateikiame šių formulių išvedimą ir pateikiame reikiamus paaiškinimus.
Puslapio naršymas.
Ryšys tarp vieno kampo sinuso ir kosinuso
Kartais jie kalba ne apie pagrindines trigonometrines tapatybes, išvardytas aukščiau esančioje lentelėje, o apie vieną vienintelį pagrindinė trigonometrinė tapatybė malonus 
. Šio fakto paaiškinimas yra gana paprastas: lygybės gaunamos iš pagrindinės trigonometrinės tapatybės, padalijus abi jos dalis iš ir atitinkamai, ir lygybes 
ir 
išplaukia iš sinuso, kosinuso, liestinės ir kotangento apibrėžimų. Išsamiau tai aptarsime tolesnėse pastraipose.
Tai yra, ypač domina lygybė, kuriai buvo suteiktas pagrindinės trigonometrinės tapatybės pavadinimas.
Prieš įrodydami pagrindinį trigonometrinį tapatumą, pateikiame jo formuluotę: vieno kampo sinuso ir kosinuso kvadratų suma yra identiškai lygi vienetui. Dabar įrodykime.
Labai dažnai naudojama pagrindinė trigonometrinė tapatybė transformacija trigonometrinės išraiškos . Tai leidžia vieno kampo sinuso ir kosinuso kvadratų sumą pakeisti vienu. Ne mažiau dažnai pagrindinė trigonometrinė tapatybė naudojama atvirkštine tvarka: vienetas pakeičiamas bet kurio kampo sinuso ir kosinuso kvadratų suma.
Tangentas ir kotangentas per sinusą ir kosinusą
Tapatybės, jungiančios liestinę ir kotangentą su vieno formos ir formos kampo sinusu ir kosinusu 
iš karto išplaukia iš sinuso, kosinuso, liestinės ir kotangento apibrėžimų. Iš tiesų, pagal apibrėžimą sinusas yra y ordinatė, kosinusas yra x abscisė, liestinė yra ordinatės ir abscisės santykis, tai yra, 
, o kotangentas yra abscisių ir ordinačių santykis, ty 
.
Dėl šio tapatybių akivaizdumo ir dažnai liestinės ir kotangento apibrėžimai pateikiami ne per abscisės ir ordinatės santykį, o per sinuso ir kosinuso santykį. Taigi kampo liestinė yra sinuso ir šio kampo kosinuso santykis, o kotangentas yra kosinuso ir sinuso santykis.
Baigiant šį skyrių, reikia pažymėti, kad tapatybės ir laikykitės visų tokių kampų, kuriems juose esančios trigonometrinės funkcijos turi prasmę. Taigi formulė galioja bet kuriai kitai nei (kitaip vardiklis bus lygus nuliui, o dalybos iš nulio neapibrėžėme), o formulė - visiems , skiriasi nuo , kur z yra bet kuris .
Ryšys tarp liestinės ir kotangento
Dar akivaizdesnė trigonometrinė tapatybė nei ankstesnės dvi yra tapatybė, jungianti vieno formos kampo liestinę ir kotangentą . Akivaizdu, kad tai vyksta bet kuriems kitiems kampams, išskyrus , kitaip nei liestinė, nei kotangentas nėra apibrėžti.
Formulės įrodymas labai paprasta. Pagal apibrėžimą ir iš kur 
. Įrodinėjimas galėjo būti atliktas kiek kitaip. Nuo ir , tada 
.
Taigi, vieno kampo liestinė ir kotangentė, kurioje jie turi prasmę, yra.
Viena iš matematikos šakų, su kuria moksleiviai susiduria su didžiausiais sunkumais, yra trigonometrija. Nieko nuostabaus: norint laisvai įsisavinti šią žinių sritį, reikia erdvinio mąstymo, gebėjimo pagal formules rasti sinusus, kosinusus, liestines, kotangentus, supaprastinti išraiškas ir mokėti naudoti skaičių pi skaičiavimuose. Be to, įrodant teoremas reikia mokėti taikyti trigonometriją, o tam reikia arba išvystytos matematinės atminties, arba gebėjimo išvesti sudėtingas logines grandines.
Trigonometrijos ištakos
Susipažinimas su šiuo mokslu turėtų prasidėti nuo kampo sinuso, kosinuso ir liestinės apibrėžimo, tačiau pirmiausia reikia išsiaiškinti, ką trigonometrija daro apskritai.
Istoriškai stačiakampiai trikampiai buvo pagrindinis šios matematikos mokslo skyriaus tyrimo objektas. 90 laipsnių kampo buvimas leidžia atlikti įvairias operacijas, kurios leidžia nustatyti visų nagrinėjamos figūros parametrų reikšmes naudojant dvi puses ir vieną kampą arba du kampus ir vieną pusę. Anksčiau žmonės pastebėjo šį modelį ir pradėjo aktyviai jį naudoti statydami pastatus, navigaciją, astronomiją ir net mene.
Pirmas lygmuo
Iš pradžių žmonės kalbėjo apie kampų ir kraštinių santykį tik stačiųjų trikampių pavyzdžiu. Tada buvo atrastos specialios formulės, kurios leido išplėsti šios matematikos dalies naudojimo kasdieniame gyvenime ribas.
Trigonometrijos studijos mokykloje šiandien pradedamos nuo stačiųjų trikampių, po kurių įgytas žinias mokiniai panaudoja fizikoje ir spręsdami abstrakčias trigonometrines lygtis, su kuriomis darbas pradedamas vidurinėje mokykloje.
Sferinė trigonometrija
Vėliau, mokslui pasiekus kitą išsivystymo lygį, sferinėje geometrijoje pradėtos naudoti formulės su sinusu, kosinusu, tangentu, kotangentu, kur galioja kitos taisyklės, o trikampio kampų suma visada yra didesnė nei 180 laipsnių. Šis skyrius nėra mokomas mokykloje, tačiau apie jo egzistavimą būtina žinoti bent jau todėl žemės paviršiaus, o bet kurios kitos planetos paviršius yra išgaubtas, o tai reiškia, kad bet koks paviršiaus žymėjimas trimatėje erdvėje bus „lanko formos“.
Paimkite gaublį ir siūlą. Pritvirtinkite siūlą prie bet kurių dviejų rutulio taškų, kad jis būtų įtemptas. Atkreipkite dėmesį – jis įgavo lanko formą. Būtent su tokiomis formomis susiduria sferinė geometrija, naudojama geodezijoje, astronomijoje ir kitose teorinėse bei taikomosiose srityse.
Taisyklingas trikampis
Šiek tiek sužinoję apie trigonometrijos naudojimo būdus, grįžkime prie pagrindinės trigonometrijos, kad geriau suprastume, kas yra sinusas, kosinusas, liestinė, kokius skaičiavimus galima atlikti su jų pagalba ir kokias formules naudoti.
Pirmas žingsnis yra suprasti sąvokas, susijusias su stačiu trikampiu. Pirma, hipotenuzė yra pusė, priešinga 90 laipsnių kampui. Ji pati ilgiausia. Prisimename, kad pagal Pitagoro teoremą jo skaitinė reikšmė yra lygi kitų dviejų kraštinių kvadratų sumos šaknei.
Pavyzdžiui, jei dvi pusės yra atitinkamai 3 ir 4 centimetrai, hipotenuzės ilgis bus 5 centimetrai. Beje, senovės egiptiečiai apie tai žinojo maždaug prieš keturis su puse tūkstančio metų.
Dvi likusios pusės, sudarančios stačią kampą, vadinamos kojomis. Be to, turime atsiminti, kad trikampio kampų suma stačiakampėje koordinačių sistemoje yra 180 laipsnių.
Apibrėžimas
Galiausiai, gerai suprasdami geometrinį pagrindą, galime pereiti prie kampo sinuso, kosinuso ir liestinės apibrėžimo.
Kampo sinusas yra priešingos kojos (t. y. pusės, priešingos norimam kampui) santykis su hipotenuze. Kampo kosinusas yra gretimos kojos ir hipotenuzės santykis.
Atminkite, kad nei sinusas, nei kosinusas negali būti didesnis už vienetą! Kodėl? Kadangi hipotenuzė pagal nutylėjimą yra ilgiausia.Nesvarbu, kokios ilgio koja bebūtų, ji bus trumpesnė už hipotenuzą, vadinasi, jų santykis visada bus mažesnis už vieną. Taigi, jei atsakydami į problemą gausite sinusą arba kosinusą, kurio reikšmė didesnė nei 1, ieškokite skaičiavimų ar samprotavimų klaidos. Šis atsakymas akivaizdžiai neteisingas.
Galiausiai kampo liestinė yra priešingos pusės ir gretimos kraštinės santykis. Tas pats rezultatas duos sinuso padalijimą iš kosinuso. Žiūrėkite: pagal formulę kraštinės ilgį padalijame iš hipotenuzės, po to padaliname iš antrosios pusės ilgio ir padauginame iš hipotenuzės. Taigi gauname tą patį santykį kaip ir liestinės apibrėžime.
Kotangentas atitinkamai yra kraštinės, esančios šalia kampo, ir priešingos pusės santykis. Tą patį rezultatą gauname padalinę vienetą iš liestinės.
Taigi, mes apsvarstėme apibrėžimus, kas yra sinusas, kosinusas, liestinė ir kotangentas, ir galime nagrinėti formules.
Paprasčiausios formulės
Trigonometrijoje neapsieisite be formulių - kaip be jų rasti sinusą, kosinusą, liestinę, kotangentą? Ir būtent to reikia sprendžiant problemas.
Pirmoji formulė, kurią reikia žinoti pradedant mokytis trigonometrijos, sako, kad kampo sinuso ir kosinuso kvadratų suma yra lygi vienetui. Ši formulė yra tiesioginė Pitagoro teoremos pasekmė, tačiau ji taupo laiką, jei norite sužinoti kampo, o ne kraštinės, reikšmę.
Daugelis mokinių negali prisiminti antrosios formulės, kuri taip pat labai populiari sprendžiant mokyklos uždaviniai: kampo liestinės vieneto ir kvadrato suma lygi vienetui, padalintam iš kampo kosinuso kvadrato. Pažvelkite atidžiau: juk tai tas pats teiginys, kaip ir pirmoje formulėje, tik abi tapatybės pusės buvo padalintos kosinuso kvadratu. Pasirodo, dėl paprasto matematinio veiksmo trigonometrinė formulė tampa visiškai neatpažįstama. Atminkite: žinodami, kas yra sinusas, kosinusas, liestinė ir kotangentas, konvertavimo taisykles ir kelias pagrindines formules, galite bet kada patys gauti reikiamą daugiau sudėtingos formulės ant popieriaus lapo.
Dvigubo kampo formulės ir argumentų pridėjimas
Dar dvi formulės, kurias turite išmokti, yra susijusios su sinuso ir kosinuso reikšmėmis kampų sumai ir skirtumui. Jie parodyti paveikslėlyje žemiau. Atkreipkite dėmesį, kad pirmuoju atveju sinusas ir kosinusas padauginami abu kartus, o antruoju pridedama sinuso ir kosinuso porinė sandauga.
Taip pat formoje yra formulių, susijusių su argumentais dvigubas kampas. Jie yra visiškai kilę iš ankstesnių – kaip praktika, pabandykite juos gauti patys, imdami alfa kampą lygus kampui beta versija.
Galiausiai atkreipkite dėmesį, kad dvigubo kampo formules galima konvertuoti, kad būtų sumažintas sinuso, kosinuso, tangento alfa laipsnis.
Teoremos
Dvi pagrindinės pagrindinės trigonometrijos teoremos yra sinuso teorema ir kosinuso teorema. Naudodami šias teoremas galite lengvai suprasti, kaip rasti sinusą, kosinusą ir liestinę, taigi ir figūros plotą, kiekvienos pusės dydį ir kt.
Sinuso teorema teigia, kad padalijus kiekvienos trikampio kraštinės ilgį iš priešingo kampo vertės, gauname tą patį skaičių. Be to, šis skaičius bus lygus dviem apibrėžto apskritimo spinduliams, tai yra apskritimui, kuriame yra visi nurodyto trikampio taškai.
Kosinuso teorema apibendrina Pitagoro teoremą, projektuodama ją į bet kokius trikampius. Pasirodo, iš dviejų kraštinių kvadratų sumos atimkite jų sandaugą, padaugintą iš greta esančio kampo dvigubo kosinuso - gauta vertė bus lygi trečiosios kraštinės kvadratui. Taigi Pitagoro teorema pasirodo esanti ypatingas kosinuso teoremos atvejis.
Klaidos dėl neatidumo
Net ir žinant, kas yra sinusas, kosinusas ir tangentas, nesunku suklysti dėl neblaivumo ar paprasčiausių skaičiavimų klaidos. Norėdami išvengti tokių klaidų, susipažinkime su populiariausiomis iš jų.
Pirma, neturėtumėte konvertuoti įprastų trupmenų į dešimtaines, kol negausite galutinio rezultato - galite palikti atsakymą formoje bendroji trupmena nebent sąlygose nurodyta kitaip. Tokios transformacijos negalima vadinti klaida, tačiau reikia atminti, kad kiekviename problemos etape gali atsirasti naujų šaknų, kurias, pagal autoriaus sumanymą, reikėtų sumažinti. Tokiu atveju sugaišite laiką nereikalingiems matematiniams veiksmams. Tai ypač pasakytina apie tokias vertybes kaip trijų ar dviejų šaknis, nes jos atsiranda atliekant užduotis kiekviename žingsnyje. Tas pats pasakytina ir apie „bjaurių“ skaičių apvalinimą.
Be to, atkreipkite dėmesį, kad kosinuso teorema taikoma bet kuriam trikampiui, bet ne Pitagoro teoremai! Jei per klaidą pamiršite atimti dvigubą kraštinių sandaugą, padaugintą iš kampo tarp jų kosinuso, gausite ne tik visiškai neteisingą rezultatą, bet ir parodysite visišką dalyko nesupratimą. Tai yra blogiau nei neatsargumo klaida.
Trečia, nepainiokite sinusų, kosinusų, liestinių, kotangentų 30 ir 60 laipsnių kampų verčių. Atsiminkite šias reikšmes, nes 30 laipsnių sinusas yra lygus 60 kosinusui ir atvirkščiai. Juos nesunku sumaišyti, dėl to neišvengiamai gausite klaidingą rezultatą.
Taikymas
Daugelis studentų neskuba pradėti studijuoti trigonometrijos, nes jos nesupranta taikomoji prasme. Kas yra sinusas, kosinusas, tangentas inžinieriui ar astronomui? Tai sąvokos, kurių dėka galite apskaičiuoti atstumą iki tolimų žvaigždžių, numatyti meteorito kritimą, nusiųsti tyrimo zondą į kitą planetą. Be jų neįmanoma pastatyti pastato, suprojektuoti automobilio, apskaičiuoti paviršiaus apkrovą ar objekto trajektoriją. Ir tai tik ryškiausi pavyzdžiai! Juk trigonometrija vienokia ar kitokia forma naudojama visur – nuo muzikos iki medicinos.
Pagaliau
Taigi jūs esate sinusas, kosinusas, tangentas. Galite naudoti juos skaičiavimuose ir sėkmingai išspręsti mokyklos problemas.
Visa trigonometrijos esmė susiveda į tai, kad nežinomi parametrai turi būti skaičiuojami iš žinomų trikampio parametrų. Iš viso yra šeši parametrai: trijų kraštinių ilgiai ir trijų kampų dydžiai. Visas užduočių skirtumas slypi tame, kad pateikiami skirtingi įvesties duomenys.
Dabar žinote, kaip rasti sinusą, kosinusą, liestinę pagal žinomus kojų ilgius arba hipotenuzą. Kadangi šie terminai reiškia ne ką kitą, kaip santykį, o santykis yra trupmena, Pagrindinis tikslasįprastos lygties ar lygčių sistemos šaknų radimas tampa trigonometrine problema. O čia jums padės įprasta mokyklinė matematika.
Dviejų kampų α ir β sinusų ir kosinusų sumos ir skirtumo formulės leidžia pereiti nuo nurodytų kampų sumos iki kampų α + β 2 ir α - β 2 sandaugos. Iš karto pažymime, kad neturėtumėte painioti sinusų ir kosinusų sumos ir skirtumo formulių su sumos ir skirtumo sinusų ir kosinusų formulėmis. Žemiau pateikiame šių formulių sąrašą, pateikiame jų išvedimą ir parodome konkrečių problemų taikymo pavyzdžius.
Yandex.RTB R-A-339285-1
Sinusų ir kosinusų sumos ir skirtumo formulės
Užrašykime, kaip atrodo sinusų ir kosinusų sumos ir skirtumo formulės
Sinusų sumos ir skirtumo formulės
sin α + sin β = 2 sin α + β 2 cos α - β 2 sin α - sin β = 2 sin α - β 2 cos α + β 2
Kosinusų sumos ir skirtumo formulės
cos α + cos β = 2 cos α + β 2 cos α - β 2 cos α - cos β = - 2 sin α + β 2 cos α - β 2, cos α - cos β = 2 sin α + β -2 α 2
Šios formulės galioja bet kokiems kampams α ir β. Kampai α + β 2 ir α - β 2 vadinami atitinkamai kampų alfa ir beta pusinės sumos ir pusinės skirtumo dalimi. Pateikiame kiekvienos formulės formulę.
Sinusų ir kosinusų sumos ir skirtumo formulių apibrėžimai
Dviejų kampų sinusų suma yra lygus šių kampų pusės sumos sinuso ir pusės skirtumo kosinuso sandaugai.
Dviejų kampų sinusų skirtumas yra lygus šių kampų pusės skirtumo sinuso ir pusės sumos kosinuso sandaugai.
Dviejų kampų kosinusų suma yra lygus šių kampų pusės sumos kosinuso ir pusės skirtumo kosinuso sandaugai.
Dviejų kampų kosinusų skirtumas yra lygus dvigubai šių kampų pusės sumos sinuso ir pusės skirtumo kosinuso sandaugai, paimtai su neigiamu ženklu.
Sinusų ir kosinusų sumos ir skirtumo formulių išvedimas
Norint išvesti dviejų kampų sinuso ir kosinuso sumos ir skirtumo formules, naudojamos sudėjimo formulės. Pateikiame juos žemiau
sin (α + β) = sin α cos β + cos α sin β sin (α - β) = sin α cos β - cos α sin β cos (α + β) = cos α cos β - sin α sin β cos ( α - β) = cos α cos β + sin α sin β
Mes taip pat vaizduojame pačius kampus kaip pusiau sumų ir pusiau skirtumų sumą.
α = α + β 2 + α - β 2 \u003d α 2 + β 2 + α 2 - β 2 β \u003d α + β 2 - α - β 2 \u003d α + β 2 - α - β 2 \u003d
Tiesiogiai pereiname prie sin ir cos sumos ir skirtumo formulių išvedimo.
Sinusų sumos formulės išvedimas
Sumoje sin α + sin β pakeičiame α ir β aukščiau pateiktomis šių kampų išraiškomis. Gauk
sin α + sin β = sin α + β 2 + α - β 2 + sin α + β 2 - α - β 2
Dabar pirmajai išraiškai taikome pridėjimo formulę, o antrajai – kampų skirtumų sinusinę formulę (žr. aukščiau pateiktas formules)
nuodėm - β 2 - cos α + β 2 sin α - β 2 sin α + β 2 + α - β 2 + sin α + β 2 - α - β 2 = sin α + β 2 cos α - β 2 + cos α β 2 sin α - β 2 + sin α + β 2 cos α - β 2 - cos α + β 2 sin α - β 2
sin α + β 2 cos α - β 2 + cos α + β 2 sin α - β 2 + sin α + β 2 cos α - β 2 - cos α + β 2 sin α - β 2 = = 2 sin α + 2 cos α – β 2
Likusių formulių išvedimo veiksmai yra panašūs.
Sinusų skirtumo formulės išvedimas
sin α - sin β = nuodėmė α + β 2 + α - β 2 - sin α + β 2 - α - β 2 sin α + β 2 + α - β 2 - sin α + β 2 - α - β 2 = nuodėmė α + β 2 cos α - β 2 + cos α + β 2 sin α - β 2 - sin α + β 2 cos α - β 2 - cos α + β 2 sin α - β 2 = = 2 sin α 2 cos α + β 2
Kosinusų sumos formulės išvedimas
cos α + cos β = cos α + β 2 + α - β 2 + cos α + β 2 - α - β 2 cos α + β 2 + α - β 2 + cos α + β 2 - α - cos β α + β 2 cos α - β 2 - sin α + β 2 sin α - β 2 + cos α + β 2 cos α - β 2 + sin α + β 2 sin α - β 2 = = 2 cos β 2 + cos α – β 2
Kosinuso skirtumo formulės išvedimas
cos α - cos β = cos α + β 2 + α - β 2 - cos α + β 2 - α - β 2 cos α + β 2 + α - β 2 - cos α + β 2 - α - cos β α + β 2 cos α - β 2 - sin α + β 2 sin α - β 2 - cos α + β 2 cos α - β 2 + sin α + β 2 sin α - β 2 = = - 2 sin α + α 2 sin α – β 2
Praktinių problemų sprendimo pavyzdžiai
Pirmiausia patikrinsime vieną iš formulių, pakeisdami į ją konkrečias kampo reikšmes. Tegu α = π 2 , β = π 6 . Apskaičiuokime šių kampų sinusų sumos reikšmę. Pirmiausia naudojame trigonometrinių funkcijų pagrindinių verčių lentelę, o tada pritaikome sinusų sumos formulę.
1 pavyzdys. Dviejų kampų sinusų sumos formulės patikrinimas
α \u003d π 2, β \u003d π 6 sin π 2 + sin π 6 \u003d 1 + 1 2 \u003d 3 2 sin π 2 + sin π 6 \u003d 2 sin π π 2 π 2 - 2 6 2 \u003d 2 sin π 3 cos π 6 \u003d 2 3 2 3 2 \u003d 3 2
Dabar panagrinėkime atvejį, kai kampų reikšmės skiriasi nuo lentelėje pateiktų pagrindinių verčių. Tegul α = 165°, β = 75°. Apskaičiuokime šių kampų sinusų skirtumo reikšmę.
2 pavyzdys. Sinuso skirtumo formulės taikymas
α = 165 ° , β = 75 ° sin α - sin β = sin 165 ° - sin 75 ° sin 165 - sin 75 = 2 sin 165 ° - sin 75 ° 2 cos 165 ° + sin 75 ° 2 = = 2 sin 45 ° cos 120 ° = 2 2 2 - 1 2 = 2 2
Naudodami sinusų ir kosinusų sumos ir skirtumo formules, galite pereiti nuo sumos arba skirtumo į trigonometrinių funkcijų sandaugą. Dažnai šios formulės vadinamos perėjimo nuo sumos prie sandaugos formulėmis. Sinusų ir kosinusų sumos ir skirtumo formulės plačiai naudojamos sprendžiant trigonometrines lygtis ir konvertuojant trigonometrines išraiškas.
Jei tekste pastebėjote klaidą, pažymėkite ją ir paspauskite Ctrl+Enter
Pateikiami santykiai tarp pagrindinių trigonometrinių funkcijų – sinuso, kosinuso, liestinės ir kotangento. trigonometrines formules. O kadangi sąsajų tarp trigonometrinių funkcijų yra gana daug, tai paaiškina ir trigonometrinių formulių gausą. Vienos formulės jungia to paties kampo trigonometrines funkcijas, kitos – daugiakampio funkcijas, kitos – leidžia sumažinti laipsnį, ketvirtos – visas funkcijas išreikšti per pusės kampo liestinę ir pan.
Šiame straipsnyje mes išvardinsime visus pagrindinius trigonometrines formules, kurių pakanka daugumai trigonometrijos problemų išspręsti. Kad būtų lengviau įsiminti ir naudoti, sugrupuosime juos pagal paskirtį ir surašysime į lenteles.
Puslapio naršymas.
Pagrindinės trigonometrinės tapatybės
Pagrindinės trigonometrinės tapatybės nustatyti ryšį tarp vieno kampo sinuso, kosinuso, liestinės ir kotangento. Jie išplaukia iš sinuso, kosinuso, liestinės ir kotangento apibrėžimo, taip pat vieneto apskritimo sąvokos. Jie leidžia išreikšti vieną trigonometrinę funkciją per bet kurią kitą.
Išsamų šių trigonometrinių formulių aprašymą, jų išvedimą ir taikymo pavyzdžius rasite straipsnyje.
Liejamos formulės
Liejamos formulės išplaukia iš sinuso, kosinuso, liestinės ir kotangento savybių, tai yra, jos atspindi trigonometrinių funkcijų periodiškumo savybę, simetrijos savybę, taip pat poslinkio tam tikru kampu savybę. Šios trigonometrinės formulės leidžia pereiti nuo darbo su savavališkais kampais prie darbo su kampais nuo nulio iki 90 laipsnių.
Straipsnyje galima išnagrinėti šių formulių pagrindimą, mnemoninę taisyklę, kaip jas įsiminti, ir jų taikymo pavyzdžius.
Papildymo formulės
Trigonometrinės sudėties formulės parodykite, kaip dviejų kampų sumos arba skirtumo trigonometrinės funkcijos išreiškiamos šių kampų trigonometrinėmis funkcijomis. Šios formulės yra šių trigonometrinių formulių išvedimo pagrindas.
Formulės dvigubai, trigubai ir kt. kampas
Formulės dvigubai, trigubai ir kt. kampas (jos dar vadinamos kelių kampų formulėmis) parodo, kaip trigonometrinės funkcijos veikia dvigubai, trigubai ir kt. kampai () išreiškiami vieno kampo trigonometrinėmis funkcijomis. Jų išvedimas pagrįstas sudėjimo formulėmis.
Išsamesnė informacija surinkta straipsnių formulėse, skirtose dvigubai, trigubai ir kt. kampas .
Pusės kampo formulės
Pusės kampo formulės parodykite, kaip pusės kampo trigonometrinės funkcijos išreiškiamos sveikojo kampo kosinusu. Šios trigonometrinės formulės kyla iš dvigubo kampo formulių.
Jų išvadas ir taikymo pavyzdžius rasite straipsnyje.
Sumažinimo formulės
Trigonometrinės mažėjančių laipsnių formulės yra skirti palengvinti perėjimą nuo natūralių trigonometrinių funkcijų galių prie sinusų ir kosinusų pirmojo laipsnio, bet kelių kampų. Kitaip tariant, jie leidžia sumažinti trigonometrinių funkcijų galias iki pirmosios.
Trigonometrinių funkcijų sumos ir skirtumo formulės
pagrindinė paskirties vieta trigonometrinių funkcijų sumos ir skirtumo formulės susideda iš perėjimo prie funkcijų sandaugos, o tai labai naudinga supaprastinant trigonometrines išraiškas. Šios formulės taip pat plačiai naudojamos sprendžiant trigonometrines lygtis, nes leidžia apskaičiuoti sinusų ir kosinusų sumą ir skirtumą.
Sinusų, kosinusų ir sinusų sandauga pagal kosinusą formulės
Perėjimas nuo trigonometrinių funkcijų sandaugos prie sumos arba skirtumo atliekamas naudojant sinusų, kosinusų ir sinusų sandaugos formules.
Autorių teisės priklauso protingiems studentams
Visos teisės saugomos.
Saugoma autorių teisių įstatymo. Jokia www.svetainės dalis, įskaitant vidinę medžiagą ir išorinį dizainą, negali būti atgaminta jokia forma arba naudojama be išankstinio raštiško autorių teisių savininko leidimo.
