Čiara (krivka) štvrtého rádu nazývame priamku definovanú algebraickou rovnicou štvrtého stupňa vzhľadom na karteziánske pravouhlé súradnice. Obdobne sú definované čiary (krivky) piateho, šiesteho a ďalších rádov.

Množina čiar (kriviek) štvrtého rádu už neobsahuje desiatky, ale tisíce čiar určitého typu. Sady liniek piateho a šiesteho rádu sú ešte rozmanitejšie. Tu uvažujeme o určitých typoch liniek štvrtého a vyššieho rádu, ktoré majú zaujímavé vlastnosti a praktické aplikácie.

Lemniscate Bernoulli

Obráťme sa na krivku opísanú bodom M v rovine tak, aby súčin p vzdialeností tohto bodu k dvom konkrétnym bodom F 1 a F 2 tej istej roviny zostal nezmenený. Takáto krivka sa nazýva lemniscate (lemniscate v gréčtine znamená „stužka“). Ak je dĺžka úsečky F 1 F 2 c, potom sa vzdialenosti od stredu O úsečky F 1 F 2 k F1 a F2 rovnajú c / 2 a súčin týchto vzdialeností sa rovná - c 2 / 4. Najprv požadujme, aby hodnota p nemenného súčinu bola presne rovná 2/4; Potom

rad riadkov transcendentná špirála

Ryža. 8

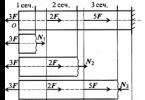
bod O bude ležať na lemniskáte a samotný lemniskát bude vyzerať ako „ležiaci osmička“ (obr. 8). Ak pokračujeme v segmente F 1 F 2 v oboch smeroch až po priesečník s lemniskátom, dostaneme dva body A 1 a A 2. Vyjadríme vzdialenosť medzi A 1 A 2 \u003d x cez známu vzdialenosť c:

Lemniškátové ohniská sú F1 (a c; 0) a F2 (c; 0). Vezmite ľubovoľný bod M (x; y). Súčin vzdialeností od ohniska k bodu M je

A podľa definície sa rovná c2:

Odmocnime obe strany rovnice:

Rozbaľte zátvorky na ľavej strane:

Otvoríme zátvorky a zbalíme nový štvorec súčtu:

Vyberieme spoločný faktor a prenesieme:

V tomto prípade a je polomer kružnice opisujúcej lemniskát. Po vykonaní jednoduchých transformácií môžeme získať explicitnú rovnicu:

Štvorčekujeme a otvárame zátvorky:

Pripomíname

Toto je kvadratická rovnica pre y." Keď to vyriešime, dostaneme

Ak vezmeme koreň a zahodíme možnosť so záporným druhým výrazom, dostaneme:

kde pozitívny variant definuje hornú polovicu lemniskátu, negatívny variant definuje spodnú.

Ak sa hodnota konštantného súčinu p nerovná 2/4, potom lemniskát zmení svoj tvar. A keď je p menšie ako c 2 /4, lemniskát pozostáva z dvoch oválov, z ktorých každý obsahuje body F 1 a F 2, v tomto poradí (obr. 9).

Ryža. 9

To. nastavením rôznych podmienok pre p a c 2 /4 získame lemniskáty rôznych typov (obr. 10).

Ryža. 10

Zoberme si teraz ľubovoľný počet bodov na rovine. F1, F2,…, Fn Dostaneme krivku, ktorej tvar bude závisieť od toho, ako sú navzájom umiestnené body F 1 , F 2 ,…, F n a aká je hodnota konštantného súčinu. Táto krivka sa nazýva lemniskát s n ohniskami.

Vyššie sme zvažovali lemniskáty s dvoma ohniskami. Ak vezmeme rôzny počet ohnísk, usporiadame ich rôznymi spôsobmi a priradíme súčinu vzdialeností tú či onú hodnotu, môžeme získať lemniskáty tých najbizarnejších obrysov. Vedieme bod ceruzky z určitého bodu A bez toho, aby sme ho zložili z papiera, aby sa nakoniec vrátil do východiskového bodu A. Potom opíše určitú krivku; požadujeme len, aby sa táto krivka nikde nepretínala

Ryža. 11

sám. Je zrejmé, že týmto spôsobom možno získať krivky, ktoré majú napríklad obrysy ľudskej hlavy alebo vtáka (obr. 11). Ukazuje sa, že pri takejto ľubovoľnej krivke je možné zvoliť počet n a usporiadanie ohnísk takým spôsobom

F1, F2,…, Fn

a priradiť takú hodnotu pre konštantný súčin vzdialeností

МF 1 МF 2 … МF n = p

že zodpovedajúci lemniskát podľa oka sa nebude líšiť od tejto krivky. Inými slovami, možné odchýlky bodu M, ktorý opisuje lemniskát, od nakreslenej krivky - nepresiahnu šírku ťahu ceruzky (ceruzku je možné vopred nabrúsiť ako chcete, aby bol ťah veľmi úzke). Tento pozoruhodný fakt, ktorý hovorí o mimoriadnej rozmanitosti a bohatosti foriem lemniskátov s mnohými ohniskami, sa pomerne rigorózne, ale veľmi ťažko dokazuje pomocou vyššej matematiky.

Pascalov slimák

Miesto bodov M a M" umiestnené na čiarach ceruzky (ktorej stred O leží na kružnici s polomerom R) vo vzdialenosti a na oboch stranách bodu P priesečníka čiar s kružnicou; teda PM = PM" = a. rovnica v pravouhlých súradniciach: (x2 + y2 - 2Rx)2 - a2(x2 + y2) = 0, v polárnych súradniciach: r = 2R cos j + a. Keď a = 2R, slučka sa stiahne do bodu, v takom prípade sa Pascalova kochlea zmení na kardioidu. Názov je pomenovaný po francúzskom vedcovi B. Pascalovi (1588-1651), ktorý ho ako prvý študoval.

Cykloidné krivky

Predstavte si, že určitá krivka sa valí bez skĺznutia pozdĺž inej krivky; akýkoľvek bod, vždy spojený s prvou krivkou, bude opisovať novú krivku. Môžete si teda predstaviť, ako sa elipsa valí po inej elipse a skúmať čiaru, po ktorej sa bude pohybovať jej stred, alebo určiť trajektóriu ohniska paraboly, ktorá sa valí po priamke atď.

Medzi krivkami vytvorenými týmto spôsobom sa rozlišujú krivky, ktoré sú trajektóriami bodu, ktorý je vždy spojený s kružnicou, ktorá sa valí bez skĺznutia po inej kružnici. Výsledné riadky sú tzv cykloidný.

Pri vytváraní cykloidných kriviek je vykresľovací bod oddelený od stredu tvoriacej (pohybujúcej sa) kružnice v určitej vzdialenosti. V konkrétnom prípade je to na obvode tvoriacej kružnice. Za tejto podmienky sú výsledné krivky rozdelené na epicykloidy a hypocykloidy v závislosti od toho, či je generujúci kruh umiestnený na vonkajšej alebo vnútornej strane pevného kruhu.

Medzi algebraické krivky patria také známe krivky ako kardioidné, astroidné, uvažujme o týchto krivkách.

Kardioidný

1. Rovnica. Kardioidu možno definovať ako trajektóriu bodu ležiaceho na obvode kružnice s polomerom r, ktorá sa valí po obvode pevnej kružnice s rovnakým polomerom. Bude to teda epicykloida s modulom m rovným 1.

Táto okolnosť nám umožňuje okamžite zapísať parametrické rovnice kardioidy a nahradiť modul m jednou vo vyššie uvedených parametrických rovniciach epicykloidy. Bude mať:

Na získanie polárnej rovnice kardioidy je vhodné vziať bod A ako pól (obr. 13) a nasmerovať polárnu os pozdĺž úsečky. Keďže štvoruholník AOO 1 M bude rovnoramenný lichobežník, potom sa polárny uhol bodu M bude rovnať uhlu natočenia tvoriacej kružnice, t.j. parameter t. Vzhľadom na túto okolnosť nahraďme y v druhej rovnici systému (1) cez sin t. Znížením takto získanej rovnosti o sin t dostaneme polárnu rovnicu kardioidy

Ryža. 13

Podľa tejto rovnice

môžeme konštatovať, že kardioid je jedným z Pascalových slimákov. Dá sa teda definovať ako konchoida kruhu.

Preložením rovnice (2) do pravouhlého súradnicového systému dostaneme:

Z tejto rovnice vyplýva, že kardioida je algebraická krivka 4. rádu.

2. Vlastnosti. V prvom rade, keďže kardioida je epicykloida s m=1, možno na ňu preniesť všetky vlastnosti epicykloidov, o ktorých sme uvažovali v predchádzajúcom odseku.

Tu sú vlastnosti a špecifikácie.

1. Dotyčnica v ľubovoľnom bode kardioidy prechádza bodom kružnice tvoriacej kružnice, diametrálne protiľahlej k bodu dotyku kružníc, a normála prechádza bodom ich dotyku.

2. Uhol, ktorý zviera dotyčnica ku kardioide s polomerovým vektorom bodu dotyku, sa rovná polovici uhla, ktorý zviera tento polomerový vektor s polárnou osou. Naozaj

Z tohto vzťahu priamo vyplýva, že uhol, ktorý zviera dotyčnica ku kardioide s osou x, sa rovná (ako vonkajší uhol trojuholníka AMN Obr. 14). Pomocou vzorca môžeme dokázať, že dotyčnice ku kardioide nakreslené na koncoch tetivy prechádzajúcej pólom sú navzájom kolmé.

Naozaj, odkedy

Ryža. 14

Poznamenávame tiež, že miestom priesečníkov týchto dotyčníc je kružnica. Rovnica prvej dotyčnice na základe rovníc (1) kardioidy bude mať tvar

a druhá dotyčnica Vylúčením parametra z týchto rovníc dostaneme rovnicu naznačeného kruhu.

3. Polomer zakrivenia v ľubovoľnom bode kardioidy je určený vzorcom

Dá sa tiež ukázať, že polomer zakrivenia je 2/3 polárnej normály N v danom bode.

Vskutku, odkiaľ na základe (4) získame Tento vzťah možno použiť na zostrojenie stredu zakrivenia kardioidy.

4. Evoluta kardioidy podľa všeobecnej vlastnosti evolúcie epicykloidy bude tiež kardioida podobná danej, s koeficientom podobnosti rovným 1/3 a otočená vzhľadom k danej o uhol 180°.

5. Dĺžka kardioidného oblúka z bodu A do ľubovoľného bodu M je určená vzorcom

Ak sa dĺžka oblúka počíta od bodu A 1, diametrálne opačného k bodu A, potom vzorec na určenie dĺžky oblúka možno zapísať ako

6. Prirodzená rovnica kardioidy sa získa, ak je parameter vylúčený z rovnosti (4) a (6). Bude to vyzerať

7. Oblasť ohraničená kardioidom je určená vzorcom

a ako je vidieť, rovná sa šesťkolesovej ploche generujúceho kruhu.

Dĺžka celej kardioidy je určená vzorcom

a ako je možné vidieť, rovná sa ôsmim priemerom generujúcej kružnice. Objem tela získaný rotáciou kardioidy okolo jej osi sa rovná

Povrch tela získaný rotáciou kardioidy okolo svojej osi sa rovná

Videli sme, že kardioida organicky súvisí s kruhom. Ide o lastúru kruhu a epicykloidu. S kružnicou má iný vzťah – kardioida je čiastková éra kružnice vzhľadom na bod patriaci do tejto kružnice.

Ryža. 15

Nech je OM kolmica spustená na dotyčnicu ku kružnici s polomerom rovným 2r nakreslenej v bode N.

Keďže OM \u003d OB + BM, alebo \u003d\u003d 2r cos + 2r, potom bude lokus bodov M kardioidný s rovnicou \u003d 2r (1 + cos)

Na záver poznamenávame, že kardioida tiež patrí do rodiny sínusových špirál a jej jednotlivé vlastnosti opakujú všeobecné vlastnosti týchto kriviek. Z týchto vlastností vyplýva najmä to, že inverzia kardioidy vzhľadom na vrchol dáva parabolu.

Astroid

1. Vlastnosti. Astroid je špeciálny prípad hypocykloidov, konkrétne hypocykloida s modulom m rovným 1/4. Ide teda o trajektóriu bodu ležiaceho na kružnici kružnice s polomerom r, ktorá sa valí po vnútornej strane ďalšej, pevnej kružnice, ktorej polomer R je štyrikrát väčší.

Parametrické rovnice astroidea možno získať vložením hypocykloidov do rovníc, m=1/4. Tu sú rovnice:

Ryža. 16

kde t, ako predtým, je uhol natočenia tvoriacej kružnice (obr. 16)

Vylúčením parametra t z rovníc (1) dostaneme:

Rovnica (2) naznačuje, že astroid je algebraická krivka šiesteho rádu.

Parametrické rovnice (1) astroidu možno zredukovať do tvaru

Vylúčením parametra t z týchto rovníc získame často používaný tvar rovnice astroidov

Za predpokladu v skôr odvodených všeobecných vzťahoch pre cykloidné krivky modul

m = -1/4, získame zodpovedajúce vzťahy pre astroid:

1) polomer zakrivenia v ľubovoľnom bode astroidu je určený vzorcom

2) dĺžka oblúka astroidea z bodu A do ľubovoľného bodu M(t) je určená vzorcom

dĺžka jednej vetvy je rovná a dĺžka celej krivky je 6R;

3) aby sme získali prirodzenú rovnicu astroidu, najprv si všimneme, že ak počiatočným bodom dĺžky oblúka nie je bod A, pre ktorý t \u003d 0, ale bod, pre ktorý t \u003d, potom dĺžka oblúk je určený vzorcom

vylúčením parametra t z rovníc (5) a (6) dostaneme prirodzenú rovnicu astroidea

4) evoluta astroida je tiež astroideum podobné danému, s koeficientom podobnosti rovným 2, pootočené voči danému o uhol /4 (obr. 16)

5) plocha ohraničená celým astroideom sa rovná objemu tela získaného rotáciou astroidea, rovná sa 32/105 R 3

povrch tela tvorený rotáciou astroida sa rovná

Prejdime teraz k úvahám o niektorých konkrétnych vlastnostiach astroidov.

Astroid je obal segmentu konštantnej dĺžky, končí. ktoré sa posúvajú po dvoch vzájomne kolmých priamkach.

Tieto priamky berieme ako súradnicové osi a s uhlom sklonu klzného segmentu ND=R cez (obr. 4) dostaneme rovnicu priamky ND v tvare

Diferencovaním tejto rovnice vzhľadom na parameter dostaneme:

Vylúčením parametra z poslednej rovnice a rovnice (7) budeme mať obalovú rovnicu v tvare t.j. astroid.

V praxi môže byť pohyb segmentu ND realizovaný pomocou takzvaných kardanových kruhov. Jedna z týchto kružníc s polomerom R je nehybná a druhá, s polomerom r, dvakrát menším, sa valí po vnútornej strane nehybnej kružnice. Akékoľvek dva diametrálne opačné body N a D valivého kruhu sa budú pohybovať pozdĺž dvoch vzájomne kolmých priemerov Ox a Oy stacionárneho kruhu. Je jasné, že obálkou priemeru valivého kruhu bude astroid.

Ryža. 17

Ryža. 18

Uvažovaný spôsob vzniku astroida možno interpretovať aj nasledovne. Obdĺžnik ODCN, ktorého dve strany ležia na dvoch vzájomne kolmých čiarach, sa zdeformuje tak, že jeho uhlopriečka si zachová dĺžku rovnajúcu sa R, obálka uhlopriečky bude astroid. Keďže v tomto prípade kolmica spadnutá z vrcholu C na uhlopriečku DN slúži ako kolmica na obálku, astroidea je miestom základne kolmic spadnutých z vrcholu C obdĺžnika k jeho diagonále.

Pre , tieto rovnice vyjadrujú priamy astroid, o ktorom sme uvažovali skôr.

Krivka alebo čiara je geometrický pojem, ktorý je v rôznych častiach definovaný odlišne.

CURVE (čiara), stopa, ktorú zanecháva pohybujúci sa bod alebo teleso. Krivka je zvyčajne znázornená iba ako hladko zakrivená čiara, ako je parabola alebo kruh. Ale matematický koncept krivky zahŕňa priamku aj obrazce zložené z úsečiek, napríklad trojuholníka alebo štvorca.

Krivky môžeme rozdeliť na ploché a priestorové. Rovinná krivka, ako je parabola alebo priamka, je vytvorená v priesečníku dvoch rovín alebo roviny a telesa, a preto leží celá v jednej rovine. Priestorovú krivku, napríklad špirálu v tvare špirálovej pružiny, nemožno získať ako priesečník žiadnej plochy alebo telesa s rovinou a neleží v jednej rovine. Krivky môžeme rozdeliť aj na uzavreté a otvorené. Uzavretá krivka, ako je štvorec alebo kruh, nemá konce, t.j. pohybujúci sa bod generujúci takúto krivku periodicky opakuje svoju dráhu.

Krivka je miesto alebo množina bodov, ktoré spĺňajú nejakú matematickú podmienku alebo rovnicu.

Napríklad kruh je ťažisko bodov v rovine, ktoré sú rovnako vzdialené od daného bodu. Krivky definované algebraickými rovnicami sa nazývajú algebraické krivky.

Napríklad rovnica priamky y = mx + b, kde m je sklon a b je segment odrezaný na osi y, je algebraická.

Krivky, ktorých rovnice obsahujú transcendentálne funkcie, ako sú logaritmy alebo goniometrické funkcie, sa nazývajú transcendentálne krivky.

Napríklad y = log x a y = tg x sú rovnice transcendentálnych kriviek.

Tvar algebraickej krivky možno určiť podľa stupňa jej rovnice, ktorý sa zhoduje s najvyšším stupňom členov rovnice.

Ak rovnica prvého stupňa, napríklad Ax + By + C = 0, potom má krivka tvar priamky.

Ak rovnica druhého stupňa, napr.

Ax 2 + By + C = 0 alebo Ax 2 + By 2 + C = 0, potom je krivka kvadratická, t.j. predstavuje jednu z kužeľosečiek; takéto krivky zahŕňajú paraboly, hyperboly, elipsy a kružnice.

Uvádzame všeobecné formy rovníc kužeľosečiek:

x 2 + y 2 \u003d r 2 - kruh,

x 2 / a 2 + y 2 / b 2 \u003d 1 - elipsa,

y \u003d os 2 – parabola,

x 2 / a 2 - y 2 / b 2 \u003d 1 - hyperbola.

Krivky zodpovedajúce rovnici tretieho, štvrtého, piateho, šiesteho atď. stupne sa nazývajú krivky tretieho, štvrtého, piateho, šiesteho atď. objednať. Vo všeobecnosti platí, že čím vyšší je stupeň rovnice, tým viac ohybov bude mať otvorená krivka.

Mnohé zložité krivky dostali špeciálne mená.

Cykloida je rovinná krivka opísaná pevným bodom kružnice, ktorá sa valí pozdĺž priamky, nazývaná tvoriaca čiara cykloidy; cykloida pozostáva zo série opakujúcich sa oblúkov.

Epicykloida je rovinná krivka opísaná pevným bodom na kružnici, ktorá sa valí pozdĺž inej pevnej kružnice mimo nej.

Hypocykloida je rovinná krivka opísaná pevným bodom kružnice, ktorá sa valí zvnútra pozdĺž pevnej kružnice.

Špirála je plochá krivka, ktorá sa odvíja jednu zákrutu za druhou z pevného bodu (alebo sa vinie okolo neho).

Matematici skúmali vlastnosti kriviek už od staroveku a názvy mnohých nezvyčajných kriviek sa spájajú s menami tých, ktorí ich študovali ako prví. Takými sú napríklad Archimedova špirála, Agnesiova kučera, Dioklov cissoid, Nikomedov cochoid a Bernoulliho lemniskát.

V rámci elementárnej geometrie pojem krivka nedostáva jednoznačnú formuláciu a niekedy sa definuje ako „dĺžka bez šírky“ alebo ako „hranica obrazca“. V elementárnej geometrii je štúdium kriviek v podstate obmedzené na príklady (, , , atď.). Elementárna geometria bez všeobecných metód prenikla pomerne hlboko do štúdia vlastností špecifických kriviek (, niektoréa tiež), v každom prípade pomocou špeciálnych techník.

Krivka je najčastejšie definovaná ako súvislé mapovanie zo segmentu na:

V tomto prípade môžu byť krivky rôzne, aj keď súzladiť sa. Takéto krivky sú tzvparametrizované krivkyalebo ak[ a , b ] = , spôsoby.

Niekedy je krivka definovaná až do , teda až do minimálneho vzťahu ekvivalencie tak, že parametrické krivky

sú ekvivalentné, ak existuje spojitý (niekedy neklesajúci) h zo segmentu [ a 1 ,b 1 ] do segmentu [ a 2 ,b 2] tak, že

Tie, ktoré určuje tento vzťah, sa nazývajú alebo jednoducho krivky.

Analytické definície

V kurzoch analytickej geometrie sa dokázalo, že medzi čiarami napísanými v karteziánskych pravouhlých (alebo dokonca všeobecne afinných) súradniciach je všeobecná rovnica druhého stupňa

Ax 2 + 2Bxy + Cy 2 + 2Dx + 2Ey + F = 0

(kde je aspoň jeden z koeficientov A, B, C nenulový) existuje len týchto osem typov riadkov:

a) elipsa;

b) hyperbola;

c) parabola (nedegenerované krivky druhého rádu);

d) pár pretínajúcich sa čiar;

e) pár rovnobežných čiar;

f) pár zhodných čiar (jedna čiara);

g) jeden bod (degenerované čiary druhého rádu);

h) "čiara" neobsahujúca žiadne body.

Naopak, akýkoľvek riadok každého z týchto ôsmich typov je napísaný v karteziánskych pravouhlých súradniciach nejakou rovnicou druhého rádu. (V kurzoch analytickej geometrie sa zvyčajne hovorí o deviatich (skôr ako ôsmich) typoch kužeľosečiek, pretože rozlišujú medzi „imaginárnou elipsou“ a „dvojicou imaginárnych rovnobežných čiar“ – geometricky sú tieto „priamky“ rovnaké, keďže obe neobsahujú jeden bod, ale analyticky sú zapísané rôznymi rovnicami.) Preto (degenerované a nedegenerované) kužeľosečky možno definovať aj ako priamky druhého rádu.

INkrivka v rovine je definovaná ako množina bodov, ktorých súradnice vyhovujú rovniciF ( X , r ) = 0 . Zároveň za funkciuF sú uložené obmedzenia, ktoré zaručujú, že táto rovnica má nekonečný počet nezhodných riešení a

táto množina riešení nevypĺňa „kus roviny“.

Algebraické krivky

Dôležitou triedou kriviek sú tie, pre ktoré je funkciaF ( X , r ) Existujez dvoch premenných. V tomto prípade krivka definovaná rovnicouF ( X , r ) = 0 , sa volá.

Algebraické krivky dané rovnicou 1. stupňa sú .

Rovnica 2. stupňa, ktorá má nekonečný počet riešení, určuje, teda degenerované a nedegenerované.

Príklady kriviek dané rovnicami 3. stupňa: , .

Príklady kriviek 4. stupňa: a .

Príklad krivky 6. stupňa: .

Príklad krivky definovanej rovnicou párneho výkonu: (multifokálna).

Algebraické krivky definované rovnicami vyšších stupňov sú uvažované v. Ich teória zároveň nadobudne väčšiu harmóniu, ak sa úvaha uskutoční na . V tomto prípade je algebraická krivka určená rovnicou tvaru

F ( z 1 , z 2 , z 3 ) = 0 ,

Kde F je polynóm troch premenných, ktoré sú bodmi.

Typy kriviek

Rovinná krivka je krivka, ktorej všetky body ležia v rovnakej rovine.

(jednoduchá čiara alebo jordánsky oblúk, tiež obrys) je množina bodov v rovine alebo priestore, ktoré sú vo vzájomnej spojitosti s úsečkami.

Segment cesty v .

analytické krivky, ktoré nie sú algebraické. Presnejšie povedané, krivky, ktoré možno definovať cez úrovňovú čiaru analytickej funkcie (alebo v multidimenzionálnom prípade systému funkcií).

sínusoida,

cykloid,

Archimedova špirála

traktor,

reťazová linka,

Hyperbolická špirála atď.

Spôsoby definovania kriviek:

analytická - krivka je daná matematickou rovnicou;

grafický - krivka sa nastavuje vizuálne na nosiči grafickej informácie;

tabuľkový - krivka je daná súradnicami radu bodov.

parametrický (najvšeobecnejší spôsob určenia rovnice krivky):

Kde - plynulé funkcie parametrovt, a

(X") 2 + (r") 2 + (z") 2 > 0 (podmienka pravidelnosti).

Často je vhodné použiť invariantný a kompaktný zápis krivky s:

kde na ľavej strane sú body krivky a pravá strana určuje jej závislosť od nejakého parametra t. Rozšírením tohto zápisu o súradnice dostaneme vzorec (1).

Cykloid.

História štúdia cykloidy je spojená s menami takých veľkých vedcov, filozofov, matematikov a fyzikov ako Aristoteles, Ptolemaios, Galileo, Huygens, Torricelli a ďalší.

Cykloid(odκυκλοειδής - okrúhly) - ktorý možno definovať ako trajektóriu bodu ležiaceho na hranici kružnice, ktorá sa valí bez kĺzania po priamke. Tento kruh sa nazýva generujúci kruh.

Jedným z najstarších spôsobov vytvárania kriviek je kinematická metóda, pri ktorej sa krivka získa ako trajektória bodu. Krivka, ktorá sa získa ako trajektória bodu upevneného na kruhu, ktorý sa valí bez skĺznutia po priamke, pozdĺž kruhu alebo inej krivky, sa nazýva cykloidná, čo v gréčtine znamená kruh, pripomínajúci kruh.

Uvažujme najprv o prípade, keď sa kružnica valí po priamke. Krivka opísaná bodom upevneným na kružnici, ktorá sa valí bez kĺzania po priamke, sa nazýva cykloida.

Nechajte kružnicu s polomerom R valiť po priamke a. C je bod upevnený na kružnici, v počiatočnom okamihu v polohe A (obr. 1). Položme na priamku úsečku AB, rovnajúcu sa obvodu kruhu, t.j. AB \u003d 2 π R. Tento segment rozdeľujeme na 8 rovnakých častí bodmi A1, A2, ..., A8 \u003d B.

Je jasné, že keď kružnica, odvaľujúca sa po priamke a, urobí jednu otáčku, t.j. sa otočí o 360, potom zaujme polohu (8) a bod C sa presunie z polohy A do polohy B.

Ak kruh urobí polovicu celej otáčky, t.j. sa otočí o 180, potom zaujme pozíciu (4) a bod C sa posunie do najvyššej polohy C4.

Ak sa kruh otočí o uhol 45, potom sa kruh posunie do polohy (1) a bod C sa posunie do polohy C1.

Obrázok 1 tiež ukazuje ďalšie body cykloidy zodpovedajúce zostávajúcim uhlom rotácie kruhu, ktoré sú násobkami 45.

Spojením zostrojených bodov hladkou krivkou získame úsek cykloidy zodpovedajúci jednej úplnej otáčke kružnice. Pri ďalších otáčkach sa získajú rovnaké úseky, t.j. cykloida bude pozostávať z periodicky sa opakujúceho úseku nazývaného cykloidný oblúk.

Venujme pozornosť polohe dotyčnice k cykloide (obr. 2). Ak cyklista jazdí po mokrej vozovke, kvapky odtrhnuté od kolesa priletia tangenciálne k cykloide a pri absencii štítov môžu postriekať chrbát cyklistu.

Prvý človek, ktorý študoval cykloidu, bol Galileo Galilei (1564-1642). Prišiel aj s jeho názvom.

Vlastnosti cykloidu:

Cykloida má množstvo pozoruhodných vlastností. Spomeňme niektoré z nich.

Nehnuteľnosť 1. (Ľadová hora.) V roku 1696 I. Bernoulli nastolil problém nájsť najstrmšiu klesajúcu krivku, alebo, inými slovami, problém, aký by mal mať tvar ľadového kopca, ktorý sa valí nadol, aby vytvoril cestu. z počiatočného bodu A do koncového bodu B v najkratšom čase (obr. 3, a). Požadovaná krivka sa nazývala „brachistochrónová“, t.j. najkratšia časová krivka.

Je jasné, že najkratšia cesta z bodu A do bodu B je segment AB. Pri takomto priamočiarom pohybe však rýchlosť naberá pomaly a čas strávený zostupom sa ukazuje ako veľký (obr. 3, b).

Rýchlosť sa získava tým rýchlejšie, čím je klesanie strmšie. Prudkým klesaním sa však dráha po zákrute predlžuje a tým sa predlžuje čas jej prejazdu.

Medzi matematikov, ktorí riešili tento problém, patrili: G. Leibniz, I. Newton, G. Lopital a J. Bernoulli. Dokázali, že požadovaná krivka je obrátená cykloida (obr. 3, a). Metódy vyvinuté týmito vedcami pri riešení problému brachistochróny položili základ pre nový smer v matematike - variačný počet.

Nehnuteľnosť 2. (Hodiny s kyvadlom.) Hodiny s obyčajným kyvadlom nemôžu bežať presne, pretože perióda kmitania kyvadla závisí od jeho amplitúdy: čím väčšia je amplitúda, tým je perióda dlhšia. Holandského vedca Christiana Huygensa (1629 - 1695) zaujímalo, akú krivku má gulička na strune kyvadla sledovať, aby doba jej kmitania nezávisela od amplitúdy. Všimnite si, že v obyčajnom kyvadle je krivka, po ktorej sa gulička pohybuje, kruh (obr. 4).

Požadovaná krivka sa ukázala ako obrátená cykloida. Ak je napríklad žľab vyrobený vo forme obrátenej cykloidy a guľa sa po ňom prechádza, potom perióda pohybu lopty pôsobením gravitácie nebude závisieť od jej počiatočnej polohy a amplitúdy (obr. 5). . Pre túto vlastnosť sa cykloida nazýva aj „tautochrón“ – krivka rovnakých časov.

Huygens vyrobil dve drevené dosky s cykloidnými okrajmi, obmedzujúcimi pohyb nite doľava a doprava (obr. 6). V tomto prípade sa samotná guľa bude pohybovať po obrátenej cykloide, a preto doba jej oscilácií nebude závisieť od amplitúdy.

Z tejto vlastnosti najmä cykloidy vyplýva, že bez ohľadu na to, z ktorého miesta zosuvu ľadu v podobe obrátenej cykloidy začneme zostup, strávime rovnaký čas až do koncového bodu.

Cykloidná rovnica

1. Cykloidnú rovnicu je vhodné napísať ako α - uhol natočenia kružnice vyjadrený v radiánoch, pričom α sa tiež rovná dráhe, ktorú prejde tvoriaca kružnica po priamke.

x=ra– r hriech α

y=r - r cos α

2. Zoberme si vodorovnú súradnicovú os ako priamku, po ktorej sa odvaľuje vytvárajúca kružnica s polomerom r.

Cykloida je opísaná parametrickými rovnicami

X = rt – r hriech t,

r = r – r cos t.

Rovnica v:

Cykloidu možno získať ako riešenie diferenciálnej rovnice:

Z príbehu o cykloide

Prvý z vedcov upozornil na cykloiduV, no vážne skúmanie tejto krivky sa začalo až v r.

Prvý, kto začal študovať cykloidu, bol Galileo Galilei (1564-1642), slávny taliansky astronóm, fyzik a pedagóg. Vymyslel aj názov „cykloid“, čo znamená: „pripomínajúci kruh“. Sám Galileo o cykloide nič nenapísal, ale jeho diela v tomto smere spomínajú študenti a nasledovníci Galilea: Viviani, Toricelli a ďalší. Toricelli, slávny fyzik, vynálezca barometra, venoval veľa času matematike. V renesancii neexistovali úzko špecializovaní vedci. Talentovaný človek sa zaoberal filozofiou, fyzikou a matematikou a všade dosiahol zaujímavé výsledky a urobil veľké objavy. O niečo neskôr ako Taliani sa cykloidu chopili Francúzi a nazvali ho „roll“ alebo „trochoid“. V roku 1634 Roberval - vynálezca známeho systému závaží systému závaží - vypočítal oblasť ohraničenú oblúkom cykloidy a jej základňou. Súčasník Galilea uskutočnil zmysluplnú štúdiu cykloidy. Medzi , teda krivky, ktorých rovnicu nemožno zapísať v tvare X , r, cykloida je prvou zo skúmaných.

O cykloide napísal:

Ruleta je taká bežná čiara, že po priamke a kruhu už nie je žiadna spoločná čiara; kreslí sa pred očami každého tak často, že sa človek musí čudovať, že o tom starí ľudia neuvažovali ... lebo toto nie je nič iné ako cesta opísaná vo vzduchu klincom kolesa.

Nová krivka si rýchlo získala popularitu a bola podrobená hĺbkovej analýze, ktorá zahŕňala, , Newton,, bratia Bernoulliovci a ďalšie osobnosti vedy XVII-XVIII storočia. Na cykloide, metódy vznikajúce v tých rokoch. Skutočnosť, že analytická štúdia cykloidy bola rovnako úspešná ako analýza algebraických kriviek, urobila veľký dojem a stala sa dôležitým argumentom v prospech „vyrovnania práv“ algebraických a transcendentálnych kriviek. Epicykloida

Niektoré typy cykloidov

Epicykloida - trajektória bodu A, ležiaceho na kružnici s priemerom D, ktorá sa bez skĺznutia valí po vodiacej kružnici s polomerom R (vonkajší dotyk).

Konštrukcia epicykloidu sa vykonáva v nasledujúcom poradí:

Zo stredu 0 sa nakreslí pomocný oblúk s polomerom rovným 000=R+r;

Z bodov 01, 02, ... 012 sa ako zo stredov ťahajú kružnice s polomerom r, až kým sa nepretnú s pomocnými oblúkmi v bodoch A1, A2, ... A12, ktoré patria do epicykloidy.

Hypocykloida

Hypocykloida - trajektória bodu A, ležiaceho na kružnici s priemerom D, ktorá sa bez kĺzania valí po vodiacej kružnici s polomerom R (vnútorný dotyk).

Konštrukcia hypocykloidy sa vykonáva v nasledujúcom poradí:

Generujúca kružnica s polomerom r a vodiaca kružnica s polomerom R sú nakreslené tak, že sa dotýkajú v bode A;

Generujúci kruh je rozdelený na 12 rovnakých častí, získajú sa body 1, 2, ... 12;

Zo stredu 0 je nakreslený pomocný oblúk s polomerom rovným 000=R-r;

Stredový uhol a je určený vzorcom a \u003d 360r / R.

Rozdeľte oblúk vodiaceho kruhu, ohraničeného uhlom a, na 12 rovnakých častí, získajte body 11, 21, ... 121;

Od stredu 0 cez body 11, 21, ... 121 sa vedú priamky k priesečníku s pomocným oblúkom v bodoch 01, 02, ... 012;

Zo stredu 0 sú nakreslené pomocné oblúky cez deliace body 1, 2, ... 12 tvoriacej kružnice;

Z bodov 01, 02, ... 012 sa ako zo stredov ťahajú kružnice s polomerom r, až kým sa nepretnú s pomocnými oblúkmi v bodoch A1, A2, ... A12, ktoré patria do hypocykloidy.

Kardioidný.

Kardioidný ( καρδία - Srdce, Kardioida je špeciálny prípad Termín „kardioida“ zaviedol Castillon v roku 1741.

Ak vezmeme za pól kruh a bod na ňom, potom dostaneme kardioidu iba vtedy, ak vyčleníme segmenty rovné priemeru kruhu. Pre iné hodnoty vynesených segmentov budú lastúrniky predĺžené alebo skrátené kardioidy. Tieto predĺžené a skrátené kardioidy sa inak nazývajú Pascalove slimáky.

Kardioida má rôzne aplikácie v strojárstve. Vo forme kardioidy vyrábajú excentry, vačky do áut. Niekedy sa používa pri kreslení ozubených kolies. Okrem toho sa používa v optickej technike.

Vlastnosti kardioidu

Kardioidný -V M na pohyblivom kruhu bude opisovať uzavretú trajektóriu. Táto plochá krivka sa nazýva kardioidná.

2) Kardioidu možno získať aj iným spôsobom. Označte bod na kruhu O a nakreslite z neho lúč. Ak z bodu A priesečník tohto lúča s kruhom, odložte segment AM, pozdĺž dĺžky rovnajúcej sa priemeru kruhu a otáčajte lúč okolo bodu O, potom bod M sa bude pohybovať pozdĺž kardioidy.

3) Kardioidu je možné znázorniť aj ako krivku dotýkajúcu sa všetkých kružníc so stredom daného kruhu a prechádzajúcich jej pevným bodom. Keď sa vytvorí niekoľko kruhov, kardioid sa ukáže byť postavený akoby sám.

4) Existuje ďalší rovnako elegantný ako neočakávaný spôsob, ako vidieť kardioidu. Na obrázku môžete vidieť bodový zdroj svetla na kruhu. Po prvom odraze lúčov od kruhu sa lúče dotýkajú kardioidy. Teraz si predstavte, že kruh je okrajmi pohára, v jednom bode odráža jasnú žiarovku. Čierna káva sa naleje do šálky, čo vám umožní vidieť jasné odrazené lúče. V dôsledku toho je kardioida zvýraznená lúčmi svetla.

Astroid.

Astroid (z gréckeho astron - hviezda a eidos - pohľad), plochá krivka opísaná bodom kruhu, ktorý sa zvnútra dotýka pevného kruhu so štvornásobkom polomeru a bez skĺznutia sa po ňom valí. Patrí medzi hypocykloidy. Astroid - algebraická krivka 6. rádu.

Astroid.

Dĺžka celého astroidu sa rovná šiestim polomerom pevného kruhu a plocha ním ohraničená sú tri osminy pevného kruhu.

Úsek dotyčnice k astroideu, uzavretý medzi dvoma vzájomne kolmými polomermi pevnej kružnice nakreslenej na špičke astroidea, sa rovná polomeru pevnej kružnice bez ohľadu na to, ako bol bod zvolený.

vlastnosti astroidov

Sú tu štyrihrot .

Dĺžka oblúka od bodu 0 po obálku

rodiny segmentov konštantnej dĺžky, ktorých konce sú umiestnené na dvoch navzájom kolmých čiarach.

Astroid je 6. rádu.

Astroidné rovnice

Rovnica v karteziánskych pravouhlých súradniciach je:| x | 2 / 3 + | y | 2/3 = R2/3parametrická rovnica:x = Rcos 3 t y = Rsin 3 t

Ako postaviť astroid

Nakreslíme dve navzájom kolmé čiary a nakreslíme sériu segmentov s dĺžkouR ktorých koncové body ležia na týchto čiarach. Na obrázku je 12 takýchto segmentov (vrátane segmentov samotných navzájom kolmých čiar). Čím viac segmentov nakreslíme, tým presnejšia bude krivka. Zostrojme teraz obálku všetkých týchto segmentov. Táto obálka bude astroid.

Záver

V príspevku sú uvedené príklady problémov s rôznymi typmi kriviek, ktoré sú definované rôznymi rovnicami alebo ktoré spĺňajú nejakú matematickú podmienku. Najmä cykloidné krivky, spôsoby ich špecifikácie, rôzne spôsoby konštrukcie, vlastnosti týchto kriviek.

Vlastnosti cykloidných kriviek sa veľmi často využívajú v mechanike pri prevodoch, čo výrazne zvyšuje pevnosť dielov v mechanizmoch.

- (z gréckeho pohľadu astron a eidos) plochá krivka opísaná bodom kruhu, ktorý sa zvnútra dotýka pevného kruhu so štvornásobkom polomeru a bez skĺznutia sa po ňom valí. Patrí medzi hypocykloidy. Astroidská algebraická ...... Veľký encyklopedický slovník

Exist., Počet synoným: 1 krivka (56) ASIS Synonym Dictionary. V.N. Trishin. 2013... Slovník synonym

- (z gréckeho pohľadu ástron hviezda a éidos), plochá krivka opísaná bodom na kruhu, ktorý sa dotýka vnútra pevného kruhu so štvornásobným polomerom a valí sa po ňom bez skĺznutia. Patrí medzi hypocykloidy. Astroid ...... encyklopedický slovník

- (astro... gr. eidos pohľad) mat. plochá krivka opísaná bodom kružnice, ktorá sa valí bez kĺzania po vnútornej strane inej pevnej kružnice s polomerom štyrikrát väčším ako polomer prvej; vyzerá ako štvorcípa hviezda. Nový slovník... Slovník cudzích slov ruského jazyka

Plochá algebra. krivka ti ro rádu, k okraju je opísaná bodom kružnice s polomerom r, valiacim sa po vnútornej strane kružnice s polomerom R=4r; hypocykloida s modulom r=4. Rovnica v karteziánskych karteziánskych súradniciach: Parametrická. rovnice... Matematická encyklopédia

Prečo je náš svet krásny? Pretože formy a farby živej prírody sa do značnej miery riadia všeobecnými zákonmi harmónie, ktoré odhaľuje dôsledná matematická analýza. Pri štúdiu prírody v nej nachádzame čoraz viac estetických čŕt, ktoré sa spravidla neodhalia hneď, ale až po podrobnom matematickom rozbore.

Osoba rozlišuje predmety okolo seba podľa tvaru. Záujem o formu predmetu môže byť diktovaný životnou nevyhnutnosťou alebo môže byť spôsobený krásou formy. Forma, ktorá je založená na kombinácii symetrie a zlatého rezu, prispieva k najlepšiemu vizuálnemu vnímaniu a dojmu zmyslu pre krásu a harmóniu.

Celok sa vždy skladá z častí, časti rôznych veľkostí sú v určitom vzťahu medzi sebou aj k celku. Princíp zlatého rezu je najvyšším prejavom štrukturálnej a funkčnej dokonalosti celku a jeho častí v umení, vede, technike a prírode.

Pri využívaní zákonov geometrie prírody v novej situácii na štúdium predmetov súvisiacich s geometrickými konštrukciami prehodnocujeme študované geometrické zákony, rozvíjame geometrickú intuíciu.

V procese plnenia tvorivých úloh rôzneho obsahu sme sa oboznámili s možnými oblasťami aplikácie geometrických poznatkov (umelci, architekti, dizajnéri a pod.).

Grafické prostriedky zobrazovania informácií sa využívajú vo všetkých sférach spoločnosti. Majú ucelený obraz, vyznačujú sa symbolikou, kompaktnosťou a relatívnou ľahkosťou čítania. Práve tieto kvality grafických obrázkov určujú ich rozšírené využitie. V blízkej budúcnosti bude mať viac ako polovica prezentovaných informácií grafickú formu prezentácie. Rozvoj teoretických základov deskriptívnej geometrie, inžinierskej grafiky a iných príbuzných vied rozšíril spôsoby získavania grafických obrazov. Popri ručných metódach tvorby grafických obrazov, zostavovaní projektovej dokumentácie sa čoraz viac využívajú počítačové metódy. Využívanie nových informačných technológií zabezpečuje tvorbu, úpravu, ukladanie, replikáciu grafických obrázkov pomocou rôznych softvérových nástrojov.

I. Úvodné informácie o algebraických krivkách

1. Astroid

Astroid (z gréckeho >-hviezda) je krivka opísaná bodom na pohyblivom kruhu, ktorý sa zvnútra dotýka pevného kruhu so štvornásobkom polomeru a otáča sa po ňom bez skĺznutia. Plocha ohraničená astroideom je /8 plochy pevného kruhu a celková dĺžka astroidea sa rovná polomeru tohto kruhu, šesťkrát.

Rovnica astroidu v karteziánskych pravouhlých súradniciach je:

x + y = R.

Konštrukcia astroidného grafu bola vykonaná v > takto:

:: Zostrojený funkčný graf pre y > 0 (polomer R = 5);

:: Vytvorili sme funkčný graf.

2. Kardioidný

Kardioida (z gréckeho >-srdce a eidos-pohľad) je plochá krivka opísaná pevným bodom kruhu, ktorý sa zvonka dotýka pevného kruhu s rovnakým polomerom a bez skĺznutia sa po ňom valí. Krivka dostala svoj názov podľa podobnosti so srdcom.

Kardioidné vykresľovanie sa tiež uskutočnilo v >.

3. Nefroid

Nefroid (z gréc. hephros-obličky, eidos-pohľad) - krivka, ktorá opisuje pevný bod kruhu valiaceho sa von pozdĺž dvakrát väčšieho kruhu. Prvýkrát vlastnosti nefroidov skúmal v 17. storočí saský šľachtic E. V. Chirngauz. Nefroid sa skladá z dvoch kardioidných.

4. Pascalov slimák.

Pascalov slimák je plochá algebraická krivka. Pomenovaný podľa Etienna Pascala (otca Blaise Pascala), ktorý ho ako prvý skúmal. Rovnica v polárnych súradniciach. Pre l = 2a sa získa kardioid.

II. Aplikácia matematického modelovania.

1. História tvorby závitovej grafiky

Niťová grafika (alebo izovlákno) je grafický obrázok vyrobený špeciálnym spôsobom pomocou nití na kartóne alebo inom pevnom podklade. Niťová grafika sa tiež niekedy nazýva izografia alebo kartónová výšivka.

V Rusku sa používa výraz > (vláknová grafika alebo niť), v anglicky hovoriacich krajinách sa používa slovné spojenie - výšivka na papieri, v nemecky hovoriacich krajinách - pojem.

Niťová grafika, ako druh umenia a remesiel, sa prvýkrát objavila v Anglicku v 17. storočí. Anglickí tkáči prišli na špeciálny spôsob tkania nití. Zatĺkali klince do dosák a v určitom poradí cez ne ťahali nite. V dôsledku toho sa získali výrobky z prelamovanej čipky, ktoré sa používali na zdobenie domu. (Vznikla verzia, že tieto práce boli akýmsi náčrtom vzorov na tkanine). Moderný spotrebný materiál vám umožňuje získať veľmi efektívne produkty.

Spolu s pôvodnou technikou nite grafiky existuje ďalší smer dizajnu nití - vyšívanie na lepenku (niť) pomocou rovnakých techník (spôsob vyplnenia rohu a kruhu).

Záujem o filamentovú grafiku sa objavil a potom zmizol. Jeden z vrcholov popularity bol na konci devätnásteho storočia. Na vyšívaní boli vydané knihy, ktoré popisovali neobvyklý spôsob vyšívania na papier, jednoduchý a ľahký, prístupný deťom. Použili sme perforované kartičky (hotové šablóny) a spôsob vyplnenia rohu, stehy >, > (na vyšívanie oblúčikov). S minimom finančných prostriedkov by si každý (a najmä deti) mohol vyrobiť luxusné suveníry na prázdniny.

Teraz sa toto umenie praktizuje v mnohých krajinách sveta.

V našej krajine existuje malé množstvo informácií o izovlákne, väčšinou na informačné účely: samostatné publikácie v časopisoch > V roku 1995 kniha minského profesora G. A. Branitského > a kniha Nagibiny M. I. > s malou kapitolou o izovlákne.

Po analýze dostupných informácií sa nám podarilo zistiť, že o tomto druhu vyšívania vychádza veľa kníh vo forme postupných inštrukcií a albumov nápadov, v ktorých sa všade používa iba reprodukčný spôsob práce.

Výhodou izovlákna je, že rýchlo beží a dá sa vymyslieť veľa zaujímavých vzorov. Tento typ kreativity rozvíja predstavivosť, zrak, jemné motorické zručnosti prstov, umelecké schopnosti a estetický vkus. Pomocou techniky niťovej grafiky môžete vyrábať nielen ozdobné panely, ale aj pohľadnice, obaly na suveníry, záložky do kníh.

A izovlákna (vláknová grafika alebo dizajn vlákna) môžu mať niekoľko smerov:

1) reprodukčná metóda: práca na šablóne, pokyny krok za krokom, distribúcia hotových vzorov a vyšívacích súprav

2) čiastočné vyhľadávanie (projekt): učenie sa kalkulovať na kartóne (t.j. vytváranie vlastných majstrovských diel), hľadanie vlastných techník a kombinácií, „hranie sa“ s pozadím, nitkami – s materiálom predstavenia

3) kombinované - keď všetko začína "abecedou", pracujeme s hotovými schémami, ale zmeníme typ materiálu (farbu) a dosiahneme "majstrovské dielo".

2. Základné techniky nitkovej grafiky

Niťová grafika je známa aj pod inými názvami: izovlákno (t.j. obrázok s niťou), grafická výšivka. Na zvládnutie techniky stačí vedieť, ako sa vypĺňa uhol, kruh a oblúk.

Recepcia 1. Vyplnenie rohu.

Na nesprávnu stranu lepenky nakreslite uhol a rozdeľte každú stranu na rovnaký počet častí. Hroty prepichneme špendlíkom alebo tenkým šidlom, navlečieme niť do ihly a vyplníme podľa schémy.

Recepcia 2. Vyplnenie kruhu.

Nakreslite kružnicu pomocou kružidla. Rozdeľte ho na 12 rovnakých častí a vyplňte podľa schémy.

Príjem 3. Plnenie oblúka.

Nakreslíme oblúk, rozdelíme ho na rovnaké časti a urobíme vpichy v deliacich bodoch. Ihlu navlečieme a naplníme podľa vzoru

III. Výskumná práca.

Konštrukcie v programe>.

Úloha 1. Rozdelenie úsečky na n rovnakých častí.

Riešenie 1. Rozdelenie na 2, 4, 8, 16 atď. časti bolo vykonané v > zostrojením stredových bodov segmentu.

Riešenie 2. Tiež sme vykonali rozdelenie segmentu na ľubovoľný počet častí v > pomocou Thalesovej vety.

Úloha 2. Rozdelenie kruhu na 6, 12, 24 častí.

Riešenie 1. Hľadali sme rôzne spôsoby, ako rozdeliť kruh na časti. V programe > sme nakreslili kruh, náhodne umiestnili body, zmerali výsledné uhly a potom > sme body posúvali po kruhu, kým sme nezískali požadovanú hodnotu. Bola to monotónna a nezaujímavá práca. Chyba prvého rozdelenia na 12 častí bola + 0,15 cm v dĺžke akordov. Začali sme analyzovať situáciu a hľadať najlepšie spôsoby riešenia úloh. V dôsledku toho sme našli niekoľko riešení na rozdelenie kruhu na 6, 12, 24 častí.

Riešenie 2. Na kružnici bolo vyznačených 6 bodov, zmerali sa všetky uhly, body sa zarovnali tak, aby sa každý uhol rovnal 60 [o]. Potom sa pomocou programu nakreslili osy každého uhla. Výsledkom bolo rozdelenie na 12 častí. A na rozdelenie na 24 častí boli opäť nakreslené osy získaných uhlov. Chyba takejto konštrukcie sa ukázala ako + 0,01 stupňa.

Riešenie 3. Pomocou programu sme postavili 3 kruhy s rovnakým polomerom (kopírovanie aplikácie), skombinovali sme ich, ako je znázornené na obrázku. Označte priesečníky kružníc. Výsledné uhly boli zmerané, ukázalo sa, že sú rovné 60 [o]. Ďalej sme postavili osy uhlov na delenie na 12 a 24 častí. Chyba takéhoto riešenia je nulová.

Úloha 3. Rozdelenie kruhu na 9, 18, 36 častí.

Keď sme našli optimálny spôsob riešenia predchádzajúceho problému, podobne sme začali hľadať spôsoby, ako rozdeliť kruh na 9, 18 a 36 častí. Rozdelenie na 18 a 36 častí je možné vykonať až po zostrojení 9 bodov aplikovaním konštrukcie osí.

Riešenie. 360 [o]: 9 = 40 [o]. Polkruh sme rozdelili na 4 oblúky približne 40 [o] a oblúk 20 [o]. Pomocou programu sme vykonali všetky potrebné merania uhlov pohybom bodov. Ďalej sme vybrali zostrojené body a pomocou príkazu > sme body premietli o 180 stupňov vzhľadom na stred kruhu na druhý polkruh. Chyba takejto konštrukcie bola + 0,04 stupňa.

Úloha 4. Konštrukcia algebraických kriviek

Astroid

Riešenie 1. Astroid je postavený na súradnicovej rovine podľa nasledujúceho algoritmu:

:: Musíte spojiť body osi y s bodmi úsečky tak, aby súčet dielikov dal 10 (napríklad: 1 a 9, 2 a 8, 3 a 7 atď.).

:: Body spojíme v rovnakom poradí vo zvyšných štvrtinách súradnicovej roviny.

Riešenie 2. Nakreslite kruh, vytvorte kolmé priemery, rozdeľte každý polomer na párny počet častí. Body sme spojili segmentmi podľa predchádzajúceho algoritmu.

Riešenie 3. Po zvládnutí optimálneho spôsobu rozdelenia kruhu na 6 častí sme dokončili stavbu 6-hviezdičkového astroidu.

Riešenie 4. Konštrukcia 8-hviezdičkového astroidu bola vykonaná s konštrukciou pravých uhlových osí.

Kardioidný

Riešenie. Na zostrojenie kardioidy bude základňou kruh. Kardioid bol postavený podľa nasledujúceho plánu:

:: nakreslil kruh a rozdelil ho na 36 častí (každá po 10 stupňoch);

:: očíslované vonkajšie body od 1 do 36 proti smeru hodinových ručičiek;

:: interné body sú očíslované podľa schémy 1;

:: spojené bodky s rovnakými vnútornými a vonkajšími číslami;

:: obálka a bude kardioid.

Schéma 1 Schéma 2

IV. Naša kreativita.

Po zvládnutí základných techník dizajnu a modelovania v > sme sa snažili realizovať v úlohe dizajnérov a umelcov. Vyvinuli sme a uviedli do praxe nasledujúce práce:

Záver, závery

>, - poznamenal Aristoteles pred 2500 rokmi. Náš súčasník Suchomlinskij veril, že >. A matematika je úžasný predmet na prekvapenie.

Po dôkladnom preštudovaní dostupného materiálu sme sa zoznámili s novou metódou vytvárania kriviek - matematickým vyšívaním pomocou známych techník na vytváranie geometrických tvarov (zostrojenie uhla, rozdelenie segmentu na rovnaké časti, spojenie bodov v určitom poradí, rozdelenie a zakrúžkujte v programe na rovnaké časti\u003e). Našli sme úžasnú podobnosť medzi matematickým vyšívaním a dlho známym druhom umeleckých remesiel - izovláknom.

Na internete, v špeciálnej literatúre, je veľa fotografií s výšivkou izovlákna, ale diagramy k nim nie sú pripojené. Dospeli sme k záveru, že matematické vyšívanie je tvorivý proces. Znalosťou základov matematického modelovania, ktoré sú načrtnuté v našej práci, uplatnením kreatívneho myslenia, logiky, trpezlivosti dokážete vytvárať individuálne > úžitkové umenie.

Matematické vyšívanie zaujalo nielen nás, ale aj mnohých žiakov školy (dievčatá aj chlapcov). Veríme, že moderné informačné technológie budú spájať matematiku a umenie.

KURZOVÁ PRÁCA

na tému:

"Praktická aplikácia vlastností pozoruhodných kriviek"

Úvod

Relevantnosť témy je preukázať aplikáciu matematických poznatkov v praktických ľudských činnostiach. Kurz štúdia analytickej geometrie neposkytuje zváženie vlastností nádherných kriviek, ktoré sa v živote bežne používajú.

Hypotéza : Použitie tohto materiálu rozširuje študentom obzory o krivkách a ich vlastnostiach a ukazuje ich praktické uplatnenie v živote človeka.

Účel tejto práce : Zhromaždite materiál na jeho aplikáciu pri samoštúdiu nádherných kriviek.

Úlohy : Pomôcť študentovi. Využite minimum času, aby ste dosiahli maximálny úžitok.

Praktický význam práce: Verím, že moja práca bude užitočná pre študentov prístupným a názorným spôsobom na pochopenie látky. Ukážte praktickú aplikáciu vlastností nádherných kriviek, naučte sa krivky stavať.

Výber témy

Pri súčasnej úrovni rozvoja technického myslenia sú potrebné poznatky o pozoruhodných krivkách. V prírode nie sú také vzácne, majú praktické uplatnenie v živote človeka. Poznatky o ich pozoruhodných vlastnostiach sa využívajú v rôznych mechanizmoch, ktoré človek v živote využíva.

Túto tému som si vybral, pretože ju považujem za zaujímavú a zmysluplnú, rozvíjajúc kognitívny záujem o analytickú geometriu, otvárajúc praktickú aplikáciu geometrie v živote. Použitie tohto materiálu na prednáškach o geometrii rozširuje obzory študentov pozdĺž kriviek študovaných v programe. V rôznych častiach matematiky a na rôznych stupňoch štúdia sa stretávame s krivkami, tretieho aj druhého rádu. Nikde sa však nehovorí o pozoruhodných vlastnostiach týchto kriviek a ešte viac o ich praktickom použití. Domnievam sa, že je veľmi dôležité, aby študenti poznali úžasné vlastnosti týchto kriviek, ktoré sú v živote hojne využívané. Štúdiom a čo i len spoznaním týchto vlastností študenti vidia skutočne praktické využitie geometrie.

K tomu som sa zoznámil s materiálom o nádherných krivkách a ich vlastnostiach v rôznych učebniciach a encyklopédiách matematiky.

1. Z histórie vývoja náuky o líniách

Pojem čiara vznikol v ľudskej mysli už v praveku. Trajektória vrhaného kameňa, obrysy kvetov a listov rastlín, kľukatá línia brehu rieky a iné prírodné úkazy oddávna priťahovali pozornosť ľudí. Mnohokrát odpozorované slúžili ako základ pre postupné etablovanie koncepcie linky. Ale trvalo dosť dlho, kým naši predkovia porovnali tvary zakrivených čiar medzi sebou. Prvé kresby na stenách jaskýň, primitívne ornamenty na domácich nádobách ukazujú, že ľudia dokázali nielen rozlíšiť priamku od krivky, ale aj rozlíšiť jednotlivé krivky. Pamiatky staroveku dosvedčujú, že všetky národy v určitom štádiu svojho vývoja mali pojmy priamka a ich obvod. Na stavbu týchto čiar boli použité najjednoduchšie nástroje.

Teória čiar sa však začala rozvíjať až s príchodom matematických teórií. Grécki vedci vytvorili teóriu línií druhého rádu. Tieto čiary boli považované za rez kužeľa rovinou, v dôsledku čoho sa v staroveku nazývali kužeľové rezy. Kónické rezy ako prvý uvažoval Menechmus, ktorý žil v 4. storočí pred Kristom. Pri hľadaní riešení rôznych problémov uvažovali grécki vedci aj o niektorých transcendentálnych líniách.

V stredoveku sa na dôležitý úspech gréckych vedcov zabudlo. Matematická veda sa opäť obrátila na štúdium kriviek až v 7. storočí. Pre štúdium línií mala prvoradý význam metóda súradníc objavená Descartesom a Fermatom, ktorá prispela k vzniku infinitezimálneho počtu. Metóda súradníc v kombinácii s analýzou infinitezimál umožnila pristúpiť k štúdiu línií všeobecným spôsobom. Rôzne problémy mechaniky, astronómie, geodézie, optiky, ktoré vznikli v 7. – 8. storočí, viedli k objaveniu mnohých nových línií a štúdiu ich geometrických mechanických vlastností. Týmito otázkami sa s veľkým nadšením zaoberali najväčší matematici tej doby – Descartes, Huygens, Leibniz, bratia Bernoulliovci.

Ďalší dôležitý krok v štúdiu čiar urobil Newton, ktorý začal s vývojom teórie kriviek tretieho rádu. Následne boli stanovené tieto úlohy: študovať krivky štvrtého a vyššieho rádu, vytvoriť všeobecnú teóriu algebraických kriviek v rovine, pristúpiť k systematickému štúdiu algebraických plôch, počnúc plochou druhého rádu. K riešeniu posledného problému veľkou mierou prispel slávny matematik VIII Leonhard Euler, akademik Akadémie vied v Petrohrade. Opísal prvú príručku o analytickej geometrii, ktorá načrtla teóriu čiar a plôch druhého rádu.

. Pozoruhodné línie tretieho rádu

Všetky priamky a krivky druhého rádu (kružnice, elipsy, paraboly, hyperboly) sú špeciálnymi prípadmi kriviek tretieho rádu.

Vo všeobecnom prípade možno rovnicu zakrivenej čiary tretieho rádu zapísať takto: x 3 + a 1 y 3 + 3a 2 x 2 y + 3a 3 xy 2 + 3a 4 x 2 + 3a 5 y 2 + 3a 6 xy + 3a 7 x + 3a 8 y + a 9 \u003d 0.

Predpokladá sa, že koeficienty súčasne nezmiznú (inak by sa získala rovnica druhého stupňa). Viac ako 70 druhov týchto liniek. Tu uvažujeme len o niektorých z nich, ktoré sú pozoruhodné svojimi vlastnosťami a aplikáciami.

Kartézsky list

. Vlastnosti formulára. Kartézsky list sa nazýva krivka 3. rádu, ktorej rovnica má v pravouhlej sústave tvar

Niekedy je vhodné použiť parametrické karteziánske rovnice, ktoré je možné získať nastavením r= TX, pridanie rovnosti (1) k tejto rovnosti a riešenie výsledného systému vzhľadom na X A y, v dôsledku toho budeme mať:

z čoho vyplýva, že karteziánsky list je racionálna krivka.

Všimnite si tiež, že polárna karteziánska rovnica má tvar

(3)

Súradnice X A pri zadajte karteziánsku rovnicu symetricky, z čoho to vyplýva krivka je symetrická vzhľadom na os y=x. Zvyčajné skúmanie singulárnych bodov vedie k záveru, že počiatkom je uzlový bod karteziánskeho listu. Rovnice dotyčníc k algebraickej krivke v jej singulárnom bode, ktorý sa zhoduje s počiatkom, možno získať, ako je dobre známe, prirovnaním skupiny členov najnižšieho stupňa z rovnice tejto krivky k nule. V našom prípade máme Z axy \u003d 0, odkiaľ dostaneme x = 0 a y = 0 - požadované rovnice dotyčníc v uzlovom bode. Tieto dotyčnice sa zhodujú so súradnicovými osami, a preto sa krivka v počiatku pretína v pravom uhle. Je ľahké vidieť, že v prvom súradnicovom uhle krivka vytvára slučku, ktorá sa pretína s priamkou y = X v bode

Body tejto slučky, kde sú dotyčnice rovnobežné so súradnicovými osami, majú súradnice

A (pozri obr. 1)

Pre konečný záver o tvare krivky je potrebné nájsť aj asymptotu Nahradením y v rovnici krivky za , vo výslednej rovnici rovnáme nule koeficienty dvoch členov s vyššími stupňami. X. Získajte

a b = - a. Karteziánsky list má teda asymptotu

y \u003d - x - a; preto v 2. a 4. súradnicovom uhle idú vetvy karteziánskeho listu do nekonečna.

Ryža. 1

Často zvážte krivku otočenú o 135 stupňov. Jej rovnice vyzerajú takto. V pravouhlom systéme: , Kde

Parametrické:

Odvodenie rovníc pootočenej krivky:

Súradnicový systém XOY sa prevedie na súradnicový systém UOV, ktorý sa získa otočením osí OX a OY v smere hodinových ručičiek o uhol a preorientovaním osi OX v opačnom smere:

Vyjadrenie starých súradníc XY z hľadiska nových UV vyzerá takto:

Po nahradení výrazov starých súradníc novou rovnicou sa karteziánsky list prevedie do nasledujúcej podoby: .

Zadáme parameter , posledná rovnica sa prepíše takto:

Alebo .

Premenné u a v nahradíme obvyklými x a y a získame kartézsku listovú rovnicu v novom súradnicovom systéme:

Nahradením predchádzajúcej rovnice do rovnice získame rovnicu karteziánskeho listu v polárnom súradnicovom systéme:

Vyriešením tohto výrazu pre ρ dostaneme:

2. Vlastnosti. Podľa Maclaurinovej vety, ak v troch bodoch algebraickej krivky 3. rádu, ležiacich na jednej priamke, nakreslíme dotyčnice k tejto krivke, potom aj body ich priesečníka s krivkou budú ležať na priamke. Pri použití na karteziánsky list sa táto veta dá ľahko dokázať. Na tento účel odvodíme predbežnú podmienku prítomnosti troch bodov karteziánskeho listu zodpovedajúcich hodnotám t 1 , t 2 A t 3 parametra na jednej priamke. Ak má rovnica priamky tvar r= kx+ b, potom hodnoty parametrov zodpovedajúce priesečníkom tejto priamky s krivkou musia spĺňať systém

Tento systém vedie k rovnici

ktorých koreňmi budú požadované hodnoty t 1 , t 2 A t 3 parametra, z čoho vyplýva, že

Táto rovnosť je podmienkou prítomnosti troch bodov M 1 (t 1) , M 2 (t 2 ), M 3 (t 3) Kartézsky list na jednej priamke.

S touto podmienkou ukážeme platnosť Maclaurinovej vety pre karteziánsky list. Vskutku, dotyčnica v bode M 1 (t 1 ) možno považovať za priamku, ktorá pretína karteziánsky list v dvoch bodoch, ktoré sa navzájom zhodujú, pre ktoré t 2 = t 1 , a v treťom bode, pre ktorý bude zodpovedajúca hodnota parametra označená T1. Podmienka (4) má formu t 1 2 T 1 = - 1. Pre dotyčnice v bodoch M 2 A M 3 získame podobné vzťahy t 2 2 T 2 = -1 a t 3 2 T 3 = -1 . Vynásobením týchto troch rovnosti máme

(t 1 t 2 t 3 ) 2 T 1 T 2 T 3 = -1 . z čoho na základe (4) usudzujeme, že a T 1 T 2 T 3 = -1, tie. bodov N 1 (T 1 ), N 2 (T 2) a N 3 (T 3) ležia na rovnakej priamke.

Určením oblasti ohraničenej slučkou karteziánskeho listu dostaneme:

. Spôsob výstavby. Najprv si všimneme, že ak sa os symetrie karteziánskeho listu berie ako os úsečky, potom jej rovnica bude mať tvar

(5)

Nech je teraz kružnica s polomerom r a stredom v bode

a priamy x= -h. Vezmite ľubovoľný bod Q tejto kružnice a nakreslite priamku QA a priamy QN, kolmo na os x (obr. 2). Z priesečníka R rovno QA s rovnou čiarou x = - h nakresliť rovnú čiaru RO kým sa nepretína v bode Q 1 s rovnou čiarou QN. Takže pointa Q na kruhu bude pridelený bod Q1. Miestom bodov Q 1 je karteziánsky list.

Aby ste to dokázali, všimnite si, že súradnice bodu Q možno napísať vo forme

uhol tvorený polomerom kružnice vedenej k bodu Q, s kladným smerom osi x. V súlade s tým rovnica priamky QA možno napísať ako

Za predpokladu, že v tejto rovnici x= -h, nájsť súradnicu

bodov R. Z toho vyplýva, že rovnica priamky RQ 1 sa zapíše do formulára

(6)

Zároveň rovnica priamky Q 1 N má formu

(7)

Vylúčením parametra z rovníc (6) a (7). w, rovnicu lokusu bodov Q 1 nájdeme v tvare

Porovnaním s rovnicou (5) sme dospeli k záveru, že nájdené miesto bodov je karteziánsky list.

Transformácia bodov kružnice na body karteziánskeho listu, uskutočnená takouto jeho konštrukciou, sa nazýva Maclaurinova transformácia.

4. Historický odkaz. Prvýkrát v dejinách matematiky je krivka, neskôr nazývaná karteziánsky list, definovaná v liste Descarta Fermatovi z roku 1638 ako krivka, pre ktorú je súčet objemov kociek postavených na úsečke a ordináte každý bod sa rovná objemu rovnobežnostenu postaveného na úsečke, ordinate a nejakej konštante . Forma krivky je prvýkrát stanovená Robervalom, ktorý nájde uzlový bod krivky, ale v jeho znázornení krivka pozostáva len zo slučky. Opakovaním tejto slučky v štyroch kvadrantoch dostane postavu, ktorá mu pripomína kvet so štyrmi okvetnými lístkami. Poetický názov krivky „jazmínový plátok“ sa však neujal. Úplnú formu krivky s prítomnosťou asymptoty určili neskôr (1692) Huygens a I. Bernoulli. Názov „karteziánsky zoznam“ sa pevne udomácnil až od začiatku 18. storočia.

Cissoid of Diokles

1. Vlastnosti formulára. Medzi mnohými spôsobmi vzdelávania cisoidy - krivku, ktorú objavili starovekí ľudia pri hľadaní riešenia slávneho problému zdvojenia kocky, sa najskôr zameriame na najjednoduchšie. Vezmite kruh (tzv výroba) s priemerom OA=2a a dotyčnicou AB Jej. Nakreslite lúč OB cez bod O a nakreslite naň úsečku OM=Slnko. Takto zostrojený bod M patrí do cissoidy. otáčanie lúča 0V pod určitým uhlom a po vykonaní uvedenej konštrukcie nájdeme druhý bod cissoidu atď. (obr. 3).

Ak sa bod O berie ako pól, odkiaľ získame polárnu rovnicu kissoidu

Pomocou vzorcov na prechod z polárnych na karteziánske súradnice nájdeme cissoidnú rovnicu v pravouhlom systéme:

(2)

Parametrické rovnice kissoidy možno získať nastavením x=ty, potom na základe rovnice (2) dospejeme k systému

Ryža. 3

Rovnica (2) ukazuje, že cisoida je algebraická krivka tretieho rádu a z rovníc (3) vyplýva, že ide o racionálnu krivku.

Cissoid je symetrický vzhľadom na os x, má nekonečné vetvy; dotyčnica k tvoriacej kružnici, t.j. rovno x = 2a slúži ako asymptota; pôvodom je hrot 1. druhu.

2. Vlastnosti. Kinematicky možno získať cisoidu ako trajektóriu stredu M nohu slnko trojuholník ABC, pohybom v rovine výkresu tak, že jeho vrchol IN posúva pozdĺž osi y a druhú nohu AC vždy prechádza pevným bodom E na osi x. (obr. 4)

V skutočnosti, označujúci stred segmentu OE cez D, všímame si to odvtedy BC=EO,ê VŠETKY=ê VEO, kde /_ VEO = /_ SVE, a preto ê NBE - rovnoramenné a od r ED=EO/2=BC/2=BM, potom segment DM rovnobežne so segmentom BE. Dovoľme si ďalej pointu TO je tu priesečník s pokračovaním segmentu DM priamka prechádzajúca bodom IN rovnobežne s osou x. Opíšme kružnicu so stredom v počiatku a polomer rovný OD , a nakreslite k nemu dotyčnicu v druhom bode priesečníka s priamkou EO. Očividne to prejde cez bod TO. Označenie priesečníka priamky DMK s kruhom cez F, Všimnite si, že trojuholníky DOF A MVK sú si navzájom rovné. Z ich rovnosti vyplýva, že D.F.= MK, čo znamená a DM= FK. Posledná rovnosť ukazuje, že ťažisko bodov M bude cissoid.

Iné spôsoby formovania cisoidy sú založené na jej vzťahu k parabole. Ukážme si to v prvom rade cisoida je čiastkovou érou paraboly vzhľadom na jej vrchol.

Rovnica tejto paraboly. Rovnica dotyčnice v ľubovoľnom bode M(x, h ) Táto parabola môže byť napísaná ako rovnica kolmice spustenej z počiatku na túto dotyčnicu budú súradnicami bodu N jej priesečník s dotyčnicou určujú vzorce

(4)

Vylúčením parametra h z týchto rovníc dostaneme rovnicu

vyjadrujúci kissoid.

Všimnite si ďalej, že súradnice bodu sú symetrické k počiatku vzhľadom na dotyčnicu k parabole o 2 = 2 px sa získajú, ak sú pravé časti vzorcov (4) zdvojené, a preto sú určené vzorcami

Vylúčením parametra h z týchto rovníc dostaneme opäť kissoidu rovnicou. Z toho vyplýva, že cisoida je ťažisko bodov symetrických k vrcholu paraboly vzhľadom na jej dotyčnice.

Treba si uvedomiť, že lokus bodov symetrických k počiatku vzhľadom na dotyčnicu k parabole môžeme považovať za trajektóriu vrcholu inej paraboly, rovnakej ako je daná, ktorá sa valí po danej parabole. Vzniká tak nový spôsob kinematického formovania cisoidy ako trajektóriu vrcholu paraboly, ktorá sa valí bez skĺznutia pozdĺž inej podobnej paraboly.

Strofoid

Strofoid (z gréčtiny stróphos - skrútená stuha a éidos - pohľad)

Nech je pevná čiara AB a bod C mimo nej vo vzdialenosti CO = A; okolo C sa otáča priamka, ktorá pretína AB v premennom bode N. Ak z bodu N odložíme segmenty NM \u003d NM "\u003d NO na obe strany priamky AB, potom ťažisko bodov M a M" pre všetky polohy rotujúceho lúča je CN strofoid. Rovnica v pravouhlých súradniciach: ; v polárnych súradniciach: r = - a cos 2j/cosj. Strofoid ako prvý skúmal E. Torricelli (1645), názov bol zavedený v polovici 19. storočia. Ryža. 6

Verziera Agnesi

Verziera (verziera) Agnesi ( niekedy Agnesiina kučera) je rovinná krivka, ťažisko bodov M, pre ktoré platí vzťah, kde OA je priemer kružnice, BC je poltetiva tejto kružnice, kolmá na OA. Agnesiina versiera bola pomenovaná po talianskej matematičke Marii Gaetana Agnesi, ktorá túto krivku študovala.

Rovnice

O = (0,0), A = (0, a)

V pravouhlom súradnicovom systéme:

Súradnice bodu M ležiaceho na versieri sú x = BM, y = OB. OA = a a podľa definície staviame proporciu

Odtiaľ

Na druhej strane, BC možno nájsť z kruhovej rovnice:

Vieme y = OB, takže vyjadrujeme:

Prirovnajte oba výrazy pre BC:

Umocnenie, prekladanie a vytváranie zátvoriek:

Vyjadríme y (y=0 nie je podľa definície vhodné):

, kde je uhol medzi OA a OC.

Vlastnosti:

1. Verzier - krivka tretieho rádu.

Priemer OA je jedinou osou symetrie krivky.

Krivka má jedno maximum - A (0; a) a dva inflexné body -

V blízkosti vrcholu A sa versier približuje ku kružnici s priemerom OA. V bode A nastáva tangencia a krivka sa zhoduje s kružnicou. To je znázornené hodnotou polomeru zakrivenia v bode A:.

Plocha pod grafom S = πa2. Vypočíta sa integráciou rovnice cez všetky .

Objem rotačného telesa versiera okolo jeho asymptoty (osi OX) .

Ané zee maria gaetana(Agnesi Maria Gaetana), rod. 16.05.1718, Milan - r. 01.09.1799, tamže. Taliansky matematik, profesor na univerzite v Bologni (od roku 1750). Agnesiho dielo „Základy analýzy pre využitie talianskej mládeže“ („Instituzioni analitiche ad uso della gioventú italiana“, v. 1-2, Mil., 1748) obsahuje prezentáciu analytickej geometrie, najmä krivku tretieho rádu. s názvom "Agnesiina kučera" sa tam uvažuje (alebo verzia), ktorej rovnica je y=a 3 / (x 2 + a 2).

Na zostrojenie tejto priamky je potrebné nakresliť kružnicu s polomerom a so stredom v bode (0, a). Potom sa od začiatku nakreslia rovné čiary a označia sa dva body. Bod A (x1, y1) je priesečník priamky a kružnice, bod B (x2,2a) je priesečník priamky a hornej horizontálnej dotyčnice kružnice. Potom sa zostrojí bod krivky (x2, y1).

Anglický matematik John Colson sa ujal prekladu Principia of Analysis z taliančiny. Pre neho, Európana 18. storočia, však nebolo ľahké prijať, že autorkou knihy je žena a že pre ňu, pre autora, môže byť krivka spojená s účesom. V dôsledku toho sa v anglickej literatúre krivka nazývala čarodejnica z Agnesi. - niečo z oblasti letov na holú horu ...

3. Pozoruhodné línie štvrtého a vyššieho rádu

Lemniscate Bernoulli

Ohniská lemniskátu sú F1 (− c; 0) a F2 (c; 0). Vezmite ľubovoľný bod M (x; y). Súčin vzdialeností od ohniska k bodu M je

A podľa definície sa rovná c2:

Odmocnime obe strany rovnice:

Rozbaľte zátvorky na ľavej strane:

Otvoríme zátvorky a zbalíme nový štvorec súčtu:

Vyberieme spoločný faktor a prenesieme:

V tomto prípade a je polomer kružnice opisujúcej lemniskát. Po vykonaní jednoduchých transformácií môžeme získať explicitnú rovnicu:

Štvorčekujeme a otvárame zátvorky:

Pripomíname

Toto je kvadratická rovnica pre y." Keď to vyriešime, dostaneme

Ak vezmeme koreň a zahodíme možnosť so záporným druhým výrazom, dostaneme:

kde pozitívny variant definuje hornú polovicu lemniskátu, negatívny variant definuje spodnú.

To. nastavením rôznych podmienok pre p a c 2 /4 získame lemniskáty rôznych typov (obr. 10).

Ryža. 10

F1, F2,…, Fn

a priradiť takú hodnotu pre konštantný súčin vzdialeností

МF 1 МF 2 … МF n = p

Pascalov slimák

Miesto bodov M a M" umiestnené na čiarach ceruzky (ktorej stred O leží na kružnici s polomerom R) vo vzdialenosti a na oboch stranách bodu P priesečníka čiar s kružnicou; teda PM = PM" = A. rovnica v pravouhlých súradniciach: ( x 2 + y 2 - 2Rx)2 - a 2(x 2 + y 2) = 0, v polárnych súradniciach: r = 2 R cos j + A. O a = 2R slučka sa stiahne do bodu, v takom prípade sa Pascalova kochlea zmení na kardioidnú. Názov je pomenovaný po francúzskom vedcovi B. Pascalovi (1588-1651), ktorý ho ako prvý študoval.

Cykloidné krivky

Medzi algebraické krivky patria také známe krivky ako kardioidné, astroidné, uvažujme o týchto krivkách.

Kardioidný

Táto okolnosť nám umožňuje okamžite zapísať parametrické rovnice kardioidy a nahradiť modul m jednou vo vyššie uvedených parametrických rovniciach epicykloidy. Bude mať:

(1)

Na získanie polárnej rovnice kardioidy je vhodné vziať bod A ako pól (obr. 13) a nasmerovať polárnu os pozdĺž úsečky. Keďže štvoruholník AOO 1 M bude rovnoramenný lichobežník, potom polárny uhol j bodu M sa bude rovnať uhlu natočenia tvoriacej kružnice, t.j. parameter t. Vzhľadom na túto okolnosť nahraďme y v druhej rovnici sústavy (1) až r sin t. Znížením takto získanej rovnosti o sin t dostaneme polárnu rovnicu kardioidy

Podľa tejto rovnice

môžeme konštatovať, že kardioid je jedným z Pascalových slimákov. Dá sa teda definovať ako konchoida kruhu.

Z tejto rovnice vyplýva, že kardioida je algebraická krivka 4. rádu.

2. Vlastnosti. V prvom rade, keďže kardioida je epicykloida s m=1, možno na ňu preniesť všetky vlastnosti epicykloidov, o ktorých sme uvažovali v predchádzajúcom odseku.

Tu sú vlastnosti a špecifikácie.

Dotyčnica v ľubovoľnom bode kardioidy prechádza bodom kružnice tvoriacej kružnice, diametrálne protiľahlej k bodu dotyku kružníc, a normála prechádza bodom ich dotyku.

Uhol m, ktorý zviera dotyčnica ku kardioide s polomerovým vektorom bodu dotyku, sa rovná polovici uhla, ktorý zviera tento polomerový vektor s polárnou osou. Naozaj

Naozaj, odkedy

Ryža. 14

Poznamenávame tiež, že miestom priesečníkov týchto dotyčníc je kružnica. Rovnica prvej dotyčnice na základe rovníc (1) kardioidy bude mať tvar

A druhá dotyčnica Vylúčením parametra z týchto rovníc dostaneme rovnicu označenej kružnice.

Polomer zakrivenia v ľubovoľnom bode kardioidy je určený vzorcom

Dá sa tiež ukázať, že polomer zakrivenia je 2/3 polárnej normály N v danom bode.

Vskutku, odkiaľ na základe (4) získame Tento vzťah možno použiť na zostrojenie stredu zakrivenia kardioidy.

Evoluta kardioidy podľa všeobecnej vlastnosti evolúcie epicykloidy bude tiež kardioida podobná danej, s koeficientom podobnosti rovným 1/3 a otočená vzhľadom k danej o uhol 180°.

Dĺžka kardioidného oblúka z bodu A do ľubovoľného bodu M je určená vzorcom

Ak sa dĺžka oblúka počíta od bodu A 1, diametrálne opačného k bodu A, potom vzorec na určenie dĺžky oblúka možno zapísať ako

(6)

Prirodzená rovnica kardioidy sa získa, ak je parameter vylúčený z rovnosti (4) a (6). Bude to vyzerať

(7)

Oblasť ohraničená kardioidom je určená vzorcom

a ako je vidieť, rovná sa šesťkolesovej ploche generujúceho kruhu.

Dĺžka celej kardioidy je určená vzorcom

a ako je možné vidieť, rovná sa ôsmim priemerom generujúcej kružnice. Objem tela získaný rotáciou kardioidy okolo jej osi sa rovná

Povrch tela získaný rotáciou kardioidy okolo svojej osi sa rovná

Nech je OM kolmica spustená na dotyčnicu ku kružnici s polomerom rovným 2r nakreslenej v bode N.

Pretože OM \u003d OB + BM, alebo r \u003d= 2r cos j + 2r, potom bude lokus bodov M kardioidný s rovnicou r \u003d 2r (1 + cos j)

Astroid

Parametrické rovnice astroidea možno získať vložením hypocykloidov do rovníc, m=1/4. Tu sú rovnice:

kde t, ako predtým, je uhol natočenia tvoriacej kružnice (obr. 16)

Vylúčením parametra t z rovníc (1) dostaneme:

Rovnica (2) naznačuje, že astroid je algebraická krivka šiesteho rádu.

Parametrické rovnice (1) astroidu možno zredukovať do tvaru

(3)

Vylúčením parametra t z týchto rovníc získame často používaný tvar rovnice astroidov

(4)

Za predpokladu v skôr odvodených všeobecných vzťahoch pre cykloidné krivky modul

m = -1/4, získame zodpovedajúce vzťahy pre astroid:

) polomer zakrivenia v ľubovoľnom bode astroidea je určený vzorcom

(5)

) dĺžka oblúka astroidea z bodu A do ľubovoľného bodu M(t) je určená vzorcom

dĺžka jednej vetvy je rovná a dĺžka celej krivky je 6R;

), aby sme získali prirodzenú rovnicu astroidu, najprv si všimneme, že ak počiatočným bodom dĺžky oblúka nie je bod A, pre ktorý t \u003d 0, ale bod, pre ktorý t \u003d p, potom dĺžka oblúk je určený vzorcom

vylúčením parametra t z rovníc (5) a (6) dostaneme prirodzenú rovnicu astroidea

) evoluta astroidea je aj astroidea podobná danej, s koeficientom podobnosti 2, pootočená voči danej o uhol p/4 (obr. 16)

) plocha ohraničená celým astroideom sa rovná objemu tela získaného rotáciou astroidea, rovná sa 32/105p R 3

povrch tela tvorený rotáciou astroida sa rovná

Prejdime teraz k úvahám o niektorých konkrétnych vlastnostiach astroidov.

Astroid je obal segmentu konštantnej dĺžky, končí. ktoré sa posúvajú po dvoch vzájomne kolmých priamkach.

Tieto priamky berieme ako súradnicové osi a s uhlom sklonu klzného segmentu ND=R cez a (obr. 4) dostaneme rovnicu priamky ND v tvare

Diferencovaním tejto rovnice vzhľadom na parameter a dostaneme:

Ryža. 17

Ryža. 18

Pre , tieto rovnice vyjadrujú priamy astroid, o ktorom sme uvažovali skôr.

. Niektoré transcendentálne línie

transcendentný sa nazývajú priamky, ktorých rovnice v pravouhlých karteziánskych súradniciach nie sú algebraické. Najjednoduchším príkladom transcendentálnych čiar je grafika funkcií y=, y= a iných goniometrických funkcií. Uvažujme o niektorých ďalších transcendentálnych líniách.

Archimedova špirála

Predstavte si nekonečne dlhú sekundovú ručičku, po ktorej od stredu ciferníka neúnavne beží malý chrobáčik stálou rýchlosťou v cm/s. Za minútu bude chyba vo vzdialenosti 60v cm od stredu, za dve - 120v atď. Vo všeobecnosti platí, že po t sekundách od začiatku behu bude vzdialenosť ploštice od stredu rovná vt cm. Počas tejto doby sa šípka otočí o uhol obsahujúci 6 t ° (napokon za jednu sekundu dokáže sa otočiť o uhol 360 °: 60 \u003d 6 °). Preto je poloha ploštice na rovine číselníka po ľubovoľnom počte t sekúnd po začiatku pohybu nasledovná. Je potrebné posunúť uhol a obsahujúci 6t ° od počiatočnej polohy šípky v smere jej otáčania a zmerať vzdialenosť r = vt cm od stredu pozdĺž novej polohy šípky. (obr. 21).

Ryža. 21.

Je zrejmé, že pomer medzi uhlom otočenia a šípky (v stupňoch) a prejdenou vzdialenosťou r (v centimetroch) bude:

Inými slovami, r je priamo úmerné a a koeficient úmernosti je k = v/6.

Priložme k nášmu bežcovi malú, ale nevyčerpateľnú nádobu s čiernou farbou a predpokladajme, že farba, ktorá vyteká cez malý otvor, zanechá na papieri stopu od chrobáka neseného spolu so šípom. Potom sa na papieri postupne objaví krivka, ktorú prvýkrát študoval Archimedes (287 - 212 pred Kr.). Na jeho počesť sa nazýva Archimedova špirála. Treba len povedať, že Archimedes nehovoril ani o sekundovej ručičke (vtedy neexistovali ani hodiny s pružinou: boli vynájdené až v 17. storočí), ani o ploštici. Kvôli prehľadnosti sme ich zaradili sem.

Ryža. 22 Obr. 23.

Archimedovu špirálu tvorí nekonečne veľa závitov. Začína v strede ciferníka a s rastúcim počtom otáčok sa od neho stále viac vzďaľuje. Na obr. 22 znázorňuje prvý obrat a časť druhého.

Pravdepodobne ste už počuli, že pomocou kompasu a pravítka nie je možné rozdeliť náhodne nasnímaný uhol na tri rovnaké časti (v špeciálnych prípadoch, keď uhol obsahuje napríklad 180°, 135° alebo 90°, problém sa dá ľahko vyriešiť). Ale ak použijete úhľadne nakreslenú Archimedovu špirálu, potom môže byť akýkoľvek uhol rozdelený na ľubovoľný počet rovnakých častí.

Rozdeľme si napríklad uhol AOB na tri rovnaké časti (obr. 23.). Ak predpokladáme, že šípka sa otočila práve do tohto uhla, potom bude chyba v bode N na strane rohu. Ale keď bol uhol rotácie trikrát menší, potom bola chyba trikrát bližšie k stredu O. Aby sme našli túto polohu, najprv rozdelíme segment ON na tri rovnaké časti. To sa dá urobiť pomocou kompasu a pravítka. Dostaneme segment ON 1 , ktorého dĺžka je trikrát menšia ako ON. Ak chcete vrátiť plošticu do špirály, musíte na tejto krivke urobiť zárez s polomerom ON 1 (opäť kompas!). Dostaneme bod M. Uhol AOM a bude trikrát menší ako uhol AON.

Cykloid

Na spodný okraj tabule pripevníme pravítko a po ňom vyvaľkáme obruč alebo kruh (kartónový alebo drevený), pritlačíme k pravítku a doske. Ak pripevníte kúsok kriedy na obruč alebo kruh (v bode dotyku s pravítkom), potom krieda nakreslí krivku (obr. 24), nazývanú cykloida (čo v gréčtine znamená „kruhový“). Jedno otočenie obruče zodpovedá jednému "oblúku" cykloidy MM"M""N", ak sa obruč odvaľuje ďalej, získajú sa ďalšie a ďalšie oblúky tej istej cykloidy.

Ryža. 24.

Aby sme na papieri postavili približne jeden oblúk cykloidy, opísaný zrolovaním obruče s priemerom rovným napríklad trom centimetrom, odložíme na rovný segment rovný 3x3,14 = 9,42 cm.

Dostaneme segment, ktorého dĺžka sa rovná dĺžke obručového ráfika, t.j. kruh s priemerom tri centimetre. Tento segment ďalej rozdelíme na určitý počet rovnakých častí, napríklad 6, a pre každý bod delenia znázorníme našu obruč v polohe, keď spočíva presne na tomto bode (obr. 24), pričom tieto polohy očíslujeme čísla:

Oh, 1, 2, 3, 4, 5, 6.

Na presun z jednej pozície do druhej sa musí obruč otočiť o jednu šestinu celej otáčky (pretože vzdialenosť medzi susednými deliacimi bodmi sa rovná šestine kruhu). Ak teda v polohe 0 bude krieda v bode M 0, tak v polohe 1 bude ležať v bode M 1 - jedna šestina kruhu od bodu dotyku, v polohe 2 - v bode M 2 - dve šestiny od kontaktné miesto, a t.d. Ak chcete získať body M 1, M 2, M 3 atď., stačí urobiť zárezy zodpovedajúcej kružnice, počnúc bodom dotyku, s polomerom rovným

Ryža. 25.

5 cm a v polohe 1 je potrebná jedna pätka, v polohe 2 - dve pätky urobené za sebou, v polohe 3 - tri pätky atď. Teraz, aby sme nakreslili cykloidu, zostáva spojiť body

M 0, M 1, M 2, M 3, M 4, M 5, M 6

hladká krivka (podľa oka).

Krivka najkratšieho klesania

Spomedzi mnohých pozoruhodných vlastností cykloidy si všimneme jednu, kvôli ktorej si zaslúžil hlasno znejúce zložité meno: „brachistochrón“. Tento názov sa skladá z dvoch gréckych slov, ktoré znamenajú „najkratší“ a „čas“.

Zvážte nasledujúcu otázku: aký tvar by mal mať dobre vyleštený kovový žľab spájajúci dva dané body A a B (obr. 26.), aby sa leštená kovová guľa kotúľala po tomto žľabe z bodu A do bodu B čo najkratšie. čas? Na prvý pohľad sa zdá, že treba zastaviť na priamom žľabe, keďže len po ňom lopta prejde najkratšou cestou z A do B. Nehovoríme však o najkratšej ceste, ale o najkratšom čase; čas závisí nielen od dĺžky dráhy, ale aj od rýchlosti behu loptičky. Ak je žľab ohnutý, jeho časť, začínajúca od bodu A, padá strmšie ako v prípade priameho žľabu a guľa, ktorá padá pozdĺž neho, nadobudne rýchlosť väčšiu ako v úseku rovnakej dĺžky. rovný žľab. Ale ak urobíme počiatočnú časť veľmi strmú a relatívne dlhú, potom časť susediaca s bodom B bude veľmi jemná a tiež relatívne dlhá; prvá časť lopty prejde rýchlo, druhá veľmi pomaly a lopta môže prísť neskoro do bodu B. Takže žľab zrejme potrebuje mať konkávny tvar, ale ohyb by nemal byť príliš výrazný.

Ryža. 26.

Ryža. 27.

Taliansky fyzik a astronóm Galileo (1564-1642) si myslel, že koryto najkratšieho času by malo byť zakrivené pozdĺž oblúka kruhu. Švajčiarski matematici, bratia Bernoulliovci, však asi pred tristo rokmi presným výpočtom dokázali, že to tak nebolo a že žľab sa musí ohnúť pozdĺž oblúka cykloidy (prevrátený nadol, obr. 27). Odvtedy si cykloida vyslúžila prezývku brachistochróna a Bernoulliho dôkazy slúžili ako začiatok nového odvetvia matematiky – variačného počtu. Ten sa zaoberá hľadaním typu kriviek, pre ktoré tá či oná veličina, ktorá nás zaujíma, dosahuje svoju najmenšiu (av niektorých otázkach aj najväčšiu) hodnotu.

logaritmická špirála

Táto krivka by mohla byť pomenovaná po Descartovi, pretože bola prvýkrát spomenutá v jednom z jeho listov (1638). Podrobnú štúdiu jeho vlastností však vykonal až o pol storočia neskôr Jacob Bernoulli. Tieto vlastnosti urobili silný dojem na súčasných matematikov. Na kamennej doske postavenej na hrobe tohto slávneho matematika sú znázornené otáčky logaritmickej špirály.

Archimedova špirála je opísaná bodom pohybujúcim sa pozdĺž lúča („nekonečná šípka“) tak, že vzdialenosť od začiatku lúča sa zväčšuje úmerne s uhlom jeho natočenia: r = ka. Logaritmická špirála sa získa, ak sa požaduje, aby sa nie samotná vzdialenosť, ale jej logaritmus nezväčšoval priamo úmerne s uhlom rotácie. Zvyčajne sa rovnica logaritmickej špirály zapisuje s použitím iného ako rovnocenného čísla e ako základu systému logaritmov (časť 25). Takýto logaritmus čísla r sa nazýva prirodzený logaritmus a označuje sa In r. Takže rovnica logaritmickej špirály je napísaná ako ln r = ka

Samozrejme, uhol natočenia a možno stále merať v stupňoch. Ale matematici to radšej merajú v radiánoch, t.j. vezmite ako mieru uhla pomer dĺžky oblúka kruhu medzi stranami stredového uhla k polomeru tohto kruhu. Potom bude otočenie šípu v pravom uhle merané číslom l 1,57, otočenie hodnotou rozšíreného uhla - číslom l 3,14 a úplné otočenie, merané v stupňoch číslom 360, v radiánoch sa bude merať číslom 2 l 6,28.

Ryža. 28.

Z mnohých vlastností logaritmickej špirály si všimneme jednu vec: každý lúč, ktorý vychádza od začiatku, pretína ľubovoľné otočenie špirály pod rovnakým uhlom. Hodnota tohto uhla závisí len od čísla k v špirálovej rovnici. V tomto prípade sa pod uhlom medzi lúčom a špirálou rozumie uhol medzi týmto lúčom a dotyčnicou špirály nakreslenej v priesečníku (obr. 28).

Záver

V priebehu zvažovania kriviek tretieho a štvrtého rádu

zoznámili sme sa s niektorými skutočne pozoruhodnými krivkami, ktoré obývajú nádherný svet analytickej geometrie, ktoré sú v našich životoch oveľa bežnejšie, ako sa zdá. Zvažovali sme ich praktické uplatnenie v živote človeka, význam ich pozoruhodných vlastností v rôznych mechanizmoch, ktoré človek v živote využíva. V tomto príspevku sme zozbierali materiál s dôrazom na praktickú konštrukciu kriviek.

Cieľ bol teda splnený a úlohy uvedené k cieľu boli vyriešené.

Literatúra

rad riadkov transcendentná špirála

1. Markushevich A.I. Pozoruhodné krivky. - M.: Krasnoproletarskaya, 1951. -23 s.; 1978., - 48 strán s ilustráciami.

História matematiky od staroveku do začiatku XIX storočia / Ed. A.P. Juškevič. - M.: Nauka, 1970, zväzok 1. - 352 s.; 1970, v. 2. - 300 s.; 1972, sv. 3 - 496 s.

Nikiforovsky V.A., Freiman L.S. Zrod novej matematiky. - M.: Nauka, 1976. - 198 s.

Savelov A.A. Ploché krivky. - M.: Fizmatgiz, 1960 - 294 s.

Ilyin V.A., Poznyak E.G. Analytická geometria. - M.: Nauka, 1971. - 232 s.

Tyshkevich R.I., Fedenko A.S. Lineárna algebra a analytická geometria. - 2. vyd. - Minsk: Vyš. Shk., 1976,544 s.

Analytické definície

Typy kriviek

Spôsoby definovania kriviek:

Cykloid.

Vlastnosti cykloidu:

Cykloidná rovnica

Z príbehu o cykloide

Niektoré typy cykloidov

Kardioidný.

Vlastnosti kardioidu

Astroid.

vlastnosti astroidov

Astroidné rovnice

Ako postaviť astroid

Záver

Cissoid of Diokles

Lemniscate Bernoulli

Kardioidný

Astroid

Archimedova špirála

Cykloid

Krivka najkratšieho klesania

logaritmická špirála

Prečítajte si tiež