Je známe, že funkcia y= f(x) môže byť definovaná implicitne pomocou rovnice týkajúcej sa premenných x a y:

F(x,y)=0.

Sformulujme podmienky, za ktorých platí rovnica F(x,y)=0 definuje jednu z premenných ako funkciu druhej. Nasledujúci

Veta (existencia implicitnej funkcie) Nech funkcia F(x,y)=0 spĺňa nasledujúce podmienky:

1) je tu bod P˳(х˳,y˳) , kde F(x˳,y˳)=0

2) F'y(x˳,y˳)≠ 0

3) funkcie F'x (x, y)a F'y (x, y) sú súvislé v niektorom okolí bodu

P 0 (X 0 ,r 0).

Potom existuje jedinečná funkcia y =f (x) definovaná na nejakom intervale obsahujúcom bod a spĺňajúca rovnicu F(x,y)=0 pre ľubovoľné x z tohto intervalu, takže f(x 0) = y0

Ak máte implicitnú funkciu z X, to znamená, že sa určí z rovnice F ( X, pri) = 0, teda za predpokladu, že pri existuje funkcia od X, získame identitu F (X, pri(X)) = 0, čo možno považovať za konštantnú funkciu. Diferencovaním tejto konštantnej funkcie dostaneme:

Ak v tomto pomere , potom môžete nájsť .

Opäť derivačným vzťahom (1) dostaneme:

Vzťah (2) možno považovať za rovnicu na určenie druhej derivácie. Opäť derivačným vzťahom (2) získame rovnicu na určenie tretej derivácie atď.

Smerová derivácia. Smerový vektor pre prípad dvoch a troch premenných (smerové kosínusy). Prírastok funkcie v danom smere. Určenie smerovej derivácie, jej vyjadrenie pomocou parciálnych derivácií. Funkčný gradient. Vzájomná poloha gradientu a čiary hladiny v danom bode pre funkciu dvoch premenných.

Derivácia z'I v smere I funkcie dvoch premenných z=f(x;y) je limitom pomeru prírastku funkcie v tomto smere k veľkosti posunutia ∆I, keďže tá má tendenciu k 0: z'i=lim∆iz /∆I

Derivácia z'I charakterizuje rýchlosť zmeny funkcie v smere i.

Ak funkcia z=f(x;y) má v bode M(x;y) spojité parciálne derivácie, potom v tomto bode existuje derivácia v ľubovoľnom smere vychádzajúca z bodu M(x;y), ktorá sa vypočíta podľa vzorca z'i =z'xˑcosα+z"yˑcosβ, kde cosα, cosβ sú kosínusy vektora smerujúceho k4.

Gradient funkcie z=f(x,y) je vektor so súradnicami f'x, f'y. Označuje sa z=(f'x,f'y) alebo .

Smerová derivácia sa rovná bodovému súčinu gradientu a jednotkového vektora, ktorý určuje smer I.

Vektor z v každom bode smeruje pozdĺž normály k čiare hladiny prechádzajúcej daným bodom v smere rastúcej funkcie.

Parciálne derivácie f'x a f'y sú derivácie funkcie z=f(x,y) pozdĺž dvoch parciálnych smerov osí Ox a Oy.

Nech z=f(x,y) je diferencovateľná funkcia v nejakej oblasti D, M(x,y) . Nech I je nejaký smer (vektor s počiatkom v bode M) a =(cosα; cosβ).

Pri pohybe týmto smerom I bod M(x,y) do bodu M1(x+∆x;y+∆y), funkcia z dostane prírastok ∆iz=f(x+∆x;y+∆y)-f(x ;y) nazval prírastok funkcie z v danom smere I.

Ak MM1=∆I, potom ∆x=∆icosα, ∆y=∆icosβ, teda ∆iz=f(x+∆icosα; y+∆icosβ)-f(x;y).

Veľmi často sa pri riešení praktických problémov (napríklad vo vyššej geodézii alebo analytickej fotogrammetrii) objavujú zložité funkcie viacerých premenných, t.j. x, y, z jednu funkciu f(x,y,z) ) sú samotné funkciami nových premenných U, V, W ).

Stáva sa to napríklad pri pohybe z pevného súradnicového systému Oxyz do mobilného systému O 0 UVW a späť. V tomto prípade je dôležité poznať všetky parciálne derivácie vzhľadom na „pevné“ – „staré“ a „pohyblivé“ – „nové“ premenné, keďže tieto parciálne derivácie zvyčajne charakterizujú polohu objektu v týchto súradnicových systémoch, a najmä ovplyvniť zhodu leteckých snímok so skutočným objektom. V takýchto prípadoch platia nasledujúce vzorce:

Teda vzhľadom na zložitú funkciu T tri „nové“ premenné U, V, W cez tri „staré“ premenné x, y, z potom:

Komentujte. Variácie v počte premenných sú možné. Napríklad: ak

Najmä ak z = f(xy), y = y(x) , potom dostaneme takzvaný vzorec „celkového derivátu“:

Rovnaký vzorec pre „celkový derivát“ v prípade:

bude mať podobu:

Možné sú aj iné variácie vzorcov (1.27) - (1.32).

Poznámka: Vzorec "totálnej derivácie" sa používa v kurze fyziky v časti "Hydrodynamika" pri odvodzovaní základného systému rovníc pohybu tekutín.

Príklad 1.10. Vzhľadom na to:

Podľa (1.31):

§7 Parciálne derivácie implicitne danej funkcie viacerých premenných

Ako viete, implicitne definovaná funkcia jednej premennej je definovaná nasledovne: funkcia nezávislej premennej X sa nazýva implicitný, ak je daný rovnicou, ktorá nie je vyriešená vzhľadom na r :

Príklad 1.11.

Rovnica

implicitne definuje dve funkcie:

A rovnica

nedefinuje žiadnu funkciu.

Veta 1.2 (existencia implicitnej funkcie).

Nechajte funkciu z \u003d f (x, y) a jeho parciálne deriváty f" X A f" r definované a súvislé v nejakej štvrti U M0 bodov M 0 (X 0 r 0 ) . okrem toho f(x 0 ,y 0 )=0 A f"(x 0 ,y 0 )≠0 , potom rovnica (1.33) určuje v okolí U M0 implicitná funkcia y= y(x) , spojité a diferencovateľné v určitom intervale D sústredený na bod X 0 , a y(x 0 )=y 0 .

Bez dôkazu.

Z vety 1.2 vyplýva, že na tomto intervale D :

to znamená, že existuje identita v

kde sa "celkový" derivát nachádza podľa (1.31)

To znamená, že (1.35) dáva vzorec na nájdenie derivácie implicitne danej funkcie jednej premennej X .

Implicitná funkcia dvoch alebo viacerých premenných je definovaná podobne.

Napríklad, ak v nejakej oblasti V priestor Oxyz rovnica je splnená:

potom za určitých podmienok na funkcii F implicitne definuje funkciu

Analogicky s (1.35) sa jeho parciálne deriváty nachádzajú takto:

Príklad 1.12. Za predpokladu, že rovnica

implicitne definuje funkciu

Nájsť z" X , z" r .

preto podľa (1.37) dostaneme odpoveď.

§8 Čiastkové deriváty druhého a vyššieho rádu

Definícia 1.9 Parciálne derivácie druhého rádu funkcie z=z(x,y) sú definované takto:

Boli štyria. Navyše za určitých podmienok na funkciách z(x,y) platí rovnosť:

Komentujte. Čiastočné deriváty druhého rádu možno označiť aj takto:

Definícia 1.10 Čiastkové derivácie tretieho rádu – osem (2 3).

Naučíme sa nájsť derivácie funkcií daných implicitne, teda danými nejakými rovnicami, ktoré navzájom spájajú premenné. X A r. Príklady implicitne definovaných funkcií:

,

Deriváty implicitných funkcií alebo deriváty implicitných funkcií sa dajú pomerne ľahko nájsť. Teraz analyzujme príslušné pravidlo a príklad a potom zistíme, prečo je to vôbec potrebné.

Aby sme našli deriváciu funkcie danej implicitne, je potrebné diferencovať obe strany rovnice vzhľadom na x. Tie členy, v ktorých je prítomné iba x, sa zmenia na obvyklú deriváciu funkcie x. A členy s y je potrebné diferencovať pomocou pravidla diferenciácie komplexnej funkcie, pretože y je funkciou x. Ak je to celkom jednoduché, tak vo výslednej derivácii termínu s x by to malo byť: derivácia funkcie od y, vynásobená deriváciou od y. Napríklad derivát termínu sa zapíše ako , derivát termínu sa zapíše ako . Ďalej, z toho všetkého je potrebné vyjadriť tento "y zdvih" a získame požadovanú deriváciu implicitne danej funkcie. Pozrime sa na to na príklade.

Príklad 1

Riešenie. Obe časti rovnice diferencujeme vzhľadom na x, za predpokladu, že y je funkciou x:

Odtiaľ dostaneme derivát, ktorý sa vyžaduje v úlohe:

Teraz niečo o nejednoznačnej vlastnosti implicitne definovaných funkcií a prečo sú potrebné špeciálne pravidlá na ich diferenciáciu. V niektorých prípadoch sa môžete uistiť, že substitúcia v danej rovnici (pozri príklady vyššie) namiesto y jej vyjadrenia prostredníctvom x vedie k tomu, že táto rovnica sa zmení na identitu. Takže. vyššie uvedená rovnica implicitne definuje nasledujúce funkcie:

Po dosadení výrazu y na druhú cez x do pôvodnej rovnice dostaneme identitu:

.

Výrazy, ktoré sme dosadili, sme získali riešením rovnice pre y.

Ak by sme mali diferencovať zodpovedajúcu explicitnú funkciu

potom by sme dostali odpoveď ako v príklade 1 - z funkcie špecifikovanej implicitne:

Ale nie každá funkcia zadaná implicitne môže byť reprezentovaná vo forme r = f(X) . Napríklad implicitne definované funkcie

nie sú vyjadrené elementárnymi funkciami, to znamená, že tieto rovnice nie je možné vyriešiť vzhľadom na hráča. Preto existuje pravidlo pre diferenciáciu funkcie dané implicitne, ktoré sme už študovali a bude dôsledne aplikované v ďalších príkladoch.

Príklad 2 Nájdite deriváciu funkcie danej implicitne:

.

Vyjadríme prvočíslo y a na výstupe deriváciu funkcie danej implicitne:

Príklad 3 Nájdite deriváciu funkcie danej implicitne:

.

Riešenie. Diferencujte obe strany rovnice vzhľadom na x:

.

Príklad 4 Nájdite deriváciu funkcie danej implicitne:

.

Riešenie. Diferencujte obe strany rovnice vzhľadom na x:

.

Vyjadríme a dostaneme deriváciu:

.

Príklad 5 Nájdite deriváciu funkcie danej implicitne:

Riešenie. Členy na pravej strane rovnice prenesieme na ľavú stranu a na pravej necháme nulu. Diferencujte obe strany rovnice vzhľadom na x.

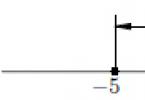
Nechajte spojitú funkciu pri od X je nastavený implicitne F(X, r) = 0, kde F(X, r), F" x(X, r), F"y(X, r) sú spojité funkcie v nejakej doméne D obsahujúcej bod ( X, pri), ktorých súradnice vyhovujú vzťahom F (X, r) = 0, F"y(X, r) ≠ 0. Potom funkcia pri od X má derivát

Dôkaz (pozri obrázok). Nechaj F"y(X, r) > 0. Keďže derivácia F"y(X, r) je spojitý, potom môžeme zostrojiť štvorec [ X 0 - δ" , X 0 + δ" , pri 0 - δ" , pri 0 + δ" ], takže pre všetky jeho body F"y (X, r) > 0, t.j. F(X, r) je monotónny v pri pri pevnom X. Tým sú splnené všetky podmienky vety o existencii implicitnej funkcie pri = f (X), také, že F(X, f (X)) º 0.
Nastavíme prírastok Δ X. nová hodnota X + Δ X sa bude zhodovať pri + Δ pri = f (X + Δ X), takže tieto hodnoty spĺňajú rovnicu F (X + Δ X, r + Δ r) = 0. Samozrejme,

Δ F = F(X + Δ X, r + Δ r) − F(X, r) = 0

a v tomto prípade

.

Od (7) máme

.

Keďže implicitná funkcia pri = f (X) je spojitý, potom Δ pri→ 0 ako Δ X→ 0, teda α → 0 a β → 0. Odkiaľ konečne máme

.

Q.E.D.

Parciálne derivácie a diferenciály vyšších rádov.

Nech parciálne derivácie funkcií z = f (X, r) definované v okolí bodu M existujú v každom bode v tomto okolí. V tomto prípade sú parciálne derivácie funkciami dvoch premenných X A pri definované v naznačenom okolí bodu M. Nazvime ich parciálne derivácie prvého rádu. Na druhej strane parciálne derivácie vzhľadom na premenné X A pri z funkcií v bode M, ak existujú, sa nazývajú parciálne derivácie funkcie druhého rádu f (M) na tomto mieste a sú označené nasledujúcimi symbolmi

Parciálne deriváty druhého rádu tvaru , , sa nazývajú zmiešané parciálne deriváty.

Rozdiely vyšších rádov

zvážime dx vo výraze pre D Y ako konštantný faktor.Potom funkcia D Y je funkciou iba argumentu X a jeho diferenciál v určitom bode X má tvar (pri zvažovaní diferenciálu od D Y budeme používať nový zápis pre diferenciály):

δ ( D Y) = δ [ f " (X) d x] = [f " (X) d x] " δ X = f "" (X) d(X) δ X .

diferenciál δ ( D Y) z diferenciálu D Y v bode X, prevzaté pri δ x = dx, sa nazýva diferenciál druhého rádu funkcie f (X) v bode X a označené d 2 r, t.j.

d 2 r = f ""(X)·( dx) 2 .

Na druhej strane, diferenciál δ( d 2 r) z diferenciálu d 2 r, prevzaté pri δ x = dx, sa nazýva diferenciál tretieho rádu funkcie f(X) a označené d 3 r atď. diferenciál δ( d n-1 y) z diferenciálu d n -1 f, prevzaté pri δ X = dx, sa nazýva diferenciál n- rád (resp n- m diferenciálne) funkcie f(X) a označené d n y.
Dokážme to pre n-tý diferenciál funkcie, vzorec

d n y = y (n) ·( dx)n, n = 1, 2, … (3.1)

Pri dôkaze používame metódu matematickej indukcie. Pre n= 1 a n= 2 vzorec (3.1) je dokázaný. Nech to platí pre diferenciály poriadku n - 1

d n −1 r=y( n−1) ( dx)n −1 ,

a funkciu r (n-1) (X) je v určitom bode rozlíšiteľné X. Potom

Prenájom δ x = dx, dostaneme

Q.E.D.
Pre hocikoho n spravodlivá rovnosť

alebo

tie. n- i derivácia funkcie r= f (X) v bode X sa rovná pomeru n-tý diferenciál tejto funkcie v bode X Komu n-tý stupeň diferenciálu argumentu.

Smerová derivácia funkcií viacerých premenných.

Zohľadňuje sa funkcia a jednotkový vektor. Priamy l cez t. M 0 so smerovým vektorom

Definícia 1. Derivácia funkcie u = u(X, r, z) podľa premennej t volal derivácia v smere l

Keďže na tomto riadku u je komplexná funkcia jednej premennej, potom derivácia vzhľadom na t sa rovná celkovej derivácii vzhľadom na t(§ 12).

Označuje sa a rovná sa

Vzorec pre deriváciu funkcie danej implicitne. Dôkaz a príklady použitia tohto vzorca. Príklady výpočtu derivácií prvého, druhého a tretieho rádu.

Obsah

Derivát prvého rádu

Nech je funkcia daná implicitne pomocou rovnice
(1) .
A nech má táto rovnica pre určitú hodnotu jedinečné riešenie. Nech je funkcia diferencovateľná funkcia v bode , A
.
Potom s touto hodnotou existuje derivácia, ktorá je určená vzorcom:
(2) .

Dôkaz

Pre dôkaz zvážte funkciu ako komplexnú funkciu premennej:
.
Aplikujeme pravidlo diferenciácie komplexnej funkcie a nájdeme deriváciu vzhľadom na premennú ľavej a pravej strany rovnice
(3) :
.
Pretože derivácia konštanty sa rovná nule a potom
(4) ;
.

Vzorec bol osvedčený.

Deriváty vyšších rádov

Prepíšme rovnicu (4) iným spôsobom:
(4) .
Okrem toho sú komplexné funkcie premennej:
;
.
Závislosť definuje rovnicu (1):
(1) .

Nájdeme deriváciu vzhľadom na premennú z ľavej a pravej strany rovnice (4).
Podľa vzorca pre deriváciu komplexnej funkcie máme:
;
.
Podľa vzorca odvodeného produktu:

.
Podľa vzorca odvodeného súčtu:


.

Pretože derivácia pravej strany rovnice (4) sa rovná nule, potom
(5) .
Nahradením derivácie tu získame hodnotu derivácie druhého rádu v implicitnej forme.

Podobným spôsobom derivovaním rovnice (5) dostaneme rovnicu obsahujúcu deriváciu tretieho rádu:
.
Nahradením nájdených hodnôt derivátov prvého a druhého rádu nájdeme hodnotu derivátu tretieho rádu.

Pokračujúcou diferenciáciou možno nájsť derivát akéhokoľvek poriadku.

Príklady

Príklad 1

Nájdite prvú deriváciu funkcie danej implicitne rovnicou:
(P1) .

Riešenie Formuly 2

Deriváciu nájdeme podľa vzorca (2):
(2) .

Presuňme všetky premenné na ľavú stranu, aby rovnica mala tvar .
.
Odtiaľ.

Nájdeme deriváciu vzhľadom na , za predpokladu, že je konštantná.
;
;
;
.

Nájdeme deriváciu vzhľadom na premennú za predpokladu, že premenná je konštantná.
;
;
;
.

Podľa vzorca (2) zistíme:
.

Výsledok môžeme zjednodušiť, ak si všimneme, že podľa pôvodnej rovnice (A.1) . Náhradník:
.
Vynásobte čitateľa a menovateľa:
.

Riešenie druhým spôsobom

Vyriešme tento príklad druhým spôsobom. Aby sme to dosiahli, nájdeme deriváciu vzhľadom na premennú ľavej a pravej časti pôvodnej rovnice (P1).

Aplikujeme:
.
Použijeme vzorec pre deriváciu zlomku:
;
.
Použijeme vzorec pre deriváciu komplexnej funkcie:
.
Pôvodnú rovnicu (P1) diferencujeme.
(P1) ;
;
.
Vynásobte a zoskupte výrazy.
;
.

Dosaďte (z rovnice (P1)):
.
Vynásobme:
.

Príklad 2

Nájdite deriváciu druhého rádu funkcie danej implicitne pomocou rovnice:
(P2.1) .

Diferencujte pôvodnú rovnicu vzhľadom na premennú za predpokladu, že je funkciou:
;
.
Aplikujeme vzorec pre deriváciu komplexnej funkcie.
.

Pôvodnú rovnicu (A2.1) diferencujeme:
;
.
Z pôvodnej rovnice (A2.1) vyplýva, že . Náhradník:
.
Rozbaľte zátvorky a zoskupte členov:
;
(P2.2) .
Nájdeme derivát prvého rádu:
(P2.3) .

Aby sme našli deriváciu druhého rádu, derivujeme rovnicu (A2.2).
;
;
;
.
Dosadíme výraz za deriváciu prvého poriadku (A2.3):
.
Vynásobme:

;
.
Odtiaľto nájdeme derivát druhého rádu.

Príklad 3

Nájdite deriváciu tretieho rádu funkcie danej implicitne pomocou rovnice:
(P3.1) .

Diferencujte pôvodnú rovnicu vzhľadom na premennú za predpokladu, že je funkciou .
;
;
;
;
;
;
(P3.2) ;

Rovnicu (A3.2) diferencujeme vzhľadom na premennú .
;
;
;
;
;
(P3.3) .

Diferencujeme rovnicu (A3.3).
;
;
;
;
;
(P3.4) .

Z rovníc (A3.2), (A3.3) a (A3.4) nájdeme hodnoty derivácií pri .
;
;
.