pohyb tuhého telesa, podobne ako pohyb bodu, môže byť zložitý.

Nechajte telo urobiť nejaký pohyb vzhľadom na súradnicový systém 0 X 1 r 1 z 1, ktorý sa zase pohybuje vzhľadom na pevné osi 0 xyz.Relatívna pohyb telesa je jeho pohyb vzhľadom na pohybujúci sa súradnicový systém 0 X 1 r 1 z 1. Pre objasnenie prenosný pohybu telesa v každom časovom okamihu, teleso by sa malo považovať za pevne pripevnené k pohyblivej referenčnej sústave a pohyb, ktorý teleso s pohyblivou referenčnou sústavou vykoná vzhľadom na pevný rám, bude prenosný pohyb. Pohyb telesa vzhľadom na pevný súradnicový systém sa nazýva absolútne.

Hlavnou úlohou kinematiky komplexného pohybu tuhého telesa je stanovenie vzťahov medzi kinematickými charakteristikami absolútnych, relatívnych a prenosných pohybov. Komplexný pohyb tuhého telesa môže pozostávať z translačných a rotačných pohybov alebo môže byť získaný pridaním translačných a rotačných pohybov. V niektorých úlohách kinematiky sa daný komplexný pohyb tuhého telesa rozloží na pohybové zložky (analýza); v iných sa vyžaduje definovať komplexný pohyb ako výsledok pridania jednoduchších (syntéza). Ako pri analýze, tak aj pri syntéze pohybov hovoríme o rozklade a pridávaní pohybov uvažovaných v danom momente (okamžité pohyby).

Sčítanie translačných pohybov tuhého telesa

Nech sa tuhé teleso súčasne zúčastňuje dvoch okamžite translačných pohybov, z ktorých jeden je translačný s rýchlosťou v 1, druhý je prenosný s rýchlosťou v 2 (obrázok 2.73). Vyberte ľubovoľný bod M telo. Nájdite absolútnu rýchlosť bodu M

v a = v r + v e = v 1 + v 2 . (2.113)

Pretože relatívny aj prenosný pohyb tuhého telesa sú okamžite translačné, potom sa relatívne, prenosné a teda podľa vzorca (2.113) absolútne rýchlosti všetkých bodov telesa budú navzájom rovnať v každom okamihu čas (rovnaký čo do veľkosti a rovnobežný v smere), t.j. absolútny pohyb telesa je tiež momentálne translačný.

Je zrejmé, že tento záver je aplikovateľný na komplexný pohyb tuhého telesa, ktorý pozostáva z troch alebo viacerých okamžitých translačných pohybov, potom vo všeobecnom prípade

Takže ako výsledok pridania okamžitých translačných pohybov tuhého telesa je výsledný pohyb okamžite translačný.

Komentujte. Okamžitý translačný pohyb tuhého telesa sa líši od translačného pohybu v tom, že počas translačného pohybu v každom časovom okamihu sú rýchlosti a zrýchlenia všetkých bodov telesa rovnaké a pri okamžitom translačnom pohybe v danom časovom okamihu sú len rýchlosti. všetky body tela sú rovnaké.

66, 67 Pridanie rotácií okolo rovnobežných osí

Zvážte prípad, keď relatívny pohyb telesa je rotácia

s uhlovou rýchlosťou okolo osi , upevnený na kľuke (obr. 1a) a prenosný - otáčaním kľuky okolo osi rovnobežne s , s uhlovou rýchlosťou . Potom bude pohyb telesa planparalelný vzhľadom na rovinu kolmú na osi.

Predpokladáme, že rotácie smerujú jedným smerom. Znázornime rez telesom rovinou kolmou na osi (obr. 1 b). Stopy osí v reze budú označené písmenami a . Potom a . V tomto prípade sú vektory a sú navzájom rovnobežné, kolmé a smerované rôznymi smermi. Potom je bod okamžitým stredom rýchlostí , a teda os rovnobežná s osami a je okamžitou osou rotácie. Na určenie uhlovej rýchlosti absolútnej rotácie telesa okolo osi a polohy samotnej osi, t.j. bodov , využívame vlastnosť okamžitého stredu rýchlostí

.

Nahradením hodnôt a týchto rovností nakoniec získame

Takže pri sčítaní dvoch rotácií smerujúcich rovnakým smerom okolo rovnobežných osí bude výsledným pohybom telesa okamžitá rotácia s absolútnou rýchlosťou okolo okamžitej osi rovnobežne s údajmi, ktorej poloha je určená proporciami (2).

V priebehu času okamžitá os otáčania mení svoju polohu a opisuje valcovú plochu.

Uvažujme teraz prípad, keď sú rotácie smerované rôznymi smermi (obr. 2).

Predpokladajme, že . Potom, ako v predchádzajúcom prípade, argumentujeme pre uhlovú rýchlosť absolútneho pohybu telesa okolo osi a polohu samotnej osi, získame

Pri sčítaní dvoch rotácií smerujúcich v opačných smeroch okolo rovnobežných osí teda bude výsledným pohybom telesa okamžitá rotácia s absolútnou uhlovou rýchlosťou okolo okamžitej osi, ktorej poloha je určená proporciami (4).

Všimnite si, že v tomto prípade bod externe rozdeľuje vzdialenosť medzi rovnobežnými osami.

Uvažujme špeciálny prípad, keď rotácie okolo rovnobežných osí smerujú rôznymi smermi, ale modulo (obr. 3).

Takýto súbor rotácií sa nazýva pár rotácií a vektory tvoria pár uhlových rýchlostí. V tomto prípade dostaneme a , teda = . Vtedy je okamžitý stred rýchlostí v nekonečne a všetky body telesa v danom čase majú rovnakú rýchlosť.

V dôsledku toho bude výsledný pohyb telesa translačný (alebo okamžite translačný) pohyb s rýchlosťou, ktorá sa číselne rovná a smeruje kolmo k rovine prechádzajúcej cez vektory a . Dvojica rotácií je teda ekvivalentná okamžitému translačnému pohybu s rýchlosťou rovnajúcou sa momentu dvojice uhlových rýchlostí týchto rotácií.

Príkladom dvojice uhlových rýchlostí je pohyb pedálu bicykla voči rámu bicykla (obr. 4).

Tento pohyb je kombináciou translačnej rotácie spolu s kľukou okolo osi a relatívnej rotácie pedálu vzhľadom na kľuku okolo osi. Pedál zostáva počas celého pohybu rovnobežne s pôvodnou polohou, t.j. robí pohyb vpred.

Pozrime sa na niekoľko príkladov.

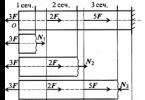
Príklad 1. Kľuka sa otáča v smere hodinových ručičiek okolo osi s uhlovou rýchlosťou a kotúč s polomerom sa otáča v smere hodinových ručičiek okolo osi s rovnakou uhlovou rýchlosťou vzhľadom na kľuku. Nájdite veľkosť a smer absolútnych rýchlostí bodov a (obr. 5).

Riešenie. Keďže uhlové rýchlosti translačného a relatívneho otáčania sú v absolútnej hodnote rovnaké a smerované rovnakým smerom, okamžitý stred otáčania disku leží v strede medzi a , t.j. . Modul absolútnej uhlovej rýchlosti otáčania disku okolo bodu sa rovná . Odtiaľto nájdeme:

, ,

, .

Príklad 2. Kľuka sa otáča okolo osi uhlovou rýchlosťou. Na kľukovom čape je voľne namontované polomerové ozubené koleso spojené so stacionárnym ozubeným kolesom polomeru. Nájdite absolútnu uhlovú rýchlosť prevodu a jeho uhlovú rýchlosť vzhľadom na kľuku (obr. 6).

Riešenie. Keďže prevod je v zábere so stojacim kolesom, absolútna rýchlosť bodu záberu prevodu s týmto kolesom je nulová, t.j. bod je okamžitý stred otáčania ozubeného kolesa. Odtiaľ alebo ,

Všimnite si, že smer otáčania ozubeného kolesa sa zhoduje so smerom otáčania kľuky.

Potom sa z rovnosti zistí absolútna uhlová rýchlosť ozubeného kolesa

Ak sa teleso súčasne zúčastňuje translačného translačného pohybu rýchlosťou a relatívneho rotačného pohybu s uhlovou rýchlosťou , potom v závislosti od ich relatívnej polohy je vhodné zvážiť tri samostatné prípady.

1. Rýchlosť translačného pohybu je kolmá na os relatívnej rotácie. V tomto prípade sú vektory a kolmé (obr. 53). On-line OS, kolmá na rovinu, v ktorej a sú umiestnené, je bod S, ktorého rýchlosť je nulová. Určte jeho vzdialenosť od bodu O.

Podľa teorému sčítania rýchlosti pre bod S máme

keďže pri otáčaní okolo osi

Vzhľadom na to, že rýchlosti a sú opačného smeru, dostaneme

Od , potom a teda body S A O sú na diaľku

Ostatné body s rýchlosťami rovnými nule sa nachádzajú na priamke prechádzajúcej bodom S, rovnobežne s osou otáčania telesa s uhlovou rýchlosťou . Existuje teda okamžitá os rotácie rovnobežná s osou relatívnej rotácie a prechádzajúca bodom S.

Pri sčítaní translačných translačných a rotačných relatívnych pohybov tuhého telesa, v ktorých je translačná rýchlosť kolmá na os relatívnej rotácie, ekvivalentný absolútny pohyb je rotácia okolo okamžitej osi rovnobežnej s osou relatívnej rotácie s uhlovou rýchlosťou zhodujúcou sa s uhlová rýchlosť relatívnej rotácie.

2. Pohyb skrutky. Pohyb, pri ktorom je rýchlosť prenosného translačného pohybu telesa rovnobežná s osou relatívnej rotácie, sa nazýva skrutkový pohyb pevného telesa (obr. 54). Os rotácie telesa sa v tomto prípade nazýva os in a o o o y. Pri špirálovom pohybe sa teleso pohybuje translačne rovnobežne s osou špirálového pohybu a otáča sa okolo tejto osi. Skrutkový pohyb nie je redukovaný na žiadny iný jednoduchý ekvivalentný pohyb.

Pri špirálovom pohybe môžu mať vektory a vektory rovnaký aj opačný smer. Skrutkovitý pohyb telesa je charakterizovaný parametrom skrutkovitého pohybu, ktorý sa považuje za hodnotu . Ak a menia sa v čase, potom sú parametre špirálového pohybu tiež premenlivé. Vo všeobecnom prípade , a , t.j. p je posunutie telesa pozdĺž osi špirálového pohybu, keď sa teleso pootočí o jeden radián.

Pre bod M máme

Ale kde r je vzdialenosť bodu od osi skrutky. Rýchlosti a sú kolmé. teda

Vzhľadom na to, dostávame

Ak sa teleso otáča konštantnou uhlovou rýchlosťou a má konštantnú rýchlosť translácie, potom sa takýto pohyb telesa nazýva konštantný skrutkový pohyb. V tomto prípade je bod tela počas pohybu vždy na povrchu kruhového valca s polomerom r. Dráha bodu je špirála. Okrem parametra v posudzovanom prípade zadajte stúpanie skrutiek, teda vzdialenosť, o ktorú sa ktorýkoľvek bod telesa posunie počas jednej otáčky telesa okolo osi špirálového pohybu. Uhol natočenia telesa pri sa vypočíta podľa vzorca . Pre jednu revolúciu tela. Čas potrebný na to.

Počas T bod sa bude pohybovať v smere rovnobežnom s osou skrutkovice o stúpanie skrutkovice.

Takto sa získa závislosť stúpania skrutky od parametra pohybu skrutky.

Rovnice pohybu bodu M telesá pozdĺž skrutkovice (obr. 102) v karteziánskych súradniciach sú vyjadrené v tomto tvare:

V týchto rovniciach sú veličiny a konštantné.

3. Všeobecný prípad. Nech rýchlosť translačného translačného pohybu a uhlová rýchlosť relatívnej rotácie zvierajú uhol . Prípad, keď už boli uvažované , a , majú všetky body tela. Takto bol získaný skrutkový pohyb so špirálovou osou vzdialenou od pôvodnej osi rotácie o .

Parameter výsledného skrutkovitého pohybu .

Všeobecný prípad translačného translačného a relatívneho rotačného pohybu tuhého telesa sa ukázal ako ekvivalentný okamžitému pohybu skrutky.

Podrobnosti Kategória: Zobrazenie: 975

POHYB SKRUTKY. Ak je pohyb nemenného systému (napríklad tuhého telesa) zložený z rotácie okolo osi a translačného pohybu pozdĺž tejto osi, potom sa takýto pohyb telesa nazýva špirálový pohyb; naznačená os sa nazýva špirálová os, alebo os otáčania - posuvná. Ak sú dané dve ľubovoľné polohy telesa pohybujúceho sa v priestore, potom prechod z polohy I do polohy II možno vykonať jedným skrutkovitým pohybom okolo určite umiestnenej špirálovej osi (Chalova veta); pričom rotačné a translačné pohyby môžu byť vykonávané buď súčasne alebo postupne v akomkoľvek poradí. Ak vezmeme do úvahy všetky dané posunutia telesa v priestore ako pozostávajúce z nekonečne malých elementárnych posunov a aplikovaním Shallovej vety na každé z nich, dostaneme nasledujúcu polohu: akýkoľvek pohyb telesa v priestore je sériou nekonečne malých špirálových posunov okolo okamžitých špirálových osí, meniace svoju polohu v každom okamihu a smer v priestore.

Skrutkovité elementárne posuny telesa okolo každej okamžitej osi sú pohyby ekvivalentné nekonečne malým skutočným posunom telesa a predstavujú ich až do nekonečne malých hodnôt vyšších rádov. Zákony pohybu skrutky, ekvivalentné akémukoľvek pohybu tuhého telesa, stanovil Mozzi (Giulio Mozzi, 1768). Pridanie dvoch špirálových pohybov tiež vedie k špirálovému pohybu.

Uvažujme komplexný pohyb tuhého telesa, ktorý sa skladá z translačných a rotačných pohybov. Zodpovedajúci príklad je znázornený na obr. 78. Tu je relatívny pohyb telesa 1 je rotácia s uhlovou rýchlosťou okolo osi Ach upevnené na plošine 2, a prenosné - translačný pohyb plošiny s rýchlosťou. Súčasne sa koleso zúčastňuje dvoch takýchto pohybov. 3, pre ktorý je relatívnym pohybom rotácia okolo svojej osi a prenosný je pohyb tej istej platformy. V závislosti od hodnoty uhla α medzi vektormi a (pre koleso je tento uhol 90°) sú tu možné tri prípady.

1. Rýchlosť translačného pohybu je kolmá na os otáčania ( ). Nech sa komplexný pohyb telesa skladá z rotačného pohybu okolo osi Ach s uhlovou rýchlosťou ω a translačný pohyb s rýchlostnou kolmou (obr. 79). Je zrejmé, že tento pohyb predstavuje (vzhľadom na rovinu P, kolmo na os Ach) planparalelny pohyb.

Ak spočítate bod A pól, potom uvažovaný pohyb, ako každý planparalelný pohyb, bude skutočne pozostávať z translačného s rýchlosťou, t. j. s rýchlosťou pólu, a z rotácie okolo osi Ach prechádzajúci cez pól.

Vektor , podľa časti 6.2, môže byť nahradený dvojicou uhlových rýchlostí a , za predpokladu , a . Zároveň aj vzdialenosť AR sa určuje z rovnosti , odkiaľ .

Vektory a po sčítaní dávajú nulu, a preto pohyb telesa v tomto prípade možno považovať za okamžitú rotáciu okolo osi pp s uhlovou rýchlosťou. Teda rotácia tela okolo osí Ach A pp prebieha s rovnakou uhlovou rýchlosťou, t.j. rotačná časť pohybu nezávisí od voľby pólu.

2. Pohyb skrutky ( ). Ak je komplexný pohyb telesa zložený z rotácie okolo osi Ach s uhlovou rýchlosťou a translačný s rýchlosťou smerujúcou rovnobežne s osou Ach(obr. 80), potom sa takýto pohyb tela nazýva skrutka. Os Ach volal os skrutky. Keď sú vektory a smerované rovnakým smerom, potom s pravidlom obrazu, ktoré sme prijali, bude skrutka správny; ak v rôznych smeroch - vľavo. Dráha, ktorú prejde počas jednej otáčky ľubovoľný bod telesa ležiaceho na osi skrutky, sa nazýva krok h skrutka. Ak sú hodnoty a konštantné, potom bude stúpanie skrutky tiež konštantné. Označuje čas jednej revolúcie cez T, získame v tomto prípade a odkiaľ .

S neustálym krokom, akýkoľvek bod M telo, neležiace na osi skrutky, opisuje špirálová čiara. Bodová rýchlosť M, umiestnený od osi skrutky v určitej vzdialenosti r, sa skladá z translačnej rýchlosti a rýchlosti na ňu kolmej, získanej pri rotačnom pohybe, ktorá sa číselne rovná ω r. Preto .

Rýchlosť smeruje tangenciálne k špirále. Ak valcová plocha, po ktorej sa bod pohybuje M, prerežte pozdĺž tvoriacej priamky a rozviňte, potom sa špirálové čiary zmenia na priame čiary naklonené k základni valca pod uhlom , kde .

3. Rýchlosť translačného pohybu zviera s osou otáčania ľubovoľný uhol. Komplexný pohyb vykonávaný telom v tomto prípade (obr. 81, a) možno považovať za všeobecný prípad pohybu voľného tuhého telesa.

Vektor (obr. 81, b) rozložíme na zložky: smerované pozdĺž () a kolmé () . Rýchlosť môže byť nahradená dvojicou uhlových rýchlostí a , po ktorej môžu byť vektory a vyradené. Vzdialenosť AC nájsť podľa vzorca.

Potom je teleso ponechané na rotáciu s uhlovou rýchlosťou a translačný pohyb s rýchlosťou. V dôsledku toho bude rozloženie rýchlostí bodov telesa v danom časovom okamihu rovnaké ako pri špirálovom pohybe okolo osi. ss s uhlovou rýchlosťou a translačnou rýchlosťou.

Po vykonaní transformácií (obr. 81, b) sme sa presunuli z pólu A k pólu S. Výsledok potvrdzuje, že vo všeobecnom prípade pohybu tuhého telesa sa pri zmene pólu () nemení uhlová rýchlosť, ale mení sa iba translačná rýchlosť ().

Keďže pri pohybe voľného tuhého telesa sa veličiny α budú neustále meniť, plynule sa bude meniť aj poloha osi. ss, ktorý sa teda nazýva okamžitá špirálová os. teda pohyb voľného tuhého telesa možno tiež považovať za zložený zo série okamžitých špirálových pohybov okolo kontinuálne sa meniacich špirálových osí.

Záver

Úlohu a miesto teoretickej mechaniky v inžinierskom vzdelávaní určuje skutočnosť, že je vedeckým základom pre mnohé oblasti modernej techniky. Asimiláciu teoretickej mechaniky komplikuje skutočnosť, že modelovanie a matematické znázornenie študovaných prírodných javov zohráva v tejto vede podstatnú úlohu. Preto pri riešení inžinierskych problémov majú študenti často značné ťažkosti. Problém formovania výskumného prístupu k úlohám stanoveným študentmi (zo sekcie "Kinematika" kurzu teoretickej mechaniky) možno vyriešiť navrhovanou učebnicou. Príručka prístupným spôsobom pokrýva hlavné témy časti „Kinematika“ so všetkými potrebnými dôkazmi. Uvádzajú sa návody na riešenie problémov a príklady ich riešenia. Úlohy na samostatnú prácu uvedené na konci kapitol príručky pomôžu zvládnuť a upevniť prezentovanú látku.

Uvažujme komplexný pohyb tuhého telesa, ktorý sa skladá z translačných a rotačných pohybov. Zodpovedajúci príklad je znázornený na obr. 207. Relatívnym pohybom telesa 1 je rotácia s uhlovou rýchlosťou c okolo osi upevnenej na plošine 2 a translačným pohybom je translačný pohyb plošiny s rýchlosťou v. Súčasne sa koleso 3 tiež podieľa na dvoch takýchto pohyboch, pre ktoré je relatívnym pohybom rotácia okolo svojej osi a prenosným pohybom je pohyb tej istej plošiny. V závislosti od hodnoty uhla a medzi vektormi a v (pre koleso je tento uhol 90°) sú tu možné tri prípady.

1. Rýchlosť translačného pohybu je kolmá na os rotácie Zložený pohyb telesa nech je zložený z rotačného pohybu okolo osi s uhlovou rýchlosťou co a translačného pohybu s rýchlosťou v, kolmej (obr. 208).

Je ľahké vidieť, že tento pohyb je (vzhľadom na rovinu П, kolmú na os ) rovinno-paralelný pohyb, podrobne študovaný v kap. XI. Ak považujeme bod A za pól, potom uvažovaný pohyb, ako každý planparalelný pohyb, bude skutočne pozostávať z translačného s rýchlosťou, t. j. s rýchlosťou pólu, a z rotácie okolo osi prechádzajúcej cez pól. .

Vektor v možno nahradiť dvojicou uhlových rýchlostí (pozri § 69) tak, že vezmeme . V tomto prípade je vzdialenosť AR určená z rovnosti odkiaľ (vzhľadom na to, že )

Súčet vektorov je nula a dostaneme, že pohyb telesa v tomto prípade možno považovať za okamžitú rotáciu okolo osi s uhlovou rýchlosťou . Tento výsledok sa predtým získal iným spôsobom (pozri § 56). Porovnaním rovností (55) a (107) vidíme, že bod P pre rez telesa je okamžitým stredom rýchlostí. Tu sa ešte raz presvedčíme, že rotácia telesa okolo osí nastáva s rovnakým uhlom rýchlosť, t.j., že rotačná časť pohybu nezávisí od voľby pólu (pozri § 52).

2. Pohyb skrutky (). Ak je komplexný pohyb telesa zložený z rotačného okolo osi s uhlovou rýchlosťou co a translačného s rýchlosťou v smerujúcom rovnobežne s osou (obr. 209), potom sa takýto pohyb telesa nazýva skrutkový. Os sa nazýva os skrutky.

Keď sú vektory nasmerované jedným smerom, potom podľa pravidla, ktoré sme prijali, bude obraz o skrutke správny; ak v rôznych smeroch, - vľavo.

Vzdialenosť prejdená počas jednej otáčky ktorýmkoľvek bodom telesa ležiaceho na osi skrutky sa nazýva stúpanie h skrutky. Ak sú hodnoty band a s konštantné, potom bude aj stúpanie skrutky konštantné. Označením času jednej otáčky cez T dostaneme v tomto prípade , odkiaľ

Pri konštantnom stúpaní opisuje každý bod M telesa, ktorý neleží na osi skrutky, špirálu. Rýchlosť bodu M, ktorý sa nachádza vo vzdialenosti od osi skrutky, sa skladá z translačnej rýchlosti v a rýchlosti na ňu kolmej, získanej pri rotačnom pohybe, ktorá sa číselne rovná Preto,

Rýchlosť smeruje tangenciálne k špirále. Ak je valcová plocha, po ktorej sa bod M pohybuje, prerezaná pozdĺž tvoriacej čiary a rozložená, potom sa špirálové čiary zmenia na priame čiary naklonené k základni valca pod uhlom.

3. Rýchlosť translačného pohybu zviera s osou otáčania ľubovoľný uhol. Komplexný pohyb vykonávaný telesom v tomto prípade (obr. 210, a) je pohyb uvažovaný v § 63 (všeobecný prípad pohybu voľného tuhého telesa).

Vektor v (obr. 210, b) rozložíme na zložky: kolmú rýchlosť smerujúcu spolu s možno nahradiť dvojicou uhlových rýchlostí (ako na obr. 208), po ktorej môžu byť vektory vyradené. AC vzdialenosť nájdeme pomocou vzorca (107).