Zvážte riešenie rovníc s jednou premennou o stupeň vyššou ako druhá.
Stupeň rovnice P(x) = 0 je stupeň polynómu P(x), t.j. najväčšia z mocnín svojich členov s nenulovým koeficientom.
Takže napríklad rovnica (x 3 - 1) 2 + x 5 \u003d x 6 - 2 má piaty stupeň, pretože po operáciách otvárania zátvoriek a privádzania podobných získame ekvivalentnú rovnicu x 5 - 2x 3 + 3 \u003d 0 piateho stupňa.
Pripomeňme si pravidlá, ktoré budú potrebné na riešenie rovníc stupňa vyššieho ako je druhý.
Výroky o koreňoch polynómu a jeho deliteľoch:
1. Polynóm n-tého stupňa má počet koreňov nepresahujúcich číslo n a korene násobnosti m sa vyskytujú presne m-krát.
2. Polynóm nepárneho stupňa má aspoň jeden skutočný koreň.
3. Ak α je koreň Р(х), potom Р n (х) = (х – α) · Q n – 1 (x), kde Q n – 1 (x) je polynóm stupňa (n – 1) .
4.
5. Redukovaný polynóm s celočíselnými koeficientmi nemôže mať zlomkové racionálne korene.
6. Pre polynóm tretieho stupňa
P 3 (x) \u003d ax 3 + bx 2 + cx + d je možná jedna z dvoch vecí: buď sa rozloží na súčin troch dvojčlenov
P 3 (x) \u003d a (x - α) (x - β) (x - γ), alebo sa rozloží na súčin dvojčlenu a štvorcového trojčlenu P 3 (x) \u003d a (x - α) ( x 2 + βx + y ).
7. Akýkoľvek polynóm štvrtého stupňa sa rozšíri na súčin dvoch štvorcových trinómov.
8. Polynóm f(x) je bezo zvyšku deliteľný polynómom g(x), ak existuje polynóm q(x) taký, že f(x) = g(x) q(x). Na delenie polynómov sa uplatňuje pravidlo „delenie rohom“.
9. Aby bol polynóm P(x) deliteľný binomom (x – c), je potrebné a postačujúce, aby číslo c bolo koreňom P(x) (dôsledok Bezoutovej vety).
10. Vietova veta: Ak x 1, x 2, ..., x n sú skutočné korene polynómu
P (x) = a 0 x n + a 1 x n - 1 + ... + a n, potom platia nasledujúce rovnosti:
x 1 + x 2 + ... + x n \u003d -a 1 / a 0,
x 1 x 2 + x 1 x 3 + ... + x n - 1 x n \u003d a 2 / a 0,
x 1 x 2 x 3 + ... + x n - 2 x n - 1 x n \u003d -a 3 / a 0,
x 1 x 2 x 3 x n \u003d (-1) n a n / a 0.
Riešenie príkladov
Príklad 1
Nájdite zvyšok po vydelení P (x) \u003d x 3 + 2/3 x 2 - 1/9 (x - 1/3).
Riešenie.
Podľa záveru Bezoutovej vety: "Zvyšok delenia polynómu binómom (x - c) sa rovná hodnote polynómu v c." Nájdite P(1/3) = 0. Preto je zvyšok 0 a číslo 1/3 je koreňom polynómu.
Odpoveď: R = 0.
Príklad 2
Rozdeľte "roh" 2x 3 + 3x 2 - 2x + 3 o (x + 2). Nájdite zvyšok a neúplný kvocient. 
Riešenie:
2x 3 + 3x 2 – 2x + 3| x + 2
2x 3 + 4x 2 2x 2 – x
X 2 – 2 x
Odpoveď: R = 3; podiel: 2x 2 - x.
Základné metódy riešenia rovníc vyšších stupňov
1. Zavedenie novej premennej
Spôsob zavedenia novej premennej je už známy z príkladu bikvadratických rovníc. Spočíva v tom, že na vyriešenie rovnice f (x) \u003d 0 sa zavedie nová premenná (substitúcia) t \u003d x n alebo t \u003d g (x) a f (x) sa vyjadrí prostredníctvom t, čím sa získa a nová rovnica r (t). Potom vyriešením rovnice r(t) nájdite korene:
(ti, t2, ..., t n). Potom sa získa množina n rovníc q(x) = t 1 , q(x) = t 2 , ... , q(x) = t n, z ktorej sa nájdu korene pôvodnej rovnice.
Príklad 1
(x 2 + x + 1) 2 - 3x 2 - 3x - 1 = 0.
Riešenie:
(x 2 + x + 1) 2 - 3 (x 2 + x) - 1 = 0.
(x 2 + x + 1) 2 - 3 (x 2 + x + 1) + 3 - 1 = 0.
Náhrada (x 2 + x + 1) = t.
t2 - 3t + 2 = 0.
t 1 \u003d 2, t 2 \u003d 1. Opačná výmena:
x 2 + x + 1 = 2 alebo x 2 + x + 1 = 1;
x 2 + x - 1 = 0 alebo x 2 + x = 0;
Odpoveď: Z prvej rovnice: x 1, 2 = (-1 ± √5) / 2, z druhej: 0 a -1.
2. Faktorizácia metódou zoskupovania a skrátených vzorcov násobenia
Základ tejto metódy tiež nie je nový a spočíva v zoskupení pojmov takým spôsobom, že každá skupina obsahuje spoločný faktor. Aby ste to dosiahli, niekedy musíte použiť nejaké umelé triky.
Príklad 1
x 4 - 3 x 2 + 4 x - 3 = 0.
Riešenie.
Predstavte si - 3x 2 = -2x 2 - x 2 a skupina:
(x 4 - 2x 2) - (x 2 - 4x + 3) = 0.
(x 4 - 2x 2 +1 - 1) - (x 2 - 4x + 3 + 1 - 1) = 0.
(x 2 - 1) 2 - 1 - (x - 2) 2 + 1 = 0.
(x 2 - 1) 2 - (x - 2) 2 \u003d 0.
(x 2 - 1 - x + 2) (x 2 - 1 + x - 2) = 0.
(x 2 - x + 1) (x 2 + x - 3) = 0.
x 2 - x + 1 \u003d 0 alebo x 2 + x - 3 \u003d 0.
Odpoveď: V prvej rovnici nie sú žiadne korene, z druhej: x 1, 2 = (-1 ± √13) / 2.
3. Faktorizácia metódou neurčitých koeficientov
Podstatou metódy je, že pôvodný polynóm sa rozloží na faktory s neznámymi koeficientmi. Pomocou vlastnosti, že polynómy sú rovnaké, ak sú ich koeficienty rovnaké pri rovnakých mocniciach, sa nájdu neznáme expanzné koeficienty.
Príklad 1
x 3 + 4 x 2 + 5 x + 2 = 0.
Riešenie.
Polynóm 3. stupňa možno rozložiť na súčin lineárnych a štvorcových faktorov.
x 3 + 4x 2 + 5x + 2 \u003d (x - a) (x 2 + bx + c),
x 3 + 4x 2 + 5x + 2 = x 3 + bx 2 + cx - ax 2 - abx - ac,
x 3 + 4x 2 + 5x + 2 \u003d x 3 + (b - a) x 2 + (cx - ab) x - ac.
Riešenie systému:
(b – a = 4,
(c – ab = 5,
(-ac=2,
(a = -1,
(b=3,
(c = 2, t.j.
x 3 + 4x 2 + 5x + 2 \u003d (x + 1) (x 2 + 3x + 2).
Korene rovnice (x + 1) (x 2 + 3x + 2) = 0 sa dajú ľahko nájsť.
Odpoveď: -1; -2.
4. Spôsob výberu koreňa najvyšším a voľným koeficientom

Metóda je založená na aplikácii teorémov:
1) Akýkoľvek celočíselný koreň polynómu s celočíselnými koeficientmi je deliteľom voľného člena.
2) Aby bol ireducibilný zlomok p / q (p je celé číslo, q prirodzený) koreňom rovnice s celočíselnými koeficientmi, je potrebné, aby číslo p bolo celočíselným deliteľom voľného člena a 0 a q je prirodzený deliteľ najvyššieho koeficientu.
Príklad 1
6x 3 + 7x 2 - 9x + 2 = 0.
Riešenie:
6: q = 1, 2, 3, 6.
Preto p/q = ±1, ±2, ±1/2, ±1/3, ±2/3, ±1/6.
Po nájdení jedného koreňa, napríklad - 2, nájdeme ďalšie korene delením rohom, metódou neurčitých koeficientov alebo Hornerovou schémou.
Odpoveď: -2; 1/2; 1/3.
Máte nejaké otázky? Neviete, ako riešiť rovnice?
Ak chcete získať pomoc tútora - zaregistrujte sa.
Prvá lekcia je zadarmo!
stránky, s úplným alebo čiastočným kopírovaním materiálu, je potrebný odkaz na zdroj.
HORNEROVÁ SCHÉMA
PRI RIEŠENÍ ROVNICE S PARAMETRMI
ZO SKUPINY "C" V PRÍPRAVE NA POUŽITIE
Kazantseva Ludmila Viktorovna
učiteľ matematiky MBOU "Uyar stredná škola č. 3"
Na voliteľných hodinách je potrebné rozširovať okruh doterajších vedomostí o riešenie úloh zvýšenej náročnosti skupiny „C“.
Táto práca sa zaoberá niektorými problémami zvažovanými v ďalších triedach.
Hornerovu schému je vhodné zaviesť po preštudovaní témy „Rozdelenie polynómu polynómom“. Tento materiál umožňuje riešiť rovnice vyššieho rádu nie spôsobom zoskupovania polynómov, ale racionálnejším spôsobom, ktorý šetrí čas.
Plán lekcie.
Lekcia 1.
1. Vysvetlenie teoretického materiálu.
2. Riešenie príkladov a B C d).
Lekcia 2.
1. Riešenie rovníc a B C d).
2. Hľadanie racionálnych koreňov polynómu
Aplikácia Hornerovej schémy pri riešení rovníc s parametrami.
Lekcia 3.
Úlohy a B C).
Lekcia 4.
1. Úlohy d), e), f), g), h).
Riešenie rovníc vyšších stupňov.
Hornerova schéma.
Veta : Nech je koreňom rovnice neredukovateľný zlomok
a o X n + a 1 X n-1 + … + a n-1 X 1 + a n = 0
s celočíselnými koeficientmi. Potom číslo R je deliteľ vedúceho koeficientu A O .
Dôsledok: Akýkoľvek celočíselný koreň rovnice s celočíselnými koeficientmi je deliteľom jej voľného člena.
Dôsledok: Ak je vodiaci koeficient rovnice s celočíselnými koeficientmi 1 , potom všetky racionálne korene, ak existujú, sú celé čísla.
Príklad 1. 2x 3 – 7x 2 + 5x - 1 = 0
Nech je teda koreňom rovnice neredukovateľný zlomokR je deliteľ čísla1:±1
q je deliteľ vedúceho termínu: ± 1; ±2
Racionálne korene rovnice treba hľadať medzi číslami:± 1; ± .
f(1) = 2 – 7 + 5 – 1 = – 1 ≠ 0
f(–1) = –2 – 7 – 5 – 1 ≠ 0
f() = – + – 1 = – +  – = 0
– = 0
Koreň je číslo .
Polynomické delenie P(x) = a O X P + a 1 X n -1 + … + a n do binomického tvaru ( x – £) Je vhodné vykonávať podľa Hornerovej schémy.
Označte neúplný kvocient P(x) na ( x – £) cez Q (X ) = b o X n -1 + b 1 X n -2 + … b n -1 ,
a zvyšok cez b n
P(x) =Q (X ) (X – £) + b n , potom máme identitu
A O X P + a 1 X n-1 + … + a n = (b o X n-1 + … + b n-1 ) (x - £) +b n
Q (X ) je polynóm, ktorého stupeň je 1 pod stupňom pôvodného polynómu. Polynomické koeficienty Q (X ) určená Hornerovou schémou.
oh oh
1
a 2
a n-1
a n
b o = a o
b 1 = a 1 + £· b o
b 2 = a 2 + £· b 1
b n-1 = a n-1 + £· b n-2
b n = a n + £· b n-1
Do prvého riadku tejto tabuľky napíšte koeficienty polynómu P(x).
Ak niektorý stupeň premennej chýba, zapíše sa do príslušnej bunky tabuľky 0.
Najvyšší koeficient kvocientu sa rovná najvyššiemu koeficientu dividendy ( A O = b o ). Ak £ je koreň polynómu, potom sa v poslednej bunke ukáže 0.
Príklad 2. Faktorizujte s celočíselnými koeficientmi
P (x) \u003d 2x 4 - 7x 3 - 3x 2 + 5x - 1
± 1.
Pasuje - 1.
Rozdeliť P(x) na (x + 1)
2
– 7
– 3
5
– 1
– 1
2
– 9
6
– 1
0
2x 4 - 7x 3 - 3x 2 + 5x - 1 = (x + 1) (2x 3 - 9x 2 + 6x - 1)
Hľadáme odmocniny celého čísla medzi voľným členom: ± 1
Keďže vedúci výraz je 1, potom korene môžu byť zlomkové čísla: - ; .
Pasuje .
2
– 9
6
– 1
2
– 8
2
0
2x 3 - 9x 2 + 6x - 1 \u003d (x -) (2x 2 - 8x + 2) = (2x - 1) (x 2 - 4x + 1)
Trinomial X 2 - 4x + 1 nefaktorizuje s celočíselnými koeficientmi.
Cvičenie:
1. Faktorizujte s celočíselnými koeficientmi:
A) X 3 – 2x 2 - 5x + 6
q: ± 1;
p: ± 1; ±2; ± 3; ±6
± 1; ±2; ± 3; ±6
Hľadanie racionálnych koreňov polynómu f (1) = 1 – 2 – 5 + 6 = 0
x = 1
1
– 2
– 5
6
1
1
– 1
– 6
0
x 3 - 2x 2 - 5x + 6 \u003d (x - 1) (x 2 - x - 6) \u003d (x - 1) (x - 3) (x + 2)
Poďme určiť korene kvadratickej rovnice
x 2 - x - 6 = 0
x = 3; x \u003d - 2
b) 2x 3 + 5x 2 + x - 2
p: ± 1; ±2
q: ± 1; ±2
± 1; ±2; ±
Nájdite korene polynómu tretieho stupňa
f(1) = 2 + 5 + 1 - 2 ≠ 0
f (–1) = – 2 + 5 – 1 – 2 = 0
Jeden z koreňov rovnice x = - 1
2
5
1
– 2
– 1
2
3
– 2
0
2x 3 + 5x 2 + x - 2 \u003d (x + 1) (2x 2 + 3x - 2) \u003d (x + 1) (x + 2) (2x - 1)
Rozšírme štvorcovú trojčlenku 2x 2 + 3x - 2 multiplikátory
2x 2 + 3x - 2 \u003d 2 (x + 2) (x -)
D = 9 + 16 = 25
x 1 \u003d - 2; x 2 =
V) X 3 – 3x 2 + x + 1
p:±1
q: ± 1
:± 1
f(1) = 1 - 3 + 1 - 1 = 0
Jedným z koreňov polynómu tretieho stupňa je x = 1
1
– 3
1
1
1
1
– 2
– 1
0
x 3 - 3x 2 + x + 1 = (x - 1) (x 2 - 2x - 1)
Nájdite korene rovnice X 2 – 2x – 1 = 0
D= 4 + 4 = 8
x 1 = 1 – 
x 2 = 1 + 
x 3 - 3 x 2 + x + 1 = (x - 1) (x - 1 +  ) (х – 1 –
) (х – 1 –  )
)
G) X 3 – 2x – 1
p:±1
q: ± 1
:± 1
Definujme korene polynómu
f(1) = 1 – 2 – 1 = – 2
f (–1) = – 1 + 2 – 1 = 0
Prvý koreň x = - 1
1
0
– 2
– 1
– 1
1
– 1
– 1
0
x 3 - 2x - 1 \u003d (x + 1) (x 2 - x - 1)
x 2 - x - 1 = 0
D = 1 + 4 = 5
x 1,2 = 
x 3 - 2x - 1 \u003d (x + 1) (x -  ) (X -
) (X -  )
)
2. Vyriešte rovnicu:
A) X 3 – 5x + 4 = 0
Definujme korene polynómu tretieho stupňa
± 1; ±2; ±4
f(1) = 1 - 5 + 4 = 0
Jedným z koreňov je x = 1
1
0
– 5
4
1
1
1
– 4
0
x 3 - 5 x + 4 = 0
(x - 1) (x 2 + x - 4) = 0
X 2 + x - 4 = 0
D = 1 + 16 = 17
x 1 =  ; X 2
=
; X 2
= 
odpoveď: 1;  ;
; 
b) X 3 – 8x 2 + 40 = 0
Určme korene polynómu tretieho stupňa.
± 1; ±2; ± 4; ±5; ± 8; ± 10; ±20; ±40
f(1) ≠ 0
f(–1) ≠ 0
f (–2) = – 8 – 32 + 40 = 0
Jedným z koreňov je x \u003d - 2
1
– 8
0
40
– 2
1
– 10
20
0
Rozložme polynóm tretieho stupňa na faktory.
x 3 - 8x 2 + 40 \u003d (x + 2) (x 2 - 10x + 20)
Nájdite korene kvadratickej rovnice X 2 – 10x + 20 = 0
D = 100 - 80 = 20
x 1 = 5 –  ; X 2
= 5 +
; X 2
= 5 + 
Odpoveď: - 2; 5 –  ; 5 +
; 5 + 
V) X 3 – 5x 2 + 3x + 1 = 0
Hľadáme odmocniny celého čísla medzi deliteľmi voľného termínu: ± 1
f (–1) = – 1 – 5 – 3 + 1 ≠ 0
f(1) = 1 - 5 + 3 + 1 = 0
Pasuje x = 1
1
– 5
3
1
1
1
– 4
– 1
0
x 3 - 5 x 2 + 3 x + 1 = 0
(x - 1) (x 2 - 4x - 1) = 0
Určíme korene kvadratickej rovnice X 2 – 4x – 1 = 0
D = 20
x = 2 +  ; x = 2 -
; x = 2 - 
odpoveď: 2 –  ; 1; 2 +
; 1; 2 + 
G) 2x 4 – 5x 3 + 5x 2 – 2 = 0
p: ± 1; ±2
q: ± 1; ±2
± 1; ±2; ±
f(1) = 2 - 5 + 5 - 2 = 0
Jeden z koreňov rovnice x = 1
2
– 5
5
0
– 2
1
2
– 3
2
2
0
2x 4 - 5x 3 + 5x 2 - 2 = 0
(x - 1) (2x 3 - 3x 2 + 2x + 2) = 0
Rovnakým spôsobom nájdeme korene rovnice tretieho stupňa.
2x 3 - 3x 2 + 2x + 2 = 0
p: ± 1; ±2
q: ± 1; ±2
± 1; ±2; ±
f(1) = 2 - 3 + 2 + 2 ≠ 0
f (–1) = – 2 – 3 – 2 + 2 ≠ 0
f(2) = 16 - 12 + 4 + 2 ≠ 0
f (–2) = – 16 – 12 – 4 + 2 ≠ 0
f() = – + 1 + 2 ≠ 0
f(–) = – – – 1 + 2 ≠ 0
Ďalší koreň rovnicex = -
2
– 3
2
2
2
– 4
4
0
2x 3 - 3x 2 + 2x + 2 = 0
(x + ) (2x 2 - 4x + 4) = 0
Poďme určiť korene kvadratickej rovnice 2x 2 – 4x + 4 = 0
x 2 - 2 x + 2 = 0
D = – 4< 0
Preto sú korene pôvodnej rovnice štvrtého stupňa
1 a –
odpoveď: –; 1
3. Nájdite racionálne korene polynómu
A) X 4 – 2x 3 – 8x 2 + 13x - 24
q: ± 1
± 1; ±2; ± 3; ± 4; ± 6; ± 8; ± 12; ± 24
Vyberme si jeden z koreňov polynómu štvrtého stupňa:
f(1) = 1 - 2 - 8 + 13 - 24 ≠ 0
f(-1) = 1 + 2 - 8 - 13 - 24 ≠ 0
f(2) = 16 - 16 - 32 + 26 - 24 ≠ 0
f(-2) = 16 + 16 - 72 - 24 ≠ 0
f(-3) = 81 + 54 - 72 - 39 - 24 = 0
Jeden z koreňov polynómu X 0= – 3.
x 4 - 2x 3 - 8x 2 + 13x - 24 \u003d (x + 3) (x 3 - 5x 2 + 7x + 8)
Poďme nájsť racionálne korene polynómu
x 3 – 5 x 2 + 7 x + 8
p: ± 1; ±2; ± 4; ± 8
q: ± 1
f(1) = 1 - 5 + 7 + 8 ≠ 0
f (–1) = – 1 – 5 – 7 – 8 ≠ 0
f(2) = 8 - 20 + 14 + 8 ≠ 0
f (–2) = – 8 – 20 – 14 + 8 ≠ 0
f(-4) = 64 - 90 - 28 + 8 ≠ 0
f(4) ≠ 0
f(–8) ≠ 0
f(8) ≠ 0
Okrem čísla X 0 = – 3 neexistujú žiadne iné racionálne korene.
b) X 4 – 2x 3 – 13x 2 – 38x – 24
p: ± 1; ±2; ± 3; ± 4; ± 6; ± 8; ± 12; ± 24
q: ± 1
f(1) = 1 + 2 - 13 - 38 - 24 ≠ 0
f (–1) = 1 – 2 – 13 + 38 – 24 = 39 – 39 = 0, to jest x = - 1 polynómový koreň
1
2
– 13
– 38
– 24
– 1
1
1
– 14
– 24
0
x 4 - 2x 3 - 13x 2 - 38x - 24 \u003d (x + 1) (x 3 - x 2 - 14x - 24)
Definujme korene polynómu tretieho stupňa X 3 - X 2 – 14x – 24
p: ± 1; ±2; ± 3; ± 4; ± 6; ± 8; ± 12; ± 24
q: ± 1
f(1) = -1 + 1 + 14 - 24 ≠ 0
f(-1) = 1 + 1 - 14 - 24 ≠ 0
f(2) = 8 + 4 - 28 - 24 ≠ 0
f (–2) = – 8 + 4 + 28 – 24 ≠ 0
Takže druhý koreň polynómu x \u003d - 2
1
1
– 14
– 24
– 2
1
– 1
– 12
0
x 4 - 2x 3 - 13x 2 - 38x - 24 \u003d (x + 1) (x 2 + 2) (x 2 - x - 12) \u003d
= (x + 1) (x + 2) (x + 3) (x - 4)
odpoveď: – 3; – 2; – 1; 4
Aplikácia Hornerovej schémy pri riešení rovníc s parametrom.
Nájdite najväčšiu celočíselnú hodnotu parametra A, pod ktorým je rovnica f (x) = 0 má tri rôzne korene, z ktorých jeden X 0 .
A) f (x) = x 3 + 8x 2 +ach+b , X 0 = – 3
Takže jeden z koreňov X 0 = – 3 , potom podľa Hornerovej schémy máme:
1
8
A
b
– 3
1
5
– 15 + a
0
0 \u003d - 3 (- 15 + a) + b
0 \u003d 45 - 3a + b
b = 3a - 45
x 3 + 8x 2 + ax + b \u003d (x + 3) (x 2 + 5x + (a - 15))
Rovnica X 2 + 5x + (a - 15) = 0 D > 0
A = 1; b = 5; c \u003d (a - 15),
D \u003d b 2 - 4ac \u003d 25 - 4 (a - 15) \u003d 25 + 60 - 4a\u003e 0,
85 – 4a > 0;
4a< 85;
a< 21
Najväčšia celočíselná hodnota parametra A, pod ktorým je rovnica
f (x) = 0 má tri korene a = 21
odpoveď: 21.
b) f(x) = x 3 – 2x 2 + ax + b, x 0 = – 1
Od jedného z koreňov X 0= – 1, potom podľa Hornerovej schémy máme
1
– 2
a
b
– 1
1
– 3
3 + a
0
x 3 - 2x 2 + ax + b = (x + 1) (x 2 - 3x + (3 + a))
Rovnica X 2 – 3 X + (3 + a ) = 0 musí mať dva korene. Toto sa robí len vtedy, keď D > 0
a = 1; b = - 3; c = (3 + a),
D \u003d b 2 - 4ac \u003d 9 - 4 (3 + a) \u003d 9 - 12 - 4a \u003d - 3 - 4a\u003e 0,
– 3-4a > 0;
– 4a< 3;
a < –
Najvyššia hodnota a = -1 a = 40
odpoveď: a = 40
G) f(x) = x 3 – 11x 2 + ax + b, x 0 = 4
Od jedného z koreňov X 0 = 4 , potom podľa Hornerovej schémy, ktorú máme
1
– 11
a
b
4
1
– 7
– 28 + a
0
x 3 - 11x 2 + ax + b \u003d (x - 4) (x 2 - 7x + (a - 28))
f (X ) = 0, Ak x = 4 alebo X 2 – 7 X + (a – 28) = 0
D > 0, to jest
D \u003d b 2 - 4ac \u003d 49 - 4 (a - 28) \u003d 49 + 112 - 4a \u003d 161 - 4a\u003e 0,
161 – 4a > 0;
– 4a< – 161; f X 0 = – 5 , potom podľa Hornerovej schémy, ktorú máme
1
13
a
b
– 5
1
8
– 40 + a
0
x 3 + 13x 2 + ax + b \u003d (x + 5) (x 2 + 8x + (a - 40))
f (X ) = 0, Ak x \u003d - 5 alebo X 2 + 8 X + (a – 40) = 0
Rovnica má dva korene, ak D > 0
D \u003d b 2 - 4ac \u003d 64 - 4 (a - 40) \u003d 64 + 1 60 - 4a \u003d 224 - 4a\u003e 0,
224- 4a > 0;
a< 56
Rovnica f (X ) má tri korene s najväčšou hodnotou a = 55
odpoveď: a = 55
a) f (X ) = X 3 + 19 X 2 + sekera + b , X 0 = – 6
Od jedného z koreňov – 6 , potom podľa Hornerovej schémy, ktorú máme
1
19
a
b
– 6
1
13
a - 78
0
x 3 + 19x 2 + ax + b = (x +6) (x 2 + 13x + (a - 78)) = 0
f (X ) = 0, Ak x \u003d - 6 alebo X 2 + 13 X + (a – 78) = 0
Druhá rovnica má dva korene, ak
Ak chcete použiť ukážku prezentácií, vytvorte si Google účet (účet) a prihláste sa: https://accounts.google.com
Popisy snímok:
Rovnice vyšších stupňov (korene polynómu v jednej premennej).
Plán prednášky. č. 1 . Rovnice vyšších stupňov v školskom kurze matematiky. č. 2. Štandardný tvar polynómu. č. 3. Celočíselné korene polynómu. Hornerova schéma. č. 4. Zlomkové korene polynómu. č. 5. Rovnice tvaru: (x + a) (x + b) (x + c) ... = A č. 6. Návratové rovnice. č. 7. Homogénne rovnice. č. 8. Metóda neurčitých koeficientov. č.9. Funkčno - grafická metóda. č.10. Vieta vzorce pre rovnice vyšších stupňov. № 11. Neštandardné metódy riešenia rovníc vyšších stupňov.
Rovnice vyšších stupňov v školskom kurze matematiky. 7. trieda. Štandardný tvar polynómu. Akcie s polynómami. Faktorizácia polynómu. V bežnej triede 42 hodín, v špeciálnej triede 56 hodín. 8 špeciálna trieda. Celočíselné korene polynómu, delenie polynómov, reciproké rovnice, rozdiel a súčet n-tej mocniny binomu, metóda neurčitých koeficientov. Yu.N. Makarychev "Dodatočné kapitoly k školskému kurzu algebry 8. ročníka", M.L. Galitsky Zbierka úloh z algebry 8. - 9. ročník. 9 špeciálna trieda. Racionálne korene polynómu. Zovšeobecnené recipročné rovnice. Vieta vzorce pre rovnice vyšších stupňov. N.Ya. Vilenkin Algebra stupeň 9 s hĺbkovým štúdiom. 11 špeciálna trieda. Identita polynómov. Polynóm vo viacerých premenných. Funkčne - grafická metóda na riešenie rovníc vyšších stupňov.
Štandardný tvar polynómu. Polynóm P(x) = a ⁿ x ⁿ + a n-1 x n-1 + … + a₂x ² + a₁x + a₀. Nazýva sa polynóm štandardnej formy. a n x ⁿ je vedúci člen polynómu a n je koeficient vedúceho člena polynómu. Pre a n = 1 sa P(x) nazýva redukovaný polynóm. a ₀ je voľný člen polynómu P(x). n je stupeň polynómu.
Celé korene polynómu. Hornerova schéma. Veta č. 1. Ak je celé číslo a koreňom polynómu P(x), potom a je deliteľom voľného člena P(x). Príklad č. 1. Vyriešte rovnicu. X⁴ + 2x³ \u003d 11x² - 4x - 4 Uveďme rovnicu do štandardného tvaru. X⁴ + 2x³ - 11x² + 4x + 4 \u003d 0. Máme polynóm P (x) \u003d x ⁴ + 2x³ - 11x² + 4x + 4 Deliče voľného člena: ± 1, ± 2, ± 4. x \u003d 1 koreň rovnice, pretože P (1) \u003d 0, x \u003d 2 je koreň rovnice, pretože P(2) = 0 Bezoutova veta. Zvyšok delenia polynómu P(x) binómom (x - a) sa rovná P(a). Dôsledok. Ak a je koreň polynómu P(x), potom P(x) je deliteľné (x - a). V našej rovnici je P (x) delené (x - 1) a (x - 2), a teda (x - 1) (x - 2). Pri delení P (x) koeficientom (x ² - 3x + 2) v kvociente dostaneme trinom x ² + 5x + 2 = 0, ktorý má korene x = (-5 ± √17) / 2
Zlomkové korene polynómu. Veta #2. Ak p / g je koreň polynómu P(x), potom p je deliteľ voľného člena, g je deliteľ koeficientu najvyššieho člena P(x). Príklad č. 2: Vyriešte rovnicu. 6x³ - 11x² - 2x + 8 = 0. Deliče voľného člena: ±1, ±2, ±4, ±8. Žiadne z týchto čísel nespĺňa rovnicu. Neexistujú žiadne celé korene. Prirodzené deliče koeficientu najvyššieho člena P(x): 1, 2, 3, 6. Možné zlomkové korene rovnice: ±2/3, ±4/3, ±8/3. Kontrolou sme presvedčení, že P (4/3) \u003d 0. X \u003d 4/3 je koreň rovnice. Podľa Hornerovej schémy delíme P(x) o (x - 4/3).
Príklady nezávislého rozhodovania. Vyriešte rovnice: 9x³ - 18x = x - 2, x ³ - x ² = x - 1, x 3 - 3x² -3x + 1 = 0, X 4 - 2x3 + 2x - 1 = 0, X4 - 3x² + 2 = 0 , x ⁵ + 5x³ - 6x² = 0, x ³ + 4x² + 5x + 2 = 0, X4 + 4x3 - x ² - 16x - 12 = 0 4x3 + x ² - x + 5 = 0 3x3 - 9x³ - 5x³ - 5x³ + 5x³ 9x + 10 = 0. Odpovede: 1) ±1/3; 2 2) ± 1, 3) -1; 2 ±√3, 4) ±1, 5) ± 1; ±√2, 6) 0; 17)-2; -1,8) -3; -1; ±2, 9) – 5/4 10) -2; - 5/3; 1.
Rovnice tvaru (x + a) (x + b) (x + c) (x + d) ... = A. Príklad č.3. Vyriešte rovnicu (x + 1)(x + 2)(x + 3)(x + 4) =24. a = 1, c = 2, c = 3, d = 4 a + d = c + c. Prvú zátvorku vynásobíme štvrtou a druhú treťou. (x + 1) (x + 4) (x + 20 (x + 3) = 24. (x² + 5x + 4) (x² + 5x + 6) = 24. Nech x² + 5x + 4 = y, potom y (y + 2) = 24, y² + 2y - 24 = 0 y₁ = - 6, y₂ = 4. x ² + 5x + 4 = -6 alebo x ² + 5x + 4 = 4. x ² + 5x + 10 = 0, D
Príklady nezávislého rozhodovania. (x + 1) (x + 3) (x + 5) (x + 7) = -15, x (x + 4) (x + 5) (x + 9) + 96 = 0, x (x + 3 )(x + 5) (x + 8) + 56 = 0, (x - 4) (x - 3) (x - 2) (x - 1) = 24, (x - 3) (x -4)( x - 5) (x - 6) \u003d 1680, (x ² - 5x) (x + 3) (x - 8) + 108 \u003d 0, (x + 4) ² (x + 10) (x - 2 ) + 243 \u003d 0 (x ² + 3x + 2) (x ² + 9x + 20) \u003d 4, Indikácia: x + 3x + 2 \u003d (x + 1) (x + 2), x ² + 9x + 20 \u003d (x + 4) (х + 5) Odpovede: 1) -4 ±√6; - 6; - 2,6) - 1; 6; (5± √97)/2 7) -7; -1; -4±√3.
Návratové rovnice. Definícia č.1. Rovnica v tvare: ax⁴ + inx ³ + cx ² + in + a \u003d 0 sa nazýva recipročná rovnica štvrtého stupňa. Definícia č.2. Rovnica v tvare: ax⁴ + vx ³ + cx ² + kvx + k² a \u003d 0 sa nazýva zovšeobecnená recipročná rovnica štvrtého stupňa. k² a: a \u003d k²; kv: v \u003d k. Príklad č. 6. Vyriešte rovnicu x ⁴ - 7x³ + 14x² - 7x + 1 = 0. Vydeľte obe strany rovnice x². x ² - 7x + 14 - 7 / x + 1 / x ² \u003d 0, (x ² + 1 / x ²) - 7 (x + 1 / x) + 14 \u003d 0. Nech x + 1 / x \ u003d r. Odmocnime obe strany rovnice. x ² + 2 + 1/ x ² = y², x ² + 1/ x ² = y² - 2. Dostaneme kvadratickú rovnicu y² - 7y + 12 = 0, y₁ = 3, y₂ = 4. x + 1/ x = 3 alebo x + 1 / x = 4. Dostaneme dve rovnice: x ² - 3x + 1 = 0, x ² - 4x + 1 = 0. Príklad č. 7. 3x⁴ - 2x³ - 31x² + 10x + 75 = 0. 75:3 = 25, 10: (- 2) = -5, (-5)² = 25. Podmienka zovšeobecnenej návratovej rovnice je splnená k = -5. Je riešený podobne ako v príklade č.6. Vydeľte obe strany rovnice x². 3x⁴ - 2x - 31 + 10 / x + 75 / x ² \u003d 0, 3 (x ⁴ + 25 / x ²) - 2 (x - 5 / x) - 31 \u003d 0. Nech x - 5 / x \ u003d y, odmocnime obe strany rovnosti x ² - 10 + 25 / x ² = y², x ² + 25 / x ² = y² + 10. Máme kvadratickú rovnicu 3y² - 2y - 1 = 0, y₁ = 1 y2 = -1/3. x - 5 / x \u003d 1 alebo x - 5 / x \u003d -1/3. Dostaneme dve rovnice: x ² - x - 5 = 0 a 3x² + x - 15 = 0
Príklady nezávislého rozhodovania. 1. 78x⁴ - 133x³ + 78x² - 133x + 78 = 0, 2. x ⁴ - 5x3 + 10x² - 10x + 4 = 0, 3. x ⁴ - x ³ - 10x² + 0, 5 x 6.³ = 2x + 4.³ - 38x² -10x + 24 \u003d 0,5.x ⁴ + 2x³ - 11x² + 4x + 4 \u003d 0,6.x ⁴ - 5x³ + 10x² -10x + 4 \u003d 1) 0. Odpovede: 3; 3/2, 2) 1;2 3) -1 ±√3; (3±√17)/2, 4) -1±√3; (7±√337)/125) 1; 2; (-5± √17)/2, 6) 1; 2.
Homogénne rovnice. Definícia. Rovnica v tvare a₀ u3 + a₁ u² v + a₂ uv² + a₃ v3 = 0 sa nazýva homogénna rovnica tretieho stupňa vzhľadom na u v. Definícia. Rovnica v tvare a₀ u⁴ + a₁ u3v + a₂ u²v² + a₃ uv3 + a₄ v4 = 0 sa nazýva homogénna rovnica štvrtého stupňa vzhľadom na u v. Príklad číslo 8. Vyriešte rovnicu (x ² - x + 1)³ + 2x⁴ (x ² - x + 1) - 3x⁶ \u003d 0 Homogénna rovnica tretieho stupňa vzhľadom na u \u003d x ² - x + 1, v \u003d x ². Obe strany rovnice vydelíme x ⁶. Najprv sme skontrolovali, že x = 0 nie je koreň rovnice. (x ² - x + 1 / x ²)³ + 2 (x ² - x + 1 / x ²) - 3 \u003d 0. (x ² - x + 1) / x ²) \u003d y, y³ + 2r - 3 = 0, y = 1 je koreň rovnice. Polynóm P (x) \u003d y³ + 2y - 3 delíme y - 1 podľa Hornerovej schémy. Najmä dostaneme trojčlenku, ktorá nemá korene. odpoveď: 1.
Príklady nezávislého rozhodovania. 1. 2(x² + 6x + 1)² + 5(X² + 6X + 1)(X² + 1) + 2(X² + 1)² = 0. 2. (X + 5)⁴ - 13X²(X + 5 + 2)² + 2(x - 2)⁴ = 0,5 (x² + x + 4)² + 3x (x² + x + 4) + 2x² = 0, Odpovede: 1) -1; -2±√3, 2) -5/3; -5/4; 5/2; 53)-1; -1/2; 2;4 4) ±√2; 3±√2, 5) Neexistujú žiadne korene.
Metóda neurčitých koeficientov. Veta číslo 3. Dva polynómy P(x) a G(x) sú zhodné práve vtedy, ak majú rovnaký stupeň a koeficienty pri rovnakých mocniciach premennej v oboch polynómoch sú rovnaké. Príklad #9. Faktor polynómu y4 - 4y³ + 5y² - 4y + 1. y4 - 4y³ + 5y² - 4y + 1 = (y² + wu + c)(y² + v₁y + c₁) = y 4 + y3 (v₁) + c s₁ + s + v₁v) + y(s₁ + s₁) + ss₁. Podľa vety č.3 máme sústavu rovníc: в₁ + в = -4, с₁ + с + в₁в = 5, slnko ₁ + св ₁ = -4, ss ₁ = 1. Je potrebné vyriešiť sústavu v celých číslach. Posledná rovnica v celých číslach môže mať riešenia: c = 1, c₁ =1; c = -1, c1 = -1. Nech с = с ₁ = 1, potom z prvej rovnice máme в₁ = -4 –в. Dosaďte v druhej rovnici systému in² + 4v + 3 = 0, in = -1, in₁ = -3 alebo in = -3, in₁ = -1. Tieto hodnoty zodpovedajú tretej rovnici systému. S c \u003d c ₁ \u003d -1 D
Príklad číslo 10. Vynásobte polynóm y³ - 5y + 2. y³ -5y + 2 \u003d (y + a) (y² + wu + c) \u003d y³ + (a + c) y² + (av + c) y + ac. Máme systém rovníc: a + b \u003d 0, av + c \u003d -5, ac \u003d 2. Možné celočíselné riešenia tretej rovnice: (2; 1), (1; 2), (-2 -1), (-1;-2). Nech a = -2, c = -1. Z prvej rovnice sústavy pri = 2, ktorá spĺňa druhú rovnicu. Nahradením týchto hodnôt do požadovanej rovnosti dostaneme odpoveď: (y - 2) (y² + 2y - 1). Druhý spôsob. Y³ - 5 rokov + 2 \u003d y³ -5 rokov + 10 - 8 \u003d (y³ - 8) - 5 (y - 2) \u003d (y - 2) (y2 + 2 roky -1).
Príklady nezávislého rozhodovania. Vynásobte polynómy: 1. y⁴ + 4y³ + 6y2 + 4y -8, 2. y⁴ - 4y3 + 7y2 - 6y + 2, 3. x ⁴ + 324, 4. y⁴ -8y3 + 24y15,5. Sol rovnica využívajúca metódu faktorizácie: a) x ⁴ -3x² + 2 = 0, b) x ⁵ + 5x³ -6x² = 0. Odpovede: 1) (y² + 2y -2) (y² + 2y + 4), 2) (y - 1)² (y² -2 roky + 2), 3) (x² -6x + 18) (x² + 6x + 18), 4) (y - 1) (y² - 3) (y² - 4 roky + 5), 5a) ± 1; ±√2, 5b) 0; 1.
Funkčne - grafická metóda na riešenie rovníc vyšších stupňov. Príklad číslo 11. Riešte rovnicu x ⁵ + 5x -42 = 0. Funkcia y \u003d x ⁵ je rastúca, funkcia y \u003d 42 - 5x klesajúca (k
Príklady nezávislého rozhodovania. 1. Pomocou vlastnosti monotónnosti funkcie dokážte, že rovnica má jeden koreň a nájdite tento koreň: a) x ³ \u003d 10 - x, b) x ⁵ + 3x³ - 11√2 - x. Odpovede: a) 2, b) √2. 2. Riešte rovnicu funkčno-grafickou metódou: a) x = ³ √x, b) l x l = ⁵ √x, c) 2 = 6 - x, d) (1/3) = x +4, d ) (x - 1)² \u003d log₂ x, e) log \u003d (x + ½)², g) 1 - √x \u003d ln x, h) √x - 2 \u003d 9 / x. Odpovede: a) 0; ±1, b) 0; 1, c) 2, d) -1, e) 1; 2, f) ½, g) 1, h) 9.
Vieta vzorce pre rovnice vyšších stupňov. Veta č. 5 (Vietova veta). Ak rovnica a x ⁿ + a x ⁿ + ... + a₁x + a₀ má n rôznych reálnych koreňov x ₁, x ₂, ..., x, potom vyhovujú rovnosti: Pre kvadratickú rovnicu ax² + in + c = o : x ₁ + x ₂ \u003d -in/a, x₁x ₂ \u003d c/a; Pre kubickú rovnicu a3x3 + a2x 2 + a1x + a0 = o: x 1 + x 2 + x 3 = -a2/a3; x1x2 + x1x33 + x2x33 = a1/a3; x₁x2x3 \u003d -a0/a3; ..., pre rovnicu n-tého stupňa: x ₁ + x ₂ + ... x \u003d - a / a, x₁x ₂ + x₁x ₃ + ... + x x \u003d a / a, ..., x₁x ₂ ... x \u003d (- 1 ) ⁿ a₀/a. Platí aj opačná veta.
Príklad č.13. Napíšte kubickú rovnicu, ktorej korene sú inverzné ku koreňom rovnice x ³ - 6x² + 12x - 18 = 0 a koeficient pri x ³ je 2. 1. Podľa Vietovej vety pre kubickú rovnicu máme: x ₁ + x ₂ + x ₃ = 6, x₁x ₂ + х₁х ₃ + х₂х ₃ = 12, х₁х₂х ₃ = 18. 2. Zostavte prevrátené hodnoty daných koreňov. 1/ x 1 + 1/ x 2 + 1/ x 3 = (x 2 x 3 + x 1 x 3 + x 1 x ₂)/ x 1 x 2 x 3 = 12/18 = 2/3. 1/ x₁ x ₂ + 1/ x₁ x 3 + 1/ x₂x ₃ = (x 3 + x 2 + x 1)/ x₁ x₂ x ₃ = 6/18 = 1/3, 1/ x₂1 x 1x = 1,8 Dostaneme rovnicu x ³ + 2/3x² + 1/3x - 1/18 = 0 2 Odpoveď: 2x³ + 4/3x² + 2/3x -1/9 = 0.
Príklady nezávislého rozhodovania. 1. Napíšte kubickú rovnicu, ktorej korene sú inverzné k druhej mocnine koreňov rovnice x ³ - 6x² + 11x - 6 = 0 a koeficient pri x ³ je 8. Odpoveď: 8x³ - 98/9x² + 28/9x -2/9 = 0. Neštandardné metódy riešenia rovníc vyšších stupňov. Príklad č.12. Vyriešte rovnicu x ⁴ -8x + 63 = 0. Rozložme ľavú stranu rovnice na faktor. Vyberte presné štvorce. X⁴ - 8x + 63 \u003d (x ⁴ + 16x² + 64) - (16x² + 8x + 1) \u003d (x ² + 8)² - (4x + 1)² \u003d (x ² + 4x + 9) ( x ² - 4x + 7) = 0. Oba diskriminanty sú záporné. Odpoveď: žiadne korene.
Príklad č.14. Vyriešte rovnicu 21x³ + x ² - 5x - 1 \u003d 0. Ak je voľný člen rovnice ± 1, rovnica sa prevedie na vyššie uvedenú rovnicu nahradením x \u003d 1 / y. 21 / y³ + 1 / y² - 5 / y - 1 \u003d 0 y³, y³ + 5y² -y - 21 \u003d 0. y \u003d -3 je koreň rovnice. (y + 3) (y² + 2y -7) \u003d 0, y \u003d -1 ± 2√2. x ₁ = -1/3, x ₂ = 1/ -1 + 2√2 = (2√2 + 1)/7, X₃ = 1/-1 -2√2 =(1-2√2)/7 . Príklad č. 15. Vyriešte rovnicu 4x³-10x² + 14x - 5 \u003d 0. Vynásobte obe strany rovnice číslom 2. 8x³ -20x² + 28x - 10 \u003d 0, (2x)³ - 5 (2x)² + 14 (2x) - 10 \u003d 0. Zavádzame novú premennú y \u003d 2x, dostaneme redukovanú rovnicu y³ - 5y² + 14y -10 \u003d 0, y \u003d 1 je koreň rovnice. (y - 1) (y² - 4 roky + 10) \u003d 0, D
Príklad č.16. Dokážte, že rovnica x ⁴ + x ³ + x - 2 = 0 má jeden kladný koreň. Nech f (x) \u003d x ⁴ + x ³ + x - 2, f '(x) \u003d 4x³ + 3x² + 1\u003e o pre x\u003e o. Funkcia f (x) sa zvyšuje pre x > o a hodnota f (o) \u003d -2. Je zrejmé, že rovnica má jeden kladný koreň p.t.d. Príklad č. 17. Vyriešte rovnicu 8x (2x² - 1) (8x⁴ - 8x² + 1) \u003d 1. I.F. Sharygin „Voliteľný kurz matematiky pre ročník 11“. M. Osvietenie 1991 str. 90. 1. d x l 1 2x² - 1 > 1 a 8x⁴ -8x² + 1 > 1 2. Urobme zmenu x \u003d útulnou, y € (0; n). Pre zostávajúce hodnoty y sa hodnoty x opakujú a rovnica nemá viac ako 7 koreňov. 2x² - 1 = 2 cos²y - 1 = cos2y, 8x4 - 8x² + 1 = 2 (2x² - 1)² - 1 = 2 cos²2y - 1 = cos4y. 3. Rovnica sa zmení na 8 coscos2ycos4y = 1. Vynásobte obe strany rovnice siny . 8 sinycosycos2ycos4y = siny . Ak použijeme vzorec dvojitého uhla 3-krát, dostaneme rovnicu sin8y \u003d siny, sin8y - siny \u003d 0
Koniec riešenia príkladu č.17. Aplikujeme vzorec pre rozdiel sínusov. 2 sin7y/2 cos9y/2 = 0 . Ak vezmeme do úvahy, že y € (0;n), y = 2ks/3, k = 1, 2, 3 alebo y = n /9 + 2ks/9, k = 0, 1, 2, 3. Ak sa vrátime k premennej x, dostaneme odpoveď: Cos2 p / 7, cos4 p / 7, cos6 p / 7, cos p / 9, ½, cos5 p / 9, cos7 p / 9. Príklady nezávislého rozhodovania. Nájdite všetky hodnoty a, pre ktoré má rovnica (x² + x)(x² + 5x + 6) = a práve tri korene. Odpoveď: 16.9. Smer: nakreslite ľavú stranu rovnice. Fmax = f(0) = 9/16. Priamka y \u003d 9/16 pretína graf funkcie v troch bodoch. Vyriešte rovnicu (x ² + 2x) ² - (x + 1) ² \u003d 55. Odpoveď: -4; 2. Vyriešte rovnicu (x + 3)⁴ + (x + 5)⁴ = 16. Odpoveď: -5; -3. Vyriešte rovnicu 2 (x ² + x + 1) ² -7 (x - 1) ² \u003d 13 (x ³ - 1). Odpoveď: -1; -1/2, 2;4 Nájdite počet reálnych koreňov rovnice x ³ - 12x + 10 = 0 na [-3; 3/2]. Pomôcka: nájdite derivát a preskúmajte monot.
Príklady na samostatné riešenie (pokračovanie). 6. Nájdite počet reálnych koreňov rovnice x ⁴ - 2x³ + 3/2 = 0. Odpoveď: 2 X₁² + x ₂² + x ₃². Odpoveď: 66. Smer: použite Vietovu vetu. 8. Dokážte, že pre a > o má ľubovoľná reálna rovnica x ³ + ax + b = o iba jeden reálny koreň. Pomôcka: Dokážte protirečením. Použite Vietovu vetu. 9. Vyriešte rovnicu 2 (x ² + 2) ² \u003d 9 (x ³ + 1). Odpoveď: ½; 1; (3 ± √13)/2. Smer: priveďte rovnicu do homogénnej podoby pomocou rovnosti X² + 2 = x + 1 + x ² - x + 1, x ³ + 1 = (x + 1) (x ² - x + 1). 10. Vyriešte sústavu rovníc x + y \u003d x ², 3y - x \u003d y². Odpoveď: (0;0), (2;2), (√2; 2 - √2), (- √2; 2 + √2). 11. Vyriešte systém: 4y² -3xy \u003d 2x -y, 5x² - 3y² \u003d 4x - 2y. Odpoveď: (o; o), (1; 1), (297/265; - 27/53).
Test. 1 možnosť. 1. Vyriešte rovnicu (x ² + x) - 8 (x ² + x) + 12 = 0. 2. Vyriešte rovnicu (x + 1) (x + 3) (x + 5) (x + 7) = - 15 3. Vyriešte rovnicu 12x²(x - 3) + 64(x - 3)² = x ⁴. 4. Vyriešte rovnicu x ⁴ - 4x³ + 5x² - 4x + 1 = 0 5. Vyriešte sústavu rovníc: x ² + 2y² - x + 2y = 6, 1,5x² + 3y² - x + 5y = 12.
Možnosť 2 1. (x ² - 4x) ² + 7 (x ² - 4x) + 12 \u003d 0. 2. x (x + 1) (x + 5) (x + 6) \u003d 24. 3. x 4 + 18 (x + 4)² = 11x² (x + 4). 4. x ⁴ - 5x³ + 6x² - 5x + 1 = 0. 5. x ² - 2xy + y² + 2x²y - 9 = 0, x - y - x²y + 3 = 0. 3 možnosť. 1. (x ² + 3x)² - 14 (x ² + 3x) + 40 \u003d 0 2. (x - 5) (x-3) (x + 3) (x + 1) \u003d - 35, 3 x4 + 8x²(x + 2) = 9(x + 2)². 4. x ⁴ - 7x³ + 14x² - 7x + 1 = 0. 5. x + y + x ² + y ² = 18, xy + x ² + y² = 19.
4 možnosť. (x ² - 2x) ² - 11 (x ² - 2x) + 24 \u003d o. (x-7)(x-4)(x-2)(x + 1) = -36. X4 + 3(x-6)2 = 4x2(6-x). X⁴ - 6x³ + 7x² - 6x + 1 = 0. X² + 3xy + y² = - 1, 2x² - 3xy - 3y² = - 4. Ďalšia úloha: Zvyšok delenia polynómu P (x) číslom (x - 1) je 4, zvyšok pri delení (x + 1) je 2 a pri delení (x - 2) je 8. Nájdite zvyšok, keď je P (x) delené (x ³ - 2x² - x + 2).
Odpovede a pokyny: možnosť č. 1 č. 2. č. 3. č. 4. č. 5. 1. - 3; ±2; 11;2;3. -5; -4; 1; 2. Homogénna rovnica: u \u003d x -3, v \u003d x² -2; -1; 3; 4.(2;1); (2/3; 4/3). Smer: 1 (-3) + 2 2 2. -6; -2; -4±√6. -3±2√3; - 4; - 2,1 ±√11; 4; - 2. Homogénna rovnica: u = x + 4, v = x² 1; 5;3±√13. (2;1); (0;3); (- tridsať). Smer: 2 2 + 1. 3. -6; 2; 4; 12-3; -2; 4; 12-6; -3; -1; 2. Homogénne u \u003d x + 2, v \u003d x² -6; ±3; 2 (2;3), (3;2), (-2 + √7; -2 - √7); (-2 - √7; -2 + √7). Poznámka: 2 -1. 4. (3±√5)/2 2±√3 2±√3; (3±√5)/2 (5 ±√21)/2 (1;-2), (-1;2). Smer: 1 4 + 2 .
Riešenie dodatočnej úlohy. Podľa Bezoutovej vety: P (1) \u003d 4, P (-1) \u003d 2, P (2) \u003d 8. P (x) \u003d G (x) (x ³ - 2x² - x + 2 ) + ax² + in + With. náhradník 1; - 1; 2. P (1) \u003d G (1) 0 + a + b + c \u003d 4, a + b + c \u003d 4. P (-1) \u003d a - b + c \u003d 2, P ( 2) = 4a² + 2b + c = 8. Vyriešením výslednej sústavy troch rovníc dostaneme: a = c = 1, c = 2. Odpoveď: x ² + x + 2.
Kritérium č. 1 – 2 body. 1 bod – jedna výpočtová chyba. Č. 2,3,4 - po 3 body. 1 bod - viedol ku kvadratickej rovnici. 2 body – jedna chyba vo výpočte. č.5. - 4 body. 1 bod - vyjadruje jednu premennú cez druhú. 2 body - získal jedno z riešení. 3 body – jedna chyba vo výpočte. Dodatočná úloha: 4 body. 1 bod - aplikovaná Bezoutova veta pre všetky štyri prípady. 2 body - zostavená sústava rovníc. 3 body – jedna chyba vo výpočte.
Vo všeobecnosti platí, že rovnica, ktorá má stupeň vyšší ako 4, sa nedá vyriešiť v radikáloch. Niekedy však stále môžeme nájsť korene polynómu vľavo v rovnici najvyššieho stupňa, ak ho predstavíme ako súčin polynómov v stupni najviac 4. Riešenie takýchto rovníc je založené na rozklade polynómu na faktory, preto vám odporúčame, aby ste si pred štúdiom tohto článku prečítali túto tému.
Najčastejšie sa treba zaoberať rovnicami vyšších stupňov s celočíselnými koeficientmi. V týchto prípadoch sa môžeme pokúsiť nájsť racionálne korene a potom vynásobiť polynóm, aby sme ho potom mohli previesť na rovnicu nižšieho stupňa, ktorú bude ľahké vyriešiť. V rámci tohto materiálu zvážime práve takéto príklady.
Rovnice vyššieho stupňa s celočíselnými koeficientmi
Všetky rovnice v tvare a n x n + a n - 1 x n - 1 + . . . + a 1 x + a 0 = 0 , môžeme zredukovať na rovnicu rovnakého stupňa vynásobením oboch strán a n n - 1 a zmenou premennej tvaru y = a n x:
a n x n + a n - 1 x n - 1 +. . . + a 1 x + a 0 = 0 a n n x n + a n - 1 a n n - 1 x n - 1 + ... + a 1 (a n) n - 1 x + a 0 (a n) n - 1 = 0 y = a n x ⇒ y n + b n - 1 r n - 1 + … + b 1 r + b 0 = 0
Výsledné koeficienty budú tiež celé čísla. Budeme teda musieť vyriešiť redukovanú rovnicu n-tého stupňa s celočíselnými koeficientmi, ktorá má tvar x n + a n x n - 1 + ... + a 1 x + a 0 = 0.
Vypočítame celočíselné korene rovnice. Ak má rovnica celé korene, musíte ich hľadať medzi deliteľmi voľného člena a 0. Poďme si ich zapísať a dosadiť do pôvodnej rovnosti jeden po druhom, pričom skontrolujeme výsledok. Keď sme získali identitu a našli jeden z koreňov rovnice, môžeme ju zapísať v tvare x - x 1 · P n - 1 (x) = 0 . Tu x 1 je koreň rovnice a P n - 1 (x) je podiel x n + a n x n - 1 + ... + a 1 x + a 0 delený x - x 1 .
Dosaďte zvyšných deliteľov v P n - 1 (x) = 0 , počnúc x 1 , pretože korene sa môžu opakovať. Po získaní identity sa koreň x 2 považuje za nájdený a rovnicu možno zapísať ako (x - x 1) (x - x 2) P n - 2 (x) \u003d 0. Tu P n - 2 (x ) bude podielom delenia P n - 1 (x) x - x 2 .
Pokračujeme v triedení deliteľov. Nájdite všetky korene celého čísla a označte ich počet ako m. Potom môže byť pôvodná rovnica reprezentovaná ako x - x 1 x - x 2 · … · x - x m · Pn - m (x) = 0 . Tu P n - m (x) je polynóm n - m -tého stupňa. Na výpočet je vhodné použiť Hornerovu schému.
Ak má naša pôvodná rovnica celočíselné koeficienty, nemôžeme skončiť pri zlomkových koreňoch.
V dôsledku toho sme dostali rovnicu P n - m (x) = 0, ktorej korene možno nájsť akýmkoľvek vhodným spôsobom. Môžu byť iracionálne alebo zložité.
Ukážme si na konkrétnom príklade, ako sa takáto schéma riešenia aplikuje.
Príklad 1
podmienka: nájdite riešenie rovnice x 4 + x 3 + 2 x 2 - x - 3 = 0 .
Riešenie
Začnime hľadaním celých koreňov.
Máme odchyt rovný mínus tri. Má deliteľov rovných 1, -1, 3 a -3. Dosadíme ich do pôvodnej rovnice a uvidíme, ktoré z nich vo výsledku dajú identity.
Pre x rovné jednej dostaneme 1 4 + 1 3 + 2 1 2 - 1 - 3 \u003d 0, čo znamená, že jedna bude koreňom tejto rovnice.
Teraz rozdeľme polynóm x 4 + x 3 + 2 x 2 - x - 3 (x - 1) do stĺpca:
Takže x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.
1 3 + 2 1 2 + 4 1 + 3 = 10 ≠ 0 (- 1) 3 + 2 (- 1) 2 + 4 - 1 + 3 = 0
Dostali sme identitu, čo znamená, že sme našli ďalší koreň rovnice, rovný - 1.
Polynóm x 3 + 2 x 2 + 4 x + 3 delíme (x + 1) v stĺpci:
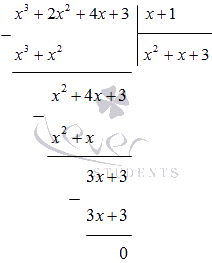
Chápeme to
x 4 + x 3 + 2 x 2 - x - 3 = (x - 1) (x 3 + 2 x 2 + 4 x + 3) = = (x - 1) (x + 1) (x 2 + x + 3)
Do rovnice x 2 + x + 3 = 0 dosadíme nasledujúceho deliteľa od -1:
1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0
Výsledné rovnosti budú nesprávne, čo znamená, že rovnica už nemá celočíselné korene.
Zvyšné korene budú koreňmi výrazu x 2 + x + 3 .
D \u003d 1 2 - 4 1 3 \u003d - 11< 0
Z toho vyplýva, že táto štvorcová trojčlenka nemá skutočné korene, ale existujú komplexne združené: x = - 1 2 ± i 11 2 .
Ujasnime si, že namiesto rozdelenia do stĺpca možno použiť Hornerovu schému. Urobíme to takto: po určení prvého koreňa rovnice vyplníme tabuľku.
V tabuľke koeficientov hneď vidíme koeficienty kvocientu z delenia polynómov, čo znamená x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.
Po nájdení ďalšieho koreňa rovného - 1 dostaneme nasledovné:
odpoveď: x \u003d - 1, x \u003d 1, x \u003d - 1 2 ± i 11 2.
Príklad 2
podmienka: vyriešte rovnicu x 4 - x 3 - 5 x 2 + 12 = 0.
Riešenie
Voľný člen má deliteľov 1 , - 1 , 2 , - 2 , 3 , - 3 , 4 , - 4 , 6 , - 6 , 12 , - 12 .
Skontrolujme ich v poradí:
1 4 - 1 3 - 5 1 2 + 12 = 7 ≠ 0 (- 1) 4 - (- 1) 3 - 5 (- 1) 2 + 12 = 9 ≠ 0 2 4 2 3 - 5 2 2 + 12 = 0
Takže x = 2 bude koreňom rovnice. Vydeľte x 4 - x 3 - 5 x 2 + 12 x - 2 pomocou Hornerovej schémy:
V dôsledku toho dostaneme x - 2 (x 3 + x 2 - 3 x - 6) = 0 .
2 3 + 2 2 - 3 2 - 6 = 0
Takže 2 bude opäť koreň. Vydeliť x 3 + x 2 - 3 x - 6 = 0 x - 2:
V dôsledku toho dostaneme (x - 2) 2 (x 2 + 3 x + 3) = 0 .
Kontrola zostávajúcich deliteľov nemá zmysel, pretože rovnosť x 2 + 3 x + 3 = 0 je rýchlejšie a pohodlnejšie riešiť pomocou diskriminantu.
Poďme vyriešiť kvadratickú rovnicu:
x 2 + 3 x + 3 = 0 D = 3 2 - 4 1 3 = - 3< 0
Dostaneme komplexne konjugovaný pár koreňov: x = - 3 2 ± i 3 2 .
Odpoveď x = -32 ± i32.
Príklad 3
podmienka: nájdite skutočné korene rovnice x 4 + 1 2 x 3 - 5 2 x - 3 = 0.
Riešenie
x 4 + 1 2 x 3 - 5 2 x - 3 = 0 2 x 4 + x 3 - 5 x - 6 = 0
Vykonáme násobenie 2 3 oboch častí rovnice:
2 x 4 + x 3 - 5 x - 6 = 0 2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0
Nahradíme premenné y = 2 x:
2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0 r 4 + r 3 - 20 r - 48 = 0
V dôsledku toho sme dostali štandardnú rovnicu 4. stupňa, ktorú je možné vyriešiť podľa štandardnej schémy. Pozrime sa na delitele, rozdelíme a nakoniec dostaneme, že má 2 skutočné korene y \u003d - 2, y \u003d 3 a dva komplexné. Nebudeme tu uvádzať celé riešenie. Na základe nahradenia budú skutočné korene tejto rovnice x = y 2 = - 2 2 = - 1 a x = y 2 = 3 2 .
odpoveď: x 1 \u003d - 1, x 2 \u003d 3 2
Ak si všimnete chybu v texte, zvýraznite ju a stlačte Ctrl+Enter
Text práce je umiestnený bez obrázkov a vzorcov.
Plná verzia práce je dostupná v záložke „Súbory úloh“ vo formáte PDF
Úvod
Riešenie algebraických rovníc vyšších stupňov s jednou neznámou je jedným z najťažších a najstarších matematických problémov. Týmito problémami sa zaoberali najvýznamnejší matematici staroveku.
Riešenie rovníc n-tého stupňa je dôležitou úlohou aj pre modernú matematiku. Záujem o ne je pomerne veľký, keďže tieto rovnice úzko súvisia s hľadaním koreňov rovníc, ktoré nie sú zohľadnené v školských osnovách matematiky.
problém: nedostatok zručností v riešení rovníc vyšších stupňov rôznymi spôsobmi u študentov im bráni úspešne sa pripraviť na záverečnú atestáciu z matematiky a matematických olympiád, školenia v špecializovanej matematickej triede.
Uvedené skutočnosti určili relevantnosť našej práce „Riešenie rovníc vyšších stupňov“.
Vlastníctvo najjednoduchších spôsobov riešenia rovníc n-tého stupňa skracuje čas na dokončenie úlohy, od ktorej závisí výsledok práce a kvalita procesu učenia.
Cieľ práce:štúdium známych metód riešenia rovníc vyšších stupňov a identifikácia najdostupnejších z nich pre praktickú aplikáciu.
Na základe tohto cieľa nasledujúce úlohy:
Študovať literatúru a internetové zdroje na túto tému;
Oboznámte sa s historickými faktami súvisiacimi s touto témou;
Opíšte rôzne spôsoby riešenia rovníc vyšších stupňov
porovnajte stupeň náročnosti každého z nich;
Oboznámiť spolužiakov s metódami riešenia rovníc vyšších stupňov;
Vytvorte súbor rovníc pre praktickú aplikáciu každej z uvažovaných metód.
Predmet štúdia- rovnice vyšších stupňov s jednou premennou.
Predmet štúdia- spôsoby riešenia rovníc vyšších stupňov.
hypotéza: neexistuje všeobecný spôsob a jediný algoritmus, ktorý umožňuje nájsť riešenia rovníc n-tého stupňa v konečnom počte krokov.
Výskumné metódy:
- bibliografická metóda (analýza literatúry k výskumnej téme);
- klasifikačná metóda;
- metóda kvalitatívnej analýzy.
Teoretický význam výskum spočíva v systematizácii metód riešenia rovníc vyšších stupňov a popise ich algoritmov.
Praktický význam- prezentoval materiál na túto tému a vývoj učebnej pomôcky pre žiakov na túto tému.
1. ROVNICE VYŠŠÍCH MOCNOSTÍ
1.1 Pojem rovnice n-tého stupňa
Definícia 1. Rovnica n-tého stupňa je rovnicou tvaru
a 0 xⁿ+a 1 X n -1 +a 2 xⁿ - ²+…+a n -1 x+a n = 0, kde koeficienty a 0, a 1, a 2…, a n -1, a n - akékoľvek reálne čísla a ,a 0 ≠ 0 .
Polynóm a 0 xⁿ+a 1 X n -1 +a 2 xⁿ - ²+…+a n -1 x+a n sa nazýva polynóm n-tého stupňa. Koeficienty sa rozlišujú podľa názvov: a 0 - senior koeficient; a n je voľný člen.
Definícia 2. Riešenia alebo korene pre danú rovnicu sú všetky hodnoty premennej X, ktoré premenia túto rovnicu na skutočnú číselnú rovnosť alebo, pre ktoré je polynóm a 0 xⁿ+a 1 X n -1 +a 2 xⁿ - ²+…+a n -1 x+a n ide na nulu. Takáto premenlivá hodnota X nazývaný aj koreň polynómu. Vyriešiť rovnicu znamená nájsť všetky jej korene alebo zistiť, že žiadne neexistujú.
Ak a 0 = 1, potom sa takáto rovnica nazýva redukovaná celočíselná racionálna rovnica n th stupňa.
Pre rovnice tretieho a štvrtého stupňa existujú vzorce Cardano a Ferrari, ktoré vyjadrujú korene týchto rovníc pomocou radikálov. Ukázalo sa, že v praxi sa používajú len zriedka. Ak teda n ≥ 3 a koeficienty polynómu sú ľubovoľné reálne čísla, potom nájdenie koreňov rovnice nie je ľahká úloha. V mnohých špeciálnych prípadoch je však tento problém vyriešený až do konca. Zastavme sa pri niektorých z nich.
1.2 Historické fakty riešenia rovníc vyšších stupňov
Už v staroveku si ľudia uvedomovali, aké dôležité je naučiť sa riešiť algebraické rovnice. Asi pred 4000 rokmi babylonskí vedci zvládli riešenie kvadratickej rovnice a vyriešili sústavy dvoch rovníc, z ktorých jedna bola druhého stupňa. Pomocou rovníc vyšších stupňov sa riešili rôzne problémy zememeračstva, architektúry a vojenských záležitostí, redukovali sa na ne mnohé a rôznorodé otázky praxe a prírodných vied, pretože presný jazyk matematiky umožňuje jednoducho vyjadriť fakty a vzťahy, ktoré sa v bežnom jazyku môžu zdať mätúce a zložité.
Univerzálny vzorec na hľadanie koreňov algebraickej rovnice n-týžiadny titul. Mnohí, samozrejme, prišli s lákavou myšlienkou nájsť vzorce pre ľubovoľnú mocninu n, ktoré by vyjadrovali korene rovnice z hľadiska jej koeficientov, teda riešili by rovnicu v radikáloch.
Až v 16. storočí sa talianskym matematikom podarilo pokročiť ďalej - nájsť vzorce pre n \u003d 3 a n \u003d 4. V tom istom čase sa Scipio, Dahl, Ferro a jeho študenti Fiori a Tartaglia zaoberali otázkou všeobecné riešenie rovníc 3. stupňa.
V roku 1545 vyšla kniha talianskeho matematika D. Cardana „Veľké umenie, alebo o pravidlách algebry“, kde sa popri iných otázkach algebry uvažuje o všeobecných metódach riešenia kubických rovníc, ako aj o metóde pre riešenie rovníc 4. stupňa, ktoré objavil jeho žiak L. Ferrari.
Kompletný výklad otázok súvisiacich s riešením rovníc 3. a 4. stupňa podal F. Viet.
V 20. rokoch 19. storočia nórsky matematik N. Abel dokázal, že korene rovníc piateho stupňa nemožno vyjadriť prostredníctvom radikálov.
Počas štúdie sa ukázalo, že moderná veda pozná mnoho spôsobov riešenia rovníc n-tého stupňa.
Výsledkom hľadania metód na riešenie rovníc vyšších stupňov, ktoré nie je možné vyriešiť metódami uvažovanými v školskom programe, sú metódy založené na aplikácii Vietovej vety (pre rovnice stup. n>2), Bezoutove vety, Hornerove schémy, ako aj Cardanov a Ferrariho vzorec na riešenie kubických a kvartických rovníc.
V príspevku sú prezentované metódy riešenia rovníc a ich typy, ktoré sa pre nás stali objavom. Patria sem - metóda neurčitých koeficientov, pridelenie plného stupňa, symetrické rovnice.
2. RIEŠENIE INTEGROVANÝCH ROVNICE VYŠŠÍCH MOCNOSTÍ S INTEGROVANÝMI KOEFICIENTMI
2.1 Riešenie rovníc 3. stupňa. Formula D. Cardano
Zvážte rovnice formulára X 3 +px+q=0. Všeobecnú rovnicu transformujeme do tvaru: X 3 +px 2 +qx+r=0. Zapíšme si vzorec súčtu kocky; Pridajme ho k pôvodnej rovnosti a nahraďme ho r. Dostaneme rovnicu: r 3 + (q-) (y-) + (r- =0. Po transformáciách máme: r 2 +py + q=0. Teraz znova napíšme vzorec súčtu kocky:
(a+b) 3 =a 3 + 3a 2 b+3ab 2 +b 3 = a 3 +b 3 + 3ab (a + b), nahradiť ( a+b)zapnuté X, dostaneme rovnicu X 3 - 3abx - (a 3 +b 3) = 0. Teraz je jasné, že pôvodná rovnica je ekvivalentná systému: a vyriešením systému dostaneme:
Získali sme vzorec na riešenie uvedenej rovnice 3. stupňa. Nesie meno talianskeho matematika Cardana.
Zvážte príklad. Vyriešte rovnicu: .
Máme R= 15 a q= 124, potom pomocou Cardanovho vzorca vypočítame koreň rovnice
Záver: tento vzorec je dobrý, ale nie je vhodný na riešenie všetkých kubických rovníc. Je však objemný. Preto sa v praxi používa zriedka.
Ale ten, kto ovláda tento vzorec, ho môže použiť pri riešení rovníc tretieho stupňa na skúške.
2.2 Vietova veta
Z kurzu matematiky poznáme túto vetu pre kvadratickú rovnicu, no málokto vie, že sa používa aj na riešenie rovníc vyšších stupňov.
Zvážte rovnicu:
faktorizujte ľavú stranu rovnice, vydeľte ≠ 0.
Pravú stranu rovnice transformujeme do tvaru
; Z toho vyplýva, že do systému môžeme zapísať nasledujúce rovnosti:
Vietou odvodené vzorce pre kvadratické rovnice a nami demonštrované pre rovnice 3. stupňa platia aj pre polynómy vyšších stupňov.
Poďme vyriešiť kubickú rovnicu:
Záver: táto metóda je univerzálna a pre študentov dostatočne jednoduchá na pochopenie, keďže Vietovu vetu poznajú zo školských osnov pre n = 2. Zároveň, aby sme našli korene rovníc pomocou tejto vety, je potrebné mať dobré výpočtové schopnosti.
2.3 Bezoutova veta
Táto veta je pomenovaná po francúzskom matematikovi z 18. storočia J. Bezoutovi.
Veta. Ak rovnica a 0 xⁿ+a 1 X n -1 +a 2 xⁿ - ²+…+a n -1 x+a n = 0, v ktorom sú všetky koeficienty celé čísla a voľný člen je iný ako nula, má celočíselný koreň, potom je tento koreň deliteľom voľného člena.
Vzhľadom na to, že polynóm n-tého stupňa je na ľavej strane rovnice, veta má inú interpretáciu.
Veta. Pri delení polynómu n-tého stupňa vzhľadom na X do dvojčlenky x-a zvyšok sa rovná hodnote dividendy, keď x = a. (list a môže označovať akékoľvek reálne alebo imaginárne číslo, t.j. akékoľvek komplexné číslo).
dôkaz: nech f(x) označuje ľubovoľný polynóm n-tého stupňa vzhľadom na premennú x a nech, keď je delený binomom ( x-a) sa stalo v súkromí q(x), a vo zvyšku R. To je zrejmé q(x) bude tam nejaký polynóm (n - 1) stupeň relatívne X a zvyšok R bude konštantná hodnota, t.j. nezávislý od X.
Ak zvyšok R bol polynóm prvého stupňa v x, potom by to znamenalo, že delenie nebolo vykonané. takže, R od X nezávisí. Definíciou delenia získame identitu: f(x)=(x-a)q(x)+R.
Rovnosť platí pre akúkoľvek hodnotu x, takže platí aj pre x=a, dostaneme: f(a)=(a-a)q(a)+R. Symbol f(a) označuje hodnotu polynómu f (X) pri x=a, q(a) označuje hodnotu q(x) pri x=a. Zvyšok R zostalo ako predtým R od X nezávisí. Práca ( x-a) q(a) = 0, pretože násobiteľ ( x-a) = 0, a multiplikátor q(a) existuje určitý počet. Preto z rovnosti dostaneme: f(a)=R, h.t.d.
Príklad 1 Nájdite zvyšok delenia polynómu X 3 - 3X 2 + 6X- 5 na dvojčlen
X- 2. Bezoutovou vetou R = f(2) = 23-322 + 62 -5 = 3. odpoveď: R= 3.
Všimnite si, že Bézoutova veta nie je taká dôležitá sama o sebe, ale kvôli svojim dôsledkom. (Príloha 1)
Zastavme sa pri úvahách o niektorých metódach aplikácie Bezoutovej vety pri riešení praktických problémov. Treba poznamenať, že pri riešení rovníc pomocou Bezoutovej vety je potrebné:
Nájdite všetkých celočíselných deliteľov voľného termínu;
Z týchto deliteľov nájdite aspoň jeden koreň rovnice;
Rozdeľte ľavú stranu rovnice o (Ha);
Napíšte súčin deliteľa a kvocientu na ľavú stranu rovnice;
Vyriešte výslednú rovnicu.
Zoberme si príklad riešenia rovnice x 3 + 4X 2 + x - 6 = 0 .
Riešenie: nájdite deliteľa voľného člena ±1 ; ± 2; ± 3; ± 6. Vypočítajte hodnoty pre x= 1, 1 3 + 41 2 + 1-6 = 0. Vydeľte ľavú stranu rovnice ( X- 1). Delenie vykonávame „rohom“, dostaneme:
Záver: Bezoutova veta, jeden zo spôsobov, ktorým sa venujeme v našej práci, sa študuje v programe mimoškolských aktivít. Je to ťažké pochopiť, pretože na to, aby ste si to osvojili, musíte z toho poznať všetky dôsledky, no zároveň je Bezoutova veta jedným z hlavných pomocníkov študentov na skúške.
2.4 Hornerova schéma
Rozdeliť polynóm binomom x-α môžete použiť špeciálny jednoduchý trik vynájdený anglickými matematikmi 17. storočia, neskôr nazývaný Hornerova schéma. Hornerova schéma okrem hľadania koreňov rovníc uľahčuje výpočet ich hodnôt. Na to je potrebné dosadiť hodnotu premennej do polynómu Pn (x) = a 0 xn+a 1 X n-1 +a 2 xⁿ - ²+…++ a n -1 x+a n. (1)
Zvážte delenie polynómu (1) binómom X-α.
Vyjadríme koeficienty neúplného kvocientu b 0 xⁿ - ¹+ b 1 xⁿ - ²+ b 2 xⁿ - ³+…+ mld -1 a zvyšok r z hľadiska koeficientov polynómu Pn( X) a číslo α. b 0 =a 0 , b 1 = α b 0 +a 1 , b 2 = α b 1 +a 2 …, mld -1 =
= α mld -2 +a n -1 = α mld -1 +a n .
Výpočty podľa Hornerovej schémy sú uvedené vo forme nasledujúcej tabuľky:
|
A 0 |
a 1 |
a 2 , |
|||
|
b 0 =a 0 |
b 1 = α b 0 +a 1 |
b 2 = α b 1 +a 2 |
r = a b n-1 +a n |
Pretože r=Pn(α), potom α je koreň rovnice. Aby sme skontrolovali, či α je viacnásobný odmocninec, Hornerovu schému možno aplikovať už na kvocient b 0 x+ b 1 x+…+ mld -1 podľa tabuľky. Ak je v stĺpci pod mld -1 opäť dostaneme 0, takže α je násobný koreň.
Zvážte príklad: vyriešte rovnicu X 3 + 4X 2 + x - 6 = 0.
Aplikujme na ľavú stranu rovnice rozklad polynómu na ľavej strane rovnice, Hornerovu schému.
Riešenie: nájdite deliteľa voľného termínu ± 1; ±2; ± 3; ± 6.
|
6 ∙ 1 + (-6) = 0 |
Koeficienty kvocientu sú čísla 1, 5, 6 a zvyšok je r = 0.
znamená, X 3 + 4X 2 + X - 6 = (X - 1) (X 2 + 5X + 6) = 0.
Odtiaľ: X- 1 = 0 alebo X 2 + 5X + 6 = 0.
X = 1, X 1 = -2; X 2 = -3. odpoveď: 1,- 2, - 3.
Záver: na jednej rovnici sme teda ukázali použitie dvoch rôznych spôsobov faktorizácie polynómov. Podľa nášho názoru je Hornerova schéma najpraktickejšia a najhospodárnejšia.
2.5 Riešenie rovníc 4. stupňa. Ferrari metóda
Cardanov študent Ludovic Ferrari objavil spôsob, ako vyriešiť rovnicu 4. stupňa. Ferrari metóda pozostáva z dvoch krokov.
I. etapa: rovnica tvaru je reprezentovaná ako súčin dvoch štvorcových trojčlenov, vyplýva to z toho, že rovnica je 3. stupňa a má aspoň jedno riešenie.
Etapa II: výsledné rovnice sa riešia pomocou faktorizácie, avšak na nájdenie požadovanej faktorizácie je potrebné vyriešiť kubické rovnice.
Cieľom je reprezentovať rovnice ako A 2 = B 2 , kde A = X 2+s,
B-lineárna funkcia X. Potom zostáva vyriešiť rovnice A = ±B.
Pre názornosť zvážte rovnicu: Oddelíme 4. stupeň, dostaneme: Pre ľubovoľné d výraz bude dokonalý štvorec. Pridajte k obom stranám rovnice, ktorú dostaneme
Na ľavej strane je plný štvorec, môžete si vybrať d takže pravá strana (2) sa stane dokonalým štvorcom. Predstavte si, že sme to dosiahli. Potom naša rovnica vyzerá takto:
Nájsť koreň neskôr nebude ťažké. Ak chcete vybrať správne d je potrebné, aby diskriminant pravej strany (3) zanikol, t.j.
Takže nájsť d, je potrebné vyriešiť túto rovnicu 3. stupňa. Táto pomocná rovnica sa nazýva solventný.
Môžeme ľahko nájsť odmocninu celého čísla rozpúšťadla: d= 1
Dosadením rovnice do (1) dostaneme
Záver: Ferrari metóda je univerzálna, no komplikovaná a ťažkopádna. Zároveň, ak je algoritmus riešenia jasný, možno touto metódou riešiť rovnice 4. stupňa.
2.6 Metóda neurčených koeficientov
Úspešnosť riešenia rovnice 4. stupňa Ferrari metódou závisí od toho, či riešime resolvent – rovnicu 3. stupňa, čo, ako vieme, nie je vždy možné.
Podstata metódy neurčitých koeficientov spočíva v tom, že typ faktorov, na ktoré sa daný polynóm rozloží, sa uhádne a koeficienty týchto faktorov (aj polynómy) sa určia vynásobením faktorov a prirovnaním koeficientov pri rovnakých mocninách mocniny. premenlivý.
Príklad: vyriešte rovnicu:
Predpokladajme, že ľavú stranu našej rovnice možno rozložiť na dva štvorcové trinómy s celočíselnými koeficientmi tak, že identická rovnosť
Je zrejmé, že koeficienty pred nimi sa musia rovnať 1 a voľné členy sa musia rovnať jednej + 1, druhý má 1.
Koeficienty, ktorým čelí X. Označme ich podľa A a na ich určenie vynásobíme obe trojčlenky na pravej strane rovnice.
V dôsledku toho dostaneme:
Vyrovnanie koeficientov pri rovnakých mocninách X na ľavej a pravej strane rovnosti (1) získame systém na hľadanie a
Vyriešenie tohto systému budeme mať
Takže naša rovnica je ekvivalentná rovnici
Keď to vyriešime, dostaneme tieto korene: .
Metóda neurčitých koeficientov je založená na týchto tvrdeniach: ľubovoľný polynóm štvrtého stupňa v rovnici možno rozložiť na súčin dvoch polynómov druhého stupňa; dva polynómy sú zhodné práve vtedy a len vtedy, ak sú ich koeficienty rovnaké pri rovnakých mocninách X.
2.7 Symetrické rovnice
Definícia. Rovnica tvaru sa nazýva symetrická, ak sa prvé koeficienty vľavo rovnajú prvým koeficientom vpravo.
Vidíme, že prvé koeficienty vľavo sa rovnajú prvým koeficientom vpravo.
Ak má takáto rovnica nepárny stupeň, potom má koreň X= - 1. Ďalej môžeme znížiť stupeň rovnice vydelením ( x+ 1). Ukazuje sa, že pri delení symetrickej rovnice ( x+ 1) získa sa symetrická rovnica párneho stupňa. Dôkaz symetrie koeficientov je uvedený nižšie. (Príloha 6) Našou úlohou je naučiť sa riešiť symetrické rovnice párneho stupňa.
Napríklad: (1)
Riešime rovnicu (1), delíme X 2 (do stredného stupňa) = 0.
Pojmy zoskupujeme so symetrickými
) + 3(X+ . Označiť pri= X+ , odmocnime obe časti, teda = pri 2 Takže 2( pri 2 alebo 2 pri 2 + 3 vyriešením rovnice dostaneme pri = , pri= 3. Ďalej sa vrátime k náhrade X+ = a X+ = 3. Dostaneme rovnice a Prvá nemá riešenie a druhá má dva korene. Odpoveď:
Záver: tento typ rovnice sa často nestretáva, ale ak sa s ním stretnete, dá sa ľahko a jednoducho vyriešiť bez toho, aby ste sa uchýlili k ťažkopádnym výpočtom.
2.8 Extrakcia plného stupňa
Zvážte rovnicu.
Ľavá strana je kocka súčtu (x + 1), t.j.
Z oboch častí vytiahneme koreň tretieho stupňa: , potom dostaneme
Kde je jediný koreň.
VÝSLEDKY ŠTÚDIE
V dôsledku práce sme dospeli k týmto záverom:
Vďaka preštudovanej teórii sme sa zoznámili s rôznymi metódami riešenia celých rovníc vyšších stupňov;
Vzorec D. Cardana sa ťažko používa a dáva vysokú pravdepodobnosť chýb vo výpočte;
− metóda L. Ferrariho umožňuje zredukovať riešenie rovnice štvrtého stupňa na kubické;
− Bezoutovu vetu je možné použiť ako pre kubické rovnice, tak aj pre rovnice štvrtého stupňa; je zrozumiteľnejšia a názornejšia pri riešení rovníc;
Hornerova schéma pomáha výrazne znížiť a zjednodušiť výpočty pri riešení rovníc. Hornerova schéma okrem nájdenia koreňov uľahčuje výpočet hodnôt polynómov na ľavej strane rovnice;
Zvlášť zaujímavé bolo riešenie rovníc metódou neurčitých koeficientov, riešenie symetrických rovníc.
V priebehu výskumnej práce sa zistilo, že študenti sa s najjednoduchšími metódami riešenia rovníc najvyššieho stupňa oboznamujú vo výberových triedach matematiky, počnúc 9. alebo 10. ročníkom, ako aj v špeciálnych kurzoch putovnej matematiky. školy. Táto skutočnosť bola zistená ako výsledok prieskumu medzi učiteľmi matematiky na MBOU "SŠ č. 9" a žiakmi, ktorí prejavujú zvýšený záujem o predmet "matematika".
Najpopulárnejšími metódami riešenia rovníc vyšších stupňov, s ktorými sa stretávame pri riešení olympijských, súťažných úloh a v dôsledku prípravy na skúšky študentov, sú metódy založené na aplikácii Bezoutovej vety, Hornerovej schémy a zavedení novej premennej. .
Ukážka výsledkov výskumnej práce, t.j. spôsoby riešenia rovníc, ktoré sa neštudujú v školských osnovách z matematiky, zaujímajú spolužiaci.
Záver
Po preštudovaní vzdelávacej a vedeckej literatúry, internetových zdrojov na vzdelávacích fórach mládeže