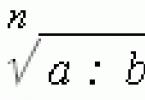
Dano je 8 primjera faktorizacije polinoma. Oni uključuju primjere rješavanja kvadratnih i bikvadratnih jednadžbi, primjere rekurzivnih polinoma i primjere pronalaženja cjelobrojnih korijena polinoma trećeg i četvrtog stupnja.
Sadržaj
Vidi također: Metode rastavljanja polinoma na faktore
Korijeni kvadratne jednadžbe
Rješenje kubnih jednadžbi
1. Primjeri s rješenjem kvadratne jednadžbe
Primjer 1.1
x 4 + x 3 - 6 x 2.
Izvadite x 2
za zagrade:
.
2 + x - 6 = 0:
.
Korijeni jednadžbe:
, .
.
Primjer 1.2
Rastavljanje polinoma trećeg stupnja na faktore:
x 3 + 6 x 2 + 9 x.
Izvadimo x iz zagrada:
.
Rješavamo kvadratnu jednadžbu x 2 + 6 x + 9 = 0:
Njegova diskriminanta je .
Budući da diskriminant nula, tada su korijeni jednadžbe višestruki: ;
.
Odavde dobivamo rastavljanje polinoma na faktore:
.
Primjer 1.3
Rastavljanje polinoma petog stupnja na faktore:
x 5 - 2 x 4 + 10 x 3.
Izvadite x 3
za zagrade:
.
Rješavamo kvadratnu jednadžbu x 2 - 2 x + 10 = 0.
Njegova diskriminanta je .
Budući da je diskriminant manji od nule, korijeni jednadžbe su složeni: ;
, .
Faktorizacija polinoma ima oblik:
.
Ako nas zanima faktoring s realnim koeficijentima, tada:
.
Primjeri rastavljanja polinoma na faktore pomoću formula
Primjeri s bikvadratnim polinomima
Primjer 2.1
Faktoriziraj bikvadratni polinom:
x 4 + x 2 - 20.
Primijenite formule:
a 2 + 2 ab + b 2 = (a + b) 2;
a 2 - b 2 = (a - b)(a + b).
;
.
Primjer 2.2
Rastavljanje polinoma na faktore koji se svodi na bikvadrat:
x 8 + x 4 + 1.
Primijenite formule:
a 2 + 2 ab + b 2 = (a + b) 2;
a 2 - b 2 = (a - b)(a + b):
;
;
.
Primjer 2.3 s rekurzivnim polinomom
Faktorisanje rekurzivnog polinoma:
.
Rekurzivni polinom ima neparan stupanj. Stoga ima korijen x = - 1
. Podijelimo polinom s x - (-1) = x + 1. Kao rezultat toga dobivamo:
.
Vršimo zamjenu:
, ;
;
;
.
Primjeri rastavljanja polinoma na faktore s cijelim korijenima
Primjer 3.1
Rastavljanje polinoma na faktore:
.
Pretpostavimo jednadžbu
6
-6, -3, -2, -1, 1, 2, 3, 6
.
(-6) 3 - 6 (-6) 2 + 11 (-6) - 6 = -504;
(-3) 3 - 6 (-3) 2 + 11 (-3) - 6 = -120;
(-2) 3 - 6 (-2) 2 + 11 (-2) - 6 = -60;
(-1) 3 - 6 (-1) 2 + 11 (-1) - 6 = -24;
1 3 - 6 1 2 + 11 1 - 6 = 0;
2 3 - 6 2 2 + 11 2 - 6 = 0;
3 3 - 6 3 2 + 11 3 - 6 = 0;
6 3 - 6 6 2 + 11 6 - 6 = 60.
Dakle, pronašli smo tri korijena:
x 1 = 1
, x 2 = 2
, x 3 = 3
.
Budući da je izvorni polinom trećeg stupnja, on nema više od tri korijena. Budući da smo pronašli tri korijena, oni su jednostavni. Zatim
.
Primjer 3.2
Rastavljanje polinoma na faktore:
.
Pretpostavimo jednadžbu
ima barem jedan cijeli korijen. Tada je to djelitelj broja 2
(član bez x ). Odnosno, cijeli korijen može biti jedan od brojeva:
-2, -1, 1, 2
.
Zamijenite ove vrijednosti jednu po jednu:
(-2) 4 + 2 (-2) 3 + 3 (-2) 3 + 4 (-2) + 2 = 6
;
(-1) 4 + 2 (-1) 3 + 3 (-1) 3 + 4 (-1) + 2 = 0
;
1 4 + 2 1 3 + 3 1 3 + 4 1 + 2 = 12;
2 4 + 2 2 3 + 3 2 3 + 4 2 + 2 = 54.
Dakle, pronašli smo jedan korijen:
x 1 = -1
.
Polinom podijelimo s x - x 1 = x - (-1) = x + 1:

Zatim,
.
Sada moramo riješiti jednadžbu trećeg stupnja:
.
Ako pretpostavimo da ova jednadžba ima korijen cijelog broja, onda je ona djelitelj broja 2
(član bez x ). Odnosno, cijeli korijen može biti jedan od brojeva:
1, 2, -1, -2
.
Zamjena x = -1
:
.
Dakle, pronašli smo drugi korijen x 2
= -1
. Bilo bi moguće, kao i u prethodnom slučaju, polinom podijeliti s , ali ćemo članove grupirati:
.
Kvadratni trinom može se rastaviti na sljedeće faktore:
A x 2 + b x + c = a ⋅ (x − x 1) ⋅ (x − x 2)
gdje je a broj, koeficijent ispred najvećeg koeficijenta,
x je varijabla (odnosno slovo),
x 1 i x 2 - brojevi, korijeni kvadratna jednadžba a x 2 + b x + c = 0 , koje se nalaze preko diskriminante.
Ako kvadratna jednadžba ima samo jedan korijen, tada dekompozicija izgleda ovako:
a x 2 + b x + c = a ⋅ (x − x 0) 2
Primjeri faktoriranja kvadratnog trinoma:
- − x 2 + 6 x + 7 = 0 ⇒ x 1 = − 1, x 2 = 7
− x 2 + 6 x + 7 = (− 1) ⋅ (x − (− 1)) (x − 7) = − (x + 1) (x − 7) = (x + 1) (7 − x)
- − x 2 + 4 x − 4 = 0; ⇒ x0 = 2
− x 2 + 4 x − 4 = (− 1) ⋅ (x − 2) 2 = − (x − 2) 2
Ako je kvadratni trinom nepotpun (b = 0 ili c = 0), tada se može rastaviti na sljedeće načine:
- c = 0 ⇒ a x 2 + b x = x (a x + b)
- b = 0 ⇒ primijenite formulu reduciranog množenja za razliku kvadrata.
Zadaci za samostalno rješavanje
broj 1. Kvadratni trinom je rastavljen na faktore: x 2 + 6 x - 27 = (x + 9) (x - a) . Pronađi .
Riješenje:
Prvo trebate izjednačiti kvadratni trinom s nulom da biste pronašli x 1 i x 2.
x 2 + 6 x − 27 = 0
a = 1, b = 6, c = − 27
D = b 2 − 4 a c = 6 2 − 4 ⋅ 1 ⋅ (− 27) = 36 + 108 = 144
D > 0 znači da će postojati dva različita korijena.
x 1,2 = − b ± D 2 a = − 6 ± 144 2 ⋅ 1 = [ − 6 + 12 2 = 6 2 = 3 − 6 − 12 2 = − 18 2 = − 9
Znajući korijene, faktoriziramo kvadratni trinom:
x 2 + 6 x − 27 = (x − (− 9)) (x − 3) = (x + 9) (x − 3)
broj 2. Jednadžba x 2 + p x + q \u003d 0 ima korijene - 5; 7. Pronađite q.
Riješenje:
1 način:(morate znati kako se kvadratni trinom rastavlja na faktore)
Ako su x 1 i x 2 korijeni kvadratnog trinoma a x 2 + b x + c, tada se on može rastaviti na sljedeće faktore: a x 2 + b x + c = a ⋅ (x − x 1) ⋅ (x − x 2) .
Budući da je u danom kvadratnom trinomu vodeći koeficijent (faktor ispred x 2) jednak jedan, dekompozicija će biti sljedeća:
x 2 + p x + q = (x − x 1) (x − x 2) = (x − (− 5)) (x − 7) = (x + 5) (x − 7) = x 2 − 7 x + 5 x - 35 = x 2 - 2 x - 35
x 2 + p x + q = x 2 − 2 x − 35 ⇒ p = − 2, q = − 35
2 načina: (morate znati Vieta teorem)
Vietin teorem:
Zbroj korijena reduciranog kvadratnog trinoma x 2 + p x + q jednak je njegovom drugom koeficijentu p sa suprotnim predznakom, a umnožak je jednak slobodnom članu q.
( x 1 + x 2 = − p x 1 ⋅ x 2 = q
q = x 1 ⋅ x 2 = (− 5) ⋅ 7 = − 35.
Prije svega, istaknimo neke često korištene nazive. Razmotrimo polinome koji sadrže samo jedno slovo, na primjer slovo x. Tada je najjednostavniji polinom u kojem postoje dva člana, od kojih jedan sadrži slovo x na prvom stupnju, a drugi uopće nema slova x, npr. 3x - 5 ili 15 - 7x ili 8z. + 7 (ovdje je umjesto slova x uzeto slovo z) itd. Takvi se polinomi nazivaju linearni binomi .
3x² - 5x + 7 ili x² + 2x - 1
ili 5y² + 7y + 8 ili z² - 5z - 2 itd.
Takvi se polinomi nazivaju kvadratni trinomi.
Zatim možemo sastaviti kubnu četvorku, na primjer:
x³ + 2x² - x + 1 ili 3x³ - 5x² - 2x - 3 itd.,
polinom četvrtog stupnja, na primjer:
x 4 - 2x³ - 3x² + 4x - 5 itd.
Koeficijente na x, na x², na x³ itd. moguće je označiti i slovima, na primjer slovima a, b, c itd. Tada dobivamo:
1) opći oblik binom linearan u x ax + b,
2) opći oblik kvadratnog trinoma (u odnosu na x): ax² + bx + c,
3) opći oblik kubnog trinoma (u odnosu na x): ax³ + bx² + cx + d, itd.
Zamjenom slova a, b, c, d ... u ovim formulama različitim brojevima, dobivamo sve vrste linearnih binoma, kvadratnih trinoma itd. Na primjer, u formuli ax² + bx + c, koja izražava opći oblik kvadratnog trinoma, slovo a zamijenimo brojem + 3, slovo b brojem -2 i slovo c brojem -1, dobijemo kvadratni trinom 3x² - 2x - 1. U konkretnom slučaju, također je moguće dobiti binom, zamjenjujući jedno od slova nulom, na primjer, ako je a = +1, b = 0 i c \u003d -3, tada dobivamo kvadratni binom x² - 3.
Može se naučiti faktorizirati neke kvadratne trinome prilično brzo na linearne faktore. Međutim, ograničili smo se na razmatranje samo takvih kvadratnih trinoma koji zadovoljavaju sljedeće uvjete:
1) koeficijent na najvišem članu (na x²) je +1,
2) možete pronaći dva cijela broja (sa predznacima ili dva relativna cijela broja) tako da je njihov zbroj jednak koeficijentu x na prvu potenciju, a njihov umnožak jednak članu bez x (gdje nema slova x na svi).
Primjeri. 1. x² + 5x + 6; lako je u umu pronaći dva broja (sa predznacima) tako da je njihov zbroj jednak +5 (koeficijent pri x) i tako da je njihov umnožak = +6 (član bez x), - ti brojevi su: + 2 i +3 [u stvari, +2 + 3 = +5 i (+2) ∙ (+3) = +6]. Koristeći ova dva broja, zamjenjujemo +5x član sa dva člana, naime: +2x + 3x (naravno, +2x + 3x = +5x); onda će naš tehnički izraz biti umjetno pretvoren u kvadrion x² + 2x + 3x + 6. Primijenimo sada tehniku grupiranja na njega, stavljajući prva dva člana u jednu grupu, a posljednja dva u drugu:
x² + 5x + 6 = x² + 2x + 3x + 6 = x (x + 2) + 3 (x + 2) = (x + 2) (x + 3).
U prvoj skupini smo stavili x u zagrade, a u drugoj +3, dobili smo dva člana za koje se pokazalo da imaju zajednički faktor (x + 2), koji je također stavljen u zagrade, a naš trinom x² + 5x + 6 rastavljen na 2 linearna faktori: x + 2 i x + 3.
2. x² - x - 12. Ovdje treba pronaći dva broja (relativna) tako da njihov zbroj bude -1 i da njihov umnožak bude -12. Takvi brojevi su: -4 i +3.
Provjerite: -4 + 3 = -1; (-4) (+3) = -12. Koristeći ove brojeve, zamjenjujemo -x član s dva člana: -x \u003d -4x + 3x, - dobivamo:
x² - x - 12 \u003d x² - 4x + 3x - 12 \u003d x (x - 4) + 3 (x - 4) \u003d (x - 4) (x + 3).
3. x² - 7x + 6; ovdje su traženi brojevi: -6 i -1. [Provjeri: -6 + (-1) = -7; (–6) (–1) = +6].
x² - 7x + 6 = x² - 6x - x + 6 = x (x - 6) - (x - 6) = (x - 6) (x - 1).
Ovdje su članovi druge skupine -x + 6 morali biti zatvoreni u zagrade, sa znakom minus ispred njih.
4. x² + 8x - 48. Ovdje treba pronaći dva broja tako da njihov zbroj bude +8, a umnožak -48. Kako umnožak mora imati predznak minus, tada željeni brojevi moraju biti s različitim predznacima, budući da zbroj naših brojeva ima predznak +, tada apsolutna vrijednost pozitivnog broja mora biti veća. odvijanje aritmetički broj 48 s dva faktora (a to se može učiniti na različite načine), dobivamo: : 48 = 4 ∙ 12. Tada su naši brojevi: +12 i -4. Ono što slijedi je jednostavno:
x² + 8x - 48 = x² + 12x - 4x - 48 = x (x + 12) - 4 (x + 12) = (x + 12) (x - 4).
5. x² + 7x - 12. Ovdje treba pronaći 2 broja tako da njihov zbroj bude +7, a umnožak = -12; 12 = 1 ∙ 12 = 2 ∙ 6 = 3 ∙ 4. Naizgled, 3 i 4 bi bili prikladni brojevi, ali moraju biti uzeti s različitim predznacima tako da njihov umnožak bude jednak -12, a onda njihov zbroj nikako nije može biti +7 [–3 + (+4) = +1, +3 + (–4) = –1]. Druge faktorizacije također ne daju tražene brojeve; stoga dolazimo do zaključka da te kvadratne trinome još nismo u mogućnosti faktorizirati na linearne faktore, budući da naša metoda nije primjenjiva na to (ne zadovoljava drugi od uvjeta koji su postavljeni na početku).
On ima kvadrat, a sastoji se od tri člana (). Tako ispada - kvadratni trinom.
Primjeri ne kvadratni trinomi:
\(x^3-3x^2-5x+6\) - kubni kvaternar
\(2x+1\) - linearni binom
Korijen kvadratnog trinoma:
Primjer:
Trinom \(x^2-2x+1\) ima korijen \(1\), jer \(1^2-2 1+1=0\)
Trinom \(x^2+2x-3\) ima korijene \(1\) i \(-3\), jer \(1^2+2-3=0\) i \((-3)^ 2-6-3=9-9=0\)
Na primjer: ako trebate pronaći korijene za kvadratni trinom \(x^2-2x+1\), izjednačavamo ga s nulom i rješavamo jednadžbu \(x^2-2x+1=0\).
\(D=4-4\cdot1=0\)
\(x=\frac(2-0)(2)=\frac(2)(2)=1\)
Spreman. Korijen je \(1\).
Rastavljanje kvadratnog trinoma na:
Kvadratni trinom \(ax^2+bx+c\) može se proširiti kao \(a(x-x_1)(x-x_2)\) ako su jednadžbe \(ax^2+bx+c=0\) veći od nule \ (x_1\) i \(x_2\) su korijeni iste jednadžbe).
Na primjer, razmotrite trinom \(3x^2+13x-10\).
Kvadratna jednadžba \(3x^2+13x-10=0\) ima diskriminant jednak 289 (veći od nule), a korijeni su jednaki \(-5\) i \(\frac(2)(3 )\). Dakle \(3x^2+13x-10=3(x+5)(x-\frac(2)(3))\). Lako je provjeriti ispravnost ove tvrdnje - ako smo , tada dobivamo izvorni trinom.
Kvadratni trinom \(ax^2+bx+c\) može se prikazati kao \(a(x-x_1)^2\) ako je diskriminant jednadžbe \(ax^2+bx+c=0\) jednaka nuli.
Na primjer, razmotrite trinom \(x^2+6x+9\).Kvadratna jednadžba \(x^2+6x+9=0\) ima diskriminantu jednaku \(0\), a jedini korijen jednak je \(-3\). Dakle, \(x^2+6x+9=(x+3)^2\) (ovdje koeficijent \(a=1\), pa nema potrebe pisati ispred zagrade). Imajte na umu da istu transformaciju može izvršiti .
Kvadratni trinom \(ax^2+bx+c\) ne faktorizira ako je diskriminant jednadžbe \(ax^2+bx+c=0\) manji od nule.
Na primjer, trinomi \(x^2+x+4\) i \(-5x^2+2x-1\) imaju diskriminant manji od nule. Stoga ih je nemoguće rastaviti na faktore.
Primjer
. Faktor \(2x^2-11x+12\).
Riješenje
:
Pronađite korijene kvadratne jednadžbe \(2x^2-11x+12=0\)
\(D=11^2-4 \cdot 2 \cdot 12=121-96=25>0\)
\(x_1=\frac(11-5)(4)=1,5;\) \(x_2=\frac(11+5)(4)=4.\)
Dakle \(2x^2-11x+12=2(x-1,5)(x-4)\)
Odgovor
: \(2(x-1,5)(x-4)\)
Dobiveni odgovor može biti zapisan na drugačiji način: \((2x-3)(x-4)\).
Primjer
. (Zadatak OGE) Kvadratni trinom rastavljen je na faktore \(5x^2+33x+40=5(x++ 5)(x-a)\). Pronađi\).
Riješenje:
\(5x^2+33x+40=0\)
\(D=33^2-4 \cdot 5 \cdot 40=1089-800=289=17^2\)
\(x_1=\frac(-33-17)(10)=-5\)
\(x_2=\frac(-33+17)(10)=-1,6\)
\(5x^2+33x+40=5(x+5)(x+1,6)\)
Odgovor
: \(-1,6\)