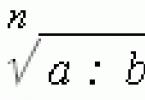
U ovom ćete članku pronaći svojstva simetrale i medijane trokuta koja mogu biti korisna u rješavanju problema.

Simetrale.

1. Sjecište simetrala trokuta je središte kružnice upisane u trokut.

Dokaz.

Doista, točke koje leže na simetrali kuta jednako su udaljene od stranica kuta. Dakle, sjecište simetrala je jednako udaljeno od svih stranica trokuta, odnosno središte je upisane kružnice.

2. Simetrala trokuta dijeli suprotnu stranicu na segmente proporcionalne susjednim stranicama:

Dokaz.

Napravimo dodatne konstrukcije. Nacrtajte pravac kroz točku paralelan s

Sjecište pravca i pravca:

∠1=∠2, jer je simetrala od ∠

∠2=∠3 kao poprijeko, kao po konstrukciji.

Dakle, ∠1=∠3 i trokut je jednakokračan, a .

Posljedično,

3. Duljina simetrale izračunava se prema sljedećim formulama:

Dokažimo drugu formulu.

Uvedimo oznaku:

Izjednačite izraze za površinu trokuta:

4. Neka je O središte upisane kružnice, simetrala kuta trokuta:

Tada je ispunjena relacija:

Dokaz:

Razmotrimo trokut:

Simetrala kuta, dakle po svojstvu simetrale trokuta

Neka onda

Izrazimo se. Prema svojstvu simetrale trokuta:

Odavde

U nekim zadacima zgodno je produžiti simetralu trokuta do sjecišta s opisanom kružnicom.

Lema o djetelini.

Zadan je trokut. Točka - točka presjeka simetrale kuta s kružnicom opisanom oko trokuta. Dopustiti biti središte kruga upisanog u trokut. Zatim

Dokaz.

Upisani kutovi koji sijeku jednake lukove su jednaki. Uočimo jednake upisane kutove:

Odavde.

Središte upisane kružnice je i simetrala kuta.

Iz trokuta

Zatim iz trokuta

dobio .

Odnosno, trokut je jednakokračan.

Odavde.

To dokazao

Dokažimo formulu (1) iz točke 3:

Dokaz:

Simetralu nastavljamo do sjecišta s opisanom kružnicom. Razmotrite trokute i . Obratite pažnju na jednake kutove:

Trokut je sličan trokutu u dva kuta. Odavde:

Po svojstvu odsječaka tetiva koje se sijeku

Zamijenite (3) u (2) i koristite (4):

Duljine odsječaka na koje simetrala dijeli stranicu trokuta izražavamo preko duljina stranica trokuta. Uvedimo oznaku:

Dobivamo sustav:

Medijani.

1. Medijane trokuta dijele se sjecišnom točkom u omjeru 2:1, računajući od vrha:

2. Neka je točka unutar trokuta takva da je ispunjena relacija: , zatim - točka sjecišta medijana trokuta.

Dokaz.

Dokažimo pomoćni teorem.

Lema.

Za proizvoljnu točku unutar trokuta vrijedi relacija:

Spustimo se s točaka i okomica na :

Iz sličnosti trokuta dobivamo:

Ako razmatramo trokute i sa zajedničkom bazom , tada dobivamo omjer:

Slično tome, dobivamo

Zbrajanjem ovih jednakosti dobivamo:

Koristimo ovu lemu da dokažemo tvrdnju 2.

Ako je jednakost (1) , zatim jednakost (2) a iz leme slijedi da je u jednakosti (2) svaki razlomak jednak .

Dokažimo da su u ovom slučaju segmenti su medijani.

Ako a , onda dobivamo . Povucimo ravne linije kroz točku, paralelne s i i razmotrimo dva para sličnih trokuta: i :

Odavde dobivamo

Iz sličnosti trokuta dobivamo, to jest, točka je sredina segmenta. Odavde.

Prema tome, je medijan trokuta.

3. Srednje strane trokuta, sijekući se, dijele ga na 6 jednakih trokuta.

Dokaz.

Dokažimo to

jer,

jer,

Posljedično,

Visine.

1. Pravci koji sadrže visine trokuta sijeku se u jednoj točki. U slučaju oštrokutnog trokuta same se visine sijeku u jednoj točki.

2. Sjecište visina trokuta ima sljedeće svojstvo: zbroj kvadrata udaljenosti od vrha trokuta i kvadrata suprotne stranice jednak je za bilo koji vrh:

Dokaz.

Dokažimo prvi dio jednakosti:

Prepišimo to u obliku:

Prema Pitagorinoj teoremi: (iz trokuta i )

(iz trokuta)

(iz trokuta)

Zamijenimo ove izraze u (1), dobivamo:

Proširujući zagrade, dobivamo:

Imamo identitet. Slično se dokazuje i drugi dio jednakosti.

3. Ako oko trokuta opišemo krug i produžimo visine trokuta do sjecišta s tim krugom,

tada je za bilo koju visinu trokuta udaljenost od osnovice visine do sjecišta nastavka visine s kružnicom jednaka udaljenosti od osnovice visine do sjecišta visina:

Ili ovako: Točke simetrične točki presjeka visina trokuta s obzirom na stranice trokuta leže na krugu opisanom oko trokuta.

Dokaz.

Dokažimo to.

Da biste to učinili, razmotrite trokuta i , I dokazati da :

Upotrijebimo znak jednakosti trokuta na stranici i dva susjedna kuta. - zajednička strana. Dokažimo jednakost dva kuta.

Dokažimo da je ∠ ∠

Neka je ∠, tada iz trokuta dobivamo to

∠. Prema tome, iz trokuta dobivamo to

Ali ∠ i ∠ temelje se na istom luku, dakle ∠ ∠ ∠

Slično, dobivamo da je ∠ ∠

4. U trokutu, točke i su baze visina povučenih iz vrhova i. Dokažite da je trokut sličan trokutu i da je koeficijent sličnosti .

Dokaz:

Središte kružnice opisane oko pravokutnog trokuta nalazi se u središtu hipotenuze . Točka leži na ovoj kružnici, jer - hipotenuza pravokutnog trokuta:

Kao upisani kutovi koji se temelje na jednom luku.

iz trokuta:

Odavde. Kut - zajednički kut trokuta i . Prema tome, trokut je sličan trokutu. Koeficijent sličnosti jednak je omjeru sličnih stranica, odnosno stranica koje leže nasuprot jednakih kutova:

Cevin teorem

Pustite u trokut

Segmenti se sijeku u jednoj točki ako i samo ako

Dokaz.

Dokažimo da je relacija (1) zadovoljena ako se segmenti sijeku u jednoj točki.

Lako je provjeriti da ako , onda

Primijenimo ovo svojstvo proporcije:

Slično:

Cevin teorem može se napisati na sljedeći način:

Ako se segmenti sijeku u jednoj točki, tada je ispunjena relacija:

Dokazati Cevin teorem u obliku sinusa, dovoljno je umjesto površina trokuta u drugi dio jednakosti (2) zamijeniti formulu za površinu svakog trokuta .

Iz predavanja Agakhanov Nazar Khangeldyevich i Vladimir Viktorovich Trushkov, CPC MIPT.

Svojstva

• Medijane trokuta sijeku se u jednoj točki, koja se naziva težište, i tom točkom ih dijeli na dva dijela u omjeru 2:1, računajući od vrha.
• Trokut je podijeljen s tri središnje strane na šest trokuta jednakih površina.
• Dulja stranica trokuta odgovara manjem medijanu.
• Od vektora koji tvore medijane možete napraviti trokut.
• Kod afinih transformacija medijan prelazi u medijan.
• Medijan trokuta dijeli ga na dva jednaka dijela.

Formule

• Formula za medijan kroz stranice (izvedena kroz Stewartov teorem ili dovršavanjem do paralelograma i korištenjem jednakosti u paralelogramu zbroja kvadrata stranica i zbroja kvadrata dijagonala):

, gdje je m c medijan na stranu c; a, b, c su stranice trokuta, pa je zbroj kvadrata medijana proizvoljnog trokuta uvijek 4/3 puta manji od zbroja kvadrata njegovih stranica.

• Formula strane u smislu medijana:

, gdje su središnje strane odgovarajućih stranica trokuta stranice trokuta.

Ako su dvije središnje strane okomite, tada je zbroj kvadrata stranica na koje su spuštene 5 puta veći od kvadrata treće stranice.

Mnemotehničko pravilo

srednji majmun,
koji ima oštro oko
skoči točno u sredinu
strane prema vrhu,
gdje je sada.

Bilješke

vidi također

Linkovi

Zaklada Wikimedia. 2010. godine.

Pogledajte što je "medijan trokuta" u drugim rječnicima:

Medijan: Medijan trokuta u planimetriji, segment koji povezuje vrh trokuta sa središtem suprotne stranice u statistici, medijan je populacijska vrijednost koja dijeli rangirane nizove podataka na pola Medijan (statistika) ... . .. Wikipedia

Medijan: Medijan trokuta u planimetriji, segment koji povezuje vrh trokuta sa središtem suprotne strane Medijan (statistika) kvantil 0,5 Medijan (trag) srednja linija traga povučena između desne i lijeve strane ... Wikipedia

Trokut i njegove središnje strane. Medijan trokuta je segment unutar trokuta koji spaja vrh trokuta sa središtem suprotne stranice, kao i pravac koji sadrži taj segment. Sadržaj 1 Svojstva 2 Formule ... Wikipedia

Pravac koji spaja vrh trokuta sa središtem njegove baze. Potpuni rječnik stranih riječi koje su ušle u upotrebu u ruskom jeziku. Popov M., 1907. medijan (lat. mediana srednja) 1) geol. isječak koji spaja vrh trokuta s ... ... Rječnik stranih riječi ruskog jezika

Medijan (od latinskog mediana sredina) u geometriji, segment koji spaja jedan od vrhova trokuta sa središtem suprotne stranice. Tri M. trokuta sijeku se u jednoj točki, koja se ponekad naziva "centrom gravitacije" trokuta, pa ... Velika sovjetska enciklopedija

Trokut je ravna crta (ili njezin segment unutar trokuta) koja povezuje vrh trokuta sa središtem suprotne stranice. Tri M. trokuta sijeku se u jednoj točki, raj se naziva težište trokuta, težište ili ... ... Matematička enciklopedija

- (od lat. mediana sredina) segment koji povezuje vrh trokuta sa sredinom suprotne stranice ... Veliki enciklopedijski rječnik

MEDIJAN, medijanci, žene. (lat. mediana, slov. sredina). 1. Ravnica povučena od vrha trokuta do sredine suprotne stranice (mat.). 2. U statistici, za niz od mnogo podataka, veličina koja ima svojstvo da je broj podataka, ... ... Objašnjavajući rječnik Ušakova

MEDIJAN, s, ženski U matematici: pravac koji povezuje vrh trokuta sa središtem suprotne stranice. Objašnjavajući rječnik Ozhegova. SI. Ozhegov, N.Yu. Švedova. 1949. 1992. ... Objašnjavajući rječnik Ozhegova

MEDIJANA (od lat. mediana sredina), isječak koji povezuje vrh trokuta sa sredinom suprotne stranice ... enciklopedijski rječnik

svojstva akorda

1. Promjer (polumjer), okomit na tetivu, dijeli ovu tetivu i oba njome stegnuta luka popola. Vrijedi i obrnuti teorem: ako promjer (radijus) raspolavlja tetivu, onda je okomit na tu tetivu.

2. Lukovi zatvoreni između paralelnih tetiva su jednaki.

3. Ako su dvije tetive kruga, AB i CD sijeku se u točki M, tada je umnožak odsječaka jedne tetive jednak umnošku odsječaka druge tetive: AM MB = CM MD.

Svojstva kruga

1. Pravac ne smije imati zajedničkih točaka s kružnicom; imaju jednu zajedničku točku s krugom ( tangens); imaju dvije zajedničke točke s njim ( sječna).

2. Kroz tri točke koje ne leže na jednoj ravnoj liniji moguće je povući kružnicu, i to samo jednu.

3. Dodirna točka dviju kružnica leži na pravcu koji spaja njihova središta.

Teorem tangente i sekante

Ako su tangenta i sekanta povučene iz točke koja leži izvan kružnice, tada je kvadrat duljine tangente jednak umnošku sekante s njezinim vanjskim dijelom: MC 2 = MA MB.

Teorem o sekanti

Ako su dvije sekante povučene iz točke koja leži izvan kružnice, tada je umnožak jedne sekante s njezinim vanjskim dijelom jednak umnošku druge sekante s njezinim vanjskim dijelom. MA MB = MC MD.

Kutovi u krugu

Središnji Kut u krugu je ravan kut s vrhom u središtu.

Kut čiji vrh leži na kružnici i čije stranice sijeku kružnicu naziva se upisani kut.

Bilo koje dvije točke na kružnici dijele je na dva dijela. Svaki od tih dijelova naziva se luk krugovi. Mjera luka može biti mjera njegovog odgovarajućeg središnjeg kuta.

Luk se zove polukrug, ako je segment koji spaja njegove krajeve promjer.

Svojstva uglova povezanih s krugom

1. Upisani kut jednak je polovici svog odgovarajućeg središnjeg kuta ili nadopunjuje polovicu tog kuta na 180°.

2. Kutovi upisani u jednu kružnicu i temeljeni na istom luku su jednaki.

3. Upisani kut na temelju promjera je 90°.

5. Kut koji čine tangenta na kružnicu i sekanta povučene kroz točku tangente jednak je polovici luka zatvorenog između njezinih stranica.

Duljine i površine

1. Opseg C radius R izračunava se formulom: C= 2 R.

2. Područje S polumjer kruga R izračunava se formulom: S = R2.

3. Duljina kružnog luka L radius R sa središnjim kutom, mjeren u radijanima, izračunava se formulom: L=R .

4. Trg S sektori radijusa R sa središnjim kutom u radijanima izračunava se formulom: S = R2 .

Upisane i opisane kružnice

Krug i trokut

središte upisane kružnice je sjecište simetrala trokuta, njegov polumjer r izračunava se formulom:

r=, gdje S je površina trokuta, i - polu-perimetar;

središte opisane kružnice je točka presjeka medijalnih okomica, njen polumjer R izračunava se po formuli:

R= , R = ;

Središte kružnice opisane oko pravokutnog trokuta nalazi se na sredini hipotenuze;

Središte opisane i upisane kružnice trokuta podudaraju se samo ako je trokut pravilan.

Krug i četverokuti

Oko konveksnog četverokuta može se opisati krug ako i samo ako je zbroj njegovih unutarnjih nasuprotnih kutova 180°:

180°;

četverokutu se može upisati kružnica ako i samo ako su zbrojevi suprotnih stranica jednaki a + c = b + d;

krug se može opisati oko paralelograma ako i samo ako je on pravokutnik;

· o trapezu je moguće opisati kružnicu ako i samo ako je taj trapez jednakokračan; središte kružnice leži u sjecištu osi simetrije trapeza sa središnjom okomitom na bočnu stranu;

Krug se može upisati u paralelogram ako i samo ako je on romb.

trokuta

Svojstva medijane trokuta

1. Medijan dijeli trokut na dva trokuta iste površine.

2. Medijane trokuta sijeku se u jednoj točki koja ih dijeli u omjeru 2:1, računajući od vrha. Ova točka se zove centar gravitacije trokut.

3. Cijeli je trokut podijeljen svojim središnjacima na šest jednakih trokuta.

Svojstva simetrale trokuta

1. Simetrala kuta je geometrijsko mjesto točaka jednako udaljenih od stranica tog kuta.

2. Simetrala unutarnjeg kuta trokuta dijeli suprotnu stranicu na odsječke proporcionalne susjednim stranicama: .

3. Sjecište simetrala trokuta je središte kružnice upisane u ovaj trokut.

Svojstva visine trokuta

1. U pravokutnom trokutu visina povučena iz vrha pravog kuta dijeli ga na dva trokuta slična izvornom.

2. U šiljastom trokutu njegove dvije visine odsijecaju od njega slične trokute.

Postoji teorija koja medijane trokuta sijeku se u jednoj točki, a ta točka dijeli svaki medijan u omjeru 2:1, gdje 2 odgovara segmentu od vrha iz kojeg je povučena središnja do točke presjeka medijana, a 1 odgovara segmentu od točke presjeka medijana do sredine stranice na koju je središnja točka nacrtan.

Da bismo dokazali ovaj teorem, razmotrimo trokut ABC s medijanama AE, BF, CD. Odnosno, točke D, E, F raspolavljaju stranice AB, BC, CA.
Ne znamo sijeku li se svi medijani u jednoj točki (to tek treba dokazati). Međutim, bilo koja dva medijana će se sjeći u jednoj točki, budući da ne mogu biti paralelna. Neka se medijane AE i BF sijeku u točki O.

Medijan BF dijeli medijan AE na dva segmenta AO i EO. Povucimo pravac kroz točku E paralelan s BF. Ovaj pravac će presijecati stranicu AC u nekoj točki L. Također povlačimo još jedan pravac paralelan s BF kroz središte segmenta AB (točka D). On će presjeći AC u točki K.

Prema Thalesovom teoremu, ako se uzastopno jednaki segmenti odvoje od njegovog vrha na jednoj strani kuta i paralelne linije se povuku kroz krajeve tih segmenata, prelazeći drugu stranu kuta, tada će te paralelne linije odrezati segmente međusobno jednake na drugoj stranici kuta.

Pogledajmo kut BCA ovog trokuta. Odsječci BE i EC su međusobno jednaki, pravci BF i EL su međusobno paralelni. Tada je prema Thalesovom teoremu CL = LF.
Ali ako pogledamo kut BAC, budući da je AD ​​= BD i DK || BF, tada je AK ​​= KF.

Kako su odsječci AF i CF međusobno jednaki (jer ih tvori središnja) i svaki od njih je podijeljen na dva jednaka odsječka, tada su sva četiri odsječka stranice AC međusobno jednaka: AK = KF = FL = LC.

Promotrimo kut EAC. Kroz krajeve tri jednaka odsječka stranice AC povučene su paralelne prave. Posljedično, oni su odrezali segmente koji su međusobno jednaki na strani AE. Segment AO sadrži dva takva segmenta, a EO samo jedan. Dakle, dokazali smo da je barem jedan medijan trokuta točkom presjeka s drugim medijanom podijeljen na dva segmenta čije su duljine u odnosu 2:1.

Sada razmotrite sjecište medijane AE s medijanom CD. Neka se sijeku u točki P.

Slično prethodnom, dokazuje se da paralelni pravci FM, CD, EN dijele stranicu AB na jednake dijelove. Zauzvrat, oni također dijele AE na tri jednaka segmenta. Štoviše, od vrha A do sjecišta medijana postoje dva takva segmenta, a nakon - jedan.

Jedan te isti segment ne može se podijeliti na tri jednaka dijela tako da kod jedne opcije podjele budu iste veličine, a kod druge - druge. Stoga se točke O i P moraju poklapati. To znači da se sva tri medijana trokuta sijeku u jednoj točki.

Da bismo dokazali da druge dvije središnje dijele sjecište u omjeru 2:1, možemo povući paralelne pravce na stranice AB i BC na isti način kao prethodni.

Srednja je jedna od glavnih linija trokuta. Taj segment i linija na kojoj leži spajaju točku na vrhu kuta trokuta sa središtem suprotne stranice istog lika. U jednakostraničnom trokutu središnja je ujedno simetrala i visina.

Svojstvo medijana, koje će uvelike olakšati rješavanje mnogih problema, je sljedeće: ako nacrtate medijane iz svakog kuta u trokutu, tada će svi oni, koji se sijeku u jednoj točki, biti podijeljeni u omjeru 2: 1. Omjer treba računati od vrha kuta.

Medijan ima svojstvo da sve dijeli na jednake dijelove. Na primjer, bilo koji medijan dijeli trokut na dva druga, jednaka po površini. A ako nacrtate sva tri medijana, tada u velikom trokutu dobijete 6 malih, također jednakih površina. Takve figure (s istim područjem) nazivaju se jednakima.

Simetrala

Simetrala je zraka koja počinje u vrhu kuta i raspolavlja taj kut. Točke koje leže na danoj zraki jednako su udaljene od stranica kuta. Svojstva simetrale dobra su pomoć pri rješavanju problema vezanih uz trokute.

U trokutu simetrala je isječak koji leži na zraki simetrale kuta i spaja vrh sa suprotnom stranom. Točka sjecišta sa stranom dijeli ga na segmente, čiji je omjer jednak omjeru strana koje su im susjedne.

Ako je krug upisan u trokut, tada će se njegovo središte poklapati sa sjecištem svih simetrala tog trokuta. Ovo se svojstvo odražava i na stereometriju - tamo piramida igra ulogu trokuta, a lopta ulogu kruga.

Visina

Baš kao središnja i simetrala, visina u trokutu prvenstveno povezuje vrh kuta i suprotnu stranicu. Ova veza rezultira sljedećim: visina je okomica povučena iz vrha na pravac koji sadrži suprotnu stranicu.

Ako je visina nacrtana u pravokutnom trokutu, tada, dodirujući suprotnu stranu, dijeli cijeli trokut na dva druga, koja su pak slična prvom.

Često se koncept okomice koristi u stereometriji za određivanje relativnih položaja linija u različitim ravninama i udaljenosti između njih. U tom slučaju segment koji obavlja funkciju okomice mora imati pravi kut s obje linije. Tada će brojčana vrijednost ovog segmenta pokazati udaljenost između dvije figure.