Тъждествени трансформации на тригонометрични изрази. Урок "Опростяване на тригонометрични изрази" Тригонометрични изрази и техните трансформации

Раздели: Математика

клас: 11

Урок 1

Тема: 11 клас (подготовка за изпит)

Опростяване на тригонометрични изрази.

Решение на най-простите тригонометрични уравнения. (2 часа)

Цели:

Систематизира, обобщава, разширява знанията и уменията на учениците, свързани с използването на тригонометрични формули и решаването на най-простите тригонометрични уравнения.

Оборудване за урока:

Структура на урока:

Оргмомент
Тестване на лаптопи. Обсъждане на резултатите.
Опростяване на тригонометрични изрази
Решение на най-простите тригонометрични уравнения
Самостоятелна работа.
Обобщение на урока. Обяснение на домашна работа.

1. Организационен момент. (2 минути.)

Учителят приветства аудиторията, обявява темата на урока, припомня, че преди това е била дадена задача да се повторят тригонометричните формули и поставя учениците за тестване.

2. Тестване. (15мин + 3мин дискусия)

Целта е да се проверят знанията на тригонометричните формули и умението да се прилагат. На бюрото на всеки ученик има лаптоп, в който има възможност за тест.

Може да има колкото искате опции, ето пример за една от тях:

I опция.

Опростете изразите:

а) основни тригонометрични тъждества

1. sin 2 3y + cos 2 3y + 1;

б) формули за добавяне

3. sin5x - sin3x;

в) превръщане на произведение в сума

6. 2sin8y cos3y;

г) формули за двоен ъгъл

7.2sin5x cos5x;

д) формули за половин ъгъл

е) формули за троен ъгъл

ж) универсално заместване

з) понижаване на степента

16. cos 2 (3x/7);

Учениците на лаптоп пред всяка формула виждат своите отговори.

Работата моментално се проверява от компютъра. Резултатите се показват на голям екран, за да могат всички да ги видят.

Също така след приключване на работата на лаптопите на учениците се показват верните отговори. Всеки ученик вижда къде е допусната грешка и какви формули трябва да повтори.

3. Опростяване на тригонометрични изрази. (25 мин.)

Целта е да се повтори, отработи и затвърди приложението на основните формули на тригонометрията. Решаване на задачи B7 от изпита.

На този етап е препоръчително да разделите класа на групи от силни (работете самостоятелно с последваща проверка) и слаби ученици, които работят с учителя.

Задача за силни ученици (предварително подготвена на печатна основа). Основният акцент е върху формулите за намаляване и двоен ъгъл, съгласно USE 2011.

Опростете изразите (за силни учащи):

Успоредно с това учителят работи със слаби ученици, като обсъжда и решава задачи на екрана под диктовката на учениците.

Изчисли:

5) sin(270º - α) + cos(270º + α)

Опростете:

Дойде ред да обсъдим резултатите от работата на силната група.

На екрана се появяват отговори, а също така с помощта на видеокамера се показва работата на 5 различни ученика (по една задача за всеки).

Слабата група вижда условието и метода на решение. Има дискусия и анализ. С използването на технически средства това става бързо.

4. Решение на най-простите тригонометрични уравнения. (30 минути.)

Целта е да се повтори, систематизира и обобщи решаването на най-простите тригонометрични уравнения, като се записват корените им. Решение на задача B3.

Всяко тригонометрично уравнение, независимо как го решаваме, води до най-простото.

При изпълнение на задачата учениците трябва да обърнат внимание на записването на корените на уравнения от частни случаи и общ вид и на избора на корени в последното уравнение.

Решете уравнения:

Запишете най-малкия положителен корен от отговора.

5. Самостоятелна работа (10 мин.)

Целта е тестване на придобитите умения, идентифициране на проблеми, грешки и начини за отстраняването им.

Предлага се разнообразна работа по избор на ученика.

Вариант за "3"

1) Намерете стойността на израза

2) Опростете израза 1 - sin 2 3α - cos 2 3α

3) Решете уравнението

Вариант за "4"

1) Намерете стойността на израза

2) Решете уравнението Запишете най-малкия положителен корен от вашия отговор.

Вариант за "5"

1) Намерете tgα, ако

2) Намерете корена на уравнението Запишете най-малкия положителен корен от вашия отговор.

6. Обобщение на урока (5 мин.)

Учителят обобщава факта, че урокът повтаря и консолидира тригонометричните формули, решението на най-простите тригонометрични уравнения.

Задава се домашна работа (предварително подготвена на хартиен носител) с проверка на място в следващия урок.

Решете уравнения:

10) Дайте отговора си като най-малкия положителен корен.

Урок 2

Тема: 11 клас (подготовка за изпит)

Методи за решаване на тригонометрични уравнения. Избор на корен. (2 часа)

Цели:

Обобщават и систематизират знанията за решаване на тригонометрични уравнения от различни видове.
Да насърчава развитието на математическото мислене на учениците, способността да наблюдават, сравняват, обобщават, класифицират.
Насърчавайте учениците да преодоляват трудностите в процеса на умствена дейност, самоконтрол, интроспекция на дейността си.

Оборудване за урока:КРМу, лаптопи за всеки ученик.

Структура на урока:

Оргмомент
Дискусия d / s и samot. работата на последния урок
Повторение на методи за решаване на тригонометрични уравнения.
Решаване на тригонометрични уравнения
Избор на корени в тригонометрични уравнения.
Самостоятелна работа.
Обобщение на урока. Домашна работа.

1. Организационен момент (2 мин.)

Учителят поздравява публиката, обявява темата на урока и плана за работа.

2. а) Анализ на домашната работа (5 мин.)

Целта е да се провери ефективността. Една работа с помощта на видеокамера се показва на екрана, останалите се събират избирателно за проверка от учителя.

б) Анализ на самостоятелна работа (3 мин.)

Целта е да се сортират грешките, да се посочат начини за преодоляването им.

На екрана са отговорите и решенията, учениците предварително са издали своите работи. Анализът върви бързо.

3. Повторение на методи за решаване на тригонометрични уравнения (5 мин.)

Целта е да се припомнят методи за решаване на тригонометрични уравнения.

Попитайте учениците какви методи за решаване на тригонометрични уравнения знаят. Подчертайте, че има така наречените основни (често използвани) методи:

променливо заместване,
факторизация,
хомогенни уравнения,

и има приложени методи:

според формулите за превръщане на сбор в произведение и произведение в сбор,
чрез формулите за намаляване,
универсално тригонометрично заместване
въвеждане на спомагателен ъгъл,
умножение по някаква тригонометрична функция.

Трябва също да се припомни, че едно уравнение може да бъде решено по различни начини.

4. Решаване на тригонометрични уравнения (30 мин.)

Целта е да се обобщят и затвърдят знанията и уменията по тази тема, да се подготви за решаване на C1 от USE.

Считам за целесъобразно уравненията за всеки метод да се решават заедно с учениците.

Ученикът диктува решението, учителят го записва на таблета, целият процес се показва на екрана. Това ще ви позволи бързо и ефективно да възстановите в паметта си вече обхванат материал.

Решете уравнения:

1) промяна на променлива 6cos 2 x + 5sinx - 7 = 0

2) факторизация 3cos(x/3) + 4cos 2 (x/3) = 0

3) хомогенни уравнения sin 2 x + 3cos 2 x - 2sin2x = 0

4) преобразуване на сумата в произведението cos5x + cos7x = cos(π + 6x)

5) преобразуване на произведението в сумата 2sinx sin2x + cos3x = 0

6) понижаване на степента на sin2x - sin 2 2x + sin 2 3x \u003d 0,5

7) универсално тригонометрично заместване sinx + 5cosx + 5 = 0.

При решаването на това уравнение трябва да се отбележи, че използването на този метод води до стесняване на областта на дефиниране, тъй като синусът и косинусът се заменят с tg(x/2). Следователно, преди да изпишете отговора, е необходимо да проверите дали числата от множеството π + 2πn, n Z са коне на това уравнение.

8) въвеждане на допълнителен ъгъл √3sinx + cosx - √2 = 0

9) умножение по някаква тригонометрична функция cosx cos2x cos4x = 1/8.

5. Избор на корени на тригонометрични уравнения (20 мин.)

Тъй като в условията на ожесточена конкуренция при влизане в университетите решението на една първа част от изпита не е достатъчно, повечето студенти трябва да обърнат внимание на задачите от втората част (C1, C2, C3).

Следователно целта на този етап от урока е да си припомним предварително изучения материал, да се подготвим за решаване на задача C1 от USE през 2011 г.

Има тригонометрични уравнения, в които трябва да изберете корените, когато изписвате отговора. Това се дължи на някои ограничения, например: знаменателят на дробта не е равен на нула, изразът под корена на четна степен е неотрицателен, изразът под знака на логаритъма е положителен и т.н.

Такива уравнения се считат за уравнения с повишена сложност и във версията USE са във втората част, а именно C1.

Решете уравнението:

Дробта е нула, ако тогава използвайки единичната окръжност, ще изберем корените (вижте Фигура 1)

Снимка 1.

получаваме x = π + 2πn, n Z

Отговор: π + 2πn, n Z

На екрана изборът на корени е показан в кръг в цветно изображение.

Продуктът е равен на нула, когато поне един от факторите е равен на нула, а дъгата в същото време не губи значението си. Тогава

Използвайки единичния кръг, изберете корените (вижте Фигура 2)

Фигура 2.

Да преминем към системата:

В първото уравнение на системата правим дневника на промените 2 (sinx) = y, получаваме уравнението след това , обратно към системата

използвайки единичния кръг, избираме корените (вижте Фигура 5),

Фигура 5

6. Самостоятелна работа (15 мин.)

Целта е да се консолидира и провери усвояването на материала, да се идентифицират грешките и да се очертаят начини за коригирането им.

Работата се предлага в три варианта, предварително подготвени на печатна основа, по избор на учениците.

Уравненията могат да се решават по всякакъв начин.

Вариант за "3"

Решете уравнения:

1) 2sin 2 x + sinx - 1 = 0

2) sin2x = √3cosx

Вариант за "4"

Решете уравнения:

1) cos2x = 11sinx - 5

2) (2sinx + √3)log 8 (cosx) = 0

Вариант за "5"

Решете уравнения:

1) 2sinx - 3cosx = 2

7. Обобщение на урока, домашна работа (5 мин.)

Учителят обобщава урока, още веднъж обръща внимание на факта, че тригонометричното уравнение може да бъде решено по няколко начина. Най-добрият начин за постигане на бърз резултат е този, който е научен най-добре от конкретен ученик.

Когато се подготвяте за изпита, трябва систематично да повтаряте формулите и методите за решаване на уравнения.

Раздават се домашни (предварително подготвени на хартиен носител) и се коментират начини за решаване на някои уравнения.

Решете уравнения:

1) cosx + cos5x = cos3x + cos7x

2) 5sin(x/6) - cos(x/3) + 3 = 0

3) 4sin 2x + sin2x = 3

4) sin 2 x + sin 2 2x - sin 2 3x - sin 2 4x = 0

5) cos3x cos6x = cos4x cos7x

6) 4sinx - 6cosx = 1

7) 3sin2x + 4 cos2x = 5

8) cosx cos2x cos4x cos8x = (1/8) cos15x

9) (2sin 2 x - sinx)log 3 (2cos 2 x + cosx) = 0

10) (2cos 2 x - √3cosx)log 7 (-tgx) = 0

11)

Видео урокът "Опростяване на тригонометрични изрази" е предназначен да развие уменията на учениците за решаване на тригонометрични задачи с помощта на основни тригонометрични тъждества. По време на видео урока се разглеждат видове тригонометрични идентичности, примери за решаване на задачи с тях. Използвайки визуални средства, за учителя е по-лесно да постигне целите на урока. Яркото представяне на материала допринася за запаметяването на важни точки. Използването на анимационни ефекти и гласова игра ви позволяват напълно да замените учителя на етапа на обяснение на материала. По този начин, използвайки тази визуална помощ в уроците по математика, учителят може да повиши ефективността на преподаването.

В началото на видео урока е обявена неговата тема. След това се припомнят тригонометричните идентичности, изследвани по-рано. Екранът показва равенствата sin 2 t+cos 2 t=1, tg t=sin t/cos t, където t≠π/2+πk за kϵZ, ctg t=cos t/sin t, вярно за t≠πk, където kϵZ, tan t · ctg t=1, при t≠πk/2, където kϵZ, наречени основни тригонометрични идентичности. Отбелязва се, че тези идентичности често се използват при решаване на проблеми, където е необходимо да се докаже равенство или да се опрости израза.

Освен това се разглеждат примери за прилагане на тези идентичности при решаване на проблеми. Първо, предлага се да се обмисли решаването на проблеми с опростяване на изрази. В пример 1 е необходимо да се опрости изразът cos 2 t- cos 4 t+ sin 4 t. За да се реши примерът, общият множител cos 2 t първо се поставя в скоби. В резултат на такова преобразуване в скоби се получава изразът 1-cos 2 t, чиято стойност от основното тъждество на тригонометрията е равна на sin 2 t. След преобразуването на израза е очевидно, че още един общ множител sin 2 t може да бъде изваден от скоби, след което изразът приема формата sin 2 t (sin 2 t + cos 2 t). От същата основна идентичност извеждаме стойността на израза в скоби, равна на 1. В резултат на опростяването получаваме cos 2 t- cos 4 t+ sin 4 t= sin 2 t.

В пример 2 изразът цена/(1- синт)+ цена/(1+ синт) също трябва да бъде опростен. Тъй като цената на израза е в числителите на двете дроби, тя може да бъде поставена в скоби като общ фактор. След това дробите в скоби се свеждат до общ знаменател чрез умножаване (1- синт)(1+ синт). След намаляване на подобни членове, 2 остава в числителя, а 1 - sin 2 t в знаменателя. От дясната страна на екрана се извиква основната тригонометрична идентичност sin 2 t+cos 2 t=1. Използвайки го, намираме знаменателя на дробта cos 2 t. След като намалим дробта, получаваме опростена форма на израза цена/(1- синт)+ цена/(1+ синт)=2/цена.

След това разглеждаме примери за доказване на идентичности, в които се прилагат придобитите знания за основните идентичности на тригонометрията. В пример 3 е необходимо да се докаже идентичността (tg 2 t-sin 2 t)·ctg 2 t=sin 2 t. Дясната страна на екрана показва три идентичности, които ще са необходими за доказателството - tg t ctg t=1, ctg t=cos t/sin t и tg t=sin t/cos t с ограничения. За доказване на тъждеството първо се отварят скобите, след което се образува произведение, което отразява израза на основното тригонометрично тъждество tg t·ctg t=1. След това, съгласно тъждеството от дефиницията на котангенс, ctg 2 t се трансформира. В резултат на трансформации се получава изразът 1-cos 2 t. Използвайки основната идентичност, намираме стойността на израза. Така се доказва, че (tg 2 t-sin 2 t)·ctg 2 t=sin 2 t.

В пример 4 трябва да намерите стойността на израза tg 2 t+ctg 2 t, ако tg t+ctg t=6. За да се оцени изразът, дясната и лявата страна на уравнението (tg t+ctg t) 2 =6 2 първо се повдигат на квадрат. Съкратената формула за умножение се показва от дясната страна на екрана. След отваряне на скобите от лявата страна на израза се образува сумата tg 2 t+2 tg t ctg t+ctg 2 t, за преобразуването на която може да се приложи едно от тригонометричните тъждества tg t ctg t=1, чиято форма се извиква от дясната страна на екрана. След преобразуването се получава равенството tg 2 t+ctg 2 t=34. Лявата страна на равенството съвпада с условието на задачата, така че отговорът е 34. Задачата е решена.

Видео урокът "Опростяване на тригонометрични изрази" се препоръчва за използване в традиционен училищен урок по математика. Също така материалът ще бъде полезен за учител, който осигурява дистанционно обучение. За формиране на умения за решаване на тригонометрични задачи.

ПОЯСНЕНИЕ НА ТЕКСТА:

"Опростяване на тригонометрични изрази".

Равенство

1) sin 2 t + cos 2 t = 1 (синус на квадрат te плюс косинус на квадрат te е равно на едно)

2) tgt =, при t ≠ + πk, kϵZ (тангенсът на te е равен на отношението на синус от te към косинус от te, когато te не е равно на pi с две плюс pi ka, ka принадлежи на zet)

3) ctgt = , при t ≠ πk, kϵZ (котангенсът на te е равен на съотношението на косинуса на te към синуса на te, когато te не е равно на пика на ka, който принадлежи на z).

4)tgt ∙ ctgt = 1 за t ≠ , kϵZ

се наричат основни тригонометрични тъждества.

Често те се използват за опростяване и доказване на тригонометрични изрази.

Разгледайте примери за използване на тези формули при опростяване на тригонометрични изрази.

ПРИМЕР 1. Опростете израза: cos 2 t - cos 4 t + sin 4 t. (израз косинус на квадрат te минус косинус на четвърта степен на te плюс синус на четвърта степен на te).

Решение. cos 2 t - cos 4 t + sin 4 t = cos 2 t∙ (1 - cos 2 t) + sin 4 t = cos 2 t ∙ sin 2 t + sin 4 t = sin 2 t (cos 2 t + sin 2 t) = sin 2 t 1= sin 2 t

(изваждаме общия множител косинус на квадрат te, в скоби получаваме разликата между единица и квадрат на косинус te, който е равен на квадрат на синус te по първото идентичност. Получаваме сбора на синуса на четвъртия степен te на произведението на косинус квадрат te и синус квадрат te. Изваждаме общия множител синус квадрат te извън скобите, в скоби получаваме сумата от квадратите на косинуса и синуса, която според основната тригонометрия идентичност, е равно на 1. В резултат на това получаваме квадрат на синус te).

ПРИМЕР 2. Опростете израза: + .

(изразът е сумата от две дроби в числителя на първия косинус te в знаменателя едно минус синус te, в числителя на втория косинус te в знаменателя на втория плюс синус te).

(Изваждаме общия множител косинус te от скоби и в скоби го привеждаме към общ знаменател, който е произведението на едно минус синус te по едно плюс синус te.

В числителя получаваме: едно плюс синус te плюс едно минус синус te, даваме подобни, числителят е равен на две след привеждане на подобни.

В знаменателя можете да приложите формулата за съкратено умножение (разлика на квадратите) и да получите разликата между единицата и квадрата на синуса te, който според основната тригонометрична идентичност

е равно на квадрата на косинус te. След като намалим с косинус te, получаваме крайния отговор: две делено на косинус te).

Разгледайте примери за използването на тези формули в доказателството на тригонометрични изрази.

ПРИМЕР 3. Докажете идентичността (tg 2 t - sin 2 t) ∙ ctg 2 t \u003d sin 2 t (произведението на разликата между квадратите на тангенса на te и синуса на te и квадрата на котангенса на te е равно на квадрата на синуса от te).

Доказателство.

Нека трансформираме лявата страна на равенството:

(tg 2 t - sin 2 t) ∙ ctg 2 t = tg 2 t ∙ ctg 2 t - sin 2 t ∙ ctg 2 t = 1 - sin 2 t ∙ ctg 2 t =1 - sin 2 t ∙ = 1 - cos 2 t = грях 2 t

(Нека отворим скобите, от получената по-рано връзка е известно, че произведението на квадратите на тангенса на te по котангенса на te е равно на едно. Припомнете си, че котангенсът на te е равен на отношението на косинуса на te към синус от te, което означава, че квадратът на котангенса е отношението на квадрата на косинус от te към квадрата на синус от te.

След намаляване със синуса на квадрат от te, получаваме разликата между единица и косинуса на квадрат от te, който е равен на синуса на квадрат от te). Q.E.D.

ПРИМЕР 4. Намерете стойността на израза tg 2 t + ctg 2 t, ако tgt + ctgt = 6.

(сумата от квадратите на тангенса на te и котангенса на te, ако сумата на тангенса и котангенса е шест).

Решение. (tgt + ctgt) 2 = 6 2

tg 2 t + 2 ∙ tgt ∙ctgt + ctg 2 t = 36

tg 2 t + 2 + ctg 2 t = 36

tg 2 t + ctg 2 t = 36-2

tg 2 t + ctg 2 t = 34

Нека повдигнем на квадрат двете части на първоначалното равенство:

(tgt + ctgt) 2 = 6 2 (квадратът на сбора от тангенса на te и котангенса на te е шест на квадрат). Припомнете си съкратената формула за умножение: Квадратът на сумата от две количества е равен на квадрата на първото плюс два пъти произведението на първото и второто плюс квадрата на второто. (a+b) 2 =a 2 +2ab+b 2 Получаваме tg 2 t + 2 ∙ tgt ∙ctgt + ctg 2 t = 36 .

Тъй като произведението на тангенса на te и котангенса на te е равно на едно, тогава tg 2 t + 2 + ctg 2 t \u003d 36 (сумата от квадратите на тангенса на te и котангенса на te и две е тридесет и шест),

Раздели: Математика

клас: 11

Урок 1

Тема: 11 клас (подготовка за изпит)

Опростяване на тригонометрични изрази.

Решение на най-простите тригонометрични уравнения. (2 часа)

Цели:

Систематизира, обобщава, разширява знанията и уменията на учениците, свързани с използването на тригонометрични формули и решаването на най-простите тригонометрични уравнения.

Оборудване за урока:

Структура на урока:

Оргмомент
Тестване на лаптопи. Обсъждане на резултатите.
Опростяване на тригонометрични изрази
Решение на най-простите тригонометрични уравнения
Самостоятелна работа.
Обобщение на урока. Обяснение на домашна работа.

1. Организационен момент. (2 минути.)

2. Тестване. (15мин + 3мин дискусия)

Може да има колкото искате опции, ето пример за една от тях:

I опция.

Опростете изразите:

а) основни тригонометрични тъждества

1. sin 2 3y + cos 2 3y + 1;

б) формули за добавяне

3. sin5x - sin3x;

в) превръщане на произведение в сума

6. 2sin8y cos3y;

г) формули за двоен ъгъл

7.2sin5x cos5x;

д) формули за половин ъгъл

е) формули за троен ъгъл

ж) универсално заместване

з) понижаване на степента

16. cos 2 (3x/7);

Учениците на лаптоп пред всяка формула виждат своите отговори.

3. Опростяване на тригонометрични изрази. (25 мин.)

Опростете изразите (за силни учащи):

Изчисли:

5) sin(270º - α) + cos(270º + α)

Опростете:

Дойде ред да обсъдим резултатите от работата на силната група.

4. Решение на най-простите тригонометрични уравнения. (30 минути.)

Всяко тригонометрично уравнение, независимо как го решаваме, води до най-простото.

Решете уравнения:

Запишете най-малкия положителен корен от отговора.

5. Самостоятелна работа (10 мин.)

Целта е тестване на придобитите умения, идентифициране на проблеми, грешки и начини за отстраняването им.

Предлага се разнообразна работа по избор на ученика.

Вариант за "3"

1) Намерете стойността на израза

2) Опростете израза 1 - sin 2 3α - cos 2 3α

3) Решете уравнението

Вариант за "4"

1) Намерете стойността на израза

2) Решете уравнението Запишете най-малкия положителен корен от вашия отговор.

Вариант за "5"

1) Намерете tgα, ако

2) Намерете корена на уравнението Запишете най-малкия положителен корен от вашия отговор.

6. Обобщение на урока (5 мин.)

Задава се домашна работа (предварително подготвена на хартиен носител) с проверка на място в следващия урок.

Решете уравнения:

10) Дайте отговора си като най-малкия положителен корен.

Урок 2

Тема: 11 клас (подготовка за изпит)

Методи за решаване на тригонометрични уравнения. Избор на корен. (2 часа)

Цели:

Обобщават и систематизират знанията за решаване на тригонометрични уравнения от различни видове.
Да насърчава развитието на математическото мислене на учениците, способността да наблюдават, сравняват, обобщават, класифицират.
Насърчавайте учениците да преодоляват трудностите в процеса на умствена дейност, самоконтрол, интроспекция на дейността си.

Оборудване за урока:КРМу, лаптопи за всеки ученик.

Структура на урока:

Оргмомент
Дискусия d / s и samot. работата на последния урок
Повторение на методи за решаване на тригонометрични уравнения.
Решаване на тригонометрични уравнения
Избор на корени в тригонометрични уравнения.
Самостоятелна работа.
Обобщение на урока. Домашна работа.

1. Организационен момент (2 мин.)

Учителят поздравява публиката, обявява темата на урока и плана за работа.

2. а) Анализ на домашната работа (5 мин.)

б) Анализ на самостоятелна работа (3 мин.)

Целта е да се сортират грешките, да се посочат начини за преодоляването им.

На екрана са отговорите и решенията, учениците предварително са издали своите работи. Анализът върви бързо.

3. Повторение на методи за решаване на тригонометрични уравнения (5 мин.)

Целта е да се припомнят методи за решаване на тригонометрични уравнения.

променливо заместване,
факторизация,
хомогенни уравнения,

и има приложени методи:

според формулите за превръщане на сбор в произведение и произведение в сбор,
чрез формулите за намаляване,
универсално тригонометрично заместване
въвеждане на спомагателен ъгъл,
умножение по някаква тригонометрична функция.

Трябва също да се припомни, че едно уравнение може да бъде решено по различни начини.

4. Решаване на тригонометрични уравнения (30 мин.)

Целта е да се обобщят и затвърдят знанията и уменията по тази тема, да се подготви за решаване на C1 от USE.

Считам за целесъобразно уравненията за всеки метод да се решават заедно с учениците.

Решете уравнения:

1) промяна на променлива 6cos 2 x + 5sinx - 7 = 0

2) факторизация 3cos(x/3) + 4cos 2 (x/3) = 0

3) хомогенни уравнения sin 2 x + 3cos 2 x - 2sin2x = 0

4) преобразуване на сумата в произведението cos5x + cos7x = cos(π + 6x)

5) преобразуване на произведението в сумата 2sinx sin2x + cos3x = 0

6) понижаване на степента на sin2x - sin 2 2x + sin 2 3x \u003d 0,5

7) универсално тригонометрично заместване sinx + 5cosx + 5 = 0.

8) въвеждане на допълнителен ъгъл √3sinx + cosx - √2 = 0

9) умножение по някаква тригонометрична функция cosx cos2x cos4x = 1/8.

5. Избор на корени на тригонометрични уравнения (20 мин.)

Такива уравнения се считат за уравнения с повишена сложност и във версията USE са във втората част, а именно C1.

Решете уравнението:

Дробта е нула, ако тогава използвайки единичната окръжност, ще изберем корените (вижте Фигура 1)

Снимка 1.

получаваме x = π + 2πn, n Z

Отговор: π + 2πn, n Z

На екрана изборът на корени е показан в кръг в цветно изображение.

Използвайки единичния кръг, изберете корените (вижте Фигура 2)

Воронкова Олга Ивановна

МБОУ „Средно училище

№ 18"

Енгелс, Саратовска област.

Учител по математика.

"Тригонометрични изрази и техните трансформации"

Въведение ……………………………………………………………………………...3

Глава 1 Класификация на задачите за използване на трансформации на тригонометрични изрази ……………………………………………………...5

1.1. Изчислителни задачи стойности на тригонометрични изрази……….5

1.2.Задачи за опростяване на тригонометрични изрази .... 7

1.3. Задачи за преобразуване на числени тригонометрични изрази ... ..7

1.4 Смесени задачи…………………………………………………….....9

Глава 2

2.1 Тематично повторение в 10 клас………………………………………...11

Тест 1………………………………………………………………………………..12

Тест 2…………………………………………………………………………………..13

Тест 3…………………………………………………………………………………..14

2.2 Последно повторение в 11 клас……………………………………………...15

Тест 1…………………………………………………………………………………..17

Тест 2…………………………………………………………………………………..17

Тест 3…………………………………………………………………………………..18

Заключение.………………………………………………………………………..19

Списък на използваната литература………………………………………..…….20

Въведение.

В днешните условия най-важният въпрос е: „Как можем да помогнем за премахването на някои пропуски в знанията на студентите и да ги предупредим за евентуални грешки на изпита?“ За да се реши този проблем, е необходимо да се постигне от учениците не формално усвояване на програмния материал, а неговото дълбоко и съзнателно разбиране, развитие на скоростта на устни изчисления и трансформации, както и развитие на умения за решаване на най-простите задачи. проблеми „в ума“. Необходимо е да се убедят учениците, че само при наличие на активна позиция, в изучаването на математика, при условие на придобиване на практически умения, умения и тяхното използване, може да се разчита на истински успех. Необходимо е да се използва всяка възможност за подготовка за изпита, включително избираемите предмети в 10-11 клас, редовно да се анализират сложни задачи с учениците, като се избира най-рационалният начин за решаването им в класната стая и допълнителните часове.положителен резултат вобластта на решаване на типични проблеми може да бъде постигната, ако учителите по математика, чрез създаванедобра основна подготовка на учениците, да търсим нови начини за решаване на проблемите, които са се отворили пред нас, активно да експериментираме, да прилагаме съвременни педагогически технологии, методи, техники, които създават благоприятни условия за ефективна самореализация и самоопределяне на учениците в нови социални условия.

Тригонометрията е неразделна част от училищния курс по математика. Добрите познания и силни умения по тригонометрия са доказателство за достатъчно ниво на математическа култура, незаменимо условие за успешното изучаване на математика, физика и редица техническидисциплини.

Уместността на работата. Значителна част от завършилите училище показват от година на година много слаба подготовка в този важен раздел на математиката, както се вижда от резултатите от минали години (процент на завършване през 2011 г.-48,41%, 2012 г.-51,05%), тъй като анализът на преминаването единният държавен изпит показа, че учениците допускат много грешки при изпълнение на задачите от този раздел или изобщо не се заемат с такива задачи. В един Въпросите от държавния изпит по тригонометрия се срещат в почти три вида задачи. Това е решението на най-простите тригонометрични уравнения в задача B5 и работа с тригонометрични изрази в задача B7 и изучаването на тригонометрични функции в задача B14, както и задачи B12, в които има формули, описващи физични явления и съдържащи тригонометрични функции . И това е само част от задачите B! Но има и любими тригонометрични уравнения с избор на корени C1 и „не много любими“ геометрични задачи C2 и C4.

Обективен. Анализирайте материала на задачите на USE B7, посветени на преобразуването на тригонометрични изрази и класифицирайте задачите според формата на тяхното представяне в тестовете.

Работата се състои от две глави, въведение и заключение. Уводът подчертава актуалността на работата. Първата глава предоставя класификация на задачите за използване на трансформации на тригонометрични изрази в тестови задачи за USE (2012).

Във втората глава се разглежда организацията на повторението на темата „Преобразуване на тригонометрични изрази“ в 10, 11 клас и се разработват тестове по тази тема.

Списъкът с литература включва 17 източника.

Глава 1. Класификация на задачите за използване на трансформации на тригонометрични изрази.

В съответствие със стандарта за средно (пълно) образование и изискванията за нивото на обучение на учениците, задачите за познаване на основите на тригонометрията са включени в кодификатора на изискванията.

Изучаването на основите на тригонометрията ще бъде най-ефективно, когато:

учениците ще бъдат положително мотивирани да повтарят вече изучен материал;

в образователния процес ще се прилага подход, ориентиран към ученика;

ще се прилага система от задачи, която допринася за разширяване, задълбочаване, систематизиране на знанията на учениците;

ще се използват съвременни педагогически технологии.

След като анализирахме литературата и интернет ресурсите за подготовка за изпита, ние предложихме една от възможните класификации на задачите B7 (KIM USE 2012-тригонометрия): задачи за изчисляванестойности на тригонометрични изрази; задачи запреобразуване на числени тригонометрични изрази; задачи за преобразуване на буквени тригонометрични изрази; смесени задачи.

1.1. Изчислителни задачи стойности на тригонометрични изрази.

Един от най-често срещаните видове прости тригонометрични задачи е изчисляването на стойностите на тригонометричните функции по стойността на една от тях:

а) Използване на основното тригонометрично тъждество и неговите следствия.

Пример 1 . Намерете дали
и
.

Решение.
,
,

защото , тогава
.

Отговор.

Пример 2 . намирам
, ако
и .

Решение.
,
,
.

защото , тогава
.

Отговор. .

б) Използване на формули за двоен ъгъл.

Пример 3 . намирам
, ако
.

Решение. , .

Отговор.
.

Пример 4 . Намерете стойността на израз
.

Решение. .

Отговор.
.

1. намирам , ако

. Отговор. -0,2

2. намирам , ако
и
. Отговор. 0,4

3. намирам

, ако . Отговор. -12.884. намирам

, ако

. Отговор. -0,845. Намерете стойността на израза:

. Отговор. 66. Намерете стойността на израз

.Отговор. -19

1.2.Задачи за опростяване на тригонометрични изрази. Формулите за намаляване трябва да бъдат добре усвоени от учениците, тъй като те ще бъдат използвани по-нататък в уроците по геометрия, физика и други свързани дисциплини.

Пример 5 . Опростете изразите
.

Решение. .

Отговор.
.

Задачи за самостоятелно решаване:

1. Опростете израза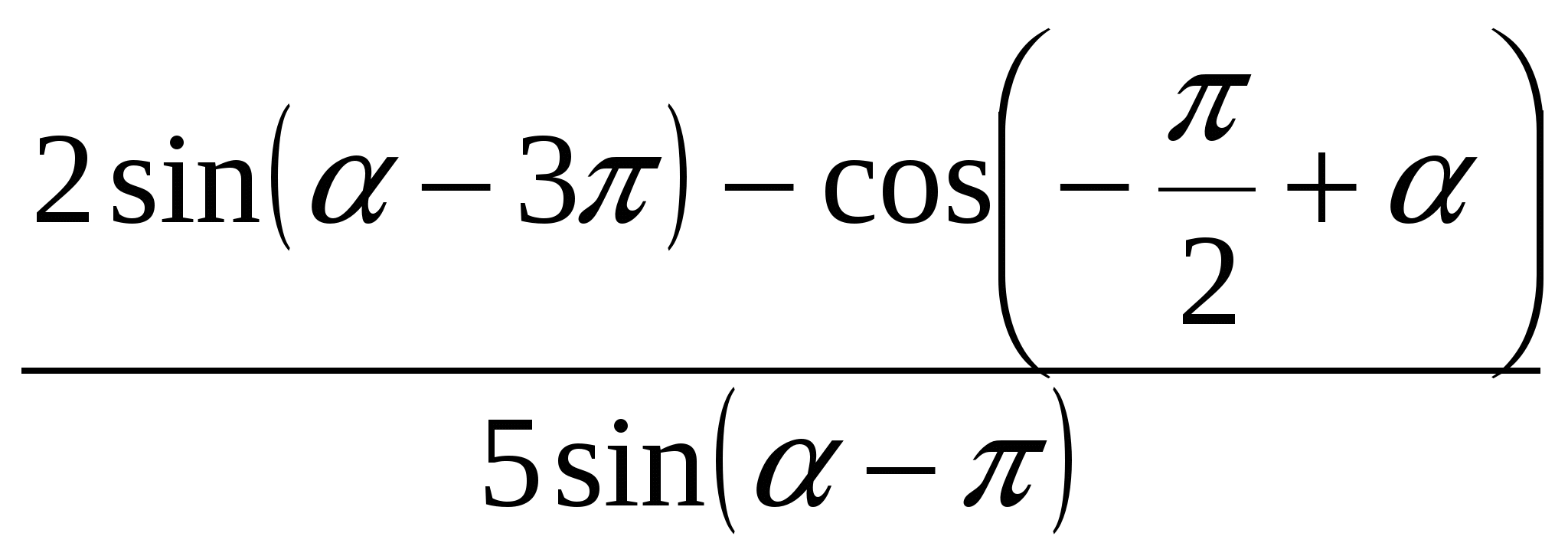

. Отговор. 0,62. намирам

, ако

и. Отговор. 10.563. Намерете стойността на израз

, ако

. Отговор. 2

1.3. Задачи за преобразуване на числени тригонометрични изрази.

При развиване на умения и способности на задачи за преобразуване на числени тригонометрични изрази трябва да се обърне внимание на познаването на таблицата със стойности на тригонометричните функции, свойствата на паритета и периодичността на тригонометричните функции.

а) Използване на точни стойности на тригонометрични функции за някои ъгли.

Пример 6 . Изчисли
.

Решение.
.

Отговор.
.

б) Използване на свойствата на паритета тригонометрични функции.

Пример 7 . Изчисли
.

Решение. .

Отговор.

в) Използване на свойствата на периодичносттатригонометрични функции.

Пример 8 . Намерете стойността на израз
.

Решение. .

Отговор.
.

Задачи за самостоятелно решаване:

1. Намерете стойността на израз

. Отговор. -40,52. Намерете стойността на израза

. Отговор. 17

3. Намерете стойността на израз
. Отговор. 6

. Отговор. -24

Отговор. -64

1.4 Смесени задачи.

Тестовата форма на сертифициране има много важни характеристики, така че е важно да се обърне внимание на задачите, свързани с използването на няколко тригонометрични формули едновременно.

Пример 9 намирам
, ако
.

Решение.
.

Отговор.
.

Пример 10 . намирам
, ако
и
.

Решение. .

защото , тогава
.

Отговор.
.

Пример 11. намирам
, ако .

Решение. , ,
,
,
,
,
.

Отговор.

Пример 12 Изчисли
.

Решение. .

Отговор.
.

Пример 13. Намерете стойността на израз
, ако
.

Решение. .

Отговор.
.

Задачи за самостоятелно решаване:

1. намирам

, ако

. Отговор. -1,75
2. намирам

, ако

. Отговор. 33. Намерете

, ако .Отговор. 0,254. Намерете стойността на израза

, ако

. Отговор. 0,35. Намерете стойността на израза

, ако

. Отговор. 5

Глава 2. Методически аспекти Организация на окончателното повторение на темата "Преобразуване на тригонометрични изрази."

Един от най-важните въпроси, допринасящи за по-нататъшното подобряване на академичните постижения, постигането на задълбочени и солидни знания сред учениците, е въпросът за повтарянето на вече изучен материал. Практиката показва, че в 10. клас е по-целесъобразно да се организира тематично повторение; в 11 клас - финално повторение.

2.1. Тематично повторение в 10. клас.

В процеса на работа върху математическия материал, повторението на всяка завършена тема или цял раздел от курса става особено важно.

С тематичното повторение знанията на учениците по темата се систематизират в последния етап от нейното преминаване или след почивка.

За тематично повторение се разпределят специални уроци, върху които се концентрира и обобщава материалът на една конкретна тема.

Повторението в урока се извършва чрез разговор с широкото участие на учениците в този разговор. След това учениците получават задача да повторят определена тема и се предупреждават, че ще има кредитна работа на тестове.

Тестът по дадена тема трябва да включва всички основни въпроси. След приключване на работата се анализират характерни грешки и се организира повторение за отстраняването им.

За уроци по тематично повторение предлагаме разг тестови работина тема "Преобразуване на тригонометрични изрази".

Тест #1

Тест #2

Тест #3

Таблица с отговори

Тест

2.2. Последно повторение в 11 клас.

Окончателното повторение се извършва на последния етап от изучаването на основните въпроси на курса по математика и се извършва в логическа връзка с изучаването на учебния материал за този раздел или курса като цяло.

Окончателното повторение на учебния материал има следните цели:

1. Активизиране на материала от целия курс на обучение за изясняване на неговата логическа структура и изграждане на система в рамките на предметните и междупредметните връзки.

2. Задълбочаване и, ако е възможно, разширяване на знанията на студентите по основните въпроси на курса в процеса на повторение.

В контекста на задължителния изпит по математика за всички завършили, постепенното въвеждане на USE кара учителите да възприемат нов подход към подготовката и провеждането на уроците, като се има предвид необходимостта да се гарантира, че всички ученици овладяват учебния материал на основно ниво, както и възможност за мотивирани студенти, които се интересуват от високи резултати за прием в университет, динамично напредване в усвояването на материала на повишено и високо ниво.

В уроците на последното повторение можете да разгледате следните задачи:

Пример 1 . Изчислете стойността на израза.Решение. =

= =

=0,5. Отговор. 0,5. Пример 2 Посочете най-голямото цяло число, което може да приеме изразът

Решение. защото
може да приема произволна стойност, принадлежаща на сегмента [–1; 1], тогава
приема произволна стойност на сегмента [–0,4; 0,4], следователно . Цялата стойност на израза е едно - числото 4.

Отговор: 4 Пример 3 . Опростете израза

Решение: Нека използваме формулата за разлагане на сумата от кубове: . Ние имаме

Ние имаме:
.

Отговор: 1

Пример 4 Изчисли
.

Решение. .

Отговор: 0,28

За уроците на финалното повторение предлагаме разработени тестове по темата "Преобразуване на тригонометрични изрази".

Посочете най-голямото цяло число, което не надвишава 1

Заключение.

След като работихме със съответната методическа литература по тази тема, можем да заключим, че способността и уменията за решаване на задачи, свързани с тригонометрични трансформации в училищния курс по математика, са много важни.

В хода на извършената работа беше извършена класификация на задачите B7. Разглеждат се тригонометричните формули, които най-често се използват в CMM от 2012 г. Дадени са примерни задачи с решения. Разработени са диференциални тестове за организиране на повторението и систематизирането на знанията при подготовката за изпита.

Препоръчително е да продължите започнатата работа, като вземете предвид решение на най-простите тригонометрични уравнения в задача B5, изучаване на тригонометрични функции в задача B14, задача B12, в която има формули, описващи физични явления и съдържащи тригонометрични функции.

В заключение бих искал да отбележа, че ефективността на полагането на изпита до голяма степен се определя от това колко ефективно е организиран процесът на подготовка на всички нива на образование, с всички категории ученици. И ако успеем да формираме у учениците самостоятелност, отговорност и готовност да продължат да учат през целия им следващ живот, тогава не само ще изпълним поръчката на държавата и обществото, но и ще повишим собственото си самочувствие.

Повторението на учебния материал изисква творческа работа от учителя. Той трябва да осигури ясна връзка между видовете повторение, да приложи дълбоко обмислена система за повторение. Овладяването на изкуството на организиране на повторението е задача на учителя. Силата на знанията на учениците до голяма степен зависи от неговото решение.

Литература.

Вигодски Я.Я., Наръчник по елементарна математика. -М .: Наука, 1970.

Задачи с повишена трудност по алгебра и началото на анализа: Учебник за 10-11 клас на гимназията / B.M. Ивлев, А.М. Абрамов, Ю.П. Дудницин, С.И. Шварцбург. – М.: Просвещение, 1990.

Приложение на основни тригонометрични формули за преобразуване на изрази (10 клас) // Фестивал на педагогическите идеи. 2012-2013 г.

Корянов А.Г. , Прокофиев А.А. Подготвяме добри ученици и отличници за изпит. - М .: Педагогически университет "Първи септември", 2012.- 103 с.

Кузнецова E.N.Опростяване на тригонометрични изрази. Решаване на тригонометрични уравнения по различни методи (подготовка за изпит). 11 клас. 2012-2013 г.

Куланин Е. Д. 3000 състезателни задачи по математика. 4-ти id., правилно. и допълнителни – М.: Ролф, 2000.

Мордкович А.Г. Методически проблеми на изучаването на тригонометрията в общообразователно училище // Математика в училище. 2002. № 6.

Пичурин Л.Ф. За тригонометрията и не само за нея: -М. Просвещение, 1985г

Решетников Н.Н. Тригонометрия в училище: -М. : Педагогически университет "Първи септември", 2006, л.к. 1.

Шабунин M.I., Прокофиев A.A. Математика. Алгебра. Начало на математическия анализ Профилно ниво: учебник за 10 клас - М .: БИНОМ. Лаборатория на знанието, 2007 г.

Образователен портал за подготовка за изпит.

Подготовка за изпита по математика „О, тази тригонометрия! http://festival.1september.ru/articles/621971/

Проект "Математика? Лесно!!!" http://www.resolventa.ru/