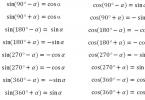Definícia. Redukčné vzorce sú vzorce, ktoré vám umožňujú prejsť od goniometrických funkcií formulára k funkciám argumentov. S ich pomocou je možné zmenšiť sínus, kosínus, tangens a kotangens ľubovoľného uhla na sínus, kosínus, tangens a kotangens uhla z intervalu od 0 do 90 stupňov (od 0 do radiánov). Redukčné vzorce nám teda umožňujú prejsť k práci s uhlami do 90 stupňov, čo je nepochybne veľmi pohodlné.

Redukčné vzorce:

Existujú dve pravidlá používania redukčných vzorcov.

1. Ak možno uhol znázorniť ako (π/2 ±a) alebo (3*π/2 ±a), potom zmeny názvu funkcie sin to cos, cos to sin, tg to ctg, ctg to tg. Ak je možné uhol znázorniť v tvare (π ±a) alebo (2*π ±a), potom Názov funkcie zostáva nezmenený.

Pozrite sa na obrázok nižšie, schematicky ukazuje, kedy zmeniť znamenie a kedy nie

2. Známka zníženej funkcie zostáva rovnaký. Ak mala pôvodná funkcia znamienko plus, potom aj redukovaná funkcia má znamienko plus. Ak mala pôvodná funkcia znamienko mínus, potom aj redukovaná funkcia má znamienko mínus.

Na obrázku nižšie sú znázornené znamienka základných goniometrických funkcií v závislosti od štvrťroka.

Príklad:

Vypočítajte

Použime redukčné vzorce:

Sin(150˚) je v druhej štvrtine, z obrázku vidíme, že znamenie hriechu v tejto štvrtine sa rovná „+“. To znamená, že daná funkcia bude mať aj znamienko „+“. Aplikovali sme druhé pravidlo.

Teraz 150˚ = 90˚ + 60˚. 90˚ je π/2. To znamená, že máme do činenia s prípadom π/2+60, preto podľa prvého pravidla zmeníme funkciu z sin na cos. V dôsledku toho dostaneme Sin(150˚) = cos(60˚) = ½.

A ešte jeden bod: redukčných vzorcov je do počtu pomerne veľa a hneď vás varujeme, aby ste sa ich všetky nenaučili naspamäť. Nie je to absolútne potrebné - existuje jeden, ktorý vám umožní jednoducho aplikovať redukčné vzorce.

Zapíšme si teda všetky redukčné vzorce vo forme tabuľky.

Tieto vzorce je možné prepísať pomocou stupňov a radiánov. Ak to chcete urobiť, zapamätajte si vzťah medzi stupňami a radiánmi a nahraďte π všade 180 stupňami.

Príklady použitia redukčných vzorcov

Účelom tohto odseku je ukázať, ako sa v praxi používajú redukčné vzorce pri riešení príkladov.

Na začiatok stojí za to povedať, že existuje nekonečné množstvo spôsobov, ako znázorniť uhol pod znamienkom goniometrických funkcií vo forme a . Je to spôsobené tým, že uhol môže mať akúkoľvek hodnotu. Ukážme si to na príklade.

Vezmime si napríklad uhol pod znamienkom goniometrickej funkcie rovný . Tento uhol môže byť reprezentovaný ako , alebo ako , alebo ako alebo mnohými inými spôsobmi.

Teraz sa pozrime, aké redukčné vzorce budeme musieť použiť v závislosti od znázornenia uhla. Vezmime .

Ak znázorníme uhol ako , potom toto zobrazenie zodpovedá redukčnému vzorcu tvaru , z ktorého získame . Tu môžeme uviesť hodnotu goniometrickej funkcie: .

Na prezentáciu už použijeme vzorec formulára , čo nás vedie k nasledujúcemu výsledku: .

Napokon, keďže zodpovedajúci redukčný vzorec má tvar .

Na záver tejto diskusie je potrebné poznamenať, že existujú určité vymoženosti pri používaní reprezentácií uhla, v ktorých má uhol hodnotu od 0 do 90 stupňov (od 0 do pi v polovičných radiánoch).

Pozrime sa na ďalší príklad použitia redukčných vzorcov.

Príklad.

Pomocou redukčných vzorcov znázornite cez sínus a tiež cez kosínus ostrého uhla.

Riešenie.

Na aplikáciu redukčných vzorcov potrebujeme znázorniť uhol 197 stupňov vo forme resp , a podľa podmienok problému musí byť uhol ostrý. To možno vykonať dvoma spôsobmi: alebo . teda alebo .

Prejdením na zodpovedajúce vzorce pre zníženie a , Získame a .

odpoveď:

A .

Mnemotechnické pravidlo

Ako sme spomenuli vyššie, nie je potrebné zapamätať si redukčné vzorce. Ak si ich pozorne prezriete, môžete identifikovať vzory, z ktorých môžete získať pravidlo, ktoré vám umožní získať ktorýkoľvek z redukčných vzorcov. Volá sa mnemotechnické pravidlo(mnemotechnika je umenie memorovania).

Mnemotechnické pravidlo obsahuje tri fázy:

Okamžite stojí za to povedať, že ak chcete použiť mnemotechnické pravidlo, musíte byť veľmi dobrí v identifikácii znakov sínus, kosínus, tangens a kotangens po štvrtinách, pretože to budete musieť robiť neustále.

Pozrime sa na aplikáciu mnemotechnického pravidla na príkladoch.

Príklad.

Pomocou mnemotechnického pravidla si zapíšte redukčné vzorce pre A , pričom uhol považujeme za uhol prvej štvrtiny.

Riešenie.

Nemusíme robiť prvý krok pravidla, pretože uhly pod znamienkami goniometrických funkcií sú už zapísané v požadovanom tvare.

Určme znamienko funkcií A . Za predpokladu, že - uhol prvej štvrtiny, uhol je tiež uhol prvej štvrtiny a uhol - uhol druhej štvrtiny. Kosínus v prvej štvrtine má znamienko plus a dotyčnica v druhej štvrtine má znamienko mínus. V tejto fáze budú mať požadované vzorce tvar a . Teraz, keď sme prišli na znamenia, môžeme prejsť na posledný krok mnemotechnického pravidla.

Keďže argument funkcie kosínus má tvar , potom treba zmeniť názov funkcie na kofunkciu, teda na sínus. A argument dotyčnice má tvar , preto by názov funkcie mal zostať rovnaký.

V dôsledku toho máme A . Môžete sa pozrieť na tabuľku redukčných vzorcov, aby ste sa uistili, že získané výsledky sú správne.

odpoveď:

A .

Ak chcete materiál spevniť, zvážte riešenie príkladu so špecifickými uhlami.

Príklad.

Pomocou mnemotechnického pravidla zredukujte na trigonometrické funkcie ostrého uhla.

Riešenie.

Najprv si predstavme uhol 777 stupňov vo forme potrebnej na uplatnenie mnemotechnického pravidla. Dá sa to urobiť dvoma spôsobmi: alebo.

Pôvodný uhol je prvý štvrtinový uhol, sínus pre tento uhol má znamienko plus.

Pre prezentáciu musí byť názov sínusu ponechaný rovnaký, ale na prezentáciu typu je potrebné zmeniť sínus na kosínus.

V dôsledku toho máme a .

odpoveď:

A .

Na záver tohto bodu zvážte príklad ilustrujúci dôležitosť správneho znázornenia uhla pod znamienkom goniometrických funkcií pre aplikáciu mnemotechnického pravidla: uhol musí byť ostrý!!!

Vypočítajme tangens uhla. V zásade, odkazom na hodnoty sínusu, kosínusu, tangensu a kotangensu v článku, môžeme okamžite odpovedať na otázku problému: .

Ak reprezentujeme uhol as alebo as , potom môžeme použiť mnemotechnické pravidlo: A , čo nás vedie k rovnakému výsledku.

Ale to je to, čo sa môže stať, ak vezmete reprezentáciu uhla, napríklad formy. V tomto prípade nás k tomuto výsledku dovedie mnemotechnické pravidlo. Tento výsledok je nesprávny a vysvetľuje sa to tým, že na znázornenie sme nemali právo použiť mnemotechnické pravidlo, pretože uhol nie je ostrý.

Dôkaz redukčných vzorcov

Vzorce redukcie odrážajú periodicitu, symetriu a vlastnosti posunu podľa uhlov a . Okamžite si všimnime, že všetky redukčné vzorce sa dajú dokázať vyradením termínu v argumentoch, pretože to znamená zmenu uhla o celé číslo o celý počet otáčok, čo nemení hodnoty goniometrických funkcií. Tento termín slúži ako odraz periodicity.

Prvý blok 16 redukčných vzorcov priamo vyplýva z vlastností sínus, kosínus, tangens a kotangens. Nemá cenu sa nimi ani zaoberať.

Prejdime k ďalšiemu bloku vzorcov. Najprv si ukážme prvé dva z nich. Ostatné vyplýva z nich. Poďme teda dokázať redukčné vzorce formulára A .

Zoberme si jednotkový kruh. Nech začiatočný bod A po otočení o uhol prejde do bodu A 1 (x, y) a po otočení o uhol do bodu A 2. Nakreslíme A 1 H 1 a A 2 H 2 – kolmice na priamku Ox.

Je ľahké vidieť, že pravouhlé trojuholníky OA 1 H 1 a OA 2 H 2 sú rovnaké v prepone a dvoch susedných uhloch. Z rovnosti trojuholníkov a polohy bodov A 1 a A 2 na jednotkovej kružnici je zrejmé, že ak má bod A 1 súradnice x a y, potom bod A 2 má súradnice −y a x. Potom nám definície sínusu a kosínusu umožňujú zapísať rovnosti a , z čoho vyplýva, že A . To dokazuje uvažované redukčné vzorce pre akýkoľvek uhol.

Zvažujem to A (v prípade potreby pozri článok základné goniometrické identity), ako aj práve osvedčené vzorce, získame a . Takže sme dokázali nasledujúce dva redukčné vzorce.

Na dôkaz redukčných vzorcov argumentom stačí reprezentovať ho ako , a potom použiť overené vzorce a vlastnosti goniometrických funkcií s opačnými argumentmi. Napríklad, .

Všetky ostatné redukčné vzorce sa dokazujú podobným spôsobom na základe už overených dvojitou aplikáciou. Napríklad sa zobrazuje ako , ale ako . A a - ako a resp.

Bibliografia.

• Algebra: Učebnica pre 9. ročník. priem. škola/Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Ed. S. A. Telyakovsky. - M.: Education, 1990. - 272 s.: ill. - ISBN 5-09-002727-7
• Bašmakov M.I. Algebra a začiatky analýzy: Učebnica. pre 10-11 ročníkov. priem. školy - 3. vyd. - M.: Školstvo, 1993. - 351 s.: chor. - ISBN 5-09-004617-4.
• Algebra a začiatok analýzy: Proc. pre 10-11 ročníkov. všeobecné vzdelanie inštitúcie / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn a ďalší; Ed. A. N. Kolmogorov. - 14. vyd. - M.: Vzdelávanie, 2004. - 384 s.: i. - ISBN 5-09-013651-3.
• Gusev V. A., Mordkovich A. G. Matematika (príručka pre študentov technických škôl): Proc. príspevok.- M.; Vyššie škola, 1984.-351 s., ill.

A ešte jedna úloha B11 na tú istú tému – zo skutočnej Jednotnej štátnej skúšky z matematiky.

Úloha. Nájdite význam výrazu:

V tomto krátkom videonávode sa naučíme, ako aplikovať redukčné vzorce za riešenie reálnych úloh B11 z Jednotnej štátnej skúšky z matematiky. Ako vidíte, máme dva trigonometrické výrazy, z ktorých každý obsahuje sínusy a kosínusy, ako aj dosť brutálne číselné argumenty.

Pred riešením týchto problémov si pripomeňme, čo sú redukčné vzorce. Takže, ak máme výrazy ako:

Potom sa prvého člena (tvaru k · π/2) môžeme zbaviť podľa špeciálnych pravidiel. Narysujme si trigonometrickú kružnicu a označme na nej hlavné body: 0, π/2; π; 3π/2 a 2π. Potom sa pozrieme na prvý člen pod znamienkom goniometrickej funkcie. Máme:

1. Ak člen, ktorý nás zaujíma, leží na zvislej osi trigonometrickej kružnice (napríklad: 3π/2; π/2 atď.), potom je pôvodná funkcia nahradená kofunkciou: sínus je nahradený kosínusom, a kosínus, naopak, sínusom.
2. Ak náš člen leží na vodorovnej osi, potom sa pôvodná funkcia nemení. Jednoducho odstránime prvý výraz vo výraze a je to.

Získame tak goniometrickú funkciu, ktorá neobsahuje členy tvaru k · π/2. Tým sa však práca s redukčnými vzorcami nekončí. Faktom je, že naša nová funkcia získaná po „vyradení“ prvého termínu môže mať pred sebou znamienko plus alebo mínus. Ako identifikovať toto znamenie? Teraz to zistíme.

Predstavme si, že uhol α zostávajúci vo vnútri goniometrickej funkcie po transformáciách má veľmi malú mieru. Čo však znamená „malá miera“? Povedzme α ∈ (0; 30°) - to je celkom dosť. Zoberme si príklad funkcie:

Potom, podľa našich predpokladov, že α ∈ (0; 30°) dospejeme k záveru, že uhol 3π/2 − α leží v tretej súradnicovej štvrtine, t.j. 3π/2 − α ∈ (π; 3π/2). Pamätajme na znak pôvodnej funkcie, t.j. y = sin x na tomto intervale. Je zrejmé, že sínus v tretej súradnicovej štvrtine je záporný, pretože podľa definície je sínus ordinátou konca pohyblivého polomeru (v skratke, sínus je súradnica y). Súradnica y v dolnej polrovine má vždy záporné hodnoty. To znamená, že v treťom štvrťroku je y tiež záporné.

Na základe týchto úvah môžeme zapísať konečný výraz:

Problém B11 - Možnosť 1

Tieto isté techniky sú celkom vhodné na riešenie problému B11 z Jednotnej štátnej skúšky z matematiky. Jediný rozdiel je v tom, že v mnohých reálnych úlohách B11 sa namiesto radiánovej miery (t.j. čísla π, π/2, 2π atď.) používa miera stupňov (t.j. 90°, 180°, 270° atď.). Pozrime sa na prvú úlohu:

Najprv sa pozrime na čitateľa. cos 41° je netabuľková hodnota, takže s tým nemôžeme nič robiť. Zatiaľ to nechajme tak.

Teraz sa pozrime na menovateľa:

sin 131° = sin (90° + 41°) = cos 41°

Je zrejmé, že ide o redukčný vzorec, takže sínus je nahradený kosínusom. Okrem toho na segmente leží uhol 41° (0°; 90°), t.j. v prvom súradnicovom kvadrante - presne tak, ako je to potrebné na použitie redukčných vzorcov. Ale potom je 90° + 41° druhá súradnicová štvrtina. Pôvodná funkcia y = sin x je tam kladná, takže v poslednom kroku dáme pred kosínus znamienko plus (inými slovami, nevložili sme nič).

Zostáva sa zaoberať posledným prvkom:

cos 240° = cos (180° + 60°) = −cos 60° = −0,5

Tu vidíme, že 180° je horizontálna os. V dôsledku toho sa samotná funkcia nezmení: bol tam kosínus - a kosínus tiež zostane. Opäť sa však vynára otázka: objaví sa plus alebo mínus pred výsledným výrazom cos 60°? Všimnite si, že 180° je tretia súradnicová štvrtina. Kosínus je tam záporný, preto bude mať nakoniec pred ním znamienko mínus. Celkovo dostaneme konštrukciu −cos 60° = −0,5 - to je tabuľková hodnota, takže všetko sa dá ľahko vypočítať.

Teraz dosadíme výsledné čísla do pôvodného vzorca a dostaneme:

Ako vidíte, číslo cos 41° v čitateli a menovateli zlomku sa ľahko zníži a zostane obvyklý výraz, ktorý sa rovná −10. V tomto prípade môže byť mínus buď vyňaté a umiestnené pred zlomkom, alebo „ponechané“ vedľa druhého faktora až do posledného kroku výpočtov. V každom prípade bude odpoveď -10. To je všetko, problém B11 je vyriešený!

Problém B14 - možnosť 2

Prejdime k druhej úlohe. Opäť máme pred sebou zlomok:

No, 27° leží v prvej súradnicovej štvrti, takže tu nič nezmeníme. Ale hriech 117° treba napísať (zatiaľ bez štvorčeka):

sin 117° = sin (90° + 27°) = cos 27°

Samozrejme, opäť pred nami redukčný vzorec: 90° je vertikálna os, preto sa sínus zmení na kosínus. Okrem toho uhol α = 117° = 90° + 27° leží v druhom súradnicovom kvadrante. Pôvodná funkcia y = sin x je tam kladná, preto je po všetkých transformáciách stále znamienko plus pred kosínusom. Inými slovami, nič sa tam nepridáva - necháme to tak: cos 27°.

Vrátime sa k pôvodnému výrazu, ktorý je potrebné vypočítať:

Ako vidíme, po transformáciách vznikla hlavná goniometrická identita v menovateli: sin 2 27° + cos 2 27° = 1. Spolu −4: 1 = −4 - tak sme našli odpoveď na druhú úlohu B11.

Ako vidíte, pomocou redukčných vzorcov sa takéto problémy z Jednotnej štátnej skúšky z matematiky riešia doslova v niekoľkých riadkoch. Žiadny sínus súčtu a kosínus rozdielu. Všetko, čo si musíme zapamätať, je len trigonometrický kruh.

Ako si zapamätať vzorce na redukciu goniometrických funkcií? Je to jednoduché, ak použijete asociáciu.Túto asociáciu som nevymyslel ja. Ako už bolo spomenuté, dobrá asociácia by mala „chytiť“, to znamená vyvolať živé emócie. Emócie vyvolané touto asociáciou nemôžem nazvať pozitívnymi. Ale dáva výsledok - umožňuje vám zapamätať si redukčné vzorce, čo znamená, že má právo na existenciu. Koniec koncov, ak sa vám to nepáči, nemusíte to používať, nie?

Redukčné vzorce majú tvar: sin(πn/2±α), cos(πn/2±α), tg(πn/2±α), ctg(πn/2±α). Pamätajte, že +α dáva pohyb proti smeru hodinových ručičiek, - α dáva pohyb v smere hodinových ručičiek.

Na prácu s redukčnými vzorcami potrebujete dva body:

1) dajte znamienko, ktoré má začiatočná funkcia (v učebniciach píšu: redukovateľná. Ale aby ste sa neplietli, je lepšie nazvať ju začiatočnou), ak za uhol prvej štvrtiny považujeme α, tzn. , malý.

2) Horizontálny priemer - π±α, 2π±α, 3π±α... - vo všeobecnosti, keď nie je zlomok, názov funkcie sa nemení. Vertikálne π/2±α, 3π/2±α, 5π/2±α... - pri zlomku sa mení názov funkcie: sínus - na kosínus, kosínus - na sínus, dotyčnica - na kotangens a kotangens — k dotyčnici.

Teraz vlastne asociácia:

vertikálny priemer (je tam zlomok) -

stáť opitý. Čo sa s ním stane skôr?

alebo uz je neskoro? Presne tak, padne.

Názov funkcie sa zmení.

Ak je priemer vodorovný, pijan už leží. Pravdepodobne spí. Nič sa mu nestane, už zaujal vodorovnú polohu. V súlade s tým sa názov funkcie nemení.

Teda sin(π/2±α), sin(3π/2±α), sin(5π/2±α) atď. dať ±cosα,

a sin(π±α), sin(2π±α), sin(3π±α), … - ±sinα.

Už vieme ako.

Ako to funguje? Pozrime sa na príklady.

1) cos(π/2+α)=?

Stávame sa π/2. Keďže +α znamená, že ideme dopredu, proti smeru hodinových ručičiek. Ocitáme sa v druhej štvrtine, kde má kosínus znamienko „-“. Názov funkcie sa mení („opitý stojí“, čo znamená, že spadne). takže,

cos(π/2+α)=-sin α.

Poďme na 2π. Keďže -α - ideme dozadu, teda v smere hodinových ručičiek. Ocitáme sa v IV štvrtine, kde má dotyčnica znamienko „-“. Názov funkcie sa nemení (priemer je vodorovný, „opilec už leží“). Teda tan(2π-α)=- tanα.

3) ctg²(3π/2-α)=?

Príklady, v ktorých je funkcia zvýšená na párnu mocninu, sú ešte jednoduchšie na riešenie. Párny stupeň „-“ ho odstráni, to znamená, že stačí zistiť, či sa názov funkcie zmení alebo zostane. Priemer je vertikálny (je tam zlomok, „stojí opitý“, spadne), názov funkcie sa zmení. Získame: ctg²(3π/2-α)= tan²α.

Patria do trigonometrickej časti matematiky. Ich podstatou je zredukovať goniometrické funkcie uhlov do „jednoduchej“ podoby. O dôležitosti ich poznania sa dá napísať veľa. Týchto vzorcov je už 32!

Nezľaknite sa, nemusíte sa ich učiť, ako mnohé iné vzorce v kurze matematiky. Netreba si zapĺňať hlavu zbytočnými informáciami, treba si zapamätať „kľúče“ či zákony a zapamätať si či odvodiť požadovaný vzorec nebude problém. Mimochodom, keď v článkoch píšem “...treba sa učiť!!!” - to znamená, že sa to naozaj treba naučiť.

Ak nepoznáte redukčné vzorce, jednoduchosť ich odvodenia vás príjemne prekvapí - existuje „zákon“, pomocou ktorého sa to dá ľahko urobiť. A môžete napísať ktorýkoľvek z 32 vzorcov za 5 sekúnd.

Uvediem len niektoré z problémov, ktoré sa objavia na Jednotnej štátnej skúške z matematiky, kde bez znalosti týchto vzorcov je vysoká pravdepodobnosť zlyhania pri ich riešení. Napríklad:

– úlohy na riešenie pravouhlého trojuholníka, kde hovoríme o vonkajšom uhle a úlohy na vnútorné uhly, niektoré z týchto vzorcov sú tiež potrebné.

- úlohy na výpočet hodnôt goniometrických výrazov; prevod numerických goniometrických výrazov; prevod doslovných goniometrických výrazov.

– úlohy na dotyčnici a geometrický význam dotyčnice, je potrebný redukčný vzorec pre dotyčnicu, ako aj iné úlohy.

– stereometrické úlohy, pri riešení je často potrebné určiť sínus alebo kosínus uhla, ktorý leží v rozsahu od 90 do 180 stupňov.

A to sú práve tie body, ktoré sa týkajú Jednotnej štátnej skúšky. A v samotnom kurze algebry je veľa problémov, ktorých riešenie sa jednoducho nezaobíde bez znalosti redukčných vzorcov.

K čomu to teda vedie a ako nám zadané vzorce uľahčujú riešenie problémov?

Napríklad musíte určiť sínus, kosínus, tangens alebo kotangens ľubovoľného uhla od 0 do 450 stupňov:

uhol alfa sa pohybuje od 0 do 90 stupňov

* * *

Takže je potrebné pochopiť „zákon“, ktorý tu funguje:

1. Určte znamienko funkcie v príslušnom kvadrante.

Dovoľte mi pripomenúť vám:

2. Pamätajte na nasledovné:

funkcia sa mení na kofunkciu

funkcia sa nemení na kofunkciu

Čo znamená pojem – funkcia sa mení na kofunkciu?

Odpoveď: sínus sa mení na kosínus alebo naopak, dotyčnica na kotangens alebo naopak.

To je všetko!

Teraz si podľa predloženého zákona sami napíšeme niekoľko redukčných vzorcov:

Tento uhol leží v treťom štvrťroku, kosínus v treťom štvrťroku je záporný. Funkciu nemeníme na kofunkciu, pretože máme 180 stupňov, čo znamená:

Uhol leží v prvej štvrtine, sínus v prvej štvrtine je kladný. Funkciu nemeníme na kofunkciu, pretože máme 360 ​​stupňov, čo znamená:

Tu je ďalšie dodatočné potvrdenie, že sínusy susedných uhlov sú rovnaké:

Uhol leží v druhej štvrtine, sínus v druhej štvrtine je kladný. Funkciu nemeníme na kofunkciu, pretože máme 180 stupňov, čo znamená:

Prepracujte každý vzorec v duchu alebo písomne ​​a budete presvedčení, že na tom nie je nič zložité.

***

V článku o riešení bola zaznamenaná nasledujúca skutočnosť - sínus jedného ostrého uhla v pravouhlom trojuholníku sa rovná kosínusu iného ostrého uhla v ňom.