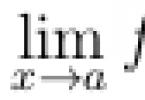Teória limitov je jednou z oblastí matematickej analýzy. Otázka riešenia limitov je pomerne rozsiahla, keďže existujú desiatky metód riešenia limitov rôznych typov. Existujú desiatky nuancií a trikov, ktoré vám umožňujú vyriešiť tento alebo ten limit. Napriek tomu sa ešte pokúsime pochopiť hlavné typy limitov, s ktorými sa v praxi najčastejšie stretávame.

Začnime samotným konceptom limitu. Najprv však krátke historické pozadie. V 19. storočí žil Francúz Augustin Louis Cauchy, ktorý dal prísne definície mnohým pojmom matan a položil ich základy. Treba povedať, že tento uznávaný matematik bol, je a bude v nočných morách všetkých študentov fyziky a matematiky, keďže dokázal obrovské množstvo teorémov matematickej analýzy a jedna veta je smrteľnejšia ako druhá. V tejto súvislosti zatiaľ nebudeme uvažovať stanovenie Cauchyho limitu, ale skúsme urobiť dve veci:

1. Pochopte, čo je to limit.
2. Naučte sa riešiť hlavné typy limitov.

Ospravedlňujem sa za niektoré nevedecké vysvetlenia, dôležité je, aby bol materiál zrozumiteľný aj pre čajník, čo je vlastne úlohou projektu.

Aký je teda limit?

A len príklad, prečo huňatá baba....

Akýkoľvek limit pozostáva z troch častí:

1) Známa ikona limitu.
2) Záznamy pod ikonou limitu, v tomto prípade . Záznam znie „X má tendenciu k jednej“. Najčastejšie - presne, aj keď namiesto „X“ v praxi existujú iné premenné. V praktických úlohách môže byť miesto jedného absolútne ľubovoľné číslo, ako aj nekonečno ().
3) Funkcie pod medzným znakom, v tomto prípade .

Samotné nahrávanie znie takto: „limita funkcie, keďže x má tendenciu k jednote“.

Pozrime sa na ďalšiu dôležitú otázku – čo znamená výraz „x“? usiluje do jedného"? A čo to vlastne znamená „usilovať sa“?
Koncept limitu je takpovediac pojmom, dynamický. Zostavme postupnosť: najprv , potom , , ..., , ….
To znamená, že výraz „x usiluje k jednej“ treba chápať takto: „x“ dôsledne preberá hodnoty ktoré sa k jednote približujú nekonečne blízko a prakticky sa s ňou zhodujú.

Ako vyriešiť vyššie uvedený príklad? Na základe vyššie uvedeného stačí nahradiť jeden do funkcie pod znakom limitu:

Takže prvé pravidlo: Keď je daný limit, najprv sa jednoducho pokúsime zapojiť číslo do funkcie.

Uvažovali sme o najjednoduchšej hranici, ale aj tie sa v praxi vyskytujú, a to nie tak zriedka!

Príklad s nekonečnom:

Poďme zistiť, čo to je? To je prípad, keď sa zvyšuje bez obmedzenia, to znamená: najprv, potom, potom, potom a tak ďalej do nekonečna.

Čo sa stane s funkciou v tomto čase?
, , , …

Takže: ak , potom má funkcia tendenciu k mínus nekonečnu:

Zhruba povedané, podľa nášho prvého pravidla namiesto „X“ dosadíme do funkcie nekonečno a dostaneme odpoveď.

Ďalší príklad s nekonečnom:

Opäť začneme zvyšovať do nekonečna a pozrieme sa na správanie funkcie:

Záver: keď sa funkcia zvyšuje bez obmedzenia:

A ďalšia séria príkladov:

Skúste si v duchu analyzovať nasledovné a zapamätajte si najjednoduchšie typy limitov:

, , , , , , , , ,
Ak máte kdekoľvek pochybnosti, môžete si vziať do ruky kalkulačku a trochu si zacvičiť.
V prípade, že , skúste zostaviť postupnosť , , . Ak potom , , .

! Poznámka: Presne povedané, tento prístup ku konštrukcii postupností niekoľkých čísel je nesprávny, ale na pochopenie najjednoduchších príkladov je celkom vhodný.

Venujte pozornosť aj nasledujúcej veci. Aj keď je limit uvedený s veľkým číslom navrchu alebo dokonca s miliónom: , potom je všetko rovnaké , pretože skôr či neskôr „X“ začne nadobúdať také gigantické hodnoty, že milión v porovnaní bude skutočný mikrób.

Čo si musíte zapamätať a pochopiť z vyššie uvedeného?

1) Keď je daný limit, najprv sa jednoducho pokúsime nahradiť číslo do funkcie.

2) Musíte pochopiť a okamžite vyriešiť tie najjednoduchšie limity, ako napr , , atď.

Okrem toho má limit veľmi dobrý geometrický význam. Pre lepšie pochopenie témy odporúčam prečítať si učebný materiál Grafy a vlastnosti elementárnych funkcií. Po prečítaní tohto článku nielenže konečne pochopíte, čo je limita, ale zoznámite sa aj so zaujímavými prípadmi, keď limita funkcie vo všeobecnosti neexistuje!

V praxi je, žiaľ, darčekov málo. A preto prejdeme k zvažovaniu zložitejších limitov. Mimochodom, na túto tému existuje intenzívny kurz vo formáte pdf, čo je užitočné najmä vtedy, ak máte VEĽMI málo času na prípravu. Ale materiály stránky, samozrejme, nie sú horšie:

Teraz budeme uvažovať o skupine limity when a funkciou je zlomok, ktorého čitateľ a menovateľ obsahuje polynómy

Príklad:

Vypočítajte limit

Podľa nášho pravidla sa pokúsime do funkcie dosadiť nekonečno. Čo získame na vrchole? Nekonečno. A čo sa deje nižšie? Tiež nekonečno. Máme teda to, čo sa nazýva druhová neistota. Niekto by si mohol myslieť, že , a odpoveď je hotová, ale vo všeobecnom prípade to tak vôbec nie je a je potrebné použiť nejakú techniku ​​riešenia, ktorú teraz zvážime.

Ako riešiť limity tohto typu?

Najprv sa pozrieme na čitateľa a nájdeme najvyššiu mocnosť:

Vedúca mocnina v čitateli je dvojka.

Teraz sa pozrieme na menovateľa a tiež ho nájdeme na najvyššiu moc:

Najvyšší stupeň menovateľa je dva.

Potom zvolíme najvyššiu mocninu čitateľa a menovateľa: v tomto príklade sú rovnaké a rovnajú sa dvom.

Spôsob riešenia je teda nasledovný: na odhalenie neistoty je potrebné vydeliť čitateľa a menovateľa najvyššou mocninou.

Tu je odpoveď a už vôbec nie nekonečno.

Čo je zásadne dôležité pri návrhu rozhodnutia?

Najprv uvedieme neistotu, ak existuje.

Po druhé, je vhodné prerušiť riešenie na prechodné vysvetlenia. Zvyčajne používam znak, ktorý nemá žiadny matematický význam, ale znamená, že riešenie je prerušené na prechodné vysvetlenie.

Po tretie, v limite je vhodné vyznačiť, čo kam ide. Keď je práca vypracovaná ručne, je pohodlnejšie to urobiť takto:

Na poznámky je lepšie použiť jednoduchú ceruzku.

Samozrejme, nemusíte nič z toho robiť, ale potom možno učiteľ upozorní na nedostatky v riešení alebo začne klásť doplňujúce otázky o zadaní. Potrebujete to?

Príklad 2

Nájdite hranicu
Opäť v čitateli a menovateli nájdeme v najvyššom stupni:

Maximálny stupeň v čitateli: 3
Maximálny stupeň v menovateli: 4
Vyberte si najväčší hodnotu, v tomto prípade štyri.
Podľa nášho algoritmu, aby sme odhalili neistotu, delíme čitateľa a menovateľa .
Kompletné zadanie môže vyzerať takto:

Vydeľte čitateľa a menovateľa podľa

Príklad 3

Nájdite hranicu
Maximálny stupeň „X“ v čitateli: 2
Maximálny stupeň „X“ v menovateli: 1 (možno napísať ako)
Na odhalenie neistoty je potrebné vydeliť čitateľa a menovateľa číslom . Konečné riešenie môže vyzerať takto:

Vydeľte čitateľa a menovateľa podľa

Zápis neznamená delenie nulou (nulou sa deliť nedá), ale delenie nekonečne malým číslom.

Odhalením druhovej neistoty sa nám to možno podarí konečné číslo, nula alebo nekonečno.

Limity s neurčitosťou typu a spôsob ich riešenia

Ďalšia skupina limitov je trochu podobná limitom, ktoré sme práve zvážili: čitateľ a menovateľ obsahujú polynómy, ale „x“ už nemá tendenciu k nekonečnu, ale k konečné číslo.

Príklad 4

Vyriešiť limit
Najprv skúsme nahradiť -1 do zlomku:

V tomto prípade sa získa takzvaná neistota.

Všeobecné pravidlo: ak čitateľ a menovateľ obsahujú polynómy a forma je neurčitá, potom to zverejniť musíte rozpočítať čitateľa a menovateľa.

Na to je najčastejšie potrebné vyriešiť kvadratickú rovnicu a/alebo použiť skrátené vzorce na násobenie. Ak ste na tieto veci zabudli, navštívte stránku Matematické vzorce a tabuľky a prečítajte si učebný materiál Horúce vzorce pre kurz školskej matematiky. Mimochodom, najlepšie je vytlačiť si to, vyžaduje sa to veľmi často a informácie sa lepšie absorbujú z papiera.

Poďme teda vyriešiť náš limit

Zohľadnite čitateľa a menovateľa

Aby ste mohli vypočítať čitateľa, musíte vyriešiť kvadratickú rovnicu:

Najprv nájdeme diskriminant:

A jeho druhá odmocnina: .

Ak je diskriminant veľký, napríklad 361, použijeme kalkulačku, funkcia extrakcie druhej odmocniny je na najjednoduchšej kalkulačke.

! Ak sa koreň nevytiahne celý (získa sa zlomkové číslo s čiarkou), je veľmi pravdepodobné, že diskriminant bol vypočítaný nesprávne alebo bol v úlohe preklep.

Ďalej nájdeme korene:

Takto:

Všetky. Čitateľ sa rozkladá na faktor.

Menovateľ. Menovateľ je už najjednoduchší faktor a neexistuje spôsob, ako ho zjednodušiť.

Samozrejme sa to dá skrátiť na:

Teraz dosadíme -1 do výrazu, ktorý zostane pod limitným znakom:

Prirodzene, v teste, teste alebo skúške nie je riešenie nikdy popísané tak podrobne. Vo finálnej verzii by mal dizajn vyzerať asi takto:

Rozložme čitateľa na faktor.

Príklad 5

Vypočítajte limit

Po prvé, „dokončená“ verzia riešenia

Rozložme čitateľa a menovateľa.

Čitateľ:
Menovateľ:



,

Čo je dôležité v tomto príklade?
Po prvé, musíte dobre rozumieť tomu, ako sa čitateľ odhaľuje, najprv sme vyňali 2 zo zátvoriek a potom sme použili vzorec pre rozdiel druhých mocnín. Toto je vzorec, ktorý musíte poznať a vidieť.

Odporúčanie: Ak je v limite (takmer akéhokoľvek typu) možné vyňať číslo zo zátvoriek, potom to vždy robíme.
Okrem toho je vhodné presunúť takéto čísla za ikonu limitu. Prečo? Áno, len aby neprekážali. Hlavná vec je nestratiť tieto čísla neskôr počas riešenia.

Upozorňujeme, že v záverečnej fáze riešenia som z ikony limitu odstránil dve a potom mínus.

! Dôležité
Počas riešenia sa fragment typu vyskytuje veľmi často. Znížte tento zlomokje zakázané . Najprv musíte zmeniť znamienko čitateľa alebo menovateľa (do zátvoriek vložte -1).
, čiže sa objaví znamienko mínus, s ktorým sa počíta pri výpočte limitu a netreba ho vôbec strácať.

Vo všeobecnosti som si všimol, že najčastejšie pri hľadaní limitov tohto typu musíte riešiť dve kvadratické rovnice, to znamená, že aj čitateľ aj menovateľ obsahujú kvadratické trojčlenky.

Metóda násobenia čitateľa a menovateľa konjugovaným výrazom

Naďalej zvažujeme neistotu formy

Ďalší typ limitov je podobný predchádzajúcemu typu. Jediná vec, okrem polynómov, pridáme korene.

Príklad 6

Nájdite hranicu

Začnime sa rozhodovať.

Najprv sa pokúsime dosadiť 3 do výrazu pod limitným znakom
Opakujem ešte raz – toto je prvá vec, ktorú musíte urobiť pre AKÝKOĽVEK limit. Táto akcia sa zvyčajne vykonáva mentálne alebo vo forme návrhu.

Bola získaná neistota formy, ktorú je potrebné odstrániť.

Ako ste si určite všimli, náš čitateľ obsahuje rozdiel koreňov. A v matematike je zvykom zbaviť sa koreňov, ak je to možné. Prečo? A život je bez nich jednoduchší.

Limita funkcie v bode a v

Limita funkcie je hlavným aparátom matematickej analýzy. S jeho pomocou sa následne určí spojitosť funkcie, derivácia, integrál a súčet radu.

Nech je funkcia y=f(X)definované v nejakom okolí bodu, snáď s výnimkou bodu samotného.

Sformulujme dve ekvivalentné definície limity funkcie v bode.

Definícia 1 (v „jazyku sekvencií“ alebo podľa Heineho). číslo b volal limit funkcie r=f(X) v bode (alebo pre ), ak pre akúkoľvek sekvenciu prípustných hodnôt argumentov konverguje (t.j.), postupnosť zodpovedajúcich funkčných hodnôt konverguje k číslu b(tj).

V tomto prípade píšu alebo na. Geometrický význam limity funkcie: znamená, že pre všetky body X, dostatočne blízko k bodu , zodpovedajúce hodnoty funkcie sa od čísla líšia tak málo, ako si želáte b.

Definícia 2 (v jazyku e-d “, alebo podľa Cauchyho). číslo b volal limit funkcie r=f(X) v bode (alebo pre ), ak pre akékoľvek kladné číslo e existuje kladné číslo d také, že pre všetky spĺňajúce nerovnosť , nerovnosť .

Zaznamenané.

Táto definícia sa dá stručne napísať takto:

Všimnite si, že to môžete napísať takto.

Geometrický význam limity funkcie: ak pre akékoľvek e-okolie bodu b je tam také d-okolie bodu , že pre všetkých z tohto d-okolia zodpovedajú zodpovedajúce hodnoty funkcie f(X) ležia v e-okolí bodu b. Inými slovami, body na grafe funkcie r=f(X) ležia vo vnútri pásu šírky 2e ohraničeného priamkami pri = b+e, pri = b- e (obrázok 17). Je zrejmé, že hodnota d závisí od výberu e, preto píšeme d = d(e).

Pri určovaní limity funkcie sa predpokladá, že X usiluje o akýmkoľvek spôsobom: zostáva menej ako (naľavo od ), väčší než (napravo od ), alebo kolísanie okolo bodu .

Existujú prípady, keď metóda aproximácie argumentu X Komu výrazne ovplyvňuje hodnotu limitu funkcie. Preto sa zavádzajú koncepty jednostranných limitov.

Definícia. Číslo sa volá limit funkcie r=f(X) vľavo v bode , ak pre ľubovoľné číslo e > 0 existuje číslo d = d(e) > 0 také, že pre , nerovnosť .

Limita vľavo sa píše takto alebo stručne (Dirichletova notácia) (obrázok 18).

Definované podobne limit funkcie vpravo , napíšme to pomocou symbolov:

V stručnosti, limit na pravej strane je označený .

Volá sa ľavá a pravá hranica funkcie jednosmerné limity . Je zrejmé, že ak , potom existujú obe jednostranné limity a .

Platí to aj naopak: ak existujú obe limity a a sú rovnaké, potom existuje limit a .

Ak, tak neexistuje.

Definícia. Nechajte funkciu r=f(X) je definovaný v intervale . číslo b volal limit funkcie r=f(X) pri X® ¥, ak pre ľubovoľné číslo e > 0 také číslo existuje M = M(e) > 0, čo pre všetkých X, uspokojenie nerovnosti nerovnosť je uspokojená. Stručne možno túto definíciu napísať takto:

Ak X® +¥, potom napíšte, ak X® -¥, potom píšu , ak = , potom sa ich spoločný význam zvyčajne označuje .

Geometrický význam tejto definície je nasledujúci: for , to for a zodpovedajúce hodnoty funkcie r=f(X) spadajú do e-okolia bodu b, t.j. body grafu ležia v páse šírky 2e, ohraničenom priamkami a (obrázok 19).

Nekonečne veľké funkcie (b.b.f)

Infinitezimálne funkcie (infinitezimálne funkcie)

Definícia. Funkcia r=f(X) sa nazýva nekonečne veľký pri , ak pre akékoľvek číslo M> 0 existuje číslo d = d( M) > 0, čo je pre každého X, uspokojenie nerovnosti, nerovnosť je uspokojená. Napíšte alebo na .

Napríklad funkcia je b.b.f. v .

Ak f(X) má tendenciu k nekonečnu a nadobúda iba kladné hodnoty, potom napíšte ; ak len záporné hodnoty, tak .

Definícia. Funkcia r=f(X), definovaný na celej číselnej osi, sa nazýva nekonečne veľký pri , ak pre akékoľvek číslo M> 0 existuje také číslo N = N(M) > 0, čo je pre každého X uspokojenie nerovnosti, zapíše sa nerovnosť. Krátky:

Napríklad existuje b.b.f. v .

Všimnite si, že ak argument X, inklinujúci k nekonečnu, naberá len prirodzené hodnoty, t.j. , potom zodpovedajúca b.b.f. sa stáva nekonečne veľkou sekvenciou. Napríklad postupnosť je nekonečne veľká postupnosť. samozrejme, akékoľvek b.b.f. v okolí bodov je neobmedzená v tejto blízkosti. Opak nie je pravdou: neobmedzená funkcia nemusí byť b.b.f. (Napríklad, )

Ak však kde b - konečné číslo, potom funkcia f(x obmedzené v blízkosti bodu.

Z definície limity funkcie totiž vyplýva, že keď je podmienka splnená. Preto pre , a to znamená, že funkcia f(X) je obmedzený.

Definícia. Funkcia r=f(X) sa nazýva nekonečne malý pri , Ak

Podľa definície limity funkcie táto rovnosť znamená: pre akékoľvek číslo existuje číslo také, že pre všetky X uspokojením nerovnosti je nerovnosť uspokojená.

B.m.f. sa určuje podobne. pri

: Vo všetkých týchto prípadoch.

Infinitezimálne funkcie sa často nazývajú nekonečne malé množstvá alebo nekonečne malý ; zvyčajne sa označujú gréckymi písmenami a, b atď.

Príklady b.m.f. slúžiť funkcie, keď

Ďalší príklad: - nekonečne malá postupnosť.

Príklad Dokáž to.

Riešenie . Funkcia 5+ X možno reprezentovať ako súčet čísla 7 a b.m.f. X- 2 (at ), t.j. je splnená rovnosť. Preto vetou 3.4.6 dostaneme .

Základné teorémy o limitách

Uvažujme teorémy (bez dôkazu), ktoré uľahčujú hľadanie limity funkcie. Formulácia viet pre prípady, keď a je podobná. V prezentovaných vetách budeme predpokladať, že limity existujú.

Veta 5.8 Limita súčtu (rozdielu) dvoch funkcií sa rovná súčtu (rozdielu) ich limit: .

Veta 5.9 Limita súčinu dvoch funkcií sa rovná súčinu ich limitov:

Všimnite si, že veta platí pre súčin ľubovoľného konečného počtu funkcií.

Dôsledok 3 Konštantný faktor môže byť za hranicou znamienka: .

Dôsledok 4 Hranica stupňa s prirodzeným exponentom sa rovná rovnakému stupňu limity: . najmä

Veta 5.10 Limit zlomku sa rovná limite čitateľa vydelenej limitou menovateľa, pokiaľ limita v menovateli nie je nula:

Príklad Vypočítajte

Riešenie .

Príklad Vypočítajte

Riešenie . Tu nemožno použiť vetu o limite zlomku, pretože limita menovateľa, at je rovná 0. Okrem toho limita čitateľa je rovná 0. V takýchto prípadoch hovoríme, že máme typová neistota. Aby sme ho rozšírili, rozložíme čitateľa a menovateľa zlomku na faktor a potom ho znížime o:

Príklad Vypočítajte

Riešenie . Tu sa zaoberáme typová neistota. Ak chcete nájsť limit daného zlomku, vydeľte čitateľa a menovateľa takto:

Funkcia je teda súčtom čísla 2 a b.m.f

Známky limitov

Nie každá funkcia, dokonca aj obmedzená, má limit. Napríklad funkcia at nemá žiadne obmedzenie. V mnohých otázkach analýzy stačí overiť existenciu limity funkcie. V takýchto prípadoch sa používajú znaky existencie limitu.

Prvý a druhý pozoruhodný limit

Definícia. Pri výpočte limity výrazov obsahujúcich goniometrické funkcie sa často používa limita

volal prvý pozoruhodný limit .

Znie: limit pomeru sínusu k jeho argumentu sa rovná jednej, keď argument smeruje k nule.

Príklad Nájsť

Riešenie . Máme neistotu formy. Veta o limite zlomku neplatí. Označme potom pri a

Príklad 3 Nájdite

Riešenie.

Definícia. Rovnosti sú tzv druhá pozoruhodná hranica .

Komentujte. Je známe, že limita číselnej postupnosti

Má limit rovný e: . Číslo e sa nazýva Neperovo číslo. Číslo e je iracionálne, jeho približná hodnota je 2,72 (e = 2, 718281828459045...). Niektoré vlastnosti čísla e spôsobujú, že je obzvlášť vhodné zvoliť toto číslo ako základ logaritmov. Logaritmy k základu e sa nazývajú prirodzené logaritmy a sú označené Všimnite si, že

Prijmime bez dôkazu tvrdenie, že funkcia inklinuje aj k číslu e

Ak to vložíte, nasleduje. Tieto rovnosti sa široko používajú pri výpočte limitov. V aplikáciách analýzy hrá dôležitú úlohu exponenciálna funkcia so základom e. Funkcia sa nazýva exponenciálna a používa sa aj zápis

Príklad Nájsť

Riešenie . Označujeme samozrejme, že máme

Výpočet limitov

Na odhalenie neistôt tvaru je často užitočné použiť princíp nahradenia infinitezimál ekvivalentnými a iné vlastnosti ekvivalentných infinitezimálnych funkcií. Ako je známe ~ X kedy ~ X o , pretože

V tomto článku vám povieme, aká je limita funkcie. Najprv si vysvetlíme všeobecné body, ktoré sú veľmi dôležité pre pochopenie podstaty tohto javu.

Koncept limitu

V matematike je zásadne dôležitý pojem nekonečna, označovaného symbolom ∞. Treba ho chápať ako nekonečne veľké + ∞ alebo nekonečne malé - ∞ číslo. Keď hovoríme o nekonečne, často máme na mysli oba tieto významy naraz, ale zápis tvaru + ∞ alebo - ∞ by sa nemal nahradiť jednoducho ∞.

Limita funkcie sa zapíše ako lim x → x 0 f (x) . V spodnej časti napíšeme hlavný argument x a pomocou šípky naznačíme, ku ktorej hodnote x0 bude inklinovať. Ak je hodnota x 0 konkrétne reálne číslo, potom máme do činenia s limitou funkcie v bode. Ak má hodnota x 0 tendenciu k nekonečnu (nezáleží na tom, či ∞, + ∞ alebo - ∞), potom by sme mali hovoriť o limite funkcie v nekonečne.

Limita môže byť konečná alebo nekonečná. Ak sa rovná konkrétnemu reálnemu číslu, t.j. lim x → x 0 f (x) = A, potom sa to nazýva konečná limita, ale ak lim x → x 0 f (x) = ∞, lim x → x 0 f (x) = + ∞ alebo lim x → x 0 f (x) = - ∞ , potom nekonečno.

Ak nevieme určiť ani konečnú, ani nekonečnú hodnotu, znamená to, že takáto hranica neexistuje. Príkladom tohto prípadu by bola hranica sínusu v nekonečne.

V tomto odseku si vysvetlíme, ako nájsť hodnotu limity funkcie v bode a v nekonečne. Aby sme to dosiahli, musíme zaviesť základné definície a pamätať si, čo sú to číselné postupnosti, ako aj ich konvergenciu a divergenciu.

Definícia 1

Číslo A je limita funkcie f (x) ako x → ∞, ak postupnosť jej hodnôt konverguje k A pre akúkoľvek nekonečne veľkú postupnosť argumentov (záporných alebo kladných).

Zápis limity funkcie vyzerá takto: lim x → ∞ f (x) = A.

Definícia 2

Ako x → ∞, limita funkcie f(x) je nekonečná, ak postupnosť hodnôt pre akúkoľvek nekonečne veľkú postupnosť argumentov je tiež nekonečne veľká (kladná alebo záporná).

Záznam vyzerá ako lim x → ∞ f (x) = ∞ .

Príklad 1

Dokážte rovnosť lim x → ∞ 1 x 2 = 0 pomocou základnej definície limity pre x → ∞.

Riešenie

Začnime napísaním postupnosti hodnôt funkcie 1 x 2 pre nekonečne veľkú kladnú postupnosť hodnôt argumentu x = 1, 2, 3, . . . , n , . . . .

1 1 > 1 4 > 1 9 > 1 16 > . . . > 1 n 2 > . . .

Vidíme, že hodnoty budú postupne klesať až k 0. Pozri na obrázku:

x = - 1 , - 2 , - 3 , . . . , - n , . . .

1 1 > 1 4 > 1 9 > 1 16 > . . . > 1 - n2 > . . .

Tu tiež môžeme vidieť monotónny pokles smerom k nule, čo potvrdzuje platnosť tohto v podmienke rovnosti:

odpoveď: Správnosť tohto v podmienke rovnosti je potvrdená.

Príklad 2

Vypočítajte limit lim x → ∞ e 1 10 x .

Riešenie

Začnime ako predtým zapisovaním postupností hodnôt f (x) = e 1 10 x pre nekonečne veľkú kladnú postupnosť argumentov. Napríklad x = 1, 4, 9, 16, 25, . . . , 102, . . . → + ∞ .

e110; e 410; e 910; e1610; e 25 10; . . . ; e 10010; . . . = = 1,10; 1,49; 2,45; 4,95; 12, 18; . . . ; 22026, 46; . . .

Vidíme, že táto postupnosť je nekonečne kladná, čo znamená f (x) = lim x → + ∞ e 1 10 x = + ∞

Prejdime k zápisu hodnôt nekonečne veľkej negatívnej postupnosti, napríklad x = - 1, - 4, - 9, - 16, - 25, . . . , - 10 2 , . . . → - ∞ .

e-110; e-410; e-910; e-1610; e-2510; . . . ; e-10010; . . . = = 0,90; 0,67; 0,40; 0,20; 0,08; . . . ; 0,000045; . . . x = 1, 4, 9, 16, 25,. . . , 102, . . . → ∞

Keďže tiež smeruje k nule, potom f (x) = lim x → ∞ 1 e 10 x = 0 .

Riešenie problému je jasne znázornené na obrázku. Modré bodky označujú postupnosť kladných hodnôt, zelené bodky sledy záporných hodnôt.

odpoveď: lim x → ∞ e 1 10 x = + ∞, pr a x → + ∞ 0, pr a x → - ∞.

Prejdime k metóde výpočtu limity funkcie v bode. Na to potrebujeme vedieť správne definovať jednostrannú hranicu. To nám bude užitočné aj pri hľadaní zvislých asymptot grafu funkcie.

Definícia 3

Číslo B je limita funkcie f (x) vľavo ako x → a v prípade, keď postupnosť jej hodnôt konverguje k danému číslu pre ľubovoľnú postupnosť argumentov funkcie x n konvergujúcich k a, ak jeho hodnoty zostávajú menšie ako a (x n< a).

Takáto hranica sa písomne ​​označuje ako lim x → a - 0 f (x) = B.

Teraz sformulujme, aká je limita funkcie vpravo.

Definícia 4

Číslo B je limita funkcie f (x) vpravo ako x → a v prípade, keď postupnosť jej hodnôt konverguje k danému číslu pre ľubovoľnú postupnosť argumentov funkcie x n konvergujúcich k a, ak jeho hodnoty zostávajú väčšie ako a (x n > a) .

Túto limitu zapíšeme ako lim x → a + 0 f (x) = B .

Limitu funkcie f (x) môžeme nájsť v určitom bode, keď má rovnaké limity na ľavej a pravej strane, t.j. lim x → a f (x) = lim x → a - 0 f (x) = lim x → a + 0 f (x) = B . Ak sú obe limity nekonečné, limita funkcie v počiatočnom bode bude tiež nekonečná.

Teraz si tieto definície objasníme napísaním riešenia konkrétneho problému.

Príklad 3

Dokážte, že v bode x 0 = 2 existuje konečná limita funkcie f (x) = 1 6 (x - 8) 2 - 8 a vypočítajte jej hodnotu.

Riešenie

Aby sme problém vyriešili, musíme si pripomenúť definíciu limity funkcie v bode. Najprv dokážme, že pôvodná funkcia má limit vľavo. Zapíšme si postupnosť funkčných hodnôt, ktoré budú konvergovať k x 0 = 2, ak x n< 2:

f(-2); f(0); f (1); f 1 1 2; f 1 3 4; f 1 7 8; f 1 15 16; . . . ; f 1 1023 1024; . . . = = 8,667; 2 667; 0,167; - 0,958; - 1 489; - 1 747; - 1 874; . . . ; - 1 998; . . . → - 2

Keďže vyššie uvedená postupnosť sa zníži na -2, môžeme napísať, že lim x → 2 - 0 1 6 x - 8 2 - 8 = - 2.

6 , 4 , 3 , 2 1 2 , 2 1 4 , 2 1 8 , 2 1 16 , . . . , 2 1 1024 , . . . → 2

Hodnoty funkcií v tejto sekvencii budú vyzerať takto:

f (6); f (4); f (3); f 2 1 2; f 2 3 4; f 2 7 8; f 2 15 16; . . . ; f 2 1023 1024; . . . = = - 7,333; - 5 333; - 3 833; - 2 958; - 2 489; - 2 247; - 2 124; . . . , - 2 001, . . . → - 2

Táto postupnosť tiež konverguje k - 2, čo znamená lim x → 2 + 0 1 6 (x - 8) 2 - 8 = - 2.

Zistili sme, že limity na pravej a ľavej strane tejto funkcie budú rovnaké, čo znamená, že limita funkcie f (x) = 1 6 (x - 8) 2 - 8 v bode x 0 = 2 existuje, a lim x -> 216 (x-8)2-8 = -2.

Priebeh riešenia môžete vidieť na obrázku (zelené bodky sú sekvenciou hodnôt konvergujúcich k x n< 2 , синие – к x n > 2).

odpoveď: Limity na pravej a ľavej strane tejto funkcie budú rovnaké, čo znamená, že limita funkcie existuje a lim x → 2 1 6 (x - 8) 2 - 8 = - 2.

Ak chcete hlbšie študovať teóriu limitov, odporúčame vám prečítať si článok o spojitosti funkcie v bode a hlavných typoch bodov nespojitosti.

Ak si všimnete chybu v texte, zvýraznite ju a stlačte Ctrl+Enter

Zvážte funkciu %%f(x)%% definovanú aspoň v nejakej prepichnutej oblasti %%\stackrel(\circ)(\text(U))(a)%% bodu %%a \in \overline( \ mathbb(R))%% rozšírený číselný riadok.

Koncept Cauchyho limity

Zavolá sa číslo %%A \in \mathbb(R)%%. limit funkcie%%f(x)%% v bode %%a \v \mathbb(R)%% (alebo v %%x%% s tendenciou k %%a \in \mathbb(R)%%), ak, čo Bez ohľadu na kladné číslo %%\varepsilon%%, existuje kladné číslo %%\delta%% tak, že pre všetky body v prepichnutom %%\delta%% susedstve bodu %%a%% funkčné hodnoty patria do %%\varepsilon %%-okolie bodu %%A%%, príp

$$ A = \lim\limits_(x \to a)(f(x)) \Šípka vľavo\forall\varepsilon > 0 ~\existuje \delta > 0 \big(x \in \stackrel(\circ)(\text (U))_\delta(a) \Šípka doprava f(x) \v \texte(U)_\varepsilon (A) \big) $$

Táto definícia sa nazýva definícia %%\varepsilon%% a %%\delta%%, ktorú navrhol francúzsky matematik Augustin Cauchy a používa sa od začiatku 19. storočia až dodnes, pretože má potrebnú matematickú prísnosť a presnosť.

Kombinovanie rôznych susedstiev bodu %%a%% tvaru %%\stackrel(\circ)(\text(U))_\delta(a), \text(U)_\delta (\infty), \ text(U) _\delta (-\infty), \text(U)_\delta (+\infty), \text(U)_\delta^+ (a), \text(U)_\delta^ - (a) %% s okolím %%\text(U)_\varepsilon (A), \text(U)_\varepsilon (\infty), \text(U)_\varepsilon (+\infty), \ text(U) _\varepsilon (-\infty)%%, dostaneme 24 definícií Cauchyho limity.

Geometrický význam

Geometrický význam limity funkcie

Poďme zistiť, aký geometrický význam má limita funkcie v bode. Zostrojme graf funkcie %%y = f(x)%% a označme na ňom body %%x = a%% a %%y = A%%.

Limita funkcie %%y = f(x)%% v bode %%x \to a%% existuje a je rovná A, ak pre ľubovoľné %%\varepsilon%% okolie bodu %%A%% možno zadať také %%\ delta%%-okolie bodu %%a%%, tak, že pre akékoľvek %%x%% z tohto %%\delta%%-okolia bude hodnota %%f(x)% % bude v %%\varepsilon%%-bodoch susedstva %%A%%.

Všimnite si, že podľa definície limity funkcie podľa Cauchyho pre existenciu limity v %%x \to a%% nezáleží na tom, akú hodnotu má funkcia v bode %%a%%. Je možné uviesť príklady, kde funkcia nie je definovaná, keď %%x = a%% alebo má inú hodnotu ako %%A%%. Limit však môže byť %%A%%.

Stanovenie Heineovho limitu

Prvok %%A \in \overline(\mathbb(R))%% sa nazýva limita funkcie %%f(x)%% v %% x \to a, a \in \overline(\mathbb( R))%% , ak pre akúkoľvek sekvenciu %%\(x_n\) \až %% z domény definície, sekvencia zodpovedajúcich hodnôt %%\big\(f(x_n)\big\)% % má tendenciu k %%A%%.

Definíciu limity podľa Heineho je vhodné použiť, keď vzniknú pochybnosti o existencii limity funkcie v danom bode. Ak je možné zostrojiť aspoň jednu sekvenciu %%\(x_n\)%% s limitom v bode %%a%% tak, že sekvencia %%\big\(f(x_n)\big\)%% nemá limit, potom môžeme konštatovať, že funkcia %%f(x)%% nemá v tomto bode limit. Ak pre dvoch rôzne sekvencie %%\(x"_n\)%% a %%\(x""_n\)%% majúce rovnaký limit %%a%%, sekvencie %%\big\(f(x"_n)\big\)%% a %%\big\(f(x""_n)\big\)%% majú rôzne limity, potom v tomto prípade neexistuje ani limita funkcie %%f(x)%%.

Príklad

Nech %%f(x) = \sin(1/x)%%. Skontrolujme, či limita tejto funkcie existuje v bode %%a = 0%%.

Najprv si zvolíme postupnosť $$ \(x_n\) = \left\(\frac((-1)^n)(n\pi)\right\) konvergujúcu k tomuto bodu. $$

Je jasné, že %%x_n \ne 0~\forall~n \in \mathbb(N)%% a %%\lim (x_n) = 0%%. Potom %%f(x_n) = \sin(\left((-1)^n n\pi\right)) \equiv 0%% a %%\lim\big\(f(x_n)\big\) = 0 %%.

Potom vezmite postupnosť konvergujúcu k rovnakému bodu $$ x"_n = \left\( \frac(2)((4n + 1)\pi) \right\), $$

pre ktoré %%\lim(x"_n) = +0%%, %%f(x"_n) = \sin(\big((4n + 1)\pi/2\big)) \equiv 1%% a %%\lim\big\(f(x"_n)\big\) = 1%%. Podobne pre sekvenciu $$ x""_n = \left\(-\frac(2)((4n + 1) ) \pi) \vpravo\), $$

tiež konvergujúce k bodu %%x = 0%%, %%\lim\big\(f(x""_n)\big\) = -1%%.

Všetky tri sekvencie poskytli rôzne výsledky, čo je v rozpore s Heineho definičnou podmienkou, t.j. táto funkcia nemá obmedzenie v bode %%x = 0%%.

Veta

Cauchyho a Heineho definície limity sú ekvivalentné.

Je uvedená formulácia hlavných viet a vlastností limity funkcie. Uvádzajú sa definície konečných a nekonečných limitov v konečných bodoch a v nekonečne (obojstrannom a jednostrannom) podľa Cauchyho a Heineho. Zohľadňujú sa aritmetické vlastnosti; teorémy súvisiace s nerovnosťami; Cauchyho konvergenčné kritérium; limita komplexnej funkcie; vlastnosti nekonečne malých, nekonečne veľkých a monotónnych funkcií. Definícia funkcie je uvedená.

Obsah

Druhá definícia podľa Cauchyho

Limita funkcie (podľa Cauchyho) ako jej argument x smeruje k x 0 je konečné číslo alebo bod v nekonečne a, pre ktorý sú splnené tieto podmienky:
1) je tam také prepichnuté okolie bodu x 0 , na ktorom je funkcia f (X) určený;
2) pre každé okolie bodu a patriace do , existuje také prepichnuté okolie bodu x 0 , na ktorom hodnoty funkcie patria do vybraného okolia bodu a:
v .

Tu a a x 0 môžu byť aj konečné čísla alebo body v nekonečne. Pomocou logických symbolov existencie a univerzálnosti možno túto definíciu napísať takto:
.

Ak vezmeme ľavé alebo pravé okolie koncového bodu za množinu, dostaneme definíciu Cauchyho limity vľavo alebo vpravo.

Veta
Cauchyho a Heineho definície limity funkcie sú ekvivalentné.
Dôkaz

Použiteľné susedstvá bodov

Potom v skutočnosti Cauchyho definícia znamená nasledovné.
Pre všetky kladné čísla existujú čísla , takže pre všetky x patriace do punktovaného okolia bodu : , hodnoty funkcie patria do okolia bodu a: ,
Kde , .

S touto definíciou nie je veľmi vhodné pracovať, pretože štvrte sú definované pomocou štyroch čísel. Dá sa to však zjednodušiť zavedením štvrtí s rovnako vzdialenými koncami. To znamená, že môžete dať ,. Potom dostaneme definíciu, ktorá sa ľahšie používa pri dokazovaní viet. Okrem toho je ekvivalentná definícii, v ktorej sa používajú ľubovoľné štvrte. Dôkaz tejto skutočnosti je uvedený v časti „Ekvivalencia Cauchyho definícií limity funkcie“.

Potom môžeme dať jednotnú definíciu limity funkcie v konečných a nekonečne vzdialených bodoch:
.
Tu pre koncové body
; ;
.
Akékoľvek okolie bodov v nekonečne je prepichnuté:
; ; .

Konečné limity funkcie v koncových bodoch

Číslo a sa nazýva limita funkcie f (X) v bode x 0 , Ak
1) funkcia je definovaná na nejakom punktovanom okolí koncového bodu;
2) pre všetky existuje také, že v závislosti od , také, že pre všetky x, pre ktoré platí nerovnosť
.

Pomocou logických symbolov existencie a univerzálnosti možno definíciu limity funkcie napísať takto:
.

Jednostranné limity.
Ľavý limit v bode (ľavý limit):
.
Pravý limit v bode (pravý limit):
.
Ľavý a pravý limit sa často označujú takto:
; .

Konečné limity funkcie v bodoch v nekonečne

Limity v bodoch v nekonečne sa určujú podobným spôsobom.
.
.
.

Nekonečné funkčné limity

Môžete tiež zaviesť definície nekonečných limitov určitých znakov rovných a :
.
.

Vlastnosti a vety limity funkcie

Ďalej predpokladáme, že uvažované funkcie sú definované v zodpovedajúcom punktovanom okolí bodu , čo je konečné číslo alebo jeden zo symbolov: . Môže to byť aj jednostranný hraničný bod, teda mať tvar alebo . Okolie je obojstranné pre obojstranný limit a jednostranné pre jednostranný limit.

Základné vlastnosti

Ak hodnoty funkcie f (X) zmeniť (alebo urobiť nedefinovaným) konečný počet bodov x 1, x 2, x 3, ... x n, potom táto zmena neovplyvní existenciu a hodnotu limity funkcie v ľubovoľnom bode x 0 .

Ak existuje konečná limita, potom existuje prepichnuté okolie bodu x 0 , na ktorom je funkcia f (X) obmedzené:
.

Nech má funkcia v bode x 0 konečná nenulová hranica:
.
Potom pre ľubovoľné číslo c z intervalu existuje takéto prepichnuté okolie bodu x 0 , za čo ,
, Ak ;
, Ak .

Ak je na niektorom prepichnutom okolí bodu , konštanta, potom .

Ak existujú konečné limity a a na nejakom prerazenom okolí bodu x 0
,
To .

Ak , a na niektorom okolí bodu
,
To .
Najmä ak je v niektorom susedstve bodu
,
potom ak , potom a ;
ak , potom a .

Ak na nejakom prerazenom okolí bodu x 0 :
,
a existujú konečné (alebo nekonečné určitého znamienka) rovnaké limity:
, To
.

Dôkazy o hlavných vlastnostiach sú uvedené na stránke
"Základné vlastnosti limity funkcie."

Nech sú funkcie a definované v niektorom prepichnutom okolí bodu. A nech existujú konečné limity:
A .
A nech C je konštanta, teda dané číslo. Potom
;
;
;
, Ak .

Ak potom.

Dôkazy aritmetických vlastností sú uvedené na stránke
"Aritmetické vlastnosti limity funkcie".

Cauchyho kritérium pre existenciu limity funkcie

Veta
Aby bola funkcia definovaná na nejakom punktovanom okolí konečného alebo v nekonečnom bode x 0 , mal v tomto bode konečnú limitu, je potrebné a postačujúce, aby pre akékoľvek ε > 0 tam bolo také prepichnuté okolie bodu x 0 , že pre všetky body a z tohto okolia platí nasledujúca nerovnosť:
.

Limita komplexnej funkcie

Veta o limite komplexnej funkcie
Nech má funkcia limit a mapuje punktované okolie bodu na punktované okolie bodu. Nech je funkcia definovaná na tomto okolí a má naň limit.
Tu sú konečné alebo nekonečne vzdialené body: . Okolie a im zodpovedajúce limity môžu byť obojstranné alebo jednostranné.
Potom existuje limita komplexnej funkcie a rovná sa:
.

Limitná veta komplexnej funkcie sa aplikuje, keď funkcia nie je definovaná v bode alebo má hodnotu odlišnú od limity. Ak chcete použiť túto vetu, musí existovať prepichnuté okolie bodu, kde množina hodnôt funkcie neobsahuje bod:
.

Ak je funkcia v bode spojitá, potom znamienko limitu možno použiť na argument spojitej funkcie:
.
Nasleduje veta zodpovedajúca tomuto prípadu.

Veta o limite spojitej funkcie funkcie
Nech existuje limita funkcie g (X) ako x → x 0 , a rovná sa t 0 :
.
Tu je bod x 0 môže byť konečná alebo nekonečne vzdialená: .
A nechajte funkciu f (t) spojitý v bode t 0 .
Potom existuje limita komplexnej funkcie f (g(x)), a rovná sa f (t 0):
.

Dôkazy teorémov sú uvedené na stránke
„Limita a kontinuita komplexnej funkcie“.

Nekonečne malé a nekonečne veľké funkcie

Infinitezimálne funkcie

Definícia
O funkcii sa hovorí, že je nekonečne malá, ak
.

Súčet, rozdiel a súčin konečného počtu nekonečne malých funkcií v je nekonečne malá funkcia v .

Súčin funkcie ohraničenej na nejakom punktovanom okolí bodu , k infinitezimálnemu at je nekonečne malá funkcia v .

Na to, aby funkcia mala konečnú limitu, je potrebné a postačujúce, že
,
kde je infinitezimálna funkcia v .

"Vlastnosti nekonečne malých funkcií".

Nekonečne veľké funkcie

Definícia
O funkcii sa hovorí, že je nekonečne veľká, ak
.

Súčet alebo rozdiel obmedzenej funkcie na nejakom prepichnutom okolí bodu a nekonečne veľkej funkcie v je nekonečne veľká funkcia v bode .

Ak je funkcia nekonečne veľká pre a funkcia je ohraničená nejakým prepichnutým okolím bodu, potom
.

Ak funkcia na nejakom prepichnutom okolí bodu spĺňa nerovnosť:
,
a funkcia je nekonečne malá pri:
, a (na niektorom prepichnutom okolí bodu), potom
.

Dôkazy vlastností sú uvedené v časti
"Vlastnosti nekonečne veľkých funkcií".

Vzťah medzi nekonečne veľkými a nekonečne malými funkciami

Z dvoch predchádzajúcich vlastností vyplýva súvislosť medzi nekonečne veľkými a nekonečne malými funkciami.

Ak je funkcia nekonečne veľká v , potom je funkcia nekonečne malá v .

Ak je funkcia nekonečne malá pre , a , potom je funkcia nekonečne veľká pre .

Vzťah medzi nekonečne malou a nekonečne veľkou funkciou možno vyjadriť symbolicky:
, .

Ak má infinitezimálna funkcia určité znamienko v , to znamená, že je kladná (alebo záporná) v niektorom punktovanom okolí bodu , potom túto skutočnosť možno vyjadriť takto:
.
Rovnakým spôsobom, ak má nekonečne veľká funkcia určité znamienko v , potom píšu:
.

Potom možno symbolickú súvislosť medzi nekonečne malými a nekonečne veľkými funkciami doplniť nasledujúcimi vzťahmi:
, ,
, .

Ďalšie vzorce týkajúce sa symbolov nekonečna nájdete na stránke
"Body v nekonečne a ich vlastnosti."

Limity monotónnych funkcií

Definícia
Zavolá sa funkcia definovaná na nejakej množine reálnych čísel X prísne zvyšovať, ak pre všetky platí nasledujúca nerovnosť:
.
V súlade s tým pre prísne klesá funkcia platí nasledujúca nerovnosť:
.
Pre neklesajúci:
.
Pre nezväčšujúce sa:
.

Z toho vyplýva, že striktne rastúca funkcia je aj neklesajúca. Striktne klesajúca funkcia je tiež nerastúca.

Funkcia sa volá monotónna, ak je neklesajúca alebo nezvyšujúca sa.

Veta
Nech funkcia neklesá na intervale kde .
Ak je hore ohraničený číslom M: potom existuje konečná limita. Ak to nie je obmedzené zhora, potom .
Ak je zdola ohraničená číslom m: tak existuje konečná hranica. Ak nie je obmedzený zdola, potom .

Ak sú body a a b v nekonečne, potom vo výrazoch medzné znamienka znamenajú, že .
Táto veta môže byť formulovaná kompaktnejšie.

Nech funkcia neklesá na intervale kde . Potom existujú jednostranné limity v bodoch a a b:
;
.

Podobná veta pre nerastúcu funkciu.

Nech sa funkcia nezvýši na intervale kde . Potom sú tu jednostranné limity:
;
.

Dôkaz vety je uvedený na stránke
"Limity monotónnych funkcií".

Definícia funkcie

Funkcia y = f (X) je zákon (pravidlo), podľa ktorého každý prvok x množiny X je spojený s jedným a len jedným prvkom y množiny Y.

Prvok x ∈ X volal argument funkcie alebo nezávislá premenná.
Prvok y ∈ Y volal funkčná hodnota alebo závislá premenná.

Množina X sa nazýva doména funkcie.
Súbor prvkov y ∈ Y, ktoré majú predobrazy v množine X, sa nazýva oblasť alebo súbor funkčných hodnôt.

Volá sa skutočná funkcia obmedzené zhora (zdola), ak existuje číslo M také, že nerovnosť platí pre všetkých:
.
Zavolá sa funkcia čísla obmedzené, ak existuje číslo M také, že pre všetky:
.

Horný okraj alebo presná horná hranica Skutočná funkcia sa nazýva najmenšie číslo, ktoré obmedzuje rozsah jej hodnôt zhora. To znamená, že toto je číslo s, pre ktoré pre každého a pre kohokoľvek existuje argument, ktorého funkčná hodnota presahuje s′: .
Horná hranica funkcie môže byť označená takto:
.

Respektíve spodný okraj alebo presná spodná hranica Skutočná funkcia sa nazýva najväčšie číslo, ktoré obmedzuje rozsah jej hodnôt zdola. To znamená, že toto je číslo i, pre ktoré pre každého a pre kohokoľvek existuje argument, ktorého funkčná hodnota je menšia ako i′: .
Infimum funkcie možno označiť takto:
.

Referencie:
L.D. Kudrjavcev. Kurz matematickej analýzy. Zväzok 1. Moskva, 2003.
CM. Nikolského. Kurz matematickej analýzy. Zväzok 1. Moskva, 1983.

Pozri tiež: