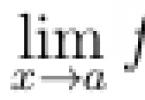číslo- dôležitý matematický pojem, ktorý sa v priebehu storočí menil.

Prvé predstavy o počte vznikli pri počítaní ľudí, zvierat, ovocia, rôznych produktov atď. Výsledkom sú prirodzené čísla: 1, 2, 3, 4, ...

Historicky prvým rozšírením pojmu číslo je pridanie zlomkových čísel k prirodzenému číslu.

Zlomok nazýva sa časť (podiel) jednotky alebo niekoľko rovnakých častí.

Určené: , kde m, n- celé čísla;

Zlomky s menovateľom 10 n, Kde n- celé číslo, tzv desiatkový: .

Medzi desatinnými zlomkami zaujíma osobitné miesto periodické zlomky: - čistý periodický zlomok, - zmiešaný periodický zlomok.

Ďalšie rozšírenie pojmu číslo je spôsobené rozvojom samotnej matematiky (algebry). Descartes v 17. storočí. predstaví koncept záporné číslo.

Čísla sa nazývajú celé čísla (kladné a záporné), zlomky (kladné a záporné) a nula racionálne čísla. Akékoľvek racionálne číslo možno zapísať ako konečný a periodický zlomok.

Na štúdium neustále sa meniacich premenných veličín sa ukázalo, že je potrebné nové rozšírenie pojmu čísla - zavedenie reálnych (reálnych) čísel - pridaním iracionálnych čísel k racionálnym číslam: iracionálne čísla sú nekonečné desatinné neperiodické zlomky.

Iracionálne čísla sa objavili pri meraní nesúmerateľných segmentov (strana a uhlopriečka štvorca), v algebre - pri extrakcii koreňov je príkladom transcendentálneho, iracionálneho čísla π, e .

čísla prirodzené(1, 2, 3,...), celý(..., –3, –2, –1, 0, 1, 2, 3,...), racionálny(reprezentovateľné ako zlomok) a iracionálny(nie je možné zobraziť ako zlomok ) tvoria súpravu skutočný (skutočný)čísla.

Komplexné čísla sa v matematike rozlišujú samostatne.

Komplexné čísla vznikajú v súvislosti s problémom riešenia štvorcov pre prípad D< 0 (здесь D– diskriminant kvadratickej rovnice). Tieto čísla dlho nenašli fyzické uplatnenie, a preto sa nazývali „imaginárne“ čísla. Teraz sa však veľmi široko používajú v rôznych oblastiach fyziky a technológie: elektrotechnika, hydro- a aerodynamika, teória pružnosti atď.

Komplexné čísla sa píšu v tvare: z= a+ bi. Tu a A b – reálne čísla, A i – pomyselná jednotka, t.j.e. i 2 = -1. číslo a volal úsečka, a b –ordinát komplexné číslo a+ bi. Dve komplexné čísla a+ bi A a–bi sa volajú konjugovať komplexné čísla.

Vlastnosti:

1. Reálne číslo A možno napísať aj vo forme komplexných čísel: a+ 0i alebo a – 0i. Napríklad 5 + 0 i a 5-0 i znamená to isté číslo 5.

2. Komplexné číslo 0 + bi volal čisto imaginárne číslo. Záznam bi znamená to isté ako 0 + bi.

3. Dve komplexné čísla a+ bi A c+ di sa považujú za rovnaké, ak a= c A b= d. V opačnom prípade sa komplexné čísla nerovnajú.

Akcie:

Doplnenie. Súčet komplexných čísel a+ bi A c+ di sa nazýva komplexné číslo ( a+ c) + (b+ d)i. teda Pri pridávaní komplexných čísel sa ich úsečky a ordináty pridávajú oddelene.

Odčítanie. Rozdiel dvoch komplexných čísel a+ bi(zmenšené) a c+ di(subtrahend) sa nazýva komplexné číslo ( a–c) + (b–d)i. teda Pri odčítaní dvoch komplexných čísel sa ich úsečky a ordináty odčítajú oddelene.

Násobenie. Súčin komplexných čísel a+ bi A c+ di sa nazýva komplexné číslo:

(ac–bd) + (inzerát+ bc)i. Táto definícia vyplýva z dvoch požiadaviek:

1) čísla a+ bi A c+ di treba násobiť ako algebraické binomy,

2) číslo i má hlavnú vlastnosť: i 2 = –1.

PRÍKLAD ( a+ bi)(a–bi)= a 2 +b 2 . teda prácadvoch konjugovaných komplexných čísel sa rovná kladnému reálnemu číslu.

divízie. Rozdeľte komplexné číslo a+ bi(deliteľné) iným c+ di (delič) - znamená nájsť tretie číslo e+ f i(chat), ktorý pri vynásobení deliteľom c+ di, výsledkom je dividenda a+ bi. Ak deliteľ nie je nula, delenie je vždy možné.

PRÍKLAD Nájsť (8 + i) : (2 – 3i) .

Riešenie. Prepíšme tento pomer ako zlomok:

Vynásobte jeho čitateľa a menovateľa 2 + 3 i a po vykonaní všetkých transformácií dostaneme:

Úloha 1: Sčítajte, odčítajte, násobte a delte z 1 na z 2

Extrahovanie druhej odmocniny: Vyriešte rovnicu X 2 = -a. Na vyriešenie tejto rovnice sme nútení používať čísla nového typu - imaginárne čísla . teda imaginárny číslo sa volá ktorého druhá mocnina je záporné číslo. Podľa tejto definície imaginárnych čísel môžeme definovať a imaginárny jednotka:

Potom pre rovnicu X 2 = – 25 dostaneme dve imaginárny koreň:

Úloha 2: Vyriešte rovnicu:

1)x 2 = – 36; 2) X 2 = – 49; 3) X 2 = – 121

Geometrické znázornenie komplexných čísel. Reálne čísla sú reprezentované bodmi na číselnej osi:

Tu je pointa A znamená číslo –3, bodka B-číslo 2 a O-nula. Naproti tomu komplexné čísla sú reprezentované bodmi na súradnicovej rovine. Na tento účel volíme pravouhlé (karteziánske) súradnice s rovnakými mierkami na oboch osiach. Potom komplexné číslo a+ bi bude reprezentovaný bodkou P s osou xA a ordinovaťb. Tento súradnicový systém je tzv komplexná rovina .

modul komplexné číslo je dĺžka vektora OP, ktoré predstavuje komplexné číslo na súradnici ( obsiahly) lietadlo. Modul komplexného čísla a+ bi označené | a+ bi| alebo) písmeno r a rovná sa:

Konjugované komplexné čísla majú rovnaký modul.

Pravidlá pre kreslenie výkresu sú takmer rovnaké ako pre výkres v karteziánskom súradnicovom systéme. Pozdĺž osí je potrebné nastaviť rozmer, pozn.

e
jednotka pozdĺž reálnej osi; Re z

imaginárna jednotka pozdĺž imaginárnej osi. som z

Úloha 3. Zostrojte nasledujúce komplexné čísla v komplexnej rovine: , , , , , , ,

1. Čísla sú presné a približné.Čísla, s ktorými sa v praxi stretávame, sú dvojakého druhu. Niektoré uvádzajú skutočnú hodnotu množstva, iné len približné. Prvé sa nazývajú presné, druhé - približné. Najčastejšie je vhodné použiť približné číslo namiesto presného, ​​najmä preto, že v mnohých prípadoch nie je možné presné číslo vôbec nájsť.

Ak teda povedia, že v triede je 29 žiakov, potom číslo 29 je presné. Ak hovoria, že vzdialenosť z Moskvy do Kyjeva je 960 km, tak tu je číslo 960 približné, pretože na jednej strane naše meracie prístroje nie sú absolútne presné, na druhej strane samotné mestá majú určitý rozsah.

Výsledkom akcií s približnými číslami je tiež približné číslo. Vykonaním niektorých operácií na presných číslach (delenie, extrakcia koreňov) môžete získať aj približné čísla.

Teória približných výpočtov umožňuje:

1) poznať stupeň presnosti údajov, vyhodnotiť stupeň presnosti výsledkov;

2) získavať údaje s primeraným stupňom presnosti dostatočným na zabezpečenie požadovanej presnosti výsledku;

3) racionalizovať proces výpočtu a oslobodiť ho od výpočtov, ktoré neovplyvnia presnosť výsledku.

2. Zaokrúhľovanie. Jedným zo zdrojov získavania približných čísel je zaokrúhľovanie. Približné aj presné čísla sú zaokrúhlené.

Zaokrúhlenie daného čísla na určitú číslicu sa nazýva nahradenie novým číslom, ktoré sa z daného čísla získa vyradením všetkých jeho číslic zapísaných napravo od číslice tejto číslice, alebo ich nahradením nulami. Tieto nuly sú zvyčajne podčiarknuté alebo písané menšie. Aby bolo zaokrúhlené číslo čo najbližšie k zaokrúhľovanému číslu, mali by ste použiť nasledujúce pravidlá: ak chcete zaokrúhliť číslo na jednu z určitej číslice, musíte zahodiť všetky číslice za číslicou tejto číslice a nahradiť s nulami v celom čísle. Do úvahy sa berú nasledovné:

1) ak je prvá (vľavo) z vyradených číslic menšia ako 5, posledná zostávajúca číslica sa nezmení (zaokrúhli sa nadol);

2) ak je prvá číslica, ktorá sa má vyradiť, väčšia ako 5 alebo rovná 5, posledná zostávajúca číslica sa zvýši o jednu (zaokrúhlenie s prebytkom).

Ukážme si to na príkladoch. Okrúhly:

a) až desatiny 12,34;

b) na stotiny 3,2465; 1038,785;

c) do tisícin 3,4335.

d) do tisíc 12375; 320729.

a) 12,34 ≈ 12,3;

b) 3,2465 ≈ 3,25; 1038,785 ≈ 1038,79;

c) 3,4335 ≈ 3,434.

d) 12375 ≈ 12 000; 320729 ≈ 321000.

3. Absolútne a relatívne chyby. Rozdiel medzi presným číslom a jeho približnou hodnotou sa nazýva absolútna chyba približného čísla. Ak je napríklad presné číslo 1,214 zaokrúhlené na desatinu, dostaneme približné číslo 1,2. V tomto prípade je absolútna chyba približného čísla 1,2 1,214 - 1,2, t.j. 0,014.

Ale vo väčšine prípadov je presná hodnota uvažovanej hodnoty neznáma, ale iba približná. Potom je absolútna chyba neznáma. V týchto prípadoch uveďte limit, ktorý neprekračuje. Toto číslo sa nazýva limitná absolútna chyba. Hovorí sa, že presná hodnota čísla sa rovná jeho približnej hodnote s chybou menšou ako je hraničná chyba. Napríklad číslo 23,71 je približná hodnota čísla 23,7125 s presnosťou 0,01, keďže absolútna chyba aproximácie je 0,0025 a menšia ako 0,01. Tu je limitná absolútna chyba 0,01 *.

Hraničná absolútna chyba približného čísla A označené symbolom Δ a. Záznam

X≈a(±Δ a)

treba chápať takto: presná hodnota množstva X je medzi číslami A– Δ a A A+ Δ A, ktoré sa nazývajú dolná a horná hranica X a označujú NG X VG X.

Napríklad, ak X≈ 2,3 (±0,1), potom 2,2<X< 2,4.

Naopak, ak 7.3< X< 7,4, тоX≈ 7,35 (±0,05). Absolútna alebo hraničná absolútna chyba necharakterizuje kvalitu vykonaného merania. Rovnakú absolútnu chybu možno považovať za významnú a nevýznamnú v závislosti od čísla, ktorým je nameraná hodnota vyjadrená. Napríklad, ak meriame vzdialenosť medzi dvoma mestami s presnosťou na jeden kilometer, potom takáto presnosť pre túto zmenu úplne postačuje, ale zároveň pri meraní vzdialenosti medzi dvoma domami na tej istej ulici bude takáto presnosť neprijateľné. V dôsledku toho presnosť približnej hodnoty veličiny závisí nielen od veľkosti absolútnej chyby, ale aj od hodnoty meranej veličiny. Preto je relatívna chyba mierou presnosti.

Relatívna chyba je pomer absolútnej chyby k hodnote približného čísla. Pomer limitnej absolútnej chyby k približnému číslu sa nazýva limitná relatívna chyba; označujú to takto: . Relatívne a okrajové relatívne chyby sa zvyčajne vyjadrujú v percentách. Napríklad, ak merania ukázali, že vzdialenosť X medzi dvoma bodmi je viac ako 12,3 km, ale menej ako 12,7 km, potom sa za jeho približnú hodnotu berie aritmetický priemer týchto dvoch čísel, t.j. ich polovičný súčet, potom sa hraničná absolútna chyba rovná polovičnému rozdielu týchto čísel. V tomto prípade X≈ 12,5 (±0,2). Tu je hraničná absolútna chyba 0,2 km a hraničná relatívna

Existuje mnoho typov čísel, jedným z nich sú celé čísla. Objavili sa celé čísla, aby sa uľahčilo počítanie nielen v pozitívnom, ale aj v negatívnom smere.

Pozrime sa na príklad:
Cez deň bola vonkajšia teplota 3 stupne. K večeru teplota klesla o 3 stupne.
3-3=0
Vonku bolo 0 stupňov. A v noci teplota klesla o 4 stupne a teplomer začal ukazovať -4 stupne.
0-4=-4

Séria celých čísel.

Takýto problém nemôžeme opísať pomocou prirodzených čísel, tento problém budeme uvažovať na súradnicovej čiare.

Dostali sme sériu čísel:
…, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, …

Tento rad čísel sa nazýva rad celých čísel.

Kladné celé čísla. Záporné celé čísla.

Séria celých čísel pozostáva z kladných a záporných čísel. Napravo od nuly sú prirodzené čísla, alebo sa tiež nazývajú kladné celé čísla. A idú vľavo od nuly záporné celé čísla.

Nula nie je ani kladné, ani záporné číslo. Je to hranica medzi kladnými a zápornými číslami.

je množina čísel pozostávajúca z prirodzených čísel, záporných celých čísel a nuly.

Rad celých čísel v kladnom a zápornom smere je nekonečné číslo.

Ak vezmeme akékoľvek dve celé čísla, potom sa budú volať čísla medzi týmito celými číslami konečná množina.

Napríklad:
Zoberme si celé čísla od -2 do 4. Všetky čísla medzi týmito číslami sú zahrnuté v konečnej množine. Naša konečná množina čísel vyzerá takto:
-2, -1, 0, 1, 2, 3, 4.

Prirodzené čísla sa označujú latinským písmenom N.
Celé čísla sa označujú latinským písmenom Z. Celá množina prirodzených čísel a celých čísel môže byť znázornená na obrázku.


Nekladné celé čísla inými slovami, sú to záporné celé čísla.
Nezáporné celé čísla sú kladné celé čísla.

V tomto článku definujeme množinu celých čísel, zvážime, ktoré celé čísla sa nazývajú kladné a ktoré záporné. Ukážeme si tiež, ako sa celé čísla používajú na popis zmien v určitých množstvách. Začnime s definíciou a príkladmi celých čísel.

Celé čísla. Definícia, príklady

Najprv si spomeňme na prirodzené čísla ℕ. Už samotný názov napovedá, že ide o čísla, ktoré sa prirodzene používajú na počítanie už od nepamäti. Aby sme pokryli pojem celých čísel, musíme rozšíriť definíciu prirodzených čísel.

Definícia 1. Celé čísla

Celé čísla sú prirodzené čísla, ich protiklady a číslo nula.

Množina celých čísel je označená písmenom ℤ.

Množina prirodzených čísel ℕ je podmnožinou celých čísel ℤ. Každé prirodzené číslo je celé číslo, ale nie každé celé číslo je prirodzené číslo.

Z definície vyplýva, že ktorékoľvek z čísel 1, 2, 3 je celé číslo. . , číslo 0, ako aj čísla - 1, - 2, - 3, . .

V súlade s tým uvedieme príklady. Čísla 39, - 589, 10000000, - 1596, 0 sú celé čísla.

Nechajte čiaru súradníc nakresliť vodorovne a nasmerovať ju doprava. Poďme sa na to pozrieť, aby sme si vizualizovali umiestnenie celých čísel na riadku.

Počiatok na súradnicovej čiare zodpovedá číslu 0 a body ležiace na oboch stranách nuly zodpovedajú kladným a záporným celým číslam. Každý bod zodpovedá jednému celému číslu.

Do ľubovoľného bodu na priamke, ktorej súradnica je celé číslo, sa môžete dostať vyčlenením určitého počtu segmentov jednotiek z počiatku.

Kladné a záporné celé čísla

Zo všetkých celých čísel je logické rozlišovať kladné a záporné celé čísla. Uveďme ich definície.

Definícia 2: Kladné celé čísla

Kladné celé čísla sú celé čísla so znamienkom plus.

Napríklad číslo 7 je celé číslo so znamienkom plus, teda kladné celé číslo. Na súradnicovej čiare toto číslo leží napravo od referenčného bodu, ktorý sa považuje za číslo 0. Ďalšie príklady kladných celých čísel: 12, 502, 42, 33, 100500.

Definícia 3: Záporné celé čísla

Záporné celé čísla sú celé čísla so znamienkom mínus.

Príklady záporných celých čísel: - 528, - 2568, - 1.

Číslo 0 oddeľuje kladné a záporné celé čísla a samo o sebe nie je ani kladné, ani záporné.

Každé číslo, ktoré je opakom kladného celého čísla, je podľa definície záporné celé číslo. Platí to aj naopak. Prevrátená hodnota akéhokoľvek záporného celého čísla je kladné celé číslo.

Je možné poskytnúť iné formulácie definícií záporných a kladných celých čísel pomocou ich porovnania s nulou.

Definícia 4: Kladné celé čísla

Kladné celé čísla sú celé čísla väčšie ako nula.

Definícia 5: Záporné celé čísla

Záporné celé čísla sú celé čísla, ktoré sú menšie ako nula.

V súlade s tým kladné čísla ležia napravo od začiatku na súradnicovej čiare a záporné celé čísla ležia naľavo od nuly.

Už sme povedali, že prirodzené čísla sú podmnožinou celých čísel. Ujasnime si tento bod. Množina prirodzených čísel pozostáva z kladných celých čísel. Na druhej strane, množina záporných celých čísel je množina čísel opačných k prirodzeným.

Dôležité!

Akékoľvek prirodzené číslo možno nazvať celým číslom, ale akékoľvek celé číslo nemožno nazvať prirodzeným číslom. Pri odpovedi na otázku, či záporné čísla sú prirodzené čísla, musíme smelo povedať – nie, nie sú.

Nekladné a nezáporné celé čísla

Uveďme niekoľko definícií.

Definícia 6. Nezáporné celé čísla

Nezáporné celé čísla sú kladné celé čísla a číslo nula.

Definícia 7. Nekladné celé čísla

Nekladné celé čísla sú záporné celé čísla a číslo nula.

Ako vidíte, číslo nula nie je ani kladné, ani záporné.

Príklady nezáporných celých čísel: 52, 128, 0.

Príklady nekladných celých čísel: - 52, - 128, 0.

Nezáporné číslo je číslo väčšie alebo rovné nule. Nekladné celé číslo je teda číslo menšie alebo rovné nule.

Pre stručnosť sa používajú výrazy „nekladné číslo“ a „nezáporné číslo“. Napríklad namiesto toho, aby ste povedali, že číslo a je celé číslo, ktoré je väčšie alebo rovné nule, môžete povedať: a je nezáporné celé číslo.

Použitie celých čísel na popis zmien veličín

Na čo sa používajú celé čísla? Po prvé, s ich pomocou je vhodné opísať a určiť zmeny v množstve akýchkoľvek objektov. Uveďme si príklad.

Nechajte určitý počet kľukových hriadeľov uskladniť v sklade. Ak sa do skladu privezie ďalších 500 kľukových hriadeľov, ich počet sa zvýši. Číslo 500 presne vyjadruje zmenu (zvýšenie) počtu dielov. Ak sa potom zo skladu odoberie 200 dielov, potom toto číslo bude charakterizovať aj zmenu počtu kľukových hriadeľov. Tentoraz smerom nadol.

Ak sa zo skladu nič neodoberie a nič nedodá, potom číslo 0 znamená, že počet dielov zostáva nezmenený.

Zrejmé pohodlie používania celých čísel na rozdiel od prirodzených čísel spočíva v tom, že ich znamienko jasne ukazuje smer zmeny hodnoty (zvýšenie alebo zníženie).

Pokles teploty o 30 stupňov možno charakterizovať ako záporné celé číslo - 30 a zvýšenie o 2 stupne - kladné celé číslo 2.

Uveďme ďalší príklad s použitím celých čísel. Tentokrát si predstavme, že máme niekomu darovať 5 mincí. Potom môžeme povedať, že máme - 5 mincí. Číslo 5 popisuje veľkosť dlhu a znamienko mínus znamená, že musíme rozdať mince.

Ak dlhujeme 2 mince jednej osobe a 3 inej osobe, celkový dlh (5 mincí) možno vypočítať pomocou pravidla sčítania záporných čísel:

2 + (- 3) = - 5

Ak si všimnete chybu v texte, zvýraznite ju a stlačte Ctrl+Enter

TO celé čísla zahŕňajú prirodzené čísla, nulu a čísla opačné k prirodzeným číslam.

Celé čísla sú kladné celé čísla.

Napríklad: 1, 3, 7, 19, 23 atď. Takéto čísla používame na počítanie (na stole je 5 jabĺk, auto má 4 kolesá atď.)

Latinské písmeno \mathbb(N) - označené množina prirodzených čísel.

Prirodzené čísla nemôžu zahŕňať záporné čísla (stolička nemôže mať záporný počet nôh) a zlomkové čísla (Ivan nedokázal predať 3,5 bicykla).

Opakom prirodzených čísel sú záporné celé čísla: −8, −148, −981, ….

Aritmetické operácie s celými číslami

Čo môžete robiť s celými číslami? Dajú sa navzájom násobiť, sčítať a odčítať. Pozrime sa na každú operáciu na konkrétnom príklade.

Sčítanie celých čísel

Dve celé čísla s rovnakými znamienkami sa sčítajú takto: sčítajú sa moduly týchto čísel a výslednému súčtu predchádza koncové znamienko:

(+11) + (+9) = +20

Odčítanie celých čísel

Dve celé čísla s rôznymi znamienkami sa sčítajú takto: od modulu väčšieho čísla sa odpočíta modul menšieho čísla a pred výslednú odpoveď sa umiestni znamienko väčšieho modulového čísla:

(-7) + (+8) = +1

Násobenie celých čísel

Ak chcete vynásobiť jedno celé číslo druhým, musíte vynásobiť moduly týchto čísel a vložiť znamienko „+“ pred výslednú odpoveď, ak pôvodné čísla mali rovnaké znamienka, a znamienko „-“, ak mali pôvodné čísla iné znaky:

(-5)\cdot (+3) = -15

(-3)\cdot (-4) = +12

Malo by sa pamätať na nasledujúce pravidlo pre násobenie celých čísel:

+ \cdot + = +

+ \cdot - = -

- \cdot + = -

- \cdot - = +

Existuje pravidlo pre násobenie viacerých celých čísel. Pripomeňme si to:

Znamienko súčinu bude „+“, ak je počet faktorov so záporným znamienkom párny a „–“, ak je počet faktorov so záporným znamienkom nepárny.

(-5) \cdot (-4) \cdot (+1) \cdot (+6) \cdot (+1) = +120

Celočíselné delenie

Delenie dvoch celých čísel sa vykonáva takto: modul jedného čísla sa vydelí modulom druhého a ak sú znamienka čísel rovnaké, pred výsledný kvocient sa umiestni znamienko „+“. a ak sú znamienka pôvodných čísel odlišné, umiestni sa znamienko „-“.

(-25) : (+5) = -5

Vlastnosti sčítania a násobenia celých čísel

Pozrime sa na základné vlastnosti sčítania a násobenia pre ľubovoľné celé čísla a, b a c:

1. a + b = b + a - komutatívna vlastnosť sčítania;
2. (a + b) + c = a + (b + c) - kombinatívna vlastnosť sčítania;
3. a \cdot b = b \cdot a - komutatívna vlastnosť násobenia;
4. (a \cdot c) \cdot b = a \cdot (b \cdot c)- asociatívne vlastnosti násobenia;
5. a \cdot (b \cdot c) = a \cdot b + a \cdot c- distributívna vlastnosť násobenia.

Toto sú čísla, ktoré sa používajú pri počítaní: 1, 2, 3... atď.

Nula nie je prirodzená.

Prirodzené čísla sa zvyčajne označujú symbolom N.

Celé čísla. Kladné a záporné čísla

Volajú sa dve čísla, ktoré sa od seba líšia iba znamienkom opak, napríklad +1 a -1, +5 a -5. Znamienko „+“ sa zvyčajne nepíše, ale predpokladá sa, že pred číslom je „+“. Takéto čísla sa nazývajú pozitívne. Volajú sa čísla, pred ktorými je znak „-“. negatívne.

Prirodzené čísla, ich protiklady a nula sa nazývajú celé čísla. Množina celých čísel je označená symbolom Z.

Racionálne čísla

Sú to konečné zlomky a nekonečné periodické zlomky. Napríklad,

Množina racionálnych čísel je označená Q. Všetky celé čísla sú racionálne.

Iracionálne čísla

Nekonečný neperiodický zlomok sa nazýva iracionálne číslo. Napríklad:

Označuje sa množina iracionálnych čísel J.

Reálne čísla

Množina všetkých racionálnych a všetkých iracionálnych čísel sa nazýva súbor skutočného (skutočného)čísla.

Reálne čísla sú reprezentované symbolom R.

Zaokrúhľovanie čísel

Zvážte číslo 8,759123... . Zaokrúhlenie na najbližšie celé číslo znamená zapísanie len tej časti čísla, ktorá je pred desatinnou čiarkou. Zaokrúhlením na desatiny sa rozumie zapísanie celej časti a jednej číslice za desatinnou čiarkou; zaokrúhliť na najbližšiu stotinu - dve číslice za desatinnou čiarkou; až tisíciny - tri číslice atď.