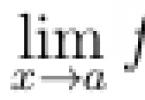Veta. Nechajte funkciu x=φ(t) súvislý v bode a a funkciu y=f(x) súvislý v bode b=φ(a). Potom komplexná funkcia y=f[φ(t)]=F(t) súvislý v bode a.

Nechaj x=φ(t) A y=f(x)- najjednoduchšie elementárne funkcie s mnohými hodnotami (X) funkcie x=φ(t) je rozsah funkcie y=f(x). Ako vieme, elementárne funkcie sú spojité v každom bode danej oblasti. Preto podľa predchádzajúcej vety komplexná funkcia y=f(φ(t)), teda superpozícia dvoch elementárnych funkcií, je spojitá. Napríklad funkcia je spojitá v akomkoľvek bode x ≠ 0, ako komplexná funkcia dvoch elementárnych funkcií x=t-1 A y = hriech x. Tiež funkcia y=ln sin x spojité v ktoromkoľvek bode intervalu (2kπ,(2k+1)π), k ∈ Z (hriech x>0).

Prednáška 4.

Kontinuita funkcií

1. Spojitosť funkcie v bode

Definícia 1. Nechajte funkciu r=f(X) je definovaný v bode X 0 a v nejakom susedstve tohto bodu. Funkcia r=f(X) sa nazýva spojitá v bode x 0 , ak v tomto bode existuje limita funkcie a tá sa rovná hodnote funkcie v tomto bode, t.j.

Takže podmienka kontinuity funkcie r=f(X) v bode X 0 je to:

Pretože
, potom rovnosť (32) možno zapísať v tvare

(33)

To znamená, že keď nájdenie limity spojitej funkcief(X) pod znakom funkcie sa dá ísť na limit, t.j. do funkcie f(X) namiesto argumentu X nahradiť jeho limitnú hodnotu X 0 .

lim hriech X= hriech(lim X);

lim arctg X=arctg(lim X); (34)

lim log X=log(lim X).

Cvičenie. Nájdite limit: 1)
; 2)
.

Definujme kontinuitu funkcie na základe konceptov prírastku argumentu a funkcie.

Pretože podmienky
A
sú identické (obr. 4), potom má rovnosť (32) tvar:

alebo
.

Definícia 2. Funkcia r=f(X) sa nazýva spojitá v bode x 0 , ak je definovaný v bode X 0 a jeho okolia a nekonečne malý prírastok v argumente zodpovedá nekonečne malému prírastku vo funkcii.

Cvičenie. Preskúmajte spojitosť funkcie r=2X 2 1.

Vlastnosti funkcií spojitých v bode

1. Ak funkcie f(X) A φ (X) sú v bode súvislé X 0, potom ich súčet
, práca
a súkromné
(vzhľadom na to
) sú funkcie spojité v bode X 0 .

2. Ak je funkcia pri=f(X) je v bode súvislý X 0 a f(X 0)>0, potom existuje také okolie bodu X 0, v ktorom f(X)>0.

3. Ak je funkcia pri=f(u) je spojitá v bode u 0 a funkcia u= φ (X) je v bode súvislý u 0 = φ (X 0 ), potom komplexná funkcia r=f[φ (X)] je v bode spojitá X 0 .

2. Spojitosť funkcie v intervale a na segmente

Funkcia r=f(X) sa nazýva priebežne v intervale (a; b), ak je spojitý v každom bode tohto intervalu.

Funkcia r=f(X) sa nazýva kontinuálne na segmente [a; b] ak je súvislý v intervale ( a; b) a v bode X=A je správne súvislý (t.j.
) a v bode X=b je ponechaná súvislá (t.j.
).

3. Body diskontinuity funkcií a ich klasifikácia

Nazývajú sa body, v ktorých je prerušená spojitosť funkcie body zlomu túto funkciu.

Ak X=X 0 – bod zlomu funkcie r=f(X), potom nie je splnená aspoň jedna z podmienok prvej definície spojitosti funkcie.

Príklad.

1.
. 2.

3)
4)
.

▼Bod zlomu X 0 sa nazýva bod zlomu prvý druh funkcie r=f(X), ak v tomto bode existujú vľavo a vpravo konečné limity funkcie (jednostranné limity), t.j.
A
. kde:

Veľkosť | A 1 -A 2 | volal funkčný skok v bode diskontinuity prvého druhu. ▲

▼Bod zlomu X 0 sa nazýva bod zlomu druhý druh funkcie r=f(X), ak aspoň jedna z jednostranných limitov (ľavá alebo pravá) neexistuje alebo sa rovná nekonečnu. ▲

Cvičenie. Nájdite body prerušenia a zistite ich typ pre funkcie:

1)
; 2)
.

4. Základné vety o spojitých funkciách

Vety o spojitosti funkcií vyplývajú priamo z príslušných viet o limitách.

Veta 1. Súčet, súčin a podiel dvoch spojitých funkcií je spojitá funkcia (pre podiel, s výnimkou tých hodnôt argumentu, v ktorých sa deliteľ nerovná nule).

Veta 2. Nechajte funkcie u=φ (X) je v bode súvislý X 0 a funkciu r=f(u) je v bode súvislý u=φ (X 0 ). Potom komplexná funkcia f(φ (X)), ktorý pozostáva zo spojitých funkcií, je v bode spojitý X 0 .

Veta 3. Ak je funkcia r=f(X) je súvislý a striktne monotónny na [ a; b] osi Oh, potom inverzná funkcia pri=φ (X) je tiež súvislý a monotónny na zodpovedajúcom segmente [ c;d] osi OU.

Každá elementárna funkcia je spojitá v každom bode, v ktorom je definovaná.

5. Vlastnosti funkcií spojitých na intervale

Weierstrassova veta. Ak je funkcia na segmente spojitá, potom na tomto segmente dosiahne svoje maximálne a minimálne hodnoty.

Dôsledok. Ak je funkcia spojitá na intervale, potom je na intervale ohraničená.

Bolzanova-Cauchyho veta. Ak je funkcia r=f(X) je spojitý na intervale [ a; b] a na svojich koncoch nadobúda nerovnaké hodnoty f(a)=A A f(b)=B,
, potom bez ohľadu na číslo S, uzavretá medzi A A IN, je tu pointa
také že f(c)=C.

Geometricky veta je jasná. Pre akékoľvek číslo S, uzavretá medzi A A IN, vo vnútri tohto segmentu je bod c taký, že f(S)=C. Rovno pri=S pretína graf funkcie aspoň v jednom bode.

Dôsledok. Ak je funkcia r=f(X) je spojitý na intervale [ a; b] a preberá hodnoty rôznych znakov na svojich koncoch, potom vo vnútri segmentu [ a; b] je tam aspoň jeden bod s, v ktorom je funkcia r=f(X) ide na nulu: f(c)=0.

Geometrické význam vety: ak graf spojitej funkcie prechádza z jednej strany osi Oh k druhému, potom pretína os Oh.

Proces štúdia funkcie pre spojitosť je neoddeliteľne spojený so schopnosťou nájsť jednostranné limity funkcie. Preto, aby ste mohli začať študovať materiál v tomto článku, je vhodné najprv preskúmať tému limity funkcie.

Funkcia f(x) je nepretržitý v bode x 0, ak sa limita vľavo rovná limite vpravo a zhoduje sa s hodnotou funkcie v bode x 0, t.j.: lim x → x 0 - 0 f (x) = lim x → x 0 + 0 f (x) = f (x0)

Táto definícia nám umožňuje odvodiť dôsledok: hodnota limity funkcie v bodoch spojitosti sa zhoduje s hodnotou funkcie v týchto bodoch.

Príklad 1

Je daná funkcia f (x) = 1 6 (x - 8) 2 - 8. Je potrebné dokázať jeho spojitosť v bode x 0 = 2.

Riešenie

Najprv určíme existenciu limity vľavo. Na tento účel používame postupnosť argumentov x n, ktorá sa redukuje na x 0 = 2 · (x n< 2) . Например, такой последовательностью может быть:

2 , 0 , 1 , 1 1 2 , 1 3 4 , 1 7 8 , 1 15 16 , . . . , 1 1023 1024 , . . . → 2

Zodpovedajúca postupnosť funkčných hodnôt vyzerá takto:

f(-2); f(0); f (1); f 1 1 2; f 1 3 4; f 1 7 8; f 1 15 16; . . . ; f 1 1023 1024; . . . = = 8. 667; 2. 667; 0 167; - 0. 958; - 1. 489; - 1. 747; - 1. 874; . . . ; - 1. 998; . . . → - 2

na výkrese sú označené zelenou farbou.

Je celkom zrejmé, že takáto postupnosť sa zníži na - 2, čo znamená lim x → 2 - 0 1 6 (x - 8) 2 - 8 = - 2.

Určme existenciu limity vpravo: použijeme postupnosť argumentov x n, ktorá sa redukuje na x 0 = 2 (x n > 2). Táto sekvencia môže byť napríklad:

6 , 4 , 3 , 2 1 2 , 2 1 4 , 2 1 8 , 2 1 16 , . . . , 2 1 1024 , . . . → 2

Zodpovedajúca postupnosť funkcií:

f (6); f (4); f (3); f 2 1 2; f 2 1 4; f 2 1 8; f 2 1 16; . . . ; f 2 1 1024; . . . = = - 7. 333; - 5. 333; - 3. 833; - 2. 958; - 2. 489; - 2. 247; - 2. 247; - 2. 124; . . . ; - 2. 001; . . . → - 2

na obrázku vyznačené modrou farbou.

A táto postupnosť sa zníži na -2, potom lim x → 2 + 0 1 6 (x - 8) 2 - 8 = - 2.

Vyššie uvedené akcie ukázali, že limity vpravo a vľavo sú rovnaké, čo znamená, že existuje limita funkcie f (x) = 1 6 x - 8 2 - 8 v bode x 0 = 2, zatiaľ čo lim x → 2 16 (x - 8) 2 - 8 = -2.

Po výpočte hodnoty funkcie v danom bode je rovnosť zrejmá:

lim x → 2 - 0 f (x) = lim x → 2 + 0 f (x) = f (2) = 1 6 (2 - 8) 2 - 8 = - 2 čo udáva spojitosť danej funkcie pri a daný bod.

Ukážme si to graficky:

odpoveď: Spojitosť funkcie f (x) = 1 6 (x - 8) 2 - 8 v danej časti bola dokázaná.

Odnímateľná prietrž prvého druhu

Funkcia má odstrániteľná prietrž prvého druhu v bode x 0, keď sa limity vpravo a vľavo rovnajú, ale nerovnajú sa hodnote funkcie v bode, t.j.:

lim x → x 0 - 0 f (x) = lim x → x 0 + 0 f (x) ≠ f (x 0)

Príklad 2

Je daná funkcia f (x) = x 2 - 25 x - 5. Je potrebné určiť body jeho zlomu a určiť ich typ.

Riešenie

Najprv označme definičný obor funkcie: D (f (x)) ⇔ D x 2 - 25 x - 5 ⇔ x - 5 ≠ 0 ⇔ x ∈ (- ∞ ; 5) ∪ (5 ; + ∞)

V danej funkcii môže ako bod zlomu slúžiť len hraničný bod definičného oboru, t.j. x 0 = 5. V tomto bode preskúmame funkciu spojitosti.

Zjednodušme výraz x 2 - 25 x - 5: x 2 - 25 x - 5 = (x - 5) (x + 5) x - 5 = x + 5.

Definujme hranice vpravo a vľavo. Pretože funkcia g(x) = x + 5 je spojitá pre akékoľvek reálne x, potom:

lim x → 5 - 0 (x + 5) = 5 + 5 = 10 lim x → 5 + 0 (x + 5) = 5 + 5 = 10

odpoveď: limity vpravo a vľavo sú rovnaké a daná funkcia v bode x 0 = 5 nie je definovaná, t.j. v tomto bode má funkcia odstrániteľnú diskontinuitu prvého druhu.

Neodstrániteľná diskontinuita prvého druhu je tiež určená bodom skoku funkcie.

Definícia 3 Príklad 3

Daná je po častiach spojitá funkcia f (x) = x + 4 , x< - 1 , x 2 + 2 , - 1 ≤ x < 1 2 x , x ≥ 1 . Необходимо изучить заданную функцию на предмет непрерывности, обозначить вид точек разрыва, составить чертеж.

Riešenie

Nespojitosti tejto funkcie môžu byť len v bode x 0 = - 1 alebo v bode x 0 = 1.

Určme limity napravo a naľavo od týchto bodov a hodnotu danej funkcie v týchto bodoch:

• naľavo od bodu x 0 = - 1 je daná funkcia f (x) = x + 4, potom z dôvodu spojitosti lineárnej funkcie: lim x → - 1 - 0 f (x) = lim x → - 1 - 0 (x + 4) = - 1 + 4 = 3;
• priamo v bode x 0 = - 1 má funkcia tvar: f (x) = x 2 + 2, potom: f (- 1) = (- 1) 2 + 2 = 3;
• na intervale (- 1 ; 1) je daná funkcia: f (x) = x 2 + 2. Na základe vlastnosti spojitosti kvadratickej funkcie máme: lim x → - 1 + 0 f (x) = lim x → - 1 + 0 (x 2 + 2) = (- 1) 2 + 2 = 3 lim x → 1 - 0 f (x) = limit x → 1 - 0 (x 2 + 2) = (1) 2 + 2 = 3
• v bode x 0 = - 1 má funkcia tvar: f (x) = 2 x a f (1) = 2 1 = 2.
• napravo od bodu x 0 je daná funkcia f (x) = 2 x. Vzhľadom na spojitosť lineárnej funkcie: lim x → 1 + 0 f (x) = lim x → 1 + 0 (2 x) = 2 1 = 2

odpoveď: nakoniec sme dostali:

• lim x → - 1 - 0 f (x) = lim x → - 1 + 0 f (x) = f (- 1) = 3 - to znamená, že v bode x 0 = - 1 je daná po častiach spojitá;
• lim x → - 1 - 0 f (x) = 3, lim x → 1 + 0 f (x) = 2 - teda v bode x 0 = 1 je definovaná neodstrániteľná diskontinuita prvého druhu (skok).

Na túto úlohu nám stačí pripraviť výkres.

Funkcia má nespojitosť druhého druhu v bode x 0, keď niektorá z limitov na ľavej hranici x → x 0 - 0 f (x) alebo na pravej hranici x → x 0 + 0 f (x) neexistuje alebo je nekonečná.

Príklad 4

Je daná funkcia f (x) = 1 x. Je potrebné preskúmať danú funkciu na spojitosť, určiť typ bodov zlomu a pripraviť výkres.

Riešenie

Zapíšme definičný obor funkcie: x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) .

Nájdite hranice napravo a naľavo od bodu x 0 = 0.

Zadajte ľubovoľnú postupnosť hodnôt argumentov konvergujúcich k x 0 vľavo. Napr.:

8 ; - 4 ; - 2 ; - 1 ; - 1 2 ; - 1 4 ; . . . ; - 1 1024 ; . . .

Zodpovedá postupnosti funkčných hodnôt:

f(-8); f(-4); f(-2); f(-1); f-12; f - 14; . . . ; f - 1 1024; . . . = = - 18; - 14; - 12; - 1; - 2; - 4; . . . ; - 1024; . . .

Je zrejmé, že táto postupnosť je nekonečne veľká záporná, potom lim x → 0 - 0 f (x) = lim x → 0 - 0 1 x = - ∞ .

Teraz určme ľubovoľnú postupnosť hodnôt argumentov konvergujúcich k x 0 sprava. Napríklad: 8 ; 4; 2; 1; 12; 14; . . . ; 1 1024; . . . , a zodpovedá postupnosti funkčných hodnôt:

f (8); f (4); f (2); f (1); f12; f14; . . . ; f 1 1024; . . . = = 18; 14; 12; 1; 2; 4; . . . ; 1024; . . .

Táto postupnosť je nekonečne veľká kladná, čo znamená lim x → 0 + 0 f (x) = lim x → 0 + 0 1 x = + ∞ .

Odpoveď: bod x 0 = 0 je bod nespojitosti funkcie druhého druhu.

Poďme na ilustráciu:

Ak si všimnete chybu v texte, zvýraznite ju a stlačte Ctrl+Enter

V tejto lekcii sa naučíme, ako vytvoriť spojitosť funkcie. Urobíme to pomocou limitiek, teda jednostranných - vpravo a vľavo, ktoré nie sú vôbec strašidelné, napriek tomu, že sú písané ako a .

Ale čo je vlastne kontinuita funkcie? Kým sa nedostaneme k striktnej definícii, najjednoduchšie je predstaviť si čiaru, ktorú je možné nakresliť bez toho, aby ste zdvihli ceruzku z papiera. Ak je takáto čiara nakreslená, potom je súvislá. Táto čiara je grafom spojitej funkcie.

Graficky je funkcia v bode spojitá, ak sa jej graf v tomto bode „nezlomí“. Graf takejto spojitej funkcie je znázornené na obrázku nižšie.

Určenie spojitosti funkcie cez limitu. Funkcia je spojitá v bode, ak sú splnené tri podmienky:

1. Funkcia je definovaná v bode .

Ak nie je splnená aspoň jedna z uvedených podmienok, funkcia nie je v bode spojitá. V tomto prípade hovoria, že funkcia trpí diskontinuitou a body na grafe, v ktorých je graf prerušený, sa nazývajú body diskontinuity funkcie. Graf takejto funkcie, ktorá trpí diskontinuitou v bode x=2, je na obrázku nižšie.

Príklad 1 Funkcia f(X) je definovaný takto:

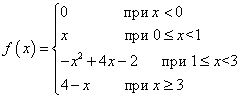
Bude táto funkcia spojitá v každom z hraničných bodov svojich vetiev, teda v bodoch X = 0 , X = 1 , X = 3 ?

Riešenie. Skontrolujeme všetky tri podmienky spojitosti funkcie v každom hraničnom bode. Prvá podmienka je splnená, od čoho funkcia definovaná v každom z hraničných bodov vyplýva z definície funkcie. Zostáva skontrolovať zostávajúce dve podmienky.

Bodka X= 0. V tomto bode nájdime ľavý limit:

.

Poďme nájsť pravý limit:

X= 0 sa musí nájsť pre tú vetvu funkcie, ktorá obsahuje tento bod, teda druhú vetvu. Nájdeme ich:

Ako vidíme, limita funkcie a hodnota funkcie v bode X= 0 sú rovnaké. Preto je funkcia v bode spojitá X = 0 .

Bodka X= 1. V tomto bode nájdime ľavý limit:

Poďme nájsť pravý limit:

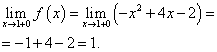
Limita funkcie a hodnota funkcie v bode X= 1 sa musí nájsť pre tú vetvu funkcie, ktorá obsahuje tento bod, teda druhú vetvu. Nájdeme ich:

.

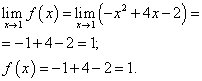Limita funkcie a hodnota funkcie v bode X= 1 sú rovnaké. Preto je funkcia v bode spojitá X = 1 .

Bodka X= 3. V tomto bode nájdime ľavý limit:

Poďme nájsť pravý limit:

Limita funkcie a hodnota funkcie v bode X= 3 sa musí nájsť pre tú vetvu funkcie, ktorá obsahuje tento bod, teda druhú vetvu. Nájdeme ich:

.

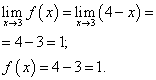Limita funkcie a hodnota funkcie v bode X= 3 sú rovnaké. Preto je funkcia v bode spojitá X = 3 .

Hlavný záver: táto funkcia je spojitá v každom hraničnom bode.

Sami si vytvorte kontinuitu funkcie v určitom bode a potom sa pozrite na riešenie

Nepretržitú zmenu funkcie možno definovať ako postupnú zmenu bez skokov, pri ktorej malá zmena v argumente znamená malú zmenu funkcie.

Ilustrujme túto nepretržitú zmenu funkcie na príklade.

Závažie nechajte visieť na nite nad stolom. Pod vplyvom tohto zaťaženia sa vlákno natiahne, takže vzdialenosť l zaťaženie od bodu zavesenia závitu je funkciou hmotnosti bremena m, teda l = f(m) , m≥0 .

Ak mierne zmeníte hmotnosť nákladu, potom vzdialenosť l zmení sa málo: malé zmeny m malé zmeny zodpovedajú l. Ak je však hmotnosť bremena blízka pevnosti nite v ťahu, potom mierne zvýšenie hmotnosti bremena môže spôsobiť pretrhnutie nite: vzdialenosť l sa náhle zvýši a bude sa rovnať vzdialenosti od bodu zavesenia k povrchu stola. Graf funkcie l = f(m) znázornené na obrázku. V reze je tento graf súvislá (plná) čiara a v bode je prerušená. Výsledkom je graf pozostávajúci z dvoch vetiev. Vo všetkých bodoch okrem funkcie l = f(m) je spojitá, ale v určitom bode má diskontinuitu.

Štúdium spojitosti funkcie môže byť buď samostatnou úlohou, alebo jednou z etáp úplného štúdia funkcie a zostavenia jej grafu.

Spojitosť funkcie na intervale

Nechajte funkciu r = f(X) definované v intervale ] a, b[ a je spojitá v každom bode tohto intervalu. Potom sa nazýva spojitý v intervale ] a, b[ . Pojem spojitosti funkcie na intervaloch tvaru ]- ∞ je definovaný podobne, b[ , ]a, + ∞[ , ]- ∞, + ∞[ . Teraz nechajme funkciu r = f(X) definované na intervale [ a, b]. Rozdiel medzi intervalom a segmentom: hraničné body intervalu nie sú zahrnuté v intervale, ale hraničné body segmentu sú zahrnuté v segmente. Tu by sme mali spomenúť takzvanú jednostrannú kontinuitu: v bode a, zostávajúci v segmente [ a, b] , môžeme sa priblížiť iba sprava a k bodu b- len vľavo. Hovoríme, že funkcia je spojitá na intervale [ a, b] , ak je spojitá vo všetkých vnútorných bodoch tohto segmentu, súvislá vpravo v bode a a je ponechaná súvislá v bode b.

Príkladom spojitej funkcie môže byť ktorákoľvek z elementárnych funkcií. Každá elementárna funkcia je spojitá na akomkoľvek intervale, na ktorom je definovaná. Napríklad funkcie a sú spojité v akomkoľvek intervale [ a, b], funkcia je spojitá na intervale [ 0 , b], funkcia je spojitá na akomkoľvek segmente, ktorý neobsahuje bod a = 2 .

Príklad 4. Preskúmajte spojitosť funkcie.

Riešenie. Pozrime sa na prvú podmienku. Funkcia nie je definovaná v bodoch - 3 a 3. Nie je splnená aspoň jedna z podmienok spojitosti funkcie po celej číselnej osi. Preto je táto funkcia v intervaloch spojitá

Príklad 5. Určte, pri akej hodnote parametra a nepretržite doména definície funkciu

Riešenie.

Nájdite pravý limit na:

.

Je zrejmé, že hodnota v bode X= 2 by sa malo rovnať sekera :

a = 1,5 .

Príklad 6. Určte, pri akých hodnotách parametrov a A b nepretržite doména definície funkciu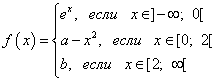

Riešenie.
Nájdite ľavostrannú hranicu funkcie v bode:

.

Preto hodnota v bode musí byť 1:

Nájdite funkciu ľavej ruky v bode:

Je zrejmé, že hodnota funkcie v bode by sa mala rovnať:

Odpoveď: funkcia je spojitá v celej oblasti definície kedy a = 1; b = -3 .

Základné vlastnosti spojitých funkcií

Matematika prišla ku konceptu spojitej funkcie štúdiom predovšetkým rôznych pohybových zákonov. Priestor a čas sú nekonečné a závislosť napríklad cesty s z času t, vyjadrené zákonom s = f(t) , uvádza príklad spojitého funkcie f(t). Teplota ohrievanej vody sa tiež neustále mení, je to tiež nepretržitá funkcia času: T = f(t) .

V matematickej analýze sú dokázané niektoré vlastnosti spojitých funkcií. Predstavme si najdôležitejšie z týchto vlastností.

1. Ak funkcia spojitá v intervale nadobúda hodnoty rôznych znamienok na koncoch intervalu, potom v určitom bode tohto intervalu nadobúda hodnotu rovnú nule. Vo formálnejšom vyjadrení je táto vlastnosť daná vetou známou ako prvá Bolzanova-Cauchyho veta.

2. Funkcia f(X), súvislé na intervale [ a, b] , preberá všetky medzihodnoty medzi hodnotami v koncových bodoch, teda medzi f(a) A f(b). Vo formálnejšom vyjadrení je táto vlastnosť daná vetou známou ako druhá Bolzanova-Cauchyho veta.

Definícia. Zavolá sa funkcia f(x), definovaná v okolí nejakého bodu x 0 súvislý v bode x 0 ak sa limita funkcie a jej hodnota v tomto bode rovnajú, t.j.

Tá istá skutočnosť môže byť napísaná inak:

Definícia. Ak je funkcia f(x) definovaná v niektorom okolí bodu x 0, ale nie je spojitá v samotnom bode x 0, potom sa nazýva výbušný a bod x 0 je bodom nespojitosti.

Príklad spojitej funkcie:

r

0 x 0 - x 0 x 0 + x

P príklad nespojitej funkcie:

Definícia. Funkcia f(x) sa nazýva spojitá v bode x 0, ak pre ľubovoľné kladné číslo >0 existuje číslo >0 také, že pre ľubovoľné x spĺňa podmienku

nerovnosť pravdivá
.

Definícia. Zavolá sa funkcia f(x). nepretržitý v bode x = x 0, ak je prírastok funkcie v bode x 0 nekonečne malá hodnota.

f(x) = f(x 0) + (x)

kde (x) je nekonečne malé pri xx 0.

Vlastnosti spojitých funkcií.

1) Súčet, rozdiel a súčin spojitých funkcií v bode x 0 je spojitá funkcia v bode x 0.

2) Podiel dvoch spojitých funkcií – je spojitá funkcia za predpokladu, že g(x) sa v bode x 0 nerovná nule.

3) Superpozícia spojitých funkcií je spojitá funkcia.

Táto vlastnosť môže byť zapísaná nasledovne:

Ak u = f(x), v = g(x) sú spojité funkcie v bode x = x 0, potom funkcia v = g(f(x)) je tiež spojitá funkcia v tomto bode.

Platnosť vyššie uvedených vlastností sa dá ľahko dokázať pomocou limitných viet.

Spojitosť niektorých elementárnych funkcií.

1) Funkcia f(x) = C, C = const je spojitá funkcia v celom definičnom obore.

2) Racionálna funkcia
je spojitá pre všetky hodnoty x okrem tých, pri ktorých sa menovateľ stáva nulou. Funkcia tohto typu je teda spojitá v celej oblasti definície.

3) Goniometrické funkcie sin a cos sú vo svojej oblasti definície spojité.

Dokážme vlastnosť 3 pre funkciu y = sinx.

Napíšme prírastok funkcie y = sin(x + x) – sinx, alebo po transformácii:

V skutočnosti existuje limit pre súčin dvoch funkcií
A
. V tomto prípade je kosínusová funkcia obmedzenou funkciou pri х0
, a preto

limit funkcie sínus
, potom je nekonečne malý priх0.

Existuje teda súčin funkcie ohraničenej a infinitezimálnej, preto tento súčin, t.j. funkcia у je nekonečne malá. V súlade s definíciami diskutovanými vyššie je funkcia y = sinx spojitou funkciou pre akúkoľvek hodnotu x = x 0 z oblasti definície, pretože jeho prírastok v tomto bode je nekonečne malá hodnota.

Body zlomu a ich klasifikácia.

Uvažujme nejakú funkciu f(x), spojitú v okolí bodu x 0, možno s výnimkou tohto bodu samotného. Z definície bodu zlomu funkcie vyplýva, že x = x 0 je bod zlomu, ak funkcia v tomto bode nie je definovaná alebo v ňom nie je spojitá.

Treba si tiež uvedomiť, že kontinuita funkcie môže byť jednostranná. Vysvetlíme si to nasledovne.

, potom sa hovorí, že funkcia je správne spojitá.

Ak jednostranný limit (pozri vyššie)
, potom sa hovorí, že funkcia zostane spojitá.

Definícia. Bod x 0 sa nazýva bod zlomu funkcia f(x), ak f(x) nie je definovaná v bode x 0 alebo nie je v tomto bode spojitá.

Definícia. Bod x 0 sa nazýva bod diskontinuity 1. druhu, ak má v tomto bode funkcia f(x) konečnú, ale nie rovnakú ľavú a pravú limitu.

Na splnenie podmienok tejto definície nie je potrebné, aby funkcia bola definovaná v bode x = x 0, stačí, aby bola definovaná naľavo a napravo od neho.

Z definície môžeme usúdiť, že v bode diskontinuity 1. druhu môže mať funkcia len konečný skok. V niektorých špeciálnych prípadoch sa niekedy nazýva aj bod diskontinuity 1. druhu odnímateľné bod zlomu, ale o tom si povieme viac nižšie.

Definícia. Bod x 0 sa nazýva bod diskontinuity 2. druhu, ak v tomto bode funkcia f(x) nemá aspoň jednu z jednostranných limitov alebo aspoň jedna z nich je nekonečná.

Spojitosť funkcie na intervale a na segmente.

Definícia. Zavolá sa funkcia f(x). spojité v intervale (segmente), ak je súvislý v ktoromkoľvek bode intervalu (segmentu).

V tomto prípade nie je potrebná spojitosť funkcie na koncoch úseku alebo intervalu, vyžaduje sa len jednostranná spojitosť na koncoch úseku alebo intervalu.

Vlastnosti funkcií spojitých na intervale.

Vlastnosť 1: (Prvá Weierstrassova veta (Carl Weierstrass (1815-1897) – nemecký matematik)). Funkcia, ktorá je na intervale spojitá, je na tomto intervale ohraničená, t.j. na segmente je splnená podmienka –M  f(x)  M.

Dôkaz tejto vlastnosti je založený na skutočnosti, že funkcia, ktorá je spojitá v bode x 0, je ohraničená v určitom jej okolí, a ak segment rozdelíte na nekonečný počet segmentov, ktoré sú „stiahnuté“ do bodu x 0, potom vzniká určité okolie bodu x 0.

Vlastnosť 2: Funkcia, ktorá je v segmente spojitá, má najväčšie a najmenšie hodnoty.

Tie. existujú hodnoty x 1 a x 2 také, že f(x 1) = m, f(x 2) = M a

m  f(x)  M

Všimnime si, že tieto najväčšie a najmenšie hodnoty môže funkcia nadobudnúť segment niekoľkokrát (napríklad f(x) = sinx).

Volá sa rozdiel medzi najväčšou a najmenšou hodnotou funkcie na segmente váhanie funguje na segmente.

Vlastnosť 3: (Druhá Bolzanova – Cauchyho veta). Funkcia, ktorá je v intervale spojitá, preberá všetky hodnoty medzi dvoma ľubovoľnými hodnotami v tomto intervale.

Vlastnosť 4: Ak je funkcia f(x) spojitá v bode x = x 0, potom existuje nejaké okolie bodu x 0, v ktorom si funkcia zachováva svoje znamienko.

Vlastnosť 5: (Prvá Bolzanova veta (1781-1848) - Cauchy). Ak je funkcia f(x) na segmente spojitá a má na koncoch segmentu hodnoty opačných znamienok, potom je vo vnútri tohto segmentu bod, kde f(x) = 0.

Tie. ak znamienko(f(a))  znamienko(f(b)), potom  x 0: f(x 0) = 0.

Príklad.

v bode x = -1 je funkcia spojitá v bode x = 1 bod nespojitosti 1. druhu

pri

Príklad. Preskúmajte spojitosť funkcie a určte typ bodov nespojitosti, ak existujú.

v bode x = 0 je funkcia spojitá v bode x = 1 bod nespojitosti 1. druhu