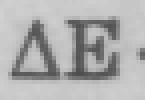Skutočný logaritmus

Logaritmus reálnych čísel a b dáva zmysel so style="max-width: 98%; height: auto; width: auto;" src="/pictures/wiki/files/55/7cd1159e49fee8eff61027c9cde84a53.png" border="0">.

Najpoužívanejšie typy logaritmov sú:

Ak logaritmické číslo považujeme za premennú, dostaneme logaritmická funkcia, Napríklad: . Táto funkcia je definovaná na pravej strane číselného radu: X> 0, je tam spojitá a diferencovateľná (pozri obr. 1).

Vlastnosti

Prirodzené logaritmy

Keď je rovnosť pravdivá

(1)

najmä

Tento rad konverguje rýchlejšie a navyše ľavá strana vzorca teraz môže vyjadrovať logaritmus akéhokoľvek kladného čísla.

Vzťah k desiatkovému logaritmu: .

Desatinné logaritmy

Ryža. 2. Logaritmická stupnica

Logaritmy na základ 10 (symbol: lg a) pred vynálezom kalkulačiek boli široko používané na výpočty. Nerovnomerná stupnica desiatkových logaritmov je zvyčajne vyznačená aj na logaritmických pravidlách. Podobná stupnica sa široko používa v rôznych oblastiach vedy, napríklad:

• Chémia - aktivita vodíkových iónov ().
• Hudobná teória - stupnica nôt, vo vzťahu k frekvenciám hudobných nôt.

Logaritmická škála je tiež široko používaná na identifikáciu exponentu v mocninných vzťahoch a koeficientu v exponente. V tomto prípade má graf zostrojený na logaritmickej mierke pozdĺž jednej alebo dvoch osí formu priamky, ktorá sa ľahšie študuje.

Komplexný logaritmus

Viachodnotová funkcia

Riemannov povrch

Komplexná logaritmická funkcia je príkladom Riemannovej plochy; jeho pomyselnú časť (obr. 3) tvorí nekonečné množstvo vetiev, stočených ako špirála. Tento povrch je jednoducho spojený; jeho jediná nula (prvého rádu) sa získa pri z= 1, singulárne body: z= 0 a (vetvové body nekonečného rádu).

Riemannova plocha logaritmu je univerzálnym pokrytím komplexnej roviny bez bodu 0.

Historický náčrt

Skutočný logaritmus

Potreba zložitých výpočtov rýchlo rástla v 16. storočí a veľa ťažkostí sa týkalo násobenia a delenia viacciferných čísel. Koncom storočia prišli viacerí matematici takmer súčasne s myšlienkou: nahradiť prácne násobenie jednoduchým sčítaním, pomocou špeciálnych tabuliek porovnávať geometrický a aritmetický postup, pričom geometrický je pôvodný. Potom je delenie automaticky nahradené nemerateľne jednoduchším a spoľahlivejším odčítaním. Ako prvý publikoval túto myšlienku vo svojej knihe „ Aritmetická integra„Michael Stiefel, ktorý sa však vážnejšie nesnažil realizovať svoj nápad.

V 20. rokoch 17. storočia Edmund Wingate a William Oughtred vynašli prvé logaritmické pravítko, ešte pred príchodom vreckových kalkulačiek – nepostrádateľného inžinierskeho nástroja.

Logaritmácia blízka modernému chápaniu – ako inverzná operácia zvyšovania moci – sa prvýkrát objavila u Wallisa a Johanna Bernoulliho a nakoniec ju legitimizoval Euler v 18. storočí. V knihe „Úvod do analýzy nekonečna“ () Euler poskytol moderné definície exponenciálnych aj logaritmických funkcií, rozšíril ich do mocninných radov a osobitne si všimol úlohu prirodzeného logaritmu.

Eulerovi sa pripisuje aj rozšírenie logaritmickej funkcie na komplexnú oblasť.

Komplexný logaritmus

Prvé pokusy rozšíriť logaritmy na komplexné čísla urobili na prelome 17.-18. storočia Leibniz a Johann Bernoulli, ale nepodarilo sa im vytvoriť holistickú teóriu, a to predovšetkým preto, že samotný pojem logaritmu ešte nebol jasne definovaný. Diskusia o tejto otázke sa uskutočnila najskôr medzi Leibnizom a Bernoullim a v polovici 18. storočia medzi d'Alembertom a Eulerom. Bernoulli a d'Alembert verili, že by sa to malo určiť log(-x) = log(x). Kompletnú teóriu logaritmov záporných a komplexných čísel publikoval Euler v rokoch 1747-1751 a v podstate sa nelíši od modernej.

Hoci spor pokračoval (D'Alembert obhajoval svoj názor a podrobne ho argumentoval v článku vo svojej Encyklopédii a v iných dielach), Eulerov názor rýchlo získal všeobecné uznanie.

Logaritmické tabuľky

Logaritmické tabuľky

Z vlastností logaritmu vyplýva, že namiesto prácneho násobenia viacciferných čísel stačí nájsť (z tabuliek) a sčítať ich logaritmy a potom pomocou tých istých tabuliek vykonať potenciáciu, teda nájsť hodnotu výsledku z jeho logaritmu. Delenie sa líši len tým, že logaritmy sa odčítajú. Laplace povedal, že vynález logaritmov „predĺžil život astronómov“ tým, že výrazne urýchlil proces výpočtov.

Pri presúvaní desatinnej čiarky v čísle na nčíslic, hodnota dekadického logaritmu tohto čísla sa zmení na n. Napríklad log8314,63 = log8,31463 + 3. Z toho vyplýva, že stačí zostaviť tabuľku desiatkových logaritmov pre čísla v rozsahu od 1 do 10.

Prvé tabuľky logaritmov publikoval John Napier ( ), a obsahovali iba logaritmy goniometrických funkcií a s chybami. Nezávisle od neho Joost Bürgi, priateľ Keplera (), zverejnil jeho tabuľky. V roku 1617 publikoval oxfordský profesor matematiky Henry Briggs tabuľky, ktoré už obsahovali desiatkové logaritmy samotných čísel, od 1 do 1000, s 8 (neskôr 14) číslicami. Chyby však boli aj v Briggsových tabuľkách. Prvé bezchybné vydanie založené na tabuľkách Vega () sa objavilo až v roku 1857 v Berlíne (Bremiwerove tabuľky).

V Rusku boli prvé tabuľky logaritmov publikované v roku 1703 za účasti L. F. Magnitského. V ZSSR bolo vydaných niekoľko zbierok logaritmických tabuliek.

• Bradis V.M.Štvormiestne matematické tabuľky. 44. vydanie, M., 1973.

Exponenciálna funkcia reálnej premennej (s kladným základom) sa určuje v niekoľkých krokoch. Po prvé, pre prírodné hodnoty - ako produkt rovnakých faktorov. Definícia sa potom podľa pravidiel rozširuje na záporné celé čísla a nenulové hodnoty. Ďalej uvažujeme zlomkové exponenty, v ktorých je hodnota exponenciálnej funkcie určená pomocou koreňov: . Pre iracionálne hodnoty je definícia už spojená so základným pojmom matematickej analýzy - s prechodom na limit, z dôvodu kontinuity. Všetky tieto úvahy nie sú v žiadnom prípade aplikovateľné na pokusy rozšíriť exponenciálnu funkciu na komplexné hodnoty indikátora a čo to je, napríklad, je úplne nejasné.

Euler po prvý raz zaviedol mocninu s komplexným exponentom s prirodzenou bázou na základe analýzy množstva konštrukcií integrálneho počtu. Niekedy veľmi podobné algebraické výrazy, keď sú integrované, dávajú úplne odlišné odpovede:

Zároveň je tu druhý integrál formálne získaný z prvého, keď je nahradený

Z toho môžeme vyvodiť záver, že pri správnej definícii exponenciálnej funkcie s komplexným exponentom súvisia inverzné goniometrické funkcie s logaritmami, a teda exponenciálna funkcia súvisí s goniometrickými.

Euler mal odvahu a predstavivosť poskytnúť primeranú definíciu exponenciálnej funkcie so základom, konkrétne:

Ide o definíciu, a preto nemožno túto formulku dokazovať, možno len hľadať argumenty v prospech rozumnosti a účelnosti takejto definície. Matematická analýza poskytuje mnoho argumentov tohto druhu. Obmedzíme sa len na jeden.

Je známe, že v skutočnosti existuje obmedzujúci vzťah: . Na pravej strane je polynóm, ktorý má zmysel aj pre zložité hodnoty pre . Limit postupnosti komplexných čísel je určený prirodzene. Postupnosť sa považuje za konvergentnú, ak postupnosť reálnych a imaginárnych častí konverguje a je akceptovaná

Poďme to nájsť. Aby sme to dosiahli, prejdeme na trigonometrický tvar a pre argument vyberieme hodnoty z intervalu. Pri tejto voľbe je jasné, že pre . ďalej

Ak chcete prejsť na limit, musíte overiť existenciu limitov a nájsť tieto limity. Je jasné že

Takže vo výraze

skutočná časť inklinuje k tomu, imaginárna časť inklinuje k tomu

Tento jednoduchý argument poskytuje jeden z argumentov v prospech Eulerovej definície exponenciálnej funkcie.

Teraz zistíme, že pri násobení hodnôt exponenciálnej funkcie sa exponenty sčítavajú. naozaj:

2. Eulerove vzorce.

Uveďme definíciu exponenciálnej funkcie. Dostaneme:

Nahradením b za -b dostaneme

Sčítaním a odčítaním týchto rovníc po členoch nájdeme vzorce

nazývané Eulerove vzorce. Vytvárajú spojenie medzi goniometrickými funkciami a exponenciálnymi funkciami s imaginárnymi exponentmi.

3. Prirodzený logaritmus komplexného čísla.

Komplexné číslo uvedené v goniometrickom tvare možno zapísať v tvare Táto forma zápisu komplexného čísla sa nazýva exponenciálna. Zachováva si všetky dobré vlastnosti trigonometrickej formy, ale je ešte stručnejšia. Ďalej je preto prirodzené predpokladať, že skutočná časť logaritmu komplexného čísla je logaritmom jeho modulu a imaginárna časť je jeho argument. To do určitej miery vysvetľuje „logaritmickú“ vlastnosť argumentu – argument súčinu sa rovná súčtu argumentov faktorov.

Exponenciálna funkcia reálnej premennej (s kladným základom) sa určuje v niekoľkých krokoch. Po prvé, pre prírodné hodnoty - ako produkt rovnakých faktorov. Definícia sa potom podľa pravidiel rozširuje na záporné celé čísla a nenulové hodnoty. Ďalej uvažujeme zlomkové exponenty, v ktorých je hodnota exponenciálnej funkcie určená pomocou koreňov: . Pre iracionálne hodnoty je definícia už spojená so základným pojmom matematickej analýzy - s prechodom na limit, z dôvodu kontinuity. Všetky tieto úvahy nie sú v žiadnom prípade aplikovateľné na pokusy rozšíriť exponenciálnu funkciu na komplexné hodnoty indikátora a čo to je, napríklad, je úplne nejasné.

Euler po prvý raz zaviedol mocninu s komplexným exponentom s prirodzenou bázou na základe analýzy množstva konštrukcií integrálneho počtu. Niekedy veľmi podobné algebraické výrazy, keď sú integrované, dávajú úplne odlišné odpovede:

Zároveň je tu druhý integrál formálne získaný z prvého, keď je nahradený

Z toho môžeme vyvodiť záver, že pri správnej definícii exponenciálnej funkcie s komplexným exponentom súvisia inverzné goniometrické funkcie s logaritmami, a teda exponenciálna funkcia súvisí s goniometrickými.

Euler mal odvahu a predstavivosť poskytnúť primeranú definíciu exponenciálnej funkcie so základom, konkrétne:

Ide o definíciu, a preto nemožno túto formulku dokazovať, možno len hľadať argumenty v prospech rozumnosti a účelnosti takejto definície. Matematická analýza poskytuje mnoho argumentov tohto druhu. Obmedzíme sa len na jeden.

Je známe, že v skutočnosti existuje obmedzujúci vzťah: . Na pravej strane je polynóm, ktorý má zmysel aj pre zložité hodnoty pre . Limit postupnosti komplexných čísel je určený prirodzene. Postupnosť sa považuje za konvergentnú, ak postupnosť reálnych a imaginárnych častí konverguje a je akceptovaná

Poďme to nájsť. Aby sme to dosiahli, prejdeme na trigonometrický tvar a pre argument vyberieme hodnoty z intervalu. Pri tejto voľbe je jasné, že pre . ďalej

Ak chcete prejsť na limit, musíte overiť existenciu limitov a nájsť tieto limity. Je jasné že

Takže vo výraze

skutočná časť inklinuje k tomu, imaginárna časť inklinuje k tomu

Tento jednoduchý argument poskytuje jeden z argumentov v prospech Eulerovej definície exponenciálnej funkcie.

Teraz zistíme, že pri násobení hodnôt exponenciálnej funkcie sa exponenty sčítavajú. naozaj:

2. Eulerove vzorce.

Uveďme definíciu exponenciálnej funkcie. Dostaneme:

Nahradením b za -b dostaneme

Sčítaním a odčítaním týchto rovníc po členoch nájdeme vzorce

nazývané Eulerove vzorce. Vytvárajú spojenie medzi goniometrickými funkciami a exponenciálnymi funkciami s imaginárnymi exponentmi.

3. Prirodzený logaritmus komplexného čísla.

Komplexné číslo uvedené v goniometrickom tvare možno zapísať v tvare Táto forma zápisu komplexného čísla sa nazýva exponenciálna. Zachováva si všetky dobré vlastnosti trigonometrickej formy, ale je ešte stručnejšia. Ďalej je preto prirodzené predpokladať, že skutočná časť logaritmu komplexného čísla je logaritmom jeho modulu a imaginárna časť je jeho argument. To do určitej miery vysvetľuje „logaritmickú“ vlastnosť argumentu – argument súčinu sa rovná súčtu argumentov faktorov.

Plán:

Úvod

• 1 Skutočný logaritmus
  • 1.1 Vlastnosti
  • 1.2 Logaritmická funkcia
  • 1.3 Prirodzené logaritmy
  • 1.4 Desatinné logaritmy
• 2 Komplexný logaritmus
  • 2.1 Definícia a vlastnosti
  • 2.2 Príklady
  • 2.3 Analytické pokračovanie
  • 2.4 Riemannov povrch
• 3 Historický náčrt
  • 3.1 Skutočný logaritmus
  • 3.2 Komplexný logaritmus
• 4 Logaritmické tabuľky
• 5 Aplikácie
Literatúra
Poznámky

Úvod

Ryža. 1. Grafy logaritmických funkcií

Logaritmus čísla b založené na a (z gréčtiny λόγος - „slovo“, „postoj“ a ἀριθμός - „číslo“) je definované ako ukazovateľ výkonu, na ktorý sa musí základňa zdvihnúť a získať číslo b. Označenie: . Z definície vyplýva, že záznamy a sú rovnocenné.

Napríklad preto.

1. Reálny logaritmus

Logaritmus reálnych čísel a b dáva zmysel, keď . Ako je známe, exponenciálna funkcia r = a X je monotónna a každá hodnota trvá iba raz a rozsah jej hodnôt obsahuje všetky kladné reálne čísla. Z toho vyplýva, že hodnota skutočného logaritmu kladného čísla vždy existuje a je jednoznačne určená.

Najpoužívanejšie typy logaritmov sú:

1.1. Vlastnosti

Dôkaz

Dokážme to.

(keďže podľa podmienky bc > 0). ■

Dôkaz

Dokážme to

(keďže podľa podmienok ■

Dôkaz

Na jej preukázanie používame identitu. Logaritmujme obe strany identity na základ c. Dostaneme:

Dôkaz

Dokážme to.

(pretože b p> 0 podľa podmienky). ■

Dôkaz

Dokážme to

Dôkaz

Logaritmujte ľavú a pravú stranu k základni c :

Ľavá strana: Pravá strana:

Rovnosť výrazov je zrejmá. Keďže logaritmy sú rovnaké, potom sú v dôsledku monotónnosti logaritmickej funkcie aj samotné výrazy rovnaké. ■

1.2. Logaritmická funkcia

Ak logaritmické číslo považujeme za premennú, dostaneme logaritmická funkcia r=log a X (pozri obr. 1). Je definovaný na . Rozsah hodnôt: .

Funkcia sa striktne zvyšuje pri a> 1 a striktne sa znižuje na 0< a < 1 . График любой логарифмической функции проходит через точку (1;0) . Функция непрерывна и неограниченно дифференцируема всюду в своей области определения.

Rovno X= 0 je ľavá vertikálna asymptota, pretože at a> 1 a pri 0< a < 1 .

Derivácia logaritmickej funkcie sa rovná:

Dôkaz

I. Dokážme to

Zapíšme si identitu e ln X = X a odlíšiť jeho ľavú a pravú stranu

Dostávame to, z čoho to vyplýva

II. Dokážme to

Logaritmická funkcia vykonáva izomorfizmus medzi multiplikatívnou grupou kladných reálnych čísel a aditívnou grupou všetkých reálnych čísel.

1.3. Prirodzené logaritmy

Vzťah k desiatkovému logaritmu: .

Ako je uvedené vyššie, derivácia prirodzeného logaritmu má jednoduchý vzorec:

Z tohto dôvodu sa v matematickom výskume prevažne používajú prirodzené logaritmy. Často sa objavujú pri riešení diferenciálnych rovníc, štúdiu štatistických závislostí (napríklad rozloženie prvočísel) atď.

Neurčitý integrál prirodzeného logaritmu možno ľahko nájsť integráciou po častiach:

Rozšírenie Taylorovho radu možno znázorniť takto:
keď platí rovnosť

(1)

najmä

Tento rad konverguje rýchlejšie a navyše ľavá strana vzorca teraz môže vyjadrovať logaritmus akéhokoľvek kladného čísla.

1.4. Desatinné logaritmy

Ryža. 2a. Logaritmická stupnica

Ryža. 2b. Logaritmická stupnica so symbolmi

Logaritmy na základ 10 (symbol: lg a) pred vynálezom kalkulačiek boli široko používané na výpočty. Nerovnomerná stupnica desiatkových logaritmov sa zvyčajne používa na posuvné pravidlá. Podobná stupnica sa používa v mnohých oblastiach vedy, napríklad:

• Fyzika - intenzita zvuku (decibely).
• Astronómia - stupnica jasnosti hviezd.
• Chémia – aktivita vodíkových iónov (pH).
• Seizmológia - Richterova stupnica.
• Hudobná teória - stupnica nôt, vo vzťahu k frekvenciám hudobných nôt.
• História je logaritmická časová mierka.

Logaritmická škála je tiež široko používaná na identifikáciu exponentu v mocninných vzťahoch a koeficientu v exponente. V tomto prípade má graf zostrojený na logaritmickej mierke pozdĺž jednej alebo dvoch osí formu priamky, ktorá sa ľahšie študuje.

2. Komplexný logaritmus

2.1. Definícia a vlastnosti

Pre komplexné čísla je logaritmus definovaný rovnakým spôsobom ako skutočný. V praxi sa takmer výlučne používa prirodzený komplexný logaritmus, ktorý označujeme a definujeme ako množinu všetkých komplexných čísel z také že e z = w . Komplexný logaritmus existuje pre ľubovoľný a jeho skutočná časť je určená jednoznačne, zatiaľ čo imaginárna časť má nekonečný počet hodnôt. Z tohto dôvodu sa nazýva viachodnotová funkcia. Ak si predstavíte w v demonštratívnej forme:

,

potom sa logaritmus nájde podľa vzorca:

Tu je skutočný logaritmus, r = | w | , k- ľubovoľné celé číslo. Hodnota získaná, keď k= 0, tzv hlavný význam zložitý prirodzený logaritmus; je zvykom brať v ňom hodnotu argumentu v intervale (− π,π] Príslušná (už jednohodnotová) funkcia je tzv. hlavná pobočka logaritmus a označuje sa . Niekedy označujú aj logaritmickú hodnotu, ktorá nie je na hlavnej vetve.

Zo vzorca vyplýva:

• Skutočná časť logaritmu je určená vzorcom:

• Logaritmus záporného čísla sa zistí podľa vzorca:

Keďže komplexné goniometrické funkcie súvisia s exponentom (Eulerov vzorec), komplexný logaritmus, ako inverzná funkcia exponenciály, súvisí s inverznými goniometrickými funkciami. Príklad takéhoto spojenia:

2.2. Príklady

Uveďme hlavnú hodnotu logaritmu pre niektoré argumenty:

Pri prevode zložitých logaritmov by ste mali byť opatrní, berúc do úvahy, že sú viachodnotové, a preto rovnosť logaritmov akýchkoľvek výrazov neznamená rovnosť týchto výrazov. Príklad chybného uvažovania:

iπ = ln(− 1) = ln((− i) 2) = 2ln(- i) = 2(− iπ / 2) = - iπ - čistá absurdita.

Všimnite si, že vľavo je hlavná hodnota logaritmu a vpravo je hodnota zo základnej vetvy ( k= − 1). Príčinou chyby je neopatrné používanie vlastnosti, ktoré vo všeobecnosti znamená v zložitom prípade celú nekonečnú množinu logaritmických hodnôt, nielen hlavnú hodnotu.

2.3. Analytické pokračovanie

Ryža. 3. Komplexný logaritmus (imaginárna časť)

Logaritmus komplexného čísla možno definovať aj ako analytické rozšírenie reálneho logaritmu na celú komplexnú rovinu. Nech krivka Γ začína v jednotke, neprechádza nulou a nepretína zápornú časť reálnej osi. Potom hlavná hodnota logaritmu v koncovom bode w krivku Γ možno určiť podľa vzorca:

Ak je Γ jednoduchá krivka (bez sebapriesečníkov), potom na čísla ležiace na nej možno bez obáv použiť logaritmické identity, napr.

Ak je dovolené, aby krivka Γ pretínala zápornú časť reálnej osi, potom prvý takýto priesečník prenesie výsledok z vetvy hlavnej hodnoty do susednej vetvy a každý nasledujúci priesečník spôsobí podobný posun pozdĺž vetiev logaritmickej funkcie ( pozri obrázok).

Z analytického pokračovacieho vzorca vyplýva, že na ľubovoľnej vetve logaritmu

Pre akýkoľvek kruh S, pokrývajúci bod 0:

Integrál sa odoberá v kladnom smere (proti smeru hodinových ručičiek). Táto identita je základom teórie zvyškov.

Môžete tiež definovať analytické pokračovanie komplexného logaritmu pomocou vyššie uvedeného radu (1), zovšeobecneného na prípad komplexného argumentu. Z typu expanzie však vyplýva, že v jednotke sa rovná nule, to znamená, že rad sa vzťahuje iba na hlavnú vetvu viachodnotovej funkcie komplexného logaritmu.

2.4. Riemannov povrch

Komplexná logaritmická funkcia je príkladom Riemannovej plochy; jeho pomyselnú časť (obr. 3) tvorí nekonečné množstvo vetiev stočených do tvaru špirály. Tento povrch je jednoducho spojený; jeho jediná nula (prvého rádu) sa získa pri z= 1, singulárne body: z= 0 a (vetvové body nekonečného rádu).

Riemannova plocha logaritmu je univerzálnym pokrytím komplexnej roviny bez bodu 0.

3. Historický náčrt

3.1. Skutočný logaritmus

Potreba zložitých výpočtov rýchlo rástla v 16. storočí a veľa ťažkostí sa týkalo násobenia a delenia viacciferných čísel a zakorenenia. Koncom storočia prišli viacerí matematici takmer súčasne s myšlienkou: nahradiť prácne násobenie jednoduchým sčítaním, pomocou špeciálnych tabuliek porovnávať geometrický a aritmetický postup, pričom geometrický je pôvodný. Potom je delenie automaticky nahradené nemerateľne jednoduchším a spoľahlivejším odčítaním a extrahovaním koreňa stupňa n prichádza k deleniu logaritmu radikálneho výrazu n. Ako prvý publikoval túto myšlienku vo svojej knihe „ Aritmetická integra„Michael Stiefel, ktorý sa však vážnejšie nesnažil realizovať svoj nápad.

V roku 1614 škótsky amatérsky matematik John Napier publikoval esej v latinčine s názvom „ Popis úžasnej tabuľky logaritmov"(lat. Mirifici Logarithmorum Canonis Descriptio ). Obsahoval stručný popis logaritmov a ich vlastností, ako aj 8-miestne tabuľky logaritmov sínusov, kosínusov a dotyčníc s krokom 1“. logaritmus, navrhnutý Napierom, sa etabloval vo vede. Napier načrtol teóriu logaritmov vo svojej ďalšej knihe „ Vytvorenie úžasnej logaritmickej tabuľky"(lat. Mirifici Logarithmorum Canonis Constructio ), ktorý posmrtne vydal v roku 1619 jeho syn.

Pojem funkcie ešte neexistoval a Napier definoval logaritmus kinematicky, porovnávajúc rovnomerný a logaritmicky pomalý pohyb; napríklad definoval logaritmus sínusu takto:

Logaritmus daného sínusu je číslo, ktoré sa vždy aritmeticky zväčšovalo rovnakou rýchlosťou, akou začal geometricky klesať celkový sínus.

V modernej notácii môže byť Napierov kinematický model reprezentovaný diferenciálnou rovnicou: dx/x = -dy/M, kde M je mierkový faktor zavedený s cieľom zabezpečiť, aby sa hodnota ukázala ako celé číslo s požadovaným počtom číslic (desatinné zlomky sa ešte veľmi nepoužívali). Napier získal M = 10000000.

Presne povedané, Napier zostavil zlú funkciu, ktorá sa teraz nazýva logaritmus. Ak označíme jeho funkciu LogNap(x), potom súvisí s prirodzeným logaritmom takto:

LogNap(M) = 0, to znamená, že logaritmus „plného sínusu“ je nula – to je to, čo Napier svojou definíciou dosiahol. .

Hlavná vlastnosť Napierovho logaritmu: ak veličiny tvoria geometrickú postupnosť, potom ich logaritmy tvoria aritmetickú postupnosť. Logaritmické pravidlá pre funkciu neper sa však líšili od pravidiel pre moderný logaritmus.

Napríklad, LogNap(ab) = LogNap(a) + LogNap(b) - LogNap(1).

Bohužiaľ, všetky hodnoty v Napierovej tabuľke obsahovali chybu výpočtu po šiestej číslici. To však nezabránilo tomu, aby nová metóda výpočtu získala veľkú popularitu a mnohí európski matematici, vrátane Keplera, začali zostavovať logaritmické tabuľky. Len o 5 rokov neskôr, v roku 1619, londýnsky učiteľ matematiky John Spidell ( John Speidell) znovu publikoval Napierove tabuľky, transformované tak, aby sa z nich skutočne stali tabuľky prirodzených logaritmov (hoci Spidell zachoval škálovanie na celé čísla). Termín „prirodzený logaritmus“ navrhol taliansky matematik Pietro Mengoli ( Pietro Mengoli)) v polovici 16. storočia.

V 20. rokoch 17. storočia Edmund Wingate a William Oughtred vynašli prvé logaritmické pravítko, ešte pred príchodom vreckových kalkulačiek – nepostrádateľného inžinierskeho nástroja.

Logaritmizácia blízka modernému chápaniu – ako inverzná operácia zvyšovania moci – sa prvýkrát objavila u Wallisa a Johanna Bernoulliho a nakoniec ju legitimizoval Euler v 18. storočí. V knihe „Úvod do analýzy nekonečna“ (1748) dal Euler moderné definície exponenciálnych aj logaritmických funkcií, rozšíril ich do mocninných radov a osobitne si všimol úlohu prirodzeného logaritmu.

Eulerovi sa pripisuje aj rozšírenie logaritmickej funkcie na komplexnú oblasť.

3.2. Komplexný logaritmus

Prvé pokusy rozšíriť logaritmy na komplexné čísla urobili na prelome 17.-18. storočia Leibniz a Johann Bernoulli, ale nepodarilo sa im vytvoriť holistickú teóriu, a to predovšetkým preto, že samotný pojem logaritmu ešte nebol jasne definovaný. Diskusia o tejto otázke sa uskutočnila najskôr medzi Leibnizom a Bernoullim a v polovici 18. storočia medzi d'Alembertom a Eulerom. Bernoulli a d'Alembert verili, že by sa to malo určiť log(-x) = log(x). Kompletnú teóriu logaritmov záporných a komplexných čísel publikoval Euler v rokoch 1747-1751 a v podstate sa nelíši od modernej.

Hoci spor pokračoval (D'Alembert obhajoval svoj názor a podrobne ho argumentoval v článku vo svojej Encyklopédii a v iných dielach), Eulerov názor rýchlo získal všeobecné uznanie.

4. Logaritmické tabuľky

Logaritmické tabuľky

Z vlastností logaritmu vyplýva, že namiesto prácneho násobenia viacciferných čísel stačí nájsť (z tabuliek) a sčítať ich logaritmy a potom pomocou tých istých tabuliek vykonať potenciáciu, teda nájsť hodnotu výsledku z jeho logaritmu. Delenie sa líši iba tým, že logaritmy sa odčítajú. Laplace povedal, že vynález logaritmov „predĺžil život astronómom“ tým, že výrazne urýchlil proces výpočtov.

Pri presúvaní desatinnej čiarky v čísle na nčíslic, hodnota dekadického logaritmu tohto čísla sa zmení na n. Napríklad log8314,63 = log8,31463 + 3. Z toho vyplýva, že stačí zostaviť tabuľku desiatkových logaritmov pre čísla v rozsahu od 1 do 10.

Prvé tabuľky logaritmov publikoval John Napier (1614) a obsahovali iba logaritmy goniometrických funkcií a s chybami. Nezávisle od neho Joost Burgi, priateľ Keplera, vydal svoje tabuľky (1620). V roku 1617 publikoval oxfordský profesor matematiky Henry Briggs tabuľky, ktoré už obsahovali desiatkové logaritmy samotných čísel, od 1 do 1000, s 8 (neskôr 14) číslicami. Chyby však boli aj v Briggsových tabuľkách. Prvé bezchybné vydanie založené na tabuľkách Vega (1783) sa objavilo až v roku 1857 v Berlíne (Bremiwerove tabuľky).

V Rusku boli prvé tabuľky logaritmov publikované v roku 1703 za účasti L. F. Magnitského. V ZSSR bolo vydaných niekoľko zbierok logaritmických tabuliek.

• Bradis V.M.Štvormiestne matematické tabuľky. 44. vydanie, M., 1973.

Bradisove tabuľky (1921) sa používali vo vzdelávacích inštitúciách a v inžinierskych výpočtoch, ktoré nevyžadovali veľkú presnosť. Obsahovali mantisy desiatkových logaritmov čísel a goniometrických funkcií, prirodzené logaritmy a niektoré ďalšie užitočné výpočtové nástroje.

• Vega G. Tabuľky sedemciferných logaritmov, 4. vydanie, M., 1971.

Profesionálna kolekcia pre presné výpočty.

• Päťmiestne tabuľky prirodzených hodnôt goniometrických veličín, ich logaritmy a logaritmy čísel, 6. vydanie, M.: Nauka, 1972.
• Tabuľky prirodzených logaritmov, 2. vydanie, v 2 zväzkoch, M.: Nauka, 1971.

V súčasnosti, s rozšírením kalkulačiek, potreba používať tabuľky logaritmov zmizla.

M, vlastnosť (komplexná analýza).

Definícia a vlastnosti

Komplexná nula nemá logaritmus, pretože komplexný exponent nemá nulovú hodnotu. Nenulová texvc môžu byť znázornené v demonštratívnej forme:

Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pozrite si math/README - pomoc s nastavením.): z=r \cdot e^(i (\varphi + 2 \pi k))\;\;, Kde Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti Matematika/README.): k- ľubovoľné celé číslo

Potom Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \mathrm(Ln)\,z sa nachádza podľa vzorca:

Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pozrite si math/README - pomoc s nastavením.): \mathrm(Ln)\,z = \ln r + i \left(\varphi + 2 \pi k \right)

Tu Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \ln\,r= \ln\,|z|- skutočný logaritmus. Z toho vyplýva:

Zo vzorca je zrejmé, že iba jedna z hodnôt má imaginárnu časť v intervale Nedá sa analyzovať výraz (spustiteľný súbor texvc . Táto hodnota sa nazýva hlavný význam zložitý prirodzený logaritmus. Zavolá sa príslušná (už jednoznačná) funkcia hlavná pobočka logaritmus a je označený Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \ln\,z. Niekedy cez Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \ln\, z označujú aj hodnotu logaritmu, ktorý neleží na hlavnej vetve. Ak Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti matematika/README.): z je reálne číslo, potom sa hlavná hodnota jeho logaritmu zhoduje s obyčajným reálnym logaritmom.

Z vyššie uvedeného vzorca tiež vyplýva, že reálna časť logaritmu je určená nasledovne prostredníctvom komponentov argumentu:

Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \operatorname(Re)(\ln(x+iy)) = \frac(1)(2) \ln(x^2+y^2)

Obrázok ukazuje, že skutočná súčiastka ako funkcia komponentov je centrálne symetrická a závisí len od vzdialenosti od začiatku. Získa sa rotáciou grafu skutočného logaritmu okolo zvislej osi. Keď sa blíži k nule, funkcia má tendenciu Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pozri math/README - pomoc s nastavením.): -\infty.

Logaritmus záporného čísla sa zistí podľa vzorca:

Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \mathrm(Ln) (-x) = \ln x + i \pi (2 k + 1) \qquad (x>0,\ k = 0, \pm 1 ,\ pm 2\bodky)

Príklady zložitých logaritmických hodnôt

Uveďme hlavnú hodnotu logaritmu ( Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \ln) a jeho všeobecné vyjadrenie ( Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \mathrm(Ln)) k niektorým argumentom:

Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \ln (1) = 0;\; \mathrm(Ln) (1) = 2k\pi i Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \ln (-1) = i \pi;\; \mathrm(Ln) (-1) = (2k+1)i \pi Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \ln (i) = i \frac(\pi) (2);\; \mathrm(Ln) (i) = i \frac(4k+1)(2) \pi

Pri prevode zložitých logaritmov by ste mali byť opatrní, berúc do úvahy, že sú viachodnotové, a preto rovnosť logaritmov akýchkoľvek výrazov neznamená rovnosť týchto výrazov. Príklad chybný zdôvodnenie:

Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pozrite si math/README – pomoc s nastavením.): i\pi = \ln(-1) = \ln((-i)^2) = 2\ln(-i) = 2(-i\pi/2 ) = -i\pi- zjavná chyba.

Všimnite si, že vľavo je hlavná hodnota logaritmu a vpravo je hodnota zo základnej vetvy ( Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pozri math/README - pomoc s nastavením.): k=-1). Príčinou chyby je neopatrné používanie nehnuteľnosti Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \log_a((b^p)) = p~\log_a b, čo vo všeobecnosti znamená v zložitom prípade celú nekonečnú množinu hodnôt logaritmu, a nielen hlavnú hodnotu.

Komplexná logaritmická funkcia a Riemannova plocha

Riemannova plocha logaritmu je vďaka svojej jednoduchej prepojenosti univerzálnym pokrytím komplexnej roviny bez bodu. Nedá sa analyzovať výraz (spustiteľný súbor texvc .

Analytické pokračovanie

Logaritmus komplexného čísla možno definovať aj ako analytické pokračovanie reálneho logaritmu do celej komplexnej roviny. Nechajte krivku Nedá sa analyzovať výraz (spustiteľný súbor texvc začína na jednotke, neprechádza nulou a neprechádza zápornou časťou reálnej osi. Potom hlavná hodnota logaritmu v koncovom bode Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti matematika/README.): w nepoctivý Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \Gamma možno určiť podľa vzorca:

Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \ln z = \int\limits_\Gamma (du \over u)

Ak Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \Gamma- jednoduchá krivka (bez vlastných priesečníkov), potom pre čísla ležiace na nej možno bez obáv použiť logaritmické identity, napríklad:

Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \ln (wz) = \ln w + \ln z, ~\forall z,w\in\Gamma\colon zw\in \Gamma

Hlavná vetva logaritmickej funkcie je spojitá a diferencovateľná v celej komplexnej rovine, s výnimkou zápornej časti reálnej osi, na ktorej sa imaginárna časť náhle zmení na Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pozri math/README - pomoc s nastavením.): 2\pi. Táto skutočnosť je však dôsledkom umelého obmedzenia imaginárnej časti hlavnej hodnoty intervalom Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): (-\pi, \pi]. Ak vezmeme do úvahy všetky vetvy funkcie, potom spojitosť nastane vo všetkých bodoch okrem nuly, kde funkcia nie je definovaná. Ak vyriešite krivku Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \Gamma prekročí zápornú časť reálnej osi, potom prvý takýto priesečník prenesie výsledok z vetvy hlavnej hodnoty do susednej vetvy a každý nasledujúci priesečník spôsobí podobný posun pozdĺž vetiev logaritmickej funkcie (pozri obrázok).

Z analytického pokračovacieho vzorca vyplýva, že na ktorejkoľvek vetve logaritmu:

Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \frac(d)(dz) \ln z = (1\over z)

Pre akýkoľvek kruh Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti matematika/README.): S, pokrývajúci bod Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pozri matematiku/README - pomoc s nastavením.): 0 :

Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \oint\limits_S (dz \over z) = 2\pi i

Integrál sa odoberá v kladnom smere (proti smeru hodinových ručičiek). Táto identita je základom teórie zvyškov.

Analytické pokračovanie komplexného logaritmu možno definovať aj pomocou radov známych pre skutočný prípad:

Z tvaru týchto radov však vyplýva, že v jednej sa súčet radu rovná nule, to znamená, že rad sa vzťahuje iba na hlavnú vetvu viachodnotovej funkcie komplexného logaritmu. Polomer konvergencie oboch radov je 1.

Spojenie s inverznými goniometrickými a hyperbolickými funkciami

Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \operatorname(Arcsin) z = -i \operatorname(Ln) (i z + \sqrt(1-z^2)) Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \operatorname(Arccos) z = -i \operatorname(Ln) (z + i\sqrt(1-z^2)) Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pozri math/README - pomoc s nastavením.): \operatorname(Arctg) z = -\frac(i)(2) \ln \frac(1+z i)(1-z i) + k \pi \; (z \ne \pm i) Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pozri math/README - pomoc s nastavením.): \operatorname(Arcctg) z = -\frac(i)(2) \ln \frac(z i-1)(z i+1) + k \pi \; (z \ne \pm i) Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \operatorname(Arsh)z = \operatorname(Ln)(z+\sqrt(z^2+1))- inverzný hyperbolický sínus Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pozrite si math/README - pomoc s nastavením.): \operatorname(Arch)z=\operatorname(Ln) \left(z+\sqrt(z^(2)-1) \right)- inverzný hyperbolický kosínus Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \operatorname(Arth)z=\frac(1)(2)\operatorname(Ln)\left(\frac(1+z)(1-z)\right)- inverzná hyperbolická dotyčnica Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \operatorname(Arcth)z=\frac(1)(2)\operatorname(Ln)\left(\frac(z+1)(z-1)\right)- inverzný hyperbolický kotangens

Historický náčrt

Prvé pokusy rozšíriť logaritmy na komplexné čísla urobili na prelome 17.-18. storočia Leibniz a Johann Bernoulli, ale nepodarilo sa im vytvoriť holistickú teóriu, predovšetkým preto, že samotný pojem logaritmu ešte nebol jasne definovaný. Diskusia o tejto otázke prebiehala najskôr medzi Leibnizom a Bernoullim a v polovici 18. storočia medzi D’Alembertom a Eulerom. Bernoulli a D'Alembert verili, že by sa to malo určiť Nedá sa analyzovať výraz (spustiteľný súbor texvc nenájdené; Pomoc s nastavením nájdete v časti math/README.): \log(-x) = \log(x), zatiaľ čo Leibniz dokázal, že logaritmus záporného čísla je imaginárne číslo. Kompletnú teóriu logaritmov záporných a komplexných čísel publikoval Euler v rokoch 1747-1751 a v podstate sa nelíši od modernej. Hoci diskusia pokračovala (D'Alembert obhajoval svoj názor a podrobne ho argumentoval v článku vo svojej Encyklopédii a v iných dielach), Eulerov prístup získal na konci 18. storočia všeobecné uznanie.

Napíšte recenziu na článok "Komplexný logaritmus"

Literatúra

Teória logaritmov

• Korn G., Korn T.. - M.: Nauka, 1973. - 720 s.
• Sveshnikov A. G., Tichonov A. N. Teória funkcií komplexnej premennej. - M.: Nauka, 1967. - 304 s.
• Fikhtengolts G. M. Priebeh diferenciálneho a integrálneho počtu. - vyd. 6. - M.: Nauka, 1966. - 680 s.

História logaritmov

• Matematika 18. storočia // / Editoval A. P. Juškevič, v troch zväzkoch. - M.: Veda, 1972. - T. III.
• Kolmogorov A. N., Juškevič A. P. (eds.). Matematika 19. storočia. Geometria. Teória analytických funkcií. - M.: Veda, 1981. - T. II.

Poznámky

1. Logaritmická funkcia. // . - M.: Sovietska encyklopédia, 1982. - T. 3.
2. , zväzok II, str. 520-522..
3. , S. 623..
4. , S. 92-94..
5. , S. 45-46, 99-100..
6. Boltyansky V. G., Efremovič V. A.. - M.: Nauka, 1982. - S. 112. - (Knižnica Kvant, číslo 21).
7. , zväzok II, str. 522-526..
8. , S. 624..
9. , S. 325-328..
10. Rybnikov K.A. História matematiky. V dvoch zväzkoch. - M.: Vydavateľstvo. Moskovská štátna univerzita, 1963. - T. II. - S. 27, 230-231..
11. , S. 122-123..
12. Klein F.. - M.: Veda, 1987. - T. II. Geometria. - s. 159-161. - 416 s.

Výňatok charakterizujúci komplexný logaritmus

Z divokej hrôzy, ktorá nás zachvátila, sme sa ako strely rútili širokým údolím, ani sme nepomysleli na to, že by sme mohli ísť rýchlo na iné „poschodie“... Jednoducho sme nemali čas na to myslieť – príliš sme sa báli.
To stvorenie letelo priamo nad nami, hlasno cvakalo rozďaveným zubatým zobákom a my sme sa ponáhľali, ako sme len mohli, špliechajúc odporné slizké striekance do strán a v duchu sme sa modlili, aby tohto strašidelného „zázračného vtáka“ zrazu zaujalo niečo iné... bolo cítiť, že je oveľa rýchlejšia a jednoducho sme nemali šancu sa od nej odtrhnúť. Ako šťastie, v blízkosti nerástol ani jeden strom, neboli tam žiadne kríky, ba ani kamene, za ktoré by sa dalo schovať, len v diaľke bolo vidieť zlovestnú čiernu skalu.
- Tu! – vykríkla Stella a ukázala prstom na ten istý kameň.
No zrazu, nečakane, priamo pred nami sa odniekiaľ zjavila bytosť, pri pohľade na ktorú nám doslova stuhla krv v žilách... Vyzeralo to akoby „priamo zo vzduchu“ a bolo naozaj desivé... obrovská čierna mŕtvola bola celá pokrytá dlhými, hrubými vlasmi, takže vyzeral ako bruchý, len tento „medveď“ bol vysoký ako trojposchodový dom... Hrčatá hlava netvora bola „korunovaná“ dvoma obrovskými zakrivenými rohy a strašidelné ústa boli zdobené párom neuveriteľne dlhých tesákov, ostrých ako nože, len pri pohľade, ktorým sa nám od strachu podlomili nohy... A potom, čo nás neuveriteľne prekvapilo, monštrum ľahko vyskočilo a. .. nadvihol lietajúce „muck“ na jeden zo svojich obrovských tesákov... Zamrzli sme v šoku.
- Poďme bežať!!! – skríkla Stella. – Poďme bežať, kým je „zaneprázdnený“!...
A boli sme pripravení znova sa ponáhľať bez toho, aby sme sa obzreli, keď zrazu za našimi chrbtom zaznel tenký hlas:
- Dievčatá, počkajte!!! Netreba utekať!... Dean ťa zachránil, nie je nepriateľ!
Prudko sme sa otočili - za nami stálo maličké, veľmi krásne čiernooké dievčatko... a pokojne hladilo príšeru, ktorá sa k nej priblížila!... Naše oči sa rozšírili prekvapením... Bolo to neuveriteľné! Iste - bol to deň prekvapení!... Dievča, pozerajúc na nás, sa prívetivo usmialo, vôbec sa nebálo chlpatej príšery stojacej vedľa nás.
- Prosím, nebojte sa ho. Je veľmi milý. Videli sme, že ťa Ovara prenasleduje a rozhodli sme sa pomôcť. Dean bol skvelý, stihol to načas. Naozaj, moja drahá?
„Dobrý“ zamrmlal, čo znelo ako slabé zemetrasenie, a sklonil hlavu a olízal dievčaťu tvár.
– Kto je Owara a prečo na nás zaútočila? - Opýtal som sa.
"Útočí na každého, je to predátor." A veľmi nebezpečné,“ odpovedalo dievča pokojne. – Môžem sa opýtať, čo tu robíte? Vy nie ste odtiaľto, dievčatá?
- Nie, nie odtiaľto. Len sme kráčali. Ale tá istá otázka pre teba - čo tu robíš?
„Idem za mamou...“ zarmútilo sa dievčatko. "Zomreli sme spolu, ale z nejakého dôvodu skončila tu." A teraz tu žijem, ale nepoviem jej to, pretože s tým nikdy nebude súhlasiť. Myslí si, že len prídem...
– Nie je lepšie jednoducho prísť? Je to tu také strašné!... – Stella pokrčila plecami.
"Nemôžem ju tu nechať samú, sledujem ju, aby sa jej nič nestalo." A tu je so mnou Dean... Pomáha mi.
Nemohla som tomu uveriť... Toto malé statočné dievčatko dobrovoľne opustilo svoje krásne a milé „poschodie“, aby žilo v tomto chladnom, hroznom a cudzom svete, chrániac svoju matku, ktorá bola nejakým spôsobom veľmi „vinná“! Nemyslím si, že by sa našlo veľa tak odvážnych a obetavých ľudí (dokonca aj dospelých!), ktorí by sa odvážili podstúpiť takýto čin... A hneď mi napadlo - možno len nepochopila, na čo sa sama odsúdi. ?!
– Ako dlho si tu, dievča, ak to nie je tajomstvo?
„Nedávno...“ odpovedalo smutne čiernooké dieťa a prstami si potiahlo čierny prameň svojich kučeravých vlasov. – Keď som zomrel, ocitol som sa v takom krásnom svete!... Bol taký milý a bystrý!... A potom som videl, že moja matka nie je pri mne a ponáhľal som sa ju hľadať. Spočiatku to bolo také strašidelné! Z nejakého dôvodu ju nikde nenašli... A potom som upadol do tohto hrozného sveta... A potom som ju našiel. Bol som tu tak vystrašený... Tak osamelý... Mama mi povedala, aby som odišiel, dokonca mi vynadala. Ale nemôžem ju opustiť... Teraz mám priateľa, môjho dobrého Deana, a už tu môžem nejako existovať.
Jej „dobrá kamarátka“ opäť zavrčala, z čoho nám so Stellou naskočila obrovská „dolná astrálna“ husia koža... Pozbieral som sa, snažil som sa trochu upokojiť a začal som sa na tento chlpatý zázrak pozerať bližšie... A on, okamžite cítil, že si ho všimli, strašne si odkryl ústa s tesákmi... Odskočil som.
- Oh, nebojte sa, prosím! "Usmieva sa na teba," "uisťovalo dievča."
Áno... Z takého úsmevu sa naučíš rýchlo behať... - pomyslel som si.
- Ako sa stalo, že ste sa s ním spriatelili? – spýtala sa Stella.
– Keď som sem prvýkrát prišiel, veľmi som sa bál, najmä keď dnes útočili také príšery ako ty. A potom jedného dňa, keď som takmer zomrel, ma Dean zachránil pred množstvom strašidelných lietajúcich „vtákov“. Tiež som sa ho najprv bála, ale potom som si uvedomila, aké má zlaté srdce... Je to najlepší kamarát! Nikdy som nič také nemal, ani keď som žil na Zemi.
- Ako si si na to tak rýchlo zvykol? Jeho vzhľad nie je celkom, povedzme, známy...
– A tu som pochopil jednu veľmi jednoduchú pravdu, ktorú som si z nejakého dôvodu na Zemi nevšimol – na vzhľade nezáleží, či má človek alebo tvor dobré srdce... Moja mama bola veľmi krásna, no občas bola veľmi nahnevaná. tiež. A potom všetka jej krása niekam zmizla... A Dean, hoci je strašidelný, je vždy veľmi láskavý a vždy ma chráni, cítim jeho láskavosť a ničoho sa nebojím. Ale na vzhľad sa dá zvyknúť...
– Viete, že tu budete veľmi dlho, oveľa dlhšie, ako žijú ľudia na Zemi? Naozaj tu chceš zostať?...
"Moja mama je tu, tak jej musím pomôcť." A keď ona opäť „odíde“ žiť na Zem, odídem aj ja... Tam, kde je viac dobra. V tomto hroznom svete sú ľudia veľmi zvláštni – akoby vôbec nežili. prečo je to tak? Viete o tom niečo?
– Kto ti povedal, že tvoja matka odíde znova žiť? – začala sa zaujímať Stella.
- Dean, samozrejme. Vie veľa, žije tu veľmi dlho. Povedal tiež, že keď budeme (moja mama a ja) opäť žiť, naše rodiny budú iné. A potom už nebudem mať túto matku... Preto chcem byť teraz s ňou.
- Ako sa s ním rozprávate, váš dekan? – spýtala sa Stella. - A prečo nám nechceš povedať svoje meno?
Ale je to pravda - stále sme nevedeli jej meno! A ani oni nevedeli, odkiaľ pochádza...
– Volal som sa Mária... Ale naozaj na tom záleží?
- Určite! – zasmiala sa Stella. - Ako s vami môžem komunikovať? Keď odídete, dajú vám nové meno, ale kým tu budete, budete musieť žiť s tým starým. Hovorila si tu s niekým iným, dievča Maria? – spýtala sa Stella a zo zvyku skákala z témy na tému.
"Áno, hovorila som..." povedalo dievčatko váhavo. "Ale sú tu takí zvláštni." A takí nešťastní... Prečo sú takí nešťastní?
– To, čo tu vidíš, prispieva k šťastiu? – prekvapila ma jej otázka. – Aj samotná miestna „realita“ vopred zabíja akékoľvek nádeje!.. Ako tu môžeš byť šťastný?
- Neviem. Keď som s mamou, zdá sa mi, že aj ja by som tu mohol byť šťastný... Pravda, je to tu veľmi strašidelné a veľmi sa jej tu nepáči... Keď som povedal, že som súhlasil, že zostanem s ona, zakričala na mňa a povedala, že som jej „bezmozgové nešťastie“... Ale ja sa neurážam... Viem, že sa len bojí. Presne ako ja...
– Možno ťa len chcela ochrániť pred tvojím „extrémnym“ rozhodnutím a chcela len, aby si sa vrátil na svoje „poschodie“? – opatrne sa spýtala Stella, aby sa neurazila.
– Nie, samozrejme... Ale ďakujem za pekné slová. Mama ma často nazývala nie veľmi dobrými menami, dokonca aj na Zemi... Ale viem, že to nebolo z hnevu. Jednoducho bola nešťastná, že som sa narodil, a často mi hovorila, že som jej zničil život. Ale nebola to moja chyba, však? Vždy som sa jej snažil urobiť radosť, ale z nejakého dôvodu sa mi to veľmi nedarilo... A nikdy som nemal otca. – Mária bola veľmi smutná a hlas sa jej triasol, akoby sa chystala plakať.
Pozreli sme sa na seba so Stellou a bol som si takmer istý, že podobné myšlienky navštívili aj ju... Už teraz sa mi naozaj nepáčila táto rozmaznaná, sebecká “matka”, ktorá namiesto toho, aby sa sama starala o svoje dieťa, jeho hrdinskú obeť vôbec som pochopil a navyše som jej aj bolestne ublížil.
"Ale Dean hovorí, že som dobrý a že ho robím veľmi šťastným!" – veselšie bľabotalo dievčatko. "A on chce byť so mnou kamarát." A iní, ktorých som tu stretol, sú veľmi chladní a ľahostajní a niekedy až zlí... Najmä tí, ktorí majú pripútané príšery...
"Potvory - čo?..." nerozumeli sme.
- No, na chrbte im sedia strašné príšery a hovoria im, čo musia robiť. A ak nepočúvajú, príšery sa im strašne posmievajú... Snažil som sa s nimi rozprávať, ale tieto príšery mi to nedovolili.
Z tohto „vysvetlenia“ sme nerozumeli absolútne nič, ale samotný fakt, že niektoré astrálne bytosti mučili ľudí, nemohol zostať „preskúmaný“, takže sme sa jej hneď spýtali, ako môžeme vidieť tento úžasný fenomén.
- Áno, všade! Najmä na „čiernej hore“. Tu je, za stromami. Chcete, aby sme išli s vami aj my?
- Samozrejme, budeme veľmi šťastní! – hneď odpovedala natešená Stella.
Aby som bol úprimný, tiež som sa naozaj neusmial nad vyhliadkou na randenie s niekým iným, „strašidelným a nepochopiteľným“, najmä sám. Ale záujem zvíťazil nad strachom a my by sme, samozrejme, išli aj napriek tomu, že sme sa trochu báli... Ale keď s nami kráčal taký obranca ako Dean, hneď to bolo veselšie...
A potom, po krátkom momente, sa pred našimi očami roztvorilo skutočné peklo, dokorán otvorené od úžasu... Vízia pripomínala obrazy Boscha (alebo Bosca, podľa toho, do akého jazyka to preložíte), „šialeného“ umelca. ktorý kedysi šokoval celý svet svojím umeleckým svetom... Samozrejme, nebol blázon, ale bol jednoducho veštec, ktorý z nejakého dôvodu mohol vidieť iba nižší Astrál. Ale musíme mu dať, čo mu patrí - stvárnil ho vynikajúco... Videl som jeho obrazy v knihe, ktorá bola v knižnici môjho otca, a stále som si pamätal ten strašidelný pocit, ktorý väčšina jeho obrazov nesie...
"Aká hrôza!" zašepkala šokovaná Stella.
Dalo by sa asi povedať, že sme tu, na „poschodiach“ už videli veľa... Ale toto sme si nevedeli predstaviť ani v najstrašnejšej nočnej more!... Za „čiernou skalou“ sa úplne otvorilo niečo nemysliteľné. .. Vyzeralo to ako obrovský plochý „kotol“ vytesaný do skaly, na dne ktorého bublala karmínová „láva“... Všade „praskal“ horúci vzduch so zvláštnymi blikajúcimi červenkastými bublinami, z ktorých vychádzala horiaca para a padali vo veľkých kvapkách na zem, alebo na ľudí, ktorí sa pod ňu v tej chvíli prepadli... Ozvali sa srdcervúce výkriky, no hneď stíchli, keďže tie najhnusnejšie stvorenia sedeli na chrbtoch tých istých ľudí, ktorí sa spokojný pohľad „ovládal“ svoje obete, nevenoval ani najmenšiu pozornosť ich utrpeniu... Pod nahými nohami ľudí červenali rozpálené kamene, karmínová zem praskajúca teplom bublala a „topila“... para vytryskla cez obrovské trhliny a spaľujúce nohy ľudí vzlykajúcich od bolesti boli vynesené do výšin, odparujúc sa ľahkým dymom... A v samom strede „jamy“ tiekla jasne červená, široká ohnivá rieka, do ktorých z času na čas tie isté ohavné príšery nečakane vrhli tú či onú mučenú entitu, ktorá po páde spôsobila len krátke špliechanie oranžových iskier, a potom, keď sa na chvíľu zmenila na nadýchaný biely oblak, zmizla. .. navždy... Bolo to skutočné peklo a ja a Stella sme chceli odtiaľ čo najskôr „zmiznúť“...
"Čo budeme robiť?" zašepkala Stella v tichom zdesení. - Chceš ísť tam dole? Môžeme im nejako pomôcť? Pozrite, koľko ich je!...
Stáli sme na čierno-hnedom, teplom vysušenom útese, pozorovali hrôzu naplnenú „kašu“ bolesti, beznádeje a násilia, ktorá sa tiahla dole, a cítili sme sa tak detsky bezmocní, že aj moja bojovná Stella tentoraz kategoricky zložila svoje nariasené „krídla“. .“ „a pri prvom zavolaní bola pripravená ponáhľať sa na svoje, také drahé a spoľahlivé, vyššie „poschodie“...