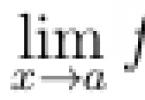Iš integracijos kelio.
Apsvarstykite kreivinį 2-osios rūšies integralą, kur L– kreivė, jungianti taškus M Ir N. Tegul funkcijos P(x, y) Ir Q(x, y) turėti ištisinių dalinių išvestinių tam tikroje srityje D, kuriame yra visa kreivė L. Nustatykime sąlygas, kurioms esant kreivinis integralas nepriklauso nuo kreivės formos L, bet tik dėl taškų vietos M Ir N.
Nubrėžkime dvi savavališkas kreives MPN Ir MQN, guli zonoje D ir sujungimo taškai M Ir N(1 pav.).
K
M N Ryžiai. 1.
Apsimeskime tai 
, tai yra 
Tada kur L– uždaras kontūras, sudarytas iš kreivių MPN Ir N.Q.M.(todėl tai gali būti laikoma savavališka). Taigi 2-osios rūšies kreivinio integralo nepriklausomumo nuo integravimo kelio sąlyga yra lygiavertė sąlygai, kad toks integralas virš bet kurio uždaro kontūro yra lygus nuliui.
Bilietas Nr.34.Pirmojo tipo paviršiaus integralas (virš paviršiaus ploto) Taikymas (medžiagos paviršiaus masė, svorio centro koordinatės, momentai, lenkto paviršiaus plotas).
Apsvarstykite atvirą paviršių S, apribotas kontūru L, ir padalykite jį į dalis tam tikromis kreivėmis S 1, S 2,…, S n. Kiekvienoje dalyje pasirinkite tašką M i ir suprojektuokite šią dalį ant paviršiaus, einančio per šį tašką, liestinės plokštumos. Projekcijoje gauname plokščią figūrą su plotu T i. Pavadinkime ρ didžiausią atstumą tarp dviejų taškų bet kurioje paviršiaus dalyje S.
Apibrėžimas 12.1. Paskambinkime plotas S paviršiai ploto sumos riba T i adresu
Pirmojo tipo paviršinis integralas.
Apsvarstykite tam tikrą paviršių S, apribotas kontūru L, ir suskaidykite į dalis S 1, S 2,…, S p(taip pat pažymėsime kiekvienos dalies plotą S p). Tegul funkcijos reikšmė nurodoma kiekviename šio paviršiaus taške f(x, y, z). Rinksimės kiekvienoje dalyje S i tašką M i (x i , y i , z i) ir sudaryti integralinę sumą
. (12.2)
Apibrėžimas 12.2. Jei integralinės sumos (12.2) yra baigtinė riba, nepriklausoma nuo paviršiaus padalijimo į dalis metodo ir taškų pasirinkimo M i, tada jis vadinamas pirmos rūšies paviršiaus integralas iš funkcijos f(M) = f(x, y, z) ant paviršiaus S ir yra paskirtas
komentuoti. 1-osios rūšies paviršinis integralas turi įprastas integralų savybes (tiesiškumas, tam tikros funkcijos integralų sumavimas per atskiras nagrinėjamo paviršiaus dalis ir kt.).
1-osios rūšies paviršinio integralo geometrinė ir fizinė reikšmė.
Jei integrandas f(M)≡ 1, tada iš 12.2 apibrėžimo išplaukia, kad jis yra lygus nagrinėjamo paviršiaus plotui S.
. (12.4)
1 tipo paviršinio integralo taikymas.
1. Išlenkto paviršiaus plotas, kurio lygtis yra z = f(x, y), galima rasti formoje:
(14.21)
(Ω – projekcija Sį O lėktuvą xy).
2. Paviršiaus masė
(14.22)
3. Akimirkos:
Statiniai paviršiaus momentai koordinačių plokštumų O atžvilgiu xy, O xz, O yz;
Paviršiaus inercijos momentai koordinačių ašių atžvilgiu;
Paviršiaus inercijos momentai koordinačių plokštumų atžvilgiu;
- (14.26)
Paviršiaus inercijos momentas kilmės atžvilgiu.
4. Paviršiaus masės centro koordinatės:
. (14.27)
Bilieto numeris 35. 1-osios rūšies paviršinio integralo apskaičiavimas (sumažinus jį į kartotinį).
Apsiribokime tuo atveju, kai paviršius S yra pateikta aiškiai, tai yra, formos lygtimi z = φ(x, y). Be to, iš paviršiaus ploto apibrėžimo matyti, kad
S i =, kur Δ σi – projekcijos plotas S iį O lėktuvą xy, A γ i– kampas tarp O ašies z ir normalus paviršiui S taške M i. Yra žinoma, kad
,
kur ( x i , y i , z i) – taško koordinates M i. Todėl,
Pakeitę šią išraišką į formulę (12.2), gauname, kad
,
Kai sumavimas dešinėje atliekamas per O plokštumos sritį Ω xy, kuri yra projekcija į šią paviršiaus plokštumą S(1 pav.).
S: z=φ(x,y)
Δσ iΩ
Šiuo atveju, dešinėje pusėje, dviejų kintamųjų funkcijai per plokščią sritį gaunama integralinė suma, kuri riboje at suteikia dvigubą integralą.Taigi buvo gauta formulė, leidžianti sumažinti apskaičiavimą 1-osios rūšies paviršinis integralas skaičiuojant dvigubą integralą:
komentuoti. Dar kartą paaiškinsime, kad kairėje (12.5) formulės pusėje yra paviršius integralas, o dešinėje - dvigubai.
Bilieto numeris 36.Antros rūšies paviršinis integralas. Vektorinio lauko srautas. Ryšys tarp pirmos ir antros rūšies paviršinių integralų.
Vektorinio lauko srautas.
Apsvarstykite vektorinį lauką A (M), apibrėžtas erdvinėje srityje G, orientuotas lygus paviršius S G ir vieneto normaliųjų lauką P (M) pasirinktoje paviršiaus pusėje S.
Apibrėžimas 13.3. 1 tipo paviršinis integralas
,
(13.1)
Kur An yra atitinkamų vektorių skaliarinė sandauga ir A p– vektorinė projekcija A vadinama normalia kryptimi vektoriaus lauko srautas ESU) per pasirinktą paviršiaus pusę S .
Pastaba 1. Jei pasirinksite kitą paviršiaus pusę, tada normalus ir atitinkamai srautas pasikeis.
Pastaba 2. Jei vektorius A nurodo skysčio tekėjimo greitį tam tikrame taške, tada integralas (13.1) nustato skysčio kiekį, tekantį per laiko vienetą paviršiumi. S teigiama kryptimi (taigi ir bendras terminas „tekėjimas“).
Tegu pateikiamas plokščias vektorinis laukas. Toliau darysime prielaidą, kad funkcijos P ir Q kartu su jų išvestinėmis yra tolydžios tam tikroje plokštumos O srityje
Panagrinėkime du savavališkus taškus srityje G. Šiuos taškus galima sujungti skirtingomis linijomis, esančiomis srityje, išilgai kurios kreivinio integralo reikšmės paprastai skiriasi.
Taigi, pavyzdžiui, apsvarstykite kreivinį integralą
ir du taškai. Apskaičiuokime šį integralą, pirma, išilgai tiesės, jungiančios taškus A ir B, ir, antra, išilgai parabolės lanko, jungiančio tuos pačius taškus. Taikydami kreivinio integralo skaičiavimo taisykles, randame
a) išilgai atkarpos
b) išilgai parabolės lanko:
Taigi matome, kad kreivinio integralo reikšmės priklauso nuo integracijos kelio, tai yra, jos priklauso nuo linijos, jungiančios taškus A ir B, tipo. Priešingai, kaip nesunku patikrinti, kreivinis integralas išilgai tos pačios linijos, jungiančios taškus, suteikia to paties dalyko vertę, lygią .
Analizuoti pavyzdžiai rodo, kad kreiviniai integralai, skaičiuojami skirtingais keliais, jungiančiais du duotus taškus, kai kuriais atvejais skiriasi vienas nuo kito, o kitais atvejais įgauna tą pačią reikšmę.
Tegu A ir B yra du savavališki srities G taškai. Apsvarstykite įvairias kreives, esančias srityje G ir jungiančias taškus A ir B.
Jei tiesinis integralas išilgai bet kurio iš šių kelių įgauna tą pačią reikšmę, tada sakoma, kad jis nepriklauso nuo integravimo kelio.
Kitos dvi teoremos pateikia sąlygas, kurioms esant tiesinis integralas nepriklauso nuo integravimo kelio.
1 teorema. Kad kreivinis integralas tam tikroje srityje G būtų nepriklausomas nuo integravimo kelio, būtina ir pakanka, kad integralas virš bet kurio uždaro kontūro, esančio šioje srityje, būtų lygus nuliui.
Įrodymas. Tinkamumas.
Tegul integralas virš bet kurio uždaro kontūro, nubrėžto srityje G, yra lygus nuliui. Parodykime, kad šis integralas nepriklauso nuo integracijos kelio. Tiesą sakant, tegul A ir B yra du taškai, priklausantys sričiai G. Sujungkime šiuos taškus dviem skirtingomis, savavališkai pasirinktomis kreivėmis, esančiomis G srityje (257 pav.).
Parodykime, kad lankai sudaro uždarą kontūrą Atsižvelgdami į kreivinių integralų savybes, gauname
nes . Bet pagal sąlygą tai tarsi uždaro ciklo integralas.
Todėl, arba Taigi, tiesinis integralas nepriklauso nuo integracijos kelio.
Būtinybė. Tegul kreivinis integralas srityje G yra nepriklausomas nuo integravimo kelio. Parodykime, kad bet kurio uždaro kontūro, esančio šioje srityje, integralas yra lygus nuliui. Iš tikrųjų panagrinėkime savavališką uždarą kontūrą, esantį G srityje, ir paimkime jame du savavališkus taškus A ir B (žr. 257 pav.). Tada
nes pagal būklę . Taigi, bet kurio uždaro kontūro L, esančio G srityje, integralas yra lygus nuliui.
Ši teorema pateikia praktiniam naudojimui patogias sąlygas, kurioms esant kreivinis integralas nepriklauso nuo integravimo kelio.
2 teorema.
Kad kreivinis integralas būtų nepriklausomas nuo integracijos kelio tiesiog sujungtoje srityje, būtina ir pakanka, kad sąlyga būtų įvykdyta kiekviename šios srities taške.
Įrodymas. Tinkamumas. Parodykime srityje, kad kreivinis integralas virš bet kurio uždaro kontūro L, esančio G srityje, yra lygus nuliui. Panagrinėkime plotą a, apribotą kontūro L. Dėl tiesiog susieto regiono G pobūdžio plotas a visiškai priklauso šiai sričiai. Remiantis Ostrogradsky-Green formule, ypač svetainėje Todėl ir todėl, . Taigi integralas per bet kurį uždarą kontūrą L srityje G yra lygus nuliui. Remdamiesi 1 teorema, darome išvadą, kad kreivinis integralas nepriklauso nuo integravimo kelio.
Būtinybė. Tegul kreivinis integralas yra nepriklausomas nuo integravimo kelio tam tikroje srityje Q. Parodykime, kad visuose srities taškuose
Tarkime, priešingai, ty tam tikru regiono tašku. Dėl dalinių išvestinių tęstinumo prielaidos skirtumas taip pat bus nuolatinė funkcija. Vadinasi, aplink tašką galima apibūdinti apskritimą a (esantį G srityje), kurio visuose taškuose, kaip ir taške, skirtumas bus teigiamas. Apskritimui pritaikykime Ostrogradsky-Green formulę.
Regionas vadinamas tiesiog sujungtu, jei jo riba yra sujungta aibė. Regionas vadinamas n-jungtu, jei jo riba skyla į n-susijusias aibes.
komentuoti. Green formulė taip pat tinka daugybei sujungtų regionų atveju.
Kad integralas (A, B – bet kurie taškai iš D) nepriklausytų nuo integracijos kelio (o tik nuo pradinio ir galutinio taškų A, B), būtina ir pakanka, kad išilgai bet kurios uždaros kreivės (išilgai bet kurios kontūras) esantis D integralas buvo lygus nuliui =0
Įrodymas (būtinybė). Tegul (4) nepriklauso nuo integravimo kelio. Apsvarstykite savavališką kontūrą C, esantį D srityje, ir pasirinkite du savavališkus šio kontūro taškus A, B. Tada kreivė C gali būti pavaizduota kaip dviejų kreivių AB=G2, AB=G1, C=Г - 1 + G2 sąjunga.
1 teorema. Kad kreivinis integralas būtų nepriklausomas nuo integravimo kelio D, būtina ir pakanka, kad
srityje D. Pakankamumas. Jei tai tiesa, Greeno formulė bet kuriam kontūrui C bus tokia 
iš kur reikalingas teiginys seka lema. Būtinybė. Pagal bet kurio kontūro lemą = 0. Tada pagal Grino formulę plotui D, kurį riboja šis kontūras, = 0. Pagal vidutinės reikšmės teoremą = mD arba = = 0. Pereinant iki ribos, sutraukiant kontūrą iki taško, gauname tai šioje vietoje.
2 teorema. Norint, kad kreivinis integralas (4) būtų nepriklausomas nuo integravimo kelio D, būtina ir pakanka, kad integrando išraiška Pdx+Qdy būtų suminis kokios nors funkcijos u srityje D. du = Pdx+Qdy. Tinkamumas. Tegul tai išsipildo, tada būtinybė. Tegul integralas yra nepriklausomas nuo integracijos kelio. Fiksuojame tam tikrą tašką A0 srityje D ir apibrėžiame funkciją u(A) = u(x,y)=
Tokiu atveju
XО (xО). Taigi yra išvestinė =P. Panašiai patikrinama, ar =Q. Remiantis padarytomis prielaidomis, funkcija u yra nuolat diferencijuojama ir du = Pdx+Qdy.
32-33. 1 ir 2 rūšies kreiviųjų integralų apibrėžimas
Kreivinis integralas per lanko ilgį (1 rūšis)
Tegul funkcija f(x,y) yra apibrėžta ir ištisinė lygiosios kreivės K lanko AB taškuose. Savavališkai padalykite lanką į n elementariųjų lankų taškais t0..tn tegul lk yra konkrečios kreivės ilgis k lankas. Paimkime savavališką kiekvieno elementariojo lanko tašką N(k,k) ir padauginkime šį tašką iš atitinkamo taško. lanko ilgis bus sudarytas iš trijų vientisų sumų:
1
=
f(k,k)lk 2 = 
Р(k,k)хk 3 = 
Q(k,k)yk, kur хk = x k -x k -1, yk = y k -y k -1
1-osios rūšies kreivinis integralas išilgai lanko bus vadinamas integralo sumos 1 riba, su sąlyga, kad max(lk) 0 
Jeigu integralinės sumos riba yra 2 arba 3 ties 0, tai ši riba vadinama. 2-osios rūšies kreivinis integralas, funkcija P(x,y) arba Q(x,y) išilgai kreivės l = AB ir žymimas: 
arba 
suma: 
+
Įprasta jį vadinti bendruoju kreiviniu 2-osios rūšies integralu ir žymėti simboliu: 
šiuo atveju funkcijos f(x,y), P(x,y), Q(x,y) vadinamos integruojamomis išilgai kreivės l = AB. Pati kreivė l vadinama kontūru arba integruojant A yra pradinis taškas, B – galutinis integracijos taškas, dl – lanko ilgio diferencialas, todėl vadinamas 1-osios rūšies kreiviniu integralu. kreivinis integralas virš kreivės lanko, o antrosios rūšies – virš funkcijos.
Iš kreivinių integralų apibrėžimo matyti, kad 1 tipo integralai nepriklauso nuo krypties, kuria kreivė l eina iš A ir B arba iš B ir A. 1-osios rūšies kreivinis integralas išilgai AB:
, 2-osios rūšies kreiviniams integralams kreivės krypties pasikeitimas lemia ženklo pasikeitimą:
Tuo atveju, kai l yra uždara kreivė, t. y. taškas B sutampa su tašku A, tada iš dviejų galimų uždaro kontūro ėjimo krypčių l vadinama teigiama kryptimi, kuria kontūro viduje esantis plotas lieka į kairę. pagarba??? apvalumas, t.y. judėjimo kryptis yra prieš laikrodžio rodyklę. Priešinga judėjimo kryptis vadinama neigiama. Kreivinis integralas AB išilgai uždaro kontūro l, einantis teigiama kryptimi, bus pažymėtas simboliu:
Erdvinei kreivei panašiai įvedamas vienas 1 tipo integralas:
ir trys 2-osios rūšies integralai:
vadinama paskutinių trijų integralų suma. bendrasis kreivinis 2-osios rūšies integralas.
Kai kurios kreivinių 1-osios rūšies integralų taikymas.
1. Integralus 
- lanko ilgis AB
2.Mechaninė 1-osios rūšies integralo reikšmė.
Jei f(x,y) = (x,y) yra medžiagos lanko linijinis tankis, tada jo masė: 
3. Medžiagos lanko masės centro koordinatės:
4. Lanko, esančio oksi plokštumoje, inercijos momentas koordinačių pradžios ir sukimosi ašių atžvilgiu ox, oy:
5. 1-osios rūšies integralo geometrinė reikšmė
Tegul funkcija z = f(x,y) – turi ilgio matmenį f(x,y)>=0 visuose medžiagos lanko taškuose, esančiuose oksi plokštumoje, tada:
, kur S yra cilindrinio paviršiaus plotas, katė susideda iš statmenų okha plokštumai, į rytus. AB kreivės taškuose M(x,y).
Kai kurios 2-osios rūšies kreiviųjų integralų taikymas.
Plokščios srities D su riba L ploto apskaičiavimas
2. Jėgos darbas. Tegul materialus taškas, veikiamas jėgos, juda ištisine plokščia kreive BC, nukreipta nuo B iki C, šios jėgos darbas yra toks:
2-oji rūšis iš integracijos kelio
Panagrinėkime 2-osios rūšies kreivinį integralą, kur L yra kreivė, jungianti taškus M ir N. Tegul funkcijos P(x, y) ir Q(x, y) turi ištisines dalines išvestines tam tikroje srityje D, kurioje kreivė L Išsiaiškinkime, kokiomis sąlygomis nagrinėjamas kreivinis integralas priklauso ne nuo kreivės L formos, o tik nuo taškų M ir N vietos.
Nubraižykime dvi savavališkas kreives MSN ir MTN, esančias D srityje ir jungiančias taškus M ir N (14 pav.).
Tarkime, kad tai yra
kur L yra uždara kilpa, sudaryta iš MSN ir NTM kreivių (taigi, ji gali būti laikoma savavališka). Taigi 2-osios rūšies kreivinio integralo nepriklausomumo nuo integravimo kelio sąlyga yra lygiavertė sąlygai, kad toks integralas virš bet kurio uždaro kontūro yra lygus nuliui.
5 teorema (Greino teorema). Tegul funkcijos P(x, y) ir Q(x, y) ir jų dalinės išvestinės yra tolydžios visuose kokios nors srities D taškuose. Tada, kad bet koks uždaras kontūras L, esantis D srityje, atitiktų sąlygą
būtina ir pakanka, kad = visuose srities D taškuose.
Įrodymas.
1) Pakankamumas: tegul sąlyga = tenkinama. Panagrinėkime savavališką uždarą kontūrą L srityje D, ribojantį sritį S, ir parašykime jam Greeno formulę:
Taigi, pakankamumas įrodytas.
2) Būtinumas: tarkime, kad sąlyga tenkinama kiekviename srities D taške, tačiau yra bent vienas šios srities taškas, kuriame -? 0. Tarkime, taške P(x0, y0) turime: - > 0. Kadangi kairėje nelygybės pusėje yra ištisinė funkcija, ar ji bus teigiama ir didesnė už kai kurias? > 0 tam tikrame mažame regione D`, kuriame yra taškas P.
Iš čia, naudodami Greeno formulę, gauname tai
čia L` yra kontūras, ribojantis plotą D`. Šis rezultatas prieštarauja sąlygai. Vadinasi, = visuose regiono D taškuose, ką ir reikėjo įrodyti.
Pastaba 1. Panašiai trimatės erdvės atveju galima įrodyti, kad būtinos ir pakankamos sąlygos kreivinio integralo nepriklausomumui
iš integracijos kelio yra:
2 pastaba. Jei sąlygos (52) tenkinamos, išraiška Pdx + Qdy + Rdz yra suminis kurios nors funkcijos u skirtumas. Tai leidžia sumažinti kreivinio integralo skaičiavimą, kad būtų galima nustatyti skirtumą tarp verčių tiek galutiniame, tiek pradiniame integravimo kontūro taškuose, nes
Šiuo atveju funkciją ir galima rasti naudojant formulę
kur (x0, y0, z0) yra taškas iš srities D, o C yra savavališka konstanta. Iš tiesų, nesunku patikrinti, ar funkcijos dalinės išvestinės, pateiktos pagal (53) formulę, yra lygios P, Q ir R.
10 pavyzdys.
Apskaičiuokite 2-osios rūšies tiesinį integralą
išilgai savavališkos kreivės, jungiančios taškus (1, 1, 1) ir (2, 3, 4).
Įsitikinkite, kad tenkinamos sąlygos (52):
Todėl funkcija egzistuoja. Raskime jį naudodami formulę (53), pateikdami x0 = y0 = z0 = 0. Tada
Taigi funkcija nustatoma iki savavališko pastovaus termino. Paimkime C = 0, tada u = xyz. Vadinasi,
30. Greeno formulė. Kreivinio integralo nepriklausomumo nuo integracijos kelio sąlygos.
Greeno formulė: Jei C yra uždara srities D riba, o funkcijos P(x,y) ir Q(x,y) kartu su jų pirmos eilės dalinėmis išvestinėmis yra ištisinės uždaroje srityje D (įskaitant C ribą). ), tada galioja Greeno formulė:, o apvažiavimas aplink kontūrą C pasirenkamas taip, kad sritis D liktų kairėje.
Iš paskaitų: Tegu pateikiamos funkcijos P(x,y) ir Q(x,y), kurios yra ištisinės D srityje kartu su pirmos eilės dalinėmis išvestinėmis. Integralas virš ribos (L), visiškai įtrauktas į D sritį ir apimantis visus D srities taškus: . Teigiama kontūro kryptis yra tada, kai ribota kontūro dalis yra į kairę.
2-osios rūšies kreivinio integralo nepriklausomumo nuo integracijos kelio sąlyga. Būtina ir pakankama sąlyga, kad pirmosios rūšies kreivinis integralas, jungiantis taškus M1 ir M2, nepriklauso nuo integracijos kelio, o priklauso tik nuo pradžios ir pabaigos taškų, yra lygybė:.
.
31. Pirmos ir antros rūšies paviršiniai integralai, jų pagrindinės savybės ir skaičiavimas.
– nurodant paviršių.
Projektuokime S į xy plokštumą ir gaukime sritį D. Sritį D padaliname linijų tinkleliu į dalis, vadinamas Di. Iš kiekvienos tiesės taško brėžiame lygiagrečias z, tada S bus padalintas į Si. Padarykime integralią sumą: . Nukreipkime didžiausią skersmenį Di į nulį:, gauname:
Tai pirmos rūšies paviršinis integralas
Taip apskaičiuojamas pirmos rūšies paviršinis integralas.
Apibrėžimas trumpai. Jei yra baigtinė integralų sumos riba, nepriklausoma nuo S skaidymo į elementarias dalis Si metodo ir taškų pasirinkimo, tada ji vadinama pirmos rūšies paviršiniu integralu.
Pereinant nuo kintamųjų x ir y prie u ir v:
P 
paviršinis integralas turi visas paprasto integralo savybes. Žr. klausimus aukščiau.
Antrosios rūšies paviršinio integralo apibrėžimas, pagrindinės jo savybės ir skaičiavimas. Ryšys su pirmosios rūšies integralu.
Tegu pateiktas paviršius S, ribojamas tiese L (3.10 pav.). Paimkime tam tikrą paviršiaus S kontūrą L, kuris neturi bendrų taškų su riba L. Kontūro L taške M galime atkurti dvi paviršiaus S normaliąsias. Pasirinkime vieną iš šių krypčių. Tašką M pažymime išilgai kontūro L pasirinkta normaliąja kryptimi.
Jei taškas M grįžta į pradinę padėtį ta pačia normaliosios krypties (o ne priešinga), tada paviršius S vadinamas dvipusiu. Mes atsižvelgsime tik į dvipusius paviršius. Dvipusis paviršius yra bet koks lygus paviršius su lygtimi .
Tegul S yra dvipusis atviras paviršius, ribojamas tiesės L, kuri neturi susikirtimo taškų. Pasirinkime tam tikrą paviršiaus pusę. Teigiama kontūro L ėjimo kryptimi vadinsime tokią kryptį, kuria judant pasirinkta paviršiaus puse, pats paviršius lieka į kairę. Dvipusis paviršius, turintis teigiamą kryptį, kuriuo galima pereiti jame nustatytus kontūrus, vadinamas orientuotu paviršiumi.
Pereikime prie antrojo tipo paviršiaus integralo konstravimo. Paimkime dvipusį paviršių S erdvėje, susidedantį iš baigtinio skaičiaus gabalėlių, kurių kiekvienas yra pateiktas formos lygtimi arba yra cilindrinis paviršius su generatoriais, lygiagrečiais Ozo ašiai.
Tegul R(x,y,z) yra funkcija, apibrėžta ir ištisinė paviršiuje S. Naudodami linijų tinklą, S savavališkai padalijame į n "elementariųjų" atkarpų ΔS1, ΔS2, ..., ΔSi, ..., ΔSn, kurie neturi bendrų vidinių taškų. Kiekvienoje atkarpoje ΔSi savavališkai pasirenkame tašką Mi(xi,yi,zi) (i=1,...,n). Tegu (ΔSi)xy yra atkarpos ΔSi projekcijos į koordinačių plokštumą Oxy plotas, paimtas su „+“ ženklu, jei normalioji paviršiaus S taške Mi(xi,yi,zi) ( i=1,...,n) formos su Ozo ašimi yra smailusis kampas, o su „–“ ženklu, jei šis kampas yra bukas. Sudarykime funkcijos R(x,y,z) integralią sumą per paviršių S kintamuosiuose x,y: . Tegu λ yra didžiausias iš skersmenų ΔSi (i = 1, ..., n).
Jei yra baigtinė riba, kuri nepriklauso nuo paviršiaus S padalijimo į „elementarias“ dalis ΔSi būdo ir nuo taškų pasirinkimo, tada ji vadinama paviršiaus integralu virš pasirinktos funkcijos R paviršiaus S pusės. (x, y, z) išilgai koordinačių x, y (arba antrojo tipo paviršinio integralo) ir žymimas 
.
Panašiai galite sudaryti paviršiaus integralus per koordinates x, z arba y, z išilgai atitinkamos paviršiaus pusės, t.y. 
Ir 
.
Jei visi šie integralai egzistuoja, tada pasirinktoje paviršiaus pusėje galime įvesti „bendrą“ integralą: .
Antrosios rūšies paviršinis integralas turi įprastas integralo savybes. Atkreipiame dėmesį tik į tai, kad bet kuris antros rūšies paviršinis integralas keičia ženklą, kai pasikeičia paviršiaus pusė.
Ryšys tarp pirmos ir antros rūšies paviršinių integralų.
Tegul paviršius S pateikiamas pagal lygtį: z = f(x,y) ir f(x,y), f"x(x,y), f"y(x,y) yra tolydžios funkcijos uždaroje sritis τ (paviršiaus S projekcijos į koordinačių plokštumą Oxy), o funkcija R(x,y,z) yra ištisinė paviršiuje S. Paviršiaus S normalioji, turinti krypties kosinusus cos α, cos β, cos γ, pasirenkama į viršutinę paviršiaus S pusę. Tada .
Bendram atvejui turime:
= 
| " |
