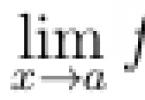Teorema. Tegul funkcija x=φ(t) ištisinis taške a, ir funkcija y=f(x) ištisinis taške b=φ(a). Tada sudėtinga funkcija y=f[φ(t)]=F(t) ištisinis taške a.

Leisti x=φ(t) Ir y=f(x)- paprasčiausios elementarios funkcijos, turinčios daug reikšmių (x) funkcijas x=φ(t) yra funkcijos apimtis y=f(x). Kaip žinome, elementarios funkcijos yra ištisinės kiekviename nurodytos srities taške. Todėl pagal ankstesnę teoremą kompleksinė funkcija y=f(φ(t)), tai yra, dviejų elementariųjų funkcijų superpozicija yra ištisinė. Pavyzdžiui, funkcija yra ištisinė bet kuriame taške x ≠ 0, kaip sudėtinga dviejų elementariųjų funkcijų funkcija x=t -1 Ir y = sin x. Taip pat funkcija y=ln sin x nuolatinis bet kuriame intervalo taške (2kπ,(2k+1)π), k ∈ Z (sin x>0).

4 paskaita.

Funkcijų tęstinumas

1. Funkcijos tęstinumas taške

1 apibrėžimas. Tegul funkcija y=f(x) yra apibrėžtas taške X 0 ir kažkurioje šio taško kaimynystėje. Funkcija y=f(x) vadinamas ištisinis taške x 0 , jei šiame taške yra funkcijos riba ir ji lygi funkcijos reikšmei šiame taške, t.y.

Taigi, funkcijos tęstinumo sąlyga y=f(x) taške X 0 ar tai:

Nes
, tada lygybę (32) galima parašyti formoje

(33)

Tai reiškia, kad kai tolydžios funkcijos ribos radimasf(x) galima eiti į ribą po funkcijos ženklu, t.y. į funkciją f(x) vietoj argumento X pakeisti jo ribinę vertę X 0 .

lim nuodėmė x=sin(lim x);

lim arctg x=arctg(lim x); (34)

lim log x=log(lim x).

Pratimas. Raskite ribą: 1)
; 2)
.

Apibrėžkime funkcijos tęstinumą, remdamiesi argumento ir funkcijos prieaugio sąvokomis.

Nes sąlygos
Ir
yra identiški (4 pav.), tada lygybė (32) yra tokia:

arba
.

2 apibrėžimas. Funkcija y=f(x) vadinamas ištisinis taške x 0 , jei jis apibrėžtas taške X 0 ir jo kaimynystėje, o be galo mažas argumento prieaugis atitinka be galo mažą funkcijos prieaugį.

Pratimas. Išnagrinėkite funkcijos tęstinumą y=2X 2 1.

Tęstinių taške funkcijų savybės

1. Jei funkcijos f(x) Ir φ (x) yra ištisiniai taške X 0, tada jų suma
, darbas
ir privatus
(turint omenyje
) yra taške ištisinės funkcijos X 0 .

2. Jei funkcija adresu=f(x) yra ištisinis taške X 0 ir f(x 0)>0, tada yra tokia taško kaimynystė X 0 , kuriame f(x)>0.

3. Jei funkcija adresu=f(u) yra tolydi taške u 0 , o funkcija u= φ (x) yra ištisinis taške u 0 = φ (x 0 ), tada sudėtinga funkcija y=f[φ (x)] yra ištisinis taške X 0 .

2. Funkcijos tęstinumas intervale ir atkarpoje

Funkcija y=f(x) vadinamas nuolatinis intervale (a; b), jei jis yra tęstinis kiekviename šio intervalo taške.

Funkcija y=f(x) vadinamas ištisinis segmente [a; b] jei jis yra tęstinis intervale ( a; b), ir taške X=A yra teisingas tęstinis (t. y.
), ir taške x=b paliekamas ištisinis (t. y.
).

3. Funkcijų nenutrūkstamumo taškai ir jų klasifikacija

Vadinami taškai, kuriuose nutrūksta funkcijos tęstinumas lūžio taškaiši funkcija.

Jeigu X=X 0 – funkcijos lūžio taškas y=f(x), tada netenkinama bent viena iš pirmojo funkcijos tęstinumo apibrėžimo sąlygų.

Pavyzdys.

1.
. 2.

3)
4)
.

▼Lūžio taškas X 0 vadinamas lūžio tašku pirmoji rūšis funkcijas y=f(x), jei šiuo metu kairėje ir dešinėje yra baigtinės funkcijos ribos (vienpusės ribos), t.y.
Ir
. Kur:

Didumas | A 1 -A 2 | paskambino funkcijos šuolis pirmosios rūšies nenutrūkstamumo taške. ▲

▼Lūžio taškas X 0 vadinamas lūžio tašku antra rūšis funkcijas y=f(x), jei bent viena iš vienpusių ribų (kairė arba dešinė) neegzistuoja arba yra lygi begalybei. ▲

Pratimas. Raskite funkcijų pertraukos taškus ir sužinokite jų tipą:

1)
; 2)
.

4. Pagrindinės tolydžių funkcijų teoremos

Funkcijų tęstinumo teoremos tiesiogiai išplaukia iš atitinkamų teoremų apie ribas.

1 teorema. Dviejų ištisinių funkcijų suma, sandauga ir koeficientas yra ištisinė funkcija (dalytui, išskyrus tas argumento reikšmes, kuriose daliklis nėra lygus nuliui).

2 teorema. Tegul funkcijos u=φ (x) yra ištisinis taške X 0 ir funkcija y=f(u) yra ištisinis taške u=φ (x 0 ). Tada sudėtinga funkcija f(φ (x)), susidedantis iš ištisinių funkcijų, taške yra tęstinis X 0 .

3 teorema. Jei funkcija y=f(x) yra ištisinis ir griežtai monotoniškas [ a; b] ašys Oi, tada atvirkštinė funkcija adresu=φ (x) taip pat yra tęstinis ir monotoniškas atitinkamame segmente [ c;d] ašys OU.

Kiekviena elementari funkcija yra ištisinė kiekviename taške, kuriame ji yra apibrėžta.

5. Funkcijų, nuolatinių intervale, savybės

Weierstrasso teorema. Jei funkcija yra ištisinė segmente, tada šiame segmente ji pasiekia didžiausias ir mažiausias reikšmes.

Pasekmė. Jei funkcija yra ištisinė intervale, tada ji yra ribojama su intervalu.

Bolzano-Koši teorema. Jei funkcija y=f(x) yra tęstinis intervale [ a; b] ir jo galuose paima nelygias vertes f(a)=A Ir f(b)=B,
, tada kad ir koks būtų skaičius SU, sudaryta tarp A Ir IN, yra taškas
toks kad f(c)=C.

Geometriškai teorema akivaizdi. Bet kokiam skaičiui SU, sudaryta tarp A Ir IN, šio segmento viduje yra taškas c, kad f(SU)=C. Tiesiai adresu=SU kerta funkcijos grafiką bent viename taške.

Pasekmė. Jei funkcija y=f(x) yra tęstinis intervale [ a; b] ir perima skirtingų ženklų reikšmes jo galuose, tada segmento viduje [ a; b] yra bent vienas taškas Su, kurioje funkcija y=f(x) pereina į nulį: f(c)=0.

Geometrinis teoremos prasmė: jei tolydžios funkcijos grafikas eina iš vienos ašies pusės Oiį kitą, tada jis kerta ašį Oi.

Funkcijos tęstinumo tyrimo procesas yra neatsiejamai susijęs su gebėjimu rasti vienpuses funkcijos ribas. Todėl norint pradėti studijuoti šio straipsnio medžiagą, patartina pirmiausia išnagrinėti funkcijos ribos temą.

F(x) funkcija yra tęstinis taške x 0, jei riba kairėje lygi riba dešinėje ir sutampa su funkcijos reikšme taške x 0, t.y.: lim x → x 0 - 0 f (x) = lim x → x 0 + 0 f (x) = f (x0)

Šis apibrėžimas leidžia išvesti išvadą: funkcijos ribos reikšmė tęstinumo taškuose sutampa su funkcijos reikšme šiuose taškuose.

1 pavyzdys

Pateikta funkcija f (x) = 1 6 (x - 8) 2 - 8. Būtina įrodyti jo tęstinumą taške x 0 = 2.

Sprendimas

Pirmiausia nustatome ribos egzistavimą kairėje pusėje. Norėdami tai padaryti, naudojame argumentų seką x n, kuri sumažinama iki x 0 = 2 · (x n< 2) . Например, такой последовательностью может быть:

2 , 0 , 1 , 1 1 2 , 1 3 4 , 1 7 8 , 1 15 16 , . . . , 1 1023 1024 , . . . → 2

Atitinkama funkcijų reikšmių seka atrodo taip:

f(-2); f (0); f (1); f 1 1 2 ; f 1 3 4 ; f 1 7 8 ; f 1 15 16 ; . . . ; f 1 1023 1024; . . . = = 8. 667; 2. 667; 0 . 167; -0. 958; - 1. 489; - 1. 747; - 1. 874; . . . ; - 1. 998; . . . → - 2

brėžinyje jie pažymėti žalia spalva.

Visiškai akivaizdu, kad tokia seka redukuojasi iki -2, o tai reiškia lim x → 2 - 0 1 6 (x - 8) 2 - 8 = - 2.

Nustatykime ribos egzistavimą dešinėje: naudojame argumentų seką x n, kuri redukuojasi iki x 0 = 2 (x n > 2). Pavyzdžiui, ši seka gali būti tokia:

6 , 4 , 3 , 2 1 2 , 2 1 4 , 2 1 8 , 2 1 16 , . . . , 2 1 1024 , . . . → 2

Atitinkama funkcijų seka:

f (6); f (4); f (3); f 2 1 2; f 2 1 4 ; f 2 1 8; f 2 1 16 ; . . . ; f 2 1 1024 ; . . . = = - 7 . 333; -5. 333; – 3. 833; – 2. 958; – 2. 489; – 2. 247; – 2. 247; – 2. 124; . . . ; – 2. 001 ; . . . → - 2

paveikslėlyje nurodyta mėlyna spalva.

Ir ši seka sumažinama iki -2, tada lim x → 2 + 0 1 6 (x - 8) 2 - 8 = - 2.

Aukščiau pateikti veiksmai parodė, kad ribos dešinėje ir kairėje yra lygios, o tai reiškia, kad taške x 0 = 2 yra funkcijos f (x) = 1 6 x - 8 2 - 8 riba, o lim x → 2 1 6 (x - 8 ) 2 - 8 = - 2 .

Apskaičiavus funkcijos reikšmę tam tikrame taške, lygybė akivaizdi:

lim x → 2 - 0 f (x) = lim x → 2 + 0 f (x) = f (2) = 1 6 (2 - 8) 2 - 8 = - 2, kuris rodo nurodytos funkcijos tęstinumą duotas taškas.

Parodykime tai grafiškai:

Atsakymas: Funkcijos f (x) = 1 6 (x - 8) 2 - 8 tęstinumas duotoje dalyje įrodytas.

Nuimamas pirmosios rūšies plyšimas

Funkcija turi pašalinamas pirmosios rūšies plyšimas taške x 0, kai ribos dešinėje ir kairėje yra lygios, bet nelygios funkcijos reikšmei taške, t.y.:

lim x → x 0 - 0 f (x) = lim x → x 0 + 0 f (x) ≠ f (x 0)

2 pavyzdys

Pateikta funkcija f (x) = x 2 - 25 x - 5. Būtina nustatyti jo lūžio taškus ir nustatyti jų tipą.

Sprendimas

Pirmiausia pažymėkime funkcijos apibrėžimo sritį: D (f (x)) ⇔ D x 2 - 25 x - 5 ⇔ x - 5 ≠ 0 ⇔ x ∈ (- ∞ ; 5) ∪ (5 ; + ∞)

Tam tikroje funkcijoje lūžio tašku gali tarnauti tik apibrėžimo srities ribinis taškas, t.y. x 0 = 5. Panagrinėkime tęstinumo funkciją šioje vietoje.

Supaprastinkime išraišką x 2 - 25 x - 5: x 2 - 25 x - 5 = (x - 5) (x + 5) x - 5 = x + 5.

Apibrėžkime ribas dešinėje ir kairėje. Kadangi funkcija g(x) = x + 5 yra ištisinė bet kuriam realiam x, tada:

lim x → 5 - 0 (x + 5) = 5 + 5 = 10 lim x → 5 + 0 (x + 5) = 5 + 5 = 10

Atsakymas: ribos dešinėje ir kairėje yra lygios, o duotoji funkcija taške x 0 = 5 neapibrėžta, t.y. šiuo metu funkcija turi pašalinamą pirmojo tipo pertrūkį.

Nepašalinamą pirmosios rūšies nepertraukiamumą taip pat lemia funkcijos šuolio taškas.

3 apibrėžimas 3 pavyzdys

Duota dalimis tolydi funkcija f (x) = x + 4 , x< - 1 , x 2 + 2 , - 1 ≤ x < 1 2 x , x ≥ 1 . Необходимо изучить заданную функцию на предмет непрерывности, обозначить вид точек разрыва, составить чертеж.

Sprendimas

Šios funkcijos nenutrūkstamumas gali būti tik taške x 0 = - 1 arba taške x 0 = 1.

Nustatykime šių taškų dešinėje ir kairėje esančias ribas ir pateiktos funkcijos reikšmę šiuose taškuose:

• į kairę nuo taško x 0 = - 1 duotoji funkcija yra f (x) = x + 4, tada dėl tiesinės funkcijos tęstinumo: lim x → - 1 - 0 f (x) = lim x → - 1 - 0 (x + 4) = -1 + 4 = 3;
• tiesiai taške x 0 = - 1 funkcija įgauna tokią formą: f (x) = x 2 + 2, tada: f (- 1) = (- 1) 2 + 2 = 3;
• intervale (- 1 ; 1) duotoji funkcija yra: f (x) = x 2 + 2. Remdamiesi kvadratinės funkcijos tęstinumo savybe, turime: lim x → - 1 + 0 f (x) = lim x → - 1 + 0 (x 2 + 2) = (- 1) 2 + 2 = 3 lim x → 1 - 0 f (x) = rib x → ​​1 - 0 (x 2 + 2) = (1) 2 + 2 = 3
• taške x 0 = - 1 funkcija turi tokią formą: f (x) = 2 x ir f (1) = 2 1 = 2.
• į dešinę nuo taško x 0 duotoji funkcija yra f (x) = 2 x. Dėl tiesinės funkcijos tęstinumo: lim x → 1 + 0 f (x) = lim x → 1 + 0 (2 x) = 2 1 = 2

Atsakymas: galiausiai gavome:

• lim x → - 1 - 0 f (x) = lim x → - 1 + 0 f (x) = f (- 1) = 3 - tai reiškia, kad taške x 0 = - 1 duotoji funkcija yra ištisinė;
• lim x → - 1 - 0 f (x) = 3, lim x → 1 + 0 f (x) = 2 - taigi taške x 0 = 1 yra apibrėžtas nepašalinamas pirmos rūšies (šuolis) pertrauka.

Mums tereikia paruošti šios užduoties piešinį.

Funkcija turi antros rūšies nenuoseklumas taške x 0, kai kuri nors iš kairiojo lim x → x 0 - 0 f (x) arba dešiniojo lim x → x 0 + 0 f (x) ribų neegzistuoja arba yra begalinė.

4 pavyzdys

Pateikta funkcija f (x) = 1 x. Būtina išnagrinėti pateiktą funkciją tęstinumui, nustatyti lūžio taškų tipą ir parengti brėžinį.

Sprendimas

Užrašykime funkcijos apibrėžimo sritį: x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) .

Raskime ribas į dešinę ir į kairę nuo taško x 0 = 0.

Nurodykime savavališką argumentų reikšmių seką, konverguojančią į x 0 kairėje. Pvz.:

8 ; - 4 ; - 2 ; - 1 ; - 1 2 ; - 1 4 ; . . . ; - 1 1024 ; . . .

Tai atitinka funkcijos reikšmių seką:

f (- 8); f (- 4); f(-2); f (-1); f - 1 2; f - 1 4; . . . ; f - 1 1024 ; . . . = = - 1 8 ; - 14; - 12; - 1; - 2; - 4; . . . ; - 1024; . . .

Akivaizdu, kad ši seka yra be galo didelė neigiama, tada lim x → 0 - 0 f (x) = lim x → 0 - 0 1 x = - ∞ .

Dabar nurodykime savavališką argumentų reikšmių seką, konverguojančią į x 0 iš dešinės. Pavyzdžiui: 8 ; 4 ; 2 ; 1 ; 12; 14; . . . ; 1 1024 ; . . . , ir ji atitinka funkcijos reikšmių seką:

f (8); f (4); f (2); f (1); f 1 2; f 1 4; . . . ; f 1 1024 ; . . . = = 18; 14; 12; 1 ; 2 ; 4 ; . . . ; 1024 ; . . .

Ši seka yra be galo didelė teigiama, o tai reiškia lim x → 0 + 0 f (x) = lim x → 0 + 0 1 x = + ∞ .

Atsakymas: taškas x 0 = 0 yra antrojo tipo funkcijos nutrūkimo taškas.

Iliustruojame:

Jei tekste pastebėjote klaidą, pažymėkite ją ir paspauskite Ctrl+Enter

Šioje pamokoje sužinosime, kaip nustatyti funkcijos tęstinumą. Tai darysime naudodami ribas, tuo tarpu vienpuses - dešinę ir kairę, kurios visai nėra baisios, nepaisant to, kad jos parašytos kaip ir .

Bet kas vis dėlto yra funkcijos tęstinumas? Kol nepasieksime griežto apibrėžimo, lengviausia įsivaizduoti liniją, kurią galima nubrėžti nepakeliant pieštuko nuo popieriaus. Jei tokia linija nubrėžta, tai ji yra ištisinė. Ši linija yra tolydžios funkcijos grafikas.

Grafiškai funkcija yra ištisinė taške, jei jos grafikas šiame taške „nenutrūksta“. Tokios tolydžios funkcijos grafikas yra parodyta paveikslėlyje žemiau.

Funkcijos tęstinumo nustatymas per ribą. Funkcija yra ištisinė taške, jei tenkinamos trys sąlygos:

1. Funkcija apibrėžiama taške .

Jei netenkinama bent viena iš išvardytų sąlygų, funkcija taške nėra tęstinė. Šiuo atveju jie sako, kad funkcija patiria netolydumą, o grafiko taškai, kuriuose grafikas nutrūksta, yra vadinami funkcijos nenutrūkstamais taškais. Tokios funkcijos, kuri nutrūksta taške x=2, grafikas yra žemiau esančiame paveikslėlyje.

1 pavyzdys. Funkcija f(x) apibrėžiamas taip:

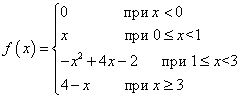
Ar ši funkcija bus ištisinė kiekviename jos šakų ribiniame taške, tai yra taškuose x = 0 , x = 1 , x = 3 ?

Sprendimas. Tikriname visas tris funkcijos tęstinumo sąlygas kiekviename ribiniame taške. Pirmoji sąlyga įvykdyta, nuo ko apibrėžta funkcija kiekviename ribiniame taške išplaukia iš funkcijos apibrėžimo. Belieka patikrinti likusias dvi sąlygas.

Taškas x= 0. Šiuo metu suraskime kairiąją ribą:

.

Raskime dešinės pusės ribą:

x= 0 turi būti rasta tai funkcijos šakai, kuri apima šį tašką, ty antrąją šaką. Mes juos randame:

Kaip matome, funkcijos riba ir funkcijos reikšmė taške x= 0 yra lygūs. Todėl funkcija taške yra ištisinė x = 0 .

Taškas x= 1. Šiuo metu suraskime kairiąją ribą:

Raskime dešinės pusės ribą:

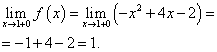
Funkcijos riba ir funkcijos reikšmė taške x= 1 reikia rasti tai funkcijos šakai, kuri apima šį tašką, tai yra, antrai šakai. Mes juos randame:

.

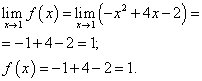Funkcijos riba ir funkcijos reikšmė taške x= 1 yra lygūs. Todėl funkcija taške yra ištisinė x = 1 .

Taškas x= 3. Šiuo metu suraskime kairiąją ribą:

Raskime dešinės pusės ribą:

Funkcijos riba ir funkcijos reikšmė taške x= 3 reikia rasti tai funkcijos šakai, kuri apima šį tašką, ty antrąją šaką. Mes juos randame:

.

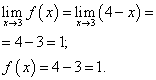Funkcijos riba ir funkcijos reikšmė taške x= 3 yra lygūs. Todėl funkcija taške yra ištisinė x = 3 .

Pagrindinė išvada: ši funkcija yra ištisinė kiekviename ribiniame taške.

Pats nustatykite funkcijos tęstinumą taške, tada pažiūrėkite į sprendimą

Nuolatinis funkcijos keitimas gali būti apibrėžtas kaip laipsniškas pasikeitimas be šuolių, kai nedidelis argumento pakeitimas reiškia nedidelį funkcijos pasikeitimą.

Iliustruojame šį nuolatinį funkcijos pokytį pavyzdžiu.

Tegul ant sriegio virš stalo kabo svarelis. Veikiant šiai apkrovai siūlas išsitempia, todėl atstumas l apkrova nuo sriegio pakabinimo taško yra apkrovos masės funkcija m, tai yra l = f(m) , m≥0 .

Jei šiek tiek pakeisite krovinio masę, tada atstumą l pasikeis mažai: maži pokyčiai m atitinka nedideli pakitimai l. Tačiau, jei apkrovos masė yra artima sriegio atsparumui tempimui, šiek tiek padidinus apkrovos masę, sriegis gali nutrūkti: atstumas l staigiai padidės ir taps lygus atstumui nuo pakabos taško iki stalo paviršiaus. Funkcijos grafikas l = f(m) parodyta paveiksle. Atkarpoje šis grafikas yra ištisinė (ištisinė) linija, o taške ji nutrūksta. Rezultatas yra grafikas, susidedantis iš dviejų šakų. Visuose taškuose, išskyrus , funkciją l = f(m) yra tęstinis, bet tam tikru momentu jis turi netolydumą.

Funkcijos tęstinumo tyrimas gali būti arba savarankiška užduotis, arba vienas iš pilno funkcijos tyrimo ir jos grafiko sudarymo etapų.

Funkcijos tęstinumas intervale

Tegul funkcija y = f(x) apibrėžtas intervale ] a, b[ ir yra tęstinis kiekviename šio intervalo taške. Tada jis vadinamas tęstiniu intervale ] a, b[. Funkcijos tęstinumo sąvoka ]-∞ formos intervaluose apibrėžiama panašiai, b[ , ]a, + ∞[ , ]- ∞, + ∞[ . Leiskite dabar funkcijai y = f(x) apibrėžtas intervale [ a, b] . Skirtumas tarp intervalo ir atkarpos: į intervalą neįtraukiami intervalo ribiniai taškai, bet į atkarpą įtraukiami atkarpos ribiniai taškai. Čia reikėtų paminėti vadinamąjį vienpusį tęstinumą: taške a, likęs segmente [ a, b] , galime priartėti tik iš dešinės ir į tašką b- tik kairėje. Sakoma, kad funkcija yra nuolatinė intervale [ a, b] , jei jis yra ištisinis visuose vidiniuose šio atkarpos taškuose, ištisinis taško dešinėje a ir paliekamas ištisinis taške b.

Tolydžios funkcijos pavyzdys gali būti bet kuri elementari funkcija. Kiekviena elementari funkcija yra ištisinė bet kuriame intervale, kuriame ji yra apibrėžta. Pavyzdžiui, funkcijos ir yra ištisinės bet kuriuo intervalu [ a, b], funkcija tęsiasi intervale [ 0 , b] , funkcija yra ištisinė bet kurioje atkarpoje, kurioje nėra taško a = 2 .

4 pavyzdys. Patikrinkite funkcijos tęstinumą.

Sprendimas. Patikrinkim pirmąją sąlygą. Funkcija neapibrėžta taškuose - 3 ir 3. Netenkinama bent viena iš funkcijos tęstinumo visoje skaičių tiesėje sąlygų. Todėl ši funkcija yra nuolatinė intervalais

5 pavyzdys. Nustatykite, kokia parametro reikšmė a nenutrūkstamas visame apibrėžimo sritis funkcija

Sprendimas.

Raskime dešinės pusės ribą:

.

Akivaizdu, kad taško vertė x= 2 turėtų būti lygus kirvis :

a = 1,5 .

6 pavyzdys. Nustatykite, kokiomis parametrų reikšmėmis a Ir b nenutrūkstamas visame apibrėžimo sritis funkcija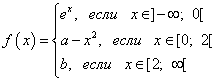

Sprendimas.
Raskime funkcijos kairiąją ribą taške:

.

Todėl taško reikšmė turi būti 1:

Raskime kairiąją funkciją taške:

Akivaizdu, kad funkcijos vertė taške turėtų būti lygi:

Atsakymas: funkcija yra nenutrūkstama visoje apibrėžimo srityje kada a = 1; b = -3 .

Pagrindinės nuolatinių funkcijų savybės

Matematika iki tolydžios funkcijos sampratos atėjo tyrinėdama, visų pirma, įvairius judėjimo dėsnius. Erdvė ir laikas yra begaliniai, o priklausomybė, pavyzdžiui, keliai s nuo laiko t, išreikštas įstatymu s = f(t) , pateikia tęstinio pavyzdį funkcijas f(t). Šildomo vandens temperatūra taip pat nuolat kinta, tai taip pat yra nuolatinė laiko funkcija: T = f(t) .

Matematinės analizės metu įrodomos kai kurios ištisinių funkcijų savybės. Pateiksime svarbiausias iš šių savybių.

1. Jei funkcija, kuri tęsiasi intervale, intervalo galuose įgauna skirtingų ženklų reikšmes, tai tam tikrame šio intervalo taške ji įgauna reikšmę, lygią nuliui. Formalesniame teiginyje ši savybė pateikiama teoremoje, žinomoje kaip pirmoji Bolzano-Cauchy teorema.

2. Funkcija f(x) , nuolatinis intervale [ a, b], ima visas tarpines vertes tarp verčių galiniuose taškuose, tai yra tarp f(a) Ir f(b). Formalesniame teiginyje ši savybė pateikiama teoremoje, žinomoje kaip antroji Bolzano-Cauchy teorema.

Apibrėžimas. Iškviečiama funkcija f(x), apibrėžta kokio nors taško x 0 kaimynystėje ištisinis taške x 0, jei funkcijos riba ir jos reikšmė šiame taške yra lygios, t.y.

Tą patį faktą galima parašyti skirtingai:

Apibrėžimas. Jei funkcija f(x) yra apibrėžta kurioje nors taško x 0 kaimynystėje, bet nėra tolydi pačiame taške x 0, tada ji vadinama sprogstamasis funkcija, o taškas x 0 yra nutrūkimo taškas.

Nepertraukiamos funkcijos pavyzdys:

y

0 x 0 - x 0 x 0 + x

P nepertraukiamos funkcijos pavyzdys:

Apibrėžimas. Funkcija f(x) vadinama tęstine taške x 0, jei bet kuriam teigiamam skaičiui >0 yra toks skaičius >0, kad bet kuris x, tenkinantis sąlygą

nelygybė tiesa
.

Apibrėžimas. Iškviečiama funkcija f(x). tęstinis taške x = x 0, jei funkcijos prieaugis taške x 0 yra be galo maža reikšmė.

f(x) = f(x 0) + (x)

kur (x) yra be galo maža, kai xx 0.

Ištisinių funkcijų savybės.

1) Tęstinių funkcijų taške x 0 suma, skirtumas ir sandauga yra taške x 0 tolydi funkcija.

2) Dviejų ištisinių funkcijų koeficientas – yra ištisinė funkcija, jei g(x) taške x 0 nėra lygus nuliui.

3) Tęstinių funkcijų superpozicija yra nuolatinė funkcija.

Ši savybė gali būti parašyta taip:

Jei u = f(x), v = g(x) yra tolydžios funkcijos taške x = x 0, tai funkcija v = g(f(x)) šiame taške taip pat yra tolydžioji funkcija.

Minėtų savybių pagrįstumą galima nesunkiai įrodyti naudojant ribines teoremas.

Kai kurių elementarių funkcijų tęstinumas.

1) Funkcija f(x) = C, C = const yra nuolatinė funkcija visoje apibrėžimo srityje.

2) Racionalioji funkcija
yra tęstinis visoms x reikšmėms, išskyrus tas, kuriose vardiklis tampa nuliu. Taigi šio tipo funkcija yra nenutrūkstama visoje apibrėžimo srityje.

3) Trigonometrinės funkcijos sin ir cos yra tolydžios savo apibrėžimo srityje.

Įrodykime funkcijos y = sinx savybę 3.

Parašykime funkcijos y = sin(x + x) – sinx prieaugį arba po transformacijos:

Iš tiesų, dviejų funkcijų sandaugai yra riba
Ir
. Šiuo atveju kosinuso funkcija yra ribota funkcija tiesх0
, ir todėl

sinuso funkcijos riba
, tada jis yra be galo mažas tiesх0.

Taigi yra ribotosios funkcijos sandauga ir be galo maža, todėl ši sandauga, t.y. funkcija у yra be galo maža. Remiantis aukščiau aptartais apibrėžimais, funkcija y = sinx yra ištisinė funkcija bet kuriai reikšmei x = x 0 iš apibrėžimo srities, nes jo prieaugis šioje vietoje yra be galo maža reikšmė.

Lūžio taškai ir jų klasifikacija.

Panagrinėkime kokią nors funkciją f(x), ištisinę taško x 0 kaimynystėje, išskyrus patį šį tašką. Iš funkcijos lūžio taško apibrėžimo išplaukia, kad x = x 0 yra lūžio taškas, jei funkcija šiame taške neapibrėžta arba jame nėra tolydi.

Taip pat reikia pažymėti, kad funkcijos tęstinumas gali būti vienpusis. Paaiškinkime tai taip.

, tada sakoma, kad funkcija yra teisinga tęstinė.

Jei vienpusė riba (žr. aukščiau)
, tada sakoma, kad funkcija paliekama ištisinė.

Apibrėžimas. Taškas x 0 vadinamas lūžio taškas funkcija f(x), jei f(x) neapibrėžtas taške x 0 arba nėra tęstinis šiame taške.

Apibrėžimas. Taškas x 0 vadinamas 1 tipo nenutrūkstamumo taškas, jei šioje vietoje funkcija f(x) turi baigtines, bet nelygias kairiąsias ir dešiniąsias ribas.

Norint patenkinti šio apibrėžimo sąlygas, nebūtina, kad funkcija būtų apibrėžta taške x = x 0, pakanka, kad ji būtų apibrėžta jo kairėje ir dešinėje.

Iš apibrėžimo galime daryti išvadą, kad 1-osios rūšies nepertraukiamumo taške funkcija gali turėti tik baigtinį šuolį. Kai kuriais ypatingais atvejais kartais vadinamas ir 1-osios rūšies nepertraukiamumo taškas nuimamas lūžio tašką, bet apie tai plačiau pakalbėsime toliau.

Apibrėžimas. Taškas x 0 vadinamas 2-osios rūšies nenutrūkstamumo taškas, jei šioje vietoje funkcija f(x) neturi bent vienos iš vienpusių ribų arba bent viena iš jų yra begalinė.

Funkcijos tęstinumas intervale ir atkarpoje.

Apibrėžimas. Iškviečiama funkcija f(x). nuolatinis intervalu (segmentas), jei jis yra tęstinis bet kuriame intervalo (segmento) taške.

Šiuo atveju funkcijos tęstinumas atkarpos ar intervalo galuose nereikalingas, atkarpos ar intervalo galuose reikalingas tik vienpusis tęstinumas.

Funkcijų, ištisinių intervale, savybės.

1 nuosavybė: (Pirmoji Weierstrasso teorema (Carl Weierstrass (1815-1897) – vokiečių matematikas)). Funkcija, kuri yra nepertraukiama intervale, yra apribota šiuo intervalu, t.y. atkarpoje tenkinama sąlyga –M  f(x)  M.

Šios savybės įrodymas pagrįstas tuo, kad funkcija, kuri yra ištisinė taške x 0, yra ribojama tam tikroje jos kaimynystėje ir jei atkarpą padalinsite į begalinį skaičių atkarpų, kurios yra „sutrauktos“ į tašką. x 0, tada susidaro tam tikra taško x 0 kaimynystė.

2 nuosavybė: Funkcija, kuri yra ištisinė segmente, įgauna didžiausias ir mažiausias reikšmes.

Tie. yra tokios reikšmės x 1 ir x 2, kad f(x 1) = m, f(x 2) = M ir

m  f(x)  M

Atkreipkime dėmesį į šias didžiausias ir mažiausias reikšmes, kurias funkcija gali įgauti segmentą kelis kartus (pavyzdžiui, f(x) = sinx).

Skirtumas tarp didžiausios ir mažiausios funkcijos reikšmių segmente vadinamas dvejonės veikia segmente.

3 nuosavybė: (Antra Bolzano – Koši teorema). Funkcija, kuri yra nuolatinė intervale, įgyja visas reikšmes tarp dviejų savavališkų šio intervalo reikšmių.

4 nuosavybė: Jei funkcija f(x) yra ištisinė taške x = x 0, tai yra taško x 0 kaimynystė, kurioje funkcija išlaiko savo ženklą.

5 nuosavybė: (Pirmoji Bolzano (1781-1848) teorema – Koši). Jei funkcija f(x) yra ištisinė atkarpoje ir atkarpos galuose turi priešingų ženklų reikšmes, tada šios atkarpos viduje yra taškas, kuriame f(x) = 0.

Tie. jei ženklas(f(a))  ženklas(f(b)), tai  x 0: f(x 0) = 0.

Pavyzdys.

taške x = -1 funkcija yra ištisinė taške x = 1 1 tipo nenutrūkstamumo taškas

adresu

Pavyzdys. Išnagrinėkite tęstinumo funkciją ir nustatykite nenutrūkstamų taškų tipą, jei tokių yra.

taške x = 0 funkcija yra ištisinė taške x = 1 1 tipo nenutrūkstamumo taškas