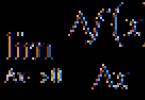Pri odvodení úplne prvého vzorca tabuľky budeme vychádzať z definície derivačnej funkcie v bode. Vezmime kam X– akékoľvek reálne číslo, tj. X– ľubovoľné číslo z oblasti definície funkcie. Zapíšme si limit pomeru prírastku funkcie k prírastku argumentu na :

Treba poznamenať, že pod medzným znamienkom sa získa výraz, ktorým nie je neistota nuly delená nulou, keďže v čitateli nie je nekonečne malá hodnota, ale práve nula. Inými slovami, prírastok konštantnej funkcie je vždy nula.

teda derivácia konštantnej funkciesa rovná nule v celej oblasti definície.

Derivácia mocninovej funkcie.

Vzorec pre deriváciu mocninnej funkcie má tvar , kde exponent p– akékoľvek reálne číslo.

Dokážme najprv vzorec pre prirodzený exponent, teda pre p = 1, 2, 3, …

Použijeme definíciu derivátu. Zapíšme si limitu pomeru prírastku mocninnej funkcie k prírastku argumentu:

Na zjednodušenie výrazu v čitateli sa obrátime na Newtonov binomický vzorec:

teda

To dokazuje vzorec pre deriváciu mocninnej funkcie pre prirodzený exponent.

Derivácia exponenciálnej funkcie.

Uvádzame odvodenie derivačného vzorca na základe definície:

Dostali sme sa do neistoty. Na jej rozšírenie uvádzame novú premennú a na adrese . Potom . Pri poslednom prechode sme použili vzorec na prechod na nový logaritmický základ.

Dosadíme do pôvodného limitu:

Ak si spomenieme na druhú pozoruhodnú limitu, dostaneme sa k vzorcu pre deriváciu exponenciálnej funkcie:

Derivácia logaritmickej funkcie.

Dokážme vzorec pre deriváciu logaritmickej funkcie pre všetkých X z domény definície a všetkých platných hodnôt bázy a logaritmus Podľa definície derivátu máme:

Ako ste si všimli, počas dôkazu sa transformácie vykonávali pomocou vlastností logaritmu. Rovnosť je pravda vďaka druhej pozoruhodnej hranici.

Derivácie goniometrických funkcií.

Aby sme odvodili vzorce pre derivácie goniometrických funkcií, budeme si musieť pripomenúť niektoré trigonometrické vzorce, ako aj prvú pozoruhodnú limitu.

Podľa definície derivácie pre funkciu sínus máme .

Použime vzorec rozdielu sínusov:

Zostáva sa obrátiť na prvý pozoruhodný limit:

Teda derivácia funkcie hriech x Existuje cos x.

Vzorec pre deriváciu kosínusu je dokázaný presne rovnakým spôsobom.

Preto derivácia funkcie cos x Existuje - hriech x.

Vzorce pre tabuľku derivácií pre tangens a kotangens odvodíme pomocou osvedčených pravidiel diferenciácie (derivácia zlomku).

Deriváty hyperbolických funkcií.

Pravidlá diferenciácie a vzorec pre deriváciu exponenciálnej funkcie z tabuľky derivácií nám umožňujú odvodiť vzorce pre derivácie hyperbolického sínusu, kosínusu, tangensu a kotangensu.

Derivácia inverznej funkcie.

Aby sme predišli zmätku pri prezentácii, označme argument funkcie, pomocou ktorej sa vykonáva diferenciácia, dolným indexom, to znamená, že ide o deriváciu funkcie. f(x) Autor: X.

Teraz poďme formulovať pravidlo na nájdenie derivácie inverznej funkcie.

Nechajte funkcie y = f(x) A x = g(y) vzájomne inverzné, definované na intervaloch resp. Ak v určitom bode existuje konečná nenulová derivácia funkcie f(x), potom v bode existuje konečná derivácia inverznej funkcie g(y), a . V inom príspevku .

Toto pravidlo je možné preformulovať pre kohokoľvek X z intervalu , potom dostaneme .

Overme si platnosť týchto vzorcov.

Nájdite inverznú funkciu pre prirodzený logaritmus (Tu r je funkcia a X- argument). Po vyriešení tejto rovnice pre X, dostaneme (tu X je funkcia a r– jej argument). teda a vzájomne inverzné funkcie.

Z tabuľky derivátov to vidíme A .

Uistime sa, že vzorce na nájdenie derivátov inverznej funkcie nás vedú k rovnakým výsledkom:

Ako vidíte, dostali sme rovnaké výsledky ako v tabuľke derivátov.

Teraz máme znalosti na to, aby sme dokázali vzorce pre derivácie inverzných goniometrických funkcií.

Začnime derivátom arcsínusu.

. Potom pomocou vzorca pre deriváciu inverznej funkcie dostaneme

Zostáva už len vykonať premeny.

Pretože rozsah arcsínus je interval , To (pozri časť o základných elementárnych funkciách, ich vlastnostiach a grafoch). Preto o tom neuvažujeme.

teda . Definičnou doménou arczínového derivátu je interval (-1; 1) .

Pre arc cosinus sa všetko robí presne rovnakým spôsobom:

Poďme nájsť derivát arkustangens.

Pretože inverzná funkcia je .

Vyjadrime arkustangens v arkkozíne, aby sme zjednodušili výsledný výraz.

Nechaj arctgx = z, Potom

teda

Derivát oblúkového kotangens sa nachádza podobným spôsobom:

Je prezentovaný dôkaz a odvodenie vzorca pre deriváciu sínus - sin(x). Príklady výpočtu derivátov sin 2x, sínus na druhú a na druhú. Odvodenie vzorca pre deriváciu sínusu n-tého rádu.

Obsah

Pozri tiež: Sínus a kosínus - vlastnosti, grafy, vzorce

Derivácia vzhľadom na premennú x od sínusu x sa rovná kosínusu x:
(sin x)′ = cos x.

Dôkaz

Na odvodenie vzorca pre deriváciu sínusu použijeme definíciu derivácie:
.

Aby sme našli túto hranicu, musíme výraz transformovať takým spôsobom, aby sme ho zredukovali na známe zákony, vlastnosti a pravidlá. Na to potrebujeme poznať štyri vlastnosti.
1) Význam prvého pozoruhodného limitu je:
(1) ;
2) Spojitosť funkcie kosínus:
(2) ;
3) Goniometrické vzorce. Budeme potrebovať nasledujúci vzorec:
(3) ;
4) Aritmetické vlastnosti limity funkcie:
Ak a , tak
(4) .

Aplikujme tieto pravidlá na naše limity. Najprv transformujeme algebraický výraz
.
Na tento účel použijeme vzorec
(3) .
V našom prípade
; . Potom
;
;
;
.

Teraz urobme náhradu. O , . Použime prvý pozoruhodný limit (1):
.

Urobme rovnakú substitúciu a použijeme vlastnosť spojitosti (2):
.

Keďže existujú vyššie vypočítané limity, použijeme vlastnosť (4):

.

Vzorec pre derivát sínusu bol osvedčený.

Príklady

Pozrime sa na jednoduché príklady hľadania derivácií funkcií obsahujúcich sínus. Nájdeme deriváty nasledujúcich funkcií:
y = hriech 2x; y = hriech 2x a y = hriech 3x.

Príklad 1

Nájdite derivát zhrešiť 2x.

Najprv nájdime derivát najjednoduchšej časti:
(2x)′ = 2(x)′ = 2 1 = 2.
Aplikujeme.
.
Tu .

(hriech 2x)′ = 2 čo 2x.

Príklad 2

Nájdite deriváciu sínusovej druhej mocniny:
y = hriech 2x.

Prepíšme pôvodnú funkciu do zrozumiteľnejšej podoby:
.
Poďme nájsť derivát najjednoduchšej časti:
.
Aplikujeme vzorec pre deriváciu komplexnej funkcie.

.
Tu .

Môžete použiť jeden z trigonometrických vzorcov. Potom
.

Príklad 3

Nájdite deriváciu sínusovej kocky:
y = hriech 3x.

Deriváty vyššieho rádu

Všimnite si, že derivát hriech x prvý rád možno vyjadriť prostredníctvom sínusu takto:
.

Nájdite deriváciu druhého rádu pomocou vzorca pre deriváciu komplexnej funkcie:

.
Tu .

Teraz si môžeme všimnúť tú diferenciáciu hriech x spôsobí, že jeho argument vzrastie o . Potom derivácia n-tého rádu má tvar:
(5) .

Dokážme to pomocou metódy matematickej indukcie.

Už sme skontrolovali, že pre , platí vzorec (5).

Predpokladajme, že vzorec (5) platí pre určitú hodnotu. Dokážme, že z toho vyplýva, že vzorec (5) je splnený pre .

Napíšme vzorec (5) na:
.
Túto rovnicu diferencujeme pomocou pravidla na derivovanie komplexnej funkcie:

.
Tu .
Tak sme našli:
.
Ak dosadíme , tak tento vzorec bude mať tvar (5).

Vzorec je osvedčený.

Pozri tiež:

Derivát

Výpočet derivácie matematickej funkcie (diferenciácia) je veľmi častým problémom pri riešení vyššej matematiky. Pre jednoduché (elementárne) matematické funkcie je to pomerne jednoduchá záležitosť, keďže tabuľky derivácií pre elementárne funkcie sú už dávno zostavené a sú ľahko dostupné. Nájdenie derivácie komplexnej matematickej funkcie však nie je triviálna úloha a často si vyžaduje značné úsilie a čas.

Nájdite derivát online

Naša online služba vám umožňuje zbaviť sa zbytočných dlhých výpočtov a nájsť derivát online v jednom momente. Navyše pomocou našej služby umiestnenej na webovej stránke www.stránka, môžete vypočítať online derivát ako z elementárnej funkcie, tak aj z veľmi komplexnej funkcie, ktorá nemá analytické riešenie. Hlavné výhody našej stránky oproti iným sú: 1) neexistujú prísne požiadavky na spôsob zadávania matematickej funkcie pre výpočet derivácie (napr. pri zadávaní funkcie sínus x ju môžete zadať ako sin x alebo sin (x) alebo sin[x] atď. d.); 2) online výpočet derivácie prebieha okamžite v režime online a absolútne zadarmo; 3) umožňujeme vám nájsť deriváciu funkcie akúkoľvek objednávku, zmena poradia derivácie je veľmi jednoduchá a zrozumiteľná; 4) umožňujeme vám nájsť derivát takmer akejkoľvek matematickej funkcie online, dokonca aj veľmi zložitých, ktoré nie je možné vyriešiť inými službami. Poskytnutá odpoveď je vždy presná a nemôže obsahovať chyby.

Používanie nášho servera vám umožní 1) vypočítať derivát online za vás, čím sa eliminujú časovo náročné a únavné výpočty, počas ktorých by ste mohli urobiť chybu alebo preklep; 2) ak vypočítate deriváciu matematickej funkcie sami, potom vám poskytneme možnosť porovnať získaný výsledok s výpočtami našej služby a uistiť sa, že riešenie je správne, alebo nájsť chybu, ktorá sa vkradla; 3) použite našu službu namiesto používania tabuliek derivátov jednoduchých funkcií, kde nájdenie požadovanej funkcie často trvá.

Všetko, čo musíte urobiť, je nájsť derivát online- je využívať našu službu na

Pre pohodlie a prehľadnosť pri štúdiu témy uvádzame súhrnnú tabuľku.

Neustáley = C Mocninná funkcia y = x p (x p) " = p x p - 1	Exponenciálna funkciay = sekera (a x) " = a x ln a Najmä vtedy, keďa = emáme y = e x (e x) " = e x
Logaritmická funkcia (log a x) " = 1 x ln a Najmä vtedy, keďa = emáme y = log x (ln x) " = 1 x	Goniometrické funkcie (sin x) " = cos x (cos x) " = - sin x (t g x) " = 1 cos 2 x (c t g x) " = - 1 hriech 2 x
Inverzné goniometrické funkcie (a r c sin x) " = 1 1 - x 2 (a r c cos x) " = - 1 1 - x 2 (a r c t g x) " = 1 1 + x 2 (a r c c t g x) " = - 1 1 + x 2	Hyperbolické funkcie (s h x) " = c h x (c h x) " = s h x (t h x) " = 1 c h 2 x (c t h x) " = - 1 h 2 x

Poďme analyzovať, ako sa získali vzorce zadanej tabuľky, alebo inými slovami, dokážeme odvodenie derivačných vzorcov pre každý typ funkcie.

Derivácia konštanty

Dôkaz 1

Aby sme odvodili tento vzorec, berieme ako základ definíciu derivácie funkcie v bode. Používame x 0 = x, kde X má hodnotu akéhokoľvek reálneho čísla, alebo inými slovami, X je ľubovoľné číslo z definičného oboru funkcie f (x) = C. Zapíšme si limitu pomeru prírastku funkcie k prírastku argumentu ako ∆ x → 0:

lim ∆ x → 0 ∆ f (x) ∆ x = lim ∆ x → 0 C - C ∆ x = lim ∆ x → 0 0 ∆ x = 0

Upozorňujeme, že výraz 0 ∆ x spadá pod medzné znamienko. Nie je to neistota „nula delená nulou“, keďže čitateľ neobsahuje nekonečne malú hodnotu, ale presne nulu. Inými slovami, prírastok konštantnej funkcie je vždy nula.

Derivácia konštantnej funkcie f (x) = C sa teda rovná nule v celej oblasti definície.

Príklad 1

Konštantné funkcie sú dané:

f 1 (x) = 3, f 2 (x) = a, a ∈ R, f 3 (x) = 4. 13 7 22 , f 4 (x) = 0 , f 5 (x) = - 8 7

Riešenie

Opíšme si dané podmienky. V prvej funkcii vidíme deriváciu prirodzeného čísla 3. V nasledujúcom príklade musíte vziať derivát z A, Kde A- akékoľvek skutočné číslo. Tretí príklad nám dáva deriváciu iracionálneho čísla 4. 13 7 22, štvrtý je deriváciou nuly (nula je celé číslo). Nakoniec v piatom prípade máme deriváciu racionálneho zlomku - 8 7.

odpoveď: derivácie daných funkcií sú nulové pre akúkoľvek real X(v celej oblasti definície)

f 1 " (x) = (3) " = 0, f 2 " (x) = (a) " = 0, a ∈ R, f 3 " (x) = 4. 13 7 22" = 0, f 4 " (x) = 0 " = 0 , f 5 " (x) = - 8 7 " = 0

Derivácia mocninovej funkcie

Prejdime k mocninovej funkcii a vzorcu pre jej deriváciu, ktorá má tvar: (x p) " = p x p - 1, kde exponent p je akékoľvek reálne číslo.

Dôkaz 2

Tu je dôkaz vzorca, keď je exponent prirodzené číslo: p = 1, 2, 3, …

Opäť sa opierame o definíciu derivátu. Zapíšme si hranicu pomeru prírastku mocninnej funkcie k prírastku argumentu:

(x p) " = lim ∆ x → 0 = ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p - x p ∆ x

Na zjednodušenie výrazu v čitateli používame Newtonov binomický vzorec:

(x + ∆ x) p - x p = C p 0 + x p + C p 1 · x p - 1 · ∆ x + C p 2 · x p - 2 · (∆ x) 2 + . . . + + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p - x p = = C p 1 x p - 1 ∆ x + C p 2 x p - 2 (∆ x) 2 + . . . + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p

Takto:

(x p) " = lim ∆ x → 0 ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p - x p ∆ x = = lim ∆ x → 0 (C p 1 x p - 1 ∆ x + C p 2 x p - 2 (∆ x) 2 + ... + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p) ∆ x = = lim ∆ x → 0 (C p 1 x p - 1 + C p 2 x p - 2 ∆ x + .. + C p p - 1 x (∆ x) p - 2 + C p p (∆ x) p - 1) = = C p 1 · x p - 1 + 0 + 0 + ... + 0 = p ! 1 ! · (p - 1) ! · x p - 1 = p · x p - 1

Dokázali sme teda vzorec pre deriváciu mocninnej funkcie, keď je exponent prirodzené číslo.

Dôkaz 3

Poskytnúť dôkazy pre prípad, keď p- akékoľvek iné reálne číslo ako nula, používame logaritmickú deriváciu (tu by sme mali pochopiť rozdiel od derivácie logaritmickej funkcie). Pre úplnejšie pochopenie sa odporúča študovať deriváciu logaritmickej funkcie a ďalej porozumieť derivácii implicitnej funkcie a derivácii komplexnej funkcie.

Uvažujme o dvoch prípadoch: kedy X pozitívne a kedy X negatívne.

Takže x > 0. Potom: x p > 0 . Logaritmujme rovnosť y = x p so základom e a aplikujme vlastnosť logaritmu:

y = x p ln y = ln x p ln y = p · ln x

V tejto fáze sme získali implicitne špecifikovanú funkciu. Definujme jeho derivát:

(ln y) " = (p · ln x) 1 y · y " = p · 1 x ⇒ y " = p · y x = p · x p x = p · x p - 1

Teraz zvážime prípad, kedy X - záporné číslo.

Ak indikátor p je párne číslo, potom je funkcia mocniny definovaná pre x< 0 , причем является четной: y (x) = - y ((- x) p) " = - p · (- x) p - 1 · (- x) " = = p · (- x) p - 1 = p · x p - 1

Potom x p< 0 и возможно составить доказательство, используя логарифмическую производную.

Ak p je nepárne číslo, potom je funkcia mocniny definovaná pre x< 0 , причем является нечетной: y (x) = - y (- x) = - (- x) p . Тогда x p < 0 , а значит логарифмическую производную задействовать нельзя. В такой ситуации возможно взять за основу доказательства правила дифференцирования и правило нахождения производной сложной функции:

y " (x) = (- (- x) p) " = - ((- x) p) " = - p · (- x) p - 1 · (- x) " = = p · (- x) p - 1 = p x p - 1

Posledný prechod je možný vďaka tomu, že ak p je teda nepárne číslo p - 1 buď párne číslo alebo nula (pre p = 1), teda pre zápor X platí rovnosť (- x) p - 1 = x p - 1.

Takže sme dokázali vzorec pre deriváciu mocninovej funkcie pre akékoľvek skutočné p.

Príklad 2

Poskytnuté funkcie:

f 1 (x) = 1 x 2 3, f 2 (x) = x 2 - 1 4, f 3 (x) = 1 x log 7 12

Určite ich deriváty.

Riešenie

Niektoré z daných funkcií transformujeme do tabuľkového tvaru y = x p na základe vlastností stupňa a potom použijeme vzorec:

f 1 (x) = 1 x 2 3 = x - 2 3 ⇒ f 1 " (x) = - 2 3 x - 2 3 - 1 = - 2 3 x - 5 3 f 2 " (x) = x 2 - 1 4 = 2 - 1 4 x 2 - 1 4 - 1 = 2 - 1 4 x 2 - 5 4 f 3 (x) = 1 x log 7 12 = x - log 7 12 ⇒ f 3" ( x) = - log 7 12 x - log 7 12 - 1 = - log 7 12 x - log 7 12 - log 7 7 = - log 7 12 x - log 7 84

Derivácia exponenciálnej funkcie

Dôkaz 4

Odvodme odvodený vzorec pomocou definície ako základu:

(a x) " = lim ∆ x → 0 a x + ∆ x - a x ∆ x = lim ∆ x → 0 a x (a ∆ x - 1) ∆ x = a x lim ∆ x → 0 a ∆ x - 1 ∆ x = 0 0

Dostali sme neistotu. Aby sme to rozšírili, napíšme novú premennú z = a ∆ x - 1 (z → 0 ako ∆ x → 0). V tomto prípade a ∆ x = z + 1 ⇒ ∆ x = log a (z + 1) = ln (z + 1) ln a . Pri poslednom prechode bol použitý vzorec pre prechod na nový logaritmický základ.

Do pôvodného limitu dosadíme:

(a x) " = a x · lim ∆ x → 0 a ∆ x - 1 ∆ x = a x · ln a · lim ∆ x → 0 1 1 z · ln (z + 1) = = a x · ln a · lim ∆ x → 0 1 ln (z + 1) 1 z = a x · ln a · 1 ln lim ∆ x → 0 (z + 1) 1 z

Pripomeňme si druhú pozoruhodnú limitu a potom dostaneme vzorec pre deriváciu exponenciálnej funkcie:

(a x) " = a x · ln a · 1 ln lim z → 0 (z + 1) 1 z = a x · ln a · 1 ln e = a x · ln a

Príklad 3

Exponenciálne funkcie sú dané:

f 1 (x) = 2 3 x, f 2 (x) = 5 3 x, f 3 (x) = 1 (e) x

Je potrebné nájsť ich deriváty.

Riešenie

Na deriváciu exponenciálnej funkcie a vlastnosti logaritmu používame vzorec:

f 1 " (x) = 2 3 x " = 2 3 x ln 2 3 = 2 3 x (ln 2 - ln 3) f 2 " (x) = 5 3 x " = 5 3 x ln 5 1 3 = 1 3 5 3 x ln 5 f 3 " (x) = 1 (e) x " = 1 e x " = 1 e x ln 1 e = 1 e x ln e - 1 = - 1 e x

Derivácia logaritmickej funkcie

Dôkaz 5

Uveďme dôkaz o vzorci pre deriváciu logaritmickej funkcie pre ľubovoľnú X v oblasti definície a akýchkoľvek prípustných hodnôt základu a logaritmu. Na základe definície derivátu dostaneme:

(log a x) " = lim ∆ x → 0 log a (x + ∆ x) - log a x ∆ x = lim ∆ x → 0 log a x + ∆ x x ∆ x = = lim ∆ x → 0 1 ∆ x log a 1 + ∆ x x = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x = = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x · x x = lim ∆ x → 0 1 x · log a 1 + ∆ x x x ∆ x = = 1 x · log a lim ∆ x → 0 1 + ∆ x x x ∆ x = 1 x · log a e = 1 x · ln e ln a = 1 x · ln a

Z naznačeného reťazca rovnosti je zrejmé, že transformácie boli založené na vlastnosti logaritmu. Rovnosť lim ∆ x → 0 1 + ∆ x x x ∆ x = e platí v súlade s druhou pozoruhodnou hranicou.

Príklad 4

Logaritmické funkcie sú dané:

f 1 (x) = log ln 3 x, f 2 (x) = ln x

Je potrebné vypočítať ich deriváty.

Riešenie

Aplikujme odvodený vzorec:

f1" (x) = (log ln 3 x)" = 1 x · ln (ln 3); f 2 " (x) = (ln x) " = 1 x ln e = 1 x

Takže derivácia prirodzeného logaritmu je jedna delená X.

Derivácie goniometrických funkcií

Dôkaz 6

Použime niekoľko goniometrických vzorcov a prvú úžasnú limitu na odvodenie vzorca pre deriváciu goniometrickej funkcie.

Podľa definície derivácie funkcie sínus dostaneme:

(sin x) " = lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x

Vzorec pre rozdiel sínusov nám umožní vykonať nasledujúce akcie:

(sin x) " = lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x = = lim ∆ x → 0 2 sin x + ∆ x - x 2 cos x + ∆ x + x 2 ∆ x = = lim ∆ x → 0 sin ∆ x 2 · cos x + ∆ x 2 ∆ x 2 = = cos x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2

Nakoniec použijeme prvý úžasný limit:

sin " x = cos x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = cos x

Takže derivácia funkcie hriech x bude cos x.

Ukážeme aj vzorec pre deriváciu kosínusu:

cos " x = lim ∆ x → 0 cos (x + ∆ x) - cos x ∆ x = = lim ∆ x → 0 - 2 sin x + ∆ x - x 2 sin x + ∆ x + x 2 ∆ x = = - lim ∆ x → 0 sin ∆ x 2 sin x + ∆ x 2 ∆ x 2 = = - sin x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = - sin x

Tie. derivácia funkcie cos x bude – hriech x.

Vzorce pre derivácie tangens a kotangens odvodíme na základe pravidiel diferenciácie:

t g " x = sin x cos x " = sin " x · cos x - sin x · cos " x cos 2 x = = cos x · cos x - sin x · (- sin x) cos 2 x = sin 2 x + cos 2 x cos 2 x = 1 cos 2 x c t g " x = cos x sin x " = cos " x · sin x - cos x · sin " x sin 2 x = = - sin x · sin x - cos x · cos x hriech 2 x = - hriech 2 x + cos 2 x hriech 2 x = - 1 hriech 2 x

Derivácie inverzných goniometrických funkcií

Časť o derivácii inverzných funkcií poskytuje komplexné informácie o dôkaze vzorcov pre derivácie arksínusu, arkkozínu, arkustangensu a arkotangensu, takže tu látku nebudeme duplikovať.

Deriváty hyperbolických funkcií

Dôkaz 7

Vzorce pre derivácie hyperbolického sínusu, kosínusu, tangensu a kotangensu môžeme odvodiť pomocou pravidla diferenciácie a vzorca pre deriváciu exponenciálnej funkcie:

s h " x = e x - e - x 2 " = 1 2 e x " - e - x " = = 1 2 e x - - e - x = e x + e - x 2 = c h x c h " x = e x + e - x 2 " = 1 2 e x " + e - x " = = 1 2 e x + - e - x = e x - e - x 2 = s h x t h " x = s h x c h x " = s h " x · c h x - s h x · c h " x c h 2 x = c h 2 x - s h 2 x c h 2 x = 1 c h 2 x c h " x = c h x s h x " = c h " x · s h x - c h x · s h " x s h 2 x = h 2 x - c h 2 x h 2 x = - 1 h 2 x

Ak si všimnete chybu v texte, zvýraznite ju a stlačte Ctrl+Enter