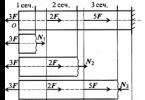
Lygtys su moduliais, sprendimų metodai. 1 dalis.

Prieš pradedant tiesioginį tokių lygčių sprendimo metodų tyrimą, svarbu suprasti modulio esmę, jo geometrinę prasmę. Suprasdami modulio apibrėžimą ir jo geometrinę reikšmę, nustatomi pagrindiniai tokių lygčių sprendimo metodai. Vadinamasis intervalų metodas atidarant modulinius skliaustus yra toks efektyvus, kad jį naudojant moduliais galima išspręsti absoliučiai bet kokią lygtį ar nelygybę. Šioje dalyje išsamiai išnagrinėsime du standartinius metodus: intervalų metodą ir lygties pakeitimo populiacija metodą.

Tačiau, kaip matysime, šie metodai visada yra veiksmingi, tačiau ne visada patogūs ir gali lemti ilgus ir net nelabai patogius skaičiavimus, kuriems išspręsti natūraliai reikia daugiau laiko. Todėl svarbu žinoti tuos metodus, kurie labai supaprastina tam tikrų lygčių struktūrų sprendimą. Abiejų lygties dalių kvadratūra, naujo kintamojo įvedimo metodas, grafinis metodas, lygčių, turinčių modulį po modulio ženklu, sprendimas. Šiuos metodus aptarsime kitame skyriuje.

Skaičiaus modulio apibrėžimas. Modulio geometrinė reikšmė.

Pirmiausia susipažinkime su geometrine modulio reikšme:

modulio numeris a (|a|) skambinti atstumas skaičių eilutėje nuo pradžios (taško 0) iki taško A(a).

Remdamiesi šiuo apibrėžimu, apsvarstykite keletą pavyzdžių:

|7| yra atstumas nuo 0 iki taško 7, žinoma, tai yra 7. → | 7 |=7

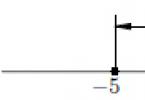
|-5| yra atstumas nuo 0 iki taško -5 ir jis lygus: 5. → |-5| = 5

Visi suprantame, kad atstumas negali būti neigiamas! Todėl |x| ≥ 0 visada!

Išspręskite lygtį: |x |=4

Šią lygtį galima perskaityti taip: atstumas nuo taško 0 iki taško x yra 4. Taip, pasirodo, kad nuo 0 galime judėti tiek į kairę, tiek į dešinę, o tai reiškia, kad judame į kairę atstumu, lygiu 4 atsidursime taške: -4, o judėdami į dešinę atsidursime taške: 4. Iš tiesų, |-4 |=4 ir |4 |=4.

Taigi atsakymas yra x=±4.

Jei atidžiai išnagrinėsite ankstesnę lygtį, pastebėsite, kad: atstumas į dešinę išilgai skaičių linijos nuo 0 iki taško yra lygus pačiam taškui, o atstumas į kairę nuo 0 iki skaičiaus yra lygus priešingai numeris! Suprasdami, kad dešinėje nuo 0 yra teigiami skaičiai, o į kairę nuo 0 yra neigiami, formuluojame skaičiaus modulio apibrėžimai: skaičiaus modulis (absoliuti reikšmė). X(|x|) vadinamas pačiu skaičiumi X, jei x ≥0, o skaičius yra X jei x<0.

Čia reikia rasti skaičių eilutės taškų aibę, atstumas nuo 0 iki kurio bus mažesnis nei 3, įsivaizduokime skaičių eilutę, joje tašką 0, eikime į kairę ir suskaičiuokime vieną (-1), du (- 2) ir trys (-3), sustokite. Tolimesni taškai, esantys toliau nei 3, arba atstumas, iki kurio nuo 0 yra didesnis nei 3, dabar einame į dešinę: vienas, du, trys, vėl sustokite. Dabar pasirenkame visus savo taškus ir gauname intervalą x: (-3; 3).

Svarbu tai aiškiai matyti, jei vis tiek nepavyksta, pieškite ant popieriaus ir pamatysite, kad ši iliustracija jums visiškai aiški, nepatingėkite ir pabandykite mintyse įžvelgti šių užduočių sprendimus:

|x |=11, x=? |x|=-5, x=?

| x |<8, х-? |х| <-6, х-?

|x|>2, x-? |x|> -3, x-?

|π-3|=? |-x²-10|=?

|√5-2|=? |2x-x²-3|=?

|x²+2|=? |х²+4|=0

|x²+3x+4|=? |-x²+9| ≤0

Atkreipkite dėmesį į keistas užduotis antrajame stulpelyje? Iš tiesų, atstumas negali būti neigiamas, todėl: |x|=-5- neturi sprendinių, žinoma, jis negali būti mažesnis už 0, todėl: |x|<-6 тоже не имеет решений, ну и естественно, что любое расстояние будет больше отрицательного числа, значит решением |x|>-3 yra visi skaičiai.

Sužinoję, kaip greitai matyti brėžinius su sprendimais, skaitykite toliau.

Instrukcija

Jei modulis vaizduojamas kaip ištisinė funkcija, tada jo argumento reikšmė gali būti teigiama arba neigiama: |х| = x, x ≥ 0; |x| = - x, x

Modulis yra lygus nuliui, o bet kurio teigiamo skaičiaus modulis yra jo modulis. Jei argumentas yra neigiamas, tada atidarius skliaustus, jo ženklas pasikeičia iš minuso į pliusą. Remiantis tuo, daroma išvada, kad priešingo moduliai yra lygūs: |-x| = |x| = x.

Kompleksinio skaičiaus modulis randamas pagal formulę: |a| = √b ² + c ² ir |a + b| ≤ |a| + |b|. Jei argumente yra teigiamas skaičius kaip daugiklis, tada jį galima išimti iš skliaustų ženklo, pavyzdžiui: |4*b| = 4*|b|.

Jei argumentas pateikiamas kaip kompleksinis skaičius, tada skaičiavimų patogumui laužtiniuose skliaustuose leidžiama reiškinio terminų tvarka: |2-3| = |3-2| = 3-2 = 1, nes (2-3) yra mažesnis už nulį.

Į laipsnį keliamas argumentas kartu yra po tos pačios eilės šaknies ženklu – jis sprendžiamas taip: √a² = |a| = ±a.

Jei jūsų laukia užduotis, kurioje nenurodyta modulio skliaustų išplėtimo sąlyga, tada jums nereikia jų atsikratyti - tai bus galutinis rezultatas. Ir jei norite juos atidaryti, turite nurodyti ženklą ±. Pavyzdžiui, reikia rasti išraiškos √(2 * (4-b)) ² reikšmę. Jo sprendimas atrodo taip: √(2 * (4-b)) ² = |2 * (4-b)| = 2 * |4-b|. Kadangi posakio 4-b ženklas nežinomas, jį reikia palikti skliausteliuose. Jei pridedate papildomą sąlygą, pvz., |4-b| >

Nulio modulis yra lygus nuliui, o bet kurio teigiamo skaičiaus modulis yra lygus jam pačiam. Jei argumentas yra neigiamas, tada atidarius skliaustus, jo ženklas pasikeičia iš minuso į pliusą. Remiantis tuo, daroma išvada, kad priešingų skaičių moduliai yra lygūs: |-x| = |x| = x.

Kompleksinio skaičiaus modulis randamas pagal formulę: |a| = √b ² + c ² ir |a + b| ≤ |a| + |b|. Jei argumente yra teigiamas sveikasis skaičius kaip daugiklis, tada jį galima išimti iš skliaustų ženklo, pavyzdžiui: |4*b| = 4*|b|.

Modulis negali būti neigiamas, todėl bet koks neigiamas skaičius paverčiamas teigiamu: |-x| = x, |-2| = 2, |-1/7| = 1/7, |-2,5| = 2,5.

Jei argumentas pateikiamas kaip kompleksinis skaičius, tada skaičiavimų patogumui leidžiama keisti laužtiniuose skliaustuose pateiktos išraiškos terminų tvarką: |2-3| = |3-2| = 3-2 = 1, nes (2-3) yra mažesnis už nulį.

Jei jūsų laukia užduotis, kurioje nenurodyta modulio skliaustų išplėtimo sąlyga, tada jums nereikia jų atsikratyti - tai bus galutinis rezultatas. Ir jei norite juos atidaryti, turite nurodyti ženklą ±. Pavyzdžiui, reikia rasti išraiškos √(2 * (4-b)) ² reikšmę. Jo sprendimas atrodo taip: √(2 * (4-b)) ² = |2 * (4-b)| = 2 * |4-b|. Kadangi posakio 4-b ženklas nežinomas, jį reikia palikti skliausteliuose. Jei pridedate papildomą sąlygą, pvz., |4-b| > 0, tada rezultatas yra 2 * |4-b| = 2 *(4 - b). Kaip nežinomas elementas taip pat gali būti pateiktas konkretus skaičius, į kurį reikia atsižvelgti, nes. tai paveiks išraiškos ženklą.

Terminas (modulis) pažodiniu vertimu iš lotynų kalbos reiškia „matuoti“. Šią sąvoką į matematiką įvedė anglų mokslininkas R. Cotesas. O vokiečių matematikas K. Weierstrassas pristatė modulio ženklą – simbolį, kuriuo rašant žymima ši sąvoka.

Susisiekus su

Pirmą kartą ši sąvoka nagrinėjama matematikoje pagal vidurinės mokyklos 6 klasės programą. Pagal vieną apibrėžimą modulis yra absoliuti tikrojo skaičiaus reikšmė. Kitaip tariant, norėdami sužinoti tikrojo skaičiaus modulį, turite atmesti jo ženklą.

Grafiškai absoliuti vertė Ažymimas kaip |a|.

Pagrindinis šios sąvokos skiriamasis bruožas yra tas, kad ji visada yra neneigiama reikšmė.

Skaičiai, kurie skiriasi vienas nuo kito tik ženklu, vadinami priešingais skaičiais. Jei reikšmė yra teigiama, tada jos priešingybė yra neigiama, o nulis yra jos pačios priešingybė.

geometrinė vertė

Jei nagrinėsime modulio sąvoką geometriniu požiūriu, tada jis žymės atstumą, kuris matuojamas vienetų segmentais nuo pradžios iki duoto taško. Šis apibrėžimas visiškai atskleidžia geometrinę tiriamo termino reikšmę.

Grafiškai tai galima išreikšti taip: |a| = O.A.

Absoliučios vertės savybės

Žemiau apžvelgsime visas šios sąvokos matematines savybes ir rašymo būdus pažodinių išraiškų forma:

Lygčių sprendimo moduliu ypatumai

Jei mes kalbame apie matematinių lygčių ir nelygybių, kuriose yra modulis, sprendimą, turite atsiminti, kad norėdami jas išspręsti, turėsite atidaryti šį ženklą.

Pavyzdžiui, jei absoliučios reikšmės ženkle yra kokia nors matematinė išraiška, tai prieš atidarant modulį būtina atsižvelgti į esamus matematinius apibrėžimus.

|A + 5| = A + 5 jei A yra didesnis arba lygus nuliui.

5-A jei A yra mažesnis už nulį.

Kai kuriais atvejais ženklas gali būti vienareikšmiškai išplėstas bet kuriai kintamojo reikšmei.

Panagrinėkime dar vieną pavyzdį. Sukonstruokime koordinačių tiesę, kurioje pažymime visas skaitines reikšmes, kurių absoliuti reikšmė bus 5.

Pirmiausia turite nubrėžti koordinačių liniją, nurodyti joje koordinačių kilmę ir nustatyti vieno segmento dydį. Be to, linija turi turėti kryptį. Dabar ant šios tiesios linijos reikia pritaikyti žymes, kurios bus lygios vieno segmento vertei.

Taigi matome, kad šioje koordinačių linijoje bus du mus dominantys taškai, kurių reikšmės yra 5 ir -5.

Šiame straipsnyje mes išsamiai išanalizuosime absoliuti skaičiaus reikšmė. Pateiksime įvairius skaičiaus modulio apibrėžimus, supažindinsime su žymėjimu ir pateiksime grafines iliustracijas. Šiuo atveju mes svarstome įvairius pavyzdžius, kaip rasti skaičiaus modulį pagal apibrėžimą. Po to išvardijame ir pagrindžiame pagrindines modulio savybes. Straipsnio pabaigoje kalbėsime apie tai, kaip nustatomas ir randamas kompleksinio skaičiaus modulis.

Puslapio naršymas.

Skaičių modulis – apibrėžimas, žymėjimas ir pavyzdžiai

Pirmiausia pristatome modulio žymėjimas. Skaičiaus a modulis bus parašytas kaip , tai yra, į kairę ir į dešinę nuo skaičiaus įdėsime vertikalias linijas, kurios sudaro modulio ženklą. Pateikime porą pavyzdžių. Pavyzdžiui, modulo -7 gali būti parašytas kaip ; 4125 modulis parašytas kaip , o modulis parašytas kaip .

Toliau pateiktas modulio apibrėžimas susijęs su sveikaisiais skaičiais ir racionaliaisiais bei neracionaliais skaičiais, kaip į sudedamąsias realiųjų skaičių aibės dalis. Kalbėsime apie kompleksinio skaičiaus modulį in.

Apibrėžimas.

Modulis a yra pats skaičius a, jei a yra teigiamas skaičius, arba skaičius −a, priešingas skaičiui a, jei a yra neigiamas skaičius, arba 0, jei a=0 .

Balsinis skaičiaus modulio apibrėžimas dažnai rašomas tokia forma , šis žymėjimas reiškia, kad jei a>0 , jei a=0 ir jei a<0 .

Įrašas gali būti pavaizduotas kompaktiškesne forma . Šis žymėjimas reiškia, kad jei (a yra didesnis arba lygus 0 ), o jei a<0 .

Taip pat yra rekordas . Čia atvejis, kai a=0 turėtų būti paaiškintas atskirai. Šiuo atveju turime , bet −0=0 , nes nulis laikomas skaičiumi, kuris yra priešingas jam pačiam.

Atnešam skaičiaus modulio radimo pavyzdžiai su duotu apibrėžimu. Pavyzdžiui, suraskime skaičių 15 ir . Pradėkime nuo suradimo. Kadangi skaičius 15 yra teigiamas, jo modulis pagal apibrėžimą yra lygus pačiam šiam skaičiui, ty . Koks yra skaičiaus modulis? Kadangi yra neigiamas skaičius, tada jo modulis yra lygus skaičiui, priešingam skaičiui, tai yra skaičiui . Taigi,.

Šios pastraipos pabaigoje pateikiame vieną išvadą, kurią labai patogu pritaikyti praktikoje ieškant skaičiaus modulio. Iš skaičiaus modulio apibrėžimo išplaukia, kad skaičiaus modulis yra lygus skaičiui po modulio ženklu, nepriklausomai nuo jo ženklo, o iš aukščiau aptartų pavyzdžių tai labai aiškiai matyti. Išsakytas teiginys paaiškina, kodėl vadinamas ir skaičiaus modulis absoliuti skaičiaus reikšmė. Taigi skaičiaus modulis ir absoliuti skaičiaus reikšmė yra vienas ir tas pats.

Skaičiaus modulis kaip atstumas

Geometriškai skaičiaus modulis gali būti interpretuojamas kaip atstumas. Atnešam skaičiaus modulio pagal atstumą nustatymas.

Apibrėžimas.

Modulis a yra atstumas nuo koordinačių linijos pradžios iki taško, atitinkančio skaičių a.

Šis apibrėžimas atitinka pirmoje pastraipoje pateiktą skaičiaus modulio apibrėžimą. Paaiškinkime šį dalyką. Atstumas nuo pradžios iki taško, atitinkančio teigiamą skaičių, yra lygus šiam skaičiui. Nulis atitinka atskaitos tašką, todėl atstumas nuo atskaitos taško iki taško, kurio koordinatė 0 yra lygus nuliui (norint patekti iš taško O nereikia atidėti nei vienos atkarpos, nei atkarpos, sudarančios kokią nors vienos atkarpos dalį iki taško, kurio koordinatė 0). Atstumas nuo pradžios iki taško, kurio koordinatė yra neigiama, yra lygus skaičiui, priešingam nurodyto taško koordinatei, nes jis yra lygus atstumui nuo pradžios iki taško, kurio koordinatė yra priešinga.

Pavyzdžiui, skaičiaus 9 modulis yra 9, nes atstumas nuo pradžios iki taško, kurio koordinatė 9, yra devyni. Paimkime kitą pavyzdį. Taškas su koordinate −3,25 yra 3,25 atstumu nuo taško O, taigi .

Skambus skaičiaus modulio apibrėžimas yra ypatingas dviejų skaičių skirtumo modulio apibrėžimo atvejis.

Apibrėžimas.

Dviejų skaičių skirtumo modulis a ir b lygus atstumui tarp koordinačių linijos taškų su koordinatėmis a ir b .

Tai yra, jei yra pateikti taškai koordinačių tiesėje A(a) ir B(b), tai atstumas nuo taško A iki taško B yra lygus skaičių a ir b skirtumo moduliui. Jei tašką O (atskaitos tašką) laikysime tašku B, tada gausime šios pastraipos pradžioje pateikto skaičiaus modulio apibrėžimą.

Skaičiaus modulio nustatymas per aritmetinę kvadratinę šaknį

Kartais randama modulio nustatymas per aritmetinę kvadratinę šaknį.

Pavyzdžiui, apskaičiuokime skaičių −30 modulius ir remdamiesi šiuo apibrėžimu. Mes turime . Panašiai apskaičiuojame dviejų trečdalių modulį: .

Skaičiaus modulio apibrėžimas pagal aritmetinę kvadratinę šaknį taip pat atitinka apibrėžimą, pateiktą šio straipsnio pirmoje pastraipoje. Parodykime. Tegul a yra teigiamas skaičius, o −a yra neigiamas. Tada Ir , jei a = 0 , tada .

Modulio ypatybės

Modulis turi keletą būdingų rezultatų - modulio savybės. Dabar pateiksime pagrindinius ir dažniausiai naudojamus iš jų. Pagrįsdami šias savybes, remsimės skaičiaus modulio apibrėžimu pagal atstumą.

Pradėkime nuo akivaizdžiausios modulio savybės − skaičiaus modulis negali būti neigiamas skaičius. Pažodine forma ši savybė turi bet kurio skaičiaus a formą. Šią savybę labai lengva pagrįsti: skaičiaus modulis yra atstumas, o atstumas negali būti išreikštas neigiamu skaičiumi.

Pereikime prie kitos modulio savybės. Skaičiaus modulis lygus nuliui tada ir tik tada, kai šis skaičius lygus nuliui. Nulio modulis pagal apibrėžimą yra lygus nuliui. Nulis atitinka pradinę vietą, joks kitas koordinačių linijos taškas neatitinka nulio, nes kiekvienas realusis skaičius yra susietas su vienu koordinačių linijos tašku. Dėl tos pačios priežasties bet koks skaičius, išskyrus nulį, atitinka kitą tašką nei pradžios taškas. Ir atstumas nuo pradžios iki bet kurio taško, išskyrus tašką O, nėra lygus nuliui, nes atstumas tarp dviejų taškų yra lygus nuliui tada ir tik tada, kai šie taškai sutampa. Aukščiau pateiktas samprotavimas įrodo, kad tik nulio modulis yra lygus nuliui.

Pirmyn. Priešingi skaičiai turi vienodus modulius, tai yra, bet kuriam skaičiui a . Iš tiesų, du koordinačių linijos taškai, kurių koordinatės yra priešingi skaičiai, yra vienodu atstumu nuo pradžios, o tai reiškia, kad priešingų skaičių moduliai yra lygūs.

Kita modulio ypatybė yra: dviejų skaičių sandaugos modulis lygus šių skaičių modulių sandaugai, tai yra, . Pagal apibrėžimą skaičių a ir b sandaugos modulis yra arba a b, jei , arba −(a b), jei . Iš realiųjų skaičių daugybos taisyklių išplaukia, kad skaičių a ir b modulių sandauga yra lygi arba a b , arba −(a b) , jei , kas įrodo nagrinėjamą savybę.

A dalinio modulis, padalytas iš b, yra lygus daliniui, dalinantis a modulį iš modulio b, tai yra, . Pagrįskime šią modulio savybę. Kadangi koeficientas yra lygus sandaugai, tada . Dėl ankstesnės nuosavybės mes turime . Belieka tik naudoti lygybę , kuri galioja pagal skaičiaus modulio apibrėžimą.

Ši modulio savybė parašyta kaip nelygybė: , a , b ir c yra savavališki realieji skaičiai. Rašytinė nelygybė yra ne kas kita trikampio nelygybė. Kad tai būtų aišku, paimkime koordinačių tiesės taškus A(a) , B(b) , C(c) ir apsvarstykime išsigimusią trikampį ABC, kurio viršūnės yra toje pačioje tiesėje. Pagal apibrėžimą skirtumo modulis yra lygus atkarpos AB ilgiui, - atkarpos AC ilgiui ir - atkarpos CB ilgiui. Kadangi bet kurios trikampio kraštinės ilgis neviršija kitų dviejų kraštinių ilgių sumos, nelygybė , todėl galioja ir nelygybė.

Ką tik įrodyta nelygybė yra daug dažnesnė formoje . Parašyta nelygybė paprastai laikoma atskira modulio savybe su formuluote: „ Dviejų skaičių sumos modulis neviršija šių skaičių modulių sumos“. Bet nelygybė tiesiogiai išplaukia iš nelygybės , jei į ją įdėsime −b vietoj b ir imsime c=0 .

Kompleksinio skaičiaus modulis

Duokim kompleksinio skaičiaus modulio nustatymas. Tebūnie mums duota kompleksinis skaičius, parašytas algebrine forma , kur x ir y yra kai kurie realieji skaičiai, atitinkamai reiškiantys tikrosią ir įsivaizduojamą kompleksinio skaičiaus z dalis ir yra įsivaizduojamas vienetas.