Taško greičio, pagreičio, trajektorijos kreivumo spindulio, liestinės, normaliosios ir dvinormės skaičiavimo formulės pagal nurodytas koordinačių priklausomybes nuo laiko. Uždavinio, kuriame pagal pateiktas judėjimo lygtis reikia nustatyti taško greitį ir pagreitį, sprendimo pavyzdys. Taip pat nustatomas trajektorijos kreivumo spindulys, liestinė, normalioji ir binormalioji.
TurinysĮvadas
Žemiau pateiktų formulių išvados ir teorijos pristatymas pateikiamos puslapyje „Materialaus taško kinematika“. Čia mes pritaikome pagrindinius šios teorijos rezultatus materialaus taško judėjimo patikslinimo koordinačių metodui.
Turėkime fiksuotą stačiakampę koordinačių sistemą, kurios centras yra fiksuotame taške. Šiuo atveju taško M padėtis vienareikšmiškai nustatoma pagal jo koordinates (x, y, z). Taško judėjimo nurodymo koordinačių metodas- tai metodas, kuriame pateikiamos koordinačių priklausomybės nuo laiko. Tai yra, pateikiamos trys laiko funkcijos (trimačiam judėjimui):
Kinematinių dydžių apibrėžimas
Žinodami koordinačių priklausomybę nuo laiko, automatiškai nustatome medžiagos taško M spindulio vektorių pagal formulę:
,
kur yra vienetiniai vektoriai (orths) x, y, z ašių kryptimi.
Diferencijuodami pagal laiką randame greičio ir pagreičio projekcijas koordinačių ašyse:
;
;
Greičio ir pagreičio moduliai:
;
.
.
Tangentinis (tangentinis) pagreitis yra viso pagreičio projekcija į greičio kryptį:
.
Tangentinio (tangentinio) pagreičio vektorius:
Normalus pagreitis:
.
;
.
Vieneto vektorius pagrindinės trajektorijos normalės kryptimi:
.
Trajektorijos kreivumo spindulys:
.
Kelio kreivumo centras:
.
.
Problemos sprendimo pavyzdys
Taško greičio ir pagreičio nustatymas pagal pateiktas jo judėjimo lygtis
Pagal pateiktas taško judėjimo lygtis nustatykite jo trajektorijos tipą ir laiko momentui raskite taško padėtį trajektorijoje, jo greitį, pilnąjį, tangentinį ir normalųjį pagreičius, taip pat kreivio spindulį. trajektorijos.
Taškinio judėjimo lygtys:
, cm;
, cm.
Sprendimas
Trajektorijos tipo nustatymas
Iš judesio lygčių neįtraukiame laiko. Norėdami tai padaryti, perrašome juos į formą:
;
.
Taikome formulę:
.
;
;
;
.
Taigi, mes gavome trajektorijos lygtį:
.
Tai parabolės su viršūne taške ir simetrijos ašyje lygtis.
Nes
, Tai
; arba
.
Panašiai gauname apribojimą koordinatei:
;
;
Taigi taško trajektorija yra parabolės lankas
,
esantis adresu
Ir .
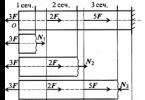
Iš taškų statome parabolę.
| 0 | 6 |
| 3 | 5,625 |
| 6 | 4,5 |
| 9 | 2,625 |
| 12 | 0 |
Nustatykite taško padėtį tuo metu.
;
.
Taško greičio nustatymas
Diferencijuodami koordinates ir laiko atžvilgiu randame greičio komponentus.
.
Norint atskirti, patogu taikyti trigonometrijos formulę:
. Tada
;
.
Apskaičiuojame greičio komponentų vertes laiko momentu:
;
.
Greičio modulis:
.
Taško pagreičio nustatymas
Atskirdami greičio komponentus ir laiko atžvilgiu randame taško pagreičio komponentus.
;
.
Apskaičiuokite pagreičio komponentų vertes vienu metu:
;
.
Pagreičio modulis:
.
Tangentinis pagreitis yra viso pagreičio projekcija į greičio kryptį:
.
Kadangi , tada tangentinio pagreičio vektorius nukreiptas priešingai greičiui .
Normalus pagreitis:
.
Vektorius ir yra nukreiptas į trajektorijos kreivumo centrą.
Trajektorijos kreivumo spindulys:
.
Taško trajektorija yra parabolės lankas
;
.
Taško greitis:.
Taško pagreitis: ; ; .
Trajektorijos kreivumo spindulys: .
Kitų dydžių apibrėžimas
Spręsdami problemą radome:
vektorius ir greičio modulis:
;
;
vektorius ir bendras pagreičio modulis:
;
;
tangentiniai ir normalūs pagreičiai:
;
;
trajektorijos kreivumo spindulys: .
Apibrėžkime likusius kiekius.
Vieneto vektorius kelio liestinės kryptimi:
.
Tangentinio pagreičio vektorius:
.
Normalus pagreičio vektorius:
.
Vieneto vektorius pagrindinės normalės kryptimi:
.
Trajektorijos kreivumo centro koordinatės:
.
Įveskime trečiąją koordinačių sistemos ašį, statmeną ašims ir . 3D sistemoje
;
.
Vieneto vektorius binormalia kryptimi:
.
judėjimo užduotys
Mes naudojame (4) lygtį ir paimame jos išvestinę laiko atžvilgiu
(8) su vienetiniais vektoriais yra greičio vektoriaus projekcijos koordinačių ašyse
Greičio projekcijos koordinačių ašyse apibrėžiamos kaip pirmosios atitinkamų koordinačių išvestinės.
Žinodami projekcijas, galite rasti vektoriaus modulį ir jo kryptį
,
(10)
Greičio nustatymas natūraliu būdu
judėjimo užduotys
Tegu pateikta materialaus taško trajektorija ir kreivinės koordinatės kitimo dėsnis. Tarkime, kad t Turėjo 1 tašką 
ir koordinatę s 1, tuo tarpu t 2 - koordinatė s 2. Per
koordinatė buvo padidinta 
, tada vidutinis taško greitis
.
Norėdami rasti greitį tam tikru laiko momentu, pereiname prie ribos
,
.
(12)
Taško greičio vektorius natūraliai nurodant judėjimą apibrėžiamas kaip pirmoji kreivinės koordinatės išvestinė.
taško pagreitis
Pagal materialaus taško pagreitį suprasti vektorinį dydį, apibūdinantį taško greičio vektoriaus dydžio ir krypties kitimo greitį laikui bėgant.
Taško pagreitis vektoriniu judesio nustatymo metodu
Apsvarstykite tašką dviem laiko taškais t 1
(
) Ir t 2
(
), Tada 
- laiko padidėjimas 
- greičio padidėjimas.
Vektorius 
visada guli judėjimo plokštumoje ir yra nukreipta į trajektorijos įgaubtą.
P 
vienas vidutinis taško pagreitis metu
t
suprasti dydį
.
(13)
Norėdami rasti pagreitį tam tikru laiko momentu, pereiname prie ribos
,
.
(14)
Taško pagreitis tam tikru metu apibrėžiamas kaip taško spindulio vektoriaus antroji laiko išvestinė arba pirmoji greičio vektoriaus išvestinė.
Pagreičio vektorius yra gretimoje plokštumoje ir yra nukreiptas į trajektorijos įdubimą.
Taško pagreitis judesio nustatymo koordinačių metodu
Judėjimo nurodymui panaudokime vektoriaus ir koordinačių ryšio lygtį
Ir paimkite antrą išvestinį iš jo
,
.
(15)
(15) lygtyje su vienetiniais vektoriais yra pagreičio vektoriaus projekcijos koordinačių ašyse
.
(16)
Pagreičio projekcijos koordinačių ašyse apibrėžiamos kaip pirmosios greičio projekcijų išvestinės arba kaip antrosios atitinkamų koordinačių išvestinės.
Pagreičio vektoriaus modulį ir kryptį galima rasti iš šių išraiškų
,
(17)
,
,
.
(18)
Taško pagreitis naudojant natūralų judėjimo nurodymo būdą
P 
Tegul taškas juda kreivine trajektorija. Apsvarstykite dvi jo pozicijas laiko akimirkomis t
(s, M, v) Ir t 1
(s 1 , M 1 , v 1).
Šiuo atveju pagreitis nustatomas per jo projekcijas į natūralios koordinačių sistemos ašis, judančias kartu su tašku M. Ašys nukreipiamos taip:
M - liestinė, nukreipta išilgai trajektorijos liestinės, į teigiamą atstumo atskaitą,
M n- pagrindinis normalus, nukreiptas išilgai normalios, esančios gretimoje plokštumoje, ir nukreiptas į trajektorijos įdubimą,
M b yra dvinormis, statmenas plokštumai M n ir su pirmosiomis ašimis sudaro dešinįjį trigubą.
Kadangi pagreičio vektorius yra gretimoje plokštumoje, tada a b = 0. Raskime pagreičio projekcijas ant kitų ašių.
.
(19)
Projektuokime (19) į koordinačių ašis
,
(20)
.
(21)
Nubrėžkite ašis per tašką M 1 lygiagrečiai ašims taške M ir raskite greičio projekcijas:
Kur - vadinamasis gretumo kampas.
Pakeiskite (22) į (20)
.
At t 0 0, cos 1 tada
.
(23)
Taško tangentinis pagreitis nustatomas pagal greičio pirmąją išvestinę arba kreivinės koordinatės antrąją laiko išvestinę.
Tangentinis pagreitis apibūdina greičio vektoriaus dydžio pokytį.
Pakeiskite (22) į (21)
.
Padauginkite skaitiklį ir vardiklį iš s gauti žinomas ribas
Kur 
(pirma žymi riba),
,
,
, Kur
- trajektorijos kreivumo spindulys.
Pakeitę apskaičiuotas ribas į (24), gauname
.
(25)
Normalus taško pagreitis nustatomas pagal greičio kvadrato santykį su trajektorijos kreivumo spinduliu duotame taške.
Normalus pagreitis apibūdina greičio vektoriaus pokytį kryptimi ir visada yra nukreiptas į trajektorijos įgaubtą.
Galiausiai gauname materialaus taško pagreičio projekcijas ant natūralios koordinačių sistemos ašių ir vektoriaus modulio
,
(26)
.
(27)
Taško judėjimas erdvėje gali būti laikomas duotu, jei žinomi jo trijų Dekarto koordinačių x, y, z kitimo dėsniai, kaip laiko funkcija. Tačiau kai kuriais erdvinio judėjimo atvejais materialūs taškai(pavyzdžiui, srityse, kurias riboja įvairių formų paviršiai), judėjimo lygtis Dekarto koordinatėse yra nepatogu, nes jos tampa pernelyg sudėtingos. Tokiais atvejais galima pasirinkti kitus tris nepriklausomus skaliarinius parametrus $q_1,(\ q)_2,\ \ q_3$, vadinamus kreivinėmis arba apibendrintomis koordinatėmis, kurios taip pat vienareikšmiškai nustato taško vietą erdvėje.
Taško M greitis, nurodant jo judėjimą kreivinėmis koordinatėmis, nustatomas kaip greičio komponentų, lygiagrečių koordinačių ašims, vektorinė suma:
\[\overrightarrow(v)=\frac(d\overrightarrow(r))(dt)=\frac(\partial \overrightarrow(r))(\partial q_1)\dot(q_1)+\frac(\partial \ overrightarrow(r))(\partial q_2)\dot(q_2)+\frac(\partial \overrightarrow(r))(\partial q_3)\dot(q_3)=v_(q_1)\overline(e_1)+v_( q_2)\overline(e_2)\+v_(q_3)\overline(e_3)\]
projekcijos vektorius greičiai atitinkamose koordinačių ašyse yra: $v_(q_i)=\overline(v\ )\cdot \overline(e_i)=H_i\dot(q_i)\ \ ,\ \ i=\overline(1,3)$
Čia $H_i=\left|(\left(\frac(\partial \overrightarrow(r))(\partial q_i)\right))_M\right|$ yra parametras, vadinamas i-tuoju Lame koeficientu ir yra lygus taško spindulio vektoriaus modulio vertės dalinei išvestinei i-osios kreivinės koordinatės, apskaičiuotos duotame taške M, atžvilgiu. Kiekvienas $\overline(e_i)$ vektorius turi kryptį, atitinkančią spindulio vektoriaus $r_i$ pabaigos taško judėjimas kaip i-osios apibendrintos koordinatės. Greičio modulis stačiakampėje kreivinėje koordinačių sistemoje gali būti apskaičiuojamas pagal priklausomybę:
Aukščiau pateiktose formulėse išvestinių ir Lame koeficientų reikšmės apskaičiuojamos pagal dabartinę taško M padėtį erdvėje.
taško koordinates sferinėje koordinačių sistemoje yra skaliariniai parametrai r, $(\mathbf \varphi ),\ (\mathbf \theta )$, skaičiuojami kaip parodyta pav. 1.
1 pav. Greičio vektorius sferinėmis koordinatėmis
Taško judėjimo lygčių sistema šiuo atveju yra tokia:
\[\left\( \begin(masyvas)(c) r=r(t) \\ \varphi =\varphi (t \\ \theta =\theta (t \end(masyvas) \right.\])
Ant pav. 1 paveiksle pavaizduotas spindulio vektorius r, nubrėžtas iš pradžios taško, kampai $(\mathbf \varphi )$ ir $(\mathbf \theta )$, taip pat nagrinėjamos sistemos koordinačių linijos ir ašys savavališkame taške M trajektorija. Matyti, kad koordinačių linijos $((\mathbf \varphi ))$ ir $((\mathbf \theta ))$ yra r spindulio rutulio paviršiuje. Ši kreivinė koordinačių sistema taip pat yra stačiakampė. Dekarto koordinatės gali būti išreikštos sferinėmis koordinatėmis taip:
Tada Lame koeficientai: $H_r=1;\ \ H_(\varphi )=rsin\varphi ;\ \ H_0=r$ ; taško greičio projekcijos sferinės koordinačių sistemos ašyse $v_r=\dot(r\ \ );$ $v_(\theta )=r\dot(\theta )$; $\ v_(\varphi )=r\dot(\varphi )sin\theta $ ir greičio vektoriaus modulis
Taško pagreitis sferinėje koordinačių sistemoje
\[\overrightarrow(a)=a_r(\overrightarrow(e))_r+a_(\varphi )(\overrightarrow(e))_(\varphi )+a_(\theta )(\overrightarrow(e))_( \theta ),\]
taško pagreičio projekcijos sferinės koordinačių sistemos ašyse
\ \
Pagreičio modulis $a=\sqrt(a^2_r+a^2_(\varphi )+a^2_(\theta ))$
1 užduotis
Taškas juda išilgai sferos susikirtimo linijos ir cilindras pagal lygtis: r = R, $\varphi $ = kt/2, $\theta $ = kt/2 , (r, $\varphi $, $\theta $ --- sferinės koordinatės). Raskite taško greičio modulį ir projekcijas sferinės koordinačių sistemos ašyse.
Raskime greičio vektoriaus projekcijas ant sferinių koordinačių ašių:
Greičio modulis $v=\sqrt(v^2_r+v^2_(\varphi )+v^2_(\theta ))=R\frac(k)(2)\sqrt((sin)^2\frac(kt )(2)+1)$
2 užduotis
Naudodamiesi 1 uždavinio sąlyga, nustatykite taško pagreičio modulį.
Raskime pagreičio vektoriaus projekcijas ant sferinių koordinačių ašių:
\ \ \
Pagreičio modulis $a=\sqrt(a^2_r+a^2_(\varphi )+a^2_(\theta ))=R\frac(k^2)(4)\sqrt(4+(sin)^2 \frac(kt)(2))$
