त्रिकोणमितीय अभिव्यक्तियों की पहचान परिवर्तन। पाठ "त्रिकोणमितीय व्यंजकों का सरलीकरण" त्रिकोणमितीय व्यंजकों को सरल कैसे करें

वीडियो पाठ "त्रिकोणमितीय अभिव्यक्तियों का सरलीकरण" को बुनियादी त्रिकोणमितीय पहचान का उपयोग करके त्रिकोणमितीय समस्याओं को हल करने में छात्रों के कौशल को बनाने के लिए डिज़ाइन किया गया है। वीडियो पाठ के दौरान, त्रिकोणमितीय सर्वसमिकाओं के प्रकारों पर विचार किया जाता है, उनका उपयोग करके समस्याओं को हल करने के उदाहरण। दृश्य साधनों का उपयोग करना, शिक्षक के लिए पाठ के उद्देश्यों को प्राप्त करना आसान होता है। सामग्री की एक विशद प्रस्तुति महत्वपूर्ण बिंदुओं को याद रखने में योगदान करती है। एनीमेशन प्रभाव और आवाज अभिनय का उपयोग आपको सामग्री को समझाने के चरण में शिक्षक को पूरी तरह से बदलने की अनुमति देता है। इस प्रकार, गणित के पाठों में इस दृश्य सहायता का उपयोग करके शिक्षक शिक्षण की प्रभावशीलता को बढ़ा सकता है।

वीडियो पाठ की शुरुआत में, इसके विषय की घोषणा की जाती है। फिर पहले अध्ययन किए गए त्रिकोणमितीय सर्वसमिकाओं को याद किया जाता है। स्क्रीन समानता प्रदर्शित करती है sin 2 t+cos 2 t=1, tg t=sin t/cos t, जहां t≠π/2+πk kϵZ के लिए, ctg t=cos t/sin t, t≠πk के लिए सही, जहाँ kϵZ, tan t · ctg t=1, t≠πk/2 पर, जहाँ kϵZ, मूल त्रिकोणमितीय सर्वसमिकाएँ कहलाती हैं। यह ध्यान दिया जाता है कि इन पहचानों का उपयोग अक्सर उन समस्याओं को हल करने में किया जाता है जहां समानता साबित करना या अभिव्यक्ति को सरल बनाना आवश्यक होता है।

इसके अलावा, समस्याओं को हल करने में इन पहचानों के उपयोग के उदाहरणों पर विचार किया जाता है। सबसे पहले, अभिव्यक्ति को सरल बनाने की समस्याओं को हल करने पर विचार करने का प्रस्ताव है। उदाहरण 1 में, cos 2 t-cos 4 t+ sin 4 t व्यंजक को सरल बनाना आवश्यक है। उदाहरण को हल करने के लिए, उभयनिष्ठ गुणनखंड cos 2 t को पहले कोष्ठक में रखा गया है। कोष्ठक में इस तरह के परिवर्तन के परिणामस्वरूप, अभिव्यक्ति 1-cos 2 t प्राप्त होती है, जिसका मान त्रिकोणमिति की मूल पहचान से sin 2 t के बराबर होता है। व्यंजक के परिवर्तन के बाद, यह स्पष्ट है कि कोष्ठकों से एक और सामान्य गुणनखंड sin 2 t निकाला जा सकता है, जिसके बाद व्यंजक sin 2 t (sin 2 t + cos 2 t) का रूप ले लेता है। उसी मूल पहचान से, हम 1 के बराबर कोष्ठक में व्यंजक का मान निकालते हैं। सरलीकरण के परिणामस्वरूप, हमें cos 2 t-cos 4 t+ sin 4 t= sin 2 t प्राप्त होता है।

उदाहरण 2 में, व्यंजक लागत/(1- सिंट)+ लागत/(1+ सिंट) को भी सरल बनाने की आवश्यकता है। चूंकि व्यंजक लागत दोनों भिन्नों के अंशों में है, इसलिए इसे एक सामान्य कारक के रूप में विभाजित किया जा सकता है। फिर कोष्ठकों में अंशों को गुणा करके एक सामान्य हर में घटा दिया जाता है (1- sint)(1+ sint)। समान पदों को कम करने के बाद, 2 अंश में रहता है, और 1 - sin 2 t हर में। स्क्रीन के दाईं ओर, मूल त्रिकोणमितीय पहचान sin 2 t+cos 2 t=1 याद किया जाता है। इसका उपयोग करते हुए, हम भिन्न cos 2 t का हर पाते हैं। अंश को कम करने के बाद, हमें अभिव्यक्ति लागत / (1- सिंट) + लागत / (1 + सिंट) \u003d 2 / लागत का सरलीकृत रूप मिलता है।

इसके बाद, हम सर्वसमिकाओं को सिद्ध करने के उदाहरणों पर विचार करते हैं जिसमें त्रिकोणमिति की मूल सर्वसमिकाओं के बारे में अर्जित ज्ञान को लागू किया जाता है। उदाहरण 3 में, सर्वसमिका को सिद्ध करना आवश्यक है (tg 2 t-sin 2 t)·ctg 2 t=sin 2 t। स्क्रीन का दाहिना भाग तीन पहचानों को प्रदर्शित करता है जिनकी आवश्यकता प्रमाण के लिए होगी - tg t ctg t=1, ctg t=cos t/sin t और tg t=sin t/cos t प्रतिबंधों के साथ। पहचान साबित करने के लिए, पहले कोष्ठक खोले जाते हैं, जिसके बाद एक उत्पाद बनता है जो मुख्य त्रिकोणमितीय पहचान tg t·ctg t=1 की अभिव्यक्ति को दर्शाता है। फिर, कोटैंजेंट की परिभाषा से पहचान के अनुसार, सीटीजी 2 टी रूपांतरित हो जाता है। परिवर्तनों के परिणामस्वरूप, व्यंजक 1-cos 2 t प्राप्त होता है। मूल पहचान का उपयोग करके, हम व्यंजक का मान ज्ञात करते हैं। इस प्रकार, यह साबित हो गया है कि (tg 2 t-sin 2 t)·ctg 2 t=sin 2 t।

उदाहरण 4 में, यदि tg t+ctg t=6 है, तो आपको व्यंजक tg 2 t+ctg 2 t का मान ज्ञात करना होगा। व्यंजक का मूल्यांकन करने के लिए, समीकरण के दाएँ और बाएँ पक्ष (tg t+ctg t) 2 =6 2 पहले वर्ग हैं। संक्षिप्त गुणन सूत्र स्क्रीन के दाईं ओर प्रदर्शित होता है। व्यंजक के बाईं ओर कोष्ठक खोलने के बाद, योग tg 2 t+2 tg t ctg t+ctg 2 t बनता है, जिसके परिवर्तन के लिए त्रिकोणमितीय सर्वसमिकाओं में से एक tg t ctg t=1 लागू किया जा सकता है, जिसका रूप स्क्रीन के दाईं ओर याद किया जाता है। परिवर्तन के बाद, समानता tg 2 t+ctg 2 t=34 प्राप्त की जाती है। समानता का बायाँ भाग समस्या की स्थिति से मेल खाता है, इसलिए उत्तर 34 है। समस्या हल हो गई है।

पारंपरिक स्कूल गणित पाठ में उपयोग के लिए वीडियो पाठ "त्रिकोणमितीय अभिव्यक्तियों को सरल बनाना" की सिफारिश की जाती है। साथ ही, दूरस्थ शिक्षा प्रदान करने वाले शिक्षक के लिए सामग्री उपयोगी होगी। त्रिकोणमितीय समस्याओं को हल करने में एक कौशल बनाने के लिए।

पाठ व्याख्या:

"त्रिकोणमितीय अभिव्यक्तियों का सरलीकरण"।

समानता

1)sin 2 t + cos 2 t = 1 (साइन स्क्वेर्ड ते प्लस कोसाइन स्क्वेयर ते एक के बराबर)

2) tgt =, t + πk, kϵZ पर (te की स्पर्शरेखा, te की ज्या और te की कोज्या के अनुपात के बराबर होती है, जब te, pi बटा दो जोड़ pi ka के बराबर नहीं होता है, ka, zet से संबंधित होता है)

3) ctgt =, t k, kϵZ पर (te का कोटैंजेंट, te की कोज्या और te की ज्या के अनुपात के बराबर होता है, जब te ka के शिखर के बराबर नहीं होता है, जो कि z से संबंधित है)।

4)tgt ctgt = 1 t , kϵZ . के लिए

मूल त्रिकोणमितीय सर्वसमिकाएँ कहलाती हैं।

अक्सर इनका उपयोग त्रिकोणमितीय व्यंजकों को सरल और सिद्ध करने में किया जाता है।

त्रिकोणमितीय व्यंजकों को सरल करते समय इन सूत्रों का उपयोग करने के उदाहरणों पर विचार करें।

उदाहरण 1. व्यंजक को सरल कीजिए: cos 2 t - cos 4 t + sin 4 t। (अभिव्यक्ति एक कोज्या चुकता ते घटा कोज्या ते की चौथी डिग्री का जोड़ ते की चौथी डिग्री का ज्या)।

समाधान। cos 2 t - cos 4 t + sin 4 t = cos 2 t∙ (1 - cos 2 t) + sin 4 t = cos 2 t sin 2 t + sin 4 t = sin 2 t (cos 2 t + sin 2 टी) = पाप 2 टी 1= पाप 2 टी

(हम उभयनिष्ठ गुणनखंड कोसाइन वर्ग ते निकालते हैं, कोष्ठक में हमें एकता और कोसाइन ते के वर्ग के बीच का अंतर मिलता है, जो पहली पहचान से साइन ते के वर्ग के बराबर होता है। हमें चौथे की ज्या का योग मिलता है। उत्पाद की डिग्री ते कोसाइन वर्ग ते और साइन वर्ग ते। सामान्य कारक साइन वर्ग ते कोष्ठक के बाहर निकाला जाएगा, कोष्ठक में हमें कोसाइन और साइन के वर्गों का योग मिलता है, जो मूल त्रिकोणमितीय के अनुसार होता है पहचान, 1 के बराबर है। परिणामस्वरूप, हमें साइन ते का वर्ग मिलता है)।

उदाहरण 2. व्यंजक को सरल कीजिए: + .

(अभिव्यक्ति पहली कोसाइन ते के अंश में दो अंशों का योग हो, हर में एक घटा साइन ते, दूसरे एक प्लस साइन ते के हर में दूसरे कोसाइन ते के अंश में)।

(हम सामान्य गुणक कोसाइन ते को कोष्ठक से बाहर निकालते हैं, और कोष्ठक में हम इसे एक सामान्य हर में लाते हैं, जो एक ऋण साइन ते बटा एक प्लस साइन ते का गुणनफल होता है।

अंश में हमें मिलता है: एक जमा साइन ते जमा एक घटा साइन ते, हम समान देते हैं, अंश समान लाने के बाद दो के बराबर होता है।

हर में, आप संक्षिप्त गुणन सूत्र (वर्गों का अंतर) लागू कर सकते हैं और साइन ते की इकाई और वर्ग के बीच का अंतर प्राप्त कर सकते हैं, जो कि मूल त्रिकोणमितीय पहचान के अनुसार है

कोसाइन ते के वर्ग के बराबर है। कोसाइन ते द्वारा कम करने के बाद, हमें अंतिम उत्तर मिलता है: दो कोसाइन ते से विभाजित)।

त्रिकोणमितीय अभिव्यक्तियों के प्रमाण में इन सूत्रों के उपयोग के उदाहरणों पर विचार करें।

उदाहरण 3. सर्वसमिका सिद्ध करें (tg 2 t - sin 2 t) ctg 2 t \u003d sin 2 t (ते की स्पर्शरेखा के वर्गों और ते की ज्या और के कोटेंगेंट के वर्ग के बीच अंतर का गुणनफल ते, ते की ज्या के वर्ग के बराबर है)।

सबूत।

आइए समानता के बाएँ पक्ष को रूपांतरित करें:

(टीजी 2 टी - पाप 2 टी) सीटीजी 2 टी = टीजी 2 टी सीटीजी 2 टी - पाप 2 टी सीटीजी 2 टी = 1 - पाप 2 टी ∙ सीटीजी 2 टी = 1 - पाप 2 टी ∙ = 1 - क्योंकि 2 टी = पाप 2 टी

(आइए कोष्ठक खोलें, पहले प्राप्त संबंध से यह ज्ञात होता है कि ते के स्पर्शरेखा द्वारा ते के स्पर्शरेखा के वर्गों का गुणनफल एक के बराबर होता है। याद रखें कि ते का कोसाइन के अनुपात के बराबर है ते से ते की ज्या है, जिसका अर्थ है कि कोटैंजेंट का वर्ग ते की ज्या के वर्ग से ते की कोज्या के वर्ग का अनुपात है।

ते के ज्या वर्ग से घटाने के बाद, हम ते के वर्ग की एकता और कोज्या के बीच का अंतर प्राप्त करते हैं, जो ते के वर्ग की ज्या के बराबर होता है)। क्यू.ई.डी.

उदाहरण 4. व्यंजक tg 2 t + ctg 2 t का मान ज्ञात कीजिए यदि tgt + ctgt = 6 है।

(यदि टेंगेंट और कोटैंजेंट का योग छह है, तो ते की स्पर्शरेखा और ते के कोटैंजेंट के वर्गों का योग)।

समाधान। (टीजीटी + सीटीजीटी) 2 = 6 2

टीजी 2 टी + 2 टीजीटी ∙सीटीजीटी + सीटीजी 2 टी = 36

टीजी 2 टी + 2 + सीटीजी 2 टी = 36

टीजी 2 टी + सीटीजी 2 टी = 36-2

टीजी 2 टी + सीटीजी 2 टी = 34

आइए मूल समानता के दोनों भागों को वर्गाकार करें:

(tgt + ctgt) 2 = 6 2 (te की स्पर्श रेखा और te की कोटंगेंट के योग का वर्ग छह वर्ग है)। संक्षिप्त गुणन सूत्र को याद करें: दो राशियों के योग का वर्ग पहले जोड़ के वर्ग के बराबर होता है जो पहले और दूसरे के गुणनफल का दुगुना होता है और दूसरे का वर्ग। (a+b) 2 =a 2 +2ab+b 2 हमें tg 2 t + 2 ∙ tgt ∙ctgt + ctg 2 t = 36 प्राप्त होता है।

चूँकि ते की स्पर्श रेखा और ते की कोटेंगेंट का गुणनफल एक के बराबर होता है, तो tg 2 t + 2 + ctg 2 t \u003d 36 (te की स्पर्शरेखा के वर्गों का योग और te और दो की कोटेंजेंट है छत्तीस),

वोरोनकोवा ओल्गा इवानोव्ना

MBOU "माध्यमिक विद्यालय"

नंबर 18"

एंगेल्स, सेराटोव क्षेत्र।

गणित के शिक्षक।

"त्रिकोणमितीय व्यंजक और उनके परिवर्तन"

परिचय …………………………………………………………………….3

अध्याय 1 त्रिकोणमितीय अभिव्यक्तियों के परिवर्तन के उपयोग के लिए कार्यों का वर्गीकरण …………………………………………………………5

1.1. गणना कार्य त्रिकोणमितीय व्यंजकों का मान……….5

1.2.त्रिकोणमितीय अभिव्यक्तियों को सरल बनाने के लिए कार्य .... 7

1.3. संख्यात्मक त्रिकोणमितीय अभिव्यक्तियों के रूपांतरण के लिए कार्य ... ..7

1.4 मिश्रित कार्य ………………………………………………………… 9

अध्याय 2

2.1 ग्रेड 10 में विषयगत दोहराव ………………………………………… 11

टेस्ट 1 ……………………………………………………………………………..12

टेस्ट 2………………………………………………………………………………………..13

टेस्ट 3………………………………………………………………………………………..14

2.2 ग्रेड 11 में अंतिम पुनरावृत्ति……………………………………………15

टेस्ट 1 ………………………………………………………………………………..17

टेस्ट 2………………………………………………………………………………………..17

टेस्ट 3………………………………………………………………………………………..18

निष्कर्ष। ………………………………………………………………………………… 19

प्रयुक्त साहित्य की सूची ……………………………………………….20

परिचय।

आज की परिस्थितियों में, सबसे महत्वपूर्ण प्रश्न है: "हम छात्रों के ज्ञान में कुछ अंतराल को खत्म करने में कैसे मदद कर सकते हैं और उन्हें परीक्षा में संभावित गलतियों के खिलाफ चेतावनी दे सकते हैं?" इस मुद्दे को हल करने के लिए, छात्रों से कार्यक्रम सामग्री की औपचारिक आत्मसात नहीं, बल्कि इसकी गहरी और सचेत समझ, मौखिक गणना और परिवर्तनों की गति का विकास, साथ ही सरलतम को हल करने के लिए कौशल का विकास करना आवश्यक है। समस्याएं "मन में"। छात्रों को यह विश्वास दिलाना आवश्यक है कि केवल एक सक्रिय स्थिति की उपस्थिति में, गणित के अध्ययन में, व्यावहारिक कौशल, कौशल और उनके उपयोग के अधीन, वास्तविक सफलता पर भरोसा किया जा सकता है। कक्षा 10-11 में वैकल्पिक विषयों सहित परीक्षा की तैयारी के लिए हर अवसर का उपयोग करना, छात्रों के साथ जटिल कार्यों का नियमित रूप से विश्लेषण करना, उन्हें कक्षा और अतिरिक्त कक्षाओं में हल करने का सबसे तर्कसंगत तरीका चुनना आवश्यक है।में सकारात्मक परिणामविशिष्ट समस्याओं को हल करने के क्षेत्र को प्राप्त किया जा सकता है यदि गणित के शिक्षक, बनाकरछात्रों का अच्छा बुनियादी प्रशिक्षण, हमारे सामने खुलने वाली समस्याओं को हल करने के नए तरीकों की तलाश करने के लिए, सक्रिय रूप से प्रयोग करने के लिए, आधुनिक शैक्षणिक तकनीकों, विधियों, तकनीकों को लागू करने के लिए जो छात्रों के प्रभावी आत्म-प्राप्ति और आत्मनिर्णय के लिए अनुकूल परिस्थितियों का निर्माण करते हैं। नई सामाजिक स्थितियां।

त्रिकोणमिति स्कूली गणित पाठ्यक्रम का एक अभिन्न अंग है। त्रिकोणमिति में अच्छा ज्ञान और मजबूत कौशल गणितीय संस्कृति के पर्याप्त स्तर का प्रमाण हैं, गणित, भौतिकी के सफल अध्ययन के लिए एक अनिवार्य शर्त, और कई तकनीकीअनुशासन।

काम की प्रासंगिकता. स्कूल के स्नातकों का एक महत्वपूर्ण हिस्सा गणित के इस महत्वपूर्ण खंड में साल-दर-साल बहुत खराब तैयारी दिखाता है, जैसा कि पिछले वर्षों के परिणामों (2011-48.41%, 2012-51.05 में पूरा होने का प्रतिशत) के परिणामों से प्रमाणित होता है। एकीकृत राज्य परीक्षा ने दिखाया कि छात्र इस विशेष खंड के असाइनमेंट को पूरा करते समय कई गलतियाँ करते हैं या ऐसे असाइनमेंट बिल्कुल भी नहीं करते हैं। एक में त्रिकोणमिति में राज्य परीक्षा के प्रश्न लगभग तीन प्रकार के कार्यों में मिलते हैं। यह कार्य B5 में सबसे सरल त्रिकोणमितीय समीकरणों का समाधान है, और कार्य B7 में त्रिकोणमितीय अभिव्यक्तियों के साथ काम करता है, और कार्य B14 में त्रिकोणमितीय कार्यों का अध्ययन, साथ ही साथ कार्य B12, जिसमें भौतिक घटना का वर्णन करने वाले सूत्र हैं और त्रिकोणमितीय कार्य शामिल हैं . और यह केवल बी कार्यों का हिस्सा है! लेकिन जड़ों C1 के चयन के साथ पसंदीदा त्रिकोणमितीय समीकरण भी हैं, और "बहुत पसंदीदा नहीं" ज्यामितीय कार्य C2 और C4 हैं।

उद्देश्य. त्रिकोणमितीय अभिव्यक्तियों के परिवर्तन के लिए समर्पित USE कार्यों B7 की सामग्री का विश्लेषण करें और परीक्षणों में उनकी प्रस्तुति के अनुसार कार्यों को वर्गीकृत करें।

कार्य में दो अध्याय होते हैं, परिचय और निष्कर्ष। परिचय कार्य की प्रासंगिकता पर जोर देता है। पहला अध्याय एकीकृत राज्य परीक्षा (2012) के परीक्षण कार्यों में त्रिकोणमितीय अभिव्यक्तियों के परिवर्तनों के उपयोग के लिए कार्यों का वर्गीकरण प्रदान करता है।

दूसरे अध्याय में, कक्षा 10, 11 में "त्रिकोणमितीय अभिव्यक्तियों का परिवर्तन" विषय की पुनरावृत्ति के संगठन पर विचार किया जाता है और इस विषय पर परीक्षण विकसित किए जाते हैं।

संदर्भों की सूची में 17 स्रोत शामिल हैं।

अध्याय 1. त्रिकोणमितीय अभिव्यक्तियों के परिवर्तनों के उपयोग के लिए कार्यों का वर्गीकरण।

माध्यमिक (पूर्ण) शिक्षा के मानक और छात्रों के प्रशिक्षण के स्तर की आवश्यकताओं के अनुसार, त्रिकोणमिति की मूल बातों के ज्ञान के लिए कार्यों को आवश्यकताओं के कोडिफायर में शामिल किया गया है।

त्रिकोणमिति की मूल बातें सीखना सबसे प्रभावी होगा जब:

छात्रों को पूर्व में पढ़ी गई सामग्री को दोहराने के लिए सकारात्मक रूप से प्रेरित किया जाएगा;

शैक्षिक प्रक्रिया में एक छात्र-केंद्रित दृष्टिकोण लागू किया जाएगा;

कार्यों की एक प्रणाली लागू की जाएगी जो छात्रों के ज्ञान के विस्तार, गहनता, व्यवस्थितकरण में योगदान करती है;

उन्नत शैक्षणिक तकनीकों का उपयोग किया जाएगा।

परीक्षा की तैयारी के लिए साहित्य और इंटरनेट संसाधनों का विश्लेषण करने के बाद, हमने कार्यों के संभावित वर्गीकरणों में से एक प्रस्तावित किया है B7 (KIM USE 2012-त्रिकोणमिति): गणना के लिए कार्यत्रिकोणमितीय अभिव्यक्तियों के मूल्य; के लिए कार्यसंख्यात्मक त्रिकोणमितीय अभिव्यक्तियों का रूपांतरण; शाब्दिक त्रिकोणमितीय अभिव्यक्तियों के परिवर्तन के लिए कार्य; मिश्रित कार्य।

1.1. गणना कार्य त्रिकोणमितीय अभिव्यक्तियों के मूल्य।

सबसे सामान्य प्रकार की सरल त्रिकोणमिति समस्याओं में से एक त्रिकोणमितीय कार्यों के मूल्यों की गणना उनमें से एक के मूल्य से होती है:

क) मूल त्रिकोणमितीय पहचान और उसके उपफलों का उपयोग।

उदाहरण 1 . खोजें अगर
तथा
.

समाधान।
,
,

इसलिये , फिर
.

उत्तर।

उदाहरण 2 . पाना
, यदि
तथा ।

समाधान।
,
,
.

इसलिये , फिर
.

उत्तर। .

b) द्विकोण सूत्रों का उपयोग।

उदाहरण 3 . पाना
, यदि
.

समाधान। , .

उत्तर।
.

उदाहरण 4 . व्यंजक का मान ज्ञात कीजिए
.

समाधान। .

उत्तर।
.

1. पाना , यदि

तथा

. उत्तर। -0.2

2. पाना , यदि
तथा
. उत्तर। 0.4

3. पाना

, यदि । उत्तर। -12.884. पाना

, यदि

. उत्तर। -0.845. व्यंजक का मान ज्ञात कीजिए:

. उत्तर। 66. व्यंजक का मान ज्ञात कीजिए

.उत्तर। -19

1.2.त्रिकोणमितीय अभिव्यक्तियों को सरल बनाने के लिए कार्य। न्यूनीकरण सूत्रों में छात्रों को अच्छी तरह से महारत हासिल होनी चाहिए, क्योंकि उनका उपयोग आगे ज्यामिति, भौतिकी और अन्य संबंधित विषयों के पाठों में किया जाएगा।

उदाहरण 5 . अभिव्यक्तियों को सरल बनाएं
.

समाधान। .

उत्तर।
.

स्वतंत्र समाधान के लिए कार्य:

1. व्यंजक को सरल कीजिए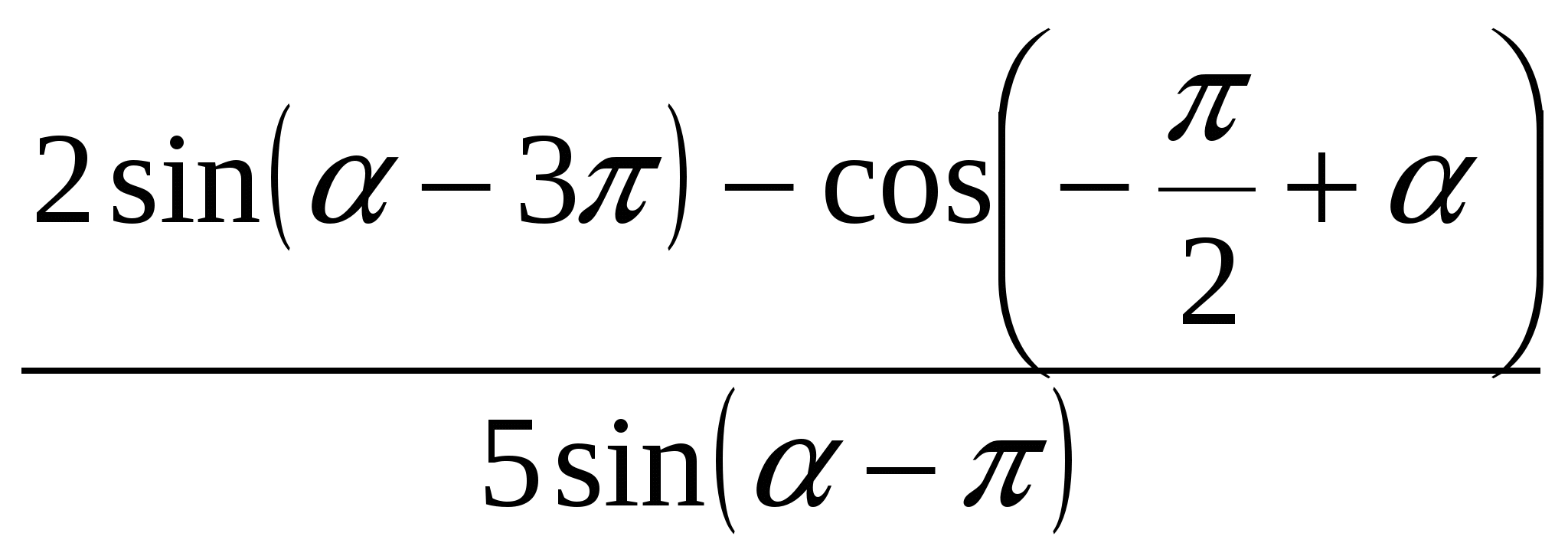

. उत्तर। 0.62. पाना

, यदि

तथा. उत्तर। 10.563. व्यंजक का मान ज्ञात कीजिए

, यदि

. उत्तर। 2

1.3. संख्यात्मक त्रिकोणमितीय अभिव्यक्तियों के परिवर्तन के लिए कार्य।

संख्यात्मक त्रिकोणमितीय अभिव्यक्तियों को परिवर्तित करने के लिए कार्यों के कौशल और क्षमताओं को विकसित करते समय, त्रिकोणमितीय कार्यों के मूल्यों की तालिका, समता के गुणों और त्रिकोणमितीय कार्यों की आवधिकता के ज्ञान पर ध्यान देना चाहिए।

a) कुछ कोणों के लिए त्रिकोणमितीय फलनों के सटीक मानों का उपयोग करना।

उदाहरण 6 . गणना
.

समाधान।
.

उत्तर।
.

b) समता के गुणों का उपयोग करना त्रिकोणमितीय फलन।

उदाहरण 7 . गणना
.

समाधान। .

उत्तर।

में) आवधिकता गुणों का उपयोग करनात्रिकोणमितीय फलन।

उदाहरण 8 . व्यंजक का मान ज्ञात कीजिए
.

समाधान। .

उत्तर।
.

स्वतंत्र समाधान के लिए कार्य:

1. व्यंजक का मान ज्ञात कीजिए

. उत्तर। -40.52. व्यंजक का मान ज्ञात कीजिए

. उत्तर। 17

3. व्यंजक का मान ज्ञात कीजिए
. उत्तर। 6

. उत्तर। -24

उत्तर। -64

1.4 मिश्रित कार्य।

प्रमाणन के परीक्षण रूप में बहुत महत्वपूर्ण विशेषताएं हैं, इसलिए एक ही समय में कई त्रिकोणमितीय सूत्रों के उपयोग से जुड़े कार्यों पर ध्यान देना महत्वपूर्ण है।

उदाहरण 9 पाना
, यदि
.

समाधान।
.

उत्तर।
.

उदाहरण 10 . पाना
, यदि
तथा
.

समाधान। .

इसलिये , फिर
.

उत्तर।
.

उदाहरण 11. पाना
, यदि ।

समाधान। , ,
,
,
,
,
.

उत्तर।

उदाहरण 12. गणना
.

समाधान। .

उत्तर।
.

उदाहरण 13 व्यंजक का मान ज्ञात कीजिए
, यदि
.

समाधान। .

उत्तर।
.

स्वतंत्र समाधान के लिए कार्य:

1. पाना

, यदि

. उत्तर। -1.75
2. पाना

, यदि

. उत्तर। 33. खोजें

, यदि ।उत्तर। 0.254. व्यंजक का मान ज्ञात कीजिए

, यदि

. उत्तर। 0.35. व्यंजक का मान ज्ञात कीजिए

, यदि

. उत्तर। 5

अध्याय 2. "त्रिकोणमितीय अभिव्यक्तियों का परिवर्तन" विषय की अंतिम पुनरावृत्ति के पद्धतिगत पहलू संगठन।

अकादमिक प्रदर्शन के और सुधार में योगदान देने वाले सबसे महत्वपूर्ण मुद्दों में से एक, छात्रों के बीच गहन और ठोस ज्ञान की उपलब्धि पहले से अध्ययन की गई सामग्री को दोहराने का मुद्दा है। अभ्यास से पता चलता है कि 10 वीं कक्षा में विषयगत पुनरावृत्ति को व्यवस्थित करना अधिक समीचीन है; 11 वीं कक्षा में - अंतिम पुनरावृत्ति।

2.1. 10 वीं कक्षा में विषयगत दोहराव।

गणितीय सामग्री पर काम करने की प्रक्रिया में, प्रत्येक पूर्ण विषय या पाठ्यक्रम के एक पूरे खंड की पुनरावृत्ति विशेष रूप से महत्वपूर्ण हो जाती है।

विषयगत पुनरावृत्ति के साथ, विषय पर छात्रों के ज्ञान को इसके पारित होने के अंतिम चरण में या एक विराम के बाद व्यवस्थित किया जाता है।

विषयगत पुनरावृत्ति के लिए, विशेष पाठ आवंटित किए जाते हैं, जिस पर एक विशेष विषय की सामग्री केंद्रित और सामान्यीकृत होती है।

इस बातचीत में छात्रों की व्यापक भागीदारी के साथ बातचीत के माध्यम से पाठ में दोहराव किया जाता है। उसके बाद, छात्रों को एक निश्चित विषय को दोहराने का कार्य दिया जाता है और चेतावनी दी जाती है कि परीक्षणों पर क्रेडिट कार्य होगा।

किसी विषय पर एक परीक्षा में उसके सभी मुख्य प्रश्न शामिल होने चाहिए। काम पूरा होने के बाद, विशिष्ट त्रुटियों का विश्लेषण किया जाता है और उन्हें खत्म करने के लिए पुनरावृत्ति का आयोजन किया जाता है।

विषयगत दोहराव के पाठों के लिए, हम विकसित टेस्ट पेपर"त्रिकोणमितीय अभिव्यक्तियों का रूपांतरण" विषय पर।

टेस्ट #1

टेस्ट #2

टेस्ट #3

उत्तर तालिका

परीक्षण

2.2. 11वीं कक्षा में अंतिम पुनरावृत्ति।

अंतिम पुनरावृत्ति गणित पाठ्यक्रम के मुख्य मुद्दों के अध्ययन के अंतिम चरण में की जाती है और इस खंड या संपूर्ण पाठ्यक्रम के लिए शैक्षिक सामग्री के अध्ययन के तार्किक संबंध में की जाती है।

शैक्षिक सामग्री की अंतिम पुनरावृत्ति के निम्नलिखित लक्ष्य हैं:

1. इसकी तार्किक संरचना को स्पष्ट करने और विषय और अंतर विषय संबंधों के भीतर एक प्रणाली का निर्माण करने के लिए संपूर्ण प्रशिक्षण पाठ्यक्रम की सामग्री को सक्रिय करना।

2. पुनरावृत्ति की प्रक्रिया में पाठ्यक्रम के मुख्य मुद्दों पर छात्रों के ज्ञान को गहरा करना और, यदि संभव हो तो विस्तार करना।

सभी स्नातकों के लिए गणित में अनिवार्य परीक्षा के संदर्भ में, यू.एस.ई. का क्रमिक परिचय शिक्षकों को पाठ तैयार करने और संचालित करने के लिए एक नया दृष्टिकोण लेता है, यह सुनिश्चित करने की आवश्यकता को ध्यान में रखते हुए कि सभी छात्र बुनियादी स्तर पर शैक्षिक सामग्री में महारत हासिल करते हैं, साथ ही विश्वविद्यालय में प्रवेश के लिए उच्च अंक प्राप्त करने में रुचि रखने वाले प्रेरित छात्रों के लिए अवसर, सामग्री को उच्च और उच्च स्तर पर महारत हासिल करने में गतिशील उन्नति।

अंतिम पुनरावृत्ति के पाठों में, आप निम्नलिखित कार्यों पर विचार कर सकते हैं:

उदाहरण 1 . अभिव्यक्ति के मूल्य की गणना करें।समाधान। =

= =

=0,5. उत्तर। 0.5. उदाहरण 2 सबसे बड़ा पूर्णांक मान निर्दिष्ट करें जो व्यंजक ले सकता है

समाधान। इसलिये
खंड से संबंधित कोई भी मान ले सकते हैं [-1; 1], फिर
खंड का कोई भी मान लेता है [-0.4; 0.4], इसलिए। व्यंजक का पूर्णांक मान एक है - संख्या 4।

उत्तर - 4 उदाहरण 3 . व्यंजक को सरल कीजिए

हल: आइए घनों के योग के गुणनखंड के लिए सूत्र का उपयोग करें: . हमारे पास है

हमारे पास है:
.

उत्तर 1

उदाहरण 4 गणना
.

समाधान। .

उत्तर: 0.28

अंतिम पुनरावृत्ति के पाठों के लिए, हम "त्रिकोणमितीय व्यंजकों का रूपांतरण" विषय पर विकसित परीक्षण प्रस्तुत करते हैं।

1 . से अनधिक सबसे बड़ा पूर्णांक निर्दिष्ट करें

निष्कर्ष.

इस विषय पर प्रासंगिक कार्यप्रणाली साहित्य के माध्यम से काम करने के बाद, हम यह निष्कर्ष निकाल सकते हैं कि स्कूल गणित पाठ्यक्रम में त्रिकोणमितीय परिवर्तनों से संबंधित कार्यों को हल करने की क्षमता और कौशल बहुत महत्वपूर्ण है।

किए गए कार्य के दौरान, B7 कार्यों का वर्गीकरण किया गया था। 2012 के सीएमएम में सबसे अधिक बार उपयोग किए जाने वाले त्रिकोणमितीय सूत्रों पर विचार किया जाता है। समाधान के साथ कार्यों के उदाहरण दिए गए हैं। परीक्षा की तैयारी में ज्ञान की पुनरावृत्ति और व्यवस्थितकरण को व्यवस्थित करने के लिए विभेदक परीक्षण विकसित किए गए हैं।

विचार करते हुए शुरू किए गए काम को जारी रखना उचित है कार्य B5 में सबसे सरल त्रिकोणमितीय समीकरणों का समाधान, कार्य B14 में त्रिकोणमितीय कार्यों का अध्ययन, कार्य B12, जिसमें भौतिक घटनाओं का वर्णन करने वाले और त्रिकोणमितीय कार्यों वाले सूत्र हैं।

अंत में, मैं यह नोट करना चाहूंगा कि परीक्षा उत्तीर्ण करने की प्रभावशीलता काफी हद तक इस बात से निर्धारित होती है कि सभी श्रेणियों के छात्रों के साथ शिक्षा के सभी स्तरों पर तैयारी प्रक्रिया को प्रभावी ढंग से कैसे व्यवस्थित किया जाता है। और अगर हम छात्रों की स्वतंत्रता, जिम्मेदारी और उनके बाद के जीवन में सीखने को जारी रखने के लिए तत्परता का प्रबंधन करते हैं, तो हम न केवल राज्य और समाज के आदेश को पूरा करेंगे, बल्कि अपने आत्म-सम्मान को भी बढ़ाएंगे।

शैक्षिक सामग्री की पुनरावृत्ति के लिए शिक्षक से रचनात्मक कार्य की आवश्यकता होती है। उसे दोहराव के प्रकारों के बीच एक स्पष्ट संबंध प्रदान करना चाहिए, पुनरावृत्ति की एक गहन सोची-समझी प्रणाली को लागू करना चाहिए। दोहराव के आयोजन की कला में महारत हासिल करना शिक्षक का कार्य है। छात्रों के ज्ञान की ताकत काफी हद तक इसके समाधान पर निर्भर करती है।

साहित्य।

वायगोडस्की हां। हां।, प्राथमिक गणित की पुस्तिका। -एम .: नौका, 1970।

बीजगणित में बढ़ी हुई कठिनाई और विश्लेषण की शुरुआत के कार्य: हाई स्कूल / बी.एम. के 10-11 ग्रेड के लिए पाठ्यपुस्तक। इवलेव, ए.एम. अब्रामोव, यू.पी. डुडनित्सिन, एस.आई. श्वार्जबर्ड। - एम .: ज्ञानोदय, 1990।

अभिव्यक्तियों के परिवर्तन के लिए मूल त्रिकोणमितीय सूत्रों का अनुप्रयोग (ग्रेड 10) // शैक्षणिक विचारों का उत्सव। 2012-2013।

कोर्यानोव ए.जी. , प्रोकोफ़िएव ए.ए. हम परीक्षा के लिए अच्छे छात्रों और उत्कृष्ट छात्रों को तैयार करते हैं। - एम .: शैक्षणिक विश्वविद्यालय "सितंबर का पहला", 2012.- 103 पी।

कुज़नेत्सोवा ई.एन.त्रिकोणमितीय व्यंजकों का सरलीकरण। विभिन्न तरीकों से त्रिकोणमितीय समीकरणों को हल करना (परीक्षा की तैयारी)। 11th ग्रेड। 2012-2013।

गणित में कुलनिन ईडी 3000 प्रतिस्पर्धी समस्याएं। चौथी आईडी।, सही। और अतिरिक्त - एम .: रॉल्फ, 2000।

मोर्दकोविच ए.जी. एक सामान्य शिक्षा स्कूल में त्रिकोणमिति का अध्ययन करने की विधि संबंधी समस्याएं // स्कूल में गणित। 2002. नंबर 6.

पिचुरिन एल.एफ. त्रिकोणमिति के बारे में और न केवल इसके बारे में: -एम। ज्ञानोदय, 1985

रेशेतनिकोव एन.एन. स्कूल में त्रिकोणमिति: -एम। : शैक्षणिक विश्वविद्यालय "सितंबर का पहला", 2006, एलके 1.

शबुनिन एम.आई., प्रोकोफिव ए.ए. गणित। बीजगणित। गणितीय विश्लेषण की शुरुआत। प्रोफाइल स्तर: ग्रेड 10 - एम के लिए पाठ्यपुस्तक। बिनोम। नॉलेज लैब, 2007.

परीक्षा की तैयारी के लिए शैक्षिक पोर्टल।

गणित में परीक्षा की तैयारी "ओह, यह त्रिकोणमिति! http://festival.1september.ru/articles/621971/

प्रोजेक्ट "गणित? आसान !!!" http://www.resolventa.ru/

अनुभाग: गणित

कक्षा: 11

पाठ 1

विषय: ग्रेड 11 (परीक्षा की तैयारी)

त्रिकोणमितीय व्यंजकों का सरलीकरण।

सरलतम त्रिकोणमितीय समीकरणों का हल। (2 घंटे)

लक्ष्य:

त्रिकोणमिति सूत्रों के उपयोग और सरलतम त्रिकोणमितीय समीकरणों के समाधान से संबंधित छात्रों के ज्ञान और कौशल को व्यवस्थित, सामान्यीकृत, विस्तारित करें।

सबक के लिए उपकरण:

पाठ संरचना:

ऑर्गमोमेंट
लैपटॉप पर परीक्षण। परिणामों की चर्चा।
त्रिकोणमितीय व्यंजकों का सरलीकरण
सरलतम त्रिकोणमितीय समीकरणों का हल
स्वतंत्र काम।
पाठ का सारांश। गृहकार्य की व्याख्या।

1. संगठनात्मक क्षण। (दो मिनट।)

शिक्षक दर्शकों को बधाई देता है, पाठ के विषय की घोषणा करता है, याद करता है कि कार्य पहले त्रिकोणमिति सूत्रों को दोहराने के लिए दिया गया था और छात्रों को परीक्षण के लिए सेट करता है।

2. परीक्षण। (15मिनट + 3मिनट की चर्चा)

लक्ष्य त्रिकोणमितीय सूत्रों के ज्ञान और उन्हें लागू करने की क्षमता का परीक्षण करना है। प्रत्येक छात्र के पास अपने डेस्क पर एक लैपटॉप होता है जिसमें एक परीक्षण विकल्प होता है।

कई विकल्प हो सकते हैं, मैं उनमें से एक का उदाहरण दूंगा:

मैं विकल्प।

अभिव्यक्तियों को सरल बनाएं:

ए) बुनियादी त्रिकोणमितीय पहचान

1. पाप 2 3y + cos 2 3y + 1;

बी) अतिरिक्त सूत्र

3. sin5x - sin3x;

सी) किसी उत्पाद को योग में परिवर्तित करना

6. 2sin8y cos3y;

d) द्विकोण सूत्र

7.2sin5x cos5x;

ई) आधा कोण सूत्र

च) ट्रिपल कोण सूत्र

छ) सार्वभौमिक प्रतिस्थापन

ज) डिग्री कम करना

16. cos 2 (3x/7);

प्रत्येक फॉर्मूले के सामने लैपटॉप पर विद्यार्थी अपने उत्तर देखते हैं।

कंप्यूटर द्वारा काम की तुरंत जाँच की जाती है। परिणाम सभी को देखने के लिए बड़ी स्क्रीन पर प्रदर्शित होते हैं।

साथ ही, काम खत्म होने के बाद छात्रों के लैपटॉप पर सही उत्तर दिखाए जाते हैं। प्रत्येक छात्र देखता है कि गलती कहां हुई और उसे किन सूत्रों को दोहराने की जरूरत है।

3. त्रिकोणमितीय व्यंजकों का सरलीकरण। (25 मि.)

लक्ष्य त्रिकोणमिति के मूल सूत्रों के अनुप्रयोग को दोहराना, काम करना और समेकित करना है। परीक्षा से B7 की समस्याओं को हल करना।

इस स्तर पर, कक्षा को मजबूत (बाद में सत्यापन के साथ स्वतंत्र रूप से काम करें) और शिक्षक के साथ काम करने वाले कमजोर छात्रों के समूहों में विभाजित करने की सलाह दी जाती है।

मजबूत छात्रों के लिए असाइनमेंट (मुद्रित आधार पर अग्रिम रूप से तैयार)। यूएसई 2011 के अनुसार, मुख्य जोर कमी और दोहरे कोण सूत्रों पर है।

अभिव्यक्तियों को सरल बनाएं (मजबूत शिक्षार्थियों के लिए):

समानांतर में, शिक्षक कमजोर छात्रों के साथ काम करता है, छात्रों के श्रुतलेख के तहत स्क्रीन पर कार्यों पर चर्चा और समाधान करता है।

गणना करें:

5) sin(270º - α) + cos(270º + α)

सरल करें:

मजबूत समूह के काम के परिणामों पर चर्चा करने की बारी थी।

उत्तर स्क्रीन पर दिखाई देते हैं, और साथ ही, एक वीडियो कैमरा की मदद से, 5 अलग-अलग छात्रों का काम प्रदर्शित होता है (प्रत्येक के लिए एक कार्य)।

कमजोर समूह स्थिति और समाधान विधि देखता है। चर्चा और विश्लेषण होता है। तकनीकी साधनों के उपयोग से यह जल्दी हो जाता है।

4. सरलतम त्रिकोणमितीय समीकरणों का हल। (30 मिनट।)

लक्ष्य सरलतम त्रिकोणमितीय समीकरणों के समाधान को दोहराना, व्यवस्थित करना और सामान्य बनाना है, उनकी जड़ों को रिकॉर्ड करना। समस्या का समाधान B3.

कोई भी त्रिकोणमितीय समीकरण, चाहे हम इसे कैसे भी हल करें, सरलतम की ओर ले जाता है।

कार्य को पूरा करते समय विद्यार्थियों को विशेष स्थितियों और सामान्य रूप के समीकरणों के मूल लिखने और अंतिम समीकरण में मूलों के चयन पर ध्यान देना चाहिए।

समीकरण हल करें:

उत्तर की सबसे छोटी सकारात्मक जड़ लिखिए।

5. स्वतंत्र कार्य (10 मि.)

लक्ष्य अर्जित कौशल का परीक्षण करना, समस्याओं, त्रुटियों और उन्हें खत्म करने के तरीकों की पहचान करना है।

छात्र की पसंद पर कई तरह के काम पेश किए जाते हैं।

"3" के लिए विकल्प

1) व्यंजक का मान ज्ञात कीजिए

2) व्यंजक को सरल कीजिए 1 - sin 2 3α - cos 2 3α

3) समीकरण हल करें

"4" के लिए विकल्प

1) व्यंजक का मान ज्ञात कीजिए

2) समीकरण हल करें अपने उत्तर की सबसे छोटी सकारात्मक जड़ लिखिए।

"5" के लिए विकल्प

1) tgα का पता लगाएं अगर

2) समीकरण का मूल ज्ञात कीजिए अपने उत्तर की सबसे छोटी सकारात्मक जड़ लिखिए।

6. पाठ का सारांश (5 मि.)

शिक्षक इस तथ्य का सार प्रस्तुत करता है कि पाठ ने त्रिकोणमितीय सूत्रों को दोहराया और समेकित किया, सरलतम त्रिकोणमितीय समीकरणों का समाधान।

अगले पाठ में स्पॉट चेक के साथ होमवर्क सौंपा गया है (मुद्रित आधार पर पहले से तैयार)।

समीकरण हल करें:

10) अपना उत्तर सबसे छोटे धनात्मक मूल के रूप में दीजिए।

पाठ 2

विषय: ग्रेड 11 (परीक्षा की तैयारी)

त्रिकोणमितीय समीकरणों को हल करने के तरीके। जड़ चयन। (2 घंटे)

लक्ष्य:

विभिन्न प्रकार के त्रिकोणमितीय समीकरणों को हल करने पर ज्ञान को सामान्य और व्यवस्थित करना।
छात्रों की गणितीय सोच के विकास को बढ़ावा देना, निरीक्षण करने, तुलना करने, सामान्यीकरण करने, वर्गीकृत करने की क्षमता।
छात्रों को मानसिक गतिविधि की प्रक्रिया में कठिनाइयों को दूर करने, आत्म-नियंत्रण, अपनी गतिविधियों का आत्मनिरीक्षण करने के लिए प्रोत्साहित करें।

सबक के लिए उपकरण:केआरएमयू, प्रत्येक छात्र के लिए लैपटॉप।

पाठ संरचना:

ऑर्गमोमेंट
चर्चा डी / एस और समोत। अंतिम पाठ का कार्य
त्रिकोणमितीय समीकरणों को हल करने के तरीकों की पुनरावृत्ति।
त्रिकोणमितीय समीकरणों को हल करना
त्रिकोणमितीय समीकरणों में जड़ों का चयन।
स्वतंत्र काम।
पाठ का सारांश। गृहकार्य।

1. आयोजन क्षण (2 मिनट।)

शिक्षक दर्शकों का अभिवादन करता है, पाठ के विषय और कार्य योजना की घोषणा करता है।

2. क) गृहकार्य का विश्लेषण (5 मि.)

लक्ष्य प्रदर्शन की जांच करना है। एक वीडियो कैमरे की मदद से एक काम स्क्रीन पर प्रदर्शित होता है, बाकी को शिक्षक द्वारा जांचने के लिए चुनिंदा रूप से एकत्र किया जाता है।

बी) स्वतंत्र कार्य का विश्लेषण (3 मिनट।)

लक्ष्य गलतियों को सुलझाना है, उन्हें दूर करने के तरीकों का संकेत देना है।

स्क्रीन पर उत्तर और समाधान हैं, छात्रों ने अपना काम पूर्व-जारी कर दिया है। विश्लेषण तेजी से हो रहा है।

3. त्रिकोणमितीय समीकरणों को हल करने के तरीकों की पुनरावृत्ति (5 मिनट।)

लक्ष्य त्रिकोणमितीय समीकरणों को हल करने के तरीकों को याद करना है।

छात्रों से पूछें कि वे त्रिकोणमितीय समीकरणों को हल करने के कौन से तरीके जानते हैं। जोर दें कि तथाकथित बुनियादी (अक्सर उपयोग की जाने वाली) विधियां हैं:

परिवर्तनीय प्रतिस्थापन,
गुणनखंडन,
सजातीय समीकरण,

और लागू तरीके हैं:

योग को उत्पाद और उत्पाद को योग में बदलने के सूत्रों के अनुसार,
कमी सूत्रों द्वारा,
सार्वभौमिक त्रिकोणमितीय प्रतिस्थापन
एक सहायक कोण का परिचय,
कुछ त्रिकोणमितीय फ़ंक्शन द्वारा गुणा।

यह भी याद रखना चाहिए कि एक समीकरण को विभिन्न तरीकों से हल किया जा सकता है।

4. त्रिकोणमितीय समीकरणों को हल करना (30 मिनट)

लक्ष्य इस विषय पर ज्ञान और कौशल को सामान्यीकृत और समेकित करना है, ताकि USE से C1 को हल करने की तैयारी की जा सके।

मैं विद्यार्थियों के साथ मिलकर प्रत्येक विधि के समीकरणों को हल करना समीचीन समझता हूँ।

छात्र समाधान निर्धारित करता है, शिक्षक टैबलेट पर लिखता है, पूरी प्रक्रिया स्क्रीन पर प्रदर्शित होती है। यह आपको अपनी मेमोरी में पहले से कवर की गई सामग्री को जल्दी और कुशलता से पुनर्स्थापित करने की अनुमति देगा।

समीकरण हल करें:

1) परिवर्तनशील परिवर्तन 6cos 2 x + 5sinx - 7 = 0

2) गुणनखंड 3cos(x/3) + 4cos 2 (x/3) = 0

3) सजातीय समीकरण sin 2 x + 3cos 2 x - 2sin2x = 0

4) योग को उत्पाद में बदलना cos5x + cos7x = cos(π + 6x)

5) उत्पाद को योग 2sinx sin2x + cos3x = 0 . में परिवर्तित करना

6) sin2x की डिग्री कम करना - पाप 2 2x + पाप 2 3x \u003d 0.5

7) सार्वभौमिक त्रिकोणमितीय प्रतिस्थापन sinx + 5cosx + 5 = 0।

इस समीकरण को हल करते समय, यह ध्यान दिया जाना चाहिए कि इस पद्धति के उपयोग से परिभाषा के क्षेत्र का संकुचन होता है, क्योंकि साइन और कोसाइन को tg(x/2) द्वारा प्रतिस्थापित किया जाता है। इसलिए, उत्तर लिखने से पहले, यह जांचना आवश्यक है कि सेट π + 2πn, n Z से संख्याएं इस समीकरण के घोड़े हैं या नहीं।

8) एक सहायक कोण का परिचय √3sinx + cosx - √2 = 0

9) किसी त्रिकोणमितीय फलन cosx cos2x cos4x = 1/8 से गुणा।

5. त्रिकोणमितीय समीकरणों के मूलों का चयन (20 मिनट)

चूंकि विश्वविद्यालयों में प्रवेश करते समय भयंकर प्रतिस्पर्धा की स्थिति में, परीक्षा के पहले भाग का समाधान पर्याप्त नहीं होता है, इसलिए अधिकांश छात्रों को दूसरे भाग (C1, C2, C3) के कार्यों पर ध्यान देना चाहिए।

इसलिए, पाठ के इस चरण का उद्देश्य 2011 में यूएसई से समस्या C1 को हल करने के लिए तैयार करने के लिए पहले से अध्ययन की गई सामग्री को याद करना है।

त्रिकोणमितीय समीकरण होते हैं जिनमें उत्तर लिखते समय आपको मूलों का चयन करना होता है। यह कुछ प्रतिबंधों के कारण है, उदाहरण के लिए: एक अंश का हर शून्य के बराबर नहीं है, एक सम अंश के मूल के नीचे का व्यंजक गैर-ऋणात्मक है, लघुगणक के चिह्न के नीचे का व्यंजक धनात्मक है, आदि।

इस तरह के समीकरणों को बढ़ी हुई जटिलता के समीकरण माना जाता है और यूएसई संस्करण में वे दूसरे भाग में हैं, अर्थात् सी 1।

प्रश्न हल करें:

भिन्न शून्य है यदि तब यूनिट सर्कल का उपयोग करके, हम जड़ों का चयन करेंगे (चित्र 1 देखें)

चित्र 1।

हमें x = + 2πn, n Z . प्राप्त होता है

उत्तर: + 2πn, n Z

स्क्रीन पर, जड़ों का चयन एक रंगीन छवि में एक वृत्त पर दिखाया गया है।

उत्पाद शून्य के बराबर होता है जब कारकों में से कम से कम एक शून्य के बराबर होता है, और चाप, एक ही समय में, अपना अर्थ नहीं खोता है। फिर

यूनिट सर्कल का उपयोग करके, जड़ों का चयन करें (चित्र 2 देखें)

पर समान परिवर्तन त्रिकोणमितीय भावनिम्नलिखित बीजीय तरकीबों का उपयोग किया जा सकता है: समान पदों को जोड़ना और घटाना; कोष्ठक से उभयनिष्ठ गुणनखंड निकालना; एक ही मूल्य से गुणा और भाग; संक्षिप्त गुणन सूत्रों का अनुप्रयोग; एक पूर्ण वर्ग का चयन; एक वर्ग त्रिपद का गुणनखंडन; परिवर्तनों को सरल बनाने के लिए नए चरों की शुरूआत।

भिन्नों वाले त्रिकोणमितीय व्यंजकों को परिवर्तित करते समय, आप अनुपात के गुणों, भिन्नों में कमी, या भिन्नों को घटाकर एक सामान्य हर में उपयोग कर सकते हैं। इसके अलावा, आप अंश के पूर्णांक भाग के चयन का उपयोग कर सकते हैं, अंश के अंश और हर को समान मान से गुणा कर सकते हैं, और यदि संभव हो तो अंश या हर की एकरूपता को भी ध्यान में रख सकते हैं। यदि आवश्यक हो, तो आप भिन्न को कई सरल भिन्नों के योग या अंतर के रूप में निरूपित कर सकते हैं।

इसके अलावा, त्रिकोणमितीय अभिव्यक्तियों को परिवर्तित करने के लिए सभी आवश्यक तरीकों को लागू करते समय, परिवर्तित अभिव्यक्तियों के अनुमेय मूल्यों की सीमा को लगातार ध्यान में रखना आवश्यक है।

आइए कुछ उदाहरण देखें।

उदाहरण 1

ए = (sin (2x - π) cos (3π - x) + sin (2x - 9π/2) cos (x + /2)) 2 + (cos (x - /2) cos ( 2x - 7π) की गणना करें। / 2) +
+ पाप (3π/2 - x) पाप (2x -5π/2)) 2

समाधान।

यह कमी सूत्रों से निम्नानुसार है:

पाप (2x - ) \u003d -sin 2x; cos (3π - x) \u003d -cos x;

पाप (2x - 9π / 2) \u003d -cos 2x; cos (x + /2) = -sin x;

कॉस (एक्स - / 2) \u003d पाप एक्स; cos (2x - 7π/2) = -sin 2x;

पाप (3π / 2 - x) \u003d -cos x; पाप (2x - 5π / 2) \u003d -cos 2x।

जहां से, तर्कों को जोड़ने और मूल त्रिकोणमितीय पहचान के सूत्रों के आधार पर, हम प्राप्त करते हैं

ए \u003d (पाप 2x cos x + cos 2x sin x) 2 + (-sin x sin 2x + cos x cos 2x) 2 \u003d sin 2 (2x + x) + cos 2 (x + 2x) \u003d
= sin 2 3x + cos 2 3x = 1

उत्तर 1।

उदाहरण 2

व्यंजक M = cos α + cos (α + β) cos + cos β - sin (α + β) sin γ + cos को उत्पाद में बदलें।

समाधान।

तर्कों को जोड़ने के सूत्रों से और त्रिकोणमितीय कार्यों के योग को उत्पाद में बदलने के लिए, उपयुक्त समूहन के बाद, हमारे पास है

М = (cos (α + β) cos γ - sin (α + β) sin γ) + cos α + (cos β + cos ) =

2cos ((β + γ)/2) cos ((β - )/2) + (cos α + cos (α + β + γ)) =

2cos ((β + )/2) cos ((β - )/2) + 2cos (α + (β + γ)/2) cos ((β + )/2)) =

2cos ((β + )/2) (cos ((β - )/2) + cos (α + (β + γ)/2)) =

2cos ((β + γ)/2) 2cos ((β - )/2 + α + (β + )/2)/2) cos ((β - )/2) - (α + ( β + )/2)/2) =

4cos ((β + )/2) cos ((α + β)/2) cos ((α + )/2)।

उत्तर: М = 4cos ((α + β)/2) cos ((α + )/2) cos ((β + γ)/2)।

उदाहरण 3.

दिखाएँ कि व्यंजक A \u003d cos 2 (x + / 6) - cos (x + / 6) cos (x - / 6) + cos 2 (x - / 6) R से सभी x के लिए लेता है। और एक ही मूल्य। यह मान ज्ञात कीजिए।

समाधान।

हम इस समस्या को हल करने के लिए दो तरीके प्रस्तुत करते हैं। पहली विधि को लागू करते हुए, पूर्ण वर्ग को अलग करके और संबंधित मूल त्रिकोणमितीय सूत्रों का उपयोग करके, हम प्राप्त करते हैं

ए \u003d (cos (x + / 6) - cos (x - / 6)) 2 + cos (x - / 6) cos (x - π / 6) \u003d

4sin 2 x sin 2 /6 + 1/2(cos 2x + cos π/3) =

पाप 2 x + 1/2 cos 2x + 1/4 = 1/2 (1 - cos 2x) + 1/2 cos 2x + 1/4 = 3/4।

समस्या को दूसरे तरीके से हल करते हुए, A को R से x का एक फलन मानें और इसके अवकलज की गणना करें। परिवर्तन के बाद, हम प्राप्त करते हैं

А´ \u003d -2cos (x + /6) sin (x + /6) + (sin (x + /6) cos (x - /6) + cos (x + /6) sin ( x + π/6)) - 2cos (x - π/6) sin (x - π/6) =

पाप 2(x + /6) + पाप ((x + /6) + (x - π/6)) - पाप 2(x - π/6) =

पाप 2x - (पाप (2x + π/3) + पाप (2x - π/3)) =

पाप 2x - 2sin 2x cos /3 = sin 2x - sin 2x 0.

इसलिए, एक अंतराल पर भिन्न फलन की स्थिरता की कसौटी के आधार पर, हम यह निष्कर्ष निकालते हैं कि

A(x) ≡ (0) = cos 2 π/6 - cos 2 /6 + cos 2 /6 = (√3/2) 2 = 3/4, x ∈ R.

उत्तर: ए = 3/4 x € R के लिए।

त्रिकोणमितीय सर्वसमिकाओं को सिद्ध करने की मुख्य विधियाँ हैं:

एक)उपयुक्त परिवर्तनों द्वारा पहचान के बाईं ओर दाईं ओर की कमी;
बी)पहचान के दाईं ओर बाईं ओर की कमी;
में)पहचान के दाएं और बाएं हिस्सों को एक ही रूप में कम करना;
जी)पहचान के बाएँ और दाएँ भागों के बीच के अंतर को शून्य करने के लिए सिद्ध किया जा रहा है।

उदाहरण 4

जाँच कीजिए कि cos 3x = -4cos x cos (x + /3) cos (x + 2π/3)।

समाधान।

इस सर्वसमिका के दाईं ओर को संगत त्रिकोणमितीय सूत्रों के अनुसार बदलने पर, हमारे पास है

4cos x cos (x + /3) cos (x + 2π/3) =

2cos x (cos ((x + /3) + (x + 2π/3)) + cos ((x + π/3) - (x + 2π/3))) =

2cos x (cos (2x + π) + cos π/3) =

2cos x cos 2x - cos x = (cos 3x + cos x) - cos x = cos 3x।

पहचान का दाहिना भाग बाईं ओर कम हो जाता है।

उदाहरण 5

सिद्ध कीजिए कि sin 2 α + sin 2 β + sin 2 – 2cos α cos β cos = 2 यदि α, β, किसी त्रिभुज के आंतरिक कोण हैं।

समाधान।

यह ध्यान में रखते हुए कि α, β, किसी त्रिभुज के आंतरिक कोण हैं, हम प्राप्त करते हैं कि

α + β + γ = और इसलिए γ = - α - β।

पाप 2 α + पाप 2 β + पाप 2 γ - 2cos α cos β cos =

पाप 2 α + पाप 2 β + पाप 2 (π - α - β) - 2cos α cos β cos (π - α - β) =

sin 2 α + sin 2 β + sin 2 (α + β) + (cos (α + β) + cos (α - β) (cos (α + β) =

sin 2 α + sin 2 β + (sin 2 (α + β) + cos 2 (α + β)) + cos (α - β) (cos (α + β) =

1/2 (1 - cos 2α) + ½ (1 - cos 2β) + 1 + 1/2 (cos 2α + cos 2β) = 2.

मूल समानता सिद्ध होती है।

उदाहरण 6

सिद्ध करें कि त्रिभुज के कोणों α, β, में से एक के लिए 60° के बराबर होने के लिए, यह आवश्यक और पर्याप्त है कि sin 3α + sin 3β + sin 3γ = 0.

समाधान।

इस समस्या की स्थिति आवश्यकता और पर्याप्तता दोनों का प्रमाण मानती है।

पहले हम सिद्ध करते हैं जरुरत.

यह दिखाया जा सकता है कि

sin 3α + sin 3β + sin 3γ = -4cos (3α/2) cos (3β/2) cos (3γ/2)।

इसलिए, इस बात को ध्यान में रखते हुए कि cos (3/2 60°) = cos 90° = 0, हम पाते हैं कि यदि α, β या में से कोई एक कोण 60° के बराबर है, तो

cos (3α/2) cos (3β/2) cos (3γ/2) = 0 और इसलिए sin 3α + sin 3β + sin 3γ = 0।

आइए अब साबित करें पर्याप्ततानिर्दिष्ट शर्त।

यदि sin 3α + sin 3β + sin 3γ = 0, तो cos (3α/2) cos (3β/2) cos (3γ/2) = 0, और इसलिए

या तो cos (3α/2) = 0, या cos (3β/2) = 0, या cos (3γ/2) = 0।

फलस्वरूप,

या 3α/2 = /2 + πk, यानी। α = π/3 + 2πk/3,

या 3β/2 = /2 + πk, यानी। β = /3 + 2πk/3,

या 3γ/2 = /2 + πk,

वे। = π/3 + 2πk/3, जहां k Z.

इस तथ्य से कि α, β, एक त्रिभुज के कोण हैं, हमारे पास है

0 < α < π, 0 < β < π, 0 < γ < π.

इसलिए, α = π/3 + 2πk/3 या β = π/3 + 2πk/3 or . के लिए

= π/3 + 2πk/3 सभी kϵZ में से केवल k = 0 फिट बैठता है।

यह इस प्रकार है कि या तो α = /3 = 60°, या β = /3 = 60°, या = /3 = 60°।

अभिकथन सिद्ध हो चुका है।

क्या आपका कोई प्रश्न है? त्रिकोणमितीय व्यंजकों को सरल बनाना नहीं जानते?
ट्यूटर की मदद लेने के लिए - रजिस्टर करें।
पहला सबक मुफ्त है!

साइट, सामग्री की पूर्ण या आंशिक प्रतिलिपि के साथ, स्रोत के लिए एक लिंक आवश्यक है।

अनुभाग: गणित

कक्षा: 11

पाठ 1

विषय: ग्रेड 11 (परीक्षा की तैयारी)

त्रिकोणमितीय व्यंजकों का सरलीकरण।

सरलतम त्रिकोणमितीय समीकरणों का हल। (2 घंटे)

लक्ष्य:

त्रिकोणमिति सूत्रों के उपयोग और सरलतम त्रिकोणमितीय समीकरणों के समाधान से संबंधित छात्रों के ज्ञान और कौशल को व्यवस्थित, सामान्यीकृत, विस्तारित करें।

सबक के लिए उपकरण:

पाठ संरचना:

ऑर्गमोमेंट
लैपटॉप पर परीक्षण। परिणामों की चर्चा।
त्रिकोणमितीय व्यंजकों का सरलीकरण
सरलतम त्रिकोणमितीय समीकरणों का हल
स्वतंत्र काम।
पाठ का सारांश। गृहकार्य की व्याख्या।

1. संगठनात्मक क्षण। (दो मिनट।)

2. परीक्षण। (15मिनट + 3मिनट की चर्चा)

कई विकल्प हो सकते हैं, मैं उनमें से एक का उदाहरण दूंगा:

मैं विकल्प।

अभिव्यक्तियों को सरल बनाएं:

ए) बुनियादी त्रिकोणमितीय पहचान

1. पाप 2 3y + cos 2 3y + 1;

बी) अतिरिक्त सूत्र

3. sin5x - sin3x;

सी) किसी उत्पाद को योग में परिवर्तित करना

6. 2sin8y cos3y;

d) द्विकोण सूत्र

7.2sin5x cos5x;

ई) आधा कोण सूत्र

च) ट्रिपल कोण सूत्र

छ) सार्वभौमिक प्रतिस्थापन

ज) डिग्री कम करना

16. cos 2 (3x/7);

प्रत्येक फॉर्मूले के सामने लैपटॉप पर विद्यार्थी अपने उत्तर देखते हैं।

3. त्रिकोणमितीय व्यंजकों का सरलीकरण। (25 मि.)

अभिव्यक्तियों को सरल बनाएं (मजबूत शिक्षार्थियों के लिए):

गणना करें:

5) sin(270º - α) + cos(270º + α)

सरल करें:

मजबूत समूह के काम के परिणामों पर चर्चा करने की बारी थी।

4. सरलतम त्रिकोणमितीय समीकरणों का हल। (30 मिनट।)

समीकरण हल करें:

उत्तर की सबसे छोटी सकारात्मक जड़ लिखिए।

5. स्वतंत्र कार्य (10 मि.)

छात्र की पसंद पर कई तरह के काम पेश किए जाते हैं।

"3" के लिए विकल्प

1) व्यंजक का मान ज्ञात कीजिए

2) व्यंजक को सरल कीजिए 1 - sin 2 3α - cos 2 3α

3) समीकरण हल करें

"4" के लिए विकल्प

1) व्यंजक का मान ज्ञात कीजिए

2) समीकरण हल करें अपने उत्तर की सबसे छोटी सकारात्मक जड़ लिखिए।

"5" के लिए विकल्प

1) tgα का पता लगाएं अगर

2) समीकरण का मूल ज्ञात कीजिए अपने उत्तर की सबसे छोटी सकारात्मक जड़ लिखिए।

6. पाठ का सारांश (5 मि.)

समीकरण हल करें:

10) अपना उत्तर सबसे छोटे धनात्मक मूल के रूप में दीजिए।

पाठ 2

विषय: ग्रेड 11 (परीक्षा की तैयारी)

त्रिकोणमितीय समीकरणों को हल करने के तरीके। जड़ चयन। (2 घंटे)

लक्ष्य:

विभिन्न प्रकार के त्रिकोणमितीय समीकरणों को हल करने पर ज्ञान को सामान्य और व्यवस्थित करना।
छात्रों की गणितीय सोच के विकास को बढ़ावा देना, निरीक्षण करने, तुलना करने, सामान्यीकरण करने, वर्गीकृत करने की क्षमता।
छात्रों को मानसिक गतिविधि की प्रक्रिया में कठिनाइयों को दूर करने, आत्म-नियंत्रण, अपनी गतिविधियों का आत्मनिरीक्षण करने के लिए प्रोत्साहित करें।

सबक के लिए उपकरण:केआरएमयू, प्रत्येक छात्र के लिए लैपटॉप।

पाठ संरचना:

ऑर्गमोमेंट
चर्चा डी / एस और समोत। अंतिम पाठ का कार्य
त्रिकोणमितीय समीकरणों को हल करने के तरीकों की पुनरावृत्ति।
त्रिकोणमितीय समीकरणों को हल करना
त्रिकोणमितीय समीकरणों में जड़ों का चयन।
स्वतंत्र काम।
पाठ का सारांश। गृहकार्य।

1. आयोजन क्षण (2 मिनट।)

2. क) गृहकार्य का विश्लेषण (5 मि.)

बी) स्वतंत्र कार्य का विश्लेषण (3 मिनट।)

लक्ष्य गलतियों को सुलझाना है, उन्हें दूर करने के तरीकों का संकेत देना है।

3. त्रिकोणमितीय समीकरणों को हल करने के तरीकों की पुनरावृत्ति (5 मिनट।)

लक्ष्य त्रिकोणमितीय समीकरणों को हल करने के तरीकों को याद करना है।

परिवर्तनीय प्रतिस्थापन,
गुणनखंडन,
सजातीय समीकरण,

और लागू तरीके हैं:

योग को उत्पाद और उत्पाद को योग में बदलने के सूत्रों के अनुसार,
कमी सूत्रों द्वारा,
सार्वभौमिक त्रिकोणमितीय प्रतिस्थापन
एक सहायक कोण का परिचय,
कुछ त्रिकोणमितीय फ़ंक्शन द्वारा गुणा।

यह भी याद रखना चाहिए कि एक समीकरण को विभिन्न तरीकों से हल किया जा सकता है।

4. त्रिकोणमितीय समीकरणों को हल करना (30 मिनट)

समीकरण हल करें:

1) परिवर्तनशील परिवर्तन 6cos 2 x + 5sinx - 7 = 0

2) गुणनखंड 3cos(x/3) + 4cos 2 (x/3) = 0

3) सजातीय समीकरण sin 2 x + 3cos 2 x - 2sin2x = 0

4) योग को उत्पाद में बदलना cos5x + cos7x = cos(π + 6x)

5) उत्पाद को योग 2sinx sin2x + cos3x = 0 . में परिवर्तित करना

6) sin2x की डिग्री कम करना - पाप 2 2x + पाप 2 3x \u003d 0.5

7) सार्वभौमिक त्रिकोणमितीय प्रतिस्थापन sinx + 5cosx + 5 = 0।

8) एक सहायक कोण का परिचय √3sinx + cosx - √2 = 0

9) किसी त्रिकोणमितीय फलन cosx cos2x cos4x = 1/8 से गुणा।

5. त्रिकोणमितीय समीकरणों के मूलों का चयन (20 मिनट)

प्रश्न हल करें:

चित्र 1।

हमें x = + 2πn, n Z . प्राप्त होता है

उत्तर: + 2πn, n Z

स्क्रीन पर, जड़ों का चयन एक रंगीन छवि में एक वृत्त पर दिखाया गया है।

यूनिट सर्कल का उपयोग करके, जड़ों का चयन करें (चित्र 2 देखें)

चित्र 2।

आइए सिस्टम पर चलते हैं:

सिस्टम के पहले समीकरण में, हम परिवर्तन लॉग 2 (sinx) = y बनाते हैं, हम तब समीकरण प्राप्त करते हैं , सिस्टम पर वापस

यूनिट सर्कल का उपयोग करके, हम जड़ों का चयन करते हैं (चित्र 5 देखें),

चित्र 5

6. स्वतंत्र कार्य (15 मि.)

लक्ष्य सामग्री को समेकित और जांचना, त्रुटियों की पहचान करना और उन्हें ठीक करने के तरीकों की रूपरेखा तैयार करना है।

काम तीन संस्करणों में पेश किया जाता है, छात्रों की पसंद पर मुद्रित आधार पर अग्रिम रूप से तैयार किया जाता है।

समीकरणों को किसी भी तरह से हल किया जा सकता है।

"3" के लिए विकल्प

समीकरण हल करें:

1) 2sin 2 x + sinx - 1 = 0

2) sin2x = √3cosx

"4" के लिए विकल्प

समीकरण हल करें:

1) cos2x = 11sinx - 5

2) (2sinx + 3)लॉग 8 (cosx) = 0

"5" के लिए विकल्प

समीकरण हल करें:

1) 2sinx - 3cosx = 2

7. पाठ का सारांश, गृहकार्य (5 मि.)

शिक्षक पाठ को सारांशित करता है, एक बार फिर इस तथ्य पर ध्यान आकर्षित करता है कि त्रिकोणमितीय समीकरण को कई तरीकों से हल किया जा सकता है। त्वरित परिणाम प्राप्त करने का सबसे अच्छा तरीका वह है जो किसी विशेष छात्र द्वारा सबसे अच्छा सीखा जाता है।

परीक्षा की तैयारी करते समय, आपको समीकरणों को हल करने के लिए सूत्रों और विधियों को व्यवस्थित रूप से दोहराने की आवश्यकता होती है।

गृहकार्य (मुद्रित आधार पर पहले से तैयार) वितरित किया जाता है और कुछ समीकरणों को हल करने के तरीकों पर टिप्पणी की जाती है।

समीकरण हल करें:

1) cosx + cos5x = cos3x + cos7x

2) 5sin(x/6) - cos(x/3) + 3 = 0

3) 4sin 2x + sin2x = 3

4) पाप 2 x + पाप 2 2x - पाप 2 3x - पाप 2 4x = 0

5) cos3x cos6x = cos4x cos7x

6) 4sinx - 6cosx = 1

7) 3sin2x + 4 cos2x = 5

8) cosx cos2x cos4x cos8x = (1/8) cos15x

9) (2sin 2 x - sinx) log 3 (2cos 2 x + cosx) = 0