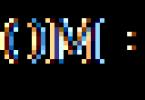Theorem: a circle can be inscribed in any triangle. a b c o. Inscribed and circumscribed circles Example of a problem on the concepts of inscribed and circumscribed circles

In this lesson we will remember the basics on which the theory of inscribed and circumscribed circles is based, we will recall the characteristics of circumscribed and inscribed quadrilaterals. In addition, we will derive formulas for finding the radii of the circumscribed and inscribed circle in various cases.

Topic: Circle

Lesson: Inscribed and Circumscribed Circles

First of all, we are talking about inscribed and circumscribed circles relative to a triangle. We are prepared for this topic because we have studied the properties of bisectors and perpendicular bisectors of a triangle.

A circle can be inscribed in any triangle (see Fig. 1).

Rice. 1

Proof:

We know that all the bisectors of a triangle intersect at one point - let it be at point O. Let's draw the bisectors AO, BO, CO. Their intersection point O is equidistant from the sides of the triangle. It is equidistant from the sides of the angle - AC and AB, since it belongs to the bisector of this angle. Likewise, it is equidistant from the sides of the angles and thus from the three sides of the triangle.

Let's drop perpendiculars from point O to the sides of the triangle - OM to side AC, OL to BC, OK to AB. These perpendiculars will be the distances from point O to the sides of the triangle, and they are equal:

Let us denote the distance from point O to the sides of the triangle as r and consider a circle with a center at point O and radius r.

The circle touches the straight line AB, because has a common point K with it, and the radius OK drawn to this point is perpendicular to the straight line AB. Similarly, the circle touches the lines AC and BC. Thus, the circle touches all those sides of the triangle, which means it is inscribed in the triangle.

So, the three bisectors of a triangle intersect at a point that is the center of the incircle.

Let's consider another theorem, it concerns the point of intersection of the perpendicular bisectors of a triangle. We know that they intersect at one point, and this point coincides with the center of the circle circumscribed about the triangle.

A circle can be drawn around any triangle.

So, a triangle is given. Let's draw the bisector p 1 to the side of the triangle BC, p 2 to the side AB, p 3 to the side AC (see Fig. 2).

According to the theorem on the properties of perpendicular bisectors, a point belonging to the perpendicular bisector of a segment is equidistant from the ends of the segment. Hence, because point Q belongs to the perpendicular bisector to segment AC. Likewise. Thus, point Q is equidistant from the vertices of the triangle. Hence QA, QB, QC are radii

Rice. 2

circle circumscribed about a triangle. Let us denote the radius as R. Point O of the intersection of the bisector perpendiculars is the center of the circumscribed circle.

Let's consider a circle inscribed in a certain quadrilateral and the properties of this quadrilateral (see Fig. 3).

Let us recall the properties of a point lying on the bisector of an angle.

An angle is given, its bisector is AL, point M lies on the bisector.

If point M lies on the bisector of an angle, then it is equidistant from the sides of the angle, that is, the distances from point M to AC and to BC of the sides of the angle are equal.

Rice. 3

The distance from a point to a line is the length of the perpendicular. From point M we draw perpendiculars MK to side AB and MR to side AC.

Consider triangles and . These are right triangles and they are equal because... have a common hypotenuse AM, and the angles are equal, since AL is the bisector of the angle. Thus, right triangles are equal in hypotenuse and acute angle, it follows that , which is what needed to be proved. Thus, a point on the bisector of an angle is equidistant from the sides of that angle.

In addition, the legs. Thus, the tangent segments drawn to a circle from one point are equal.

So let's go back to the quadrilateral. The first step is to draw bisectors in it.

All bisectors of a quadrilateral intersect at one point - point O, the center of the inscribed circle.

From point O we lower perpendiculars to the sides of the quadrilateral to points K, L, M, N and determine the points of tangency (see Fig. 3).

Tangents drawn to a circle from one point are equal to each other, so a pair of equal tangents emerge from each vertex: , , , .

Rice. 3

If a circle can be inscribed in a quadrilateral, then the sums of its opposite sides are equal. It's easy to prove:

Let's expand the brackets:

Thus, we have proven a simple but important theorem.

If a circle can be inscribed in a quadrilateral, then the sums of its opposite sides are equal.

The converse theorem is true.

If in a quadrilateral the sums of opposite sides are equal, then a circle can be inscribed in it.

Consider a circle circumscribed about a quadrilateral.

Given a circle with center O and an arbitrary quadrilateral ABCD. Let's consider the properties of this quadrilateral. All four perpendicular bisectors of a given quadrilateral intersect at one point: this point is the center of the circumcircle.

Proving that all four perpendicular bisectors intersect at one point would be tedious. There is another sign. Let's consider the angle ےА, this is the inscribed angle of a circle, it rests on the arc and is measured by half the degree measure of this arc (see Fig. 4). Let us denote the angle ےА as , then the arc . Similarly, we designate the opposite angle ےС as , it is inscribed in the circle and rests on the arc . Hence the arc.

Rice. 4

The arcs make up a complete circle. From here:

Dividing the resulting expression by two, we get:

So, we have proven the direct theorem.

Theorem

If a circle is circumscribed around a quadrilateral, the sum of its opposite angles is .

This is a necessary and sufficient sign, that is, the converse theorem is true.

If the sum of the opposite angles of a quadrilateral is , a circle can be drawn around this quadrilateral.

Based on these theorems, we note that it is impossible to describe a circle around a parallelogram, since its opposite angles are equal and their sum is not equal (see Fig. 5).

Rice. 5

A circle could be described around a parallelogram if its opposite angles were equal to 90°, that is, if it were a rectangle, thus a circle could be described around a rectangle (see Fig. 6).

Rice. 6

It is also impossible to describe a circle around a rhombus, but it can be inscribed, since all sides of a rhombus are equal, and thus the sums of the opposite sides of a rhombus are equal.

In addition, in a rhombus, each diagonal is a bisector; the point of intersection of the bisectors is equidistant from all sides of the rhombus (see Fig. 7).

Rice. 7

So, we have proven that a circle can be inscribed in any triangle, and the center of this circle coincides with the intersection point of the bisectors of the triangle. We also proved that a circle can be described around any triangle, and its center will coincide with the point of intersection of the perpendicular bisectors. In addition, we saw that some quadrilaterals can be inscribed with a circle, and to do this it is necessary that the sums of the opposite sides of the quadrilateral be equal. We also showed that around some quadrilaterals it is possible to describe a circle, and a necessary and sufficient condition for this is the equality of the sum of opposite angles.

Bibliography

Alexandrov A.D. and others. Geometry, 8th grade. - M.: Education, 2006.
Butuzov V.F., Kadomtsev S.B., Prasolov V.V. Geometry, 8th grade. - M.: Education, 2011.
Merzlyak A.G., Polonsky V.B., Yakir S.M. Geometry, 8th grade. - M.: VENTANA-GRAF, 2009.

Uztest.ru ().
Mschool.kubsu.ru ().
Ege-study.ru ().

Homework

THEOREM ABOUT THE CIRCLE DESCRIBED AROUND A POLYGON: Around any regular polygon it is possible to describe a circle, and only one. THEOREM ABOUT A CIRCLE INSCRIBED INTO A REGULAR POLYGON: A circle can be inscribed in any regular polygon, and only one.

SPa4a4 rRN Calculation of the area of a regular polygon, its side and the radius of the inscribed circle and the radius of the inscribed circle

Areas of regular polygons Areas of regular polygons NAMES AND AREA OF POLYGONS Number of sides Name of the polygonArea of a regular polygon 3Triangle0.433a 2 4Quadrilateral1.000a 2 5Pentagon1.720a 2 6Hexagon2.598a 2 7Heptagon3.634a 2 8Octagon4.828a 2 9Octagon6.182a 2 10Decagon7.694a 2 nn- square

0 inscribed angles. Hippocrates of Chios The proof presented in modern textbooks that an inscribed angle is measured by half the arc on which it rests is given in Euclid's Elements. This proposal, however, is also referred to by Hippocrates of Chios (5th century BC) in his work on “holes”. The works of Hippocrates indicate that already in the second half of the 5th century. BC e. a large number of theorems set forth in Euclid’s Elements were known, and geometry reached a high level of development. The fact that an inscribed angle based on a diameter is a right angle was known to the Babylonians 4000 years ago. Its first proof is attributed by Pamphylia, a Roman writer from the time of Nero, to Thales of Miletus.

0 regular polygons Regular quadrangles, hexagons and octagons are found in Egyptian and Babylonian ancient monuments in the form of images on walls and decorations carved from stone. Ancient Greek scientists began to show great interest in regular figures since the time of Pythagoras. Dividing a circle into a number of equal parts to construct regular polygons was important for the Pythagoreans, who argued that numbers underlie all phenomena in the world. The doctrine of regular polygons, begun in the school of Pythagoras, continued and developed in the 7th century. BC e., was systematized by Euclid and set forth in Book IV of the Elements. In addition to constructing a regular triangle, quadrilateral, pentagon and hexagon, Euclid also solves the problem of constructing a regular fifteen-sided triangle using only a compass and a ruler. This figure attracted the attention of the ancients, since it was noticed that the arc of the angle of inclination of the ecliptic to the equator represents the entire circle, that is, it is subtended by the side of a regular fifteen-sided triangle.

A B C O1 O2 O1 is the center of the circumscribed circle, O2 is the center of the inscribed circle Necessity: Sufficiency: D AB + CD = BC + AD and, therefore, AB = CD = BAD = ADC, but BAD + ABC = 180 Hence ADC + ABC = 180 , and a circle can be inscribed around the trapezoid ABCD. In addition, AB + CD = BC + AD and, therefore, a circle can be inscribed in ABCD. It is necessary and sufficient that the trapezoid be equilateral and the lateral side equal to half the sum of the bases.

Definition 2

A polygon that satisfies the condition of definition 1 is called circumscribed about a circle.

Figure 1. Inscribed circle

Theorem 1 (about a circle inscribed in a triangle)

Theorem 1

You can inscribe a circle into any triangle, and only one.

Proof.

Consider triangle $ABC$. Let's draw bisectors in it that intersect at point $O$ and draw perpendiculars from it to the sides of the triangle (Fig. 2)

Figure 2. Illustration of Theorem 1

Existence: Let us draw a circle with center at point $O$ and radius $OK.\ $Since point $O$ lies on three bisectors, it is equidistant from the sides of triangle $ABC$. That is, $OM=OK=OL$. Consequently, the constructed circle also passes through the points $M\ and\ L$. Since $OM,OK\ and\ OL$ are perpendiculars to the sides of the triangle, then by the circle tangent theorem, the constructed circle touches all three sides of the triangle. Therefore, due to the arbitrariness of a triangle, a circle can be inscribed in any triangle.

Uniqueness: Suppose that another circle with center at point $O"$ can be inscribed in triangle $ABC$. Its center is equidistant from the sides of the triangle, and, therefore, coincides with point $O$ and has a radius equal to length $OK$ But then this circle will coincide with the first one.

The theorem is proven.

Corollary 1: The center of a circle inscribed in a triangle lies at the point of intersection of its bisectors.

Here are a few more facts related to the concept of an inscribed circle:

Not every quadrilateral can fit a circle.

In any circumscribed quadrilateral, the sums of opposite sides are equal.

If the sums of the opposite sides of a convex quadrilateral are equal, then a circle can be inscribed in it.

Definition 3

If all the vertices of a polygon lie on a circle, then the circle is called circumscribed about the polygon (Fig. 3).

Definition 4

A polygon that satisfies definition 2 is said to be inscribed in a circle.

Figure 3. Circumscribed circle

Theorem 2 (about the circumcircle of a triangle)

Theorem 2

Around any triangle you can describe a circle, and only one.

Proof.

Consider triangle $ABC$. Let us draw perpendicular bisectors in it, intersecting at point $O$, and connect it with the vertices of the triangle (Fig. 4)

Figure 4. Illustration of Theorem 2

Existence: Let's construct a circle with center at point $O$ and radius $OC$. Point $O$ is equidistant from the vertices of the triangle, that is, $OA=OB=OC$. Consequently, the constructed circle passes through all the vertices of a given triangle, which means that it is circumscribed about this triangle.

Uniqueness: Suppose that another circle can be described around the triangle $ABC$ with its center at the point $O"$. Its center is equidistant from the vertices of the triangle, and, therefore, coincides with the point $O$ and has a radius equal to the length $OC. $ But then this circle will coincide with the first one.

The theorem is proven.

Corollary 1: The center of the circle circumscribed about the triangle coincides with the point of intersection of its bisectoral perpendiculars.

Here are a few more facts related to the concept of a circumcircle:

It is not always possible to describe a circle around a quadrilateral.

In any cyclic quadrilateral, the sum of opposite angles is $(180)^0$.

If the sum of the opposite angles of a quadrilateral is $(180)^0$, then a circle can be drawn around it.

An example of a problem on the concepts of inscribed and circumscribed circles

Example 1

In an isosceles triangle, the base is 8 cm and the side is 5 cm. Find the radius of the inscribed circle.

Solution.

Consider triangle $ABC$. By Corollary 1, we know that the center of the incircle lies at the intersection of the bisectors. Let us draw the bisectors $AK$ and $BM$, which intersect at the point $O$. Let's draw a perpendicular $OH$ from point $O$ to side $BC$. Let's draw a picture:

Figure 5.

Since the triangle is isosceles, then $BM$ is both the median and the altitude. By the Pythagorean theorem $(BM)^2=(BC)^2-(MC)^2,\ BM=\sqrt((BC)^2-\frac((AC)^2)(4))=\sqrt (25-16)=\sqrt(9)=$3. $OM=OH=r$ -- the required radius of the inscribed circle. Since $MC$ and $CH$ are segments of intersecting tangents, then by the theorem on intersecting tangents, we have $CH=MC=4\cm$. Therefore, $BH=5-4=1\ cm$. $BO=3-r$. From the triangle $OHB$, according to the Pythagorean theorem, we obtain:

\[((3-r))^2=r^2+1\] \ \ \

Answer:$\frac(4)(3)$.

Proofs of theorems on the properties of the circumscribed circle of a triangle

Perpendicular bisector to a line segment

Definition 1. Perpendicular bisector to a segment called a straight line perpendicular to this segment and passing through its middle (Fig. 1).

Theorem 1. Each point of the perpendicular bisector to a segment is located at the same distance from the ends this segment.

Proof . Let's consider an arbitrary point D lying on the perpendicular bisector to the segment AB (Fig. 2), and prove that triangles ADC and BDC are equal.

Indeed, these triangles are right triangles in which legs AC and BC are equal, and leg DC is common. The equality of triangles ADC and BDC implies the equality of segments AD and DB. Theorem 1 is proven.

Theorem 2 (Converse to Theorem 1). If a point is at the same distance from the ends of a segment, then it lies on the perpendicular bisector to this segment.

Proof . Let us prove Theorem 2 by contradiction. For this purpose, assume that some point E is at the same distance from the ends of the segment, but does not lie on the perpendicular bisector to this segment. Let us bring this assumption to a contradiction. Let us first consider the case when points E and A lie on opposite sides of the perpendicular bisector (Fig. 3). In this case, the segment EA intersects the perpendicular bisector at some point, which we will denote by the letter D.

Let us prove that the segment AE is longer than the segment EB. Really,

Thus, in the case when points E and A lie on opposite sides of the perpendicular bisector, we have a contradiction.

Now consider the case when points E and A lie on the same side of the perpendicular bisector (Fig. 4). Let us prove that the segment EB is longer than the segment AE. Really,

The resulting contradiction completes the proof of Theorem 2

Circle circumscribed about a triangle

Definition 2. A circle circumscribed about a triangle, is called a circle passing through all three vertices of the triangle (Fig. 5). In this case the triangle is called triangle inscribed in a circle or inscribed triangle.

Properties of the circumscribed circle of a triangle. Theorem of sines

Figure	Drawing	Property
Perpendicular bisectors to the sides of the triangle		intersect at one point .

Center circle circumscribed about an acute triangle		Center described about acute-angled inside triangle.
Center circle circumscribed about a right triangle		The center described about rectangular middle of the hypotenuse .
Center circle circumscribed about an obtuse triangle		Center described about obtuse-angled triangle circle lies outside triangle.
		,
Square triangle		S= 2R 2 sin A sin B sin C ,
Circumradius		For any triangle the equality is true:

Perpendicular bisectors to the sides of a triangle

All perpendicular bisectors , drawn to the sides of an arbitrary triangle, intersect at one point .

Circle circumscribed about a triangle

Any triangle can be surrounded by a circle . The center of a circle circumscribed about a triangle is the point at which all the perpendicular bisectors drawn to the sides of the triangle intersect.

Center of the circumscribed circle of an acute triangle

Center described about acute-angled triangle circle lies inside triangle.

Center of the circumscribed circle of a right triangle

The center described about rectangular triangle circle is middle of the hypotenuse .

Center of the circumscribed circle of an obtuse triangle

Center described about obtuse-angled triangle circle lies outside triangle.

For any triangle the following equalities are true (sine theorem):

where a, b, c are the sides of the triangle, A, B, C are the angles of the triangle, R is the radius of the circumscribed circle.

Area of a triangle

For any triangle the equality is true:

S= 2R 2 sin A sin B sin C ,

where A, B, C are the angles of the triangle, S is the area of the triangle, R is the radius of the circumscribed circle.

Circumradius

For any triangle the equality is true:

where a, b, c are the sides of the triangle, S is the area of the triangle, R is the radius of the circumscribed circle.

Proofs of theorems on the properties of the circumscribed circle of a triangle

Theorem 3. All perpendicular bisectors drawn to the sides of an arbitrary triangle intersect at one point.

Proof . Let's consider two perpendicular bisectors drawn to sides AC and AB of triangle ABC, and denote their intersection point with the letter O (Fig. 6).