Признаци за успоредност на две прави

Теорема 1. Ако в пресечната точка на две прави на секанс:

диагонално разположените ъгли са равни, или

съответните ъгли са равни, или

сборът от едностранните ъгли е 180°, тогава

линиите са успоредни(Фиг. 1).

Доказателство. Ние се ограничаваме до доказателство за случай 1.

Да предположим, че при пресичането на правите a и b със секуща AB напречно лежащите ъгли са равни. Например ∠ 4 = ∠ 6. Нека докажем, че a || b.

Да приемем, че правите a и b не са успоредни. Тогава те се пресичат в някаква точка M и следователно един от ъглите 4 или 6 ще бъде външният ъгъл на триъгълника ABM. Нека за определеност ∠ 4 е външният ъгъл на триъгълника ABM, а ∠ 6 е вътрешният. От теоремата за външния ъгъл на триъгълник следва, че ∠ 4 е по-голямо от ∠ 6, а това противоречи на условието, което означава, че правите a и 6 не могат да се пресичат, следователно са успоредни.

Следствие 1. Две различни прави в равнина, перпендикулярна на една и съща права, са успоредни(фиг. 2).

Коментирайте. Начинът, по който току-що доказахме случай 1 от теорема 1, се нарича метод на доказателство чрез противоречие или свеждане до абсурд. Този метод получи първото си име, защото в началото на разсъждението се прави предположение, което е противоположно (противоположно) на това, което се изисква да се докаже. Нарича се свеждане до абсурд поради факта, че, спорейки въз основа на направеното предположение, стигаме до абсурдно заключение (абсурд). Получаването на такова заключение ни принуждава да отхвърлим предположението, направено в началото, и да приемем това, което трябваше да бъде доказано.

Задача 1.Да се ​​построи права, минаваща през дадена точка M и успоредна на дадена права a, която не минава през точка M.

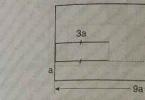
Решение. Начертаваме права p през точка M, перпендикулярна на правата a (фиг. 3).

След това начертаваме права b през точката M, перпендикулярна на правата p. Правата b е успоредна на правата a съгласно следствието от теорема 1.

От разглеждания проблем следва важен извод:
През точка, която не е на дадена права, винаги може да се начертае права, успоредна на дадената права..

Основното свойство на успоредните прави е следното.

Аксиома за успоредни прави. През дадена точка, която не е на дадена права, има само една права, успоредна на дадената права.

Разгледайте някои свойства на успоредните прави, които следват от тази аксиома.

1) Ако права пресича едната от двете успоредни прави, то тя пресича другата (фиг. 4).

2) Ако две различни прави са успоредни на третата права, то те са успоредни (фиг. 5).

Следващата теорема също е вярна.

Теорема 2. Ако две успоредни прави се пресичат със секанс, тогава:

ъглите на лежане са равни;

съответните ъгли са равни;

сборът от едностранните ъгли е 180°.

Следствие 2. Ако правата е перпендикулярна на една от двете успоредни прави, тогава тя е перпендикулярна и на другата.(виж фиг.2).

Коментирайте. Теорема 2 се нарича обратна на Теорема 1. Заключението на Теорема 1 е условието на Теорема 2. А условието на Теорема 1 е заключението на Теорема 2. Не всяка теорема има обратна, т.е. ако дадена теорема е вярна, тогава обратната теорема може да е невярна.

Нека обясним това с примера на теоремата за вертикалните ъгли. Тази теорема може да се формулира по следния начин: ако два ъгъла са вертикални, те са равни. Обратната теорема би била следната: ако два ъгъла са равни, тогава те са вертикални. И това, разбира се, не е вярно. Два равни ъгъла изобщо не трябва да са вертикални.

Пример 1Две успоредни прави се пресичат от трета. Известно е, че разликата между два вътрешни едностранни ъгъла е 30°. Намерете тези ъгли.

Решение. Нека фигура 6 отговаря на условието.

ГЛАВА III.
ПАРАЛЕЛНИ ЛИНИИ

§ 35. ЗНАЦИ ЗА УСПОРЕДНОСТ НА ДВЕ ПРАВИ.

Теоремата, че два перпендикуляра на една права са успоредни (§ 33) дава знак, че две прави са успоредни. Възможно е да се изведат по-общи признаци на успоредност на две прави.

1. Първият признак на паралелизъм.

Ако при пресичането на две прави с трета вътрешните ъгли, разположени напречно, са равни, то тези прави са успоредни.

Нека правите AB и CD пресичат правата EF и / 1 = / 2. Вземете точката O - средата на отсечката KL на секущата EF (фиг. 189).

Нека пуснем перпендикуляра OM от точка O към правата AB и да го продължим, докато се пресече с правата CD, AB_|_MN. Нека докажем, че CD_|_MN.
За да направите това, помислете за два триъгълника: MOE и NOK. Тези триъгълници са равни един на друг. Наистина: / 1 = / 2 по условието на теоремата; OK = OL - по конструкция;
/ MOL = / NOK като вертикални ъгли. Така страната и двата прилежащи към нея ъгъла на един триъгълник са съответно равни на страната и двата прилежащи към нея ъгъла на друг триъгълник; Следователно, /\ MOL = /\ NOK, и оттам
/ LMO = / знам но / LMO е директно, следователно, и / KNO също е директен. Така правите AB и CD са перпендикулярни на една и съща права MN, следователно са успоредни (§ 33), което трябваше да се докаже.

Забележка. Пресечната точка на правите MO и CD може да се установи чрез завъртане на триъгълника MOL около точка O на 180°.

2. Вторият знак за паралелизъм.

Да видим дали правите AB и CD са успоредни, ако при пресичането на третата им права EF съответните ъгли са равни.

Нека някои съответни ъгли са равни, например / 3 = / 2 (отклонение 190);
/ 3 = / 1, като ъглите са вертикални; означава, / 2 ще бъде равно / 1. Но ъглите 2 и 1 са вътрешни напречни ъгли и вече знаем, че ако при пресичането на две прави с трета вътрешните напречни ъгли са равни, тогава тези прави са успоредни. Следователно AB || CD.

Ако при пресичането на две прави от третата съответните ъгли са равни, то тези две прави са успоредни.

На това свойство се основава изграждането на успоредни прави с помощта на линийка и чертожен триъгълник. Това става по следния начин.

Нека прикрепим триъгълника към линийката, както е показано на чертеж 191. Ще преместим триъгълника така, че едната му страна да се плъзга по линийката, и ще начертаем няколко прави линии по всяка друга страна на триъгълника. Тези линии ще бъдат успоредни.

3. Третият знак за паралелизъм.

Да знаем, че при пресичането на две прави AB и CD с третата права сумата от всички вътрешни едностранни ъгли е равна на 2 д(или 180°). Дали в този случай правите AB и CD ще бъдат успоредни (фиг. 192).

Позволявам / 1 и / 2 вътрешни едностранни ъгъла и добавете до 2 д.
Но / 3 + / 2 = 2дкато съседни ъгли. Следователно, / 1 + / 2 = / 3+ / 2.

Оттук / 1 = / 3, и тези ъгли са вътрешно разположени на кръст. Следователно AB || CD.

Ако при пресичането на две прави с трета сумата от вътрешните едностранни ъгли е равна на 2 d, тогава двете прави са успоредни.

Упражнение.

Докажете, че правите са успоредни:
а) ако външните напречни ъгли са равни (фиг. 193);
б) ако сборът на външните едностранни ъгли е 2 д(дявол 194).

Тази глава е посветена на изучаването на успоредни прави. Това е името, дадено на две прави линии в равнина, които не се пресичат. Виждаме сегменти от успоредни линии в околната среда - това са два ръба на правоъгълна маса, два ръба на корица на книга, две тролейбусни ленти и т.н. Паралелните линии играят много важна роля в геометрията. В тази глава ще научите какво представляват аксиомите на геометрията и от какво се състои аксиомата на успоредните прави - една от най-известните аксиоми на геометрията.

В раздел 1 отбелязахме, че две прави или имат една обща точка, тоест се пресичат, или нямат нито една обща точка, тоест не се пресичат.

Определение

Успоредността на правите a и b се означава по следния начин: a || b.

Фигура 98 показва прави a и b, перпендикулярни на права c. В раздел 12 установихме, че такива прави a и b не се пресичат, т.е. те са успоредни.

Ориз. 98

Наред с успоредните прави често се разглеждат и успоредни отсечки. Двата сегмента се наричат паралеленако лежат на успоредни прави. На фигура 99 отсечките AB и CD са успоредни (AB || CD), а отсечките MN и CD не са успоредни. По същия начин се определя паралелността на сегмент и права линия (фиг. 99, b), лъч и права линия, сегмент и лъч, два лъча (фиг. 99, c).

Ориз. 99Признаци за успоредност на две прави

Директно с се нарича секущапо отношение на правите a и b, ако ги пресича в две точки (фиг. 100). При пресичането на прави a и b секансът c образува осем ъгъла, които са обозначени с числа на фигура 100. Някои двойки от тези ъгли имат специални имена:

кръстосани ъгли: 3 и 5, 4 и 6;
едностранни ъгли: 4 и 5, 3 и 6;
съответните ъгли: 1 и 5, 4 и 8, 2 и 6, 3 и 7.

Ориз. 100

Помислете за три признака за успоредност на две прави, свързани с тези двойки ъгли.

Теорема

Доказателство

Да предположим, че при пресичането на прави a и b със секуща AB ъглите на лежащите са равни: ∠1 = ∠2 (фиг. 101, а).

Нека докажем, че a || b. Ако ъглите 1 и 2 са прави (фиг. 101, b), тогава правите a и b са перпендикулярни на правата AB и следователно са успоредни.

Ориз. 101

Да разгледаме случая, когато ъгли 1 и 2 не са прави.

От средата O на сегмента AB начертайте перпендикуляр OH към правата a (фиг. 101, c). На линията b от точка B отделяме сегмента VH 1, равен на сегмента AH, както е показано на фигура 101, c, и начертаваме сегмента OH 1. Триъгълниците ONA и OH 1 V са равни по две страни и ъгъл между тях (AO = BO, AN = VN 1, ∠1 = ∠2), следователно ∠3 = ∠4 и ∠5 = ∠6. От равенството ∠3 = ∠4 следва, че точката H 1 лежи на продължението на лъча OH, т.е. точките H, O и H 1 лежат на една и съща права линия, а от равенството ∠5 = ∠6 тя следва, че ъгъл 6 е права (тъй като ъгъл 5 е прав ъгъл). Правите a и b са перпендикулярни на правата HH 1, така че са успоредни. Теоремата е доказана.

Теорема

Доказателство

Нека в пресечната точка на правите a и b секансът със съответните ъгли е равен, например ∠1 = ∠2 (фиг. 102).

Ориз. 102

Тъй като ъгли 2 и 3 са вертикални, тогава ∠2 = ∠3. От тези две равенства следва, че ∠1 = ∠3. Но ъгли 1 и 3 са напречни, така че правите a и b са успоредни. Теоремата е доказана.

Теорема

Доказателство

Нека в пресечната точка на прави a и b секансът със сумата от едностранните ъгли е 180°, например ∠1 + ∠4 = 180° (виж фиг. 102).

Тъй като ъгли 3 и 4 са съседни, тогава ∠3 + ∠4 = 180°. От тези две равенства следва, че напречните ъгли 1 и 3 са равни, следователно правите a и b са успоредни. Теоремата е доказана.

Практически начини за рисуване на успоредни линии

Признаците на успоредни прави са в основата на начините за конструиране на успоредни прави с помощта на различни инструменти, използвани в практиката. Помислете например за метод за конструиране на успоредни линии с помощта на чертожен квадрат и линийка. За да изградим права линия, минаваща през точката M и успоредна на дадената права a, прилагаме чертожен квадрат към правата a и линийка към нея, както е показано на фигура 103. След това, премествайки квадрата по линийката, ние ще гарантира, че точката M е от страната на квадрата и ще начертае линия b. Правите a и b са успоредни, тъй като съответните ъгли, означени на фигура 103 с буквите α и β, са равни.

Ориз. 103Фигура 104 показва метод за конструиране на успоредни прави с помощта на Т-квадрат. Този метод се използва в практиката на рисуване.

Ориз. 104Подобен метод се използва при извършване на дърводелски работи, където се използва фаска за маркиране на успоредни линии (две дървени дъски, закрепени с панта, фиг. 105).

Ориз. 105

Задачи

186. На фигура 106 прави a и b се пресичат от права c. Докажете, че a || b ако:

а) ∠1 = 37°, ∠7 = 143°;
б) ∠1 = ∠6;
в) ∠l = 45°, а ъгъл 7 е три пъти по-голям от ъгъл 3.

Ориз. 106

187. Според фигура 107 докажете, че AB || Д.Е.

Ориз. 107

188. Отсечките AB и CD се пресичат в общата им среда. Докажете, че правите AC и BD са успоредни.

189. Използвайки данните от фигура 108, докажете, че BC || AD.

Ориз. 108

190. На фигура 109 AB = BC, AD = DE, ∠C = 70°, ∠EAC = 35°. Докажете, че DE || КАТО.

Ориз. 109

191. Отсечката VK е ъглополовяща на триъгълника ABC. През точката K е прекарана права, пресичаща страната BC в точка M, така че BM = MK. Докажете, че правите KM и AB са успоредни.

192. В триъгълник ABC ъгъл A е 40°, а ъгъл ALL, съседен на ъгъл ACB, е 80°. Докажете, че ъглополовящата на ъгъл ALL е успоредна на правата AB.

193. В триъгълник ABC ∠A = 40°, ∠B = 70°. Правата BD е прекарана през върха B, така че лъч BC е ъглополовяща на ъгъл ABD. Докажете, че правите AC и BD са успоредни.

194. Начертайте триъгълник. През всеки връх на този триъгълник, с помощта на квадрат и линийка, начертайте права линия, успоредна на срещуположната страна.

195. Начертайте триъгълник ABC и отбележете точка D на страната AC. През точка D с помощта на квадрат и линийка начертайте прави линии, успоредни на другите две страни на триъгълника.

Тази глава е посветена на изучаването на успоредни прави. Това е името, дадено на две прави линии в равнина, които не се пресичат. Виждаме сегменти от успоредни линии в околната среда - това са два ръба на правоъгълна маса, два ръба на корица на книга, две тролейбусни ленти и т.н. Паралелните линии играят много важна роля в геометрията. В тази глава ще научите какво представляват аксиомите на геометрията и от какво се състои аксиомата на успоредните прави - една от най-известните аксиоми на геометрията.

В раздел 1 отбелязахме, че две прави или имат една обща точка, тоест се пресичат, или нямат нито една обща точка, тоест не се пресичат.

Определение

Успоредността на правите a и b се означава по следния начин: a || b.

Фигура 98 показва прави a и b, перпендикулярни на права c. В раздел 12 установихме, че такива прави a и b не се пресичат, т.е. те са успоредни.

Ориз. 98

Наред с успоредните прави често се разглеждат и успоредни отсечки. Двата сегмента се наричат паралеленако лежат на успоредни прави. На фигура 99 отсечките AB и CD са успоредни (AB || CD), а отсечките MN и CD не са успоредни. По същия начин се определя паралелността на сегмент и права линия (фиг. 99, b), лъч и права линия, сегмент и лъч, два лъча (фиг. 99, c).

Ориз. 99Признаци за успоредност на две прави

Директно с се нарича секущапо отношение на правите a и b, ако ги пресича в две точки (фиг. 100). При пресичането на прави a и b секансът c образува осем ъгъла, които са обозначени с числа на фигура 100. Някои двойки от тези ъгли имат специални имена:

кръстосани ъгли: 3 и 5, 4 и 6;
едностранни ъгли: 4 и 5, 3 и 6;
съответните ъгли: 1 и 5, 4 и 8, 2 и 6, 3 и 7.

Ориз. 100

Помислете за три признака за успоредност на две прави, свързани с тези двойки ъгли.

Теорема

Доказателство

Да предположим, че при пресичането на прави a и b със секуща AB ъглите на лежащите са равни: ∠1 = ∠2 (фиг. 101, а).

Нека докажем, че a || b. Ако ъглите 1 и 2 са прави (фиг. 101, b), тогава правите a и b са перпендикулярни на правата AB и следователно са успоредни.

Ориз. 101

Да разгледаме случая, когато ъгли 1 и 2 не са прави.

От средата O на сегмента AB начертайте перпендикуляр OH към правата a (фиг. 101, c). На линията b от точка B отделяме сегмента VH 1, равен на сегмента AH, както е показано на фигура 101, c, и начертаваме сегмента OH 1. Триъгълниците ONA и OH 1 V са равни по две страни и ъгъл между тях (AO = BO, AN = VN 1, ∠1 = ∠2), следователно ∠3 = ∠4 и ∠5 = ∠6. От равенството ∠3 = ∠4 следва, че точката H 1 лежи на продължението на лъча OH, т.е. точките H, O и H 1 лежат на една и съща права линия, а от равенството ∠5 = ∠6 тя следва, че ъгъл 6 е права (тъй като ъгъл 5 е прав ъгъл). Правите a и b са перпендикулярни на правата HH 1, така че са успоредни. Теоремата е доказана.

Теорема

Доказателство

Нека в пресечната точка на правите a и b секансът със съответните ъгли е равен, например ∠1 = ∠2 (фиг. 102).

Ориз. 102

Тъй като ъгли 2 и 3 са вертикални, тогава ∠2 = ∠3. От тези две равенства следва, че ∠1 = ∠3. Но ъгли 1 и 3 са напречни, така че правите a и b са успоредни. Теоремата е доказана.

Теорема

Доказателство

Нека в пресечната точка на прави a и b секансът със сумата от едностранните ъгли е 180°, например ∠1 + ∠4 = 180° (виж фиг. 102).

Тъй като ъгли 3 и 4 са съседни, тогава ∠3 + ∠4 = 180°. От тези две равенства следва, че напречните ъгли 1 и 3 са равни, следователно правите a и b са успоредни. Теоремата е доказана.

Практически начини за рисуване на успоредни линии

Признаците на успоредни прави са в основата на начините за конструиране на успоредни прави с помощта на различни инструменти, използвани в практиката. Помислете например за метод за конструиране на успоредни линии с помощта на чертожен квадрат и линийка. За да изградим права линия, минаваща през точката M и успоредна на дадената права a, прилагаме чертожен квадрат към правата a и линийка към нея, както е показано на фигура 103. След това, премествайки квадрата по линийката, ние ще гарантира, че точката M е от страната на квадрата и ще начертае линия b. Правите a и b са успоредни, тъй като съответните ъгли, означени на фигура 103 с буквите α и β, са равни.

Ориз. 103Фигура 104 показва метод за конструиране на успоредни прави с помощта на Т-квадрат. Този метод се използва в практиката на рисуване.

Ориз. 104Подобен метод се използва при извършване на дърводелски работи, където се използва фаска за маркиране на успоредни линии (две дървени дъски, закрепени с панта, фиг. 105).

Ориз. 105

Задачи

186. На фигура 106 прави a и b се пресичат от права c. Докажете, че a || b ако:

а) ∠1 = 37°, ∠7 = 143°;
б) ∠1 = ∠6;
в) ∠l = 45°, а ъгъл 7 е три пъти по-голям от ъгъл 3.

Ориз. 106

187. Според фигура 107 докажете, че AB || Д.Е.

Ориз. 107

188. Отсечките AB и CD се пресичат в общата им среда. Докажете, че правите AC и BD са успоредни.

189. Използвайки данните от фигура 108, докажете, че BC || AD.

Ориз. 108

190. На фигура 109 AB = BC, AD = DE, ∠C = 70°, ∠EAC = 35°. Докажете, че DE || КАТО.

Ориз. 109

191. Отсечката VK е ъглополовяща на триъгълника ABC. През точката K е прекарана права, пресичаща страната BC в точка M, така че BM = MK. Докажете, че правите KM и AB са успоредни.

192. В триъгълник ABC ъгъл A е 40°, а ъгъл ALL, съседен на ъгъл ACB, е 80°. Докажете, че ъглополовящата на ъгъл ALL е успоредна на правата AB.

193. В триъгълник ABC ∠A = 40°, ∠B = 70°. Правата BD е прекарана през върха B, така че лъч BC е ъглополовяща на ъгъл ABD. Докажете, че правите AC и BD са успоредни.

194. Начертайте триъгълник. През всеки връх на този триъгълник, с помощта на квадрат и линийка, начертайте права линия, успоредна на срещуположната страна.

195. Начертайте триъгълник ABC и отбележете точка D на страната AC. През точка D с помощта на квадрат и линийка начертайте прави линии, успоредни на другите две страни на триъгълника.

ABи ОТдпресечено от третата линия MN, тогава образуваните в този случай ъгли получават следните имена по двойки:

съответните ъгли: 1 и 5, 4 и 8, 2 и 6, 3 и 7;

вътрешни кръстосани ъгли: 3 и 5, 4 и 6;

външни кръстосани ъгли: 1 и 7, 2 и 8;

вътрешни едностранни ъгли: 3 и 6, 4 и 5;

външни едностранни ъгли: 1 и 8, 2 и 7.

И така, ∠ 2 = ∠ 4 и ∠ 8 = ∠ 6, но по доказаното ∠ 4 = ∠ 6.

Следователно ∠ 2 = ∠ 8.

3. Съответни ъгли 2 и 6 са еднакви, тъй като ∠ 2 = ∠ 4 и ∠ 4 = ∠ 6. Уверяваме се също, че другите съответни ъгли са равни.

4. Сума вътрешни едностранни ъгли 3 и 6 ще бъдат 2d, защото сумата съседни ъгли 3 и 4 е равно на 2d = 180 0 и ∠ 4 може да бъде заменено с идентичното ∠ 6. Също така се уверете, че сбор от ъгли 4 и 5 е равно на 2d.

5. Сума външни едностранни ъглище бъде 2d, защото тези ъгли съответно са равни вътрешни едностранни ъгликато ъгли вертикален.

От обосновката, доказана по-горе, получаваме обратни теореми.

Когато в пресечната точка на две линии на произволна трета линия получаваме, че:

1. Вътрешните напречни ъгли са еднакви;

или 2.Външните напречни ъгли са еднакви;

или 3.Съответните ъгли са еднакви;

или 4.Сумата от вътрешните едностранни ъгли е равна на 2d = 180 0 ;

или 5.Сумата на външната едностранна е 2d = 180 0 ,

тогава първите две линии са успоредни.