Розглянемо розв'язання рівнянь з одного змінного ступеня вище за другий.
ступенем рівняння Р(х) = 0 називається ступінь многочлена Р(х), тобто. найбільша зі ступенів його членів з коефіцієнтом, що не дорівнює нулю.
Приміром, рівняння (х 3 – 1) 2 + x 5 = x 6 – 2 має п'яту ступінь, т.к. після операцій розкриття дужок та приведення подібних отримаємо рівносильне рівняння х 5 – 2х 3 + 3 = 0 п'ятого ступеня.
Згадаймо правила, які знадобляться для вирішення рівнянь ступеня вище за другий.
Твердження про коріння багаточлена та його дільників:
1. Багаточлен n-го ступеня має число коренів, що не перевищує число n, причому коріння кратності m зустрічаються рівно m разів.
2. Багаточлен непарної міри має хоча б один дійсний корінь.
3. Якщо α – корінь Р(х), то Р n (х) = (х – α) · Q n – 1 (x), де Q n – 1 (x) – багаточлен ступеня (n – 1).
4.
5. Наведений многочлен з цілими коефіцієнтами може мати дробових раціональних коренів.
6. Для багаточлена третього ступеня
Р 3 (х) = ах 3 + bx 2 + cx + d можливе одне з двох: або він розкладається у добутку трьох двочленів
Р 3 (x) = а(х – α)(х – β)(х – γ), або розкладається у добуток двочлена та квадратного тричлена Р 3 (x) = а(х – α)(х 2 + βх + γ ).
7. Будь-який багаточлен четвертого ступеня розкладається на твір двох квадратних тричленів.
8. Багаточлен f(x) ділиться на многочлен g(х) без залишку, якщо існує багаточлен q(x), що f(x) = g(x) · q(x). Для поділу багаточленів застосовується правило «поділу куточком».
9. Для ділимості многочлена P(x) на двочлен (x - c) необхідно і достатньо, щоб число було коренем P(x) (Наслідок теореми Безу).
10. Теорема Вієта: Якщо х 1 , х 2 , …, х n – дійсне коріння багаточлена
Р(х) = а 0 х n + а 1 х n - 1 + … + а n, то мають місце такі рівності:
х 1 + х 2 + … + х n = -а 1/а 0
х 1 · х 2 + х 1 · х 3 + … + х n - 1 · х n = a 2 / а 0,
х 1 · х 2 · х 3 + … + х n - 2 · х n - 1 · х n = -a 3 / а 0,
х 1 · х 2 · х 3 · х n = (-1) n a n / а 0 .
Рішення прикладів
приклад 1.
Знайти залишок від поділу Р(х) = х 3 + 2/3 x 2 – 1/9 (х – 1/3).
Рішення.
За наслідком з теореми Безу: «Залишок від поділу багаточлена на двочлен (х – с) дорівнює значенню багаточлена від с». Знайдемо Р(1/3) = 0. Отже, залишок дорівнює 0 та число 1/3 – корінь багаточлена.
Відповідь: R = 0.
приклад 2.
Розділити «куточком» 2х3+3x2 – 2х+3 на (х+2). Знайти залишок та неповне приватне. 
Рішення:
2х 3 + 3x 2 - 2х + 3 | х + 2
2х 3 + 4 x 2 2x 2 – x
X 2 – 2 x
Відповідь: R = 3; приватне: 2х2 – х.
Основні методи вирішення рівнянь вищих ступенів
1. Введення нової змінної
Метод введення нової змінної вже знайомий з прикладу біквадратних рівнянь. Він у тому, що з вирішення рівняння f(x) = 0 вводять нову змінну (підстановку) t = x n чи t = g(х) і виражають f(x) через t, отримуючи нове рівняння r(t). Вирішуючи потім рівняння r(t), знаходять коріння:
(t 1, t 2, …, t n). Після цього одержують сукупність n рівнянь q(x) = t 1 , q(x) = t 2 , … , q(x) = t n , з яких знаходять коріння вихідного рівняння.
приклад 1.
(х 2 + х + 1) 2 - 3х 2 - 3x - 1 = 0.
Рішення:
(х 2 + х + 1) 2 - 3 (х 2 + x) - 1 = 0.
(х 2 + х + 1) 2 - 3 (х 2 + x + 1) + 3 - 1 = 0.
Заміна (х 2 + х + 1) = t.
t 2 - 3t + 2 = 0.
t 1 = 2, t 2 = 1. Зворотна заміна:
х 2 + х + 1 = 2 або х 2 + х + 1 = 1;
х 2 + х - 1 = 0 або х 2 + х = 0;
Відповідь: З першого рівняння: х 1, 2 = (-1 ± √5)/2, з другого: 0 та -1.
2. Розкладання на множники методом угруповання та формул скороченого множення
Основа даного методу також не нова і полягає в групуванні доданків таким чином, щоб кожна група містила загальний множник. І тому іноді доводиться застосовувати деякі штучні прийоми.
приклад 1.
х 4 - 3x2 + 4х - 3 = 0.
Рішення.
Представимо - 3x2 = -2x2 - x2 і згрупуємо:
(Х 4 - 2x 2) - (X 2 - 4х + 3) = 0.
(х 4 - 2x 2 +1 - 1) - (x 2 - 4х + 3 + 1 - 1) = 0.
(х 2 - 1) 2 - 1 - (x - 2) 2 + 1 = 0.
(х 2 - 1) 2 - (x - 2) 2 = 0.
(х 2 - 1 - х + 2) (х 2 - 1 + х - 2) = 0.
(х 2 - х + 1) (х 2 + х - 3) = 0.
х 2 - х + 1 = 0 або х 2 + х - 3 = 0.
Відповідь: У першому рівнянні немає коріння, з другого: х 1, 2 = (-1 ± √13)/2.
3. Розкладання на множник методом невизначених коефіцієнтів
Суть методу у тому, що вихідний многочлен розкладається на множники з невідомими коефіцієнтами. Використовуючи властивість, що багаточлени рівні, якщо рівні їхні коефіцієнти за однакових ступенів, знаходять невідомі коефіцієнти розкладання.
приклад 1.
х 3 + 4x 2 + 5х + 2 = 0.
Рішення.
Багаточлен 3-го ступеня можна розкласти у добуток лінійного та квадратного множників.
х 3 + 4x 2 + 5х + 2 = (х - а) (x 2 + bх + c),
х 3 + 4x 2 + 5х + 2 = х 3 + bx 2 + cх - ax 2 - abх - ac,
х 3 + 4x 2 + 5х + 2 = х 3 + (b - a) x 2 + (cх - ab) х - ac.
Вирішивши систему:
(b - a = 4,
(c - ab = 5,
(-ac = 2,
(a = -1,
(b = 3,
(C = 2, тобто.
x 3 + 4x 2 + 5x + 2 = (x + 1) (x 2 + 3x + 2).
Коріння рівняння (х + 1) (x 2 + 3х + 2) = 0 легко.
Відповідь: -1; -2.
4. Метод підбору кореня за старшим та вільним коефіцієнтом

Метод спирається застосування теорем:
1) Кожен корінь многочлена з цілими коефіцієнтами є дільником вільного члена.
2) Для того, щоб нескоротний дріб p/q (p – ціле, q – натуральне) був коренем рівняння з цілими коефіцієнтами, необхідно, щоб число p було цілим дільником вільного члена а 0, а q – натуральним дільником старшого коефіцієнта.
приклад 1.
6х3 + 7x2 - 9х + 2 = 0.
Рішення:
6: q = 1, 2, 3, 6.
Отже, p/q = ±1, ±2, ±1/2, ±1/3, ±2/3, ±1/6.
Знайшовши один корінь, наприклад - 2, інше коріння знайдемо, використовуючи розподіл куточком, метод невизначених коефіцієнтів або схему Горнера.
Відповідь: -2; 1/2; 1/3.
Залишились питання? Не знаєте, як розв'язувати рівняння?
Щоб отримати допомогу репетитора – зареєструйтесь.
Перший урок – безкоштовно!
сайт, при повному або частковому копіюванні матеріалу посилання на першоджерело обов'язкове.
СХЕМА ГІРНЕРА
У РІШЕННІ РІВНЯНЬ З ПАРАМЕТРАМИ
З ГРУПИ «С» ПІДГОТОВКА ДО ЄДІ
Казанцева Людмила Вікторівна
вчитель математики МБОУ «Уярська ЗОШ №3»
На факультативних заняттях необхідно розширити коло наявних знань з допомогою рішення завдань підвищеної складності групи «З».
Дана робота висвітлює частину питань, що розглядаються на додаткових заняттях.
Доцільно запровадити схему Горнера після вивчення теми «Ділення багаточлена на багаточлен». Цей матеріал дозволяє вирішувати рівняння вищих порядків не способом угруповання багаточленів, а раціональнішим шляхом, що економить час.
План занять.
Заняття 1.
1. Пояснення теоретичного матеріалу.
2. Рішення прикладів а Б В Г).
Заняття 2.
1. Розв'язання рівнянь а Б В Г).
2. Знаходження раціонального коріння багаточлена
Застосування схеми Горнера під час вирішення рівнянь з параметрами.
Заняття 3.
Завдання а Б В).
Заняття 4.
1. Завдання г), д), е), ж), з).
Вирішення рівнянь вищих ступенів.
Схема Горнер.
Теорема : Нехай нескоротний дріб є коренем рівняння.
a o x n + a 1 x n-1 + … + a n-1 x 1 + a n = 0
з цілими коефіцієнтами. Тоді число рє дільником старшого коефіцієнта а о .
Слідство: Будь-який цілий корінь рівняння з цілими коефіцієнтами є дільником його вільного члена.
Слідство: Якщо старший коефіцієнт рівняння з цілими коефіцієнтами дорівнює 1 , то всі раціональні коріння, якщо вони існують – цілі.
Приклад 1. 2х 3 - 7х 2 + 5х - 1 = 0
Нехай нескоротний дріб є коренем рівняння, тодір є дільником числа1: ± 1
q є дільником старшого члена: ± 1; ± 2
Раціональне коріння рівняння треба шукати серед чисел:±1; ±.
f(1) = 2 – 7 + 5 – 1 = – 1 ≠ 0
f(–1) = –2 – 7 – 5 – 1 ≠ 0
f() = – + – 1 = – +  – = 0
– = 0
Коренем є число .
Поділ багаточлену Р(х) = а о х п + a 1 x n -1 + … + a n на двочлен ( х – £)зручно виконувати за схемою Горнер.
Позначимо неповне приватне Р(х)на ( х – £)через Q (x ) = b o x n -1 + b 1 x n -2 + … b n -1 ,
а залишок через b n
Р(х) =Q (x ) (x – £) + b n , то має місце тотожність
а о х п + a 1 x n-1 + … + a n = (b o x n-1 + … + b n-1 ) (х - £) +b n
Q (x ) - багаточлен, ступінь якого на 1 нижче від ступеня вихідного многочлена. Коефіцієнти многочлена Q (x ) визначаються за схемою Горнер.
а про
a 1
a 2
a n-1
a n
b o = a про
b 1 = a 1 + £· b o
b 2 = a 2 + £· b 1
b n-1 = a n-1 + £· b n-2
b n = a n + £· b n-1
У першому рядку цієї таблиці записують коефіцієнти багаточлена Р(х).
Якщо якийсь ступінь змінної відсутній, то у відповідній клітині таблиці пишеться 0.
Старший коефіцієнт приватного дорівнює старшому коефіцієнту поділеного ( а о = b o ). Якщо £ є коренем багаточлена, то в останній клітині виходить 0.
Приклад 2. Розкласти на множники з цілими коефіцієнтами
Р(х) = 2х 4 - 7х 3 - 3х 2 + 5х - 1
±1.
Підходить – 1.
Ділимо Р(х)на (х + 1)
2
– 7
– 3
5
– 1
– 1
2
– 9
6
– 1
0
2х 4 - 7х 3 - 3х 2 + 5х - 1 = (х + 1) (2х 3 - 9х 2 + 6х - 1)
Шукаємо ціле коріння серед вільного члена: ± 1
Оскільки старший член дорівнює 1, то корінням можуть бути дробові числа: – ; .
Підходить .
2
– 9
6
– 1
2
– 8
2
0
2х 3 – 9х 2 + 6х – 1 =(х – ) (2х 2 - 8х + 2) = (2х - 1) (х 2 - 4х + 1)
Тричлен х 2 - 4х + 1на множники з цілими коефіцієнтами не розкладається.
Завдання:
1. Розкладіть на множники з цілими коефіцієнтами:
а) х 3 - 2х 2 - 5х + 6
q: ± 1;
р: ±1; ±2; ±3; ±6
:± 1; ±2; ±3; ±6
Знаходимо раціональне коріння багаточлена f (1) = 1 – 2 – 5 + 6 = 0
х = 1
1
– 2
– 5
6
1
1
– 1
– 6
0
х 3 – 2х 2 – 5х + 6 = (х – 1) (х 2 – х – 6) = (х – 1) (х – 3) (х + 2)
Визначимо коріння квадратного рівняння
х 2 – х – 6 = 0
х = 3; х = - 2
б) 2х 3 + 5х 2 + х – 2
р: ±1; ± 2
q: ± 1; ± 2
:± 1; ±2; ±
Знайдемо коріння багаточлена третього ступеня
f (1) = 2 + 5 + 1 – 2 ≠ 0
f (-1) = - 2 + 5 - 1 - 2 = 0
Один із коренів рівняння х = - 1
2
5
1
– 2
– 1
2
3
– 2
0
2х 3 + 5х 2 + х – 2 = (х + 1) (2х 2 + 3х – 2) = (х + 1) (х + 2) (2х – 1)
Розкладемо квадратний тричлен 2х 2 + 3х - 2на множники
2х 2 + 3х - 2 = 2 (х + 2) (х - )
D = 9 + 16 = 25
х 1 = - 2; х 2 =
в) х 3 - 3х 2 + х + 1
р: ± 1
q : ± 1
:± 1
f (1) = 1 - 3 + 1 - 1 = 0
Одним із коренів багаточлена третього ступеня є х = 1
1
– 3
1
1
1
1
– 2
– 1
0
х 3 – 3х 2 + х + 1 = (х – 1) (х 2 – 2х – 1)
Знайдемо коріння рівняння х 2 - 2х - 1 = 0
D = 4 + 4 = 8
х 1 = 1 – 
х 2 = 1 + 
х 3 – 3х 2 + х + 1 = (х - 1) (х - 1 +  ) (х – 1 –
) (х – 1 –  )
)
г) х 3 - 2х - 1
р: ± 1
q : ± 1
:± 1
Визначимо коріння багаточлена
f (1) = 1 – 2 – 1 = – 2
f (-1) = - 1 + 2 - 1 = 0
Перший корінь х = - 1
1
0
– 2
– 1
– 1
1
– 1
– 1
0
х 3 – 2х – 1 = (х + 1) (х 2 – х – 1)
х 2 – х – 1 = 0
D = 1 + 4 = 5
х 1,2 = 
х 3 - 2х - 1 = (х + 1) (х -  ) (х –
) (х –  )
)
2. Розв'язати рівняння:
а) х 3 - 5х + 4 = 0
Визначимо коріння багаточлена третього ступеня
:± 1; ±2; ± 4
f (1) = 1 - 5 + 4 = 0
Одним з коренів є х = 1
1
0
– 5
4
1
1
1
– 4
0
х 3 - 5х + 4 = 0
(х - 1) (х 2 + х - 4) = 0
х 2 + х - 4 = 0
D = 1 + 16 = 17
х 1 =  ; х 2
=
; х 2
= 
Відповідь: 1;  ;
; 
б) х 3 - 8х 2 + 40 = 0
Визначимо коріння багаточлена третього ступеня.
:± 1; ±2; ±4; ±5; ±8; ±10; ±20; ± 40
f(1) ≠ 0
f (–1) ≠ 0
f (-2) = - 8 - 32 + 40 = 0
Одним з коренів є х = - 2
1
– 8
0
40
– 2
1
– 10
20
0
Розкладемо багаточлен третього ступеня на множники.
х 3 – 8х 2 + 40 = (х + 2) (х 2 – 10х + 20)
Знайдемо коріння квадратного рівняння х 2 - 10х + 20 = 0
D = 100 - 80 = 20
х 1 = 5 –  ; х 2
= 5 +
; х 2
= 5 + 
Відповідь: - 2; 5 –  ; 5 +
; 5 + 
в) х 3 - 5х 2 + 3х + 1 = 0
Шукаємо ціле коріння серед дільників вільного члена: ± 1
f (–1) = – 1 – 5 – 3 + 1 ≠ 0
f (1) = 1 - 5 + 3 + 1 = 0
Підходить х = 1
1
– 5
3
1
1
1
– 4
– 1
0
х 3 - 5х 2 + 3х + 1 = 0
(х - 1) (х 2 - 4х - 1) = 0
Визначаємо коріння квадратного рівняння х 2 - 4х - 1 = 0
D = 20
х = 2+  ; х = 2 -
; х = 2 - 
Відповідь: 2 –  ; 1; 2 +
; 1; 2 + 
г) 2х 4 - 5х 3 + 5х 2 – 2 = 0
р: ±1; ± 2
q: ± 1; ± 2
:± 1; ±2; ±
f (1) = 2 - 5 + 5 - 2 = 0
Один із коренів рівняння х = 1
2
– 5
5
0
– 2
1
2
– 3
2
2
0
2х 4 - 5х 3 + 5х 2 - 2 = 0
(х - 1) (2х 3 - 3х 2 + 2х + 2) = 0
Знаходимо за такою ж схемою коріння рівняння третього ступеня.
2х 3 - 3х 2 + 2х + 2 = 0
р: ±1; ± 2
q: ± 1; ± 2
:± 1; ±2; ±
f (1) = 2 – 3 + 2 + 2 ≠ 0
f (–1) = – 2 – 3 – 2 + 2 ≠ 0
f(2) = 16 – 12 + 4 + 2 ≠ 0
f (–2) = – 16 – 12 – 4 + 2 ≠ 0
f() = – + 1 + 2 ≠ 0
f(–) = – – – 1 + 2 ≠ 0
Наступний корінь рівняннях = -
2
– 3
2
2
2
– 4
4
0
2х 3 - 3х 2 + 2х + 2 = 0
(х + ) (2х 2 - 4х + 4) = 0
Визначимо коріння квадратного рівняння 2х 2 - 4х + 4 = 0
х 2 - 2х + 2 = 0
D = - 4< 0
Отже, корінням вихідного рівняння четвертого ступеня є
1 та –
Відповідь: –; 1
3. Знайдіть раціональне коріння багаточлена
а) х 4 - 2х 3 - 8х 2 + 13х - 24
q : ± 1
:± 1; ±2; ±3; ±4; ±6; ±8; ±12; ± 24
Підберемо один із коренів багаточлена четвертого ступеня:
f (1) = 1 – 2 – 8 + 13 – 24 ≠ 0
f (–1) = 1 + 2 – 8 – 13 – 24 ≠ 0
f (2) = 16 – 16 – 32 + 26 – 24 ≠ 0
f (–2) = 16 + 16 – 72 – 24 ≠ 0
f (-3) = 81 + 54 - 72 - 39 - 24 = 0
Один із коренів багаточлена х 0= – 3.
х 4 – 2х 3 – 8х 2 + 13х – 24 = (х + 3) (х 3 – 5х 2 + 7х + 8)
Знайдемо раціональне коріння багаточлена
х 3 - 5х 2 + 7х + 8
р: ±1; ±2; ±4; ± 8
q : ± 1
f (1) = 1 – 5 + 7 + 8 ≠ 0
f (–1) = – 1 – 5 – 7 – 8 ≠ 0
f(2) = 8 – 20 + 14 + 8 ≠ 0
f (–2) = – 8 – 20 – 14 + 8 ≠ 0
f (–4) = 64 – 90 – 28 + 8 ≠ 0
f(4) ≠ 0
f (–8) ≠ 0
f(8) ≠ 0
Крім числа x 0 = – 3 інших раціональних коренів немає.
б) х 4 - 2х 3 - 13х 2 - 38х - 24
р: ±1; ±2; ±3; ±4; ±6; ±8; ±12; ± 24
q : ± 1
f (1) = 1 + 2 – 13 – 38 – 24 ≠ 0
f (–1) = 1 – 2 – 13 + 38 – 24 = 39 – 39 = 0, тобто х = - 1корінь багаточлена
1
2
– 13
– 38
– 24
– 1
1
1
– 14
– 24
0
х 4 – 2х 3 – 13х 2 – 38х – 24 = (х + 1) (х 3 – х 2 – 14х – 24)
Визначимо коріння багаточлена третього ступеня х 3 - х 2 - 14х - 24
р: ±1; ±2; ±3; ±4; ±6; ±8; ±12; ± 24
q : ± 1
f (1) = – 1 + 1 + 14 – 24 ≠ 0
f (–1) = 1 + 1 – 14 – 24 ≠ 0
f (2) = 8 + 4 – 28 – 24 ≠ 0
f (–2) = – 8 + 4 + 28 – 24 ≠ 0
Значить, другий корінь багаточлена х = - 2
1
1
– 14
– 24
– 2
1
– 1
– 12
0
х 4 – 2х 3 – 13х 2 – 38х – 24 = (х + 1) (х 2 + 2) (х 2 – х – 12) =
= (х + 1) (х + 2) (х + 3) (х - 4)
Відповідь: – 3; – 2; – 1; 4
Застосування схеми Горнера під час вирішення рівнянь з параметром.
Знайдіть найбільше значення параметра а,при якому рівняння f (х) = 0має три різних кореня, один з яких х 0 .
а) f (х) = х 3 + 8х 2 + ах +b х 0 = – 3
Так один із коренів х 0 = – 3 , то за схемою Горнера маємо:
1
8
а
b
– 3
1
5
– 15 + а
0
0 = - 3 (- 15 + а) + b
0 = 45 - 3а + b
b = 3а - 45
х 3 + 8х 2 + ах + b = (х + 3) (х 2 + 5х + (а – 15))
Рівняння х 2 + 5х + (а - 15) = 0 D > 0
а = 1; b = 5; с = (а - 15),
D = b 2 - 4ac = 25 - 4 (a - 15) = 25 + 60 - 4a > 0,
85 – 4a > 0;
4a< 85;
a< 21
Найбільше значення параметра а,при якому рівняння
f (х) = 0має три корені, а = 21
Відповідь: 21.
б) f(x) = x 3 - 2x 2 + ax + b, x 0 = – 1
Так як один з коренів х 0= – 1, то за схемою Горнера маємо
1
– 2
a
b
– 1
1
– 3
3+а
0
x 3 – 2x 2 + ax + b = (x + 1) (x 2 – 3x + (3 + a))
Рівняння x 2 – 3 x + (3 + a ) = 0 повинно мати два корені. Це виконується лише в тому випадку, коли D > 0
a = 1; b = - 3; c = (3 + a),
D = b 2 - 4ac = 9 - 4 (3 + a) = 9 - 12 - 4a = - 3 - 4a > 0,
– 3 – 4a > 0;
– 4a< 3;
a < –
Найбільше значення а = - 1 а = 40
Відповідь: а = 40
г) f(x) = x 3 - 11x 2 + ax + b, x 0 = 4
Так як один з коренів х 0 = 4 , то за схемою Горнера маємо
1
– 11
a
b
4
1
– 7
– 28 + а
0
x 3 – 11x 2 + ax + b = (x – 4) (x 2 – 7x + (a – 28))
f (x ) = 0, якщо х = 4або x 2 – 7 x + (a – 28) = 0
D > 0, тобто
D = b 2 – 4ac = 49 – 4 (a – 28) = 49 + 112 – 4a = 161 – 4a >0,
161 - 4a > 0;
– 4a< – 161; f x 0 = – 5 , то за схемою Горнера маємо
1
13
a
b
– 5
1
8
– 40 + а
0
x 3 + 13x 2 + ax + b = (x +5) (x 2 +8x + (a – 40))
f (x ) = 0, якщо х = - 5або x 2 + 8 x + (a – 40) = 0
Рівняння має два корені, якщо D > 0
D = b 2 – 4ac = 64 – 4 (a – 40) = 64 + 1 60 – 4a = 224 – 4a >0,
224– 4a >0;
a< 56
Рівняння f (x ) має три корені при найбільшому значенні а = 55
Відповідь: а = 55
ж) f (x ) = x 3 + 19 x 2 + ax + b , x 0 = – 6
Так як один з коренів – 6 , то за схемою Горнера маємо
1
19
a
b
– 6
1
13
а – 78
0
x 3 + 19x 2 + ax + b = (x +6) (x 2 + 13x + (a – 78)) = 0
f (x ) = 0, якщо х = - 6або x 2 + 13 x + (a – 78) = 0
Друге рівняння має два корені, якщо
Щоб скористатися попереднім переглядом презентацій, створіть собі обліковий запис Google і увійдіть до нього: https://accounts.google.com
Підписи до слайдів:
Рівняння вищих ступенів (коріння багаточлена від однієї змінної).
План лекції. №1. Рівняння вищих ступенів у шкільному курсі математики. №2. Стандартний вид багаточлену. № 3. Цілі коріння многочлена. Схема Горнер. № 4. Дробове коріння багаточлена. № 5. Рівняння виду: (х + а) (х + в) (х + с) … = А № 6. Поворотні рівняння. № 7. Однорідні рівняння. №8. Метод невизначених коефіцієнтів. № 9. Функціонально – графічний метод. № 10. Формули Вієта для рівнянь вищих ступенів. № 11. Нестандартні методи розв'язання рівнянь вищих ступенів.
Рівняння вищих ступенів у шкільному курсі математики. 7 клас. Стандартний вид багаточлену. Дії із багаточленами. Розкладання многочлена на множники. У звичайному класі 42 години, у спеціалізованому класі 56 годин. 8 спецклас. Цілі коріння многочлена, розподіл багаточленів, поворотні рівняння, різницю і сума п – их ступенів двочлена, метод невизначених коефіцієнтів. Ю.М. Макарічев «Додаткові розділи до шкільного курсу алгебри 8 класу», М.Л.Галицький Збірник завдань з алгебри 8 – 9 клас». 9 спецклас. Раціональне коріння багаточлена. Узагальнені поворотні рівняння. Формули Вієта для рівнянь вищих ступенів. Н.Я. Віленкін «Алгебра 9 клас із поглибленим вивченням. 11 спецклас. Тотожність багаточленів. Багаточлен від кількох змінних. Функціонально – графічний метод розв'язання рівнянь вищих ступенів.
Стандартний вид багаточлену. Багаточлен Р(х) = а ⁿ х ⁿ + а п-1 х п-1 + … + а₂х ² + а₁х + а₀. Називається багаточлен стандартного вигляду. а п х ⁿ – старший член багаточлена а п – коефіцієнт при старшому члені многочлена. При а п = 1 Р(х) називається наведеним багаточлен. а ₀ - вільний член многочлена Р(х). п – ступінь многочлена.
Цілі коріння многочлена. Схема Горнер. Теорема № 1. Якщо ціле число а є коренем многочлена Р(х), то а дільник вільного члена Р(х). Приклад №1. Розв'яжіть рівняння. Х⁴ + 2х³ = 11х² – 4х – 4 Наведемо рівняння до стандартного вигляду. Х⁴ + 2х³ - 11х² + 4х + 4 = 0. Маємо багаточлен Р(х) = х⁴ + 2х³ - 11х² + 4х + 4 Дільники вільного члена: ± 1, ± 2, ±4. х = 1 корінь рівняння, т.к. Р(1) = 0, х = 2 корінь рівняння, т.к. Р(2) = 0 Теорема Безу. Залишок від розподілу многочлена Р(х) на двочлен (х – а) дорівнює Р(а). Слідство. Якщо а – корінь многочлена Р(х), то Р(х) поділяється на (х – а). У нашому рівнянні Р(х) ділиться на (х – 1) і (х – 2), отже, і (х – 1) (х – 2). При розподілі Р(х) на (х ² - 3х + 2) у приватному виходить тричлен х ² + 5х + 2 = 0, який має коріння х = (-5 ± √17)/2
Дробне коріння багаточлена. Теорема №2. Якщо р/g корінь багаточлена Р(х), то р – дільник вільного члена, g – дільник коефіцієнта старшого члена Р(х). Приклад № 2. Розв'яжіть рівняння. 6х³ - 11х² - 2х + 8 = 0. Дільники вільного члена: ±1, ±2, ±4, ±8. Жодне з цих чисел не задовольняє рівняння. Цілого коріння немає. Натуральні дільники коефіцієнта старшого члена Р(х): 1, 2, 3, 6. Можливе дробове коріння рівняння: ±2/3, ±4/3, ±8/3. Перевіркою переконуємося, що Р(4/3) = 0. Х = 4/3 корінь рівняння. За схемою Горнера розділимо Р(х) на (х – 4/3).
Приклади самостійного рішення. Розв'яжіть рівняння: 9х³ - 18х = х – 2, х³ - х² = х – 1, х³ - 3х² -3х + 1 = 0, Х⁴ - 2х³ + 2х – 1 = 0, Х⁴ - 3х² + 2 = 0 , х ⁵ + 5х³ - 6х² = 0, х ³ + 4х² + 5х + 2 = 0, Х⁴ + 4х³ - х ² - 16х – 12 = 0 4х³ + х ² - х + 5 = 0 3х⁴ + 5х³ + 10 = 0. Відповіді: 1) ±1/3; 2 2) ±1, 3) -1; 2 ±√3 , 4) ±1, 5) ± 1; ±√2 , 6) 0; 1 7) -2; -1, 8) -3; -1; ±2, 9) - 5/4 10) -2; - 5/3; 1.
Рівняння виду (х + а) (х + в) (х + с) (х + d) ... = А. Приклад №3. Розв'яжіть рівняння (х + 1) (х + 2) (х + 3) (х + 4) = 24. а = 1, в = 2, с = 3, d = 4 а + d = в + с. Перемножуємо першу дужку з четвертою та другу з третьою. (х + 1) (х + 4) (х + 20 (х + 3) = 24. (х ² + 5х + 4) (х ² + 5х + 6) = 24. Нехай х ² + 5х + 4 = у тоді у(у + 2) = 24, у² + 2у – 24 = 0 у₁ = - 6, у₂ = 4. х ² + 5х + 4 = -6 або х ² + 5х + 4 = 4. х ² + 5х + 10 = 0, Д
Приклади самостійного рішення. (х + 1) (х + 3) (х + 5) (х + 7) = -15, х (х + 4) (х + 5) (х + 9) + 96 = 0, х (х + 3) )(х + 5)(х + 8) + 56 = 0, (х - 4)(х - 3)(х - 2)(х - 1) = 24, (х - 3)(х -4)( х - 5) (х - 6) = 1680, (х - 5х) (х + 3) (х - 8) + 108 = 0, (х + 4) ² (х + 10) (х - 2) + 243 = 0 (х ² + 3х + 2) (х ² + 9х + 20) = 4, Вказівка: х + 3х + 2 = (х + 1) (х + 2), х ² + 9х + 20 = (х + 4) (х + 5) Відповіді: 1) -4 ± √ 6; - 6; - 2. 6) - 1; 6; (5± √97)/2 7) -7; -1; -4±3.
Поворотні рівняння. Визначення №1. Рівняння виду: ах⁴ + вх ³ + сх ² + вх + а = 0 називається поворотним рівнянням четвертого ступеня. Визначення №2. Рівняння виду: ах⁴ + вх ³ + сх ² + квх + к² а = 0 називається узагальненим поворотним рівнянням четвертого ступеня. к² а: а = к²; кв: в = к. Приклад №6. Розв'яжіть рівняння х ⁴ - 7х³ + 14х² - 7х + 1 = 0. Ділимо обидві частини рівняння на х ² . х ² - 7х + 14 - 7 / х + 1 / х ² = 0, (х ² + 1 / х ²) - 7 (х + 1 / х) + 14 = 0. Нехай х + 1 / х = у. Зводимо обидві частини рівності квадрат. х ² + 2 + 1/ х ² = у² , х ² + 1/ х ² = у² - 2. Отримуємо квадратне рівняння у² - 7у + 12 = 0, у ₁ = 3, у ₂ = 4. х + 1 / х = 3 або х + 1/ х = 4. Отримуємо два рівняння: х ² - 3х + 1 = 0, х ² - 4х + 1 = 0. Приклад №7. 3х⁴ - 2х³ - 31х² + 10х + 75 = 0. 75:3 = 25, 10:(– 2) = -5, (-5)² = 25. Умова узагальненого поворотного рівняння виконується к= -5. Вирішується аналогічно до прикладу №6. Ділимо обидві частини рівняння на х ². 3х⁴ - 2х – 31 + 10/х + 75/х² = 0, 3(х⁴ + 25/х²) – 2(х – 5/х) – 31 = 0. Нехай х – 5/х = у, зводимо обидві частини рівності квадрат х ² - 10 + 25/ х ² = у² , х ² + 25/ х ² = у² + 10. Маємо квадратне рівняння 3у² - 2у – 1 = 0, у₁ = 1, у₂ = - 1/ 3. х - 5/х = 1 або х - 5/х = -1/3. Отримуємо два рівняння: х ² - х - 5 = 0 і 3х ² + х - 15 = 0
Приклади самостійного рішення. 1. 78х⁴ - 133х³ + 78х² - 133х + 78 = 0,2. - 38х² -10х + 24 = 0, 5. х⁴ + 2х³ - 11х² + 4х + 4 = 0, 6. х⁴ - 5х³ + 10х² -10х + 4 = 0. Відповіді: 1) 2/3; 3/2, 2) 1; 2 3) -1 ±√3; (3±√17)/2, 4) -1±√3; (7±√337)/12 5) 1; 2; (-5± √17)/2, 6) 1; 2.
Однорідні рівняння. Визначення. Рівняння виду а₀ u³ + а₁ u² v + а₂ uv² + а₃ v³ = 0 називається однорідним рівнянням третього ступеня щодо u v . Визначення. Рівняння виду а₀ u⁴ + а₁ u³v + а₂ u²v² + а₃ uv³ + а₄ v⁴ = 0 називається однорідним рівнянням четвертого ступеня щодо u v . Приклад №8. Розв'яжіть рівняння (х ² - х + 1)³ + 2х⁴(х ² - х + 1) – 3х⁶ = 0 Однорідне рівняння третього ступеня щодо u = х ²-х + 1, v = х². Ділимо обидві частини рівняння на х ⁶. Попередньо перевірили, що х = 0 не є коренем рівняння. (х ² - х + 1/х ²)³ + 2(х ² - х + 1/х ²) – 3 = 0. (х ² - х + 1)/х ²) = у, у ³ + 2у – 3 = 0, у = 1 корінь рівняння. Ділимо багаточлен Р(х) = у³ + 2у – 3 на у – 1 за схемою Горнера. У приватному отримуємо тричлен, який не має коріння. Відповідь: 1.
Приклади самостійного рішення. 1. 2(х ² + 6х + 1)² + 5(Х² + 6Х + 1)(Х² + 1) + 2(Х² + 1)² = 0, 2. (Х + 5)⁴ - 13Х²(Х + 5)² + 36Х⁴ = 0, 3. 2(Х² + Х + 1)² - 7(Х – 1)² = 13(Х³ - 1), 4. 2(Х -1)⁴ - 5(Х² - 3Х + 2)² + 2(х – 2)⁴ = 0,5. -2±√3, 2) -5/3; -5/4; 5/2; 5 3) -1; -1/2; 2;4 4) ±√2; 3±√2, 5) Коренів немає.
Метод невизначених коефіцієнтів. Теорема №3. Два многочлени Р(х) і G(х) тотожні тоді й тільки тоді, коли вони мають однаковий ступінь та коефіцієнти при однойменних ступенях змінної в обох багаточленах рівні. Приклад №9. Розкласти на множники багаточлен у⁴ - 4у ³ + 5у ² - 4у + 1. у ⁴ - 4у ³ + 5у ² - 4у + 1 = (у ² + ву + с) (у² + в₁у + с₁) = у ⁴ +у³ (в₁ + в) + у² (с₁ + с + в₁в) + у (вс ₁ + св ₁) + сс ₁. Відповідно до теореми №3 маємо систему рівнянь: в₁ + в = -4, с₁ + с + в₁в = 5, вс + + св ₁ = -4, сс ₁ = 1. Необхідно вирішити систему в цілих числах. Останнє рівняння у цілих числах може мати розв'язки: с = 1, с₁ =1; с = -1, с₁ = -1. Нехай з = с ₁ = 1, тоді з першого рівняння маємо в ₁ = -4 - ст. Підставляємо у друге рівняння системи в ² + 4в + 3 = 0, в = -1, в ₁ = -3 або в = -3, в ₁ = -1. Ці значення відповідають третьому рівнянню системи. При с = с ₁ = -1 Д
Приклад №10. Розкласти на множники многочлен у ³ - 5у + 2. у ³ -5у + 2 = (у + а) (у ² + ву + с) = у ³ + (а + в) у ² + (ав + с) у + ас. Маємо систему рівнянь: а + в = 0, ав + с = -5, ас = 2. Можливі цілі рішення третього рівняння: (2; 1), (1; 2), (-2; -1), (-1 ;-2). Нехай а = -2, з = -1. З першого рівняння системи = 2, що задовольняє другому рівнянню. Підставляючи дані значення шукану рівність отримаємо відповідь: (у – 2) (у² + 2у – 1). Другий спосіб. У - 5у + 2 = у -5у + 10 - 8 = (у - 8) - 5 (у - 2) = (у - 2) (у + 2у -1).
Приклади самостійного рішення. Розкладіть на множники багаточлени: 1. у⁴ + 4у³ + 6у² +4у -8, 2. у⁴ - 4у³ + 7у² - 6у + 2, 3. х⁴ + 324, 4. у⁴ -8у³ + 24у² -32у + 1. Розв'яжіть рівняння, використовуючи метод розкладання на множники: а) х ⁴ -3х² + 2 = 0, б) х ⁵ +5х³ -6х² = 0. Відповіді: 1) (у² +2у -2) 2) (у – 1)²(у² -2у + 2), 3) (х ² -6х + 18)(х ² + 6х + 18), 4) (у – 1)(у – 3)(у² - 4у + 5), 5а) ±1; ±√2 , 5б) 0; 1.
Функціонально – графічний метод розв'язання рівнянь вищих ступенів. Приклад №11. Розв'яжіть рівняння х ⁵ + 5х -42 = 0. Функція у = х ⁵ зростаюча, функція у = 42 – 5х спадна (к
Приклади самостійного рішення. 1. Використовуючи властивість монотонності функції, доведіть, що рівняння має єдиний корінь, і знайдіть цей корінь: а) х ³ = 10 – х, б) х ⁵ + 3х³ - 11√2 – х. Відповіді: а) 2; б) √2. 2. Розв'яжіть рівняння, використовуючи функціонально – графічний метод: а) х = ³ х, б) l х l = ⁵ √х, в) 2 = 6 – х, г) (1/3) = х +4, д ) (х – 1)² = log₂ х, е) log = (х + ½)², ж) 1 - √х = ln х, з) √х – 2 = 9/х. Відповіді: а) 0; ±1, б) 0; 1, в) 2, г) -1, д) 1; 2, е) ½, ж) 1, з) 9.
Формули Вієта для рівнянь вищих ступенів. Теорема №5 (Теореме Вієта). Якщо рівняння а х ⁿ + а х ⁿ + … + а₁х + а₀ має n різних дійсних коренів х ₁, х ₂, … , х, то вони задовольняють рівностям: Для квадратного рівняння ах ² + вх + с = о: х ₁ ₂ = -в/а, х₁х ₂ = с/а; Для кубічного рівняння а₃х ³ + а₂х ² + а₁х + а₀ = о: х ₁ + х ₂ + х ₃ = -а₂/а₃; х₁х ₂ + х₁х ₃ + х₂х ₃ = а₁/а₃; х₁х₂х ₃ = -а₀/а₃; …, для рівняння n – ступеня: х ₁ + х ₂ + … х = - а / а, х₁х ₂ + х₁х ₃ + … + х х = а / а, … , х₁х ₂·… · х = (- 1 ) ⁿ а₀/а. Виконується і зворотна теорема.
Приклад №13. Напишіть кубічне рівняння, коріння якого обернене корінням рівняння х ³ - 6х² + 12х – 18 = 0, а коефіцієнт при х ³ дорівнює 2. 1. За теоремою Вієта для кубічного рівняння маємо: х ₁ + х ₂ + х ₃ ₂ + х₁х ₃ + х₂х ₃ = 12, х₁х₂х ₃ = 18. 2. Складаємо зворотні величини даним корінням і для них застосовуємо зворотну теорему Вієта. 1/ х ₁ + 1/ х ₂ + 1/ х ₃ = (х₂х ₃ + х₁х ₃ + х₁х ₂)/ х₁х₂х ₃ = 12/18 = 2/3. 1/ х₁х ₂ + 1/ х₁х ₃ + 1/ х₂х ₃ = (х ₃ + х ₂ + х ₁)/ х₁х₂х ₃ = 6/18 = 1/3, 1/ х₂. Отримуємо рівняння х³ +2/3х² + 1/3х – 1/18 = 0 · 2 Відповідь: 2х³ + 4/3х² + 2/3х -1/9 = 0.
Приклади самостійного рішення. 1. Напишіть кубічне рівняння, коріння якого обернене квадратам коренів рівняння х ³ - 6х² + 11х – 6 = 0, а коефіцієнт при х ³ дорівнює 8. Відповідь: 8х³ - 98/9х² + 28/9х -2/9 = 0. Нестандартні методи розв'язків рівнянь вищих ступенів. Приклад №12. Розв'яжіть рівняння х ⁴ -8х + 63 = 0. Розкладемо ліву частину рівняння на множники. Виділимо точні квадрати. Х⁴ - 8х + 63 = (х ⁴ + 16х² + 64) – (16х² + 8х + 1) = (х ² + 8)² - (4х + 1)² = (х ² + 4х + 9)(х ² - 4х + 7) = 0. Обидва дискримінанти негативні. Відповідь: немає коріння.
Приклад №14. Розв'яжіть рівняння 21х³ + х ² - 5х – 1 = 0. Якщо вільний член рівняння дорівнює ± 1, то рівняння перетворюється на наведене рівняння за допомогою заміни х = 1/у. 21/у³ + 1/у² - 5/у – 1 = 0 · у³, у³ + 5у² -у – 21 = 0. у = -3 корінь рівняння. (у + 3) (у + 2у -7) = 0, у = -1 ± 2√2. х ₁ = -1/3, х ₂ = 1/ -1 + 2√2 = (2√2 + 1)/7, Х₃ = 1/-1 -2√2 =(1-2√2)/7 . Приклад №15. Розв'яжіть рівняння 4х³-10х² + 14х – 5 = 0. Помножимо обидві частини рівняння на 2. 8х³ -20х² + 28х – 10 = 0, (2х)³ - 5(2х)² + 14·(2х) -10 = 0. Введемо нову змінну у = 2х, отримаємо наведене рівняння у - 5у + 14у -10 = 0, у = 1 корінь рівняння. (у - 1) (у ² - 4у + 10) = 0, Д
Приклад №16. Довести, що рівняння х ⁴ + х ³ + х – 2 = 0 має один позитивний корінь. Нехай f(х) = х ⁴ + х ³ + х – 2, f'(х) = 4х³ + 3х² + 1 > о при х > о. Функція f(х) зростаюча за х > о, а значення f(о) = -2. Вочевидь, що рівняння має одне позитивний корінь ч.т.д. Приклад №17. Розв'яжіть рівняння 8х(2х² - 1)(8х⁴ - 8х² + 1) = 1. І.Ф.Шарігін «Факультативний курс з математики для 11 класу».М. Освіта 1991 стр90. 1. l х l 1 2х² - 1 > 1 і 8х⁴ -8х² + 1 > 1 2. Зробимо заміну х = cosy у € (0; п). При інших значеннях, значення х повторюються, а рівняння має не більше 7 коренів. 2х² - 1 = 2 cos²y - 1 = cos2y, 8х⁴ - 8х² + 1 = 2 (2х² - 1)² - 1 = 2 cos²2y - 1 = cos4y. 3. Рівняння набуває вигляду 8 cosycos2ycos4y = 1. Помножуємо обидві частини рівняння на siny . 8 sinycosycos2ycos4y = siny . Застосовуючи 3 рази формулу подвійного кута, отримаємо рівняння sin8y = siny , sin8y – siny = 0
Закінчення рішення прикладу №17. Застосовуємо формулу різниці синусів. 2 sin7y/2 · cos9y/2 = 0. Враховуючи, що у € (0;п), у = 2пк/3, к = 1, 2, 3 або у = п /9 + 2пк/9, до =0, 1, 2, 3. Повертаючись до змінної х отримуємо відповідь: Cos2 п/7, cos4 п/7, cos6 п/7, cos п/9, ½, cos5 п/9, cos7 п/9. Приклади самостійного рішення. Знайти всі значення а, при яких рівняння (х ² + х) (х ² + 5х + 6) = а має рівно три корені. Відповідь: 9/16. Вказівка: побудувати графік лівої частини рівняння. Fmax = f(0) = 9/16. Пряма у = 9/16 перетинає графік функції у трьох точках. Розв'яжіть рівняння (х ² + 2х) ² - (х + 1) ² = 55. Відповідь: -4; 2. Розв'яжіть рівняння (х + 3)⁴ + (х + 5)⁴ = 16. Відповідь: -5; -3. Розв'яжіть рівняння 2(х ² + х + 1)² -7(х – 1)² = 13(х ³ - 1). Відповідь: -1; -1/2, 2;4 Знайдіть число дійсних коренів рівняння х ³ - 12х + 10 = 0 на [-3; 3/2]. Вказівка: знайти похідну та дослідити на монот.
Приклади самостійного рішення (продовження). 6. Знайдіть число дійсних коренів рівняння х ⁴ - 2х³ + 3/2 = 0. Відповідь: 2 7. Нехай х ₁, х ₂, х ₃ - коріння багаточлена Р(х) = х ³ - 6х² -15х + 1. Знайдіть Х₁² + х₂² + х₃². Відповідь: 66. Вказівка: застосуйте теорему Вієта. 8. Доведіть, що при а > про і довільному речовинному рівнянні х ³ + ах + в = о має лише один речовий корінь. Вказівка: проведіть доказ протилежного. Застосуйте теорему Вієта. 9. Розв'яжіть рівняння 2(х ² + 2)² = 9(х ³ + 1). Відповідь: ½; 1; (3 ± √13)/2. Вказівка: приведіть рівняння до однорідного, використовуючи рівність Х² + 2 = х + 1 + х ² - х + 1, х ³ + 1 = (х + 1)(х ² - х + 1). 10. Розв'яжіть систему рівнянь х + у = х², 3у – х = у². Відповідь: (0; 0), (2; 2), (√2; 2 - √2), (- √2; 2 + √2). 11. Розв'яжіть систему: 4у² -3ху = 2х -у, 5х² - 3у² = 4х - 2у. Відповідь: (о;о), (1;1),(297/265; - 27/53).
Контрольна робота. 1 варіант. 1. Розв'яжіть рівняння (х ² + х) - 8 (х ² + х) + 12 = 0. 2. Розв'яжіть рівняння (х + 1) (х + 3) (х + 5) (х + 7) = - 15 3. Розв'яжіть рівняння 12х²(х – 3) + 64(х – 3)² = х ⁴. 4. Розв'яжіть рівняння х ⁴ - 4х³ + 5х² - 4х + 1 = 0 5. Розв'яжіть систему арівань: х ² + 2у² - х + 2у = 6, 1,5 х² + 3у² - х + 5у = 12.
2 варіант 1. (х ² - 4х) ² + 7 (х ² - 4х) + 12 = 0. 2. х (х + 1) (х + 5) (х + 6) = 24. 3. х ⁴ + 18(х + 4)² = 11х²(х + 4). 4. х⁴ - 5х³ + 6х² - 5х + 1 = 0. 5. х² - 2ху + у² + 2х²у - 9 = 0, х - у - х²у + 3 = 0. 3 варіант. 1. (х ² + 3х) ² - 14 (х ² + 3х) + 40 = 0 2. (х - 5) (х-3) (х + 3) (х + 1) = - 35. 3. х4 + 8х ² (х + 2) = 9 (х + 2) ². 4. х ⁴ - 7х ³ + 14х ² - 7х + 1 = 0. 5. х + у + х ² + у ² = 18, ху + х ² + у ² = 19.
4 варіант. (х ² - 2х) ² - 11 (х ² - 2х) + 24 = о. (Х-7) (Х-4) (Х-2) (Х + 1) = -36. Х⁴ + 3(х -6)² = 4х²(6 – х). Х⁴ - 6х³ + 7х² - 6х + 1 = 0. Х² + 3ху + у² = - 1, 2х² - 3ху – 3у² = - 4. Додаткове завдання: Залишок від поділу багаточлена Р(х) на (х – 1) дорівнює 4, залишок від розподілу на (х + 1) дорівнює2, а при розподілі на (х – 2) дорівнює 8. Знайти залишок від розподілу Р(х) на (х ³ - 2х ² - х + 2).
Відповіді та вказівки: варіант №1 №2. №3. №4. №5. 1. - 3; ±2; 1 1;2;3. -5; -4; 1; 2. Однорідне рівняння: u = x -3, v = x² -2; -1; 3; 4. (2; 1); (2/3; 4/3). Вказівка: 1 · (-3) + 2 · 2 2. -6; -2; -4±√6. -3±2√3; - 4; - 2. 1±√11; 4; - 2. Однорідне рівняння: u = x + 4, v = x ² 1; 5;3±√13. (2; 1); (0; 3); (- 3; 0). Вказівка: 2 · 2 + 1. 3. -6; 2; 4; 12 -3; -2; 4; 12 -6; -3; -1; 2. Однорідне u = x + 2, v = x ² -6; ±3; 2 (2;3), (3;2), (-2 + √7; -2 - √7); (-2 - √7; -2 + √7). Вказівка: 2-1. 4. (3±√5)/2 2±√3 2±√3; (3±√5)/2 (5±√21)/2 (1;-2), (-1;2). Вказівка: 1 · 4 + 2 .
Вирішення додаткового завдання. За теоремою Безу: Р(1) = 4, Р(-1) = 2, Р(2) = 8. Р(х) = G(x) (х ³ - 2х ² - х + 2) с. Підставляємо 1; - 1; 2. Р(1) = G(1) · 0 + а + в + с = 4, а + в + с = 4. Р(-1) = а – + с = 2, Р(2) = 4а² + 2в + с = 8. Вирішуючи отриману систему із трьох рівнянь отримаємо: а = в = 1, с = 2. Відповідь: х ² + х + 2.
Критерій №1 – 2 бали. 1 бал – одна обчислювальна помилка. № 2,3,4 – по 3 бали. 1 бал – призвели до квадратного рівняння. 2 бали – одна обчислювальна помилка. № 5. - 4 бали. 1 бал – висловили одну змінну через іншу. 2 бали – отримали одне із рішень. 3 бали – одна обчислювальна помилка. Додаткове завдання: 4 бали. 1 бал – застосували теорему Безу для всіх чотирьох випадків. 2 бали – склали систему рівнянь. 3 бали – одна обчислювальна помилка.
У випадку рівняння, що має ступінь вище 4 , не можна дозволити в радикалах. Але іноді ми все ж таки можемо знайти коріння багаточлена, що стоїть ліворуч у рівнянні вищого ступеня, якщо представимо його у вигляді твору багаточленів у ступеню не більше 4-х. Вирішення таких рівнянь базується на розкладі багаточлена на множники, тому радимо вам повторити цю тему перед вивченням цієї статті.
Найчастіше доводиться мати справу з рівняннями найвищих ступенів із цілими коефіцієнтами. У цих випадках ми можемо спробувати знайти раціональне коріння, а потім розкласти багаточлен на множники, щоб потім перетворити його на рівняння нижчого ступеня, яке буде просто вирішити. В рамках цього матеріалу ми розглянемо такі приклади.
Рівняння вищого ступеня із цілими коефіцієнтами
Усі рівняння, що мають вигляд a n x n + a n – 1 x n – 1 + . . . + a 1 x + a 0 = 0 ми можемо привести до рівняння тієї ж ступеня за допомогою множення обох частин на a n n - 1 і здійснивши заміну змінної виду y = a n x:
a n x n + a n - 1 x n - 1 +. . . + a 1 x + a 0 = 0 a n · x n + a n - 1 · a n n - 1 · x n - 1 + … + a 1 · (a n) n - 1 · x + a 0 · (a n) n - 1 = 0 y = a n x ⇒ y n + b n - 1 y n - 1 + … + b 1 y + b 0 = 0
Ті коефіцієнти, що вийшли у результаті, також будуть цілими. Таким чином, нам потрібно буде вирішити наведене рівняння n-го ступеня з цілими коефіцієнтами, що має вигляд x n + a n x n - 1 + … + a 1 x + a 0 = 0 .
Обчислюємо цілі корені рівняння. Якщо рівняння має ціле коріння, потрібно шукати їх серед дільників вільного члена a 0 . Випишемо їх і підставлятимемо у вихідну рівність по черзі, перевіряючи результат. Як тільки ми здобули тотожність і знайшли один із коренів рівняння, то можемо записати його у вигляді x - x 1 · P n - 1 (x) = 0 . Тут x 1 є коренем рівняння, а P n - 1 (x) є приватним від поділу x n + a n x n - 1 + … + a 1 x + a 0 на x - x 1 .
Підставляємо решту виписаних дільників у P n - 1 (x) = 0 , почавши з x 1 , оскільки коріння може повторюватися. Після отримання тотожності корінь x 2 вважається знайденим, а рівняння може бути записано у вигляді (x - x 1) (x - x 2) · P n - 2 (x) = 0. Тут P n - 2 (x) буде приватним від розподілу P n - 1 (x) на x - x 2 .
Продовжуємо і надалі перебирати дільники. Знайдемо всі цілі коріння і позначимо їх кількість як m. Після цього вихідне рівняння можна як x - x 1 x - x 2 · … · x - x m · P n - m (x) = 0 . Тут P n - m (x) є многочленом n - m-ного ступеня. Для підрахунку зручно використати схему Горнера.
Якщо у нас вихідне рівняння має цілі коефіцієнти, ми не можемо отримати в результаті дробове коріння.
У нас у результаті вийшло рівняння P n - m (x) = 0, коріння якого може бути знайдено будь-яким зручним способом. Вони можуть бути ірраціональними чи комплексними.
Покажемо на прикладі, як застосовується така схема рішення.
Приклад 1
Умова:Знайдіть розв'язок рівняння x 4 + x 3 + 2 x 2 - x - 3 = 0 .
Рішення
Почнемо з знаходження цілого коріння.
Ми маємо вільний член, рівний мінус трьом. Він має дільники, рівні 1 , - 1 , 3 і - 3 . Підставимо їх у вихідне рівняння та подивимося, які з них дадуть у результаті тотожності.
При x , що дорівнює одиниці, ми отримаємо 1 4 + 1 3 + 2 · 1 2 - 1 - 3 = 0 , отже, одиниця буде коренем даного рівняння.
Тепер виконаємо поділу багаточлена x 4 + x 3 + 2 x 2 - x - 3 на (х - 1) у стовпчик:
Отже, x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.
1 3 + 2 · 1 2 + 4 · 1 + 3 = 10 ≠ 0 (-1) 3 + 2 · (- 1) 2 + 4 · - 1 + 3 = 0
У нас вийшло тотожність, значить, ми знайшли ще один корінь рівняння, рівний - 1 .
Ділимо багаточлен x 3 + 2 x 2 + 4 x + 3 на (х + 1) у стовпчик:
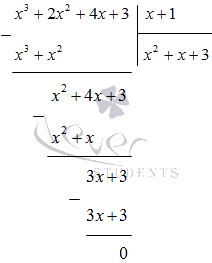
Отримуємо, що
x 4 + x 3 + 2 x 2 - x - 3 = (x - 1) (x 3 + 2 x 2 + 4 x + 3) = = (x - 1) (x + 1) (x 2 + x + 3)
Підставляємо черговий дільник на рівність x 2 + x + 3 = 0 , починаючи з - 1:
1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0
Рівності, отримані в результаті, будуть невірними, отже, рівняння більше немає цілого коріння.
Коріння, що залишилося, буде корінням виразу x 2 + x + 3 .
D = 1 2 - 4 · 1 · 3 = - 11< 0
З цього випливає, що цей квадратний тричлен не має дійсних коренів, але є комплексно пов'язані: x = - 1 2 ± i 11 2 .
Уточнимо, що замість поділу в стовпчик можна застосовувати схему Горнера. Це робиться так: після того, як ми визначили перший корінь рівняння, заповнюємо таблицю.
У таблиці коефіцієнтів ми одразу можемо побачити коефіцієнти частки від поділу многочленів, отже, x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3 .
Після знаходження наступного кореня, що дорівнює - 1, ми отримуємо наступне:
Відповідь:х = - 1, х = 1, x = - 1 2 ± i 11 2 .
Приклад 2
Умова:розв'яжіть рівняння x 4 - x 3 - 5 x 2 + 12 = 0 .
Рішення
У вільного члена є дільники 1 , - 1 , 2 , - 2 , 3 , - 3 , 4 , - 4 , 6 , - 6 , 12 , - 12 .
Перевіряємо їх по порядку:
1 4 - 1 3 - 5 · 1 2 + 12 = 7 ≠ 0 (-1) 4 - (- 1) 3 - 5 · (- 1) 2 + 12 = 9 ≠ 0 2 4 · 2 3 - 5 · 2 2 + 12 = 0
Значить x = 2 буде коренем рівняння. Розділимо x 4 - x 3 - 5 x 2 + 12 на х - 2, скориставшись схемою Горнера:
У результаті отримаємо x - 2 (x 3 + x 2 - 3 x - 6) = 0 .
2 3 + 2 2 - 3 · 2 - 6 = 0
Значить, 2 знову буде коренем. Розділимо x 3 + x 2 - 3 x - 6 = 0 на x - 2:
У результаті отримаємо (x – 2) 2 · (x 2 + 3 x + 3) = 0 .
Перевірка дільників, що залишилися, сенсу не має, оскільки рівність x 2 + 3 x + 3 = 0 швидше і зручніше вирішити за допомогою дискримінанта.
Розв'яжемо квадратне рівняння:
x 2 + 3 x + 3 = 0 D = 3 2 - 4 · 1 · 3 = - 3< 0
Отримуємо комплексно пов'язану пару коренів: x = - 3 2 ± i 3 2 .
Відповідь: x = - 3 2 ± i 3 2 .
Приклад 3
Умова:знайдіть для рівняння x 4 + 1 2 x 3 - 5 2 x - 3 = 0 дійсне коріння.
Рішення
x 4 + 1 2 x 3 - 5 2 x - 3 = 0 2 x 4 + x 3 - 5 x - 6 = 0
Виконуємо домноження 2 3 обох частин рівняння:
2 x 4 + x 3 - 5 x - 6 = 0 2 4 · x 4 + 2 3 x 3 - 20 · 2 · x - 48 = 0
Замінюємо змінні y = 2 x:
2 4 · x 4 + 2 3 x 3 - 20 · 2 · x - 48 = 0 y 4 + y 3 - 20 y - 48 = 0
У результаті у нас вийшло стандартне рівняння 4-го ступеня, яке можна вирішити за стандартною схемою. Перевіримо дільники, розділимо і отримаємо в результаті, що воно має 2 дійсних кореня y = - 2, y = 3 і два комплексних. Рішення цілком тут ми не наводитимемо. Через заміну дійсним корінням даного рівняння будуть x = y 2 = - 2 2 = - 1 і x = y 2 = 3 2 .
Відповідь: x 1 = - 1 , x 2 = 3 2
Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl+Enter
Текст роботи розміщено без зображень та формул.
Повна версія роботи доступна у вкладці "Файли роботи" у форматі PDF
Вступ
Розв'язання рівнянь алгебри вищих ступенів з одним невідомим являє собою одну з найважчих і найдавніших математичних завдань. Цими завданнями займалися найвидатніші математики давнини.
Розв'язання рівнянь n-ого ступеня є важливим завданням і для сучасної математики. Інтерес до них досить великий, оскільки ці рівняння тісно пов'язані з пошуком коренів рівнянь, що не розглядаються шкільною програмою з математики.
Проблема:відсутність навичок вирішення рівнянь вищих ступенів різними способами в учнів заважає їм успішно підготуватися до підсумкової атестації з математики та математичних олімпіадів, навчання у профільному математичному класі.
Перелічені факти визначили актуальністьнашої роботи «Рішення рівнянь найвищих ступенів».
Володіння найпростішими способами розв'язання рівнянь n-го ступеня скорочує час до виконання завдання, від якого залежить результат роботи та якість процесу навчання.
Мета роботи:вивчення відомих способів вирішення рівнянь вищих ступенів та виявлення найбільш доступних з них для практичного застосування.
Виходячи з поставленої мети, у роботі визначено такі завдання:
Вивчити літературу та Інтернет-ресурси на цю тему;
Ознайомитись з історичними фактами, що стосуються цієї теми;
Описати різні способи вирішення рівнянь вищих ступенів
порівняти ступінь складності кожного з них;
Ознайомити однокласників зі способами розв'язання рівнянь вищих ступенів;
Створити добірку рівнянь для практичного застосування кожного із розглянутих способів.
Об'єкт дослідження- Рівняння вищих ступенів з однією змінною.
Предмет дослідження- способи розв'язання рівнянь вищих ступенів.
Гіпотеза:загального способу та єдиного алгоритму, що дозволяє за кінцеве число кроків знаходити рішення рівнянь n-го ступеня, не існує.
Методи дослідження:
- бібліографічний метод (аналіз літератури на тему дослідження);
- метод класифікації;
- метод якісного аналізу
Теоретична значимістьдослідження полягає у систематизації способів вирішення рівнянь вищих ступенів та опис їх алгоритмів.
Практична значимість- пред'явлений матеріал з цієї теми та розробка навчального посібника для учнів з цієї теми.
1.РІВНЯННЯ ВИЩИХ СТУПЕНІВ
1.1 Поняття рівняння n-ого ступеня
Визначення 1.Рівнянням n-ого ступеня називається рівняння виду
a 0 xⁿ+a 1 x n -1 +a 2 xⁿ - ²+…+a n -1 x+a n = 0, де коефіцієнти a 0, a 1, a 2…, a n -1, a n- будь-які дійсні числа, причому ,a 0 ≠ 0 .
Багаточлен a 0 xⁿ+a 1 x n -1 +a 2 xⁿ - ²+…+a n -1 x+a n називають многочленом n-ого ступеня. Коефіцієнти розрізняють за назвами: a 0 - Старший коефіцієнт; a n-вільний член.
Визначення 2. Рішення або коріння для даного рівнянняє всі значення змінної х, які звертають це рівняння у вірну числову рівність або при якому багаточлен a 0 xⁿ+a 1 x n -1 +a 2 xⁿ - ²+…+a n -1 x+a n перетворюється на нуль. Таке значення змінної хназивають також коренем багаточлена. Вирішити рівняння - це означає знайти всі його коріння або встановити, що їх немає.
Якщо a 0 = 1, то таке рівняння називають наведеним цілим раціональним рівнянням n -йступеня.
Для рівнянь третього та четвертого ступеня існують формули Кардано та Феррарі, що виражають коріння цих рівнянь через радикали. З'ясувалося, що на практиці вони рідко користуються. Отже, якщо n ≥ 3, а коефіцієнти многочлена довільні дійсні числа, пошук коренів рівняння − завдання непросте. Тим не менш, у багатьох окремих випадках це завдання вирішується до кінця. Зупинимося на деяких із них.
1.2 Історичні факти вирішення рівнянь вищих ступенів
Вже в давнину люди усвідомили, як важливо навчитися вирішувати рівняння алгебри. Близько 4000 років тому вавилонські вчені володіли розв'язком квадратного рівняння та вирішували системи двох рівнянь, з яких одне – другого ступеня. За допомогою рівнянь вищих ступенів вирішувалися різноманітні завдання землемірства, архітектури та військової справи, до них зводилися багато і різноманітні питання практики та природознавства, оскільки точна мова математики дозволяє просто висловити факти та співвідношення, які, будучи викладеними звичайною мовою, можуть здатися заплутаними та складними .
Універсальної формули для знаходження коренів рівняння алгебри n-ийступеня немає. Багатьом, зрозуміло, спадала на думку приваблива думка знайти для будь-якого ступеня n формули, які б виражали коріння рівняння через його коефіцієнти, тобто, вирішували б рівняння в радикалах.
Тільки в 16 столітті італійським математикам вдалося просунутися далі - знайти формули для n=3 і n=4. Одночасно питанням про загальне вирішення рівнянь 3-го ступеня займалися Сципіон, Даль, Ферро та його учні Фіорі та Тарталья.
В 1545 вийшла книга італійського математика Д. Кардано «Велике мистецтво, або про правила алгебри», де поряд з іншими питаннями алгебри розглядаються загальні способи вирішення кубічних рівнянь, а також метод вирішення рівнянь 4-го ступеня, відкритий його учнем Л. Феррарі.
Повний виклад питань, пов'язаних з вирішенням рівнянь 3-го та 4-го ступенів, дав Ф. Вієт.
У 20-х роках 19 століття, норвезький математик Н. Абель довів, що коріння рівнянь п'ятого ступеня не можуть бути виражені через радикали.
У результаті дослідження було виявлено, що сучасної науці відомо безліч способів розв'язання рівнянь n-ого ступеня.
Результатом пошуку методів вирішення рівнянь вищих ступенів, що не піддаються вирішенню способами, що розглядаються у шкільній програмі, стали способи, що ґрунтуються на застосуванні теореми Вієта (для рівнянь ступеня n>2), теореми Безу, схеми Горнера, а також формула Кардано та Феррарі для вирішення кубічних рівнянь та рівнянь четвертого ступеня.
У роботі представлені методи вирішення рівнянь та їх види, які стали відкриттям. До них можна віднести метод невизначених коефіцієнтів, виділення повного ступеня, симетричні рівняння.
2. РІШЕННЯ ЦІЛІХ РІВНЯНЬ ВИЩИХ СТУПЕНІВ З ЦІЛИМИ КОЕФІЦІЄНТАМИ
2.1 Розв'язання рівнянь третього ступеня. Формула Д. Кардано
Розглянемо рівняння виду x 3 +px+q=0.Перетворимо рівняння загального вигляду на вигляд: x 3 +px 2 +qx+r=0.Запишемо формулу куба суми; Складемо з початковою рівністю та замінимо на y. Отримаємо рівняння: y 3 + (q -) (y -) + (r - = 0).Після перетворень, маємо: y 2 + py + q = 0.Тепер знову запишемо формулу куба суми:
(a + b) 3 =a 3 + 3a 2 b + 3ab 2 + b 3 = a 3 + b 3 + 3ab (a + b),замінимо ( a + b)на x, отримаємо рівняння x 3 - 3abx - (a 3 +b 3) = 0. Тепер видно, що вихідне рівняння рівносильне системі: і Вирішуючи систему, отримаємо:
Ми отримали формулу для вирішення наведеного рівняння 3-го ступеня. Вона носить ім'я італійського математика Кардано.
Розглянемо приклад. Вирішити рівняння: .
Маємо р= 15 і q= 124, тоді використовуючи формулу Кардано обчислимо корінь рівняння
Висновок: ця формула хороша, але не підходить для вирішення всіх кубічних рівнянь. Водночас вона громіздка. Тому практично нею користуються рідко.
Але той, хто опанує цю формулу, може використовувати її при вирішенні рівнянь третього ступеня на ЄДІ.
2.2 Теорема Вієта
З курсу математики ми знаємо цю теорему для квадратного рівняння, але мало хто знає, що її використовують і для вирішення рівнянь найвищих ступенів.
Розглянемо рівняння:
розкладемо ліву частину рівняння на множники, розділимо на ≠ 0.
Праву частину рівняння перетворимо на вигляд
; звідси слід, можна записати у систему такі рівності:
Формули, виведені Вієтом для квадратних рівнянь і продемонстровані нами для рівнянь 3-го ступеня, вірні й багаточленів вищих ступенів.
Розв'яжемо кубічне рівняння:
Висновок: даний спосіб універсальний і досить легкий для розуміння учнями, тому що теорема Вієта їм знайома за шкільною програмою для n = 2. Разом з тим, щоб знаходити коріння рівнянь за допомогою даної теореми необхідно мати хороші обчислювальні навички.
2.3 Теорема Безу
Ця теорема названа на ім'я французького математика XVIII століття Ж. Безу.
Теорема.Якщо рівняння a 0 xⁿ+a 1 x n -1 +a 2 xⁿ - ²+…+a n -1 x+a n = 0, у якому всі коефіцієнти цілі числа, причому вільний член відмінний від нуля, має цілий корінь, цей корінь є дільником вільного члена.
Враховуючи, що в лівій частині рівняння багаточлен n-го ступеня, теорема має й інше трактування.
Теорема.При розподілі многочлена n-го ступеня щодо xна двочлен x - aзалишок дорівнює значенню поділеного при x = a. (літера aможе означати будь-яке дійсне чи уявне число, тобто. будь-яке комплексне число).
Доведення:нехай f(x) позначає собою довільний многочлен n-го ступеня щодо змінної x і нехай при його розподілі на двочлен ( x-a) вийшло у приватному q(x), а в залишку R. Очевидно, що q(x)буде деякий багаточлен (n - 1)-го ступеня щодо x, а залишок Rбуде величиною незмінною, тобто. не залежить від x.
Якби залишок Rбув многочленом першого ступеня щодо x, це означало б, що розподіл не виконано. Отже, Rвід xне залежить. За визначенням поділу отримуємо тотожність: f(x)=(x-a) q(x)+R.
Рівність справедлива за будь-якого значення x, отже, вона справедлива і при x=a, Отримаємо: f(a)=(a-a) q(a)+R. Символ f(a) позначає значення багаточлена f (x) при x=a, q(a)позначає значення q(x) при x=a.Залишок Rзалишився таким, яким він був раніше, оскільки Rвід xне залежить. Твір ( x-a) q(a) = 0, оскільки множник ( x-a) = 0,а множник q(a)є кілька. Тому з рівності отримаємо: f(a)= R,ч.т.д.
приклад 1.Знайти залишок від поділу багаточлена x 3 - 3x 2 + 6x- 5 на двочлен
x- 2. За теоремою Безу : R=f(2) = 23-322 + 62 -5 = 3. Відповідь: R= 3.
Зазначимо, що теорема Безу важлива не так сама по собі, як своїми наслідками. (Додаток 1)
Зупинимося на розгляді деяких прийомів застосування теореми Безу до вирішення практичних завдань. Слід зазначити, що при розв'язанні рівнянь за допомогою теореми Безу необхідно:
Знайти всі цілі дільники вільного члена;
З цих дільників знайти хоча б один корінь рівняння;
Ліву частину рівняння розділити на (х-а);
Записати в лівій частині рівняння добуток дільника та приватного;
Вирішити отримане рівняння.
Розглянемо з прикладу рішення рівняння х 3 + 4х 2 + х - 6 = 0 .
Рішення: знаходимо дільники вільного члена ±1 ; ± 2; ± 3; ± 6. Обчислимо значення при х= 1, 1 3 + 41 2 + 1-6 = 0. Розділимо ліву частину рівняння на ( х- 1). Розподіл виконаємо «куточком», отримаємо:
Висновок: теорема Безу один із тих способів, які ми розглядаємо в нашій роботі, вивчається у програмі факультативних занять. Вона важка у розумінні, тому що, щоб їй володіти, треба знати всі наслідки з неї, але при цьому теорема Безу є одним із головних помічників учнів на ЄДІ.
2.4 Схема Горнера
Для поділу багаточлена на двочлен х-αможна використовувати спеціальний нескладний прийом, вигаданий англійськими математиками XVII століття, згодом названою схемою Горнера. Крім знаходження коренів рівнянь, за схемою Горнера можна просто обчислювати їх значення. Для цього необхідно підставити значення змінної багаточлен Pn (x) = a 0 xn+a 1 x n-1 +a 2 xⁿ - ²+…++ a n -1 x+a n. (1)
Розглянемо поділ багаточлена (1) на двочлен x-α.
Виразимо коефіцієнти неповного приватного b 0 xⁿ - ¹+ b 1 xⁿ - ²+ b 2 xⁿ - ³+…+ bn -1 та залишок rчерез коефіцієнти многочлена Pn( x) та число α. b 0 =a 0 , b 1 = α b 0 +a 1 , b 2 = α b 1 +a 2 …, bn -1 =
= α bn -2 +a n -1 = α bn -1 +a n .
Обчислення за схемою Горнера представлені у вигляді таблиці:
|
а 0 |
a 1 |
a 2 , |
|||
|
b 0 =а 0 |
b 1 = α b 0 +a 1 |
b 2 = α b 1 +a 2 |
r=α b n-1 +a n |
Оскільки r=Pn(α),то α – корінь рівняння. Для того щоб перевірити, чи не є α кратним коренем, схему Горнера можна застосувати вже до приватного b 0 x+ b 1 x+…+ bn -1 за таблицею. Якщо у стовпці під bn -1 вийде знову 0, отже α – кратний корінь.
Розглянемо приклад: розв'язати рівняння х 3 + 4х 2 + х - 6 = 0.
Застосуємо до лівої частини рівняння розкладання на множники багаточлена, що стоїть у лівій частині рівняння, схему Горнера.
Рішення: знаходимо дільники вільного члена ± 1; ±2; ± 3; ± 6.
|
6 ∙ 1 + (-6) = 0 |
Коефіцієнти частки - числа 1, 5, 6, а залишок r = 0.
Значить, х 3 + 4х 2 + х - 6 = (х - 1) (х 2 + 5х + 6) = 0.
Звідси: х- 1 = 0 або х 2 + 5х + 6 = 0.
х = 1, х 1 = -2; х 2 = -3. Відповідь: 1,- 2, - 3.
Висновок: таким чином, на одному рівнянні ми показали застосування двох різних способів розкладання множників багаточленів. На наш погляд, схема Горнера найбільш практична та економічна.
2.5 Розв'язання рівнянь 4-го ступеня. Метод Феррарі
Учень Кардано Людовік Феррарі виявив спосіб розв'язання рівняння 4-го ступеня. Метод Ferrari складається з двох етапів.
I етап: рівняння виду представляється у вигляді добутку двох квадратних тричленів це випливає з того, що рівняння третього ступеня і хоча б одне рішення.
II етап: отримані рівняння вирішуються за допомогою розкладання на множники, проте для того, щоб знайти потрібне розкладання на множники, доводиться вирішувати кубічні рівняння.
Ідея у тому, щоб уявити рівняння як A 2 =B 2 , де A= x 2+s,
B-лінійна функція від x. Тоді залишається розв'язати рівняння A = ±B.
Для наочності розглянемо рівняння: Усамітним 4-й ступінь, отримаємо: Для будь-якого dвираз буде повним квадратом. Додамо до обох частин рівняння отримаємо
У лівій частині повний квадрат можна підібрати dщоб права частина (2) стала повним квадратом. Уявімо, що ми досягли цього. Тоді наше рівняння виглядає так:
Знайти корінь згодом не складе жодних труднощів. Щоб правильно підібрати dтреба, щоб дискримінант правої частини (3) звернувся нанівець, тобто.
Отже, щоб знайти d, Треба вирішити це рівняння 3-го ступеня. Таке допоміжне рівняння називають резольвентою.
Легко знаходимо цілий корінь резольвенти: d = 1
Підставивши в (1) рівняння отримаємо
Висновок: метод Феррарі універсальний, але складний і громіздкий. Разом про те, якщо алгоритм рішення зрозумілий, то рівняння 4-го ступеня можна вирішувати даним методом.
2.6 Метод невизначених коефіцієнтів
Успіх вирішення рівняння 4-го ступеня методом Феррарі залежить від того, чи вирішили ми резольвенту - рівняння 3-го ступеня, що, як ми знаємо, не завжди вдається.
Суть методу невизначених коефіцієнтів полягає в тому, що вид співмножників, на які розкладається даний многочлен, вгадується, а коефіцієнти цих співмножників (також багаточленів) визначається шляхом перемноження співмножників та прирівнювання коефіцієнтів при однакових ступенях змінної.
Приклад: розв'яжіть рівняння:
Припустимо, що ліву частину нашого рівняння можна розкласти на два квадратні тричлени з цілими коефіцієнтами такі, що справедливо тотожну рівність
Очевидно, що коефіцієнти перед них повинні бути рівними 1, а вільні члени - в одного + 1, в іншого – 1.
Невизначеними залишаються коефіцієнти, що стоять перед х. Позначимо їх через аі і щоб їх визначити, перемножимо обидва тричлени правої частини рівняння.
В результаті отримаємо:
Прирівнюючи коефіцієнти за однакових ступенів ху лівій та правій частинах рівності (1), отримуємо систему для знаходження та
Вирішивши цю систему, матимемо
Отже, наше рівняння рівносильне рівнянню
Вирішивши його, отримуємо такі коріння: .
Метод невизначених коефіцієнтів спирається на такі твердження: будь-який багаточлен четвертого ступеня, що стоїть у рівнянні, можна розкласти на твір двох багаточленів другого ступеня; два многочлени тотожно рівні тоді і лише тоді, коли рівні їх коефіцієнти при однакових ступенях х.
2.7 Симетричні рівняння
Визначення.Рівняння виду називається симетричним, якщо перші коефіцієнти, що стоять у рівнянні зліва, рівні першим коефіцієнтам, що стоять праворуч.
Ми, що перші коефіцієнти зліва рівні першим коефіцієнтам справа.
Якщо таке рівняння має непарний ступінь, воно має корінь х= - 1. Далі ми можемо знизити рівень рівняння, поділивши його на ( х+ 1). Виявляється, що при розподілі симетричного рівняння на ( х+ 1) виходить симетричне рівняння парного ступеня. Доказ симетричності коефіцієнтів наведено нижче. (Додаток 6) Наше завдання – навчитися вирішувати симетричні рівняння парного ступеня.
Наприклад: (1)
Розв'яжемо рівняння (1), поділимо на х 2 (На середній ступінь) = 0.
Згрупуємо доданки з симетричними
) + 3(x+. Позначимо у= x+ , Зведемо обидві частини в квадрат, звідси = у 2 Отже, 2( у 2 або 2 у 2 + 3 розв'язавши рівняння, отримаємо у = , у= 3. Далі повернемося до заміни x+ = і x+ = 3. Отримаємо рівняння і перше не має рішення, а друге має два корені. Відповідь:.
Висновок: даний вид рівнянь не часто зустрічається, але якщо він вам попався, його можна вирішити легко і просто не вдаючись до громіздких обчислень.
2.8 Виділення повного ступеня
Розглянемо рівняння.
Ліва частина є куб суми (х+1), тобто.
Витягаємо корінь третього ступеня з обох частин: , далі отримаємо
Звідки єдине коріння.
РЕЗУЛЬТАТИ ДОСЛІДЖЕННЯ
За результатами роботи ми дійшли таких висновків:
Завдяки вивченій теорії ми познайомилися з різними методами розв'язання цілих рівнянь вищих ступенів;
Формула Д. Кардано є складною у застосуванні і дає більшу ймовірність припуститися помилок при обчисленні;
− метод Л. Феррарі дозволяє звести рішення рівняння четвертого ступеня до кубічного;
− теорема Безу може застосовуватися як для кубічних рівнянь, так і для рівнянь четвертого ступеня; вона більш зрозуміла та наочна у застосуванні до розв'язання рівнянь;
Схема Горнера допомагає суттєво скоротити та спростити обчислення у вирішенні рівнянь. Крім знаходження коренів, за схемою Горнера можна простіше обчислювати значення многочленів, які у лівої частини рівняння;
Особливий інтерес викликали розв'язання рівнянь методом невизначених коефіцієнтів, розв'язання симетричних рівнянь.
У ході дослідницької роботи було з'ясовано, що з найпростішими способами вирішення рівнянь вищого ступеня учні знайомляться на заняттях факультативу з математики, починаючи з 9-го чи 10-го класів, а також спецкурсах виїзних математичних шкіл. Цей факт встановлено в результаті опитування вчителів математики МБОУ «ЗОШ № 9» та учнів, які виявляють підвищений інтерес до предмета «математика».
Найбільш затребуваними методами вирішення рівнянь вищих ступенів, які зустрічаються при вирішенні олімпіадних, конкурсних завдань та в результаті підготовки до іспитів учнями, є методи, що ґрунтуються на застосуванні теореми Безу, схеми Горнера та запровадження нової змінної.
Демонстрація результатів дослідницької роботи, тобто. способів розв'язання рівнянь, що не вивчаються у шкільній програмі з математики, зацікавила однокласників.
Висновок
Вивчивши навчальну та наукову літературу, Інтернет-ресурси у молодіжних освітніх форумах