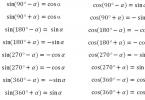Definiție. Formulele de reducere sunt formule care vă permit să treceți de la funcțiile trigonometrice ale formei la funcțiile de argument. Cu ajutorul lor, sinusul, cosinusul, tangenta și cotangenta unui unghi arbitrar pot fi reduse la sinusul, cosinusul, tangenta și cotangenta unui unghi din intervalul de la 0 la 90 de grade (de la 0 la radiani). Astfel, formulele de reducere ne permit să trecem la lucrul cu unghiuri în 90 de grade, ceea ce este, fără îndoială, foarte convenabil.

Formule de reducere:

Există două reguli pentru utilizarea formulelor de reducere.

1. Dacă unghiul poate fi reprezentat ca (π/2 ±a) sau (3*π/2 ±a), atunci se modifică numele funcției sin la cos, cos la sin, tg la ctg, ctg la tg. Dacă unghiul poate fi reprezentat sub forma (π ±a) sau (2*π ±a), atunci Numele funcției rămâne neschimbat.

Uită-te la poza de mai jos, arată schematic când să schimbi semnul și când nu

2. Semnul funcției reduse rămâne la fel. Dacă funcția inițială avea semnul plus, atunci funcția redusă are și semnul plus. Dacă funcția inițială avea semnul minus, atunci funcția redusă are și semnul minus.

Figura de mai jos prezintă semnele funcțiilor trigonometrice de bază în funcție de trimestru.

Exemplu:

calculati

Să folosim formulele de reducere:

Sin(150˚) este în al doilea trimestru; din figură vedem că semnul păcat în acest trimestru este egal cu „+”. Aceasta înseamnă că funcția dată va avea și semnul „+”. Am aplicat a doua regulă.

Acum 150˚ = 90˚ +60˚. 90˚ este π/2. Adică avem de-a face cu cazul π/2+60, prin urmare, conform primei reguli, schimbăm funcția din sin în cos. Ca rezultat, obținem Sin(150˚) = cos(60˚) = ½.

Și încă un punct: există destul de multe formule de reducere la număr și vă vom avertiza imediat să nu le învățați pe de rost. Nu este absolut nevoie de acest lucru - există unul care vă permite să aplicați cu ușurință formule de reducere.

Deci, să notăm toate formulele de reducere sub forma unui tabel.

Aceste formule pot fi rescrise folosind grade și radiani. Pentru a face acest lucru, amintiți-vă doar relația dintre grade și radiani și înlocuiți π cu 180 de grade peste tot.

Exemple de utilizare a formulelor de reducere

Scopul acestui paragraf este de a arăta modul în care formulele de reducere sunt utilizate în practică pentru a rezolva exemple.

Pentru început, merită să spunem că există un număr infinit de moduri de a reprezenta un unghi sub semnul funcțiilor trigonometrice sub forma și . Acest lucru se datorează faptului că unghiul poate lua orice valoare. Să arătăm asta cu un exemplu.

De exemplu, să luăm unghiul de sub semnul funcției trigonometrice egal cu . Acest unghi poate fi reprezentat ca , sau cum , sau cum , sau în multe alte moduri.

Acum să vedem ce formule de reducere va trebui să folosim în funcție de reprezentarea unghiului. Hai sa luam .

Dacă reprezentăm unghiul ca , atunci acestei reprezentări îi corespunde o formulă de reducere de forma , din care obținem . Aici putem indica valoarea funcției trigonometrice: .

Pentru prezentare vom folosi deja o formulă a formei , ceea ce ne conduce la următorul rezultat: .

În fine, deoarece formula de reducere corespunzătoare are forma .

Pentru a încheia această discuție, este de remarcat mai ales că există anumite facilități atunci când se utilizează reprezentări unghiulare în care unghiul are o valoare de la 0 la 90 de grade (de la 0 la pi în jumătate de radiani).

Să ne uităm la un alt exemplu de utilizare a formulelor de reducere.

Exemplu.

Folosind formule de reducere, reprezentați prin sinus și, de asemenea, prin cosinusul unui unghi ascuțit.

Soluţie.

Pentru a aplica formulele de reducere, trebuie să reprezentăm un unghi de 197 de grade sub forma sau , iar în funcție de condițiile problemei, unghiul trebuie să fie ascuțit. Acest lucru se poate face în două moduri: sau . Prin urmare, sau .

Revenind la formulele corespunzătoare pentru reducerea și , obținem și .

Răspuns:

Și .

Regulă mnemonică

După cum am menționat mai sus, nu este necesară memorarea formulelor de reducere. Dacă le priviți cu atenție, puteți identifica tipare din care puteți obține o regulă care vă permite să obțineți oricare dintre formulele de reducere. El este numit regula mnemonică(mnemonica este arta memorării).

Regula mnemonică conține trei etape:

Merită să spuneți imediat că pentru a aplica regula mnemonică trebuie să fiți foarte bun la identificarea semnelor sinusului, cosinusului, tangentei și cotangentei pe sferturi, deoarece va trebui să faceți acest lucru în mod constant.

Să ne uităm la aplicarea regulii mnemonice folosind exemple.

Exemplu.

Folosind o regulă mnemonică, notează formulele de reducere pentru Și , considerând unghiul ca fiind unghiul primului sfert.

Soluţie.

Nu trebuie să facem primul pas al regulii, deoarece unghiurile de sub semnele funcțiilor trigonometrice sunt deja scrise în forma necesară.

Să determinăm semnul funcțiilor Și . Cu condiția ca - unghiul primului sfert, unghiul este, de asemenea, unghiul primului sfert și unghiul - unghiul celui de-al doilea sfert. Cosinusul din primul sfert are semnul plus, iar tangenta din al doilea sfert are semnul minus. În această etapă, formulele necesare vor avea forma și . Acum că ne-am dat seama de semne, putem trece la pasul final al regulii mnemonice.

Întrucât argumentul funcției cosinus are forma , atunci numele functiei trebuie schimbat in cofunction, adica in sine. Iar argumentul tangentă are forma , prin urmare, numele funcției trebuie lăsat același.

Ca rezultat avem Și . Vă puteți uita la tabelul cu formule de reducere pentru a vă asigura că rezultatele obținute sunt corecte.

Răspuns:

Și .

Pentru a consolida materialul, luați în considerare rezolvarea unui exemplu cu unghiuri specifice.

Exemplu.

Folosind o regulă mnemonică, reduceți la funcțiile trigonometrice ale unui unghi ascuțit.

Soluţie.

În primul rând, să ne imaginăm unghiul de 777 de grade în forma necesară pentru aplicarea regulii mnemonice. Acest lucru se poate face în două moduri: sau.

Unghiul original este primul sfert de unghi, sinusul pentru acest unghi are un semn plus.

Pentru prezentare, numele sinusului trebuie lăsat același, dar pentru a prezenta tipul, sinusul trebuie schimbat în cosinus.

Ca urmare, avem și .

Răspuns:

Și .

Pentru a încheia acest punct, luați în considerare un exemplu care ilustrează importanța reprezentării corecte a unui unghi sub semnul funcțiilor trigonometrice pentru aplicarea regulii mnemonice: unghiul trebuie sa fie ascutit!!!

Să calculăm tangenta unghiului. În principiu, referindu-ne la materialul din valorile articolului de sinus, cosinus, tangentă și cotangentă, putem răspunde imediat la întrebarea problemei: .

Dacă reprezentăm unghiul ca sau ca , atunci putem folosi regula mnemonică: Și , ceea ce ne duce la același rezultat.

Dar asta se poate întâmpla dacă luați o reprezentare a unui unghi, de exemplu, a formei. În acest caz, regula mnemonică ne va conduce la acest rezultat. Acest rezultat este incorect, iar acest lucru se explică prin faptul că pentru reprezentare nu am avut dreptul să aplicăm regula mnemonică, întrucât unghiul nu este acut.

Dovada formulelor de reducere

Formulele de reducere reflectă periodicitatea, simetria și proprietățile deplasării prin unghiuri și . Să observăm imediat că toate formulele de reducere pot fi dovedite prin eliminarea termenului din argumente, deoarece înseamnă schimbarea unghiului cu un număr întreg de rotații complete, iar acest lucru nu schimbă valorile funcțiilor trigonometrice. Acest termen servește ca o reflectare a periodicității.

Primul bloc de 16 formule de reducere decurge direct din proprietățile sinusului, cosinusului, tangentei și cotangentei. Nici măcar nu merită să ne oprim asupra lor.

Să trecem la următorul bloc de formule. Mai întâi, să le demonstrăm pe primele două. Restul urmează de la ei. Deci, să demonstrăm formulele de reducere ale formei Și .

Să luăm în considerare cercul unității. Fie punctul inițial A, după rotirea cu un unghi, să meargă la punctul A 1 (x, y), iar după rotire cu un unghi, la punctul A 2. Să desenăm A 1 H 1 și A 2 H 2 – perpendiculare pe dreapta Ox.

Este ușor de observat că triunghiurile dreptunghiulare OA 1 H 1 și OA 2 H 2 sunt egale ca ipotenuză și două unghiuri adiacente. Din egalitatea triunghiurilor și locația punctelor A 1 și A 2 pe cercul unitar, devine clar că dacă punctul A 1 are coordonatele x și y, atunci punctul A 2 are coordonatele -y și x. Apoi definițiile sinusului și cosinusului ne permit să scriem egalitățile și , din care rezultă că Și . Aceasta dovedește formulele de reducere luate în considerare pentru orice unghi.

Având în vedere că Și (dacă este necesar, vezi articolul identități trigonometrice de bază), precum și formulele tocmai dovedite, obținem și . Deci am demonstrat următoarele două formule de reducere.

Pentru a demonstra formulele de reducere cu un argument, este suficient să îl reprezentați ca și apoi să folosiți formulele și proprietățile dovedite ale funcțiilor trigonometrice cu argumente opuse. De exemplu, .

Toate celelalte formule de reducere sunt dovedite în mod similar pe baza celor deja dovedite prin dublă aplicare. De exemplu, apare ca , dar ca . Și și - ca și respectiv.

Bibliografie.

• Algebră: Manual pentru clasa a IX-a. medie scoala/Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Ed. S. A. Telyakovsky.- M.: Educație, 1990. - 272 p.: il. - ISBN 5-09-002727-7
• Bashmakov M. I. Algebra și începuturile analizei: manual. pentru clasele 10-11. medie şcoală - Ed. a 3-a. - M.: Educaţie, 1993. - 351 p.: ill. - ISBN 5-09-004617-4.
• Algebră iar începutul analizei: Proc. pentru clasele 10-11. educatie generala instituții / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn și alții; Ed. A. N. Kolmogorov.- ed. a XIV-a - M.: Educație, 2004. - 384 p.: il. - ISBN 5-09-013651-3.
• Gusev V. A., Mordkovich A. G. Matematică (un manual pentru cei care intră în școlile tehnice): Proc. indemnizatie.- M.; Superior scoala, 1984.-351 p., ill.

Și încă o problemă B11 pe aceeași temă - de la adevăratul examen de stat unificat la matematică.

Sarcină. Găsiți sensul expresiei:

În acest scurt tutorial video vom învăța cum să aplicăm formule de reducere pentru rezolvarea unor probleme reale B11 de la Examenul Unificat de Stat la matematică. După cum puteți vedea, avem două expresii trigonometrice, fiecare conținând sinusuri și cosinusuri, precum și câteva argumente numerice destul de brutale.

Înainte de a rezolva aceste probleme, să ne amintim ce sunt formulele de reducere. Deci, dacă avem expresii ca:

Atunci putem scăpa de primul termen (de forma k · π/2) după reguli speciale. Să desenăm un cerc trigonometric și să marchem punctele principale pe el: 0, π/2; π; 3π/2 și 2π. Apoi ne uităm la primul termen sub semnul funcției trigonometrice. Avem:

1. Dacă termenul care ne interesează se află pe axa verticală a cercului trigonometric (de exemplu: 3π/2; π/2 etc.), atunci funcția inițială este înlocuită cu o co-funcție: sinusul este înlocuit cu cosinus, iar cosinus, dimpotrivă, prin sinus.
2. Dacă termenul nostru se află pe axa orizontală, atunci funcția inițială nu se schimbă. Pur și simplu eliminăm primul termen din expresie și gata.

Astfel, obținem o funcție trigonometrică care nu conține termeni de forma k · π/2. Cu toate acestea, munca cu formule de reducere nu se termină aici. Cert este că noua noastră funcție, obținută după „aruncarea” primului termen, poate avea în față un semn plus sau minus. Cum să identifici acest semn? Acum vom afla.

Să ne imaginăm că unghiul α rămas în interiorul funcției trigonometrice după transformări are o măsură de grad foarte mică. Dar ce înseamnă „măsură mică”? Să spunem α ∈ (0; 30°) - este suficient. Să luăm un exemplu de funcție:

Apoi, urmând presupunerile noastre că α ∈ (0; 30°), concluzionăm că unghiul 3π/2 − α se află în al treilea sfert de coordonate, i.e. 3π/2 − α ∈ (π; 3π/2). Să ne amintim semnul funcției originale, adică. y = sin x pe acest interval. Evident, sinusul din al treilea trimestru de coordonate este negativ, deoarece, prin definiție, sinusul este ordonata de la capătul razei în mișcare (pe scurt, sinusul este coordonata y). Ei bine, coordonata y din semiplanul inferior ia întotdeauna valori negative. Aceasta înseamnă că în al treilea trimestru y este și negativ.

Pe baza acestor reflecții, putem nota expresia finală:

Problema B11 - Opțiunea 1

Aceleași tehnici sunt destul de potrivite pentru rezolvarea problemei B11 de la examenul de stat unificat la matematică. Singura diferență este că în multe probleme reale B11, în loc de o măsură în radian (adică numere π, π/2, 2π etc.) este utilizată o măsură a gradului (adică 90°, 180°, 270° și etc.). Să ne uităm la prima sarcină:

Să ne uităm mai întâi la numărător. cos 41° este o valoare non-tabulară, așa că nu putem face nimic cu ea. Să lăsăm așa deocamdată.

Acum să ne uităm la numitor:

sin 131° = sin (90° + 41°) = cos 41°

Evident, aceasta este o formulă de reducere, deci sinusul este înlocuit cu un cosinus. În plus, unghiul de 41° se află pe segment (0°; 90°), adică în primul cadran de coordonate - exact așa cum este necesar pentru aplicarea formulelor de reducere. Dar atunci 90° + 41° este al doilea trimestru de coordonate. Funcția originală y = sin x este pozitivă acolo, așa că punem un semn plus în fața cosinusului la ultimul pas (cu alte cuvinte, nu am pus nimic).

Rămâne să ne ocupăm de ultimul element:

cos 240° = cos (180° + 60°) = −cos 60° = −0,5

Aici vedem că 180° este axa orizontală. În consecință, funcția în sine nu se va schimba: a existat un cosinus - și cosinusul va rămâne și el. Dar se pune din nou întrebarea: va apărea plus sau minus înaintea expresiei rezultate cos 60°? Rețineți că 180° este al treilea trimestru de coordonate. Cosinusul de acolo este negativ, prin urmare, cosinusul va avea în cele din urmă un semn minus în fața lui. În total, obținem construcția −cos 60° = −0,5 - aceasta este o valoare tabelară, deci totul este ușor de calculat.

Acum înlocuim numerele rezultate în formula originală și obținem:

După cum puteți vedea, numărul cos 41° în numărătorul și numitorul fracției este ușor de redus, iar expresia obișnuită rămâne, care este egală cu −10. În acest caz, minusul poate fi fie scos și plasat în fața semnului fracției, fie „păstrat” lângă al doilea factor până la ultima etapă a calculelor. În orice caz, răspunsul va fi -10. Gata, problema B11 este rezolvata!

Problema B14 - opțiunea 2

Să trecem la a doua sarcină. Avem din nou o fracție în fața noastră:

Ei bine, 27° se află în primul trimestru de coordonate, așa că nu vom schimba nimic aici. Dar păcatul 117° trebuie scris (fără pătrat deocamdată):

sin 117° = sin (90° + 27°) = cos 27°

Evident, din nou înaintea noastră formula de reducere: 90° este axa verticală, prin urmare sinusul se va schimba în cosinus. În plus, unghiul α = 117° = 90° + 27° se află în al doilea cadran de coordonate. Funcția originală y = sin x este pozitivă acolo, prin urmare, după toate transformările, mai există un semn plus în fața cosinusului. Cu alte cuvinte, acolo nu se adaugă nimic - o lăsăm așa: cos 27°.

Revenim la expresia originală care trebuie calculată:

După cum vedem, după transformări, principala identitate trigonometrică a apărut la numitor: sin 2 27° + cos 2 27° = 1. Total −4: 1 = −4 - deci am găsit răspunsul la a doua problemă B11.

După cum puteți vedea, cu ajutorul formulelor de reducere astfel de probleme de la examenul unificat de stat la matematică sunt rezolvate literalmente în câteva rânduri. Fără sinus al sumei și cosinus al diferenței. Tot ce trebuie să ne amintim este doar cercul trigonometric.

Cum să ne amintim formulele pentru reducerea funcțiilor trigonometrice? Este usor daca folosesti o asociere.Asociatia asta nu a fost inventata de mine. După cum am menționat deja, o asociere bună ar trebui să „prindă”, adică să evoce emoții vii. Nu pot numi pozitive emoțiile cauzate de această asociere. Dar dă un rezultat - vă permite să vă amintiți formulele de reducere, ceea ce înseamnă că are dreptul de a exista. La urma urmei, dacă nu-ți place, nu trebuie să-l folosești, nu?

Formulele de reducere au forma: sin(πn/2±α), cos(πn/2±α), tg(πn/2±α), ctg(πn/2±α). Amintiți-vă că +α dă mișcare în sens invers acelor de ceasornic, - α dă mișcare în sensul acelor de ceasornic.

Pentru a lucra cu formule de reducere, aveți nevoie de două puncte:

1) pune semnul pe care îl are funcția inițială (în manuale se scrie: reductibil. Dar ca să nu ne încurcăm, este mai bine să o numim inițială), dacă considerăm că α este unghiul primului sfert, adică , mic.

2) Diametru orizontal - π±α, 2π±α, 3π±α... - în general, când nu există fracție, numele funcției nu se schimbă. Vertical π/2±α, 3π/2±α, 5π/2±α... - când există o fracție, numele funcției se schimbă: sinus - în cosinus, cosinus - în sinus, tangentă - în cotangentă și cotangent - a tangentă.

Acum, de fapt, asociația:

diametru vertical (există o fracție) -

stând beat. Ce se va întâmpla cu el devreme?

sau e prea tarziu? Așa e, va cădea.

Numele funcției se va schimba.

Dacă diametrul este orizontal, bețiul este deja culcat. Probabil că doarme. Nu i se va întâmpla nimic; el și-a asumat deja o poziție orizontală. În consecință, numele funcției nu se schimbă.

Adică sin(π/2±α), sin(3π/2±α), sin(5π/2±α), etc. da ±cosα,

și sin(π±α), sin(2π±α), sin(3π±α), … - ±sinα.

Știm deja cum.

Cum functioneaza? Să ne uităm la exemple.

1) cos(π/2+α)=?

Devenim π/2. Deoarece +α înseamnă că mergem înainte, în sens invers acelor de ceasornic. Ne aflăm în al doilea trimestru, unde cosinusul are semnul „-“. Se schimbă numele funcției („un beat stă în picioare”, ceea ce înseamnă că va cădea). Asa de,

cos(π/2+α)=-sin α.

Să ajungem la 2π. Din moment ce -α - mergem înapoi, adică în sensul acelor de ceasornic. Ne aflăm în trimestrul IV, unde tangenta are semnul „-“. Numele funcției nu se schimbă (diametrul este orizontal, „bețiul este deja culcat”). Astfel, tan(2π-α)=- tanα.

3) ctg²(3π/2-α)=?

Exemplele în care o funcție este ridicată la o putere pară sunt și mai simplu de rezolvat. Gradul par „-” îl elimină, adică trebuie doar să aflați dacă numele funcției se schimbă sau rămâne. Diametrul este vertical (există o fracție, „stă beat”, va cădea), numele funcției se schimbă. Se obține: ctg²(3π/2-α)= tan²α.

Ele aparțin secțiunii de trigonometrie a matematicii. Esența lor este de a reduce funcțiile trigonometrice ale unghiurilor la o formă „simplu”. Se pot scrie multe despre importanța cunoașterii lor. Există deja 32 dintre aceste formule!

Nu vă alarmați, nu trebuie să le învățați, ca multe alte formule dintr-un curs de matematică. Nu este nevoie să vă umpleți capul cu informații inutile, trebuie să vă amintiți „cheile” sau legile, iar amintirea sau derivarea formulei necesare nu va fi o problemă. Apropo, când scriu în articole „... trebuie să înveți!!!” - asta înseamnă că chiar trebuie învățat.

Dacă nu sunteți familiarizat cu formulele de reducere, atunci simplitatea derivării lor vă va surprinde plăcut - există o „lege” cu ajutorul căreia acest lucru se poate face cu ușurință. Și poți scrie oricare dintre cele 32 de formule în 5 secunde.

Voi enumera doar câteva dintre problemele care vor apărea la Examenul Unificat de Stat la matematică, unde fără cunoașterea acestor formule există o mare probabilitate de a eșua în rezolvarea lor. De exemplu:

– probleme pentru rezolvarea unui triunghi dreptunghic, unde vorbim despre unghiul exterior, și probleme pentru unghiurile interne, unele dintre aceste formule sunt și ele necesare.

– sarcini privind calcularea valorilor expresiilor trigonometrice; conversia expresiilor trigonometrice numerice; conversia expresiilor trigonometrice literale.

– probleme asupra tangentei și semnificația geometrică a tangentei, se impune o formulă de reducere a tangentei, precum și alte probleme.

– probleme stereometrice, în cursul rezolvării este adesea necesar să se determine sinusul sau cosinusul unui unghi care se află în intervalul de la 90 la 180 de grade.

Și acestea sunt doar acele puncte care se referă la examenul de stat unificat. Și în cursul de algebră în sine există multe probleme, a căror rezolvare pur și simplu nu se poate face fără cunoașterea formulelor de reducere.

Deci, la ce duce acest lucru și cum formulele specificate ne facilitează rezolvarea problemelor?

De exemplu, trebuie să determinați sinusul, cosinusul, tangenta sau cotangenta oricărui unghi de la 0 la 450 de grade:

unghiul alfa variază de la 0 la 90 de grade

* * *

Deci, este necesar să înțelegeți „legea” care funcționează aici:

1. Determinați semnul funcției în cadranul corespunzător.

Lasă-mă să-ți amintesc:

2. Amintiți-vă următoarele:

funcția se schimbă în cofuncție

funcția nu se schimbă în cofuncție

Ce înseamnă conceptul - o funcție se schimbă într-o cofuncție?

Răspuns: sinusul se schimbă în cosinus sau invers, tangentă la cotangentă sau invers.

Asta e tot!

Acum, conform legii prezentate, vom scrie noi înșine câteva formule de reducere:

Acest unghi se află în al treilea sfert, cosinusul în al treilea sfert este negativ. Nu schimbăm funcția într-o cofuncție, deoarece avem 180 de grade, ceea ce înseamnă:

Unghiul se află în primul sfert, sinusul în primul sfert este pozitiv. Nu schimbăm funcția într-o cofuncție, deoarece avem 360 de grade, ceea ce înseamnă:

Iată o altă confirmare suplimentară că sinusurile unghiurilor adiacente sunt egale:

Unghiul se află în al doilea sfert, sinusul în al doilea trimestru este pozitiv. Nu schimbăm funcția într-o cofuncție, deoarece avem 180 de grade, ceea ce înseamnă:

Lucrează fiecare formulă mental sau în scris și vei fi convins că nu este nimic complicat.

***

În articolul despre soluție, a fost remarcat următorul fapt - sinusul unui unghi ascuțit dintr-un triunghi dreptunghic este egal cu cosinusul altui unghi ascuți din acesta.