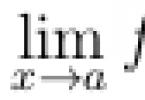Teoria limitelor este una dintre ramurile analizei matematice. Problema rezolvării limitelor este destul de extinsă, deoarece există zeci de metode de rezolvare a limitelor de diferite tipuri. Există zeci de nuanțe și trucuri care vă permit să rezolvați cutare sau cutare limită. Cu toate acestea, vom încerca în continuare să înțelegem principalele tipuri de limite care sunt cel mai des întâlnite în practică.

Să începem cu însăși conceptul de limită. Dar mai întâi, un scurt context istoric. Acolo a trăit un francez, Augustin Louis Cauchy, în secolul al XIX-lea, care a dat definiții stricte multor concepte de matan și a pus bazele acestuia. Trebuie spus că acest respectat matematician a fost, este și va fi în coșmarurile tuturor studenților la fizică și matematică, deoarece a demonstrat un număr imens de teoreme de analiză matematică, iar una este mai letală decât cealaltă. În acest sens, nu vom lua în considerare încă determinarea limitei Cauchy, dar să încercăm să facem două lucruri:

1. Înțelege ce este o limită.
2. Învață să rezolvi principalele tipuri de limite.

Îmi cer scuze pentru unele explicații neștiințifice, este important ca materialul să fie de înțeles chiar și pentru un ceainic, care, de fapt, este sarcina proiectului.

Deci care este limita?

Și doar un exemplu de ce să-i faci buniței...

Orice limită constă din trei părți:

1) Cunoscuta pictogramă limită.
2) Intrări sub pictograma limită, în acest caz . Intrarea scrie „X tinde spre unu”. Cel mai adesea - exact, deși în loc de „X” în practică există și alte variabile. În sarcinile practice, locul unuia poate fi absolut orice număr, precum și infinitul ().
3) Funcții sub semnul limită, în acest caz .

Înregistrarea în sine se citește astfel: „limita unei funcții ca x tinde spre unitate”.

Să ne uităm la următoarea întrebare importantă - ce înseamnă expresia „x”? se straduieste catre unul"? Și ce înseamnă chiar „străduiți”?
Conceptul de limită este un concept, ca să spunem așa, dinamic. Să construim o secvență: mai întâi , apoi , , …, , ….
Adică expresia „x se straduieste la unu” ar trebui înțeles astfel: „x” preia constant valorile care se apropie de unitatea infinit apropiată și practic coincid cu ea.

Cum se rezolvă exemplul de mai sus? Pe baza celor de mai sus, trebuie doar să înlocuiți unul în funcție de sub semnul limită:

Deci, prima regulă: Când se oferă vreo limită, mai întâi încercăm pur și simplu să conectăm numărul în funcție.

Am considerat cea mai simplă limită, dar acestea apar și în practică, și nu atât de rar!

Exemplu cu infinit:

Să ne dăm seama ce este? Acesta este cazul când crește fără limită, adică: mai întâi, apoi, apoi, apoi și așa mai departe la infinit.

Ce se întâmplă cu funcția în acest moment?
, , , …

Deci: dacă , atunci funcția tinde spre minus infinit:

În linii mari, conform primei noastre reguli, în loc de „X” înlocuim infinitul în funcție și obținem răspunsul.

Un alt exemplu cu infinit:

Din nou începem să creștem la infinit și să ne uităm la comportamentul funcției:

Concluzie: când funcția crește fără limită:

Și încă o serie de exemple:

Vă rugăm să încercați să analizați mental următoarele pentru dvs. și să vă amintiți cele mai simple tipuri de limite:

, , , , , , , , ,
Dacă aveți îndoieli oriunde, puteți lua un calculator și puteți exersa puțin.
În cazul în care , încercați să construiți secvența , , . Daca atunci , , .

! Notă: Strict vorbind, această abordare de a construi secvențe de mai multe numere este incorectă, dar pentru înțelegerea celor mai simple exemple este destul de potrivită.

Acordați atenție și la următorul lucru. Chiar dacă o limită este dată cu un număr mare în vârf, sau chiar cu un milion: , atunci este tot la fel , deoarece mai devreme sau mai târziu „X” va începe să capete valori atât de gigantice încât un milion în comparație va fi un adevărat microb.

Ce trebuie să rețineți și să înțelegeți din cele de mai sus?

1) Când se oferă o limită, mai întâi încercăm pur și simplu să substituim numărul în funcție.

2) Trebuie să înțelegeți și să rezolvați imediat cele mai simple limite, cum ar fi , , etc.

Mai mult, limita are o semnificație geometrică foarte bună. Pentru o mai bună înțelegere a temei, vă recomand să citiți materialul didactic Grafice și proprietăți ale funcțiilor elementare. După ce ați citit acest articol, nu numai că veți înțelege în sfârșit ce este o limită, dar veți și face cunoștință cu cazuri interesante în care limita unei funcții în general nu exista!

În practică, din păcate, sunt puține cadouri. Și, prin urmare, trecem la considerarea unor limite mai complexe. Apropo, pe acest subiect există curs intensivîn format pdf, care este util mai ales dacă aveți FOARTE puțin timp de pregătit. Dar materialele site-ului, desigur, nu sunt mai rele:

Acum vom lua în considerare grupul de limite când , iar funcția este o fracție al cărei numărător și numitor conțin polinoame

Exemplu:

Calculați limita

Conform regulii noastre, vom încerca să substituim infinitul în funcție. Ce obținem în vârf? Infinit. Și ce se întâmplă mai jos? De asemenea, infinitul. Astfel, avem ceea ce se numește incertitudinea speciei. S-ar putea crede că , și răspunsul este gata, dar în cazul general nu este deloc cazul și este necesar să se aplice o tehnică de soluție, pe care o vom lua în considerare acum.

Cum se rezolvă limitele de acest tip?

Mai întâi ne uităm la numărător și găsim cea mai mare putere:

Puterea principală în numărător este două.

Acum ne uităm la numitor și îl găsim și la cea mai mare putere:

Cel mai înalt grad al numitorului este doi.

Apoi alegem cea mai mare putere a numărătorului și numitorului: în acest exemplu, acestea sunt aceleași și egale cu doi.

Deci, metoda de rezolvare este următoarea: pentru a dezvălui incertitudinea, este necesar să se împartă numărătorul și numitorul la cea mai mare putere.

Iată-l, răspunsul, și deloc infinit.

Ce este esențial important în proiectarea unei decizii?

În primul rând, indicăm incertitudinea, dacă există.

În al doilea rând, este indicat să întrerupeți soluția pentru explicații intermediare. De obicei folosesc semnul, nu are nicio semnificație matematică, dar înseamnă că soluția este întreruptă pentru o explicație intermediară.

În al treilea rând, în limită este indicat să marchezi ce se întâmplă unde. Când lucrarea este întocmită manual, este mai convenabil să o faceți astfel:

Este mai bine să folosiți un creion simplu pentru note.

Desigur, nu trebuie să faceți nimic din toate acestea, dar apoi, poate, profesorul va sublinia deficiențele soluției sau va începe să pună întrebări suplimentare despre sarcină. Ai nevoie de el?

Exemplul 2

Găsiți limita
Din nou la numărător și numitor găsim în cel mai înalt grad:

Gradul maxim la numărător: 3
Gradul maxim la numitor: 4
Alege cel mai mare valoare, în acest caz patru.
Conform algoritmului nostru, pentru a dezvălui incertitudinea, împărțim numărătorul și numitorul la .
Sarcina completă ar putea arăta astfel:

Împărțiți numărătorul și numitorul la

Exemplul 3

Găsiți limita
Gradul maxim de „X” la numărător: 2
Gradul maxim de „X” la numitor: 1 (se poate scrie ca)
Pentru a dezvălui incertitudinea, este necesar să împărțiți numărătorul și numitorul la . Soluția finală ar putea arăta astfel:

Împărțiți numărătorul și numitorul la

Notația nu înseamnă împărțire la zero (nu poți împărți la zero), ci împărțire cu un număr infinitezimal.

Astfel, descoperind incertitudinea speciei, putem fi capabili număr final, zero sau infinit.

Limite cu incertitudine de tip și metodă de rezolvare a acestora

Următorul grup de limite este oarecum similar cu limitele luate în considerare: numărătorul și numitorul conțin polinoame, dar „x” nu mai tinde spre infinit, ci spre număr finit.

Exemplul 4

Rezolvați limita
Mai întâi, să încercăm să înlocuim -1 în fracția:

În acest caz, se obține așa-numita incertitudine.

Regula generala: dacă numărătorul și numitorul conțin polinoame și există incertitudine cu privire la forma , atunci pentru a o dezvălui trebuie să factorizezi numărătorul și numitorul.

Pentru a face acest lucru, cel mai adesea trebuie să rezolvați o ecuație pătratică și/sau să utilizați formule de înmulțire abreviate. Dacă aceste lucruri au fost uitate, atunci vizitați pagina Formule și tabele matematiceși citiți materialul didactic Formule fierbinți pentru cursul școlar de matematică. Apropo, cel mai bine este să-l imprimați; este solicitat foarte des, iar informațiile sunt absorbite mai bine din hârtie.

Deci, hai să ne rezolvăm limita

Factorizați numărătorul și numitorul

Pentru a factoriza numărătorul, trebuie să rezolvați ecuația pătratică:

Mai întâi găsim discriminantul:

Și rădăcina pătrată a acesteia: .

Dacă discriminantul este mare, de exemplu 361, folosim un calculator; funcția de extragere a rădăcinii pătrate este pe cel mai simplu calculator.

! Dacă rădăcina nu este extrasă în întregime (se obține un număr fracționar cu virgulă), este foarte probabil ca discriminantul să fi fost calculat incorect sau să fi fost o greșeală de tipar în sarcină.

În continuare găsim rădăcinile:

Prin urmare:

Toate. Numătorul este factorizat.

Numitor. Numitorul este deja cel mai simplu factor și nu există nicio modalitate de a-l simplifica.

Evident, poate fi scurtat la:

Acum înlocuim -1 în expresia care rămâne sub semnul limită:

Desigur, într-un test, test sau examen, soluția nu este niciodată descrisă atât de detaliat. În versiunea finală, designul ar trebui să arate cam așa:

Să factorizăm numărătorul.

Exemplul 5

Calculați limita

În primul rând, versiunea „termină” a soluției

Să factorizăm numărătorul și numitorul.

Numărător:
Numitor:



,

Ce este important în acest exemplu?
În primul rând, trebuie să înțelegeți bine cum este dezvăluit numărătorul, mai întâi am scos 2 dintre paranteze și apoi am folosit formula pentru diferența de pătrate. Aceasta este formula pe care trebuie să o cunoști și să o vezi.

Recomandare: Dacă într-o limită (de aproape orice tip) este posibil să scoatem un număr din paranteze, atunci o facem întotdeauna.
Mai mult, este recomandabil să mutați astfel de numere dincolo de pictograma limită. Pentru ce? Da, doar ca să nu stea în cale. Principalul lucru este să nu pierdeți aceste numere mai târziu în timpul soluției.

Vă rugăm să rețineți că, în etapa finală a soluției, le-am scos pe cele două din pictograma limită și apoi pe minus.

! Important
În timpul soluției, fragmentul tip apare foarte des. Reduceți această fracțieeste interzis . Mai întâi trebuie să schimbați semnul numărătorului sau numitorului (puneți -1 din paranteze).
, adică apare un semn minus, care se ia în considerare la calcularea limitei și nu este nevoie să o pierzi deloc.

În general, am observat că cel mai adesea în găsirea limitelor de acest tip trebuie să rezolvi două ecuații pătratice, adică atât numărătorul cât și numitorul conțin trinoame pătratice.

Metoda de înmulțire a numărătorului și numitorului cu expresia conjugată

Continuăm să luăm în considerare incertitudinea formei

Următorul tip de limite este similar cu tipul anterior. Singurul lucru, pe lângă polinoame, vom adăuga rădăcini.

Exemplul 6

Găsiți limita

Să începem să decidem.

Mai întâi încercăm să înlocuim 3 în expresia de sub semnul limită
Repet încă o dată - acesta este primul lucru pe care trebuie să-l faci pentru ORICE limită. Această acțiune este de obicei efectuată mental sau în formă de proiect.

S-a obținut o incertitudine a formei care trebuie eliminată.

După cum probabil ați observat, numărătorul nostru conține diferența rădăcinilor. Și în matematică se obișnuiește să scapi de rădăcini, dacă este posibil. Pentru ce? Și viața este mai ușoară fără ele.

Limita unei funcții la un punct și la

Limita unei funcții este principalul aparat de analiză matematică. Cu ajutorul acestuia, continuitatea unei funcții, derivata, integrala și suma unei serii sunt ulterior determinate.

Fie funcția y=f(X)definit într-o anumită vecinătate a punctului, cu excepția, poate, a punctului însuși.

Să formulăm două definiții echivalente ale limitei unei funcții într-un punct.

Definiția 1 (în „limbajul secvențelor”, sau conform Heine). Număr b numit limita functiei y=f(X) la punct (sau pentru ), dacă pentru orice succesiune de valori de argument admisibile care converg către (adică ), succesiunea valorilor funcției corespunzătoare converge către număr b(adică).

În acest caz ei scriu sau la. Sensul geometric al limitei unei funcții: înseamnă că pentru toate punctele X, suficient de aproape de punct , valorile corespunzătoare ale funcției diferă cât de puțin se dorește de număr b.

Definiția 2 (în „limbă e-d ", sau după Cauchy). Număr b numit limita functiei y=f(X) la punct (sau pentru ), dacă pentru orice număr pozitiv e există un număr pozitiv d astfel încât pentru toți care satisfac inegalitatea , inegalitatea .

Înregistrate.

Această definiție poate fi scrisă pe scurt după cum urmează:

Rețineți că puteți scrie așa.

Semnificația geometrică a limitei funcției: dacă pentru orice e-vecinătate a punctului b există o asemenea d-vecinație a punctului , că pentru toți din acest cartier d valorile corespunzătoare ale funcției f(X) se află în vecinătatea e-punctului b. Cu alte cuvinte, punctele de pe graficul funcției y=f(X) se află în interiorul unei fâșii de lățime 2e delimitată de linii drepte la = b+e, la = b- e (Figura 17). Evident, valoarea lui d depinde de alegerea lui e, deci scriem d = d(e).

La determinarea limitei unei funcţii se presupune că X se străduiește pentru în orice fel: rămânând mai puţin decât (în partea stângă a ), mai mare ca (la dreapta de ), sau fluctuează în jurul unui punct .

Există cazuri când metoda de aproximare a unui argument X La afectează semnificativ valoarea limitei funcției. Prin urmare, sunt introduse conceptele de limite unilaterale.

Definiție. Numărul este sunat limita functiei y=f(X) stânga la punct , dacă pentru orice număr e > 0 există un număr d = d(e) > 0 astfel încât pentru , inegalitatea .

Limita din stânga este scrisă astfel sau pe scurt (notația Dirichlet) (Figura 18).

Definit în mod similar limita funcției din dreapta , să-l scriem folosind simboluri:

Pe scurt, limita din dreapta este notată cu .

Limitele stânga și dreapta ale unei funcții sunt numite limite cu sens unic . Evident, dacă , atunci există ambele limite unilaterale și .

Este adevărat și invers: dacă ambele limite există și și sunt egale, atunci există o limită și .

Dacă, atunci nu există.

Definiție. Lasă funcția y=f(X) este definită în intervalul . Număr b numit limita functiei y=f(X) la X® ¥, dacă pentru orice număr e > 0 există un astfel de număr M = M(e) > 0, care pentru toți X, satisfacerea inegalității inegalitatea este satisfăcută. Pe scurt, această definiție poate fi scrisă după cum urmează:

Dacă X® +¥, apoi scrieți dacă X® -¥, atunci ei scriu , dacă = , atunci sensul lor comun este de obicei notat .

Sensul geometric al acestei definiții este următorul: pentru , pentru și valorile corespunzătoare ale funcției y=f(X) se încadrează în e-vecinătatea punctului b, adică punctele graficului se află într-o fâșie de lățime 2e, delimitată de linii drepte și (Figura 19).

Funcții infinit de mari (b.b.f)

Funcții infinitezimale (funcții infinitezimale)

Definiție. Funcţie y=f(X) se numește infinit de mare la , dacă pentru orice număr M> 0 există un număr d = d( M) > 0, care este pentru toată lumea X, satisfăcând inegalitatea, inegalitatea este satisfăcută.Scrie sau la .

De exemplu, funcția este b.b.f. la .

Dacă f(X) tinde spre infinit la și ia numai valori pozitive, apoi scrieți ; dacă numai valori negative, atunci .

Definiție. Funcţie y=f(X), definită pe întreaga axă numerică, se numește infinit de mare la , dacă pentru orice număr M> 0 există un astfel de număr N = N(M) > 0, care este pentru toată lumea X satisfacand inegalitatea se scrie inegalitatea. Mic de statura:

De exemplu, există b.b.f. la .

Rețineți că dacă argumentul X, tinzând spre infinit, ia numai valori naturale, adică. , apoi b.b.f corespunzător. devine o succesiune infinit de mare. De exemplu, secvența este o secvență infinit de mare. Evident, orice b.b.f. în zona înconjurătoare puncte este nelimitat în această vecinătate. Reversul nu este adevărat: o funcție nemărginită poate să nu fie b.b.f. (De exemplu, )

Cu toate acestea, dacă unde b - număr final, apoi funcția f(x limitatîn vecinătatea punctului.

Într-adevăr, din definiţia limitei unei funcţii rezultă că atunci când condiţia este îndeplinită. Prin urmare, pentru , și aceasta înseamnă că funcția f(X) este limitat.

Definiție. Funcţie y=f(X) se numește infinitezimal la , Dacă

Prin definiția limitei unei funcții, această egalitate înseamnă: pentru orice număr există un număr astfel încât pentru toți X satisfacerea inegalității, inegalitatea este satisfăcută.

B.m.f. se determină în mod similar. la

: În toate aceste cazuri.

Funcțiile infinitezimale sunt adesea numite cantități infinitezimale sau infinitezimal ; de obicei notate cu literele grecești a, b etc.

Exemple de b.m.f. servesc funcţii când

Un alt exemplu: - o succesiune infinitezimală.

Exemplu Demonstrează că.

Soluţie . Caracteristica 5+ X poate fi reprezentat ca suma numărului 7 și b.m.f. X- 2 (la ), adică egalitatea este satisfăcută. Prin urmare, prin Teorema 3.4.6 obținem .

Teoreme de bază despre limite

Să luăm în considerare teoreme (fără dovezi) care facilitează găsirea limitelor unei funcții. Formularea teoremelor pentru cazurile când și este similară. În teoremele prezentate, vom presupune că limitele există.

Teorema 5.8 Limita sumei (diferenței) a două funcții este egală cu suma (diferenței) limitelor lor: .

Teorema 5.9 Limita produsului a două funcții este egală cu produsul limitelor lor:

Rețineți că teorema este valabilă pentru produsul oricărui număr finit de funcții.

Corolarul 3 Factorul constant poate fi luat dincolo de semnul limită: .

Corolarul 4 Limita unui grad cu exponent natural este egală cu același grad al limitei: . În special,

Teorema 5.10 Limita unei fracții este egală cu limita numărătorului împărțită la limita numitorului, cu excepția cazului în care limita numitorului este zero:

Exemplu calculati

Soluţie .

Exemplu calculati

Soluţie . Aici nu se poate aplica teorema asupra limitei unei fracții, deoarece limita numitorului, la este egală cu 0. În plus, limita numărătorului este egală cu 0. În astfel de cazuri spunem că avem incertitudinea de tip. Pentru a o extinde, factorizăm numărătorul și numitorul fracției, apoi le reducem cu:

Exemplu calculati

Soluţie . Aici avem de-a face incertitudinea de tip. Pentru a afla limita unei fracții date, împărțiți numărătorul și numitorul la:

Funcția este suma numărului 2 și b.m.f., prin urmare

Semne ale limitelor

Nu orice funcție, chiar și una limitată, are o limită. De exemplu, funcția la nu are limită. În multe întrebări de analiză, este suficient doar să verificăm existența unei limite a unei funcții. În astfel de cazuri, se folosesc semne ale existenței unei limite.

Prima și a doua limită remarcabilă

Definiție. Când se calculează limitele expresiilor care conțin funcții trigonometrice, limita este adesea folosită

numit prima limită remarcabilă .

Se citește: limita raportului dintre sinus și argumentul său este egală cu unu atunci când argumentul tinde spre zero.

Exemplu Găsi

Soluţie . Avem incertitudinea formei. Teorema limitei fracțiilor nu se aplică. Să notăm atunci la și

Exemplu 3 Găsiți

Soluţie.

Definiție. Se numesc egalităţi a doua limită remarcabilă .

cometariu. Se știe că limita unei secvențe de numere

Are o limită egală cu e: . Numărul e se numește numărul Neper. Numărul e este irațional, valoarea sa aproximativă este 2,72 (e = 2, 718281828459045...). Unele proprietăți ale numărului e fac să fie deosebit de convenabilă alegerea acestui număr ca bază a logaritmilor. Logaritmii la baza e sunt numiți logaritmi naturali și sunt notați cu Rețineți că

Să acceptăm fără dovezi afirmația că funcția tinde și spre numărul e

Dacă îl pui, urmează. Aceste egalități sunt utilizate pe scară largă în calcularea limitelor. În aplicațiile de analiză, un rol important îl joacă funcția exponențială cu baza e. Funcția se numește exponențială și se folosește și notația

Exemplu Găsi

Soluţie . Notăm în mod evident, cu Avem

Calculul limitelor

Pentru a dezvălui incertitudinile formei, este adesea util să se aplice principiul înlocuirii infinitezimale cu unele echivalente și alte proprietăți ale funcțiilor infinitezimale echivalente. După cum este cunoscut ~ X când ~ X la , pentru că

În acest articol vă vom spune care este limita unei funcții. Mai întâi, să explicăm punctele generale care sunt foarte importante pentru înțelegerea esenței acestui fenomen.

Conceptul de limită

În matematică, conceptul de infinit, notat cu simbolul ∞, este fundamental important. Ar trebui înțeles ca un număr infinit de mare + ∞ sau un număr infinitezimal - ∞. Când vorbim despre infinit, deseori ne referim la ambele sensuri simultan, dar notația formei + ∞ sau - ∞ nu trebuie înlocuită pur și simplu cu ∞.

Limita unei funcții se scrie ca lim x → x 0 f (x) . În partea de jos scriem argumentul principal x, iar cu ajutorul unei săgeți indicăm spre ce valoare x0 va tinde. Dacă valoarea x 0 este un număr real concret, atunci avem de-a face cu limita funcției într-un punct. Dacă valoarea x 0 tinde spre infinit (nu contează dacă ∞, + ∞ sau - ∞), atunci ar trebui să vorbim despre limita funcției la infinit.

Limita poate fi finită sau infinită. Dacă este egal cu un anumit număr real, de ex. lim x → x 0 f (x) = A, atunci se numește limită finită, dar dacă lim x → x 0 f (x) = ∞, lim x → x 0 f (x) = + ∞ sau lim x → x 0 f (x) = - ∞ , apoi infinit.

Dacă nu putem determina nici o valoare finită, nici o valoare infinită, înseamnă că o astfel de limită nu există. Un exemplu al acestui caz ar fi limita sinusului la infinit.

În acest paragraf vom explica cum să găsim valoarea limitei unei funcții într-un punct și la infinit. Pentru a face acest lucru, trebuie să introducem definiții de bază și să ne amintim ce sunt secvențele de numere, precum și convergența și divergența lor.

Definiția 1

Numărul A este limita funcției f (x) ca x → ∞ dacă succesiunea valorilor sale converge către A pentru orice succesiune infinit de argumente (negativă sau pozitivă).

Scrierea limitei unei funcții arată astfel: lim x → ∞ f (x) = A.

Definiția 2

Ca x → ∞, limita unei funcții f(x) este infinită dacă șirul de valori pentru orice succesiune infinit de argumente este, de asemenea, infinit de mare (pozitivă sau negativă).

Intrarea arată ca lim x → ∞ f (x) = ∞ .

Exemplul 1

Demonstrați egalitatea lim x → ∞ 1 x 2 = 0 folosind definiția de bază a limitei pentru x → ∞.

Soluţie

Să începem prin a scrie o secvență de valori a funcției 1 x 2 pentru o secvență pozitivă infinit de valori a argumentului x = 1, 2, 3, . . . , n , . . . .

1 1 > 1 4 > 1 9 > 1 16 > . . . > 1 n 2 > . . .

Vedem că valorile vor scădea treptat, tinzând spre 0. Vezi in poza:

x = - 1 , - 2 , - 3 , . . . , - n , . . .

1 1 > 1 4 > 1 9 > 1 16 > . . . > 1 - n 2 > . . .

Aici putem observa și o scădere monotonă spre zero, ceea ce confirmă validitatea acesteia în condiția de egalitate:

Răspuns: Corectitudinea acestui lucru în condiția de egalitate este confirmată.

Exemplul 2

Calculați limita lim x → ∞ e 1 10 x .

Soluţie

Să începem, ca mai înainte, prin a scrie secvențe de valori f (x) = e 1 10 x pentru o succesiune pozitivă infinit de argumente. De exemplu, x = 1, 4, 9, 16, 25, . . . , 10 2 , . . . → + ∞ .

e 1 10 ; e 4 10 ; e 9 10 ; e 16 10 ; e 25 10 ; . . . ; e 100 10 ; . . . = = 1, 10; 1, 49; 2, 45; 4, 95; 12, 18; . . . ; 22026, 46; . . .

Vedem că această succesiune este infinit pozitivă, ceea ce înseamnă f (x) = lim x → + ∞ e 1 10 x = + ∞

Să trecem la scrierea valorilor unei secvențe negative infinit de mare, de exemplu, x = - 1, - 4, - 9, - 16, - 25, . . . , - 10 2 , . . . → - ∞ .

e - 1 10 ; e - 4 10 ; e - 9 10 ; e - 16 10 ; e - 25 10 ; . . . ; e - 100 10 ; . . . = = 0, 90; 0, 67; 0, 40; 0, 20; 0, 08; . . . ; 0,000045; . . . x = 1, 4, 9, 16, 25, . . . , 10 2 , . . . → ∞

Deoarece tinde și spre zero, atunci f (x) = lim x → ∞ 1 e 10 x = 0 .

Soluția problemei este prezentată clar în ilustrație. Punctele albastre indică o secvență de valori pozitive, punctele verzi indică o secvență de valori negative.

Răspuns: lim x → ∞ e 1 10 x = + ∞ , pr și x → + ∞ 0 , pr și x → - ∞ .

Să trecem la metoda de calcul a limitei unei funcții într-un punct. Pentru a face acest lucru, trebuie să știm cum să definim corect o limită unilaterală. Acest lucru ne va fi util și pentru a găsi asimptotele verticale ale graficului unei funcții.

Definiția 3

Numărul B este limita funcției f (x) din stânga ca x → a în cazul în care succesiunea valorilor sale converge către un număr dat pentru orice succesiune de argumente a funcției x n convergentă către a, dacă valorile sale rămân mai mici decât a (x n< a).

O astfel de limită este notată în scris ca lim x → a - 0 f (x) = B.

Acum să formulăm care este limita unei funcții din dreapta.

Definiția 4

Numărul B este limita funcției f (x) din dreapta ca x → a în cazul în care succesiunea valorilor sale converge către un număr dat pentru orice succesiune de argumente a funcției x n convergentă către a, dacă valorile sale rămân mai mari decât a (x n > a).

Scriem această limită ca lim x → a + 0 f (x) = B .

Putem găsi limita unei funcții f (x) la un anumit punct când are limite egale pe laturile stânga și dreapta, i.e. lim x → a f (x) = lim x → a - 0 f (x) = lim x → a + 0 f (x) = B . Dacă ambele limite sunt infinite, limita funcției de la punctul de plecare va fi, de asemenea, infinită.

Acum vom clarifica aceste definiții notând soluția unei probleme specifice.

Exemplul 3

Demonstrați că există o limită finită a funcției f (x) = 1 6 (x - 8) 2 - 8 în punctul x 0 = 2 și calculați valoarea acesteia.

Soluţie

Pentru a rezolva problema, trebuie să ne amintim definiția limitei unei funcții într-un punct. Mai întâi, să demonstrăm că funcția originală are o limită în stânga. Să scriem o secvență de valori ale funcției care va converge către x 0 = 2 dacă x n< 2:

f(-2); f (0); f (1) ; f 1 1 2 ; f 1 3 4 ; f 1 7 8 ; f 1 15 16; . . . ; f 1 1023 1024; . . . = = 8, 667; 2, 667; 0, 167; - 0, 958; - 1, 489; - 1.747; - 1.874; . . . ; - 1.998; . . . → - 2

Deoarece șirul de mai sus se reduce la - 2, putem scrie că lim x → 2 - 0 1 6 x - 8 2 - 8 = - 2.

6 , 4 , 3 , 2 1 2 , 2 1 4 , 2 1 8 , 2 1 16 , . . . , 2 1 1024 , . . . → 2

Valorile funcției din această secvență vor arăta astfel:

f (6); f (4); f (3); f 2 1 2 ; f 2 3 4 ; f 2 7 8 ; f 2 15 16 ; . . . ; f 2 1023 1024; . . . = = - 7, 333; - 5, 333; - 3, 833; - 2.958; - 2, 489; - 2, 247; - 2, 124; . . . , - 2.001, . . . → - 2

Această secvență converge și la - 2, ceea ce înseamnă lim x → 2 + 0 1 6 (x - 8) 2 - 8 = - 2.

Am constatat că limitele din partea dreaptă și stângă ale acestei funcții vor fi egale, ceea ce înseamnă că limita funcției f (x) = 1 6 (x - 8) 2 - 8 în punctul x 0 = 2 există, și lim x → 2 1 6 (x - 8) 2 - 8 = - 2 .

Puteți vedea progresul soluției în ilustrație (punctele verzi sunt o secvență de valori care converg la x n< 2 , синие – к x n > 2).

Răspuns: Limitele din partea dreaptă și stângă ale acestei funcții vor fi egale, ceea ce înseamnă că limita funcției există, iar lim x → 2 1 6 (x - 8) 2 - 8 = - 2.

Pentru a studia mai profund teoria limitelor, vă sfătuim să citiți articolul despre continuitatea unei funcții într-un punct și principalele tipuri de puncte de discontinuitate.

Dacă observați o eroare în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter

Luați în considerare funcția %%f(x)%% definită cel puțin într-o zonă perforată %%\stackrel(\circ)(\text(U))(a)%% din punctul %%a \in \overline( \ mathbb(R))%% linie numerică extinsă.

Conceptul de limită Cauchy

Numărul %%A \în \mathbb(R)%% este numit limita functiei%%f(x)%% la punctul %%a \in \mathbb(R)%% (sau la %%x%% care tinde spre %%a \in \mathbb(R)%%), dacă, ce Indiferent de numărul pozitiv %%\varepsilon%%, există un număr pozitiv %%\delta%% astfel încât pentru toate punctele din vecinătatea punctului %%\delta%% a punctului %%a%% valorile funcției aparțin %%\varepsilon %%-vecinătatea punctului %%A%%, sau

$$ A = \lim\limits_(x \to a)(f(x)) \Leftrightarrow \forall\varepsilon > 0 ~\exists \delta > 0 \big(x \in \stackrel(\circ)(\text (U))_\delta(a) \Rightarrow f(x) \in \text(U)_\varepsilon (A) \big) $$

Această definiție se numește definiția %%\varepsilon%% și %%\delta%%, propusă de matematicianul francez Augustin Cauchy și folosită de la începutul secolului al XIX-lea până în zilele noastre deoarece are rigoarea și acuratețea matematică necesară.

Combinând diferite vecinătăți ale punctului %%a%% din forma %%\stackrel(\circ)(\text(U))_\delta(a), \text(U)_\delta (\infty), \ text(U) _\delta (-\infty), \text(U)_\delta (+\infty), \text(U)_\delta^+ (a), \text(U)_\delta^ - (a) %% cu împrejurimile %%\text(U)_\varepsilon (A), \text(U)_\varepsilon (\infty), \text(U)_\varepsilon (+\infty), \ text(U) _\varepsilon (-\infty)%%, obținem 24 de definiții ale limitei Cauchy.

Sensul geometric

Sensul geometric al limitei unei funcții

Să aflăm care este semnificația geometrică a limitei unei funcții într-un punct. Să construim un grafic al funcției %%y = f(x)%% și să marchem punctele %%x = a%% și %%y = A%% pe ea.

Limita funcției %%y = f(x)%% în punctul %%x \to a%% există și este egală cu A dacă pentru orice %%\varepsilon%% vecinătate a punctului %%A%% se poate specifica o astfel de %%\ delta%%-vecinătate a punctului %%a%%, astfel încât pentru orice %%x%% din acest %%\delta%%-vecinătate valoarea %%f(x)% % va fi în punctele de vecinătate %%\varepsilon%% %%A%%.

Rețineți că prin definirea limitei unei funcții conform lui Cauchy, pentru existența unei limite la %%x \to a%%, nu contează ce valoare ia funcția în punctul %%a%%. Pot fi date exemple în care funcția nu este definită când %%x = a%% sau ia o altă valoare decât %%A%%. Cu toate acestea, limita poate fi %%A%%.

Determinarea limitei Heine

Elementul %%A \in \overline(\mathbb(R))%% se numește limita funcției %%f(x)%% la %% x \to a, a \in \overline(\mathbb( R))%% , dacă pentru orice secvență %%\(x_n\) \la un%% din domeniul definiției, secvența valorilor corespunzătoare ​​%%\big\(f(x_n)\big\)% % tinde spre %%A%%.

Definiția unei limite conform Heine este convenabil de utilizat atunci când apar îndoieli cu privire la existența unei limite a unei funcții la un punct dat. Dacă este posibil să construiți cel puțin o secvență %%\(x_n\)%% cu o limită în punctul %%a%% astfel încât secvența %%\big\(f(x_n)\big\)%% nu are limită, atunci putem concluziona că funcția %%f(x)%% nu are nicio limită în acest moment. Dacă pentru doi variat secvențele %%\(x"_n\)%% și %%\(x""_n\)%% având la fel limită %%a%%, secvențele %%\big\(f(x"_n)\big\)%% și %%\big\(f(x""_n)\big\)%% au variat limite, atunci în acest caz nu există nici o limită a funcției %%f(x)%%.

Exemplu

Fie %%f(x) = \sin(1/x)%%. Să verificăm dacă limita acestei funcții există în punctul %%a = 0%%.

Să alegem mai întâi o secvență $$ \(x_n\) = \left\(\frac((-1)^n)(n\pi)\right\) care converge în acest punct. $$

Este clar că %%x_n \ne 0~\forall~n \in \mathbb(N)%% și %%\lim (x_n) = 0%%. Atunci %%f(x_n) = \sin(\left((-1)^n n\pi\right)) \equiv 0%% și %%\lim\big\(f(x_n)\big\) = 0 %%.

Apoi luați o secvență care converge către același punct $$ x"_n = \left\( \frac(2)((4n + 1)\pi) \right\), $$

pentru care %%\lim(x"_n) = +0%%, %%f(x"_n) = \sin(\big((4n + 1)\pi/2\big)) \equiv 1%% și %%\lim\big\(f(x"_n)\big\) = 1%%. În mod similar, pentru secvența $$ x""_n = \left\(-\frac(2)((4n + 1) ) \pi) \dreapta\), $$

de asemenea, convergând către punctul %%x = 0%%, %%\lim\big\(f(x""_n)\big\) = -1%%.

Toate cele trei secvențe au dat rezultate diferite, ceea ce contrazice condiția definiției Heine, adică. această funcție nu are limită în punctul %%x = 0%%.

Teorema

Definițiile Cauchy și Heine ale limitei sunt echivalente.

Este dată formularea principalelor teoreme și proprietăți ale limitei unei funcții. Sunt date definiții ale limitelor finite și infinite în puncte finite și la infinit (bilaterale și unilaterale) conform lui Cauchy și Heine. Sunt luate în considerare proprietățile aritmetice; teoreme legate de inegalități; criteriul de convergență Cauchy; limita unei funcții complexe; proprietăți ale funcțiilor infinitezimale, infinit de mari și monotone. Este dată definiția unei funcții.

Conţinut

A doua definiție după Cauchy

Limita unei funcții (după Cauchy) ca argumentul ei x tinde spre x 0 este un număr finit sau un punct la infinit a pentru care sunt îndeplinite următoarele condiții:
1) există o astfel de vecinătate perforată a punctului x 0 , pe care funcția f (X) determinat;
2) pentru orice vecinătate a punctului a aparținând , există o astfel de vecinătate perforată a punctului x 0 , pe care valorile funcției aparțin vecinătății selectate a punctului a:
la .

Aici a și x 0 pot fi, de asemenea, numere finite sau puncte la infinit. Folosind simbolurile logice ale existenței și universalității, această definiție poate fi scrisă după cum urmează:
.

Dacă luăm vecinătatea stângă sau dreaptă a unui punct final ca mulțime, obținem definiția unei limite Cauchy la stânga sau la dreapta.

Teorema
Definițiile Cauchy și Heine ale limitei unei funcții sunt echivalente.
Dovada

Cartierele de puncte aplicabile

Apoi, de fapt, definiția Cauchy înseamnă următoarele.
Pentru orice numere pozitive, există numere, astfel încât pentru toate x aparținând vecinătății punctate a punctului: , valorile funcției aparțin vecinătății punctului a: ,
Unde , .

Această definiție nu este foarte convenabilă pentru a lucra, deoarece cartierele sunt definite folosind patru numere. Dar se poate simplifica prin introducerea cartierelor cu capete echidistante. Adică poți pune , . Apoi vom obține o definiție care este mai ușor de utilizat atunci când demonstrăm teoreme. Mai mult, este echivalent cu definiția în care sunt folosite cartiere arbitrare. Dovada acestui fapt este dată în secțiunea „Echivalența definițiilor Cauchy ale limitei unei funcții”.

Apoi putem da o definiție unificată a limitei unei funcții în puncte finite și infinit îndepărtate:
.
Aici pentru puncte finale
; ;
.
Orice vecinătate de puncte la infinit este perforată:
; ; .

Limite finite ale funcției la punctele finale

Numărul a se numește limita funcției f (X)în punctul x 0 , Dacă
1) funcția este definită pe o vecinătate perforată a punctului final;
2) pentru orice există astfel încât să depindă de , astfel încât pentru orice x pentru care , inegalitatea este valabilă
.

Folosind simbolurile logice ale existenței și universalității, definiția limitei unei funcții poate fi scrisă după cum urmează:
.

Limite unilaterale.
Limită din stânga într-un punct (limită din stânga):
.
Limită dreaptă într-un punct (limită dreaptă):
.
Limitele din stânga și din dreapta sunt adesea indicate după cum urmează:
; .

Limitele finite ale unei funcții în puncte la infinit

Limitele în puncte la infinit sunt determinate într-un mod similar.
.
.
.

Limite infinite ale funcției

De asemenea, puteți introduce definiții ale limitelor infinite ale anumitor semne egale cu și:
.
.

Proprietăţi şi teoreme ale limitei unei funcţii

În plus, presupunem că funcțiile luate în considerare sunt definite în vecinătatea perforată corespunzătoare a punctului , care este un număr finit sau unul dintre simbolurile: . Poate fi, de asemenea, un punct limită unilateral, adică să aibă forma sau . Cartierul este bilateral pentru o limită cu două laturi și unilateral pentru o limită unilaterală.

Proprietăți de bază

Dacă valorile funcției f (X) schimbați (sau faceți nedefinit) un număr finit de puncte x 1, x 2, x 3, ... x n, atunci această modificare nu va afecta existența și valoarea limitei funcției la un punct arbitrar x 0 .

Dacă există o limită finită, atunci există o vecinătate perforată a punctului x 0 , pe care funcția f (X) limitat:
.

Fie funcția să aibă în punctul x 0 limită finită diferită de zero:
.
Atunci, pentru orice număr c din intervalul , există o astfel de vecinătate perforată a punctului x 0 , pentru ce ,
, Dacă ;
, Dacă .

Dacă, pe o vecinătate perforată a punctului, , este o constantă, atunci .

Dacă există limite finite și și pe o vecinătate perforată a punctului x 0
,
Acea .

Dacă , și pe o anumită vecinătate a punctului
,
Acea .
În special, dacă se află într-un anumit punct
,
atunci dacă , atunci și ;
dacă , atunci și .

Dacă pe o vecinătate perforată a unui punct x 0 :
,
și există limite egale finite (sau infinite ale unui anumit semn):
, Acea
.

Dovezile principalelor proprietăți sunt date pe pagină
„Proprietățile de bază ale limitei unei funcții”.

Fie funcțiile și să fie definite într-o vecinătate perforată a punctului. Și să fie limite finite:
Și .
Și să fie C o constantă, adică un număr dat. Apoi
;
;
;
, Dacă .

Daca atunci.

Pe pagină sunt date dovezi ale proprietăților aritmetice
„Proprietăți aritmetice ale limitei unei funcții”.

Criteriul Cauchy pentru existența unei limite a unei funcții

Teorema
Pentru o funcție definită pe o vecinătate perforată a unui punct finit sau infinit x 0 , a avut o limită finită în acest punct, este necesar și suficient ca pentru orice ε > 0 exista o astfel de vecinătate perforată a punctului x 0 , că pentru orice puncte și din această vecinătate este valabilă următoarea inegalitate:
.

Limita unei funcții complexe

Teoremă asupra limitei unei funcții complexe
Fie ca funcția să aibă o limită și mapați o vecinătate perforată a unui punct pe o vecinătate perforată a unui punct. Lăsați funcția să fie definită pe această vecinătate și aveți o limită asupra acesteia.
Iată punctele finale sau infinit îndepărtate: . Vecinătățile și limitele lor corespunzătoare pot fi fie cu două laturi, fie unilaterale.
Atunci există o limită a unei funcții complexe și este egală cu:
.

Teorema limită a unei funcții complexe se aplică atunci când funcția nu este definită într-un punct sau are o valoare diferită de limită. Pentru a aplica această teoremă, trebuie să existe o vecinătate perforată a punctului în care mulțimea de valori a funcției nu conține punctul:
.

Dacă funcția este continuă în punctul , atunci semnul limită poate fi aplicat argumentului funcției continue:
.
Următoarea este o teoremă corespunzătoare acestui caz.

Teoremă asupra limitei unei funcții continue a unei funcții
Să existe o limită a funcției g (X) ca x → x 0 , și este egal cu t 0 :
.
Aici este punctul x 0 poate fi finit sau infinit distant: .
Și fie funcția f (t) continuă în punctul t 0 .
Atunci există o limită a funcției complexe f (g(x)), și este egal cu f (t 0):
.

Pe pagină sunt date dovezi ale teoremelor
„Limita și continuitatea unei funcții complexe”.

Funcții infinitezimale și infinit de mari

Funcții infinitezimale

Definiție
Se spune că o funcție este infinitezimală dacă
.

Sumă, diferență și produs a unui număr finit de funcții infinitezimale la este o funcție infinitezimală la .

Produsul unei funcții mărginit pe o vecinătate perforată a punctului , la o infinitezimală la este o funcție infinitezimală la .

Pentru ca o funcție să aibă o limită finită, este necesar și suficient ca
,
unde este o funcție infinitezimală la .

„Proprietăți ale funcțiilor infinitezimale”.

Funcții infinit de mari

Definiție
Se spune că o funcție este infinit de mare dacă
.

Suma sau diferența unei funcții mărginite, pe o vecinătate perforată a punctului , și o funcție infinit de mare la este o funcție infinit de mare la .

Dacă funcția este infinit de mare pentru , și funcția este mărginită pe o vecinătate perforată a punctului , atunci
.

Dacă funcția , pe o vecinătate perforată a punctului , satisface inegalitatea:
,
iar funcția este infinitezimală la:
, și (pe vreo vecinătate perforată a punctului), apoi
.

Dovezile proprietăților sunt prezentate în secțiune
„Proprietăți ale funcțiilor infinit de mari”.

Relația dintre funcțiile infinit de mari și infinitezimale

Din cele două proprietăți anterioare rezultă legătura dintre funcțiile infinit de mari și infinitezimale.

Dacă o funcție este infinit de mare la , atunci funcția este infinitezimală la .

Dacă o funcție este infinitezimală pentru , și , atunci funcția este infinit mare pentru .

Relația dintre o funcție infinitezimală și o funcție infinit de mare poate fi exprimată simbolic:
, .

Dacă o funcție infinitezimală are un anumit semn la , adică este pozitivă (sau negativă) pe o vecinătate perforată a punctului , atunci acest fapt poate fi exprimat astfel:
.
În același mod, dacă o funcție infinit de mare are un anumit semn la , atunci ei scriu:
.

Apoi legătura simbolică dintre funcțiile infinit de mici și infinit de mari poate fi completată cu următoarele relații:
, ,
, .

Formule suplimentare referitoare la simbolurile infinitului pot fi găsite pe pagină
„Punctează la infinit și proprietățile lor”.

Limitele funcţiilor monotone

Definiție
Se numește o funcție definită pe un set de numere reale X strict crescând, dacă pentru toate acestea sunt valabile următoarea inegalitate:
.
În consecință, pentru strict în scădere Funcționează următoarea inegalitate:
.
Pentru nedescrescătoare:
.
Pentru necrescătoare:
.

Rezultă că o funcție strict crescătoare este, de asemenea, nedescrescătoare. O funcție strict descrescătoare este, de asemenea, necreștetoare.

Funcția este numită monoton, dacă nu este în scădere sau în creștere.

Teorema
Fie ca funcția să nu scadă pe intervalul în care .
Dacă este mărginită mai sus de numărul M: atunci există o limită finită. Dacă nu este limitat de sus, atunci.
Dacă este limitată de jos de numărul m: atunci există o limită finită. Dacă nu este limitat de jos, atunci.

Dacă punctele a și b sunt la infinit, atunci în expresii semnele limită înseamnă că .
Această teoremă poate fi formulată mai compact.

Fie ca funcția să nu scadă pe intervalul în care . Atunci există limite unilaterale în punctele a și b:
;
.

O teoremă similară pentru o funcție care nu crește.

Fie ca funcția să nu crească pe intervalul în care . Apoi există limite unilaterale:
;
.

Dovada teoremei este prezentată pe pagină
„Limitele funcțiilor monotone”.

Definiția funcției

Funcţie y = f (X) este o lege (regulă) conform căreia fiecare element x al mulțimii X este asociat cu unul și un singur element y al mulțimii Y.

Elementul x ∈ X numit argumentul funcției sau variabila independenta.
Elementul y ∈ Y numit valoarea functiei sau variabilă dependentă.

Se numește mulțimea X domeniul functiei.
Set de elemente y ∈ Y, care au preimagini în setul X, se numește zonă sau set de valori ale funcției.

Funcția reală este numită limitat de sus (de jos), dacă există un număr M astfel încât inegalitatea să fie valabilă pentru toți:
.
Se apelează funcția de număr limitat, dacă există un număr M astfel încât pentru toate:
.

Marginea superioară sau limita superioară exactă O funcție reală se numește cel mai mic număr care își limitează intervalul de valori de sus. Adică acesta este un număr s pentru care, pentru toată lumea și pentru oricare, există un argument a cărui valoare a funcției depășește s′: .
Limita superioară a unei funcții poate fi notată după cum urmează:
.

Respectiv marginea de jos sau limita inferioară exactă O funcție reală se numește cel mai mare număr care își limitează intervalul de valori de jos. Adică acesta este un număr i pentru care, pentru toată lumea și pentru oricare, există un argument a cărui valoare a funcției este mai mică decât i′: .
Infimul unei funcții poate fi notat astfel:
.

Referinte:
L.D. Kudryavtsev. Curs de analiză matematică. Volumul 1. Moscova, 2003.
CM. Nikolsky. Curs de analiză matematică. Volumul 1. Moscova, 1983.

Vezi si: