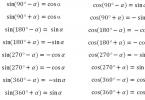Визначення. Формулами приведення називають формули, які дозволяють перейти від тригонометричних функцій виду до функцій аргументу. З їх допомогою синус, косинус, тангенс та котангенс довільного кута можна привести до синуса, косінусу, тангенсу та котангенсу кута з інтервалу від 0 до 90 градусів (від 0 до радіан). Таким чином, формули приведення дозволяють переходити до роботи з кутами в межах 90 градусів, що, безсумнівно, дуже зручно.

Формули наведення:

Для використання формул приведення є два правила.

1. Якщо кут можна подати у вигляді (π/2 ±a) або (3*π/2 ±a), то назва функції змінюється sin на cos, cos на sin, tg на ctg, ctg на tg. Якщо ж кут можна уявити у вигляді (π ±a) або (2*π ±a), то назва функції залишається без змін.

Подивіться на малюнок нижче, там схематично зображено, коли слід міняти знак, а коли ні

2. Знак наведеної функції залишається тим самим. Якщо вихідна функція мала знак плюс, то і наведена функція має знак плюс. Якщо вихідна функція мала знак мінус, то і наведена функція має знак мінус.

На малюнку нижче подано знаки основних тригонометричних функцій залежно від чверті.

Приклад:

Обчислити

Скористаємося формулами приведення:

Sin(150˚) знаходиться у другій чверті, на малюнку бачимо що знак sin у цій чверті дорівнює "+". Отже, у наведеної функції теж буде знак «+». Це ми застосували друге правило.

Тепер 150˚ = 90˚ +60˚. 90˚ це π/2. Тобто маємо справу з випадком π/2+60, отже, за першим правилом змінюємо функцію з sin на cos. У результаті отримуємо Sin(150˚) = cos(60˚) = ½.

І ще один момент: формул приведення досить багато за кількістю, і відразу застережемо Вас від заучування їх усіх напам'ять. У цьому немає необхідності – існує , що дозволяє легко застосовувати формули приведення.

Отже, запишемо усі формули наведення у вигляді таблиці.

Ці формули можна переписати з використанням градусів та радіан. Для цього достатньо згадати про зв'язок між градусами і радіанами і скрізь замінити π на 180 градусів.

Приклади використання формул приведення

Мета цього пункту полягає в тому, щоб показати, як формули наведення використовуються на практиці при вирішенні прикладів.

Спочатку варто сказати, що існує нескінченна кількість способів представлення кута під знаком тригонометричних функцій у вигляді і . Це з тим, що кут може набувати будь-яке значення. Покажемо на прикладі.

Наприклад візьмемо кут під знаком тригонометричної функції рівним. Цей кут можна уявити як , або як , або як , або ще безліччю інших способів.

А тепер давайте подивимося, які формули приведення нам доведеться використовувати залежно від уявлення кута. Наприклад візьмемо .

Якщо ми представимо кут як , то цьому уявленню відповідає формула приведення виду , звідки отримуємо . Ми можемо вказати значення тригонометричної функції: .

Для подання ми вже будемо використовувати формулу виду , що призводить до наступного результату: .

Нарешті, так як відповідна формула приведення має вигляд .

На закінчення цих міркувань варто особливо відзначити, що існують певні зручності при використанні уявлень кута, в яких кут має величину від 0 до 90 градусів (від 0 до пі навпіл радіан).

Розглянемо приклад застосування формул приведення.

приклад.

Використовуючи формули наведення, уявіть через синус, а також через косинус гострого кута.

Рішення.

Щоб застосувати формули приведення, нам потрібно кут 197 градусів подати у вигляді або , причому за умовою завдання кут має бути гострим. Це можна зробити двома способами: або . Таким чином, або .

Звернувшись до відповідних формул приведення і , отримуємо і .

Відповідь:

і .

Мнемонічне правило

Як ми згадували вище, формули приведення заучувати напам'ять необов'язково. Якщо уважно на них подивитися, то можна виявити закономірності, з яких можна отримати правило, що дозволяє отримати будь-яку формулу приведення. Його називають мнемонічним правилом(Мнемоніка - мистецтво запам'ятовування).

Мнемонічне правило містить три етапи:

Відразу варто сказати, що для застосування мнемонічного правила потрібно дуже добре вміти визначати знаки синуса, косинуса, тангенсу та котангенсу по чвертях, тому що робити це доведеться постійно.

Розберемо застосування мнемонічного правила на прикладах.

приклад.

Використовуючи менімонічне правило, запишіть формули приведення для і рахуючи кут кутом першої чверті.

Рішення.

Перший крок правила нам робити не доведеться, тому що кути під знаками тригонометричних функцій вже записані у потрібному вигляді.

Визначимо знак функцій і . За умови, що - кут першої чверті, кут теж є кутом першої чверті, а кут - кутом другої чверті. Косінус у першій чверті має знак плюс, а тангенс у другій чверті має знак мінус. На цьому етапі шукані формули матимуть вигляд і . Зі знаками розібралися, можна переходити до заключного кроку мнемонічного правила.

Оскільки аргумент функції косинус має вигляд , то назву функції потрібно поміняти на кофункцію, тобто на синус. А аргумент тангенсу має вигляд Отже, назву функції потрібно залишити колишньою.

У результаті маємо та . Можна заглянути до таблиці формул приведення, щоб переконатися у правильності отриманих результатів.

Відповідь:

та .

Для закріплення матеріалу розглянемо рішення прикладу з конкретними кутами.

приклад.

Використовуючи менімонічне правило, приведіть до тригонометричних функцій гострого кута.

Рішення.

Для початку уявімо кут 777 градусів у вигляді, необхідному для застосування мнемонічного правила. Це можна зробити двома способами: або .

Початковий кут є кутом першої чверті, синус для цього кута має знак плюс.

Для подання назву синуса потрібно залишити колишнім, а для подання виду синус доведеться поміняти на косинус.

У результаті маємо і .

Відповідь:

та .

На закінчення цього пункту розглянемо приклад, що ілюструє важливість правильного представлення кута під знаком тригонометричних функцій для застосування мнемонічного правила: кут повинен бути гострим!

Обчислимо тангенс кута. У принципі, звернувшись до матеріалу статті значення синуса, косинуса, тангенсу та котангенсу, ми можемо відразу дати відповідь на запитання задачі: .

Якщо ми представимо кут як або як, то можна скористатися мнемонічним правилом: і що призводить до того ж результату.

А ось що може вийти, якщо взяти уявлення кута, наприклад, виду. При цьому менімонічне правило приведе нас до такого результату. Цей результат невірний, а пояснюється це тим, що для подання ми не мали права застосовувати менімонічне правило, оскільки кут не є гострим.

Доказ формул наведення

Формули приведення відображають періодичність, симетричність та властивості зсуву на кути та . Відразу зауважимо, що це формули приведення можна доводити, відкинувши в аргументах доданок , оскільки воно означає зміна кута ціле число повних оборотів, але це змінює значення тригонометричних функцій. Це доданок і є відображенням періодичності.

Перший блок з 16 формул приведення безпосередньо випливає із властивостей синуса, косинуса, тангенсу та котангенсу. На них навіть не варто зупинятися.

Переходимо до наступного блоку формул. Спочатку доведемо перші дві з них. Інші випливають із них. Отже, доведемо формули наведення виду і .

Розглянемо одиничне коло. Нехай початкова точка A після повороту на кут перетворюється на точку A 1 (x, y) , а після повороту на кут - у точку A 2 . Проведемо A 1 H 1 та A 2 H 2 – перпендикуляри до прямої Ox.

Нескладно бачити, що прямокутні трикутники OA 1 H 1 і OA 2 H 2 рівні по гіпотенузі і двох кутів, що прилягають до неї. З рівності трикутників та розташування точок A 1 і A 2 на одиничному колі стає видно, що якщо точка A 1 має координати x і y то точку A 2 має координати −y і x . Тоді визначення синуса та косинуса дозволяють нам записати рівності та звідки випливає, що і . Цим доведено аналізовані формули приведення для будь-якого кута.

Враховуючи що і (при необхідності дивіться статтю основні тригонометричні тотожності), а також щойно доведені формули, отримуємо і . Так ми довели дві наступні формули приведення.

Для доказу формул приведення з аргументом досить його подати як , після чого використовувати доведені формули та властивості тригонометричних функцій з протилежними аргументами. Наприклад, .

Аналогічно доводяться й інші формули приведення з урахуванням вже доведених шляхом дворазового застосування. Наприклад, представляється як , а як . А й – як і відповідно.

Список літератури.

• Алгебра:Навч. для 9 кл. середовищ. шк./Ю. Н. Макарічев, Н. Г. Міндюк, К. І. Нешков, С. Б. Суворова; За ред. С. А. Теляковського.- М.: Просвітництво, 1990.- 272 с.: Іл.- ISBN 5-09-002727-7
• Башмаков М. І.Алгебра та початку аналізу: Навч. для 10-11 кл. середовищ. шк. - 3-тє вид. - М: Просвітництво, 1993. - 351 с.: іл. - ISBN 5-09-004617-4.
• Алгебрата початку аналізу: Навч. для 10-11 кл. загальноосвіт. установ / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудніцин та ін; За ред. А. Н. Колмогорова. - 14-те вид. - М.: Просвітництво, 2004. - 384 с.: Іл. - ISBN 5-09-013651-3.
• Гусєв В. А., Мордкович А. Г.Математика (посібник для вступників до технікумів): Навч. посібник.- М.; Вищ. шк., 1984.-351 с., іл.

І ще одне завдання B11 на ту саму тему — із реального ЄДІ з математики.

Завдання. Знайдіть значення виразу:

У цьому короткому відеоуроці ми дізнаємося, як застосовувати формули приведеннядля вирішення реальних завдань B11 з ЄДІ з математики. Як ви бачите, перед нами — два тригонометричні вирази, кожний з яких містить синуси та косинуси, а також досить звірячі числові аргументи.

Перш ніж розв'язувати ці завдання, давайте згадаємо, що таке формули приведення. Отже, якщо у нас є вирази виду:

То ми можемо позбутися першого доданку (виду k · π/2) за спеціальними правилами. Накреслимо тригонометричне коло, відзначимо на ньому основні точки: 0, π/2; π; 3π/2 та 2π. Потім дивимося на перший доданок під знаком тригонометричної функції. Маємо:

1. Якщо цікавий для нас доданок лежить на вертикальній осі тригонометричного кола (наприклад: 3π/2; π/2 і т.д.), то вихідна функція замінюється на ко-функцию: синус замінюється косинусом, а косинус — навпаки, синусом.
2. Якщо ж наш доданок лежить на горизонтальній осі, то вихідна функція не змінюється. Просто прибираємо перший доданок у виразі - і все.

Таким чином, ми отримаємо тригонометричну функцію, що не містить доданків виду k · π/2. Однак на цьому робота з формулами наведення не закінчується. Справа в тому, що перед нашою новою функцією, отриманою після «відкидання» першого доданка, може стояти знак плюс чи мінус. Як визначити цей знак? Ось зараз і дізнаємось.

Припустимо, що кут α, що залишився всередині тригонометричної функції після перетворень, має дуже малу градусну міру. Але що означає «малий захід»? Припустимо, α ∈ (0; 30 °) - цього цілком достатньо. Розглянемо для прикладу функцію:

Тоді, дотримуючись наших припущень, що α ∈ (0; 30°), укладаємо, що кут 3π/2 − α лежить у третій координатній чверті, тобто. 3π/2 − α ∈ (π; 3π/2). Згадуємо символ вихідної функції, тобто. y = sin x у цьому інтервалі. Очевидно, що синус у третій координатній чверті негативний, оскільки за визначенням синус це ордината кінця рухомого радіусу (коротше синус це координата y). Ну, а координата y в нижній напівплощині завжди набуває негативних значень. Значить, і в третій чверті y теж негативний.

На підставі цих роздумів ми можемо записати остаточний вираз:

Завдання B11 - 1 варіант

Ось ці самі прийоми цілком підходять для вирішення завдання B11 з ЄДІ з математики. Різниця лише в тому, що в багатьох реальних завданнях B11 замість радіанної міри (тобто чисел π, π/2, 2π тощо) використовується градусний захід (тобто 90°, 180°, 270° і і т.д.). Давайте подивимося на перше завдання:

Спочатку розберемося з чисельником. cos 41 ° - це нетабличне значення, тому ми нічого не можемо зробити з ним. Поки що так і залишимо.

Тепер дивимося на знаменник:

sin 131° = sin (90° + 41°) = cos 41°

Очевидно, що перед нами є формула приведення, тому синус замінився на косинус. З іншого боку, кут 41° лежить на відрізку (0°; 90°), тобто. у першій координатній чверті саме так, як потрібно для застосування формул приведення. Але тоді 90 ° + 41 ° - це друга координатна чверть. Вихідна функція y = sin x там позитивна, тому ми поставили перед косинусом на останньому етапі знак «плюс» (тобто не поставили нічого).

Залишилося розібратися з останнім елементом:

cos 240° = cos (180° + 60°) = −cos 60° = −0,5

Тут бачимо, що 180° — це горизонтальна вісь. Отже, сама функція не зміниться: був косинус і залишиться теж косинус. Але знову постає питання: плюс чи мінус стоятиме перед отриманим виразом cos 60°? Зауважимо, що 180 ° - це третя координатна чверть. Косинус там негативний, отже, перед косинусом у результаті стоятиме знак «мінус». Отже, отримуємо конструкцію −cos 60° = −0,5 — це табличне значення, тому все легко вважається.

Тепер підставляємо отримані числа у вихідну формулу та отримуємо:

Як бачимо, число cos 41° у чисельнику та знаменнику дробу легко скорочується, і залишається звичайний вираз, який дорівнює -10. При цьому мінус можна або винести і поставити перед знаком дробу, або «тримати» поряд з другим множником до останнього кроку обчислень. Відповідь у будь-якому випадку вийде -10. Все, завдання B11 вирішено!

Завдання B14 - 2 варіант

Переходимо до другого завдання. Перед нами знову дріб:

Ну, 27° у нас лежить у першій координатній чверті, тож тут нічого міняти не будемо. А ось sin 117 ° треба розписати (поки без жодного квадрата):

sin 117° = sin (90° + 27°) = cos 27°

Очевидно, перед нами знову формула приведення: 90 ° - це вертикальна вісь, отже, синус зміниться на косинус. Крім того, кут α = 117 ° = 90 ° + 27 ° лежить у другій координатній чверті. Вихідна функція y = sin x там позитивна, отже, перед косинус після всіх перетворень все одно залишається знак «плюс». Іншими словами, там нічого не додається - так і залишаємо: cos 27 °.

Повертаємося до вихідного виразу, який потрібно обчислити:

Як бачимо, у знаменнику після перетворень виникла основна тригонометрична тотожність: sin 2 27° + cos 2 27° = 1. Разом −4: 1 = −4 — ось ми і знайшли відповідь до другого завдання B11.

Як бачите, за допомогою формул приведення такі завдання з ЄДІ з математики вирішуються буквально в кілька рядків. Жодних синусів суми та косінусів різниці. Все, що нам потрібно пам'ятати, — це лише тригонометричне коло.

Як запам'ятати формули наведення тригонометричних функцій? Це легко, якщо використовувати асоціацію. Ця асоціація придумана не мною. Як мовилося раніше, хороша асоціація має «чіпляти», тобто викликати яскраві емоції. Не можу назвати емоції, викликані цією асоціацією, позитивними. Але вона дає результат — дає змогу запам'ятовувати формули наведення, а отже, має право на існування. Зрештою, якщо вона вам не сподобається, ви її можете не використовувати, правильно?

Формули приведення мають вигляд: sin(πn/2±α), cos(πn/2±α), tg(πn/2±α), ctg(πn/2±α). Запам'ятовуємо, що +α дає рух проти годинникової стрілки — α — рух за годинниковою стрілкою.

Для роботи з формулами наведення потрібні два пункти:

1) ставимо знак, який має початкова функція (у підручниках пишуть: наведена. Але щоб не заплутатися, краще назвати її початковою), якщо вважати α кутом I чверті, тобто маленьким.

2) Горизонтальний діаметр – π±α, 2π±α, 3π±α… – загалом, коли немає дробу – назва функції не змінює. Вертикальний ?

Тепер, власне, асоціація:

вертикальний діаметр (є дріб)

п'яний стоїть. Що з ним станеться рано

чи пізно? Правильно, впаде.

Назва функції зміниться.

Якщо діаметр горизонтальний — п'яний вже лежить. Спить, мабуть. З ним уже нічого не станеться, він уже прийняв горизонтальне становище. Відповідно, назва функції не змінюється.

Тобто sin(π/2±α), sin(3π/2±α), sin(5π/2±α) тощо. дають ±cosα,

а sin(π±α), sin(2π±α), sin(3π±α), … – ±sinα.

Як вже знаємо.

Як це працює? Дивимось на прикладах.

1) cos(π/2+α)=?

Стаємо на π/2. Оскільки +α — отже, йдемо вперед проти годинникової стрілки. Потрапляємо у ІІ чверть, де косинус має знак «-«. Назва функції змінюється («п'яний стоїть», отже – впаде). Отже,

cos(π/2+α)=-sin α.

Стаємо на 2π. Оскільки -α - йдемо назад, тобто за годинниковою стрілкою. Потрапляємо до IV чверть, де тангенс має знак «-«. Назва функції не змінюється (діаметр горизонтальний, п'яний вже лежить). Таким чином, tg(2π-α)=- tgα.

3) ctg²(3π/2-α)=?

Приклади, у яких функція зводиться парний ступінь, вирішуються ще простіше. Четний ступінь «-» прибирає, тобто треба лише з'ясувати, змінюється назва функції чи залишається. Діаметр вертикальний (є дріб, «п'яний стоїть», впаде), назва функції змінюється. Отримуємо: ctg²(3π/2-α)= tg²α.

Вони належать до розділу "тригонометрія" в математиці. Суть їх полягає у приведенні тригонометричних функцій кутів до «простішого» виду. Про важливість їхнього знання написати можна багато. Цих формул аж 32 штуки!

Не лякайтеся, вчити їх не треба, як і багато інших формул в курсі математики. Зайвою інформацією голову забивати не потрібно, необхідно запам'ятовувати «ключики» чи закони, і згадати чи вивести потрібну формулу проблемою не буде. До речі, коли я пишу у статтях «… потрібно вивчити!» - Це означає, що дійсно, це необхідно саме вивчити.

Якщо ви з формулами приведення не знайомі, то простота їх виведення вас приємно здивує – є «закон», за допомогою якого це легко зробити. І будь-яку із 32 формул ви напишіть за 5 секунд.

Перелічу лише деякі завдання, які будуть на ЄДІ з математики, де без знання цих формул є велика ймовірність зазнати фіаско у вирішенні. Наприклад:

- Завдання на рішення прямокутного трикутника, де йдеться про зовнішній вугіллі, та й завдання на внутрішні кути деякі з цих формул теж необхідні.

- Завдання на обчислення значень тригонометричних виразів; перетворення числових тригонометричних виразів; перетворення буквених тригонометричних виразів.

- Завдання на дотичну та геометричний зміст дотичної, потрібна формула приведення для тангенсу, а також інші завдання.

- стереометричні завдання, по ходу рішення нерідко потрібно визначити синус або косинус кута, що лежить в межах від 90 до 180 градусів.

І це лише ті моменти, які стосуються ЄДІ. А в самому курсі алгебри є безліч завдань, при вирішенні яких без знання формул приведення просто не обійтися.

То що до чого наводиться і як обумовлені формули спрощують для нас вирішення завдань?

Наприклад, вам потрібно визначити синус, косинус, тангенс чи котангенс будь-якого кута від 0 до 450 градусів:

кут альфа лежить в межах від 0 до 90 градусів

* * *

Отже, необхідно усвідомити «закон», який тут працює:

1. Визначте знак функції у відповідній чверті.

Нагадаю їх:

2. Запам'ятайте наступне:

функція змінюється на кофункцію

функція на кофункцію не змінюється

Що означає поняття – функція змінюється на кофункцію?

Відповідь: синус змінюється на косинус чи навпаки, тангенс на котангенс чи навпаки.

От і все!

Тепер за поданим законом запишемо кілька формул приведення самостійно:

Цей кут лежить у третій чверті, косинус у третій чверті негативний. Функцію на кофункцію не міняємо, тому що у нас 180 градусів, значить:

Кут лежить у першій чверті, синус у першій чверті позитивний. Не змінюємо функцію на кофункцію, тому що у нас 360 градусів, значить:

Ось вам ще додаткове підтвердження того, що синуси суміжних кутів рівні:

Кут лежить у другій чверті, синус у другій чверті позитивний. Не змінюємо функцію на кофункцію, тому що у нас 180 градусів, значить:

Пропрацюйте подумки чи письмово кожну формулу, і переконаєтеся, що нічого складного немає.

***

У статті на рішення було зазначено такий факт - синус одного гострого кута в прямокутному трикутнику дорівнює косинус іншого гострого кута в ньому.