Triunghi . Triunghi acut, obtuz și dreptunghic.

Picioare și ipotenuză. Triunghi isoscel și echilateral.

Suma unghiurilor unui triunghi.

Unghiul exterior al unui triunghi. Semne de egalitate a triunghiurilor.

Linii și puncte remarcabile într-un triunghi: înălțimi, mediane,

bisectoare, mediană e perpendiculare, ortocentre,

centrul de greutate, centrul unui cerc circumscris, centrul unui cerc înscris.

Teorema lui Pitagora. Raportul de aspect într-un triunghi arbitrar.

Triunghi este un poligon cu trei laturi (sau trei unghiuri). Laturile unui triunghi sunt adesea indicate prin litere mici care corespund majusculelor reprezentând vârfurile opuse.

Dacă toate cele trei unghiuri sunt acute (Fig. 20), atunci aceasta este triunghi acut . Dacă unul dintre unghiuri este drept(C, Fig.21), acesta este triunghi dreptunghic; laturia, bformând un unghi drept se numesc picioare; laturăcopus unghiului drept se numeste ipotenuză. Dacă unul dintre unghiuri obtuze (B, Fig. 22), acesta este triunghi obtuz.


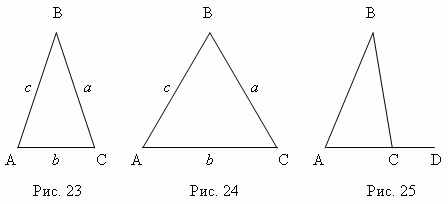
Triunghiul ABC (Fig. 23) - isoscel, Dacă Două laturile sale sunt egale (A= c); aceste laturi egale se numesc lateral, este sunat terțul bază triunghi. Triunghi ABC (Fig. 24) – echilateral, Dacă Toate laturile sale sunt egale (A = b = c). În general ( A ≠ b ≠ c) avem scalen triunghi .

Proprietățile de bază ale triunghiurilor. În orice triunghi:

1. Opus laturii mai mari se află unghiul mai mare și invers.

2. Unghiurile egale sunt opuse laturi egale și invers.

În special, toate unghiurile în echilateral triunghiul sunt egale.

3. Suma unghiurilor unui triunghi este 180 º .

Din ultimele două proprietăți rezultă că fiecare unghi într-un echilateral

triunghiul este 60 º.

4. Continuând una dintre laturile triunghiului (AC, Fig. 25), primim extern

unghiul BCD . Unghiul exterior al unui triunghi este egal cu suma unghiurilor interne,

nu adiacent cu acesta : BCD = A + B.

5. Orice latura unui triunghi este mai mică decât suma celorlalte două laturi și mai mare

diferențele lor (A < b + c, A > b – c;b < A + c, b > A – c;c < A + b,c > A – b).

Semne de egalitate a triunghiurilor.

Triunghiurile sunt congruente dacă sunt, respectiv, egale:

A ) două laturi și unghiul dintre ele;

b ) două colțuri și latura adiacentă acestora;

c) trei laturi.

Semne de egalitate ale triunghiurilor dreptunghiulare.

Două dreptunghiular Triunghiurile sunt egale dacă este îndeplinită una dintre următoarele condiții:

1) picioarele lor sunt egale;

2) catetul și ipotenuza unui triunghi sunt egale cu catetul și ipotenuza celuilalt;

3) ipotenuza și unghiul ascuțit ale unui triunghi sunt egale cu ipotenuza și unghiul ascuțit ale celuilalt;

4) cateta și unghiul ascuțit adiacent al unui triunghi sunt egale cu cateta și unghiul ascuțit adiacent al celuilalt;

5) catetul și unghiul ascuțit opus al unui triunghi sunt egale cu cateta și unghiul acut opus celuilalt.

Minunate linii și puncte în triunghi.

Înălţime triunghiul esteperpendicular,coborât de la orice vârf în partea opusă ( sau continuarea ei). Această parte se numeștebaza triunghiului . Cele trei altitudini ale unui triunghi se intersectează întotdeaunala un moment dat, numit ortocentru triunghi. Ortocentrul unui triunghi acut (punctul O , Fig. 26) este situat în interiorul triunghiului șiortocentrul unui triunghi obtuz (punctul O , fig.27) – in afara; Ortocentrul unui triunghi dreptunghic coincide cu vârful unghiului drept.

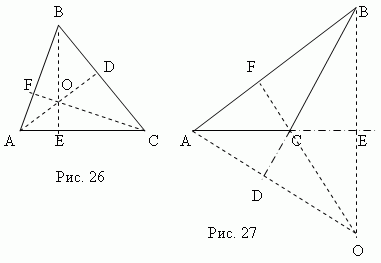
Median - Acest segment de linie , legând orice vârf al unui triunghi de mijlocul laturii opuse. Trei mediane ale unui triunghi (AD, BE, CF, fig.28) se intersectează la un punct O , aflat mereu în interiorul triunghiului si fiind al lui centrul de greutate. Acest punct împarte fiecare mediană într-un raport de 2:1, numărând de la vârf.

Bisectoare - Acest segment bisectoare unghi de la vârf la punct intersecții cu partea opusă. Trei bisectoare ale unui triunghi (AD, BE, CF, fig.29) se intersectează la un punct Oh, mereu întins în interiorul triunghiuluiȘi fiind centrul cercului înscris(vezi secțiunea „Inscrisși poligoane circumscrise").

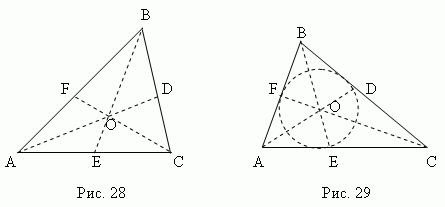
Bisectoarea împarte partea opusă în părți proporționale cu laturile adiacente ; de exemplu, în Fig. 29 AE: CE = AB: BC.

Perpendiculară mediană este o perpendiculară trasă din mijloc puncte de segment (laturi). Trei bisectoare perpendiculare ale triunghiului ABC(KO, MO, NU, Fig. 30 ) se intersectează într-un punct O, adică centru cerc circumscris (punctele K, M, N – punctele mijlocii ale laturilor triunghiului ABC).

Într-un triunghi ascuțit, acest punct se află în interiorul triunghiului; în obtuz - în exterior; într-un dreptunghiular - în mijlocul ipotenuzei. Ortocentrul, centrul de greutate, circumcentrul și cercul înscris coincid doar într-un triunghi echilateral.

Teorema lui Pitagora. Într-un triunghi dreptunghic, pătratul lungimiiIpotenuza este egală cu suma pătratelor lungimilor catetelor.

Dovada teoremei lui Pitagora rezultă clar din Fig. 31. Luați în considerare un triunghi dreptunghic ABC cu picioare a, b si ipotenuza c.

Să construim un pătrat AKMB folosind ipotenuza AB ca o parte. Apoicontinuați laturile triunghiului dreptunghic ABC astfel incat sa obtina un patrat CDEF , a cărui parte este egalăa + b .Acum este clar că aria pătratului CDEF este egal cu ( a+b) 2 . Pe de altă parte, aceasta aria este egală cu suma zone patru triunghiuri dreptunghiulareși pătratul AKMB, adică

c 2 + 4 (ab / 2) = c 2 + 2 ab,

de aici,

c 2 + 2 ab= (a+b) 2 ,

si in final avem:

c 2 =A 2 +b 2 .

Raportul de aspect într-un triunghi arbitrar.

În cazul general (pentru un triunghi arbitrar) avem:

c 2 =A 2 +b 2 – 2ab· cos C,

unde C – unghiul dintre laturiAȘi b .

Denumiri standard

Triunghi cu vârfuri A, BȘi C este desemnat ca (vezi figura). Un triunghi are trei laturi:

Lungimile laturilor unui triunghi sunt indicate prin litere latine mici (a, b, c):

Un triunghi are următoarele unghiuri:

Valorile unghiurilor de la vârfurile corespunzătoare sunt în mod tradițional notate cu litere grecești (α, β, γ).

Semne de egalitate a triunghiurilor

Un triunghi pe planul euclidian poate fi determinat în mod unic (până la congruență) de următoarele triplete de elemente de bază:

1. a, b, γ (egalitatea pe două laturi și unghiul care se află între ele);
2. a, β, γ (egalitate pe latură și două unghiuri adiacente);
3. a, b, c (egalitatea pe trei laturi).

Semne de egalitate a triunghiurilor dreptunghiulare:

1. de-a lungul piciorului și ipotenuzei;
2. pe două picioare;
3. de-a lungul piciorului și unghiului ascuțit;
4. de-a lungul ipotenuzei și unghiului ascuțit.

Unele puncte din triunghi sunt „pereche”. De exemplu, există două puncte din care toate laturile sunt vizibile fie la un unghi de 60°, fie la un unghi de 120°. Sunt chemați puncte Torricelli. Există, de asemenea, două puncte ale căror proiecții pe laturi se află la vârfurile unui triunghi regulat. Acest - Apollonius arată. Se numesc puncte și așa ceva puncte Brocard.

Direct

În orice triunghi, centrul de greutate, ortocentrul și centrul cercului circumferitor se află pe aceeași linie dreaptă, numită linia lui Euler.

Linia dreaptă care trece prin centrul cercului circumferitor și punctul Lemoine se numește Axa Brocard. Punctele Apollonius se află pe el. Punctul Torricelli și punctul Lemoine se află, de asemenea, pe aceeași linie. Bazele bisectoarelor exterioare ale unghiurilor unui triunghi se află pe o dreaptă numită axa bisectoarelor externe. Punctele de intersecție ale liniilor care conțin laturile ortotriunghiului cu liniile care conțin laturile triunghiului se află și ele pe aceeași linie. Această linie se numește axul ortocentric, este perpendicular pe dreapta lui Euler.

Dacă luăm un punct de pe cercul circumferitor al unui triunghi, atunci proiecțiile sale pe laturile triunghiului se vor afla pe aceeași dreaptă, numită Simson e hetero acest punct. Liniile lui Simson de puncte diametral opuse sunt perpendiculare.

Triunghiuri

• Se numește un triunghi cu vârfuri la bazele trasate printr-un punct dat triunghiul cevian acest punct.
• Un triunghi cu vârfuri în proiecțiile unui punct dat pe laturi se numește gazon sau triunghiul pedalei acest punct.
• Un triunghi cu vârfuri în al doilea punct de intersecție al dreptelor trasate prin vârfuri și un punct dat cu cercul circumscris se numește triunghi circumferenţial. Triunghiul circumferențial este similar cu triunghiul gazonului.

Cercuri

• Cerc înscris- un cerc care atinge toate cele trei laturi ale triunghiului. Ea este singura. Centrul cercului înscris se numește în centru.
• Cerc circular- un cerc care trece prin toate cele trei vârfuri ale triunghiului. Cercul circumscris este, de asemenea, unic.
• Excerciază- un cerc care atinge o latură a triunghiului și continuarea celorlalte două laturi. Există trei astfel de cercuri într-un triunghi. Centrul lor radical este centrul cercului înscris al triunghiului medial, numit Ideea lui Spiker.

Punctele de mijloc ale celor trei laturi ale unui triunghi, bazele celor trei altitudini ale sale și punctele de mijloc ale celor trei segmente care leagă vârfurile sale de ortocentrul se află pe un cerc numit cerc de nouă puncte sau Cercul lui Euler. Centrul cercului de nouă puncte se află pe linia lui Euler. Un cerc de nouă puncte atinge un cerc înscris și trei excercuri. Se numește punctul de tangență dintre cercul înscris și cercul de nouă puncte Punctul Feuerbach. Dacă din fiecare vârf ne așezăm în afara triunghiului pe linii drepte care conțin laturile, orteze egale în lungime cu laturile opuse, atunci cele șase puncte rezultate se află pe același cerc - Cercul Conway. Trei cercuri pot fi înscrise în orice triunghi în așa fel încât fiecare dintre ele să atingă două laturi ale triunghiului și alte două cercuri. Se numesc astfel de cercuri Cercuri Malfatti. Centrele cercurilor circumscrise celor șase triunghiuri în care triunghiul este împărțit prin mediane se află pe un cerc, care se numește circumferinta lui Lamun.

Un triunghi are trei cercuri care ating două laturi ale triunghiului și cercul circumferitor. Se numesc astfel de cercuri semiinscris sau Cercuri Verrier. Segmentele care leagă punctele de tangență ale cercurilor Verrier cu cercul circumscripțional se intersectează într-un punct numit Ideea lui Verrier. Acesta servește ca centru al unei homoteții, care transformă un cerc circumscripțional într-un cerc înscris. Punctele de contact ale cercurilor Verrier cu laturile se află pe o linie dreaptă care trece prin centrul cercului înscris.

Segmentele care leagă punctele de tangență ale cercului înscris cu vârfurile se intersectează într-un punct numit punctul Gergonne, iar segmentele care leagă vârfurile cu punctele de tangență ale excercurilor sunt în punctul Nagel.

Elipse, parabole și hiperbole

Conica înscrisă (elipsă) și perspectorul acesteia

Un număr infinit de conice (elipse, parabole sau hiperbole) pot fi înscrise într-un triunghi. Dacă înscriem o conică arbitrară într-un triunghi și conectăm punctele tangente cu vârfuri opuse, atunci liniile drepte rezultate se vor intersecta într-un punct numit perspectivă paturi. Pentru orice punct al planului care nu se află pe o latură sau pe prelungirea sa, există o conică înscrisă cu un perspector în acest punct.

Elipsa Steiner descrisă și cevianele care trec prin focarele sale

Puteți înscrie o elipsă într-un triunghi, care atinge laturile din mijloc. O astfel de elipsă se numește inscripţionată elipsa Steiner(perspectiva sa va fi centroidul triunghiului). Elipsa circumscrisă, care atinge liniile care trec prin vârfurile paralele cu laturile, se numește descris de elipsa Steiner. Dacă transformăm un triunghi într-un triunghi obișnuit folosind o transformare afină („înclinare”), atunci elipsa lui Steiner înscrisă și circumscrisă se va transforma într-un cerc înscris și circumscris. Liniile Chevian trasate prin focarele elipsei Steiner descrise (punctele Scutin) sunt egale (teorema lui Scutin). Dintre toate elipsele descrise, elipsa Steiner descrisă are cea mai mică zonă, iar dintre toate elipsele înscrise, elipsa Steiner înscrisă are cea mai mare zonă.

Elipsa Brocard și perspectorul ei - punctul Lemoine

Se numește o elipsă cu focare în punctele Brocard Elipsa Brocard. Perspectiva sa este punctul Lemoine.

Proprietățile unei parabole înscrise

Parabola Kiepert

Perspectivele parabolelor înscrise se află pe elipsa Steiner descrisă. Focalizarea unei parabole înscrise se află pe cercul circumferitor, iar directricea trece prin ortocentru. O parabolă înscrisă într-un triunghi și având ca directriță directricea lui Euler se numește Parabola Kiepert. Perspectorul său este al patrulea punct de intersecție al cercului circumscris și al elipsei Steiner circumscrise, numit punctul Steiner.

Hiperbola lui Kiepert

Dacă hiperbola descrisă trece prin punctul de intersecție al înălțimilor, atunci este echilaterală (adică asimptotele sale sunt perpendiculare). Punctul de intersecție al asimptotelor unei hiperbole echilaterale se află pe cercul de nouă puncte.

Transformări

Dacă liniile care trec prin vârfuri și un punct care nu se află pe laturi și prelungirile lor sunt reflectate în raport cu bisectoarele corespunzătoare, atunci imaginile lor se vor intersecta și într-un punct, care se numește conjugat izogonal cel original (dacă punctul se află pe cercul circumscris, atunci liniile rezultate vor fi paralele). Multe perechi de puncte remarcabile sunt conjugate izogonal: circumcentrul și ortocentrul, centroidul și punctul Lemoine, punctele Brocard. Punctele Apollonius sunt conjugate izogonal cu punctele Torricelli, iar centrul cercului înscris este conjugat izogonal cu el însuși. Sub acțiunea conjugării izogonale, liniile drepte se transformă în conice circumscrise, iar conicele circumscrise în drepte. Astfel, hiperbola Kiepert și axa Brocard, hiperbola Jenzabek și linia dreaptă Euler, hiperbola Feuerbach și linia centrelor cercurilor înscrise și circumscrise sunt conjugate izogonal. Cercurile circumferinte ale triunghiurilor punctelor conjugate izogonal coincid. Focarele elipselor înscrise sunt conjugate izogonal.

Dacă, în loc de un cevian simetric, luăm un cevian a cărui bază este la fel de îndepărtată de mijlocul laturii ca și baza celui original, atunci și astfel de cevian se vor intersecta într-un punct. Transformarea rezultată se numește conjugarea izotomică. De asemenea, convertește linii drepte în conice descrise. Punctele Gergonne și Nagel sunt conjugate izotomic. În cadrul transformărilor afine, punctele conjugate izotomic sunt transformate în puncte conjugate izotomic. Cu conjugarea izotomică, elipsa Steiner descrisă va merge în linia dreaptă infinit de distanță.

Dacă în segmentele tăiate de laturile triunghiului din cercul circumscris, înscriem cercuri care ating laturile de la bazele cevianelor trasate printr-un anumit punct, apoi conectăm punctele de tangență ale acestor cercuri cu cercul circumscris cu vârfuri opuse, atunci astfel de linii drepte se vor intersecta într-un punct. Se numește o transformare plană care potrivește punctul inițial cu cel rezultat transformare izocirculară. Compoziția conjugatelor izogonale și izotomice este compoziția unei transformări izocirculare cu sine. Această compoziție este o transformare proiectivă, care lasă laturile triunghiului pe loc și transformă axa bisectoarelor exterioare într-o linie dreaptă la infinit.

Dacă extindem laturile unui triunghi Chevian dintr-un anumit punct și luăm punctele lor de intersecție cu laturile corespunzătoare, atunci punctele de intersecție rezultate se vor afla pe o singură dreaptă, numită polar triliniar punct de start. Axa ortocentrică este polara triliniară a ortocentrului; polara triliniară a centrului cercului înscris este axa bisectoarelor externe. Polarii triliniari ai punctelor situate pe o conică circumscrisă se intersectează într-un punct (pentru un cerc circumscris acesta este punctul Lemoine, pentru o elipsă Steiner circumscrisă este centroidul). Compoziția unei conjugări izogonale (sau izotomice) și a unui polar triliniar este o transformare de dualitate (dacă un punct conjugat izogonal (izotomic) la un punct se află pe polara triliniară a unui punct, atunci polara triliniară a unui punct izogonal (izotomic) conjugată la un punct se află pe polara triliniară a unui punct).

Cuburi

Raporturi într-un triunghi

Notă:în această secțiune, , , sunt lungimile celor trei laturi ale triunghiului și , , sunt unghiurile situate, respectiv, opuse acestor trei laturi (unghiuri opuse).

Inegalitatea triunghiulară

Într-un triunghi nedegenerat, suma lungimilor celor două laturi ale sale este mai mare decât lungimea celei de-a treia laturi, într-un triunghi degenerat este egală. Cu alte cuvinte, lungimile laturilor unui triunghi sunt legate de următoarele inegalități:

Inegalitatea triunghiului este una dintre axiomele metricii.

Teorema Sumei Triunghiului Unghiului

Teorema sinusurilor

,

unde R este raza cercului circumscris triunghiului. Din teoremă rezultă că dacă a< b < c, то α < β < γ.

Teorema cosinusului

Teorema tangentei

Alte rapoarte

Rapoartele metrice dintr-un triunghi sunt date pentru:

Rezolvarea triunghiurilor

Calcularea laturilor și unghiurilor necunoscute ale unui triunghi pe baza celor cunoscute a fost numită istoric „rezolvarea triunghiurilor”. Se folosesc teoremele trigonometrice generale de mai sus.

Aria unui triunghi

Cazuri speciale Notare

Pentru zonă sunt valabile următoarele inegalități:

Calcularea ariei unui triunghi în spațiu folosind vectori

Fie vârfurile triunghiului în punctele , , .

Să introducem vectorul zonă. Lungimea acestui vector este egală cu aria triunghiului și este îndreptată normal pe planul triunghiului:

Să stabilim , unde , , sunt proiecțiile triunghiului pe planurile de coordonate. în care

si asemanator

Aria triunghiului este .

O alternativă este să calculați lungimile laturilor (folosind teorema lui Pitagora) și apoi folosind formula lui Heron.

Teoreme triunghiulare

Această secțiune nu este completată.

Triunghi- aceasta este o figură formată din trei puncte și trei segmente, în timp ce cele trei puncte nu se află pe aceeași linie, ci trei segmente leagă aceste puncte în perechi. Pentru a fi mai precis, punctele unui triunghi sunt numite vârfuri, iar segmentele sunt numite laturi. Un triunghi este desemnat prin vârfurile sale, iar în locul cuvântului lung triunghi este desenat simbolul Δ.

Să aruncăm acum o privire mai atentă la tipurile de triunghiuri.

1. Un triunghi isoscel este un triunghi care are două laturi identice, care sunt numite și laterale, a treia latură, diferită de cele două, se numește bază.
2. Un triunghi echilateral este un triunghi cu laturile egale, numit uneori și triunghi regulat.
3. Un triunghi dreptunghic este un triunghi care are un unghi drept (90 de grade).
4. Un triunghi ascuțit este un triunghi în care toate unghiurile sunt acute (adică mai puțin de 90 de grade).
5. Un triunghi obtuz este un triunghi în care unul dintre unghiuri este obtuz (adică mai mult de 90 de grade).

În principiu, este ușor să ne amintim caracteristicile fiecărui tip de triunghi, astfel încât numele vorbesc de la sine.

Luați, de exemplu, triunghiul ABC. A, B, C sunt vârfurile sale, iar AB, BC și AC sunt laturile sale, respectiv.

Acum să ne uităm la structura acestui triunghi mai detaliat. Unghiul triunghiului ABC la vârful A este unghiul format din jumătăți de drepte AB și AC. În mod similar, putem determina unghiurile care se află la vârful B și la vârful C.

Altitudinea unui triunghi este perpendiculara care coboară de la un vârf dat la linia opusă vârfului.

Bisectoarea unui triunghi este bisectoarea unui unghi dintr-un triunghi dat care leagă un vârf de un punct de pe latura opusă.

Mediana unui triunghi, care este trasă dintr-un vârf dat, este un segment care leagă acest vârf cu punctul de mijloc al laturii opuse a triunghiului.

Linia mediană a unui triunghi este un segment care leagă punctele de mijloc a două laturi ale unui triunghi dat. Există, de asemenea, o anumită teoremă la această denumire, care spune că linia de mijloc a unui triunghi este întotdeauna paralelă cu a treia latură și este, de asemenea, egală cu jumătate din aceasta.

Toate aceste notații (mediană, bisectoare, înălțime, linie mediană a unui triunghi) vor fi cu siguranță necesare în rezolvarea problemelor practice. Mai mult, fără a cunoaște proprietățile acestor vârfuri, este puțin probabil să poți rezolva orice problemă legată de triunghiuri.

pe laturile a, b, respectiv c;
Teorema cosinusului

A

2

= b

2

+c

2

- 2bccosα

a+c a-c	=	tg	α + γ; 2	=	ctg	β 2
		tg	α - γ 2		tg	α - γ 2

R=

c 2

= m

c


Triunghi echilateral

S=

Dacă trei puncte care nu se află pe aceeași dreaptă sunt legate prin segmente, obținem un triunghi. Una dintre laturile unui triunghi este adesea numită baza sa.

Teorema. Suma unghiurilor unui triunghi este 180 0

Dacă toate cele trei unghiuri ale unui triunghi sunt acute, atunci triunghiul se numește unghiular acut.

Dacă unul dintre unghiurile unui triunghi este obtuz, atunci triunghiul se numește obtuz-unghiular.

Dacă unul dintre unghiurile unui triunghi este drept, atunci triunghiul se numește dreptunghiular. Latura unui triunghi dreptunghic opus unghiului drept se numește ipotenuză, iar celelalte două părți sunt picioare.

În orice triunghi, unghiul mai mare se află opus laturii mai mari; laturi opuse egale - unghiuri egale și invers. Orice latură a unui triunghi este mai mică decât suma celorlalte două laturi și, de asemenea, mai mare decât diferența celorlalte două laturi.

Continuând una dintre laturile triunghiului, obținem un unghi extern. Unghi ABD - extern.

Semne de egalitate a triunghiurilor

Dacă două triunghiuri sunt congruente, atunci elementele (laturile și unghiurile) unui triunghi sunt, respectiv, egale cu elementele celuilalt triunghi.

Teorema. Două triunghiuri sunt congruente dacă două laturi și unghiul dintre ele ale unui triunghi sunt, respectiv, egale cu două laturi și unghiul dintre ele ale celuilalt.

Teorema. Două triunghiuri sunt congruente dacă o latură și două unghiuri adiacente ale unui triunghi sunt egale cu latura și, respectiv, două unghiuri adiacente ale celuilalt.

Teorema. Două triunghiuri sunt congruente dacă trei laturi ale unui triunghi sunt, respectiv, egale cu trei laturi ale celuilalt.

Mediana, bisectoarea și înălțimea unui triunghi

Segmentul care leagă vârful unui triunghi cu mijlocul laturii opuse se numește median triunghi.

Se numește raza care emană din vârful unui unghi și care îl împarte în două unghiuri egale bisectoare. Bisectoarea împarte partea opusă în părți proporționale cu laturile adiacente acesteia.

Se numește perpendiculara trasată de la vârful unui triunghi pe linia care conține latura opusă înălţime triunghi.

Puncte remarcabile ale triunghiului. 1) Bisectoarele unui triunghi se intersectează într-un punct.

2) Bisectoarele perpendiculare pe laturile triunghiului se intersectează într-un punct.

3) Altitudinile triunghiului (sau prelungirile lor) se intersectează într-un punct.

4) Medianele unui triunghi se intersectează într-un punct.

Triunghi isoscel

Un triunghi se numește isoscel dacă cele două laturi ale sale sunt egale. Se numesc laturi egale laturi, iar tertul - bază triunghi isoscel.

Un triunghi în care toate laturile sunt egale se numește echilateral.

Teorema.Într-un triunghi isoscel, unghiurile de bază sunt egale.

Teorema.Într-un triunghi isoscel, bisectoarea trasată la bază este mediana și altitudinea.

Știința geometriei ne spune ce sunt un triunghi, un pătrat și un cub. În lumea modernă, toată lumea, fără excepție, îl studiază în școli. De asemenea, știința care studiază direct ce este un triunghi și ce proprietăți are este trigonometria. Ea explorează în detaliu toate fenomenele legate de date. Vom vorbi despre ce este un triunghi astăzi în articolul nostru. Tipurile lor vor fi descrise mai jos, precum și unele teoreme asociate acestora.

Ce este un triunghi? Definiție

Acesta este un poligon plat. Are trei colțuri, așa cum reiese din numele său. Are, de asemenea, trei laturi și trei vârfuri, primul dintre ele sunt segmente, al doilea sunt puncte. Știind cu ce sunt egale două unghiuri, îl puteți găsi pe al treilea scăzând suma primelor două din numărul 180.

Ce tipuri de triunghiuri există?

Ele pot fi clasificate după diverse criterii.

În primul rând, ele sunt împărțite în unghi acut, unghi obtuz și dreptunghiular. Primele au unghiuri ascuțite, adică cele care sunt egale cu mai puțin de 90 de grade. În unghiurile obtuze, unul dintre unghiuri este obtuz, adică unul egal cu mai mult de 90 de grade, celelalte două sunt acute. Triunghiurile acute includ și triunghiuri echilaterale. Astfel de triunghiuri au toate laturile și unghiurile egale. Toate sunt egale cu 60 de grade, acest lucru poate fi calculat cu ușurință împărțind suma tuturor unghiurilor (180) la trei.

Triunghi dreptunghic

Este imposibil să nu vorbim despre ce este un triunghi dreptunghic.

O astfel de figură are un unghi egal cu 90 de grade (dreaptă), adică două dintre laturile sale sunt perpendiculare. Cele două unghiuri rămase sunt acute. Ele pot fi egale, atunci va fi isoscel. Teorema lui Pitagora este legată de triunghiul dreptunghic. Folosind-o, puteți găsi a treia latură, cunoscând primele două. Conform acestei teoreme, dacă adăugați pătratul unui catete la pătratul celuilalt, puteți obține pătratul ipotenuzei. Pătratul catetei poate fi calculat scăzând pătratul catetei cunoscute din pătratul ipotenuzei. Vorbind despre ce este un triunghi, ne putem aminti și un triunghi isoscel. Acesta este unul în care două dintre laturi sunt egale și două unghiuri sunt, de asemenea, egale.

Ce sunt catetul și ipotenuza?

Un catete este una dintre laturile unui triunghi care formează un unghi de 90 de grade. Ipotenuza este latura rămasă care este opusă unghiului drept. Puteți coborî o perpendiculară de pe picior. Raportul dintre latura adiacentă și ipotenuză se numește cosinus, iar latura opusă se numește sinus.

- care sunt caracteristicile sale?

Este dreptunghiulară. Picioarele sale sunt trei și patru, iar ipotenuza este cinci. Dacă vezi că catetele unui triunghi dat sunt egale cu trei și patru, poți fi sigur că ipotenuza va fi egală cu cinci. De asemenea, folosind acest principiu, puteți determina cu ușurință că catetul va fi egal cu trei dacă al doilea este egal cu patru, iar ipotenuza este egală cu cinci. Pentru a demonstra această afirmație, puteți aplica teorema lui Pitagora. Dacă două catete sunt egale cu 3 și 4, atunci 9 + 16 = 25, rădăcina lui 25 este 5, adică ipotenuza este egală cu 5. Un triunghi egiptean este și un triunghi dreptunghic ale cărui laturi sunt 6, 8 și 10. ; 9, 12 și 15 și alte numere cu raportul 3:4:5.

Ce altceva ar putea fi un triunghi?

Triunghiurile pot fi, de asemenea, înscrise sau circumscrise. Figura în jurul căreia este descris cercul se numește înscris, toate vârfurile sale sunt puncte situate pe cerc. Un triunghi circumscris este unul în care este înscris un cerc. Toate laturile sale intră în contact cu el în anumite puncte.

Cum este localizat?

Aria oricărei figuri este măsurată în unități pătrate (metri pătrați, milimetri pătrați, centimetri pătrați, decimetri pătrați etc.) Această valoare poate fi calculată într-o varietate de moduri, în funcție de tipul de triunghi. Aria oricărei figuri cu unghiuri poate fi găsită prin înmulțirea laturii sale cu perpendiculara căzută pe ea din colțul opus și împărțind această cifră la două. De asemenea, puteți găsi această valoare înmulțind cele două părți. Apoi înmulțiți acest număr cu sinusul unghiului situat între aceste laturi și împărțiți acest rezultat la doi. Cunoscând toate laturile unui triunghi, dar neștiind unghiurile acestuia, puteți găsi zona într-un alt mod. Pentru a face acest lucru, trebuie să găsiți jumătate din perimetru. Apoi scădeți alternativ diferite laturi din acest număr și înmulțiți cele patru valori rezultate. Apoi, găsiți din numărul care a ieșit. Aria unui triunghi înscris poate fi găsită înmulțind toate laturile și împărțind numărul rezultat la cel circumscris în jurul lui, înmulțit cu patru.

Aria unui triunghi circumscris se găsește în acest fel: înmulțim jumătate din perimetru cu raza cercului care este înscris în el. Dacă atunci aria sa poate fi găsită după cum urmează: pătratează latura, înmulțiți cifra rezultată cu rădăcina lui trei, apoi împărțiți acest număr la patru. Într-un mod similar, puteți calcula înălțimea unui triunghi în care toate laturile sunt egale, pentru a face acest lucru, trebuie să înmulțiți una dintre ele cu rădăcina a trei, apoi împărțiți acest număr la doi.

Teoreme legate de triunghi

Principalele teoreme care sunt asociate cu această figură sunt teorema lui Pitagora descrisă mai sus și cosinusurile. Al doilea (din sinusuri) este că, dacă împărțiți orice latură la sinusul unghiului opus acesteia, puteți obține raza cercului care este descris în jurul ei, înmulțită cu două. Al treilea (cosinus) este că dacă din suma pătratelor celor două laturi scădem produsul lor înmulțit cu doi și cosinusul unghiului situat între ele, atunci obținem pătratul celei de-a treia laturi.

Triunghiul Dali - ce este?

Mulți, când se confruntă cu acest concept, cred la început că acesta este un fel de definiție în geometrie, dar nu este deloc așa. Triunghiul Dali este numele comun pentru trei locuri care sunt strâns legate de viața celebrului artist. „Vârfurile” sale sunt casa în care a locuit Salvador Dali, castelul pe care l-a dăruit soției sale, precum și muzeul de picturi suprarealiste. În timpul unui tur al acestor locuri puteți afla multe fapte interesante despre acest artist creativ unic, cunoscut în întreaga lume.