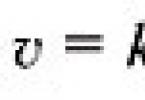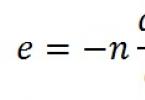Isospin of nucleons and nuclei

Both the ground and excited states of nuclei - in addition to energy, spin and parity discussed in previous seminars - are characterized by quantum numbers, which are called isospin and isospin projection. (In the literature, these quantum numbers are usually denoted either by the symbols T and T z, or I and I z).
The introduction of these quantum numbers is due to the fact that nuclear forces are invariant under the substitution protons into neutrons. This is especially pronounced in the spectra of so-called “mirror” nuclei, i.e. isobaric nuclei in which the number of protons of one is equal to the number of neutrons of the other. (See, for example, the spectra of 13 C and 13 N nuclei). For all known pairs of such nuclei, the spectra of the lowest excited states are similar: the spins and parities of the lowest states are the same, and the excitation energies are close.
From the point of view of isospin theory, a neutron and a proton are the same particle - a nucleon with isospin I = 1/2 - in two different states, differing in the projection of the isospin onto a selected axis (I z = I 3) in isospin space. There can be only two such projections for the moment I = 1/2: I z = +1/2 (proton) and I z = -1/2 (neutron). (Quantum isospin theory is constructed by analogy with spin theory. However, isospin space does not coincide with ordinary coordinate space.)
A system of Z protons and N neutrons - the nucleus - has an isospin projection

Nuclear (i.e. strong) interactions do not depend on the isospin projection, or, more precisely, strong interactions are invariant with respect to rotations in isospin space.
However, nuclear forces depend on the magnitude of isospin! The lowest energy states of the nucleon system, i.e. The ground state of the nucleus is the state with the lowest possible isospin value, which is equal to

The 48 Ca nucleus has 20 protons and 28 neutrons. Consequently, the projection of isospin I z of this nucleus is equal to
I z = (20 - 28) / 2 = - 4. Ground state isospin I = |I z | = 4.
Particles or systems of particles that have the same isospin and different isospin projections constitute isospin multiplets (doublets, triplets, etc.). The peculiarity of the members of such a multiplet is that they participate in the strong interaction in the same way. The simplest example of a doublet is a neutron and a proton. The states of the mirror nuclei 13 C and 13 N are another example (see Spectra of nuclei.)

2.6. Electromagnetic moments of nucleons and nuclei.

Electromagnetic moments determine the potential of interaction of a nucleus or particles with external electric and magnetic fields:

Here Ze is the charge of the nucleus, D is the electric dipole moment of the nucleus, Q is the quadrupole moment of the nucleus, and is the magnetic dipole moment. The higher tensor dimension terms of the interaction potential (2.18) make a negligibly small contribution to the interaction.
Electric dipole moment of nuclei in the ground state is equal to zero (up to small terms associated with weak interactions in nuclei). The equality to zero of the moment D i is a consequence of the parity of the square of the wave function of the ground state of the nucleus:

The square of the wave function of the ground state of the nucleus is an even function of the coordinates, z is an odd function. The integral over three-dimensional space of the product of an even and odd function is always equal to 0.
The square of a ψ-function has positive parity if the ψ-function itself has a certain parity (+ or -). This is true for contributions to the ψ function from strong and parity-preserving electromagnetic interactions. Small additions to the ψ-function from weak (parity-non-conserving) interactions can give a deviation from zero for the dipole moments of nuclei and particles. The role of these contributions is of great interest to modern physics, so attempts to measure the neutron dipole moment do not stop.
Quadrupole electric moment nucleus in the coordinate system associated with the nucleus (internal quadrupole moment)

Since the average value of a physical quantity in quantum mechanics, by definition,

the internal quadrupole moment, up to constants, is the difference between the average value of 2z 2 and the average value of the sum of squares x 2 and y 2. Therefore, for spherical nuclei Q = 0, for those elongated relative to the internal axis of rotation z Q > 0, and for oblate nuclei Q< 0.

Magnetic dipole moment particles is an operator in the space of wave functions of particles and is related to the operators of orbital and spin moments by the relation

In the coordinate system associated with the particle, there is no orbital motion. The value of the magnetic moment is defined as the diagonal matrix element of the operator (2.21) in the state with the maximum value of the projection of the moment onto the z axis. The action of the spin projection operator gives

The observed value of the nuclear magnetic moment (in nuclear magnetons) is proportional to the value of the nuclear spin. The proportionality coefficient is called the nuclear gyromagnetic ratio:

The total moment of the electron shell-nucleus system consists of the moment of the electron shell I and the spin of the nucleus J. Since the magnitude of the magnetic field created by electrons in the region of the nucleus is proportional to I, and the magnetic moment of the nucleus is associated with J (2.24), the interaction potential is a function of the scalar product of these vectors:

This interaction potential, included in the full Hamiltonian of the atom, is responsible for the experimental fact that states with different values of the scalar product of the vectors I and J have different shifts in the energies of atomic levels. Since the magnitude of the shift depends on the nuclear magneton, it is small compared to the magnitude thin splitting of atomic levels, which are caused by the interaction of the magnetic moment of the electron shell with an external magnetic field. Therefore, the splitting of atomic levels that occurs due to the interaction of the magnetic moment of the nucleus with the magnetic field of the atom is called ultra-thin. The number of hyperfine splitting states is equal to the number of different values of the scalar product of vectors. Let's define this quantity through the squares of quantum vectors F, J, I:

Thus, the number of levels of hyperfine splitting is equal to the number of different values of the vector F, which can take the following values

F = |J - I| , |J - I + 1|, .... , J + I - 1 , J + I.

The number of different values of the vector F is equal to 2K + 1, where K is the smallest of the vectors J, I. Since for potassium the number of hyperfine splitting levels is 4, this value does not correspond to the case when the electron shell moment 5/2 is less than the spin of the nucleus (then the number of levels was would be equal to 6). Therefore, the number of hyperfine splitting levels is 4 = 2J + 1 and the nuclear spin is J = 3/2.

Chapter 10

ULTRAFINE SPLITTING IN HYDROGEN

§ 1. Basic states for a system of two particles with spin 1/2

§2. Hamiltonian of the ground state of hydrogen

§ 3. Energy levels

§ 6. Projection matrix for spin 1

§ 1. Basic states for a system of two particles with spin 1 / 2

In this chapter we'll look at the "hyperfine splitting" of hydrogen, an interesting example of what we can already do with quantum mechanics. Here we will no longer have two states, but more. The instructiveness of this example is that it will introduce us to the methods of quantum mechanics applied to more complex problems. This example itself is quite complex, and once you understand how to handle it, it will immediately become clear to you how to generalize it to other possible problems.

As you know, a hydrogen atom consists of an electron and a proton; The electron sits close to the proton and can exist in one of many discrete energy states, in each of which its pattern of motion is different. Thus, the first excited state lies at 3/4 of the Rydberg, or 10 ev, above the ground state. But even the so-called ground state of hydrogen is not actually a separate state with a specific energy, because the electron and proton have spins. These spins are responsible for the “hyperfine structure” in energy levels, which splits all energy levels into several almost identical levels.

The spin of an electron can be directed either up or down; the proton too his own the spin can face up or down. Therefore, for every dynamic state of the atom there are four possible spin states. In other words, when a physicist talks about the “ground state” of hydrogen, he actually means the “four ground states,” and not just the lowest of them. The four spin states do not have exactly the same energy; there are small shifts relative to what would be observed in the absence of spins. These shifts, however, are many, many times smaller than those 10 ev, which lie between the ground state and the next higher state.

As a result, the energy of each dynamic state is split into a number of very close levels - this is the so-called hyperfine splitting.

The energy differences between the four spin states are what we want to calculate in this chapter. Hyperfine splitting is caused by the interaction of the magnetic moments of the electron and proton; it results in slightly different magnetic energies for each spin state. These energy shifts are only about a ten-millionth of an electron volt, which is really much less than 10 ev!

It is precisely because of such a large gap that we have the right to consider the ground state of hydrogen to be a “four-level system”, without worrying about the fact that in fact there are many more states at higher energies. We intend to limit ourselves here to studying the hyperfine structure of only the ground state of the hydrogen atom.

For our purposes, various details are not important to us location electron and proton, because all of them, so to speak, have already been produced by the atom, they all turned out by themselves when the atom got into the ground state. It is enough to know only that the electron and proton are not far from each other, in some specific spatial relationship. In addition, they can have all sorts of mutual spin orientations. And we only want to consider spin effects.

The first question to answer is: what are basic states for this system? But this question is posed incorrectly. Things like the only one basis does not exist, and any system of basis states that you choose will not be the only one. It is always possible to create new systems from linear combinations of old ones. For basic states there are always many choices and they are all equally valid.

This means we need to ask: not “what is the basis?”, but “what is it?” Can choose?". And you have the right to choose whatever you want, as long as it’s convenient for you.

It's usually best to start with a base that physically most obvious. It does not necessarily have to solve some problem or be directly important in some way, no, it should generally only make it easier to understand what is happening.

We choose the following basic states:

Condition 1. Both the electron and the proton have their backs facing upward.

State 2. The electron's spin is up, and the proton's is down.

State 3. The spin of an electron is downward, while that of a proton is

State 4. Both the electron and the proton have their backs looking

To briefly write these four states, we introduce the following notation:

Condition 1:|+ +>; the electron has spin up, the proton has a spin up.

State 2:| + ->; the electron has spin up,

the proton has a spin down.

State 3:|- + >; the electron has spin down, the proton has a spin up.

State 4:|- - >; the electron has spin down, the proton has a spin down. (10.1)

remember, that first the plus or minus sign refers to the electron, second - to the proton. To keep these symbols at your fingertips, they are summarized in Fig. 10.1.

Fig. 10.1. Set of basic states

for the ground state of the hydrogen atom.

We denote these states | + +>, | + ->> |- +>.

At times it will be more convenient to denote these states as |1>, |2>, |3> and |4>.

You might say, “But the particles interact, and maybe these states are not the right basis states at all. It's like you're looking at both particles independently." Yes indeed! Interaction poses the question: what is Hamiltonian systems? But the question is how describe system, does not concern interaction. Whatever we choose as a basis has nothing to do with what happens after. It may turn out that the atom is not capable stay in one of these basic states, even if that’s where it all started. But that's another question. This is a question of how amplitudes change over time in a chosen (fixed) basis. By choosing basis states, we are simply choosing "unit vectors" for our description.

Since we have already touched on this, let's take a look at the general problem of finding a set of basic states when there is not one particle, but more. You know the basis states for one particle. An electron, for example, is completely described in real life (not in our simplified cases, but in real life) by specifying the amplitudes of being in one of the following states:

| Electron spin up with momentum p> or

| Electron spin down with momentum p>.

In reality, there are two infinite collections of states, one for each value of p. This means that you can say that the electronic state |y> is completely described only when you know all the amplitudes

where + and - represent the components of angular momentum along some axis, usually the axis z, a p- impulse vector. Therefore, for every conceivable impulse there must be two amplitudes (a doubly infinite set of basic states). That's all that is needed to describe a single particle.

In the same way, basic states can be written when there is not one particle, but more. For example, if it were necessary to consider an electron and a proton in a more complex case than ours, then the basic states could be as follows: Electron with momentum p 1 moves spin up, and the proton with momentum R 2 moves backwards. And so on for other spin combinations. If there are more than two particles, the idea remains the same. So you see what to paint possible basic states are actually very easy. The only question is what the Hamiltonian is.

To study the ground state of hydrogen, we do not need to use complete sets of basis states for different momenta. We specify and fix certain momentum states of the proton and electron when we pronounce the words “ground state”. The details of the configuration - the amplitudes for all pulsed basis states - can be calculated, but this is another task. And now we are only touching on the influence of spin, so we will limit ourselves to only four basic states (10.1). The next question is: what is the Hamiltonian for this set of states?

§ 2. Hamiltonian of the ground state of hydrogen

You'll find out in a minute. But first I want to remind you of one thing: all sorts of things a state can always be represented as a linear combination of basic states. For any state |y|> we can write

Recall that complete parentheses are just complex numbers, so they can be denoted in the usual way by WITH i, Where i=l, 2, 3 or 4, and write (10.2) in the form

Setting the amplitude quadruple WITH i completely describes the spin state |y>. If this four changes in time (as it will in fact), then the rate of change in time is given by the operator N^. The task is to find this operator H^.

There is no general rule for how to write the Hamiltonian of an atomic system, and finding the correct formula requires more skill than finding the system of basis states. We were able to give you a general rule on how to write down a system of basis states for any problem in which there is a proton and an electron, but it is too difficult to describe the general Hamiltonian of such a combination at this level. Instead, we will lead you to the Hamiltonian with some heuristic reasoning, and you will have to accept it as correct because the results will agree with experimental observations.

Recall that in the previous chapter we were able to describe the Hamiltonian of a single spin-1/2 particle using sigma matrices or exactly equivalent sigma operators. The properties of the operators are summarized in Table. 10.1. These operators, which are simply a convenient, concise way of remembering matrix elements of the type, were useful for describing the behavior separate particles with spin 1/2. The question arises whether it is possible to find a similar means for describing a system with two spins. Yes, and very simple. Look here. We will invent a thing that we will call “electron-sigma” and which we will represent by the vector operator s e with three components s e x , s e y and s e z . Further let's agree that when one of them acts

Table 10.1· PROPERTIES OF SIGMA OPERATORS

on any of our four basic states of the hydrogen atom, then it acts on only the spin of the electron, and as if there were only one electron, by itself. Example: what is s y e|-+>? Since s y acting on an electron with spin down gives - i, multiplied by the state with an electron whose spin is up, then

s e y |-+>=- i|++>.

(When s y e acts on a combined state, it flips the electron without affecting the proton, and multiplies the result by - i.) Acting on other states, s e at will give

Let us recall once again that the operator s e acts only on first spin symbol, i.e. per spin electron.

Now we define the corresponding proton-sigma operator for the proton spin. Its three components s p x , s p y, s p z, act in the same way as s e, but only on proton spin. For example, if s p x acts on each of the four basic states, then it will turn out (again using Table 10.1)

As you can see, nothing difficult. In general, things can be more complicated. For example, the product of operators s e y s p z . When there is such a product, then first what the right operator wants is done, and then what the left one requires. For example,

Note that these number operators do nothing; we used this when we wrote s e x (-1)=(-1) s e x . We say that operators “commute” with numbers, or that numbers “can be dragged” through an operator. Practice and show that the product s e X s p z gives the following result for four states:

If we go through all the valid operators, each once, then there can be a total of 16 possibilities. Yes, sixteen, if we also include the “unit operator” 1. Firstly, there is a triple s e X, s e y, s e z, then three s p x , s p y , s p z , for a total of six. In addition, there are nine products of the form s e X sp y , total 15. And another single operator, leaving all states untouched. That's all sixteen!

Notice now that for a four-state system, the Hamilton matrix must be a 4x4 matrix of coefficients, and there will be 16 numbers in it. It is easy to show that any 4X4 matrix, and in particular the Hamilton matrix, can be written as a linear combination of the sixteen double spin matrices corresponding to the system of operators we have just composed. Therefore, for an interaction between a proton and an electron that involves only their spins, we can expect that the Hamilton operator can be written as a linear combination of the same 16 operators. The only question is how.

But first, we know that the interaction does not depend on our choice of axes for the coordinate system. If there is no external disturbance - something like a magnetic field, highlighting some direction in space - then the Hamiltonian cannot depend on our choice of axial directions x, y And z. This means that the Hamiltonian cannot have terms such as s e x by itself. This would look ridiculous, because someone in a different coordinate system would come to different results.

The only possible terms are those with an identity matrix, say a constant A(multiplied by 1^), and some combination of sigmas that does not depend on coordinates, some “invariant” combination. The only one scalar an invariant combination of two vectors is their scalar product, which for our sigmas has the form

This operator is invariant with respect to any rotation of the coordinate system. So the only possibility for a Hamiltonian with suitable symmetry in space is a constant times the identity matrix plus a constant times that dot product, i.e.

This is our Hamiltonian. This is the only thing that, based on symmetry in space, it can be equal to, there is no external field yet. A permanent member won't tell us much; it simply depends on the level we have chosen to count energies. One could equally well accept E 0 =0. And the second term will tell us everything that is needed in order to find the splitting of levels in hydrogen.

If you like, you can think about the Hamiltonian differently. If there are two magnets with magnetic moments m e and m p close to each other, then their mutual energy depends, among other things, on m e · m R. And we, as you remember, found out that the thing that we called in classical physics m e, in quantum mechanics appears under the name m e s e . Likewise, what looks like m p in classical physics usually turns out to be m p s p in quantum mechanics (where m p is the magnetic moment of the proton, which is almost 1000 times smaller than m e and has the opposite sign). This means that (10.5) states that the interaction energy is similar to the interaction of two magnets, but not completely, because the interaction of two magnets depends on the distance between them. But (10.5) can be considered (and in fact is) a kind of average interaction. The electron somehow moves inside the atom, and our Hamiltonian gives only the average interaction energy. In general, all this suggests that for the prescribed location of the electron and proton in space, there is an energy proportional to the cosine of the angle between the two magnetic moments (classically speaking). This classical qualitative picture can help you understand where everything comes from, but the only thing that matters is that (10.5) is the correct quantum mechanical formula.

The order of magnitude of the classical interaction between two magnets would be given by the product of the two magnetic moments divided by the cube of the distance between them. The distance between an electron and a proton in a hydrogen atom, roughly speaking, is equal to half the atomic radius, i.e. 0.5 A. Therefore, we can roughly estimate that the constant A should be equal to the product of the magnetic moments m e and m p divided by the cube of half an angstrom. This targeting results in numbers that fall just in the right area. But it turns out that A You can calculate more accurately, you just have to understand the complete theory of the hydrogen atom, which we are not yet capable of. In fact A was calculated to the nearest 30 ppm. As you can see, in contrast to the constant re-throw A ammonia molecules, which according to theory cannot be calculated well, our constant A for hydrogen May be calculated from a more detailed theory. But nothing can be done; for our present purposes we will have to count A a number that can be determined from experience, and analyze the physics of the matter.

Taking Hamiltonian (10.5), we can substitute it into the equation

and see what spin interaction does to energy levels. To do this, you need to count sixteen matrix elements H ij = i| H|j> corresponding to any two of the four basic states (10.1).

Let's start by calculating what is equal to Н^ |j> for each of the four basic states. Eg,

Using the method described a little earlier (remember Table 10.1, it will make things very easy), we will find what each pair of a does with |+ +>· The answer is:

This means that (10.7) turns into

Table 10.2· spin operators FOR THE HYDROGEN ATOM

And since all our four basic states are orthogonal, this immediately leads to

Remembering that N| i>=<.i>|H|j>*, we can immediately write a differential equation for the amplitude WITH 1:

That's all! Only one member.

To now obtain the remaining Hamilton equations, we must patiently go through the same procedures with H^, acting on other conditions. First, practice checking that all the sigma products in the table. 10.2 are written correctly. Then with their help you will get

And then, multiplying them all in order from the left by all other state vectors, we obtain the following Hamiltonian matrix H ij :

This, of course, means that the differential equations for the four amplitudes WITH i look like

But before moving on to their solution, it’s hard to resist telling you about one clever rule that Dirac derived. It will help you feel how much you already know, although we will not need it in our work. From equations (10.9) and (10.12) we have

“Look,” said Dirac, “I can also write the first and last equations in the form

and then they will all become alike. Now I'll come up with a new operator, which I'll denote R spin. exchange and which, according to definition, will have the following properties:

This operator, as you see, only exchanges the spin directions of two particles. Then I can write the entire system of equations (10.15) as one simple operator equation:

This is the Dirac formula. The spin exchange operator provides a convenient rule to remember s e ·s p. (As you can see, you now know how to do everything. All doors are open for you.)

§ 3. Energy levels

We are now ready to calculate the energy levels of the ground state of hydrogen by solving the Hamiltonian equations (10.14). We want to find the energies of stationary states. This means that we must find those special states |y> for which each of the amplitudes belonging to |y> C i=i|y> has the same time dependence, namely e - w t . Then the state will have energy E=hw. This means that we are looking for a set of amplitudes for which

where is the four coefficients A i does not depend on time. To see if we can get these amplitudes, let's plug (10.17) into (10.14) and see what happens. Each ihdC i /dt in (10.14) will go into E.C. i . And after reduction by a common exponential factor, each WITH i will turn into A i; we get

This is what needs to be solved to find a 1 , A 2 , A 3 and A 4 . Really, it’s very nice of the first equation that it does not depend on the others, which means that one solution is immediately visible. If you select E=A, That

a 1=1, a 2 =a 3 =a 4 =0

will give a solution. (Of course, if we accept everything A equal to zero, then this will also be a solution, but it will not give a state!) We will consider our first solution to be a state | I>:

His energy

E I =A.

All this immediately gives the key to the second solution, obtained from the last equation in (10.18):

A 1 =A 2 =A 3 =0, A 4 =1, E=A.

We will call this solution the state | II>:

|//> = |4> = |-->,(10.20)

E(a) 2 + a 3 ) = A(a 2 + a 3 ). (10.21)

Subtracting, we will have

Taking a look at this and remembering the ammonia we already know, we see that there are two solutions here:

These are mixtures of states | 2 > and | 3 >. Designating them | III> and | IV> and inserting the factor 1/Ts2 for correct normalization, we have

E III =A(10.24)

We found four stationary states and their energies. Note, by the way, that our four states are orthogonal to each other, so they can also be considered basic states if desired. Our problem is completely solved.

The three states have equal energy A, and the last one - BEHIND. The mean is zero, which means that when in (10.5) we chose E 0 = 0, Thus, we decided to count all energies from their average value. The energy level diagram of the ground state of hydrogen will look like in Fig. 10.2.

Fig. 10.2. Energy level diagram of the ground state of atomic hydrogen.

The difference in energies between the state | IV> and any of the others equals 4 A. An atom that happens to be in the states | I>, may fall from there to the state | IV>and emit light: not optical light, because the energy is very small, but a microwave quantum. Or, if we illuminate hydrogen gas with microwaves, we will notice the absorption of energy because the atoms are in a state | IV>they will intercept it and go to one of the higher states, but all this only at frequency w=4 A/h. This frequency has been measured experimentally; the best result, obtained relatively recently, is this:

The error is only three hundred billionths! Probably no fundamental physical quantity is better measured than this; This is one of the most outstanding measurements in physics in terms of accuracy. The theorists were very happy when they managed to calculate the energy with an accuracy of 3·10 -5; but by this time it was measured with an accuracy of 2·10 -11, i.e. a million times more accurate than in theory. So experimenters are far ahead of theorists. In the theory of the ground state of the hydrogen atom and You, and we are in the same position. You can also take the meaning A from experience - and everyone, in the end, has to do the same.

You've probably heard before about the "21-cm line" of hydrogen. This is the wavelength of the spectral line at 1420 MHz between hyperfine states. Radiation at this wavelength is emitted or absorbed by atomic hydrogen gas in galaxies. This means, with the help of radio telescopes tuned to waves 21 cm(or approximately 1420 MHz), one can observe the speed and location of condensations of atomic hydrogen. By measuring the intensity, you can estimate its quantity. By measuring the shift in frequency caused by the Doppler effect, the movement of gas in a galaxy can be determined. This is one of the great radio astronomy programs. So we are now talking about something very real, this is not some kind of artificial task.

§ 4. Zeeman splitting

Although we have completed the task of finding the energy levels of the ground state of hydrogen, we will still continue to study this interesting system. To say something else about it, for example to calculate the rate at which a hydrogen atom absorbs or emits radio waves of length 21 cm, you need to know what happens to him when he is outraged. We need to do what we did with the ammonia molecule - after we found the energy levels, we went further and found out what happens when the molecule is in an electric field. And after this it was not difficult to imagine the influence of the electric field of a radio wave. In the case of the hydrogen atom, the electric field does nothing with the levels, except that it shifts them all by some constant value proportional to the square of the field, and this is not interesting to us, because it does not change differences energies. This time it's important magnetic field. This means that the next step is to write the Hamiltonian for the more complex case when the atom sits in an external magnetic field.

What is this Hamiltonian? We will simply tell you the answer, because we cannot give any “proof”, except to say that this is exactly how the atom is structured.

The Hamiltonian has the form

Now it consists of three parts. First member A(s e ·s p) represents the magnetic interaction between an electron and a proton; it is the same as if there was no magnetic field. The influence of the external magnetic field is manifested in the remaining two terms. Second term (-m e s e · IN) is the energy that an electron would have in a magnetic field if it were alone there. In the same way, the last term (-m р s R · IN) would be the energy of a single proton. According to classical physics, the energy of both of them together would be the sum of their energies; According to quantum mechanics, this is also correct. The interaction energy arising due to the presence of a magnetic field is simply the sum of the energies of interaction of an electron with a magnetic field and a proton with the same field, expressed through sigma operators. In quantum mechanics, these terms are not actually energies, but referring to the classical formulas for energy helps to remember the rules for writing the Hamiltonian. As if. be that as it may, (10.27) is the correct Hamiltonian.

Now you need to go back to the beginning and solve the whole problem again. But most of the work has already been done; we just need to add the effects caused by the new members. Let us assume that the magnetic field B is constant and directed along z. Then to our old Hamiltonian operator N^ you need to add two new pieces; let's designate them N^":

Using the table. 10.1, we immediately receive

Look how convenient it is! Operator N", acting on each state, it simply gives a number multiplied by the same state. In the matrix i|H"|j> there is therefore only diagonal elements, and one can simply add the coefficients from (10.28) to the corresponding diagonal terms in (10.13), so that the Hamiltonian equations (10.14) become

The form of the equations has not changed, only the coefficients have changed. And bye IN does not change over time, you can do everything the same as before.

Substituting

, we get

Fortunately, the first and fourth equations are still independent of the others, so the same technique will be used again. One solution is state | I>, for which

Another solution

The other two equations require more work because the coefficients A 2 and a 3 are no longer equal to each other. But they are very similar to the pair of equations that we wrote for the ammonia molecule. Looking back at equations (7.20) and (7.21), the following analogy can be drawn (remember that the subscripts 1 and 2 there correspond to subscripts 2 and 3 here):

Previously, energies were given by formula (7.25), which had the form

Substituting (10.33) here, we obtain for the energy

In ch. 7 we are used to calling these energies E I And E II , now we will label them E III And E IV :

So, we have found the energies of four stationary states of the hydrogen atom in a constant magnetic field. Let's check our calculations, for which we'll direct IN to zero and see if we get the same energies as in the previous paragraph. You see that the weight is ok. At B= 0energy E I , E II And E III contact + A, a E IV - V - BEHIND. Even our numbering of states is consistent with the previous one. But when we turn on the magnetic field, each energy will begin to change in its own way. Let's see how this happens.

First, recall that for an electron, m e is negative and almost 1000 times greater than m p, which is positive. This means that m e +m p and m e -m p are both negative and almost equal to each other. Let's denote them -m and -m":

(Both mi and m" are positive and almost coincide in magnitude with m e, which is approximately equal to one Bohr magneton.) Our quartet of energies will then turn into

Energy E I initially equal to A and increases linearly with growth IN at speed m. Energy E II is also equal at first A, but with growth IN linear decreases the slope of its curve is -m . Changing these levels from IN shown in Fig. 10.3. The figure also shows energy graphs E III And E IV . Their dependence on IN different. At small IN they depend on IN quadratic; At first their slope is zero, and then they begin to bend and when large B approach straight lines with a slope ±m", close to the slope e i And E II

The shift in atomic energy levels caused by the action of a magnetic field is called Zeeman effect. We say that the curves in FIG. 10.3 show Zeeman splitting ground state of hydrogen.

Fig. 10.3. Ground state energy levels

hydrogen in a magnetic fieldIN .

Curves E III and E IV approaching dotted lines

A±m"B.

When there is no magnetic field, one simply gets one spectral line from the hyperfine structure of hydrogen. State transitions | IV> and any of the other three occur with the absorption or emission of a photon whose frequency is 1420 MHz:1/h, multiplied by the energy difference 44. But when the atom is in a magnetic field B, then much more lines are obtained. Transitions can occur between any two of the four states. This means that if we have atoms in all four states, then energy can be absorbed (or emitted) in any of the six transitions shown in Fig. 10.4 with vertical arrows.

Fig. 10.4. Transitions between energy levels of the ground state of hydrogen in a certain magnetic fieldIN.

Many of these transitions can be observed using the Rabi molecular beam technique, which we described in Chap. 35, § 3 (issue 7).

What causes the transitions? They arise if, along with a strong constant field B apply a small disturbing magnetic field that varies with time. We observed the same thing under the action of an alternating electric field on an ammonia molecule. Only here the culprit of the transitions is the magnetic field acting on the magnetic moments. But the theoretical calculations are the same as in the case of ammonia. The easiest way to obtain them is to take a disturbing magnetic field rotating in the plane hu, although the same will happen from any oscillating horizontal field. If you insert this perturbing field as an additional term into the Hamiltonian, you get solutions in which the amplitudes change with time, as was the case with the ammonia molecule. This means you can easily and accurately calculate the probability of transition from one state to another. And you will find that all this is consistent with experience.

§ 5. States in a magnetic field

Now let's look at the shape of the curves in Fig. 10.3. Firstly, if we talk about large fields, the dependence of energy on the field is quite interesting and easy to explain. For sufficiently large IN(namely when mB/A>>1) in formulas (10.37) we can neglect unity. The four energies take the form

These are the equations of the four lines in Fig. 10.3. These formulas can be physically understood as follows. The nature of stationary states in zero the field is completely determined by the interaction of two magnetic moments. Mixing of basic states | + -> and | - +> in stationary states |III>and | IV>caused by this interaction. However, one can hardly expect that each of our particles (both proton and electron) strong external fields will be influenced by the field of another particle; each will act as if it were alone in the external field. Then (as we have already seen many times) the spin of the electron will be directed along the external magnetic field (along it or against it).

Let the electron spin be directed upward, i.e., along the field; its energy will be -m e B. The proton can stand in different ways. If its spin is also directed upward, then its energy is -m p B. Their sum is equal to -(m e +m p) B=mB. And this is exactly what it is E I , and this is very nice, because we are describing the state |+ +>=| I>. There's a little extra dick A(now (m B>>A), representing the interaction energy between a proton and an electron when their spins are parallel. (From the very beginning we believed A positive, because it should have been so according to the theory in question; the same thing happens experimentally.) But the proton’s spin can also be directed downward. Then its energy in the external field will turn into +m P B, and together with the electron their energy will be -(m e -m p) B= m IN. And the energy of interaction turns into - A. Their sum will give energy E III , in (10.38). So the state | III>in strong fields it becomes the state |+ ->.

Let the electron spin now be directed downwards. Its energy in the external field is equal to m e IN. If the proton also looks down, then their total energy is equal to (m e +m p) B = - m Plus interaction energy A(the backs are now parallel). This just leads to energy E II in (10.38) and corresponds to the state |- ->=| II>, which is very nice. And finally, if the electron has a spin down and the proton has a spin up, then we get the energy (m e -m p )B-A (minus A because the backs are opposite), i.e. E IV . And the state responds |- +>.

“Wait a minute,” you’ll probably say. “States | Ill>and | IV>- is not states | + - > and | - + >; they are theirs mixtures." True, but the mixing here is barely noticeable. Indeed, at 5 = 0 they are mixtures, but we have not yet found out what happens at large IN. When we used the analogy between (10.33) and the formulas of Chap. to obtain the energy of stationary states. 7, then at the same time it was possible to take the amplitudes from there. They will be obtained from (7.23):

Attitude a 2 /a 3 - this is of course this time C 2 /C 3 Inserting similar quantities from (10.33), we obtain

where instead of E you need to take suitable energy (or E III , or E IV ). For example, for the state | III>we have

This means that for large IN at the state | ///> WITH 2 >>C 3 ;state almost completely becomes state | 2>= |+ ->. In the same way, if in (10.39) we substitute e iv , then it turns out that (C 2 /C 3) IV >simply turns into state |3> = |- +>. You see that the coefficients in the linear combinations of our basis states that make up the stationary states themselves depend on IN.

The state we call | III>, in very weak fields it is a mixture of |+ -> and |- +> in a 1:1 ratio, but in strong fields it shifts entirely to |+ ->. Likewise, the state | IV>, which in weak fields is also a mixture of |+ -> and |- +> in the proportion 1:1 (with the opposite sign), goes into the state | - +), when the spins are no longer connected to each other due to a strong external field.

I would like to draw your attention, in particular, to what is happening in very weak magnetic fields. There is one energy ( -3A), which does not change when a weak magnetic field is turned on. And there is another energy ( +A), which, when a weak magnetic field is turned on, splits into three different energy levels. In weak energy fields with increasing IN change as shown in Fig. 10.5. Let's say that we have somehow selected a set of hydrogen atoms, all of which have the same energy - 3A. If we pass them through the Stern-Gerlach device (with not very strong fields), we will find that they simply pass entirely through. (Since their energy does not depend on IN, then, according to the principle of virtual work, the magnetic field gradient does not create any force that would be felt by them.) Suppose, on the other hand, we selected a group of atoms with energy + A and passed them through the Stern-Gerlach device, say through the device S.(Again, the fields in the instrument should not be so strong as to destroy the interior of the atom; it is assumed that the fields are so small that the energies can be considered linearly dependent on IN.) We would get three bunches. On states | I> and | II>opposite forces act, their energies change according to IN linearly with slope ±m, so strength are similar to the forces acting on a dipole whose m z = ±m , and state | III> goes right through. We return again to Chap. 3. A hydrogen atom with energy +A is a particle with spin 1. This energy state is a "particle" for which j=1, and can be described (with respect to some system of axes in space) in terms of basic states |+ S>, | 0S> and |- S>, which we used in Chap. 3. On the other hand, when a hydrogen atom has an energy of -3 A, it is a particle with spin zero. (We remind you that everything said, strictly speaking, is true only for infinitesimal magnetic fields.) So, the states of hydrogen in a zero magnetic field can be grouped as follows:

In ch. 35 (issue 7) we said that for any particle the components of the angular momentum along any axis can take only certain values, always differing by h. Thus, the z-component of angular momentum J z may be equal jh,(j-1) h, (j- 2)h,..., (-j)h, Where j- particle spin (which can be integer or half-integer). Usually they write

J z =mh,(10.43)

Where T stands in place of any of the numbers j, j-1, j- 2, . . .,-j(we didn’t say this at the time). Therefore, you will often find in books the numbering of the four main states using the so-called quantum numbers j And m[often referred to as the "total angular momentum quantum number" ( j) and "magnetic quantum number" (m)]. Instead of our state symbols | I>, |II> etc. many people often write states in the form | j, m>. They would depict our table of states for the zero field in (10.41) and (10.42) in the form of a table. 10.3. There's no new physics here, it's just a matter of notation.

Table 10.3· STATES OF THE HYDROGEN ATOM IN ZERO FIELD

§ 6. Projection matrix for spin 1

Now we would like to apply our knowledge of the hydrogen atom to one special problem. In ch. 3 we talked about the fact that the particle with spin 1, located in one of the basic states (+, 0, -) in relation to the Stern-Gerlach device with some particular orientation (say, in relation to the device S), will have a certain amplitude of being in one of three states in relation to the device T, oriented in space differently. There are nine such amplitudes jT|iS> , which together form a projection matrix. In ch. 3, § 7, we wrote down the elements of this matrix for various orientations without proof T towards S. Now we want to show you one of the ways to output them.

In the hydrogen atom, we have found a system with spin 1, composed of two particles with spin 1/2. In ch. 4 we have already learned how to convert amplitudes for spin 1/2. This knowledge can be applied to obtain a transformation for spin 1. Here's how it's done: you have a system (a hydrogen atom with energy + A) with spin 1. Let us pass it through a filter S Stern-Gerlach so that we now know that it is in one of the basic states with respect to S, let's say in |+ S). What is the amplitude of it ending up in one of the basic states, say |+ T), in relation to the device T? If you call the instrument coordinate system S system x, y, z, that state |+ S> - this is what was recently called the |+ +> state. But imagine that some friend of yours drew his axle z along the axis T. He will relate his states to some system x", y", z". Its up and down states for the electron and proton would be different from yours. His state “plus - plus”, which can be written | +"+">, noting the “hatchedness” of the system, there is a state |+ T> particles with spin 1. Are you interested in T|+ S> that there is simply a different way of recording amplitude.

The amplitude can be found as follows. IN yours spin system electron from state | + +> points upward. This means that he has some amplitude e to be in your friend's system spin up and some amplitude e to be in this system spin down. Likewise, proton able + + U has spin up in your system and the amplitudes p and p turn out to be spin up or down in the "primed" system. Since we are talking about two different particles, the amplitude of that both particles together V his the system will turn out to be with their backs up, equal to the product of the amplitudes

We put e and p icons under the amplitudes to make it clear what we are doing. But both of them are simply transformation amplitudes for a particle with spin 1/2, so in fact they are the same numbers. In fact, these are the same amplitudes that we described in Chap. 4 were called T|+ S> > and which we have listed in the table. 4.1 and 4.2.

But now, however, we are threatened with confusion in notation. You must be able to distinguish the amplitude T|+ S) for a particle with spin 1/2 of what we are Also called T|+ S>, but for back 1-there is nothing in common between them! I hope you won't be too confused if we for a while Let us introduce other notations for amplitudes for spin 1/2. They are given in table. 10.4. For states of spin 1 particles we will continue to use the notation | + S, | 0S> and |- S>.

Table 10.4· AMPLITUDES for SPIN 1 / 2

In our new notation (10.44) simply becomes

This is exactly the amplitude T|+ S> for spin 1. Now let's, for example, assume that your friend has a coordinate system, i.e. a "hatched" device T, rotated around yours axes z by angle j; then from the table 4.2 turns out

This means that from (10.44) the amplitude for spin 1 will be equal to

Now you understand how we will proceed next.

But it would be good to carry out calculations in the general case for all states. If a proton and electron are in our system (system S) both look up, then the amplitudes of what is in the other system (system T)they will be in one of four possible states,

We can then write the |+ +> state as the following linear combination:

In the same way it is easy to show that

C |0 S> the situation is a little more complicated, because

But each of the states | + - > and | - +> can be expressed through the “hatched” states and substituted into the sum:

Multiplying the sum (10.50) and (10.51) by 1/T2, we get

this implies

Now we have all the necessary amplitudes. The coefficients in (10.48), (10.49) and (10.52) are matrix elements

jT| iS>. Let's put them into one matrix:

We expressed the spin 1 transformation in terms of amplitudes a, b, with and d spin 1/2 transformations.

If, for example, the system T rotated relative to S at angle a around the axis at(see Fig. 3.6, p. 64), then the amplitudes in table. 10.4 is just matrix elements R y(a) in table. 4.2:

Substituting them into (10.53), we obtain formulas (3.38), which are given on page 80 without proof.

But what happened to the state | IV)?! This is a spin-zero system; this means that she has only one state - it in all coordinate systems same. You can check that everything turns out this way if you take the difference (10.50) and (10.51); we get

But (ad-bc) - this is the determinant of the matrix for spin 1/2, it is simply equal to one. It turns out

|IV">=|IV> for any relative orientation of the two coordinate systems.

* For those who skipped over ch. 4, you will have to skip this paragraph too.

*Remember that classically U= -m·B, so the energy is least when the torque is directed along the field. For positively charged particles, the magnetic moment is parallel to the spin, for negative ones - vice versa. This means that in (10.27) m R is a positive number, and (m e - negative.

*Crampton, Kleppner, Ramsey, Physical Review Letters, 11, 338 (1963).

*In reality the condition is

but, as usual, we will identify states with constant vectors, which at t=0 coincide with real vectors.

* This operator is now called the spin exchange operator.

* For these operators, however, it turns out that nothing depends on their order.

, molecules and ions and, accordingly, spectral lines, due to the interaction of the magnetic moment of the nucleus with the magnetic field of electrons. The energy of this interaction depends on the possible mutual orientations of the nuclear spin and electron spins.

Respectively, hyperfine splitting- splitting of energy levels (and spectral lines) into several sublevels caused by such interaction.

According to classical concepts, an electron orbiting a nucleus, like any charged particle moving in a circular orbit, has a magnetic dipole moment. Similarly, in quantum mechanics, the orbital angular momentum of an electron creates a certain magnetic moment. The interaction of this magnetic moment with the magnetic moment of the nucleus (due to nuclear spin) leads to hyperfine splitting (that is, it creates a hyperfine structure). However, the electron also has spin, which contributes to its magnetic moment. Therefore, hyperfine splitting exists even for terms with zero orbital momentum.

The distance between the sublevels of the hyperfine structure is an order of magnitude smaller than that between the levels of the fine structure (this order of magnitude is essentially determined by the ratio of the electron mass to the mass of the nucleus).

Abnormal ultrafine structure is caused by the interaction of electrons with the quadrupole electric moment of the nucleus.

Story

Hyperfine splitting was observed by A. A. Michelson in 1881, but was explained only after W. Pauli suggested the presence of a magnetic moment in atomic nuclei in 1924.

Write a review about the article "Ultrafine structure"

Literature

Landau L.D., Lifshits E.M. Theoretical physics . Volume 3. Quantum mechanics (non-relativistic theory).
Shpolsky E.V. Atomic physics. - M.: Nauka, 1974.

Excerpt characterizing hyperfine structure

“There’s no point in having fun,” Bolkonsky answered.
While Prince Andrei met with Nesvitsky and Zherkov, on the other side of the corridor, Strauch, an Austrian general who was at Kutuzov’s headquarters to monitor the food supply of the Russian army, and a member of the Gofkriegsrat, who had arrived the day before, walked towards them. There was enough space along the wide corridor for the generals to freely disperse with three officers; but Zherkov, pushing Nesvitsky away with his hand, said in a breathless voice:
- They're coming!... they're coming!... move aside! please the way!
The generals passed by with an air of desire to get rid of bothersome honors. The face of the joker Zherkov suddenly expressed a stupid smile of joy, which he seemed unable to contain.
“Your Excellency,” he said in German, moving forward and addressing the Austrian general. – I have the honor to congratulate you.
He bowed his head and awkwardly, like children learning to dance, began to shuffle first with one foot and then with the other.
The general, a member of the Gofkriegsrat, looked sternly at him; without noticing the seriousness of the stupid smile, he could not refuse a moment’s attention. He narrowed his eyes to show that he was listening.
“I have the honor to congratulate you, General Mack has arrived, he’s completely healthy, he just got a little hurt here,” he added, beaming with a smile and pointing to his head.
The general frowned, turned away and walked on.
– Gott, wie naiv! [My God, how simple it is!] - he said angrily, walking away a few steps.
Nesvitsky hugged Prince Andrei with laughter, but Bolkonsky, turning even paler, with an angry expression on his face, pushed him away and turned to Zherkov. The nervous irritation into which the sight of Mack, the news of his defeat and the thought of what awaited the Russian army led him, found its outcome in anger at Zherkov’s inappropriate joke.
“If you, dear sir,” he spoke shrilly with a slight trembling of his lower jaw, “want to be a jester, then I cannot prevent you from doing so; but I declare to you that if you dare to act up in my presence next time, I will teach you how to behave.
Nesvitsky and Zherkov were so surprised by this outburst that they silently looked at Bolkonsky with their eyes open.
“Well, I just congratulated,” said Zherkov.
– I’m not joking with you, please remain silent! - Bolkonsky shouted and, taking Nesvitsky by the hand, walked away from Zherkov, who could not find what to answer.
“Well, what are you talking about, brother,” Nesvitsky said calmingly.

Although we have completed the task of finding the energy levels of the ground state of hydrogen, we will still continue to study this interesting system. To say something else about it, for example to calculate the rate at which a hydrogen atom absorbs or emits radio waves of length 21 cm, you need to know what happens to him when he is outraged. We need to do what we did with the ammonia molecule - after we found the energy levels, we went further and found out what happens when the molecule is in an electrical field. And after this it was not difficult to imagine the influence of the electric field of a radio wave. In the case of the hydrogen atom, the electric field does nothing with the levels, except that it shifts them all by some constant value proportional to the square of the field, and this is not interesting to us, because it does not change differences energies. This time it's important magnetnew field. This means that the next step is to write the Hamiltonian for the more complex case when the atom sits in an external magnetic field.

What is this Hamiltonian? We will simply tell you the answer, because we cannot give any “proof”, except to say that this is exactly how the atom is structured.

The Hamiltonian has the form

Now it consists of three parts. First member A(σ e ·σ p) represents the magnetic interaction between electron and proton; it is the same as if there was no magnetic field. The influence of the external magnetic field is manifested in the remaining two terms. Second term (— μ e σ e· B) is the energy that an electron would have in a magnetic field if it were alone there. In the same way, the last term (- μ р σ р ·В) would be the energy of a single proton. According to classical physics, the energy of both of them together would be the sum of their energies; According to quantum mechanics, this is also correct. The interaction energy arising due to the presence of a magnetic field is simply the sum of the energies of interaction of an electron with a magnetic field and a proton with the same field, expressed through sigma operators. In quantum mechanics, these terms are not actually energies, but referring to the classical formulas for energy helps to remember the rules for writing the Hamiltonian. Be that as it may, (10.27) is the correct Hamiltonian.

Now you need to go back to the beginning and solve the whole problem again. But most of the work has already been done; we just need to add the effects caused by the new members. Let us assume that the magnetic field B is constant and directed along z. Then to our old Hamiltonian operator N you need to add two new pieces; let's designate them N′:

Look how convenient it is! The operator H′, acting on each state, simply gives a number multiplied by the same state. In the matrix<¡|H′| j>there is therefore only diagonal elements, and one can simply add the coefficients from (10.28) to the corresponding diagonal terms in (10.13), so that the Hamiltonian equations (10.14) become

The form of the equations has not changed, only the coefficients have changed. And bye IN does not change over time, you can do everything the same as before.
Substituting WITH= a l e-(¡/h)Et, we get

Fortunately, the first and fourth equations are still independent of the others, so the same technique will be used again. One solution is the state |/>, for which

The other two equations require more work because the coefficients of a 2 and a 3 are no longer equal to each other. But they are very similar to the pair of equations that we wrote for the ammonia molecule. Looking back at equations (7.20) and (7.21), the following analogy can be drawn (remember that the subscripts 1 and 2 there correspond to subscripts 2 and 3 here):

Previously, energies were given by formula (7.25), which had the form

In Chapter 7 we used to call these energies E I and E II, now we will designate them E III And E IV

So, we have found the energies of four stationary states of the hydrogen atom in a constant magnetic field. Let's check our calculations, for which we'll direct IN to zero and see if we get the same energies as in the previous paragraph. You see that everything is fine. At B=0 energy E I, E II And E III contact +A, a E IV - V - 3A. Even our numbering of states is consistent with the previous one. But when we turn on the magnetic field, each energy will begin to change in its own way. Let's see how this happens.

First, recall that the electron μe negative and almost 1000 times greater μ p, which is positive. This means that μ e +μ р and μ e -μ р are both negative and almost equal to each other. Let's denote them -μ and -μ′:

(AND μ , and μ′ are positive and almost coincide in value with μ e, which is approximately equal to one Bohr magneton.) Our quartet of energies will then turn into

Energy E I initially equal to A and increases linearly with growth IN with speed μ. Energy E II is also equal at first A, but with growth IN linear decreases the slope of its curve is - μ . Changing these levels from IN shown in Fig. 10.3. The figure also shows energy graphs E III And E IV. Their dependence on IN different. At small IN they depend on IN quadratic; At first their slope is zero, and then they begin to bend and when large B approach straight lines with a slope ± μ ′ close to the slope E I And E II.

The shift in atomic energy levels caused by the action of a magnetic field is called Zeeman effect. We say that the curves in FIG. 10.3 show Zeeman splitting ground state of hydrogen. When there is no magnetic field, one simply gets one spectral line from the hyperfine structure of hydrogen. State transitions | IV> and any of the other three occur with the absorption or emission of a photon whose frequency is 1420 MHz:1/h, multiplied by the energy difference 4A. But when the atom is in a magnetic field B, then there are much more lines. Transitions can occur between any two of the four states. This means that if we have atoms in all four states, then energy can be absorbed (or emitted) in any of the six transitions shown in Fig. 10.4 with vertical arrows. Many of these transitions can be observed using the Rabi molecular beam technique, which we described in Chap. 35, § 3 (issue 7).

What causes the transitions? They arise if, along with a strong constant field IN apply a small disturbing magnetic field that varies with time. We observed the same thing under the action of an alternating electric field on an ammonia molecule. Only here the culprit of the transitions is the magnetic field acting on the magnetic moments. But the theoretical calculations are the same as in the case of ammonia. The easiest way to obtain them is to take a disturbing magnetic field rotating in the plane hu, although the same will happen from any oscillating horizontal field. If you insert this perturbing field as an additional term into the Hamiltonian, you get solutions in which the amplitudes change with time, as was the case with the ammonia molecule. This means you can easily and accurately calculate the probability of transition from one state to another. And you will find that all this is consistent with experience.

9. Compare the obtained value with the theoretical one, calculated through universal constants.

The report must contain:

1. Optical design of the spectrometer with a prism and a rotating prism;

2. Table of measurements of deviation angles of lines - mercury reference points and their average values;

3. Table of measurements of deviation angles of hydrogen lines and their average values;

4. The values of the found frequencies of hydrogen lines and the interpolation formulas used for the calculations;

5. Systems of equations used to determine the Rydberg constant using the least squares method;

6. The obtained value of the Rydberg constant and its value calculated from the universal constants.

3.5.2. Spectroscopic determination of nuclear moments

3.5.2.1. Experimental determination of parameters of hyperfine splitting of spectral lines.

To measure the ultrafine structure of spectral lines, it is necessary to use spectral instruments with high resolving power, therefore in this work we use a spectral instrument with crossed dispersion, in which a Fabry-Perot interferometer is placed inside a prism spectrograph (see Fig. 3.5.1 and section 2.4.3.2,

rice. 2.4.11).

The dispersion of a prism spectrograph is sufficient to separate spectral emission lines caused by transitions of the valence electron in an alkali metal atom, but is completely insufficient to resolve the hyperfine structure of each of these lines. Therefore, if we used only a prism spectrograph, we would obtain an ordinary emission spectrum on a photographic plate, in which the components of the hyperfine structure would merge into one line, the spectral width of which is determined only by the resolution of the ICP51.

The Fabry-Perot interferometer makes it possible to obtain an interference pattern within each spectral line, which is a sequence of interference rings. The angular diameter of these rings θ, as is known from the theory of the Fabry-Perot interferometer, is determined by the ratio of the thickness of the standard air layer t and the wavelength λ:

		θ k = k

where k is the interference order for a given ring.

Thus, each spectral line is not just a geometric image of the entrance slit, constructed by the optical system of the spectrograph in the plane of the photographic plate, each of these images now turns out to be intersected by segments of interference rings. If there is no hyperfine splitting, then within a given spectral line one system of rings corresponding to different orders of interference will be observed.

If within a given spectral line there are two components with different wavelengths (hyperfine splitting), then the interference pattern will be two systems of rings for wavelengths λ and λ ", shown in Fig. 3.5.2 with solid and dotted lines, respectively.

Rice. 3.5.2. Interference structure of a spectral line consisting of two close components.

The linear diameter of the interference rings d in the small angle approximation is related to the angular diameter θ by the relation:

d = θ×F 2,

where F 2 is the focal length of the spectrograph camera lens.

Let us obtain expressions relating the angular and linear diameters of the interference rings to the wavelength of the radiation that forms the interference pattern in the Fabry-Perot interferometer.

In the small angle approximation cos θ 2 k ≈ 1− θ 8 k and for two lengths

waves λ and λ "the conditions for the interference maximum of the kth order will be written accordingly:

				4λ"
θk = 8	−k	θ" k = 8	−k

From here, for the difference between the wavelengths of the two components, we obtain:

d λ = λ" −λ =		(θ k 2	− θ" k 2 )
d λ = λ" −λ =		(θ k 2	− θ" k 2 )

The angular diameter (k +1) of the 1st order of wavelength is determined by
ratio:
	8 − (k +1)
	8 − (k +1)
k+ 1

From (3.5.9) and (3.5.11) we obtain:

	= θ2			− θ2

				k+ 1

Excluding t					from (3.5.10)-(3.5.12) we obtain:
d λ =			θk 2 − θ" k 2

		k θ2 − θ2
					k+ 1

At small angles, the order of interference is given by the relation

k = 2 λ t (see (3.5.8)), so equality (3.5.13) takes the form:

d λ =			θk 2 − θ" k 2
d λ =
	2 t θ 2			− θ2
				k+ 1

Moving on to wave numbers ν =					We get:
Moving on to wave numbers ν =					We get:
		1 d k 2 − d "k 2
d ν =
d ν =			− d 2
			k+ 1

Now, to determine d ~ ν, we need to measure the linear diameters of two systems of interference rings for two components of the hyperfine structure inside the spectral line under study. To increase the accuracy of determining d ~ ν, it makes sense to measure the diameters of the rings, starting from the second and ending with the fifth. Further rings are located close to each other and the error in determining the difference in the squares of the diameters of the rings grows very quickly. You can average the entire right-hand side (3.5.16), or separately the numerator and denominator.