Each individual value is completely determined by its distribution function. Also, to solve practical problems, it is enough to know a few numerical characteristics, which makes it possible to present the main features random variable in short form.
These quantities are primarily expected value and dispersion .
Expected value- the average value of a random variable in probability theory. Designated as .
by the most in a simple way mathematical expectation of a random variable X(w), are found as integralLebesgue with respect to the probability measure R original probability space![]()
You can also find the mathematical expectation of a value as Lebesgue integral from X by probability distribution R X quantities X:
![]()
where is the set of all possible values X.
Mathematical expectation of functions from a random variable X is through distribution R X. For example, if X- random variable with values in and f(x)- unambiguous Borelfunction X , then:
If a F(x)- distribution function X, then the mathematical expectation is representable integralLebesgue - Stieltjes (or Riemann - Stieltjes):
![]()
while the integrability X in what sense ( * ) corresponds to the finiteness of the integral
![]()
In specific cases, if X It has discrete distribution with likely values x k, k=1, 2, . , and probabilities , then
![]()
if X has an absolutely continuous distribution with a probability density p(x), then
![]()
in this case, the existence of a mathematical expectation is equivalent to the absolute convergence of the corresponding series or integral.
Properties of the mathematical expectation of a random variable.
- Expected value constant value is equal to this value:
C- constant;
- M=C.M[X]
- The mathematical expectation of the sum of randomly taken values is equal to the sum of their mathematical expectations:
![]()
- The mathematical expectation of the product of independent random variables = the product of their mathematical expectations:
M=M[X]+M[Y]
if X and Y independent.
if the series converges:
![]()
Algorithm for calculating the mathematical expectation.
Properties of discrete random variables: all their values can be renumbered natural numbers; equate each value with a non-zero probability.
1. Multiply the pairs in turn: x i on the pi.
2. Add the product of each pair x i p i.
For example, for n = 4 :
Distribution function of a discrete random variable stepwise, it increases abruptly at those points whose probabilities have a positive sign.
Example: Find the mathematical expectation by the formula.
The mathematical expectation (average value) of a random variable X , given on a discrete probability space, is the number m =M[X]=∑x i p i , if the series converges absolutely.
Service assignment. With an online service the mathematical expectation, variance and standard deviation are calculated(see example). In addition, a graph of the distribution function F(X) is plotted.
Properties of the mathematical expectation of a random variable
- The mathematical expectation of a constant value is equal to itself: M[C]=C , C is a constant;
- M=C M[X]
- The mathematical expectation of the sum of random variables is equal to the sum of their mathematical expectations: M=M[X]+M[Y]
- The mathematical expectation of the product of independent random variables is equal to the product of their mathematical expectations: M=M[X] M[Y] if X and Y are independent.
Dispersion Properties
- The dispersion of a constant value is equal to zero: D(c)=0.
- The constant factor can be taken out from under the dispersion sign by squaring it: D(k*X)= k 2 D(X).
- If random variables X and Y are independent, then the variance of the sum is equal to the sum of the variances: D(X+Y)=D(X)+D(Y).
- If random variables X and Y are dependent: D(X+Y)=DX+DY+2(X-M[X])(Y-M[Y])
- For the variance, the computational formula is valid:
D(X)=M(X 2)-(M(X)) 2
Example. The mathematical expectations and variances of two independent random variables X and Y are known: M(x)=8 , M(Y)=7 , D(X)=9 , D(Y)=6 . Find the mathematical expectation and variance of the random variable Z=9X-8Y+7 .
Solution. Based on the properties of mathematical expectation: M(Z) = M(9X-8Y+7) = 9*M(X) - 8*M(Y) + M(7) = 9*8 - 8*7 + 7 = 23 .
Based on the dispersion properties: D(Z) = D(9X-8Y+7) = D(9X) - D(8Y) + D(7) = 9^2D(X) - 8^2D(Y) + 0 = 81*9 - 64*6 = 345
Algorithm for calculating the mathematical expectation
Properties of discrete random variables: all their values can be renumbered by natural numbers; Assign each value a non-zero probability.- Multiply the pairs one by one: x i by p i .
- We add the product of each pair x i p i .
For example, for n = 4: m = ∑x i p i = x 1 p 1 + x 2 p 2 + x 3 p 3 + x 4 p 4
Example #1.
| x i | 1 | 3 | 4 | 7 | 9 |
| pi | 0.1 | 0.2 | 0.1 | 0.3 | 0.3 |
The mathematical expectation is found by the formula m = ∑x i p i .
Mathematical expectation M[X].
M[x] = 1*0.1 + 3*0.2 + 4*0.1 + 7*0.3 + 9*0.3 = 5.9
The dispersion is found by the formula d = ∑x 2 i p i - M[x] 2 .
Dispersion D[X].
D[X] = 1 2 *0.1 + 3 2 *0.2 + 4 2 *0.1 + 7 2 *0.3 + 9 2 *0.3 - 5.9 2 = 7.69
Standard deviation σ(x).
σ = sqrt(D[X]) = sqrt(7.69) = 2.78
Example #2. A discrete random variable has the following distribution series:
| X | -10 | -5 | 0 | 5 | 10 |
| R | a | 0,32 | 2a | 0,41 | 0,03 |
Solution. The value a is found from the relationship: Σp i = 1
Σp i = a + 0.32 + 2 a + 0.41 + 0.03 = 0.76 + 3 a = 1
0.76 + 3 a = 1 or 0.24=3 a , whence a = 0.08
Example #3. Determine the distribution law of a discrete random variable if its variance is known, and x 1
p 1 =0.3; p2=0.3; p3=0.1; p 4 \u003d 0.3
d(x)=12.96
Solution.
Here you need to make a formula for finding the variance d (x) :
d(x) = x 1 2 p 1 +x 2 2 p 2 +x 3 2 p 3 +x 4 2 p 4 -m(x) 2
where expectation m(x)=x 1 p 1 +x 2 p 2 +x 3 p 3 +x 4 p 4
For our data
m(x)=6*0.3+9*0.3+x 3 *0.1+15*0.3=9+0.1x 3
12.96 = 6 2 0.3+9 2 0.3+x 3 2 0.1+15 2 0.3-(9+0.1x 3) 2
or -9/100 (x 2 -20x+96)=0
Accordingly, it is necessary to find the roots of the equation, and there will be two of them.
x 3 \u003d 8, x 3 \u003d 12
We choose the one that satisfies the condition x 1
Distribution law of a discrete random variable
x 1 =6; x2=9; x 3 \u003d 12; x4=15
p 1 =0.3; p2=0.3; p3=0.1; p 4 \u003d 0.3
There will also be tasks for an independent solution, to which you can see the answers.
Mathematical expectation and variance are the most commonly used numerical characteristics of a random variable. They characterize the most important features of the distribution: its position and degree of dispersion. The mathematical expectation is often referred to simply as the mean. random variable. Dispersion of a random variable - a characteristic of dispersion, dispersion of a random variable around its mathematical expectation.
In many problems of practice, a complete, exhaustive description of a random variable - the law of distribution - either cannot be obtained, or is not needed at all. In these cases, they are limited to an approximate description of a random variable using numerical characteristics.
Mathematical expectation of a discrete random variable
Let's come to the concept of mathematical expectation. Let the mass of some substance be distributed between the points of the x-axis x1 , x 2 , ..., x n. Moreover, each material point has a mass corresponding to it with a probability of p1 , p 2 , ..., p n. It is required to choose one point on the x-axis, which characterizes the position of the entire system of material points, taking into account their masses. It is natural to take the center of mass of the system of material points as such a point. This is the weighted average of the random variable X, in which the abscissa of each point xi enters with a "weight" equal to the corresponding probability. The mean value of the random variable thus obtained X is called its mathematical expectation.
The mathematical expectation of a discrete random variable is the sum of the products of all its possible values and the probabilities of these values:
Example 1 Organized a win-win lottery. There are 1000 winnings, 400 of which are 10 rubles each. 300 - 20 rubles each 200 - 100 rubles each. and 100 - 200 rubles each. What is the average winnings for a person who buys one ticket?
Solution. We will find the average win if the total amount of winnings, which is equal to 10*400 + 20*300 + 100*200 + 200*100 = 50,000 rubles, is divided by 1000 (the total amount of winnings). Then we get 50000/1000 = 50 rubles. But the expression for calculating the average gain can also be represented in the following form:
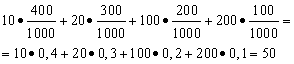
On the other hand, under these conditions, the amount of winnings is a random variable that can take on the values of 10, 20, 100 and 200 rubles. with probabilities equal to 0.4, respectively; 0.3; 0.2; 0.1. Therefore, the expected average payoff is equal to the sum of the products of the size of the payoffs and the probability of receiving them.
Example 2 The publisher decided to publish a new book. He is going to sell the book for 280 rubles, of which 200 will be given to him, 50 to the bookstore, and 30 to the author. The table gives information about the cost of publishing a book and the likelihood of selling a certain number of copies of the book.
Find the publisher's expected profit.
Solution. The random variable "profit" is equal to the difference between the income from the sale and the cost of the costs. For example, if 500 copies of a book are sold, then the income from the sale is 200 * 500 = 100,000, and the cost of publishing is 225,000 rubles. Thus, the publisher faces a loss of 125,000 rubles. The following table summarizes the expected values of the random variable - profit:
| Number | Profit xi | Probability pi | xi p i |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Total: | 1,00 | 25000 |
Thus, we obtain the mathematical expectation of the publisher's profit:
![]() .
.
Example 3 Chance to hit with one shot p= 0.2. Determine the consumption of shells that provide the mathematical expectation of the number of hits equal to 5.
Solution. From the same expectation formula that we have used so far, we express x- consumption of shells:
![]() .
.
Example 4 Determine the mathematical expectation of a random variable x number of hits with three shots, if the probability of hitting with each shot p = 0,4 .
Hint: find the probability of the values of a random variable by Bernoulli formula .
Expectation Properties
Consider the properties of mathematical expectation.
Property 1. The mathematical expectation of a constant value is equal to this constant:
Property 2. The constant factor can be taken out of the expectation sign:
![]()
Property 3. The mathematical expectation of the sum (difference) of random variables is equal to the sum (difference) of their mathematical expectations:
Property 4. The mathematical expectation of the product of random variables is equal to the product of their mathematical expectations:
Property 5. If all values of the random variable X decrease (increase) by the same number FROM, then its mathematical expectation will decrease (increase) by the same number:
![]()
When you can not be limited only to mathematical expectation
In most cases, only the mathematical expectation cannot adequately characterize a random variable.
Let random variables X and Y are given by the following distribution laws:
| Meaning X | Probability |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| Meaning Y | Probability |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
The mathematical expectations of these quantities are the same - equal to zero:
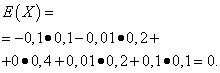
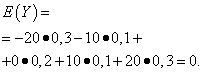
However, their distribution is different. Random value X can only take values that are little different from the mathematical expectation, and the random variable Y can take values that deviate significantly from the mathematical expectation. A similar example: the average wage does not make it possible to judge the proportion of high- and low-paid workers. In other words, by mathematical expectation one cannot judge what deviations from it, at least on average, are possible. To do this, you need to find the variance of a random variable.
Dispersion of a discrete random variable
dispersion discrete random variable X is called the mathematical expectation of the square of its deviation from the mathematical expectation:
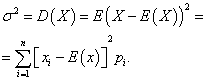
The standard deviation of a random variable X is the arithmetic value of the square root of its variance:
![]() .
.
Example 5 Calculate variances and standard deviations of random variables X and Y, whose distribution laws are given in the tables above.
Solution. Mathematical expectations of random variables X and Y, as found above, are equal to zero. According to the dispersion formula for E(X)=E(y)=0 we get:

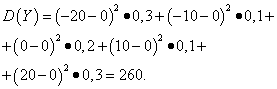
Then the standard deviations of random variables X and Y constitute
![]() .
.
Thus, with the same mathematical expectations, the variance of the random variable X very small and random Y- significant. This is a consequence of the difference in their distribution.
Example 6 The investor has 4 alternative investment projects. The table summarizes the data on the expected profit in these projects with the corresponding probability.
| Project 1 | Project 2 | Project 3 | Project 4 |
| 500, P=1 | 1000, P=0,5 | 500, P=0,5 | 500, P=0,5 |
| 0, P=0,5 | 1000, P=0,25 | 10500, P=0,25 | |
| 0, P=0,25 | 9500, P=0,25 |
Find for each alternative the mathematical expectation, variance and standard deviation.
Solution. Let us show how these quantities are calculated for the 3rd alternative:
The table summarizes the found values for all alternatives.
All alternatives have the same mathematical expectation. This means that in the long run everyone has the same income. The standard deviation can be interpreted as a measure of risk - the larger it is, the greater the risk of the investment. An investor who doesn't want much risk will choose project 1 because it has the smallest standard deviation (0). If the investor prefers risk and high returns in a short period, then he will choose the project with the largest standard deviation - project 4.
Dispersion Properties
Let us present the properties of the dispersion.
Property 1. The dispersion of a constant value is zero:
Property 2. The constant factor can be taken out of the dispersion sign by squaring it:
![]() .
.
Property 3. The variance of a random variable is equal to the mathematical expectation of the square of this value, from which the square of the mathematical expectation of the value itself is subtracted:
![]() ,
,
where ![]() .
.
Property 4. The variance of the sum (difference) of random variables is equal to the sum (difference) of their variances:
Example 7 It is known that a discrete random variable X takes only two values: −3 and 7. In addition, the mathematical expectation is known: E(X) = 4 . Find the variance of a discrete random variable.
Solution. Denote by p the probability with which a random variable takes on a value x1 = −3 . Then the probability of the value x2 = 7 will be 1 − p. Let's derive the equation for mathematical expectation:
E(X) = x 1 p + x 2 (1 − p) = −3p + 7(1 − p) = 4 ,
where we get the probabilities: p= 0.3 and 1 − p = 0,7 .
The law of distribution of a random variable:
| X | −3 | 7 |
| p | 0,3 | 0,7 |
We calculate the variance of this random variable using the formula from property 3 of the variance:
D(X) = 2,7 + 34,3 − 16 = 21 .
Find the mathematical expectation of a random variable yourself, and then see the solution
Example 8 Discrete random variable X takes only two values. It takes the larger value of 3 with a probability of 0.4. In addition, the variance of the random variable is known D(X) = 6 . Find the mathematical expectation of a random variable.
Example 9 An urn contains 6 white and 4 black balls. 3 balls are taken from the urn. The number of white balls among the drawn balls is a discrete random variable X. Find the mathematical expectation and variance of this random variable.
Solution. Random value X can take the values 0, 1, 2, 3. The corresponding probabilities can be calculated from rule of multiplication of probabilities. The law of distribution of a random variable:
| X | 0 | 1 | 2 | 3 |
| p | 1/30 | 3/10 | 1/2 | 1/6 |
Hence the mathematical expectation of this random variable:
M(X) = 3/10 + 1 + 1/2 = 1,8 .
The variance of a given random variable is:
D(X) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .
Mathematical expectation and dispersion of a continuous random variable
For a continuous random variable, the mechanical interpretation of the mathematical expectation will retain the same meaning: the center of mass for a unit mass distributed continuously on the x-axis with density f(x). In contrast to a discrete random variable, for which the function argument xi changes abruptly, for a continuous random variable, the argument changes continuously. But the mathematical expectation of a continuous random variable is also related to its mean value.
To find the mathematical expectation and variance of a continuous random variable, you need to find definite integrals . If a density function of a continuous random variable is given, then it enters directly into the integrand. If a probability distribution function is given, then by differentiating it, you need to find the density function.
The arithmetic average of all possible values of a continuous random variable is called its mathematical expectation, denoted by or .
As already known, the distribution law completely characterizes a random variable. However, the distribution law is often unknown and one has to limit oneself to lesser information. Sometimes it is even more profitable to use numbers that describe a random variable in total; such numbers are called numerical characteristics of a random variable.
Mathematical expectation is one of the important numerical characteristics.
The mathematical expectation is approximately equal to the average value of a random variable.
Mathematical expectation of a discrete random variable is the sum of the products of all its possible values and their probabilities.
If a random variable is characterized by a finite distribution series:
| X | x 1 | x 2 | x 3 | … | x n |
| R | p 1 | p 2 | p 3 | … | r p |
then the mathematical expectation M(X) is determined by the formula:
The mathematical expectation of a continuous random variable is determined by the equality:
where is the probability density of the random variable X.
Example 4.7. Find the mathematical expectation of the number of points that fall out when a dice is thrown.
Solution:
Random value X takes the values 1, 2, 3, 4, 5, 6. Let's make the law of its distribution:
| X | ||||||
| R |
Then the mathematical expectation is:
Properties of mathematical expectation:
1. The mathematical expectation of a constant value is equal to the constant itself:
M(S)=S.
2. The constant factor can be taken out of the expectation sign:
M(CX) = CM(X).
3. The mathematical expectation of the product of two independent random variables is equal to the product of their mathematical expectations:
M(XY) = M(X)M(Y).
Example 4.8. Independent random variables X and Y are given by the following distribution laws:
| X | Y | ||||||
| R | 0,6 | 0,1 | 0,3 | R | 0,8 | 0,2 |
Find the mathematical expectation of a random variable XY.
Solution.
Let's find the mathematical expectations of each of these quantities:
random variables X and Y independent, so the desired mathematical expectation:
M(XY) = M(X)M(Y)=
Consequence. The mathematical expectation of the product of several mutually independent random variables is equal to the product of their mathematical expectations.
4. The mathematical expectation of the sum of two random variables is equal to the sum of the mathematical expectations of the terms:
M(X + Y) = M(X) + M(Y).
Consequence. The mathematical expectation of the sum of several random variables is equal to the sum of the mathematical expectations of the terms.
Example 4.9. 3 shots are fired with probabilities of hitting the target equal to p 1 = 0,4; p2= 0.3 and p 3= 0.6. Find the mathematical expectation of the total number of hits.
Solution.
The number of hits on the first shot is a random variable X 1, which can take only two values: 1 (hit) with probability p 1= 0.4 and 0 (miss) with probability q 1 = 1 – 0,4 = 0,6.
The mathematical expectation of the number of hits in the first shot is equal to the probability of hitting:
Similarly, we find the mathematical expectations of the number of hits in the second and third shots:
M(X 2)= 0.3 and M (X 3) \u003d 0,6.
The total number of hits is also a random variable consisting of the sum of hits in each of the three shots:
X \u003d X 1 + X 2 + X 3.
The desired mathematical expectation X we find by the theorem of mathematical, the expectation of the sum.
- the number of boys among 10 newborns.
It is quite clear that this number is not known in advance, and in the next ten children born there may be:
Or boys - one and only one of the listed options.
And, in order to keep in shape, a little physical education:
- long jump distance (in some units).
Even the master of sports is not able to predict it :)
However, what are your hypotheses?
2) Continuous random variable - takes all numeric values from some finite or infinite range.
Note : abbreviations DSV and NSV are popular in educational literature
First, let's analyze a discrete random variable, then - continuous.
Distribution law of a discrete random variable
- this is conformity between the possible values of this quantity and their probabilities. Most often, the law is written in a table: 
The term is quite common row
distribution, but in some situations it sounds ambiguous, and therefore I will adhere to the "law".
And now very important point: since the random variable necessarily will accept one of the values, then the corresponding events form full group and the sum of the probabilities of their occurrence is equal to one:
or, if written folded:
So, for example, the law of the distribution of probabilities of points on a die has the following form: 
No comment.
You may be under the impression that a discrete random variable can only take on "good" integer values. Let's dispel the illusion - they can be anything:
Example 1
Some game has the following payoff distribution law: 
…probably you have been dreaming about such tasks for a long time :) Let me tell you a secret - me too. Especially after finishing work on field theory.
Solution: since a random variable can take only one of three values, the corresponding events form full group, which means that the sum of their probabilities is equal to one: ![]()
We expose the "partisan": ![]()
– thus, the probability of winning conventional units is 0.4.
Control: what you need to make sure.
Answer:
It is not uncommon when the distribution law needs to be compiled independently. For this use classical definition of probability, multiplication / addition theorems for event probabilities and other chips tervera:
Example 2
There are 50 lottery tickets in the box, 12 of which are winning, and 2 of them win 1000 rubles each, and the rest - 100 rubles each. Draw up a law of distribution of a random variable - the size of the winnings, if one ticket is randomly drawn from the box.
Solution: as you noticed, it is customary to place the values of a random variable in ascending order. Therefore, we start with the smallest winnings, and namely rubles.
In total, there are 50 - 12 = 38 such tickets, and according to classical definition:
is the probability that a randomly drawn ticket will not win.
The rest of the cases are simple. The probability of winning rubles is:
Checking: - and this is a particularly pleasant moment of such tasks!
Answer: the required payoff distribution law: ![]()
The following task for an independent decision:
Example 3
The probability that the shooter will hit the target is . Make a distribution law for a random variable - the number of hits after 2 shots.
... I knew that you missed him :) We remember multiplication and addition theorems. Solution and answer at the end of the lesson.
The distribution law completely describes a random variable, but in practice it is useful (and sometimes more useful) to know only some of it. numerical characteristics .
Mathematical expectation of a discrete random variable
In simple terms, this average expected value with repeated testing. Let a random variable take values with probabilities ![]() respectively. Then the mathematical expectation of this random variable is equal to sum of products all its values by the corresponding probabilities:
respectively. Then the mathematical expectation of this random variable is equal to sum of products all its values by the corresponding probabilities:
or in folded form: ![]()
Let's calculate, for example, the mathematical expectation of a random variable - the number of points dropped on a dice:
Now let's recall our hypothetical game: 
The question arises: is it even profitable to play this game? ... who has any impressions? So you can’t say “offhand”! But this question can be easily answered by calculating the mathematical expectation, in essence - weighted average probabilities of winning:
Thus, the mathematical expectation of this game losing.
Don't trust impressions - trust numbers!
Yes, here you can win 10 or even 20-30 times in a row, but in the long run we will inevitably be ruined. And I would not advise you to play such games :) Well, maybe only for fun.
From all of the above, it follows that the mathematical expectation is NOT a RANDOM value.
Creative task for independent research:
Example 4
Mr X plays European roulette according to the following system: he constantly bets 100 rubles on red. Compose the law of distribution of a random variable - its payoff. Calculate the mathematical expectation of winnings and round it up to kopecks. How average does the player lose for every hundred bet?
Reference : European roulette contains 18 red, 18 black and 1 green sector ("zero"). In the event of a “red” falling out, the player is paid a double bet, otherwise it goes to the casino’s income
There are many other roulette systems for which you can create your own probability tables. But this is the case when we do not need any distribution laws and tables, because it is established for certain that the mathematical expectation of the player will be exactly the same. Only changes from system to system




