Lesson content

Adding fractions with the same denominators

Adding fractions is of two types:

1. Adding fractions with the same denominators
2. Adding fractions with different denominators

Let's start with adding fractions with the same denominators. Everything is simple here. To add fractions with the same denominators, you need to add their numerators, and leave the denominator unchanged. For example, let's add the fractions and . We add the numerators, and leave the denominator unchanged:

This example can be easily understood if we think of a pizza that is divided into four parts. If you add pizza to pizza, you get pizza:

Example 2 Add fractions and .

The answer is an improper fraction. If the end of the task comes, then it is customary to get rid of improper fractions. To get rid of improper fraction, you need to select the whole part in it. In our case whole part stands out easily - two divided by two is equal to one:

This example can be easily understood if we think of a pizza that is divided into two parts. If you add more pizzas to the pizza, you get one whole pizza:

Example 3. Add fractions and .

Again, add the numerators, and leave the denominator unchanged:

This example can be easily understood if we think of a pizza that is divided into three parts. If you add more pizzas to pizza, you get pizzas:

Example 4 Find the value of an expression

This example is solved in exactly the same way as the previous ones. The numerators must be added and the denominator left unchanged:

Let's try to depict our solution using a picture. If you add pizzas to a pizza and add more pizzas, you get 1 whole pizza and more pizzas.

As you can see, adding fractions with the same denominators is not difficult. It is enough to understand the following rules:

1. To add fractions with the same denominator, you need to add their numerators, and leave the denominator unchanged;

Adding fractions with different denominators

Now we will learn how to add fractions with different denominators. When adding fractions, the denominators of those fractions must be the same. But they are not always the same.

For example, fractions can be added because they have the same denominators.

But fractions cannot be added immediately, because these fractions have different denominators. In such cases, fractions must be reduced to the same (common) denominator.

There are several ways to reduce fractions to the same denominator. Today we will consider only one of them, since the rest of the methods may seem complicated for a beginner.

The essence of this method lies in the fact that first (LCM) of the denominators of both fractions is sought. Then the LCM is divided by the denominator of the first fraction and the first additional factor is obtained. They do the same with the second fraction - the LCM is divided by the denominator of the second fraction and the second additional factor is obtained.

Then the numerators and denominators of the fractions are multiplied by their additional factors. As a result of these actions, fractions that had different denominators turn into fractions that have the same denominators. And we already know how to add such fractions.

Example 1. Add fractions and

First of all, we find the least common multiple of the denominators of both fractions. The denominator of the first fraction is the number 3, and the denominator of the second fraction is the number 2. The least common multiple of these numbers is 6

LCM (2 and 3) = 6

Now back to fractions and . First, we divide the LCM by the denominator of the first fraction and get the first additional factor. LCM is the number 6, and the denominator of the first fraction is the number 3. Divide 6 by 3, we get 2.

The resulting number 2 is the first additional factor. We write it down to the first fraction. To do this, we make a small oblique line above the fraction and write down the found additional factor above it:

We do the same with the second fraction. We divide the LCM by the denominator of the second fraction and get the second additional factor. LCM is the number 6, and the denominator of the second fraction is the number 2. Divide 6 by 2, we get 3.

The resulting number 3 is the second additional factor. We write it to the second fraction. Again, we make a small oblique line above the second fraction and write the found additional factor above it:

Now we are all set to add. It remains to multiply the numerators and denominators of fractions by their additional factors:

Look closely at what we have come to. We came to the conclusion that fractions that had different denominators turned into fractions that had the same denominators. And we already know how to add such fractions. Let's complete this example to the end:

Thus the example ends. To add it turns out.

Let's try to depict our solution using a picture. If you add pizzas to a pizza, you get one whole pizza and another sixth of a pizza:

Reduction of fractions to the same (common) denominator can also be depicted using a picture. Bringing the fractions and to a common denominator, we get the fractions and . These two fractions will be represented by the same slices of pizzas. The only difference will be that this time they will be divided into equal shares (reduced to the same denominator).

The first drawing shows a fraction (four pieces out of six) and the second picture shows a fraction (three pieces out of six). Putting these pieces together we get (seven pieces out of six). This fraction is incorrect, so we have highlighted the integer part in it. The result was (one whole pizza and another sixth pizza).

Note that we have painted this example in too much detail. AT educational institutions it is not customary to write in such a detailed manner. You need to be able to quickly find the LCM of both denominators and additional factors to them, as well as quickly multiply the additional factors found by your numerators and denominators. While at school, we would have to write this example as follows:

But there is also the other side of the coin. If detailed notes are not made at the first stages of studying mathematics, then questions of the kind “Where does that number come from?”, “Why do fractions suddenly turn into completely different fractions? «.

To make it easier to add fractions with different denominators, you can use the following step-by-step instructions:

1. Find the LCM of the denominators of fractions;
2. Divide the LCM by the denominator of each fraction and get an additional multiplier for each fraction;
3. Multiply the numerators and denominators of fractions by their additional factors;
4. Add fractions that have the same denominators;
5. If the answer turned out to be an improper fraction, then select its whole part;

Example 2 Find the value of an expression .

Let's use the instructions above.

Step 1. Find the LCM of the denominators of fractions

Find the LCM of the denominators of both fractions. The denominators of the fractions are the numbers 2, 3 and 4

Step 2. Divide the LCM by the denominator of each fraction and get an additional multiplier for each fraction

Divide the LCM by the denominator of the first fraction. LCM is the number 12, and the denominator of the first fraction is the number 2. Divide 12 by 2, we get 6. We got the first additional factor 6. We write it over the first fraction:

Now we divide the LCM by the denominator of the second fraction. LCM is the number 12, and the denominator of the second fraction is the number 3. Divide 12 by 3, we get 4. We got the second additional factor 4. We write it over the second fraction:

Now we divide the LCM by the denominator of the third fraction. LCM is the number 12, and the denominator of the third fraction is the number 4. Divide 12 by 4, we get 3. We got the third additional factor 3. We write it over the third fraction:

Step 3. Multiply the numerators and denominators of fractions by your additional factors

We multiply the numerators and denominators by our additional factors:

Step 4. Add fractions that have the same denominators

We came to the conclusion that fractions that had different denominators turned into fractions that have the same (common) denominators. It remains to add these fractions. Add up:

The addition didn't fit on one line, so we moved the remaining expression to the next line. This is allowed in mathematics. When an expression does not fit on one line, it is carried over to the next line, and it is necessary to put an equal sign (=) at the end of the first line and at the beginning of a new line. The equal sign on the second line indicates that this is a continuation of the expression that was on the first line.

Step 5. If the answer turned out to be an improper fraction, then select the whole part in it

Our answer is an improper fraction. We must single out the whole part of it. We highlight:

Got an answer

Subtraction of fractions with the same denominators

There are two types of fraction subtraction:

1. Subtraction of fractions with the same denominators
2. Subtraction of fractions with different denominators

First, let's learn how to subtract fractions with the same denominators. Everything is simple here. To subtract another from one fraction, you need to subtract the numerator of the second fraction from the numerator of the first fraction, and leave the denominator the same.

For example, let's find the value of the expression . To solve this example, it is necessary to subtract the numerator of the second fraction from the numerator of the first fraction, and leave the denominator unchanged. Let's do this:

This example can be easily understood if we think of a pizza that is divided into four parts. If you cut pizzas from a pizza, you get pizzas:

Example 2 Find the value of the expression .

Again, from the numerator of the first fraction, subtract the numerator of the second fraction, and leave the denominator unchanged:

This example can be easily understood if we think of a pizza that is divided into three parts. If you cut pizzas from a pizza, you get pizzas:

Example 3 Find the value of an expression

This example is solved in exactly the same way as the previous ones. From the numerator of the first fraction, you need to subtract the numerators of the remaining fractions:

As you can see, there is nothing complicated in subtracting fractions with the same denominators. It is enough to understand the following rules:

1. To subtract another from one fraction, you need to subtract the numerator of the second fraction from the numerator of the first fraction, and leave the denominator unchanged;
2. If the answer turned out to be an improper fraction, then you need to select the whole part in it.

Subtraction of fractions with different denominators

For example, a fraction can be subtracted from a fraction, since these fractions have the same denominators. But a fraction cannot be subtracted from a fraction, because these fractions have different denominators. In such cases, fractions must be reduced to the same (common) denominator.

The common denominator is found according to the same principle that we used when adding fractions with different denominators. First of all, find the LCM of the denominators of both fractions. Then the LCM is divided by the denominator of the first fraction and the first additional factor is obtained, which is written over the first fraction. Similarly, the LCM is divided by the denominator of the second fraction and a second additional factor is obtained, which is written over the second fraction.

The fractions are then multiplied by their additional factors. As a result of these operations, fractions that had different denominators turn into fractions that have the same denominators. And we already know how to subtract such fractions.

Example 1 Find the value of an expression:

These fractions have different denominators, so you need to bring them to the same (common) denominator.

First, we find the LCM of the denominators of both fractions. The denominator of the first fraction is the number 3, and the denominator of the second fraction is the number 4. The least common multiple of these numbers is 12

LCM (3 and 4) = 12

Now back to fractions and

Let's find an additional factor for the first fraction. To do this, we divide the LCM by the denominator of the first fraction. LCM is the number 12, and the denominator of the first fraction is the number 3. Divide 12 by 3, we get 4. We write the four over the first fraction:

We do the same with the second fraction. We divide the LCM by the denominator of the second fraction. LCM is the number 12, and the denominator of the second fraction is the number 4. Divide 12 by 4, we get 3. Write a triple over the second fraction:

Now we are all set for subtraction. It remains to multiply the fractions by their additional factors:

We came to the conclusion that fractions that had different denominators turned into fractions that had the same denominators. And we already know how to subtract such fractions. Let's complete this example to the end:

Got an answer

Let's try to depict our solution using a picture. If you cut pizzas from a pizza, you get pizzas.

This is the detailed version of the solution. Being at school, we would have to solve this example in a shorter way. Such a solution would look like this:

Reduction of fractions and to a common denominator can also be depicted using a picture. Bringing these fractions to a common denominator, we get the fractions and . These fractions will be represented by the same pizza slices, but this time they will be divided into the same fractions (reduced to the same denominator):

The first drawing shows a fraction (eight pieces out of twelve), and the second picture shows a fraction (three pieces out of twelve). By cutting off three pieces from eight pieces, we get five pieces out of twelve. The fraction describes these five pieces.

Example 2 Find the value of an expression

These fractions have different denominators, so you first need to bring them to the same (common) denominator.

Find the LCM of the denominators of these fractions.

The denominators of the fractions are the numbers 10, 3 and 5. The least common multiple of these numbers is 30

LCM(10, 3, 5) = 30

Now we find additional factors for each fraction. To do this, we divide the LCM by the denominator of each fraction.

Let's find an additional factor for the first fraction. LCM is the number 30, and the denominator of the first fraction is the number 10. Divide 30 by 10, we get the first additional factor 3. We write it over the first fraction:

Now we find an additional factor for the second fraction. Divide the LCM by the denominator of the second fraction. LCM is the number 30, and the denominator of the second fraction is the number 3. Divide 30 by 3, we get the second additional factor 10. We write it over the second fraction:

Now we find an additional factor for the third fraction. Divide the LCM by the denominator of the third fraction. LCM is the number 30, and the denominator of the third fraction is the number 5. Divide 30 by 5, we get the third additional factor 6. We write it over the third fraction:

Now everything is ready for subtraction. It remains to multiply the fractions by their additional factors:

We came to the conclusion that fractions that had different denominators turned into fractions that have the same (common) denominators. And we already know how to subtract such fractions. Let's finish this example.

The continuation of the example will not fit on one line, so we move the continuation to the next line. Don't forget about the equal sign (=) on the new line:

The answer turned out to be a correct fraction, and everything seems to suit us, but it is too cumbersome and ugly. We should make it easier. What can be done? You can reduce this fraction.

To reduce a fraction, you need to divide its numerator and denominator by (gcd) the numbers 20 and 30.

So, we find the GCD of the numbers 20 and 30:

Now we return to our example and divide the numerator and denominator of the fraction by the found GCD, that is, by 10

Got an answer

Multiplying a fraction by a number

To multiply a fraction by a number, you need to multiply the numerator of the given fraction by this number, and leave the denominator the same.

Example 1. Multiply the fraction by the number 1.

Multiply the numerator of the fraction by the number 1

The entry can be understood as taking half 1 time. For example, if you take pizza 1 time, you get pizza

From the laws of multiplication, we know that if the multiplicand and the multiplier are interchanged, then the product will not change. If the expression is written as , then the product will still be equal to . Again, the rule for multiplying an integer and a fraction works:

This entry can be understood as taking half of the unit. For example, if there is 1 whole pizza and we take half of it, then we will have pizza:

Example 2. Find the value of an expression

Multiply the numerator of the fraction by 4

The answer is an improper fraction. Let's take a whole part of it:

The expression can be understood as taking two quarters 4 times. For example, if you take pizzas 4 times, you get two whole pizzas.

And if we swap the multiplicand and the multiplier in places, we get the expression. It will also be equal to 2. This expression can be understood as taking two pizzas from four whole pizzas:

Multiplication of fractions

To multiply fractions, you need to multiply their numerators and denominators. If the answer is an improper fraction, you need to select the whole part in it.

Example 1 Find the value of the expression .

Got an answer. It is desirable to reduce this fraction. The fraction can be reduced by 2. Then the final solution will take the following form:

The expression can be understood as taking a pizza from half a pizza. Let's say we have half a pizza:

How to take two-thirds from this half? First you need to divide this half into three equal parts:

And take two from these three pieces:

We'll get pizza. Remember what a pizza looks like divided into three parts:

One slice from this pizza and the two slices we took will have the same dimensions:

In other words, we are talking about the same pizza size. Therefore, the value of the expression is

Example 2. Find the value of an expression

Multiply the numerator of the first fraction by the numerator of the second fraction, and the denominator of the first fraction by the denominator of the second fraction:

The answer is an improper fraction. Let's take a whole part of it:

Example 3 Find the value of an expression

Multiply the numerator of the first fraction by the numerator of the second fraction, and the denominator of the first fraction by the denominator of the second fraction:

The answer turned out to be a correct fraction, but it will be good if it is reduced. To reduce this fraction, you need to divide the numerator and denominator of this fraction by the largest common divisor(gcd) numbers 105 and 450.

So, let's find the GCD of the numbers 105 and 450:

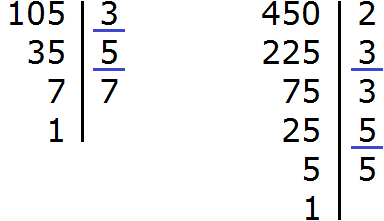
Now we divide the numerator and denominator of our answer to the GCD that we have now found, that is, by 15

Representing an integer as a fraction

Any whole number can be represented as a fraction. For example, the number 5 can be represented as . From this, the five will not change its meaning, since the expression means “the number five divided by one”, and this, as you know, is equal to five:

Reverse numbers

Now we will get acquainted with interesting topic in mathematics. It's called "reverse numbers".

Definition. Reverse to numbera is the number that, when multiplied bya gives a unit.

Let's substitute in this definition instead of a variable a number 5 and try to read the definition:

Reverse to number 5 is the number that, when multiplied by 5 gives a unit.

Is it possible to find a number that, when multiplied by 5, gives one? It turns out you can. Let's represent five as a fraction:

Then multiply this fraction by itself, just swap the numerator and denominator. In other words, let's multiply the fraction by itself, only inverted:

What will be the result of this? If we continue to solve this example, we get one:

This means that the inverse of the number 5 is the number, since when 5 is multiplied by one, one is obtained.

The reciprocal can also be found for any other integer.

You can also find the reciprocal for any other fraction. To do this, it is enough to turn it over.

Division of a fraction by a number

Let's say we have half a pizza:

Let's divide it equally between two. How many pizzas will each get?

It can be seen that after splitting half of the pizza, two equal pieces were obtained, each of which makes up a pizza. So everyone gets a pizza.

Division of fractions is done using reciprocals. Reciprocals allow you to replace division with multiplication.

To divide a fraction by a number, you need to multiply this fraction by the reciprocal of the divisor.

Using this rule, we will write down the division of our half of the pizza into two parts.

So, you need to divide the fraction by the number 2. Here the dividend is a fraction and the divisor is 2.

To divide a fraction by the number 2, you need to multiply this fraction by the reciprocal of the divisor 2. The reciprocal of the divisor 2 is a fraction. So you need to multiply by

The numerator, and that by which it is divided is the denominator.

To write a fraction, first write its numerator, then draw a horizontal line under this number, and write the denominator under the line. The horizontal line separating the numerator and denominator is called a fractional bar. Sometimes it is depicted as an oblique "/" or "∕". In this case, the numerator is written to the left of the line, and the denominator to the right. So, for example, the fraction "two-thirds" will be written as 2/3. For clarity, the numerator is usually written at the top of the line, and the denominator at the bottom, that is, instead of 2/3, you can find: ⅔.

To calculate the product of fractions, first multiply the numerator of one fractions to another numerator. Write the result to the numerator of the new fractions. Then multiply the denominators as well. Specify the final value in the new fractions. For example, 1/3? 1/5 = 1/15 (1 × 1 = 1; 3 × 5 = 15).

To divide one fraction by another, first multiply the numerator of the first by the denominator of the second. Do the same with the second fraction (divisor). Or, before performing all the steps, first “flip” the divisor, if it’s more convenient for you: the denominator should be in place of the numerator. Then multiply the denominator of the dividend by the new denominator of the divisor and multiply the numerators. For example, 1/3: 1/5 = 5/3 = 1 2/3 (1 × 5 = 5; 3 × 1 = 3).

Sources:

• Basic tasks for fractions

Fractional numbers allow you to express the exact value of a quantity in different ways. With fractions, you can perform the same mathematical operations as with integers: subtraction, addition, multiplication, and division. To learn how to decide fractions, it is necessary to remember some of their features. They depend on the type fractions, the presence of an integer part, a common denominator. Some arithmetic operations after execution require reduction of the fractional part of the result.

You will need

• - calculator

Instruction

Look carefully at the numbers. If there are decimals and irregulars among the fractions, it is sometimes more convenient to first perform actions with decimals, and then convert them to the wrong form. Can you translate fractions in this form initially, writing the value after the decimal point in the numerator and putting 10 in the denominator. If necessary, reduce the fraction by dividing the numbers above and below by one divisor. Fractions in which the whole part stands out, lead to the wrong form by multiplying it by the denominator and adding the numerator to the result. This value will become the new numerator fractions. To extract the whole part from the initially incorrect fractions, divide the numerator by the denominator. Write the whole result from fractions. And the remainder of the division becomes the new numerator, the denominator fractions while not changing. For fractions with an integer part, it is possible to perform actions separately, first for the integer and then for the fractional parts. For example, the sum of 1 2/3 and 2 ¾ can be calculated:
- Converting fractions to the wrong form:
- 1 2/3 + 2 ¾ = 5/3 + 11/4 = 20/12 + 33/12 = 53/12 = 4 5/12;
- Summation separately of integer and fractional parts of terms:
- 1 2/3 + 2 ¾ = (1+2) + (2/3 + ¾) = 3 + (8/12 + 9/12) = 3 + 17/12 = 3 + 1 5/12 = 4 5 /12.

Rewrite them through the separator ":" and continue the usual division.

To get the final result, reduce the resulting fraction by dividing the numerator and denominator by one whole number, the largest possible in this case. In this case, there must be integer numbers above and below the line.

note

Don't do arithmetic with fractions that have different denominators. Choose a number such that when the numerator and denominator of each fraction are multiplied by it, as a result, the denominators of both fractions are equal.

Useful advice

When recording fractional numbers the dividend is written above the line. This quantity is referred to as the numerator of a fraction. Under the line, the divisor, or denominator, of the fraction is written. For example, one and a half kilograms of rice in the form of a fraction will be written as follows: 1 ½ kg of rice. If the denominator of a fraction is 10, it is called a decimal fraction. In this case, the numerator (dividend) is written to the right of the whole part separated by a comma: 1.5 kg of rice. For the convenience of calculations, such a fraction can always be written in the wrong form: 1 2/10 kg of potatoes. To simplify, you can reduce the numerator and denominator values ​​by dividing them by a single whole number. In this example, dividing by 2 is possible. The result is 1 1/5 kg of potatoes. Make sure that the numbers you are going to do arithmetic with are in the same form.

Instruction

It is customary to separate ordinary and decimal fractions, acquaintance with which begins in high school. At present, there is no such field of knowledge where this would not be applied. Even in we are talking about the first 17th century, and all at once, which means 1600-1625. You also often have to deal with elementary operations on , as well as their transformation from one form to another.

Reducing fractions to a common denominator is perhaps the most important operation on. It is the basis of all calculations. So let's say there are two fractions a/b and c/d. Then, in order to bring them to a common denominator, you need to find the least common multiple (M) of the numbers b and d, and then multiply the numerator of the first fractions on (M/b), and the second numerator on (M/d).

Comparing fractions is another important task. To do this, give the given simple fractions to a common denominator and then compare the numerators, whose numerator is greater, that fraction is greater.

In order to perform the addition or subtraction of ordinary fractions, you need to bring them to a common denominator, and then perform the necessary mathematical operation from these fractions. The denominator remains unchanged. Suppose you need to subtract c/d from a/b. To do this, you need to find the least common multiple M of the numbers b and d, and then subtract the other from one numerator without changing the denominator: (a*(M/b)-(c*(M/d))/M

It is enough just to multiply one fraction by another, for this you just need to multiply their numerators and denominators:
(a / b) * (c / d) \u003d (a * c) / (b * d) To divide one fraction by another, you need to multiply the dividend fraction by the reciprocal of the divisor. (a/b)/(c/d)=(a*d)/(b*c)
It is worth recalling that in order to get a reciprocal, you need to swap the numerator and denominator.

In mathematics different types numbers have been studied since its inception. There are a large number of sets and subsets of numbers. Among them are integers, rational, irrational, natural, even, odd, complex and fractional. Today we will analyze information about the last set - fractional numbers.

Definition of fractions

Fractions are numbers consisting of a whole part and fractions of a unit. Just like integers, there are an infinite number of fractional numbers between two integers. In mathematics, operations with fractions are performed, since with integers and natural numbers. It is quite simple and can be learned in a couple of lessons.

The article presents two types

Common fractions

Ordinary fractions are the integer part a and two numbers written through the fractional bar b/c. Common fractions can be extremely handy if the fractional part cannot be represented in rational decimal form. In addition, it is more convenient to perform arithmetic operations through a fractional line. The top part is called the numerator, the bottom part is the denominator.

Actions with ordinary fractions: examples

Basic property of a fraction. At multiplying the numerator and denominator by the same number that is not zero, the result is a number equal to the given one. This property of a fraction helps to bring a denominator for addition (this will be discussed below) or reduce a fraction, making it more convenient for counting. a/b = a*c/b*c. For example, 36/24 = 6/4 or 9/13 = 18/26

Reduction to a common denominator. To bring the denominator of a fraction, you need to represent the denominator in the form of factors, and then multiply by the missing numbers. For example, 7/15 and 12/30; 7/5*3 and 12/5*3*2. We see that the denominators differ by two, so we multiply the numerator and denominator of the first fraction by 2. We get: 14/30 and 12/30.

Compound fractions- ordinary fractions with a highlighted integer part. (A b/c) To represent a compound fraction as a common fraction, multiply the number in front of the fraction by the denominator and then add it to the numerator: (A*c + b)/c.

Arithmetic operations with fractions

It will not be superfluous to consider the well-known arithmetic operations only when working with fractional numbers.

Addition and subtraction. Adding and subtracting fractions is just as easy as whole numbers, with the exception of one difficulty - the presence of a fractional bar. When adding fractions with the same denominator, it is necessary to add only the numerators of both fractions, the denominators remain unchanged. For example: 5/7 + 1/7 = (5+1)/7 = 6/7

If the denominators of two fractions are different numbers, you first need to bring them to a common one (as discussed above). 1/8 + 3/2 = 1/2*2*2 + 3/2 = 1/8 + 3*4/2*4 = 1/8 + 12/8 = 13/8. Subtraction occurs according to exactly the same principle: 8/9 - 2/3 \u003d 8/9 - 6/9 \u003d 2/9.

Multiplication and division. Actions with fractions by multiplication occur according to the following principle: numerators and denominators are multiplied separately. AT general view the multiplication formula looks like this: a/b *c/d = a*c/b*d. In addition, as you multiply, you can reduce the fraction by eliminating the same factors from the numerator and denominator. In another language, the numerator and denominator are divisible by the same number: 4/16 = 4/4*4 = 1/4.

To divide one ordinary fraction by another, you need to change the numerator and denominator of the divisor and perform the multiplication of two fractions, according to the principle discussed earlier: 5/11: 25/11 = 5/11 * 11/25 = 5*11/11*25 = 1/5

Decimals

Decimals are the more popular and commonly used version of fractional numbers. They are easier to write down in a line or present on a computer. The structure of the decimal fraction is as follows: first the whole number is written, and then, after the decimal point, the fractional part is written. At their core, decimal fractions are compound fractions, but their fractional part is represented by a number divided by a multiple of 10. Hence their name. Operations with decimal fractions are similar to operations with integers, since they are also written in the decimal number system. Also, unlike ordinary fractions, decimals can be irrational. This means that they can be infinite. They are written as 7,(3). The following entry is read: seven whole, three tenths in the period.

Basic operations with decimal numbers

Addition and subtraction of decimal fractions. Performing actions with fractions is no more difficult than with whole natural numbers. The rules are exactly the same as those used when adding or subtracting natural numbers. They can also be considered a column in the same way, but if necessary, replace the missing places with zeros. For example: 5.5697 - 1.12. In order to perform a column subtraction, you need to equalize the number of numbers after the decimal point: (5.5697 - 1.1200). So, the numerical value will not change and can be counted in a column.

Actions with decimals cannot be produced if one of them has an irrational form. To do this, you need to convert both numbers to ordinary fractions, and then use the techniques described earlier.

Multiplication and division. Multiplying decimals is similar to multiplying natural numbers. They can also be multiplied by a column, simply ignoring the comma, and then separated by a comma in the final value the same number of digits as the sum after the decimal point was in two decimal fractions. For example, 1.5 * 2.23 = 3.345. Everything is very simple, and should not cause difficulties if you have already mastered the multiplication of natural numbers.

Division also coincides with the division of natural numbers, but with a slight digression. To split into decimal number column, you must discard the comma in the divisor, and multiply the dividend by the number of digits after the decimal point in the divisor. Then perform division as with natural numbers. With incomplete division, you can add zeros to the dividend on the right, also adding a zero after the decimal point.

Examples of actions with decimal fractions. Decimals are a very handy tool for arithmetic counting. They combine the convenience of natural, whole numbers and the precision of common fractions. In addition, it is quite simple to convert one fraction to another. Operations with fractions are no different from operations with natural numbers.

1. Addition: 1.5 + 2.7 = 4.2
2. Subtraction: 3.1 - 1.6 = 1.5
3. Multiplication: 1.7 * 2.3 = 3.91
4. Division: 3.6: 0.6 = 6

In addition, decimals are suitable for representing percentages. So, 100% = 1; 60% = 0.6; and vice versa: 0.659 = 65.9%.

That's all you need to know about fractions. The article considered two types of fractions - ordinary and decimal. Both are quite easy to calculate, and if you have a complete mastery of natural numbers and operations with them, you can safely start learning fractional ones.

To express a part as a fraction of the whole, you need to divide the part by the whole.

Task 1. There are 30 students in the class, four are missing. What proportion of students are missing?

Solution:

Answer: there are no students in the class.

Finding a fraction from a number

To solve problems in which it is required to find a part of a whole, the following rule is true:

If a part of the whole is expressed as a fraction, then to find this part, you can divide the whole by the denominator of the fraction and multiply the result by its numerator.

Task 1. There were 600 rubles, this amount was spent. How much money have you spent?

Solution: to find from 600 rubles, you need to divide this amount into 4 parts, thereby we will find out how much money is one fourth:

600: 4 = 150 (p.)

Answer: spent 150 rubles.

Task 2. It was 1000 rubles, this amount was spent. How much money has been spent?

Solution: From the condition of the problem, we know that 1000 rubles consists of five equal parts. First we find how many rubles are one fifth of 1000, and then we find out how many rubles are two fifths:

1) 1000: 5 = 200 (p.) - one fifth.

2) 200 2 \u003d 400 (p.) - two fifths.

These two actions can be combined: 1000: 5 2 = 400 (p.).

Answer: 400 rubles were spent.

The second way to find a part of a whole:

To find a part of a whole, you can multiply the whole by a fraction expressing that part of the whole.

Task 3. According to the charter of the cooperative, for the validity of the reporting meeting, it must be attended by at least members of the organization. The cooperative has 120 members. With what composition can the reporting meeting be held?

Solution:

Answer: the reporting meeting can be held if there are 80 members of the organization.

Finding a number by its fraction

To solve problems in which it is required to find the whole by its part, the following rule is true:

If a part of the desired integer is expressed as a fraction, then to find this integer, you can divide this part by the numerator of the fraction and multiply the result by its denominator.

Task 1. We spent 50 rubles, this amounted to the original amount. Find the original amount of money.

Solution: from the description of the problem, we see that 50 rubles is 6 times less than the initial amount, i.e., the initial amount is 6 times more than 50 rubles. To find this amount, you need to multiply 50 by 6:

50 6 = 300 (r.)

Answer: the initial amount is 300 rubles.

Task 2. We spent 600 rubles, this amounted to the initial amount of money. Find the original amount.

Solution: we will assume that the desired number consists of three thirds. By condition, two-thirds of the number are equal to 600 rubles. First, we find one third of the initial amount, and then how many rubles are three-thirds (initial amount):

1) 600: 2 3 = 900 (p.)

Answer: the initial amount is 900 rubles.

The second way to find the whole by its part:

To find a whole by the value of its part, you can divide this value by a fraction that expresses this part.

Task 3. Line segment AB, equal to 42 cm, is the length of the segment CD. Find the length of a segment CD.

Solution:

Answer: segment length CD 70 cm

Task 4. Watermelons were brought to the store. Before lunch, the store sold, after lunch - brought watermelons, and it remains to sell 80 watermelons. How many watermelons were brought to the store in total?

Solution: first, we find out what part of the imported watermelons is the number 80. To do this, we take the total number of imported watermelons as a unit and subtract from it the number of watermelons that we managed to sell (sell):

And so, we learned that 80 watermelons is from total imported watermelons. Now we will find out how many watermelons of the total amount is, and then how many watermelons are (the number of watermelons brought):

2) 80: 4 15 = 300 (watermelons)

Answer: in total, 300 watermelons were brought to the store.