Інструкція

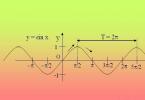
Найменший позитивний періодкосинуса теж дорівнює 2?. Розгляньте доказ цього на прикладі функції y=cos(x). Якщо T буде довільним періодом косинуса, то cos(a+T)=cos(a). Якщо a=0, cos(T)=cos(0)=1. Зважаючи на це, найменшим позитивним значенням T, при якому cos(x)=1, є 2?.

З огляду на той факт, що 2? - періодсинуса та косинуса, це ж буде і періодом котангенсу, а також тангенсу, однак не мінімальним, оскільки, як , найменший позитивний періодтангенсу і котангенсу дорівнює? Переконатися в цьому зможете, розглянувши наступний: точки, що відповідають (х) і (х +?) на тригонометричному колі, мають діаметрально протилежне розташування. Відстань від точки (х) до точки (х+2?) відповідає половині кола. За визначенням тангенсу та котангенсу tg(x+?)=tgx, а ctg(x+?)=ctgx, а значить, найменший позитивний періодкотангенсу та ?.

Зверніть увагу

Не плутайте функції y=cos(x) та y=sin(x) - маючи однаковий період, ці функції зображуються по-різному.

Корисна порада

Для більшої наочності зобразіть тригонометричну функцію, яка розраховує найменший позитивний період.

Джерела:

• Довідник з математики, шкільна математика, вища математика

Тригонометричні функції періодичні, тобто повторюються через певний період. Завдяки цьому достатньо дослідити функцію на цьому проміжку та поширити знайдені властивості на всі інші періоди.

Інструкція

Щоб знайти період тригонометричної функції, зведеної в ступінь, оцініть парність ступеня. Для зменшення стандартного періоду в два рази. Наприклад, якщо вам дана функція у = 3 cos ^ 2х, то стандартний період 2П зменшиться в 2 рази, таким чином, період дорівнюватиме П. Зверніть , функції tg, ctg в будь-якій мірі періодичні П.

По шкільних уроках математики кожен пам'ятає графік синуса, рівномірними хвилями вдалину. Аналогічну властивість - повторюватися через певний проміжок - мають і багато інших функцій. Вони називаються періодичними. Періодичність - дуже важлива властивість функції, що часто зустрічається у різних завданнях. Тому корисно вміти визначати, чи функція є періодичною.

Інструкція

Якщо F(x) - функція аргументу x, вона називається періодичною, якщо є таке число T, що з будь-якого x F(x + T) = F(x). Це число T називається періодом функції.

Періодів може бути кілька. Наприклад, функція F = const для будь-яких значень аргументу приймає одне й те саме значення, тому будь-яке число може вважатися її періодом.

Зазвичай математика цікавить найменший не рівний нулю період функції. Його для стислості і називають просто періодом.

Класичний приклад періодичних функцій – тригонометричні: синус, косинус та тангенс. Їх період однаковий і дорівнює 2?, тобто sin(x) = sin(x + 2?) = sin(x + 4?) і таке інше. Однак, зрозуміло, тригонометричні функції – не єдині періодичні.

Щодо простих, базових функцій єдиний спосіб встановити їх періодичність чи неперіодичність – обчислення. Для складних функцій вже є кілька простих правил.

Якщо F(x) - періодична функція з періодом T, і для неї визначена похідна, то ця похідна f(x) = F?(x) - теж періодична функція з періодом T. Адже значення похідної в точці x дорівнює тангенсу кута нахилу дотичної графіка її первісної в цій точці до осі абсцис, а оскільки первісна періодично повторюється, то має повторюватися і похідна. Наприклад, похідна від функції sin(x) дорівнює cos(x) і вона періодична. Беручи похідну cos(x), ви отримаєте –sin(x). Періодичність зберігається постійно.

Однак протилежне не завжди вірне. Так, функція f(x) = const періодична, та її первісна F(x) = const*x + C - немає.

Якщо F(x) - періодична функція з періодом T, то G(x) = a*F(kx + b), де a, b, і k - константи і k не дорівнює нулю - теж періодична функція, і її період дорівнює T/k. Наприклад sin(2x) - періодична функція, та її період дорівнює?. Наочно це можна так: помножуючи x на якесь число, ви стискаєте графік функції по горизонталі саме в стільки разів

Якщо F1(x) і F2(x) - періодичні функції, та його періоди рівні T1 і T2 відповідно, то сума цих функцій також може бути періодичною. Однак її період не буде простою сумою періодів T1 та T2. Якщо результат розподілу T1/T2 - раціональне число, то сума функцій періодична, та її період дорівнює найменшому загальному кратному (НОК) періодів T1 і T2. Наприклад, якщо період першої функції дорівнює 12, а період другої - 15, то період їх суми дорівнюватиме НОК (12, 15) = 60.

Наочно це можна так: функції йдуть з різною «шириною кроку», але якщо відношення їх ширин раціонально, то рано чи пізно (а точніше, саме через НОК кроків), вони знову зрівняються, і їхня сума почне новий період.

Однак якщо співвідношення періодів ірраціональне, то сумарна функція не буде періодичною. Наприклад, нехай F1(x) = x mod 2 (залишок від поділу x на 2), а F2(x) = sin(x). T1 тут дорівнюватиме 2, а T2 дорівнює 2?. Співвідношення періодів дорівнює? - ірраціональному числу. Отже, функція sin(x) + x mod 2 не є періодичною.

Багато математичних функцій мають одну особливість, що полегшує їх побудову, - це періодичністьтобто повторюваність графіка на координатній сітці через рівні проміжки.

Інструкція

Найвідомішими періодичними функціями математики є синусоїда та косінусоїда. Ці функції мають хвилеподібний характер і основний період, що дорівнює 2П. Також окремим випадком періодичної функції є f(x)=const. На позицію х підходить будь-яке число, основного періоду дана функція немає, оскільки є пряму.

Взагалі функція є періодичною, якщо є таке ціле число N, яке на відміну від нуля і задовольняє правилу f(x)=f(x+N), таким чином забезпечуючи повторюваність. Період функції - і є найменше число N, але з нуль. Тобто, наприклад, функція sin x дорівнює функції sin (x+2ПN), де N=±1, ±2 тощо.

Іноді при функції може стояти множник (наприклад, sin 2x), який збільшить або скоротить період функції. Для того щоб знайти період по графіку, необхідно визначити екстремуми функції - найвищу та найнижчу точки графіка функції. Так як синусоїда та косінусоїда мають хвилеподібний характер, це досить легко зробити. Від даних точок побудуйте перпендикулярні прямі до перетину віссю Х.

Відстань від верхнього екстремуму до нижнього буде половиною періоду функції. Найзручніше обчислювати період від перетину графіка з віссю Y і, відповідно, нульової позначки по осі х. Після цього необхідно помножити отримане значення на два та отримати основний період функції.

Для простоти побудови графіків синусоїди і косінусоїди необхідно відзначити, що якщо при функції стоїть ціле число, то її період подовжиться (тобто 2П необхідно помножити на цей коефіцієнт) і графік буде виглядати м'якше, плавно-а якщо число дробове, навпаки, скоротиться і графік стане більш «гострим», стрибкоподібним на вигляд.

Мета: узагальнити та систематизувати знання учнів на тему “Періодичність функцій”; формувати навички застосування властивостей періодичної функції, знаходження найменшого позитивного періоду функції, побудови графіків періодичних функцій; сприяти підвищенню інтересу до вивчення математики; виховувати спостережливість, акуратність.

Обладнання: комп'ютер, мультимедійний проектор, картки із завданнями, слайди, годинники, таблиці орнаментів, елементи народного промислу

"Математика - це те, за допомогою чого люди керують природою і собою"
О.М. Колмогоров

Хід уроку

I. Організаційний етап.

Перевірка готовності учнів до уроку. Повідомлення теми та завдань уроку.

ІІ. Перевірка домашнього завдання.

Домашнє завдання перевіряємо на зразки, найбільш складні моменти обговорюємо.

ІІІ. Узагальнення та систематизація знань.

1. Усна фронтальна робота.

Запитання теорії.

1) Сформуйте визначення періоду функції
2) Назвіть найменший позитивний період функцій y=sin(x), y=cos(x)
3). Назвіть найменший позитивний період функції y=tg(x), y=ctg(x)
4) Доведіть за допомогою кола вірність співвідношень:

y=sin(x) = sin(x+360º)
y=cos(x) = cos(x+360º)
y=tg(x) = tg(x+18) 0º)
y=ctg(x) = ctg(x+180º)

tg(x+π n)=tgx, n € Z
ctg(x+π n)=ctgx, n € Z

sin(x+2π n)=sinx, n € Z
cos(x+2π n)=cosx, n € Z

5) Як побудувати графік періодичної функції?

Усні вправи.

1) Довести такі співвідношення

a) sin(740º ) = sin(20º )
b) cos(54º) = cos(-1026º)
c) sin(-1000º) = sin(80º )

2. Довести, що кут 540º є одним з періодів функції y=cos(2x)

3. Довести, що кут 360º є одним із періодів функції y=tg(x)

4. Дані вирази перетворити так, щоб кути, що входять до них, по абсолютній величині не перевищували 90º .

a) tg375º
b) ctg530º
c) sin1268º
d) cos(-7363º)

5. Де ви зустрічалися зі словами ПЕРІОД, ПЕРІОДІЧНІСТЬ?

Відповіді учнів: Період у музиці – побудова, у якому викладено більш менш завершена музична думка. Геологічний період – частина епохи і поділяється на епохи з періодом від 35 до 90 млн. років.

Період напіврозпаду радіоактивної речовини. Періодичний дріб. Періодична печатка – друковані видання, що з'являються у певні терміни. Періодична система Менделєєва.

6. На малюнках зображено частини графіків періодичних функцій. Визначте період функції. Визначити період функції.

Відповідь: Т=2; Т=2; Т=4; Т = 8.

7. Де в житті ви зустрічалися з побудовою елементів, що повторюються?

Відповідь учнів: Елементи орнаментів, народна творчість.

IV. Колективне розв'язання задач.

(Розв'язання задач на слайдах.)

Розглянемо один із способів дослідження функції на періодичність.

При цьому способі обходяться труднощі, пов'язані з доказом того, що той чи інший період є найменшим, а також відпадає необхідність торкатися питань про арифметичні дії над періодичними функціями та про періодичність складної функції. Міркування спирається лише визначення періодичної функції і такий факт: якщо Т – період функції, те й nT(n?0) – її період.

Завдання 1. Знайдіть найменший позитивний період функції f(x)=1+3(x+q>5)

Рішення: Припустимо, що Т-період цієї функції. Тоді f(x+T)=f(x) всім x € D(f), тобто.

1+3(x+T+0,25)=1+3(x+0,25)
(x+T+0,25)=(x+0.25)

Покладемо x=-0,25 отримаємо

(T) = 0<=>T = n, n € Z

Ми отримали, що всі періоди цієї функції (якщо вони існують) знаходяться серед цілих чисел. Виберемо серед цих чисел найменше додатне число. Це 1 . Перевіримо, чи не буде воно і справді періодом 1 .

f(x+1) =3(x+1+0,25)+1

Оскільки (T+1)=(T) за будь-якого Т, то f(x+1)=3((x+0.25)+1)+1=3(x+0,25)+1=f(x ), тобто. 1 – період f. Оскільки 1 – найменше з усіх позитивних чисел, то T=1.

Завдання 2. Показати, що функція f(x)=cos 2 (x) періодична і визначити її основний період.

Завдання 3. Знайдіть основний період функції

f(x)=sin(1,5x)+5cos(0,75x)

Допустимо Т-період функції, тоді для будь-якого хсправедливе співвідношення

sin1,5(x+T)+5cos0,75(x+T)=sin(1,5x)+5cos(0,75x)

Якщо х = 0, то

sin(1,5T)+5cos(0,75T)=sin0+5cos0

sin(1,5T)+5cos(0,75T)=5

Якщо х=-Т, то

sin0+5cos0=sin(-1,5Т)+5cos0,75(-Т)

5 = - sin (1,5 Т) + 5 cos (0,75 Т)

sin(1,5Т)+5cos(0,75Т)=5 – sin(1,5Т)+5cos(0,75Т)=5

Склавши, отримаємо:

10cos (0,75 Т) = 10

2π n, n € Z

Виберемо з усіх "підозрілих" на період чисел найменше позитивне і перевіримо, чи воно періодом для f. Це число

f(x+)=sin(1,5x+4π )+5cos(0,75x+2π )= sin(1,5x)+5cos(0,75x)=f(x)

Отже – основний період функції f.

Завдання 4. Перевіримо, чи є періодичною функція f(x)=sin(x)

Нехай Т - період функції f. Тоді для будь-якого х

sin|x+Т|=sin|x|

Якщо х=0, то sin|Т|=sin0, sin|Т|=0 Т=π n, n € Z.

Припустимо. Що за деякого n число π n є періодом

розглянутої функції π n>0. Тоді sin|π n+x|=sin|x|

Звідси випливає, що n має бути одночасно і парним і непарним числом, а це неможливо. Тому ця функція не є періодичною.

Завдання 5. Перевірити, чи є періодичною функцією

f(x)=

Нехай Т – період f, тоді

, Звідси sinT = 0, Т = π n, n € Z. Припустимо, що при деякому n число π n дійсно є періодом цієї функції. Тоді і число 2π n буде періодом

Оскільки чисельники рівні, то рівні та його знаменники, тому

Отже, функція f не періодична.

Робота у групах.

Завдання групи 1.

Завдання групи 2.

Перевірте, чи є функція f періодичною і знайдіть її основний період (якщо існує).

f(x)=cos(2x)+2sin(2x)

Завдання групи 3.

Після закінчення роботи гурту презентують свої рішення.

VI. Підбиття підсумків уроку.

Рефлексія.

Вчитель видає учням картки з малюнками і пропонує зафарбувати частину першого малюнка відповідно до того, в якому обсязі, як їм здається, вони оволоділи способами дослідження функції на періодичність, а в частині другого малюнка відповідно до свого внеску в роботу на уроці.

VII. Домашнє завдання

1). Перевірте, чи є функція f періодичною і знайдіть її основний період (якщо вона існує)

b). f(x)=x 2 -2x+4

c). f(x)=2tg(3x+5)

2). Функція y=f(x) має період Т=2 та f(x)=x 2 +2x при х € [-2; 0]. Знайдіть значення виразу -2f(-3)-4f(3,5)

Література/

1. Мордковіч А.Г.Алгебра та початку аналізу з поглибленим вивченням.
2. Математика. Підготовка до ЄДІ. За ред. Лисенка Ф.Ф., Кулабухова С.Ю.
3. Шереметьєва Т.Г. , Тарасова Є.А.Алгебра та початку аналізу для 10-11 класів.

По шкільних уроках математики кожен пам'ятає графік синуса, рівномірними хвилями вдалину. Аналогічним властивістю - повторюватися через певний інтервал - мають і інші функції. Вони називаються періодичними. Періодичність - дуже значуща якість функції, що часто зустрічається в різних завданнях. Отже благотворно вміти визначати, чи є функція періодичною.

Інструкція

1. Якщо F(x) - функція доводу x, вона називається періодичною, якщо є таке число T, що з кожного x F(x + T) = F(x). Це число T і називається періодом функції. Періодів може бути кілька. Скажімо, функція F = const для будь-яких значень аргументу приймає одне й те саме значення, а тому всяке число може вважатися її періодом. Традиційно математика хвилює мінімальний не рівний нулю період функції. Його для стислості і називають примітивним періодом.

2. Типовий приклад періодичних функцій – тригонометричні: синус, косинус та тангенс. Їх період ідентичний і дорівнює 2?, тобто sin (x) = sin (x + 2?) = sin (x + 4?) і так далі. Втім, зрозуміло, тригонометричні функції – не виняткові періодичні.

3. Щодо примітивних, базових функцій винятковий спосіб встановити їх періодичність чи непериодичность - обчислення. Для важких функцій вже є кілька примітивних правил.

4. Якщо F(x) - періодична функція з періодом T, і для неї визначена похідна, то ця похідна f(x) = F?(x) - теж періодична функція з періодом T. Чай значення похідної в точці x дорівнює тангенсу кута нахилу дотичної графіка її первісної в цій точці до осі абсцис, а від того, що первісна періодично повторюється, то повинна повторюватися і похідна. Скажімо, похідна від функції sin(x) дорівнює cos(x) і вона періодична. Беручи похідну cos(x), ви отримаєте –sin(x). Періодичність зберігається постійно. Проте протилежне не незмінно правильно. Так, функція f(x) = const періодична, та її первісна F(x) = const*x + C - немає.

5. Якщо F(x) - періодична функція з періодом T, то G(x) = a*F(kx + b), де a, b, і k - константи і k не дорівнює нулю - теж періодична функція, і її період дорівнює T/k. Скажімо sin(2x) - періодична функція, і її період дорівнює? Наочно це можна так: помножуючи x на яке-небудь число, ви стискаєте графік функції по горизонталі саме в стільки разів

6. Якщо F1(x) і F2(x) - періодичні функції, та його періоди рівні T1 і T2 відповідно, то сума цих функцій також може бути періодичною. Втім, її період не буде легкою сумою періодів T1 і T2. Якщо результат розподілу T1/T2 - розумне число, то сума функцій періодична, та її період дорівнює найменшому загальному кратному (НОК) періодів T1 і T2. Скажімо, якщо період першої функції дорівнює 12, а період 2-й - 15, то період їх суми дорівнюватиме НОК (12, 15) = 60. Наочно це можна так: функції йдуть з різною «шириною кроку», але якщо відношення їх ширин осмислено, то рано чи пізно (а точніше, саме через НОК кроків), вони знову зрівняються, та його сума почне новий період.

7. Проте якщо співвідношення періодів ірраціонально, то сумарна функція не буде періодичною. Скажімо, нехай F1(x) = x mod 2 (залишок від поділу x на 2), а F2(x) = sin(x). T1 тут дорівнюватиме 2, а T2 дорівнює 2?. Співвідношення періодів дорівнює? - ірраціональному числу. Отже, функція sin(x) + x mod 2 не є періодичною.

Багато математичних функцій мають одну специфіку, що полегшує їх побудову, – це періодичністьтобто повторюваність графіка на координатній сітці через рівні інтервали.

Інструкція

1. Найвідомішими періодичними функціями математики є синусоїда та косінусоїда. Ці функції мають хвилеподібний характер і стрижневий період, що дорівнює 2П. Також окремим випадком періодичної функції є f(x)=const. На позицію х підходить всяке число, основного періоду дана функція не має, тому що є прямою.

2. Взагалі функція є періодичною, якщо є таке ціле число N, яке відмінно від нуля і задовольняє правилу f(x)=f(x+N), таким чином забезпечуючи повторюваність. Період функції – це найменше число N, але з нуль. Тобто, скажімо, функція sin x дорівнює функції sin (x+2ПN), де N=±1, ±2 тощо.

3. Іноді при функції може стояти множник (скажімо sin 2x), який збільшить або скоротить період функції. Для того щоб виявити період по графіку, потрібно визначити екстремуми функції – найвищу та найнижчу точки графіка функції. Тому що синусоїда і косінусоїда мають хвилеподібну вдачу, це досить легко зробити. Від даних точок побудуйте перпендикулярні прямі до перетину віссю Х.

4. Відстань від верхнього екстремуму до нижнього буде половиною періоду функції. Комфортніше кожного обчислювати період від перетину графіка з віссю Y і відповідно нульової позначки по осі х. Після цього необхідно помножити отримане значення на два і отримати стрижневий період функції.

5. Для простоти побудови графіків синусоїди і косінусоїди слід зауважити, що якщо при функції стоїть ціле число, то її період подовжиться (тобто 2П необхідно помножити на цей показник) і графік виглядатиме більш м'яко, плавно; а якщо число дробове, навпаки, скоротиться і графік стане більш «гострим», стрибкоподібним на вигляд.

Відео на тему

По шкільних уроках математики кожен пам'ятає графік синуса, рівномірними хвилями вдалину. Аналогічну властивість - повторюватися через певний проміжок - мають і багато інших функцій. Вони називаються періодичними. Періодичність - дуже важлива властивість функції, що часто зустрічається у різних завданнях. Тому корисно вміти визначати, чи функція є періодичною.

Інструкція

• Якщо F(x) - функція аргументу x, вона називається періодичною, якщо є таке число T, що з будь-якого x F(x + T) = F(x). Це число T і називається періодом функції. Періодів може бути кілька. Наприклад, функція F = const для будь-яких значень аргументу приймає одне й те саме значення, тому будь-яке число може вважатися її періодом. Зазвичай математика цікавить найменший не рівний нулю період функції. Його для стислості і називають просто періодом.
• Класичний приклад періодичних функцій – тригонометричні: синус, косинус та тангенс. Їх період однаковий і дорівнює 2π, тобто sin(x) = sin(x + 2π) = sin(x + 4π) тощо. Однак, зрозуміло, тригонометричні функції – не єдині періодичні.
• Щодо простих, базових функцій єдиний спосіб встановити їх періодичність чи неперіодичність – обчислення. Для складних функцій вже є кілька простих правил.
• Якщо F(x) - періодична функція з періодом T, і для неї визначена похідна, то ця похідна f(x) = F′(x) - теж періодична функція з періодом T. Адже значення похідної в точці x дорівнює тангенсу кута нахилу дотичної графіка її первісної в цій точці до осі абсцис, а оскільки первісна періодично повторюється, то має повторюватися і похідна. Наприклад, похідна від функції sin(x) дорівнює cos(x) і вона періодична. Беручи похідну cos(x), ви отримаєте –sin(x). Періодичність зберігається незмінно. Однак протилежне не завжди вірне. Так, функція f(x) = const періодична, та її первісна F(x) = const*x + C - немає.
• Якщо F(x) - періодична функція з періодом T, то G(x) = a*F(kx + b), де a, b, і k - константи і k не дорівнює нулю - теж періодична функція, і її період дорівнює T/k. Наприклад sin(2x) - періодична функція, та її період дорівнює π. Наочно це можна так: помножуючи x на якесь число, ви стискаєте графік функції по горизонталі саме в стільки разів
• Якщо F1(x) і F2(x) - періодичні функції, та його періоди рівні T1 і T2 відповідно, то сума цих функцій також може бути періодичною. Однак її період не буде простою сумою періодів T1 та T2. Якщо результат розподілу T1/T2 - раціональне число, то сума функцій періодична, та її період дорівнює найменшому загальному кратному (НОК) періодів T1 і T2. Наприклад, якщо період першої функції дорівнює 12, а період другої - 15, то період їх суми дорівнюватиме НОК (12, 15) = 60. Наочно це можна представити так: функції йдуть з різною «шириною кроку», але якщо відношення їх ширин раціонально, рано чи пізно (а точніше, саме через НОК кроків), вони знову зрівняються, і їх сума почне новий період.
• Однак якщо співвідношення періодів ірраціональне, то сумарна функція не буде періодичною. Наприклад, нехай F1(x) = x mod 2 (залишок від поділу x на 2), а F2(x) = sin(x). T1 тут дорівнюватиме 2, а T2 дорівнює 2π. Співвідношення періодів дорівнює π - ірраціональному числу. Отже, функція sin(x) + x mod 2 не є періодичною.