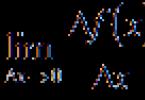При виведенні першої формули таблиці виходити з визначення похідної функції у точці. Візьмемо, де x- будь-яке дійсне число, тобто, x- Будь-яке число з області визначення функції. Запишемо межу відношення збільшення функції до збільшення аргументу при:

Слід зазначити, що під знаком межі виходить вираз, який не є невизначеністю нуль ділити на нуль, тому що в чисельнику знаходиться не нескінченно мала величина, а саме нуль. Іншими словами, збільшення постійної функції завжди дорівнює нулю.

Таким чином, похідна постійної функціїдорівнює нулю по всій області визначення.

Похідна статечної функції.

Формула похідної статечної функції має вигляд де показник ступеня p- Будь-яке дійсне число.

Доведемо спочатку формулу для натурального показника ступеня, тобто для p = 1, 2, 3, …

Будемо користуватися визначенням похідної. Запишемо межу відношення збільшення статечної функції до збільшення аргументу:

Для спрощення виразу в чисельнику звернемося до формули бінома Ньютона:

Отже,

Цим доведено формулу похідної статечної функції для натурального показника.

Похідна показової функції.

Висновок формули похідної наведемо на основі визначення:

Прийшли до невизначеності. Для її розкриття введемо нову змінну, причому при. Тоді. В останньому переході ми використали формулу переходу до нової основи логарифму.

Виконаємо підстановку у вихідну межу:

Якщо згадати другу чудову межу, то прийдемо до формули похідної показової функції:

Похідна логарифмічна функція.

Доведемо формулу похідної логарифмічної функції всім xв галузі визначення та всіх допустимих значеннях підстави aлогарифму. За визначенням похідної маємо:

Як Ви помітили, за доказом перетворення проводилися з використанням властивостей логарифму. Рівність справедливо з другого чудової межі.

Похідні тригонометричних функцій.

Для виведення формул похідних тригонометричних функцій нам доведеться згадати деякі формули тригонометрії, а також перша чудова межа.

За визначенням похідної для функції синуса маємо .

Скористаємося формулою різниці синусів:

Залишилося звернутися до першої чудової межі:

Таким чином, похідна функції sin xє cos x.

Абсолютно аналогічно доводиться формула похідної косинуса.

Отже, похідна функції cos xє -sin x.

Виведення формул таблиці похідних для тангенсу та котангенсу проведемо з використанням доведених правил диференціювання (похідна дробу).

Похідні гіперболічні функції.

Правила диференціювання та формула похідної показової функції з таблиці похідних дозволяють вивести формули похідних гіперболічного синуса, косинуса, тангенсу та котангенсу.

Похідна зворотної функції.

Щоб при викладі не було плутанини, давайте позначати в нижньому індексі аргумент функції, за яким виконується диференціювання, тобто це похідна функції f(x)по x.

Тепер сформулюємо правило знаходження похідної зворотної функції.

Нехай функції y = f(x)і x = g(y)взаємно зворотні, визначені на інтервалах та відповідно. Якщо у точці існує кінцева відмінна від нуля похідна функції f(x), то в точці існує кінцева похідна зворотної функції g(y), причому . В іншому записі .

Можна це правило переформулювати для будь-кого xз проміжку, тоді отримаємо .

Перевіримо справедливість цих формул.

Знайдемо зворотну функцію для натурального логарифму (тут y- функція, а x- Аргумент). Дозволивши це рівняння щодо x, отримаємо (тут x- функція, а y- Її аргумент). Тобто, та взаємно зворотні функції.

З таблиці похідних бачимо, що і .

Переконаємося, що формули знаходження похідних зворотної функції призводять нас до цих результатів:

Як бачите, отримали такі ж результати, як і в таблиці похідних.

Тепер ми маємо знання для доказу формул похідних зворотних тригонометричних функцій.

Почнемо з похідної арксинусу.

. Тоді за формулою похідної зворотної функції отримуємо

Залишилось провести перетворення.

Оскільки областю значень арксинусу є інтервал , то (Дивіться розділ основні елементарні функції, їх властивості та графіки). Тому, а не розглядаємо.

Отже, . Областю визначення похідної арксинусу є проміжок (-1; 1) .

Для арккосинусу все робиться абсолютно аналогічно:

Знайдемо похідну арктангенсу.

Для зворотної функцією є .

Виразимо арктангенс через арккосинус, щоб спростити отриманий вираз.

Нехай arctgx = zтоді

Отже,

Так само знаходиться похідна арккотангенса:

Процес знаходження похідної функції називається диференціюванням.Похідну доводиться знаходити у низці завдань курсу математичного аналізу. Наприклад, при знайденні точок екстремуму та перегину графіка функції.

Як знайти?

Щоб знайти похідну функції потрібно знати таблицю похідних елементарних функцій та застосовувати основні правила диференціювання:

1. Винесення константи за знак похідної: $$ (Cu)" = C(u)" $$
2. Похідна суми / різниці функцій: $$ (u \pm v)" = (u)" \pm (v)" $$
3. Похідна робота двох функцій: $$ (u \cdot v)" = u"v + uv" $$
4. Похідна дробу : $$ \bigg (\frac(u)(v) \bigg)" = \frac(u"v - uv")(v^2) $$
5. Похідна складної функції: $$ (f(g(x)))" = f"(g(x)) \cdot g"(x) $$

Приклади рішення

Приклад 1

Знайти похідну функції $ y = x^3 - 2x^2 + 7x - 1$

Рішення

Похідна суми / різниці функцій дорівнює сумі / різниці похідних: $$ y" = (x^3 - 2x^2 + 7x - 1)" = (x^3)" - (2x^2)" + (7x)" - (1)" = $$ Використовуючи правило похідної статечної функції $ (x^p)" = px^(p-1) $ маємо: $$ y" = 3x^(3-1) - 2 \cdot 2 x^(2-1) + 7 - 0 = 3x^2 - 4x + 7 $$ Також було враховано, що похідна від константи дорівнює нулю. Якщо не вдається вирішити своє завдання, то надсилайте його до нас. Ми надамо детальне рішення. Ви зможете ознайомитися з ходом обчислення та отримати інформацію. Це допоможе вчасно отримати залік у викладача!

Відповідь

$$ y" = 3x^2 - 4x + 7 $$

З правочні матеріали на тему «похідна». Основний шкільний рівень.
Теоретичні відомості для учнів, викладачів та репетиторів з математики. На допомогу проведення занять.

Визначення:похідної функції у точці називається межа відношення збільшення функції до збільшення змінної, тобто

Таблиця похідних основних математичних функцій:

Правила обчислення похідних

Похідна сумадвох будь-яких виразів дорівнює сумі похідних цих виразів (похідна суми дорівнює сумі похідних)

Похідна різницідвох будь-яких виразів дорівнює різниці похідних цих доданків (похідна різниці дорівнює різниці похідних).

Похідна від творудвох множників дорівнює добутку похідної першого множника на другий плюс добуток першого множника на похідну другого (сума взятих почергово похідних від множників).
Коментар репетитора з математики:коли я короткими фразами нагадую учневі про правило обчислення похідної від твору, я говорю так: похідна першого множника на другий плюс обмін штрихами!

Похідна від приватногодвох виразів дорівнює приватній різниці по черзі взятих похідних від множників і квадрата знаменника.

Похідна від числа на функцію. Щоб знайти похідну від твору числа на буквене вираз (на функцію) потрібно помножити це число на похідну цього виразу.

Похідна складної функції:

Для обчислення похідної складної функції необхідно знайти похідну зовнішньої функції та помножити її на похідну внутрішньої функції.

Ваші коментарі та відгуки до сторінки з похідними:
Олександр С.
Дуже потрібна була таблиця. В інтернеті одна із самих. За пояснення та правила теж велике спасибі. Хоча б за одним прикладом ще до них і взагалі було б добре було. Ще раз виличезне Дякую.

Колпаков О.М, репетитор з математики:добре, постараюся найближчим часом доповнити сторінку прикладами.

Віртуальний математичний довідник.
Ковпаков Олександр Миколайович, репетитор з математики.

Обчислення похідної- Одна з найважливіших операцій у диференціальному обчисленні. Нижче наведено таблицю знаходження похідних простих функцій. Більш складні правила диференціювання дивіться в інших уроках:

• Таблиця похідних експоненційних та логарифмічних функцій

Використовуйте наведені формули як довідкові значення. Вони допоможуть у вирішенні диференціальних рівнянь та завдань. На малюнку, в таблиці похідних простих функцій, наведена "шпаргалка" основних випадків знаходження похідної у зрозумілому для застосування вигляді, поряд з ним дано пояснення для кожного випадку.

Похідні простих функцій

1. Похідна від числа дорівнює нулю
с = 0
Приклад:
5 '= 0

Пояснення:
Похідна показує швидкість зміни значення функції за зміни аргументу. Оскільки число ніяк не змінюється за жодних умов - швидкість його зміни завжди дорівнює нулю.

2. Похідна змінноїдорівнює одиниці
x' = 1

Пояснення:
При кожному збільшенні аргументу (х) на одиницю значення функції (результату обчислень) збільшується на цю саму величину. Таким чином, швидкість зміни значення функції y = x точно дорівнює швидкості зміни значення аргументу.

3. Похідна змінної та множника дорівнює цьому множнику
сx = с
Приклад:
(3x)' = 3
(2x)' = 2
Пояснення:
В даному випадку, при кожній зміні аргументу функції ( х) її значення (y) зростає в зразів. Таким чином, швидкість зміни значення функції по відношенню до швидкості зміни аргументу точно дорівнює величині з.

Звідки випливає, що
(cx + b)" = c
тобто диференціал лінійної функції y=kx+b дорівнює кутовому коефіцієнту нахилу прямої (k).

4. Похідна змінною за модулемдорівнює частці цієї змінної до її модуля
|x|"= x / | x | за умови, що х ≠ 0
Пояснення:
Оскільки похідна змінної (див. формулу 2) дорівнює одиниці, похідна модуля відрізняється лише тим, що значення швидкості зміни функції змінюється на протилежне при перетині точки початку координат (спробуйте намалювати графік функції y = | x | і переконайтеся в цьому самі. Саме таке значення і повертає вираз x / |x|.< 0 оно равно (-1), а когда x >0 – одиниці. Тобто при негативних значеннях змінної х при кожному збільшенні зміні аргументу значення функції зменшується на таке саме значення, а при позитивних - навпаки, зростає, але точно на таке ж значення.

5. Похідна змінної у ступенідорівнює добутку числа цього ступеня та змінної до ступеня, зменшеної на одиницю
(x c)" = cx c-1, за умови, що x c і сx c-1 визначені а з ≠ 0
Приклад:
(x 2)" = 2x
(x 3)" = 3x 2
Для запам'ятовування формули:
Знесіть ступінь змінної "вниз" як множник, а потім зменшіть самий ступінь на одиницю. Наприклад, для x 2 - двійка виявилася попереду ікса, та був зменшена ступінь (2-1=1) просто дала нам 2х. Те саме сталося для x 3 - трійку "спускаємо вниз", зменшуємо її на одиницю і замість куба маємо квадрат, тобто 3x2. Дещо "не науково", але дуже просто запам'ятати.

6.Похідна дроби 1/х
(1/х)" = - 1 / x 2
Приклад:
Оскільки дріб можна подати як зведення в негативний ступінь
(1/x)" = (x -1)" , Тоді можна застосувати формулу з правила 5 похідних таблиці
(x -1)" = -1x -2 = - 1 / х 2

7. Похідна дроби зі змінним довільним ступенему знаменнику
(1 / x c)" = - c/x c+1
Приклад:
(1/x2)" = - 2/x3

8. Похідне коріння(Похідна змінної під квадратним коренем)
(√x)" = 1 / (2√x)або 1/2 х -1/2
Приклад:
(√x)" = (х 1/2)" означає можна застосувати формулу з правила 5
(х 1/2)" = 1/2 х -1/2 = 1 / (2√х)

9. Похідна змінної під коренем довільного ступеня
(n√x)" = 1 / (nn√xn-1)

Дата: 10.05.2015

Як знайти похідну?

Правила диференціювання.

Щоб знайти похідну від будь-якої функції, треба освоїти лише три поняття:

2. Правила диференціювання.

3. Похідна складної функції.

Саме у такому порядку. Це натяк.)

Зрозуміло, непогано б ще мати уявлення про похідну взагалі). Про те, що таке похідна, та як працювати з таблицею похідних – доступно розказано у попередньому уроці. Тут ми займемося правилами диференціювання.

Диференціювання – це операція знаходження похідної. Більше за цим терміном нічого не ховається. Тобто. вирази "Знайти похідну функції"і "продиференціювати функцію"- це одне і теж.

Вираз "правила диференціювання"відноситься до знаходження похідної від арифметичних операцій.Таке розуміння дуже допомагає уникнути каші у голові.

Зосередимося і згадаємо всі арифметичні операції. Їх чотири). Додавання (сума), віднімання (різниця), множення (твор) і поділ (приватне). Ось вони, правила диференціювання:

У табличці наведено п'ятьправил на чотириарифметичні дії. Я не обрахувався.) Просто правило 4 - це елементарне слідство з правила 3. Але воно настільки популярне, що має сенс записати (і запам'ятати!) його як самостійну формулу.

Під позначеннями Uі Vмаються на увазі якісь (цілком будь-які!) функції U(x)і V(x).

Розглянемо кілька прикладів. Спочатку – найпростіші.

Знайти похідну функції y = sinx - x 2

Тут ми маємо різницядвох елементарних функцій Застосовуємо правило 2. Вважатимемо, що sinx - це функція U, а x 2 – функція V.Маємо повне право написати:

y" = (sinx - x 2)" = (sinx)"- (x 2)"

Вже краще, правда?) Залишилося знайти похідні від синуса та квадрата ікса. І тому існує таблиця похідних. Просто шукаємо у таблиці потрібні нам функції ( sinxі x 2), дивимося, які вони похідні і записуємо відповідь:

y" = (sinx)" - (x 2)" = cosx - 2x

Ось і всі справи. Правило 1 диференціювання суми працює так само.

А якщо у нас кілька доданків? Нічого страшного.) Розбиваємо функцію на доданки і шукаємо похідну від кожного доданку незалежно від інших. Наприклад:

Знайти похідну функції y = sinx - x 2 + cosx - x +3

Сміливо пишемо:

y" = (sinx)" - (x 2)" + (cosx)" - (x)" + (3)"

Наприкінці уроку дам поради щодо полегшення життя при диференціюванні.)

Практичні поради:

1. Перед диференціюванням дивимося, чи не можна спростити вихідну функцію.

2. У заморочених прикладах розписуємо рішення докладно, з усіма дужками та штрихами.

3. При диференціюванні дробів з постійним числом у знаменнику, перетворюємо поділ на множення та користуємося правилом 4.