Trojuholník . Ostrý, tupý a pravouhlý trojuholník.

Nohy a hypotenzia. Rovnoramenný a rovnostranný trojuholník.

Súčet uhlov trojuholníka.

Vonkajší uhol trojuholníka. Znaky rovnosti trojuholníkov.

Pozoruhodné čiary a body v trojuholníku: výšky, mediány,

osi, medián e kolmice, ortocentrum,

ťažisko, stred kružnice opísanej, stred kružnice vpísanej.

Pytagorova veta. Pomer strán v ľubovoľnom trojuholníku.

Trojuholník je mnohouholník s tromi stranami (alebo tromi uhlami). Strany trojuholníka sú často označené malými písmenami, ktoré zodpovedajú veľkým písmenám reprezentujúcim opačné vrcholy.

Ak sú všetky tri uhly ostré (obr. 20), potom toto ostrý trojuholník . Ak je jeden z uhlov správny(C, obr. 21), to jest správny trojuholník; stranya, btvoriace pravý uhol sú tzv nohy; stranecoproti pravému uhlu sa nazýva hypotenzia. Ak jeden z tupé uhly (B, obr. 22), to jest tupý trojuholník.


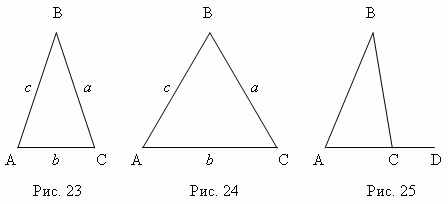
Trojuholník ABC (obr. 23) - rovnoramenné, Ak dva jeho strany sú rovnaké (a= c); tieto rovné strany sa nazývajú bočné, volá sa tretia strana základ trojuholník. Trojuholník ABC (obr. 24) – rovnostranný, Ak Všetky jeho strany sú rovnaké (a = b = c). Všeobecne ( a ≠ b ≠ c) máme scalene trojuholník .

Základné vlastnosti trojuholníkov. V akomkoľvek trojuholníku:

1. Oproti väčšej strane leží väčší uhol a naopak.

2. Rovnaké uhly ležia oproti rovnakým stranám a naopak.

Najmä všetky uhly v rovnostranný trojuholníky sú rovnaké.

3. Súčet uhlov trojuholníka je 180 º .

Z posledných dvoch vlastností vyplýva, že každý uhol v rovnostrane

trojuholník je 60 º.

4. Pokračovaním jednej zo strán trojuholníka (AC, obr. 25), dostaneme externé

uhol BCD . Vonkajší uhol trojuholníka sa rovná súčtu vnútorných uhlov,

nesusedí s ním : BCD = A + B.

5. akýkoľvek strana trojuholníka je menšia ako súčet ostatných dvoch strán a väčšia

ich rozdiely (a < b + c, a > b – c;b < a + c, b > a – c;c < a + b,c > a – b).

Znaky rovnosti trojuholníkov.

Trojuholníky sú zhodné, ak sa navzájom rovnajú:

a ) dve strany a uhol medzi nimi;

b ) dva rohy a k nim priľahlá strana;

c) tri strany.

Znaky rovnosti pravouhlých trojuholníkov.

Dva pravouhlý trojuholníky sú rovnaké, ak je splnená jedna z nasledujúcich podmienok:

1) ich nohy sú rovnaké;

2) rameno a prepona jedného trojuholníka sú rovnaké ako rameno a prepona druhého;

3) prepona a ostrý uhol jedného trojuholníka sú rovnaké ako prepona a ostrý uhol druhého;

4) noha a priľahlý ostrý uhol jedného trojuholníka sa rovnajú ramenu a susednému ostrému uhlu druhého;

5) noha a opačný ostrý uhol jedného trojuholníka sa rovnajú nohe a opačný ostrý uhol toho druhého.

Nádherné čiary a body v trojuholníku.

Výška trojuholník jekolmý,znížené z akéhokoľvek vrcholu na opačnú stranu ( alebo jej pokračovanie). Táto strana je tzvzákladňa trojuholníka . Tri výšky trojuholníka sa vždy pretínajúv jednom bode, volal ortocentrum trojuholník. Ortocentrum ostrého trojuholníka (bod O , Obr. 26) sa nachádza vo vnútri trojuholníka aortocentrum tupého trojuholníka (bod O , obr.27) – vonku; Ortocentrum pravouhlého trojuholníka sa zhoduje s vrcholom pravého uhla.

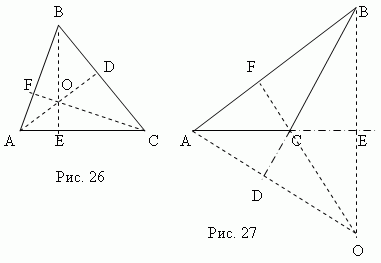
Medián - Toto úsečka , spájajúci ľubovoľný vrchol trojuholníka so stredom opačnej strany. Tri stredy trojuholníka (AD, BE, CF, obr. 28) pretínajú v jednom bode O , ktorý vždy leží vo vnútri trojuholníka a byť jeho ťažisko. Tento bod rozdeľuje každý medián v pomere 2:1, počítajúc od vrcholu.

Bisector - Toto osový segment uhol od vrcholu k bodu križovatky s opačnou stranou. Tri osi trojuholníka (AD, BE, CF, obr. 29) pretínajú v jednom bode Oh, vždy ležal vnútri trojuholníka A bytie stred vpísanej kružnice(pozri časť „Popísanéa ohraničené polygóny“).

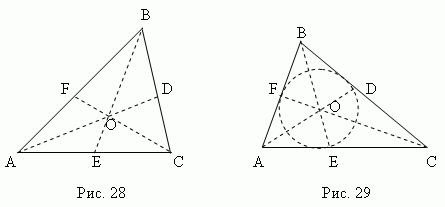
Osa rozdeľuje opačnú stranu na časti proporcionálne k susedným stranám ; napríklad na obr. 29 AE: CE = AB: BC.

Stredná kolmá je kolmica vedená zo stredu segmentové body (strany). Tri odvislé osi trojuholníka ABC(KO, MO, NO, obr. 30 ) pretínajú v jednom bode O, ktorý je stred opísaný kruh (body K, M, N – stredy strán trojuholníka ABC).

V ostrom trojuholníku tento bod leží vo vnútri trojuholníka; v tupom - vonku; v obdĺžnikovom - v strede prepony. Ortocentrum, ťažisko, circumcenter a vpísaná kružnica sa zhodujú iba v rovnostrannom trojuholníku.

Pytagorova veta. V pravouhlom trojuholníku štvorec dĺžkyPrepona sa rovná súčtu štvorcov dĺžok nôh.

Dôkaz Pytagorovej vety jasne vyplýva z obr. Predstavte si pravouhlý trojuholník ABC s nohami a, b a preponu c.

Postavme štvorec AKMB pomocou prepony AB ako vedľajšia. Potompokračujte stranami pravého trojuholníka ABC tak, aby dostal štvorec CDEF , ktorej strana je rovnáa + b.Teraz je jasné, že plocha námestia CDEF sa rovná ( a+b) 2 . Na druhej strane toto plocha sa rovná súčtu oblasti štyri pravouhlé trojuholníky a štvorec AKMB, tj

c 2 + 4 (ab / 2) = c 2 + 2 ab,

odtiaľ,

c 2 + 2 ab= (a+b) 2 ,

a nakoniec tu máme:

c 2 =a 2 + b 2 .

Pomer strán v ľubovoľnom trojuholníku.

Vo všeobecnom prípade (pre ľubovoľný trojuholník) máme:

c 2 =a 2 + b 2 – 2ab· cos C,

kde C - uhol medzi stranamia A b .

Štandardné označenia

Trojuholník s vrcholmi A, B A C je označený ako (pozri obrázok). Trojuholník má tri strany:

Dĺžky strán trojuholníka sú označené malými latinskými písmenami (a, b, c):

Trojuholník má tieto uhly:

Hodnoty uhla v zodpovedajúcich vrcholoch sa tradične označujú gréckymi písmenami (α, β, γ).

Znaky rovnosti trojuholníkov

Trojuholník na euklidovskej rovine možno jednoznačne určiť (až do zhody) pomocou nasledujúcich trojíc základných prvkov:

1. a, b, γ (rovnosť na dvoch stranách a uhol medzi nimi);
2. a, β, γ (rovnosť na strane a dva susedné uhly);
3. a, b, c (rovnosť na troch stranách).

Znaky rovnosti pravouhlých trojuholníkov:

1. pozdĺž nohy a hypotenzie;
2. na dvoch nohách;
3. pozdĺž nohy a ostrého uhla;
4. pozdĺž prepony a ostrého uhla.

Niektoré body v trojuholníku sú „spárované“. Napríklad existujú dva body, z ktorých sú viditeľné všetky strany buď pod uhlom 60° alebo pod uhlom 120°. Volajú sa Torricelliho bodky. Existujú aj dva body, ktorých priemety na strany ležia vo vrcholoch pravidelného trojuholníka. toto - Apollonius body. Body a podobne sú tzv Brocard body.

Priamy

V akomkoľvek trojuholníku ležia ťažisko, ortocentrum a stred kružnice opísanej na tej istej priamke, tzv. Eulerova línia.

Priama čiara prechádzajúca stredom opísanej kružnice a bodom Lemoine sa nazýva Os Brocard. Ležia na nej Apolloniove body. Torricelliho bod a bod Lemoine tiež ležia na tej istej priamke. Základny vonkajších osi uhlov trojuholníka ležia na jednej priamke tzv os vonkajších osi. Priesečníky priamok obsahujúcich strany pravouhlého trojuholníka s priamkami obsahujúcimi strany trojuholníka tiež ležia na tej istej priamke. Táto linka je tzv ortocentrická os, je kolmá na Eulerovu priamku.

Ak vezmeme bod na kružnici opísanej trojuholníku, potom jeho priemet na strany trojuholníka bude ležať na rovnakej priamke, tzv. Simson je rovný tento bod. Simsonove čiary diametrálne opačných bodov sú kolmé.

Trojuholníky

• Trojuholník s vrcholmi na základniach prekreslený daným bodom sa nazýva cevický trojuholník tento bod.
• Trojuholník s vrcholmi v priemetoch daného bodu na strany sa nazýva drn alebo pedálový trojuholník tento bod.
• Trojuholník s vrcholmi v druhých priesečníkoch čiar vedených cez vrcholy a daný bod s kružnicou opísanou sa nazýva obvodový trojuholník. Obvodový trojuholník je podobný drnovému trojuholníku.

Kruhy

• Vpísaný kruh- kruh dotýkajúci sa všetkých troch strán trojuholníka. Ona je jediná. Stred vpísanej kružnice je tzv stred.
• Kruhový kruh- kružnica prechádzajúca všetkými tromi vrcholmi trojuholníka. Jedinečný je aj opísaný kruh.
• Zakrúžkovať- kruh dotýkajúci sa jednej strany trojuholníka a pokračovanie ďalších dvoch strán. V trojuholníku sú tri takéto kruhy. Ich radikálnym stredom je stred vpísanej kružnice mediálneho trojuholníka, tzv Spikerova pointa.

Stredy troch strán trojuholníka, základne jeho troch výšok a stredy troch segmentov spájajúcich jeho vrcholy s ortocentrom ležia na jednej kružnici tzv. kruh deviatich bodov alebo Eulerov kruh. Stred deväťbodovej kružnice leží na Eulerovej priamke. Kruh s deviatimi bodmi sa dotýka vpísanej kružnice a troch kružníc. Dotykový bod medzi vpísanou kružnicou a kružnicou deviatich bodov sa nazýva Feuerbachov bod. Ak z každého vrcholu položíme smerom von z trojuholníka na rovné čiary obsahujúce strany, ortézy rovnakej dĺžky ako protiľahlé strany, potom výsledných šesť bodov leží na tej istej kružnici - Conwayov kruh. Do akéhokoľvek trojuholníka možno vpísať tri kruhy tak, že sa každý z nich dotýka dvoch strán trojuholníka a dvoch ďalších kruhov. Takéto kruhy sa nazývajú Malfattiho kruhy. Stredy opísaných kružníc šiestich trojuholníkov, na ktoré je trojuholník rozdelený strednicami, ležia na jednej kružnici, ktorá je tzv. obvod Lamuna.

Trojuholník má tri kruhy, ktoré sa dotýkajú dvoch strán trojuholníka a kružnice opísanej. Takéto kruhy sa nazývajú polozapísaný alebo Verrierove kruhy. Segmenty spájajúce body dotyku Verrierových kružníc s kružnicou opísanou sa pretínajú v jednom bode tzv. Verrierova pointa. Slúži ako stred homotety, ktorá premieňa opísaný kruh na vpísaný kruh. Body dotyku Verrierových kružníc so stranami ležia na priamke, ktorá prechádza stredom vpísanej kružnice.

Úsečky spájajúce dotykové body vpísanej kružnice s vrcholmi sa pretínajú v jednom bode tzv. Gergonne bod, a segmenty spájajúce vrcholy s dotykovými bodmi kružníc sú v Nagelov bod.

Elipsy, paraboly a hyperboly

Vpísaná kužeľosečka (elipsa) a jej perspektor

Do trojuholníka možno vpísať nekonečné množstvo kužeľosečiek (elipsy, paraboly alebo hyperboly). Ak do trojuholníka vpíšeme ľubovoľnú kužeľosečku a spojíme dotykové body s protiľahlými vrcholmi, potom sa výsledné priamky pretnú v jednom bode tzv. vyhliadka poschodová. Pre každý bod roviny, ktorý neleží na boku alebo na jej predĺžení, je v tomto bode vpísaná kužeľosečka s perspektorom.

Opísaná Steinerova elipsa a ceviany prechádzajúce jej ohniskami

Do trojuholníka môžete vpísať elipsu, ktorá sa v strede dotýka strán. Takáto elipsa sa nazýva vpísaná Steinerova elipsa(jeho perspektívou bude ťažisko trojuholníka). Opísaná elipsa, ktorá sa dotýka priamok prechádzajúcich vrcholmi rovnobežnými so stranami, sa nazýva opísaná Steinerovou elipsou. Ak transformujeme trojuholník na pravidelný trojuholník pomocou afinnej transformácie („zošikmenie“), potom sa jeho vpísaná a opísaná Steinerova elipsa premení na vpísanú a opísanú kružnicu. Chevovské čiary nakreslené cez ohniská opísanej Steinerovej elipsy (Scutinove body) sú rovnaké (Scutinova veta). Zo všetkých opísaných elips má najmenšiu plochu opísaná Steinerova elipsa a zo všetkých vpísaných elips má najväčšiu plochu vpísaná Steinerova elipsa.

Brocardova elipsa a jej perspektor - bod Lemoine

Volá sa elipsa s ohniskami v bodoch Brocard Brokartová elipsa. Jeho perspektíva je bod Lemoine.

Vlastnosti vpísanej paraboly

Kiepertova parabola

Perspektívy vpísaných parabol ležia na opísanej Steinerovej elipse. Ohnisko vpísanej paraboly leží na opísanej kružnici a priamka prechádza ortocentrom. Nazýva sa parabola vpísaná do trojuholníka s Eulerovou osou Kiepertova parabola. Jeho hľadiskom je štvrtý priesečník opísanej kružnice a opísanej Steinerovej elipsy, tzv. Steinerov bod.

Kiepertova hyperbola

Ak opísaná hyperbola prechádza priesečníkom výšok, potom je rovnostranná (to znamená, že jej asymptoty sú kolmé). Priesečník asymptot rovnostrannej hyperboly leží na kružnici deviatich bodov.

Premeny

Ak sa čiary prechádzajúce vrcholmi a nejakým bodom neležiacim po stranách a ich predĺženia odrážajú vzhľadom na zodpovedajúce osi, potom sa ich obrazy tiež pretnú v jednom bode, ktorý je tzv. izogonálne konjugovať pôvodný (ak bod ležal na opísanej kružnici, tak výsledné priamky budú rovnobežné). Mnoho párov pozoruhodných bodov je izogonálne konjugovaných: circumcenter a ortocentrum, centroid a Lemoine bod, Brocardove body. Apolloniove body sú izogonálne konjugované s Torricelliho bodmi a stred vpísaného kruhu je izogonálne konjugovaný sám so sebou. Pôsobením izogonálnej konjugácie sa priamky premenia na opísanú kužeľosečku a opísanú kužeľosečku na priamku. Kiepertova hyperbola a Brocardova os, Jenzabekova hyperbola a Eulerova priamka, Feuerbachova hyperbola a čiara stredov vpísanej a opísanej kružnice sú teda izogonálne konjugované. Opísané kružnice trojuholníkov izogonálne združených bodov sa zhodujú. Ohniská vpísaných elipsy sú izogonálne konjugované.

Ak namiesto symetrického cevianu vezmeme cevian, ktorého základňa je rovnako vzdialená od stredu strany ako základňa pôvodného, ​​potom sa aj takéto ceviany pretnú v jednom bode. Výsledná transformácia je tzv izotomická konjugácia. Tiež prevádza priame čiary na opísané kužeľosečky. Body Gergonne a Nagel sú izotomicky konjugované. Pri afinných transformáciách sa izotomicky konjugované body transformujú na izotomicky konjugované body. S izotomickou konjugáciou sa opísaná Steinerova elipsa dostane do nekonečne vzdialenej priamky.

Ak do segmentov odrezaných stranami trojuholníka od kružnice opísanej vpíšeme kružnice, ktoré sa dotýkajú strán v základniach cevianov pretiahnutých určitým bodom, a potom spojíme dotykové body týchto kružníc s kružnicou opísanou s opačnými vrcholmi, potom sa takéto priamky pretnú v jednom bode. Zavolá sa rovinná transformácia, ktorá sa zhoduje s pôvodným bodom s výsledným izokruhová transformácia. Zloženie izogonálnych a izotomických konjugátov je zložením izokruhovej transformácie so sebou samým. Táto kompozícia je projektívnou transformáciou, ktorá ponecháva strany trojuholníka na mieste a transformuje os vonkajších osi na priamku v nekonečne.

Ak predĺžime strany Chevovho trojuholníka určitého bodu a vezmeme ich priesečníky s príslušnými stranami, tak výsledné priesečníky budú ležať na jednej priamke, tzv. trilineárne polárneštartovací bod. Ortocentrická os je trilineárna polárna ortocentra; trilineárna polárna stredu vpísanej kružnice je osou vonkajších osi. Trilineárne poláre bodov ležiacich na opísanej kužeľosečke sa pretínajú v jednom bode (pre opísanú kružnicu je to Lemoineov bod, pre opísanú Steinerovu elipsu je to ťažisko). Zloženie izogonálneho (alebo izotomického) konjugátu a trilineárnej polárnej je transformáciou duality (ak bod izogonálne (izotomicky) konjugovaný s bodom leží na trilineárnej poláre bodu, potom trilineárna polárna bodu izogonálne (izotomicky) konjugovaný s bodom leží na trilineárnej poláre bodu).

Kocky

Pomery v trojuholníku

Poznámka: v tejto sekcii sú , , dĺžky troch strán trojuholníka a , , sú uhly ležiace proti týmto trom stranám (opačné uhly).

Trojuholníková nerovnosť

V nedegenerovanom trojuholníku je súčet dĺžok jeho dvoch strán väčší ako dĺžka tretej strany, v zdegenerovanom trojuholníku je rovný. Inými slovami, dĺžky strán trojuholníka súvisia s nasledujúcimi nerovnosťami:

Trojuholníková nerovnosť je jednou z axióm metrík.

Veta o súčte trojuholníka

Sínusová veta

,

kde R je polomer kružnice opísanej trojuholníku. Z vety vyplýva, že ak a< b < c, то α < β < γ.

Kosínusová veta

Tangentová veta

Iné pomery

Metrické pomery v trojuholníku sú dané pre:

Riešenie trojuholníkov

Výpočet neznámych strán a uhlov trojuholníka na základe známych sa historicky nazýval „riešiace trojuholníky“. Používajú sa vyššie uvedené všeobecné trigonometrické vety.

Oblasť trojuholníka

Špeciálne prípady Notácia

Pre oblasť platia nasledujúce nerovnosti:

Výpočet plochy trojuholníka v priestore pomocou vektorov

Nech sú vrcholy trojuholníka v bodoch , , .

Predstavme si plošný vektor . Dĺžka tohto vektora sa rovná ploche trojuholníka a je nasmerovaná kolmo na rovinu trojuholníka:

Stanovme , kde , , sú priemety trojuholníka na súradnicové roviny. V čom

a podobne

Plocha trojuholníka je .

Alternatívou je vypočítať dĺžky strán (pomocou Pytagorovej vety) a následne použiť Heronov vzorec.

Trojuholníkové teorémy

Táto časť nie je dokončená.

Trojuholník- ide o obrazec pozostávajúci z troch bodov a troch úsečiek, pričom tri body neležia na tej istej priamke, ale tri úsečky spájajú tieto body v pároch. Presnejšie povedané, body trojuholníka sa nazývajú jeho vrcholy a segmenty sa nazývajú strany. Trojuholník je označený svojimi vrcholmi a namiesto dlhého slova trojuholník je nakreslený symbol Δ.

Poďme sa teraz bližšie pozrieť na typy trojuholníkov.

1. Rovnoramenný trojuholník je trojuholník, ktorý má dve rovnaké strany, ktoré sa tiež nazývajú bočné, tretia strana, odlišná od týchto dvoch, sa nazýva základňa.
2. Rovnostranný trojuholník je trojuholník s rovnakými stranami, niekedy nazývaný aj pravidelný trojuholník.
3. Pravý trojuholník je trojuholník, ktorý má pravý uhol (90 stupňov).
4. Ostrý trojuholník je trojuholník, v ktorom sú všetky uhly ostré (to znamená menšie ako 90 stupňov).
5. Tupý trojuholník je trojuholník, v ktorom je jeden z uhlov tupý (to znamená viac ako 90 stupňov).

V zásade je ľahké zapamätať si vlastnosti každého typu trojuholníka, takže názvy hovoria samy za seba.

Vezmite si napríklad trojuholník ABC. A, B, C sú jeho vrcholy a AB, BC a AC sú jeho strany.

Teraz sa pozrime na štruktúru tohto trojuholníka podrobnejšie. Uhol trojuholníka ABC vo vrchole A je uhol, ktorý zvierajú polovičné priamky AB a AC. Podobne môžeme určiť uhly, ktoré ležia vo vrchole B a vo vrchole C.

Nadmorská výška trojuholníka je kolmica, ktorá klesá z daného vrcholu k priamke, ktorá je oproti vrcholu.

Osa trojuholníka je osová časť uhla daného trojuholníka, ktorá spája vrchol s bodom na opačnej strane.

Medián trojuholníka, ktorý je nakreslený z daného vrcholu, je úsečka spájajúca tento vrchol so stredom protiľahlej strany trojuholníka.

Stredová čiara trojuholníka je úsečka, ktorá spája stredy dvoch strán daného trojuholníka. Toto označenie má aj určitú vetu, ktorá hovorí, že stredná čiara trojuholníka je vždy rovnobežná s treťou stranou a tiež sa rovná jej polovici.

Všetky tieto zápisy (medián, os, výška, stredná čiara trojuholníka) budú určite potrebné pri riešení praktických úloh. Navyše bez znalosti vlastností týchto vrcholov je nepravdepodobné, že budete schopní vyriešiť akýkoľvek problém súvisiaci s trojuholníkmi.

na stranách a, b, c;
Kosínusová veta

a

2

= b

2

+c

2

- 2bccosα

a+c a-c	=	tg	α + γ; 2	=	ctg	β 2
		tg	α - γ 2		tg	α - γ 2

R=

c 2

= m

c


Rovnostranný trojuholník

S=

Ak sú tri body, ktoré neležia na tej istej priamke, spojené úsečkami, dostaneme trojuholník. Jedna zo strán trojuholníka sa často nazýva jeho základňa.

Veta. Súčet uhlov trojuholníka je 1800

Ak sú všetky tri uhly trojuholníka ostré, nazývame trojuholník ostrý uhlový.

Ak je jeden z uhlov trojuholníka tupý, potom sa trojuholník nazýva tupo-uhlové.

Ak je jeden z uhlov trojuholníka pravý, nazývame trojuholník pravouhlý. Strana pravouhlého trojuholníka oproti pravému uhlu sa nazýva hypotenzia a ďalšie dve strany sú nohy.

V akomkoľvek trojuholníku leží väčší uhol oproti väčšej strane; protiľahlé rovnaké strany - rovnaké uhly a naopak. Každá strana trojuholníka je menšia ako súčet ostatných dvoch strán a tiež väčšia ako rozdiel ostatných dvoch strán.

Pokračovaním jednej zo strán trojuholníka dostaneme vonkajší uhol. Uhol ABD - externé.

Znaky rovnosti trojuholníkov

Ak sú dva trojuholníky zhodné, potom sa prvky (strany a uhly) jedného trojuholníka rovnajú prvkom druhého trojuholníka.

Veta. Dva trojuholníky sú zhodné, ak sa dve strany a uhol medzi nimi jedného trojuholníka rovná dvom stranám a uhol medzi nimi druhého trojuholníka.

Veta. Dva trojuholníky sú rovnaké, ak sa strana a dva susedné uhly jedného trojuholníka rovnajú strane a dvom susedným uhlom druhého.

Veta. Dva trojuholníky sú zhodné, ak sa tri strany jedného trojuholníka rovnajú trom stranám druhého trojuholníka.

Medián, stred a výška trojuholníka

Úsečka spájajúca vrchol trojuholníka so stredom protiľahlej strany sa nazýva medián trojuholník.

Lúč vychádzajúci z vrcholu uhla a rozdeľujúci ho na dva rovnaké uhly sa nazýva bisector. Osa rozdeľuje opačnú stranu na časti proporcionálne k susedným stranám.

Kolmica vedená z vrcholu trojuholníka na priamku obsahujúcu opačnú stranu sa nazýva výška trojuholník.

Pozoruhodné body trojuholníka. 1) Priečnice trojuholníka sa pretínajú v jednom bode.

2) Odvesne na strany trojuholníka sa pretínajú v jednom bode.

3) Výšky trojuholníka (alebo ich predĺženia) sa pretínajú v jednom bode.

4) Strednice trojuholníka sa pretínajú v jednom bode.

Rovnoramenný trojuholník

Trojuholník sa nazýva rovnoramenný, ak sú jeho dve strany rovnaké. Rovné strany sa nazývajú strany a tretia strana - základ rovnoramenný trojuholník.

Trojuholník, v ktorom sú všetky strany rovnaké, sa nazýva rovnostranný.

Veta. V rovnoramennom trojuholníku sú základné uhly rovnaké.

Veta. V rovnoramennom trojuholníku je stred pripojená k základni stred a nadmorská výška.

Geometria nám hovorí, čo je trojuholník, štvorec a kocka. V modernom svete to všetci bez výnimky študujú v školách. Tiež veda, ktorá priamo študuje, čo je trojuholník a aké má vlastnosti, je trigonometria. Podrobne skúma všetky javy súvisiace s údajmi. O tom, čo je trojuholník, si dnes povieme v našom článku. Ich typy budú popísané nižšie, ako aj niektoré vety s nimi spojené.

čo je trojuholník? Definícia

Toto je plochý polygón. Má tri rohy, ako je zrejmé z jeho názvu. Má tiež tri strany a tri vrcholy, prvý z nich sú segmenty, druhý sú body. Keď viete, čomu sa dva uhly rovnajú, môžete nájsť tretí odčítaním súčtu prvých dvoch od čísla 180.

Aké typy trojuholníkov existujú?

Môžu byť klasifikované podľa rôznych kritérií.

V prvom rade sa delia na ostré, tupouhlé a pravouhlé. Prvé z nich majú ostré uhly, to znamená tie, ktoré sa rovnajú menej ako 90 stupňov. V tupých uhloch je jeden z uhlov tupý, to znamená taký, ktorý sa rovná viac ako 90 stupňom, ostatné dva sú ostré. Medzi akútne trojuholníky patria aj rovnostranné trojuholníky. Takéto trojuholníky majú všetky strany a uhly rovnaké. Všetky sú rovné 60 stupňom, to sa dá ľahko vypočítať vydelením súčtu všetkých uhlov (180) tromi.

Správny trojuholník

Nemožno nehovoriť o tom, čo je pravouhlý trojuholník.

Takáto postava má jeden uhol rovný 90 stupňom (rovný), to znamená, že dve jej strany sú kolmé. Zvyšné dva uhly sú ostré. Môžu sa rovnať, potom to bude rovnoramenné. Pytagorova veta súvisí s pravouhlým trojuholníkom. Pomocou neho môžete nájsť tretiu stranu a poznať prvé dve. Podľa tejto vety, ak pridáte druhú mocninu jednej nohy ku štvorcu druhej, môžete získať druhú mocninu prepony. Druhá mocnina vetvy sa dá vypočítať odčítaním druhej mocniny známej vetvy od druhej mocniny prepony. Keď už hovoríme o tom, čo je trojuholník, môžeme si spomenúť aj na rovnoramenný trojuholník. Toto je taká, v ktorej sú dve strany rovnaké a dva uhly sú tiež rovnaké.

Čo sú nohy a hypotenzia?

Noha je jedna zo strán trojuholníka, ktorý zviera uhol 90 stupňov. Prepona je zostávajúca strana, ktorá je oproti pravému uhlu. Môžete z nej spustiť kolmicu na nohu. Pomer priľahlej strany k prepone sa nazýva kosínus a opačná strana sa nazýva sínus.

- aké sú jeho vlastnosti?

Je obdĺžnikový. Jeho nohy sú tri a štyri a jeho prepona je päť. Ak vidíte, že nohy daného trojuholníka sa rovnajú trom a štyrom, môžete si byť istí, že prepona bude rovná piatim. Pomocou tohto princípu môžete tiež ľahko určiť, že noha sa bude rovnať trom, ak sa druhá rovná štyrom a prepona sa rovná piatim. Na dôkaz tohto tvrdenia môžete použiť Pytagorovu vetu. Ak sa dve nohy rovnajú 3 a 4, potom 9 + 16 = 25, koreň z 25 je 5, to znamená, že prepona sa rovná 5. Egyptský trojuholník je tiež pravouhlý trojuholník, ktorého strany sa rovnajú 6, 8 a 10; 9, 12 a 15 a ďalšie čísla v pomere 3:4:5.

Čo iné môže byť trojuholník?

Trojuholníky môžu byť tiež vpísané alebo ohraničené. Obrazec, okolo ktorého je kruh opísaný, sa nazýva vpísaný, všetky jeho vrcholy sú body ležiace na kruhu. Opísaný trojuholník je taký trojuholník, do ktorého je vpísaný kruh. Všetky jeho strany s ním v určitých bodoch prichádzajú do kontaktu.

Ako sa nachádza?

Plocha ľubovoľného čísla sa meria v štvorcových jednotkách (metre štvorcové, milimetre štvorcové, centimetre štvorcové, decimetre štvorcové atď.) Túto hodnotu je možné vypočítať rôznymi spôsobmi v závislosti od typu trojuholníka. Oblasť ľubovoľnej postavy s uhlami možno nájsť vynásobením jej strany kolmicou, ktorá na ňu spadne z opačného rohu, a vydelením tohto čísla dvoma. Túto hodnotu môžete zistiť aj vynásobením dvoch strán. Potom vynásobte toto číslo sínusom uhla umiestneného medzi týmito stranami a vydeľte tento výsledok dvoma. Ak poznáte všetky strany trojuholníka, ale nepoznáte jeho uhly, môžete nájsť oblasť iným spôsobom. Aby ste to dosiahli, musíte nájsť polovicu obvodu. Potom od tohto čísla striedavo odčítajte rôzne strany a vynásobte výsledné štyri hodnoty. Ďalej nájdite z čísla, ktoré vyšlo. Oblasť vpísaného trojuholníka možno nájsť vynásobením všetkých strán a vydelením výsledného čísla číslom opísaným okolo neho, vynásobeným štyrmi.

Oblasť opísaného trojuholníka sa nachádza týmto spôsobom: polovicu obvodu vynásobíme polomerom kruhu, ktorý je v ňom vpísaný. Ak potom jeho obsah nájdete takto: odmocnite stranu, vynásobte výsledné číslo odmocninou troch a potom toto číslo vydeľte štyrmi. Podobným spôsobom môžete vypočítať výšku trojuholníka, v ktorom sú všetky strany rovnaké, musíte jednu z nich vynásobiť odmocninou troch a potom toto číslo vydeliť dvoma.

Vety týkajúce sa trojuholníka

Hlavné vety, ktoré sú spojené s týmto obrazcom, sú Pytagorova veta opísaná vyššie a kosínusy. Druhý (zo sínusov) je, že ak vydelíte ktorúkoľvek stranu sínusom uhla oproti nej, môžete získať polomer kruhu, ktorý je okolo nej opísaný, vynásobený dvoma. Tretím (kosínusom) je, že ak od súčtu druhých mocnín dvoch strán odpočítame ich súčin vynásobený dvomi a kosínus uhla nachádzajúceho sa medzi nimi, dostaneme druhú mocninu tretej strany.

Daliho trojuholník - čo to je?

Mnohí, keď čelia tomuto konceptu, si najprv myslia, že ide o nejaký druh definície v geometrii, ale vôbec to tak nie je. Dalího trojuholník je spoločný názov pre tri miesta, ktoré sú úzko späté so životom slávneho umelca. Jeho „vrcholmi“ sú dom, v ktorom žil Salvador Dalí, hrad, ktorý daroval svojej manželke, ako aj múzeum surrealistických obrazov. Počas prehliadky týchto miest sa môžete dozvedieť veľa zaujímavých faktov o tomto jedinečnom kreatívnom umelcovi, známom po celom svete.